1 引言
大规模MIMO(Multiple-Input Multiple-Output)系统采用多天线收发技术,能有效提高通信容量与信号覆盖范围[1]。为保证通信的质量和效率,通信系统发射机需保持线性特性。然而由于发射机调制器同相/正交(In-phase/Quadrature,I/Q)支路间不理想的幅度增益和相位偏差、发射机不同射频链间的耦合效应、功率放大器 (Power Amplifier,PA)放大电路的非线性特性[2]等,导致发射机中存在I/Q不平衡、射频串扰及PA非线性等多种射频失真[3],致使通信系统性能下降。如何对大规模MIMO系统发射机射频失真进行补偿成为一个亟需解决的问题。
针对发射机射频失真问题,国内外学者提出了多种解决方案。如文献[4]中提出了基于交叉记忆多项式模型的射频失真补偿方案、文献[5]中提出基于平行Hammerstein模型的射频失真补偿方案。在众多补偿方案中,数字预失真(Digital Pre-Distortion,DPD)方法[6]由于其在实现的复杂性、准确性等方面具有良好的综合性能而成为非线性补偿中广泛采用的技术。数字预失真技术通过在失真系统之前人为地加入一个特性与失真系统相反的DPD模块来补偿失真系统。由于神经网络强大的非线性逼近能力,基于神经网络的DPD技术被广泛采用。文献[7]提出使用单路实值时延神经网络(Real-Valued Timed-Delay Neural Network,RVTDNN)对MIMO发射机中的PA非线性问题进行预失真处理的方案。RVTDNN为双隐层的全连接神经网络,兼顾网络的复杂性与预失真性能,在MIMO系统中能够取得良好的射频失真补偿效果。但随着射频元件和天线阵列维度的增加,大规模MIMO系统发射机中的射频失真问题变得极为复杂。如继续采用文献[7]中的方案,则难以获得理想的射频失真补偿性能。针对上述问题,本文提出基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿方案,基于串扰严重程度对射频链路进行分组,并通过多路RVTDNN网络实现多路预失真处理,从而降低预失真网络复杂度,提高射频失真补偿性能。
RVTDNN由输入层、输出层与隐藏层组成,其中输入层的神经元数目取决于系统的射频链路数和网络的记忆深度,输出层的神经元数目取决于系统的射频链路数。如何确定RVTDNN的隐藏层神经元数目和网络的记忆深度也是本文研究的问题之一。目前确定上述网络超参数的方法主要有经验法和超参数优化法两类。其中经验法的性能主要取决于经验值与尝试次数,需要进行大量的实验,耗费时间且难以获得理想的超参数值。而超参数优化法则可依靠优化算法进行迭代运算,得到较为理想的超参数值。文献[8]提出了基于遗传算法[9]的超参数优化方案,相较于经验法能减少求解超参数的时间。但遗传算法在种群数目较小时容易陷入局部最小值,导致无法求得全局最优解,而增大种群数目又会导致计算复杂度增加。针对这个问题,本文提出基于量子遗传算法的DPD网络超参数优化方案。量子遗传算法在种群数目较小时依然能求得全局最优解,进而降低了求解超参数的时间复杂度。
本文结构如下:第2节给出大规模MIMO系统发射机射频失真模型,第3节提出基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿方案与基于量子遗传算法的DPD网络超参数优化方案,第4节进行仿真与分析,第5节对全文进行总结。
2 大规模MIMO系统发射机失真模型
大规模MIMO系统发射机结构如图1所示,其中[X1(n),X2(n)...XP(n)]为发射机输入信号,[Y1(n),Y2(n)...YP(n)]为输出信号,P为射频链路数。在理想状况下,Yi(n)与Xi(n)之间具有线性关系。但由于发射机中的射频元件在制造过程中存着在技术、工艺等方面的限制,收发机的射频链路中不可避免地存在着非理想特性,进而产生I/Q不平衡、射频链路串扰、功率放大器非线性等多种射频失真问题。大规模MIMO系统具有天线数量巨大、载波频率高、调制阶数高的特点,这将放大射频失真对系统性能的影响,因此Yi(n)与Xi(n)之间将产生复杂的非线性关系。
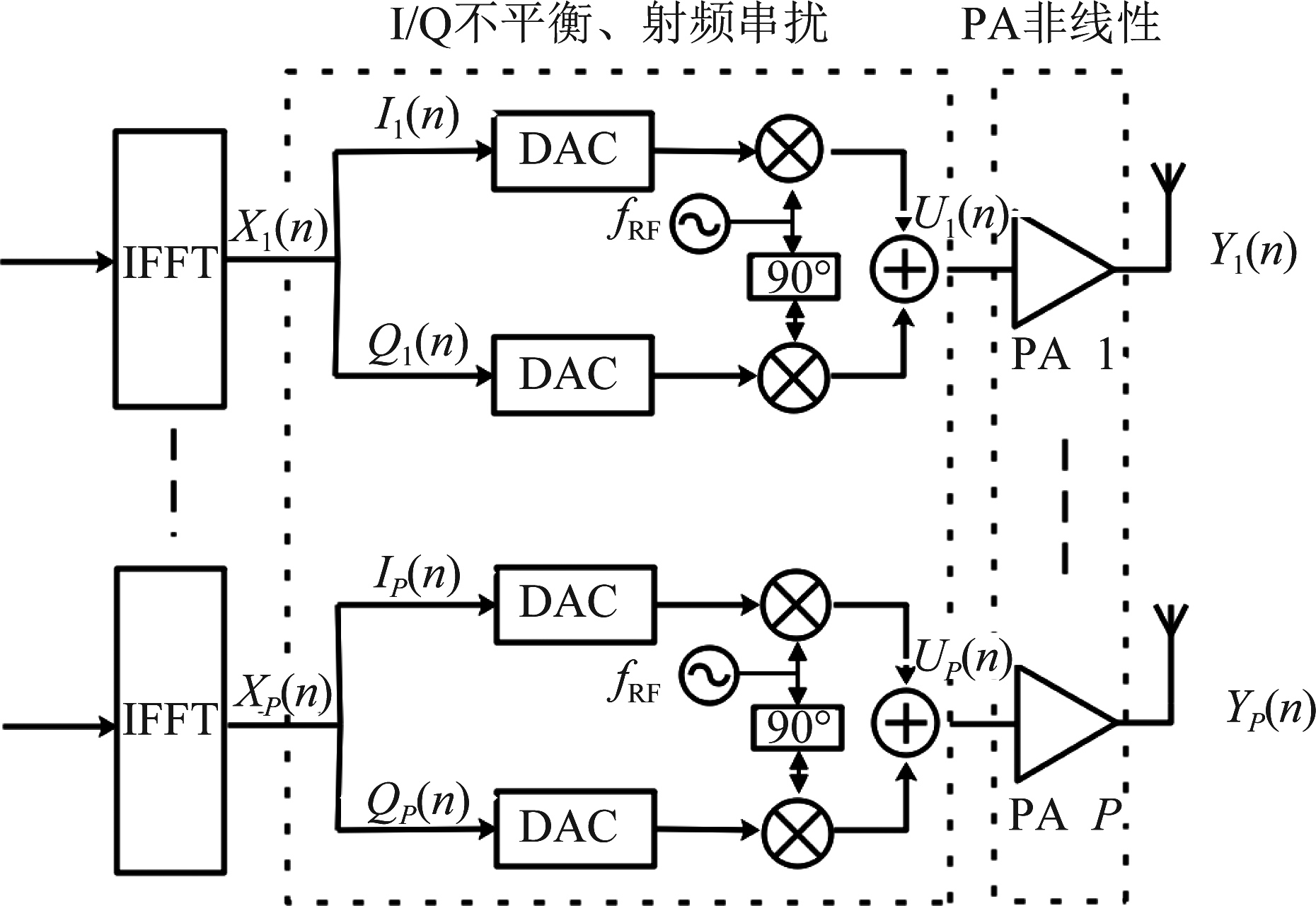
图1 大规模 MIMO系统发射机结构
Fig.1 Transmitter structure of Massive MIMO system
理想情况下,发射机同相与正交支路信号在幅度上具有相同的增益,相位差为90°。在实际情况中,发射机物理上很难实现上述情况,所以同相与正交支路存在I/Q不平衡现象。第i条射频链路上的发射信号Xi(n)在受到I/Q不平衡的影响后改变为:
(i=1,2…P)
(1)
其中μi与νi为I/Q不平衡参数,表达式为
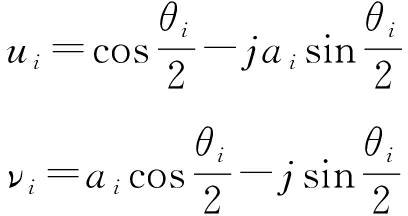
θi与ai分别为相位不平衡与幅度不平衡参量。在理想情况下满足θi=0,ai=1。
由于不同射频链间产生耦合,I/Q不平衡信号Qi(n)在串扰影响下变为:
Ui(n)=Fi(Q1(n),Q2(n)...QP(n)) (i=1,2…P)
(2)
式中,Fi(·)为对应第i条射频串扰特性的非线性函数。
经过射频链路串扰的信号通过PA后,会进一步产生非线性失真。PA的非线性失真具有记忆性,可用有记忆多项式模型[3]表示:
(3)
其中K为记忆多项式的阶数,G为PA记忆效应的记忆深度,akg为多项式的系数。
可见,发射机输出信号Yi(n)与输入信号Xi(n)之间呈现复杂的非线性关系,发射机射频失真的影响不可忽略。因此,需要对发射机的射频失真进行补偿。
3 基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿方案
3.1 基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿模型
在大规模MIMO系统中,使用单路RVTDNN预失真网络会导致射频失真补偿性能不够理想。针对这个问题,本文提出基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿模型,如图2所示。由于间距较远的射频链路间的串扰可以忽略,故可对大规模MIMO发射机的射频链路进行分组,将串扰严重的L条射频链路分为一组,并通过同一个RVTDNN进行预失真处理,M为总组数。通过将射频链路分组,减少了每个RVTDNN处理的射频链路数目,从而减少了RVTDNN的内部神经元数目,简化了网络结构。
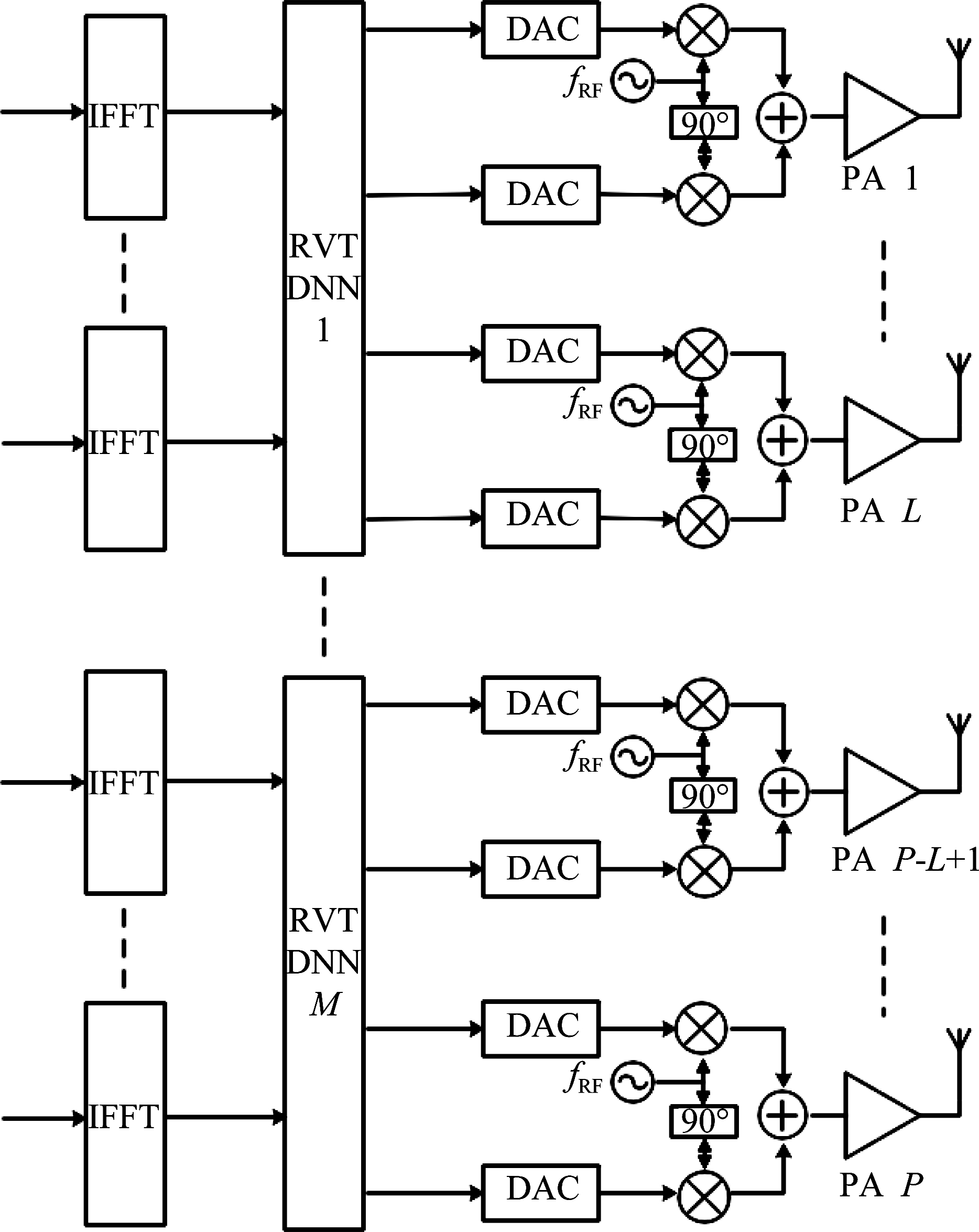
图2 基于多路RVTDNN的发射机射频失真补偿模型
Fig.2 Transmitter RF distortion compensation model based on multiple RVTDNN
将射频链路分组后,大规模MIMO系统发射机射频失真补偿采用多路RVTDNN预失真网络,其中每个RVTDNN结构如图3所示。RVTDNN预失真网络包含输入层、输出层及两个隐藏层。
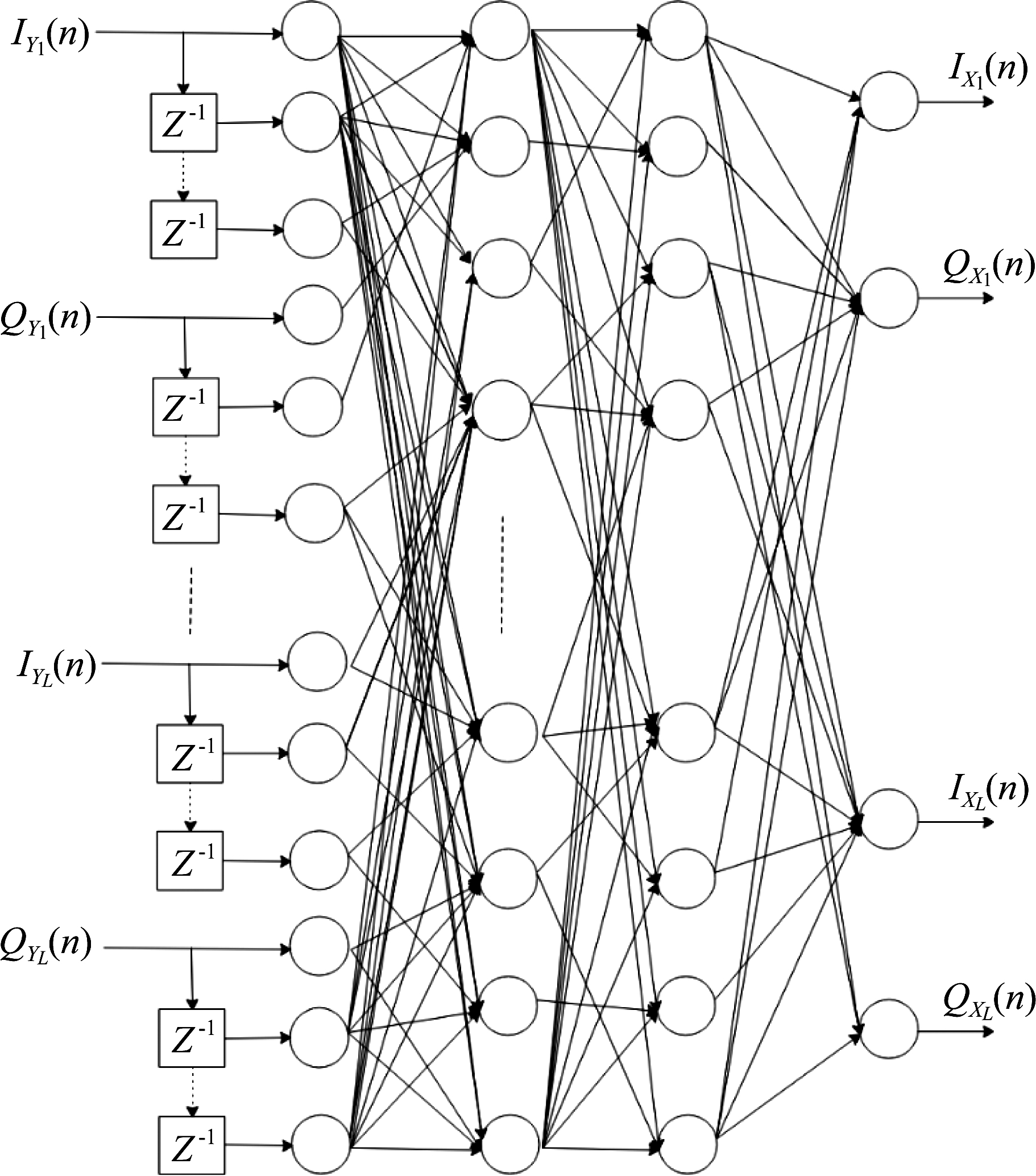
图3 RVTDNN结构
Fig.3 Structure of RVTDNN
每路RVTDNN训练方式相同,以第一路RVTDNN训练过程为例对网络训练方式进行说明。RVTDNN作为预失真网络提供发射机射频失真的逆特性,因此在训练过程中以式(3)中的[Y1(n),Y2(n)…YL(n)]作为输入信号,以[X1(n),X2(n)…XL(n)]作为输出信号对RVTDNN进行训练,其中L为每组射频链路数目。考虑到功率放大器的记忆特性,引入时延单元Z-1。考虑同相正交支路不平衡特性,将输入、输出信号的实部虚部分开,最终输入到RVTDNN的训练集信号为:
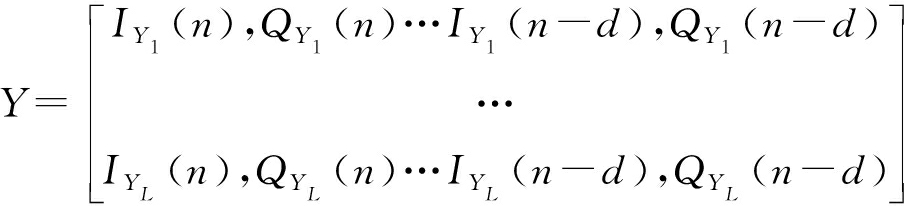
其中为d为网络记忆深度。RVTDNN输出的训练集信号为:
X=[IX1(n),QX1(n)…IXL(n),QXL(n)]
3.2 基于量子遗传算法的射频预失真网络超参数优化
为优化射频预失真网络结构,本节基于量子遗传算法解决射频预失真网络的超参数优化问题,确定RVTDNN网络记忆深度、第一隐藏层和第二隐藏层神经元数目。
量子遗传算法将量子态、量子门等量子概念引入到遗传算法中,是量子计算与遗传算法相结合的产物[10]。在遗传算法中,一条染色体表示问题的某一确定可行解。量子遗传算法使用具有叠加性的量子位表示一条染色体,因此该染色体可以代表问题所有的可行解,增加了解空间的多样性。所以相较于遗传算法,量子遗传算法提高了在相同种群数量下寻得最优解的概率,使用更小的种群数即可达到和遗传算法相同的寻优效果。
量子遗传算法在迭代过程中,后代是由父代的量子门旋转、量子交叉、量子变异操作得到。量子旋转门作用于父代中量子染色体的基态,改变概率幅的分布。之后对父代中的每条染色体进行量子交叉与量子变异操作,得到子代。
在基于量子遗传算法的预失真网络超参数优化中,将RVTDNN网络超参数标记为(D,N1,N2),对应于超参数寻优的一个可行解,其中D代表网络记忆深度,N1和N2分别代表第一隐藏层和第二隐藏层神经元数目。使用训练集训练RVTDNN网络结构,之后使用测试集计算RVTDNN的预测信号与真实信号之间的归一化均方误差(Normalization Mean-Square Error,NMSE),并将其作为量子遗传算法适应度函数:
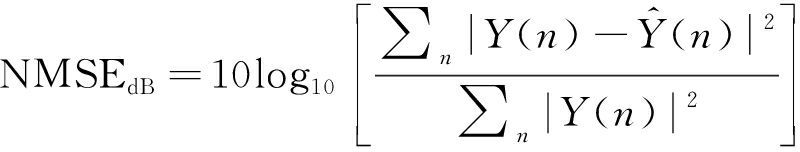
(4)
其中Y(n)为信号真实值,![]() 为神经网络预测信号值。NMSEdB越小,则适应度越高。每次迭代保留适应度高的个体,淘汰适应度低的个体,多次迭代后最终获得超参数的优化结果。
为神经网络预测信号值。NMSEdB越小,则适应度越高。每次迭代保留适应度高的个体,淘汰适应度低的个体,多次迭代后最终获得超参数的优化结果。
4 仿真实验与结果分析
使用Python进行仿真实验。为避免网络训练过程中出现过拟合现象,采用增加训练集的方式,训练集包含50000组数据,测试集包含400000组数据。射频失真模型中多项式阶数K=3,PA记忆深度G=4[11],每路RVTDNN处理天线数L=4。
4.1 超参数优化方案性能比较
在RVTDNN预失真网络训练阶段,需要设置网络迭代次数(epoch)。随着迭代次数增多,训练的神经网络损失值(loss)降低,网络预测精度升高,但是网络训练的时间加长。为了在预测精度与训练时间之间进行折中,首先分析RVTDNN训练过程中,网络迭代次数与loss值之间的关系。
图4所示为RVTDNN迭代次数与loss值之间的关系。从图中可以看出,初始阶段随着迭代次数增大,loss值快速下降。当迭代次数超过20时,loss值下降速度趋于平缓。因此在后续仿真实验中,将RVTDNN预失真网络训练的迭代次数选取为20。
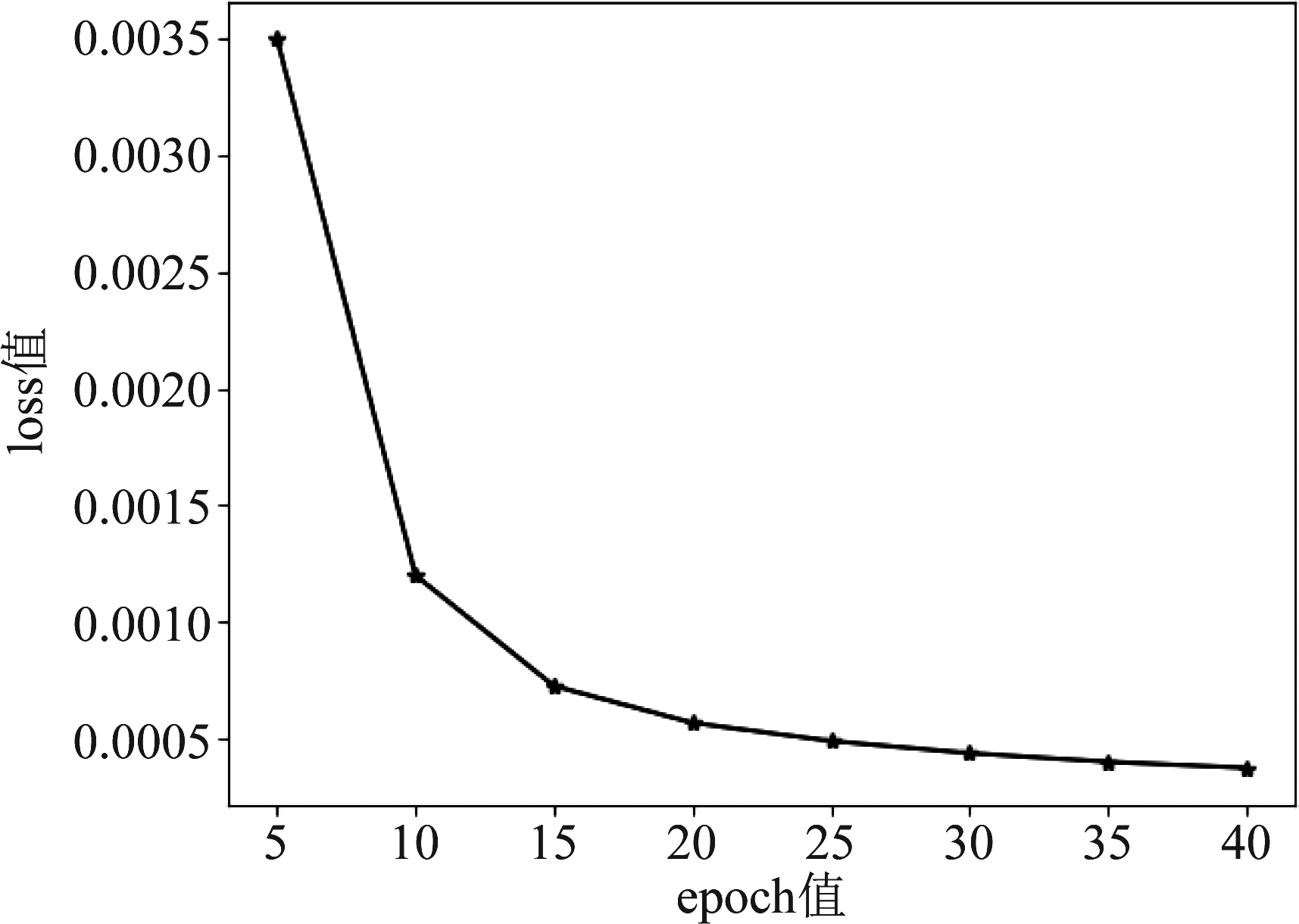
图4 迭代次数与loss值的关系曲线
Fig.4 The relationship between the number of iterations and the loss value
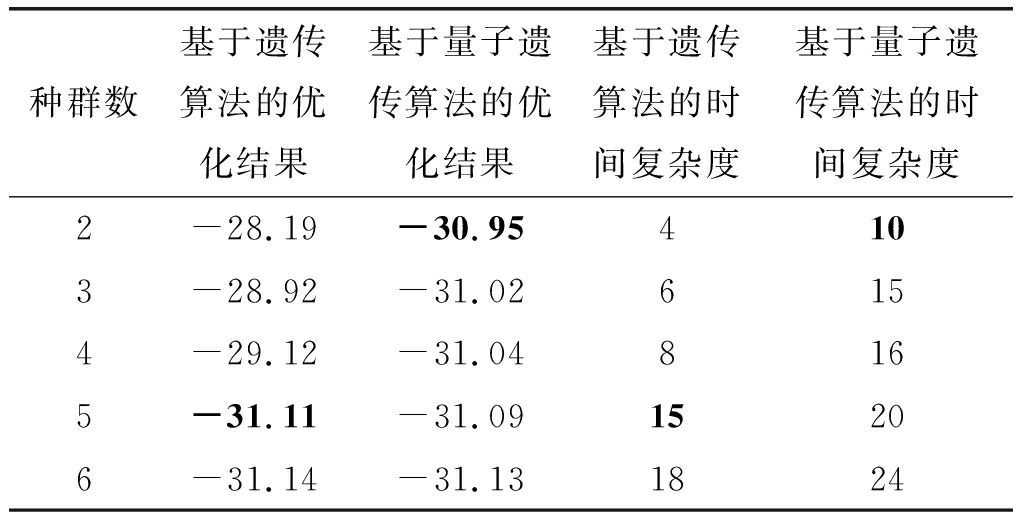
接下来验证基于量子遗传算法的RVTDNN预失真网络超参数优化方案的性能,并与基于遗传算法的预失真网络超参数优化方案进行比较。将优化算法的时间复杂度表示为种群数与算法收敛时迭代次数的乘积,即优化算法在寻优过程中所训练的神经网络数目。表1给出了在不同种群数下分别基于量子遗传算法与遗传算法进行超参数优化后,RVTDNN的最小均方误差值与优化算法的时间复杂度。从表中数据可以看出,种群数目小时,量子遗传算法寻优结果明显优于遗传算法寻优结果,量子遗传算法在种群数为2时便可近似达到遗传算法在种群数为5时的寻优效果,从而使超参数优化的时间复杂度减小![]()
表1 两种不同超参数优化算法的仿真结果
Tab.1 Simulation results based on two different optimization algorithms
种群数基于遗传算法的优化结果基于量子遗传算法的优化结果基于遗传算法的时间复杂度基于量子遗传算法的时间复杂度2-28.19-30.954103-28.92-31.026154-29.12-31.048165-31.11-31.0915206-31.14-31.131824
4.2 基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿方案性能
为研究基于多路RVTDNN的大规模MIMO系统发射机射频失真补偿方案对发射机性能的改进程度,在大规模MIMO发射机模型基础上加入高斯白噪声信道[12]与理想接收机来计算系统误码率并评估发射机射频失真补偿方案的性能。
图5给出发射机射频失真补偿方案的误码率性能曲线。六条性能曲线从上至下分别对应于不对发射信号进行射频失真补偿处理的误码率、使用单路RVTDNN[7]对发射信号补偿时的误码率、使用本文提出的多路RVTDNN对发射信号补偿但未进行超参数优化时的误码率、使用遗传算法优化多路RVTDNN后对发射信号进行补偿的误码率、使用本文提出的基于量子遗传算法方案优化多路RVTDNN后对发射信号进行补偿的误码率、以及发射机无射频失真时的系统误码率。超参数优化方案中遗传算法和量子遗传算法的种群数均设置为2。
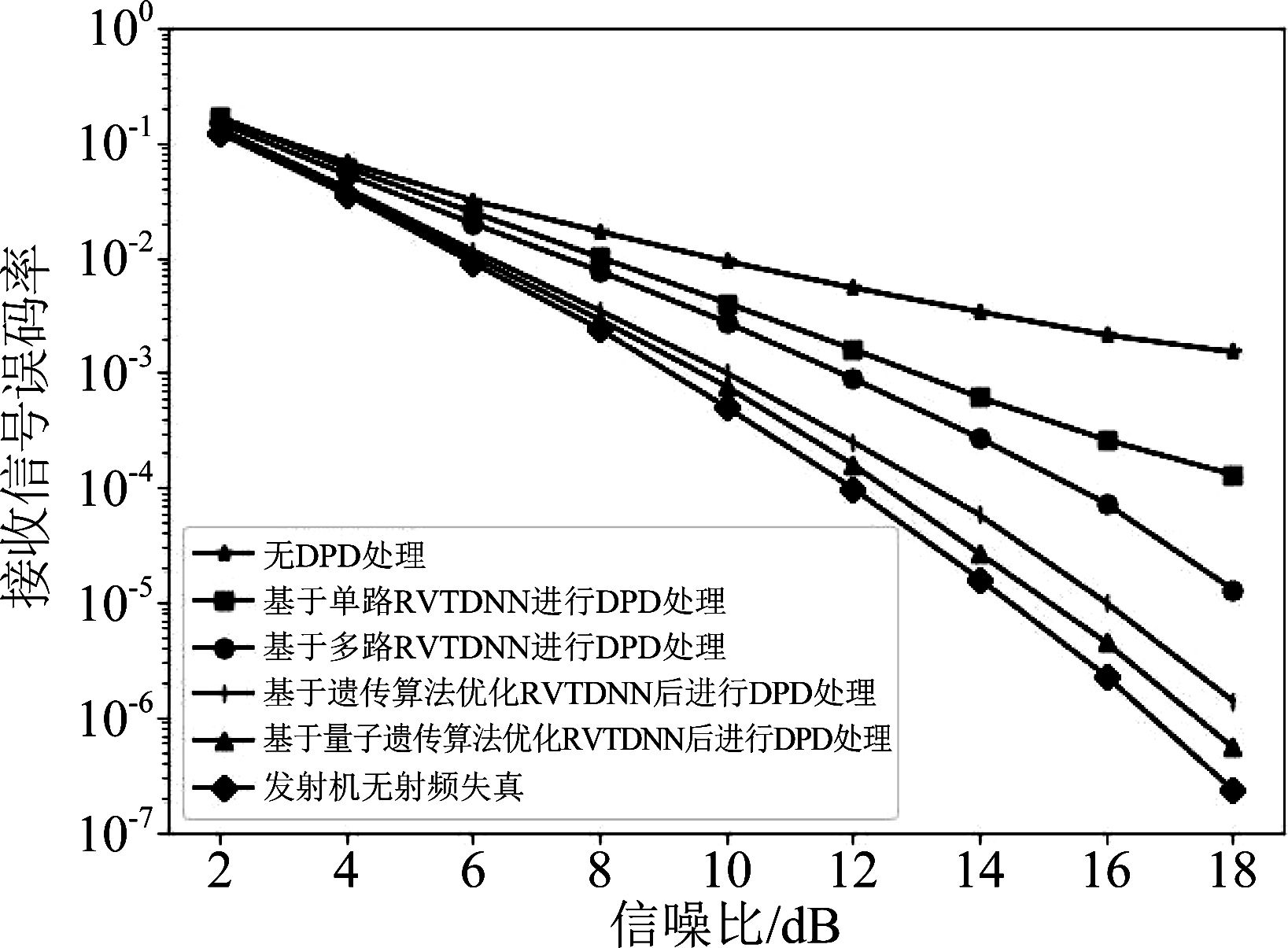
图5 接收信号误码率
Fig.5 Bit error rate of received signal
由图5可见,如不对发射信号进行预失真处理,由于射频失真的影响,系统性能较差。使用文献[7]中基于单路RVTDNN的射频失真补偿方案后,误码率虽有所下降,但系统性能依然不够理想。使用基于多路RVTDNN的射频失真补偿方案后,误码率大幅下降,系统的性能有了明显提升。对RVTDNN预失真网络做超参数优化后,可进一步降低系统的误码率,提高系统性能。在两种超参数优化方案中,本文中基于量子遗传算法的超参数优化方案相较于基于遗传算法的方案具有更好的性能,能够接近于无发射机射频失真时的误码率性能。
5 结论
为解决大规模MIMO系统发射机的多种射频失真问题,本文提出了基于多路实值时延神经网络的大规模MIMO系统发射机射频失真补偿方案,对大规模MIMO系统发射机中的I/Q不平衡、射频链路串扰、功率放大器非线性等多种射频失真问题提供了统一解决方案。该方案通过将射频链路分组减少了每路RVTDNN处理的射频链路数量,降低了预失真网络复杂度,提高了射频失真补偿性能。为了解决预失真网络超参数寻优问题,进一步提出了基于量子遗传算法的预失真网络超参数优化方案。从仿真结果可以看出,该方案提高了发射机的性能,降低了系统的误码率,减少了寻找超参数的时间。
[1] LIU Xin, CHEN Wenhua, CHEN Long, et al. Linearization for hybrid beamforming array utilizing embedded over-the-air diversity feedbacks[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(12): 5235-5248.
[2] XU Jin, JIANG Weiliang, MA Linhua, et al. Augmented time-delay twin support vector regression-based behavioral modeling for digital predistortion of RF power amplifier[J]. IEEE Access, 2019, 7: 59832-59843.
[3] 艾渤, 李波, 钟章队. 宽带功率放大器预失真原理[M]. 北京: 科学出版社, 2011: 1-169.
AI Bo, LI Bo, ZHONG Zhangdui. Wideband power amplifier predistortion principle[M]. Beijing: Science Press, 2011: 1-169.(in Chinese)
[4] BASSAM S A, HELAOUI M, GHANNOUCHI F M. Crossover digital predistorter for the compensation of crosstalk and nonlinearity in MIMO transmitters[J]. IEEE Transactions on Microwave Theory and Techniques, 2009, 57(5): 1119-1128.
[5] AMIN S, LANDIN P N, H NDEL P, et al. Behavioral modeling and linearization of crosstalk and memory effects in RF MIMO transmitters[J].IEEE Transactions on Microwave Theory and Techniques, 2014, 62(4): 810- 823.
NDEL P, et al. Behavioral modeling and linearization of crosstalk and memory effects in RF MIMO transmitters[J].IEEE Transactions on Microwave Theory and Techniques, 2014, 62(4): 810- 823.
[6] SU Gongzhe, CHEN Wenhua, ZHANG Silong, et al. A robust and low sampling rate digital predistortion algorithm for broadband PA modeling and predistortion[C]∥WAMICON 2014. Tampa, FL, USA. IEEE, 2014: 1- 4.
[7] JARAUT P, RAWAT M, GHANNOUCHI F M. Composite neural network digital predistortion model for joint mitigation of crosstalk, ![]() I/Q
I/Q![]() imbalance, nonlinearity in MIMO transmitters[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(11): 5011-5020.
imbalance, nonlinearity in MIMO transmitters[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(11): 5011-5020.
[8] WANG Siqi, ROGER M, SARRAZIN J, et al. Hyperparameter optimization of two-hidden-layer neural networks for power amplifiers behavioral modeling using genetic algorithms[J]. IEEE Microwave and Wireless Components Letters, 2019, 29(12): 802- 805.
[9] 王一, 杨俊安, 刘辉. 一种基于遗传算法的SVM决策树多分类方法[J]. 信号处理, 2010, 26(10): 1495-1499.
WANG Yi, YANG Jun’an,LIU Hui. A GA-based SVM decision-tree multi-classification method[J]. Signal Processing, 2010, 26(10): 1495-1499.(in Chinese)
[10] 郝昭昕, 孙进平. 基于量子遗传算法的MIMO雷达正交信号波形设计[J]. 信号处理, 2019, 35(6): 1064-1071.
HAO Zhaoxin, SUN Jinping. MIMO radar orthogonal waveform design based on quantum genetic algorithm[J]. Journal of Signal Processing, 2019, 35(6): 1064-1071.(in Chinese)
[11] 李明玉, 何松柏, 李晓东. 基于测量的记忆多项式功率放大器特征模型[J]. 电子测量与仪器学报, 2009, 23(8): 49-55.
LI Mingyu, HE Songbai, LI Xiaodong. Measurement-based memory polynomial behavioral modeling of RF power amplifiers[J]. Journal of Electronic Measurement and Instrument, 2009, 23(8): 49-55.(in Chinese)
[12] SALAHAT E, SALEH H. Novel average bit error rate analysis of generalized fading channels subject to additive white generalized Gaussian noise[C]∥2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP). Atlanta, GA, USA. IEEE, 2014: 1107-1111.




