1 引言
随着电子信息技术的高速发展和应用需求的不断增长,雷达、通信等多功能系统在军事、民用多个领域呈现一体化趋势。例如,舰船和无人机[1]等武器平台需要集成侦察、干扰、探测、通信等多个系统以提高作战效能[2]。另外,有相当一部分5G/B5G新兴应用需要雷达感知与无线通信的联合设计。特别地,对于未来的车联网[3]应用领域,节点车辆需要通过雷达设备感知路况,并用通信设备与其他节点车辆进行信息交流。而在这过程中,信号的一体化设计和处理是核心难点。若不在信号层面进行统一的设计,则在日益拥堵的电磁环境下,不同功能之间势必会产生强烈的同频干扰。雷达通信一体化系统的研究始于缩减战机、舰船等平台的体积,通过共用硬件资源,可大幅减少雷达、通信等设备占用体积,为隐身设计、燃油储备和武器弹药腾出空间[4]。在国内外专家学者多年的研究下,一体化系统历经了独立式结构、联合式结构和综合式结构的发展演进[5],已经在控制显示、处理、通道和孔径等一体化方面取得一定成果,如今正在向微小型一体化硬件系统和信号一体化[6]发展。
信号一体化即用同一信号同时承载雷达和通信两种功能。一体化信号分为两种途径:正交信号和共享信号。正交信号中雷达信号和通信信号相互独立,通过时间、空间、频率、极化、编码等多个维度正交叠加成一个信号,维度灵活但同时波形设计的复杂度也更高;共享信号即通过在雷达信号上调制通信信息或者将通信信号改进使其符合雷达探测要求,其中正交频分复用(OFDM)信号被多次试验证明为一种良好的共享信号[7-8]。然而,为了不失真地传输通信信息,通常需要在OFDM信号添加导频和循环前缀等信号成分,这些信号结构和高随机的通信信息会恶化模糊函数的距离旁瓣[9],进而限制探测性能。因此,需要探索OFDM共享信号旁瓣抑制技术,以满足未来军用、民用等诸多领域的雷达通信一体化要求。
近年来,国内外专家学者就雷达通信一体化信号的旁瓣抑制技术进行了深入研究,其中,刘永军在OFDM共享波形设计[10-13]方面取得了连续性的成果,包括推导了距离和速度估计的克拉美罗下界并提出了一种自适应超分辨距离和速度估计方法[12],另外通过Gold码预调制[13]解决模糊函数对通信信息敏感的问题,但Gold序列长度需与载波长度相同;李晓柏[14]以完全互补码对OFDM信号进行扩频,然后辅以分段匹配滤波方法来降低近端旁瓣,但是该方法会降低频谱利用率;Guo[15]通过半正定规划(Semi-Definitive Programming, SDP)算法优化子载波加权,以在保持低旁瓣和高分辨率的情况下,实现频谱置零(Spectral Nulling);Zuo[16]同样采用凸优化方法优化子载波加权以降低旁瓣。可见,在匹配滤波的框架下,波形优化方法需要权衡分辨率和旁瓣,预调制方法存在频谱利用率不足的问题。鉴于此,部分学者提出失配滤波算法[9],通过构造模糊函数,将距离向旁瓣推离观测窗口,使观测范围内目标探测不受限于旁瓣和波形,但是该方法会造成信噪比损失,且信噪比损失随观测窗口增大而增大。为此,本文进一步提出融合失配处理和LMS滤波的旁瓣抑制技术。通过失配滤波控制脉压旁瓣分布,使之满足LMS旁瓣对消条件,可突破传统单一失配处理的约束,进而能在不减小观测范围的条件下减少信噪比损失,或在相同信噪比损失下提升观测范围。
2 OFDM雷达通信一体化信号模型
2.1 信号模型与系统框架
20世纪末60年代,数字处理技术还未成熟时,多载波调制技术就已应用于军事无线通信中,但因实现复杂无法普及,并且早期子载波之间需要添加保护间隔来达到正交要求,如今OFDM技术通过设置子载波间隔为时长的倒数保证正交,子载波频谱之间的重叠提高了频谱利用率。OFDM信号的载波频谱结构如下图1所示,其主要思想是将一个宽带信道分解为N个并行窄子信道,每个子信道带宽小于信道相干带宽时,子信道近似经历平坦衰落,这样可有效避免大带宽信号的频谱选择性衰落,同时提高频谱利用率,且通过快速逆傅里叶变换(Inverse Fast Fourier Transform, IFFT)和快速傅里叶变换(Fast Fourier Transform, FFT)可实现OFDM调制和解调[17]。
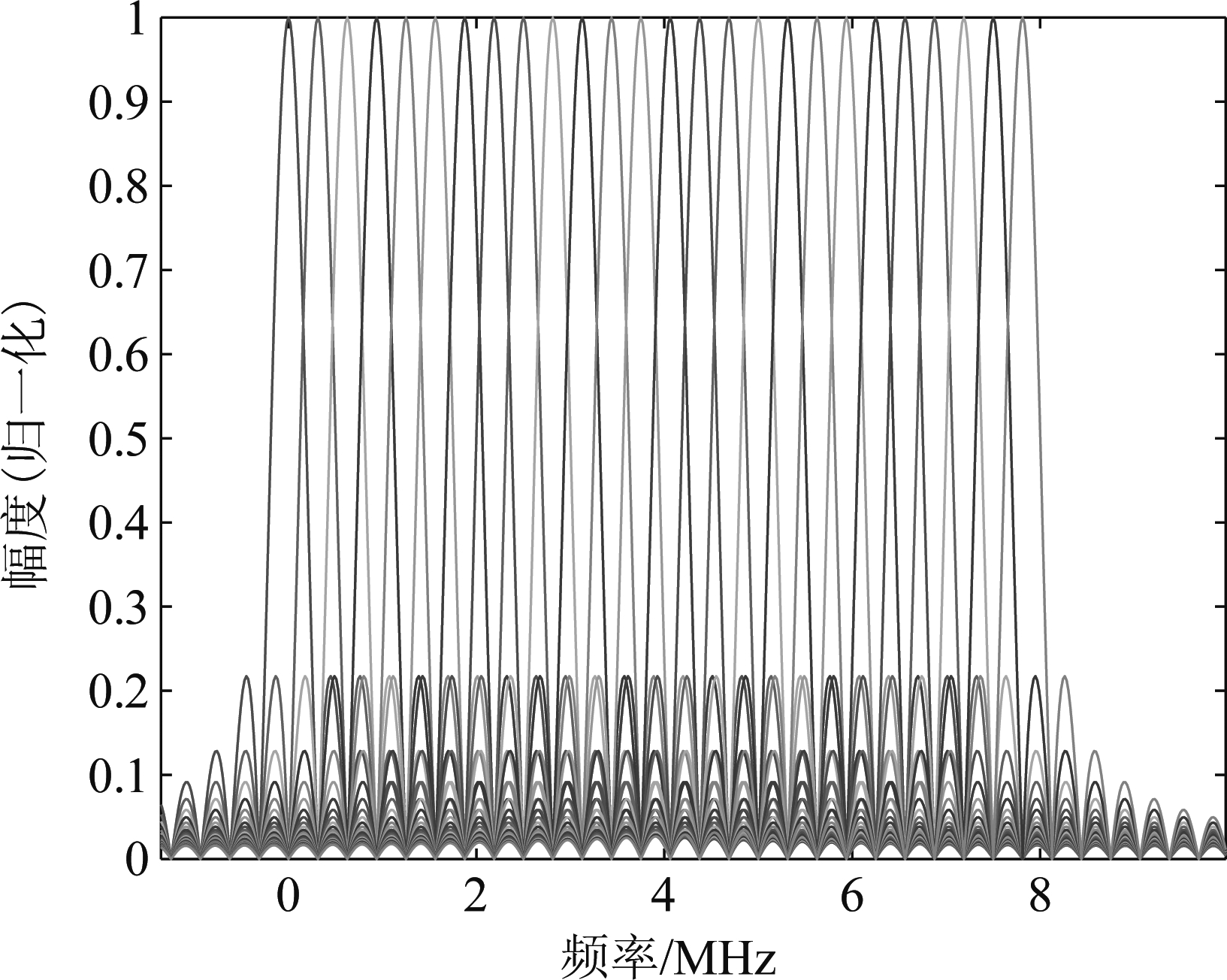
图1 OFDM的载波频谱结构
Fig.1 The carrier spectrum structure of OFDM
假设雷达发射连续的OFDM通信帧,每个通信帧由Ns个符号构成,OFDM符号载波数为Nc。一个完整的OFDM符号由有效OFDM符号和循环前缀构成,其中,完整的OFDM符号持续时长为Ts,有效OFDM符号持续时间为Tu,循环前缀时长为Tg,且Ts=Tu+Tg,OFDM符号的子载波间隔为有效时长的倒数,即
那么一个OFDM通信帧的基带表达式如下:
(1)
式中,A(m,n)表示第n个OFDM时域符号的第m个子载波上传输的码元信息,其中包含通信信息C(m,n)和导频信息P(m,n),其大小取决于选用的数字调制方式,rect(·)表示矩形窗函数。
基于OFDM雷达通信一体化信号的发射和接收方案如图2所示。
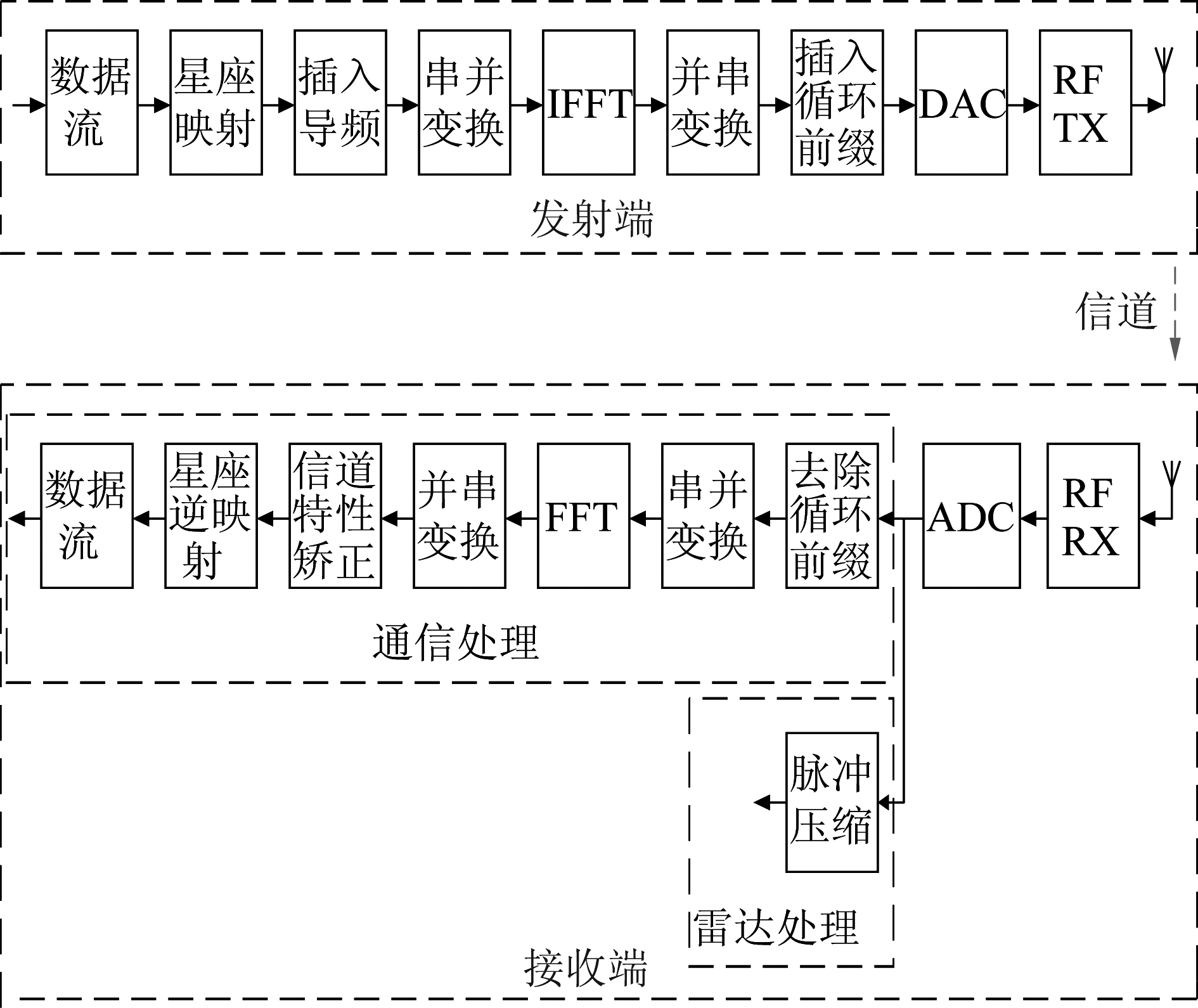
图2 基于OFDM雷达通信一体化的信号发射和接收方案
Fig.2 Signal transmitting and receiving scheme based on OFDM radar communication integration
在发送端,一个信息速率为Rb的二进制数据流经过星座映射得到一个码元复数序列,插入相应的导频信息P后,串并变换为Nc个并行子数据流{Am,n,m=0,1...,Nc,n=0,1,...,Ns},每个子数据流的符号速率为Rb/Nc。在第m个符号周期内,这Nc个并行符号{Am,n,n=0,1,...,Nc}经过IFFT,将OFDM复包络的频域样值变换为时域样值,再进行并串变换,将并行的时域样值按照时间顺序变换为串行的时域样值,然后在每个OFDM符号前插入循环前缀,通过数模转换后,将离散的复包络变换为连续的复包络,最后经过上变频搬移到射频fc,经由功率放大器发送出去。
在接收端,接收天线接收信号后,将信号分别送入通信信号处理模块和雷达信号处理模块,通信信号处理与发送端的处理过程相反。雷达信号处理主要是对回波进行脉冲压缩以提高信号的输出信噪比。脉冲压缩可分别通过匹配滤波与失配滤波实现,下面分别分析OFDM信号在匹配滤波和失配滤波的框架下脉冲压缩结果。
2.2 回波模型与脉冲压缩
假设同一发射信号经过K个目标的散射到达雷达接收天线,则距离雷达rk的目标的回波时延为
多普勒频移为
其中νk是目标径向速度,c是光速。雷达天线的接收回波r(t)表示[18]:
n(t),k=1,…,K
(2)
其中gk表示第k个目标的后向散射系数,n(t)表示均值为0方差为σn的高斯白噪声。
若在匹配滤波框架下,回波r(t)经过脉冲压缩后,表示为:
(3)
其中χ(τk)=
s(t-τk)s*(t)dt表示不同时延下s(t)的自相关函数,wn=n(t)s*(t)dt表示噪声经过匹配滤波器的输出。文献[9]推导了带有导频等信息的OFDM信号的自相关的数学表达式,详细分析了由导频、通信信息以及循环前缀带来的伪峰和高旁瓣。以表3中设置的参数为仿真参数,在匹配滤波框架下,仿真OFDM信号的零多普勒距离模糊图。
如图3所示,OFDM信号的自相关存在较高伪峰和旁瓣,循环前缀所造成的伪峰高度与其时长有关,一般取有效时长的
伪峰高度为-13.99 dB,旁瓣高度取决于信号能量,同时OFDM信号的导频和通信信息会产生随机的栅瓣,因此,OFDM信号的自相关不可避免存在旁瓣高的问题。
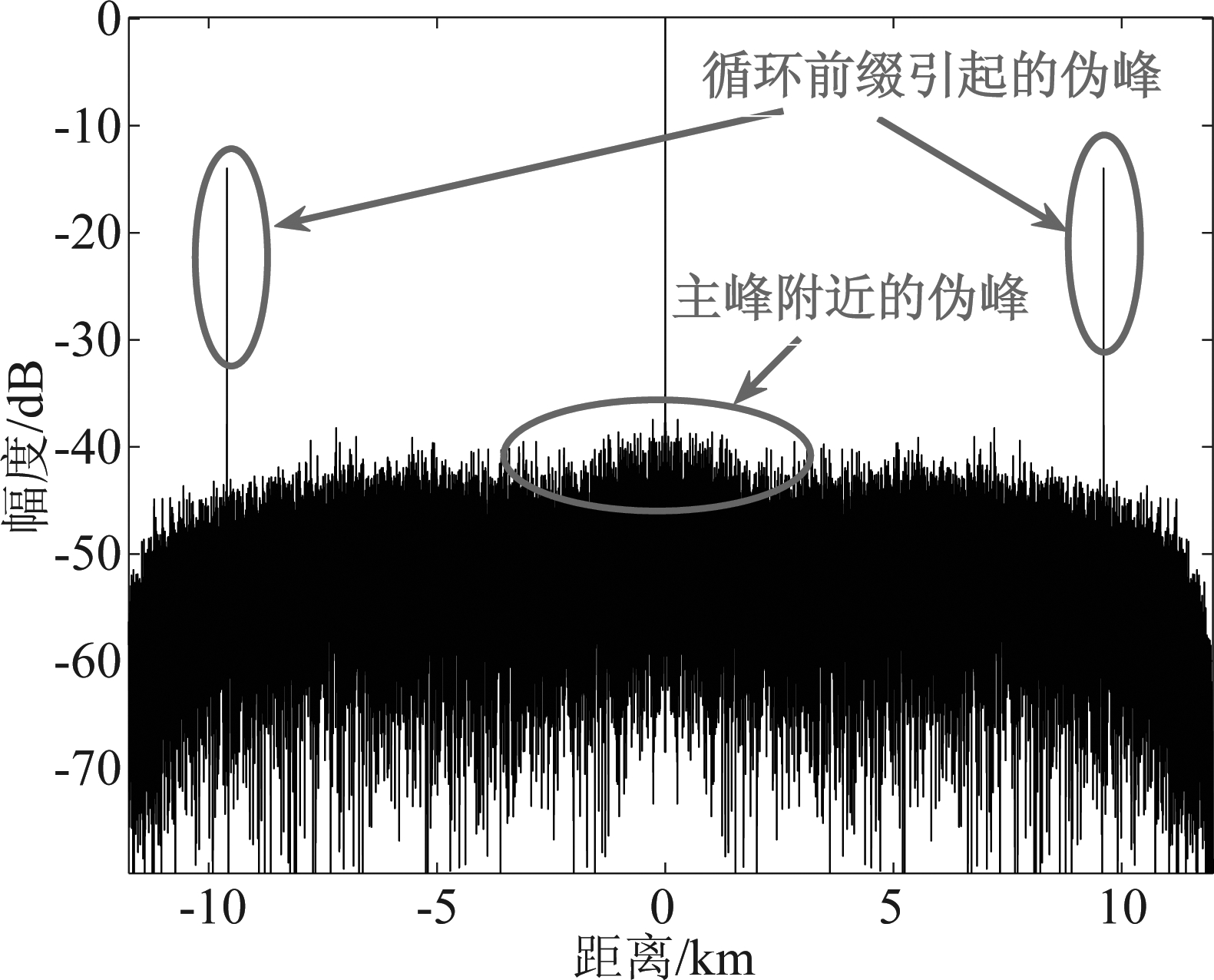
图3 匹配滤波框架下OFDM信号的距离模糊图
Fig.3 The range fuzzy image of OFDM signal under the framework of matched filtering
若在失配滤波框架下,回波r(t)经过脉冲压缩后,表示为:
(4)
式中h(t)表示失配滤波器的传递函数,χ′(τk)=s(t-τk)h(-t)dt表示不同时延下s(t)与失配滤波器的卷积结果,也为失配滤波框架下模糊函数的零多普勒距离响应。
表示噪声经过失配滤波器的输出。在发射波s(t)已知的情况下,可设计失配滤波的传递函数h(t)设计旁瓣和伪峰在模糊平面的分布,即峰值近端为置0凹槽,远端为旁瓣,h(t)的求解算法在第3小节中进行详细的叙述。以表3中设置的参数为仿真参数,在失配滤波框架下,仿真OFDM信号的零多普勒距离模糊图。
如图4所示,峰值的左右两侧是置零窗口,置零窗口外是旁瓣,这里将该置零窗口称为“凹槽”。凹槽分布在峰值两侧,分为左侧凹槽和右侧凹槽,当观测窗口大于两侧凹槽中的最短凹槽长度时,观测窗口内的所有目标均在凹槽内,而不会受到旁瓣的干扰。以表3中设置的参数为OFDM信号的仿真参数,设置失配滤波的凹槽长度6.4 km,在0 km处设置一个RCS为1的强目标,同时在凹槽的边缘5.86 km处设置一个RCS为0.02的弱目标,仿真OFDM信号的回波脉压结果,如图5所示,相比匹配滤波器,失配滤波具有可以有效识别弱目标的优点。然而,失配滤波器存在信噪比损失。信噪比损失定义为失配滤波器的信噪比和匹配滤波器的信噪比之差,即:
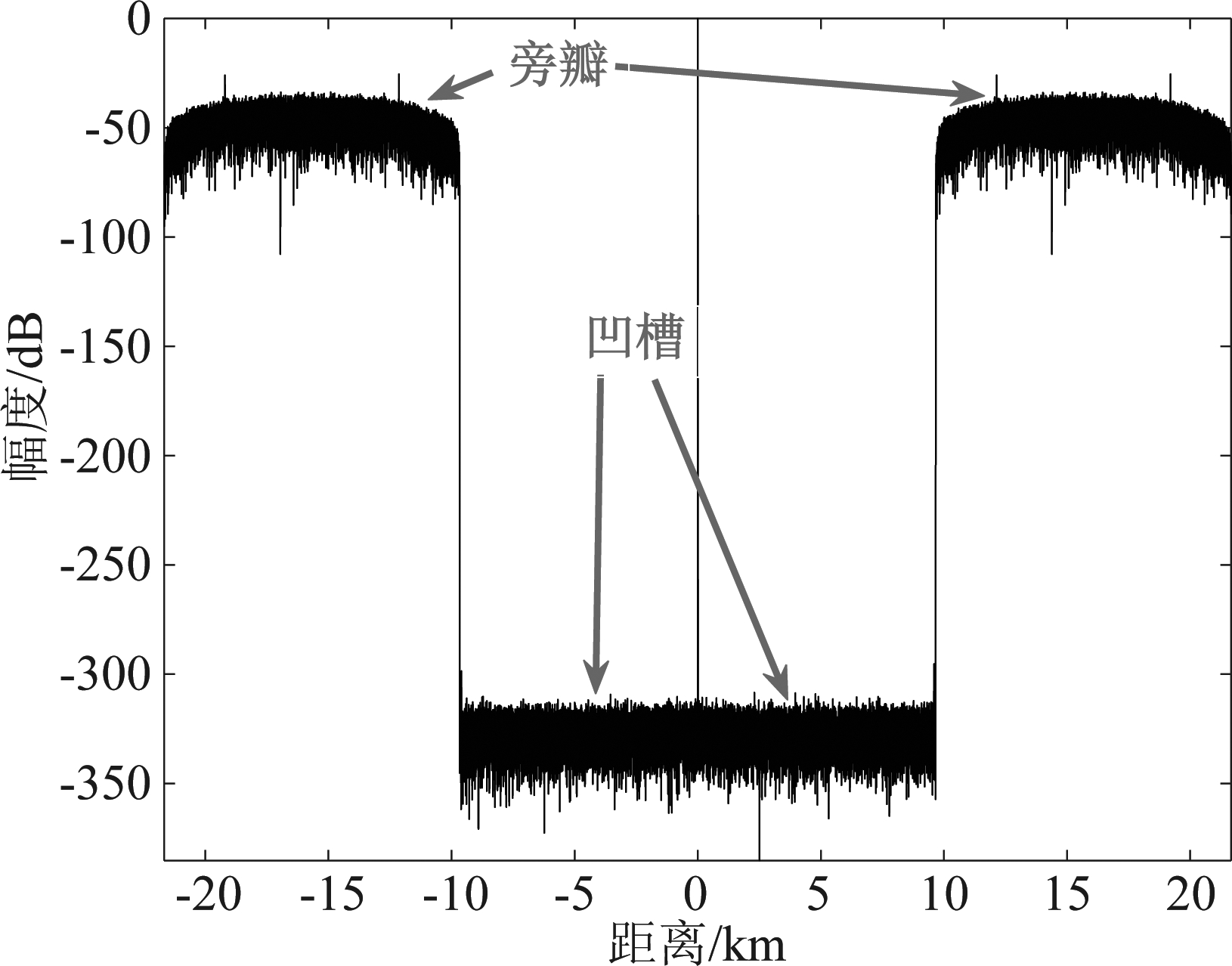
图4 失配滤波框架下OFDM信号的距离模糊图
Fig.4 The range fuzzy image of OFDM signal in the frame of mismatch filtering
SNR_Loss=10log10(SNRMMF)-10log10(SNRMF)
(5)
根据文献[9],在相同的噪声功率下,若失配滤波器和匹配滤波器能量相同时,则信噪比损失为失配滤波器输出峰值相对匹配滤波器输出峰值的能量的损失。
图5中,在相同的滤波器能量下,相对匹配滤波器,失配滤波器的峰值能量损失为7.15 dB,将图5(a)中的弱目标放大,如图5(b)中红色线所示,此弱目标的SNR<15 dB,根据雷达的检测理论,该弱目标无法被有效检测。
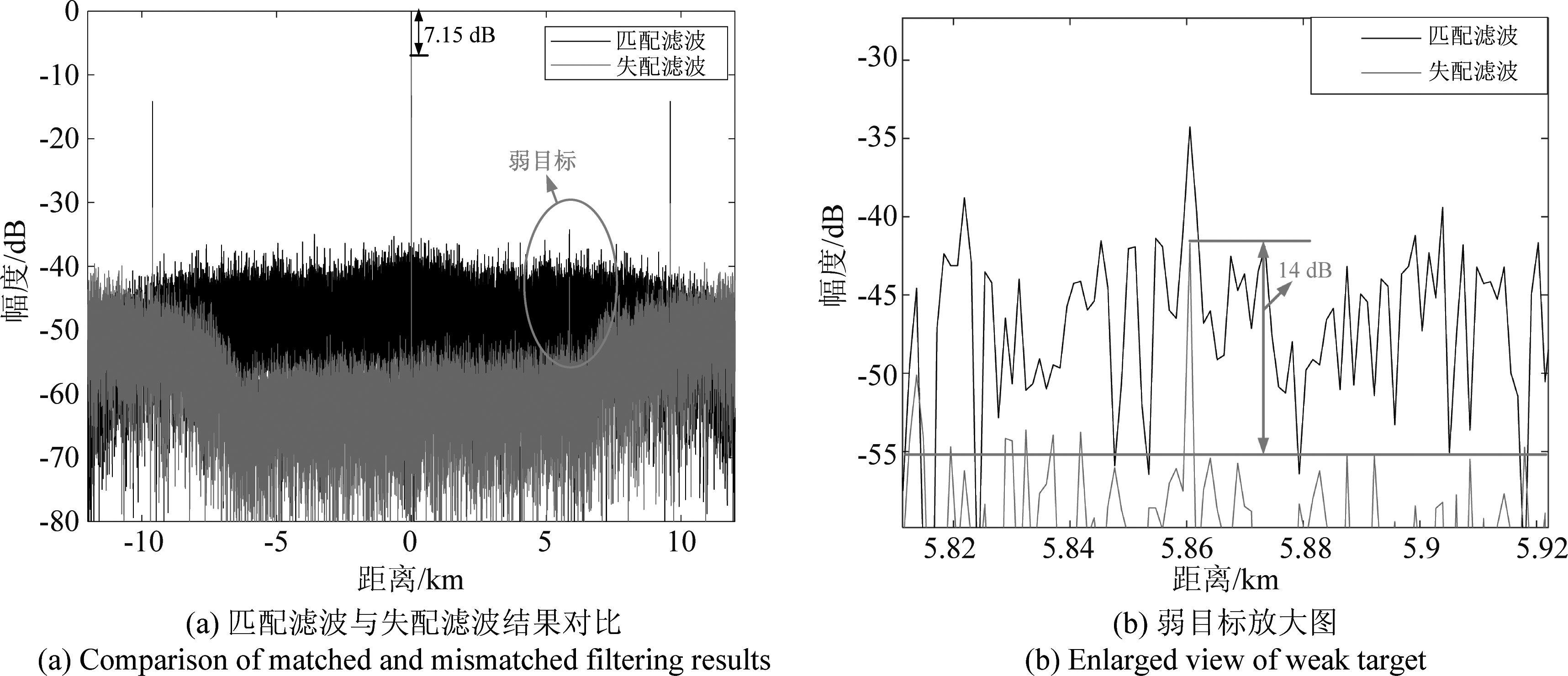
图5 匹配滤波与失配滤波结果对比及弱目标放大图
Fig.5 Comparison of matched and mismatched filtering results and weak target amplification
在相同的仿真参数下,若要保证失配滤波的输出峰值和匹配滤波的输出峰值相同,则需要增大7.15 dB的失配滤波器能量。如图6所示,对比相同滤波器能量下的失配滤波输出,相同峰值下失配滤波输出中噪底水平随着滤波器能量提升了7.15 dB,而5.86 km处的弱目标的SNR仍为14 dB,因此需要寻找降低信噪比损失的方法。由实验知,信噪比损失随凹槽增大。若缩减凹槽长度,可减少信噪比损失,如图7(a)中黑色线所示,凹槽缩短时,峰值的能量损失降至6.15 dB,但这会导致观测距离缩短,将原本位于凹槽边缘的弱目标放大,如图7(b)所示,该弱目标被凹槽外的旁瓣淹没。
图6 相同能量下和相同峰值下失配滤波对比及弱目标放大图
Fig.6 Comparison of mismatch filtering results under the same energy and the same peak value and Enlarged view of weak target
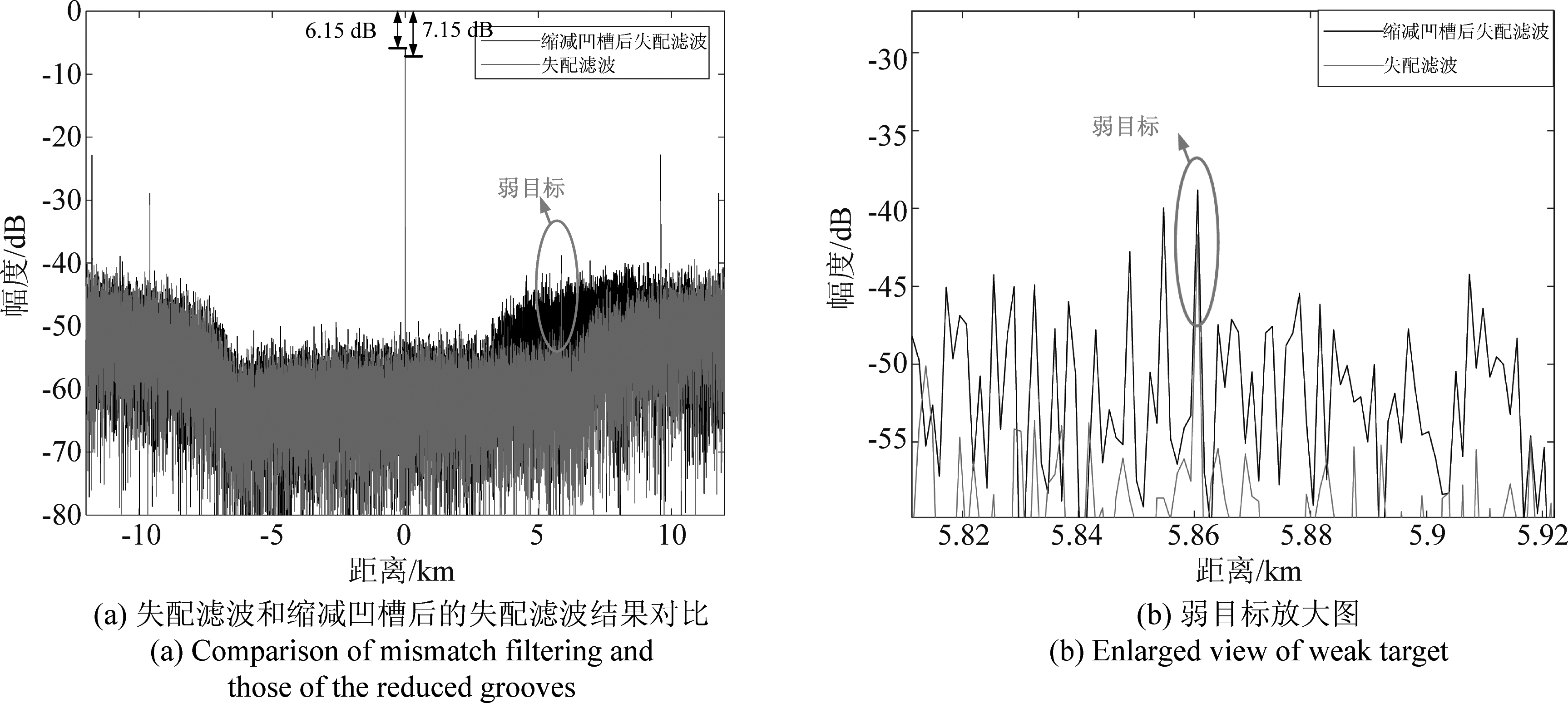
图7 失配滤波和缩减凹槽后失配滤波对比及弱目标放大图
Fig.7 Comparison of mismatch filtering and those of the reduced grooves and Enlarged view of weak target
为了突破信噪比损失与观测窗口宽度之间的约束,在不减小观测范围的条件下降低信噪比损失,本文提出了融合LMS滤波和失配处理的旁瓣抑制方法,下面详细阐述本文算法。
3 融合LMS滤波和失配处理的旁瓣抑制方法
在失配滤波框架下,若将峰值右侧的凹槽长度置0,则可缩短一半的总凹槽长度,进而减少信噪比损失,但是峰值右侧的旁瓣则会淹没弱目标。针对此问题,本文提出结合LMS算法滤除右侧旁瓣,以提高弱目标的检测概率。在保证峰值左侧凹槽长度满足雷达的观测范围时,将右侧凹槽长度置0,则回波经过失配处理后,输出的有效观测区域内不包含左侧旁瓣,只包含多个目标的峰值和目标右侧旁瓣,且右侧旁瓣为首个收到的目标右侧旁瓣以及之后到达的目标旁瓣的叠加。而LMS算法作为一种滤波算法,通过输入参考信号,滤除输入信号中参考信号的线性叠加信号。同理,当输入信号为多个目标峰值和多个目标右侧旁瓣的线性叠加信号时,设置参考信号为点目标的右侧旁瓣,可将该输入信号中不同目标的峰值右侧旁瓣分量线性叠加而成的信号滤除。因此通过融合LMS滤波算法,可降低右侧凹槽外的旁瓣,从而削弱凹槽长度的限制。在保证观测范围的情况下,缩减凹槽的长度,以此减少信噪比损失。
在无源雷达场景中,LMS滤波通常用于杂波对消,如果不考虑噪声,杂波对消器的功能是从回波通道的信号中减去与参考直达波及其延迟信号相关的杂波分量,保留具有多普勒频移的目标回波信号,其原理框图如图8所示,x(n)为待滤波信号,y(n)为参考信号,e(n)为滤波输出,M为滤波器阶数,w向量表示滤波器权值。
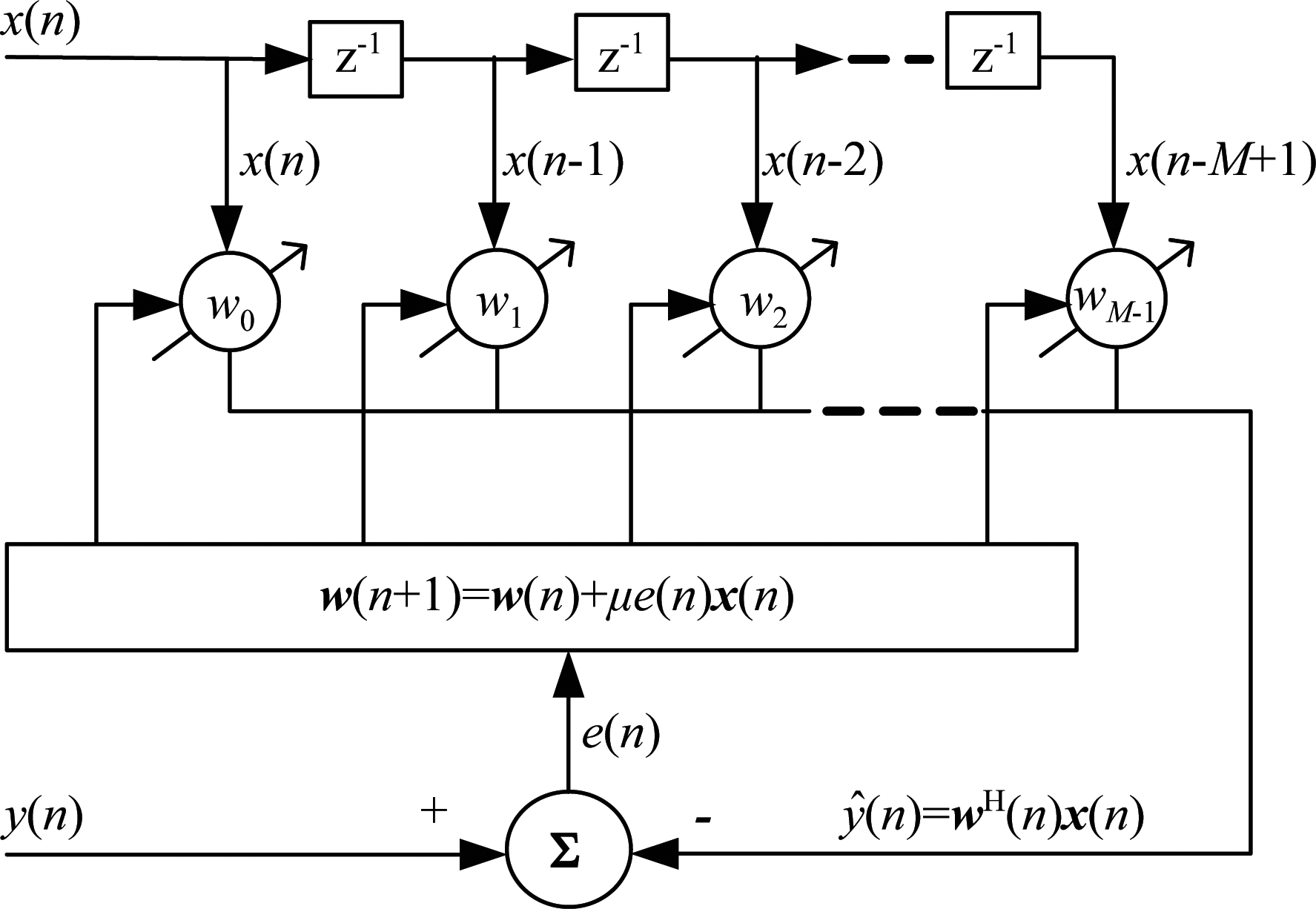
图8 LMS自适应滤波原理框图
Fig.8 LMS adaptive filtering principle block diagram
假设当前为n时刻,在该滤波器中,x(n)=[x(n),x(n-1),…,x(n-M+1)]T是输入信号矢量,w(n)=[w0(n),w1(n),…,wM-1(n)]T为n时刻滤波器的权值矢量,滤波器的算法流程如下:
其中,
是步长因子,它控制着算法的稳定性和收敛速度,λmax为输入信号矢量x(n)的自相关矩阵中的最大特征值。
若将LMS滤波引入旁瓣抑制,旁瓣对消器实现的就是从有效区域内回波信号的脉压结果(包含主瓣、右侧旁瓣)中减去点目标的脉压的右侧旁瓣及其延迟旁瓣相关的旁瓣分量。因此,本文方法中,z″为LMS滤波器的输入信号,
为LMS滤波器的参考信号。如图9所示。
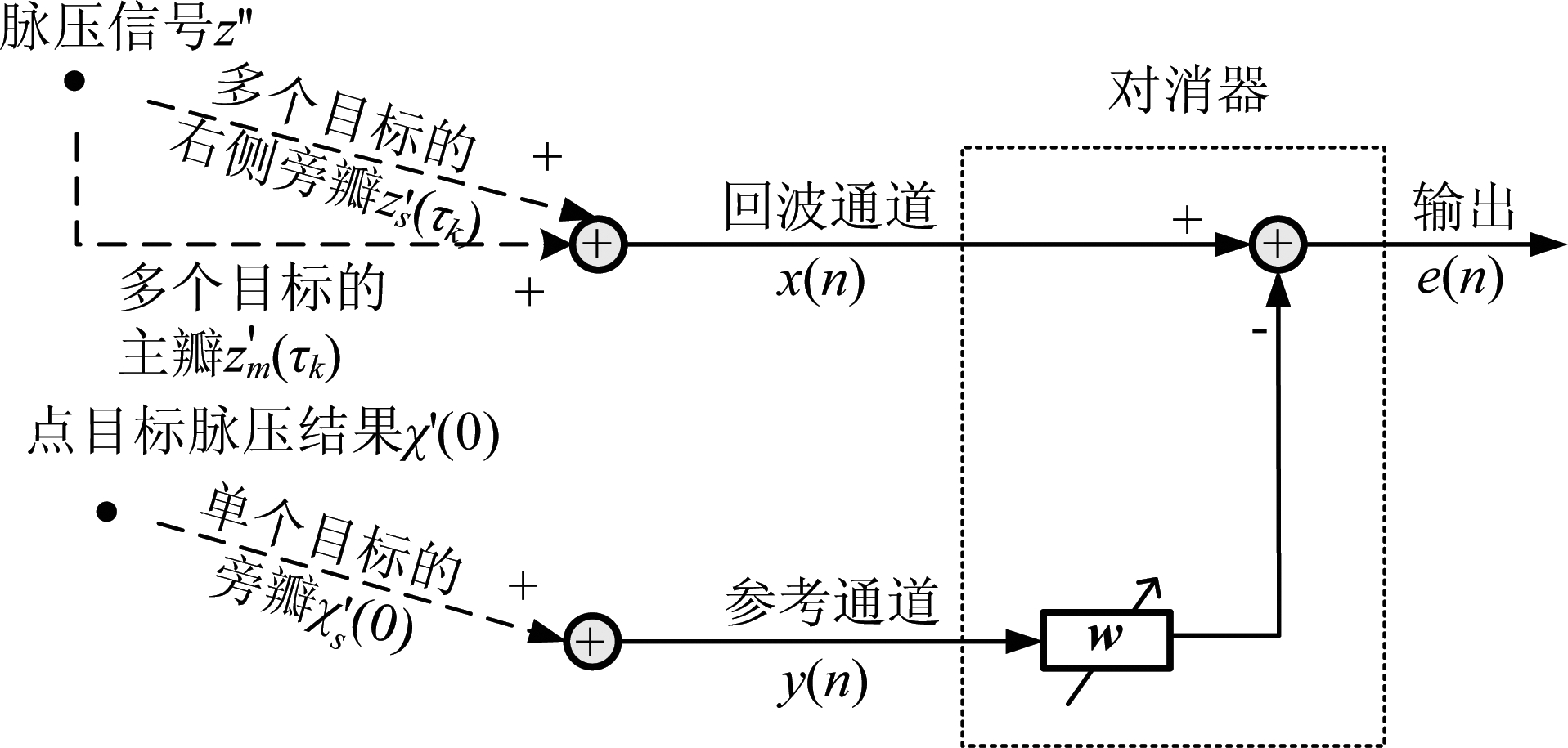
图9 LMS滤波旁瓣抑制原理框图
Fig.9 Block diagram of LMS filter sidelobe suppression principle
其中表示为模糊函数的零多普勒距离响应,χ′(0)的右侧旁瓣,z″是z′有效区域内的脉压结果,表示为:
(6)
上式中,z′s(τk)表示第k个目标的脉压旁瓣分量,z′m(τk)表示第k个目标的脉压主瓣分量。
若雷达回波采用匹配滤波方法,由于主瓣左侧没有凹槽,有效观测范围内主瓣的左右两侧都存在旁瓣。然后,从表1的步骤3得,LMS滤波是用当前时刻减去前一时刻加权矢量计算所得估计值,获得滤波器输出。若峰值左侧存在旁瓣,则估计值不为0,那么目标的峰值也会被对消掉。若要保留主瓣,只需让前一时刻的估计值为零即主峰时刻减去零便可保留主峰,前一时刻估计值为零即权值为零或主峰前滤波器的输入为零。权值的更新是滤波器自适应更新,无法准确的控制,可让主峰前滤波器的输入为零,即主峰前无旁瓣。但是无论是传统匹配滤波还是失配滤波,接收端均用线性卷积方法计算,线性卷积的起始时刻不可能为峰值。因此,在失配滤波的框架下,峰值左侧增加置零凹槽,可在LMS滤波中保留主瓣,并且降低峰值右侧的旁瓣。
表1 LMS滤波算法流程
Tab.1 LMS filtering algorithm flow
1.输入:x(n)=[x(n),x(n-1),…,x(n-M+1)]T,n=0,1,2,...,L。y(n),n=0,1,2,...,N。2.初始化:n=0,w(0)=0,μ=μopt3.计算y(n)的估计值:^y(n)=wH(n)x(n)=∑M-1i=0w*i(n)x(n-i)4.计算误差信号e(n):e(n)=y(n)-^y(n)5.更新LMS自适应权值:w(n+1)=w(n)+μe(n)x(n)6.再次进入步骤3,直到n=L。
不同于匹配滤波的相关处理,失配滤波是针对波形设计一个数字滤波器,使得滤波器的输出为接近冲击函数的理想波形。然而构造过程为圆周卷积,实际回波处理过程中,多采用线性卷积,旁瓣不可能为0,但是利用圆周卷积和线性卷积之间的关系,可将主瓣周围的旁瓣可置0,即形成一个凹槽,旁瓣被推离到观测范围之外。
假设OFDM雷达通信一体化信号的离散采样信号表示为s(n),n=0,1,...,N,失配滤波器传递函数s1(n)的构造方法如下:
表2 失配处理算法流程
Tab.2 The process of mismatch processing algorithm
1.将原始OFDM信号s(n)的左右两侧补零,可得s'(n)=[zeros(1,N_right),s(n),zeros(1,N_left)],令M=N+N_right+N_left2.计算发射波s(n)的能量:En=∑Nn=0s(n)23.构造圆周卷积理想输出Q(n):Q(n)=[zeros(1,M-1),En]4.解算失配滤波器传递函数s1(n):s1(n)=IFFT FFT(Q(n))FFT(s'(n))
由步骤4可知,s1(n)与s′(n)的圆周卷积结果为Q(n)。如图10(a)所示,红色线段表示Q(n)的第1个至第N_right个采样点,绿色线段表示Q(n)的第N_left+N至M-1个采样点,蓝色线段则是Q(n)的第M个采样点,表示电平为En的峰值。记发射信号s(n)与传递函数s1(n)的线性卷积结果为β(n),则β(n)的采样点数L为N+M-1。如图10(b)所示,依据圆周卷积和线性卷积之间的关系可知,β(n)的峰值电平为En,且包含了旁瓣和凹槽。其中峰值左侧的凹槽(图中绿色线段)为补入s(n)右侧的零,峰值右侧的凹槽(图中红色线段)为补入s(n)左侧的零。因此,若用s1(n)对s(n)进行脉冲压缩处理,则可将距离模糊图的高旁瓣、伪峰等外推,使主峰附近的旁瓣为零,进而获得采样点数为Lrange的观测窗口,且Lrange=min(N_left,N_right)。另外,通过控制补入s(n)左侧和右侧的零点数目,可控制凹槽总长度和左右两侧凹槽的长度比例。
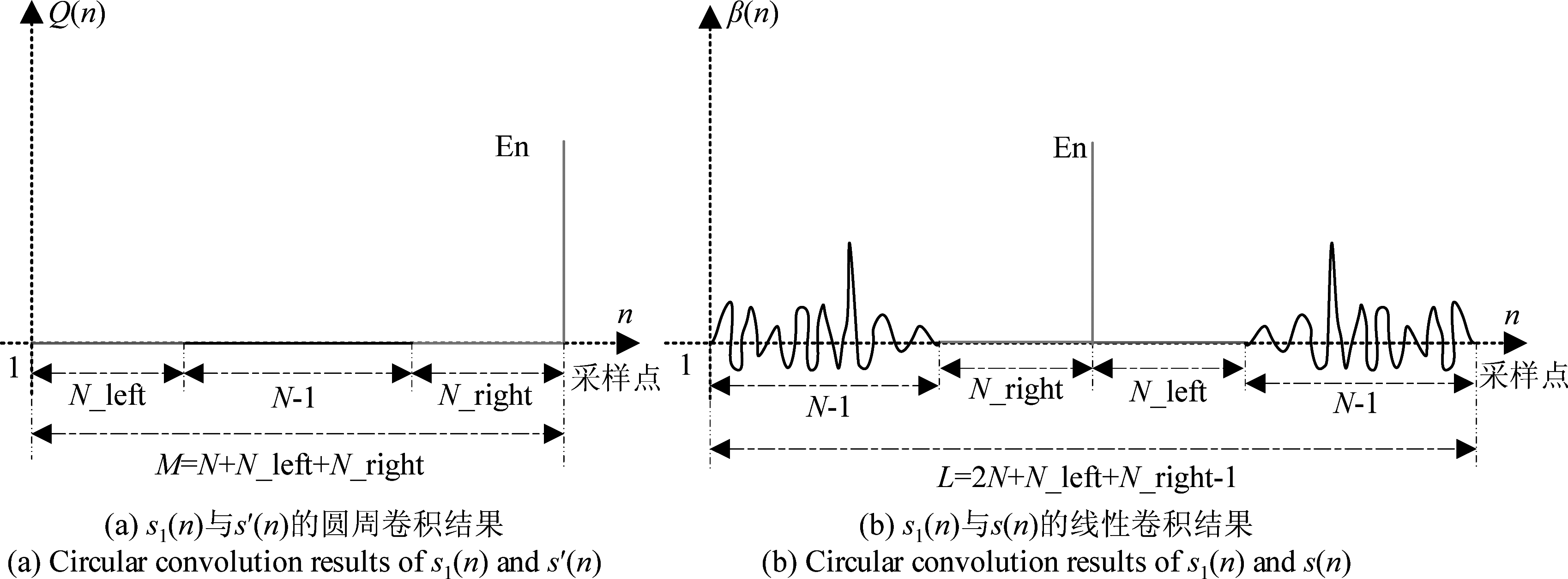
图10 圆周卷积结果与线性卷积结果的关系示意图
Fig.10 Schematic diagram of the relationship between circular convolution results and linear convolution results
然而,与传统的匹配滤波相比,上述失配滤波器的输出信噪比并非最大,存在信噪比损失问题。特别地,雷达的观测窗口越长,信噪比损失越大。结合LMS滤波滤除峰值右侧的旁瓣,可使观测窗口Lrange扩大至
且
因此相比失配处理算法,本文算法可在不减小雷达观测窗口长度的条件下,缩短凹槽,减少信噪比损失,或在相同信噪比损失条件下成倍提升雷达观测窗口长度。
综上,本节所提算法的算法框架如图11。
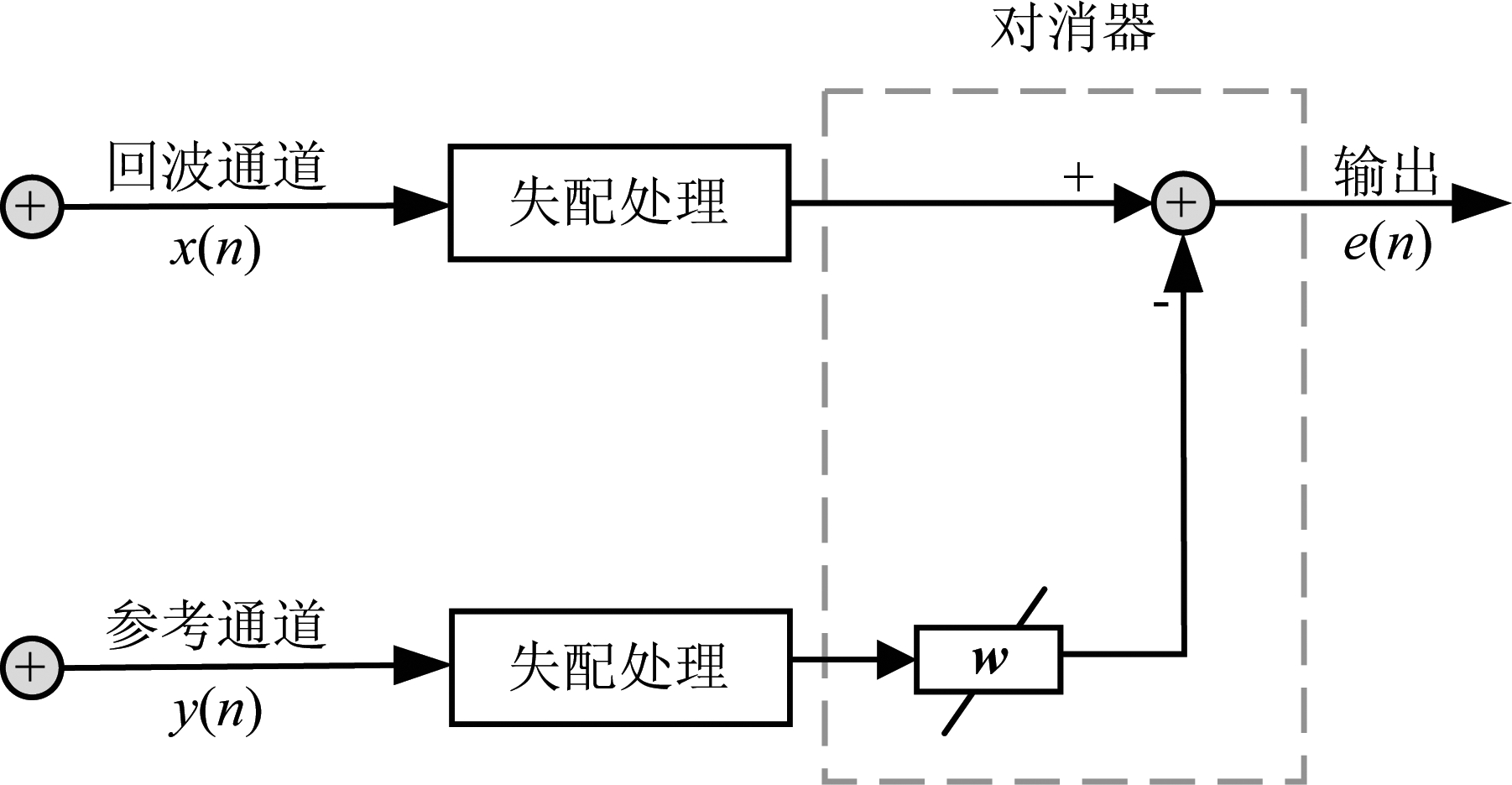
图11 融合失配处理和LMS滤波算法框架
Fig.11 Fusion mismatch processing and LMS filtering algorithm framework
4 仿真实验
4.1 仿真模型
为保证通信的传输速率,本文中一体化系统的工作于连续波体制下,但本文所提方法适用于通用场景中。下面以图12所示典型场景为例,一体化系统中整合了一体化波形发射天线和雷达接收天线与通信接收天线,一体化系统可接收雷达回波也可与其他通信设备进行通信。
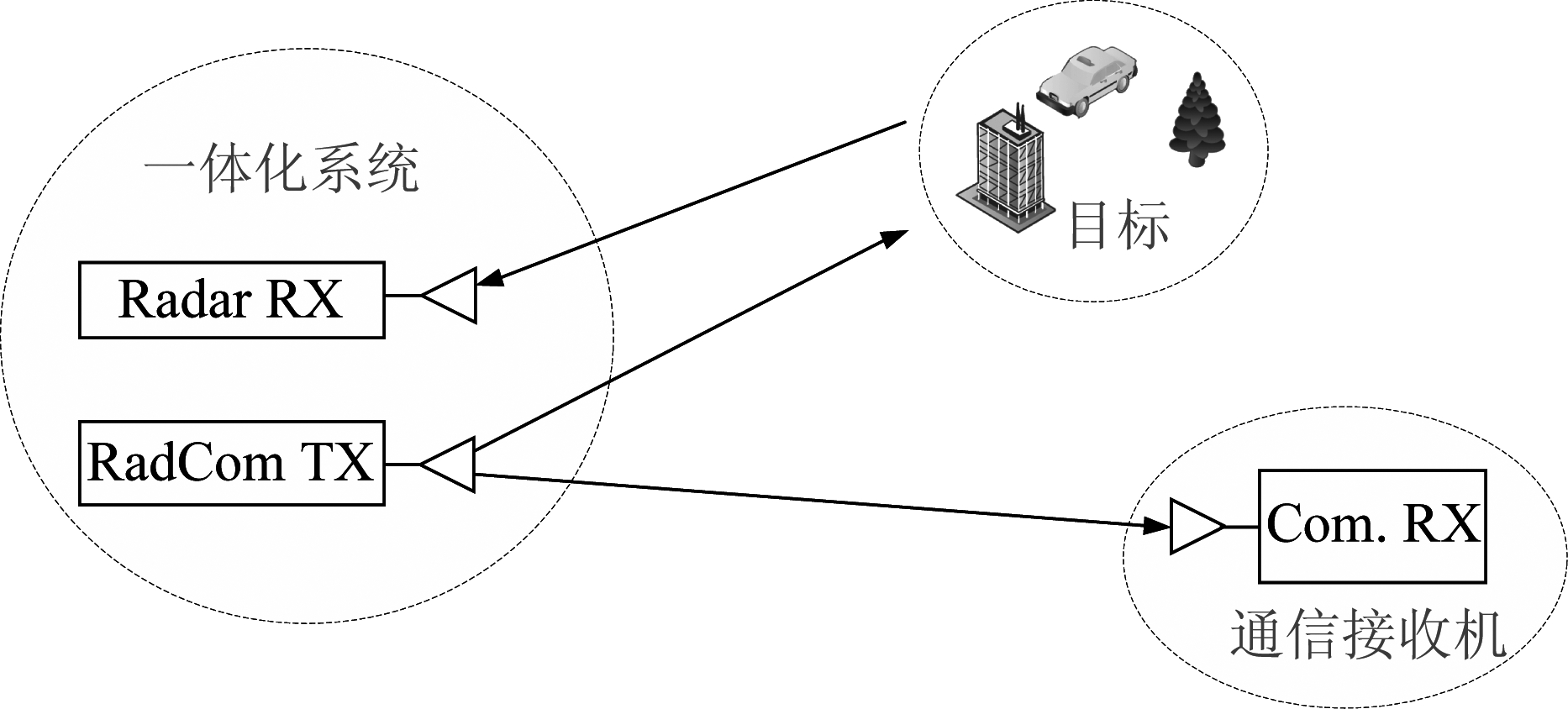
图12 典型的一体化场景
Fig.12 Tipical RadCom scenario
本文OFDM信号中通信信息的调制方式是16QAM,导频的参数设置参考4G通信协议[19],数字调制方式为PSK,导频序列为m伪随机序列。雷达的重复周期为一个OFDM符号时长。下面给出OFDM信号的仿真参数,如表3所示。
表3 OFDM信号参数
Tab.3 OFDM Signal Parameters
参数参数值信号带宽/MHz128采样率/MHz180 子载波间隔Δf/kHz15.625子载波数8192每个符号有效时间/μs64循环前缀(CP)时间/μs16每个符号的持续时间/μs80导频频域载波间隔6距离分辨率/m1.17
4.2 仿真结果
根据表3 的参数,在失配滤波的框架下,仿真OFDM信号的距离模糊函数形式,结果如图13所示,由图知,观测范围Lrange等于两侧凹槽中较短一侧凹槽的长度,即观测范围Lrange=min(Lleft,Lright),当Lleft=Lright时,观测范围Lrange=Lleft=Lright,此时凹槽总长度L=Lleft+Lright=2*Lleft=2*Lright,其中Lleft为左侧凹槽的长度(km),Lright为右侧凹槽的长度(km)。从以上结论看出,为保证观测范围,凹槽的长度至少为观测长度的两倍。如图13所示,通过失配滤波,原本淹没在匹配滤波旁瓣下的弱目标浮现出来,凹槽可在观测范围内避免旁瓣的干扰,但同时也存在较大的信噪比损失,即在相同的滤波器能量下,信号经过失配滤波器的峰值功率小于匹配滤波的脉压峰值功率,如下图,经过实验发现,该信噪比损失的大小与凹槽长度L有关,在20 dB的信噪比下,改变凹槽的长度并统计信噪比损失,仿真结果如图14所示。
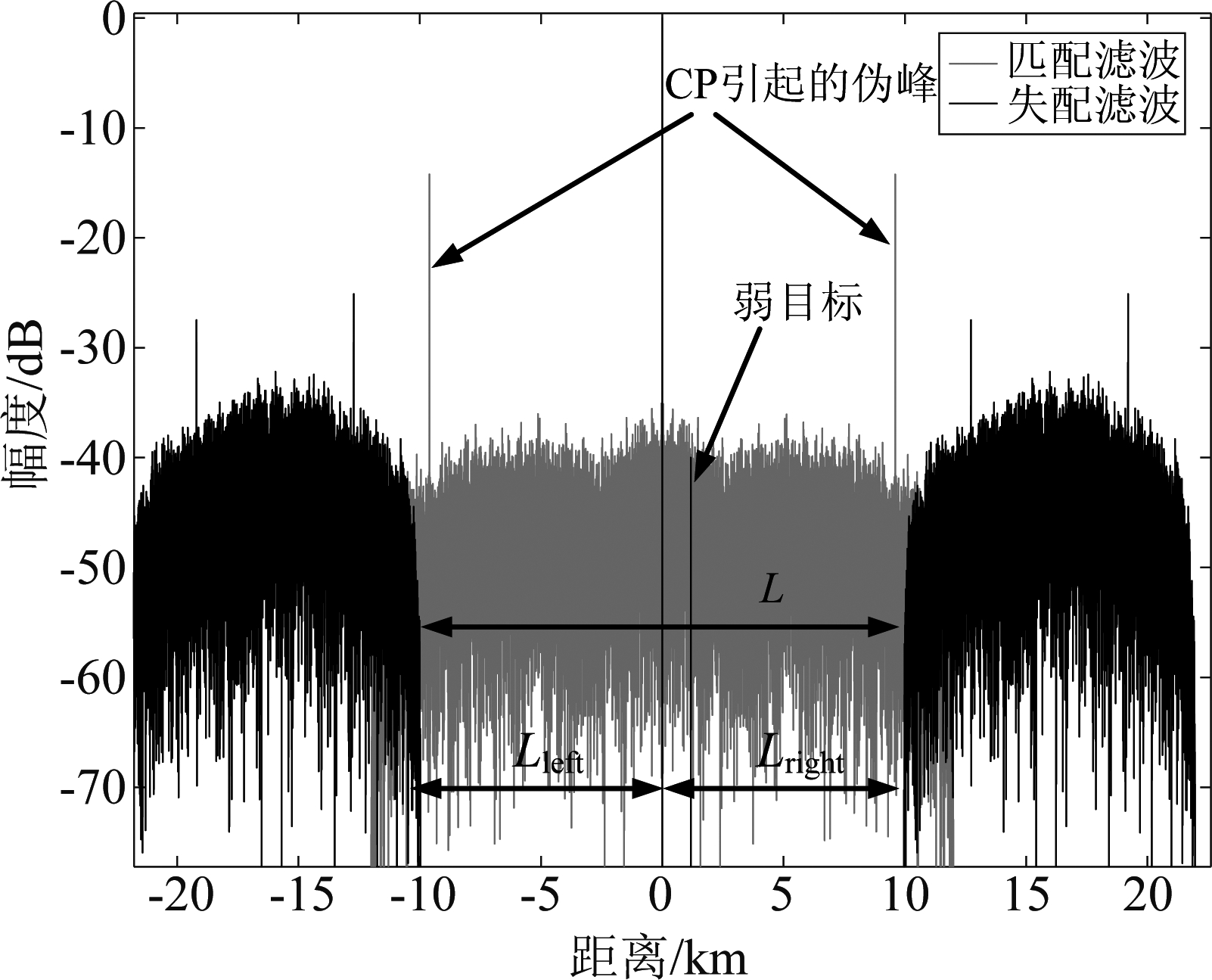
图13 失配滤波距离模糊函数形式
Fig.13 Mismatched filter point extension function
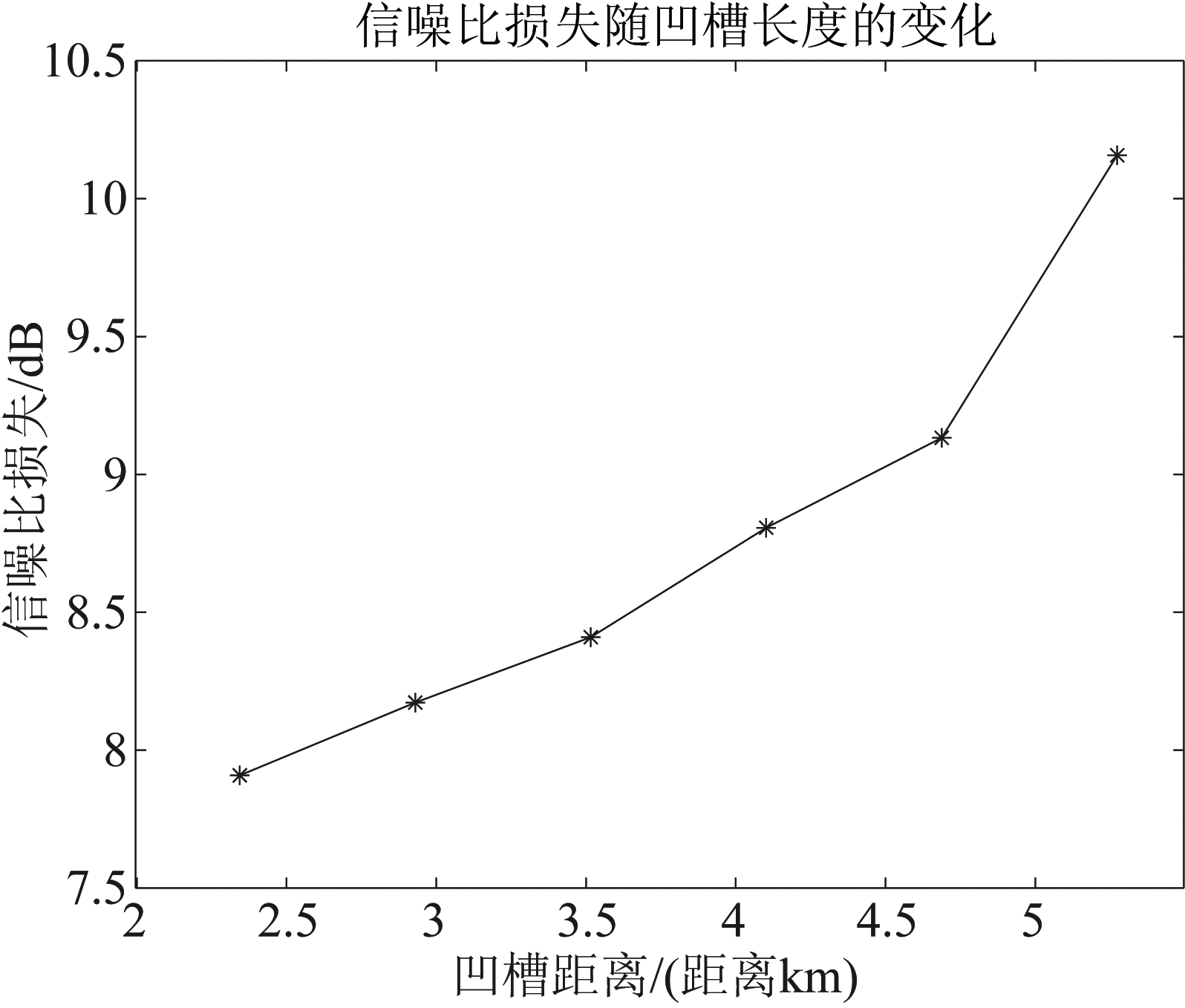
图14 20 dB信噪比下,信噪比损失随凹槽长度的变化
Fig.14 At 20 dB SNR,the SNR loss varies with the groove length
图14表明:凹槽长度与信噪比损失存在正比例关系,即随着凹槽(凹槽长度为观测距离的2倍)的增大,信噪比损失会增大。在本文方法中,回波经过失配滤波后,经过LMS滤波可对消峰值右侧的旁瓣,此时观测范围
不再受限于右侧凹槽,而等于凹槽总长度L,即
在相同的观测范围下,即
时,可将右侧凹槽置零,即Lright=0,此时凹槽的总长度L=Lleft+Lright=Lleft,凹槽的总长度相比失配滤波方法减少了一半,从而减少信噪比损失。
假设观测范围1.2 km,回波存在一个强目标和一个弱目标,分别位于0 km和1.17 km,RCS分别为1和0.025,回波的输入信噪比为20 dB。在失配滤波方法中,两侧凹槽长度Lleft=Lright=1.2 km,凹槽总长度L=Lleft+Lright=2.4 km;在相同的观测范围下,本文方法的左侧凹槽
km,右侧凹槽
km,凹槽总长度
km。控制失配滤波方法和本文方法中滤波器能量与匹配滤波器能量相同,使用失配滤波方法和本文方法对回波进行脉压处理。结果如图15(a)所示,失配滤波的信噪比损失为10.17 dB,本文方法的信噪比损失为7.16 dB,相比失配滤波方法,本文方法脉压主峰的信噪比损失减少了约3 dB,将弱目标放大,如图15(b),失配滤波方法和本文方法的噪声功率相同,失配滤波方法中弱目标的SNR=14 dB,而本文方法中弱目标的SNR=17 dB,在相同的虚警概率下,本文方法的弱目标的检测概率更高。同时,在相同的信噪比损失下,即本文方法中凹槽Lleft=Lright=1.2 km,在距离3 km的地方设置一个RCS为0.1的目标,并对回波进行脉冲压缩仿真。
图15 脉冲压缩效果对比
Fig.15 Pulse compression effect comparison
结果如图16,在图16(a)中,将失配滤波和本文方法的脉压结果分为凹槽区和高旁瓣区,经过本文方法,高旁瓣区的旁瓣和伪峰被抑制,位于高旁瓣区的目标也有效凸显出来;由图16(b)可知,本文
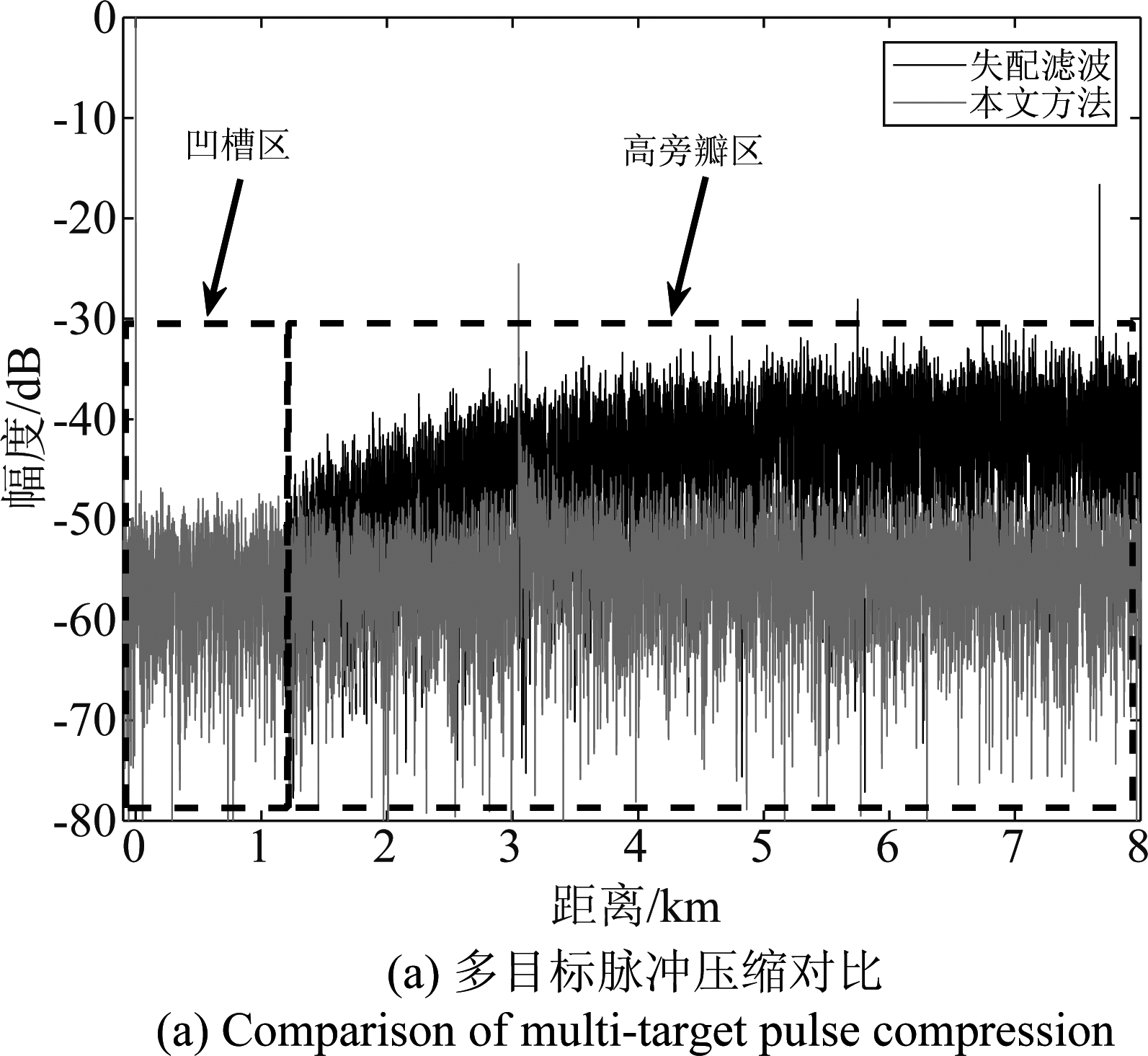
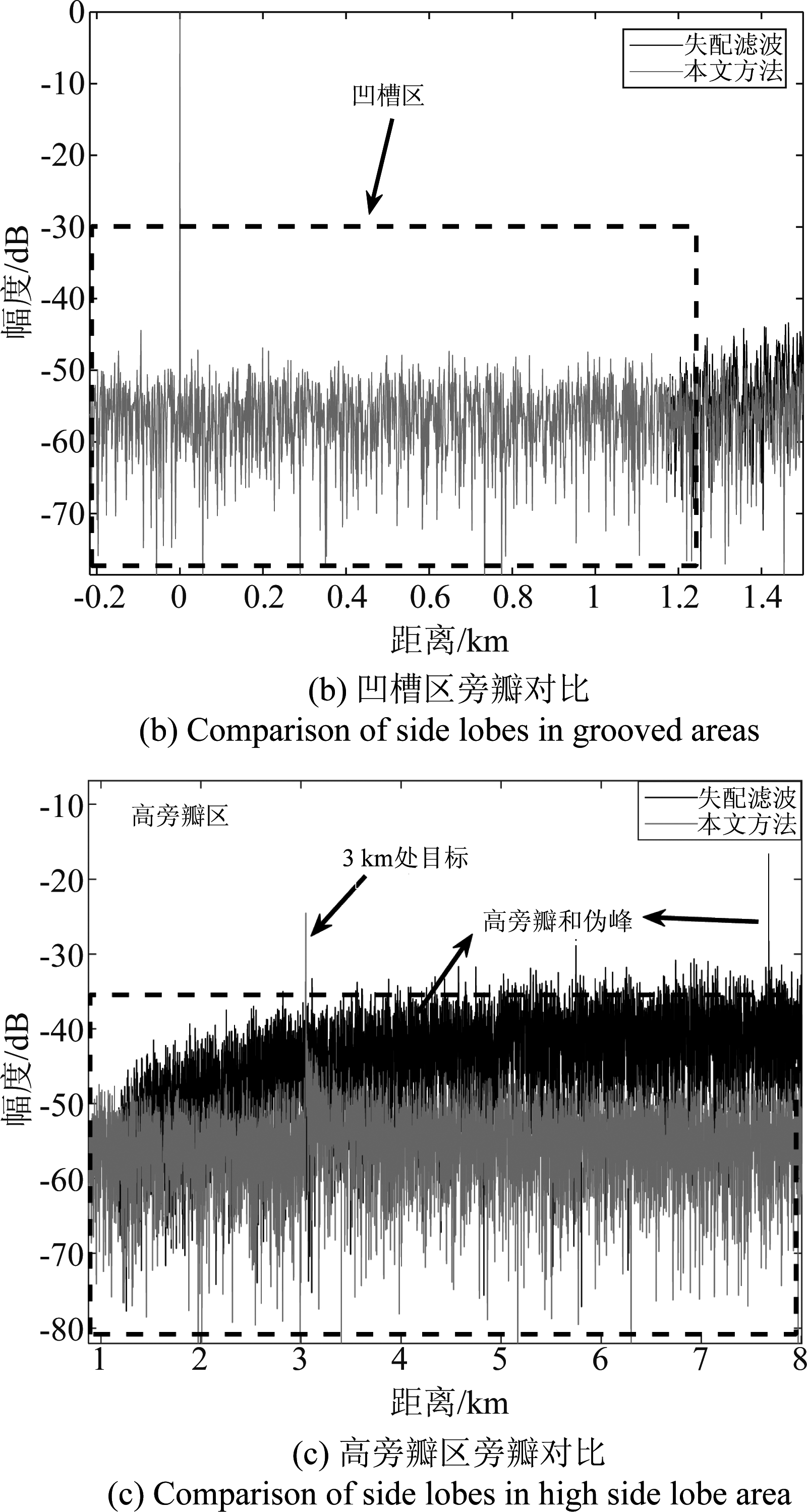
图16 多目标脉冲压缩效果对比
Fig.16 Effect comparison of multi-target pulse compression
方法与失配滤波方法的凹槽区旁瓣高度相同,其旁瓣高度取决于信噪比;由图16(c)可知,在高旁瓣区,失配滤波方法中旁瓣和伪峰仍然很高,而在本文方法中,经过LMS滤波,旁瓣和伪峰被有效抑制,3 km处的目标很好的显示出来,由此可知,观测范围可扩大到2.4 km以上,即观测范围增大了至少一倍。
5 结论
在如今频谱资源竞争愈发激烈的背景下,通信频段不断向雷达频段靠近,雷达通信一体化成为近年来的研究热点。共享信号由于时空频的高度一体化备受学者的亲睐,其中OFDM共享信号因其高频谱利用率和通信速率以及良好的模糊函数特性,在多项实验中被证明是一种良好的一体化信号。但是在雷达信号处理中,OFDM信号若使用传统的匹配滤波技术,其积分旁瓣比很高,并且存在伪峰,不能应用于密集目标以及弱目标探测的场景。近年,部分学者提出的失配滤波算法在一体化信号处理中有很大的潜力,但是该算法使得观测窗口宽度受限于信噪比损失。鉴于此,本文通过将失配处理与LMS滤波深度融合,可有效突破信噪比损失与观测窗口宽度之间的约束,进而在不减小观测范围的条件下降低信噪比损失,并且在相同的信噪比损失下,提高一倍的雷达探测范围。
[1] 田旋旋, 胡念平. 基于OFDM的无人机雷达通信一体化设计方法[J]. 信号处理, 2020, 36(10): 1714-1720.
TIAN Xuanxuan, HU Nianping. Design method of radar-communication integration using OFDM signals for UAVs[J]. Journal of Signal Processing, 2020, 36(10): 1714-1720.(in Chinese)
[2] TAVIK G C, HILTERBRICK C L, EVINS J B, et al. The advanced multifunction RF concept[J]. IEEE Transactions on Microwave Theory and Techniques, 2005, 53(3): 1009-1020.
[3] HAN Liang, WU Ke. Multifunctional transceiver for future intelligent transportation systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2011, 59(7): 1879-1892.
[4] 肖博, 霍凯, 刘永祥. 雷达通信一体化研究现状与发展趋势[J]. 电子与信息学报, 2019, 41(3): 739-750.
XIAO Bo, HUO Kai, LIU Yongxiang. Development and prospect of radar and communication integration[J]. Journal of Electronics & Information Technology, 2019, 41(3): 739-750.(in Chinese)
[5] 刘永军. 基于OFDM的雷达通信一体化设计方法研究[D]. 西安: 西安电子科技大学, 2019.
LIU Yongjun. Study on integrated radar and communications design method based on OFDM[D]. Xi′an: Xidian University, 2019.(in Chinese)
[6] 梁兴东, 李强, 王杰, 等. 雷达通信一体化技术研究综述[J]. 信号处理, 2020, 36(10): 1615-1627.
LIANG Xingdong, LI Qiang, WANG Jie, et al. Joint wireless communication and radar sensing: Review and future prospects[J]. Journal of Signal Processing, 2020, 36(10): 1615-1627.(in Chinese)
[7] 邵启红, 万显荣, 张德磊, 等. 基于OFDM波形的短波通信与超视距雷达集成实验研究[J]. 雷达学报, 2012, 1(4): 370-379.
SHAO Qihong, WAN Xianrong, ZHANG Delei, et al. Experimental study on shortwave communication and OTHR integrated system based on OFDM waveform[J]. Journal of Radars, 2012, 1(4): 370-379.(in Chinese)
[8] STURM C, WIESBECK W. Waveform design and signal processing aspects for fusion of wireless communications and radar sensing[J]. Proceedings of the IEEE, 2011, 99(7): 1236-1259.
[9] 雍萍, 王杰, 葛俊祥. 基于失配处理的OFDM雷达通信一体化共享信号旁瓣抑制技术[J]. 信号处理, 2020, 36(10): 1698-1707.
YONG Ping, WANG Jie, GE Junxiang. A novel side-lobe suppression technology for the OFDM-based joint radar and communication waveforms using the mismatching[J]. Journal of Signal Processing, 2020, 36(10): 1698-1707.(in Chinese)
[10] LIU Yongjun, LIAO Guisheng, XU Jingwei, et al. Adaptive OFDM integrated radar and communications waveform design based on information theory[J]. IEEE Communications Letters, 2017, 21(10): 2174-2177.
[11] LIU Yongjun, LIAO Guisheng, YANG Zhiwei. Robust OFDM integrated radar and communications waveform design based on information theory[J]. Signal Processing, 2019, 162: 317-329.
[12] LIU Yongjun, LIAO Guisheng, CHEN Yufeng, et al. Super-resolution range and velocity estimations with OFDM integrated radar and communications waveform[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11659-11672.
[13] 刘永军, 廖桂生, 杨志伟. 基于OFDM的雷达通信一体化波形模糊函数分析[J]. 系统工程与电子技术, 2016, 38(9): 2008-2018.
LIU Yongjun, LIAO Guisheng, YANG Zhiwei. Ambiguity function analysis of integrated radar and communication waveform based on OFDM[J]. Systems Engineering and Electronics, 2016, 38(9): 2008-2018.(in Chinese)
[14] 李晓柏, 杨瑞娟, 程伟, 等. 新的互补序列在雷达通信一体化中的应用[J]. 系统工程与电子技术, 2021, 43(3): 693- 699.
LI Xiaobai, YANG Ruijuan, CHENG Wei, et al. Application of a novel complementary signal to integrated radar and communication[J]. Systems Engineering and Elect-ronics, 2021, 43(3): 693- 699.(in Chinese)
[15] GUO T, QIU R. OFDM waveform design compromising spectral nulling, side-lobe suppression and range resolution[C]∥2014 IEEE Radar Conference. Cincinnati, OH, USA. IEEE, 2014: 1424-1429.
[16] ZUO Jiajun,YANG Ruijuan,LUO Shaohua,et al.Range sidelobe suppression for OFDM-integrated radar and communication signal[J]. The Journal of Engineering, 2019, 2019(21): 7624-7627.
[17] 周炯槃, 庞沁华, 续大我, 等. 通信原理[M]. 北京：北京邮电大学出版社, 2002: 448- 456.
ZHOU Jiongpan, PANG Qinhua, XU Dawo, et al. Principle of Communication[M]. Beijing:Beijing University of Posts and Telecommunications Press, 2002: 448- 456.(in Chinese)
[18] [美]Mark, A.Richards. 雷达信号处理基础[M]. 北京: 电子工业出版社, 2008: 115-121.
MARK A. Richards. Fundamentals of Radar Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2008: 115-121.(in Chinese)
[19] 张长青. 5G系统定义的帧结构分析[J]. 邮电设计技术, 2019(6): 42- 46.
ZHANG Changqing. Frame structure analysis of 5G system definition[J]. Designing Techniques of Posts and Telecommunications, 2019(6): 42- 46.(in Chinese)
