1 引言
被动声纳目标检测分为窄带检测和宽带检测。窄带检测适用于具有稳定线谱的水中目标,国内外学者分别运用线谱的窄能量、频率方差、空时稳定性、幅相起伏性、功率谱熵等特征完成窄带检测[1,2]。但是窄带检测没有考虑海洋传播信道随频率的变化,而且待检测的目标往往是非合作的,采用窄带检测可能导致稳定性差的问题。宽带检测运用足够宽的宽带信号进行目标检测,往往可以得到更加稳定的效果,对宽带检测的研究是近年来的一个热门课题。
对于常规波束形成,能量检测法(Conventional Energy Detection, CED)是常用的宽带检测方法,是理论上在非相干噪声场中单一目标的最优检测器。M.Bono 提出了子带峰值能量检测(Subband Peak Energy Detection, SPED),用于解决宽带能量检测的目标轨迹模糊问题[3]。在SPED的基础上,杨晨辉提出了波束域峰值能量检测方法[4],性能优于SPED。王聪提出了基于频率着色的宽带能量检测方法[5],提高了方位时间历程图的显示性能。
从匹配场波束形成的角度来看,宽带检测方法分为非相干处理方法和相干处理方法。非相干处理方法的处理单元为单个频点的匹配处理,该方法的输出为多个频率点的匹配处理的均值。单个频点的匹配处理考虑了单个频点内的空间相关性,但是均值的处理方法忽略了各个频点之间的相干信息。目前的处理算法大多采用这种空间相干处理、频率间非相干处理的方法[6]。为了降低旁瓣和提高定位精度,相干处理方法考虑了各频点之间的相干性,但是这种处理方法的性能依赖于各频点的归一化系数的选择,对噪声比较敏感。
最早的宽带相干处理方法是Clay实现的时域宽带相干匹配场处理[7]。该方法将测量得到的脉冲响应与建模得到的脉冲响应相匹配,从而实现了对声源的定位。Brienzo和Hodgkiss在爆炸声源定位试验中对该算法进行了验证[8-9]。Clay提出的时域宽带相干匹配场处理需要知道声源的频谱,这对于被动声纳的应用来说是难以实现的。Hursky在研究高频段的时域宽带相干匹配场处理时,利用双水听器的时域互相关实现了在声源频谱未知时的声源定位[10]。Westwood实现了频域的宽带相干匹配场处理[11],其输出结果为频域互相关的相干累加。在单个频点的接收数据的归一化问题上,Michalopoulou提出了以第一个阵元为参考量进行归一化的方法[12],这种归一化方法适用于高信噪比的情况。孟华等对被动声纳宽带相干处理技术进行了总结,并且提出了一种改进的阵元归一化方法,提高了宽带相干处理器的检测性能[13]。赵博将并行遗传算法应用于匹配场声源定位[14],提升了计算速度。周悦将匹配场处理建立在机器学习的框架下,基于信息理论准则对拷贝场和测量场进行距离度量[15],性能优于传统的匹配场估计方法。韦先声将传统的基于声压水听器的匹配场处理扩展到基于矢量水听器的匹配场处理[16],对比了不同匹配量下的相干处理器和非相干处理器的匹配性能。
匹配检测处理算法的加权向量为声源到水听器的传播损失声压。传播损失声压可以通过建模得到。水下声传播模型按照建模的维度不同,可以分为时域模型和频域模型[17]。直接对时域的波动方程的建模产生了时域模型,包括有限元法,有限差分法,边界元法;此外,考虑到声传播的时间尺度远小于海洋环境参数变化的时间尺度,因此可以将时域的波动方程转化为频域的亥姆霍兹方程,对亥姆霍兹方程的建模产生了频域模型,包括射线法,简正波法,抛物方程法。Jensen在基准问题的求解中,比较了基于简正波模型的双向耦合模式和单向耦合模式的建模精度,可以认为双向耦合模式是精确建模,在后向散射可忽略的场景下,单向耦合模式与双向耦合模式的精度相当[18]。从计算量上来看,单向耦合模式的计算量远小于双向耦合模式。随着计算能力的提升,有限元法被用于基准问题的求解,这也进一步验证了双向耦合模式的准确度[19]。
本文基于Hursky提出的双水听器时域互相关方法[10],提出了一种基于多水听器互相关的被动声纳宽带目标检测方法。与用于声源定位的双水听器互相关方法不同的是,本文提出的方法考虑的是如何在低信噪比下利用多个水听器的相干性实现宽带目标检测。本文的第二部分介绍了被动声纳宽带检测模型,第三部分介绍了多水听器互相关方法,第四部分通过对42个水听器的仿真实验验证了本文的方法可以在极低信噪比下实现宽带目标检测,检测能力优于双水听器。此外,宽带滤波器系数的求解需要多次求解水声模型,这会导致计算量非常大,本文提出了利用模型的互易性快速计算宽带滤波器系数的加速方案,极大地缩短了计算时间。
2 问题描述
考虑M个水听器对同一个宽带声源的接收声压信号。声源的位置为r0,声源发射信号为s(t)。用水听器的深度和到声源的距离表示水听器的位置,M个水听器的位置分别记为r1,r2…rM,接收声压信号分别为p1(t),p2(t)…pM(t)。被动声纳宽带目标检测问题可以描述为:在声源位置r0和声源发射信号s(t)未知的情况下,如何利用M个水听器的接收信号p1(t),p2(t)…pM(t)判断有无目标,即s(t)是否不为0。
通过傅里叶合成,我们可以进一步探讨M个水听器的接收信号。考虑声波在海洋波导中的传播,将海洋波导当做信道,考虑声源-海洋波导-水听器这一信道传输问题。声源在第m个水听器处激发的声压场为声源频谱中各个单频信号激发的声压场的傅里叶合成,即
(1)
其中p(r0,rm,t)表示位置为r0的声源在位置rm处激发的声压场,S(ω)为s(t)的频谱,g(r0,rm,ω)表示当角频率为ω时从r0到rm的信道频率响应。通常g(r0,rm,ω)用传播损失声压来表示,此时S(ω)为距离声源位置1 m处测得的频谱。
式(1)的傅里叶变换是无法直接进行数值计算的。我们可以考虑如下几个因素,从而将式(1)转化为可以用实数快速傅里叶变换(Real Fast Fourier Transform, RFFT)来计算的形式:
1)实际的水听器都是有一定的接收带宽的,这个接收带宽可以用最大角频率ωmax来表示,即接收声压信号的能量在角频率ωmax以上是可以忽略的。
2)声源发射信号是实信号,因此S(ω)是共轭对称的。
3)g(r0,rm,ω)是通过水声模型计算得到的,水声模型推导的起点是亥姆霍兹方程,而亥姆霍兹方程关于角频率是共轭对称的,因此g(r0,rm,ω)关于角频率也是共轭对称的。
4)对时间轴和频率轴进行离散化。将发射信号和接收信号的起始时刻都约定为0,如果要在时长为T的时间窗中计算接收声压信号,那么可以对时域和频域做如下的离散化,
tj=jΔt, j=0,1…(N-1)
(2)
(3)
其中
(4)
Δt表示时域采样间隔,Δω表示频域的采样间隔。对式(4)做简单的移项,式(4)等价于Δf=1/T,这说明频域的物理分辨率取决于信号长度,信号时长越长,在频域可以达到更高的物理分辨率。
按照Jensen[12]的推导,用离散求和代替式(1)中的积分,同时考虑频率轴的离散化导致的时间轴的周期延拓,可以得到以T为周期的接收声压信号为,
p(r0,rm,tj)= ![]() ∑n≠0p(r0,rm,tj+nT)
∑n≠0p(r0,rm,tj+nT)
(5)
其中Re{·}表示取实部,并且
(6)
如果T足够长,那么式(5)中的混叠项是可以忽略的,此时,
p(r0,rm,tj)= ![]()
(7)
式(7)中的求和项可以由实数快速傅里叶变换同时计算tj的N个采样点的值。
第m个水听器的接收信号为声源在rm处激发的声场与环境噪声的叠加,即,
pm(t)=p(r0,rm,t)+n(rm,t)
(8)
其中n(rm,t)表示在rm处的环境噪声。
当各个水听器的间距大于二分之一波长时,可以认为各个水听器处的环境噪声是不相关的。
3 多水听器互相关方法
在本文提出的多水听器互相关方法中,首先将M个水听器的接收信号等分为两组,分别对两组中的每一个水听器的接收信号通过宽带滤波进行信道解调,然后计算两组水听器累加后的解调信号的互相关系数,最后通过互相关系数计算互相关指标作为检测量,可以实现在接收端的信噪比的提升。
3.1 信道解调
信道解调是和信道传输相反的过程。假设声源的位置为r,通过宽带滤波可以计算得到在第m个水听器处的接收信号为pm(t)的声源发射信号,即
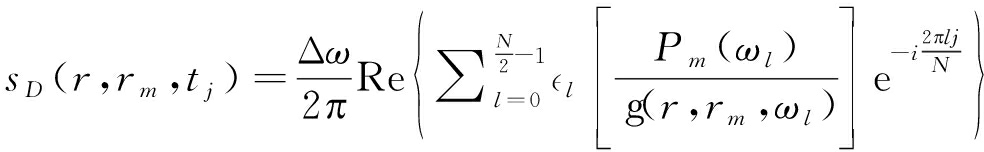
(9)
其中sD(r,rm,tj)表示第m个水听器在声源位置r处的解调信号,Pm(ωl)表示pm(t)的频谱。
将式(9)中的Pm(ωl)表示为接收信号分量和环境噪声分量之和,有,
 nD(r,rm,tj)
nD(r,rm,tj)
(10)
其中P(r0,rm,ωl)是p(r0,rm,t)的频谱,nD(r,rm,tj)表示环境噪声n(rm,t)对于声源位置r的解调信号。
根据式(10),当r=r0时,有,
sD(r0,rm,t)=s(t)+nD(r0,rm,t)
(11)
3.2 多水听器互相关的计算
多水听器互相关计算流程图如图1所示。
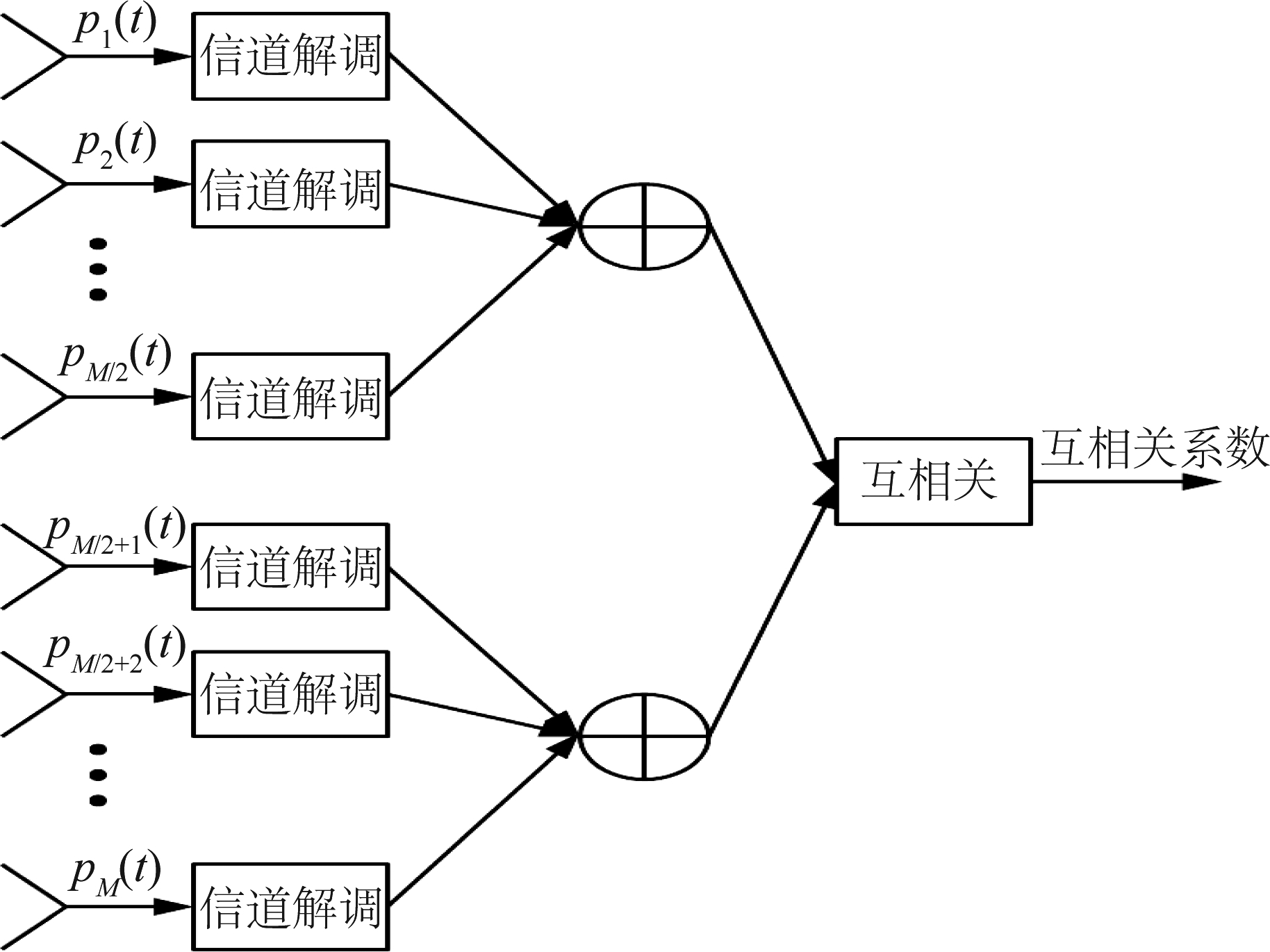
图1 多水听器互相关计算流程图
Fig.1 Multi-hydrophone correlation calculation flowchart
在图1中,将M个水听器等分为两组,其中前M/2个水听器为第一组,后M/2个水听器为第二组。以第一组水听器为例,将M/2个水听器的接收信号p1(t),p2(t)…pM/2(t)关于假定的声源位置r分别进行信道解调,并且将M/2个解调信号相加,得到第一组水听器的输出信号,记为![]() 同样可以得到第二组水听器的输出信号,记为
同样可以得到第二组水听器的输出信号,记为![]() 最后对
最后对![]() 和
和![]() 计算时域的互相关,得到的互相关系数如下,
计算时域的互相关,得到的互相关系数如下,
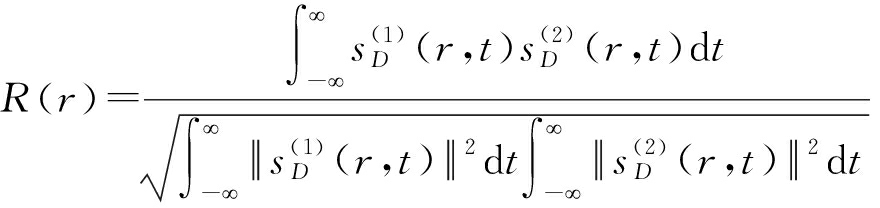
(12)
其中R(r)为![]() 和
和![]() 的互相关系数。
的互相关系数。
根据式(11),如果假定的声源位置与实际的声源位置一致,即r=r0,此时
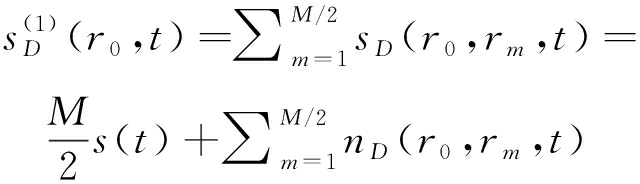
(13)
nD(r0,rm,t)是环境噪声的解调信号,水听器距离足够远时环境噪声是不相关的,此时其解调信号也是不相关的。在式(13)中,声源信号s(t)是相干叠加,而环境噪声的解调信号是非相干叠加,信噪比提升了M/2倍。在实际应用中,M取决于品质因数(Figure of Merit, FOM)、声源级和噪声级。对于![]() 也有同样的结论。在本方法中,我们将对假定的声源位置进行网格式的搜索。如果有目标,即s(t)不为0,那么
也有同样的结论。在本方法中,我们将对假定的声源位置进行网格式的搜索。如果有目标,即s(t)不为0,那么![]() 和
和![]() 的互相关系数会比较大,那么R(r0)在高信噪比情况下会接近于1。如果无目标,即s(t)为0,那么根据式(10),对于搜索网格中每个假定的声源位置,解调信号只包含噪声项,此时对于任意的声源位置r,R(r)都在0附近。我们用互相关指标
的互相关系数会比较大,那么R(r0)在高信噪比情况下会接近于1。如果无目标,即s(t)为0,那么根据式(10),对于搜索网格中每个假定的声源位置,解调信号只包含噪声项,此时对于任意的声源位置r,R(r)都在0附近。我们用互相关指标![]() 作为检测量,
作为检测量,![]() 反映了在搜索网格上R(r)的最大值和1的接近程度,如下式,
反映了在搜索网格上R(r)的最大值和1的接近程度,如下式,
(14)
3.3 用互易性原理加速计算
在式(14)中,我们需要对搜索网格中每一个声源位置计算互相关系数R(r)。假设搜索网格中的声源位置的数量是K,将需要搜索的声源位置记为r(1),r(2)…r(K),那么对于每个频点ωl,我们总共需要知道K×M个滤波器系数,表示成集合的形式为,
Gl={g(r(k),rm,ωl)|k=1…K,m=1…M}
(15)
g(r(k),rm,ωl)是通过声场模型计算得到的。声场模型的计算通常分为两部分:模型求解和声场计算。其中模型求解是指根据海洋波导参数计算得到一组能够表示声场的参数,声场计算是指根据模型求解得到的参数计算声场。在本文涉及到的双向耦合模式和单向耦合模式这两种声场模型中,模型求解都是计算每个距离段上的前向散射系数和后向散射系数,其中双向耦合模式需要求解全局耦合方程,单向耦合模式需要求解推进式的耦合方程;两种模型的声场计算是将局部的简正波解和散射系数进行加权求和,其计算量相比于模型求解是可以忽略的。例如,我们计算了声源位置为r(k)的单向耦合模式的各个距离段的散射系数,那么我们可以通过非常少的计算量得到g(r(k),r1,ωl),g(r(k),r2,ωl)…g(r(k),rM,ωl)总共M个滤波器系数。因此我们可以将式(15)中的Gl按照k的值划分成K个子集,如下式,
(16)
(17)
显然有,
(18)
每个子集的计算需要一次模型求解和M次声场计算。用TGl表示计算Gl需要的计算时间,用Tmodel表示模型求解的计算时间,用Tfield表示声场计算的计算时间,那么有,
TGl=KTmodel+KMTfield
(19)
当搜索网格很大,或者网格尺寸很小时,K的值会很大,此时计算Gl需要很长的时间,这给有限的计算资源带来了很大的挑战,因此对Gl的计算加速是很有必要的。
利用声场模型的互易性原理,可以对Gl的计算进行加速。互易性原理是指,交换声源和水听器的位置,信道传输函数不变。从物理上严格地讲,交换前后的信道传输函数应该是完全一致的,但是由于建模过程中引入的假设可能会导致互易性的失效,比如绝热近似假设了各个距离段之间没有能量的耦合传递,这个假设违背了界面处的声压连续性和质点振速连续性,因此不满足互易性。此外,由于数值方法的引入,交换前后的信道传输函数也无法做到完全一致,只能达到非常高的相似度。在后续的仿真实验中,我们对互易性原理进行了验证。按照互易性原理,有
g(r(k),rm,ωl)=g(rm,r(k),ωl)
(20)
将式(20)代入(15),有
Gl={g(rm,r(k),ωl)|k=1…K,m=1…M}
(21)
按照类似的推导,我们将式(21)划分为如下的M个子集,
(22)
(23)
并且有,
(24)
此时Gl的计算时间为
TGl=MTmodel+KMTfield
(25)
对比式(25)和式(19),我们通过互易性原理的运用,将模型求解次数从K次变成了M次。M表示水听器的个数,K表示搜索网格的网格点数,在实际应用中通常有M≪K。同时对于声场模型而言,通常有Tfield≪Tmodel,因此我们可以认为式(25)相比于式(19)在计算量上降低了K/M倍。
4 仿真实验与分析
4.1 海洋波导参数
仿真的海洋波导是一个随距离变化的浅海波导,如图2所示。
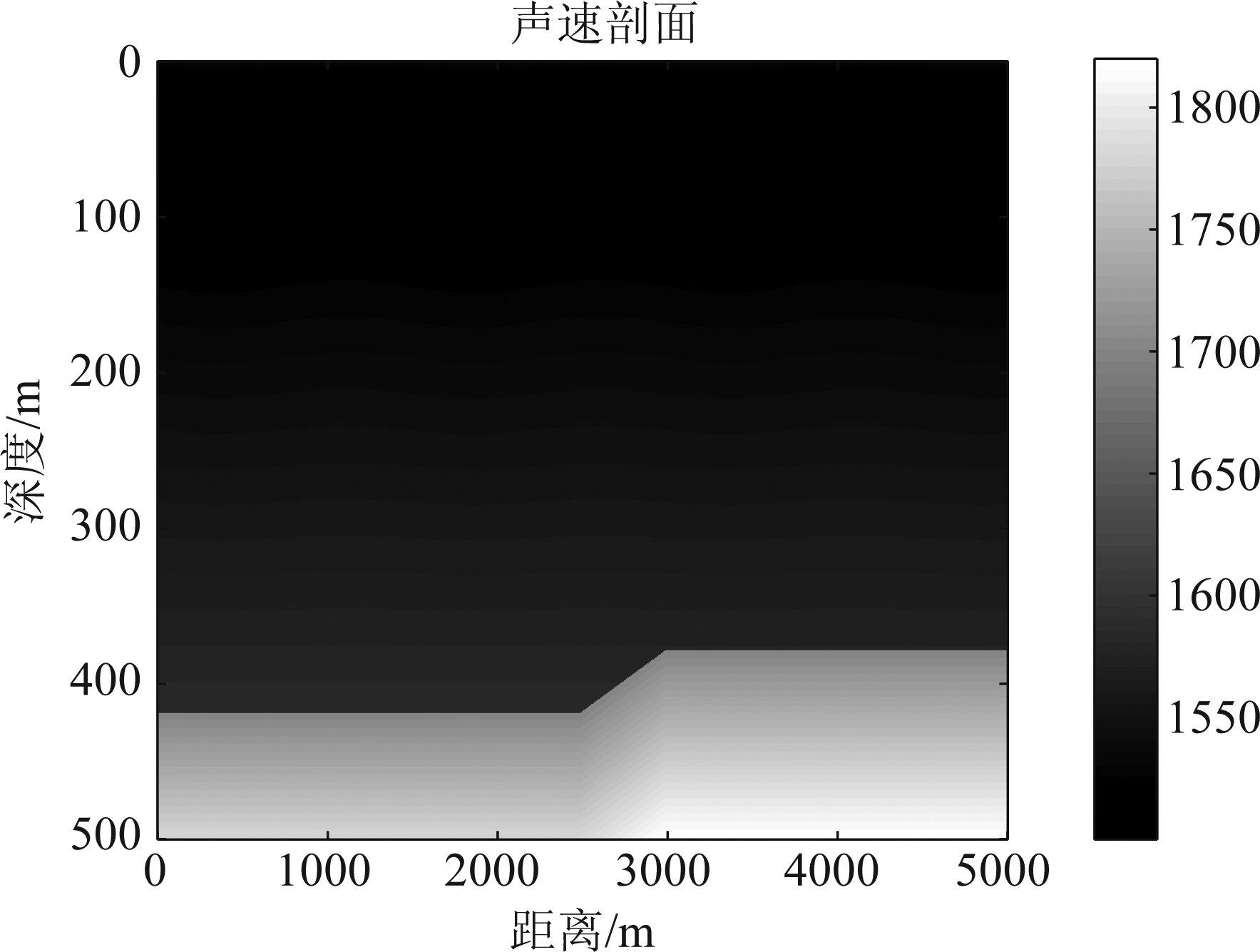
图2 浅海波导示意图
Fig.2 Schematic diagram of shallow sea waveguide
图2所示的海洋波导包括一个海水层和一个沉积层。其中在2500 m到3000 m之间有一个海底斜坡。海水层的密度为1000 kg/m3,沉积层的密度为2000 kg/m3。海面的均方根粗糙度为0.5 m,海底的均方根粗糙度为0.5 m。计算域的深度为500 m,底部为理想刚性海底。海水层的介质吸收系数为每波长0 dB,沉积层的介质吸收系数为每波长1 dB。
4.2 互易性原理的验证
本文通过仿真得到了声源和水听器的位置交换前后的接收信号,计算了两者的互相关系数来验证单向耦合模式的互易性。声源和水听器的深度都是50 m。水听器到声源的距离分别为1000 m,2000 m,3000 m。声源的发射信号为线性调频信号,其波形和频谱如图3。
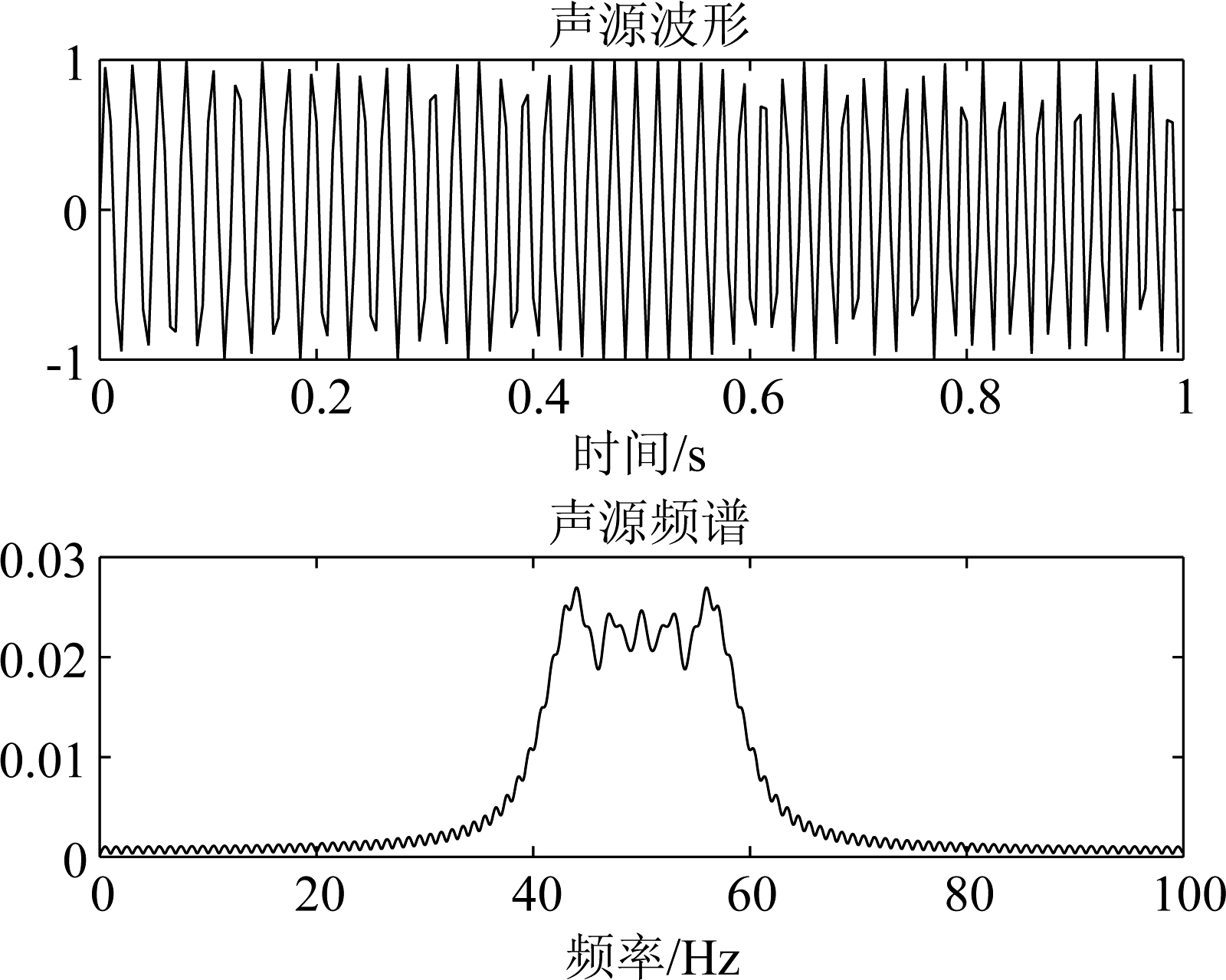
图3 声源的波形和频谱
Fig.3 Waveform and frequency spectrum of sound source
图4为水听器和声源位置交换前后的接收信号波形。
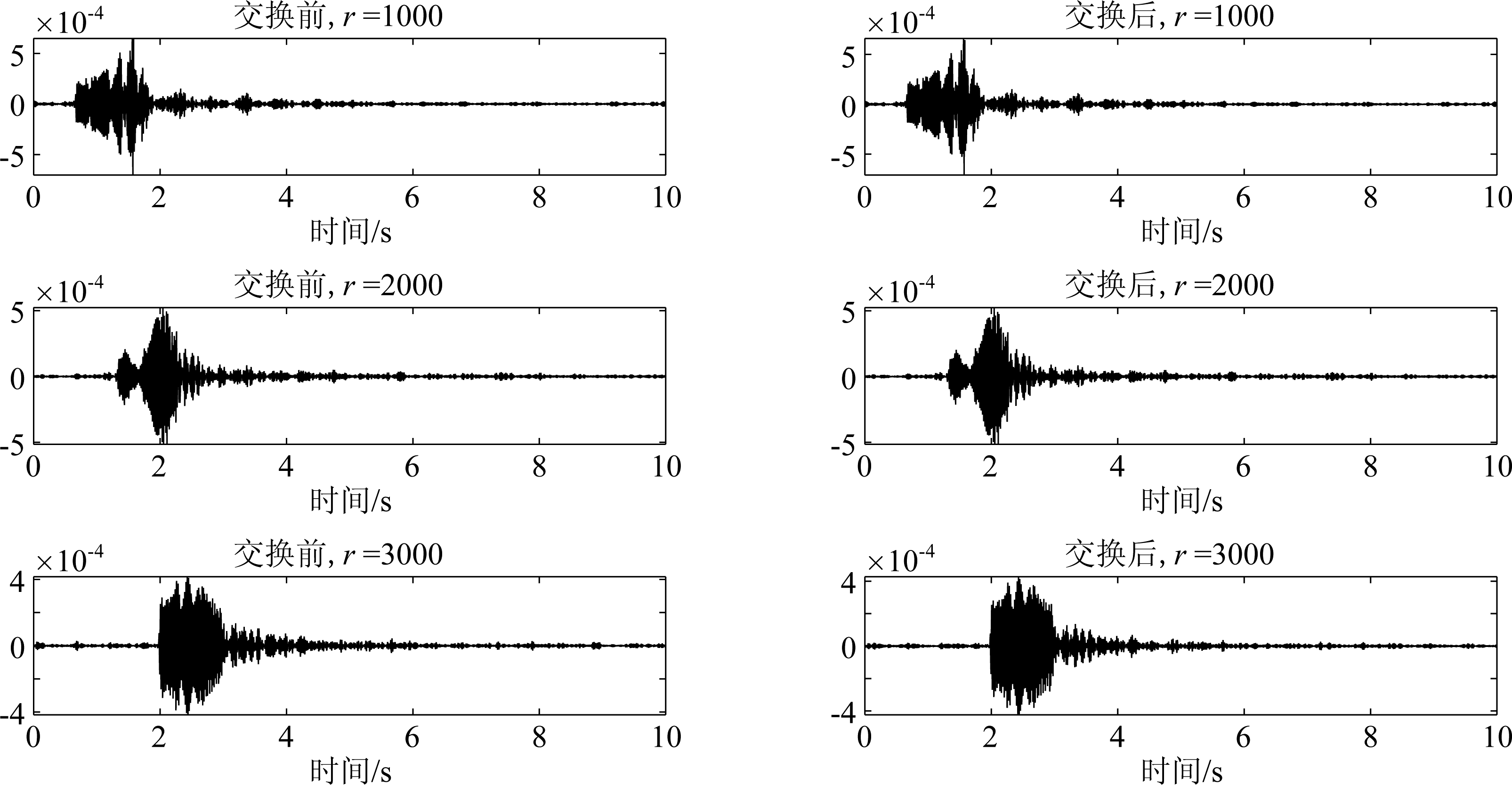
图4 交换前后的接收信号的波形
Fig.4 Waveform of the received signal before and after the exchange
表1是距离为1000 m,2000 m,3000 m时,交换前后的波形的互相关系数。从互相关系数上来看,交换前后的接收信号是非常相似的,这说明单向耦合模式满足互易性。
表1 互相关系数
Tab.1 Correlation coefficient

距离互相关系数1000 m0.99962000 m0.99993000 m0.9885
图5是直接计算宽带滤波器系数和用互易性原理计算宽带滤波器系数的计算时间的对比。声源位置的搜索点数是40000, 水听器数量为42。从图5中可以看出,在30 Hz到70 Hz的频率范围内,直接计算滤波器系数的计算时间大约为1000 s,运用互易性原理计算滤波器系数的计算时间大约为1 s,两个计算时间的比值与我们在式(25)和式(19)得出的计算时间的比值是相符的。
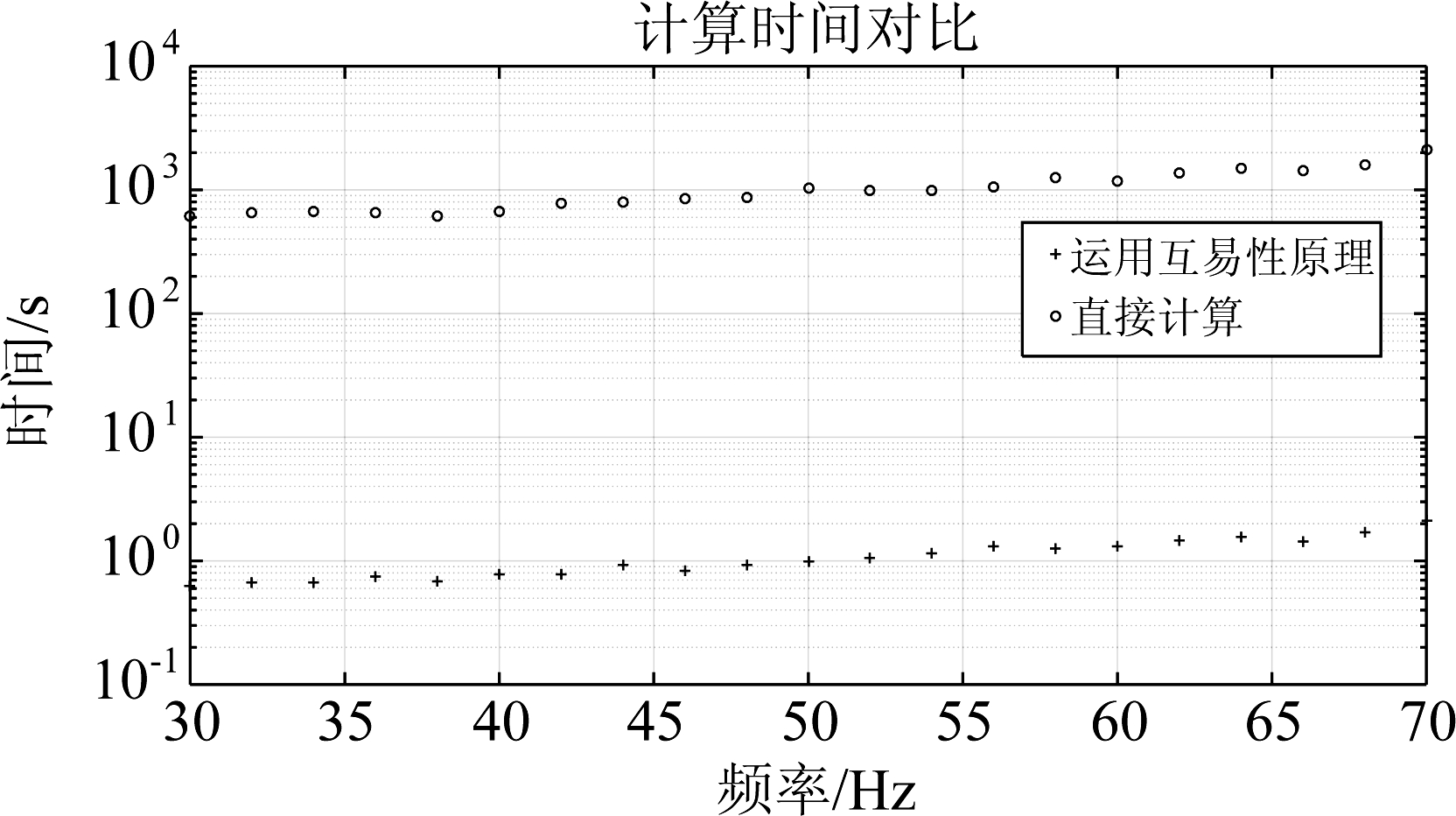
图5 直接计算滤波器系数与运用互易性原理 计算滤波器系数的计算时间
Fig.5 Calculation time for direct calculation and calculation using the principle of reciprocity of filter coefficients
4.3 多水听器互相关方法的目标检测仿真实验
本文通过仿真测试了水听器数量为2和42两种情况下的目标检测结果。在两种情况下,声源和水听器的深度都是50 m。水听器数量为2时(双水听器),两个水听器到声源的距离分别为2000 m和2500 m。水听器数量为42时(多水听器),前21个水听器到声源的距离分别为2000 m,2010 m…2200 m,后21个水听器到声源的距离分别为2500 m,2510 m…2700 m。水听器数量为2时,本文提出的方法等价于Hursky提出的双水听器互相干方法。在距离维度上,搜索范围是-2000 m到2000 m,每5 m设置一个搜索网格。在深度维度上,搜索的范围是0 m到500 m,每10 m设置一个搜索网格。
声源的波形和频谱如图3,为线性调频信号。通过双向耦合模式对海洋波导中的声传播进行建模,得到各个水听器的接收信号。信道解调采用单向耦合模式,并且运用互易性原理对计算进行加速。在接收信号中加入互不相关的白噪声用于模拟不同信噪比下的接收信号。在有目标和无目标两种场景下,分别进行了500次仿真实验。
图6是双水听器的检测量的分布,图7是多水听器的检测量的分布。在图6和图7中,信噪比均指距离为2000 m处的第一个水听器的接收信号的信噪比,其中离散点线表示有目标的检测量,实线表示无目标的检测量。从检测量上看,多水听器的检测量具有很好的可区分性,在信噪比为-21 dB时仍有一定的可区分性,在信噪比高于-15 dB时是完全可区分的,此时选择适当的阈值,可以达到0虚警率,100%检测率。相比于多水听器,双水听器的检测量的可区分性较低,只有在信噪比为3 dB时才有一定的可区分性,在其他更低的信噪比的情况下,无法检测目标。

图6 双水听器的检测量分布
Fig.6 The distribution of dual hydrophones
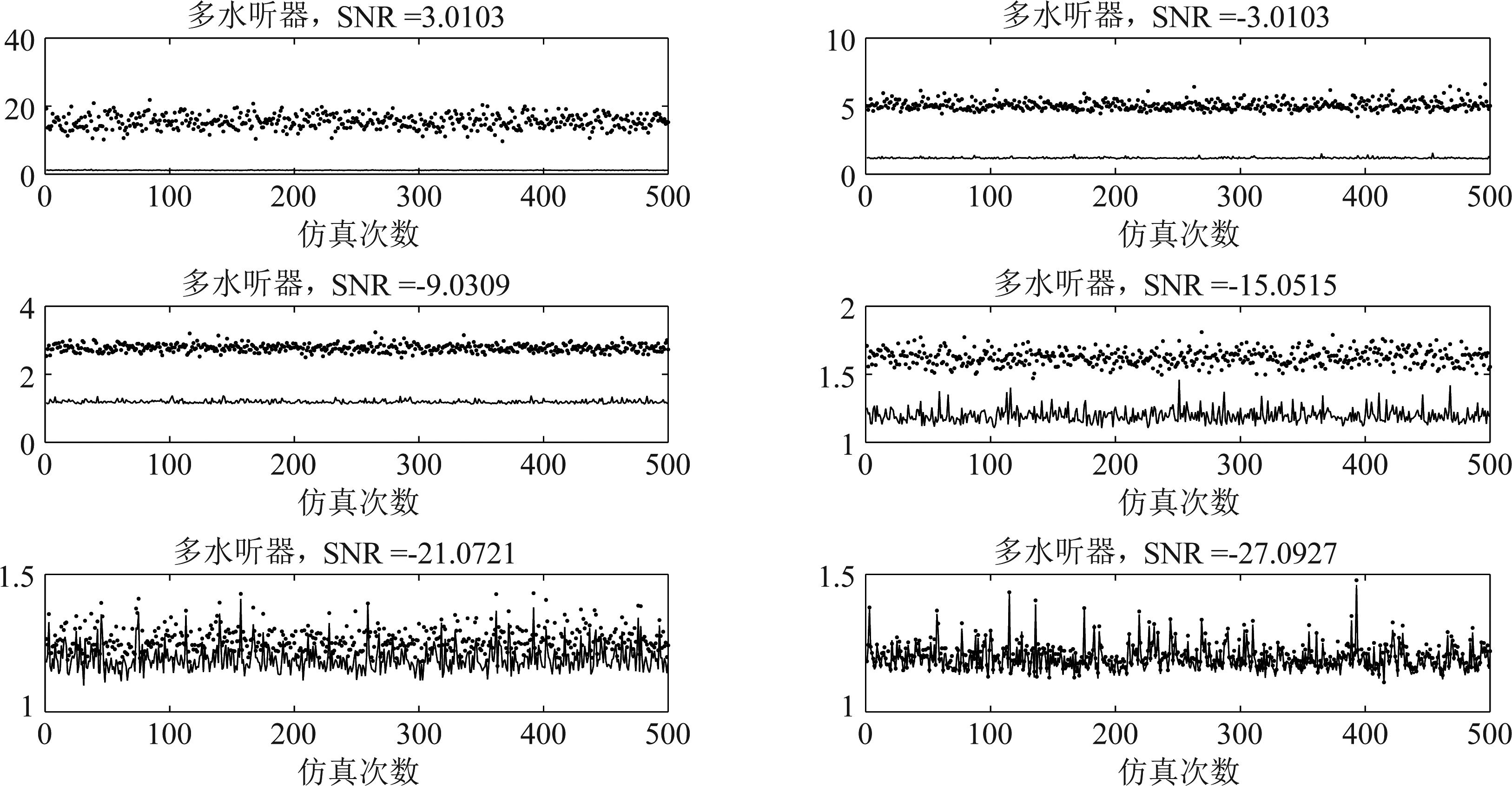
图7 多水听器的检测量分布
Fig.7 The distribution of mutiple hydrophones
图8是在不同的虚警率下的检测概率随信噪比的变化曲线。多水听器的处理方法在信噪比为-15 dB时检测概率为100%,在-21 dB时仍有一定的检测概率。双水听器处理方法只有在信噪比为3 dB时才具有一定的检测能力,此外检测概率都很低。
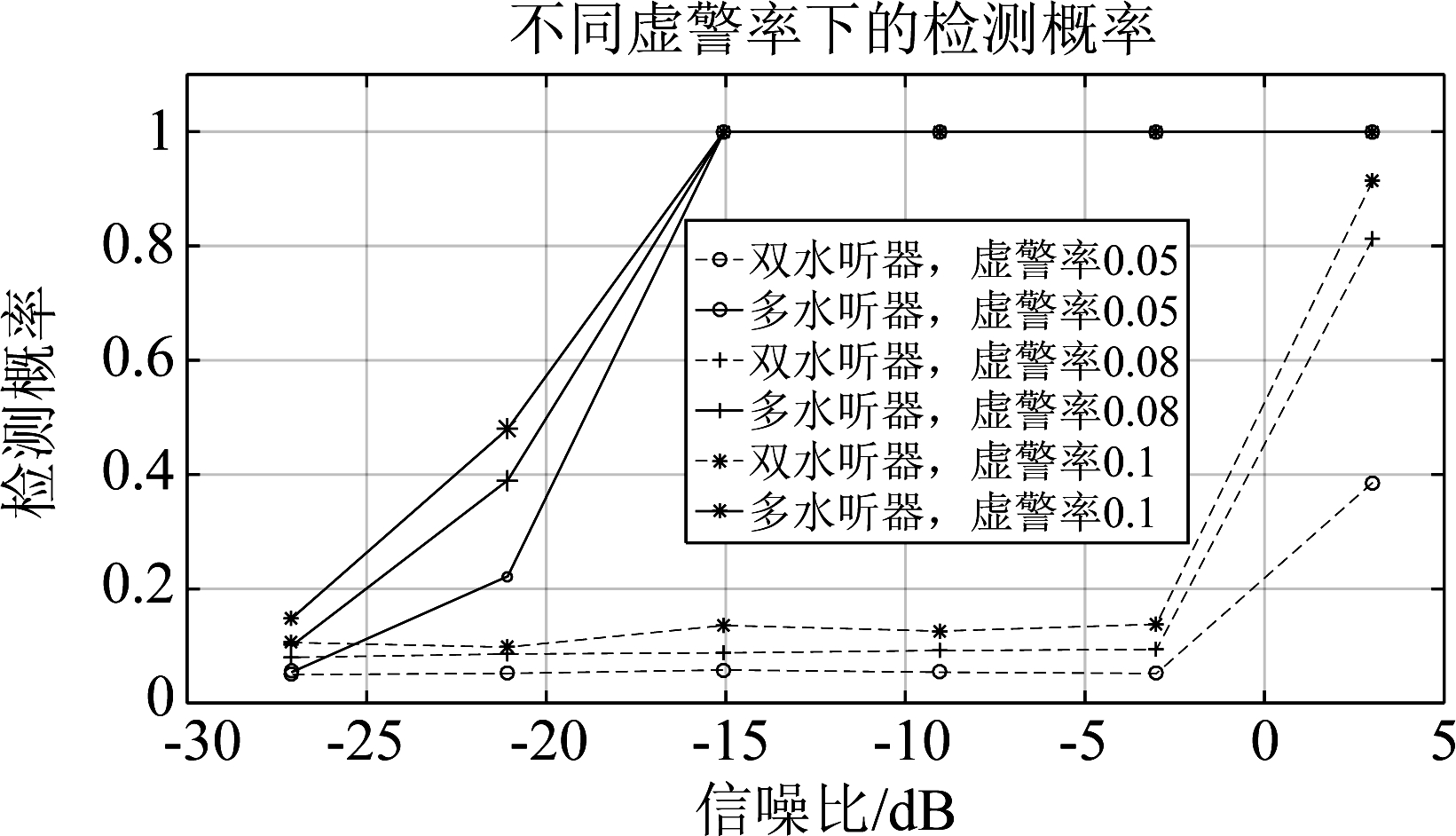
图8 检测概率曲线
Fig.8 Detection probability curve
图9是双水听器的检测率和虚警率随着阈值的变化,图10是多水听器的检测率和虚警率随着阈值的变化。检测率和虚警率两条曲线离得越远,检测性能对于阈值的选择更加鲁棒。在信噪比为-21 dB时,多水听器的两条曲线很接近了,这时检测器对阈值的选择是很敏感的,而在信噪比高于-15 dB时,两条曲线离得很远。对于双水听器的检测率和虚警率曲线,只有在信噪比为3 dB时离得较远。
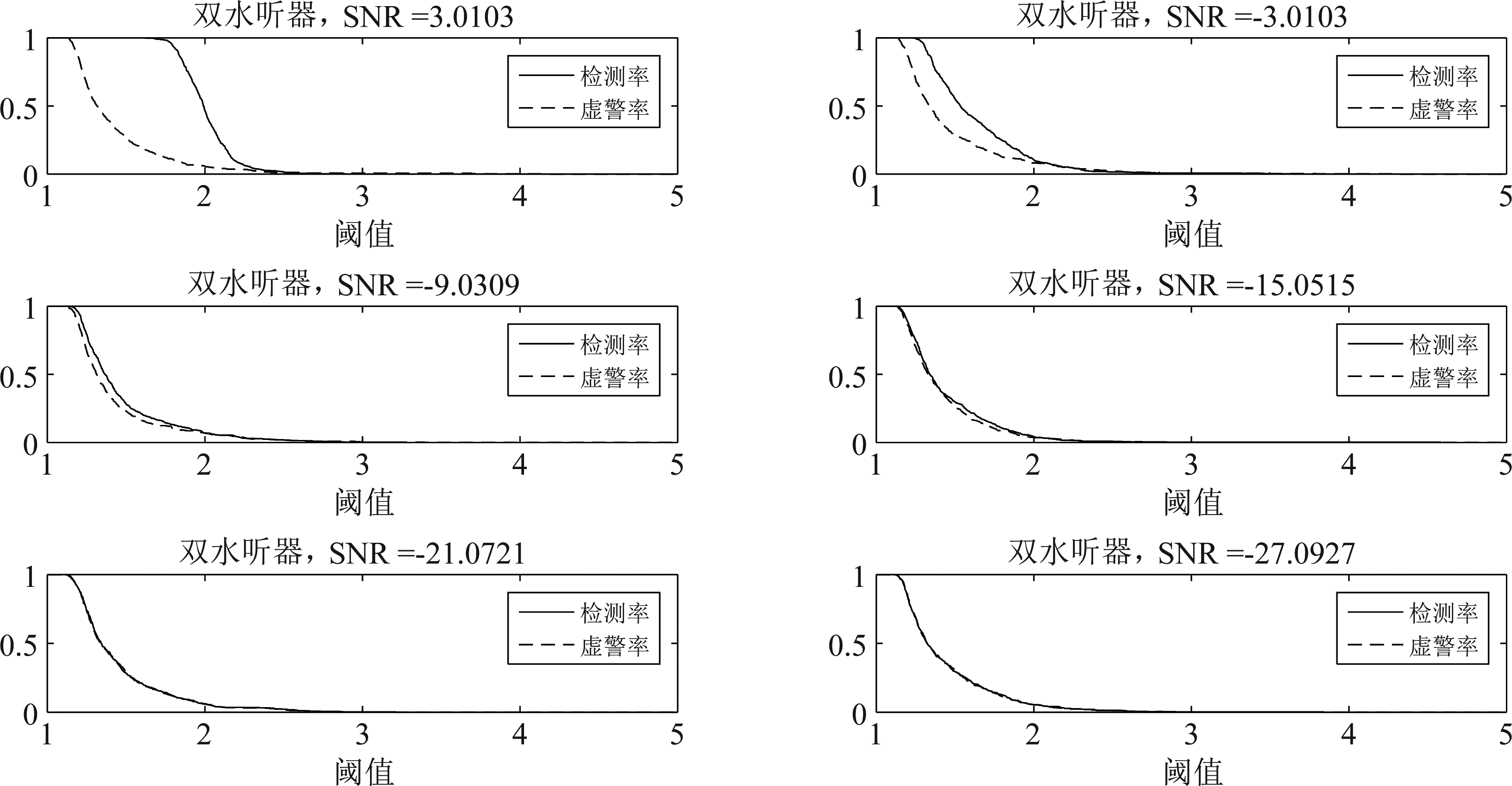
图9 双水听器的检测率和虚警率随着阈值的变化
Fig.9 Detection rate and false alarm rate of dual hydrophone varying with threshold
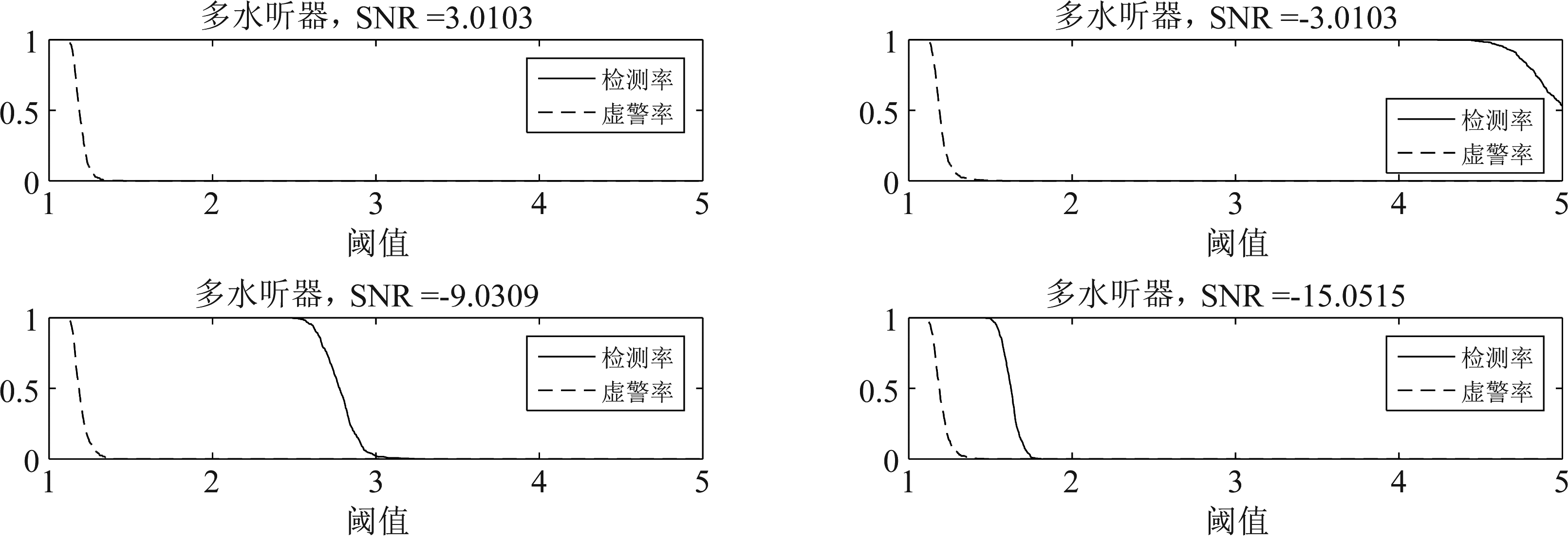

图10 多水听器的检测率和虚警率随着阈值的变化
Fig.10 Detection rate and false alarm rate of multiple hydrophone varying with threshold
图11是ROC曲线。从ROC曲线上看,随着噪声的增加,双水听器的ROC曲线变成了对角线,此时没有检测能力,而多水听器的ROC曲线在信噪比高于-15 dB时都是直角,在信噪比为-21 dB时仍然有一定的检测能力,在信噪比为-27 dB时其检测能力仍略优于双水听器的检测能力。
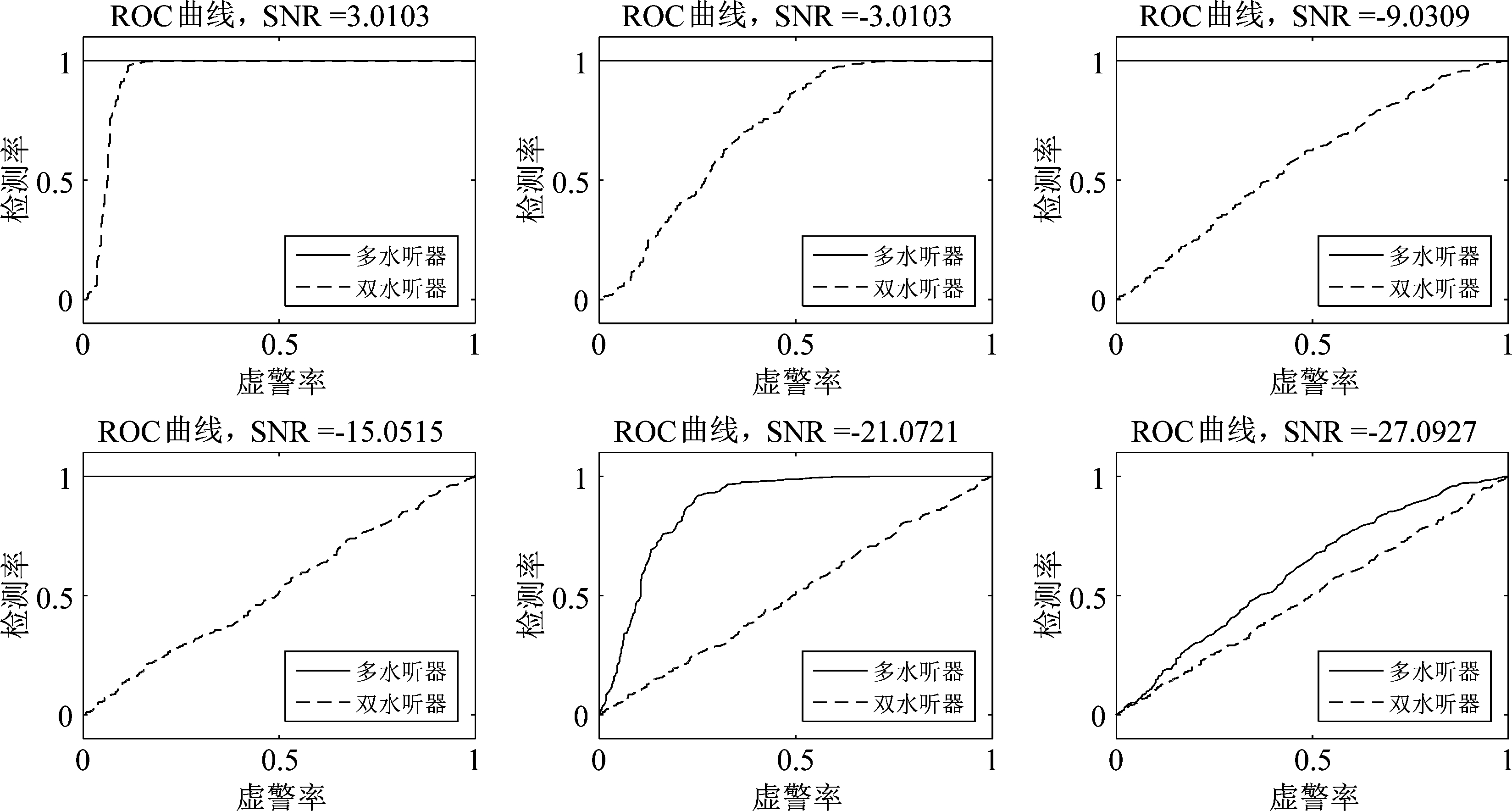
图11 ROC曲线
Fig.11 ROC curve
从检测量的分布,不同虚警率下的检测概率,检测率和虚警率随阈值的变化,以及ROC曲线上看,多水听器的检测性能均优于双水听器,增加水听器的数量可以有效地抑制噪声对检测结果的影响,对多个水听器的解调信号的求和操作实现了信号的相干叠加,噪声的非相干叠加,实现了信噪比的提升。
5 结论
本文提出的多水听器互相关方法,通过宽带滤波计算每个水听器的接收信号的解调信号,将多个解调信号相加从而提升了信噪比。此外,考虑到宽带滤波器系数的计算量很大,本文提出了运用水声模型的互易性原理的计算加速方案,极大地降低了滤波器系数的计算量。与双水听器相比,多水听器互相关方法在低信噪比情况下的检测性能更优。仿真实验验证了本文方法的优越性。
[1] 周胜增, 杜选民. 被动声呐宽带检测与窄带检测的比较研究[J]. 声学技术, 2017, 36(5): 329-330.
ZHOU Shengzeng, DU Xuanmin. Comparative research of wideband and narrowband for passive sonar[J].Technical acoustics, 2017, 36(5): 329-330.(in Chinese)
[2] 夏文杰, 蔡志明. 未知正弦信号的功率谱熵检测性能分析[J]. 信号处理, 2018, 34(12): 1499-1507.
XIA Wenjie, CAI Zhiming. Performance analysis of power spectrum entropy detection for unknown sinusoidal signals[J]. Journal of Signal Processing, 2018, 34(12): 1499-1507.(in Chinese)
[3] BONO M, SHAPO B, MCCARTY P, et al. Subband energy detection in passive array processing[C]. Adaptive Sensor Array Processing (ASAP) Workshop,2001: 25-30.
[4] 杨晨辉, 马远良, 杨益新. 峰值能量检测及其在被动声纳显示中的应用[J]. 应用声学, 2003, 22(5): 31-35.
YANG Chenhui, MA Yuanliang, YANG Yixin. Peak energy detection with application to passive sonar display[J]. Applied Acoustics, 2003, 22(5): 31-35.(in Chinese)
[5] 王聪, 刘厚雄, 孙超, 等. 基于频率着色的被动声纳宽带能量检测方法[J]. 哈尔滨工程大学学报, 2021, 42(4): 456- 462.
WANG Cong, LIU Houxiong, SUN Chao, et al. Passive sonar broadband energy detection using frequency coloring[J]. Journal of Harbin Engineering University, 2021, 42(4): 456- 462.(in Chinese)
[6] 李启虎. 数字式声纳设计原理[M]. 合肥: 安徽教育出版社, 2003: 210-214.
LI Qihu. Principles of Digital Sonar Design[M]. Hefei: Anhui Education Press, 2003: 210-214. (in Chinese)
[7] CLAY C S. Optimum time domain signal transmission and source location in a waveguide[J]. The Journal of the Acoustical Society of America, 1987, 81(3): 660- 664.
[8] BRIENZO R K, HODGKISS W S. Broadband matched-field processing[J]. The Journal of the Acoustical Society of America, 1993, 94(5): 2821-2831.
[9] HODGKISS W S, BRIENZO R K. Broadband source detection and range/depth localization via full-wavefield (matched field) processing[J]. International Conference on Acoustics, Speech, and Signal Processing, 1990, 5:2743- 2746.
[10] HURSKY P, PORTER M B, SIDERIUS M. High frequency (8-16kHz) model-based source localization[J]. The Journal of the Acoustical Society of America, 2004, 115(6): 3021-3032.
[11] WESTWOOD E K. Broadband matched-field source localization[J]. The Journal of the Acoustical Society of America, 1992, 91(5): 2777-2789.
[12] MICHALOPOULOU Z H. Robust multi-tonal matched-field inversion: a coherent approach[J]. The Journal of the Acoustical Society of America, 1998, 104(1): 163-170.
[13] 孟华, 曹占启. 被动声纳宽带相干处理技术研究[J]. 舰船电子工程, 2020, 40(4): 149-153.
MENG Hua, CAO Zhanqi. Coherent broadband passive sonar signal processing[J]. Ship Electronic Engineering, 2020, 40(4): 149-153.(in Chinese)
[14] 赵博. 并行计算技术在匹配场声源定位中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
ZHAO Bo. Application of parallel computation technology in matched field source location[D]. Harbin: Harbin Engineering University, 2012.(in Chinese)
[15] 周悦. 信息准则理论下的匹配场声源定位[D]. 杭州: 浙江大学, 2015.
ZHOU Yue. Matched-field acoustic source localization under information theory criteria[D]. Hangzhou: Zhejiang University, 2015.(in Chinese)
[16] 韦先声. 基于矢量水听器阵的匹配场声源定位研究[D]. 长沙: 国防科技大学, 2014.
WEI Xiansheng. Research on matched-field source localization based on the vector array[D]. Changsha: National University of Defense Technology, 2014.(in Chinese)
[17] ETTER P. Underwater acoustic modelling and simulation, third edition[EB/OL]. 2003. https:∥www.researchgate.net/publication/322931166_Underwater_Acoustic_Modelling_and_Simulation_Third_Edition.
[18] JENSEN F B, FERLA C M. Numerical solutions of range-dependent benchmark problems in ocean acoustics[J]. The Journal of the Acoustical Society of America, 1990, 87(4): 1499-1510.
[19] JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics, second edition[EB/OL].
2011.https:∥www.researchgate.net/publication/321525193_Computational_Ocean_Acoustics.



