1 引言
随着雷达干扰技术的发展,当前雷达面临着越来越多的干扰,这极大的影响了雷达的正常工作。雷达干扰按照入射角度可分为主瓣干扰与副瓣干扰,副瓣干扰通过副瓣隐匿、自适应波束形成(Adaptive Digitial Beam Forming, ADBF)等方法可以很好的抑制;而主瓣抗干扰的抑制则相对困难,因此主瓣抗干扰问题也成为雷达领域研究的热门问题。文献[1]利用辅助通道作为差波束,实现了和差主瓣干扰相消(Mainlobe Cancellation, MLC),但这种算法无法同时对抗主、副瓣干扰;文献[2]将ADBF和MLC进行级联,实现了主副瓣干扰的分布抑制,但文献[1-2]均未涉及干扰抑制后的目标波达角(Direction of Arrival, DOA)的估计; YANG[3]提出了一种特征投影矩阵预处理(Eigenprojection Matrix Preprocessing, EMP)与协方差矩阵重建的方法,在抑制主瓣干扰的同时对副瓣干扰进行了抑制,并保证其波束指向不偏移,提高了抗干扰能力,但这种方法只能对抗一个主瓣干扰,文献[4]在此基础上进行了改进,能同时对抗多个主瓣干扰,但无法估计目标DOA。一部分学者研究通过多输入多输出雷达系统对抗主瓣干扰,文献[5]通过选择合适的频率步进,使欺骗式假目标位于波束形成方向图的零点,从而能够有效对抗主瓣欺骗干扰,文献[6]通过对雷达回波脉压后的一维距离像作时频分析,成功实现了对主瓣间歇采样转发干扰的抑制,但以上方法均只能对抗欺骗式主瓣干扰。
还有一部分学者将盲分离技术引入到主瓣干扰对抗中[7-9],文献[7]提出了基于特征矩阵近似联合对角化(Joint Approximate Diagonalization of Eigenmatrices,JADE)的抗主瓣干扰算法,文献[8]提出了基于Fast Independent Component Analysis(FastICA)算法的雷达抗主瓣干扰技术,相比于文献[7]提高了运算速度,但该算法抗噪能力较弱,且无法估计目标DOA。脉压输出SINR(Signal to Interference plus Noise Ratio)和目标DOA估计精度通常被作为衡量抗干扰效果的重要指标。为了在抑制干扰的同时对目标DOA进行估计,文献[9]利用四阶累积量进行盲分离,同时进行了DOA估计,但这种方法随着快拍数的增加,运算时间快速增长,难以满足实时性要求。文献[10]结合了分维算法和稀疏贝叶斯进行抗干扰,但这种方法要求阵列为面阵,不适用于线性阵列。针对线阵的抗干扰与测向,文献[11]利用阻塞矩阵预处理(Block Matrix Preprocessing, BMP),构建了基于正交匹配追踪(Orthogonal Matching Pursuit, OMP)的稀疏恢复,实现了目标检测和DOA估计,但这种方法要求各阵元具有较高的信噪比,信噪比较低时效果较差。
文献[12-13]利用联合盲源分离技术(Joint Blind Source Separation, JBSS)实现了分布式阵列的联合抗干扰,但该方法计算效率较低;文献[14]联合JADE与稀疏贝叶斯抑制了主瓣干扰,但该方法在低信噪比条件下性能较差。
不论是脉压输出的SINR,还是对目标DOA估计的精度,都受接收信号信噪比的影响,信噪比越高,抗干扰效果越好。但在实际场景中,单个阵列接收信号的信噪比往往较低,而当前各种抗干扰方法普遍要求较高的信噪比,当信噪比较低时抗干扰效果会严重退化甚至失效。因此,为了进一步提高抗干扰性能,有必要研究能够适用于更低信噪比情况的抗干扰方法。本文基于子阵思想,提出了一种适用于低信噪比环境的抗干扰方法,新方法能抑制主瓣干扰与副瓣干扰,对目标回波信号进行检测,并能估计回波信号DOA,具有良好的抗干扰性能。
新方法主要有两个创新点:1.将全阵列划分为多个子阵列,通过子阵级ADBF提高了信噪比,同时保留了目标回波信号入射导向矢量信息,结合后续的稀疏恢复方法对目标信号进行了精确提取,改善了抗干扰效果,特别是在低信噪比情况下,比当前其他算法抗干扰效果更好。2.在通过子阵级ADBF提高信噪比的基础上,利用多测量向量降维提升法[15](Reduce Multiple measurement vectors and Boost, ReMBo)和交叉方向乘子法(Alternating Direction Method of Multiplier, ADMM)进行快速的稀疏恢复,比起其他算法,具有更高的计算效率,特别是在快拍数较大时,满足雷达抗干扰实时性的要求;同时对ReMBo算法进行了改进,提高了抗噪声能力,使新方法的性能进一步提高。本文组织结构为:第1节为引言,第2节介绍信号模型,第3节介绍本文算法原理,第4节为仿真验证,最后是总结。
2 信号模型
如图1所示,考虑N元均匀线性阵列,阵元间距d=λ/2为半波长,其波束指向为θz。假设多个主瓣、副瓣干扰信号与一个目标回波信号共同作用于该阵列。其中主瓣干扰数量为p,旁瓣干扰的数量为q,且所有信号相互独立。按照如图1所示的方式,将整个阵列划分为L个子阵,且每个子阵列有Ns=N-L+1个阵元,具体的,将第1个阵元至第N-L+1个阵元作为第1个子阵,将第2个阵元至第N-L+2个阵元作为第2个子阵,以此类推。假设Ns>p+q+1,考虑K个快拍,则整个阵列接收到的信号可表示为:
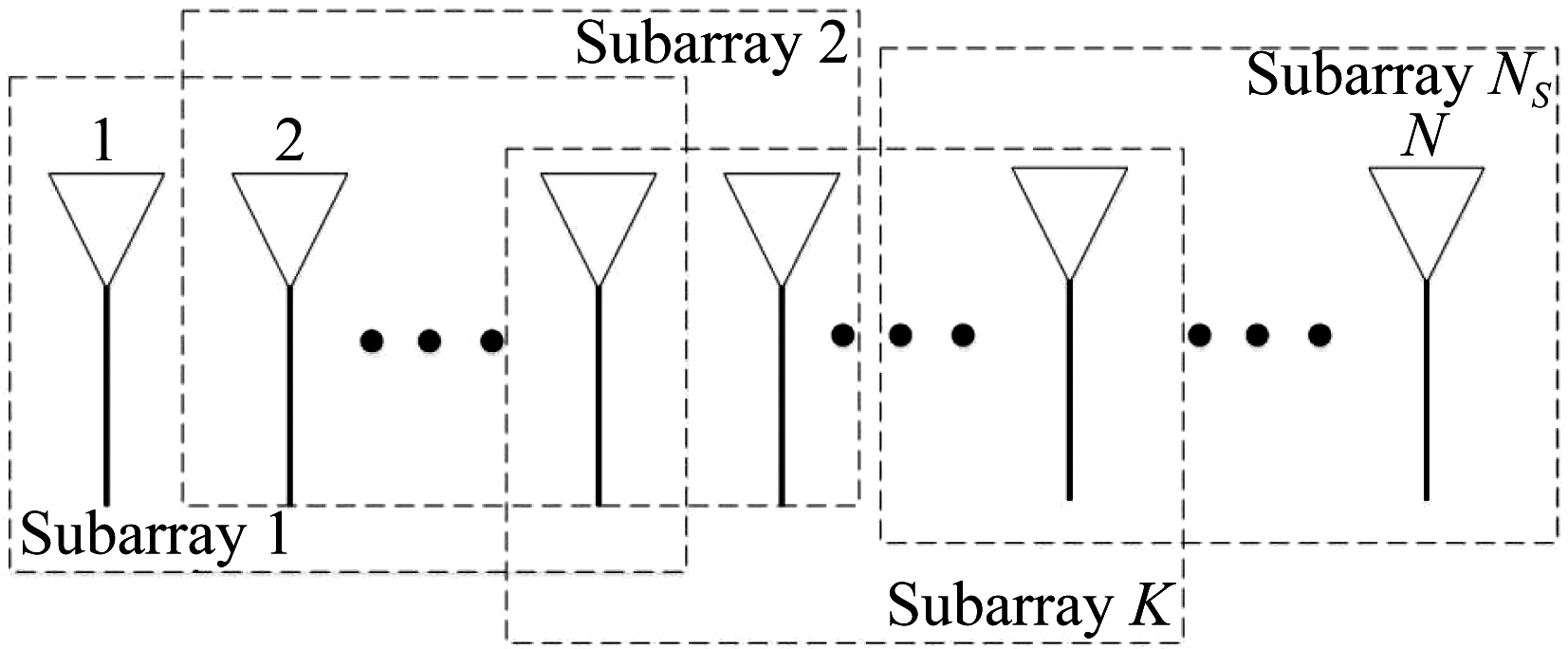
图1 子阵划分示意图
Fig.1 Diagram of subarray division
X(n)=AS(n)+v(n)=a(θ0)s0(n)+ 
(1)
其中,S(n)=[s0(n),s1(n),s2(n),…,sp+q(n)]T包含各信源的时域信息,第1个信源为目标回波,第2个至第p+1个信源为主瓣干扰信号,后q个信源为副瓣干扰信号,v(n)为噪声信号。A=[a(θ0),a(θ1),…,a(θp+q)]∈CN×(1+p+q)是阵列混合矩阵,包含各个信源的入射角度信息,其中:
a(θi)=[1,exp(-jβi),exp(-j 2βi),…, exp(-j(N-1)βi)]T,βi=2πdsin(θi)/λ
(2)
第k个子阵接收到的信号为:
Xk(n)=AkS(n)+vk(n)=ak(θ0)s0(n)+ 
(3)
其中,Ak=[ak(θ0),ak(θ1),ak(θ2),…,ak(θp+q)]∈CN×(1+p+q)是第k个子阵列的混合矩阵。ak(θm)∈CNS×1表示第m+1个信源对第k个子阵的入射导向矢量,其中:
ak(θi)=[exp(-j(k-1)βi),exp(-jkβi),…, exp(-j(k+N-L)βi)]T=exp(-j(k-1)βi)[1, exp(-jβi),…,exp(-j(N-L-1)βi)]T= exp(-j(k-1)βi)a1(θi)
(4)
其中,a1(θm)=[1,exp(-jβm),…,exp(-j(N-L-1)βm)]T∈CNs×K为第m+1个信源对第1个子阵的入射导向矢量。联立式(3)～(4)可得:
Xk(n)=exp(-j(k-1)β0)ak(θ0)s0(n)+ 
(5)
由式(5)可知,不同子阵接收到来自同一信号源的信号数据仅相差了一个固定的相位。整个阵列接收信号的协方差矩阵为:
RX=E[XXH]=P0a(θ0)a(θ0)H+ 
(6)
其中,P0为目标回波信号的能量,Pj为第j个干扰信号的能量,
为噪声功率。一般采用观测样本数据的协方差矩阵代替接收信号的协方差矩阵,则整个阵列与第1子阵接收信号的协方差矩阵可分别表示为:
(7)
(8)
3 算法原理
3.1 通过ADBF抑制第1子阵列回波数据中的副瓣干扰
首先利用ADBF抑制第1子阵中的副瓣干扰信号。对其接收信号的协方差矩阵进行特征分解可得:
(9)
其中,λ1≥λ2≥…λp+q≥λp+q+1≥…≥λNs,λNs=λmin,特征值最大的p+q+1个特征值对应的特征向量u1,u2,…,up+q+1张成信号子空间Us,对角矩阵Λs=diag(λ1,λ2,…,λp+q+1),其余的特征向量up+q+2,up+q+3,…,uNS张成噪声子空间Us,对角矩阵Λs=diag(λp+q+2,λp+q+3,…,λNs)。
3.1.1 寻找主瓣干扰对应的特征矩阵与特征向量
由文献[16]可知,如果将主瓣干扰与回波信号(统称为主瓣内信号)的特征值降低到噪声水平,使用ADBF技术抑制副瓣干扰就不会在主瓣方向上形成零陷,也不会造成主瓣偏移或失真。因此为了保证ADBF的过程不对后续的主瓣干扰抑制产生影响,我们需要进行协方差矩阵重构。要重构协方差矩阵,首先需要找到主瓣内信号对应的特征向量,本文利用向量相关系数寻找其对应的特征向量。根据相关系数的定义,可得各特征向量uj与波束指向导向矢量a1(θz)的相关系数为:
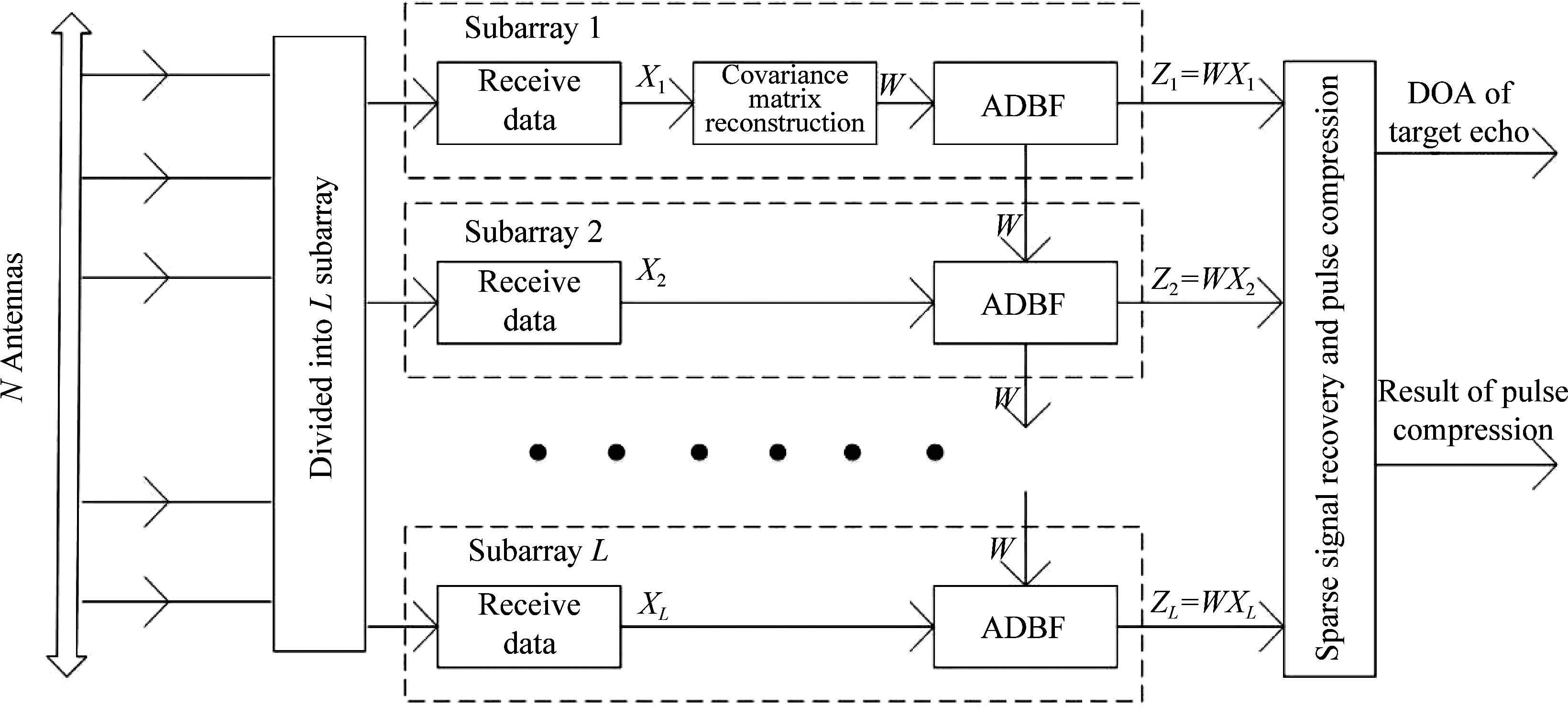
图2 算法流程图
Fig.2 Algorithm flow chart
(10)
其中uj,(1≤j≤p+q+1)对应的信号源的来波方向。显然信号的来波方向越接近波束指向方向,ρ(uj,a1(θz))越大。另一方面,当阵元数N与波长已知时,可得主瓣宽度为[17]:
(11)
由式(10)～(11)可得:若uj对应的主瓣内信号,则:
ρ(uj,a1(θz))≥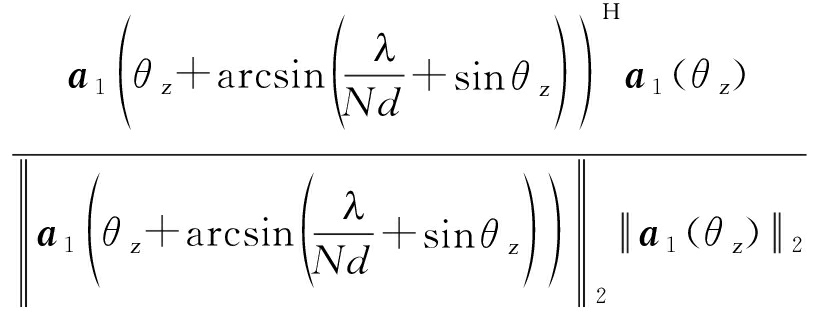 
(12)
将式(12)作为判断条件,判断uj是否为主瓣内信号对应的特征向量,可得主瓣内信号对应的所有特征向量,并得到其张成的子空间与其对应的特征值,记为UM,λM:
(13)
其中,uMj表示第j个主瓣内信号对应的特征向量。而信号子空间中存在的其他特征值与特征向量为副瓣干扰信号对应的特征值与特征向量,记为:USS,λSS。
3.1.2 ADBF抑制副瓣干扰
为了重构协方差矩阵,用噪声特征值的平均值代替主瓣内信号的特征值与噪声的每一个特征值:
(14)
其中,
分别表示重构后主瓣内信号对应的第i个特征值和噪声信号对应的第j个特征值。协方差矩阵可以重构为:
(15)
其中,
为重构后的主瓣内信号特征值,
Un表示协方差矩阵重构后噪声信号对应的特征矩阵与特征向量。基于重构的协方差矩阵,可得ADBF的自适应权向量:
(16)
将w作用于第1子阵的接收信号,会在所有副瓣方向形成零陷,同时保证波束指向不改变,即当p+1≤j≤p+q时:
wHa1(θj)≈0
(17)
经过ADBF后的输出z1(n):
z1(n)=wHX1=wH(a1(θ0)s0(n)+ 
(18)
其中,
为残余的噪声信号。由于阵列雷达的主瓣波束通常较窄,主瓣干扰信号与目标回波信号的来波方向接近于波束指向方向,即:θz≈θ0,θz≈θi(1<i<p)。联立式(16)(18),有:
(19)
可以发现,第1子阵接收信号中的副瓣干扰信号已经被抑制,只剩下主瓣干扰信号与目标回波信号。由式(16)可得,自适应权向量的模值为:
(20)
由于噪声信号为高斯白噪声,所以经过ADBF后,噪声信号的整体幅值降低为原来的
倍,残余的噪声信号
可以被视为能量降低为原来
倍的高斯白噪声。由式(19)可知,第1子阵中的主瓣干扰信号和目标回波信号近似保持不变。因此,通过子阵级ADBF,整体信噪比提高了10log10(NS)dB。
3.2 抑制其余子阵列回波信号中的副瓣干扰信号
首先证明一个引理。引理1:用于抑制第1子阵的接收数据X1(n)中副瓣干扰信号的自适应权向量w,同样适用于抑制其他子阵接收数据中的副瓣干扰信号,且同样能够提高整体信噪比。证明如下:
将w作用于第k个子阵的接收数据Xk(n),由式(5)可得输出为:
zk(n)=wHXk(n)=wH(exp(-j(k-1)β0)a1(θ0)s0(n)+ 
exp(-j(k-1)β0)wHa1(θ0)s0(n)+ 
(21)
由式(15)、(19)可知:
所以有:
zk(n)≈exp(-j(k-1)β0)s0(n)+ 
(22)
由于噪声信号vk(n)也为高斯白噪声信号,由式(20)可知,第k个子阵中的噪声信号的整体幅值也降低为原来的
倍,而主瓣干扰信号与目标回波信号近似保持不变,因此整体信噪比提高了10log10(NS)dB,这与第1子阵所达到的效果一致,引理1得证。
根据引理1,将w作用于所有子阵接收数据,即可抑制所有子阵中的副瓣干扰信号。利用所有子阵ADBF后的输出数据构建新的阵列数据Z(n):
Z(n)=[z1(n),z2(n),…,zL(n)]T∈CL×K
(23)
联立式(22)、(23)可得:
Z(n)≈[1,exp(-jβ0),…,exp(-j(L-1)β0)]Ts0(n)+ 
(24)
其中
表示各子阵输出中残留的噪声信号。
3.3 子阵分级处理方法的优势
由式(24)可知,各信号的入射导向矢量信息在Z(n)中被保留。相比于全阵列接收数据X(n),Z(n)可以看做阵元数为L,且噪声能量降低的阵列接收数据。其中残留的噪声信号整体幅值降低为原来的倍,而主瓣干扰信号与目标回波信号的幅值近似保持不变。因此Z(n)与X(n)相比,信噪比提高了10log10(NS)dB,并且抑制了副瓣干扰。
但同时阵元数由N降低为L,根据文献[18],通常情况下,阵元数由N降低为L带来的影响,与整体信噪比降低10log10(N/L)dB带来的影响相当;不过当L选择合适时,这种阵元数降低带来的影响远小于信噪比提高带来的收益,整体上会获得10log10(NSL/N)dB信噪比的收益。为了达到最好的输出性能,我们选择L的原则,通常是使信噪比收益10log10(NSL/N)dB最大,即选择
此时信噪比收益最大。
虽然全阵处理能够得到更高的信噪比增益,但是全阵处理会损失信号的入射导向矢量信息,而本文所提的子阵分级处理方法不仅能够提高信噪比,还保留了主瓣内信号的入射导向矢量信息,这为后续的处理奠定了基础。通过后续的处理,我们能够对目标回波信号进行精确提取,进一步提高信噪比,从而获得比全阵处理更好的抗干扰性能,这也正是子阵分级处理方法的优势。
3.4 基于稀疏恢复抑制主瓣干扰并估计目标DOA
稀疏恢复算法具有良好的DOA估计能力,但其在信噪比低下时性能恶化,因此文献[10]的方法在低信噪比时效果会急剧恶化,但在3.3中,本文利用子阵级ADBF提高了信噪比,在信噪比提高后,再考虑使用稀疏恢复的方法对DOA进行估计,其效果会得到很大的提高。由此,在3.3的基础上,本文考虑构建稀疏表示,以固定步长将主瓣角度范围内的所有角度离散网格化,并将其中每一个离散的网格点作为原子构建角度原子库,假设原子库总数为G,原子库
其中
为第i个原子,βYi=2πdsin(θYi)/λ。令H为稀疏矩阵,可构建如下稀疏表示:
s.t.||Z(n)-ΦH
≤ξ
(25)
由于0范数的求解问题为NP-Hard问题,可将其松弛为1范数求解,并利用正则化因子λ将其转化为如下形式:
(26)
正则化因子λ用来平衡误差量与稀疏度,若λ太小,稀疏性无法得到保证;若λ太大,得到的解过于稀疏,波形失真大,这两种情况都会导致输出性能变差。实际中可采用帕累托曲线法或文献[19]中提出的自适应连续格式来确定参数λ。问题式(26)为一个多测量向量问题(Multiple Measurement Vectors, MMV),在快拍数较多时直接计算效率很低,为了提高运算速度,本文采用如下方法进行优化计算。
3.4.1 降维、建模
首先进行降维处理,对矩阵Z(n)进行特征分解,Z(n)=UΓVT,定义矩阵VS为矩阵V的前p+q+1列构成的子矩阵,其次,定义HS=HVS,ZS=ZVS,问题式(26)可降维为:
(27)
为了提高优化计算效率,需将其转化单测量优化问题(Single Measurement Vectors, SMV)。根据文献[18]所提出的ReMBo算法的原理,基于随机投影向量,定义一个长度为p+q+1的随机向量r,可将问题式(27)转化为单测量向量问题。但由文献[18]可知,由于r的选择是完全随机的,使的ReMBo算法处理含噪声问题时,行支撑很难得到保持,效果不理想。为了更好的解决含噪声问题,本文将r看做变量,并约束其模值为1,对这个变量进行不断的迭代优化。这避免了由r的随机性带来的,在含噪声情况下,从MMV到SMV的转换使得行支撑很难得到保持的问题,从而提高了算法的抗噪能力,使得算法在低信噪比下具有更好的性能。此外,在稀疏恢复前,本文还利用子阵级ADBF提高了信噪比,这两种改进措施使得本文所提的算法在低信噪比条件下比传统方法性能更好。由此可将问题式(27)转化为如下形式:
s.t. ||r||1=1
(28)
以上问题含有关于矩阵HS的极小化项,因此求解复杂度很高。而实际中我们不需要得到变量HS的最优解,只需要得到最优解时
的行支撑即可对DOA进行估计。因此为了提高计算效率,可以将问题式(28)转化为如下等价形式:
s.t. ||r||1=1
(29)
运用假设法可以证明问题式(28)和问题式(29)是等价的,且问题式(28)中的最优解d*与问题式(29)中的最优解具有相同的行支撑,因此可以通过求解d*对DOA进行估计。上述问题中的d和r是无关的、可分离的。对于这种可分离的多目标带约束的优化问题,为了提高运算效率,可以使用ADMM算法进行快速求解。
3.4.2 使用ADMM算法进行稀疏恢复
定义lc是关于集合C={e:||e||2=1}的示性函数,即:
问题式(29)可以写成:
s.t. e=r
(30)
根据ADMM算法的原理,可知其增广拉格朗日函数为:
Qμ(d,r,e,b)=||ZSr-Φd
+λ||d||1+ 
(31)
其中,b∈Rp+q+1是拉格朗日乘子,μ>0是罚函数。上述问题求解过程可以分为以下四个子问题:
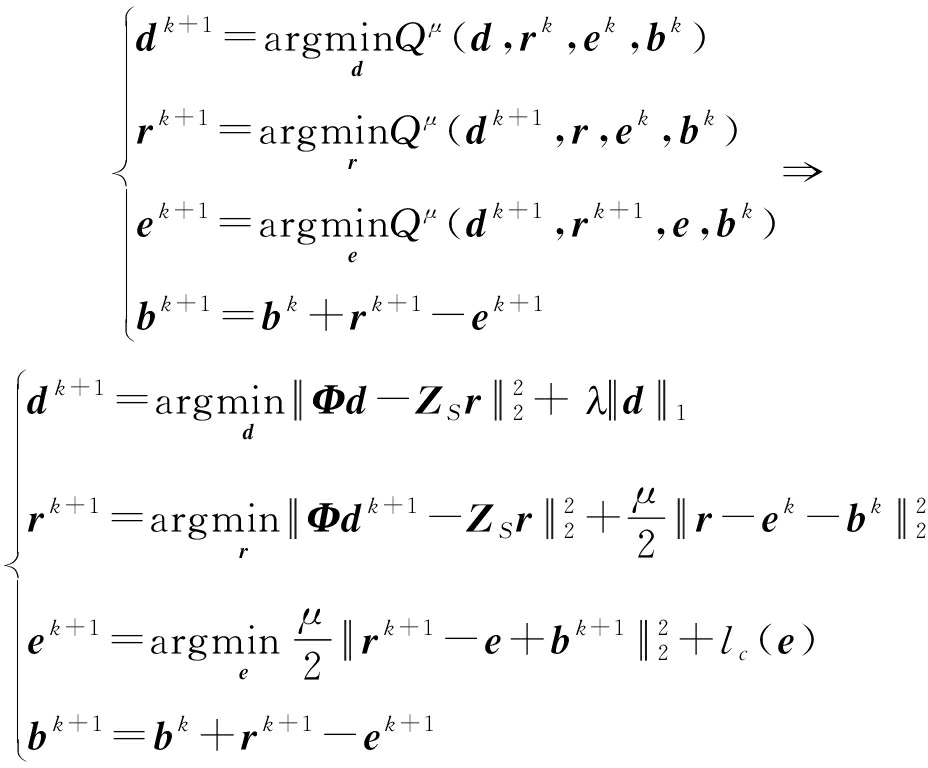
(32)
子问题1是一个l1正则化问题,可以使用基于近似可分离的稀疏恢复算法(Sparse Reconstruction by Separable Approximation, SpaRSA)快速求解。子问题4通过式(32)可直接求得。而子问题2和子问题3分别有如下闭式解:
(33)
(34)
由文献[20]可知,由于子问题2、3、4都有闭式解,因此只要子问题1的求解算法是全局收敛的,则本文所提的算法是全局收敛的。本文采用SpaRSA算法求解子问题1,而SpaRSA算法本身就是全局收敛的,因此本文所提的算法是收敛的。依次迭代求解上述4个子问题,直至收敛,即可得到稀疏向量d的解,选择d中绝对值最大的p+1个元素对应p+1个原子构建矩阵AM,即为主瓣干扰信号与目标回波信号混合矩阵的估计:
(35)
其中,
为稀疏向量d中绝对值第i大的元素对应的原子库Φ中的原子。
3.4.3 利用最小二乘法恢复信号波形并识别目标回波信号
为了得到主瓣干扰信号与目标回波信号的波形估计,我们构建如下优化问题:
(36)
其中S为主瓣干扰信号与目标回波信号的时域波形估计。问题式(36)为最小二乘问题,有闭式解:
(37)
至此,我们恢复了主瓣干扰信号与目标回波信号的波形,对S*中每一个信号进行脉冲压缩,即可辨别目标回波信号与主瓣干扰信号,同时利用稀疏向量还可以得到对应信号的DOA估计。
4 仿真结果
仿真实验时阵列采用20元等距均匀线阵,将其按照图1所示的方式划分为10个子阵列,阵元间距为半波长,主波束指向为10°。根据文献[19]的方法,设定参数λ=1,罚函数μ=0.2,角度网格化的步长为0.01°。雷达发射信号为线性调频信号,发射频率为1 MHz,脉宽100 μs,采样频率为2 MHz,快拍数为1000。假设电磁环境中存在一个静止目标,2个主瓣压制干扰,2个副瓣干扰,目标信噪比为SNR=5 dB,位于(10°,521-th),前者为角度,后者为距离门。主瓣干扰的干噪比与入射角度分别为10 dB、20 dB和8.75°、11.4°。副瓣干扰干噪比均为30 dB,分别位于-18.75°、31.4°方向。
图3给出了阵列接收到的信号直接进行脉冲压缩的结果,可以看见由于干扰的存在,无峰值存在,无法辨别是否含有目标回波信号。图4给出了经过本文算法处理后的各分离信号的脉压输出结果,可以看到,信号1和信号3的脉压结果无峰,为干扰信号;信号2的脉压结果显示有一个峰,为目标回波信号。通过数据游标可知其峰位于距离门521的位置,与仿真设计基本一致。证明本文方法是有效的。
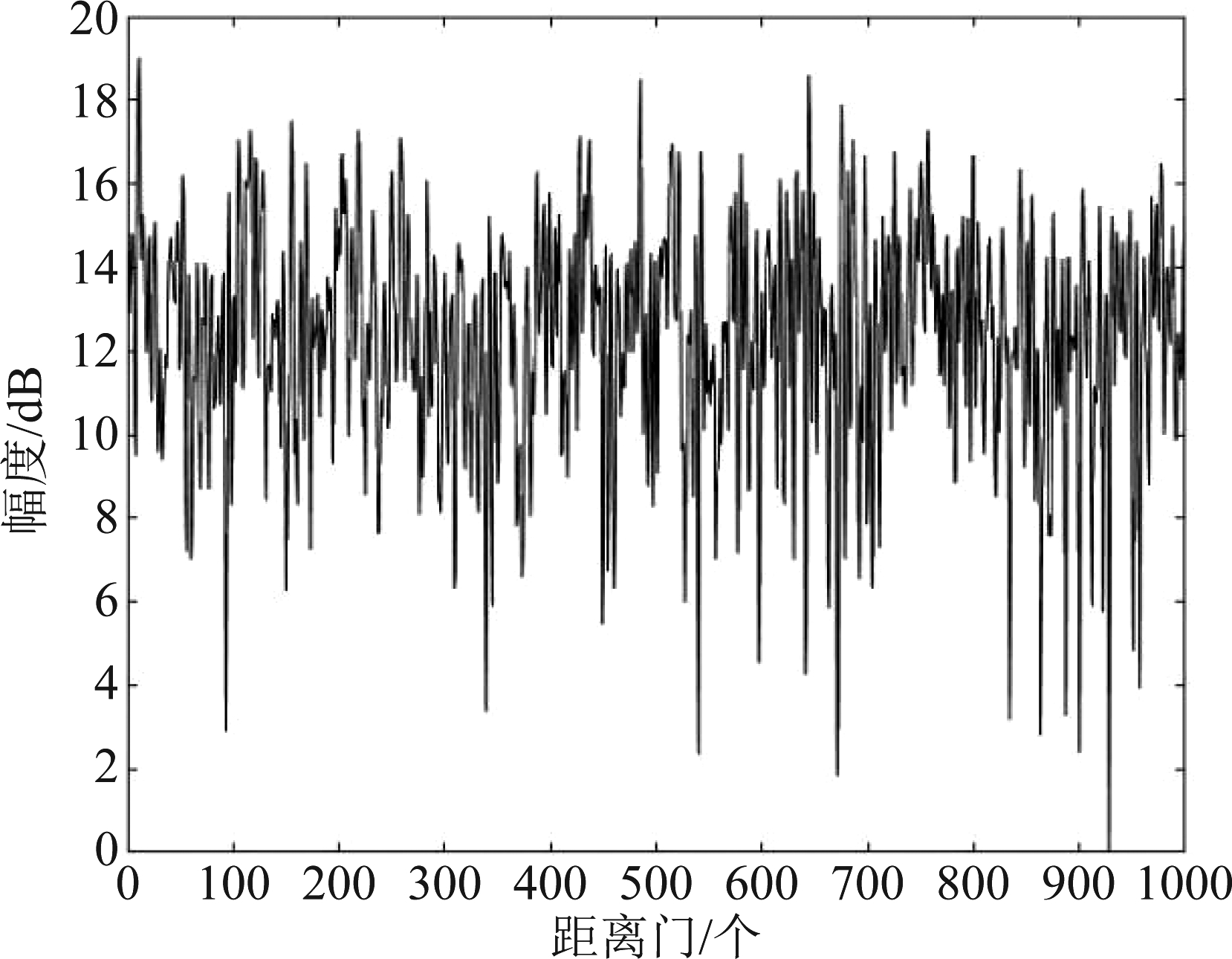
图3 直接脉压结果图
Fig.3 Results of direct pulse compression
图4 本文方法处理后的各信号的脉压输出结果
Fig.4 Pulse compression output results by the new method
为了检验本文算法的性能,将本文方法与当前流行的其他方法进行比较,主要检验输出SINR、DOA估计误差、算法的运算速度三个方面。
图5给出了在信噪比变化的情况下,本文方法与文献[8]、文献[9]、文献[11]中的方法的输出SINR和输出SINR上界的对比,可以发现,由于采用了子阵分级处理方式改善了信噪比环境,本文方法整体上具有更高的输出信噪比,比其他方法更加接近输出SINR上界,能够更好的抑制干扰,检测目标回波信号。图6给出了在设定环境下,本文方法与文献[9]、文献[11]的方法进行500次蒙卡罗特实验,得到的目标回波DOA的估计。可以看到,本文方法的目标DOA估计误差很小,且整体误差小于文献[9]和文献[11]的方法,因此本方法具有良好的DOA估计性能。
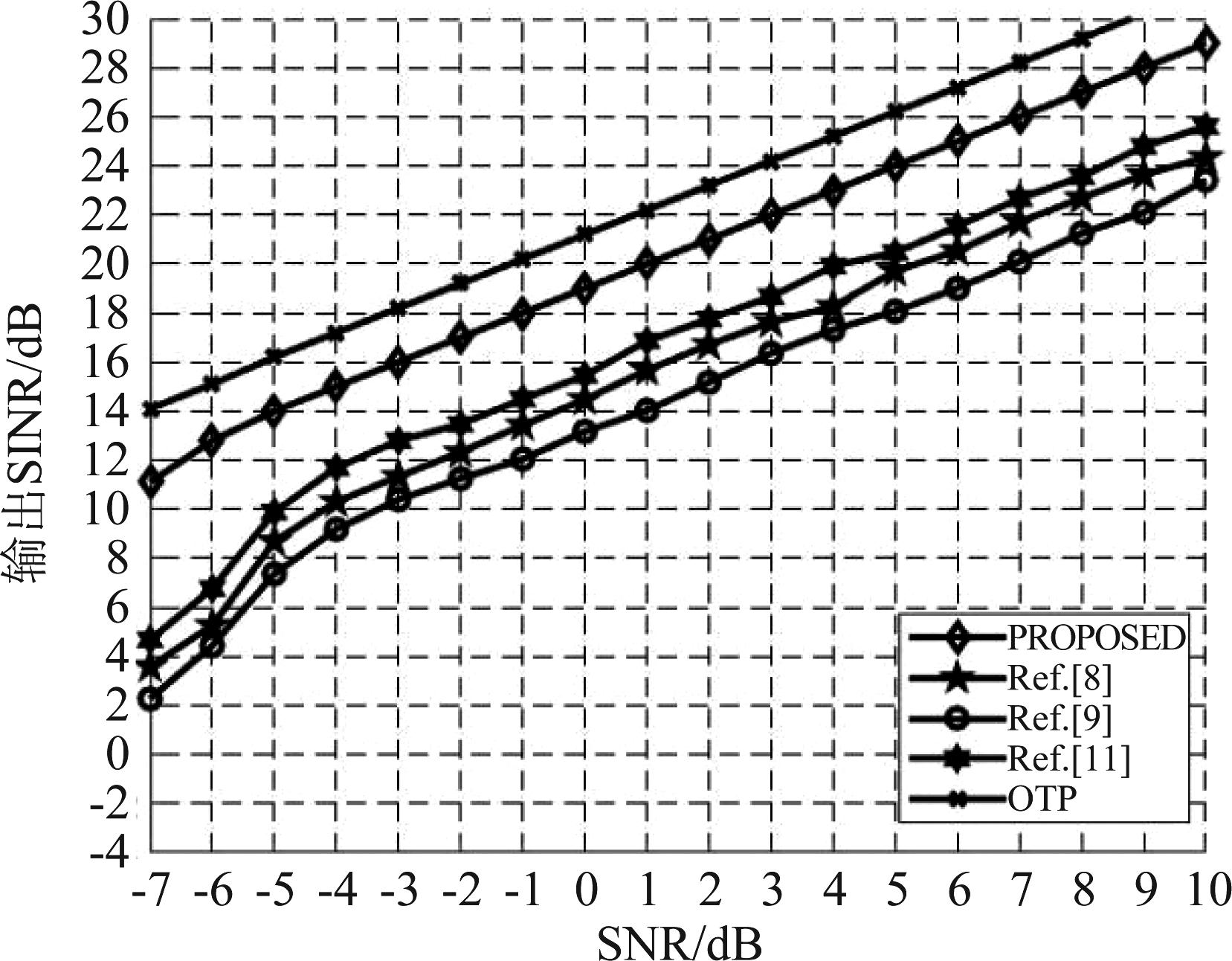
图5 不同算法的脉冲压缩输出SINR
Fig.5 SINR of pulse compression of different algorithms
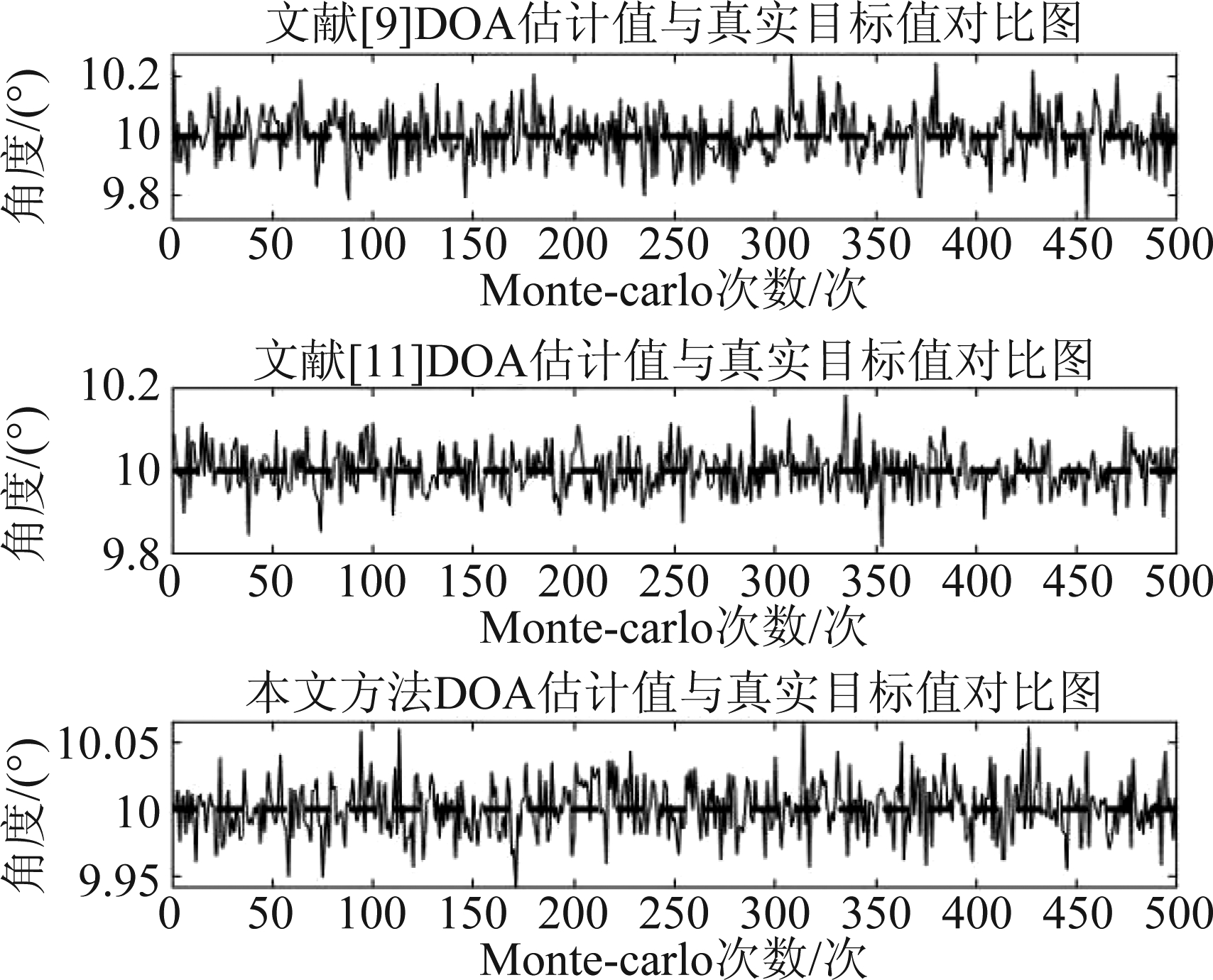
图6 不同算法的DOA估计结果
Fig.6 DOA estimation results of different algorithms
图7给出了在快拍数变化的情况下,本文方法与文献[9]、文献[11]的方法运算时间的对比。可以发现,当快拍数增加时,运算时间都在增加,但本文方法整体运算时间均低于文献[9]、文献[11]的方法,且当快拍数越大时,本文算法的运算时间优势越大。说明本文提出的降维与ADMM算法相结合进行稀疏恢复的方法,能够快速有效的抑制干扰,具有良好的实时性,更符合实际需求。图8给出了在信噪比变化的情况下,本文方法与文献[9]、文献[11]和Multiple Signal Classification(MUSIC)算法的DOA估计误差,同时还给出了DOA估计最小均方误差下界,可以发现,随着信噪比的增大,估计误差逐渐减小;相比于其他方法,本文方法整体的DOA估计误差更小,更加接近DOA估计最小均方误差下界,测角性能更好,具备更强的稳定性。
图7 不同算法的运算时间
Fig.7 Operational time of different algorithms
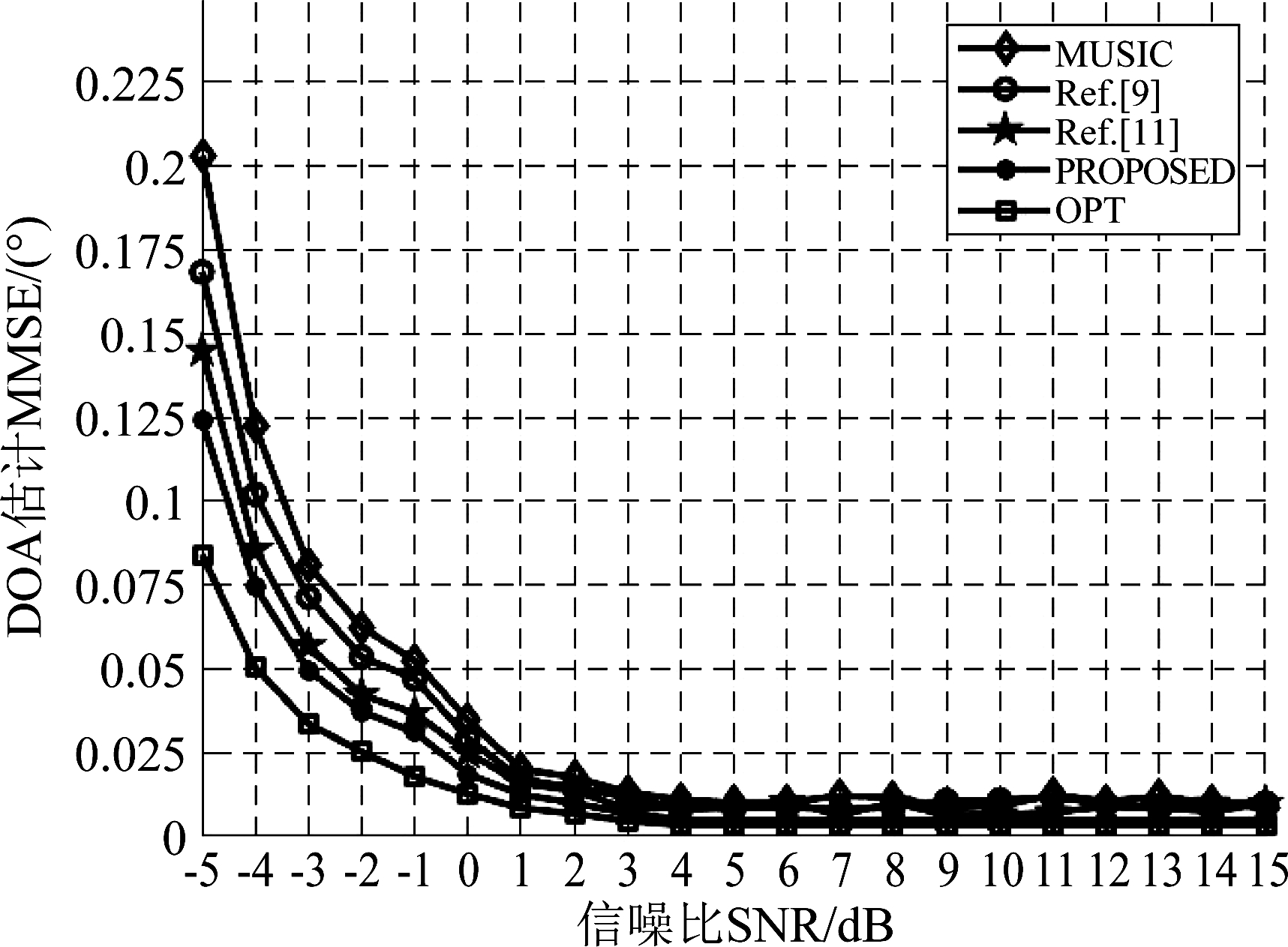
图8 不同算法的DOA估计均方差
Fig.8 DOA estimated mean square error of different algorithms
5 结论
针对低信噪比条件下的雷达抗干扰算法性能恶化的问题,本文提出了一种子阵分级处理与稀疏恢复联合的抗干扰方法,通过协方差矩阵重构与自适应波束形成,抑制了副瓣干扰;利用子阵分级处理思想,提高了信噪比,构建了新的阵列数据,并进行了稀疏表示;改进了ReMBo算法,使得算法抗干扰能力更强,同时使用ADMM算法与改进的ReMBo算法进行了快速高效的稀疏恢复,分离了主瓣干扰与目标回波信号,实现了主瓣干扰抑制;利用脉冲压缩识别了目标回波信号,估计了目标波达角。
仿真结果表明,本文方法能有效对抗主瓣、副瓣干扰,同时还能估计目标波达角。相比于当前流行的其他抗干扰方法,本文方法具备更高的输出SINR,更高的DOA估计精度与更高的运算效率,特别是在信噪比低下的条件下,本文方法优势更加突出,符合雷达抗干扰的实际需求。
[1] 廖桂生, 王彤, 保铮. 基于和差波束的自适应干扰对消技术[J]. 西安电子科技大学学报, 1997, 24(S1): 116-123.
LIAO Guisheng, WANG Tong, BAO Zheng. Interference suppression by sum and difference channels for radar systems[J]. Journal of Xidian University, 1997, 24(S1): 116-123.(in Chinese)
[2] YU K B, MURROW D J. Combining sidelobe canceller and mainlobe canceller for adaptive monopulse radar processing: US6867726[P]. 2005-03-15.
[3] YANG Xiaopeng, ZHANG Z, ZENG Tao, et al. Mainlobe interference suppression based on eigen-projection processing and covariance matrix reconstruction[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1369-1372.
[4] QIAN Junhui, HE Zishu. Mainlobe interference suppression with eigenprojection algorithm and similarity constraints[J]. Electronics Letters, 2016, 52(3): 228-230.
[5] 兰岚, 廖桂生, 许京伟, 等. FDA-MIMO雷达非自适应波束形成抗主瓣欺骗式干扰研究[J]. 信号处理, 2019, 35(6): 944-950.
LAN Lan, LIAO Guisheng, XU Jingwei, et al. Main-beam deceptive jamming suppression with Non-adaptive Beam-forming in FDA-MIMO radar[J]. Journal of Signal Processing, 2019, 35(6): 944-950.(in Chinese)
[6] 陈静, 李晗, 张洪纲, 等. 分布式雷达主瓣间歇采样转发干扰抑制方法[J]. 信号处理, 2018, 34(11): 1368-1376.
CHEN Jing, LI Han, ZHANG Honggang, et al. Main-lobe interrupted sampling repeater jamming suppression method in distributed radar[J]. Journal of Signal Processing, 2018, 34(11): 1368-1376.(in Chinese)
[7] 王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32(10): 46- 49.
WANG Jianming, WU Guangxin, ZHOU Weiguang. A study on radar mainlobe jamming suppression based on blind source separation algorithm[J]. Modern Radar, 2010, 32(10): 46- 49.(in Chinese)
[8] 王文涛, 张剑云, 李小波, 等. Fast ICA应用于雷达抗主瓣干扰算法研究[J]. 信号处理, 2015, 31(4): 497-503.
WANG Wentao, ZHANG Jianyun, LI Xiaobo, et al. A study on radar mainlobe jamming suppression algorithm based on fast ICA[J]. Journal of Signal Processing, 2015, 31(4): 497-503.(in Chinese)
[9] 周必雷, 王永良, 李荣锋, 等. 一种主瓣灵巧干扰环境下的盲距离-角度联合估计方法[J]. 电子学报, 2019, 47(9): 1819-1829.
ZHOU Bilei, WANG Yongliang, LI Rongfeng, et al. A blind range-direction estimation method in mainlobe smart jamming[J]. Acta Electronica Sinica, 2019, 47(9): 1819-1829.(in Chinese)
[10] 周必雷, 李荣锋, 段克清, 等. 一种基于稀疏重构的主瓣拖曳式干扰抑制方法[J]. 中国科学: 信息科学, 2019, 49(7): 838- 852.
ZHOU Bilei, LI Rongfeng, DUAN Keqing, et al. A sparse reconstruction algorithm for mainlobe towed jamming suppression[J]. Scientia Sinica (Informationis), 2019, 49(7): 838- 852.(in Chinese)
[11] 周必雷, 王永良, 段克清, 等. 一种主瓣干扰环境下的雷达目标参数“同维”稀疏估计方法[J]. 电子学报, 2019, 47(6): 1201-1208.
ZHOU Bilei, WANG Yongliang, DUAN Keqing, et al. A “same dimension” sparse estimation method for radar target parameter in mainlobe jamming[J]. Acta Electronica Sinica, 2019, 47(6): 1201-1208.(in Chinese)
[12] GE Mengmeng, CUI Guolong, YU Xianxiang, et al. Mainlobe jamming suppression via blind source separation[C]. 2018 IEEE Radar Conference (RadarConf18). Oklahoma City, OK, USA. IEEE, 2018: 0914-0918.
[13] GE Mengmeng, CUI Guolong, Mainlobe jamming suppression for distributed radar via joint blind source separation [J]. IET Radar, Sonar& Navigation, 2019, 13(7):1189-1199.
[14] ZHOU Bilei, LI Rongfeng, LIU Weijian, et al. A BSS-based space-time multi-channel algorithm for complex-jamming suppression[J]. Digital Signal Processing, 2019, 87: 86-103.
[15] LIU Lufeng, DU Xinpeng, CHENG Lizhi. Stable signal recovery via randomly enhanced adaptive subspace pursuit method[J]. IEEE Signal Processing Letters, 2013, 20(8): 823- 826.
[16] DAI Huanyao, WANG Xuesong, LI Yongzhen, et al. Main-lobe jamming suppression method of using spatial polarization characteristics of antennas[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2167-2179.
[17] STUTZMAN W, THIELE G. Antenna theory and design [M]. Wiley, Hoboken, NJ, 2012.
[18] MISHALI M, ELDAR Y C. Reduce and boost: Recovering arbitrary sets of jointly sparse vectors[J]. IEEE Transactions on Signal Processing, 2008, 56(10): 4692- 4702.
[19] WRIGHT S J, NOWAK R D, FIGUEIREDO M A T. Sparse reconstruction by separable approximation[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2479-2493.
[20] AFONSO M V, BIOUCAS-DIAS J M, FIGUEIREDO M A T. Fast image recovery using variable splitting and constrained optimization[J]. IEEE Transactions on Image Processing, 2010, 19(9): 2345-2356.
