 2,1范数和神经网络的非线性特征选择方法
2,1范数和神经网络的非线性特征选择方法 2,1范数和神经网络的非线性特征选择方法
2,1范数和神经网络的非线性特征选择方法随着机器学习的发展,学习任务的特征维度不断增加[1-3]。而在高维特征数据中,与任务不相关的特征数据或噪声特征数据存在的规模也不断增加[4]。这些特征数据不仅会降低学习任务的性能和效率,还会给结果的解释增加困难性。为了解决上述问题,特征选择和特征压缩变换常被用来降低特征的规模[5]。相较于特征压缩变换,特征选择能够不改变原始特征的物理属性及数据结构,更加有利于保留学习任务的可解释性[6]。
按照特征选择模型和学习任务模型的关系来说,特征选择算法可分为过滤式(filter)特征选择算法、包裹式(wrapped)特征选择算法以及嵌入式(embedded)特征选择算法[7]。过滤式特征选择算法通过某一种法则计算所有特征的权值,并根据权值大小排列挑选出重要的特征,例如ReliefF,拉普拉斯分数(Laplacian Score, LS)[8]和最小冗余最大相关算法(Minimum Redundancy Maximum Relevance, mRMR)[9];包裹式特征选择算法将所有特征分成不同的子集,用分类器对所有子集进行评价,挑选分类性能最好的特征子集作为最终的特征选择结果,例如序列特征选择(Sequential Feature Selection, SFS)算法[10]和遗传算法(Genetic Algorithm, GA)[11];嵌入式特征选择算法则是将特征选择的过程和学习的过程结合在一起,在模型训练的过程中筛选出与任务相关的重要特征,例如线性判别分析(Linear Discriminant Analysis, LDA)[12],最小二乘法(Least Square Method, LSM)[13],和随机森林(Random Forests, RF)[14]。对于这三类特征选择算法来说,过滤式算法的特征选择过程与分类学习过程相互独立,挑选的特征子集往往不是最佳的特征子集;包裹式特征选择算法由于依赖分类器来评价所有特征子集的性能,因此计算复杂度较高。而嵌入式特征选择算法将特征选择的过程融入分类模型的构建中,能够挑选出分类准确率较高的子集。
通常,正则化嵌入式特征选择算法在目标函数中加入惩罚项进行约束,来对目标函数的求解加以引导[5]。在目标函数构建中挑选符合学习任务的惩罚项,能够对最终的分类结果带来积极的影响。其中,最常使用的约束项 p范数,因此对于
p范数,因此对于 p范数的正则化是当前研究热点。例如,Hoerl等人提出了基于
p范数的正则化是当前研究热点。例如,Hoerl等人提出了基于 2范数的有偏估计岭回归,其中的
2范数的有偏估计岭回归,其中的 2范数对所有系数计算平方和根,因此该方法对于误差较大的离群值十分敏感[15]。但对于结构相似的特征子集,
2范数对所有系数计算平方和根,因此该方法对于误差较大的离群值十分敏感[15]。但对于结构相似的特征子集, 2范数无法收缩系数得到稀疏解。为解决该问题,Tibshirani等人提出了基于
2范数无法收缩系数得到稀疏解。为解决该问题,Tibshirani等人提出了基于 1范数的最小绝对值收敛和选择算子(LASSO)算法[16]。
1范数的最小绝对值收敛和选择算子(LASSO)算法[16]。 1范数采用正则化系数的绝对值进行求和,能够将大部分的系数收缩至零[17]。因此,基于
1范数采用正则化系数的绝对值进行求和,能够将大部分的系数收缩至零[17]。因此,基于 1范数的模型能得到稀疏解。而
1范数的模型能得到稀疏解。而 1范数的模型只能解决单个任务的特征选择问题,并且对噪声数据十分敏感。G.Obozinski等人针对该问题提出了一种将
1范数的模型只能解决单个任务的特征选择问题,并且对噪声数据十分敏感。G.Obozinski等人针对该问题提出了一种将 1范数和
1范数和 2范数结合的联合
2范数结合的联合 2,1范数[18]。随后,Lai等人提出了一种鲁棒的局部判别分析方法,用
2,1范数[18]。随后,Lai等人提出了一种鲁棒的局部判别分析方法,用 2,1范数代替
2,1范数代替 2范数构造类间散布矩阵。同时,他们在投影矩阵上施加了
2范数构造类间散布矩阵。同时,他们在投影矩阵上施加了 2,1范数,以保证联合稀疏性和鲁棒性[19]。Yang等人提出了一种将LDA和
2,1范数,以保证联合稀疏性和鲁棒性[19]。Yang等人提出了一种将LDA和 2,1范数正则化相结合的特征选择方法来实现特征选择。在这种方法中,他们使用
2,1范数正则化相结合的特征选择方法来实现特征选择。在这种方法中,他们使用 2,1范数项对变换矩阵的行施加稀疏约束[20]。
2,1范数项对变换矩阵的行施加稀疏约束[20]。 2,1范数利用组内和组间的联合关系,在全局的范围内使关联特征之间的系数为零,保证了系数的稀疏性和可解释性。因此,
2,1范数利用组内和组间的联合关系,在全局的范围内使关联特征之间的系数为零,保证了系数的稀疏性和可解释性。因此, 2,1范数在特征选择领域得到了广泛的应用[21]。
2,1范数在特征选择领域得到了广泛的应用[21]。
一般情况下,基于联合 2,1范数的正则化利用联合稀疏性去除噪声值和异常值,每个特征属性共有稀疏的系数,同时基于联合
2,1范数的正则化利用联合稀疏性去除噪声值和异常值,每个特征属性共有稀疏的系数,同时基于联合 2,1范数的正则化方法具有很强的鲁棒性。通常基于联合
2,1范数的正则化方法具有很强的鲁棒性。通常基于联合 2,1正则化的问题通过等价转换进行求解[22]。Liu等人提出了一种基于一阶黑箱法的
2,1正则化的问题通过等价转换进行求解[22]。Liu等人提出了一种基于一阶黑箱法的 2,1范数优化方法[23]。由于光滑凸优化的复杂度的值优于非光滑凸优化的复杂度最小值,他们将非光滑
2,1范数优化方法[23]。由于光滑凸优化的复杂度的值优于非光滑凸优化的复杂度最小值,他们将非光滑 2,1范数正则化问题重新表述为等价的光滑凸优化问题。Nie等人通过拉格朗日函数求解约束下的目标函数,并利用迭代的方式求解最优值,将
2,1范数正则化问题重新表述为等价的光滑凸优化问题。Nie等人通过拉格朗日函数求解约束下的目标函数,并利用迭代的方式求解最优值,将 2,1正则化约束下最小值求解问题变换为易于求解的参数收敛问题[24]。然而,这些方法大多采用最小化
2,1正则化约束下最小值求解问题变换为易于求解的参数收敛问题[24]。然而,这些方法大多采用最小化 2,1范数的线性函数,从线性角度来进行求解,因此对异常数据非常敏感[25]。此外,实际的特征数据结构往往更为复杂,不具备线性结构,而线性的求解模型可能对于具有非线性结构的特征数据产生一定的限制。
2,1范数的线性函数,从线性角度来进行求解,因此对异常数据非常敏感[25]。此外,实际的特征数据结构往往更为复杂,不具备线性结构,而线性的求解模型可能对于具有非线性结构的特征数据产生一定的限制。
除了已有基于 2,1范数的线性求解模型存在的问题,
2,1范数的线性求解模型存在的问题, 2,1范数同时还具有旋转不变性和非光滑的特性,导致优化过程中迭代次数庞大,算法复杂度高,并且收敛速度较慢。为了解决这一问题,并提高基于
2,1范数同时还具有旋转不变性和非光滑的特性,导致优化过程中迭代次数庞大,算法复杂度高,并且收敛速度较慢。为了解决这一问题,并提高基于 2,1范数的特征选择算法性能,本文提出引入具有非线性结构的BP神经网络以此优化基于联合
2,1范数的特征选择算法性能,本文提出引入具有非线性结构的BP神经网络以此优化基于联合 2,1范数的特征选择算法,来获得更好的分类准确率。该模型的基本思想是将
2,1范数的特征选择算法,来获得更好的分类准确率。该模型的基本思想是将 2,1范数约束项加入到神经网络中的目标函数求解中,具体来说是在目标函数中加入神经网络输入层和第一层神经元间权重矩阵的
2,1范数约束项加入到神经网络中的目标函数求解中,具体来说是在目标函数中加入神经网络输入层和第一层神经元间权重矩阵的 2,1范数。通过神经网络的自我迭代学习过程中,权重矩阵的
2,1范数。通过神经网络的自我迭代学习过程中,权重矩阵的 2,1范数对学习过程进行引导,使得神经网络输入层和第一层神经元间权重矩阵具有稀疏性和鲁棒性,最终在目标函数收敛后由权重矩阵的行的
2,1范数对学习过程进行引导,使得神经网络输入层和第一层神经元间权重矩阵具有稀疏性和鲁棒性,最终在目标函数收敛后由权重矩阵的行的 2范数值来实现特征选择。
2范数值来实现特征选择。
本文余下章节的结构如下:第2节介绍基于神经网络优化 2,1范数的非线性特征选择的具体实现方法;第3节将本文提出的特征选择算法和经典的特征选择算法进行了比较,并对实验结果进行分析和讨论;第4节对全文进行总结。
2,1范数的非线性特征选择的具体实现方法;第3节将本文提出的特征选择算法和经典的特征选择算法进行了比较,并对实验结果进行分析和讨论;第4节对全文进行总结。
 2,1范数和神经网络的非线性特征选择方法
2,1范数和神经网络的非线性特征选择方法为了将重点落在原理的实现上,我们选择了最基础的后向传播神经网络(Back Propagation,BP)结构,且只使用了一层隐藏层。因此,神经网络的模型只由输入层,隐藏层和输出层构成。本章节使用的各参数定义如表1所示。
表1 各参数定义
Tab.1 Definition of parameters

符号定义xi输入层第i个神经元的输出hj隐藏层第j个神经元的输出y^k输出层第k个神经元的输出yk输出层第k个神经元对应输出的真实值wji输入层神经元xi和隐藏层神经元hj之间的权重值vkj隐藏层神经元hj和输出层神经元y^k之间的权重值a输入层的偏置量b隐藏层的偏置量f隐藏层神经元的激活函数g输出层神经元的激活函数
一般来说,BP神经网络的正向传播过程的输出如公式(1)所示:
(1)
隐藏层的激活函数使用了sigmoid函数,其中sigmoid函数的导数可以用自身![]() (x)进行表示,更加便于后向传播过程中对于系数的迭代。sigmoid函数公式和其导数如下:
(x)进行表示,更加便于后向传播过程中对于系数的迭代。sigmoid函数公式和其导数如下:
![]()
![]()
(2)
![]()
![]() (x)[1-
(x)[1-![]() (x)]
(x)]
(3)
为了使模型更适合多分类任务,且避免概率分值不平衡,我们采用交叉熵损失函数作为神经网络的损失函数,将最大概率输出为输出。交叉熵损失定义函数为:
(4)
同时,输出层的激活函数配合使用softmax函数:
(5)
为了将 2,1范数引入BP神经网络对神经网络的学习过程进行引导,这里在输出层的损失函数中加入输入层和第一层隐藏层之间的权重矩阵的
2,1范数引入BP神经网络对神经网络的学习过程进行引导,这里在输出层的损失函数中加入输入层和第一层隐藏层之间的权重矩阵的 2,1范数。因此,损失函数修改为:
2,1范数。因此,损失函数修改为:
(6)
其中,λ为正则化参数,防止过拟合。且 2,1范数表示为:
2,1范数表示为:
(7)
其中,a为w的总列数,b为w的总行数。因此,最终的求解问题表示为:
(8)
对于||W||2,1矩阵的偏导数的求解过程可表示为:
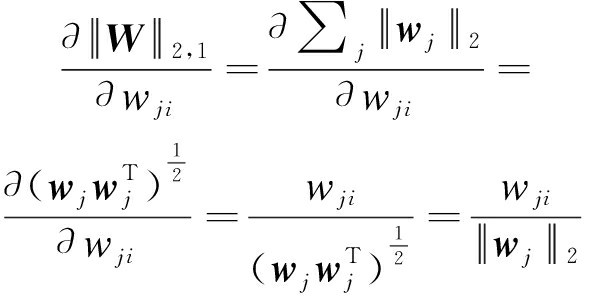
(9)
经过每一次前向传播和后向传播的迭代,输出与真实标签之间的误差会越来越小,此时设定迭代收敛的最小阈值来终止学习过程。为了直观地反映特征选择的结果,最后计算了权重矩阵W的 2范数。综上所述,我们将本文提出的方法命名为BPFS。
2范数。综上所述,我们将本文提出的方法命名为BPFS。
为了评估BPFS的性能,我们将BPFS特征选择方法与六种具有代表性的特征选择方法进行了比较,其中包括相关系数(Correlation Coefficient,CC)、ReliefF、mRMR经典的特征选择算法,以及通过线性方法优化范数的RFS[23]、SDFS[26]和L21-RLDA[27]特征选择算法。此外,选取公开的UCI数据集中的8个数据集对这些方法进行了验证,八个数据集分别为Binalpha[28],Control[29],Corel5k[28],Crowdsowrced[30],Isolet[31],Movementlibras[32],Segment[28],Sensorless[33]。表2显示了关于这些数据集的详细信息。
表2 各数据集信息
Tab.2 Information of datasets
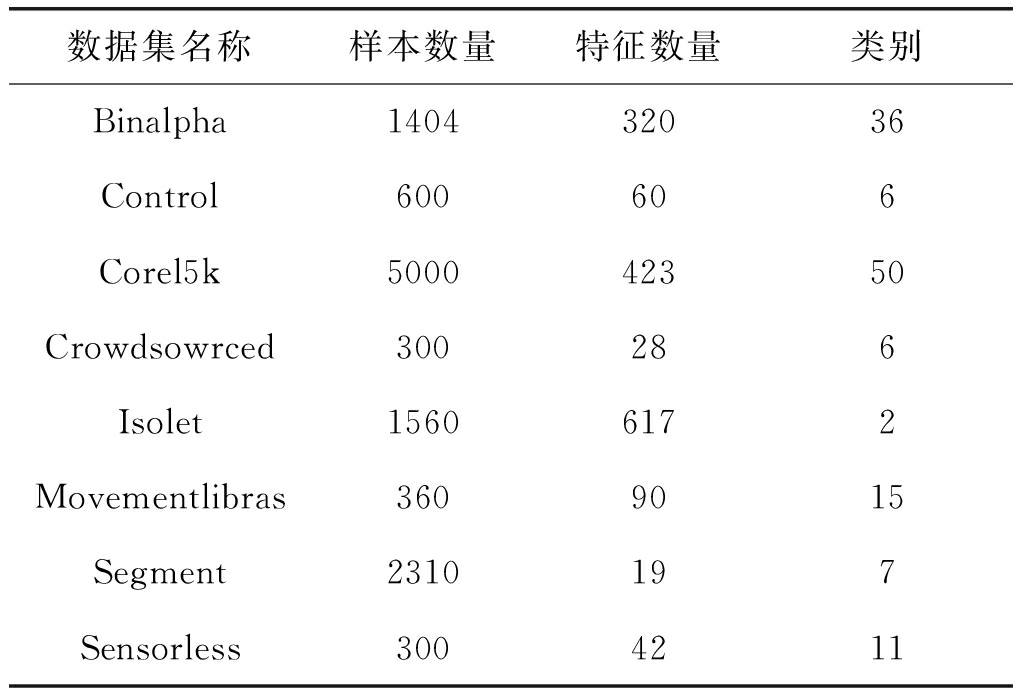
数据集名称样本数量特征数量类别Binalpha140432036Control600606Corel5k500042350Crowdsowrced300286Isolet15606172Movementlibras3609015Segment2310197Sensorless3004211
首先,我们使用七种特征选择方法选择不同数量下的特征。然后使用线性的支持向量机分类器(Support Vector Machine, SVM)和非线性的随机森林(Random Forest,RF)分类器分别对各结果进行分类,并且每次按照取百分之七十的数据作为训练集,剩下的数据作为测试集,重复多次取平均值作为分类准确度。为了提高效率,直接将数据集的所有样本和特征构成的矩阵作为输入传入输入层。需要注意的是,所有数据集都被零均值标准化。对于每次的分类结果,计算并记录平均准确度以及收敛性来检验所提出方法的性能。所有代码均在MATLAB上实现,其中SVM分类器是由LIBSVM工具箱实现的,RF分类器是使用内置函数实现。
算法的收敛速度能力一定程度反应了算法的效率和稳定性。为了加快计算速度和方便比较,将BP神经网络特征选择过程的迭代次数设为常数2500,各数据集收敛情况如图1所示。
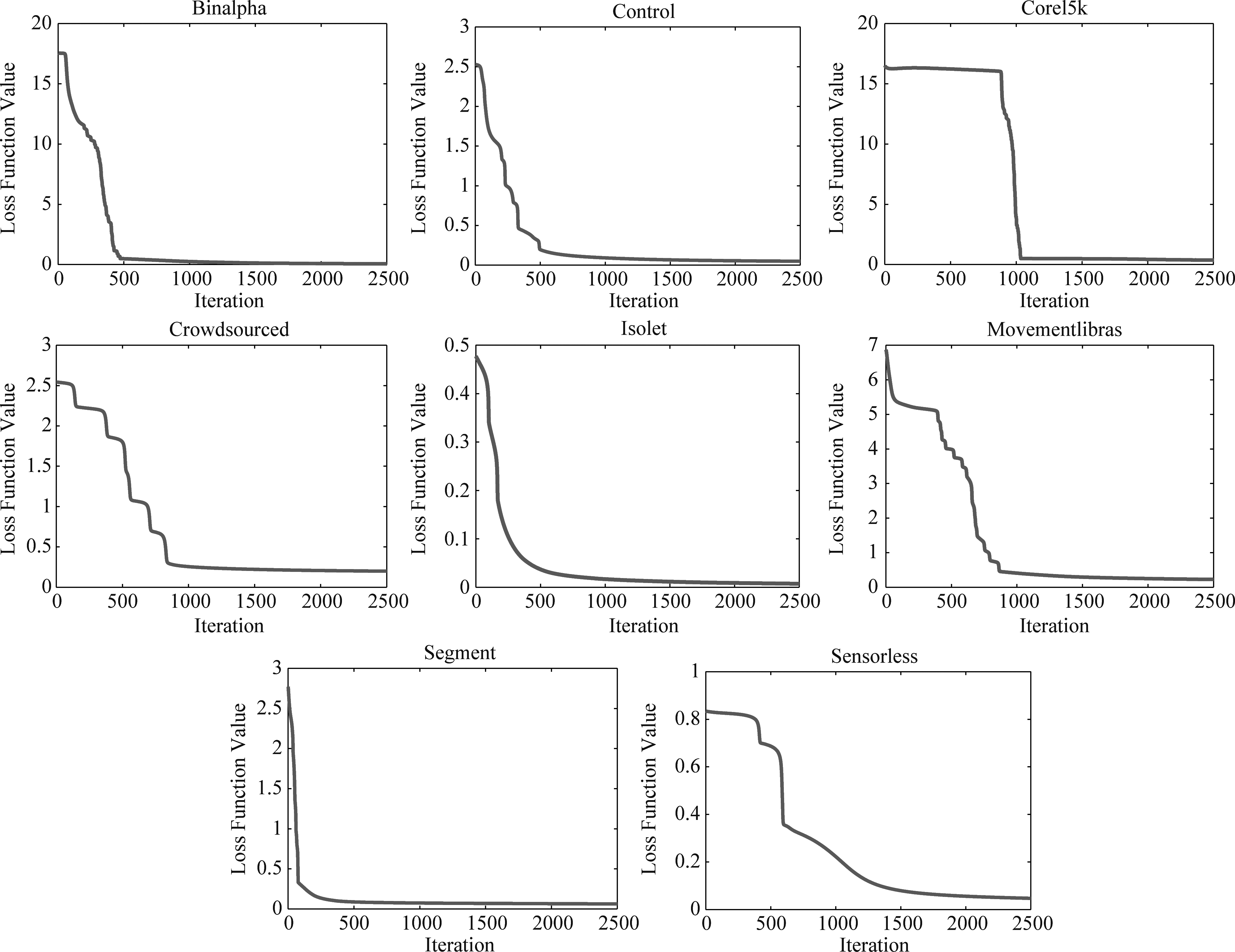
图1 BPFS在各数据集中的收敛结果
Fig.1 Iteration results of BPFS in all dataset
可以看到,在迭代2500的时候,所有数据集都很好的实现了收敛。大部分的数据在迭代次数为500至1000左右时实现了收敛,其中收敛效果最好的是Segment数据集,在迭代次数不到500时实现收敛。而Sensorless数据集收敛稍慢些,到近2000次迭代才收敛。因此,BPFS具备达到局部极小值的可能性。
图2和表3展示了SVM分类器下的7种算法在各数据集上的不同维度的分类准确度和所有维度下的平均分类准确度。
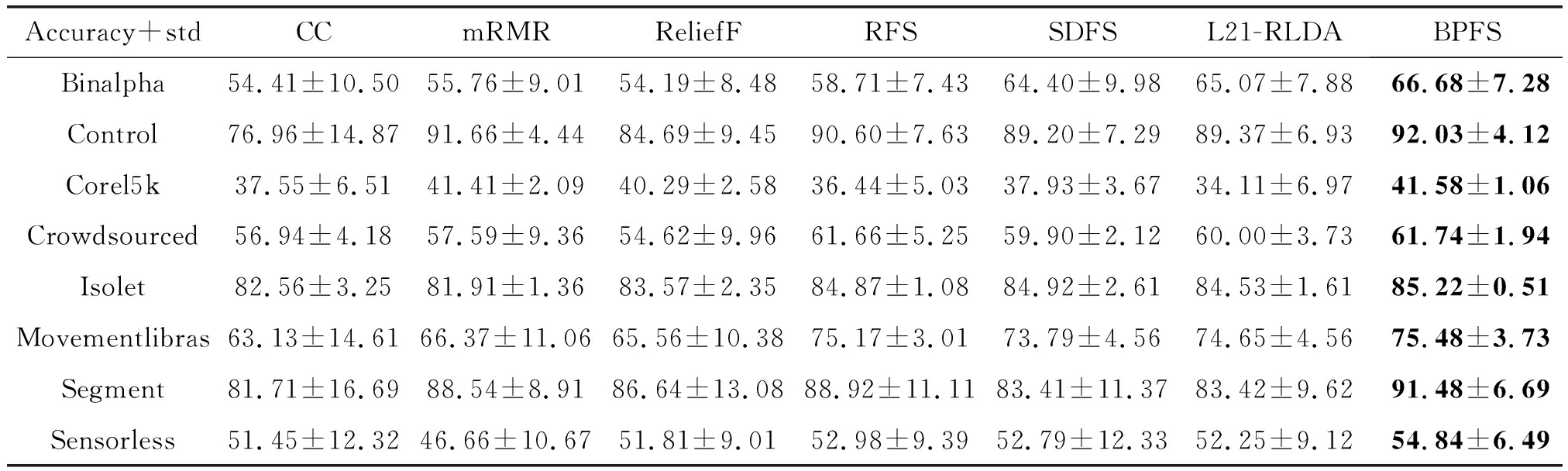
从图2可以看到,不同数据集各算法的分类准确度结果,每种方法的精度随着选择的特征数量增加变得更加精确。在SVM的结果中,BPFS算法在部分数据集中得到的分类结果相较其他算法具有一定的优势,并且在很多数据集结果中都是最先趋于平滑,快速地调整误差并选择有更具有代表的特征。不过需要注意的是,在Control,Crowdsourced和Movementlibras数据集中,BPFS算法并未取得明显的优势,尤其在Control和Crowdsourced数据集中提取的特征数量增长中后期。可能因为本文进行实验的BPFS使用的是简单基础的神经网络结构,对于特征量庞大的数据集需要更深的网络来实现更好的拟合。另外,结合表3所有维度平均分类准确度中的方差来看,BPFS算法在所有数据集中都取得了十分小的方差,因此,BPFS算法相较于其他算法具有更好的稳定性。
表3 七种特征选择方法在SVM分类器下的平均分类准确率和方差(%),其中加粗的是该数据集下准确率最高的方法
Tab.3 Mean accuracy and variance (%) of seven algorithm in SVM, and the bold form is the best accuracy
Accuracy+stdCCmRMRReliefFRFSSDFSL21-RLDABPFSBinalpha54.41±10.5055.76±9.0154.19±8.4858.71±7.4364.40±9.9865.07±7.8866.68±7.28Control76.96±14.8791.66±4.4484.69±9.4590.60±7.6389.20±7.29 89.37±6.9392.03±4.12Corel5k37.55±6.5141.41±2.0940.29±2.5836.44±5.0337.93±3.6734.11±6.9741.58±1.06Crowdsourced56.94±4.1857.59±9.3654.62±9.9661.66±5.2559.90±2.1260.00±3.7361.74±1.94Isolet82.56±3.2581.91±1.3683.57±2.3584.87±1.0884.92±2.6184.53±1.6185.22±0.51Movementlibras63.13±14.6166.37±11.0665.56±10.3875.17±3.0173.79±4.5674.65±4.5675.48±3.73Segment81.71±16.6988.54±8.9186.64±13.0888.92±11.1183.41±11.3783.42±9.6291.48±6.69Sensorless51.45±12.3246.66±10.6751.81±9.0152.98±9.3952.79±12.3352.25±9.1254.84±6.49
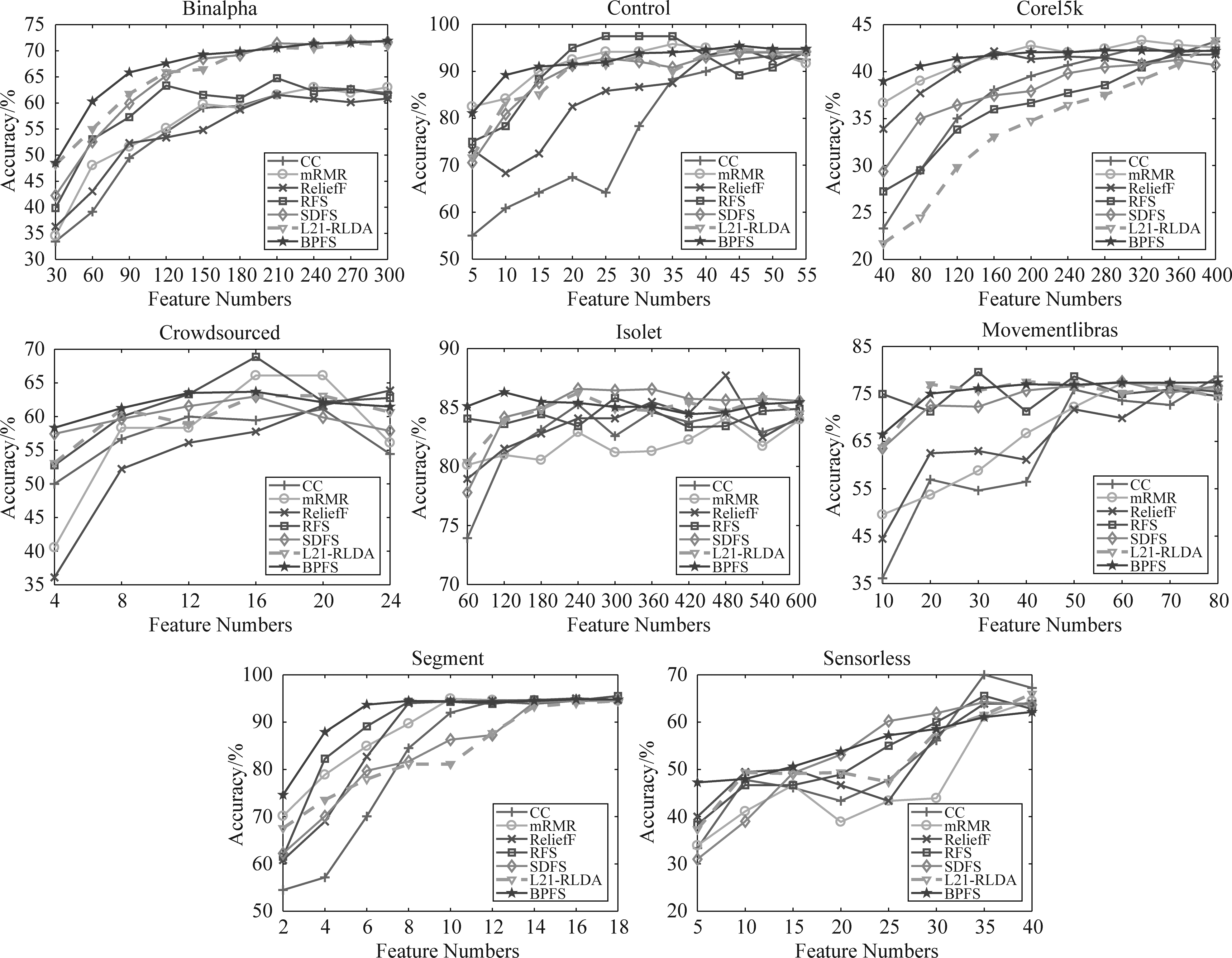
图2 7种算法在SVM分类器下各数据集上的分类准确度
Fig.2 Accuracy result of seven algorithm in SVM
同理,我们可以得到在RF分类器下的7种算法在各数据集上的不同维度的分类准确度和所有维度下的平均分类准确度,如图3和表4所示。
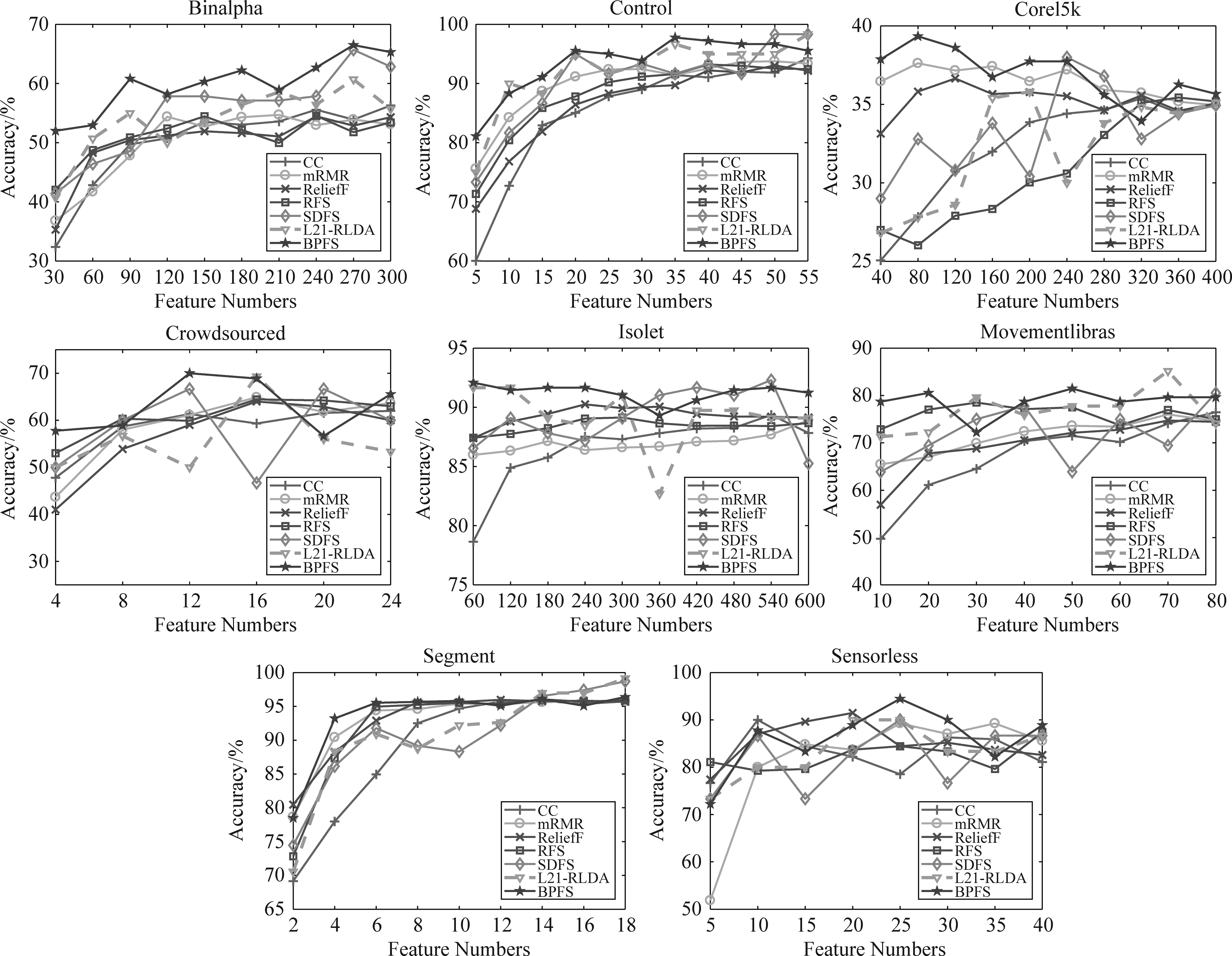
图3 7种算法在RF分类器下各数据集上的分类准确度
Fig.3 Accuracy result of seven algorithm in RF
在图3中可以看到BPFS算法在大部分的数据集中取了不错的结果,而在表4中可以看到BPFS算法在所有的数据集中得到了最高的平均分类准确度。因此,基于非线性结构的BPFS在不同的数据集中能够发挥较好的作用,在神经网络的协助下选择出更重要的特征。
表4 七种特征选择方法在RF分类器下的平均分类准确率和方差(%),其中加粗的是该数据集下准确率最高的方法
Tab.4 Mean accuracy and variance (%) of seven algorithm in RF, and the bold form is the best accuracy
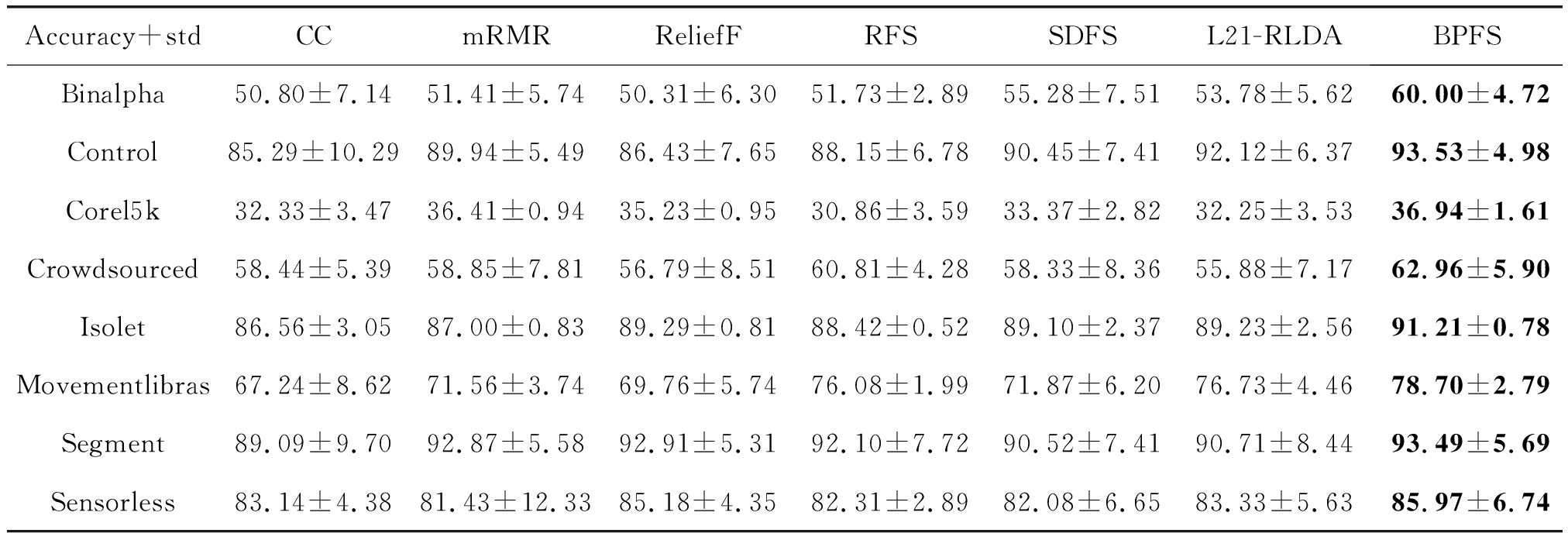
Accuracy+stdCCmRMRReliefFRFSSDFSL21-RLDABPFSBinalpha50.80±7.1451.41±5.7450.31±6.3051.73±2.8955.28±7.5153.78±5.6260.00±4.72Control85.29±10.2989.94±5.4986.43±7.6588.15±6.7890.45±7.4192.12±6.3793.53±4.98Corel5k32.33±3.4736.41±0.9435.23±0.9530.86±3.5933.37±2.8232.25±3.5336.94±1.61Crowdsourced58.44±5.3958.85±7.8156.79±8.5160.81±4.2858.33±8.3655.88±7.1762.96±5.90Isolet86.56±3.0587.00±0.8389.29±0.8188.42±0.5289.10±2.3789.23±2.5691.21±0.78Movementlibras67.24±8.6271.56±3.7469.76±5.7476.08±1.9971.87±6.2076.73±4.4678.70±2.79Segment89.09±9.7092.87±5.5892.91±5.3192.10±7.7290.52±7.4190.71±8.4493.49±5.69Sensorless83.14±4.3881.43±12.3385.18±4.3582.31±2.8982.08±6.6583.33±5.6385.97±6.74
结合表3和表4分析BPFS算法在SVM分类器和RF分类器下的结果可以得到,RF分类器下BPFS的结果在大部分数据集上比SVM分类器下BPFS的结果高,只有在Corel5k数据集上低于SVM分类器。这可能因为Corel5k数据集中的相关联的特征较多,线性的SVM分类器能够更好地处理这些线性特征。同理,在Sensorless数据集的结果中可以看到,RF分类器下所有算法的平均分类准确度都要远远高于SVM分类器下所有算法的平均分类准确度。这两个数据集在SVM分类器和RF分类器下造成的差异的原因可能是因为Sensorless数据集中的特征结构是非线性的结构,且冗余特征较多,因此在RF分类器中都取得了不错的表现。
通过这些统计数据综合看来,一方面,通过 2,1范数诱导神经网络获得稀疏的网络结构,使得BPFS能够筛选出具有代表性的特征;另一方面,利用神经网络的非线性求解
2,1范数诱导神经网络获得稀疏的网络结构,使得BPFS能够筛选出具有代表性的特征;另一方面,利用神经网络的非线性求解 2,1范数的模型结合了神经网络原有学习能力强等优点,帮助BPFS获得更好的泛化性。因此,BPFS具有一定稳定性和有效性,整体性能也有一定的优势。
2,1范数的模型结合了神经网络原有学习能力强等优点,帮助BPFS获得更好的泛化性。因此,BPFS具有一定稳定性和有效性,整体性能也有一定的优势。
本文提出了一种利用神经网络非线性结构优化基于 2,1范数的特征选择方法BPFS。该方法在神经网络的目标函数中加入输入层和隐藏层之间权值矩阵的
2,1范数的特征选择方法BPFS。该方法在神经网络的目标函数中加入输入层和隐藏层之间权值矩阵的 2,1范数作为约束项。一方面,利用神经网络神经元的非线性结构求解目标函数;另一方面,利用
2,1范数作为约束项。一方面,利用神经网络神经元的非线性结构求解目标函数;另一方面,利用 2,1范数引导神经网络的学习过程,使得目标函数收敛的同时,输入层和隐藏层之间权值矩阵足够稀疏,来实现特征选择的过程。同时,本文虽然使用了基本的后向传播模型,但是对于神经网络进行了一定的设计选择,使BPFS更加适合分类任务。最后,UCI数据库中的8个数据集被用来测试BPFS和6个经典的特征选择算法的性能,并在线性SVM和RF两种分类器下进行了实验。实验结果表明,BPFS可以有效选择对分类任务有较大贡献率的特征,并且跟其他六种算法相比,整体上表现优异。下一步工作的重点可以放在对神经网络框架的进一步研究。
2,1范数引导神经网络的学习过程,使得目标函数收敛的同时,输入层和隐藏层之间权值矩阵足够稀疏,来实现特征选择的过程。同时,本文虽然使用了基本的后向传播模型,但是对于神经网络进行了一定的设计选择,使BPFS更加适合分类任务。最后,UCI数据库中的8个数据集被用来测试BPFS和6个经典的特征选择算法的性能,并在线性SVM和RF两种分类器下进行了实验。实验结果表明,BPFS可以有效选择对分类任务有较大贡献率的特征,并且跟其他六种算法相比,整体上表现优异。下一步工作的重点可以放在对神经网络框架的进一步研究。
[1] YI S, HE Z, JING X Y, et al. Adaptive weighted sparse principal component analysis for robust unsupervised feature selection[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(6): 2153-2163.
[2] GUI J, SUN Z, JI S, et al. Feature selection based on structured sparsity: A comprehensive study[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 28(7): 1490-1507.
[3] XUE B, ZHANG M, BROWNE W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE Transactions on Evolutionary Computation, 2015, 20(4): 606-626.
[4] WANG Q, WAN J, NIE F, et al. Hierarchical feature selection for random projection[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(5): 1581-1586.
[5] PEREIRA R B, PLASTINO A, ZADROZNY B, et al. Categorizing feature selection methods for multi-label classification[J]. Artificial Intelligence Review, 2018, 49(1): 57-78.
[6] DU X, NIE F, WANG W, et al. Exploiting combination effect for unsupervised feature selection by l2,0-norm[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 30(1): 201-214.
[7] SAEYS Y, INZA I, LARRANAGA P. A review of feature selection techniques in bioinformatics[J]. Bioinformatics, 2007, 23(19): 2507-2517.
[8] HE X, CAI D, NIYOGI P. Laplacian score for feature selection[J]. Advances in Neural Information Processing Systems, 2005, 18: 507-514.
[9] PENG H, LONG F, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238.
[10] INZA I, SIERRA B, BLANCO R, et al. Gene selection by sequential search wrapper approaches in microarray cancer class prediction[J]. Journal of Intelligent & Fuzzy Systems, 2002, 12(1): 25-33.
[11] OH I S, LEE J S, MOON B R. Hybrid genetic algorithms for feature selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(11): 1424-1437.
[12] LIN S W, CHEN S C. PSOLDA: A particle swarm optimization approach for enhancing classification accuracy rate of linear discriminant analysis[J]. Applied Soft Computing, 2009, 9(3):1008-1015.
[13] PENG H, LIU C L. Discriminative feature selection via employing smooth and robust hinge loss[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 30(3): 788-802.
[14] MAYER J, RAHMAN R, GHOSH S, et al. Sequential feature selection and inference using multi-variate random forests[J]. Bioinformatics, 2018, 34(8): 1336-1344.
[15] HOERL A E, KENNARD R W. Ridge regression: biased estimation for nonorthogonal problems[J]. Technometrics A Journal of Statistics for the Physical Chemical & Engineering Sciences, 2000, 42(1): 80.
[16] TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, 1996, 58(1):267-288.
[17] OGUTU J O, SCHULZ-STREECK T, PIEPHO H P. Genomic selection using regularized linear regression models: ridge regression, lasso, elastic net and their extensions[J]. BMC Proceedings, 2012, 6(2):10.
[18] OBOZINSKI G,TASKAR B, JORDAN M. Multi-task feature selection, statistics department[J]. UC Berkeley, Tech. Rep, 2006, 2(2.2):2.
[19] LAI Z, LIU N, SHEN L, et al. Robust locally discriminant analysis via capped norm[J]. IEEE Access, 2019, 7:4641-4652.
[20] YANG L, LIU X, NIE F, et al. Robust and efficient linear discriminant analysis with L2,1-norm for feature selection[J]. IEEE Access, 2020, 8:44100-44110.
[21] ARGYRIOU A, EVGENIOU T, PONTIL M. Convex multi-task feature learning[J]. Machine Learning, 2008, 73(3):243-272.
[22] XIANG S, NIE F, MENG G, et al. Discriminative least squares regression for multiclass classification and feature selection[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(11):1738-1754.
[23] LIU J, JI S, YE J. Multi-task feature learning via efficient 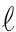 2,1-norm minimization[C]. In Proceedings of the Twenty-fifth Conference on Uncertainty in Artificial Intelligence, 2009:339-348.
2,1-norm minimization[C]. In Proceedings of the Twenty-fifth Conference on Uncertainty in Artificial Intelligence, 2009:339-348.
[24] NIE F, HUANG H, CAI X, et al. Efficient and robust feature selection via joint 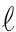 2,1-norms minimization[C]. International Conference on Neural Information Processing Systems. Curran Associates Inc, 2010, 23: 1813-1821.
2,1-norms minimization[C]. International Conference on Neural Information Processing Systems. Curran Associates Inc, 2010, 23: 1813-1821.
[25] ZHANG H, WANG J, SUN Z, et al. Feature selection for neural networks using group lasso regularization[J]. IEEE Transactions on Knowledge and Data Engineering, 2020, 32(4):659-673.
[26] WANG Z, NIE F, TIAN L, et al. Discriminative feature selection via a structured sparse subspace learning module[C]. Proc. Twenty-Ninth Int. Joint Conf. Artif. Intell. 2020: 3009-3015.
[27] ZHAO H, WANG Z, NIE F. A new formulation of linear discriminant analysis for robust dimensionality reduction[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 31(4): 629-640.
[28] WU X, XU X, LIU J, et al. Supervised feature selection with orthogonal regression and feature weighting[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 32(5): 1831-1838.
[29] ALCOCK R J, MANOLOPOULOS Y. Time-series similarity queries employing a feature-based approach[C]. 7th Hellenic Conference on Informatics, 1999: 27-29.
[30] JOHNSON B A, IIZUKA K. Integrating OpenStreetMap crowdsourced data and Landsat time-series imagery for rapid land use/land cover (LULC) mapping: Case study of the Laguna de Bay area of the Philippines[J]. Applied Geography, 2016, 67:140-149.
[31] FANTY M, COLE R. Spoken letter recognition[J]. Advances in Neural Information Processing Systems, 1990, 3: 220-226.
[32] DIAS D B, MADEO R C B, ROCHA T, et al. Hand movement recognition for brazilian sign language: a study using distance-based neural networks[C]. 2009 International Joint Conference on Neural Networks. IEEE, 2009: 697-704.
[33] PASCHKE F, BAYER C, BATOR M, et al. Sensorlose zustandsüberwachung an synchronmotoren[C]. Proceedings 23. Workshop Computational Intelligence, 2013: 211.
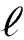 2,1-Norm Based Feature Selection and Neural Network
2,1-Norm Based Feature Selection and Neural NetworkReference format: FAN Xinyu, XU Xueyuan, WU Xia. Nonlinear solution for 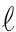 2,1-norm based feature selection and neural network[J]. Journal of Signal Processing, 2021, 37(9): 1644-1652. DOI: 10.16798/j.issn.1003- 0530.2021.09.008.
2,1-norm based feature selection and neural network[J]. Journal of Signal Processing, 2021, 37(9): 1644-1652. DOI: 10.16798/j.issn.1003- 0530.2021.09.008.
范馨予 女,1996年生,湖南衡阳人。北京师范大学人工智能学院研究生,主要研究方向为特征选择、神经网络和情感识别等。
E-mail: fxyrin@gmail.com
徐雪远 男,1992年生,安徽滁州人。北京师范大学人工智能学院博士生,主要研究方向为特征选择、盲源分离和情感识别等。
E-mail: xuxueyuan@mail.bnu.edu.cn
邬 霞(通讯作者) 女,1978年生,湖南郴州人。北京师范大学人工智能学院教授,博士生导师,主要研究方向为人工智能、脑科学和神经影像的数据处理等。
E-mail: wuxia@bnu.edu.cn