1 引言
直接序列扩频(Direct Sequence Spread Spectrum)信号,因其具有良好的保密性、抗干扰、低截获概率、抗多径干扰性以及良好的码分多址通信能力,被广泛应用于卫星、雷达、通信以及各种军事和民用通信领域[1-2],这无疑给通信对抗情报侦察提出了严峻的挑战。如何实现复杂电磁环境下扩频信号检测和参数盲估计具有重要的意义。
目前伪码序列盲估计典型方法主要包括自相关搜索法[3]、矩阵分解算法[4-6]、神经网络算法[7-8]和子空间追踪算法[9]等。自相关搜索法需要对观测序列每个采样点计算一次测度函数,先估计出伪码序列起始点,最后估计出伪码序列,在观测序列较长时,计算量较大。矩阵分解算法是基于矩阵分解理论,对观测信号的相关矩阵进行特征值或者奇异值分解,利用分解得到的最大和次大特征向量实现伪码序列估计,算法抗噪性能较强,但进行矩阵分解时会产生正比于矩阵维度三次方的计算量,导致算法收敛速度较慢。神经网络算法通过训练,可使权值向量收敛于相关矩阵的最大特征向量,进而实现伪码序列的盲估计,但是其效果受初值以及训练参数的影响很大。子空间追踪算法是特征分解算法的一种快速算法,通过自适应迭代的方式使权值收敛到主特征向量以完成伪码序列的盲估计,算法存在抗噪性能不强的问题。
针对现有算法存在的计算量大或抗噪性能较差的问题,本文提出一种基于k-means聚类的直扩信号伪码序列和信息序列盲估计算法。算法主要分为两步,信息序列估计和伪码序列估计。首先将采样后的接收信号按照信息码宽度分割得到若干段信息向量,然后利用k-means算法将向量聚为两类,随后将两类向量的信息码分别赋值为±1,最后按照分割顺序排列即可完成信息序列盲估计。在此基础上,对数据向量进行同相相加反向相减的操作以改善信噪比,然后按照伪码宽度对数据向量进行再分割并聚类,随后对两类向量进行±1的赋值,最后按照分割顺序排列,即可完成伪码序列估计。
本方法可以在伪码序列未知的情况下,直接对信息序列进行估计。对于伪码序列估计,传统的基于矩阵分解的方法,在伪码周期长采样点多的情况下,相关矩阵会变得巨大,矩阵分解的计算量会急剧增加,计算速度会严重下降。通常采用的办法是利用码片速率对信号再次进行采样,但是这样浪费了大量采样点信息会导致算法抗噪性能下降,本方法解决了这一问题。
2 信号模型
通过加性高斯白噪声信道后,接收机接收到的短码直扩基带信号模型为
r(t)=s(t)+n(t)=m(t)p(t)+n(t)
(1)
其中s(t)为基带直接序列扩频信号,
为取值为{+1,-1} 的等概率分布的信息序列,信息码片宽度为Tb,g(t)为宽度为Tb的矩形窗函数;
为取值为{+1,-1} 的伪码序列,Tc为伪码码片宽度;q(t)为发射滤波器、信道冲激函数和接收滤波器的卷积;伪码序列的长度为N,由于信号采用短码扩频方式,信号具有一周期伪码扩展一位信息码的特点,即Tb=NTc。n(t)是均值为零,方差为
的高斯白噪声且与s(t)不相关。
3 直扩信号信息码序列盲估计
3.1 盲估计原理
由于本文研究的信号类型为短码直扩信号,具有一周期伪码扩展一位信息码的特点,所以又可将信号写作如下形式
(2)
其中,
为一个周期的伪码波形;ak为取值为{+1,-1} 的等概率分布的信息序列;本文假设已经估计得到伪码周期(信息码宽度)Tb、伪码宽度Tc以及信号失步点[10-11]。根据伪码周期和伪码宽度,可计算得到伪码序列长度。根据信号失步点,可以对接收信号进行同步,保证信号严格从信息码序列和伪码序列同步处开始。随后将同步后的信号进行采样得到信号向量r,按照采样周期为Ts,随后再将向量r按照信息码片的宽度L=Tb/Ts进行分割。分割后得到M个信息码片向量,此时每个码片向量都包含一个完整周期的伪码序列,并且每个码片都在时间上严格对准,分割后得到的码片向量可以表示为
x(k)=s(k)+n(k)=
akp+n(k)(k=1,2,3,...,M)
(3)
其中s(k)表示第k段有用信号;ak表示第k段扩频序列扩展的信息码;p表示一个完整周期的伪码波形p0(t)采样后的向量;n(k)为高斯白噪声。
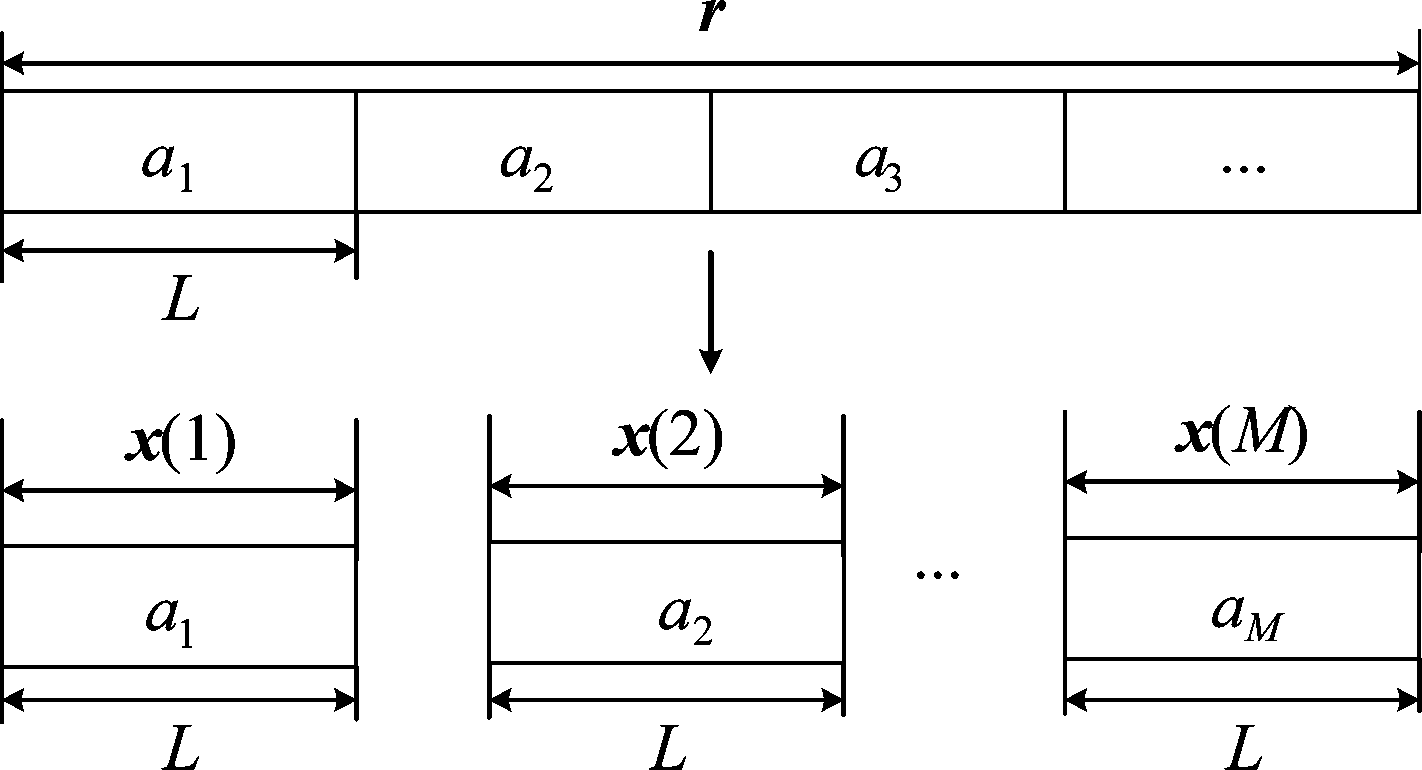
图1 信号分割示意图
Fig.1 Schematic diagram of signal segmentation
在非协作方对直扩信号进行盲估计时,由于直扩信号自身的特点,最终估计得到的信息序列和伪码序列可能与原始序列之间存在180°的相位模糊,即估计得到的序列可能为原序列或者原序列的反码,在没有其他信息(如扩频码的类型)的条件下,整体的相位模糊是无法消除的。但是这并不影响用估计得到的序列来对接收解扩或者主动发出干扰信号[12]。所以非协作方在进行直扩信号信息或伪码序列盲估计时,在没有其他附加信息的条件下,估计得到原始序列或者原始序列的反码即可达到序列盲估计的目的。
信息序列可以表示为
a=[a1,a2,a3,...,aM]
(4)
其中ak取值为±1,且满足均匀分布。由于在进行信息序列盲估计时估计得到±a都能达到盲估计的目的,因此在进行序列估计时,关键在于将取值不同的两类信息码进行分类,而二者的具体取值则不影响最终盲估计的效果。观察式(3)可以发现,不同的信息向量x(k)差别恰好在于信息码ak的取值上(同时存在高斯白噪声的干扰),因此只要将信息向量聚为两类即可完成信息码ak的分类,最后只需将已聚类完成后的两类向量的信息码分别赋值为±1,再按照分割顺序k排列即可完成信息序列的盲估计。由于需要指定聚类的类簇数量,所以本文选择k-means算法作为聚类算法。
3.2 k-means算法
K均值聚类(k-means)算法是最常用的聚类算法之一,它的作用是将相似的样本自动归到一个类别中。基本思想是以空间中的K个点作为类簇中心,将数据集中的每个点分到距离其最近的类簇当中去,随后按照每个类簇的所有点重新更新类簇中心,然后再迭代进行分配点和更新类簇中心的步骤,直到类簇中中心不再进行改变,或者改变小于某一阈值,算法结束。算法的具体流程为:
步骤1 从数据集中随机选择k个样本作为初始类簇中心向量{μ1,μ2,...,μk},对应的类簇分别为{C1,C2,...,Ck}。
步骤2 计算数据集中各样本点xj到各类簇中心向量之间的马氏距离
djk=‖xj-μk‖
(5)
步骤3 将xj划到距离最近的类簇,并得到各类簇的向量个数nk。
步骤4 计算新的类簇中心
(6)
步骤5 重复步骤2和3,直到类簇中心不再发生变化或改变小于所设置的阈值。
3.3 信息码片估计算法步骤
步骤1 将接收到的信号连续采样,采样周期为Ts,随后按照信息码宽度L=Tb/Ts对观测信号进行分割,得到M个信息码片向量{x(1),x(2),...,x(M)}。
步骤2 采用k-means算法将M个信息码片向量{x(1),x(2),...,x(M)}聚为两类,两个类簇分别记为C1和C2,用
代表第k个码片的信息码估计值,将第一类码片信息码值令为+1,第二类码片令为-1,即:
步骤3 将聚类后各信息码的估计值按照分割顺序k排列,即可完成信息序列盲估计,用
表示盲估计信息序列,则:
4 伪码序列盲估计
4.1 信号预处理
在进行信息序列估计时已分割得到M个信息码片向量{x(1),x(2),...,x(M)},每个向量x(k)都包含一个完整周期的伪码序列,此时将任意一个信息码片按照伪码宽度Lc=Tc/Ts进行再分割,都可以得到N个伪码码片向量,向量可以表示为
y(k)=q(k)+n(k)=
bkq+n(k)(k=1,2,...,N)
(7)
其中bk为第k段向量中包含的伪码;q为q(t)采样后得到的向量,向量长度为Lc=Tc/Ts;n(k)为高斯白噪声。
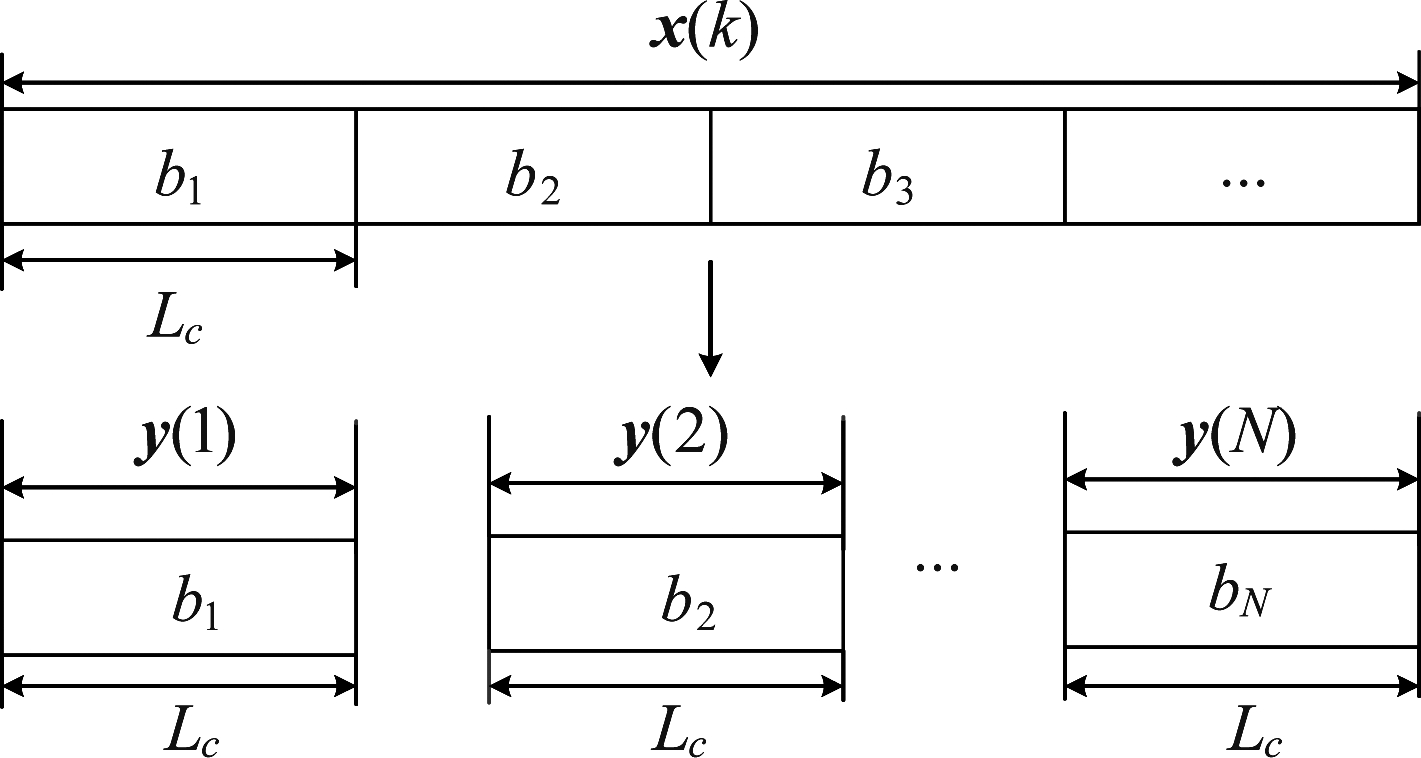
图2 信息码片分割示意图
Fig.2 Information slice segmentation diagram
在分割得到N个伪码向量的基础上,再采用与信息码估计相同的步骤可以完成伪码序列的估计。但此时估计出来的伪码序列误码率会很高,并且采用不同的信息码片会得到不同的结果。这是由于进行伪码序列盲估计时,仅仅使用了一个信息码片的数据,浪费了大量的观测数据导致信噪比较低,估计的效果差。
为了改善码片向量的信噪比,提高伪码序列估计的正确率。在信息码片进行分割之前,首先对已分类的信息码片向量进行预处理,预处理的方式是对两类信息码片向量进行同相累加反相相减的操作。假设估计得到信息码ak为+1的向量为:
x+1(i)=p+n(i)(i=1,2,3,…,m)
(8)
信息码ak为-1的向量为:
x-1(j)=-p+n(j)(j=1,2,3,…,n)
(9)
其中m为信息码为+1的信息码片的数量;n为信息码为-1的码片数量,且m+n=M;p为一周期伪码波形p0(t)经过采样得到的向量。
假设每个码片的信噪比为:
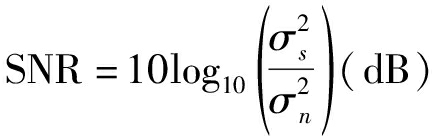
(10)
其中
为信号的方差,为噪声的方差。
首先分别对ak=±1的两类信息码片向量进行同相累加:
(11)
(12)
随后再对两类码片向量进行反相相减:
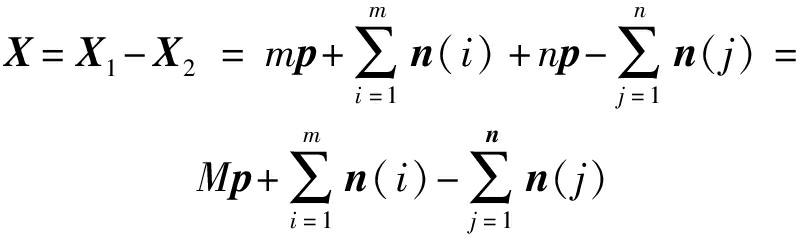
(13)
对信号进行同相相加反相相减的处理之后,信号幅度变成了原来的M倍,信号的方差则变为原来的M2倍;而噪声由原来的n(i)变为:
(14)
噪声的方差变为:
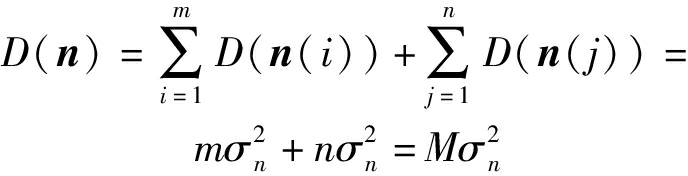
(15)
信噪比则提升为:
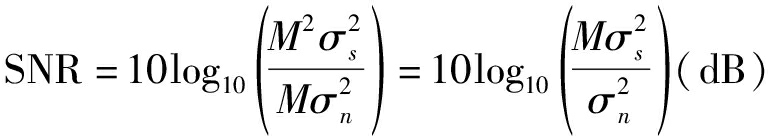
(16)
通过比较式(16)和式(10)可以得出信噪比提升了10log10(M)(dB),并且信息码片数量M的值越大,对码片信噪比改善程度就越高。信号预处理后,将已改善信噪比的信息码片按照伪码宽度Tc进行分割,随后再使用k-means算法对分割后码片进行聚类,聚类后操作与信息码估计一致,即可完成伪码序列的估计。
4.2 伪码估计步骤
步骤1 在完成信息码估计的基础上,首先对信息码片采用同相相加反相相减的方法改善信噪比。
步骤2 完成改善信噪比的操作以后,再对信息码片按照伪码宽度Lc=Tc/Ts进行分割,得到N个伪码码片向量{y(1),y(2),...,y(N)}。
步骤3 将N个伪码码片向量{y(1),y(2),...,y(N)}用k-means算法聚为两类,两个类簇分别记为C1和C2,这里使用的是k-means算法中的二分类情况。用
代表第k个码片的伪码估计值,将第一类码片信息码值令为+1,第二类码片令为-1,即:
步骤4 将聚类后伪码码片按照分割顺序排列,即可得到伪码序列估计,用
表示盲估计信息序列,则:
5 算法复杂度分析及仿真实验
5.1 算法复杂度分析
算法的复杂度指的是算法实现时所使用的乘法以及加法次数,奇异值分解算法的复杂度主要包括两个部分,分别为构造相关矩阵和奇异值分解[5],信息序列估计和伪码序列估计的复杂度分别为O(L2M+M3)和O(M2L+L3);神经网络算法复杂度在于输入向量与权值向量的乘法所消耗的复杂度,每次训练消耗的复杂度再乘以训练次数,即为神经网络方法最终的复杂度。而本文算法复杂度主要来源于k-means算法进行迭代时计算向量距离类簇中心马氏距离距离时所使用的复杂度,此外算法复杂度还与k-means算法迭代次数有关,三种算法的复杂度对比如表1所示。
表1 算法复杂度对比
Tab.1 Comparison of algorithm complexity
算法名称伪码序列盲估计信息序列盲估计奇异值分解算法神经网络算法O(M2L+L3)O(k1ML)O(L2M+M3)O(k1ML+ML)本文算法O(k2ML+k3L)O(k2ML)
其中,M为信息码片的数量;L为每个信息码片向量的长度;k1为神经网络方法迭代次数,k2和k3分别为两次k-means算法的迭代次数。
经过实验验证在对码片进行二分类时,信息码片数量在1000以内、信噪比大于-22 dB的条件下,k-means算法的迭代次数通常维持在5次以内。再结合表1数据可以看出,本文算法在算法复杂度方面要明显优于奇异值分解算法,并且奇异值算法在伪码序列和信息序列长度增长时,算法的运算量会急剧的增加。与神经网络算法的比较来看,两种方法的复杂度主要取决于迭代次数和训练次数,在序列长度增长时,算法复杂度二者相当。
5.2 仿真实验
实验1 算法可行性分析
短码直扩信号采用BPSK调制,PN码为长度N=255的Gold序列,信息码片宽度Tb=25.5 μs,伪码宽度为Tc=0.1 μs,采样速率为fs=100 MHz,假设PN码和信息码同步的时刻Tx=0。在实验中,每次均匀随机产生一位信息码,然后用它去调制PN码序列产生一周期Tb的信号,再加入零均值高斯白噪声,就生成一个信息码片数据,信噪比SNR取-8 dB,信息码片数量M取500,验证算法的可行性。图3(a)是本文算法估计信息序列与原始信息序列的对比,图3(b)表示伪码序列估计结果与原始伪码序列估计的对比结果(为了直观展示对比效果,图上仅显示前50个码片的对比效果),实验结果表明本文算法能够有效的估计信息码以及扩频码。
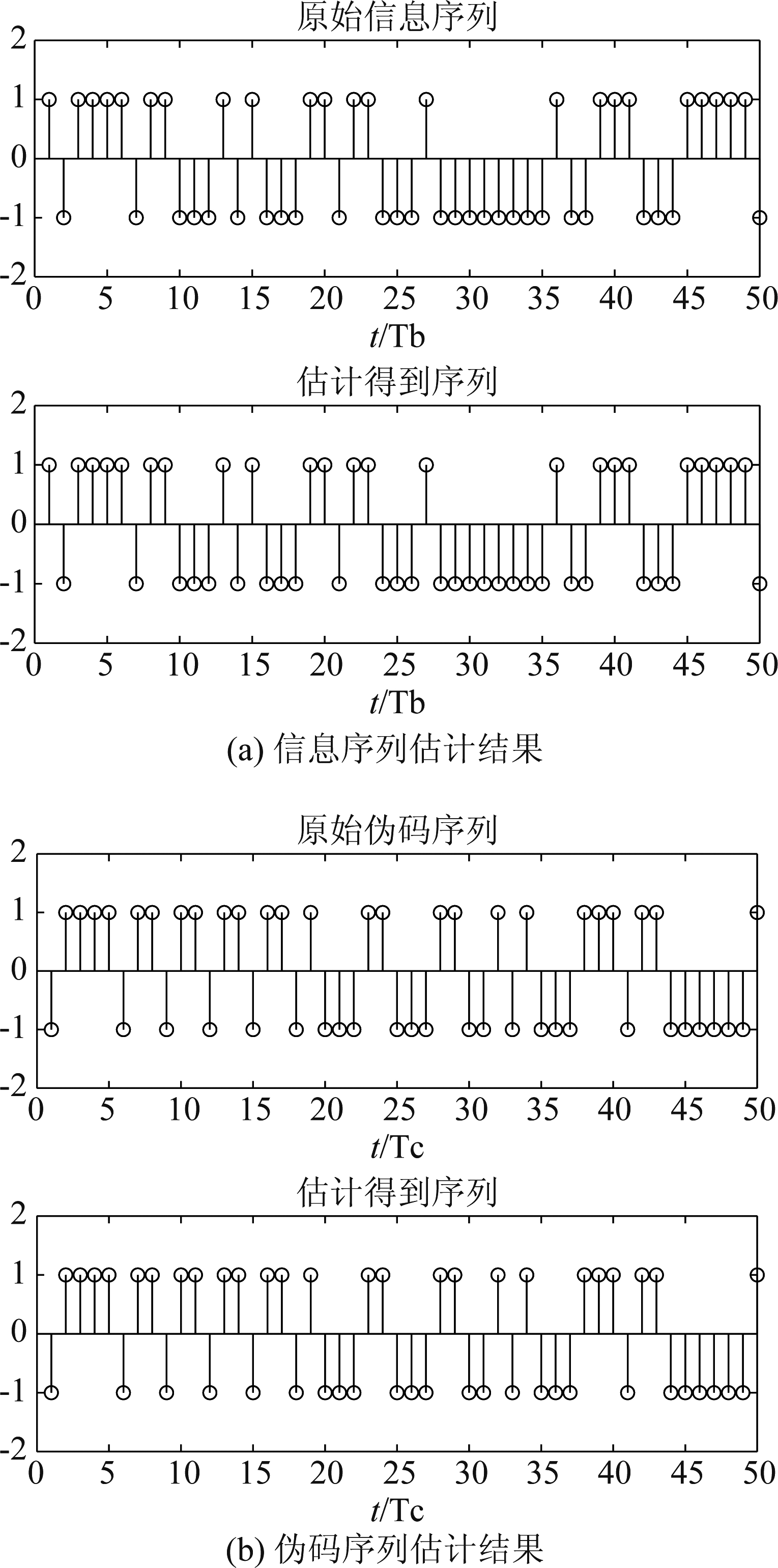
图3 算法盲估计序列和原始序列对比图
Fig.3 Comparison diagram of blind estimation sequence and original sequence
实验2 算法抗噪性能分析
为了阐明算法的性能,定义序列盲估计误码率为:
误码率=极性错误码元数量/序列长度(估计序列与原序列同相时)
误码率=极性相同码元数量/序列长度(估计序列与原序列反相时)
短码直扩信号采用BPSK调制,PN码分别取长度255的Gold序列,信息码片宽度Tb=25.5 μs,伪码宽度为Tb=0.1 μs,采样速率为fs=100 MHz,假设PN码和信息码同步的时刻Tx=0。在进行误码率随信噪比的变化性能仿真时,信息码长度M取500,信噪比取-22 dB到0 dB,对每个信噪比做100次蒙特卡洛仿真,图4(a)为信息序列盲估计误码率随信噪比的变化曲线,图4(b)为伪码序列盲估计误码率随信噪比的变化曲线,实验结果可以看出本算法在低信噪比条件下也能保持较高的估计正确率。
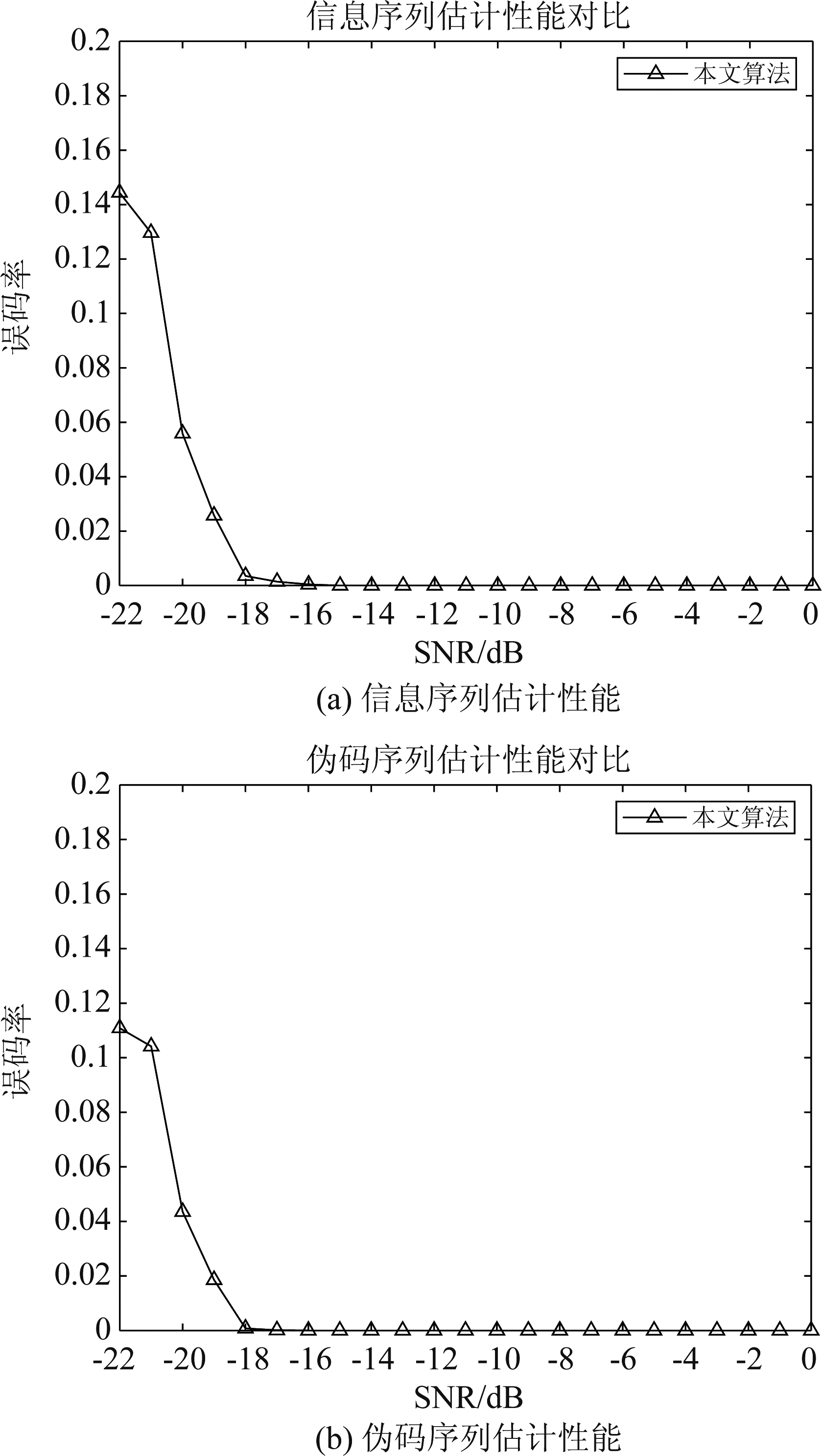
图4 信息序列与伪码序列估计性能
Fig.4 Information sequences and Pseudo-Noise sequences estimate performance
实验3 算法抗噪性能对比
短码直扩信号采用BPSK调制,PN码为长度N=255的Gold序列,信息码片宽度Tb=25.5 μs,伪码宽度为Tb=0.1 μs,采样速率为fs=100 MHz,假设PN码和信息码同步的时刻Tx=0。在进行误码率随信噪比的变化性能仿真时,信息码长度M取1000,信噪比取-22 dB到0 dB,对每个信噪比做100次蒙特卡洛仿真,图5(a)为信息序列盲估计误码率随信噪比的变化曲线,可以看出本文算法与奇异值分解算法的抗噪性能相当且优于神经网络方法;图5(b)为伪码序列盲估计误码率随信噪比的变化曲线,可以看出本文算法在伪码盲估计的抗噪性能优于神经网络方法和奇异值分解算法相当。且在此条件下,当信噪比大于-19 dB时,可以做到0误码率。
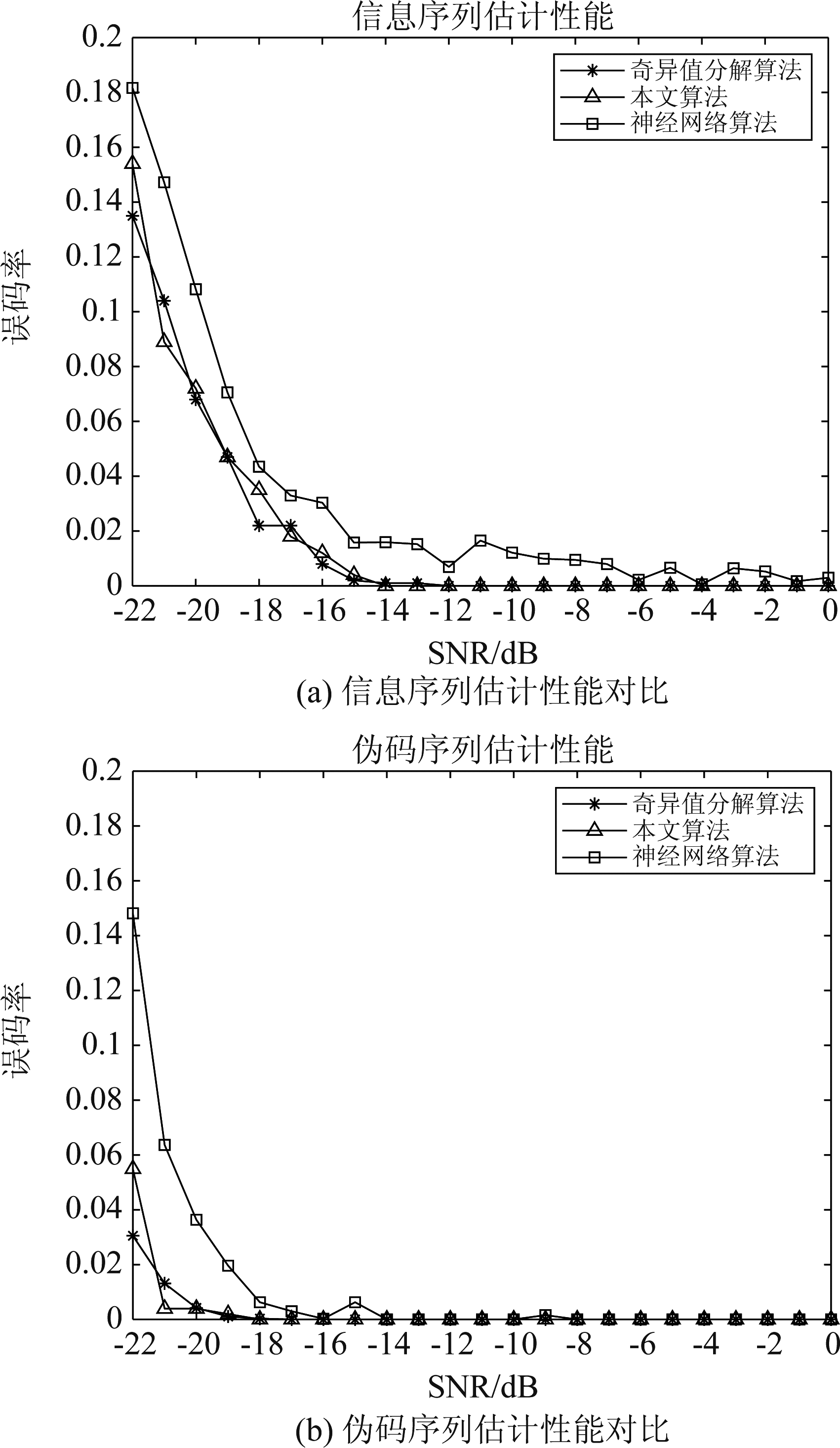
图5 信息序列与伪码序列估计性能
Fig.5 Information sequences and Pseudo-Noise sequences estimate performance
6 结论
本文针对现有的矩阵分解算法运算量大,收敛速度慢的问题,提出了一种基于k-means聚类的直扩信号信息序列和伪码序列盲估计算法。算法根据短码直扩信号一周期伪码扩展一位信息码的特点,将接收信号采样后按照信息码片宽度分割,使用k-means算法将码片聚为两类,随后将两类码片的信息码值分别赋值为+1和-1,最后按照分割顺序排列即可得到信息序列的盲估计。在此基础上对信息码片进行同相相加反相相减的处理以改善信噪比,随后再对处理后的信息码片按照伪码宽度进行分割,最后再对伪码向量进行聚类,即可完成伪码序列估计。实验验证了算法的可行性,并且相较于现有算法具有抗噪性能好、算法复杂度低的优点。
[1] COOK C, MARSH H.An introduction to spread spectrum[J].IEEE Communications Magazine, 1983, 21(2): 8-16.
[2] 解辉, 马俊涛, 姚智刚, 等.基于改进传播算子的DS-SS信号扩频序列盲估计方法[J].电子学报, 2020, 48(1): 9-16.
XIE Hui, MA Juntao, YAO Zhigang, et al.Blind estimation of the spread spectrum sequence of DS-SS signals based on improved propagator method[J].Acta Electronica Sinica, 2020, 48(1): 9-16.(in Chinese)
[3] 詹亚锋, 曹志刚, 马正新.DSSS信号的扩频序列估计[J].电子与信息学报, 2005, 27(2): 169-172.
ZHAN Yafeng, CAO Zhigang, MA Zhengxin.Spread spectrum sequence estimation for DSSS signals[J].Journal of Electronics and Information Technology, 2005, 27(2): 169-172.(in Chinese)
[4] BUREL G, BOUDER C.Blind estimation of the pseudo-random sequence of a direct sequence spread spectrum signal[C]∥MILCOM 2000 Proceedings.21st Century Military Communications.Architectures and Technologies for Information Superiority(Cat.No.00CH37155).Los Angeles, CA, USA.IEEE, 2000: 967-970.
[5] 沈斌, 王建新.基于奇异值分解的直扩信号伪码序列及信息序列盲估计方法[J].电子与信息学报, 2014, 36(9): 2098-2103.
SHEN Bin, WANG Jianxin.Blind estimation of the PN sequence and information sequence of a DSSS signal based on SVD[J].Journal of Electronics & Information Technology, 2014, 36(9): 2098-2103.(in Chinese)
[6] 邱钊洋, 李天昀.面向中频的短码直扩信号数字盲解扩算法[J].系统工程与电子技术, 2020, 42(10): 2366-2373.
QIU Zhaoyang, LI Tianyun.Digital blind despreading algorithm for IF short code DSSS signal[J].Systems Engineering and Electronics, 2020, 42(10): 2366-2373.(in Chinese)
[7] 陆俊, 陆思羽, 刘万洪, 等.直扩信号PN码序列估计的神经网络方法[J].无线电工程, 2011, 41(12): 15-17.
LU Jun, LU Siyu, LIU Wanhong, et al.Neural networks estimation algorithm for PN sequence of direct sequence spread spectrum signals[J].Radio Engineering, 2011, 41(12): 15-17.(in Chinese)
[8] 赵德芳, 张天骐, 金翔, 等.基于BP神经网络的直扩信号扩频码盲识别[J].电讯技术, 2010, 50(10): 28-35.
ZHAO Defang, ZHANG Tianqi, JIN Xiang, et al.DSSS signal spread spectrum codes blind identification based on BP neural network[J].Telecommunication Engineering, 2010, 50(10): 28-35.(in Chinese)
[9] 张红波, 吕明.基于子空间跟踪的扩频码盲估计算法[J].系统工程与电子技术, 2006, 28(10): 1470-1472,1532.
ZHANG Hongbo, LÜ Ming.Blind estimation of PN spreading sequence based on subspace tracking[J].Systems Engineering and Electronics, 2006, 28(10): 1470-1472,1532.(in Chinese)
[10] 朱孝武, 唐斌.基于DS-SS信号相位特性的参数估计[J].电子与信息学报, 2005, 27(9): 1425-1428.
ZHU Xiaowu, TANG Bin.A novel parameter estimation approach to the DS-SS signal with low signal noise ratio[J].Journal of Electronics and Information Technology, 2005, 27(9): 1425-1428.(in Chinese)
[11] 董占奇, 胡捍英, 于宏毅.基于延迟相乘-相关及谱分析的直扩信号检测与符号周期、码片时宽估计分析[J].电子与信息学报, 2008, 30(4): 840-842.
DONG Zhanqi, HU Hanying, YU Hongyi.The detection, symbol period and chip width estimation of DSSS signals based on delay-multiply, correlation and spectrum analysis[J].Journal of Electronics & Information Technology, 2008, 30(4): 840-842.(in Chinese)
[12] 张天骐, 李立忠, 张刚.直扩信号的盲处理[M].北京: 国防工业出版社, 2012.
ZHANG Tianqi, LI Lizhong, ZHANG Gang.Blind processing for signal of direct sequence spread spectrum[M].Beijing: National Defense Industry Press, 2012.(in Chinese)
