1 引言
滑动聚束模式通过方位波束扫描提升了星载合成孔径雷达(Synthetic Aperture Radar,SAR)方位分辨率,同时利用方位波束“足印”的移动拓展了传统聚束模式的观测范围[1]。星载斜视滑动聚束模式通过斜视角度调整能够实现卫星单航过多角度多次观测的能力。此外,斜视滑动聚束模式避免传统星载SAR只能正侧视或小角度斜视成像的观测制约,大幅度提升了星载SAR观测灵活性。能够在不同斜视角下实现灵活观测、提升了星载SAR单航多角度观测能力[2]。星载斜视滑动聚束模式在隐蔽目标探测、军事打击与评估、舰船目标检测与跟踪、洋流测速等方面将有广阔的应用前景。因此,斜视滑动聚束模式将在未来星载SAR系统中得到广泛应用,是未来星载SAR最主要成像模式之一[3-5]。
方位波束扫描角度和斜视角度的增加,使得滑动聚束模式的多普勒总带宽大于系统脉冲重复频率(Pulse Repetition Frequency,PRF),这会导致方位频谱的混叠。近年来,国内外众多学者对滑动聚束模式的频谱混叠问题进行了研究[6],重点对机载平台子孔径频谱的方位向拼接准则[7],大斜视模型的两步式算法[8]、基于子孔径的地面动目标参数估计和聚焦[9]等问题进行了研究,提出了基于波束域[10]、子孔径分块[7-12]和全孔径去斜处理的改进成像算法[13]来消除二维频谱混叠。与机载SAR不同,星载SAR斜距受到轨道高度、地球曲率等因素影响,采用等效斜距模型进行处理会带来较大的相位误差,而高阶斜距模型可以很好地满足星载SAR斜距的计算精度[14-16]。由于目前国内外对星载滑动聚束SAR信号处理方法的研究相对较少或多停留在正侧视和小角度斜视的场景下,多数没有考虑到用等效斜距模型会对星载斜距计算带来的严重误差,本文围绕下面几个方面展开。
在星载斜视滑动聚束模式下,斜视附加多普勒带宽显著增加,且瞬时多普勒中心呈非线性变化,这些给多普勒解混叠带来困难。为了解决这些问题,本文提出了一种基于子孔径处理的星载斜视滑动聚束成像算法。该算法改进了传统子孔径划分方式,并通过两维频谱拓展拼接和距离频率依赖的多普勒滤波来解决子孔径数据仍存在的多普勒混叠,然后再利用基于四阶斜距模型改进的CS算法完成聚焦成像,最后通过计算机仿真验证了方法的有效性。
本文第2节主要分析了斜视滑动聚束模式的方位时频关系,总结了多普勒解混叠过程中需要重点考虑的问题。第3节详细阐述了改进子孔径处理的星载斜视滑动聚束成像算法,并在第4节开展了相应的仿真验证。
2 时频特性分析
星载斜视滑动聚束模式成像几何关系如图1所示,假设星载SAR平台运动速度为νs,方位波束扫描范围为[θs,θe],其中θs为方位波束起始扫描角,θe为终止扫描角,O为方位波束扫描旋转中心,P(x,r)是成像测绘带中任意一个点目标。
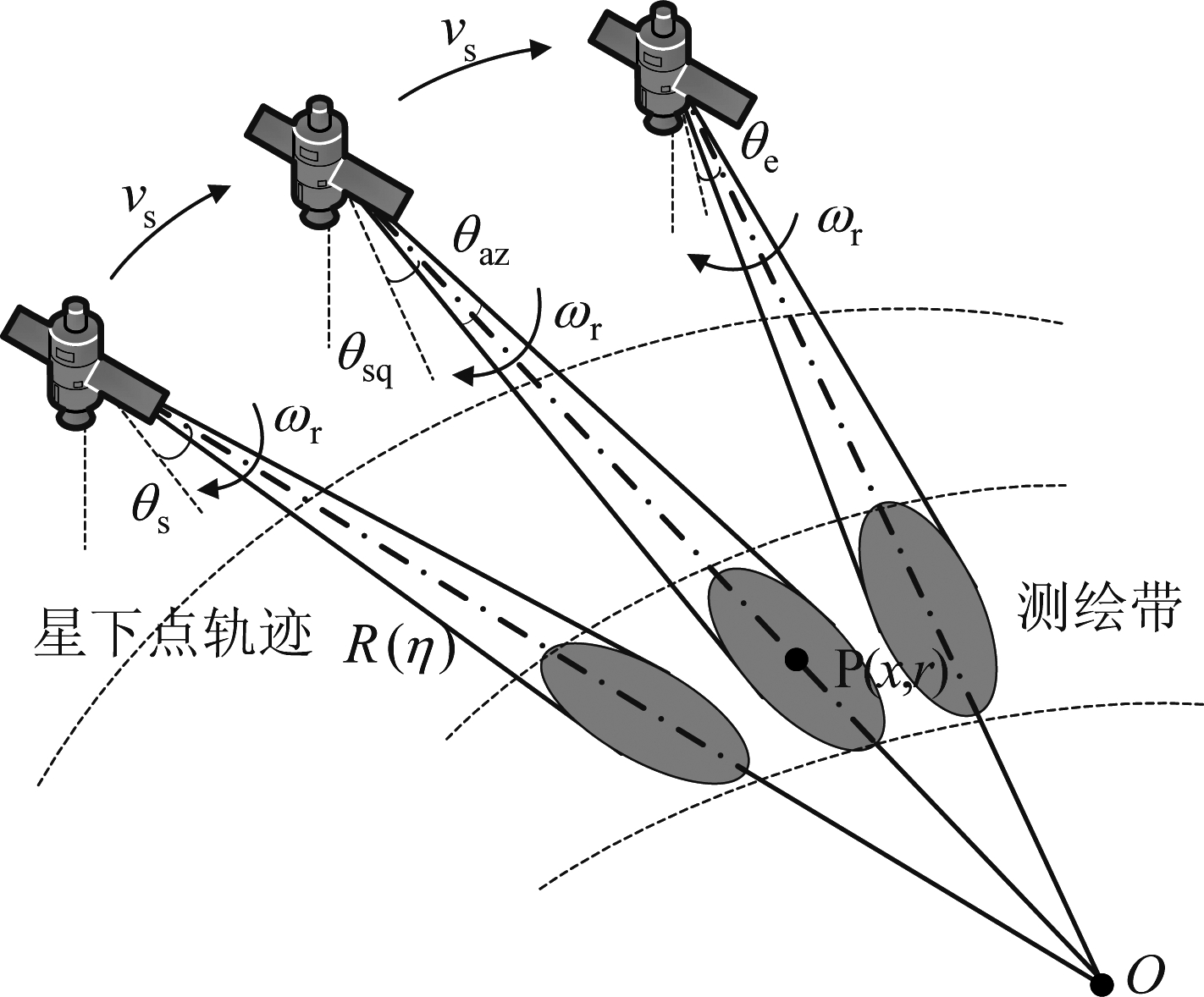
图1 星载斜视滑动聚束SAR成像几何
Fig.1 Imaging geometry of spaceborne squint sliding spotlight SAR
对于任意点目标P来说,它的方位多普勒频率fa可表示为:
(1)
其中,c为光速, fc和fr分别表示载波频率和距离向频率, fr的范围为[-Br/2,Br/2],Br为信号带宽。θm为成像中心时刻斜视角,η为方位时间,△θ∈[-θaz/2,θaz/2]是目标所在照射波束的角度位置,用瞬时斜视角为中心的角度变化量来表示,θaz=0.886λ/(La·cos θm)为3 dB波束宽度,La为方位向天线长度。假设滑动聚束模式的方位总工作时间为T,斜视滑动聚束SAR的多普勒总带宽Btot可以表示为方位瞬时频率最大值与最小值之差
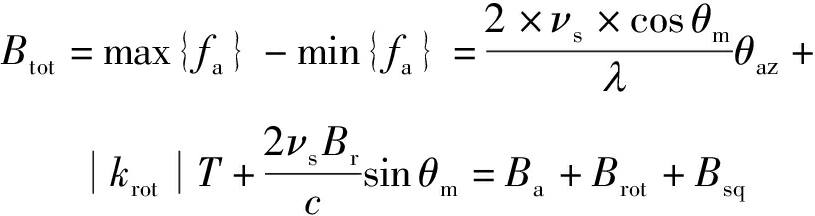
(2)
式中,第一项Ba称为方位波束多普勒带宽;第二项Brot表示由方位波束扫描导致多普勒中心变化引起的波束扫描带宽;第三项Bsq是由斜视角导致的附加带宽,当斜视角度较小时Bsq可被忽略。
斜视滑动聚束模式的方位波束瞬时多普勒中心频率fdm可以表示为:
(3)
上式对η求导,可得系统的多普勒中心变化率krot
(4)
由于滑动聚束SAR波束从后向前进行扫描,方位波束扫描角速度ωr、方位向调频率Ka和多普勒中心变化率krot均为负,且满足|krot|<|Ka|。假设方位波束扫描角速度ωr保持不变,根据fdm和krot的表达式可知,斜视滑动聚束的方位时频关系如图2所示。
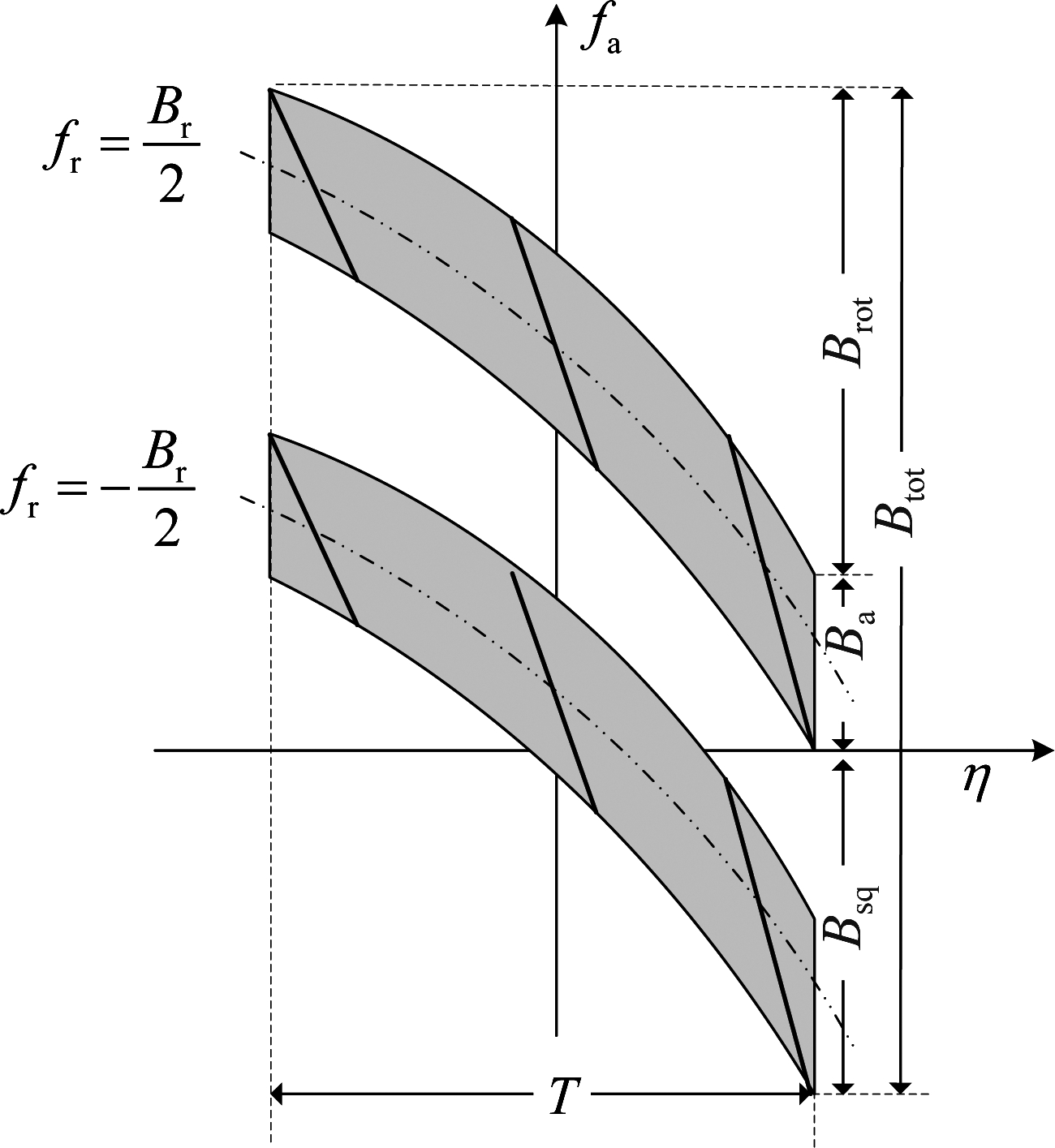
图2 斜视滑动聚束时频关系图
Fig.2 Time-frequency relationship of squint sliding spotlight SAR
为了分析斜视附加带宽Bsq和多普勒中心变化率krot对多普勒总带宽及方位多普勒解混叠的影响,根据表1中仿真参数,图3给出了斜视滑动聚束模式下斜视附加带宽和多普勒中心变化率的变化曲线。从图3(a)斜视附加带宽与斜视角的变化关系可以看出,当中心斜视角θm等于10°、距离向带宽Br等于100 MHz时,斜视附加带宽Bsq与方位波束带宽Ba之和最小为1.63Ba,通常设定星载SAR的PRF值为1.3~1.6Ba,大于系统PRF;此外,随着信号带宽和斜视角的增加,斜视附加带宽Bsq甚至会超过方位波束带宽Ba。图3(b)给出了在±5°的方位扫描角度下多普勒中心变化率随方位时间η的变化曲线,当方位中心时刻斜视角为10°,krot的变化达到了100 Hz/s;当方位中心时刻斜视角为20°,krot的变化将近300 Hz/s。
表1 仿真参数
Tab.1 Simulation parameters
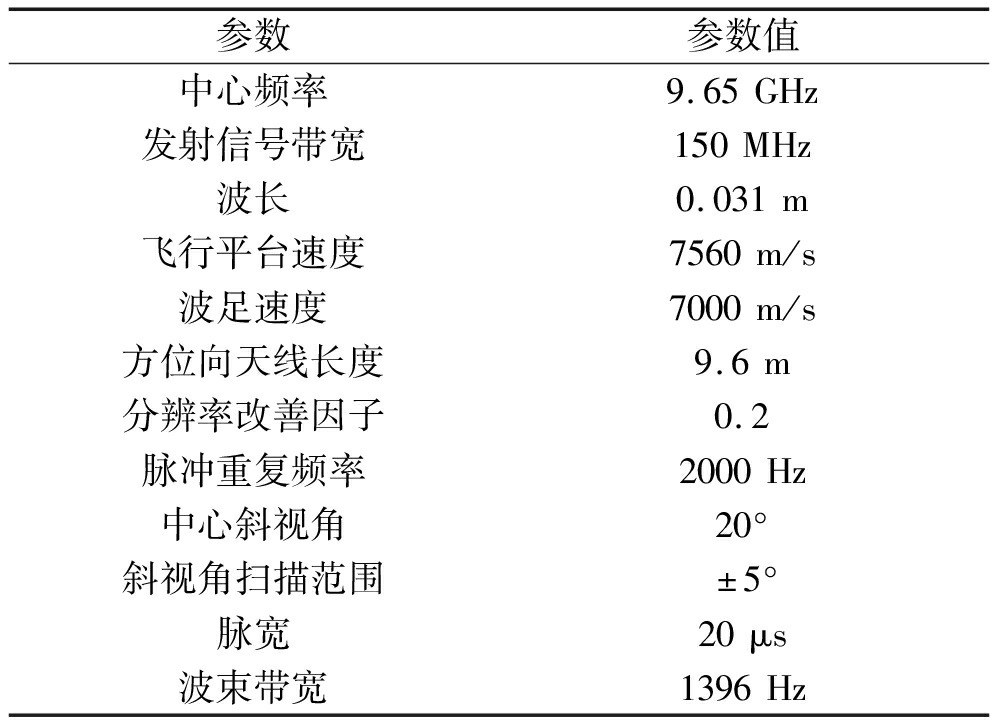
参数参数值中心频率9.65GHz发射信号带宽150MHz波长0.031m飞行平台速度7560m/s波足速度7000m/s方位向天线长度9.6m分辨率改善因子0.2脉冲重复频率2000Hz中心斜视角20°斜视角扫描范围±5°脉宽20μs波束带宽1396Hz
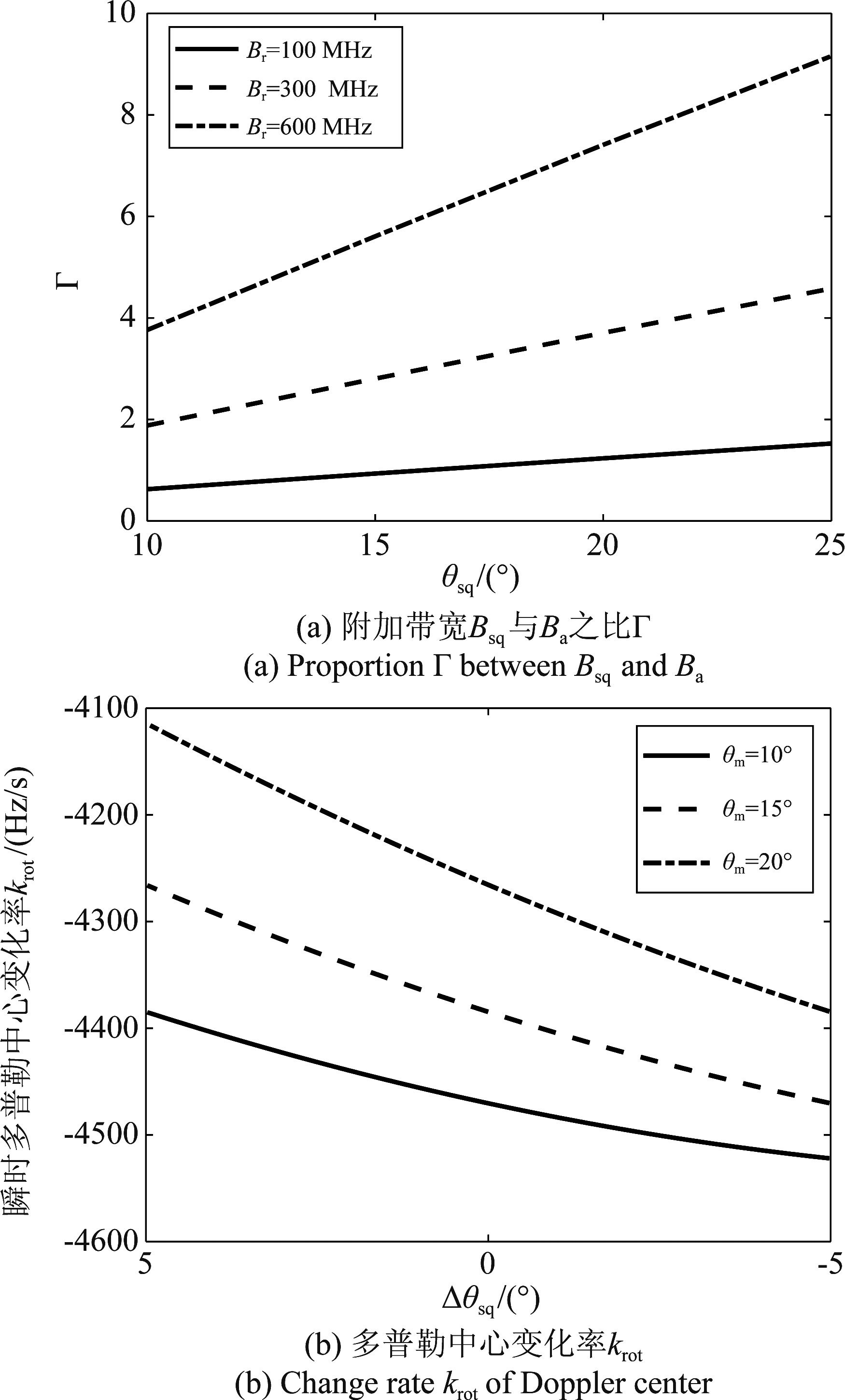
图3 斜视滑动聚束模式下多普勒参数
Fig.3 Doppler parameters in squint sliding spotlight mode
结合图2中的斜视滑动聚束模式的方位时频关系和图3中的多普勒参数仿真结果,可得斜视滑动聚束模式下的时频关系具备以下特点:
(1)随着方位斜视角度和发射信号带宽增加,斜视附加多普勒带宽Bsq不断增加,甚至可能会超出方位波束多普勒带宽Ba,此时系统PRF难以大于瞬时多普勒总带宽;
(2)随着方位波束扫描角度的增加,方位波束多普勒中心krot呈非线性变化,且中心斜视角θm越大,krot的非线性效应就越明显。
滑动聚束模式的多普勒解混叠方法主要分为子孔径分块处理和全孔径“去斜”处理两大类,这两类方法都与瞬时多普勒总带宽和瞬时多普勒中心变化率密切相关。在星载正侧视和小角度斜视滑动聚束模式下,系统PRF大于瞬时多普勒总带宽,且瞬时多普勒中心基本呈线性变化,而这些在斜视滑动聚束模式下难以满足。因此,传统滑动聚束模式多普勒解混叠的子孔径分块处理方法和全孔径“去斜”处理方法都无法直接适用于处理斜视滑动聚束模式。
3 信号处理成像算法
基于子孔径数据分块的斜视滑动聚束SAR成像算法主要由三部分组成:子孔径数据分块预处理、基于四阶斜距模型的CS成像聚焦处理和子孔径拼接处理。方位向子孔径数据分开进行处理,消除了多普勒中心非线性变化的影响。通过两维频谱延拓、拼接和滤波,升高了系统采样率,解决了子孔径数据仍存在的多普勒混叠问题。利用基于四阶斜距模型的CS算法对每段数据分别进行处理、子孔径拼接和方位压缩得到聚焦的SAR图像。本文提出的成像算法的详细流程如图4所示。
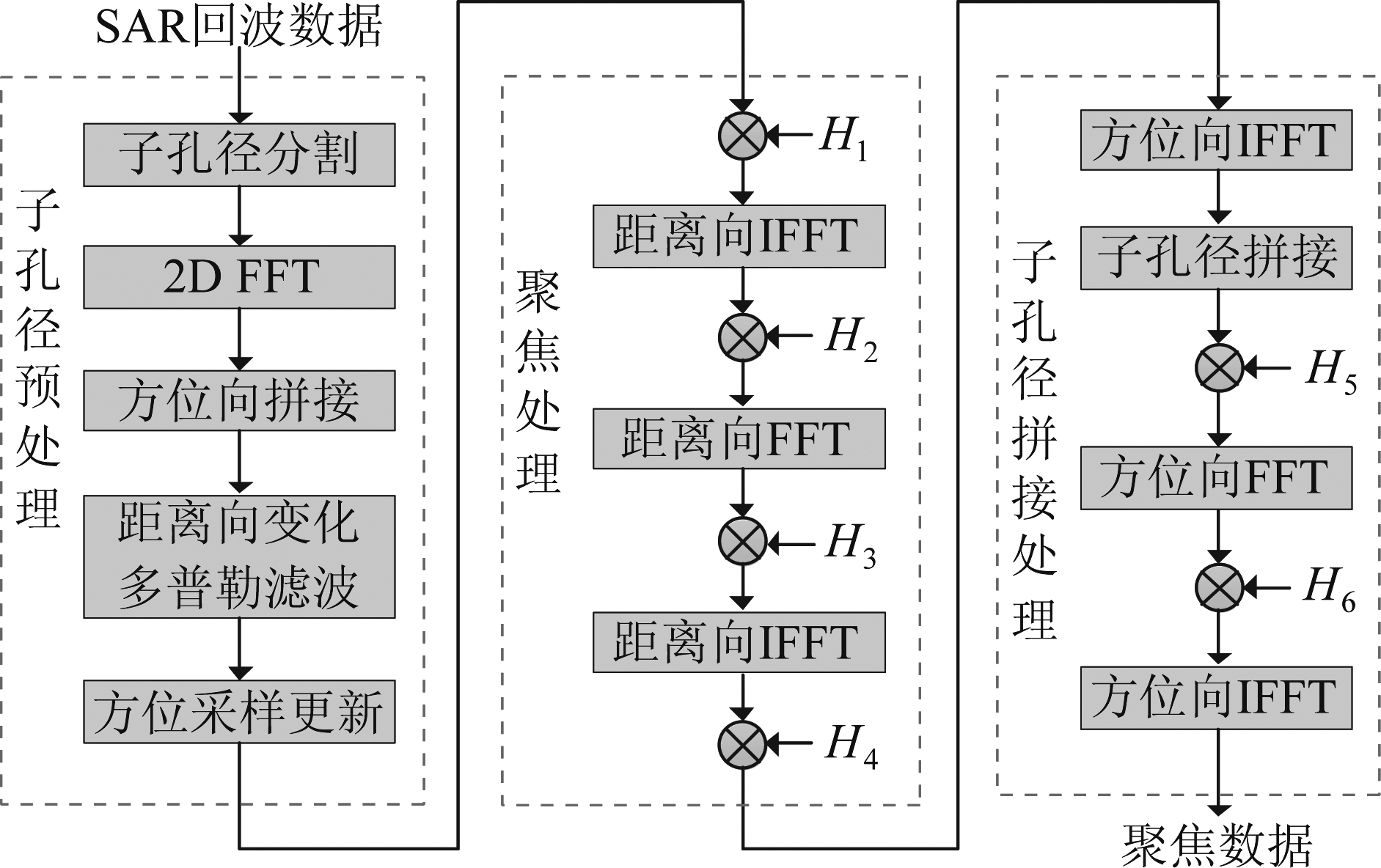
图4 成像算法流程图
Fig.4 Imaging algorithm flow diagram
3.1 子孔径划分及方位预处理
如图5所示,子孔径处理的第一步是将全孔径数据按照方位采样时间T划分为N(N≥2)个子孔径。全孔径数据的精确划分,关乎数据处理效率、孔径拼接和最终的成像质量。
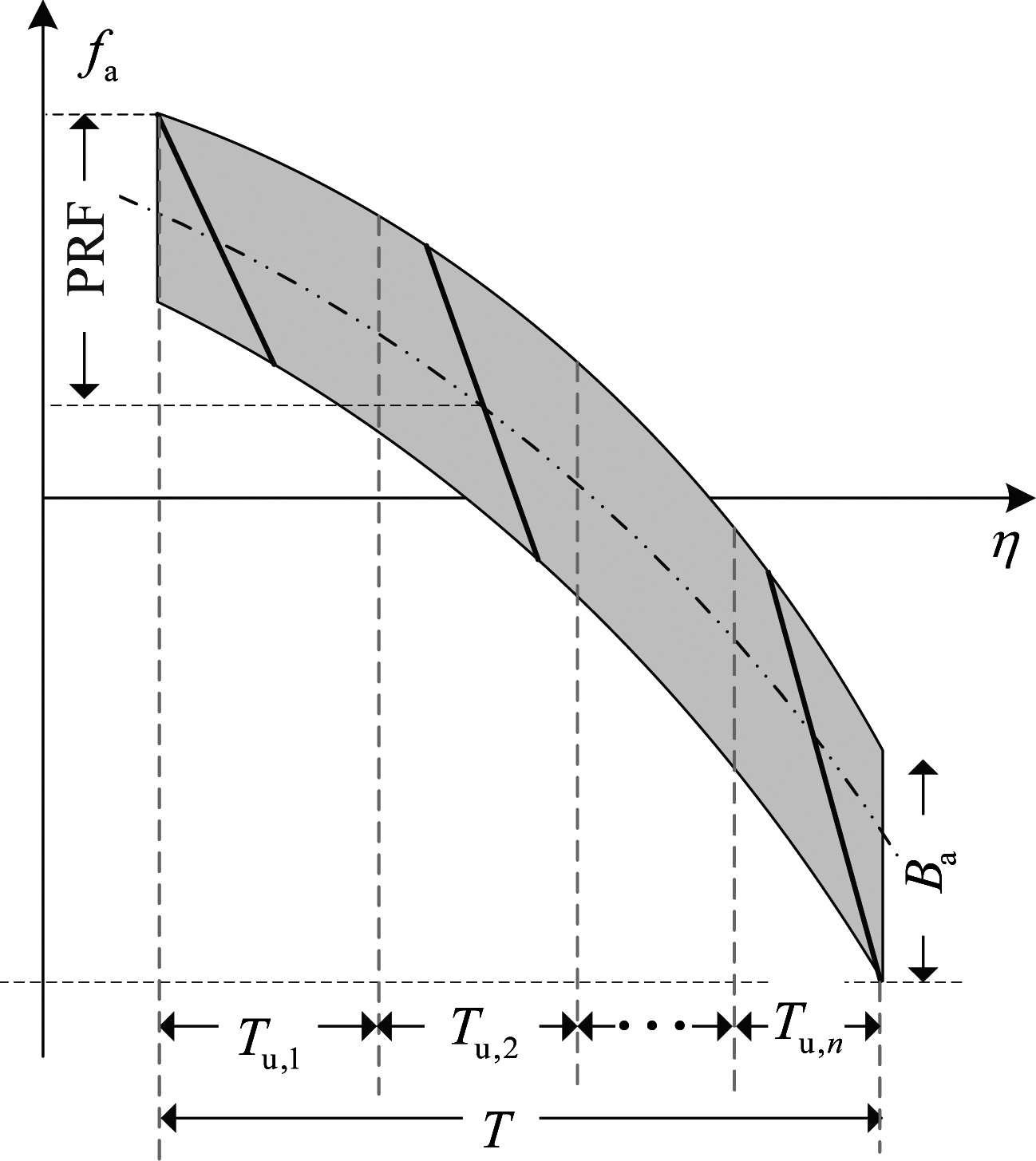
图5 子孔径划分示意图
Fig.5 Sub-aperture partitioning diagram
设子孔径的方位向带宽为Bsub_tot,n,其中n=1,2,…,N。参考等式(2),任意子孔径的方位向带宽同样由三部分组成:
Bsub_tot,n=Ba+Bsq+|krot(ηs,n)|Tu,n n=1,2, …,N
(5)
这里Tu,n为第n个子孔径长度。鉴于任意子块内的方位斜视角变化较小,本文将第n(n=1,2,…,N)个子块起始时刻的多普勒中心变化率的绝对值|krot(ηs,n)|,作为该子块的多普勒中心变化率。采样定理要求系统PRF大于任意Bsub_tot,n,则子孔径上限可以表示为:
(6)
由图3可知min(Bsq/Ba)>0.6,这表明PRF<Ba+Bsq,不满足采样定理;且带入等式(7)计算得Tu,n为负数,与客观事实相矛盾。针对上述问题,本文提出了二维频域马赛克拼接和多普勒滤波的信号预处理方法,步骤如图4所示[13]。首先,在满足采样定理的前提下对等式(7)子孔径分割准则做如下修改
(7)
图6(a)为分割后子块回波数据从二维时域变化到二维频域后的频谱。之所以在单个PRF采样范围内出现图中A1、B2、C3多个点目标的方位频谱,是因为受到斜视附加带宽Bsq的影响。接着,对混叠频谱进行延拓,复制的数量为nF,nF可以表示为:
(8)
复制后的频谱如图6(b)所示。然后,借助距离频率变化的多普勒滤波器采集有效回波信号经过多普勒滤波后的二维频谱如图6(c)所示,此时fa∈[-nF·PRF/2,nF·PRF/2]。由于单个目标的方位总带宽可能小于nF·PRF,为减少数据量,可将系统的方位采样率降为δ·PRF。此时,方位频率fa应满足
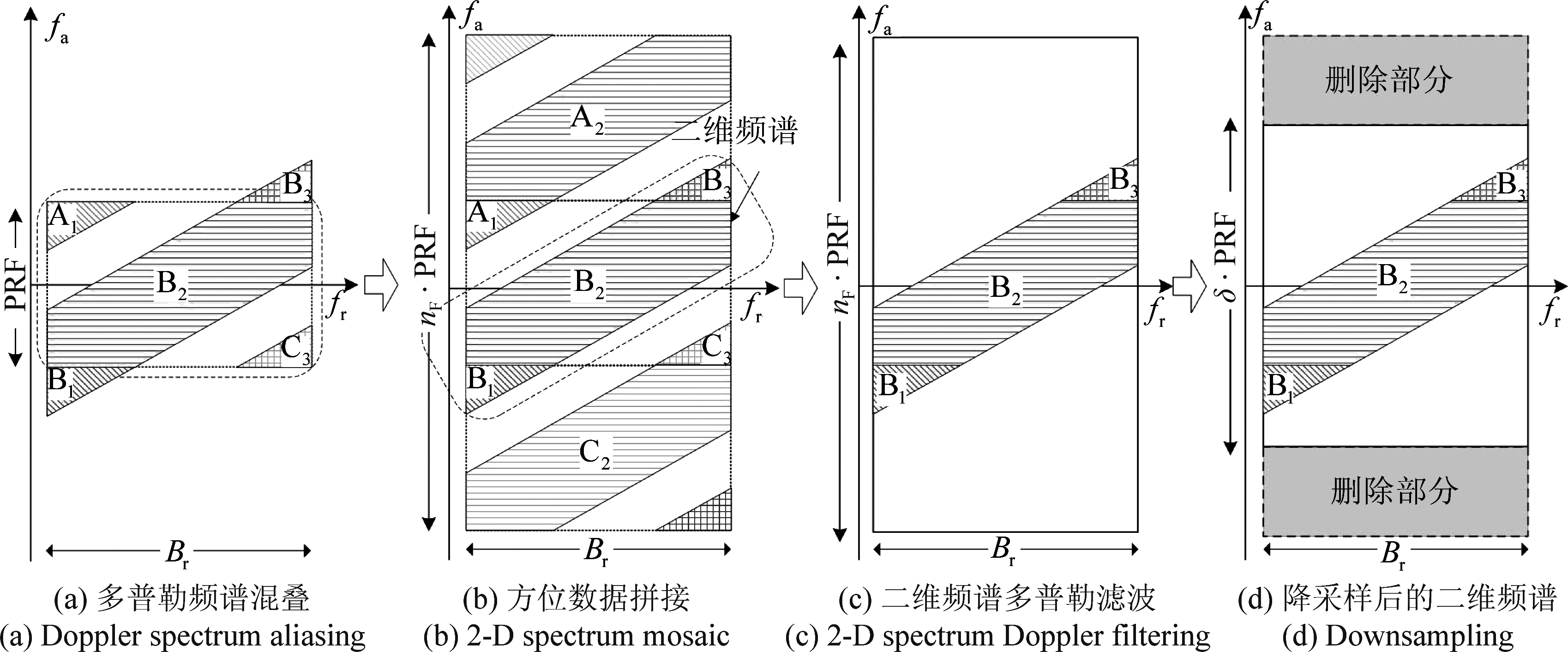
图6 二维频谱方位预处理
Fig.6 2-D spectrum azimuth preprocessing
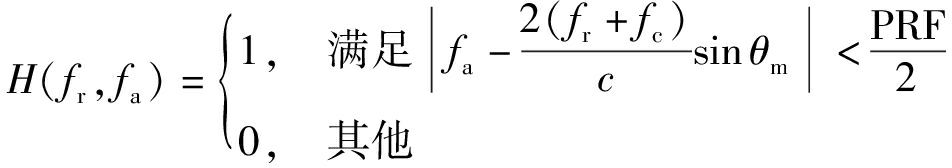
(9)
(10)
此时,δ为过采样率,满足![]() 如图6(d)所示,粗实线框表示数据的采集范围,粗虚线框代表频谱的数据冗余。通过子孔径的预处理,提升了系统PRF,分离出期望采集的二维频谱,消除了krot非线性变化和斜视附加带宽Bsq造成的频谱混叠对采集回波的干扰,减少了数据冗余和计算量。
如图6(d)所示,粗实线框表示数据的采集范围,粗虚线框代表频谱的数据冗余。通过子孔径的预处理,提升了系统PRF,分离出期望采集的二维频谱,消除了krot非线性变化和斜视附加带宽Bsq造成的频谱混叠对采集回波的干扰,减少了数据冗余和计算量。
3.2 信号聚焦
星载SAR工作轨道高、观测范围大,其斜距受到轨道高度、地球曲率等多重因素的影响。由于传统的CS算法建立在机载双曲斜距模型(Hyperbolic Range Model,HRM)的基础上,在用传统的CS算法对大斜视场景下的信号进行处理的过程中发现,采用等效斜距模型会带来较大的相位误差。可采用四阶斜距模型代替原有的双曲线模型,来弥补相位引起的误差[13-16]。四阶模型的计算公式为:
(11)
这里,R0为最短斜距,λ为波长,η为方位向时间。ξ1,ξ2,ξ3和ξ4是高次相参数。由于斜视场景高分辨率星载滑动聚束SAR模式的合成孔径时间较长,故改进Chirp Scaling算法的处理流程如图4所示。使用CS算法,需要对其中频率次数大于2的相位进行补偿,补偿函数H1可以表示为:
(12)
其中m=λfr/c,
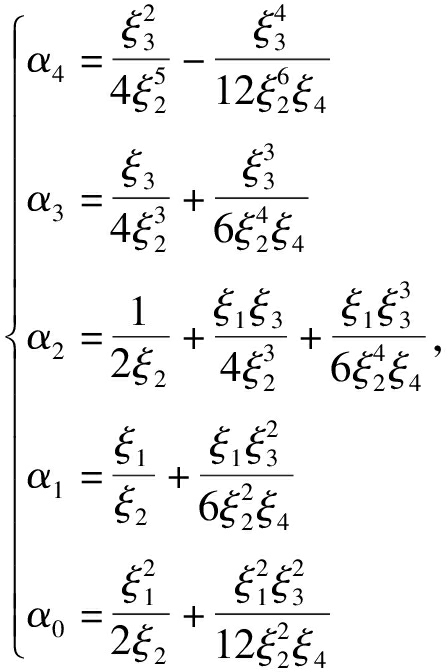 且
且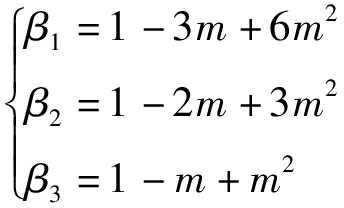
(13)
基于四阶模型的频率变标因子为H2,H2可以表示为:
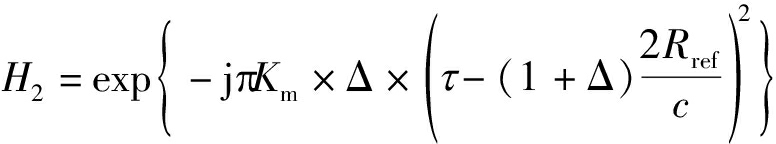
(14)
其中
(15)
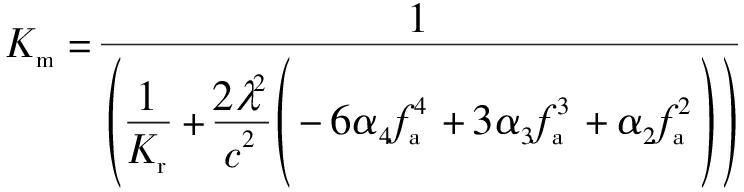
(16)
上式中的Rref为参考斜距,Kr和Km分别为初始时刻的距离向调频率和CS处理后的调频率。距离向FFT的补偿因子为H3,H3可以表示为:
(17)
通过距离向FFT,完成距离相位补偿。通过距离IFFT,进行高阶相位补偿
![]()
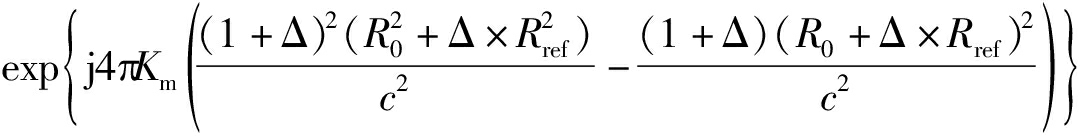
(18)
3.3 子孔径拼接
通过方位IFFT,将频谱变到时域。对单个子孔径按照时间坐标的先后顺序,进行子孔径拼接。在拼接后通过去斜函数H5对方位频谱进行去斜处理:
H5=exp{jπkrot(ηm)η2}
(19)
其中,krot(ηm)为中心斜视角θm对应的多普勒中心调频率。用固定斜率去斜后的方位向总带宽![]() 可以表示为:
可以表示为:
(20)
△fdm(η)=fdm(η)-(krot(η)×η+fdm(ηm))
(21)
其中, fdm(η)为斜视场景下任意时刻的多普勒中心, fdm(ηm)为中心斜视角对应的多普勒中心频率。由于星载滑动聚束SAR通过方位预处理将系统采样率从初始的PRF提升为δ·PRF。在方位向FFT后,通过补偿因子H6,完成方位向补偿。H6可以表示为:
(22)
最后,通过方位向IFFT完成了信号聚焦处理。
4 仿真结果
为验证本文改进的子孔径方位预处理成像方法的有效性,设置一个包含5个点目标、相对几何位置如图7(a)所示的成像场景,并进行仿真验证。SAR回波数据如图7(b)所示,雷达方位向总工作时间9 s,将整个回波数据分成36块子孔径数据,其中第4和第20块子孔径数据分别如图7(c)和(d)所示,可以看出二维频谱在方位向仍存在多普勒混叠现象,子孔径数据的多普勒混叠主要由斜视角导致。图7(e)给出了5个点目标经方位去斜后的二维频谱。图7(f)给出了点阵目标经方位去斜后的仿真结果。
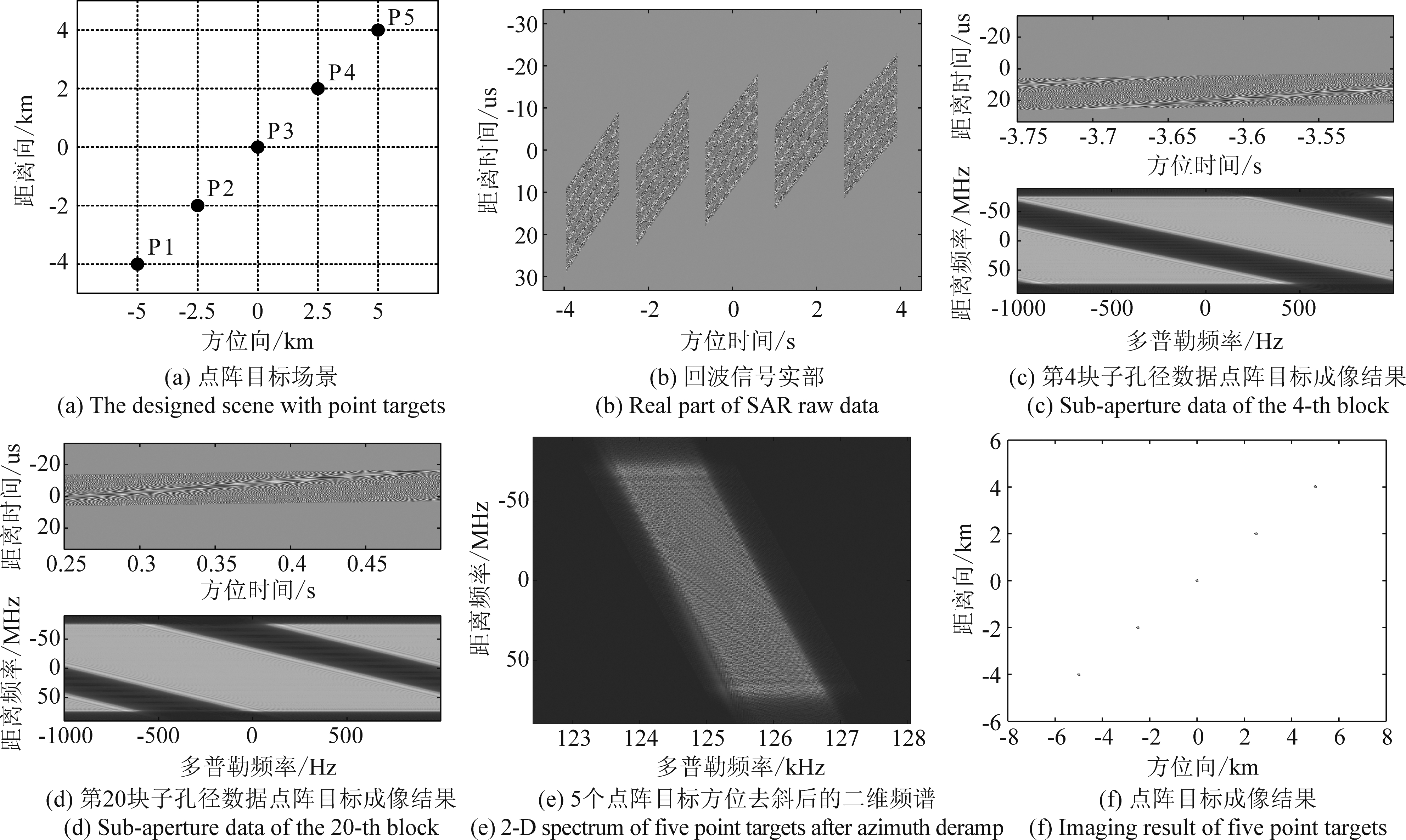
图7 点阵目标成像仿真结果
Fig.7 Imaging results of simulated point targets
在信号处理过程中,方位波束带宽Ba始终存在;波束扫描带宽Brot存在于图7(b)~(d)当中,通过子孔径划分将其打散,并在子孔径拼接后进行去斜处理消除了Brot对成像的影响;斜视附加带宽Bsq存在于信号处理全程,其对信号处理的影响集中在子孔径分割后方位预处理前的图7(b)~(d)。通过本文提出的方位信号预处理方法升高了系统采样率,消除了Bsq对后续处理的影响。图8给出了P1、P3和P5三个点目标的等高线,三个点目标取得了较好的聚焦效果。

图8 不同位置的点目标等高线图
Fig.8 Contour of targets at different positions
为了进一步分析成像结果,表2给出了点目标P1、P3和P5的具体成像性能指标,其中PSLR和ISLR分别表示峰值旁瓣比和积分旁瓣比。三个点目标的距离向分辨率的理论值均为0.886 m、方位向分辨率的理论值分别为0.944 m、0.920 m、0.944 m,对比表中的数据可以看出,各点成像结果性能指标与理论分析基本相符,从而验证了本文提出的星载斜视滑动聚束SAR的子孔径算法的有效性。
表2 点目标成像性能指标
Tab.2 Measured imaging parameters of simulated point targets
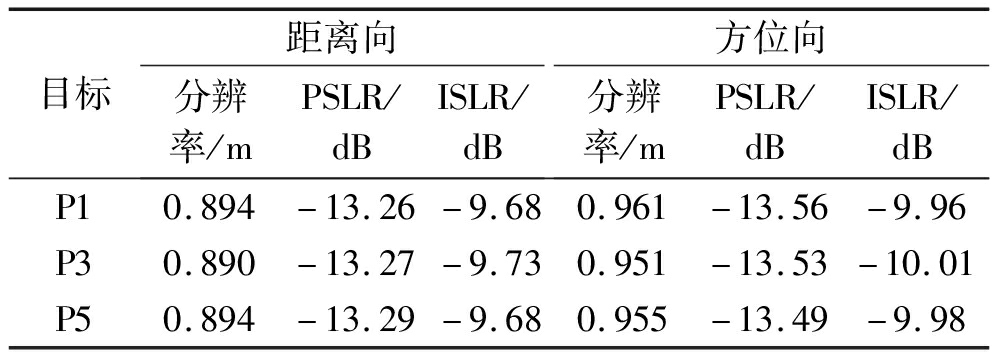
目标距离向分辨率/mPSLR/dBISLR/dB方位向分辨率/mPSLR/dBISLR/dBP10.894-13.26-9.680.961-13.56-9.96P30.890-13.27-9.730.951-13.53-10.01P50.894-13.29-9.680.955-13.49-9.98
5 结论
本文重点对星载斜视滑动聚束SAR的子孔径算法进行研究,通过子孔径分块和方位预处理,提升了系统采样率,消除了大斜视观测场景下,非线性多普勒中心和距离方位耦合带宽引起的频谱混叠。子孔径划分实现了回波数据分段并行处理,这会大大提高系统的运算速度和处理效率。利用星载高阶斜距模型,经过距离方位脉冲压缩、高阶相位补偿,子孔径拼接和去斜等处理步骤,并通过实验仿真,得到了精确聚焦的图像,验证了该方法的有效性。
[1] 王云霞.高分辨率多模式星载SAR成像方法研究[D].成都: 电子科技大学, 2020.
WANG Yunxia.Study of high-resolution Muti-mode spaceborne SAR imaging method[D].Chengdu: University of Electronic Science and Technology of China, 2020.(in Chinese)
[2] 邓云凯, 禹卫东, 张衡, 等.未来星载SAR技术发展趋势[J].雷达学报, 2020, 9(1): 1-33.
DENG Yunkai, YU Weidong, ZHANG Heng, et al.Forthcoming spaceborne SAR development[J].Journal of Radars, 2020, 9(1): 1-33.(in Chinese)
[3] 胡善清, 李慧星, 李炳沂, 等.嵌入式GPU滑动聚束SAR实时成像方法[J].北京理工大学学报, 2020, 40(9): 1018-1025.
HU Shanqing, LI Huixing, LI Bingyi, et al.The real-time imaging method for sliding spotlight SAR based on embedded GPU[J].Transactions of Beijing Institute of Technology, 2020, 40(9): 1018-1025.(in Chinese)
[4] 龙腾, 丁泽刚, 肖枫, 等.星载高分辨频率步进SAR成像技术[J].雷达学报, 2019, 8(6): 782-792.
LONG Teng, DING Zegang, XIAO Feng, et al.Spaceborne high-resolution stepped-frequency SAR imaging technology[J].Journal of Radars, 2019, 8(6): 782-792.(in Chinese)
[5] HE Feng, DONG Zhen, ZHANG Yongsheng, et al.Processing of spaceborne squinted sliding spotlight and HRWS TOPS mode data using 2-D baseband azimuth scaling[J].IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 938-955.
[6] WANG Yunxia, ZHANG Shunsheng, JIA Yuming.Processing azimuth-time domain aliasing in spaceborne sliding-spotlight SAR imaging[C]∥2020 14th European Conference on Antennas and Propagation(EuCAP).Copenhagen, Denmark.IEEE, 2020: 1-5.
[7] 张劲东, 陈家瑞, 朱岱寅, 等.一种斜视滑动聚束SAR子孔径处理成像方法[J].数据采集与处理, 2017, 32(4): 776-784.
ZHANG Jindong, CHEN Jiarui, ZHU Daiyin, et al.Imaging method for sub-aperture processing for squinted sliding spotlight SAR[J].Journal of Data Acquisition and Processing, 2017, 32(4): 776-784.(in Chinese)
[8] LIANG Yi, DANG Yanfeng, LI Guofei, et al.A two-step processing method for diving-mode squint SAR imaging with subaperture data[J].IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 811-825.
[9] HUANG Penghui, MA Jingtao, XU Huajian, et al.Moving target focusing in SAR imagery based on subaperture processing and DART[J].IEEE Geoscience and Remote Sensing Letters, 2021, 18(2): 311-315.
[10] 韩晓磊, 李世强, 王宇, 等.斜视滑动聚束模式SAR成像算法研究[J].电子与信息学报, 2013, 35(12): 2843-2849.
HAN Xiaolei, LI Shiqiang, WANG Yu, et al.Study on squint sliding spotlight mode SAR imaging[J].Journal of Electronics & Information Technology, 2013, 35(12): 2843-2849.(in Chinese)
[11] LI Ning, BIE Bowen, SUN Guangcai, et al.A high-squint TOPS SAR imaging algorithm for maneuvering platforms based on joint time-Doppler deramp without subaperture[J].IEEE Geoscience and Remote Sensing Letters, 2020, 17(11): 1899-1903.
[12] 赵莉, 陈家瑞, 柏磊.一种滑动聚束SAR子孔径成像算法[J].舰船电子对抗, 2019, 42(5): 70-73,78.
ZHAO Li, CHEN Jiarui, BAI Lei.A sliding spotligt SAR sub-aperture imaging algorithm[J].Shipboard Electronic Countermeasure, 2019, 42(5): 70-73,78.(in Chinese)
[13] XU Wei, DENG Yunkai, HUANG Pingping, et al.Full-aperture SAR data focusing in the spaceborne squinted sliding-spotlight mode[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4596-4607.
[14] LUO Yunhua, ZHAO Bingji, HAN Xiaolei, et al.A novel high-order range model and imaging approach for high-resolution LEO SAR[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3473-3485.
[15] WANG Pengbo, HAN Yu, CHEN Jie, et al.A refined chirp scaling algorithm for high-resolution spaceborne SAR based on the fourth-order model[C]∥2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS.Melbourne, VIC, Australia.IEEE, 2013: 2051-2054.
[16] HUANG Lijia, QIU Xiaolan, HU Donghui, et al.Focusing of medium-earth-orbit SAR with advanced nonlinear chirp scaling algorithm[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 500-508.




