1 引言
认知无线电(Cognitive Radio,CR)[1]能够通过系统的频谱感知能力和学习能力,根据通信环境改变信号的调制样式、通信频率、发射功率等无线电参数,实现频谱资源更高效率的利用。对于接收方而言,需要准确知道信号的调制样式才能通过解调获得传递的信息。因此,为了应对通信过程中信号调制样式变化,需要信号调制样式识别方法具有识别多种调制样式的能力,且同时具有识别准确率高、鲁棒性强、运算复杂度低的特点。
传统的信号调制样式识别方法根据分类策略的不同,可以划分成基于决策理论的方法[2-3]和基于模式识别的方法[4-10]。基于决策理论方法通常有着较高的计算复杂度,并且需要大量的先验知识,因此其运算效率较低且灵活性差[11]。基于模式识别方法的通过提取专家特征对调制信号进行识别,而一种专家特征只能有效识别几种特定的调制信号,因此通用性较差。深度学习方法由数据驱动,其优秀的特征提取和分类能力已经在计算机视觉[12-13]、自然语言处理[14-15]等研究领域得到了验证。近年来,研究者们也开始关注深度学习方法在信号调制样式识别问题上的研究与应用[16-23]。
文献[16]中作者使用卷积神经网络(Convolutional Neural Network,CNN)对11种不同调制样式的I/Q信号进行识别,实验结果显示,在信噪比(Signal-to-noise Ratio,SNR)大于4dB时最高识别准确率可以达到87.4%。文献[17]中作者提出了基于降噪自编码器和神经网络的调制识别方法,通过信号的功率谱图识别调制样式,在信噪比超过-4 dB时,该方法对6种调制信号的识别准确率超过95%。文献[18]中作者在DenseNet的基础上进行改进提出了特征融合网络,该方法以信号的频谱图作为输入来识别调制样式,实验结果显示,在信噪比为0dB以上时,该算法对9种调制信号的识别准确率超过90%。文献[19]中作者利用长短期记忆网络(Long Short-Term Memory,LSTM)对4种卫星幅相信号进行调制识别和解调,在信噪比为6 dB时,识别准确率接近98%。文献[16-19]都是单独利用CNN或者LSTM对信号调制样式进行识别,而文献[20-23]使用了CNN与LSTM结合的网络架构。通过CNN减少频率变化,由LSTM提取时序特征,充分利用了CNN与LSTM在建模能力上的互补性[24]。实验结果表明,CNN与LSTM结合的网络架构相比单独的CNN和LSTM网络能够更好地提取I/Q信号特征,从而更有效地识别信号调制样式。
基于CNN-LSTM的网络模型虽然能够对多种调制信号进行有效的识别,但是现阶段的研究工作[21-23]为了追求更高的识别准确率,而忽略了算法复杂度的增加,导致算法对嵌入式设备上的计算能力和存储能力要求较高,最终使得算法难以在实际通信环境中部署应用。然而,如果仅仅是单纯地降低算法的复杂度,则可能造成算法性能的损失,使得识别准确率较低[20]。为了在降低复杂度的同时保证算法有足够的识别性能,本文提出了一种基于多尺度时序特征(Multi-scale Temporal Features,MSTF)的识别算法。该算法通过减小网络宽度、采用小尺寸卷积核和使用降维卷积单元实现了算法复杂度的降低,同时通过增加网络深度以及跨层连接CNN层提取的不同尺度的时序数据,实现了更高语义层次信息的多样化表达,保证了算法拥有较高的识别准确率。实验结果显示,在SNR大于4 dB时,MSTF算法对11种调制信号的识别准确率达到90%以上;与同等识别准确率的算法相比,MSTF算法的训练时间缩短了17%以上,在嵌入式设备树莓派4B上的推理时间缩短了约67%。
2 MSTF算法
MSTF算法的神经网络结构如图1所示,大致可以分为包含卷积模块和连接层(Concatenate)的多尺度时序数据提取部分、LSTM模块以及输出层。

图1 MSTF算法网络结构图
Fig.1 Network structure diagram of the MSTF algorithm
2.1 多尺度时序数据提取部分
MSTF算法中多尺度时序数据提取部分的结构如图2所示,包括了卷积单元、降维卷积单元和连接(Concatenate)层。卷积单元和降维卷积单元有着相同的结构,都是由卷积层、批标准化(Batch Normalization,BN)层和线性整流单元(Rectified Linear Unit, ReLU)组成,其结构如图3所示,不同之处仅仅在于卷积层中卷积核大小的不同。
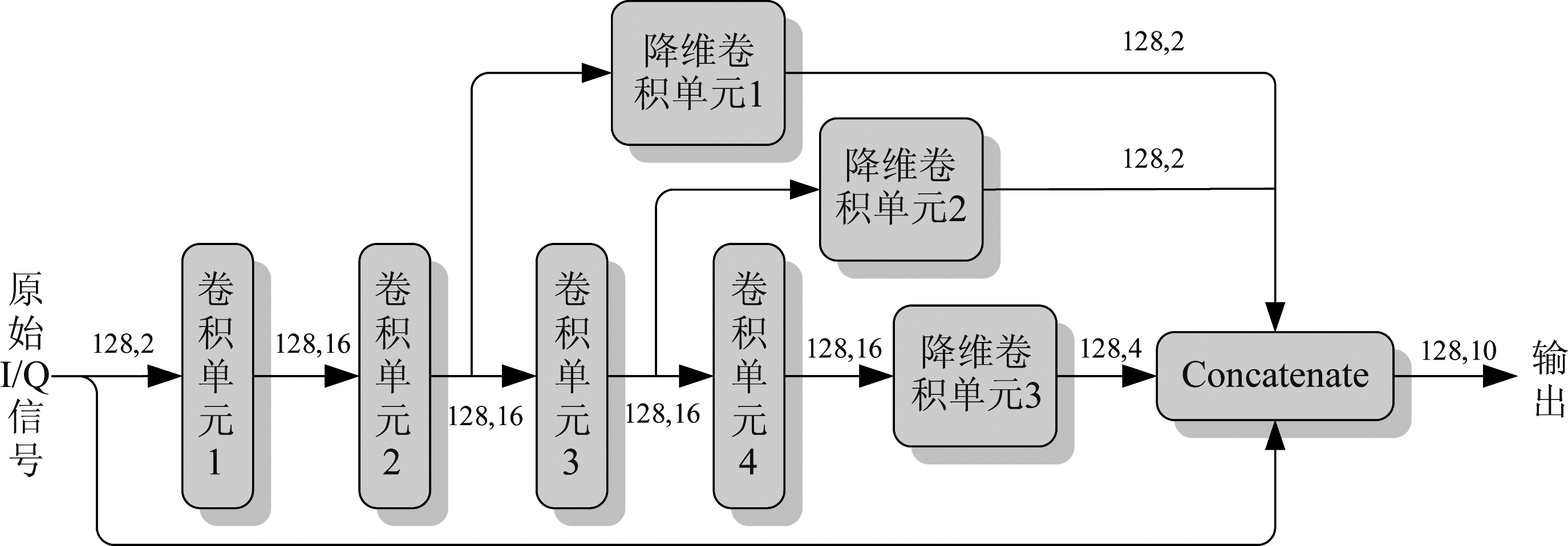
图2 多尺度时序数据提取部分结构图
Fig.2 Structure diagram of multi-scale temporal data extraction section
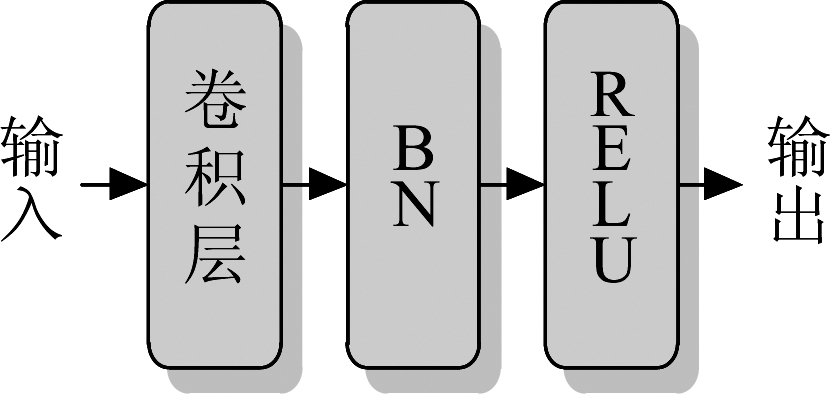
图3 卷积单元和降维卷积单元结构图
Fig.3 Structure diagram of convolution unit and reduced dimensional convolution unit
MSTF算法中卷积层采用的是一维卷积层,计算过程如公式(1)所示,其中,y、h和u分别表示输出序列、卷积核序列和输入序列,k表示输出序列上元素的坐标,N表示输入序列的长度。BN层能够对数据进行标准化处理,让每一层卷积层的输入保持相似分布,加快网络的训练速度并提高网络的泛化能力。BN层的计算过程如公式(2)~(5)所示,其中,n指的是batch size,即一次训练所抓取的数据样本数量,μ是均值,σ2是方差,xi是原始输入数据,![]() 是标准化之后的数据,ε的作用是防止分母为0,通常取值1×10-3,γ和β是可学习的重构参数。ReLU则是作为激活函数使用,其数学表达式如公式(6)所示。
是标准化之后的数据,ε的作用是防止分母为0,通常取值1×10-3,γ和β是可学习的重构参数。ReLU则是作为激活函数使用,其数学表达式如公式(6)所示。
(1)
(2)
(3)
(4)
(5)
ReLU(x)=max(0,x)
(6)
图2中卷积单元和降维卷积单元中卷积层的参数设置如表1所示。原始I/Q信号的I相和Q相数据可以看作在时间轴上采样得到的一维网格数据,输入格式为[128,2]。CNN擅长处理具有网格结构的数据[25],MSTF算法中利用卷积单元对原始I/Q信号进行特征的提取。通过浅层拥有小卷积核的卷积层可以提取局部和细节的特征,通过深层拥有大卷积核的卷积层则可以获得更为全局、语义层次更高的特征。其中,卷积单元1中卷积层的卷积核大小为1,其主要作用是提取I、Q之间的特征信息。随着卷积层的加深,卷积层输出特征图的感受野值越来越大,由于感受野值表示特征图上网格元素在原始输入数据上映射区域的大小,因此对于时序I/Q信号数据而言,不同卷积单元的输出可以理解为不同的时间尺度的时序数据。
表1 不同卷积单元内卷积层参数设置
Tab.1 Parameter settings for convolutional units and reduced dimensional convolution unit
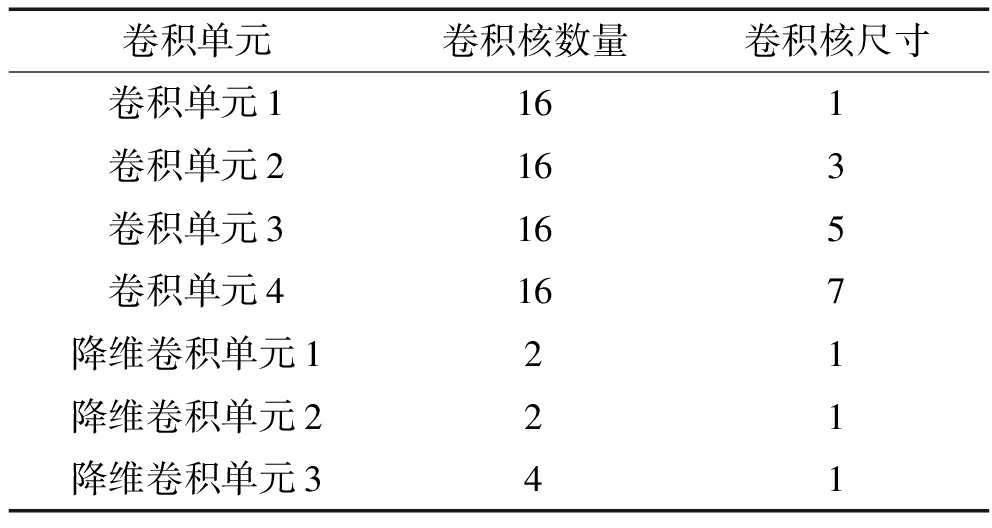
卷积单元卷积核数量卷积核尺寸卷积单元1161卷积单元2163卷积单元3165卷积单元4167降维卷积单元121降维卷积单元221降维卷积单元341
为了充分利用卷积层的输出,增加信息表达的丰富度,MSTF算法利用连接层以跨层连接的方式将不同层次、不同时间尺度的数据进行拼接,如图4所示。为了降低拼接后数据的维度并减少后续的计算量,MSTF算法利用降维卷积单元对卷积单元2、3、4的输出进行降维,以卷积单元2的输出为例,其数据格式为[128,16],降维后的数据格式为[128,2],数据量减少了8倍。由于卷积单元4的输出蕴含更加抽象的特征,因此其降维后的通道数最多,可以增加其在拼接数据中的权重。此外,MSTF算法使用原始I/Q数据代替卷积单元1的输出作为单位时间尺度的时序数据进行拼接,主要原因是原始I/Q数据不需要进行降维,可以减少计算量。

图4 数据拼接示意图
Fig.4 Schematic diagram of data stitching
2.2 LSTM模块
LSTM擅长处理存在时序关系的数据,可以有效提取输入的多尺度时序数据中包含的时序特征。LSTM有两个传输状态:细胞状态(Cell State)和隐层状态(Hidden State),状态传递示意图如图5所示。其中,细胞状态是长期状态,可以传递存在长期依赖的信息。
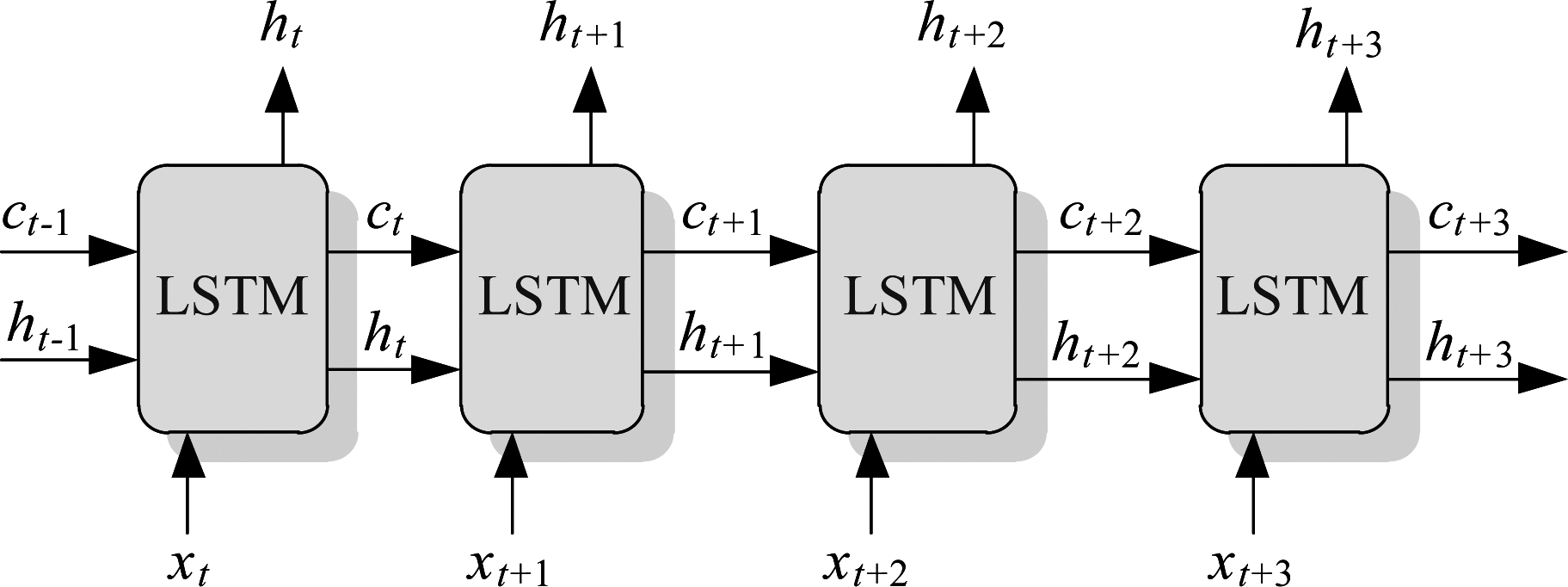
图5 LSTM状态传递示意图
Fig.5 Schematic diagram of LSTM state transfer
LSTM内部信息流动如图6所示,其内部的门控单元包括遗忘门(Forget Gate)、输入门(Input Gate)和输出门(Output Gate),并通过3个数据处理过程实现信息的遗忘、更新和积累。遗忘门的数据处理过程如公式(7)所示,其中,ft为当前时刻遗忘门的门控状态,ht-1为上一时刻的隐层输出,xt为当前时刻的输入,Wf为权重参数,bf为偏置,σ(*)表示Sigmoid函数。
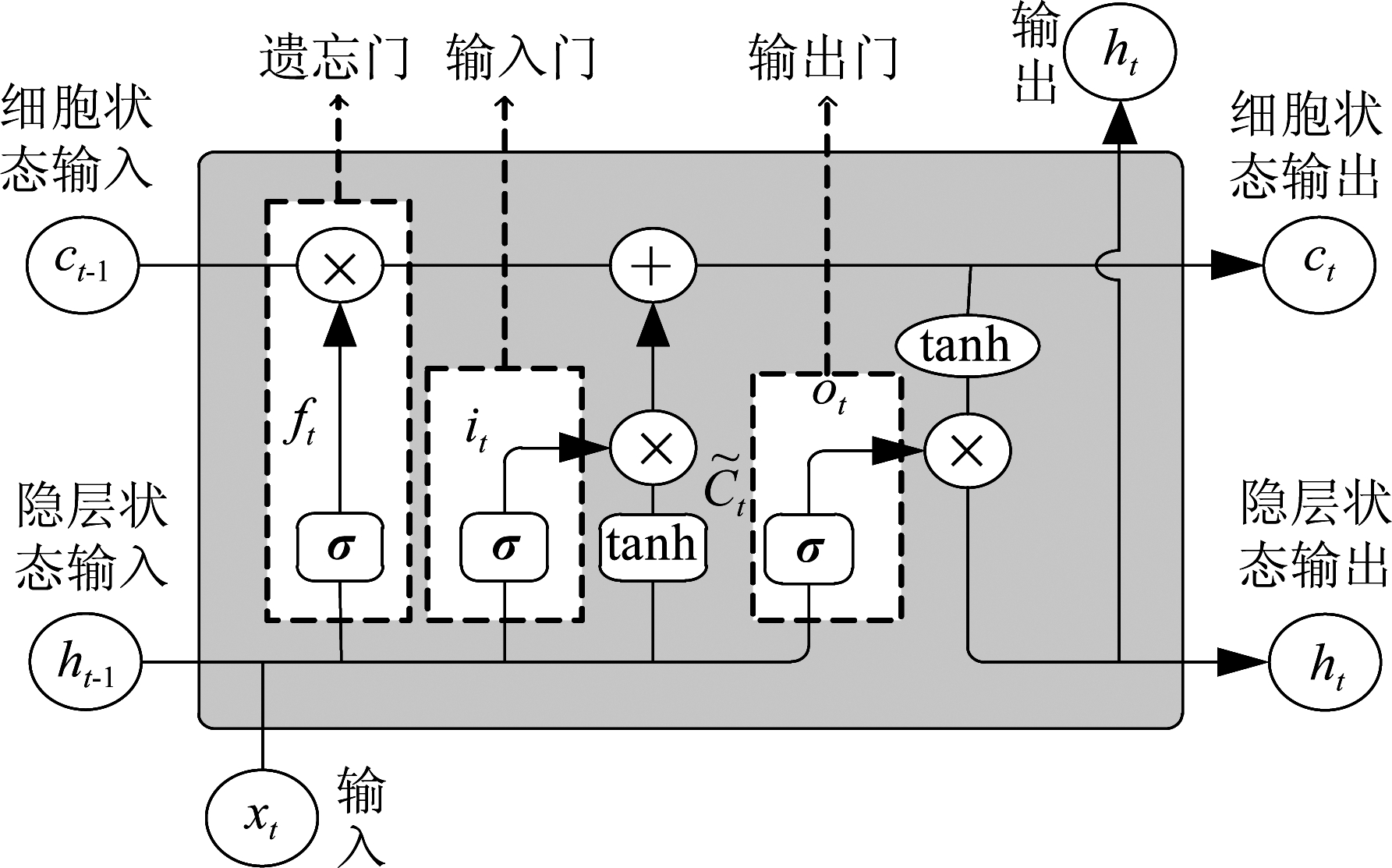
图6 LSTM结构图
Fig.6 Structure diagram of LSTM
ft=σ(Wf·[ht-1,xt]+bf)
(7)
输入门的数据处理过程如公式(8)~(10)所示,其中,it为输入门控状态,![]() 为即将加入细胞状态的候选信息. tanh(*)表示tanh函数,Ct和Ct-1分别表示当前时刻和上一时刻的细胞状态。
为即将加入细胞状态的候选信息. tanh(*)表示tanh函数,Ct和Ct-1分别表示当前时刻和上一时刻的细胞状态。
it=σ(Wi·[ht-1,xt]+bi)
(8)
(9)
(10)
输出门的数据处理过程如公式(11)和公式(12)所示,其中,ht表示当前时刻的输出。
ot=σ(Wo·[ht-1,xt]+bo)
(11)
ht=ot*tanh(Ct)
(12)
MSTF算法的LSTM模块由两层隐藏单元数(Units)分别为32和11的LSTM层组成,通过它们可以学习到更高语义层次的表示和更加抽象的特征。另外,设置第二层LSTM的单元数等于类别数,既将该层输出与信号调制样式建立起了对应关系,同时也降低了数据的维度,使得LSTM模块的输出为仅包含11个数据元素的一维向量。
2.3 输出层
MSTF算法的输出层是使用Softmax函数为激活函数的全连接层,隐藏单元数等于需要识别的类别数。Softmax函数可以将各个输出节点的输出值变成一个概率分布,概率的大小介于 0~1之间且和为1,以最大概率值索引所代表的类别作为识别结果。输出层的计算过程分为两步,第一步计算各个输出节点的输出值y:
y=WT·x+b
(13)
其中,WT为权重矩阵,x为输入向量,b为偏置。第二步是Softmax函数计算:
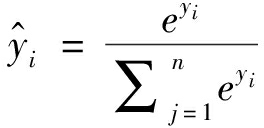
(14)
其中,n即为全连接层的隐藏单元数,e为自然常数,yi为第i个输出节点的输出值,![]() 为对应的概率值。
为对应的概率值。
2.4 算法实现
算法的训练包括前向计算和反向传播两个过程,MSTF算法描述如图7所示。训练开始前,需要对神经网络的权重参数以及训练过程的超参数进行初始化,参数的含义及初始化值如表2所示。其中,θ表示整个网络的权重参数,包括了不同网络层权重参数的随机初始化值,W和WD分别表示卷积单元和降维卷积单元中卷积层的权重参数,WL和WFC分别表示LSTM层和全连接层的网络权重参数。

图7 MSTF算法描述
Fig.7 Description of MSTF algorithm
表2 参数初始化
Tab.2 Initialization of parameters
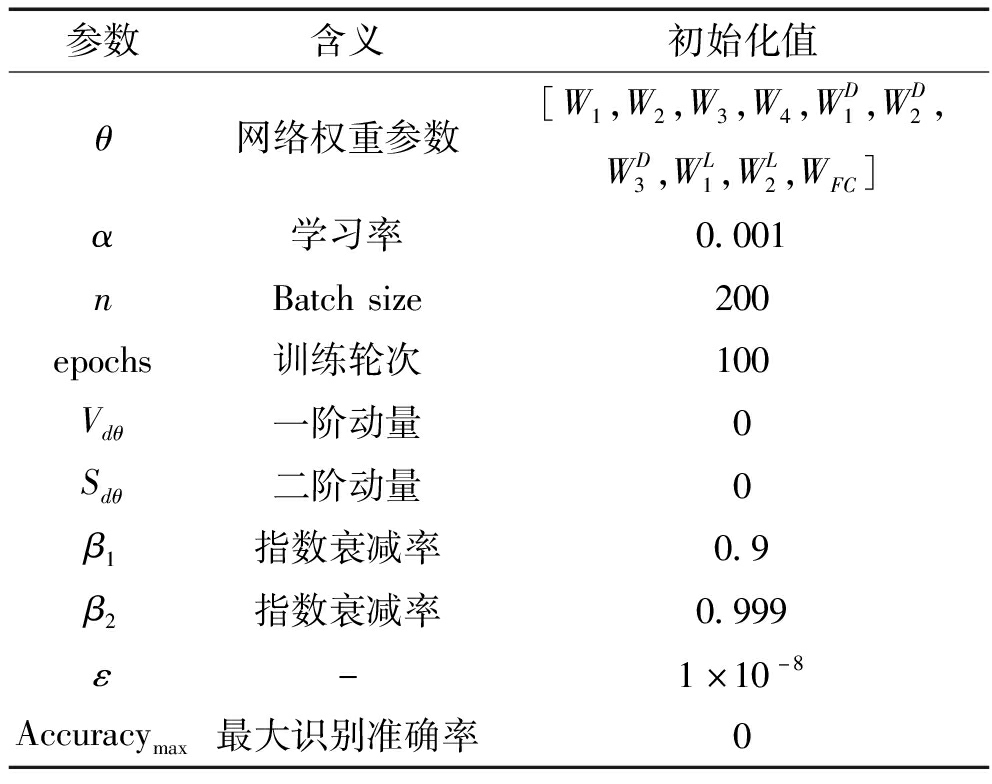
参数含义初始化值θ网络权重参数[W1,W2,W3,W4,WD1,WD2,WD3,WL1,WL2,WFC]α学习率0.001nBatchsize200epochs训练轮次100Vdθ一阶动量0Sdθ二阶动量0β1指数衰减率0.9β2指数衰减率0.999ε-1×10-8Accuracymax最大识别准确率0
前向计算过程为图7中的6~17行,其中,6~8行是4层卷积单元的计算,9~11行是降维卷积单元的计算,Conv(*)、BN(*)和ReLU(*)分别表示卷积计算、BN层计算和ReLU激活函数,计算方式如2.1节所述;第12行是不同尺度时序数据的拼接;13~15行是LSTM模块,LSTM(*)表示LSTM层的计算,计算方式如2.2节所述;16行是输出层的计算,计算方式如2.3节所述;17行是使用多分类交叉熵损失函数计算损失值。18~19行为采用Adam优化算法进行反向传播以更新网络权重θ,更新过程如公式(15)~(17)所示。算法验证过程为21~25行,评估标准采用识别准确率(Accuracy),即识别正确的样本数量占总样本数量的比例,最终保存的是识别准确率最高的网络模型。
Vdθ=β1Vdθ+(1-β1)dθ
(15)
Sdθ=β2Sdθ+(1-β2)dθ2
(16)
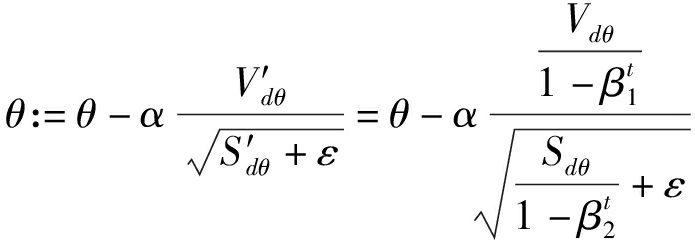
(17)
3 算法复杂度分析
3.1 相关工作
文献[20-23]提出的算法同样是结合CNN与LSTM两种网络构建算法模型,本文将它们作为对比算法与MSTF算法进行比较,对比算法与MSTF算法的网络参数如表3所示。除了文献[20]算法采用CNN与LSTM并联的连接方式外,其他算法均采用级联的方式。另外,文献[23]算法在实际训练和预测过程中采用的是双流CNN-LSTM结构,表中仅列出了单流网络的参数。
表3 对比算法与MSTF算法的网络参数
Tab.3 Network parameters of the compared algorithms and the MSTF algorithm
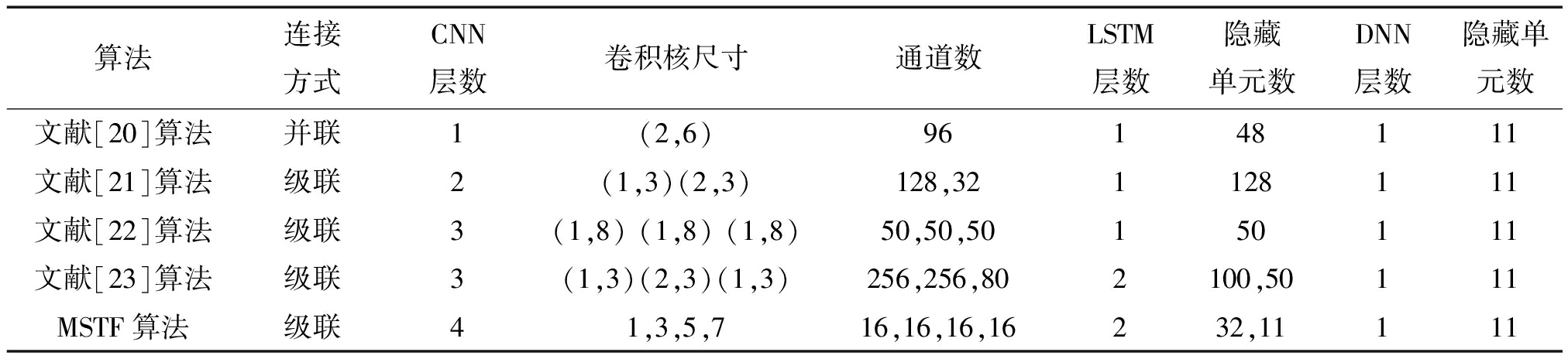
算法连接方式CNN层数卷积核尺寸通道数LSTM层数隐藏单元数DNN层数隐藏单元数文献[20]算法并联 1(2,6)96148111文献[21]算法级联 2(1,3)(2,3)128,321128111文献[22]算法级联3(1,8) (1,8) (1,8)50,50,50150111文献[23]算法级联3(1,3)(2,3)(1,3)256,256,802100,50111MSTF算法级联41,3,5,716,16,16,16232,11111
对于原始I/Q信号数据,对比算法会通过维度扩展后将其作为图像数据输入,而MSTF算法则是将其直接作为时序数据输入,如图8所示。因此MSTF算法可以使用一维卷积层直接在原始数据上提取I、Q之间的特征以及不同尺度的时序数据,实现完整和丰富的信息表达。MSTF算法卷积层的输出可以直接输入到LSTM层进行时序特征提取,而对比算法由于卷积层输出数据格式的问题,需要再次对数据进行维度压缩(Squeeze)或者数据展平(Flatten)后才能由LSTM层处理,增加了数据处理的步骤。
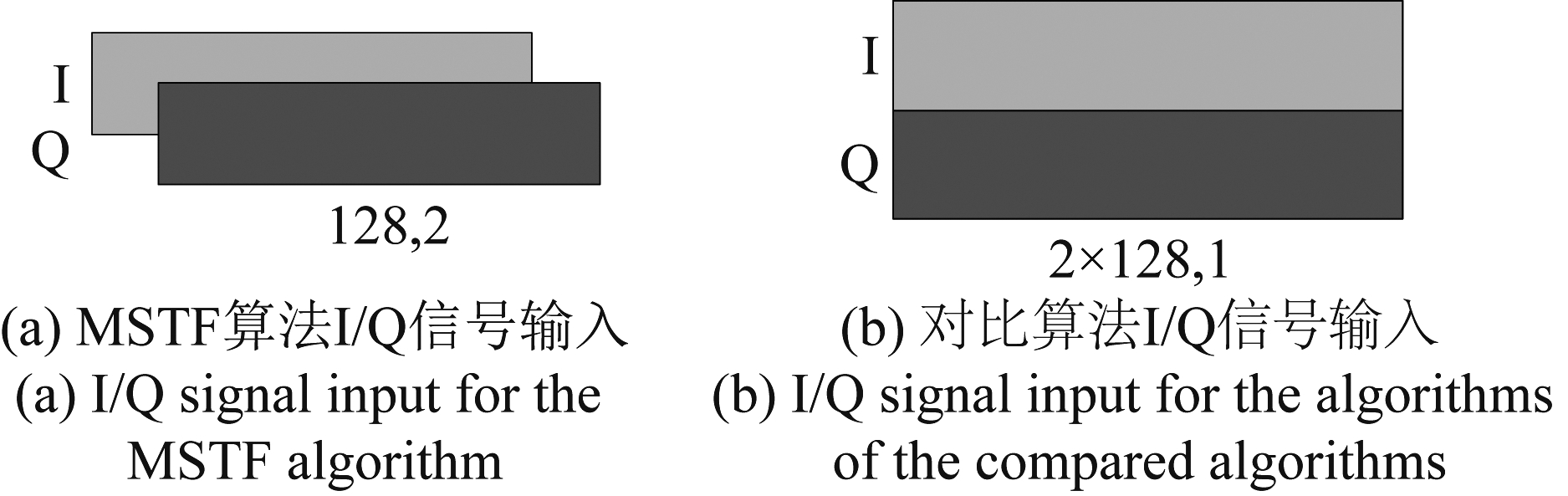
图8 I/Q信号输入示意图
Fig.8 Schematic diagram of I/Q signal input
从表3中数据可以发现,在所有算法中MSTF算法的网络层数最多,并且无论是卷积层还是LSTM层的通道数都小于对比算法。对比算法通过增加网络宽度来学习更丰富的特征,其中文献[23]算法甚至采用了双流网络模型。但是网络宽度的增加相比网络深度的增加,会带来更多的计算量,并且可能由于提取重复特征而造成更多的冗余计算。因此MSTF算法选择增加网络的层数,并且通过跨层连接的方式融合卷积层提取的不同尺度的时序数据来丰富信息的表达,最终使得算法的性能得到提升。另外,在跨层连接时通过降维卷积单元以少量的参数实现了数据维度的大幅下降。
3.2 算法复杂度分析
对于深度学习算法,可以通过模型的乘加数(Multiply-accumulate Operations,MAdds)来衡量算法的计算量,从而在理论上评估模型的速度。但是在实际的训练或者推理过程中,因为针对每一层网络,计算设备都需要从内存中读取数据和权重参数并进行计算,最后还需要将计算结果写回内存中,所以会涉及大量的内存访问,此时模型的参数量则是成为影响算法运算速度的关键因素。因此,算法的复杂度需要综合模型的计算量和参数量来进行分析,对比算法和MSTF算法的模型参数量和MAdds如表4所示。
表4 对比算法和MSTF算法的模型参数量和MAdds
Tab.4 Amount of model parameters of the compared algorithm and the MSTF algorithm
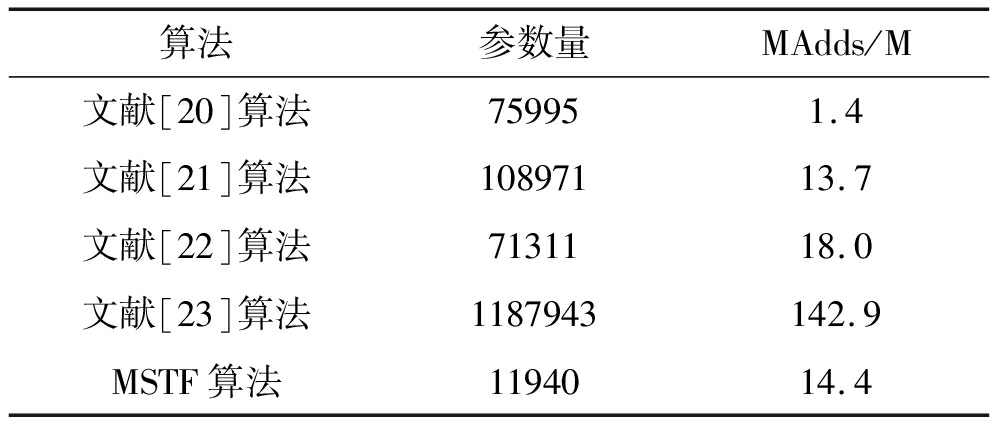
算法参数量MAdds/M文献[20]算法759951.4文献[21]算法10897113.7文献[22]算法7131118.0文献[23]算法1187943142.9MSTF算法1194014.4
虽然MSTF算法的拥有所有算法中最深的网络深度,但是从表4可以发现,在模型参数量方面MSTF算法远远少于对比算法,约为文献[20]算法和文献[22]算法的16%,与文献[21]算法和文献[23]算法相比则分别仅有它们的11%和1%;在模型计算量方面MSTF算法的MAdds多于文献[20]和文献[21]算法,少于文献[22]和文献[23]算法。其中,与模型参数量之间的差距相比,MSTF算法与文献[21]算法模型计算量之间的差距并不大。因此综合分析模型参数量和计算量两方面因素,MSTF算法的复杂度仅高于文献[20]算法而低于其他的对比算法。
4 实验验证
4.1 实验数据集
本文采用的数据集是文献[26]中作者利用GNU Radio软件平台仿真生成的I/Q信号数据集RML2016.10a,具体信息如表5所示。其中,信噪比间隔为2,每种调制信号在每个信噪比下的样本数为1000个。
表5 RML2016.10a数据集信息
Tab.5 Information of the RML2016.10a dataset

调制信号种类调制信号样本数量信噪比范围/dB每符号采样数数据格式11数字调制:BPSK、QPSK、8PSK、16QAM、64QAM、BFSK、CPFSK、PAM4;模拟调制:WB-FM、AM-SSB、AM-DSB220000-20^188[2, 128]
实验过程中,训练集、验证集和测试集按照8∶1∶1的比例进行划分,为了保证训练集、验证集和测试集的样本平衡以及它们之间的独立同分布,在划分时对每种调制信号每种信噪比下的样本按照比例随机划分。
4.2 实验环境
本文在Ubuntu 18.04 64位操作系统上,使用Python 3.7.3以及Tensorflow 2.1.0深度学习框架完成网络的搭建和训练。实验硬件共有两类:PC设备和嵌入式设备。PC设备被用于网络的训练,嵌入式设备被用于测试算法的推理时间,设备详细的参数信息如表6所示。
表6 硬件设备信息
Tab.6 Information of the hardware device

设备CPUGPU内存PCIntel Core i7-7700K 4.20 GHz(八核)GTX108016 GBJetson NanoARM Cortex-A57 1.43 GHz(四核)NVIDIA Maxwell架构,128个CUDA核心4 GB树莓派4BARM Cortex-A72 1.5 GHz(四核)无4 GB
5 实验结果
5.1 算法识别准确率对比
对比算法与MSTF算法在测试集上的识别准确率如表7所示,各信噪比下的识别准确率如图9所示。综合来看,文献[21]算法、文献[23]算法和MSTF算法有着最高的识别准确率,文献[20]算法和文献[22]算法与前面三种算法的识别准确率相比有显著的差距:文献[20]算法在测试集上的识别准确率与前面三种算法相差约9%,在4 dB时的识别准确率相差约14%;文献[22]算法则分别相差约5%和8%。在通过图9可以看到,文献[21]算法、文献[23]算法和MSTF算法的识别准确率曲线近似于重合,当SNR大于等于4 dB时识别准确率均超过90%,而文献[22]算法的识别准确率约为83%,结果最差的是文献[20]算法低于80%。
表7 对比算法与MSTF算法的识别准确率
Tab.7 Recognition accuracy of the compared algorithms and the MSTF algorithm
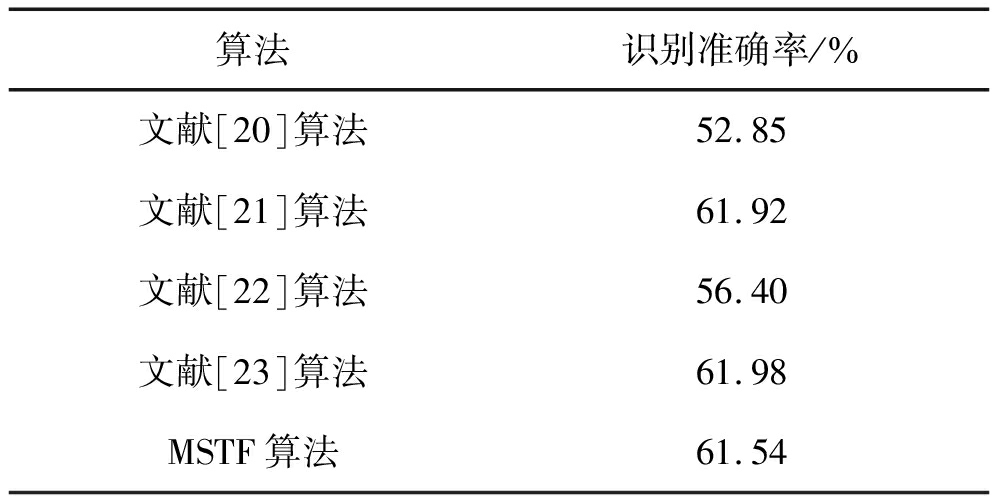
算法识别准确率/%文献[20]算法52.85文献[21]算法61.92文献[22]算法56.40文献[23]算法61.98MSTF算法61.54
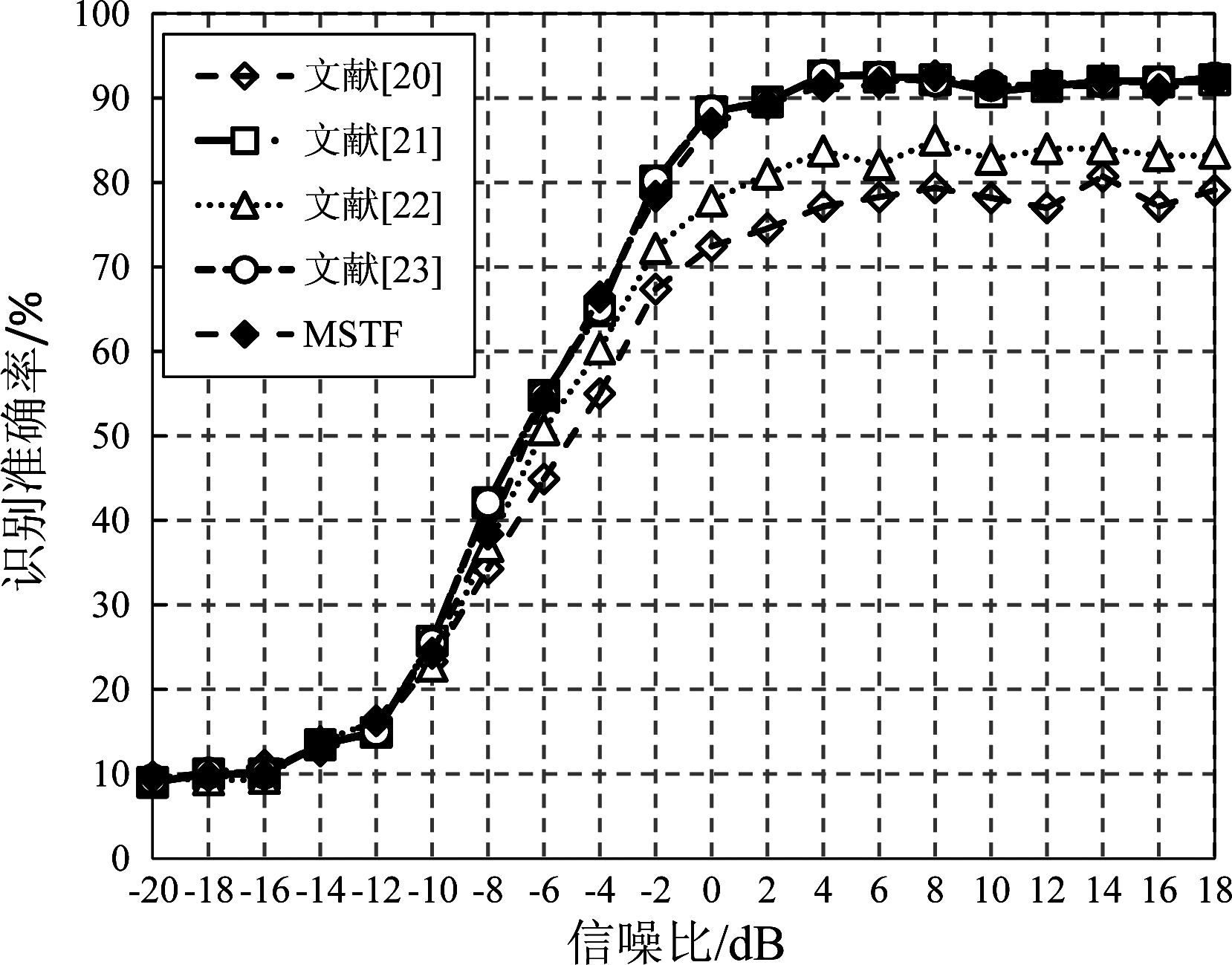
图9 对比算法与MSTF算法在不同信噪比下的识别准确率
Fig.9 Recognition accuracy at various SNRs of the compared algorithms and the MSTF algorithm
MSTF算法的网络更深,可以提取更高层次的特征,同时通过多尺度的时序数据的融合也使得LSTM层也能够提取更加丰富的时序特征,因此能够有效地识别信号的调制样式。文献[21]算法通过更多的通道数和隐藏单元数增加信息的表达,虽然提升了算法的性能,但是这也大大增加了模型参数量。文献[23]算法采用双流CNN-LSTM结构,分别对I、Q数据和A、P数据进行处理,通过增加输入数据种类和网络模型数量取得了所有算法中最好的分类性能,但同时也成倍的增加了整个算法的计算复杂度。文献[22]算法表现不佳的主要原因是仅仅使用了大卷积核,缺失了细节的特征,同时也没有提取I、Q之间的特征信息。文献[20]算法的不足是网络结构过于简单,只有一层CNN和一层LSTM,算法复杂度较低,不能很好地学习数据的一般特征。
混淆矩阵是精度评价的一种方法,列代表预测类别,行代表数据的真实归属类别,当预测类别和真实归属类别相同时则表示识别正确。通过混淆矩阵能够直观的了解到算法对不同调制信号的识别性能,对比算法与MSTF算法在信噪比为4 dB时的混淆矩阵如图10所示。对比图10中的五幅图可以看到,除真实类别为WBFM的行外,文献[21]算法、文献[23]算法和MSTF算法的混淆矩阵有一条清晰的对角线,表明这三种算法能够对除WBFM调制信号之外的其他10种信号进行有效地识别;文献[22]算法除了WBFM调制信号之外,还在16QAM和64QAM之间产生了混淆;文献[20]算法对多种调制信号的识别都产生了混淆,性能表现最差。
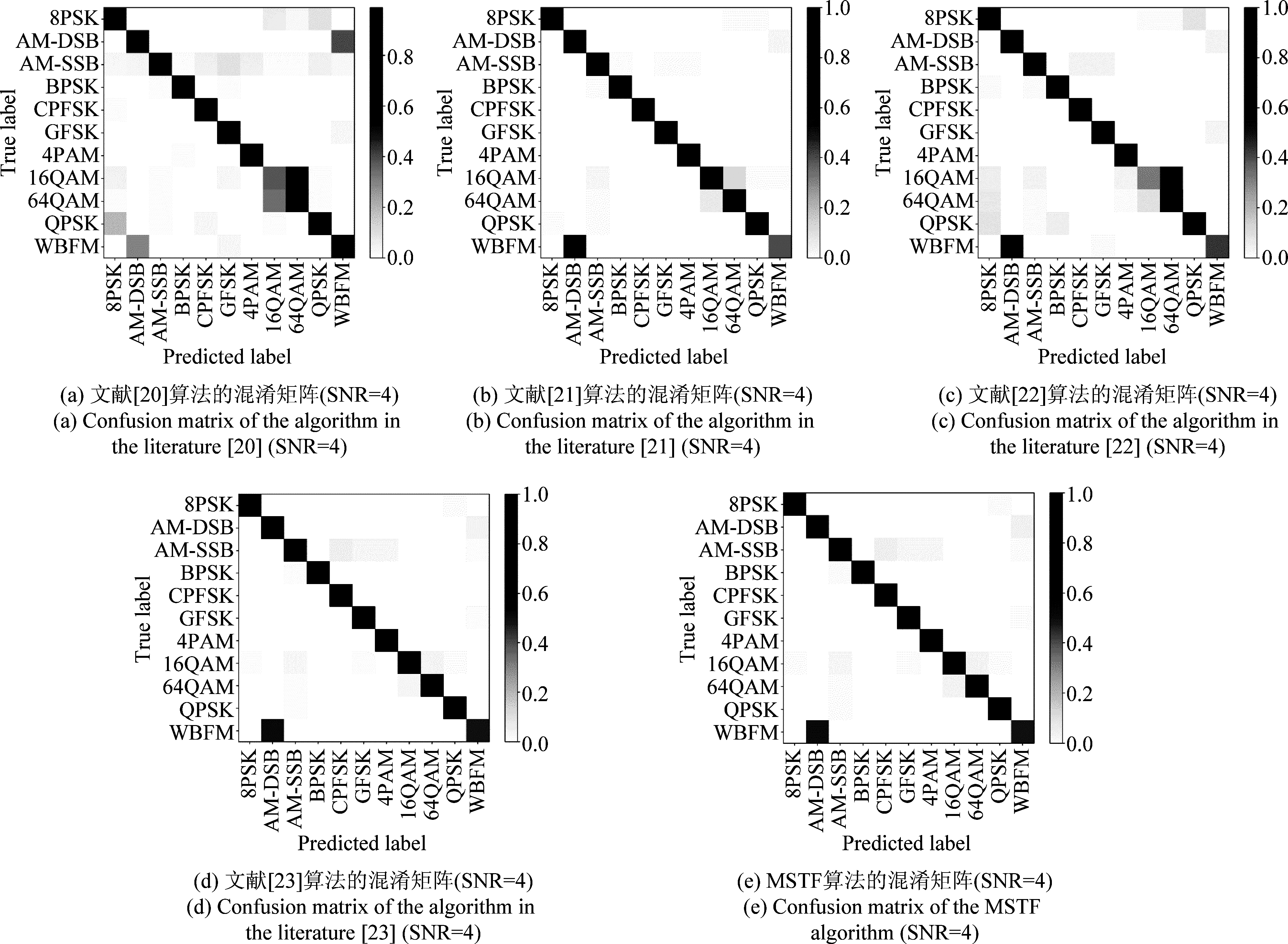
图10 对比算法与MSTF算法的混淆矩阵(SNR=4)
Fig.10 Confusion matrixes of the compared algorithms and the MSTF algorithm(SNR=4)
另外,五种算法对WBFM调制信号都不能进行有效的识别,可能的原因是RML2016.10a数据集中AM-DSB和WBFM调制信号的原始I/Q数据十分相似,而对比算法和MSTF算法的复杂度较低,难以提取有效的特征对两种信号进行区分和识别。为了解决这一问题,可以研究新的复杂度更高的算法,或者是在MSTF算法的基础上,使用另外的分类算法对AM-DSB和WBFM调制信号进行辅助处理。
5.2 算法速度对比
算法的实际运行速度可以通过训练时间和推理时间来进行对比,对比算法以及MSTF算法在PC设备上的训练时间如表8所示,在不同设备上的推理时间如表9所示。其中,算法推理时间的对比实验主要关注的是不同算法推理过程需要的时间,为了保证实验有足够的数据量,本文使用完整的RML2016.10a数据集作为输入数据进行测试。
表8 对比算法与MSTF算法的训练时间
Tab.8 Training duration of the compared algorithm and the MSTF algorithm
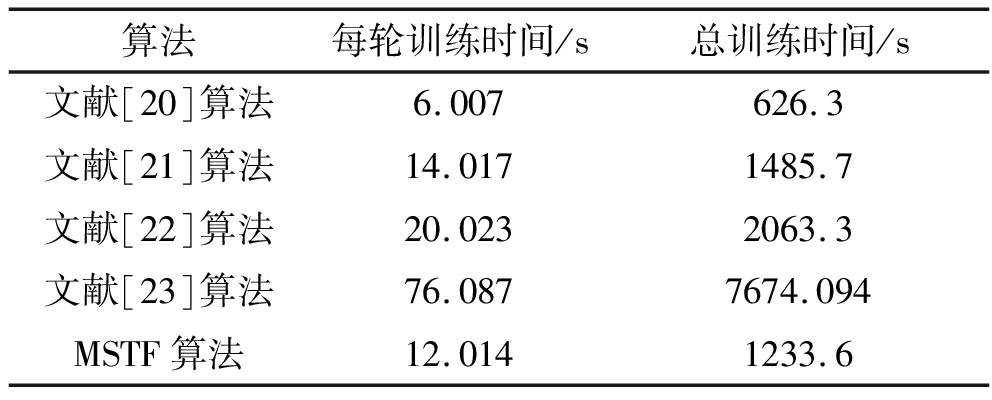
算法每轮训练时间/s总训练时间/s文献[20]算法6.007626.3文献[21]算法14.0171485.7文献[22]算法20.0232063.3文献[23]算法76.0877674.094MSTF算法12.0141233.6
表9 对比算法与MSTF算法在不同设备上的推理时间
Tab.9 Inference duration of the compared algorithms with the MSTF algorithm on different devices
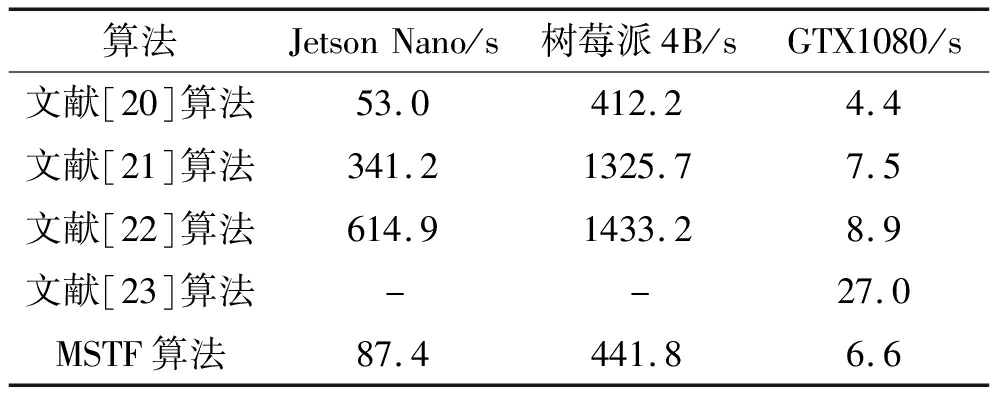
算法JetsonNano/s树莓派4B/sGTX1080/s文献[20]算法53.0412.24.4文献[21]算法341.21325.77.5文献[22]算法614.91433.28.9文献[23]算法--27.0MSTF算法87.4441.86.6
从表8可以看出,无论是每轮训练时间还是总训练时间,五种算法之间从少到多的顺序与复杂度理论分析的结果一致,MSTF算法的训练时间多于文献[22]算法,少于其他对比算法。从表9中数据可以发现,五种算法在同一种设备上推理时间的对比结果同样与算法复杂度理论分析的结果一致。另外,通过不同设备上推理时间的对比结果可以发现,算法对同样数据进行推理所需要的时间随着设备性能的下降而增加,同时不同算法推理时间之间的差距也变得越来越大。其中,文献[23]算法由于算法复杂度过高,所需占用的计算资源较多,导致在嵌入式设备Jetson Nano和树莓派4B上无法正常运行。
在实际工程应用中需要综合考虑硬件设备的体积、功耗等因素,因此嵌入式设备的计算能力难以达到与GTX1080显卡同等的性能水平,更可能的是与Jetson Nano或者是树莓派4B开发板近似的计算能力。MSTF算法与同等识别准确率的文献[21]算法和文献[23]算法相比,在Jetson Nano上的推理时间缩短了74%以上,在树莓派4B上的推理时间缩短了67%以上。因此在设备性能受限的情况下,综合考虑算法的识别准确率以及推理速度,MSTF算法更适合进行嵌入式部署应用。
6 结论
针对现阶段基于深度学习的信号调制识别方法的算法复杂度较高,难以工程实施的问题,本文提出了一种基于多尺度时序特征的信号调制样式识别算法。该算法将I/Q信号作为时序数据输入,通过多层CNN提取不同尺度的时序数据,然后采用连接层将不同尺度的时序数据进行融合,并输入到LSTM网络进行时序特征的提取,最终经过输出层输出信号的调制样式。同时通过对网络结构进行设计和优化,包括减少网络宽度、采用小尺寸卷积核和使用降维卷积单元等,减少了模型参数量,降低了算法复杂度。实验结果证明,本文提出算法与同等识别准确率的算法相比,有着更低的算法复杂度,模型参数量和训练时间更少,在嵌入式设备Jetson Nano和树莓派上的推理时间也更短,具有高效性和实用价值。
[1] MITOLA J, MAGUIRE G Q.Cognitive radio: Making software radios more personal[J].IEEE Personal Communications, 1999, 6(4): 13-18.
[2] SILLS J A.Maximum-likelihood modulation classification for PSK/QAM[C]∥MILCOM 1999.IEEE Military Communications.Conference Proceedings(Cat.No.99CH36341).Atlantic City, NJ, USA.IEEE, 1999: 217-220.
[3] WEI Wen, MENDEL J M.Maximum-likelihood classification for digital amplitude-phase modulations[J].IEEE Transactions on Communications, 2000, 48(2): 189-193.
[4] HASSAN K, DAYOUB I, HAMOUDA W, et al.Automatic modulation recognition using wavelet transform and neural network[J].2009 9th International Conference on Intelligent Transport Systems Telecommunications,(ITST), 2009: 234-238.
[5] DONG Shuli, LI Zhipeng, ZHAO Linfeng.A modulation recognition algorithm based on cyclic spectrum and SVM classification[C]∥2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference(ITNEC).Chongqing, China.IEEE, 2020: 2123-2127.
[6] SMITH A, EVANS M, DOWNEY J.Modulation classification of satellite communication signals using cumulants and neural networks[C]∥2017 Cognitive Communications for Aerospace Applications Workshop(CCAA).Cleveland, OH, USA.IEEE, 2017: 1-8.
[7] FLOHBERGER M, GAPPMAIR W, KOUDELKA O.Modulation classifier for signals used in satellite communications[C]∥2010 5th Advanced Satellite Multimedia Systems Conference and the 11th Signal Processing for Space Communications Workshop.Cagliari, Italy.IEEE, 2010: 198-202.
[8] 闫文君, 凌青, 张立民.四阶时延矩STBC-OFDM信号调制方式识别[J].信号处理, 2020, 36(1): 1-8.
YAN Wenjun, LING Qing, ZHANG Limin.Blind modulation classification of STBC-OFDM based on fourth-order lag moment[J].Journal of Signal Processing, 2020, 36(1): 1-8.(in Chinese)
[9] 代翱, 张海剑, 孙洪.联合时域和时频域特征的数字调制信号自动分类[J].信号处理, 2016, 32(11): 1283-1292.
DAI Ao, ZHANG Haijian, SUN Hong.Digital modulations automatic classification using the combination of several features extracted from time and time-frequence domain[J].Journal of Signal Processing, 2016, 32(11): 1283-1292.(in Chinese)
[10] 田上成, 王可人, 金虎.卫星通信中数字调相信号调制方式识别方法研究[J].信号处理, 2011, 27(2): 271-275.
TIAN Shangcheng, WANG Keren, JIN Hu.Automatic recognition for the digital phase modulated signals in satellite communication[J].Signal Processing, 2011, 27(2): 271-275.(in Chinese)
[11] 曾创展, 贾鑫, 朱卫纲.通信信号调制方式识别方法综述[J].通信技术, 2015, 48(3): 252-257.
ZENG Chuangzhan, JIA Xin, ZHU Weigang.Modulation classification of communication signals[J].Communications Technology, 2015, 48(3): 252-257.(in Chinese)
[12] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al.Deep residual learning for image recognition[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Las Vegas, NV, USA.IEEE, 2016: 770-778.
[13] SZEGEDY C, LIU Wei, JIA Yangqing, et al.Going deeper with convolutions[C]∥2015 IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Boston, MA, USA.IEEE, 2015: 1-9.
[14] CHEN Qian, ZHU Xiaodan, LING Zhenhua, et al.Enhanced LSTM for natural language inference[C]∥Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics(Volume 1: Long Papers).Vancouver, Canada.Stroudsburg, PA, USA: Association for Computational Linguistics, 2017:1657-1668.
[15] DEVLIN J, CHANG M W, LEE K, et al.Bert: Pre-training of deep bidirectional transformers for language understanding[J].arXiv preprint arXiv:1810.04805, 2018.
[16] O’SHEA T J, CORGAN J, CLANCY T C.Convolutional radio modulation recognition networks[C]∥Engineering Applications of Neural Networks, 2016: 213-226.
[17] 王彬, 王海旺, 李勇斌.脉冲噪声环境下的水声通信信号调制识别方法[J].信号处理, 2020, 36(12): 2107-2115.
WANG Bin, WANG Haiwang, LI Yongbin.Modulation recognition method of underwater acoustic communication signals in impulsive noise environment[J].Journal of Signal Processing, 2020, 36(12): 2107-2115.(in Chinese)
[18] ZHANG Tingping, SHUAI Cong, ZHOU Yaru.Deep learning for robust automatic modulation recognition method for IoT applications[J].IEEE Access, 2020, 8: 117689-117697.
[19] 查雄, 彭华, 秦鑫, 等.基于循环神经网络的卫星幅相信号调制识别与解调算法[J].电子学报, 2019, 47(11): 2443-2448.
ZHA Xiong, PENG Hua, QIN Xin, et al.Satellite amplitude-phase signals modulation identification and demodulation algorithm based on the cyclic neural network[J].Acta Electronica Sinica, 2019, 47(11): 2443-2448.(in Chinese)
[20] 翁建新, 赵知劲, 占锦敏.利用并联CNN-LSTM的调制样式识别算法[J].信号处理, 2019, 35(5): 870-876.
WENG Jianxin, ZHAO Zhijin, ZHAN Jinmin.Modulation recognition algorithm by using parallel CNN-LSTM[J].Journal of Signal Processing, 2019, 35(5): 870-876.(in Chinese)
[21] WU Yanlun, LI Xingjian, FANG Jun.A deep learning approach for modulation recognition via exploiting temporal correlations[C]∥2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications(SPAWC).Kalamata, Greece.IEEE, 2018: 1-5.
[22] WEST N E, O’SHEA T.Deep architectures for modulation recognition[C]∥2017 IEEE International Symposium on Dynamic Spectrum Access Networks(DySPAN).Baltimore, MD, USA.IEEE, 2017: 1-6.
[23] ZHANG Zufan, LUO Hao, WANG Chun, et al.Automatic modulation classification using CNN-LSTM based dual-stream structure[J].IEEE Transactions on Vehicular Technology, 2020, 69(11): 13521-13531.
[24] SAINATH T N, VINYALS O, SENIOR A, et al.Convolutional, long short-term memory, fully connected deep neural networks[C]∥2015 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP).South Brisbane, QLD, Australia.IEEE, 2015: 4580-4584.
[25] GOODFELLOW I, BENGIO Y, COURVILLE A, et al.Deep learning[M].Cambridge: MIT press, 2016:326.
[26] O’SHEA T J, WEST N.Radio machine learning dataset generation with gnu radio[C]∥Proceedings of the GNU Radio Conference,2016:1(1).





