1 引言
地基干涉合成孔径雷达(Ground-Based Interferometric Synthetic Aperture Radar, GB-InSAR)由星载SAR发展而来,拥有高精度、连续监测等优点[1]。但由于大气扰动等环境因素影响,雷达在观测时,信号观测相位会产生延迟,严重影响雷达测量精度[2]。因此,必须对大气相位实现补偿,保证测量的精度。
常规大气相位补偿方法分为三种。第一种是根据场景中未发生形变或已知形变的参考点,对整幅图像进行插值处理,实现大气相位补偿[3-5];第二种是基于气象数据,根据理论模型估计出大气干涉相位,进行补偿[6];第三种是基于PS(Permanent Scatterer,永久散射体)技术,对于不同的监测场景,建立不同的参数模型,实现大气相位参数的估计[7-11]。
第一种方法依赖参考点,需要这些参考点在监测过程中不发生形变,或者准确获取他们的形变信息,才能实现准确的空间维插值与补偿;第二种方法是基于大气折射率与温度、湿度、气压的理论关系,仅在良好天气条件下才能获取较好的补偿效果;第三种方法在GB-InSAR领域普遍应用,该方法要求对大气相位进行准确的参数建模,补偿精度严重依赖于模型的准确度。
针对上述问题,本文提出了一种基于气象数据辅助的GB-InSAR大气相位补偿方法。对于多幅GB-InSAR图像,首先基于折射率经验模型,基于气象数据估计出所有PS点的大气相位曲线,其次与他们的实际干涉相位曲线进行互相关运算,根据相关系数选择出稳定PS点,然后利用稳定PS点,采用线性插值、局部加权回归(locally weighted scatterplot smoothing,Lowess)、神经网络3种插值拟合方法进行大气相位估计[12-14],并与常规补偿方法进行了对比分析,评估了本文方法的有效性与优劣性。
2 常规线性斜距补偿方法
一个点的时序列幅度值标准差与均值比,为这个点的幅度离差值,根据幅度离差值,设定门限,选择出散射特性稳定的点作为PS点,即PS技术[8]。这个方法在GB-InSAR里得到广泛采用。
一个PS点的干涉大气相位Δφ可以建模为[15]:
(1)
其中,λ为波长,rm为距离,n(r,t)为大气折射率,与空间r和时间t相关。
当认为大气介质均匀时,折射率n在空间r上不发生变化,可将公式(1)改写为
(2)
然后将Δφ(t)建模为随斜距线性变化的分量
(3)
其中β0为常数分量,β1表示与斜距相关的线性系数。
基于PS技术建立线性方程组
Δθ=Xβ+ε
(4)
其中,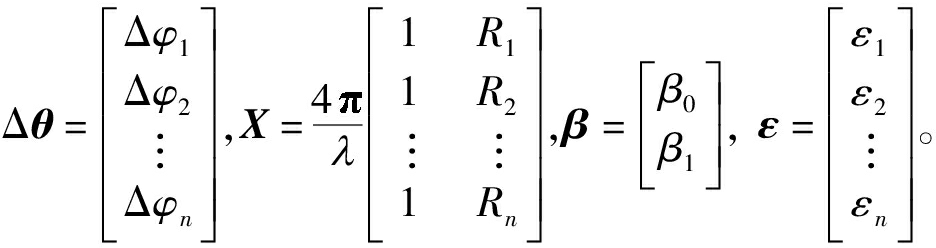
Δθ为n个解缠相位Δφ1,Δφ2,…, Δφn构成的n×2维矩阵,X为1与n个PS点距离R构成的2×n的矩阵,β为待估计的2×1维向量,ε为n×1维的随机误差向量,ε1,ε2,…, εn为各PS点的模型误差相位。采用最小二乘法对β进行迭代估计,每次估计设定阈值,剔除不可靠PS点[16]。
除了最基本的线性斜距模型外,常用参数模型还包括高阶斜距模型、斜距-高程模型等,如式(5)、(6)。
(5)
(6)
其中β0、β1、β2是各模型中待估计的未知参数,R、h分别代表目标点的斜距和高程。
但当干涉图大气相位出现复杂的非线性变化时,采用线性斜距模型、高阶斜距模型、斜距-高程模型等,均无法准确补偿。
3 改进方法
3.1 稳定PS点筛选
3.1.1 干涉相位估计
折射指数n(t1)可由t1时刻的大气干湿度、干气压和相对湿度计算[6]。
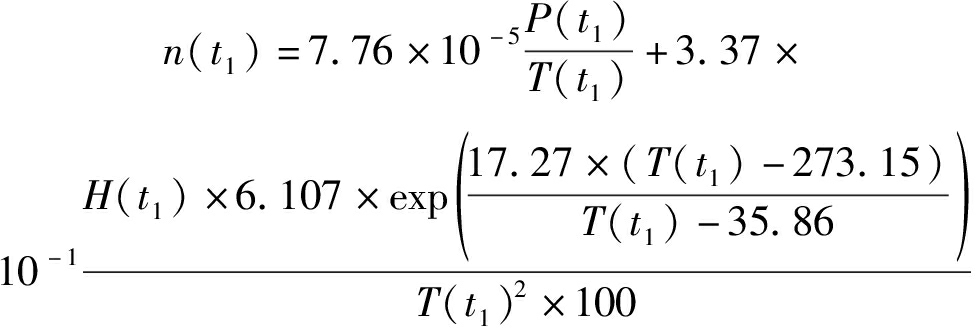
(7)
其中,T(t1)为干温度,单位为K;P(t1)为干气压,单位为hPa;H(t1)为相对湿度,单位为%。
则Δn(t)为
Δn(t)=n(t1)-n(t2)
(8)
将式(8)带入式(2)则可求得大气干涉相位。
3.1.2 相关系数选择
已知干湿度、干气压、相对湿度数据时,基于式(2)、(8)可以实现对大气相位的定量计算。基于气象数据估计出所有PS的大气相位曲线,然后与他们的实际干涉相位曲线进行对比,利用皮尔逊相关系数法计算相关系数。
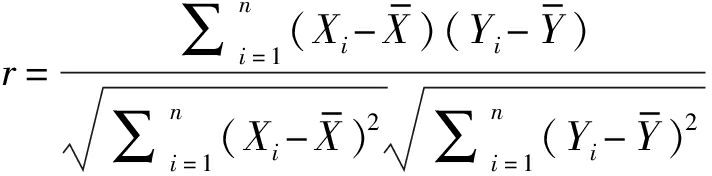
(9)
式中,X,Y分别表示两个样本,![]() 表示样本平均值,r为皮尔逊相关系数,它的大小反映了曲线的相关程度。在本文中,X,Y分别是基于折射率经验模型,由气象数据估计出的所有PS点的大气相位,和它们的实际干涉相位。通过设定合理的相干系数阈值,将互相关系数高于该阈值的点作为稳定PS点。
表示样本平均值,r为皮尔逊相关系数,它的大小反映了曲线的相关程度。在本文中,X,Y分别是基于折射率经验模型,由气象数据估计出的所有PS点的大气相位,和它们的实际干涉相位。通过设定合理的相干系数阈值,将互相关系数高于该阈值的点作为稳定PS点。
3.2 不同插值拟合方法补偿大气相位
选出稳定PS点后,根据稳定PS是离散、非均匀的分布在图像上的特点,需要采用一种适用于该类型数据的二维插值方法,本文选择如下三种插值方法补偿大气相位。
3.2.1 双线性插值
双线性插值是一次线性插值的扩展[10]。
已知Q11=(x1,y1),Q12=(x1,y2),Q21=(x2,y1)及Q22=(x2,y2)四个点的值。
为求得点f=(x,y)的值,可以通过(10),(11)两次一次线性插值,得到式(12)
(10)
(11)
(12)
在本文中,将稳定PS点作为已知点,利用线性插值,计算出所有PS点的大气干涉相位。由于插值计算每一个PS点的干涉相位是利用了临近稳定PS点的相位,因此,可以实现非线性大气相位的有效估计。
3.2.2 Lowess(局部加权回归)
首先计算已知点到指定点距离集合D。
(13)
其中,xi,yi为指定点的坐标信息,x,y为已知点的坐标信息集合。
根据设定的窗口dspan,选择窗口范围内距离指定点最小的点集合
D(dspan)={(xi-dspan,yi-dspan)...(xi,yi)...(xi+dspan,yi+dspan)}
(14)
每一个距离指定点的点n都具有自己的权值wn,它的大小为:
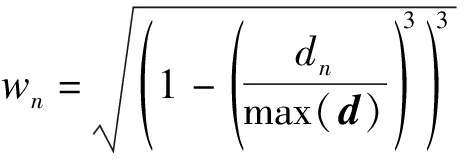
(15)
其中,d为集合里的点到指定点的距离集合,dn为窗口内第n个点到指定点的距离。
利用这些点做加权回归,其损失函数为:
(16)
其中,w, f(x,y),(x,y)分别为窗口内所有点的权值矩阵,所有点的值矩阵与位置信息矩阵,θT为待估计的参数矩阵,可采用最小二乘法估计。得到回归函数后,将指定点xi,yi带入回归函数得到该点插值f(xi,yi)。
利用局部加权回归构建一个拟合曲面f(x,y)。f(x,y)为估计的大气干涉相位值。
同线性插值,本文将稳定PS点作为已知点,利用Lowess,计算出所有PS点的大气干涉相位。Lowess做拟合时,会采用多点进行线性加权回归,且采用距离作为权值,可以很好的实现对非线性大气相位的估计。
3.2.3 BP神经网络拟合
BP神经网络图:
本文将PS点的坐标信息作为输入,PS点的干涉相位值作为期望输出,组成样本对输入网络,设定精度ε,当网络输出值与期望PS点的干涉相位值的误差E<ε,训练结束。否则,通过误差反向传播的方法修正权值。误差E的计算方式:
(17)
式中:![]() 为网络的期望输出;
为网络的期望输出;![]() 为网络的实际输出;m为学习样本个数。
为网络的实际输出;m为学习样本个数。
BP神经网络神经元设定激活函数经常是S型函数:
(18)
神经网络经常用来处理非线性问题,但神经网络拟合过后的模型与输入训练数据大小有较高关系,因此,当稳定点数量较少时,神经网络模型容易与预期不符。
3.2.4 方法流程
主要步骤:
(1)稳定PS点筛选:基于折射率经验模型,利用气象数据估计出大气相位曲线,其次与PS点的实际干涉曲线进行互相关运算,通过设定的相关系数阈值实现稳定PS点的选择。
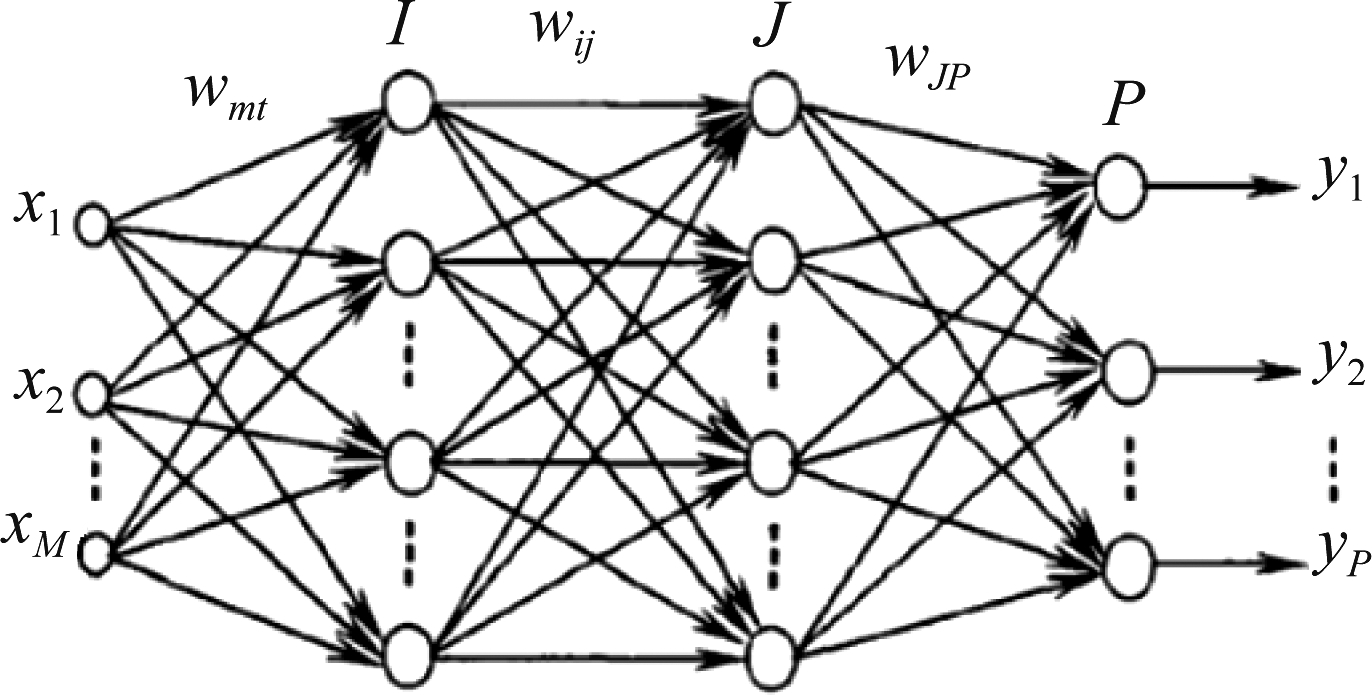
图1 神经网络结构图
Fig.1 Neural network structure diagram
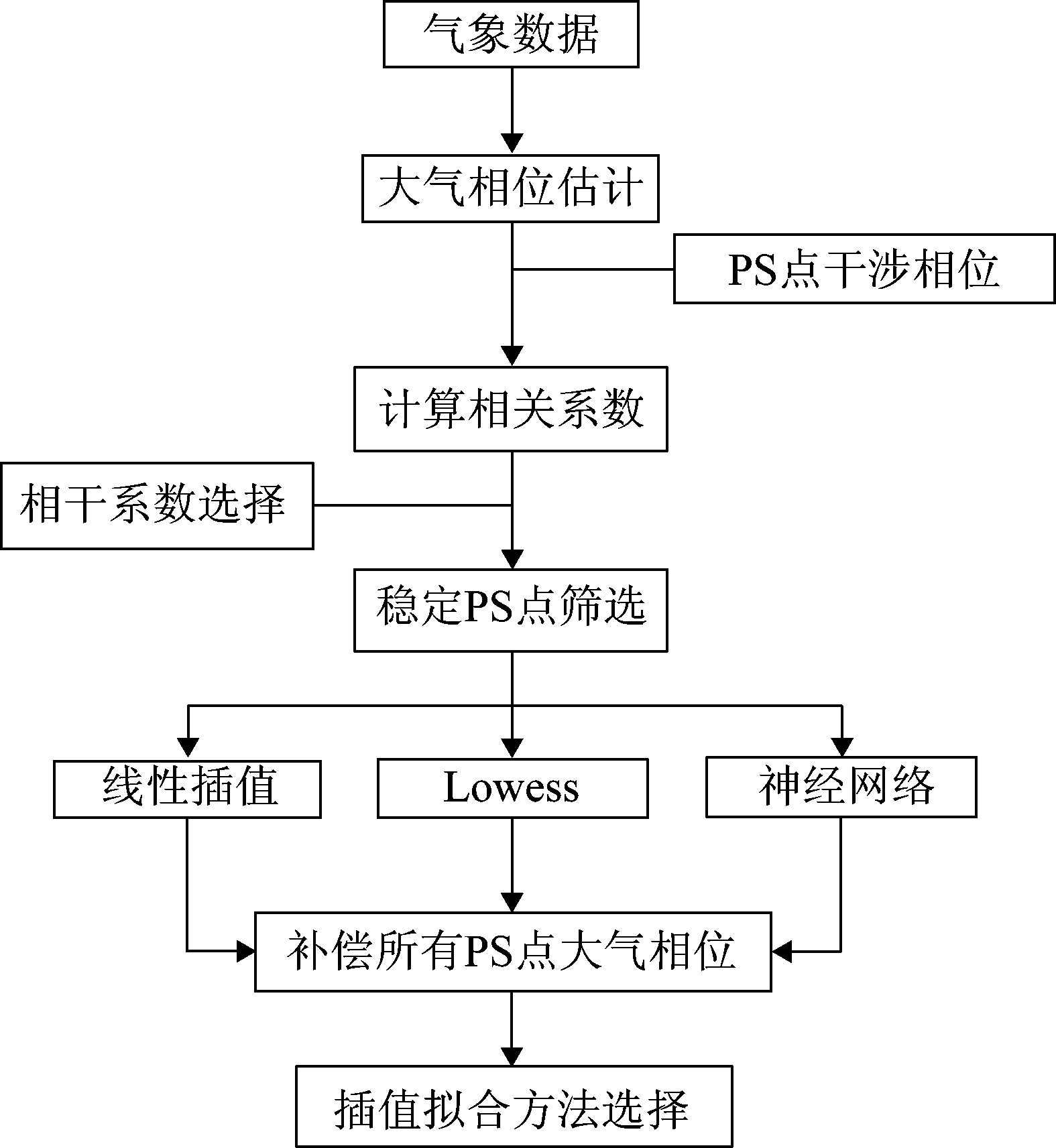
图2 方法流程图
Fig.2 Method flow chart
(2)插值拟合补偿:利用稳定PS点,采用线性插值、Lowess、神经网络三种插值方法补偿所有PS点大气相位,选出合适的插值补偿方法。
4 实验信息
本实验选定的区域为重庆九道拐,其位于重庆市万州区,图3(a)为场景照片,该区域为典型的植被山体边坡,该边坡位于万州区钟鼓楼街道、李家沟东北侧、长江北岸,该边坡体积约为25万方,纵向长约170 m、横向宽约300 m,平均厚度8 m。雷达在该区域的观测视角范围为60°,观测距离为400 m到1100 m。
实验采用一部滑轨雷达对该区域进行连续监测,雷达图片如图3(b)所示,实验选取了30幅图片,时间从2020年12月22日16:00到20:30。该滑轨雷达由北京理工雷科公司研发,其工作在Ku波段,测量周期为3~10 min,空间分辨率(1 km处)为0.3 m×4.0 m,最远探测距离5 km。

图3 场景图片与雷达图片
Fig.3 Scene images and radar images
图4(a)所示为极坐标系下该区域的雷达获取图像。将第一幅雷达图像与最后一幅雷达图像做干涉处理后获取干涉相位图如图4(b)所示。
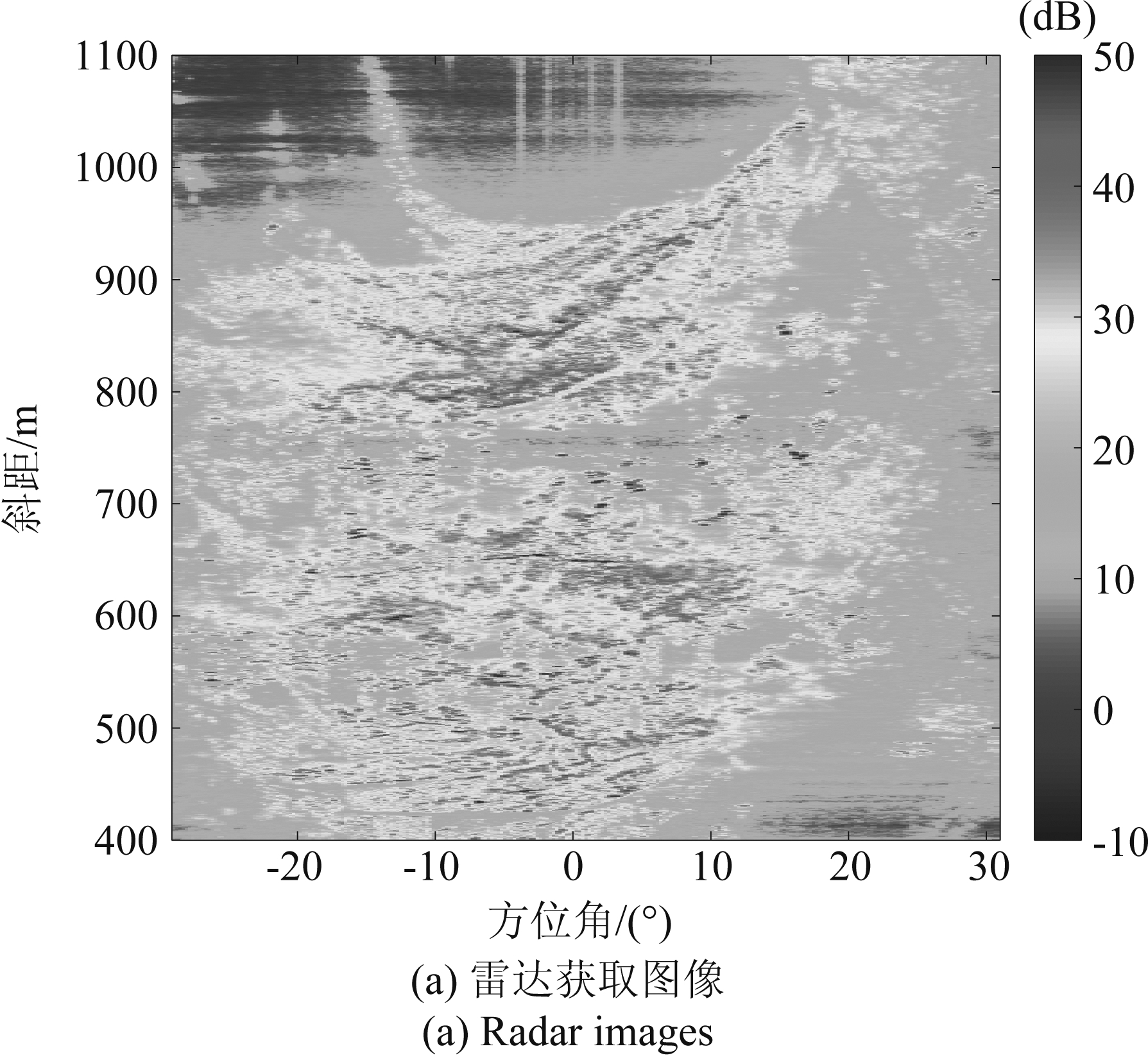
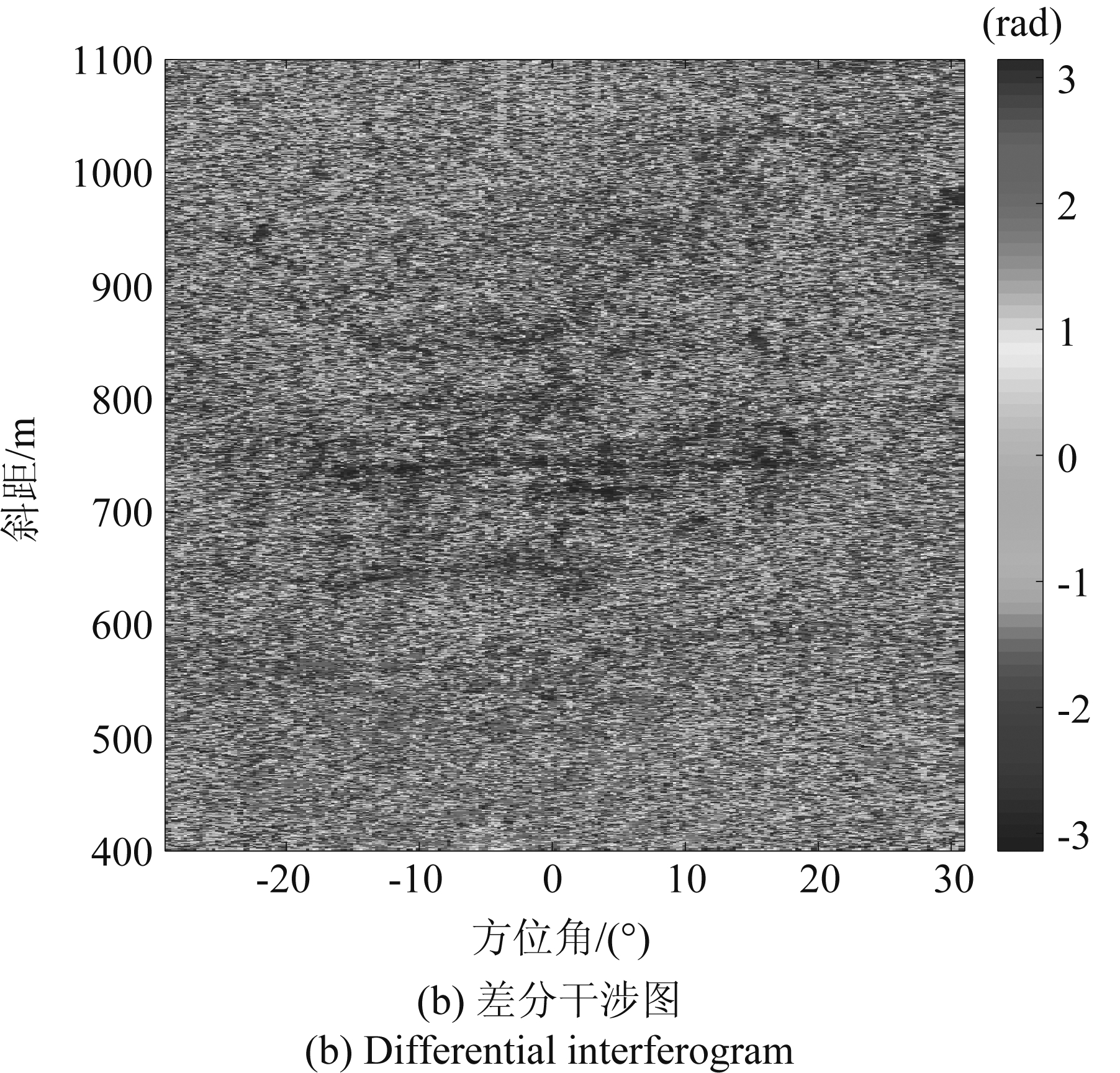
图4 雷达图像与差分干涉图
Fig.4 Radar image and differential interferogram
图5所示为利用幅度离差法选择PS点的结果。此时设定的幅度离差门限为0.25,幅度门限位-30 dB。选择后PS点总计为11364个。
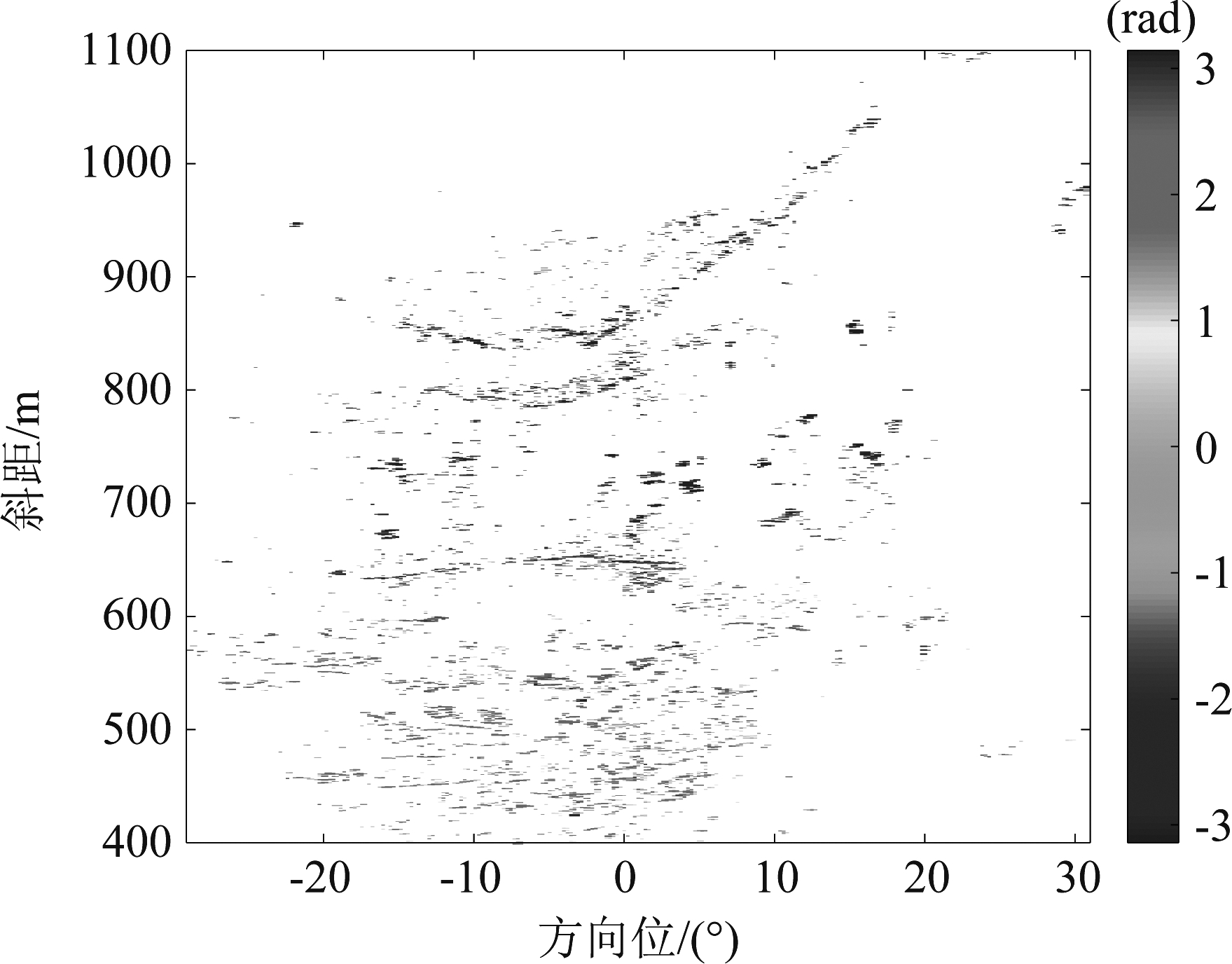
图5 PS选择结果
Fig.5 PS selection results
分析雷达图像时,利用时序列相差仅为5~6 min的相邻雷达图像进行干涉处理。本文采用30幅雷达图像,获得29幅干涉相位图。一般情况下,在短时间内,大气的变化很小,如下图6(a)和图6(b)所示。但在某些时刻,大气变化复杂,如下图6(c)和图6(d)所示,为了解决图6(c)和图6(d)所示大气不均匀变化导致的情况,本文提出气象数据筛选稳定PS点后,拟采用3种插值拟合方法对大气相位进行补偿,分别将3种方法的结果与常规线性模型补偿结果进行对比,分析不同插值拟合方法的优缺点,选出最合适的方案补偿干涉相位图中的非线性大气相位分量。
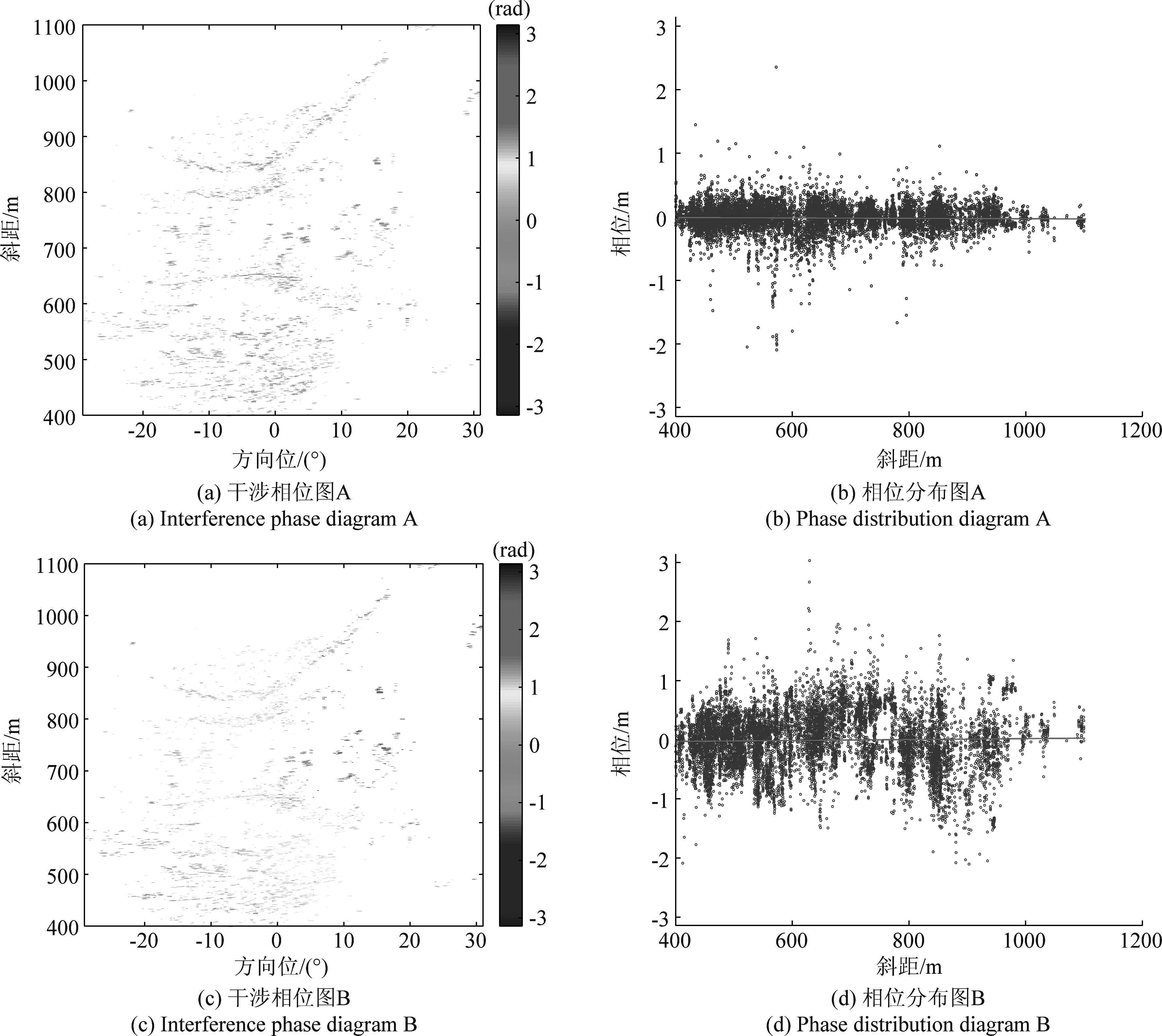
图6 短时间基线干涉相位图A和B
Fig.6 Short-time baseline interference phase diagrams A and B
根据该区域内气象站,获得2020年12月22日16:00到20:30气象变化数据(湿度、温度、大气压)分别如下图7(b)、(c)、(d)所示,基于公式(2)、(8),求出大气干涉相位,如图7(a)所示。

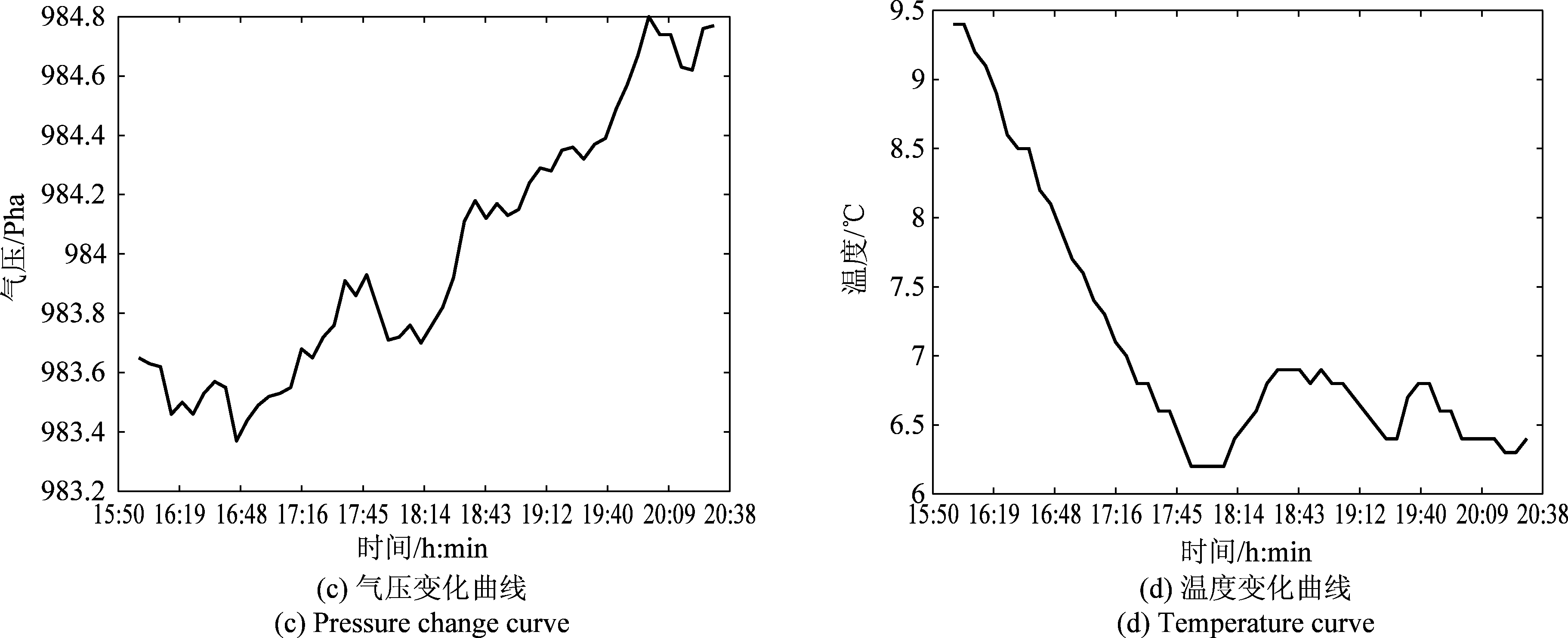
图7 温湿度、气压变化曲线其求得的大气干涉相位曲线
Fig.7 Temperature, humidity, pressure curve of atmospheric interference phase curve obtained
5 实验结果
5.1 稳定PS点筛选
利用幅度离差法得到11364个PS点,取这段时间内所有PS点的变化相位与气象数据下的大气干涉相位求相关系数,设定阈值为0.9,选出6179个稳定PS点。它们的分布如图8所示,为了直观表示稳定点与大气相位的相关性,选取相关系数最高的点与气象数据下的大气干涉相位作对比,如图9所示,此时,PS点与气象数据下的大气干涉相位相关系数为0.97。可以从图中看出,它们的变化趋势高度相似。
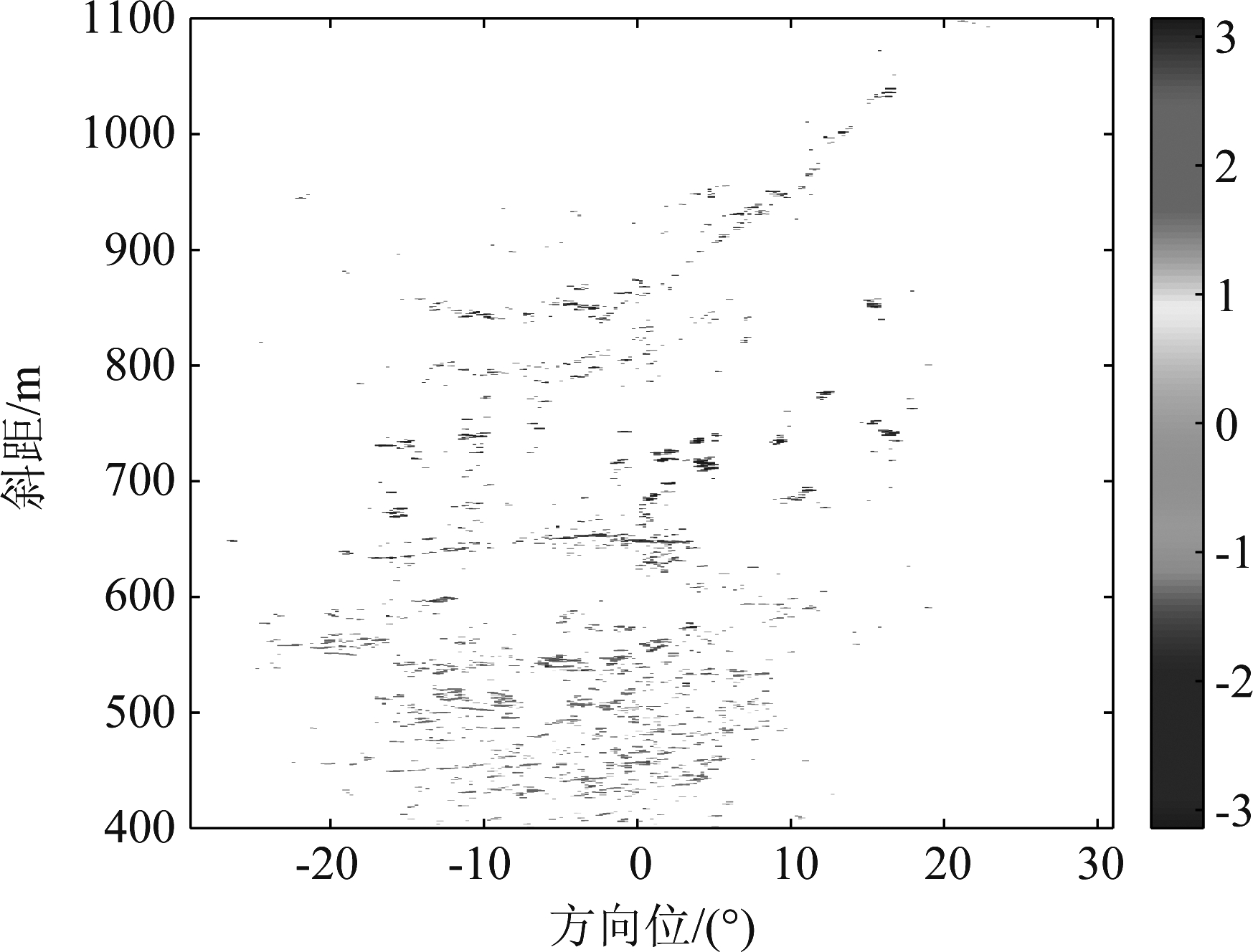
图8 稳定点空间分布图
Fig.8 Spatial distribution of stable points

图9 高相关系数点与气象数据下大气干涉相位图
Fig.9 Phase diagram of atmospheric interference between high correlation coefficient points and meteorological data
5.2 插值拟合结果
筛选出稳定PS点后,利用其坐标及相位信息进行插值拟合,估算所有PS点的大气相位,然后对其进行补偿。以图6中干涉相位图B为例进行分析。
图10(a)、图10(b)、图10(c)所示为三种插值方法的补偿结果,所有PS点补偿后相位均在0 rad左右,相较于图10(d)常规线性斜距方法下补偿结果,空变性的大气相位得到了有效补偿。但对于图10(a)红框中的PS点,由于这些点处在稳定PS点的范围外,采用线性插值方法无法进行估计。相对于其他两种插值方法,线性插值在此处具有缺陷。
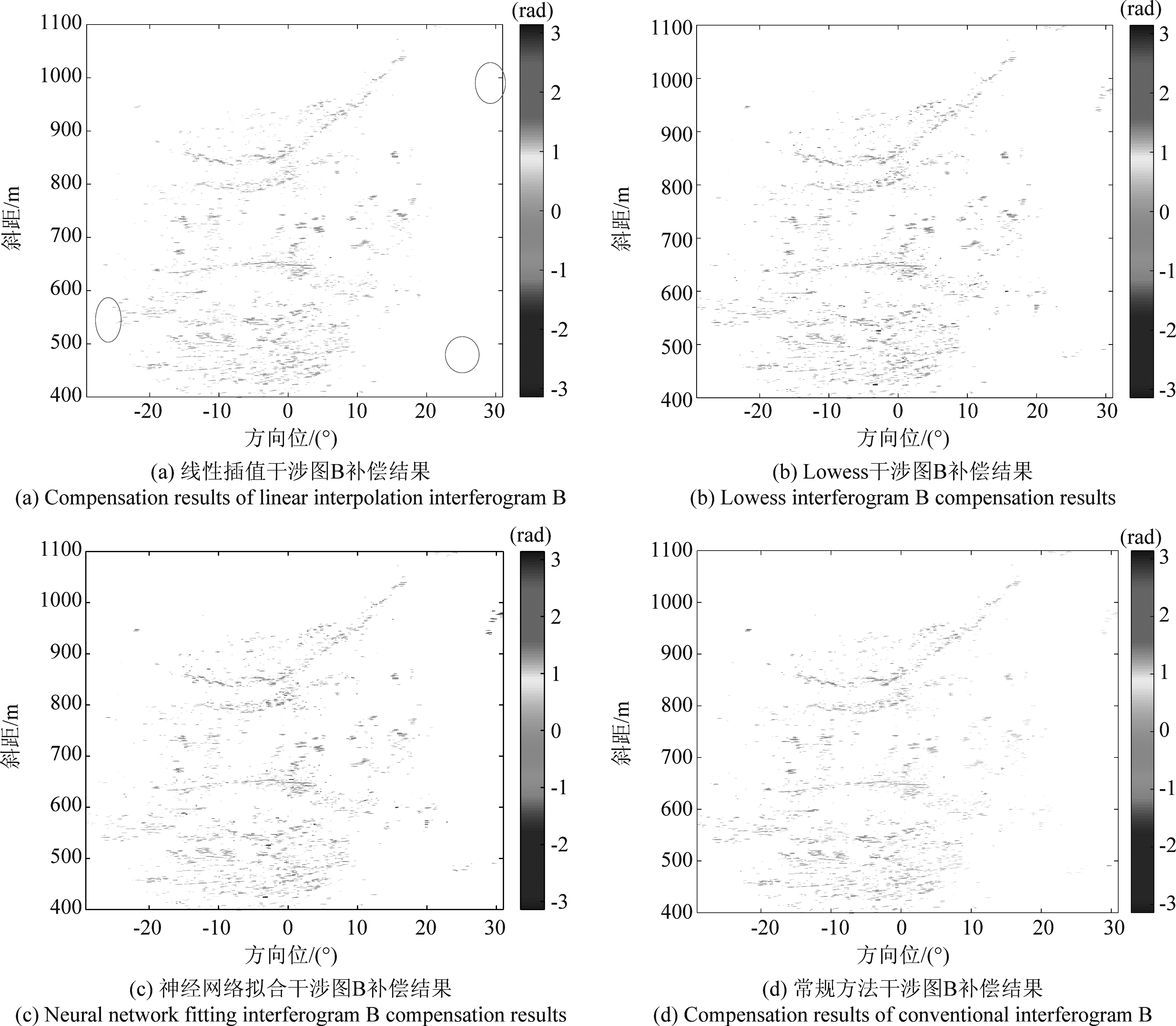
图10 几种方法补偿干涉图B的结果
Fig.10 Results of several methods for compensating interferogram B
为了更加直观的对比几种插值方法的补偿结果,从不同斜距处选择4个幅度离差值最小的PS点作为参考。图11(a)所示为所选参考点的空间分布图,图11(b)中,明显可以看出4个点的大气相位随着时间累积。图11(c)为常规方法补偿后4个点的相位变化曲线,参考点2的相位值随时间增大,说明大气相位有残余,并随时间累积。图11(d)、图11(e)、图11(f)分别为线性插值、神经网络和Lowess拟合方法的补偿结果,在图中,4个点相位变化皆较为随机,显示三种插值拟合效果较常规方法更好。

图11 不同方法补偿下参考点的相位累积相位变化曲线
Fig.11 The phase accumulation phase change curve of the reference point under different compensation methods
将29幅图利用几种补偿方法后的相位图累加得到相位累积图,相位累积图可以表明区域在观测时间内PS点累积相位变化。图12(a)为常规方法下的补偿结果,可以看出,常规方法补偿后,大气仍具有空变性,而在图12(b)、图12(c)、图12(d)三种插值拟合方法下的补偿结果中,大气的空变性得到有效改善。
但如前文所示,图12(b)线性插值的结果里,红框区域1、2、3内不存在PS点,这些区域内PS点的无法进行大气相位补偿。在图(c)神经网络补偿结果中,红框区域1、2内的PS点补偿结果显示该点相位变化较大,结果不可靠。而在图(d)Lowess拟合补偿结果中,红色区域1、2、3内PS点相位值却均在0 rad左右,红框区域内PS点得到了较好补偿。
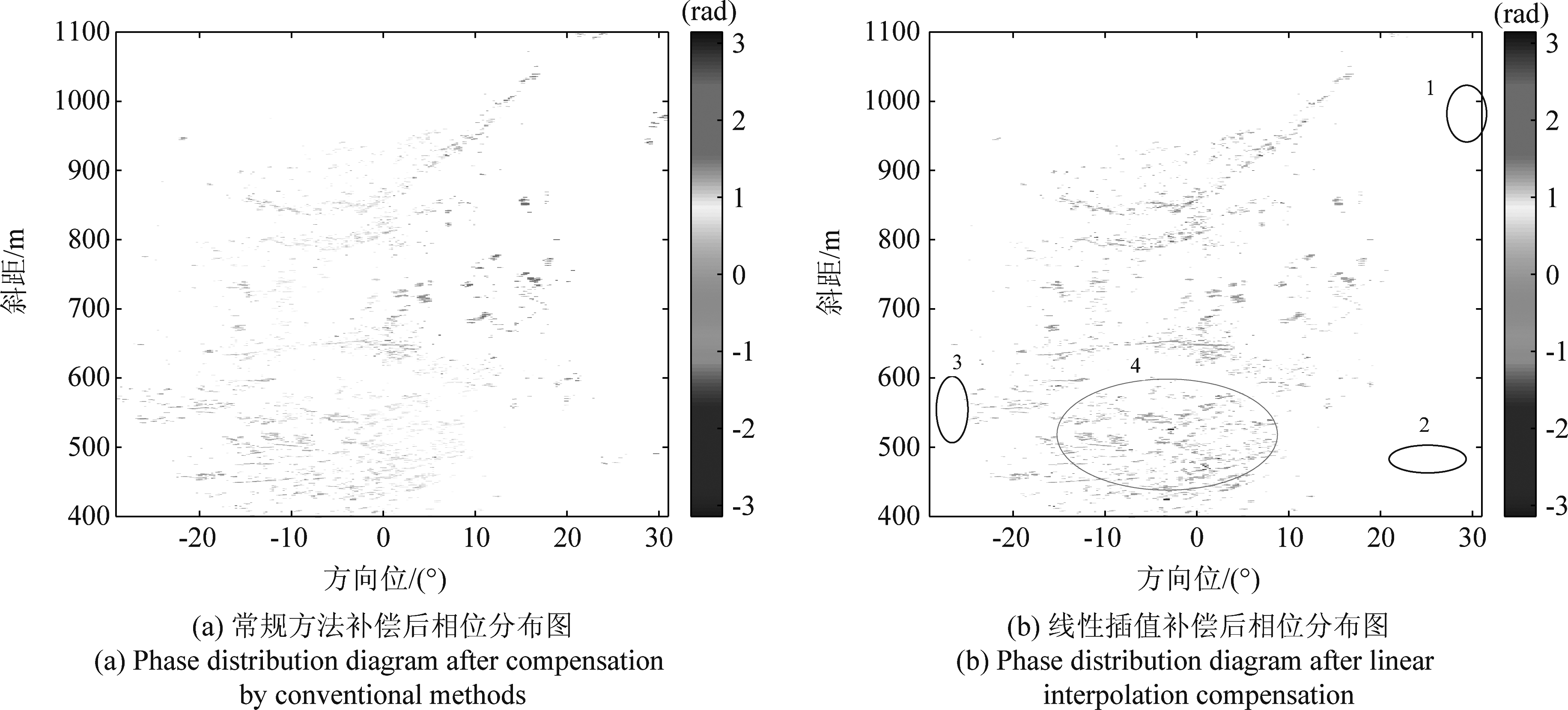
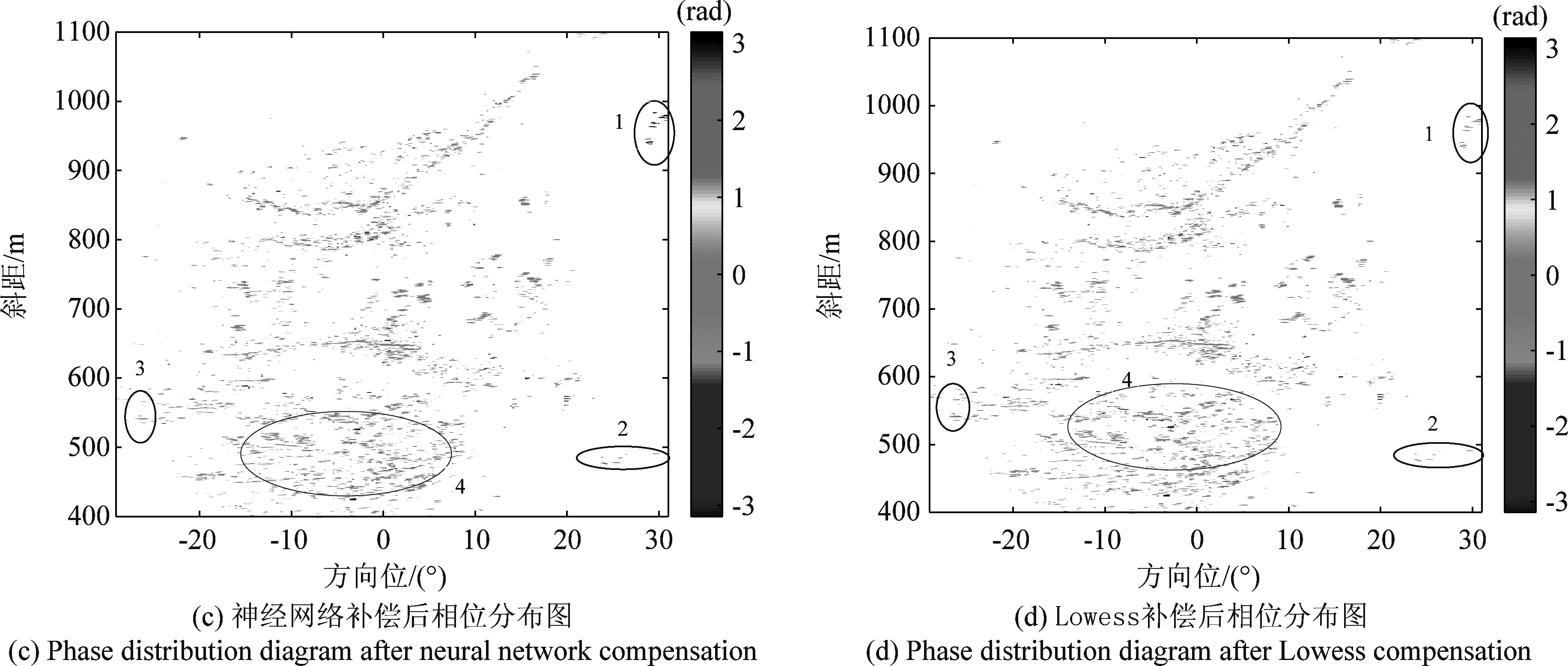
图12 不同方法补偿后相位分布图
Fig.12 Phase distribution diagram after compensation by different methods
分析造成此种情况原因:幅度离差后,红色区域内只选出了较少PS点,经过稳定点筛选,这些区域内只存在极少或不存在稳定PS点,导致线性插值和神经网络在拟合时这些区域不存在参考点,线性插值无法实现,神经网络拟合结果不可靠,而Lowess拟合时利用窗口点内做局部加权回归,构建了平滑曲面,使这些区域的值得到了有效估计,补偿后效果较好。因此,当区域内PS点较少时,密度小时,lowess取得的补偿效果较线性插值与神经网络拟合结果好。
在图12(b)、图12(c)、图12(d)中蓝色区域4中,PS数量多,分布较密集,经过稳定点选择后,区域内稳定PS较多,三种拟合插值方法在此区域补偿后的结果都在0 rad左右。因此,当区域内PS点数量较多,密度较大时,三种插值拟合方法都可得到较好结果。
三种方法中,线性插值计算量最小,神经网络次之,Lowess计算量较其他两种方法较大。
6 结论
大气相位对地基干涉雷达的测量带了不可忽视的误差。本文提出一种基于气象数据辅助的GB-InSAR大气相位补偿方法,选取了重庆九道拐29幅干涉相位图,利用相位图、参考点相位变化曲线、补偿后的累积相位图将本文方法与常规方法对比,有效的证明了本文方法解决了常规方法无法有效补偿大气相位非线性变化的干涉相位图的问题。
本文还有一些不足之处。首先本文方法需要实时获取气象数据,当观测区域过大时,需要布设多个气象站,获取不同区域内气象数据,从而准确筛选不同区域内的稳定点;其次,筛选稳定点的相关系数阈值需要人为设定;最后当大气条件变化过于复杂时,基于折射率经验模型估计大气相位的准确性较低,会影响到对稳定PS的选择,有待深入研究。
[1] 刘斌, 葛大庆, 李曼, 等.地基合成孔径雷达干涉测量技术及其应用[J].国土资源遥感, 2017, 29(1): 1-6.
LIU Bin,GE Daqing,LI Man,et al.Ground-based interferometric synthetic aperture radar and its applications[J].Remote Sensing for Land & Resources, 2017, 29(1): 1-6.(in Chinese)
[2] 曾涛,邓云开,胡程,等.地基差分干涉雷达发展现状及应用实例[J].雷达学报,2019,8(1):154-170.
ZENG Tao, DENG Yunkai, HU Cheng, et al.Development state and application examples of ground-based differential interferometric radar[J].Journal of Radars, 2019, 8(1): 154-170.(in Chinese)
[3] IANNINI L, MONTI GUARNIERI A.Atmospheric phase screen in ground-based radar: Statistics and compensation[J].IEEE Geoscience and Remote Sensing Letters, 2011, 8(3): 537-541.
[4] 黄长军, 夏红梅, 周吕.基于GCP方法的地基In SAR大气扰动误差改正分析[J].测绘与空间地理信息, 2018, 41(10): 8-11.
HUANG Changjun, XIA Hongmei, ZHOU Lv.Atmospheric disturbance error correction in GB-in SAR based on ground control point[J].Geomatics & Spatial Information Technology, 2018, 41(10): 8-11.(in Chinese)
[5] 周校,王鹏,邢诚.基于GB-SAR的建筑物微变形测量研究[J].测绘地理信息,2012,37(5):40-43.
ZHOU Xiao, WANG Peng, XING Cheng.Micro deformation mearsurement of building based on GB-SAR[J].Journal of Geomatics, 2012, 37(5): 40-43.(in Chinese)
[6] 董杰,董妍.基于气象数据的地基雷达大气扰动校正方法研究[J].测绘工程,2014,23(10):72-75.
DONG Jie, DONG Yan.Atmospheric artifact compensation for deformation monitoring with ground-based radar[J].Engineering of Surveying and Mapping, 2014, 23(10): 72-75.(in Chinese)
[7] NOFERINI L, PIERACCINI M, MECATTI D, et al.Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry[J].IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(7): 1459-1471.
[8] HU Cheng, DENG Yunkai, TIAN Weiming, et al.A PS processing framework for long-term and real-time GB-SAR monitoring[J].International Journal of Remote Sensing, 2019, 40(16): 6298-6314.
[9] HU Cheng, DENG Yunkai, TIAN Weiming, et al.A compensation method for a time-space variant atmospheric phase applied to time-series GB-SAR images[J].Remote Sensing, 2019, 11(20): 2350.
[10] 胡程,邓云开,田卫明,等.地基干涉合成孔径雷达图像非线性大气相位补偿方法[J].雷达学报,2019,8(6):831-840.
HU Cheng, DENG Yunkai, TIAN Weiming, et al.A compensation method of nonlinear atmospheric phase applied for GB-InSAR images[J].Journal of Radars, 2019, 8(6): 831-840.(in Chinese)
[11] 朱嘉鑫,邓云开,田卫明,等.基于K-means算法的时序GB-InSAR图像PS实时选择方法[J].信号处理,2021,37(3):349-357.
ZHU Jiaxin, DENG Yunkai, TIAN Weiming, et al.Real-time selection method of time series GB-InSAR image PS based on K-means algorithm[J].Journal of Signal Processing, 2021, 37(3): 349-357.(in Chinese)
[12] 陆佳炜, 陈泳恩.基于二维插值的图像变形算法[J].微型电脑应用, 2003, 19(4): 13-16,2.
LU Jiawei, CHEN Yong’en.Image deformation algorithm based on two-dimensional interpolation[J].Microcomputer Applications, 2003, 19(4): 13-16,2.(in Chinese)
[13] 徐晓丹, 刘华文, 姚明海, 等.一种基于局部加权回归的分类方法[J].计算机工程与科学, 2015, 37(10): 1959-1964.
XU Xiaodan, LIU Huawen, YAO Minghai, et al.A novel classification method based on locally weighted regression[J].Computer Engineering & Science, 2015, 37(10): 1959-1964.(in Chinese)
[14] 郭旭东,洪瑞凯,涂晋升,等.基于BP神经网络的GB-SAR大气改正模型[J].测绘科学技术,2018, 6(4): 374-386.
GUO Xudong, HONG Ruikai, TU Jinsheng,et al.GB-SAR Atmospheric Correction Model Based on BP Neural Network[J].Science and Technology of Surveying and Mapping,2018,6(4): 374-386.(in Chinese)
[15] 张祥, 陆必应, 宋千.地基SAR差分干涉测量大气扰动误差校正[J].雷达科学与技术, 2011, 9(6): 502-506, 512.
ZHANG Xiang, LU Biying, SONG Qian.Atmospheric disturbance correction in ground-based SAR differential interferometry[J].Radar Science and Technology, 2011, 9(6): 502-506,512.(in Chinese)
[16] HU Cheng, ZHU Mao, ZENG Tao, et al.High-precision deformation monitoring algorithm for GBSAR system: Rail determination phase error compensation[J].Science China Information Sciences, 2016, 59(8): 1-16.



