1 引言
多输入多输出(Multiple Input Multiple Output, MIMO)系统与正交频分多路复用(Orthogonal Frequency Division Multiplexing, OFDM)技术结合,使无线链路上的高速数据传输和宽带多媒体服务成为可能[1]。MIMO-OFDM已经得到了广泛的研究并成为一个成熟的领域。信噪比(Signal to Noise Rate, SNR)是度量通信系统传输质量可靠性不可或缺的参数[2]。信噪比估计已经成为通信系统的重要组成部分,特别是随着5G非授权频段中的频谱感知、功率控制、自适应调制和编码(Adaptive Modulation and Coding, AMC)以及软译码技术的出现[3]。在非协作通信应用背景下,准确的信噪比信息可用于提高无线通信系统的传输,信道估计结果,也可提高系统性能,且为后续的调制识别和解调提供了先验信息。所以,本文研究了MIMO-OFDM信号的SNR盲估计。
迄今为止,有关MIMO-OFDM信号 SNR盲估计的文献很少,大多数都是针对OFDM信号[4-6]。常用SNR估计技术包含两类:一种是需要数据辅助的估计方法[7-8],另一种是不具数据辅助的估计方法[9-10]。在文献[11]中,假设信道在频域中缓慢变化,在发送端使用两个OFDM训练符号,在输出端对接收到的信号进行加减得到两个新信号,通过相邻子载波的频域信道系数的差值估计噪声方差。再利用信道估计器估计信道系数来计算信噪比。该方法在单径信道下性能良好,但在较复杂的信道环境下性能较差;文献[12]在单输入多输出(Single Input Multiple Output, SIMO)系统中,根据多路信号的协方差矩阵进行奇异值分解,通过最大特征值来估计信噪比,但该方法不能直接运用在MIMO系统里,因为在MIMO系统接收端的信号都是通过不同发射天线发送过来的,收发两端的信道响应系数是不一样的;文献[13]采用半盲训练符号分析自适应传输参数,利用前导符号的周期结构估计信噪比,该算法计算复杂度高且估计精度较低。文献[14]先要选择发送信号合适的循环后缀长度,确保MIMO系统可以转换成多个单通道系统,然后基于信号的循环平稳性估计信噪比;文献[15]所提出的SNR估计算法是先基于前导符号估计出信道系数,再利用QR分解法估计噪声方差,该方法是应用在收发天线数都为2的情况下,并没有更多的扩展且对信道估计依赖大。对于以上所提出的研究方法,有的是在SISO系统里研究的,在MIMO系统里不可以直接应用,且对于MIMO-OFDM信号,目前大部分的研究是基于训练序列的,不适合应用在非协作通信场合。
针对以上研究的不足,本文对MIMO-OFDM信号SNR盲估计提出了新的方法,首先对每根接收天线上的接收信号去循环前缀(Cyclic Prefix, CP)和FFT变换,将时域卷积模型转换为频域线性瞬时混合模型,对接收信号做自相关、特征值分解(Eigen Value Decomposition, EVD)、估计发射天线数和噪声功率,其次是根据盲源分离(Blind Source Separation, BSS)思想把接收信号分开来获得源信号的估计,从而估计出信噪比。
2 系统模型
本文所研究的是收发天线位置相对集中的集中式MIMO-OFDM系统。该模型如图1所示,在发送端,经过一系列变换得到OFDM信号后,通过Nt根发射天线发送出去;在接收端,对Nr根接收天线上的接收到信号进行OFDM解调,经过一个信噪比估计模块,再进行MIMO解码,星座解映射得到比特输出。
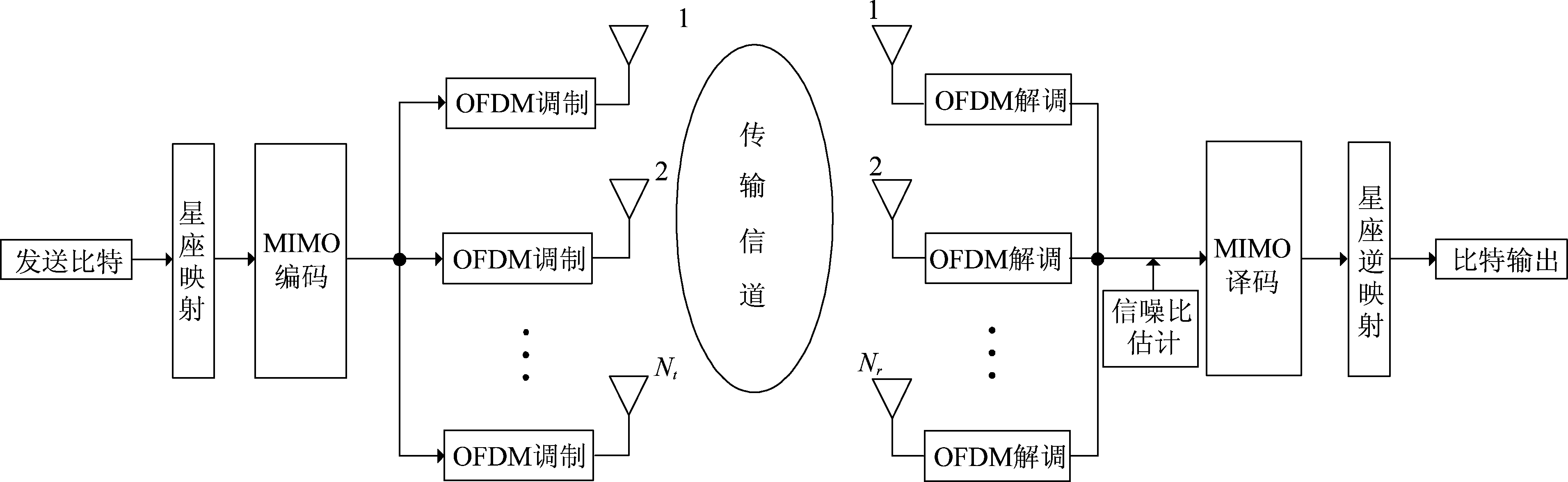
图1 MIMO-OFDM系统模型图
Fig.1 MIMO-OFDM system model diagram
假设MIMO-OFDM的子载波数为N,Ng为OFDM符号的循环前缀,发射天线数为Nt,接收天线数为Nr。第nt根发送天线上的基带OFDM时域信号为:
(1)
其中
是第nt根发送天线、第m个子载波上的第l个频域符号,其均值为0,方差为
且独立同分布,所以有:
是克罗内克函数;Ts=Tu+Tg是整个符号持续时间,其中Tu表示有用符号持续时间,Tg是循环前缀持续时间。g(t)为矩形成形脉冲函数,其表达式为:
(2)
设信号经过平坦衰落信道,且第nt个发射天线与第nr个接收天线之间的信道脉冲响应为:
hnr,nt(τ,t)=hnr,nt(t)δ(τ-τ0)
(3)
式中,δ(·)为狄利克雷函数。
在MIMO-OFDM系统的接收端,每路信号以叠加方式同时到达,频偏和初始时延不予考虑,第nr根接收天线上的接收信号为:
(4)
式中,νnr(t)是第nr根接收天线上的AWGN,均值为0,方差为
且与信号相互独立。
利用T=Tu/N对ynr(t)进行采样,去除CP后,得到第l个接收符号为:
(5)
其中,Tu=NT,Tg=NgT,Ts=NsT。对信号
进行N点FFT运算,可得到第nr根接收天线上的解调信号为:
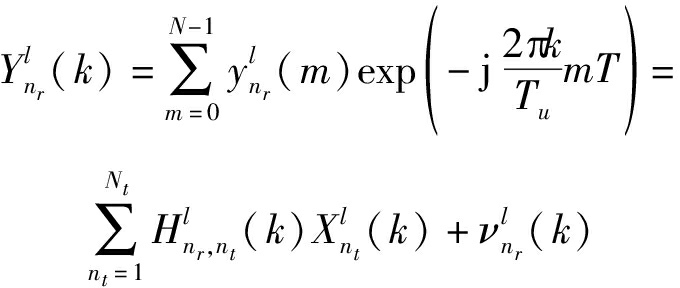
(6)
将式(6)表示成频域形式:
(7)
因为子载波存在正交性,所以Hnr,nt应为对角矩阵。因此,式(7)可变为:
(8)
忽略子载波索引,MIMO-OFDM系统用矩阵形式表示为:
Y=HX+V
(9)
其中,
为第m个子载波上的接收信号向量,
为第m个子载波上的发送向量,
为第m个子载波上的AWGN。H为第m个子载波的信道响应表示为:
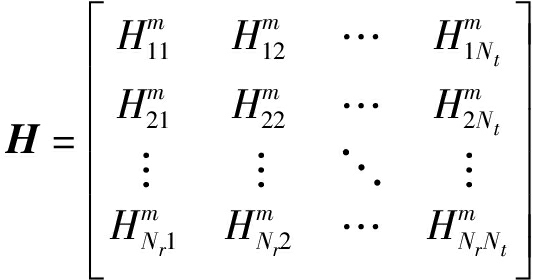
(10)
3 MIMO-OFDM信号信噪比盲估计
根据第2节建立的集中式MIMO-OFDM信号模型,本节给出了信噪比的盲估计算法,算法的主要思想是根据噪声子空间计算噪声功率和利用线性瞬时混合盲源分离方法估计源信号,为了准确估计源信号和噪声功率,一般假设,接收信号矢量维数应不小于源信号矢量维数,即Nr≥Nt[16]。
3.1 发射天线数估计
根据信噪比的估计公式和JADE算法的使用,需要知道信源数,即发射天线数。在很多文献里都是假设已知Nt,但实际场景并没有这么理想化,因此本文利用MDL准则估计Nt。估计过程为:
(1)求Y(k)的自相关矩阵
RY=E{Y(k)[Y(k)]H}
(11)
式中[·]H表示共轭转置。
(2)对RY进行EVD,将得到Nr个特征值按降序排序。
(3)用MDL算法估计发射天线数[17]。
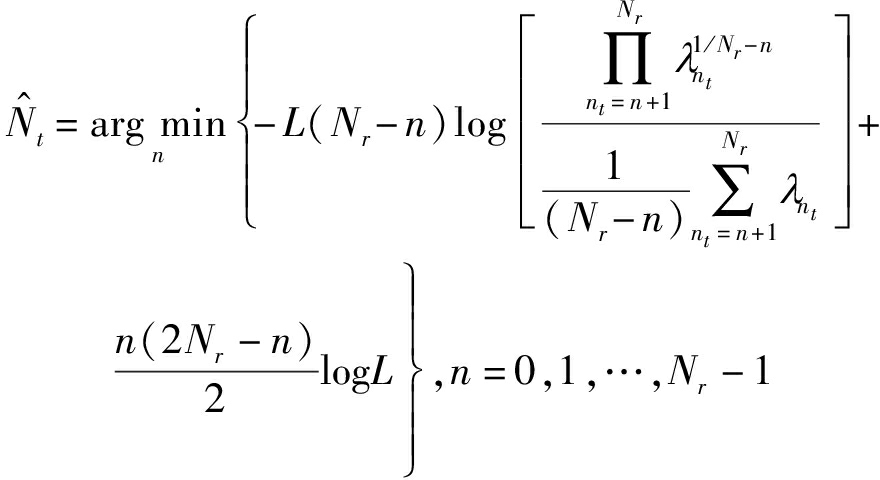
(12)
式中,λnt为第nt个特征值,L代表单根天线上的符号数。
3.2 噪声方差估计
根据式(11),对RY做特征值分解RY=U×D×UH,其中
而
是元素为0的矩阵,
为信号子空间对应的特征值。
根据2.1节估计的发射天线数
因此,噪声方差可近似为:
(13)
3.3 信号功率估计
在MIMO-OFDM系统里,源信号的传输会受到来自信道和噪声的影响,从而减小了SNR估计精度。为了降低估计误差,要消除信道和噪声对信号功率估计的影响,估计出源信号。文献[18]比较了常用的3种ICA分离算法,如:JADE、EASI、Fast ICA。其中在数据量较少时,JADE的收敛性能较好且误比特率较低,对数据量的要求也较低,不需要进行处理,可直接对复信号进行分离。因此本文利用JADE算法来估计源信号。
在进行BSS之前,先做白化处理。白化矩阵B表示为:
(14)
则白化信号可表示为:
(15)
其中V=BH。
定义信号矢量z的四阶累积量
另外对于任意一个Nr×Nr的矩阵M,有一个累积量矩阵A=Oz(M)与之对应:
(16)
根据式(15)可知:
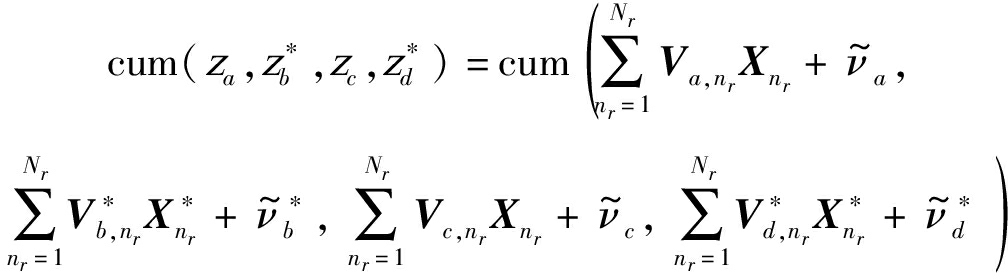
(17)
根据
这一特征和它的其他性质可得到:
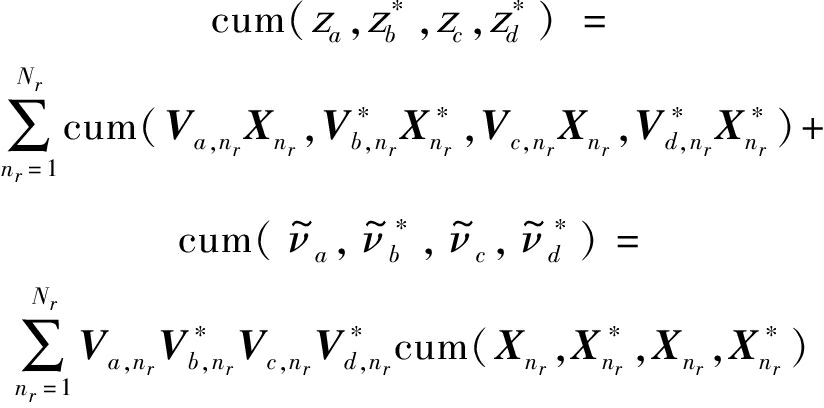
(18)
令
则由式(18)可知
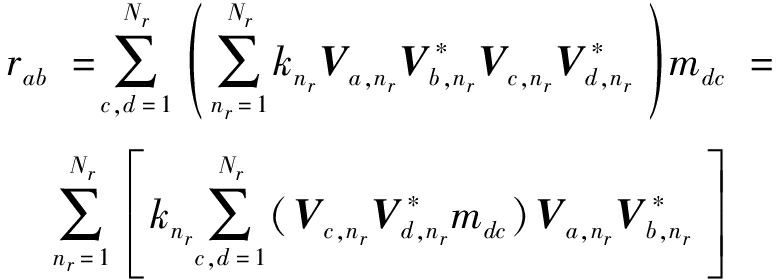
(19)
(20)
其中unr是正交矩阵V的第nr列,
根据式(20)可知只需找到一个正交矩阵
使得矩阵
对任意的M都为对角矩阵,这时
就是V的估计,到此正交矩阵V的估计问题就转换为对角集合Oz(Ma)(a=1,2,…)的联合对角化问题。
由文献[20]可得,对存在四阶累积量的Nr维的复随机向量z,存在
个实数
和个矩阵
满足
Oz(Ma)=λaMa
(21)
根据式(21),求得Nr个矩阵Oz(Ma)(a=1,2,…,Nr),然后联合对角化这Nr个矩阵,得到的
是正交矩阵,源信号的估计为
即分离矩阵为
因此可以通过源信号的估计来计算发送信号的功率。
(22)
由公式(12)、(13)和(22)可得,MIMO-OFDM信号的SNR定义式为接收信号总功率
与噪声总功率
的比值,即[21]:
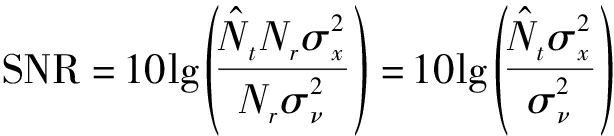
(23)
综上所述,以下是该方法的具体步骤:
步骤1 根据式(11)计算Y(k)的RY。
步骤2 对RY进行EVD,将得到Nr个特征值按降序排序。根据式(12)估计出发送天线数。
步骤3 利用(13)计算Y(k)的平均噪声功率。
步骤4 通过BSS的思想估计出源信号,利用式(22)计算发送信号功率。
步骤5 根据式(23)得出MIMO-OFDM的信噪比SNR。
算法模型如图2 所示。
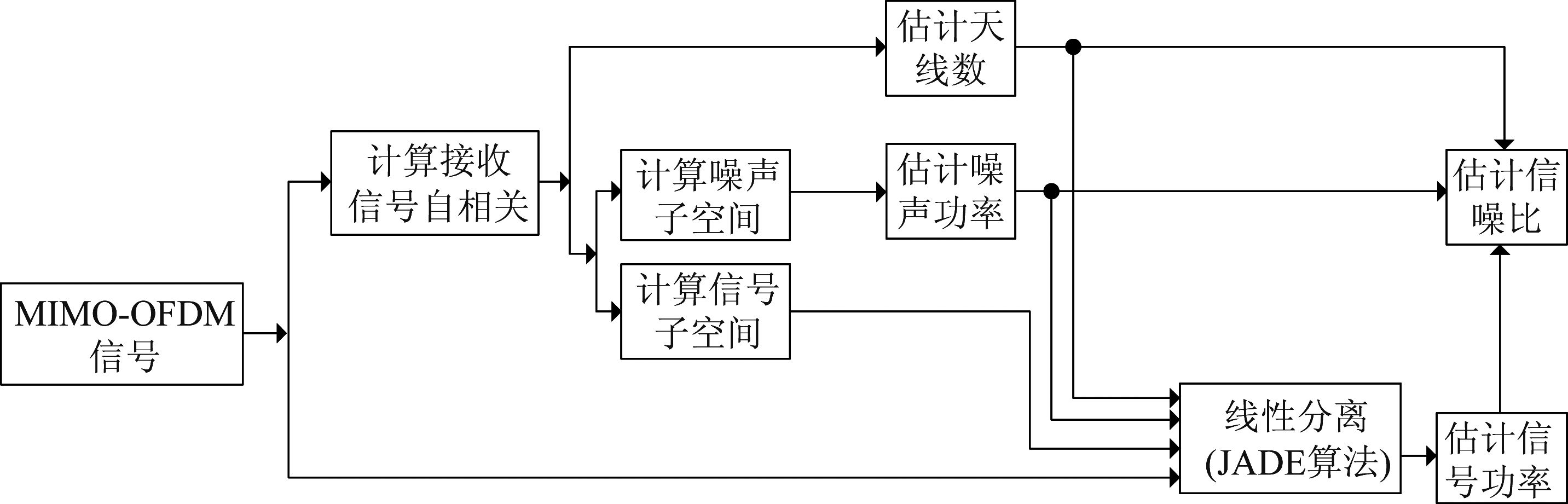
图2 算法模型
Fig.2 Algorithm model
4 仿真结果及性能分析
本文利用MATLAB软件进行实验来验证该方法的有效性,所采用的性能评价指标为估计均方误差Gvari,定义为:
(24)
其中,
为每次估计的信噪比值,s为对应的输入信噪比。
实验1 MDL算法对发射天线数Nt的估计性能分析。在不同SNR、Nt×Nr及子载波数N下研究MDL准则对Nt估计的均方根误差(Root Mean Square Error, RMSE),采用的调制方式为QPSK调制, SNR∈[-2010]dB,蒙特卡罗仿真次数为500。
图3为N=128时的估计性能图。当SNR≥2 dB时,在不同Nt×Nr条件下,其均方根误差都达到了0,并且,在同一Nr下,随着Nt的减少,估计性能越好;且在同一Nt下, Nr的增加使得估计性能也略有提高。因为收发端天线数差距越大,则分集增益越高,有助于减少信道衰落和噪声的影响,鲁棒性越好。
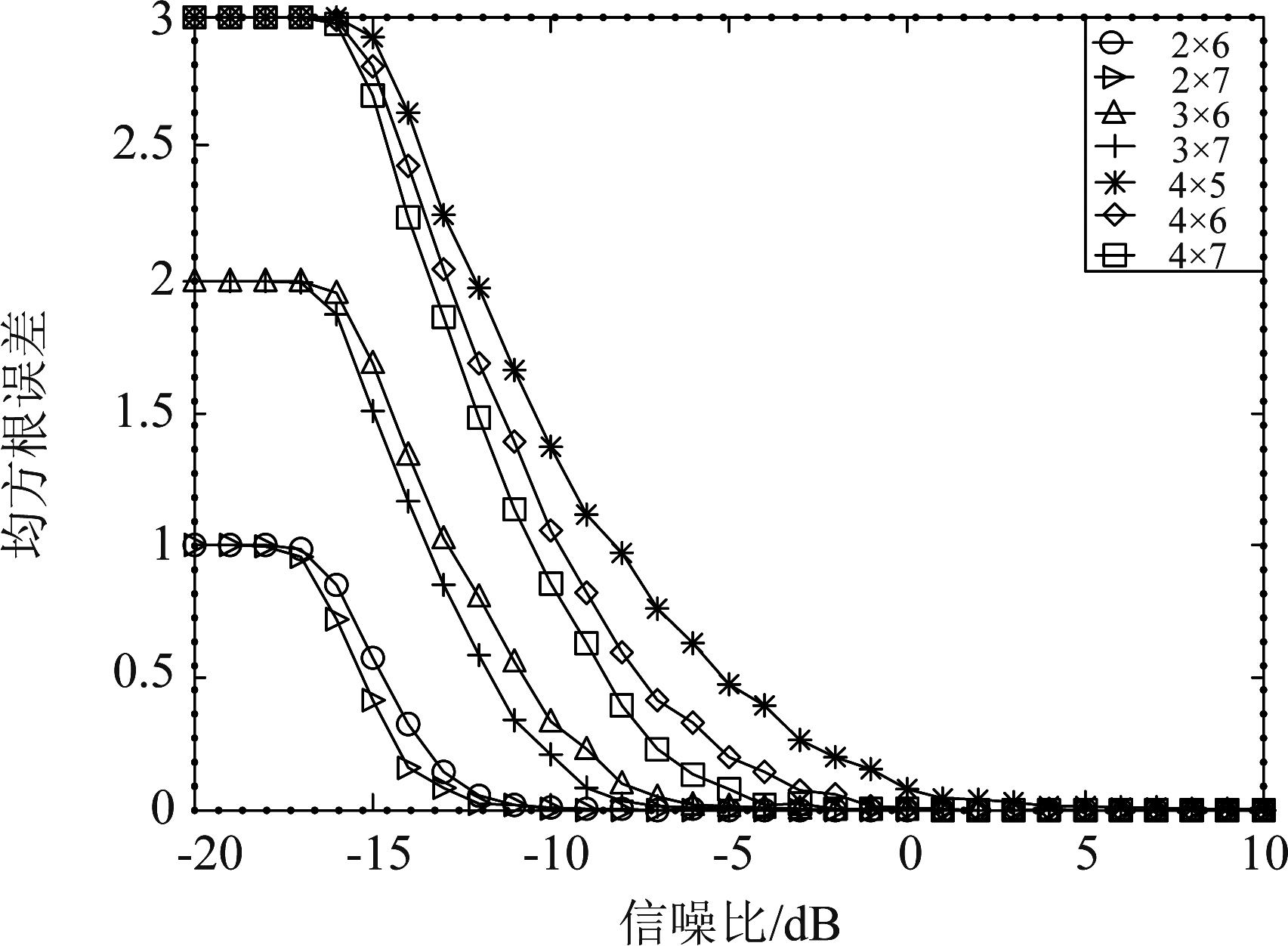
图3 不同Nt×Nr下Nt的估计性能
Fig.3 Nt Estimated performance under different Nt×Nr conditions
图4为当采用QPSK调制,Nt×Nr=3×6时MDL准则在不同N下对Nt估计的RMSE。如图可得,随着SNR的增长,MDL准则在不同N下的估计性能趋于一致,且估计性能随着N的增加而增加,这是因为做自相关的向量数越多,噪声分量消除得越多,估计性能就更好。图5为MDL准则对Nt的估计,由式(12)可知,寻找最小幅度值所对应的n作为发射天线数的估计,由图可知,对不同的Nt都能够准确的估计出来。
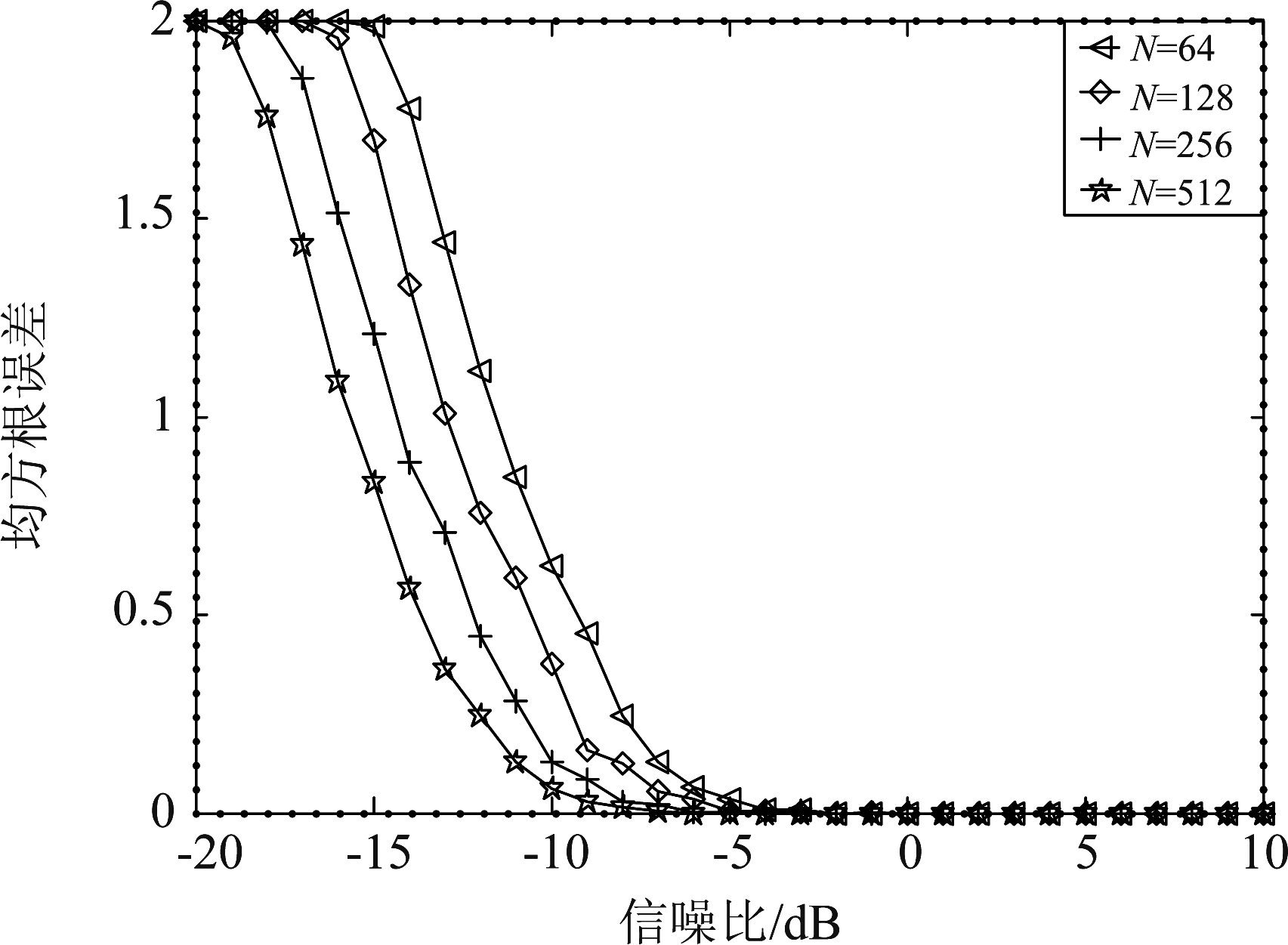
图4 不同子载波数下Nt的估计性能
Fig.4 Nt Estimation performance under different subcarrier number
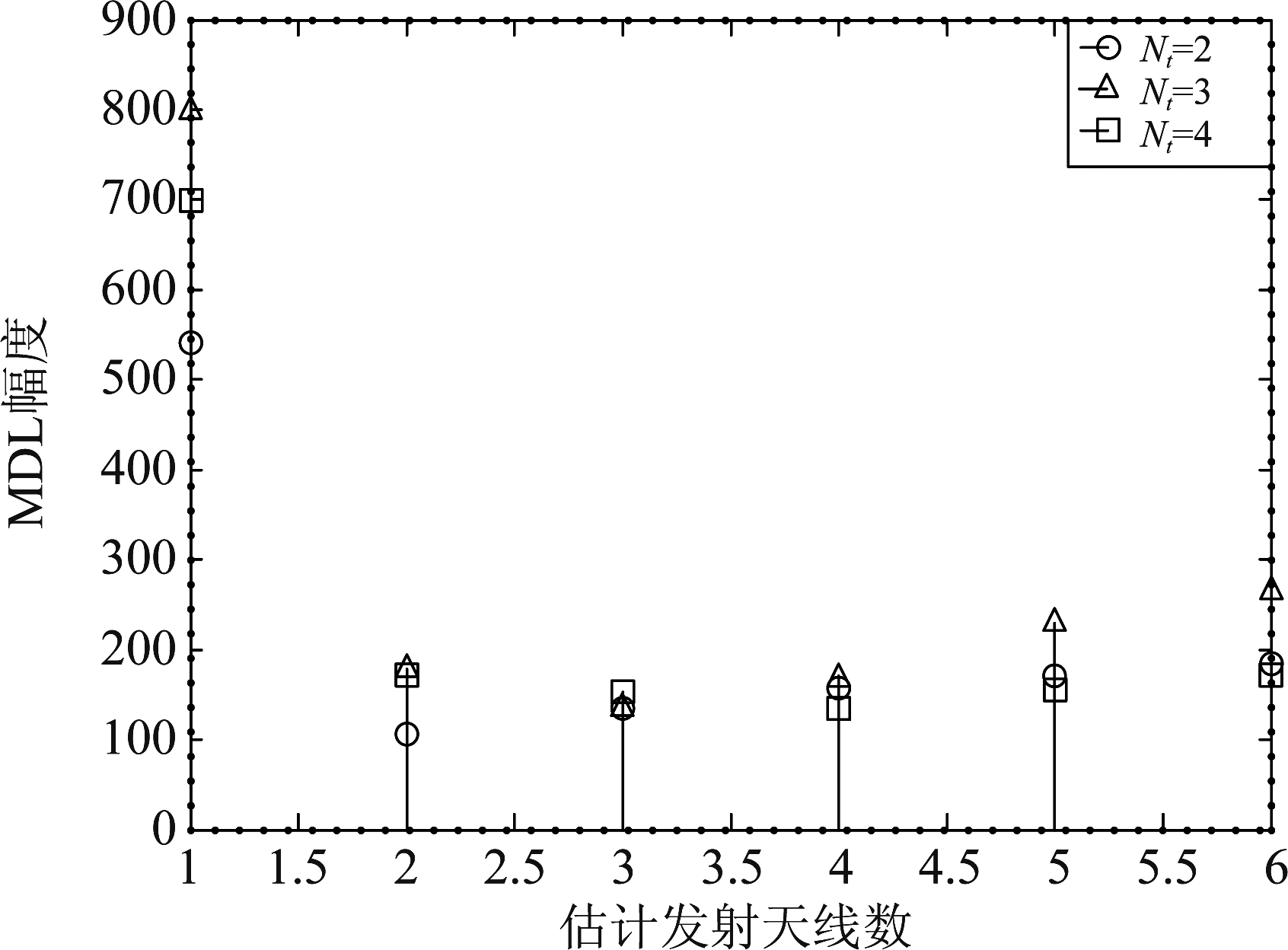
图5 MDL对发送天线的估计
Fig.5 MDL estimation of the transmitting antenna
实验2 证明MIMO-OFDM系统源信号的估计性能。本实验选取三个相互独立的OFDM 基带信号作为信源。信噪比SNR=20 dB,接收信号维数为6,采用JADE算法进行源信号的估计,结果如图6所示,绘制了信号的星座图。
图6中的(a),(b)和(c)分别为发送信号,混合信号和估计信号。可以得出,JADE准则把信号成功的分离出来,并准确的估计出了源信号。
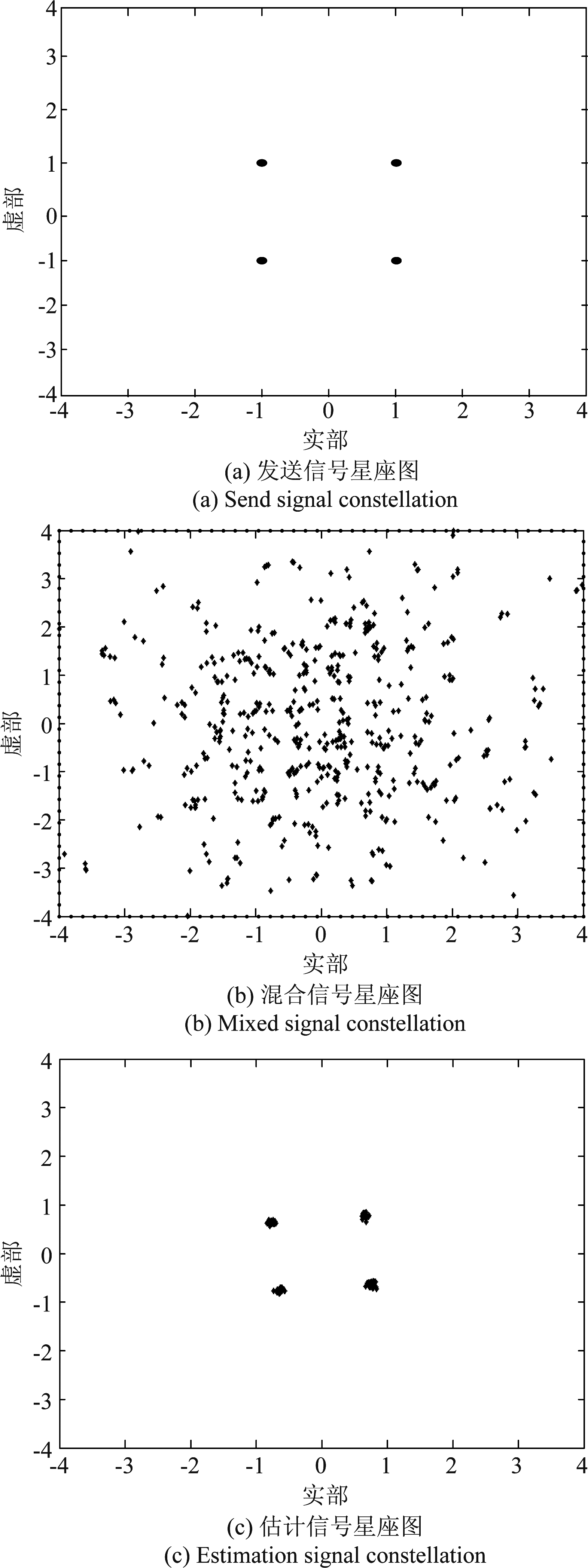
图6 MIMO-OFDM系统源信号的估计性能图
Fig.6 Performance diagram of separation estimation of MIMO-OFDM system source signal
实验3 真实的SNR和估计的SNR值的比较。仿真条件:输入信噪比为[-1050]dB,MIMO-OFDM系统中的调制方式为QPSK,N=128,Ng=32,符号个数为100,Monte Carlo仿真次数为1000。
图7显示了在Nr一定时,不同Nt下真实SNR和估计SNR的值,由图可以得出,当Nr保持不变时,随着Nt的减少,SNR的估计值和真实值越来越接近。根据式(23)和图3可知,信噪比估计受到发射天线数估计和源信号估计的影响,发射天线数的估计在Nr一定时,随着Nt的减少,估计准确率越好,SNR较低时,Nt和源信号的估计会产生较大的误差,从而影响算法的估计正确率。图8显示了在Nt一定时,不同Nr下真实SNR和估计SNR的值。从图中可以得出,Nr的变化对SNR的估计影响不大。
图7 当Nr=6时,不同Nt下真实SNR和估计SNR的比较
Fig.7 When Nr=6,the comparison between the real SNR and the estimated SNR under different Nt conditions
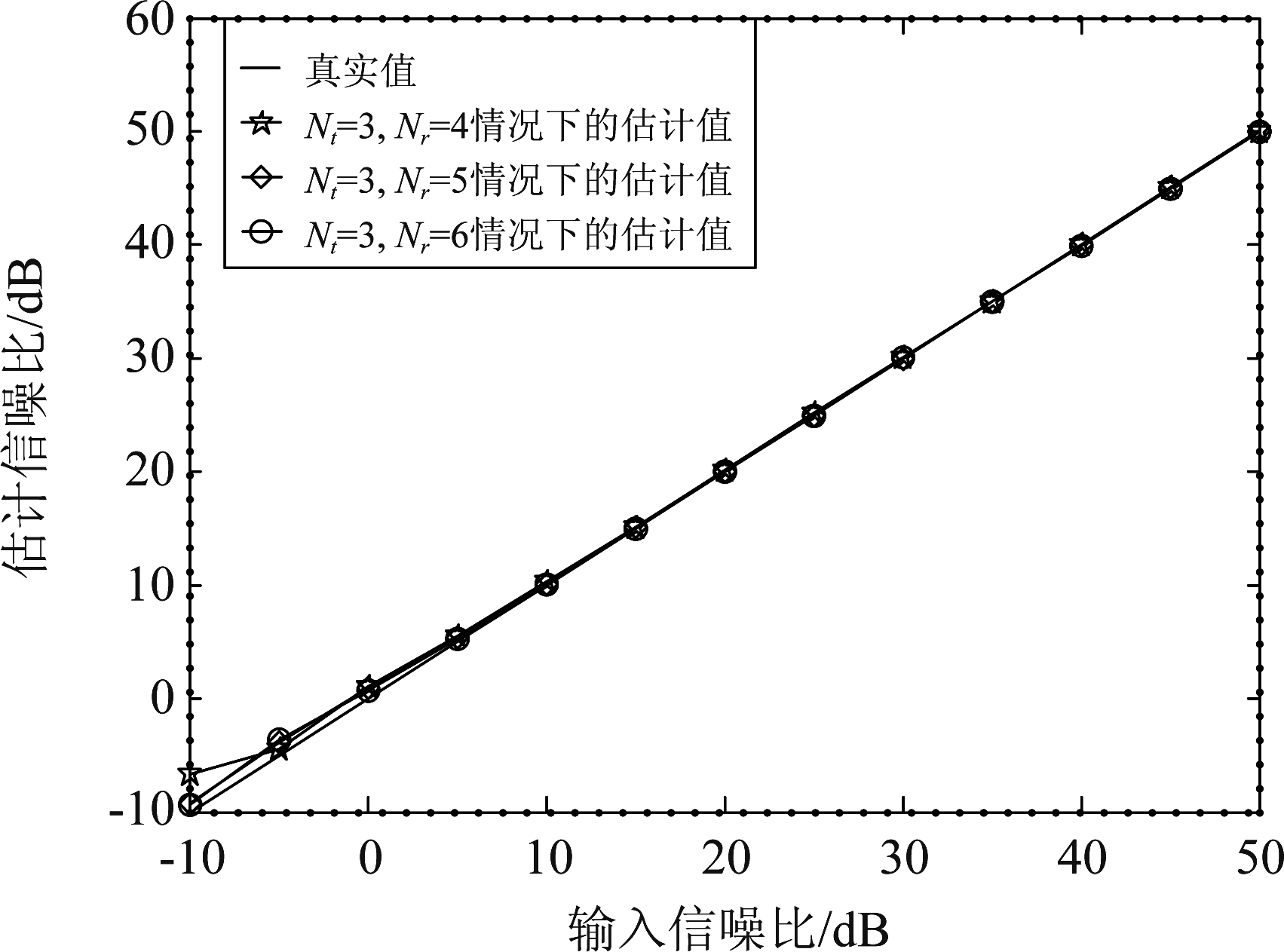
图8 当Nt=3时,不同Nr下真实SNR和估计SNR的比较
Fig.8 When Nt=3, the comparison between the real SNR and the estimated SNR under different Nr conditions
实验4 验证了当SNR是[050]dB时,不同接收天线数Nr和不同符号数L对SNR估计的影响,Nt=3,其他仿真条件如实验3所示。从图9和图10可以知道,SNR较低时,估计性能的差异在不同接收天线数下比较大,随着Nr的增加,MIMO-OFDM信号的SNR估计性能越好,这是因为,如果Nt保持恒定Nr增多会导致噪声子空间的相对维度变大,
的估计更加准确。随着SNR的增长,不同Nr下估计性能相近。另外,OFDM符号数目的增长也可以显著提高该方法的估计性能。因为对自相关矩阵EVD,符号数的增加,使信号特征值与噪声特征值之间的边界区别越大。
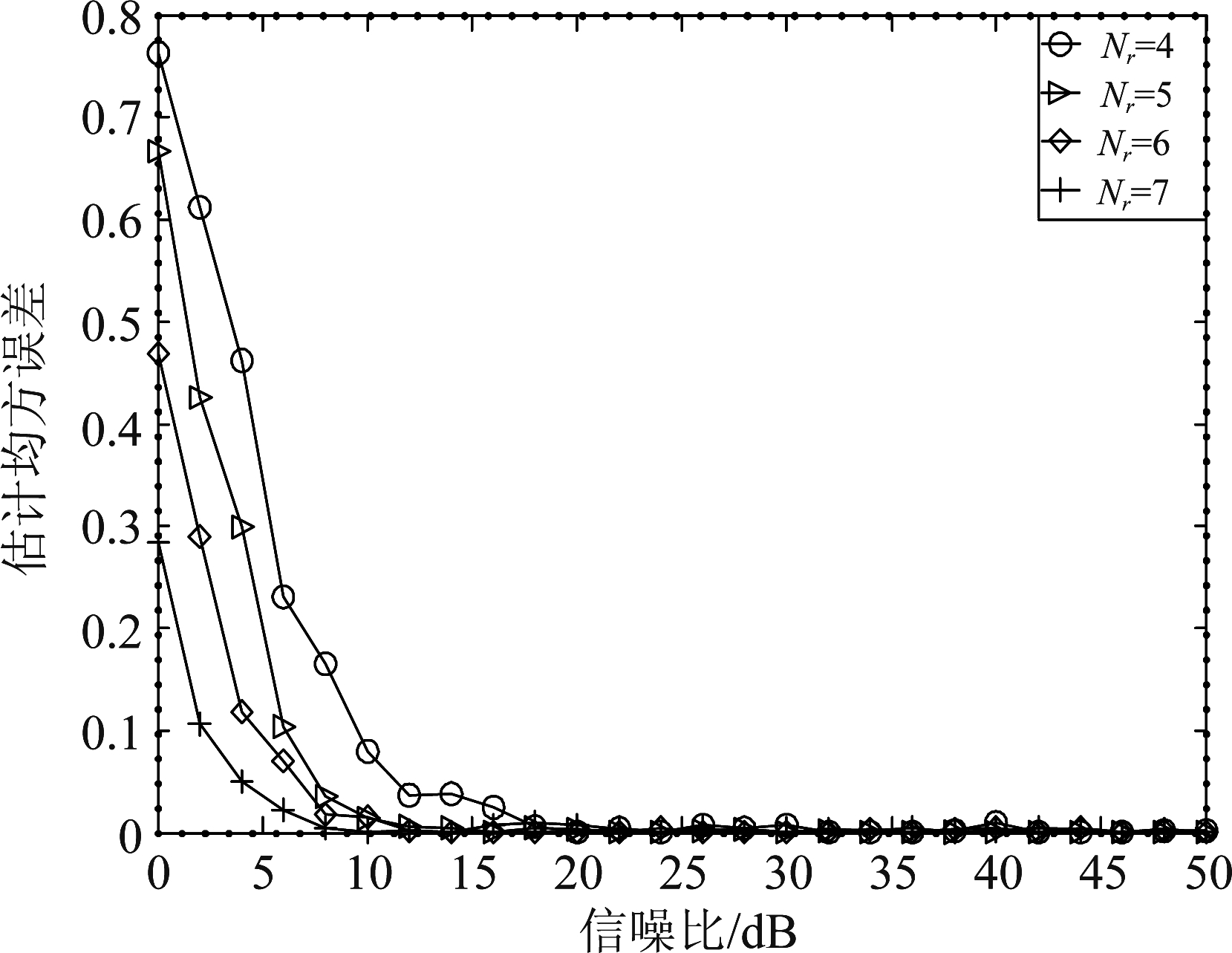
图9 当Nt=3,L=100时,不同Nr下信噪比的估计性能
Fig.9 When Nt=3,L=100, the estimated performance of SNR under different Nr conditions
图10 当Nt=3, L=300时,不同Nr下信噪比的估计性能
Fig.10 When Nt=3, L=300, the estimated performance of SNR under different Nr conditions
实验5 该文中的SNR估计算法与文献[13]和Boumard所提出的方法的性能比较。图11是在相同仿真条件下,不同SNR估计方法的性能比较,从图11可知,本文方法的估计正确率比文献[13]和Boumard所提出的算法要高。由理论分析可得,本文方法估计的信噪比即受到天线数和源信号估计的影响,也会受到噪声估计的影响。文献[13]采用的方法是半盲的,通过前导序列对信道进行估计。因此,本文所提出的方法不仅估计性能好,易于实现,而且更加适合于MIMO-OFDM系统的SNR盲估计。
图11 SNR估计性能对比
Fig.11 Comparison of SNR estimated performance
5 结论
本文针对MIMO-OFDM信号SNR的盲估计问题,研究了一种基于特征值分解和特征值矩阵联合近似对角化的SNR盲估计算法,基于不同Nt、Nr和L对该方法做了实验,并讨论了该方法的性能,最后将本文算法与其他算法做了比较。从实验结果得出,该算法适合非合作通信系统,具有良好的性能,当SNR>3 dB时,估计的均方误差小于0.1。
[1] KHAN A, ZAIB A, ULLAH I, et al.MIMO iterative receiver SNR estimation strategies for link to system interfacing[J].International Journal of Communication Systems, 2020, 33(6): e4303.DOI:10.1002/dac.4303.
[2] RAJENDER G, ANILKUMAR T.Channel estimation using Kalman filter for MIMO-OFDM communication system[J].International Journal of Recent Technology and Engineering, 2019, 8(2S11): 3075-3077.
[3] WANG Wentao, SHEN Yuyao, WANG Yongqing.Low-complexity non-data-aided SNR estimation for multilevel constellations[J].IEEE Communications Letters, 2020, 24(1): 113-116.
[4] ALOUI A, RHOUMA O B, REBAI C.Preamble based SNR estimation for IEEE 802.15.4g MR-OFDM[C]∥2018 25th IEEE International Conference on Electronics, Circuits and Systems(ICECS).Bordeaux, France.IEEE, 2018: 325-328.
[5] LIU Yu, ZHANG Tianqi, LI Can, et al.SNR estimation for OFDM signals in frequency selective fading channels[C]∥2014 7th International Congress on Image and Signal Processing.Dalian, China.IEEE, 2014: 1068-1072.
[6] 刘明骞, 郭菲, 李兵兵, 等.Underlay认知网络中时频重叠OFDM信号的信噪比盲估计[J].电子学报, 2018, 46(6): 1510-1514.
LIU Mingqian, GUO Fei, LI Bingbing, et al.Blind SNR estimation of time-frequency overlapped OFDM signals for underlay cognitive radio networks[J].Acta Electronica Sinica, 2018, 46(6): 1510-1514.(in Chinese)
[7] ZIVKOVIC M, MATHAR R.Preamble-based SNR estimation algorithm for wireless MIMO OFDM systems[C]∥2009 6th International Symposium on Wireless Communication Systems.Siena, Italy.IEEE, 2009: 96-100.
[8] YAN Chaoxing, WANG Hua, KUANG Jingming, et al.Design of data-aided SNR estimator robust to frequency offset for MPSK signals[C]∥2010 IEEE 71st Vehicular Technology Conference.Taipei, Taiwan, China.IEEE, 2010: 1-5.
[9] SOCHELEAU F X, AISSA-EL-BEY A, HOUCKE S.Non data-aided SNR estimation of OFDM signals[J].IEEE Communications Letters, 2008, 12(11): 813-815.
[10] 许维伟,叶江峰,胡茂海.一种基于奇异值分解的改进信噪比盲估计算法[J].太赫兹科学与电子信息学报,2016,14(5):771-777.
XU Weiwei,YE Jiangfeng,HU Maohai.Improved blind SNR estimation algorithm based on singular value decomposition[J].Journal of Terahertz Science and Electronic Information Technology, 2016,14(5):771-777.(in Chinese)
[11] BOUMARD S.Novel noise variance and SNR estimation algorithm for wireless MIMO OFDM systems[C]∥GLOBECOM′03.IEEE Global Telecommunications Conference(IEEE Cat.No.03CH37489).San Francisco, CA, USA.IEEE, 2003: 1330-1334.
[12] 漆雪梅, 沈彩耀, 张效义.SIMO信道中基于奇异值分解的盲信噪比估计算法[J].信号处理, 2011, 27(4): 552-557.
QI Xuemei, SHEN Caiyao, ZHANG Xiaoyi.A blind SNR estimation algorithm based on SVD over SIMO channels[J].Signal Processing, 2011, 27(4): 552-557.(in Chinese)
[13] BABU M S, RAO K K.Fast converging semi-blind SNR estimation for wireless MIMO-OFDM systems[C]∥2011 IEEE International Conference on Signal Processing, Communications and Computing(ICSPCC).Xi’an, China.IEEE, 2011: 1-6.
[14] HONG Shunli, LI Youming, GAO Yao, et al.Blind SNR estimation for MIMO-OFDM system[C] ∥IET International Communication Conference on Wireless Mobile and Computing(CCWMC 2011).Shanghai.IET, 2011: 6-9.
[15] JIAO Fei, REN Guangliang, ZHANG Zhe.A new noise variance and post detection SNR estimation method for MIMO OFDM systems[C]∥2008 11th IEEE International Conference on Communication Technology.Hangzhou, China.IEEE, 2008: 179-182.
[16] 阮宗利, 李立萍, 钱国兵, 等.基于含噪复值ICA信号模型的快速不动点算法[J].电子与信息学报, 2014, 36(5): 1094-1099.
RUAN Zongli, LI Liping, QIAN Guobing, et al.Fast fixed-point algorithm based on complex ICA signal model with noise[J].Journal of Electronics & Information Technology, 2014,36(5):1094-1099.(in Chinese)
[17] LI Tao, LI Yongzhao, CIMINI L J, et al.Hypothesis testing based fast-converged blind estimation of transmit-antenna number for MIMO systems[J].IEEE Transactions on Vehicular Technology,2018,67(6): 5084-5095.
[18] 许宏吉, 刘琚, 谷波, 等.空时分组码通信中的一类ICA盲检测方案[J].通信学报, 2007(6): 12-19.
XU Hongji, LIU Ju, GU Bo, et al.ICA based blind detection scheme in space-time block coding communications[J].Journal on Communications, 2007(6): 12-19.(in Chinese)
[19] CARDOSO J F, SOULOUMIAC A.Blind beamforming for non-Gaussian signals[J].IEE Proceedings F Radar and Signal Processing, 1993, 140(6): 362.
[20] 付卫红,杨小牛,刘乃安.基于四阶累积量的稳健的通信信号盲分离算法[J].电子与信息学报,2008(8):1853-1856.
FU Weihong, YANG Xiaoniu, LIU Naian.Robust algorithm for communication signal blind separation fourth-order-cumulant-based[J].Journal of Electronics & Information Technology, 2008(8):1853-1856.(in Chinese)
[21] 张天骐,范聪聪,葛宛营,等.基于ICA和特征提取的MIMO信号调制识别算法[J].电子与信息学报,2020,42(9):2208-2215.
ZHANG Tianqi,FAN Congcong,GE Wanying,et al.MIMO signal modulation recognition algorithm based on ICA and feature extraction[J].Journal of Electronics & Information Technology, 2020,42(9):2208-2215.(in Chinese)
