1 引言
在实际的工程应用和物理系统中,不确定性和非线性普遍存在[1-3]。滤波是指从含有噪声的观测序列推演出目标的真实状态,滤波技术是信息处理的核心技术[3-4]。非线性滤波在火箭制导与控制[1]、飞机和舰船的惯性导航[2]、卫星轨道和姿态估计[4]、生物医学图像[5]等领域有着广泛的应用。
对于复杂高维状态空间模型中的参数估计问题,许多单个非线性滤波算法难以奏效,因此有效划分模型状态空间显得尤为必要[1,5-6]。在实际问题中,由于机动目标跟踪中测量系统的高度非线性和不确定性,所以基于递推贝叶斯理论的线性最优滤波器,即卡尔曼滤波器(Kalman filtering, KF),难以获得目标状态的模型决策和后验状态估计的闭式解析解。因此,如何实现自适应的模型预测和稳态非线性滤波是机动目标跟踪的两个关键难题。近年来,多种数值逼近方法得到了研究与发展[1,5-6]。
对于模型预测的问题,尽管传统的马尔可夫概率能够有效预测有限固定结构的模型切换,然而它对机动目标的动态模型切换适应性较差,因为该方法仅依靠前一时刻的状态来预测当前模型,而忽略了先验约束信息的影响[1,10]。从信息论的角度看,充分利用系统约束信息将有助于实现状态空间降维,提高模型预测的可靠性和状态滤波的准确性[4,7-9]。Wang等人[10]提出了将先验概率添加到蒙特卡罗(Monte Carlo, MC)聚类分析,显著提高算法的准确性和计算效率。同样源于蒙特卡罗方法,Doucet.A 等人[6]提出了顺序蒙特卡罗(sequential Monte Carlo, SMC)采样也称为粒子滤波(particle filtering, PF)方法,该方法统一了几种不同科学学科中离散时间动态模型的重要性采样框架。交互多模型(interacting multiple model, IMM)算法是静态多模型(stationary multiple model, SMM)结构的主流估计方法,该算法通过概率加权融合模型信息,采用单个非线性滤波方法(例如EKF,UKF等)产生状态估计[1]。然而该算法在模型交互过程中忽略了当前观测信息的影响,因此对于模型不确定性较为明显的情况,标准IMM估计器的性能更多的依赖于滤波器的选择[1,4,6]。对于动态多模型(dynamic multiple model, DMM)估计器,可根据Rao-Blackwell理论对状态空间进行模型划分,在文献[6]和[11]中,系统的状态模型被视为潜变量且服从高斯线性模型,其估计流程与模型状态的滤波过程相互独立。
对于状态非线性滤波问题,对状态后验分布的近似计算仅在高置信度区域(又叫感兴趣区域area of interest, AOI)内是准确的[11]。然而在实际应用中,系统约束或状态变量之间的约束通常被视为准确测量[7,12]。例如,扩展卡尔曼滤波(extended Kalman filtering, EKF)算法通过截断泰勒序列(Taylor-serious)近似非线性函数。对于一般非线性系统的情形,该滤波算法是有效且常用的估计方法。然而,对于某些复杂的非线性情况,由于将观测量投影到约束超平面上而不是约束方向上导致投影偏差,使得基点估计值无法收敛到状态真实值[12]。针对无迹卡尔曼滤波在测量信息存在多峰分布时无法有效描述状态后验分布的问题,本文作者[8]提出了一种用于非线性高斯模式的约束无迹卡尔曼滤波(unscented Kalman filtering, UKF)算法,有效改善了滤波性能,提高了被动机动目标跟踪性能。然而该算法需要满足协方差矩阵满足正定的前提条件,否则可能导致UKF算法失效。为了消除该项限制条件,容积卡尔曼滤波(cubture Kalman filtering, CKF)算法采用三自由度球面-径向积分对贝叶斯积分进行数值近似。Zhu等人[13]引入状态向量的先验信息重构伪测量,从而可以有效地抑制球面和径向积分运算对观测噪声的敏感性。然而,UKF和CKF均需要满足线性高斯假设的前提,该项局限性严重制约了该类算法在非高斯状态模型空间中的应用。针对该问题,本文作者[9]提出了一种高斯混合模型(Gaussian mixture model, GMM)粒子滤波框架,该算法通过引入辅助变量构建重要性函数,融合不同区域的观测似然分布,以使得目标状态的数值近似更加接近真实状态的后验分布。Angel.F 等人[11]提出了广义的迭代后验线性化滤波算法,并在理论上阐述了该算法的收敛分析。该类方法的核心思想是状态变量的更新演化只依赖于动态系统和观测模型的第一和第二两阶矩,因此该方法可扩展应用到非高斯状态空间模型。
根据上述分析可知,目标机动运动的模型不确定性来源于数据模型难以精确建立,状态滤波的不稳定性来源于非线性模型的不可预测性。在现有公开的文献里,通常将数据建模的模糊性和非线性测量模型的不确定性两个问题分开处理,并且许多约束归类为硬约束形式。不同于硬约束需严格满足的前提条件,软约束可采用正则化方法来近似实现[6,8-9,14]。为此,本文提出了一种正则UKF状态约束的鲁棒多模型滤波算法,该算法的主要贡献在于以下两个方面:⑴构建系统软空时约束模型,将其同时融入模型选择和非线性状态滤波的动态演化过程,通过加权蒙特卡罗重要性样本优选状态模型,从而消减机动目标运动过程中数据模型的模糊性以提高模型预测的准确性。⑵通过添加正则约束项构建增广目标函数来实现软约束,结合无迹变换技术融合多似然区域状态滤波输出,从而减小非线性的不可预测性造成的预测偏差以提高状态滤波精度。这两部分互为截断先验和反馈补偿,组成了机动目标非线性动态系统实现稳定闭环控制的必不可少的关键要素。
2 提出的算法
2.1 问题描述
和
分别表示nX和nZ维空间上的状态向量和观测序列。p(X0)是状态向量的初始先验分布。考虑动态系统模型为
(1)
Zk=h(Xk)+ek,ek～N(0ne×1,Σe)
(2)
式中,k表示离散时间, f和h分别是确定的非线性函数。
是状态模型。υk 和 ek分别是nυ维和ne维的过程噪声和观测噪声。为了统计简单,假设为相互独立的加性白高斯噪声,标准差分别为Συ>0和Σe>0。
类似扩展卡尔曼滤波,可采用对观测方程局部线性化处理来近似上述状态空间模型状态的先验概率。给出如下定义
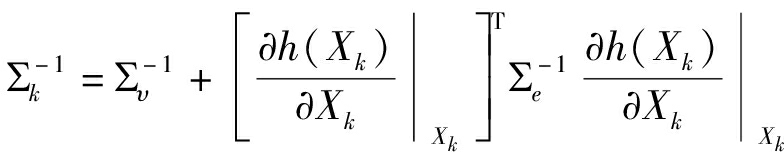
(3)
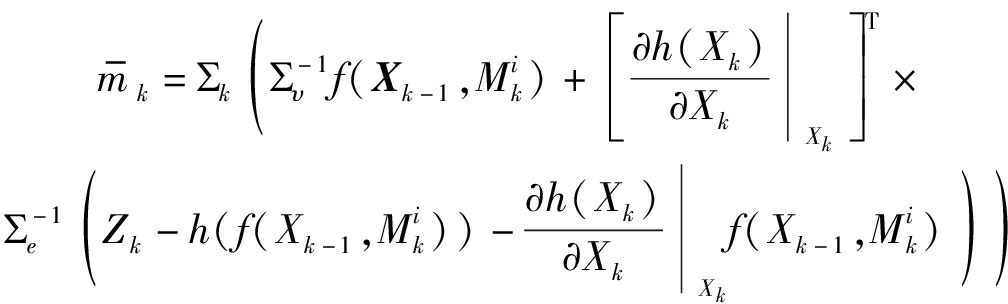
(4)
其中,上标T表示转置。
是观测模型非线性测量函数的雅可比矩阵,定义式子为
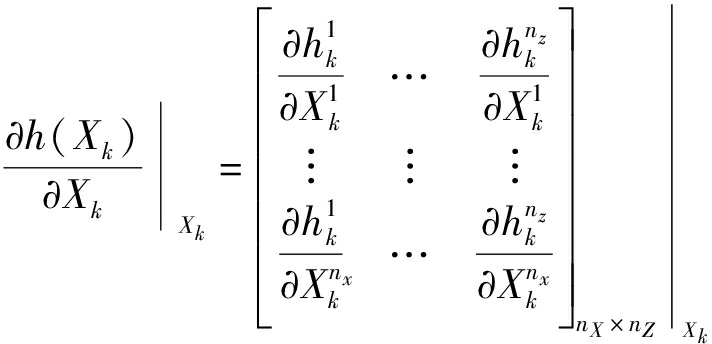
(5)
从而,目标状态估计近似的高斯分布表示为
(6)
在实际的物理系统中,因为噪声能量是衰减的,即随机噪声分布是有界的。因此在数学上,可根据截断理论构建系统状态空间上的软约束模型。对观测模型中观测噪声的概率密度函数p(ek)进行截断约束,即
p(ek)=0,if ek∉IX(Zk)⊂RnZ
(7)
其中,RnZ表示系统观测的nZ维连通域,IX(Zk)表示可行域,是观测连通区域的子区域。
在贝叶斯推理框架下,随着时间推移递推参数估计,我们考虑上一时刻状态值对下一时刻目标状态后验分布的影响,构建在状态估计推演过程中的时间约束模型,根据全概率公式推导目标状态后验概率密度函数为
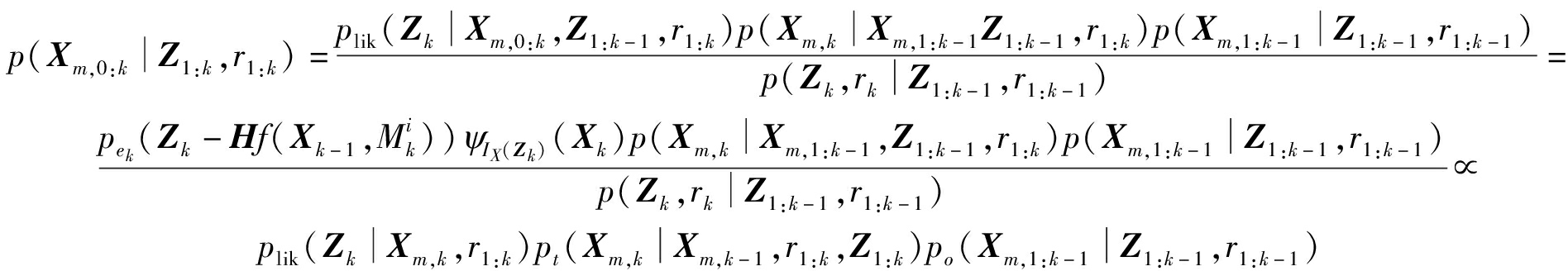
(8)
式中, Xm,k表示模型状态,plik(·)是观测似然函数,ψIX(Zk)(Xk)是辅助指示函数,p0(·)和pt(·)分别是原始先验概率密度函数和截断修正先验概率密度函数,表示历史状态和当前观测对状态估计的影响。
由于目标状态后验分布的数值积分涉及到高维积分计算,因此本文根据Rao-blackwell理论将其分解为状态模型估计和模型状态滤波两个问题。通过蒙特卡罗随机重要性样本优选状态模型,采用拟牛顿法修正截断先验概率,考虑历史状态反馈和当前观测信息对多模型状态估计的影响,结合无迹变换技术融合状态滤波输出,提出算法流程如图1所示,算法实现步骤详见2.2节和2.3节。
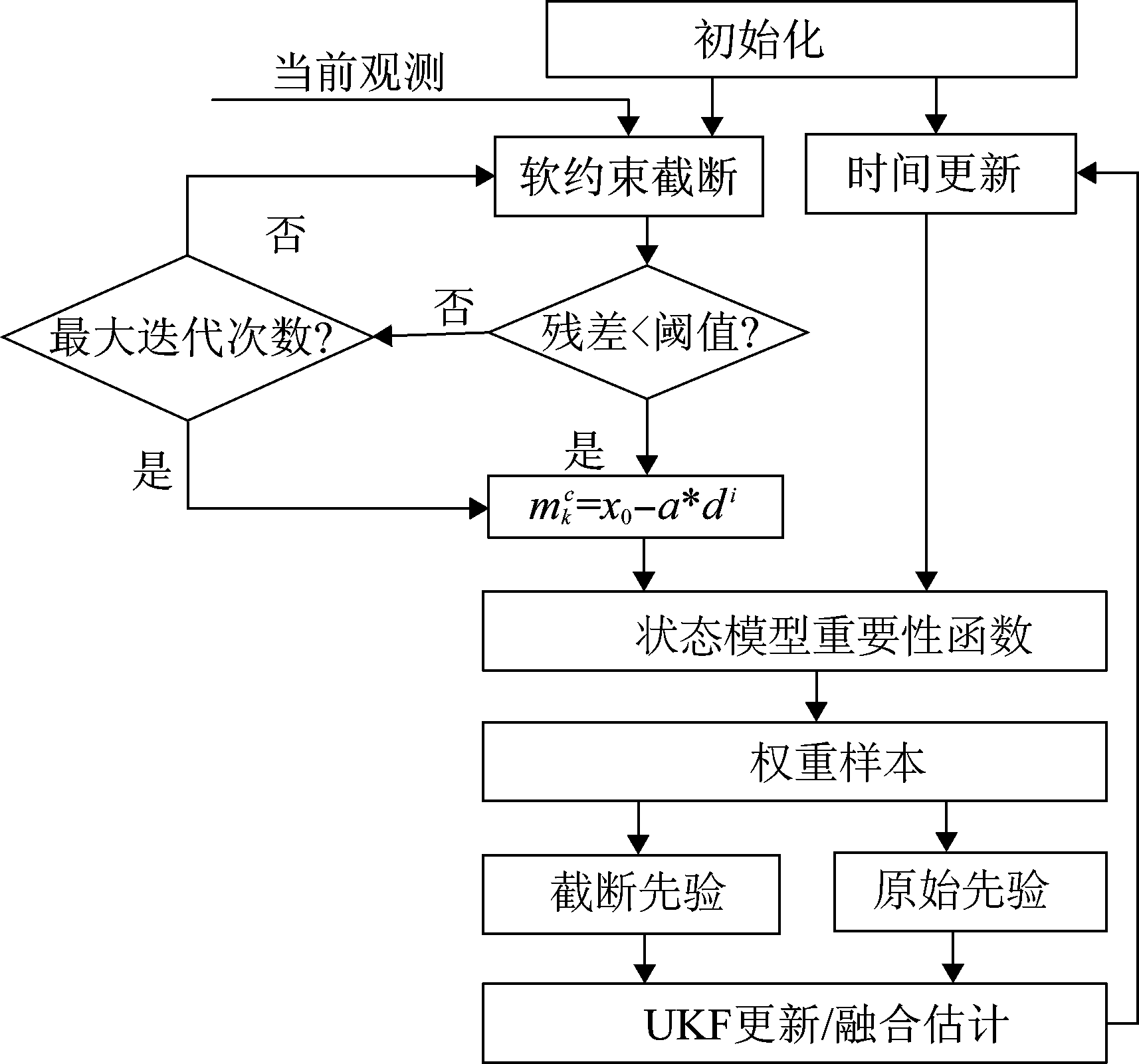
图1 提出算法框架
Fig.1 Block of the proposed algorithm
2.2 模型选择
考虑多模型分布的情况,系统观测似然函数表示为
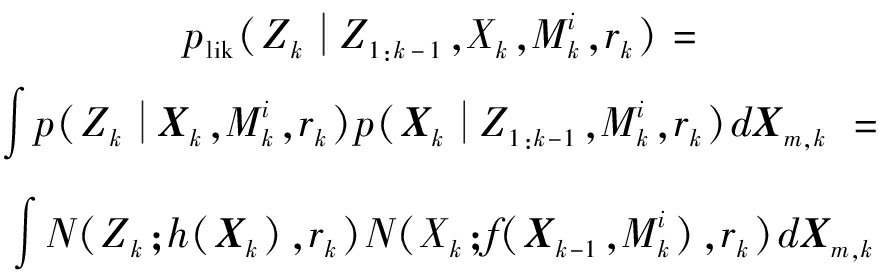
(9)
其中,rk表示系统潜在的辅助变量集。
我们通过加权重要性随机采样样本来预测模型概率,因此构建高置信度的重要性函数对于提高正确模型的匹配程度至为关键。将空时约束信息作为辅助变量融入蒙特卡罗采样过程,重要性密度函数π(·)可由下式迭代计算
(10)
其中,αk是截断修正先验的权重因子,可由模糊逻辑公式计算。
根据重要性函数随机采样Ns个模型样本,表示为
对样本权重进行时间更新,即
i=1,...,K
(11)
并且,将重要性样本权值归一化为
(12)
2.3 近似修正的先验函数
本小节同时考虑系统截断先验和后验状态估计反馈,以近似求解截断先验的分布。根据最小二乘法则构建目标函数,通过添加内外正则化惩罚项以实现系统空时软约束,因此修正的目标函数为
λA‖H
+λI‖F
(13)
其中,
是先验估计的均值,Σt和Σf分别为截断先验估计和反馈状态估计的方差。‖H和 ‖F分别为系统的内外正则惩罚项,λA和λI分别为其正则惩罚因子。请注意,在求解过程中需满足过程噪声协方差的逆
存在,从而保证矩阵可Cholesky分解。
本文选择待估计变量的自然对数为障碍函数,构建无约束的增广目标函数,从而可采用拟牛顿迭代方法进行数值求解。该方法的基本思想是保持每一个迭代点xk是可行域的内点,对于不满足约束条件的点,当迭代点靠近边界时,增广目标函数值骤然增大以示“惩罚”,从而阻止迭代点穿越边界。该算法结构简单、适应性强,但需严格要求初始值定位在可行域内,即x0∈RnX。否则,取权重最大的变量作为初始值,即
(14)
遍历可行域求得最优解,即
(15)
其中,上标c表示满足约束条件的含义。
是步长,=1,di为搜索方向。
我们认为在可行域内修正的先验概率密度近似服从正态分布,
为可行域的中心,据此计算其统计一阶矩作为正态分布的方差
即
(16)
2.4 重构无迹卡尔曼滤波
数值近似估计器的本质是递归优化,其关键步骤是状态变量的时间更新和观测更新。无迹变换方法的直观思想是用固定数量的参数近似一个高斯分布比近似任意的非线性函数更为容易[15]。因此,我们在式(16)的基础上根据下述步骤进行模型状态的非线性滤波。
步骤1 根据采样规则[15],利用修正先验概率密度函数的均值和方差产生满足约束条件的2nX+1个Sigma点Xi以及相应的权值wi。即
(17)
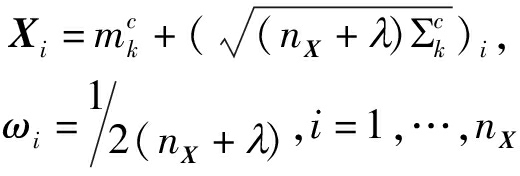
(18)
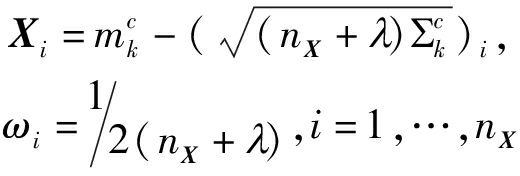
(19)
式中,λ是尺寸因子,决定Sigma点的选取范围,可以是满足nX+λ≠0的任意值。wi是第i个Sigma点的权值,且
步骤2 一步预测。
(20)
(21)
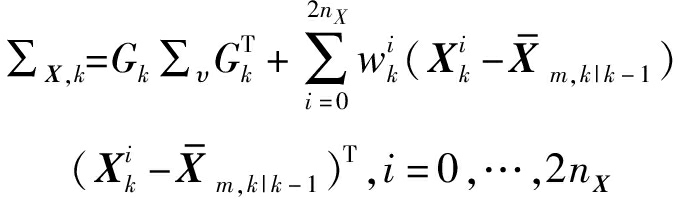
(22)
步骤3 测量更新。计算测量更新
预测协方差ΣZ以及状态与测量的互协方差ΣXZ,即
(23)
(24)
(25)
步骤4 计算滤波增益Kk+1,目标状态均值
和协方差Σk+1。即
(26)
(27)
(28)
2.5 融合状态输出
最后,对所有状态模型集下的状态滤波输出进行加权融合,得到最终的状态估计输出为
(29)
(30)
式中,
表示第k时刻第i个状态模型样本的权重,由公式(11)和(12)确定。
3 仿真实验及分析
仿真实验考虑一个位于[0 m,0 m]T的雷达观测在二维空间[0 km,30 km]×[0 km,12 km]中运动的目标。目标状态由位置、速度和转弯率构成,表示为
目标的运动模型如式(1),并且状态转移矩阵为
FCT=
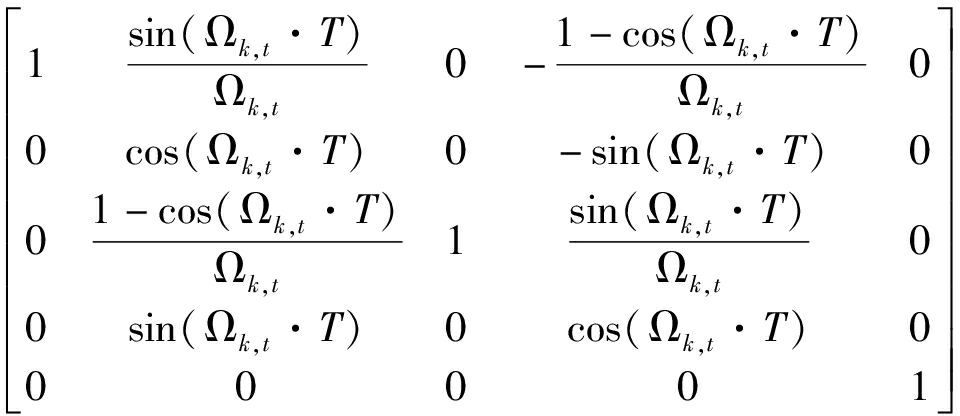
(31)
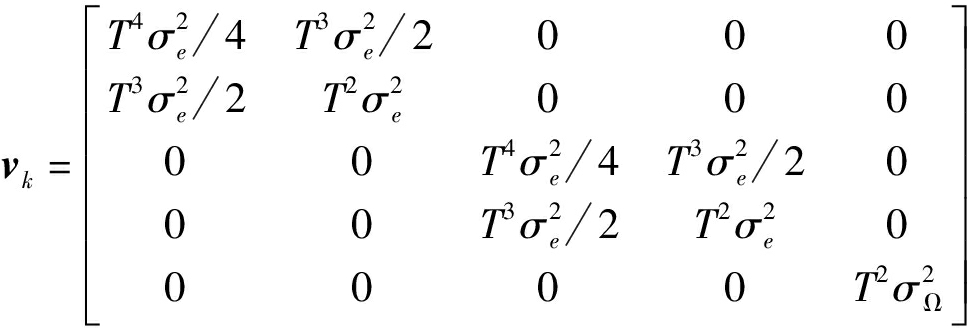
(32)
其中,Ωk,t为第k时刻目标t的转弯率,T=1 s为雷达的采样时间间隔,过程噪声标准差为σν=0.1 km/s2,σΩ=0.1 rad/s2。雷达的观测模型如式(2),并且
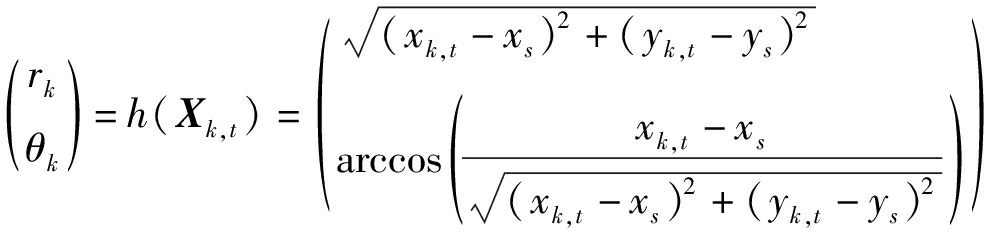
(33)
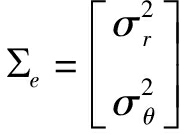
(34)
其中,r和θ分别是雷达测距和测角,各自的噪声标准差分别为σr=0.1 km和σθ=3 mrad。
为了评估本文提出滤波算法的性能,选择传统的交互多模型滤波算法(Interacting multiple model extended Kalman filtering, IMMEKF)和交互多模型无迹卡尔曼滤波(Interacting multiple model unscented Kalman filtering, IMMUKF),以及基于Rao-blackwell理论的多模型粒子滤波(Multiple model Rao-blackwell particle filtering, MMRBPF)算法进行比较,所有实验进行100次蒙特卡罗仿真实验。
目标运动仿真轨迹设计如图2所示,由5段运动(匀速—匀转弯—匀速—匀转弯—匀速)连接而成。图2同时给出了提出算法的滤波轨迹,通过轨迹对比可知,本文提出多模型滤波算法跟踪机动目标运动的滤波轨迹与模拟仿真的目标轨迹有较强的一致性,没有发生明显的跟丢现象。图3给出了四种滤波算法跟踪机动目标的位置均方根误差(root mean square error, RMSE),提出滤波算法能够很好地捕捉到目标机动运动的发生,据此可以推论提出算法能够鲁棒地处理机动目标跟踪中的状态模型不确定问题。
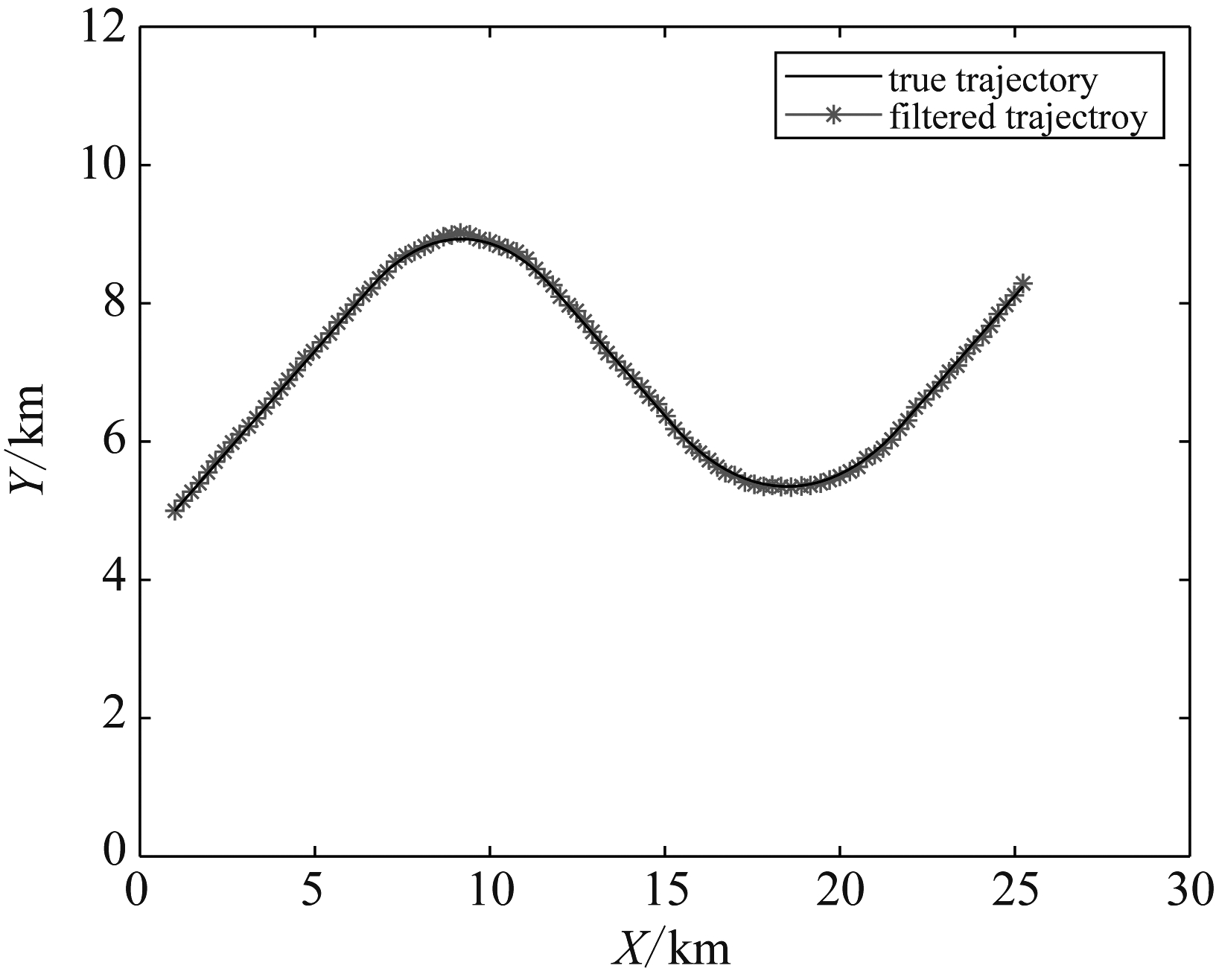
图2 仿真和滤波轨迹
Fig.2 Simulated and filtered trajectories
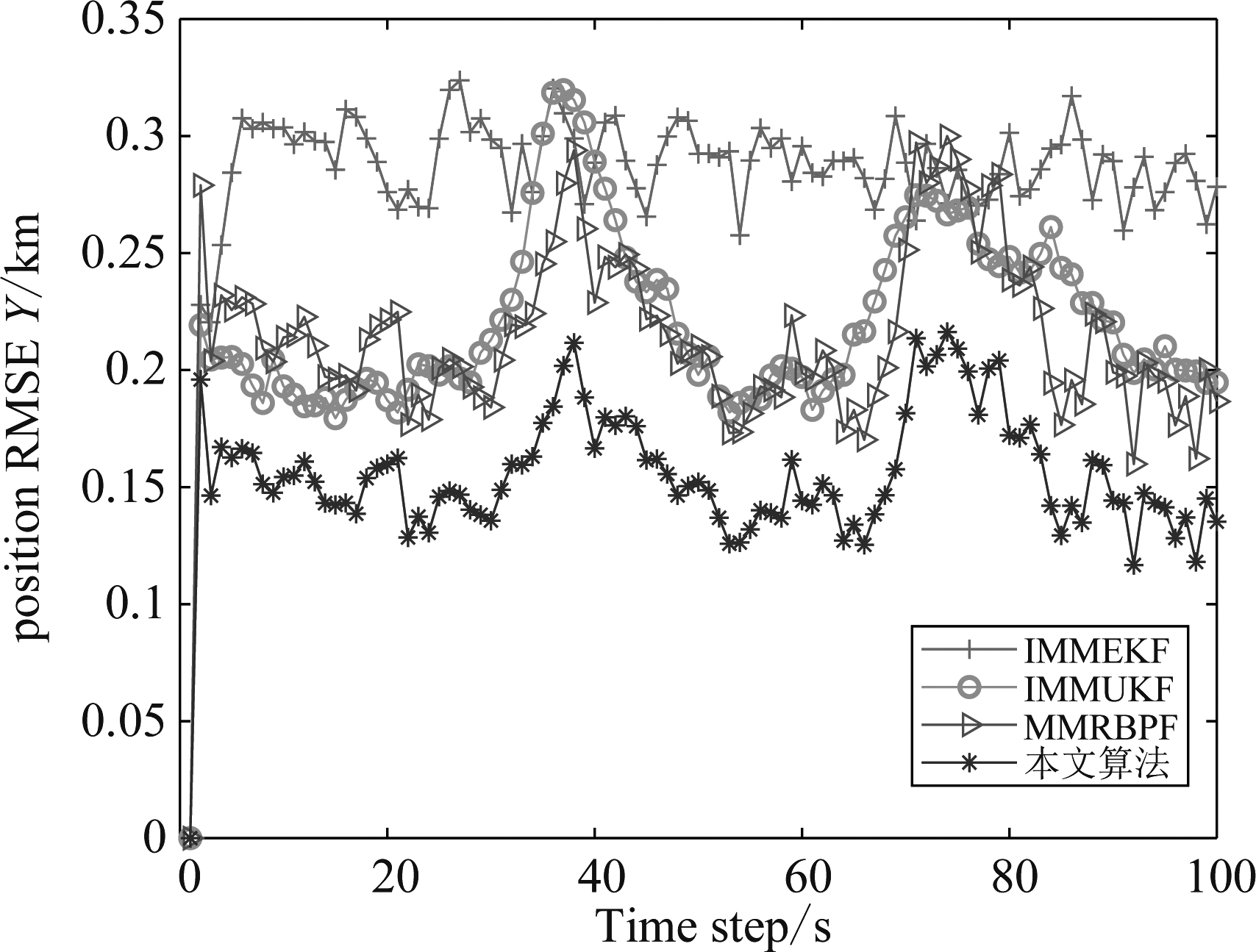
图3 滤波误差
Fig.3 Position RMSE
图4和图5分别给出了四种滤波算法在x轴和y轴运动方向跟踪机动目标的位置均方根误差。从定量比较结果可以看出,相比于传统交互多模型滤波器和多模型粒子滤波器,本文提出算法的跟踪效果在滤波精度方面表现出较大优势。这主要是因为正则状态约束能够有效提高状态模型和模型状态在动态演化过程中对随机噪声的抗干扰能力,从而提高了动态模型的切换效率和后验状态估计的准确性。
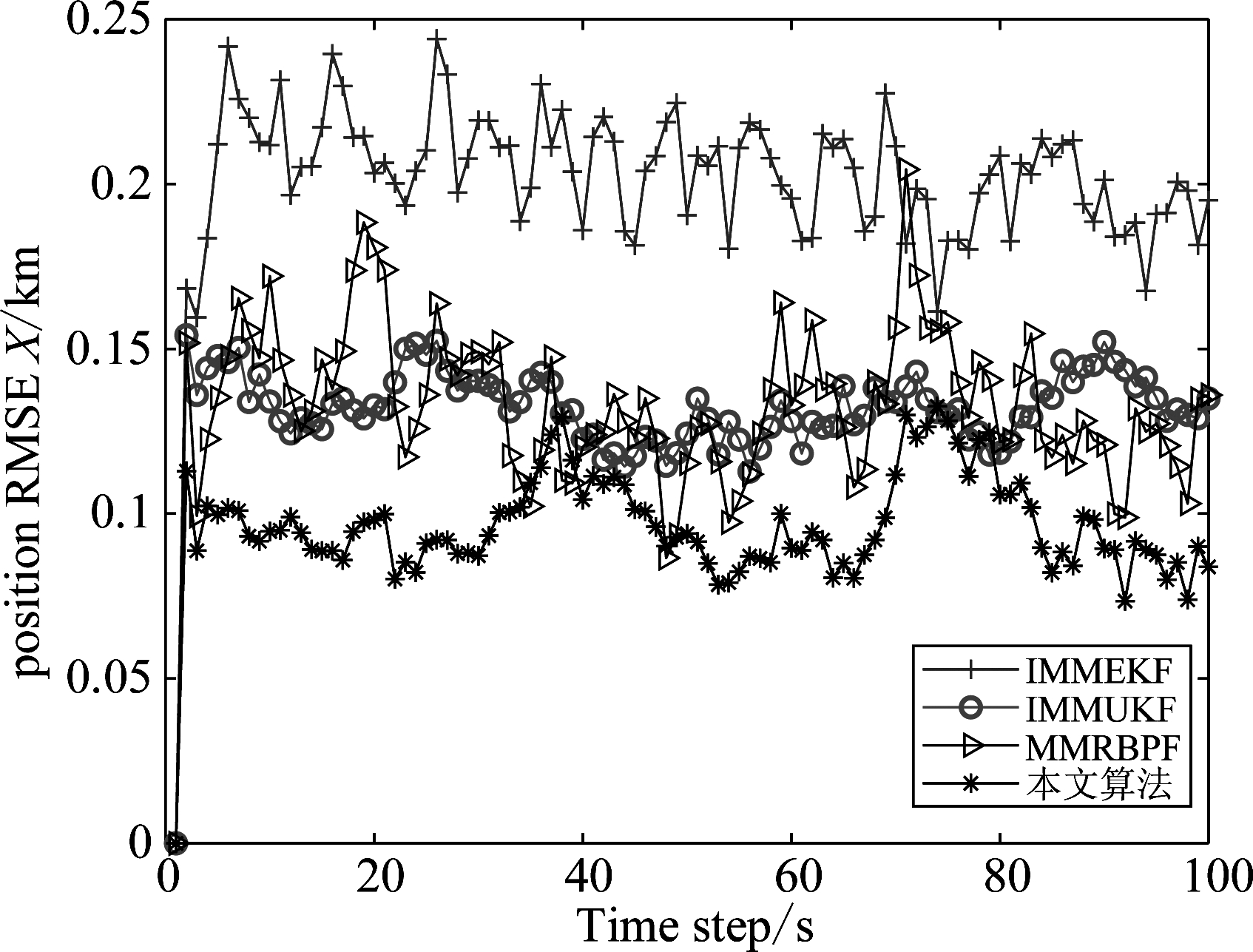
图4 X轴方向上滤波误差
Fig.4 Position RMSE in x-coordinate
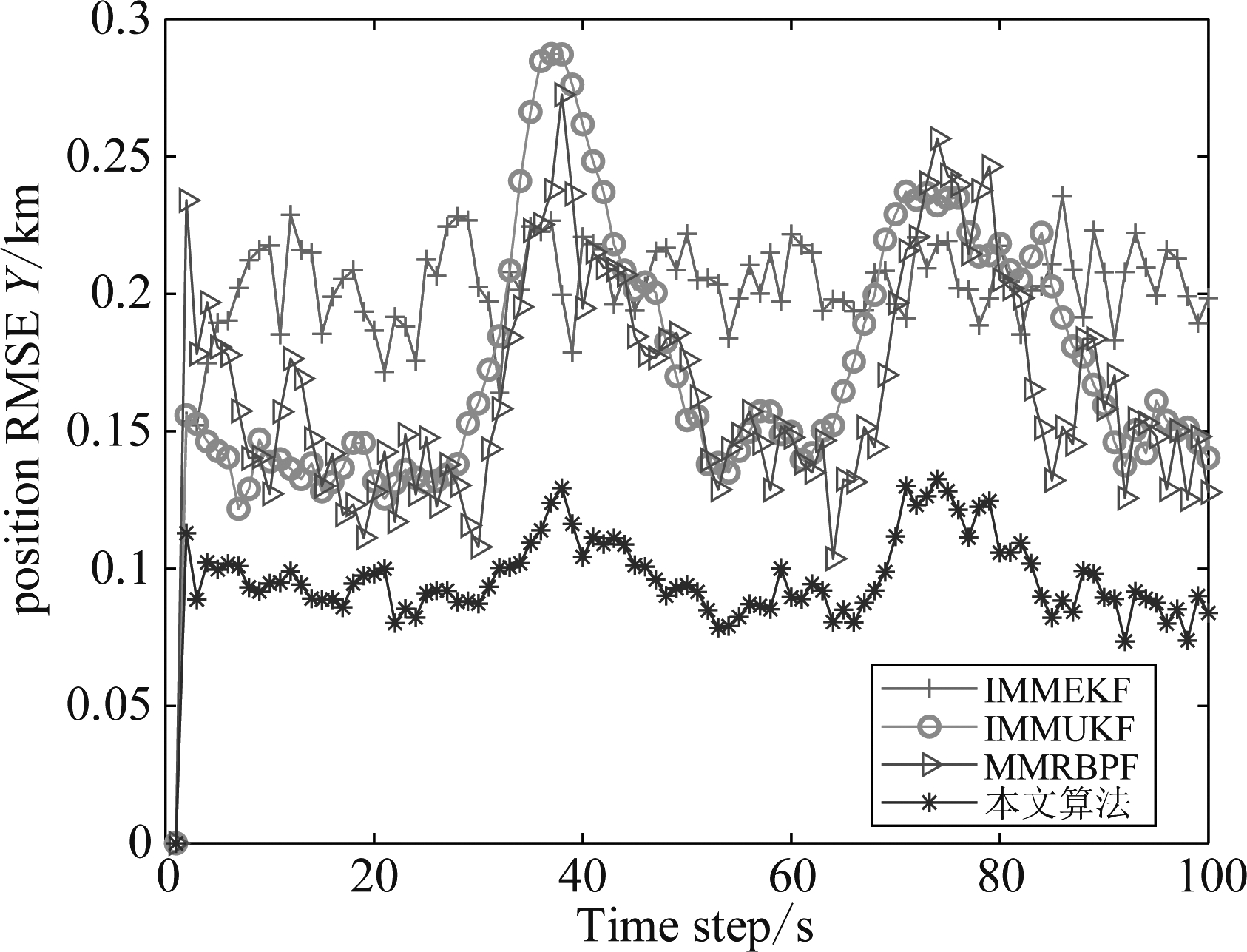
图5 Y轴方向上滤波误差
Fig.5 Position RMSE in y-coordinate
另外,为了比较提出算法的实时性能。统计IMMEKF、IMMUKF、MMRBPF和本文提出滤波算法四种方法执行一轮MC实验所需的平均时间,如表1所示。可以看出,相比于传统的基于IMM交互算法的多模型估计器,提出算法的MC实验执行时间有所增加,主要原因是该算法在状态模型选择和模型状态非线性滤波过程中均进行迭代优化。而相比于基于Rao-blackwell理论的多模型粒子滤波算法,提出算法的滤波精度相当,而一轮MC实验的平均执行时间减小了一个数量级。
表1 一个Monte Carlo 轮的平均执行时间
Tab.1 Average execution time for one Monte Carlo experiment
算法执行时间/sIMMEKF0.029IMMUKF0.043MMRBPF3.132本文算法0.207
4 结论
为了提高机动目标运动过程中数据模型切换的准确性、多模型滤波器抗击多模态似然和观测噪声干扰的能力,提出了一种正则UK状态约束的多模型滤波器,结合无迹变化和软约束正则化技术提出了一种模型状态非线性滤波器的实现算法。与交互多模型滤波器一样,所提出的滤波器考虑了目标运动的不确定性和测量系统的非线性,从而使该滤波器适合处理目标机动运动跟踪问题。另外,我们提出的正则UK状态约束的多模型滤波算法具有以下特点:(1)构建系统空时软约束模型,并将其同时施加到状态模型选择和模型状态非线性滤波过程中。通过加权蒙特卡罗重要性样本优选状态模型,从而消减数据模型的模糊性以提高模型预测的准确性。(2)通过添加内外正则化惩罚项构建增广目标函数以实现软约束,结合无迹变换技术融合多模态似然的非线性滤波输出。从而减小非线性的不可预测性造成的预测偏差以提高状态滤波精度。该两部分互为先验修正和反馈补偿,组成了机动目标非线性动态系统实现稳定闭环控制的必不可少的关键要素,实现了对有效观测信息的优化跟踪。仿真结果表明,本文提出的正则UK状态约束的多模型滤波器具有比交互多模型滤波器更强的机动目标跟踪性能。
[1] BAR-SHALOM Y, LI X R, KIRUBARAJAN T.Estimation with applications to tracking and navigation[M].New York, USA: John Wiley & Sons, Inc., 2001.
[2] PARK M S, CHWA D, HONG S K.Antisway tracking control of overhead cranes with system uncertainty and actuator nonlinearity using an adaptive fuzzy sliding-mode control[J].IEEE Transactions on Industrial Electronics, 2008, 55(11): 3972-3984.
[3] 张宏伟, 谢维信.平滑约束无迹卡尔曼滤波器[J].信号处理, 2019, 35(3): 466-471.
ZHANG Hongwei, XIE Weixin.Smoothly constrained unscented Kalman filter[J].Journal of Signal Processing, 2019, 35(3): 466-471.(in Chinese)
[4] CRASSIDIS J L, JUNKINS J L.Optimal estimation of dynamic systems[M].Second edition.Chapman and Hall/CRC, USA, 2011：249-253.
[5] WANG Shiying, SHEN Yan.Multi-modal image fusion based on saliency guided in NSCT domain[J].IET Image Processing, 2020, 14(13): 3188-3201.
[6] DOUCET A, GODSILL S, ANDRIEU C.On sequential Monte Carlo sampling methods for Bayesian filtering[J].Statistics and Computing, 2000, 10(3): 197-208.
[7] SIMON D.Kalman filtering with state constraints: A survey of linear and nonlinear algorithms[J].IET Control Theory & Applications, 2010, 4(8): 1303-1318.
[8] ZHANG Hongwei, XIE Weixin.Constrained unscented Kalman filtering for bearings-only maneuvering target tracking[J].Chinese Journal of Electronics, 2020, 29(3): 501-507.
[9] ZHANG Hongwei, XIE Weixin.Constrained auxiliary particle filtering for bearings-only maneuvering target tracking[J].Journal of Systems Engineering and Electronics, 2019, 30(4): 684-695.
[10] CHROBAK A, ZI
KOWSKI G, CHROBAK D.Application of local information entropy in cluster Monte Carlo algorithms[M]∥Theory, Application, and Implementation of Monte Carlo Method in Science and Technology.IntechOpen, 2019.
[11] GARC
A-FERN
NDEZ F, HOSTETTLER R, S
RKK S.Rao-blackwellized posterior linearization backward SLAM[J].IEEE Transactions on Vehicular Technology, 2019, 68(5): 4734-4747.
[12] DE GEETER J, VAN BRUSSEL H, DE SCHUTTER J, et al.A smoothly constrained Kalman filter[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(10): 1171-1177.
[13] ZHU Bing, ZHENG Zewei, XIA Xiaohua.Constrained adaptive model-predictive control for a class of discrete-time linear systems with parametric uncertainties[J].IEEE Transactions on Automatic Control, 2020, 65(5): 2223-2229.
[14] BOYD S, VANDENBERGHE L, FAYBUSOVICH L.Convex Optimization[J].IEEE Transactions on Automatic Control, 2006, 51(11):1859-1859.
[15] JULIER S J, UHLMANN J K, DURRANT-WHYTE H F.A new approach for filtering nonlinear systems[C]∥Proceedings of 1995 American Control Conference-ACC′95.Seattle, WA, USA.IEEE, 1995: 1628-1632.
