1 引言
近年来物联网、自动驾驶、远程医疗等技术高速发展,无线网络中连接的设备数量呈指数性增长[1]。海量设备接入不仅意味着数据流量的需求急剧增加,需要在系统容量上达到一定的水平,而且还需要考虑大规模数据传输时的安全性问题。随着网络需求的持续增长,研究人员在不断探索新的网络体系结构、通信技术以及传输技术,以满足急剧变化的需求。目前D2D、半双工和全双工、NOMA等通过广泛研究已获得极大进展。
随着移动终端和多媒体的迅速发展,对高速率数据传输的需求增加,D2D通信也被认为是有效缓解无线网络压力的有效手段[2]。D2D用户(D2D User,DU)主要通过复用蜂窝用户(Cellular User,CU)的频谱资源进行传输,无需通过基站(Base Station,BS),能够显著提高系统的频谱利用率和吞吐量。为提高异构网络的吞吐量,对产生的干扰进行协调是必不可少的。近年来,国内外相关研究主要集中于研究联合系统的资源分配来解决异构网络下的干扰管理。文献[3]在异构蜂窝场景下研究系统资源分配问题,在确保满足系统服务质量(Quality of Service,QoS)的基础上最小化总信道带宽。文献[4]考虑了包含宏蜂窝用户,DU和毫微微小区用户的上行链路加权和速率最大化问题,并通过启发式次优分配算法处理空闲子信道。文献[5]通过信道状态信息(Channel State Information,CSI)不确定的鲁棒性,从而为能量收集辅助下的D2D通信提供支持,以最大程度地保证D2D通信和速率。文献[6]同样在异构蜂窝网络下考虑D2D资源分配方案,为了实现绿色通信需求,假定不完美CSI的情况下,将CU和DU的信道分配问题通过获取加权分配矩阵来解决。文献[7]则在异构蜂窝网络下提出了一种基于Stackelberg博弈的能效优化算法,建立了跨层与层内干扰价格系数与D2D发送功率之间的函数关系,避免了干扰系数直接迭代而产生的误差,有效提高了D2D能效。
NOMA同样作为当前无线通信发展中提高频谱利用率的一个有效手段,为未来无线通信的发展带来了更大的机遇[8]。相比以往的OMA技术,NOMA能够支持用户在功率域或码域上实现传输。因此,国内外诸多研究聚焦于将NOMA技术应用于蜂窝通信。文献[9]提出了使用NOMA的D2D上行协调直连或中继传输模型,直连阶段BS与近端CU直接进行通信,而在协作阶段远端CU则利用中继转接来自BS的信息,并依据NOMA原理设计了近端CU到远端CU的D2D通信。文献[10]研究背景与文献[9]类似,主要研究了下行链路系统中的协作NOMA的性能,通过引入D2D协助基站与信道条件不太理想的移动终端进行通信,并制定了下行链路下的最佳DU配对以及最佳功率控制方案,结果表明所提出的框架具有显著优势。文献[11]在NOMA增强型D2D系统,作者求解出了采用解码转发中继的中断概率解析式,并假设在接收器处有完美的连续干扰消除,通过使用NOMA功率分配,获得了与强用户中断的最小概率相对应的功率分配系数的最优值。文献[12]中引入了电池高效协作NOMA与中继D2D通信合作的模型,在NOMA方案中引入不同的操作模式,以减少发射器和接收器端的电池功耗,目的是通过有效部署NOMA小区扇区模型来优化系统能量。上述文献[9-12]大多数是将NOMA应用到蜂窝通信,在蜂窝通信协作转发时会涉及到D2D。此外,其优化问题如果是优化系统和速率,那么涉及到协作转发过程将会使最终和速率的求解较为复杂繁琐,所以一部分文献采用中断概率评估通信质量。当然,已有一些文献针对NOMA增强型D2D通信展开了研究。文献[13]中首次提出了一种基于NOMA的D2D通信系统。该系统模型中通过引入采用NOMA传输的D2D组的理念,传统的D2D对主要聚焦于一对一通信,即一对D2D中只有一个发送端以及一个接收端。而该D2D组则是一个D2D发送端与多个D2D接收端,使得一个D2D发射机可以同时与多个D2D接收机采用NOMA机制在相同频谱资源下彼此间进行通信。文献[14]提出一种基于NOMA技术的D2D系统吞吐量最大化资源分配算法,利用自适应惩罚函数法处理约束条件,然后提出一种基于爬山策略的自适应遗传算法实现问题求解。文献[15]在NOMA增强的D2D场景中,提出了一种基于Stackelberg博弈的联合信道和功率分配算法,通过基于惩罚函数的粒子群优化(Particle Swarm Optimization,PSO)算法对D2D用户的功率分配进行优化。
现有文献关于NOMA增强型D2D通信的研究鲜少有涉及到同时优化功率分配因子与发射功率,然而根据链路条件的差异设定合适的分配因子也是十分必要的。因此,本文在传统D2D的基础上考虑NOMA因素,使一个D2D发射机可以同时与多个D2D接收机通信,在此系统模型下考虑进行信道分配,并设计相应算法联合优化功率分配因子与发射功率,研究系统中D2D和速率最大化问题。
2 系统模型
研究表明,上行链路资源的利用率通常低于下行链路资源,因此共享上行链路资源可以提高资源利用率[16]。而且,当复用上行链路资源时,BS相比于移动终端可以更好地处理来自D2D对的干扰,因此本文考虑了单小区上行链路传输场景。如图1所示,BS位于小区中央,其中的c个蜂窝用户分别表示为{CU1,CU2,…,CUc}与d组D2D用户在小区中随机分布。CU以传统蜂窝模式与BS通信,D2D组不同于传统D2D对,模型中每组D2D包含一个D2D发射机与两个D2D接收机,发射机处采用NOMA传输协议发送叠加信号向D2D接收机处,接收端再通过串行干扰消除(Serial Interference Cancellation,SIC)技术解码出所需信号。系统中共包含d个D2D发送机,表示为{DU1,DU2,…,DUd},2d个D2D接收机,表示为{DU11,DU12;DU21,DU22;…DUd1,DUd2}。此外,系统中共有K个子信道,BS为每个CU预先分配一个正交子信道,因此各个CU之间不会产生干扰。假设每个正交子信道内包含一个CU和一组采用NOMA叠加编码的DU。令矩阵BD×k={bdk}表示子信道分配矩阵,其中
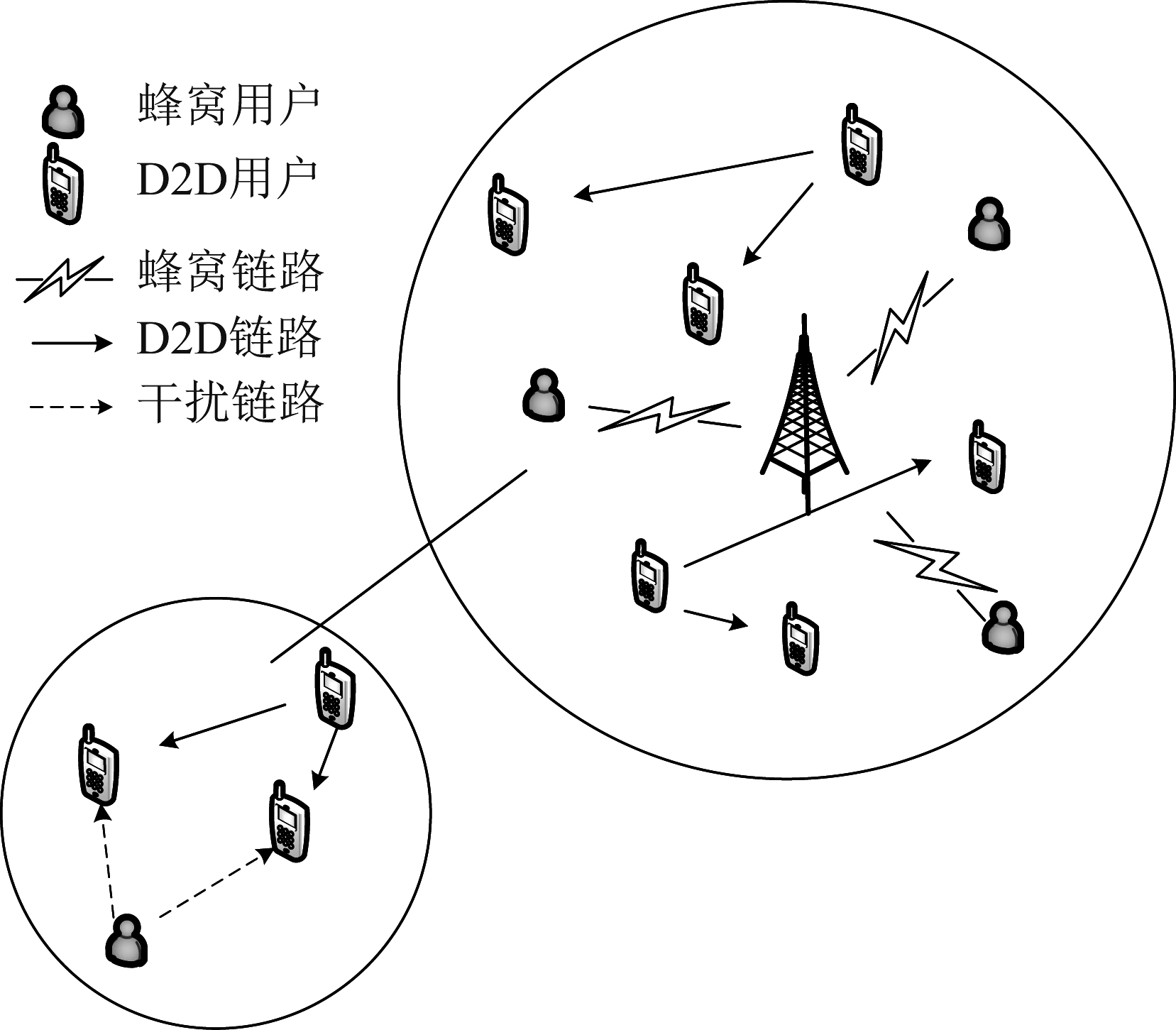
图1 系统模型
Fig.1 System model
(1)
由于系统中各个子信道之间是正交关系,因此,可先分析单一子信道中CU和D2D的干扰情况。假设第k个子信道被预先分配给某个蜂窝用户c,且同时被一组D2D用户DUd-DUd1,DUd2复用。
2.1 模型分析
A、D2D用户分析
采用NOMA协议发送叠加编码,D2D组发送的信号可以写成如下形式
(2)
其中,αk、βk分别表示D2D发送叠加信号时的功率分配因子,且满足
表示D2D发送端的发送功率,x1、x2分别表示发送给D2D接收端DUd1,DUd2的信号。
此时,D2D接收端d1处接收到的信号为
(3)
其中,
表示从D2D发射机到接收机d1这条通信链路的信道系数,
表示从CU到D2D接收机d1这条干扰链路的信道系数。w1表示该链路上均值为0,方差为n0的高斯白噪声。
上文指出,该系统模型下功率分配因子满足αk>βk,在NOMA原理下,接收端DUd1处首先解码信号x1,将信号x2看作噪声处理。此时信号x1的接收信干噪比为
(4)
其中
表示D2D发射机到接收机d1的链路增益。pc表示第k个子信道中CU的发送功率,
表示CU到D2D接收端d1的干扰链路增益。n0表示高斯白噪声的功率。
因此,接收端d1处信号x1的速率可表示为
(5)
同理,接收端d2接收到信号表示为
(6)
其中,
同样表示D2D发射机到接收机d2的信道系数,
表示从CU到D2D接收机d2的干扰链路的信道系数。w2表示高斯白噪声。
利用SIC检测技术,接收端d2处首先将信号x2看作噪声来解码信号x1,然后去除信号x1的干扰后解码信号x2。此时d2处信号x2的接收信干噪比表示为
(7)
其中,
表示D2D发射机到接收机d2的链路增益。
表示子信道中CU到D2D接收机d2的干扰链路增益。
此时,d2处信号x2的可实现速率为
(8)
B、蜂窝用户分析
在第k个子信道中,蜂窝链路传输的信号为xc,此时BS端的信干噪比可表示为
(9)
其中,pc表示CU向BS发送信号xc的功率。
分别表示同一子信道中CU到BS的通信链路增益以及D2D发送端到BS的干扰链路增益。n0表示蜂窝通信链路的高斯白噪声功率。
因此,子信道内蜂窝通信的速率可表示为
(10)
2.2 信道分配和功率控制的优化问题制定
本文目标是最大化系统中D2D对和速率,因此根据以上分析,最优化问题可以表示为
(11)
s.t.
bdk={0,1}
(12)
(13)
(14)
<αk<1
(15)
(16)
Rxi≥rd i∈{1,2}
(17)
(18)
其中,
为需要优化的变量。BD×k={bdk}表示系统的信道分配矩阵,bdk表示信道分配因子,是一个二进制变量,当D2D对复用子信道时,bdk=1,否则bdk=0。Α={α1,α2,α3,…,αK}表示系统中各个子信道功率分配因子的集合,
表示各个子信道中D2D发送功率的集合。Pmax表示D2D发送功率的最大阈值,约束条件(12)、(15)、(16)式分别限制了待优化变量的合理取值范围,由于上文已经指定αk>βk,因此要求αk至少大于
约束条件式(13)限制了每个正交子信道只能复用一组D2D对,约束条件式(14)则限制了每组D2D对只能复用一条正交子信道。rd、rc分别表示D2D发射机到单个D2D接收机的最小传输速率与CU到BS的最小传输速率。约束条件(17)表明D2D通信的和速率要优于最小阈值,约束条件(18)表明要D2D通信链路的实现首先要保证蜂窝通信传输时的QoS。
最优化问题(11)是一个混合整数非线性问题,由于其中含有二进制变量bdk,因此可将该问题分解为两个独立的子问题进行求解:信道分配和功率控制。首先,给定D2D发射功率与功率分配因子,在信道分配阶段基于Coalition博弈为D2D组分配子信道。其次,给定信道分配的结果,然后再对D2D发送功率
与功率分配因子αk进行联合优化,以最大化整个系统中D2D对的和速率。
3 基于Coalition博弈的信道分配
将子信道分配问题建模为Coalition博弈,根据系统中D2D通信的和速率获得联盟博弈中各个玩家的效用函数,进而提出了一种用于子信道分配的Coalition博弈算法。
信道分配阶段,给定的功率分配因子αk以及D2D发送功率的条件下优化信道分配矩阵BD×k={bdk},因此,本阶段的最优化问题及其约束条件可表述为如下所示,
(19)
s.t.(13)～(16)
其中,
Coalition博弈作为一种合作性博弈,主要指博弈的玩家通过合作均能够提高各自的收益,或者是合作关系中某些参与者收益不变的基础上存在一些参与者收益增加,而使整个联盟的收益从整体上看是增加的。下面介绍基于Coalition博弈的一些重要定义。
定义1 (Coalition博弈)可表示为
其中
表示博弈玩家的集合,U表示每个联盟的效用函数。
针对子信道分配问题,每个正交子信道中的一组D2D用户和一个蜂窝用户作为具有合作关系的一组博弈玩家,共同形成一个子信道联盟,因此
在本文的系统模型中,不同组的D2D用户占据不同的子信道,系统中k个正交子信道也将形成k个不相交联盟,不存在同一博弈玩家同属于两个不同的联盟的情况。因此,信道分配阶段Coalition博弈的限制条件如下:
(20)
信道分配阶段的优化问题已于上文给出,优化目标依旧是最大化系统中D2D通信的和速率。因此,对于任意联盟玩家,其效用函数可以表示为:
(21)
其中Rx1、Rx2的具体表达式已于上文给出,分别表示同一子信道中D2D信号x1、x2的传输速率。在一个子信道中,由于D2D复用蜂窝频谱,因此通信过程中CU发送的信号会对D2D组造成干扰,从而影响D2D用户的可实现速率。而在子信道中将CU和DU看作具有合作关系的一组博弈玩家,将子信道中D2D通信的可实现速率作为该合作博弈的效用函数。
为了使博弈中各个联盟的效用函数最大,应该明确定义出博弈玩家决定加入联盟或退出联盟的偏好关系,即每组D2D用户将根据其偏好选择共享某个CU所在子信道。下面即对联盟
中D2D用户的偏好关系进行如下定义:
定义2 (偏好关系≻d)对于系统中任一组D2D用户d,存在任意两个联盟
其中k≠k′,则偏好关系可表示为
对于博弈中的任意联盟,如果
表明D2D用户d更倾向于加入联盟而不是
因此,D2D用户d在联盟和联盟
中的偏好关系可以量化为如下数学形式:
(22)
博弈算法将根据上述偏好关系对系统中D2D用户逐一分配合适的子信道。若D2D用户根据上述定义的偏好关系需要更换联盟,此时需要将D2D用户切换到新的合作联盟,并更新当前系统中合作联盟信息。因此,博弈算法中的交换操作定义如下:
定义3 (交换操作)给定一个联盟分组
如果博弈玩家D2D用户d∈D需要执行从到
的交换操作,那么新的博弈分组将被更新为:
(23)
上述定义3给出了博弈玩家D2D用户d在博弈过程中的交换操作,当且仅当满足偏好关系
时,才会执行从到的交换操作。也就是说,对于每个D2D用户d∈D,如果满足式(22)中定义的偏好关系,即新的合作联盟
的收益严格优于当前合作联盟的收益,那么第d个D2D组就会离开当前联盟加入到新的联盟,执行上述交换操作。
进行有限次的交换操作后,系统中所有合作联盟将收敛到纳什均衡。下面将给出纳什均衡的定义。
定义4 (纳什均衡)如果任何D2D对均不会通过更改其复用的子信道来增加自身的可实现速率,那么该联盟即收敛到纳什均衡。
假设经过有限次交换操作后的D2D组与蜂窝用户的最终联盟分组为Γfin,下面将证明其达到纳什均衡。
假设最终的联盟分组Γfin未达到纳什均衡。也就是说,存在某个D2D对d∈D,其当前所在联盟和另一随机选择的新的联盟满足偏好关系
此时,该D2D组将执行操作离开当前联盟加入到联盟这意味着先前的Γfin并非最终的联盟分组,需要依据最新的交换操作更新为新的Γfin。因此,上述所提出的Coalition算法的最终分组Γfin是可以收敛到纳什稳定的。
根据如上所述相关定义和交换操作,算法1表示基于Coalition博弈的子信道分配算法的主要算法流程。
表1 基于Coalition博弈的子信道分配算法
Tab.1 Sub-channel allocation algorithm based on Coalition game
算法1主要算法流程1.初始化:给定D2D组发送功率pkd,功率分配因子αk,蜂窝用户发送功率pc;2.随机生成正交子信道中单个D2D组与蜂窝用户的分组Γini,令Γcur→Γini;3.While4.选择一组D2Di∈D,其所在联盟表示为Γc∈Γcur;5.选择另外一个联盟表示为Γc′∈Γcur;且满足Γc≠Γc′;6.计算RD2D(Γc)与RD2D(Γc′);7.IfD2D对i从联盟Γc到联盟Γc′的交换操作满足式(22)8.D2D对i离开联盟Γc加入到新的联盟Γc′;9.更新当前联盟情况为→Γcur;10.Endif11.直到所有子信道联盟均收敛到纳什均衡Γfin;12.Endwhile
4 功率控制
上一节中主要解决了DU与CU的子信道分配问题,完成对信道分配因子bdk的优化,本节则主要解决DU的功率控制问题,在给定信道分配矩阵BD×k的情况下,通过优化功率分配因子α和D2D发送功率p使系统中D2D和速率最大化。
4.1 功率控制优化问题分析
本阶段的最优化问题及其约束条件可表述为如下所示:
(24)
s.t.(15)～(18)
其中,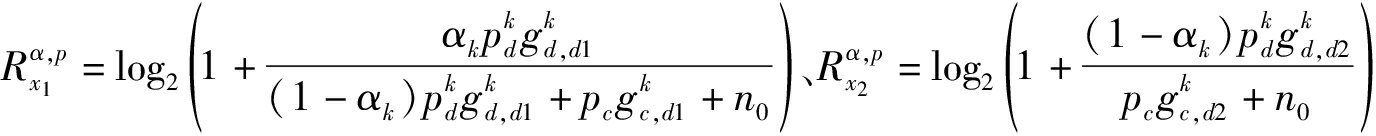
分别表示子信道分配完成后,第k个正交子信道内D2D信号x1、x2的和速率。
由于所有子信道都是正交关系,因此功率控制问题可以分解为K个子问题,其中每个子问题独立。因此本节将重点讨论子信道k上的优化问题
(25)
功率控制阶段需要优化的变量主要包含两个:αk和
首先需要考虑待优化变量和优化目标的关系。在第k个子信道内,根据D2D对和速率表达式Rk=Rx1+Rx2,分别对
求偏导,可以得到
(26)
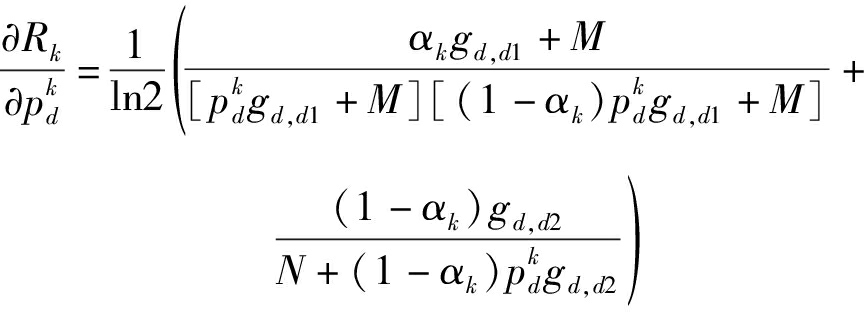
(27)
其中,M=pcgc,d1+n0,N=pcgc,d2+n0。根据式(27)可知,
恒成立,即D2D对和速率是关于
的增函数,随着D2D发送功率的增加,子信道内D2D对的传输速率也增加。而根据式(26),只能判断关于αk的偏导表达式中分母恒正,分子的正负将取决于子信道中的链路增益。因此,若某个子信道内D2D对和速率是关于αk的增函数,应尽量增大αk使D2D对获得更高的和速率;相反,若某个子信道内D2D对和速率是关于αk的减函数,在其取值范围内应尽量减小αk。
4.2 发送功率和功率分配因子联合优化算法
本文优化问题是一个非凸函数,功率控制阶段待优化变量有两个,因此可以同时考虑功率分配因子αk与D2D发送功率的联合优化求解。
首先约束条件式(17)可以写成如下形式
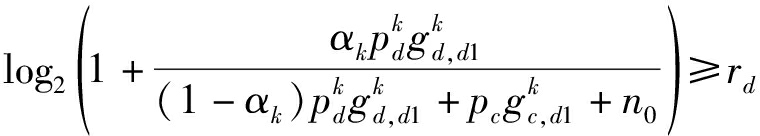
(28)
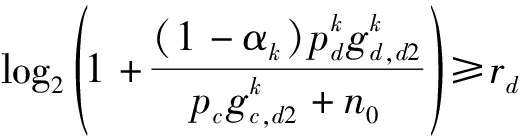
(29)
上述(28)、(29)式中包含变量
假设给定D2D通信的最小传输阈值rd,则αk与的关系可以表述为如下的函数表达式
(30)
(31)
其中,δ=2rd-1。上述式(30)与式(31)给出了功率分配因子αk关于D2D发送功率的函数关系式,可以表述为如下区域。
如图所示,A(pd)、B(pd)与Pmax共同定义了可行解域的边界值,横坐标表示D2D发送功率
纵坐标表示功率分配因子αk。其中
分别是式(30)与式(31)取等时的函数表达式,Pmax则是D2D发送功率的最大阈值。图中三条曲线围起来的区域即是与αk的联合可行解域。A(pd)与B(pd)交于点a,点a的横坐标即是在联合控制算法中可以取得的最小值。表示为
(32)
前文已经证明系统中D2D对和速率随着发送功率单调递增,而各个子信道中D2D用户数据传输速率关于αk的增减性取决于子信道中的链路增益。因此若是关于αk的减函数,则b点能使D2D用户获得最大的和速率;相反,若是关于αk的增函数,则c点能使D2D用户获得最大的和速率。
图2表明,曲线A(pd)与B(pd)随着
的增大均逐渐达到收敛。若Pmax小于两曲线达到收敛时的发送功率pcon,则此时最佳D2D对发送功率设为Pmax,最佳功率分配因子αk可以根据Pmax计算得出。若曲线收敛时的发送功率pcon小于Pmax,最佳D2D对发送功率取为Pmax,最佳功率分配因子αk即为收敛时的值。
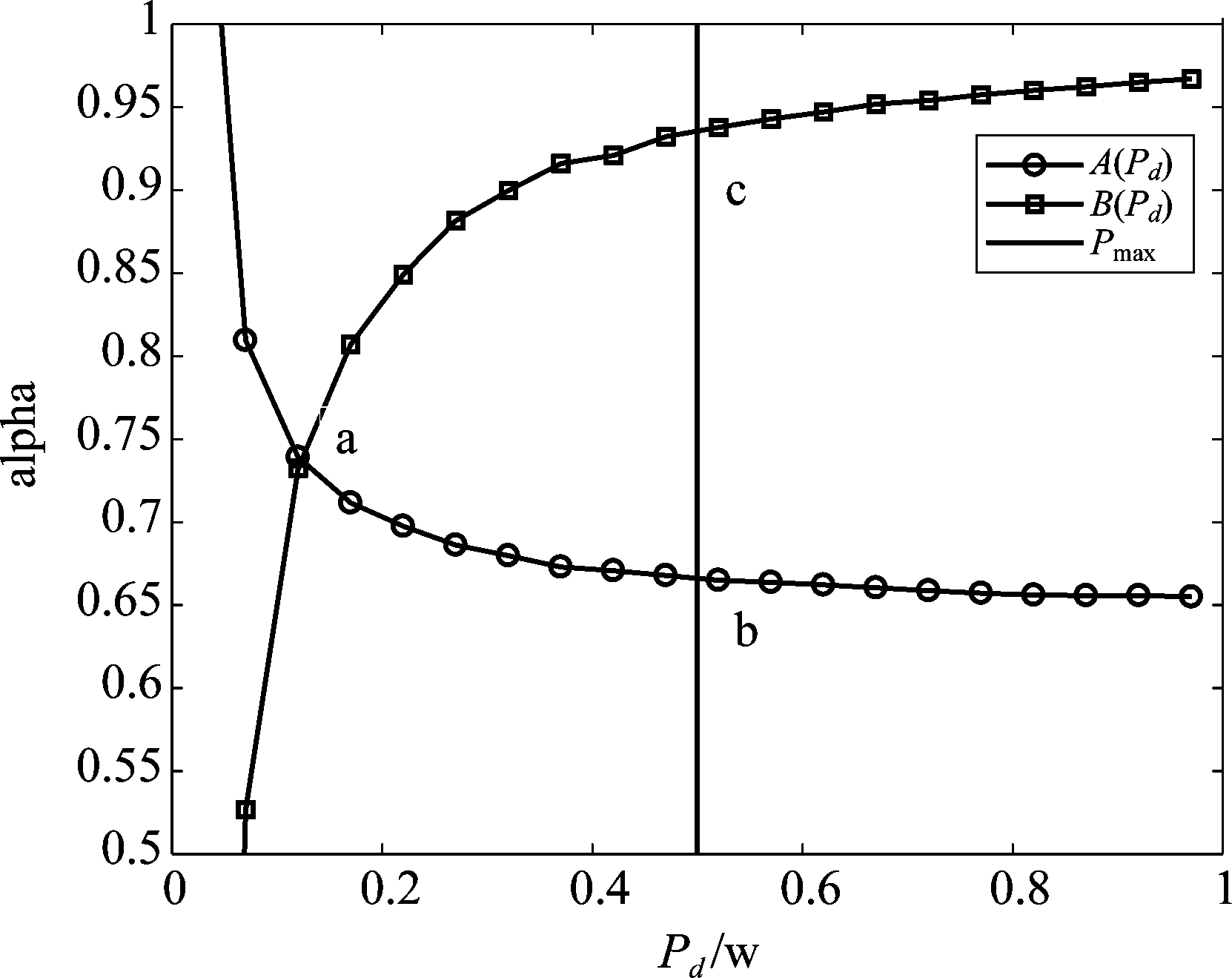
图2 D2D发送功率
与功率分配因子αk的可行解域
Fig.2 The feasible solution domain of D2D transmission power and power allocation factor αk
根据上述数学分析,D2D发送功率与功率分配因子αk的联合优化算法的主要算法流程如下所示:
表2 功率控制联合优化算法
Tab.2 Power control joint optimization algorithm
算法2主要算法流程1.初始化:设置δ,蜂窝用户发送功率pc;给定D2D对与蜂窝用户的资源分配情况;2.For 对于系统中所以D2D对3.计算:Ik=gd,d1N-gd,d2M;4.If Ik<05.根据式(32)计算可行解域内pkd可以取得的最小值:6.Pini=δ(1-δ)(pcgc,d2+n0)gd,d2-δ(pcgc,d1+n0)gd,d17.再对发送功率pkd进行迭代:pkd_next=pkd+Δp;8.While9.利用上述求解的pkd、pkd_next并根据A(pd)计算此时的功率分配因子αk、αk_next;10.If αk-αk_next≤Δα11.将pkd_next、αk_next赋值给pkd、αk;12.迭代发送功率:pkd_next=pkd+Δp;13.再次根据步骤10判断:若满足,跳出while循环,不满足重新更新pkd、pkd_next后返回再次执行步骤8;EndifEndwhile14.Ifpcon≥pmax15.根据A(pd)更新功率分配因子αk,其中pkd=pmax;16.根据式(25)计算系统D2D对和速率,其中pkd=pmax;Else17.根据式(25)计算系统D2D对和速率,其中pkd=pmax;EndifElse18.重复步骤5^17,其中根据B(pd)对αk进行更新;19.Endif20.Endfor
5 数值仿真和分析
本章数值仿真参数设置如下:
表3 仿真参数设置
Tab.3 Simulation parameter settings
参数数值蜂窝小区半径(R)500m子信道个数(K)10个蜂窝用户个数(C)10个系统中D2D对数(D)10组D2D通信距离(L)20^60m路径损耗指数(θ)3高斯白噪声(n0)-174dBm/Hz子信道带宽(B)15kHzDT端最大发射功率(Pmax)28dBm蜂窝用户端发送功率(pc)30dBmD2D链路传输速率最低阈值(rd)2bit/s·Hz
本章仿真采用的信道模型同样考虑在多径和阴影衰落的影响下,参考文献[16]中的路径损耗模型,则不同链路的路径增益可以表示为
g=ξL＾(-θ)
(33)
其中,ξ表示呈指数分布的快衰落模型,L表示各通信链路发送端到接收端的距离,θ为路径损耗常数。
近年来对蜂窝与D2D联合系统下的资源分配问题已经有诸多文献展开了研究。文献[9]中采用匈牙利算法为蜂窝网络中的中心用户与边缘用户分配频谱资源,本文则将匈牙利算法应用到异构蜂窝网络下的子信道分配问题,与本文所提的Coalition博弈算法及进行对比。另外,本文将PSO算法应用到NOMA增强型D2D通信下的功率控制优化问题,与本文所提出的基于可行解域的功率控制联合优化算法进行了对比。
上文已经提到D2D和NOMA作为5G通信中的关键技术,均可提高频谱效率,提高系统容量。因此为探究NOMA下的D2D通信是否比传统D2D通信更具优势,本小节采用matlab进行仿真,比较两种场景下的D2D对和速率。
图3所示为两种场景下的D2D和速率对比图,分别为传统的一对一通信和NOMA增强型D2D通信。为尽量保持公平性,NOMA增强型D2D中每个子信道内仅有一组D2D对,包含一个发射机和两个接收机用户,而传统D2D通信中每个子信道内有两个D2D对。如图所示,随着D2D通信距离的增加,D2D传输的速率也随之降低,但引入NOMA的D2D通信与传统的一对一D2D通信相比,能够显著提高D2D通信的可实现速率。因而将NOMA技术引入D2D通信中不仅进一步提高了频谱效率,还增加了系统容量,具有一定的研究意义。
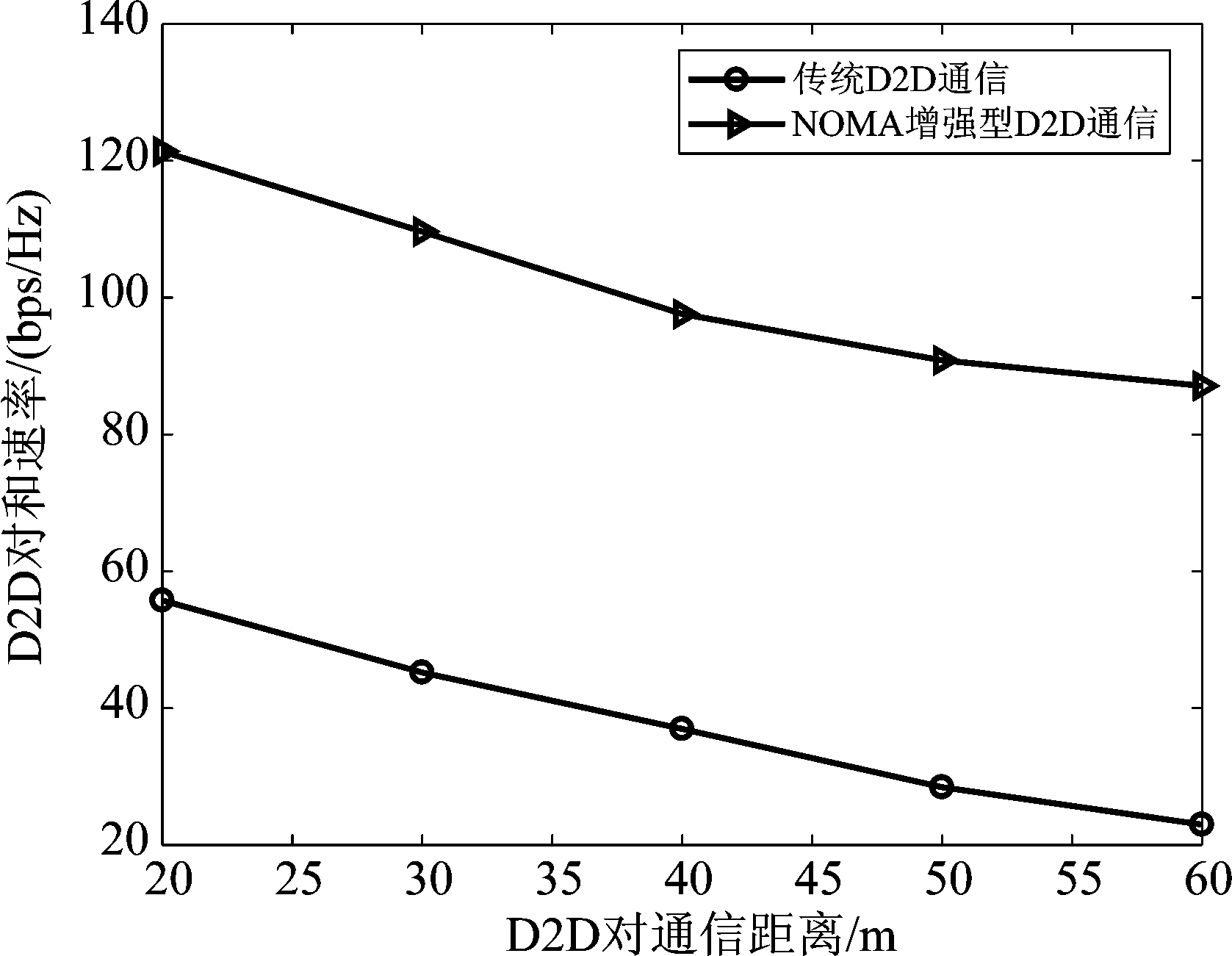
图3 D2D和速率对比示意图
Fig.3 D2D sum rate comparison diagram
图4所示为系统中D2D组和速率随蜂窝用户发送功率Pc变化的关系示意图。图中针对子信道分配问题与不同的方法展开比较,包含三种方法:本文所提出的Coalition博弈算法、匈牙利算法以及随机分配算法。为保证公平性,仅在子信道分配阶段比较三种算法性能,功率控制阶段的算法均采用本章提出的功控联合优化算法。由图4可知,在本章系统模型中,随着CU发送功率的增加D2D组和速率呈下降趋势。由于DU与CU共享同一频谱资源,因此二者间存在严重的跨层干扰,因此若要提高D2D的传输速率,则需在满足蜂窝最小传输阈值的基础上尽量减小蜂窝用户的发送功率。此外,从图4中明显可以看出,对于子信道分配问题,Coalition算法和匈牙利算法明显优于随机分配算法,因而在对系统资源分配问题进行研究时考虑子信道的最佳分配问题是十分有必要的。其次,图4表明本文所提出Coalition博弈算法与匈牙利算法性能上接近,但在计算复杂度方面,假设系统中包含c个蜂窝用户与d组D2D用户,那么匈牙利算法的复杂度为Ο(cd),而Coalition算法的复杂度为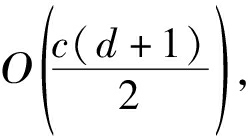
在系统中蜂窝用户和D2D用户组数量较多的情况下采用本文算法可显著降低计算复杂度。
图4 D2D和速率随Pc变化曲线图
Fig.4 D2D sum rate change curve with Pc
图5所示为系统中D2D对和速率随D2D发送功率阈值Pmax变化的关系示意图。根据上文理论分析,D2D对和速率是关于发送功率阈值Pmax的增函数,因此,图5(a)、(b)中D2D通信和速率均随着Pmax的增大呈现单调递增的趋势。由于本文针对资源分配问题拆分成了两个独立问题分别进行分析,因此图5(a)与5(b)分别针对子信道分配问题以及功率控制问题分别进行数值仿真分析。如图5(a)所示,对于子信道分配问题分别对比了Coalition博弈算法、匈牙利算法以及随机分配算法。从图中可以得到,Coalition博弈算法和匈牙利算法下D2D通信的和速率明显高于随机分配算法,因此表明合理进行频谱资源分配可以有效提升系统性能。如图5(b)所示,对于功率控制问题分别对比了本文所提出的联合优化算法和智能算法PSO算法,其中PSO算法中粒子个数设定为100个。根据图5(b)可以看出,本文提出的联合优化算法在性能上是低于PSO算法的,PSO算法主要是基于迭代全局搜索最优值,其最终的结果可能会依赖迭代次数以及粒子个数,而本文提出的算法根据两个自变量的取值范围构成联合可行解域,再通过优化问题的增减性判断自变量可以取得的最优值。图6所示为本文所提算法与PSO算法运行时间的比较示意图。仿真采用的CPU为intel core i5 10th GEN,运行内存为16G,程序运行时CPU使用率26.4%,内存占用671.8 MB。通过仿真图可以看出本文算法运行时间明显低于PSO算法,本文算法运行时间为2×10^(-4)s,而PSO算法运行时间为1.55×10^(-2)s。主要原因是本文提出的基于可行解域的联合优化算法可以根据信道增益直接获取最优解,不需要在变量的取值范围内进行搜索,有效降低了运行时间。虽然本文提出的联合优化算法的D2D和速率略低于PSO算法,但是针对非凸优化问题提出了可行解域,避免了PSO算法的全局搜索,大大降低了计算复杂度。
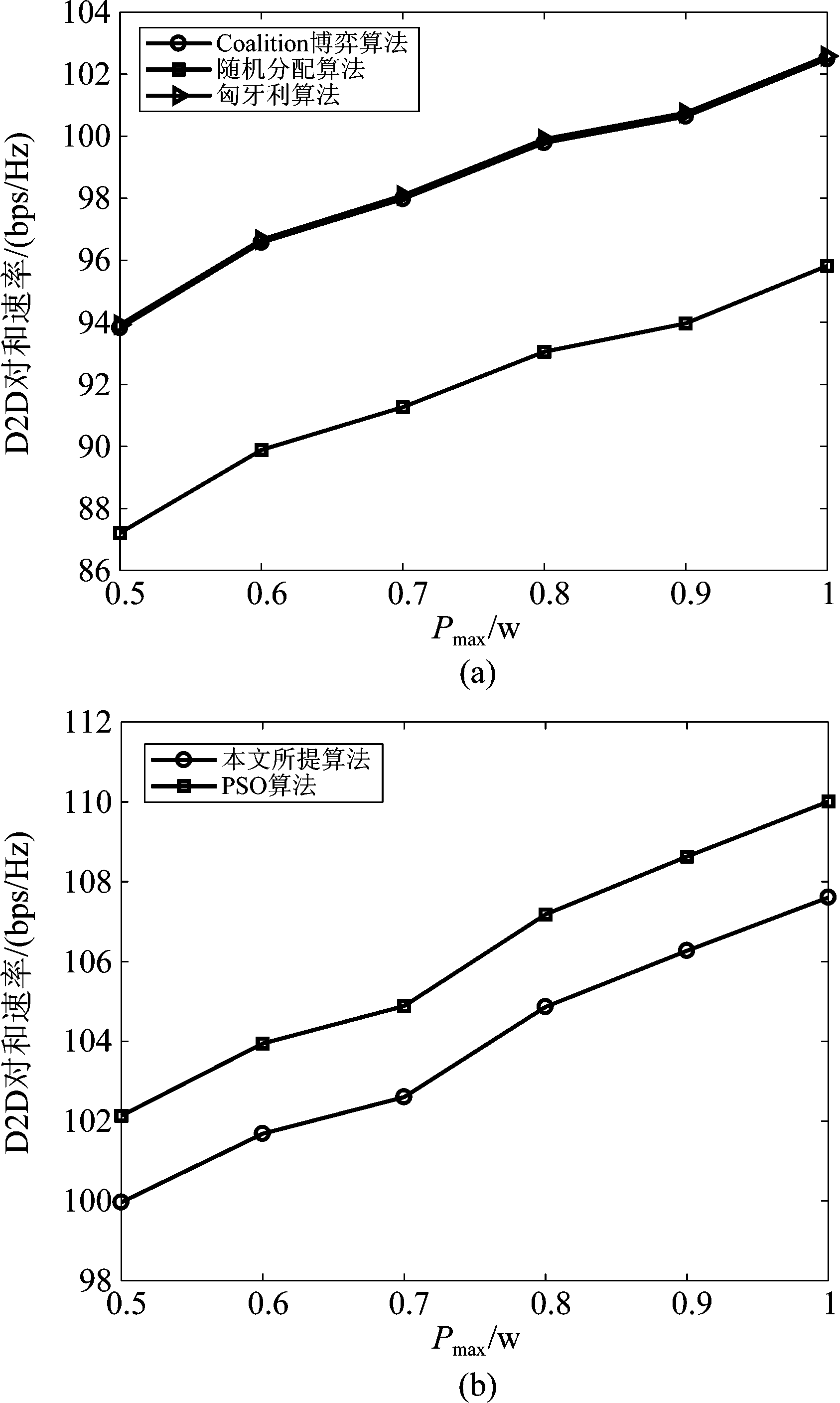
图5 D2D和速率随Pmax变化曲线图
Fig.5 D2D sum rate change curve with Pmax
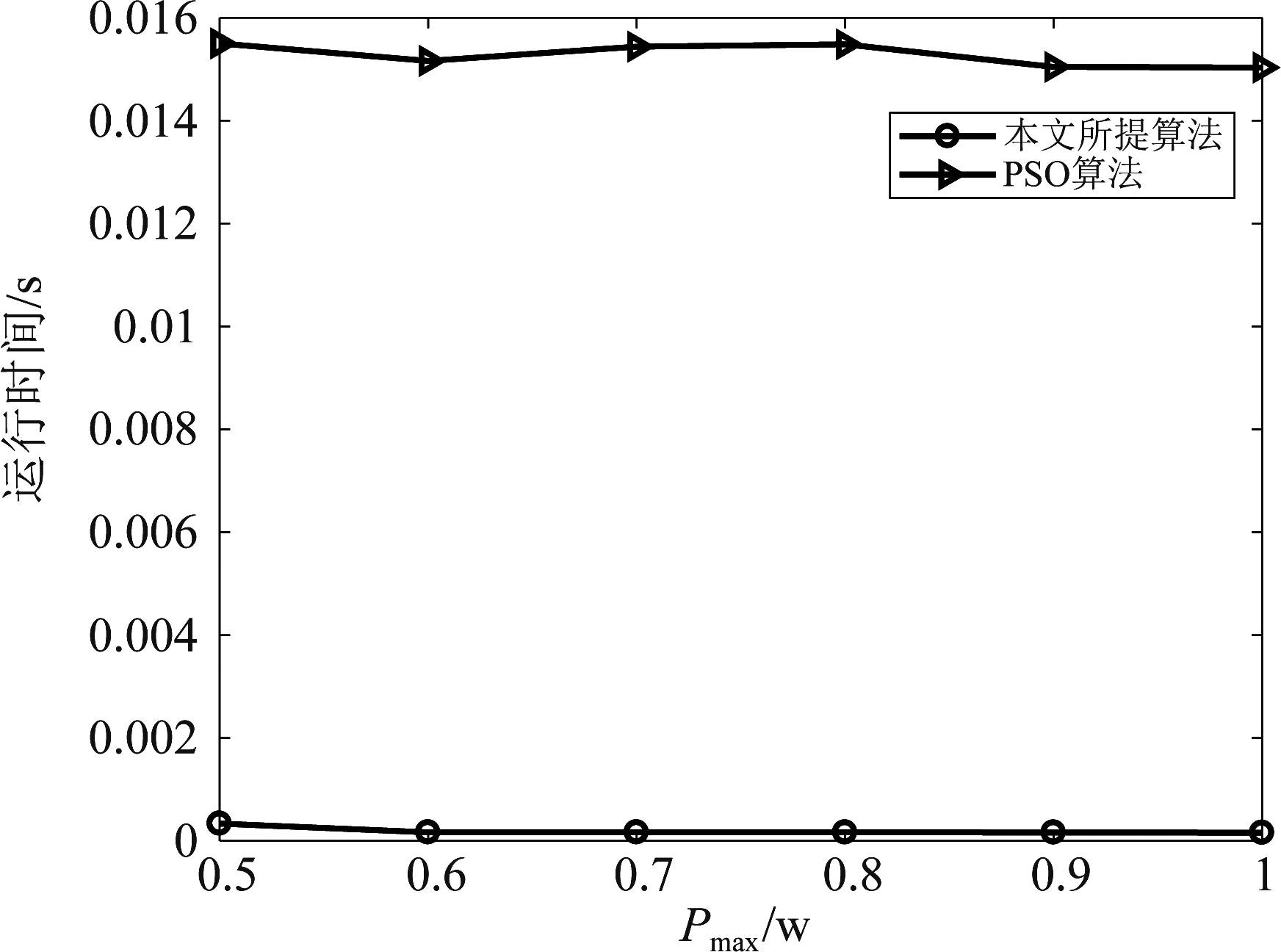
图6 运行时间对比图
Fig.6 Comparison of running time
图7所示为系统中蜂窝通信和速率随D2D用户发送功率阈值Pmax变化的关系示意图。图中分别表示系统中CU的数量分别为8、10和12时,采用本文所提的Coalition博弈算法与基于发送功率与功率分配因子的联合优化算法进行资源分配时系统中蜂窝通信的和速率。为降低DU与CU的跨层干扰,本章假定一个子信道中只能存在一组D2D组,根据上图所示,随着系统中CU与DU数量的增加,蜂窝用户的和速率也逐步升高。本文系统模型中最大化D2D通信的和速率是要首先保证蜂窝通信传输质量,根据约束条件式(18),蜂窝传输质量与D2D发送功率成反比,即随着D2D发送功率的升高,蜂窝传输质量会由于跨层干扰的影响而降低。因此根据图7所示,设定CU传输速率的最小阈值,此时可以限定DU发送功率最大阈值。
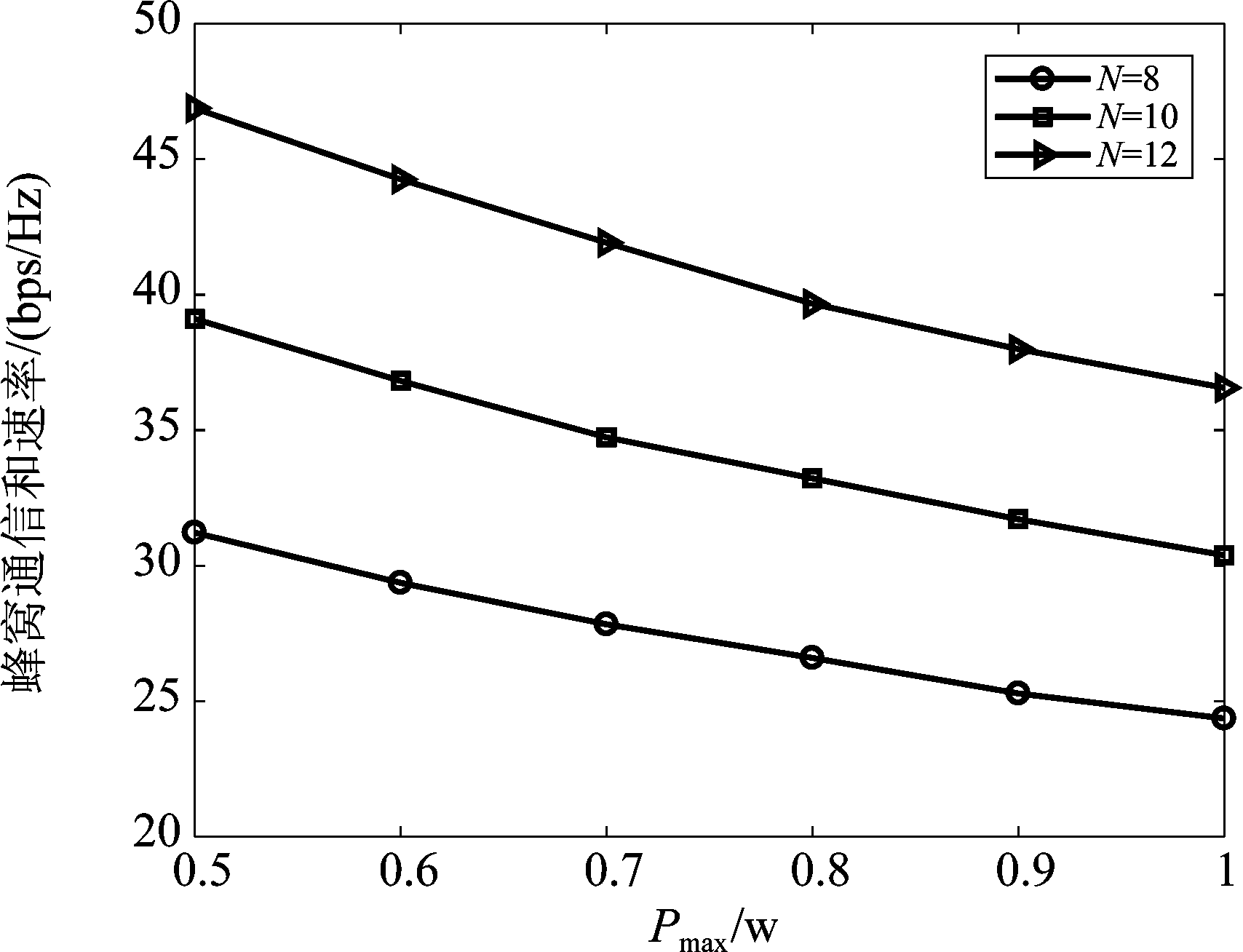
图7 蜂窝通信和速率随Pmax变化曲线图
Fig.7 Cellular communication sum rate change curve with Pmax
6 结论
本文主要研究异构蜂窝网络中NOMA增强型D2D通信的资源分配问题,主要目的是确保蜂窝传输质量又使系统中D2D和速率最大化。首先在本文系统模型中,为降低CU与DU间的跨层干扰的影响,假定一个子信道最多只能被一组D2D组复用,每个D2D组包括一个发射机与两个接收机,发射机处采用NOMA原理发送叠加信号向两个接收机,接收端出再通过SIC解码出所需信号,该系统模型下不仅能够有效减少跨层干扰,多接收端的形式还能有效提高频谱利用率。其次针对上述系统模型的特点,将资源分配问题拆分成子信道分配和功率控制两个独立问题分别进行分析。针对子信道分配问题,提出Coalition博弈模型,将同一子信道内的蜂窝用户与D2D用户看作一个合作的整体来最大化二者共同的利益。针对功率控制问题,由于本文优化问题是一个非凸函数,且不能简单的将其转化为凸函数进行求解,因此本文根据D2D发送功率与功率分配因子的可行解域,提出相应的联合优化算法来最大化D2D对和速率。最后仿真结果表明本文所提出的NOMA增强型D2D通信的资源分配算法不仅具有较好系统性能还有效降低了计算复杂度。
[1] CHEN Yali, AI Bo, NIU Yong, et al.Resource allocation for device-to-device communications underlaying heterogeneous cellular networks using coalitional games[J].IEEE Transactions on Wireless Communications, 2018,17(6): 4163-4176.
[2] HAYATI M, KALBKHANI H, SHAYESTEH M G.Energy-efficient relay selection and power allocation for multi-source multicast network-coded D2D communications[J].AEU-International Journal of Electronics and Communications, 2021, 128:153522.
[3] PARK J H, KWON D, KIM D K.Resource allocation for GBR services in D2D-enabled communication[J].Electronics, 2020, 9(10):1585.
[4] ESLAMI L,MIRJALILY G, DAVIDSON T N, et al.Spectrum-efficient QoS-aware resource assignment for FFR-based D2D-enabled heterogeneous networks[J].IEEE Access,2020,8: 218186-218198.
[5] MA Yanbo,LIU Ting,CUI Lin, et al.Robust resource allocation with power outage guarantees for energy harvesting aided device-to-device communication[J].IEEE Access,2020,8: 124563-124578.
[6] LIN Zefang, SONG Hui, PAN Daru.A joint power and channel scheduling scheme for underlay D2D communications in the cellular network[J].Sensors, 2019, 19(21):4799.
[7] 杨佳颖,李汀,解培中.异构蜂窝网络中基于Stackelberg博弈的能效优化算法[J].信号处理,2020,36(11):1923-1930.
YANG Jiaying, LI Ting, XIE Peizhong.Energy efficiency optimization algorithm for heterogeneous cellular network based on Stackelberg game[J].Journal of Signal Processing, 2020, 36(11): 1923-1930.(in Chinese)
[8] TIAN Feiyan, CHEN Xiaoming.Multiple-antenna techniques in nonorthogonal multiple access: a review[J].Frontiers of Information Technology & Electronic Engineering, 2019, 20(12): 1665-1697.
[9] XU Yao, WANG Gang, LI Bo, et al.Performance of D2D aided uplink coordinated direct and relay transmission using NOMA[J].IEEE Access,2019,7: 151090-151102.
[10] HUU P, ARFAOUI M A, SHARAFEDDINE S, et al.A low-complexity framework for joint user pairing and power control for cooperative NOMA in 5G and beyond cellular networks[J].IEEE Transactions on Communications, 2020,68(11): 6737-6749.
[11] DASH S P, JOSHI S.Performance analysis of a cooperative D2D communication network with NOMA[J].IET Communications,2020,14(16): 2731-2739.
[12] JAIN P, GUPTA A, TANWAR S, et al.Customized NOMA and sector model for battery efficient beyond 5G green networks[J].IEEE Network,2020,34(6):281-287.
[13] ZHAO Jingjing, LIU Yuanwei, CHAI KoK Keong, et al.NOMA-based D2D communications: towards 5G[C]∥ 59th Annual IEEE Global Communications Conference(IEEE GLOBECOM).Washington, 2016:1-6.
[14] 宋勇春,王茜竹,高正念.基于HAGA的D2D-NOMA资源分配优化算法[J/OL].计算机工程,2021:1-7.
SONG Yongchun,WANG Qianzhu,GAO Zhengnian.D2D-NOMA resource allocation optimization algorithm based on HAGA[J/OL].Computer Engineering,2021:1-7.(in Chinese)
[15] GU Wenying, ZHU Qi.Stackelberg game based social-aware resource allocation for NOMA enhanced D2D communications[J].Electronics,2019,8(11):1360.
[16] YUAN Yiling, YANG Tao, FENG Hui, et al.An iterative matching-Stackelberg game model for channel power allocation in D2D underlaid cellular networks[J].IEEE Transactions on Wireless Communications, 2018, 17(11):7456-7471.
