1 引言
相较于传统的线阵和面阵,共形阵列天线附着于载体表面,可以有效节省空间、满足空气动力学要求、扩大波束扫描范围、实现较高天线增益、获得较大的有效孔径。在星载、弹载雷达、航空航天飞行器等领域有重要应用[1]。在共形阵列的诸多研究方向中,利用阵列接收信号实现波束控制、波达方向(Direction Of Arrival, DOA)估计等算法有广泛的应用[2-11],其中在共形阵列方向图综合优化方面,文献[2]针对共形水听器阵列单元方向图指向不一致的问题,利用二阶锥规划实现方向图综合。文献[3]针对粒子群算法在共形天线方向图优化中易陷入局部最优的问题,利用惯性权重因子对传统的粒子群算法进行了改进,有效地获得各天线单元的幅值。在共形阵列波束形成方面,文献[4]基于共形阵列提出一种通过子阵分割以及FFT内插的快速波束形成方法。文献[5]提出一种基于共形阵列的零陷展宽方法,提高了干扰抑制的鲁棒性。在共形阵列参数估计方面,文献[6-7]利用多重信号分类法(Multiple Signal Classification, MUSIC)、子空间拟合等算法研究了锥面、柱面共形阵列的DOA估计和极化参数估计方法以及算法的估计精度。文献[8]基于锥面共形阵列提出一种降维MUSIC算法,通过构造同极化接收子阵实现了信源方位信息和极化信息的去耦合,有效地降低了极化-DOA联合估计的计算量。文献[9]针对未知互耦条件下的多输入多输出(Multiple-Input Multiple-Output, MIMO)系统中的共形阵列,提出一种基于张量技术的二维DOA估计方法。文献[10]利用非圆信号的阵列拓展性实现去耦合,并针对相干信源的情况,推导了锥面共形阵列非圆信号的空间平滑算法,有效地提升了低信噪比时的参数估计精度。
在阵列建模方面,传统的标量阵列如线阵、面阵由于阵元方向图指向一致,因此不需考虑信号极化矢量以及阵元方向图的影响。在极化敏感阵列方面,文献[11]首先给出极化敏感阵列模型,并将经典的超分辨算法移植到极化敏感阵列;文献[12]基于双正交偶极子构成的线阵或面阵研究了极化域空域联合谱估计。经典极化敏感阵列阵元方向图指向一致,(因此在建模时只需统一计算信号极化矢量在阵元方向图上的投影。)受共形载体曲率影响,共形阵列阵元方向图指向取决于载体的曲率,因此接收信号的相对幅度由信号极化矢量在阵元单元方向图的投影决定。在共形阵列建模方面,文献[13]将子阵分割和虚拟内插算法相结合实现柱面共形阵列的DOA估计。但其只考虑了阵元方向图的幅度信息,并未考虑信号和阵元的极化信息。共形阵列建模的难点在于全局信号极化矢量在阵元局部方向图的投影,文献[14-15]指出可通过欧拉旋转变换进行全局直角坐标系和局部直角坐标系的坐标变换。文献[16]基于欧拉旋转,通过三次欧拉旋转变换,建立了共形阵列全局直角坐标系和局部直角坐标系的旋转关系,最后在全局极坐标系下,将每个入射信号的极化矢量投影到每个阵元的极化方向图中得到阵元的极化响应,进而得到导向矢量[17-19]。文献[16]首次给出共形阵列建模方法的统一框架,为共形阵列信号处理奠定了基础。
分析文献[16]可知,其给出的共形阵列建模方法,仅讨论了信号极化矢量与阵元极化方向图在全局极坐标系下的投影。理论上该极化投影可以在局部极坐标系、局部直角坐标系、全局直角坐标系、全局极坐标系四种坐标系下进行。文献[20]利用流形分离技术和MUSIC算法实现任意阵列的极化DOA估计,文献[21]提出一种广义信号子空间拟合算法,实现了相干源情况下的降维DOA估计。上述方法在建立接收信号模型时均涉及到在全局坐标系下进行投影,因此研究不同的极化投影方式有助于将流形分离,广义信号子空间拟合(Generalized Signal-Subspace Fitting, GSSF)等算法应用于共形阵列,实现快速DOA估计等。此外,在全局坐标系下进行极化投影由于涉及坐标旋转反变换因此有更高的计算复杂度,在局部坐标系下的投影具有较低的计算复杂度,更易于实现。
综上,本文针对共形阵列建模中入射信号极化矢量在阵元极化方向图上投影的重点、难点问题,在利用欧拉旋转法实现坐标系变换的基础上,推导了全局直角坐标,局部极坐标、局部直角坐标等三种坐标系下,入射信号极化矢量在阵元极化方向图上的投影,得到共形阵列导向矢量,完成共形阵列信号建模,推导了四种方法建模所需要的复杂度,并利用全局坐标系下极化投影方法验证广义信号子空间拟合算法应用于共形阵列的可行性。本文在给出多种共形阵列建模方法的同时,析清了共形阵列建模的理论框架,丰富了共形阵列建模的理论内涵,是对已有基于欧拉旋转的共形阵列建模理论的有益补充。本文内容具体安排如下,首先给出共形阵列数学模型以及求解用于极化投影的阵元方向图极化响应,其次,提出了三种极化投影方式并推导其计算复杂度,最后通过仿真实验验证了本文方法的有效性,并对本文进行总结。
2 共形阵列数学模型
如图1所示,对单极化阵元构成的共形阵列,由入射信号到阵元间的波程差得到空域导向矢量A(θ,φ),由入射信号极化矢量在阵元极化方向图上的投影建立共形阵列极化域导向矢量,并最终得到共形阵列导向矢量,完成共形阵列建模。
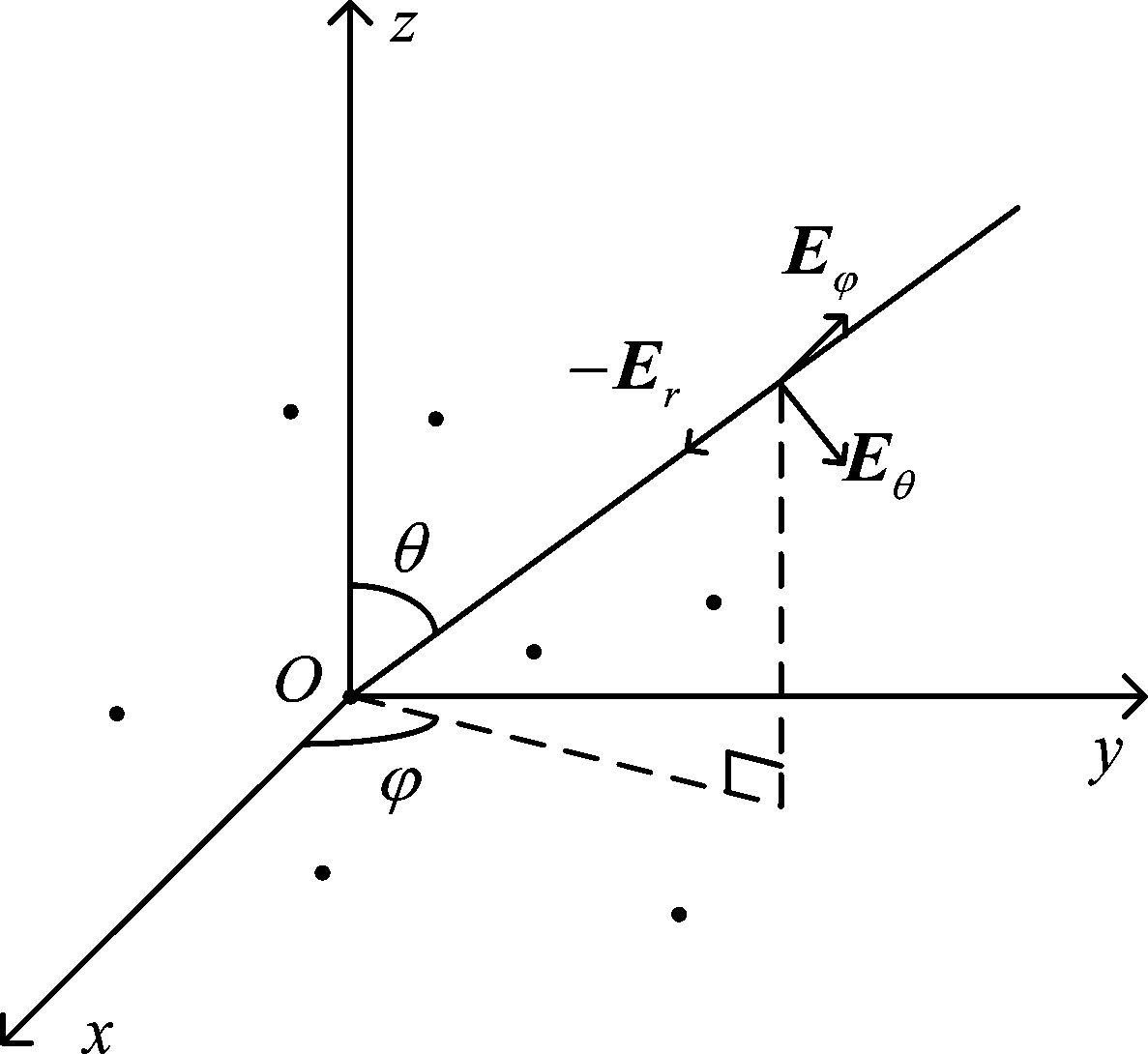
图1 三维任意形状阵列坐标系示意图
Fig.1 Schematic diagram of arbitrary shape array coordinate system
在窄带远场假设条件下,考虑任意一个N元共形阵列,阵列信号的接收模型为:
(1)
式中,X(t)为N×1的快拍数据矢量,N为阵元个数;S(t)为M×1的入射信号矢量,M为信源个数;N(t)为N×1噪声矢量。![]() 为导向矢量。由于共形天线单元指向及极化形式存在差异,不同极化形式的阵元对入射信号的极化响应不同,因此共形阵列导向矢量中除包含由波程差引起的空域导向矢量以外,还应包含阵元对入射信号的极化响应矢量,共形阵列导向矢量
为导向矢量。由于共形天线单元指向及极化形式存在差异,不同极化形式的阵元对入射信号的极化响应不同,因此共形阵列导向矢量中除包含由波程差引起的空域导向矢量以外,还应包含阵元对入射信号的极化响应矢量,共形阵列导向矢量![]() 由下式给出。
由下式给出。
(2)
A(θ,φ)=[a(θ1,φ1)a(θ2,φ2)…a(θM,φM)]
(3)
a(θi,φi)=[exp(-jωr1·vi)exp(-jωr2·vi)…
exp(-jωrN·vi)]T
(4)
P(θ,φ,γ,η)=[p(θ1,φ1,γ1,η1)p(θ2,φ2,γ2,η2)
…p(θM,φM,γM,ηM)]
(5)
p(θi,φi,γi,ηi)=[p1ip2i…pNi]T
(6)
其中,![]() 为空域导向矢量A(θ,φ)和极化矢量P(θ,φ,γ,η)的Hadamard积(⊙为矩阵的Hadamard积);θ,φ,γ,η分别为入射信号俯仰角、方位角、极化角、极化相位差;ω=2π/λ,λ为波长;rk为第k个阵元的位置矢量rk=[xk,yk,zk];vi为第i个信源的方向矢量vi=[sin θicos φi,sin θisin φi,cos θi]T;极化响应pki为第i个信号的极化矢量ui在第k个阵元方向图gk上的投影。
为空域导向矢量A(θ,φ)和极化矢量P(θ,φ,γ,η)的Hadamard积(⊙为矩阵的Hadamard积);θ,φ,γ,η分别为入射信号俯仰角、方位角、极化角、极化相位差;ω=2π/λ,λ为波长;rk为第k个阵元的位置矢量rk=[xk,yk,zk];vi为第i个信源的方向矢量vi=[sin θicos φi,sin θisin φi,cos θi]T;极化响应pki为第i个信号的极化矢量ui在第k个阵元方向图gk上的投影。
3 阵元方向图极化响应
由第2节可知,共形阵列导向矢量由空域导向矢量和极化域矢量共同确定。空域导向矢量的形式由阵元位置矢量及信源方向矢量确定;极化域导向矢量由入射信号极化矢量在每个阵元方向图的极化投影构成,其中入射信号极化矢量一般在全局坐标系下表示,各阵元方向图一般在局部坐标系中表示,而极化投影需要在同一坐标系下进行,因此需要在全局坐标系和各阵元局部坐标系之间进行坐标系变换,以实现极化投影。针对该问题,本文采用欧拉旋转变换完成全局、局部坐标系变换。
3.1 全局直角坐标系到局部直角坐标系的欧拉旋转变换
阵元方向图通常在局部极坐标系下表示,通过将入射信号方向矢量在局部极坐标系下表示,可得入射信号在阵元局部极坐标系下的入射角,进而得到阵元方向图响应。
入射信号方向矢量在局部极坐标系下的表示,可通过全局直角坐标系到局部直角坐标系的欧拉旋转变换实现。对于如图2给定的常见共形阵列,按照欧拉旋转的旋转准则,计算全局直角坐标系到每个阵元局部直角坐标系所需的欧拉旋转角D、E、F以及对应的欧拉旋转变换矩阵R。常见共形阵列的欧拉旋转角和旋转矩阵如下:

图2 三种常见的共形阵列
Fig.2 Three common conformal arrays
锥面共形阵列:
Dnm=θn+2π(m-1)/Mn,Enm=π/2-β,Fnm=0
(7)
柱面共形阵列:
Dnm=θn+2π(m-1)/Mn,Enm=π/2,Fnm=0
(8)
球面共形阵列:
Dnm=θn+2π(m-1)/Mn,
Enm=π/2-sin -1[(rs-nh)/rs],Fnm=0
(9)
欧拉旋转矩阵R如下。
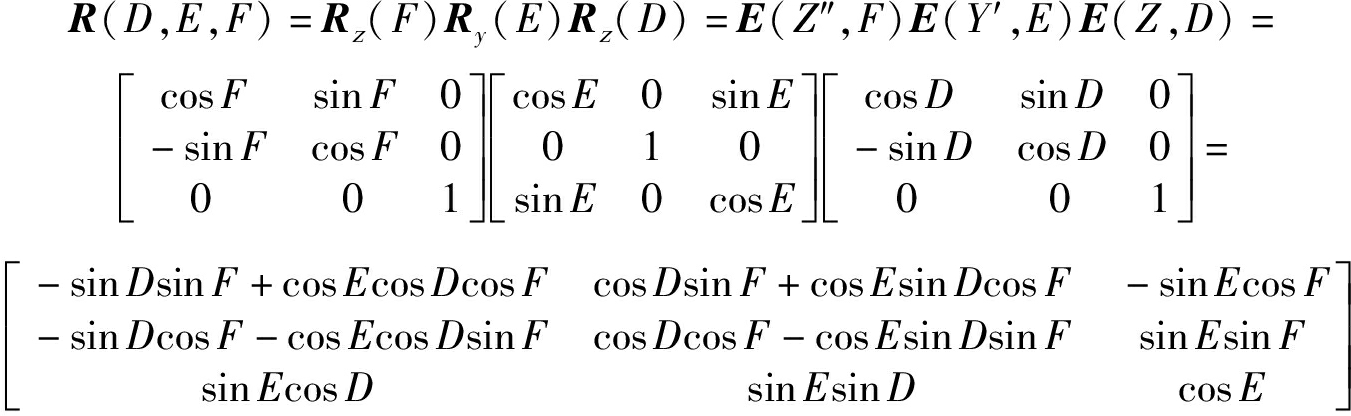
(10)
上式中局部直角坐标系的定义如下,以阵元切平面为![]() 平面,切平面法线为
平面,切平面法线为![]() 轴。D为第一次,以Z轴为旋转轴沿Z轴负方向逆时针旋转的角度。E为第二次,以Y为旋转轴逆时针旋转的角度。F为第三次,以Z为旋转轴逆时针旋转的角度,n为从下至上的圆环序号,m为每个圆环逆时针方向阵元序号,Mn为第n层包含的阵元总数,rs为球面共形阵列的半径。
轴。D为第一次,以Z轴为旋转轴沿Z轴负方向逆时针旋转的角度。E为第二次,以Y为旋转轴逆时针旋转的角度。F为第三次,以Z为旋转轴逆时针旋转的角度,n为从下至上的圆环序号,m为每个圆环逆时针方向阵元序号,Mn为第n层包含的阵元总数,rs为球面共形阵列的半径。
3.2 局部极坐标系下共形天线单元对入射信号的响应
通过欧拉旋转变换,将全局极坐标系下的入射信号方向(θ,φ)转化至局部极坐标系![]() 再依据阵元的局部方向图得到其对入射信号的响应
再依据阵元的局部方向图得到其对入射信号的响应![]() 由单位矢量的极坐标和直角坐标的关系可得,入射信号方向矢量在全局直角坐标下的表示为:
由单位矢量的极坐标和直角坐标的关系可得,入射信号方向矢量在全局直角坐标下的表示为:
x=sin θcos φ,y=sin θsin φ,z=cos θ
(11)
利用求得的欧拉旋转矩阵将其变换到局部直角坐标系:
(12)
根据式(11)中直角坐标和极坐标关系,可以得到入射信号单位矢量在阵元局部极坐标系下的表示:
(13)
利用求得的局部极坐标系下第i个信号在第k个阵元上的入射俯仰方位角![]() 以及已知的阵元局部方向图,可求得阵元在局部极坐标系下对入射信号的响应:
以及已知的阵元局部方向图,可求得阵元在局部极坐标系下对入射信号的响应:
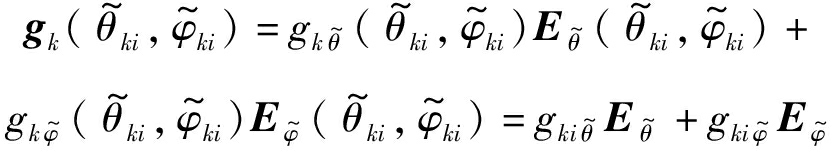
(14)
其中,![]() 为局部极坐标系下
为局部极坐标系下![]() 方向基向量;
方向基向量;![]() 为局部极坐标系下
为局部极坐标系下![]() 方向基向量。
方向基向量。![]() 表示第i个信号在第k个阵元上的方向图响应,记作
表示第i个信号在第k个阵元上的方向图响应,记作![]()
4 入射信号极化矢量在阵元极化方向图上的投影
第2节给出了由波程差引起的空域导向矢量的表达形式。极化域导向矢量由入射信号极化矢量在阵元极化方向图上的投影决定,该投影要保证在同一坐标系下完成,根据共形阵列建模过程可知,共有全局极坐标、直角坐标,局部极坐标、直角坐标四种坐标系,极化投影在以上四种坐标系中均可实现,现有文献[16]主要讨论了在全局极坐标下的投影方法,本文对另外三种坐标系下的投影方法进行了补充,并验证了四种坐标系投影结果的一致性,完善了共形阵列建模的理论框架。
4.1 信源全局极坐标系下的极化矢量
全局极坐标系下的信号极化矢量为:
ui=uiθEθ+uiφEφ
(15)
uiθ=sin(γi)exp(jηi),uiφ=cos(γi)
(16)
tanγ=Aθ/Aφ, η=φθ-φφ,
(γ∈[0,π/2], η∈[0,2π))
(17)
其中,Eθ为全局极坐标系下θ方向基向量,Eφ为全局极坐标系下φ方向基向量。γ为极化角,η为极化相位差。Aθ,Aφ为θ,φ方向电场幅度,φθ,φφ为θ,φ方向相位。
4.2 三种极化投影方式
第i个入射信号在共形阵列上的极化投影矢量可以表示为:
p(θi,φi,γi,ηi)=[p1i p2i … pNi]T
(18)
利用式(5)得到极化矢量P,并利用空域导向矢量A和极化矢量P得到共形阵列的导向矢量![]()
(19)
如图3所示,在利用信号极化矢量投影到阵元方向图的方法来计算极化投影pki时,可以在全局极坐标系、全局直角坐标系、局部直角坐标系、局部极坐标系等四种坐标系下进行,其中全局极坐标系中的投影方法(如图3(a)所示)在文献[16]中论述,以下分别对其他三种投影方法进行说明(如图3(b)、(c)、(d)所示)。
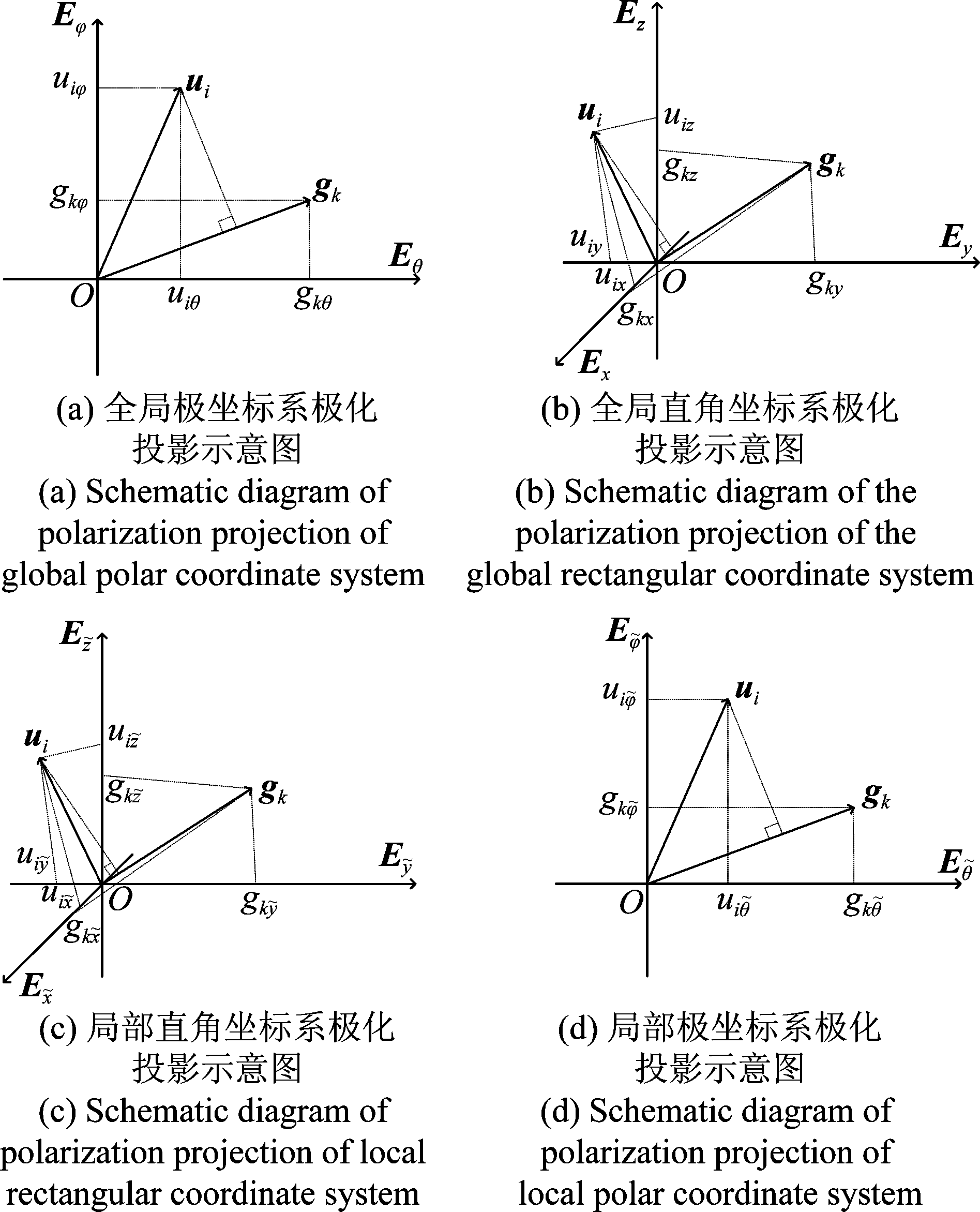
图3 入射信号极化矢量在阵元极化方向图的投影
Fig.3 The projection of the polarization vector of the incident signal on the polarization pattern of the array element
4.2.1 全局直角坐标系下极化投影
全局直角坐标系下极化投影需求得全局直角坐标系下方向图响应g和信号极化矢量u,第i个入射信号在第k个阵元方向图上的极化响应可在全局直角坐标系下表示为:
(20)
极坐标系与直角坐标系单位矢量之间的变换关系如下[12]:
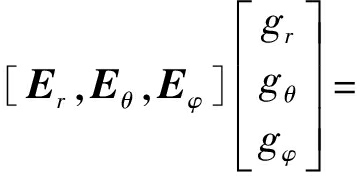
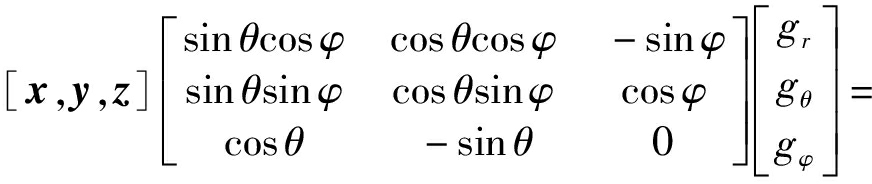
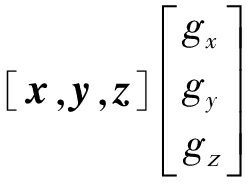
(21)
上式给出了同一矢量在全局极坐标系和直角坐标系中的坐标变换关系,局部坐标系下变换关系同理,Er,Eθ,Eφ表示基向量,gr,gθ,gφ表示相应坐标系下的坐标,同理gx,gy,gz表示同一矢量在直角坐标系下的直角坐标。
首先求解方向图极化响应在全局直角坐标系下的表示。第3节中推导出局部极坐标系下方向图极化响应![]() 由于电场强度方向垂直于传播方向,因此
由于电场强度方向垂直于传播方向,因此![]() 则由式(21)极坐标和直角坐标关系以及求得的
则由式(21)极坐标和直角坐标关系以及求得的![]() 可得式(20)中局部直角坐标系下单元方向图的
可得式(20)中局部直角坐标系下单元方向图的![]() 方向分量
方向分量![]() 为:
为:
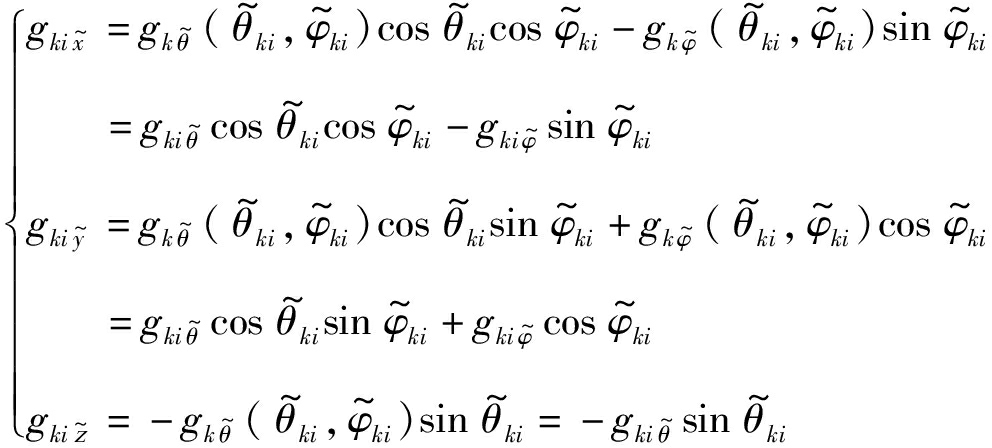
(22)
再由欧拉旋转可求得方向图响应在全局直角坐标系下的表示:
(23)
其中,第i个信号在第k个阵元上的方向图响应和俯仰方位角由式(13)、(14)给出。![]() 为第k个阵元的旋转矩阵Rk的逆矩阵。
为第k个阵元的旋转矩阵Rk的逆矩阵。
信号极化矢量在全局直角坐标下的表示方法如下。第i个入射信号的极化矢量可在全局直角坐标系下表示为:
ui(θk,φk)=uiθ(θi,φi)Eθ(θi,φi)+
uiφ(θi,φi)Eφ(θi,φi)=uixEx+uiyEy+uizEz
(24)
类似于式(22),上式中可求得基向量Ex,Ey,Ez方向的分量uix,uiy,uiz为:
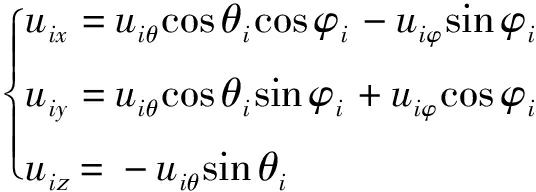
(25)
最后利用在全局直角坐标系下的信号极化矢量和阵元方向图响应可以求得第i个信号在第k个阵元上的极化投影为:
pki=ui·gk=uix·gkix+uiy·gkiy+uiz·gkiz
(26)
4.2.2 局部直角坐标系下极化投影
局部直角坐标系下极化投影需求得局部直角坐标系下方向图响应g和信号极化矢量u。第i个入射信号在第k个阵元方向图上的极化响应,可在局部直角坐标系下表示为:
(27)
上式中局部坐标系下每个阵元单元方向图的![]() 方向分量
方向分量![]() 在(23)中给出。
在(23)中给出。
信号极化矢量在全局直角坐标下的表示方法如下。将全局极坐标系下的信号极化矢量ui在局部直角坐标下表示:
ui(θi,φi)=uiθ(θi,φi)Eθ(θi,φi)+
![]()
(28)
式(25)已推导出全局直角坐标系下信号极化矢量的uix,uiy,uiz分量,因此上式中局部直角坐标系下信号极化矢量的![]() 方向分量
方向分量![]() 需经欧拉旋转变换得到:
需经欧拉旋转变换得到:
(29)
利用局部直角坐标系下的信号极化矢量和阵元方向图响应可以求得第i个信号在第k个阵元上的极化投影为:
(30)
4.2.3 局部直角坐标系下极化投影
局部极坐标系下极化投影需求得局部极坐标系下方向图响应g和信号极化矢量u。第i个入射信号在第k个阵元方向图上的极化响应,可在局部极坐标系下表示为:
(31)
信号极化矢量在全局直角坐标下的表示方法如下。将全局极坐标系下的信号极化矢量ui在局部极坐标系下表示:
ui(θi,φi)=uiθ(θi,φi)Eθ(θi,φi)+
![]()
(32)
根据式(21)中同一矢量在不同坐标系下的坐标关系,可得上式中信号极化矢量的![]() 方向分量
方向分量![]()
(33)
其中,![]() 在式(29)中推导得出。局部坐标下的
在式(29)中推导得出。局部坐标下的![]() 由式(13)给出。
由式(13)给出。
则利用在局部极坐标系下的信号极化矢量和阵元方向图响应可以求得极化投影为:
(34)
4.3 共形阵列建模复杂度分析
四种方法建模流程图及复杂度如图4所示。
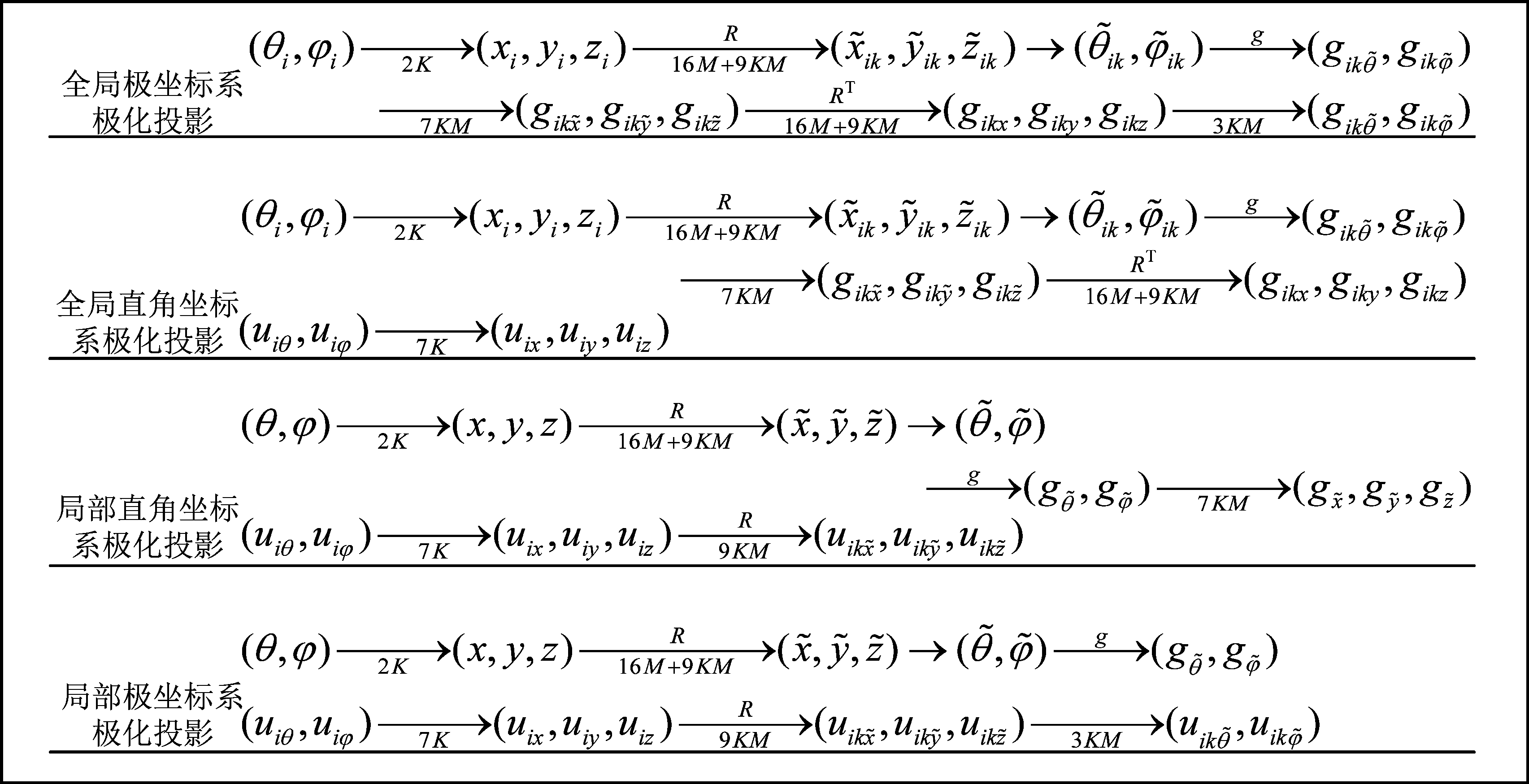
图4 四种方法建模流程图及计算复杂度
Fig.4 Four methods of modeling flowchart and computational complexity
计算复杂度采取文献[8]的定义,主要计算建模过程中实数乘法的次数。共形阵列建模计算量主要体现在全局坐标系下欧拉旋转变换、方向图响应计算、局部坐标系下欧拉旋转变换等方面。
设K为信源数,M为阵元数,上图中R表示欧拉旋转变换,g表示计算方向图响应函数。计算不同建模方法所需的实数乘法次数。其中,由式(11)可知,K个信号极坐标转化到直角坐标需要的实数乘法次数为2K次,由(10)可知,M个阵元的旋转矩阵R所需计算量为16M次,全局和局部坐标系下欧拉旋转的计算量为9KM次。观察式(25)可得,信号极化分量从全局极坐标系转化到全局直角坐标系的计算量为7K次,而由于不同阵元在同一方向的方向图极化分量不同,因此方向图响应分量从局部极坐标系转化到局部直角坐标系则需要7KM次乘法。又因为不同方向图表达式不同且不同建模方法都需进行相同的方向图计算,因此不影响计算复杂度的相对大小。由上图可知,文献[16]在全局极坐标系下进行极化投影所需计算量为(2K+16M+9KM+7KM+16M+9KM+3KM)=(28KM+32M+2K);本文所提出全局直角坐标系下极化投影计算量为(2K+16M+9KM+7KM+16M+9KM+7K)=(25KM+32M+9K);局部直角坐标系所需计算量为(2K+16M+9KM+7KM+7K+9KM)=(25KM+16M+9K);局部极坐标系所需计算量为(2K+16M+9KM+7K+9KM+3KM)=(21KM+16M+9K)。
若取信源数为K=1,阵元数M=8,四种方法所需计算量如表1所示。
表1 四种方法建模计算复杂度比较(实数乘法次数)
Tab.1 Comparison of modeling calculation amount of four methods(Real number addition times)

阵形文献[16]极化投影结果全局直角坐标极化投影结果局部直角坐标极化投影结果局部极坐标极化投影结果任意阵型482465337305
若以文献[16]中全局极坐标系极化投影所需实数乘法次数为基准,四种建模方法所需的计算复杂度之比为1.0∶0.97∶0.69∶0.63。可以看出,局部极坐标系极化投影用时最短,文献[16]用时最长。整体而言,相比于全局坐标系下投影的方法,局部坐标系下投影方法由于可以同时进行信号方向矢量和极化分量的欧拉旋转,因此可减少一次欧拉旋转矩阵R的计算,因此局部坐标系下极化投影复杂度更低。
5 共形阵列建模仿真实验
为验证本文方法的有效性,分别对锥面、柱面、球面等三种常见的共形阵列在四种坐标系下进行极化投影,对得到的四种建模结果进行对比。
仿真实验1 有效性验证
在仿真实验中采用单极化阵元,不失一般性,取圆环数目为1,各阵元均匀分布,阵元个数为8个。对于锥面共形阵列,半顶角取20°,坐标原点到圆环的距离取0.5 m;对于柱面共形阵列,圆环半径取0.2 m;对于球面共形阵列,球半径取0.2 m,坐标原点到圆环的距离取0.1 m。单元方向图取
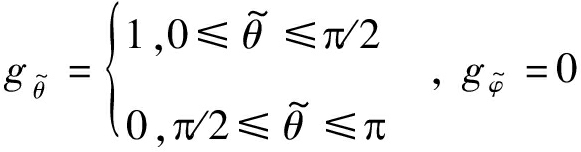
(35)
信源个数为1个,波长取0.1 m,信源的俯仰角为15°,方位角为0°,极化方式为45°线极化,极化相位差为0°,考虑遮蔽效应。根据以上仿真条件,得到不同投影方式下得到的极化矢量。对比本文建模方法和在全局极坐标系下投影的建模方法用以验证本文方法的有效性,建模结果如表2、表3、表4所示。
从表2、表3、表4结果可以看出,本文方法和文献[16]方法得到的极化矢量相同,验证了本文所提三种极化投影建模方法的有效性。
表2 锥面共形阵列四种方法得到的极化矢量pki
Tab.2 Polarization vector pki obtained by four methods of cone conformal array
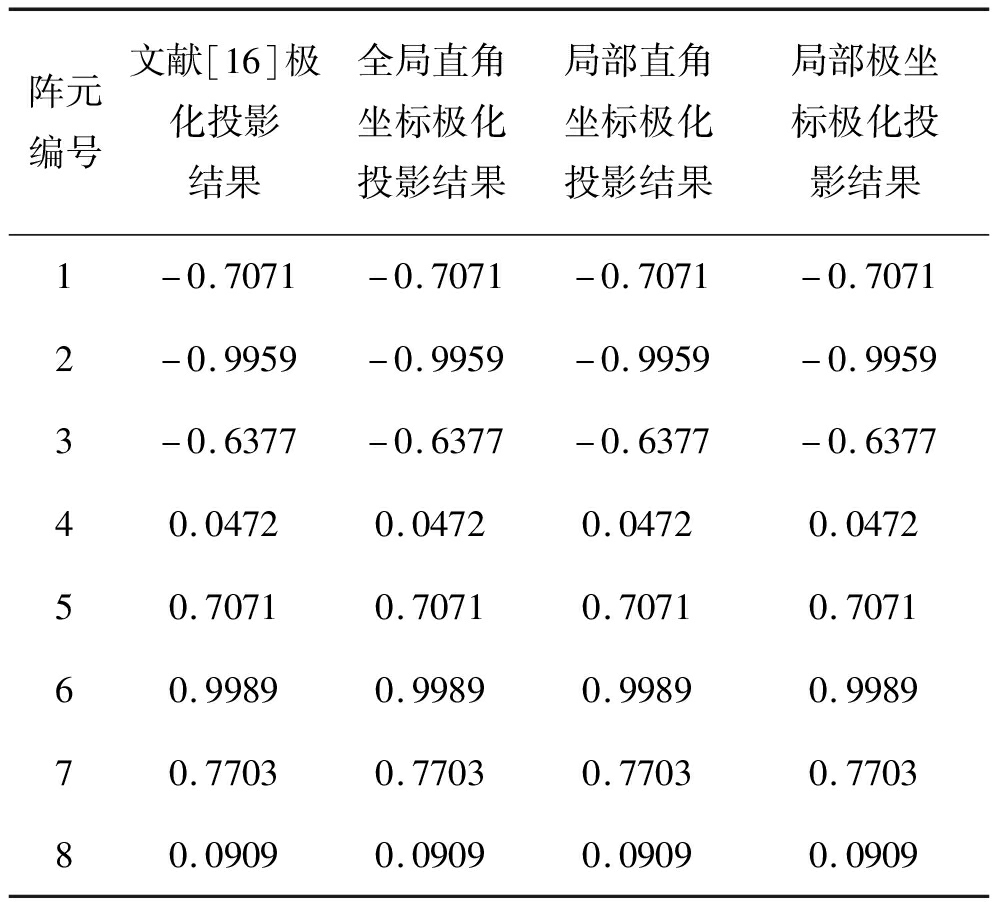
阵元编号文献[16]极化投影结果全局直角坐标极化投影结果局部直角坐标极化投影结果局部极坐标极化投影结果1-0.7071-0.7071-0.7071-0.70712-0.9959-0.9959-0.9959-0.99593-0.6377-0.6377-0.6377-0.637740.04720.04720.04720.047250.70710.70710.70710.707160.99890.99890.99890.998970.77030.77030.77030.770380.09090.09090.09090.0909
表3 柱面共形阵列四种方法得到的极化矢量pki
Tab.3 Polarization vector pki obtained by four methods of cylindrical conformal array
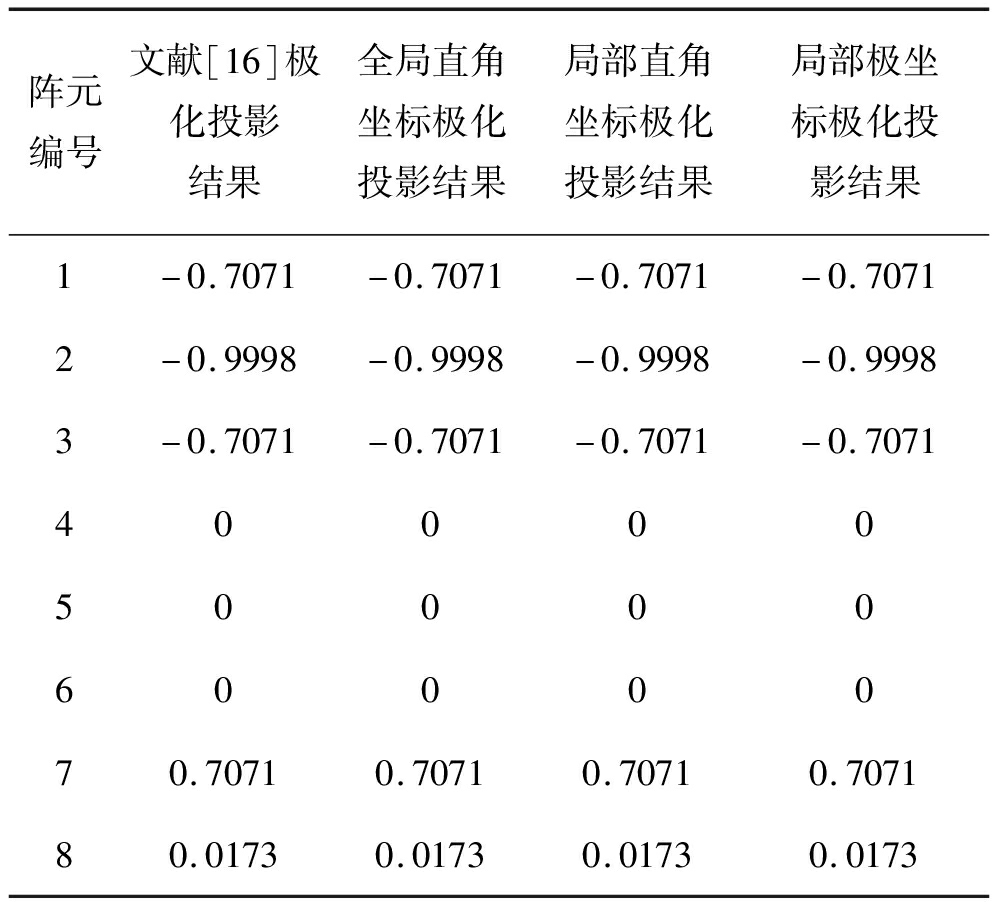
阵元编号文献[16]极化投影结果全局直角坐标极化投影结果局部直角坐标极化投影结果局部极坐标极化投影结果1-0.7071-0.7071-0.7071-0.70712-0.9998-0.9998-0.9998-0.99983-0.7071-0.7071-0.7071-0.707140000500006000070.70710.70710.70710.707180.01730.01730.01730.0173
表4 球面共形阵列四种方法得到的极化矢量pki
Tab.4 Polarization vector pki obtained by four methods of spherical conformal array
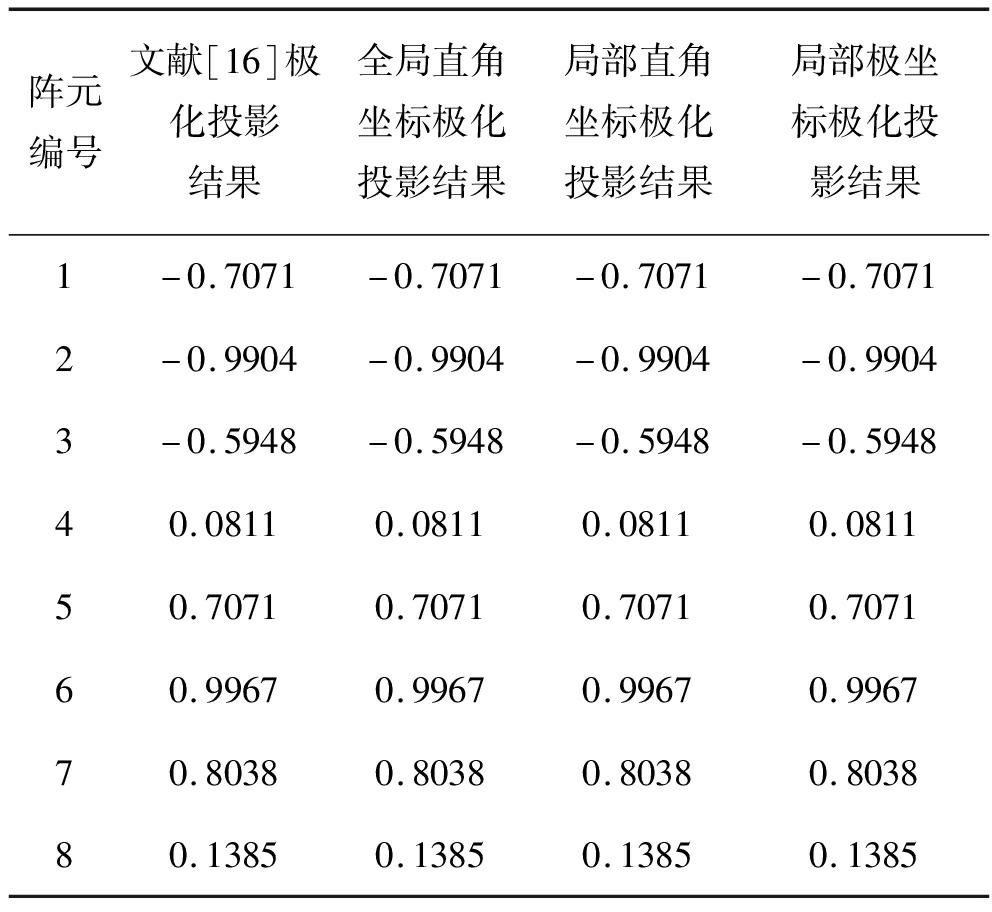
阵元编号文献[16]极化投影结果全局直角坐标极化投影结果局部直角坐标极化投影结果局部极坐标极化投影结果1-0.7071-0.7071-0.7071-0.70712-0.9904-0.9904-0.9904-0.99043-0.5948-0.5948-0.5948-0.594840.08110.08110.08110.081150.70710.70710.70710.707160.99670.99670.99670.996770.80380.80380.80380.803880.13850.13850.13850.1385
仿真实验2 全局坐标系建模方法在广义信号子空间拟合算法中的应用
为验证所提出建模方法的适用性,本文利用较有应用价值的广义信号子空间拟合算法进行验证,广义信号子空间拟合算法实现了DOA和极化信息的解耦合,相比于传统子空间类算法广义信号子空间拟合可直接进行DOA估计而无需考虑极化信息,减少计算量,且适用于相干信源,但现有文献并未对共形阵列下的广义信号子空间拟合算法进行讨论。文献[21]详细介绍了广义信号子空间拟合算法,这里不做具体展开。针对共形阵列,采用文献[21]中的表达形式,算法要求将导向矢量模型在全局直角坐标下投影,可将阵列流形重写为:
A=[Sθ1,φ1FGθ1,φ1hγ1,η1,Sθ2,φ2FGθ2,φ2hγ2,η2,…,
SθK,φKFGθK,φKhγK,ηK]
(36)
K为信源数,S为对角化空域导向矢量,F为全局直角坐标系下的方向图响应,Gθi,φi为全局坐标系下的坐标转换矩阵,hγi,ηi为全局极坐标下信号极化矢量,Gθi,φihγi,ηi为全局直角坐标系下信号极化矢量,对应式(25)。文献[21]中采用的是一般的双正交偶极子组成的极化敏感阵列,各阵元指向相同,可不考虑方向图影响,全局直角坐标下的方向图响应矩阵F退化为极化敏感矩阵,只取决于阵元摆放方式,当阵型固定,极化敏感矩阵F固定不变。而共形阵列由于阵元方向图指向不同,对于不同方向的信号,方向图响应矩阵F不同,需用欧拉旋转变换进行计算,即通过式(22)、(23)计算F,最后在全局直角坐标系下投影得到共形阵列导向矢量。
文献[21]指出,广义信号子空间拟合代价函数为:
(37)
Q=Sθ,φFθ,φGθ,φ
(38)
上式中Es为L个最大特征值对应的信号子空间,L为不相关信源个数,![]() 为矩阵Q的正交投影矩阵。
为矩阵Q的正交投影矩阵。
在仿真实验中选取柱面共形阵列,采用单极化阵元,圆环数目为1,各阵元均匀分布,阵元个数为12个,信源个数为2个,波长取0.1 m,信号形式为复正弦信号,采用相干信源,信噪比为20,快拍数取200,信号参数为(θ1,φ1,γ1,η1)=(90°,20°,45°,0°),(θ2,φ2,γ2,η2)=(90°,40°,45°,0°),假设信号均从同一平面入射,相干信源方位角谱峰搜索结果如图5所示。
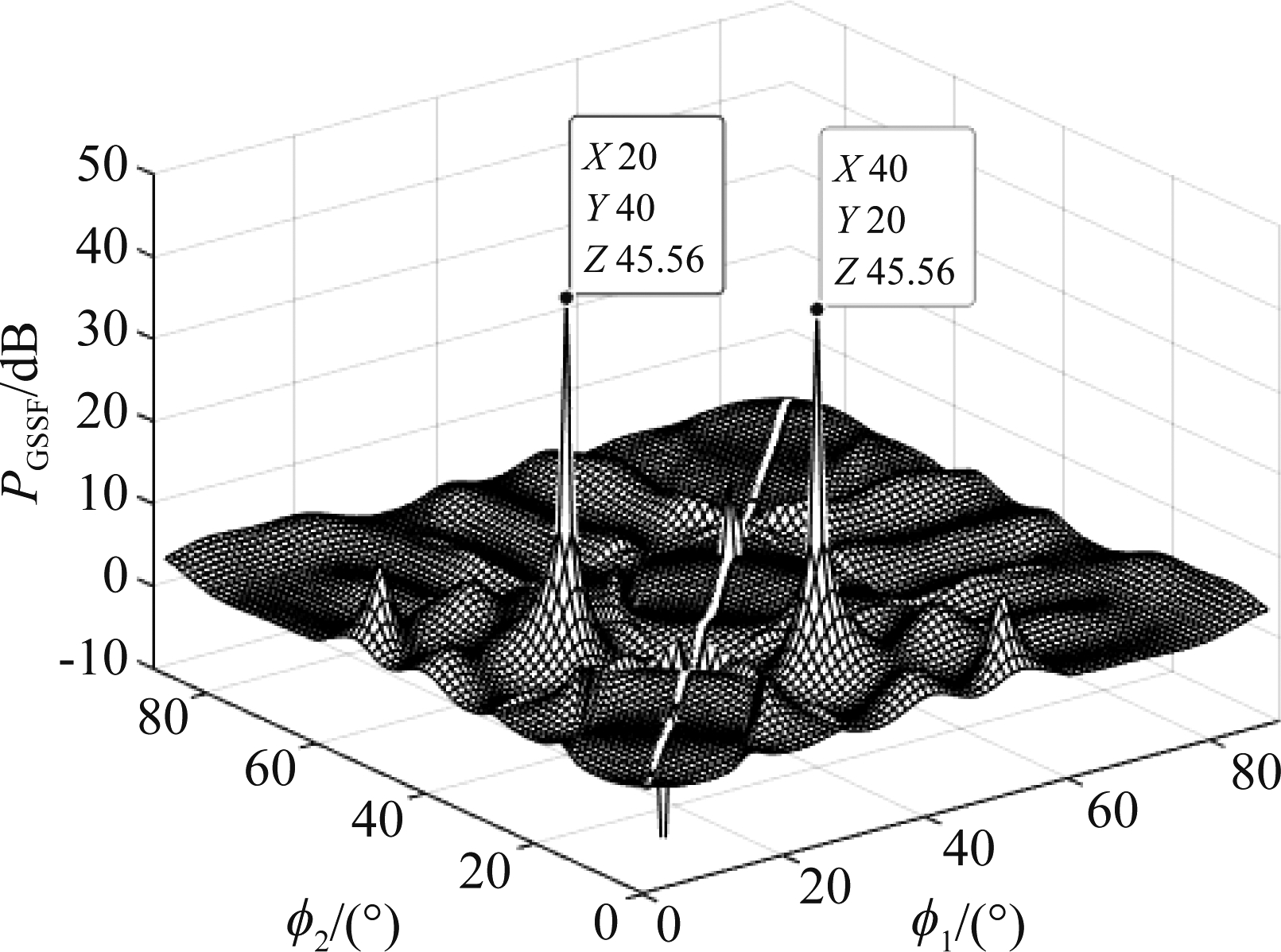
图5 广义信号子空间拟合谱峰搜索结果
Fig.5 Generalized subspace fitting spectrum peak search results
从图中可以看出,相干信源得到分辨,在预期位置出现两相干信源方位角,利用全局直角坐标系下投影对共形阵列建模可将广义信号子空间拟合算法应用于共形阵列中,验证了将广义信号子空间拟合算法用于共形阵列的可行性。
仿真实验3 时间复杂度分析
仿真条件同实验1,对四种建模方法分别进行100000次重复实验,统计计算机仿真平均运行时间,对比四种方法运行时间,结果如表5所示。
表5 四种建模方法平均消耗时间(时间:μs)
Tab.5 The average running time of the four methods of modeling(time: μs)
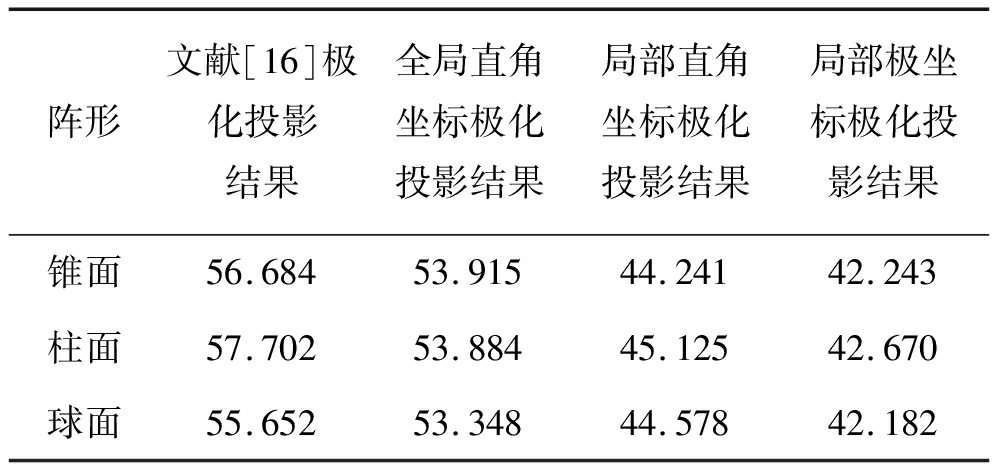
阵形文献[16]极化投影结果全局直角坐标极化投影结果局部直角坐标极化投影结果局部极坐标极化投影结果锥面56.68453.91544.24142.243柱面57.70253.88445.12542.670球面55.65253.34844.57842.182
以文献[16]中全局极坐标系极化投影所需运行时间为基准,锥面共形阵列四种建模方法所需的相对时间比为1.0∶0.95∶0.78∶0.74;柱面共形阵列四种建模方法所需的相对时间比为1.0∶0.93∶0.78∶0.74;球面共形阵列四种建模方法所需的相对时间比为1.0∶0.95∶0.80∶0.76。对比表1中四种方法所需理论相对时间和表5中四种方法所需相对时间可知,共形阵列理论建模复杂度和实际复杂度基本吻合,理论运行时间和实际运行时间的主要误差来源于方向图极化响应的运算时间,由于不同阵元方向图表达式不同,且四种方法均需计算相同的方向图极化响应,因此表1中的理论推导忽略了方向图极化响应的影响。
对比表5中不同建模方法的运行时间,本文中局部极坐标系下的投影用时最短,文献[16]方法用时最长。与理论时间相符合。
6 结论
本文针对锥面、柱面、球面等三种典型的共形阵列天线,对基于欧拉旋转的共形阵列建模方法进行了补充,提出在全局直角坐标系、局部直角坐标系、局部极坐标系下进行极化投影过程得到极化矢量的方法,丰富了共形阵列建模的理论内涵。仿真结果表明,本文所提三种建模方法与已有建模方法的结果一致,证明了方法的有效性;其中,全局坐标系下极化投影共形阵列建模方法更便于将广义信号子空间拟合、流形分离等算法应用于共形阵列,具有较好的实用价值,局部坐标系下极化投影共形阵列建模方法的计算复杂度更低,在实际应用中可根据不同的需求采取不同的建模方法。
[1] ZHANG Xiaowen, LIAO Guisheng, YANG Zhiwei, et al.Parameter estimation based on Hough transform for airborne radar with conformal array[J].Digital Signal Processing, 2020, 107.
[2] LIU Dali, LI Lei, CHEN Xinhong.Pattern synthesis of a practical conformal hydrophone array via second-order cone programming[J].Cluster Computing, 2019, 22: 8379-8386.
[3] YU Xiaomeng, ZHANG Yan, DONG Tao, et al.A novel and efficient synthesis approach on antenna radiation pattern for conformal array[C]∥2016 IEEE International Conference on Communication Systems(ICCS),2016: 1-4.
[4] LU Yiling, XIANG Yin, ZHAO Yikun, et al.Fast digital beamforming for conformal array[C]∥2019 IEEE International Conference on Signal, Information and Data Processing(ICSIDP), 2019: 1-4.
[5] WANG Zhanze, SUN Yuze, LI Shuai, et al.Null widening method for conformal array based on covariance matrix enhancement[J].The Journal of Engineering, 2019, 2019(60): 6390-6393.
[6] 刘帅,周洪娟,金铭,等.锥面共形阵列天线的极化-DOA估计[J].系统工程与电子技术,2012,34(2):253-257.
LIU Shuai, ZHOU Hongjuan, JIN Ming, et al.Polarization-DOA estimation for conical conformal array antennas[J].Systems Engineering and Electronics, 2012, 34(2): 253-257.(in Chinese)
[7] 周义建,王布宏,齐子森, 等.柱面共形阵列天线WSF算法DOA估计性能分析[J].空军工程大学学报(自然科学版),2008(4):74-78.
ZHOU Yijian, WANG Buhong, QI Zisen, et al.Performance analysis of WSF algorithm DOA estimation of cylindrical confomal array antenna[J].Journal of Air Force Engineering University(Natural Science Edtion), 2008(4): 74-78.(in Chinese)
[8] 刘帅,韩勇,闫锋刚,等.锥面共形阵列极化-DOA估计的降维MUSIC算法[J].哈尔滨工业大学学报,2017,49(5):36-41.
LIU Shuai, HAN Yong, YAN Fenggang, et al.Polarization-DOA estimation for conical conformal array based on dimension reduced MUSIC[J].Journal of Harbin Institute of Technology, 2017, 49(5): 36-41.(in Chinese)
[9] LAN Xiaoyu, WANG Lening, WANG Yupeng, et al.Tensor 2-D DOA estimation for a cylindrical conformal antenna array in a massive MIMO system under unknown mutual coupling[J].IEEE Access, 2018, 6: 7864-7871.
[10] 张羚,郭英,邹峰,等.锥面共形阵列非圆信号2D-DOA估计[J].系统工程与电子技术,2018,40(5):989-996.
ZHANG Ling, GUO Ying, ZOU Feng, et al.2D-DOA estimation on conical conformal array antennas for non-circular signals[J].Systems Engineering and Electronics, 2018, 40(5): 989-996.(in Chinese)
[11] FERRARA E, PARKS T, Direction finding with an array of antennas having diverse polarizations[J].IEEE Transactions on Antennas and Propagation, 1983, 31(2): 231-236.
[12] 庄钊文,徐振海,肖顺平,等.极化敏感阵列信号处理[M].北京:国防工业出版社,2005:200-226.
ZHUANG Zhaowen, XU Zhenhai, XIAO Shunping, et al.Signal processing of polarization sensitive Array[M].Beijing: National Defense Industry Press, 2005: 200-226.(in Chinese)
[13] YANG Peng, YANG Feng, NIE Zaiping.DOA estimation with sub-array divided technique and interporlated ESPRIT algorithm on a cylindrical conformal array antenna[J].Progress in Electromagnetics Research, 2010, 103: 201-216.
[14] Burger H A.Use of euler rotation angles for generating antenna patterns[J].IEEE Antennas and Propagation Magazine, 1995, 37(2): 56-63.
[15] MILIGAN T.More applications of euler rotation angles[J].IEEE Antennas and Propagation Magazine, 1999, 41(4): 78-83.
[16] 王布宏,郭英,王永良,等.共形天线阵列流形的建模方法[J].电子学报,2009,37(3):481-484.
WANG Buhong, GUO Ying, WANG Yongliang, et al.Array manifold modeling for conformal array antenna[J].Acta Electronica Sinica, 2009, 37(3): 481-484.(in Chinese)
[17] 齐子森,郭英,姬伟峰,等.锥面共形阵列天线盲极化DOA估计算法[J].电子学报,2009,37(9):1919-1925.
QI Zisen, GUO Ying, JI Weifeng.et al.Blind DOA estimation algorithm for conical conformal array antenna with respect to polarization diversity[J].Acta Electronica Sinica, 2009, 37(9): 1919-1925.(in Chinese)
[18] 匡开锋,徐友根,刘志文.共形阵列非圆信号波达方向估计算法[J].信号处理,2015,31(5):551-558.
KUANG Kaifeng, XU Yougen, LIU Zhiwen.Direction of arrival estimation for noncircular signals using conformal array[J].Journal of Signal Processing, 2015, 31(5): 551-558.(in Chinese)
[19] 侯青松,郭英,王布宏,等.共形阵列天线振动条件下稳健的DOA估计及位置误差校正[J].信号处理,2010,26(11):1756-1760.
HOU Qingsong, GUO Ying, WANG Buhong, et al.Robust direction finding and position errors calibration for conformal array antenna in the presence of vibration[J].Journal of Signal Processing, 2010, 26(11): 1756-1760.(in Chinese)
[20] ZHUANG Jie, XIONG Hao, WANG Wei, et al.Application of manifold separation to parametric localization for incoherently distributed sources[J].IEEE Transactions on Signal Processing, 2018, 66(11): 2849-2860.
[21] 徐友根,刘志文.广义信号子空间拟合角度-极化联合估计[J].北京理工大学学报,2010,30(7):835-839.
XU Yougen, LIU Zhiwen.Joint angle-polarization estimation via generalized signal-subspace fitting[J].Transactions of Beijing Institute of Technology, 2010, 30(7): 835-839.(in Chinese)


