1 引言
谐波信号参数估计是统计信号处理和时间序列分析领域的典型问题。许多实际问题都可以建模为谐波信号模型,如雷达、声呐、无线通信和地震数据等[1-5]。谐波参数估计方法主要有参数化方法和非参数化方法。
参数化方法通常需要信号的先验信息,如信号模型假设。参数化法主要有:MUSIC方法、ESPRIT方法和非线性最小二乘方法等。MUSIC方法利用协方差矩阵的信号子空间和噪声子空间的正交性获得信号参数的估计。该方法参数估计精度较高,但在信噪比较小时信号分辨率低,且具有较大的计算量[6]。ESPRIT方法应用信号子空间的旋转不变性得到谐波参数估计,该方法计算量较MUSIC方法小,但信噪比较大时,估计精度低于MUSIC方法[7]。非线性最小二乘方法利用总残差最小作为目标函数获得信号的参数估计,该方法具有良好的统计性能,但需要已知模型阶数,且无法获得全局最优解[8]。
非参数化方法直接利用观测数据或观测数据自相关延迟序列得到信号的参数估计。非参数化方法通常不需要观测过程的先验信息,因此非参数化方法更具有鲁棒性。非参数化估计方法主要有:极大似然估计法、周期图法和三步迭代估计法等。极大似然法利用观测信号的联合密度函数的最大化来估计谐波信号参数,当样本容量足够大时,其估计结果为无偏估计[9]。周期图估计法应用离散傅里叶变换得到谐波参数的估计,该方法简单易行,但估计精度不高[10]。三步迭代估计法将谐波参数估计分为两个过程,首先利用傅里叶变换得到参数的初估计,然后构造基于观测信号的统计量对参数进行迭代更新估计。该方法只需三次迭代就能达到与最小二乘法相同的估计精度与渐近分布[11]。
随着稀疏信号表示和压缩感知的发展[12-13],近年来,国内外学者结合参数化方法和非参数化方法发展了半参数化方法,并应用于雷达等领域[14-15]。半参数化方法中有一类稀疏估计方法,该类方法只需待估参数满足稀疏性的弱假设。但大多数稀疏估计方法在权衡数据拟合和稀疏性之间需要超参数的选择,超参数的选择一般比较困难[14-15]。2011年,Stoica等提出了一种基于加权协方差拟合准则的稀疏迭代协方差估计(sparse iterative covariance-based estimation, SPICE)的稀疏估计方法[16],后来有学者将其应用到雷达和DOA估计等领域[17-19]。SPICE方法基于加权协方差拟合准则构建目标函数获得功率谱参数的估计,不需要超参数的选择,具有高分辨率和全局收敛性。但该方法获得的功率谱参数估计值与真实值之间存在一定的偏差。2019年,Yu Zheng等人对基于SPICE方法提出了一种改进的SPICE方法用于DOA估计。该方法首先利用SPICE方法得到DOA参数的初估计,然后利用渐近最小方差准则对功率谱参数进行迭代校正,因此提高了功率谱参数估计的精度[15],但当观测数据长度较大时,该方法计算量较大。受Capon方法和振幅相位估计方法(Gohberg-Semencul, G-S)因子分解的启发[20-21],本文提出了一种基于稀疏迭代协方差估计的谐波频率与功率谱参数的快速估计方法。所提方法充分利用了观测数据协方差矩阵的Toeplitz结构和导向矢量的指数形式。该方法通过SPICE方法得到谐波信号频率和功率谱参数的初估计,然后基于渐近最小方差准构造功率谱参数表达式对功率谱进行迭代校正。为节约参数的估计时间,在参数迭代过程中,采用快速傅里叶变换对矩阵求逆和矩阵与向量相乘部分进行求解。仿真实验表明,本文所提出方法对谐波信号的功率谱和频率估计精度较高,同时计算效率较高。
2 谐波信号模型
考虑如下的谐波模型:
(1)
其中:y(n)为观测数据,ε(n)为加性噪声,N为样本数,
为谐波分量个数, fk为第k个频率,ak为第k个复振幅。另外,模型(1)满足以下假设:
(i)fk≠fl,k≠l且fk∈(0,2π);
(ii)令
则x(n)与ε(n)不相关,且{ak}各分量间不相关;
(iii)ε(n)为高斯随机序列,且ε(n)～N(0,σ2)。
本文的主要目的从观测数据{y(n); n=1,2,…,N}估计频率{fk}和功率谱{|ak|2}。
为了得到模型(1)中的频率和功率谱参数估计,我们将式(1)改写为:
(2)
其中,C为网格数,wc=2πc/C为第c个网格对应的频率,uc为第c个网格对应的复振幅。当网格数C充分大时,即C≫K,模型(1)中频率参数fk就有可能对应模型(2)中网格上的某个值wc,功率谱|ak|2对应模型(2)中网格上的某个值|uc|2[16]。
进一步,式(2)的矩阵形式为:
y=Bu+ε
(3)
在式(3)中,y=[y(1),y(2),…,y(N)]T,B=[b0,b1,…,bC-1],bc=[eiwc,eiwc2,…,eiwcN]T, u=[u0,u1,…,uC-1]T,ε=[ε(1),ε(2),…,ε(N)]T,(·)T表示转置。
由假设条件(i)和(ii),可得到观测数据的协方差矩阵R为:
R=E{yy*}=BPB*+σ2IN
(4)
其中,E{·}代表数学期望,(·)*代表共轭转置,IN表示N阶单位矩阵。在式(4)中, P=diag{p0,p2,…,pC-1},其中pc=|uc|2,diag{·}表示对角矩阵。
为便于问题的讨论,将协方差矩阵R表示为:
(5)
其中,P1=diag{p0,p2,…,pC-1,σ2,…,σ2}
diag{p0,p2,…,pC-1,pC,…,pC+N-1},B1=[B,IN][b0,b1,…,bC-1,bC,…,bC+N-1]。
3 基于稀疏迭代协方差估计的谐波频率与功率谱的快速估计
3.1 SPICE算法
考虑如下基于加权协方差拟合准则的目标函数[16]:
(6)
其中,c=1,…,C+N-1,‖·‖F代表Frobenius范数,(·)-1/2表示矩阵的Hermitan正定方根,样本协方差矩阵
进一步,式(6)可表示为如下优化问题[16]:
(7)
其中
表示矩阵的迹,‖·‖表示Euclidean范数。
显然,式(7)可转化为如下优化问题:
(8)
其中dc=‖bc‖2/‖y‖2。
因为
则‖y‖2是
的无偏一致估计。于是式(8)可表示为如下约束最小化问题[16]:
(9)
定义β=pB*R-1y=[β0,β1,…,βC+N-1],式(9)可表示为:
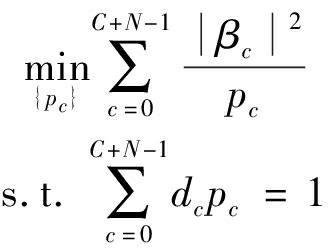
(10)
进一步,根据柯西-施瓦茨不等式可得{pc;c=0,1,…,C-1}的闭式解[16]:
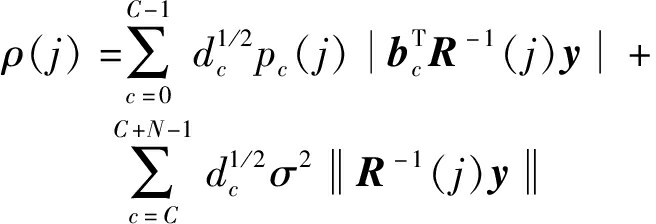
(11)
(12)
(13)
其中j表示迭代次数。下面给出基于SPICE方法的谐波信号频率和功率谱估计步骤如下:
步骤1 输入y,令B1=[b0,b1,…,bC+N-1],其中bc=[eiwc,eiwc2,…,eiwcN]T,wc=2πc/C,c=0,1,…,C+N-1,计算dc=‖bc‖2/‖y‖2,设η=10-3;
步骤2 初始化
其中
为{pc(0);c=0,1,…,C-1}中前N个最小的集合;
步骤3 构造矩阵
其中P1(j)=diag{p0(j),…,pC-1(j),σ2(j),…,σ2(j)};
步骤4 通过式(11)计算ρ(j);
步骤5 由式(12)和式(13)更新σ2(j)和p(j),其中p(j)=[p0(j),p1(j),...,pC-1(j)];
步骤6 重复步骤3～5,当‖p(j)-p(j-1)‖/‖p(j)‖≤η且‖σ2(j)-σ2(j-1)‖/‖σ2(j)‖≤η时,则中止迭代更新,输出
和
否则,继续重复步骤3～5;
步骤7 根据功率谱的前K个峰值得到功率谱和频率估计。
3.2 功率谱迭代校正估计
由3.1节可知,SPICE方法不需要选择超参数,对谐波信号的频率能进行很好的估计,但是该方法对谐波信号的功率谱估计存在一定的偏差。基于此,文献[17]提出了一种基于渐近最小方差(asymptotically minimum variance, AMV)准则的改进的SPICE方法,并应用于DOA功率谱估计,本文将其命名为校正稀疏迭代协方差估计(adjust sparse iterative covariance-based estimation, ASPICE)方法。
首先,将协方差矩阵R向量化表示为:
vec(R)r(p)
(14)
假设p可从r(p)中识别,即满足p1=p2⟺r(p1)=r(p2),则可得关于p的下界[22]:
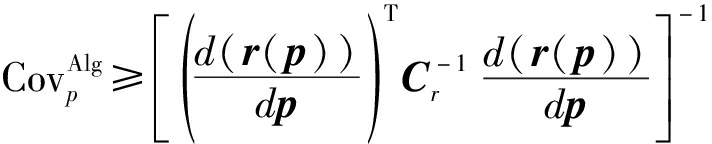
(15)
其中:d(·)/d(·)表示求导运算, Alg表示与r(p)相关的算法。在式(15)中,Cr=R*⊗R,其中⊗表示Kronecker积。由文献[23],式(15)关于p的下界可转化为如下关于r(p)的非线性最小二乘目标函数的解:
(16)
其中
由式(16),可得功率谱{pc;c=0,1,…,C-1}迭代校正表达式[17]:
(17)
tr(R-1(j))/tr(R-2(j))
(18)
综上所述,基于ASPICE方法的谐波频率和功率谱估计具体步骤如下:
步骤1 通过SPICE算法得到
和σ2(0);
步骤2 构造矩阵
其中P1(j)=diag{p0(j),…,pC-1(j),σ2(j),…,σ2(j)};
步骤3 由式(17)和式(18)更新σ2(j)和p(j),其中p(j)=[p0(j),p1(j),...,pC-1(j)];
步骤4 重复步骤3～5,满足‖p(j)-p(j-1)‖/‖p(j)‖≤η和‖σ2(j)-σ2(j-1)‖/‖σ2(j)‖≤η时,终止迭代更新,输出p和σ2,否则继续重复步骤2～3;
步骤5 根据功率谱的前K个峰值得到功率谱和频率估计。
3.3 F-ASPICE算法
上一节,我们给出了ASPICE算法关于谐波频率和功率谱的估计,相比于SPICE算法,ASPICE算法不仅对谐波信号的频率能进行很好的估计,并且提高了功率谱的估计精度,但当数据长度较大时,该算法的计算量较大。为保证谐波参数的估计精度较高同时计算量较小,本文受文献[20-21]启发,对ASPICE算法进行改进,并将改进后的算法命名为快速-校正稀疏迭代协方差估计(fast-adjust sparse iterative covariance-based estimation, F-ASPICE)。通过分析,我们发现ASPICE算法的计算量主要源于每次迭代中与协方差矩阵R相关的计算。
1)对协方差矩阵R的时间计算复杂度分析。在每次迭代中,如果直接利用式(5),即矩阵直接相乘得到协方差矩阵R,时间计算复杂度为O(CN2+C2N)。由于协方差矩阵R可表示为R=BPB*+σ2IN,而矩阵BPB*又可表示为:
(19)
其中,
显然,R具有Toeplitz矩阵结构。于是,R可通过快速离散傅里叶变换(Fast Discrete Fourier Transform, FFT)计算得到:
R=Toeplitz(r*,r)+σ2IN
(20)
令r=[r0,r1,...,rN-1],由于
则r可由下式可得:
r=((FFT(p)C-1)1∶N
(21)
也就是说,
可由
进行C点FFT后保留前N个得到。由式(20)～(21),协方差矩阵R的计算量来源于FFT的计算,其计算复杂度为O(Clog2C)。
2)对矩阵R-1的时间计算复杂度分析。在每次迭代中,若直接计算R-1,计算时间复杂度为O(N3)。由于R=BPB*+σ2IN,则R可改写为:
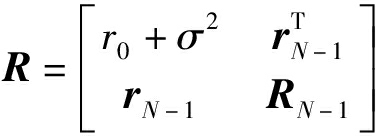
(22)
其中
由文献[21],R-1可由Gohberg-Semencul(G-S)分解可得:
(23)
其中
为Toeplitz下三角矩阵,ti为N维列向量,ZN为N阶矩阵,其具体形式为:
(24)
令
其中
表示为向量的倒置,如
在式(23)中,为得到LN(ti,ZN),i=1,2,必须要确定wN-1和αN-1。下面利用Levinson-Durbin algorithm(LDA)算法[20]确定wN-1和αN-1,具体步骤如下:
步骤1 初始化
和α1=r0+σ2+r1w1;
步骤2 计算
其中t=2,...,N-1;
步骤3 由步骤2可得αN-1,wN-1。
由上可知协方差矩阵R-1的时间计算复杂度为O(N2)。
3)对矩阵R-1y的时间计算复杂度分析。在每次迭代中,先直接计算R-1,计算时间复杂度为O(N3),再计算R-1y,则R-1y计算复杂度为O(N3+N2)。对R-1进行G-S分解后,R-1y可以表示成Toeplitz矩阵乘积和向量乘积之和,由于LN(t1,ZN)和LN(t2,ZN)均为Toeplitz下三角矩阵,故可将LN(t1,ZN)和LN(t2,ZN)分别扩充为循环矩阵C1和C2,记
和
分别表示循环矩阵
和
的第一列,将y扩充为y1 
令
由文献[21]知,由FFT和快速离散傅里叶反变换(Inverse Fast Fourier Transform,IFFT)可快速计算Toeplitz矩阵和向量的乘积,α可通过下式快速可得:
(25)
R-1y可取α的前N个分量得到,即
R-1y=(α)1∶N
(26)
由式(23)～(26)可知,R-1y时间计算复杂度为O(N2+Nlog2N)。
4)关于矩阵
的计算复杂度分析。在每次迭代中,若直接计算将
与R-1y相乘,其
的时间计算复杂度为O(NC)。
考虑到
的指数形式,对向量R-1y可采用FFT快速得到
即
(27)
由式(27)可知,的计算复杂度为O(Clog2C)。
综上分析, ASPICE算法的每次迭代的时间计算复杂度为O(N3+C2N+CN2),而本文提出的F-ASPICE算法的每次迭代的时间计算复杂度为O(N2+Clog2C+Nlog2N)。两种方法计算复杂度与观测长度N和网格数C相关,相比于 ASPICE算法,本文所提算法计算复杂度低于ASPICE算法一个数量级。ASPICE算法和F-ASPICE算法的理论时间复杂度分析如表1所示。基于F-ASPICE算法的频率和功率谱估计具体流程如下图1所示。
表1 ASPICE算法和F-ASPICE算法时间复杂度分析
Tab.1 Time complexity analysis of ASPICE algorithm and F-ASPICE algorithm
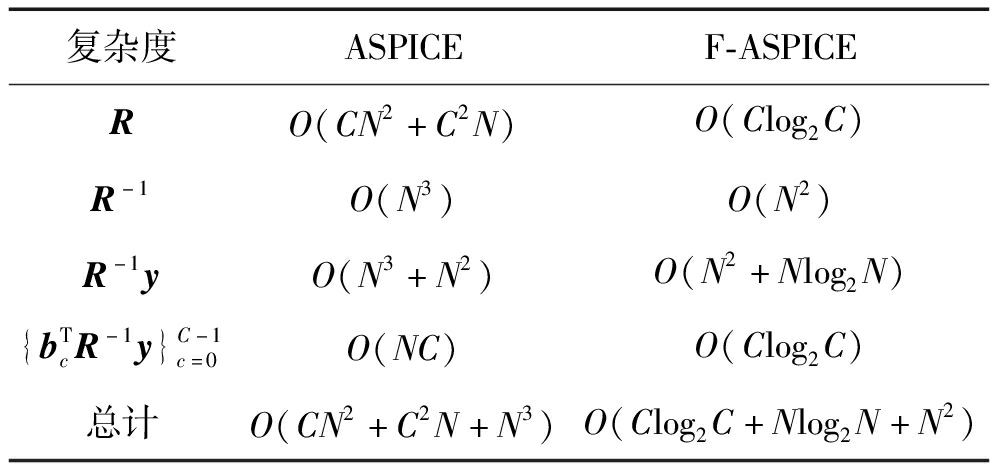
复杂度ASPICEF-ASPICERO(CN2+C2N)O(Clog2C)R-1O(N3)O(N2)R-1yO(N3+N2)O(N2+Nlog2N){bTcR-1y}C-1c=0O(NC)O(Clog2C)总计O(CN2+C2N+N3)O(Clog2C+Nlog2N+N2)
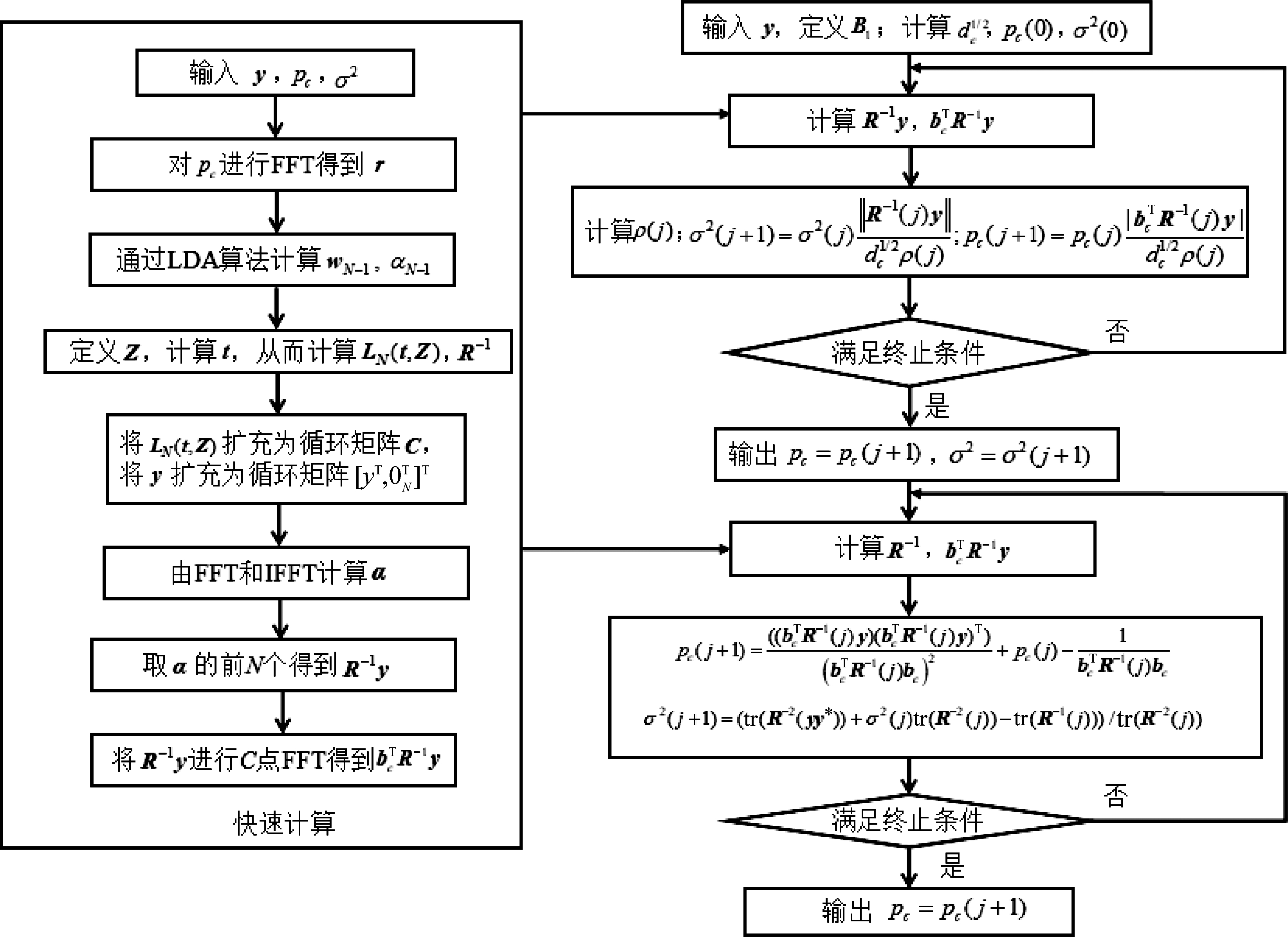
图1 基于F-ASPICE算法估计流程图
Fig.1 Estimation flow chart based on F-ASPICE algorithm
4 仿真实验
为验证本文所提方法的有效性,我们进行如下的仿真实验,并选用SPICE算法和ASPICE算法进行比对。考虑如下的谐波模型
(28)
其中, f1=0.30×2π, f2=0.35×2π, f3=0.5×2π, f4=0.55×2π,a1=2eiφ1,a2=3eiφ2, a3=2.5eiφ3,a4=3.5eiφ4,{φk;k=1,2,3,4}在[0,2π]服从独立同分布的均匀分布。加性噪声{ε(n)}是一列独立同分布的高斯随机变量,且{ε(n)}～N(0,σ2)。
在仿真实验中,信噪比(Signal-Noise-Ratio,SNR)定义为:
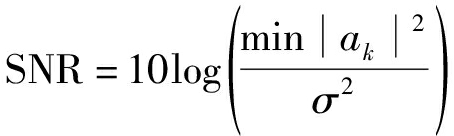
(29)
为考虑参数的估计结果,在所有仿真实验中,我们采用100次独立重复的实验,得到参数的均方根误差(Root-Mean-Square Error, RMSE)和对数均方根误差log(RMSE)。本节所有的计算均在Intel Core 2.67 GHz 处理器和3.25 GB RAM 惠普台式计算机上使用可编程式数学软件MATLAB7.1实施。
1)网格数C的选择
为验证不同网格数C下,本文所提算法的估计精度,我们考虑SNR=5 dB,观测数据长度分别为N=100和300时,取网格数C=N,2N,3N和4N四种不同情形下,三种不同算法估计精度。图2(a)展示了SPICE算法,ASPICE算法和F-ASPICE算法在N=100和SNR=5 dB时,取不同网格数频率参数估计的log(RMSE)曲线图。图2(b)展示了三种算法在N=300和SNR=5 dB时,取不同网格数频率参数估计的log(RMSE)曲线图。图3(a)和(b)分别为三种不同算法在N=100和 SNR=5 dB时以及N=300和 SNR=5 dB时,取不同网格数的功率谱参数估计RMSE曲线图。
从图2和图3我们能够看到,随着网格数的增加,三种算法得到的频率和功率谱的均方根误差不断减小。并且,在C≥2N时,即网格数大于等于两倍数据长度后,参数的均方根误差几乎没有变动,即并不是网格数取得越大,参数的估计精度就越高,因此,为节约计算时间,在后续的实验中,我们将取网格数为数据长度的两倍,即C=2N。另外,从图2和图3可知,三种算法所得频率估计精度较高,但利用本文算法得到的频率参数估计精度略低于其他两种算法;对于功率谱参数的估计,ASPICE算法估计精度最高,本文所提F-ASPICE算法次之,SPICE算法估计精度最差。
图2 三种算法基于不同网格数下的频率估计的log(RMSE)
Fig.2 Three algorithms are based on the log(RMSE)of frequency estimation with different grid numbers
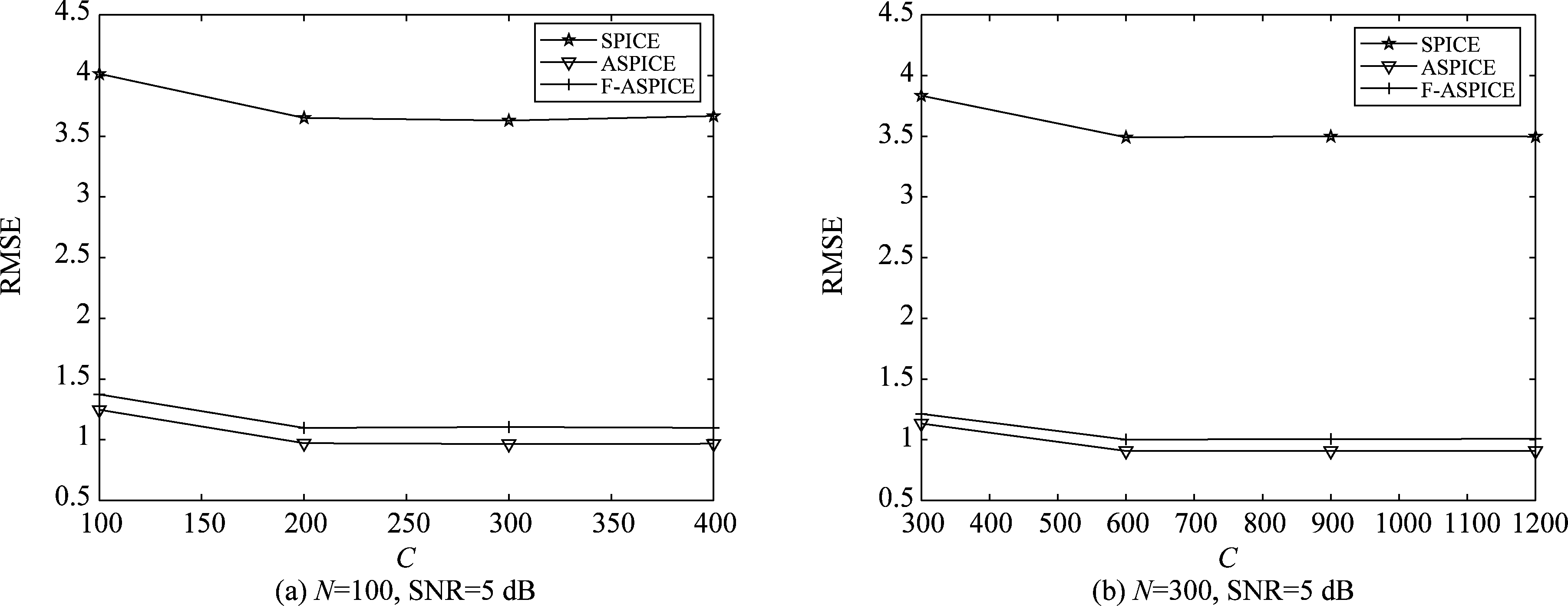
图3 三种算法基于不同网格数下的功率谱估计的RMSE
Fig.3 Three algorithms are based on the RMSE of power spectrum estimation with different grid numbers
2)参数估计
图4和图5展现了不同信噪比情形下,观测数据长度N=100,网格数C=2N时三种不同算法的频谱图。图4和图5的横坐标均为归一化后的频率,纵坐标为功率谱。从以上实验结果可知,随着信噪比的增加,三种算法得到的参数估计精度越高;在不同信噪比下,三种算法都能很好的估计频率参数;但对谐波功率谱参数的估计,在信噪比为5 dB时,SPICE算法估计较差,ASPICE和F-ASPICE两种算法的估计精度相当。
图4 N=100,SNR=5 dB时,三种算法的频谱图
Fig.4 Spectrum graphs of the three algorithms with N=100 and SNR=5 dB
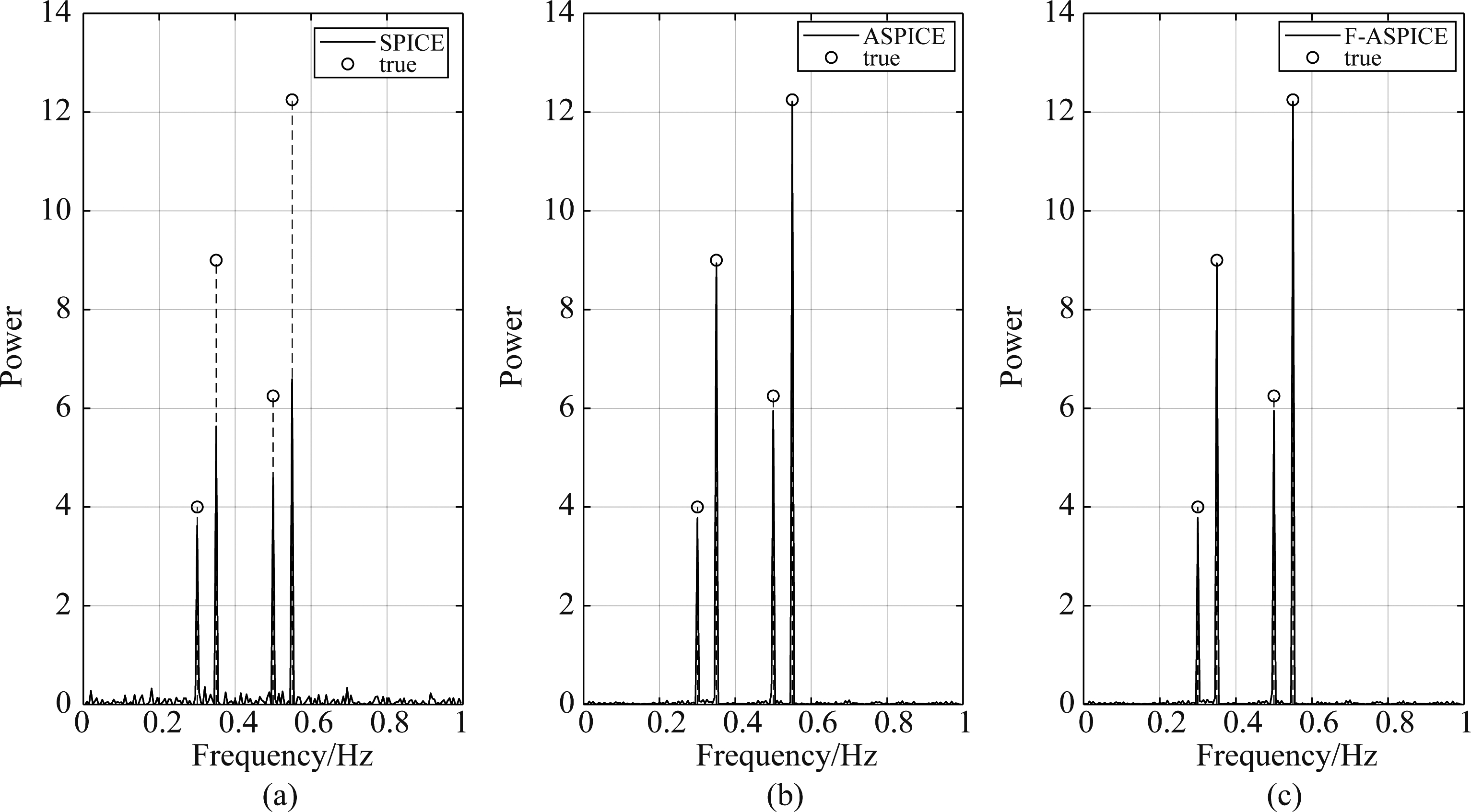
图5 N=100,SNR=10 dB时,三种算法的频谱图
Fig.5 Spectrum graphs of the three algorithms with N=100 and SNR=10 dB
为进一步考察数据长度和信噪比对参数估计的影响,图6展示了数据长度N=100和N=200时,三种算法在不同信噪比下功率谱估计的RMSE。图6(a)为观测数据长度N=100时,SPICE算法、ASPICE算法和F-ASPICE算法功率谱估计的RMSE随SNR变化曲线图。图6(b)为观测数据长度N=300时,三种算法功率谱估计的RMSE随SNR变化曲线图。从图6我们可以看到,随着数据长度的增加,三种算法的均方根误差越小;随着信噪比的增大,三种算法的均方根误差越小,且SPICE算法功率谱估计的均方误差最大,本文所提F-ASPICE算法功率谱估计的均方误差和ASPICE算法功率谱估计的均方误差相当。
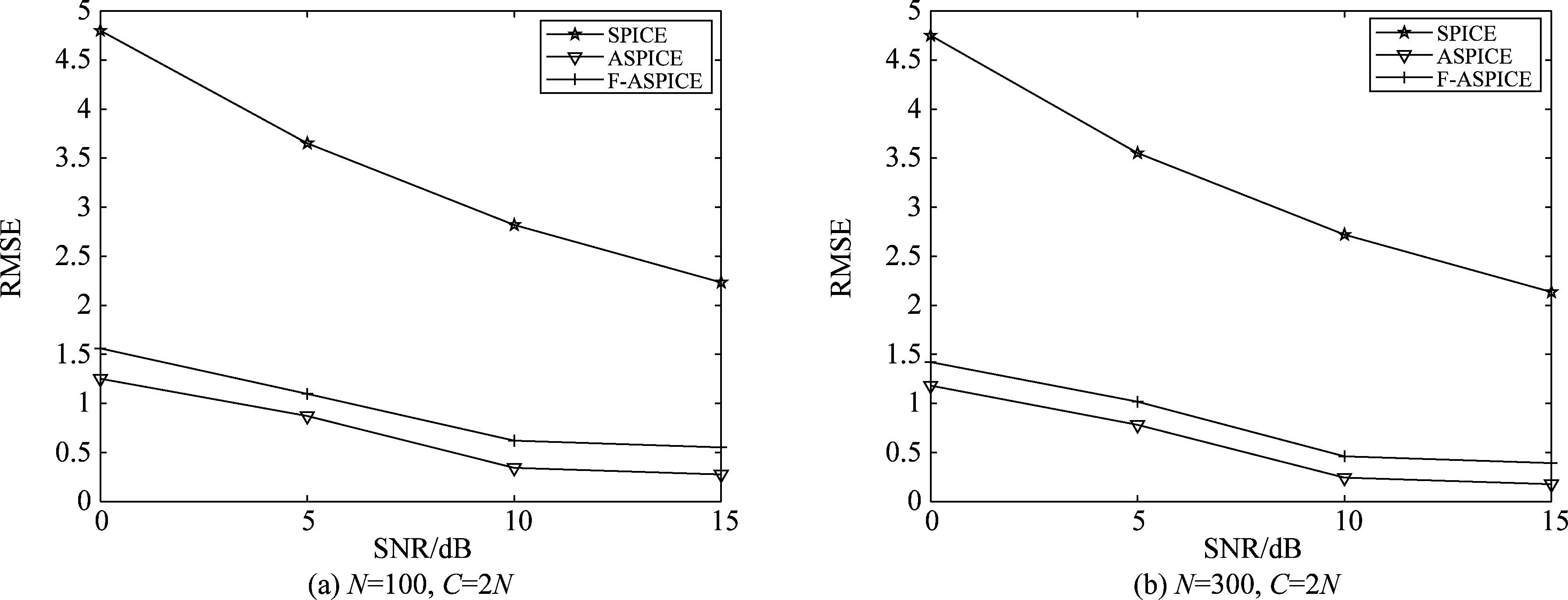
图6 不同信噪比下三种算法功率谱估计的RMSE
Fig.6 RMSE of power spectrum estimation of three algorithms with different SNR
3)计算复杂度
为比较SPICE算法,ASPICE算法和F-ASPICE算法时间计算复杂度,本文分别在信噪比SNR=0 dB,SNR=5 dB时,比较三种算法在不同观测数据长度下的运行时间。图7(a)为SNR=0 dB时,SPICE算法,ASPICE算法和F-ASPICE算法的运行时间随着数据长度变化的曲线图。图7(b)为SNR=5dB时,SPICE算法、ASPICE算法和F-ASPICE算法的运行时间随着数据长度变化的曲线图。从图7可以看出,信噪比对不同算法的运行时间没有影响;随着数据长度的增加,SPICE和ASPICE算法运行时间呈指数增长,但本文所提算法运行时间增加缓慢,当SNR=0 dB和数据长度N=900时,SPICE算法需要2010.9 s,ASPICE算法需要2698.5 s,而本文所提算法仅需688.56 s,因而证实了本文所提算法的计算效率更高。
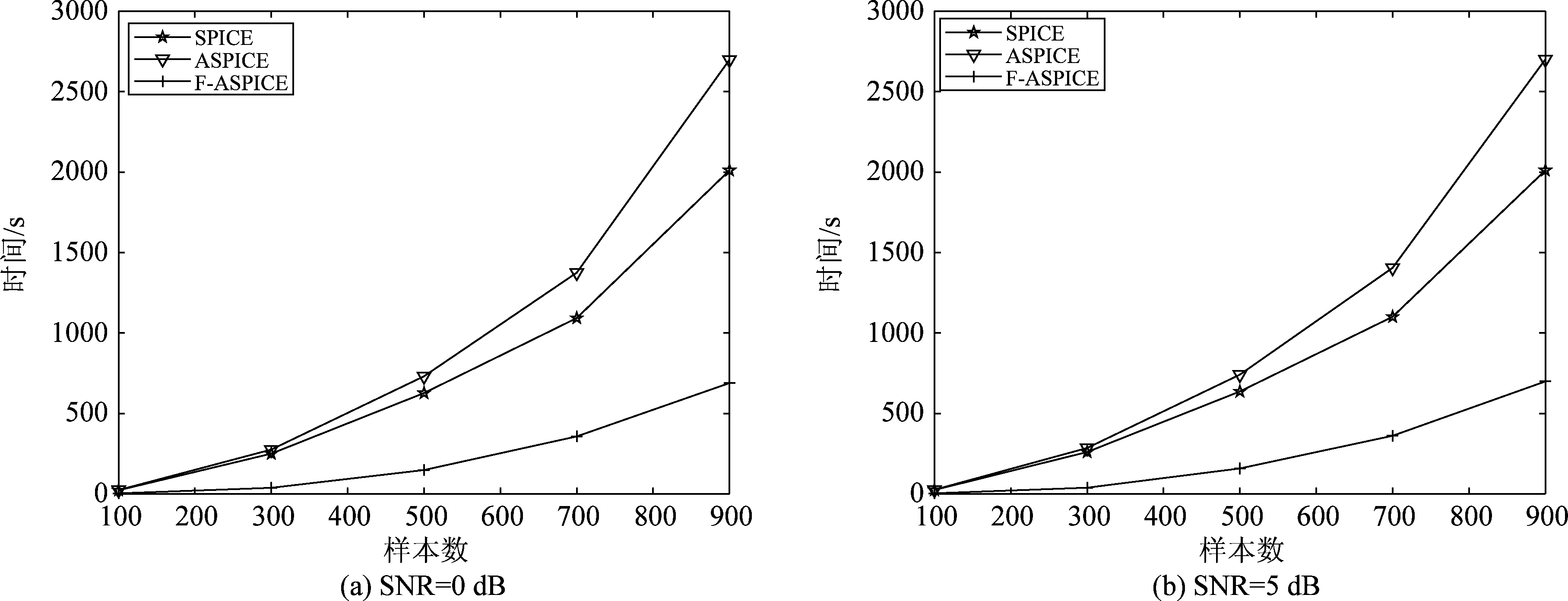
图7 三种算法在不同数据长度下的运行时间
Fig.7 The running time of the three algorithms at different data lengths
5 结论
本文研究了谐波信号的频率和功率谱参数估计。利用渐近最小方差准则,以及观测数据协方差矩阵的Toeplitz结构和导向矢量的指数形式,提出了一种基于稀疏迭代协方差矩阵的谐波信号功率谱和频率参数的快速估计方法。仿真实验表明,本文所提算法对谐波信号的功率谱和频率估计精度较高,同SPICE算法和ASPICE算法相比,本文提出的算法具有更高的计算效率。如何将本文方法推广到二维谐波的参数估计将作为我们下一步研究的方向。
[1] 王洪雁, 于若男.基于稀疏和低秩恢复的稳健DOA估计方法[J].电子与信息学报, 2020, 42(3): 589-596.
WANG Hongyan, YU Ruonan.Sparse and low rank recovery based robust DOA estimation method[J].Journal of Electronics & Information Technology, 2020, 42(3): 589-596.(in Chinese)
[2] DAI Z G, LIU Z H, WANG J Y.Iterative adaptive approach for seismic data restoration[J].Journal of Seismic Exploration, 2019, 28(4): 333-345.
[3] 代志刚, 刘智慧, 王锦妍.基于迭代最小化稀疏学习的三维地震数据重建[J].石油地球物理勘探, 2020, 55(1): 36-45,5.
DAI Zhigang, LIU Zhihui, WANG Jinyan.3Dseismic data reconstruction based on sparse learning via iterative minimization[J].Oil Geophysical Prospecting, 2020, 55(1): 36-45,5.(in Chinese)
[4] 杨鑫, 郭英.基于空时频协方差矩阵重构的高效跳频信号DOA估计[J].信号处理, 2020, 36(2): 250-256.
YANG Xin, GUO Ying.Efficient frequency hopping signal DOA estimation based on spatial time-frequency covariance matrix reconstruction[J].Journal of Signal Processing, 2020, 36(2): 250-256.(in Chinese)
[5] HAMOULEH KHEIROLLAHPOUR K, MAHMOUDI A, DUMITRESCU B.DOA estimation in the autocorrelation domain for coprime array[J].Digital Signal Processing, 2021, 110: 102940.
[6] SCHMIDT R.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.
[7] ROY R, PAULRAJ A, KAILATH T.ESPRIT——A subspace rotation approach to estimation of parameters of cisoids in noise[J].IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(5): 1340-1342.
[8] GOLUB G, PEREYRA V.Separable nonlinear least squares: The variable projection method and its applications[J].Inverse Problems, 2003, 19(2): R1-R26.
[9] RIFE D C, BOORSTYN R R.Multiple tone parameter estimation from discrete-time observations[J].The Bell System Technical Journal, 1976, 55(9): 1389-1410.
[10] NANDI S, PRASAD A, KUNDU D.An efficient and fast algorithm for estimating the parameters of two-dimensional sinusoidal signals[J].Journal of Statistical Planning and Inference, 2010, 140(1): 153-168.
[11] BAI Z D, RAO C R, CHOW M, et al.An efficient algorithm for estimating the parameters of superimposed exponential signals[J].Journal of Statistical Planning and Inference, 2003, 110(1/2): 23-34.
[12] DUARTE M F, ELDAR Y C.Structured compressed sensing: From theory to applications[J].IEEE Transactions on Signal Processing, 2011, 59(9): 4053-4085.
[13] 雷蕾, 岑翼刚, 崔丽鸿, 等.小波模极大值点的信号稀疏表示及重建[J].信号处理, 2013, 29(11): 1519-1525.
LEI Lei, CEN Yigang, CUI Lihong, et al.Sparse representation and reconstruction of signals via wavelet modulus maxima[J].Journal of Signal Processing, 2013, 29(11): 1519-1525.(in Chinese)
[14] 王琦森, 余华, 李杰, 等.基于稀疏贝叶斯学习的空间紧邻信号DOA估计算法[J].电子与信息学报, 2021, 43(3): 708-716.
WANG Qisen, YU Hua, LI Jie, et al.Sparse Bayesian learning based algorithm for DOA estimation of closely spaced signals[J].Journal of Electronics & Information Technology, 2021, 43(3): 708-716.(in Chinese)
[15] ZHAO Wanqing, BEACH T H, REZGUI Y.Automated model construction for combined sewer overflow prediction based on efficient LASSO algorithm[J].IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 49(6): 1254-1269.
[16] STOICA P, BABU P, LI Jian.SPICE: A sparse covariance-based estimation method for array processing[J].IEEE Transactions on Signal Processing, 2011, 59(2): 629-638.
[17] ZHENG Yu, LIU Lutao, YANG Xudong.SPICE-ML algorithm for direction-of-arrival estimation[J].Sensors(Basel, Switzerland), 2019, 20(1): E119.
[18] 王伟东, 张群飞, 史文涛, 等.基于矢量水听器阵的迭代稀疏协方差矩阵拟合波达方向估计方法[J].西北工业大学学报, 2020, 38(1): 14-23.
WANG Weidong, ZHANG Qunfei, SHI Wentao, et al.Iterative sparse covariance matrix fitting direction of arrival estimation method based on vector hydrophone array[J].Journal of Northwestern Polytechnical University, 2020, 38(1): 14-23.(in Chinese)
[19] ZHANG Yongchao, JAKOBSSON A, ZHANG Yin, et al.Wideband sparse reconstruction for scanning radar[J].IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(10): 6055-6068.
[20] GLENTIS G O.A fast algorithm for APES and capon spectral estimation[J].IEEE Transactions on Signal Processing, 2008, 56(9): 4207-4220.
[21] LIU Z S, LI H, LI J.Efficient implementation of Capon and APES for spectral estimation[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1314-1319.
[22] DELMAS J P.Asymptotically minimum variance second-order estimation for noncircular signals with application to DOA estimation[J].IEEE Transactions on Signal Processing, 2004, 52(5): 1235-1241.
[23] ABEIDA H, DELMAS J P.Efficiency of subspace-based DOA estimators[J].Signal Processing, 2007, 87(9): 2075-2084.
