1 引言
三星时差定位通过三颗卫星各自测量的关于辐射源的同一脉冲到达时间(time of arrival, TOA)形成两路时差,结合辐射源在地球表面的约束,便能对雷达等脉冲辐射源进行定位和跟踪。若辐射源的脉冲重复间隔(pulse repetition interval, PRI)小于时差窗宽度,即为高重频辐射源。三星对单个高重频辐射源进行时差定位和跟踪,会在脉冲配对时造成时差窗内出现多个脉冲,导致脉冲配对不唯一,这在实际定位和跟踪中会在侦察区域内出现大量模糊定位点,有可能会产生完全错误的定位结果。
国内外的学者针对解模糊问题已做出大量研究,但大部分都是解相位差模糊。针对解时差(time difference of arrival, TDOA)模糊,李涛等人于2004年对高重频雷达辐射源定位进行了研究,研究表明由于脉冲配对产生模糊导致了TDOA模糊,模糊TDOA之间相差了整数倍的PRI,并进一步提出真实定位点和虚假定位点的概念。文献定义了定位点的发散度,之后根据真实定位点趋向于收敛而虚假定位点具有发散特性这一特点,通过不断删减发散度大于一定阈值的虚假定位点来达到解模糊的目的[1]。梁景修对时差模糊观测条件下的无源定位算法作了相应总结,提出了三种解决定位模糊问题的方式:a)通过多次测量,利用数据相关方法消除定位模糊,最终获得辐射源的真实位置。b)利用辐射源脉冲信号时差的直方图消除定位模糊。c)利用时差结合测向信息解决高重频雷达定位模糊问题。文献对比了三种解决方案的优劣,最终得出时差结合测向的解模糊算法相较于其他两种方法是实现高重频辐射源快速精确定位的有效方法[2]。任文娟在梁景修的基础上对测向信息在TDOA解模糊中的应用进行了深入研究[3]。针对跳频信号相关函数由于存在周期副峰而导致的时差模糊问题,姚山峰等人提出了两种消除模糊的算法,即单跳时差平均法和相关函数包络拟合法,两种算法可以有效消除时差周期模糊问题[4]。文献[5]针对高重频运动辐射源无源定位系统遭遇的脉冲配对时差模糊问题,提出了一种基于频差和频差变化率的动目标定位反演解时差模糊算法,然而引入测频必然会使系统复杂。文献[6]针对低轨双星时差定位系统中出现的雷达信号定位模糊问题,提出了一种基于时差序列变化趋势匹配(Variation Trendline Matching of TDOA,VTMT)的解模糊算法,实验证明该算法在长基线时差定位系统中有较高的应用价值。
国外和一部分国内学者更倾向于在多目标定位中解时差关联模糊[7]和利用贝叶斯滤波相关算法[8]解模糊。文献[9]在双站无人机时差定位的研究中将每组时差都用高斯混合模型(Gaussian Mixed Model,GMM)逼近并赋予其权值,权值的大小代表着该时差量测为真实量测的概率,经过多次贝叶斯滤波之后,真实的辐射源航迹将获得较大的权值,会从诸多虚假航迹中筛选出来。但是此算法的缺陷是随着滤波次数的增加,其计算复杂度呈指数倍的增长,为解决这一问题,文献[10]指出可以通过修剪低权重的航迹来减少航迹分裂(track splitting, TS)所带来的计算复杂度。之后又有学者提出了减少高斯混合成分(mixture reduction, MR)的算法来弥补剪枝带来的信息缺失[11-13]。
以上文献大多仅针对静止辐射源以及利用测向,测频等辅助手段解时差模糊。另外应用场景也大多为地面观测站或者无人机系统,而多星时差定位场景下产生的模糊时差数量要更加繁多,因此本文提出了一种基于非线性卡尔曼滤波结合高斯和(Gaussian sum, GS)滤波[14]的三星仅时差跟踪解模糊算法,对地球表面做等高程巡航运动的高重频辐射源进行有效的无模糊跟踪。这里的非线性卡尔曼滤波可选择扩展卡尔曼滤波(extended Kalman filter, EKF)[15]、无迹卡尔曼滤波(unscented Kalman filter, UKF)[16]和容积卡尔曼滤波(cubature Kalman filter, CKF)[17],由于CKF在解决高维状态估计和发散问题上性能更加优越,因此本文采用CKF结合高斯和滤波,具体思路为:首先利用三星时差定位得出的所有模糊定位结果作为滤波初始值,之后利用CKF结合高斯和滤波得到模糊情况下的所有滤波结果,通过剪枝删减其中权重较小的高斯成分,最后加权平均得到最终滤波结果。
2 模糊时差建模
2.1 模糊时差出现的原因
对辐射源进行时差定位时,正常情况为PRI大于二分之一的时差窗的宽度,即两卫星在时差窗内各有一个到达脉冲并配对得到真实的时差;若辐射源为高重频辐射源,即其PRI小于二分之一的时差窗宽度时,会在时差窗内出现多个脉冲,造成脉冲配对一对多的现象,所有模糊时差之间相差整数倍的PRI,模糊配对情况如图1所示。
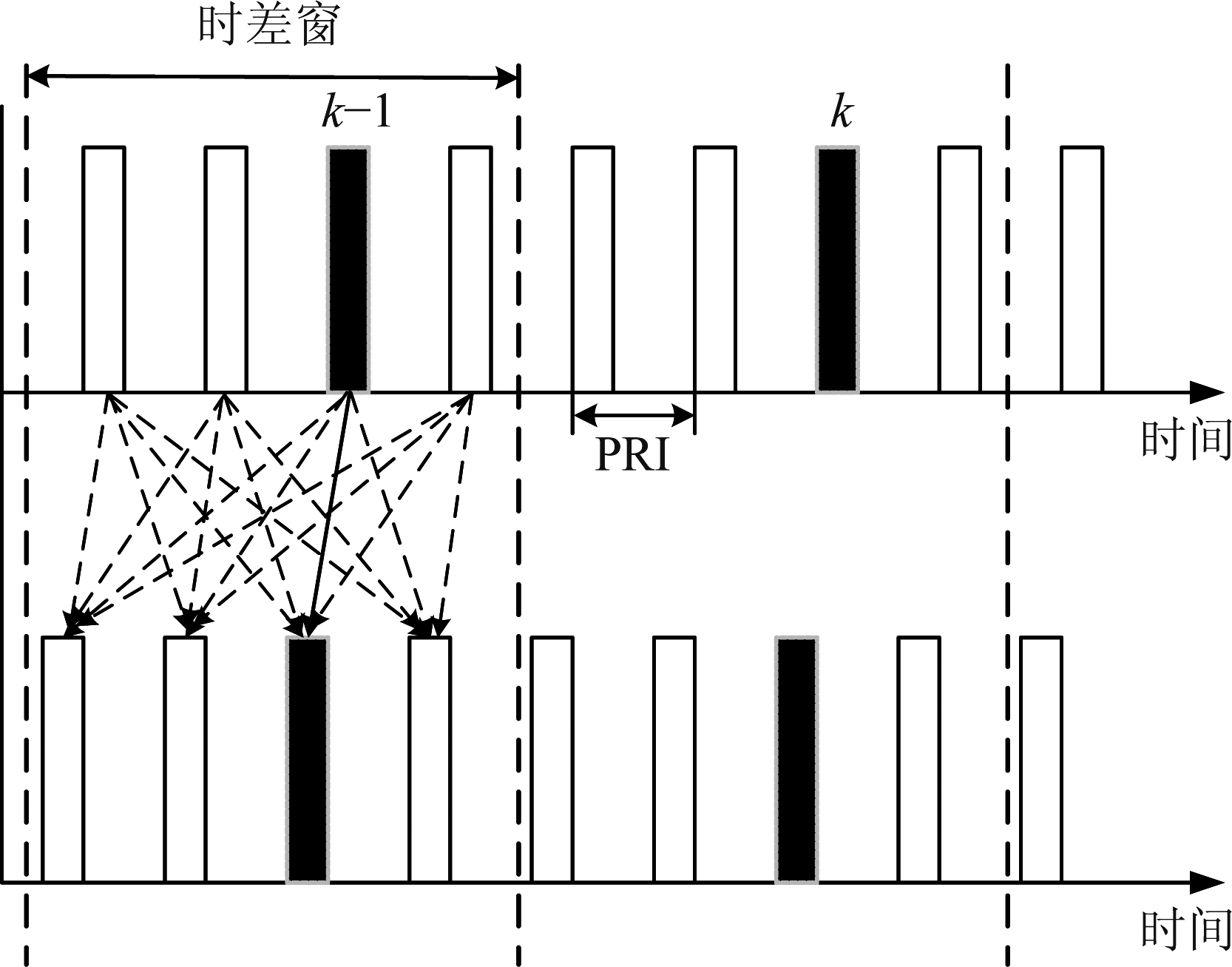
图1 高重频辐射源脉冲信号模糊配对情况
Fig.1 Ambiguous matching of high pulse repetition frequency radiation emitter signal
2.2 时差窗及模糊时差数计算方法
对模糊时差数的求解首先需计算三星时差定位的时差窗,值得注意的是,为保证良好定位效果,要求三星与地心不共面,设卫星为si(i=1,2,3),高重频辐射源为u,则三星时差窗计算模型如图2所示。
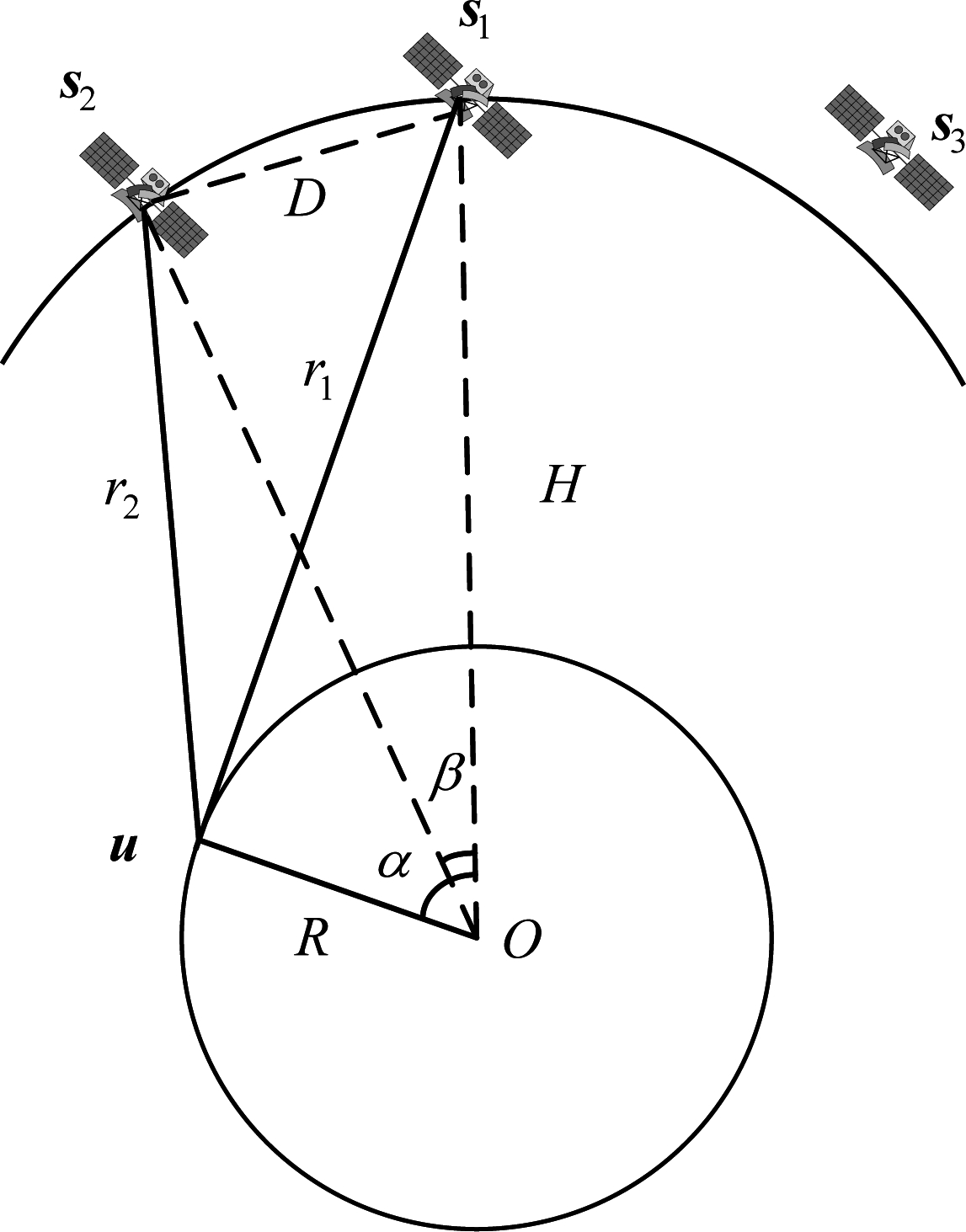
图2 三星时差窗计算模型
Fig.2 Triple satellites window of TDOA calculation model
以卫星s1和s2的时差窗为例,时差窗范围为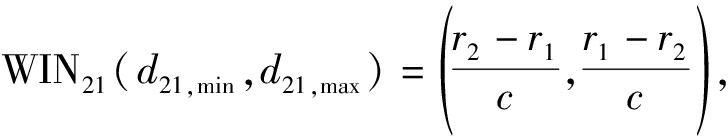 式中c为已知的信号传播速度,d21,min和d21,max分别为时差窗的下限和上限,此时u为s1与地球的切点,设s1和s2的星间距为D,卫星轨道高度为H,地球半径为R,则有
式中c为已知的信号传播速度,d21,min和d21,max分别为时差窗的下限和上限,此时u为s1与地球的切点,设s1和s2的星间距为D,卫星轨道高度为H,地球半径为R,则有
(1)
(2)
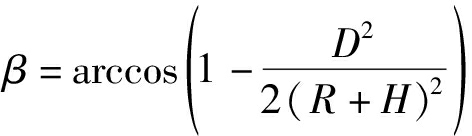
(3)
(4)
由于所有模糊时差数之间相差了整数倍的PRI,因此k时刻下WIN21(d21,min,d21,max)内的时差模糊数N21,k可由式(5)得出:
d21,min≤d21,true+N·PRI≤d21,max
(5)
其中d21,true为真实的时差,满足上式的整数N的个数即为时差模糊数N21,k。k时刻s1和s3的时差窗范围WIN31(d31,min,d31,max)及时差模糊数N31,k计算同上,将两时差窗内的模糊时差数两两配对结合高程量测共得到N21,k·N31,k组量测,即代入定位方程中可求得N21,k·N31,k个定位结果![]()
但是所有![]() 必须要满足在三星的共同可视范围内,若此定位点在三星的共同可视范围内,则满足
必须要满足在三星的共同可视范围内,若此定位点在三星的共同可视范围内,则满足
(6)
最后将不满足式(6)的结果删除即可得到最终的模糊量测数。
2.3 时差高斯混合模型近似
对于其时差量测(即距离差量测),都可以确定唯一一条双曲线,并且双曲线周围有一个σ区域,表示辐射源位置的不确定性。以卫星1和卫星2为例(卫星1和卫星3同理),图3给出了距离差量测r21的双曲线,并给定了基于r21+σr/2和r21-σr/2两条双曲线界定的一个σ区域。所有模糊量测和真实量测都为双曲线上的一个分段,对于每个分段都是一个高斯分布,其量测的均值是分段的中心,协方差由概率误差椭圆定义。这里规定每个高斯成分相互独立。
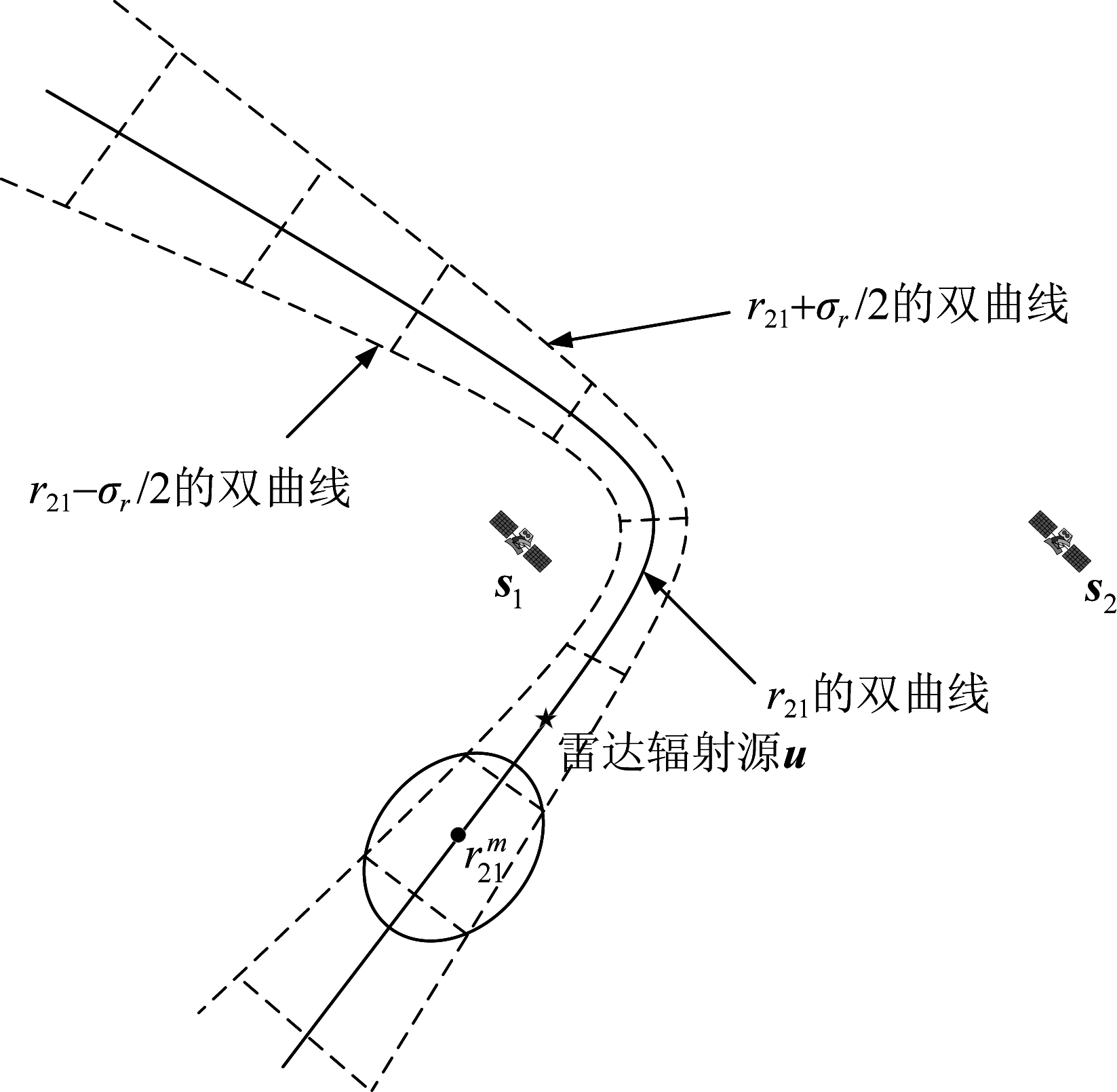
图3 s1和s2距离差量测转换为高斯混合模型近似
Fig.3 Conversion of range difference measurement between s1 and s2 into its Gaussian mixed model approximation
假设k时刻利用2.2节方法共可以得到Nk组量测,每一组量测都是均值为![]() 协方差矩阵为
协方差矩阵为![]() 的高斯分量,即k时刻下所有量测的概率密度函数为如下的高斯分布加权和:
的高斯分量,即k时刻下所有量测的概率密度函数为如下的高斯分布加权和:
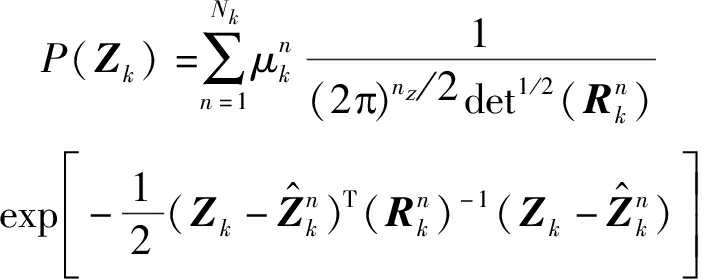
(7)
式中,nz为量测的维数,每组量测的权值都相同,为![]()
3 状态方程和观测方程
本节给出辐射源的状态方程和观测方程,为减小误差,使用WGS-84椭球模型来描述地球面。假设辐射源在地球表面做等高程巡航运动,k时刻辐射源在经纬高大地坐标系中的纬度为Bk,经度为Lk,高度为Hk,纬度方向的速度为VN,k,经度方向的速度为VE,k,由于是等高程运动,因此高度方向速度VH,k为零,Hk不变。相比于地固坐标系的六维状态矢量![]() 本文状态方程使用经纬高大地坐标系下的四维状态矢量来提高估计精度[18],即XG,k=[Bk,Lk,VN,k,VE,k]T。则等高程巡航运动辐射源的状态方程为:
本文状态方程使用经纬高大地坐标系下的四维状态矢量来提高估计精度[18],即XG,k=[Bk,Lk,VN,k,VE,k]T。则等高程巡航运动辐射源的状态方程为:
XG,k=Fk-1XG,k-1+Γk-1wk-1
(8)
式中,Fk-1为状态转移矩阵,其表达为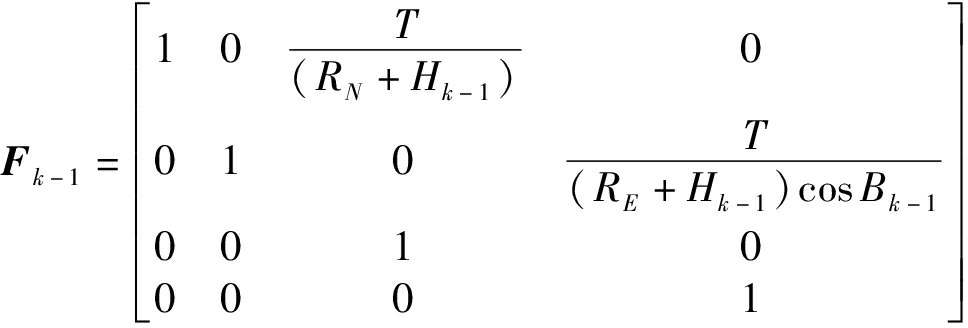 ,T为观测时间间隔,RN为当地卯酉圈曲率半径,其表达为
,T为观测时间间隔,RN为当地卯酉圈曲率半径,其表达为![]() 其中a=6378137 m为地球半长轴,第一偏心率平方e2=0.00669437999013,RE为当地子午圈曲率半径,其表达为
其中a=6378137 m为地球半长轴,第一偏心率平方e2=0.00669437999013,RE为当地子午圈曲率半径,其表达为![]() 其中wN,k-1和wE,k-1分别为辐射源在k-1时刻时的纬度方向加速度噪声和经度方向加速度噪声,其加速度噪声协方差阵
其中wN,k-1和wE,k-1分别为辐射源在k-1时刻时的纬度方向加速度噪声和经度方向加速度噪声,其加速度噪声协方差阵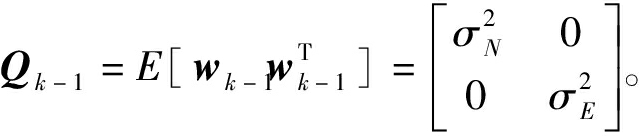 Γk-1为系统扰动矩阵,其表达为Γk-1=
Γk-1为系统扰动矩阵,其表达为Γk-1=
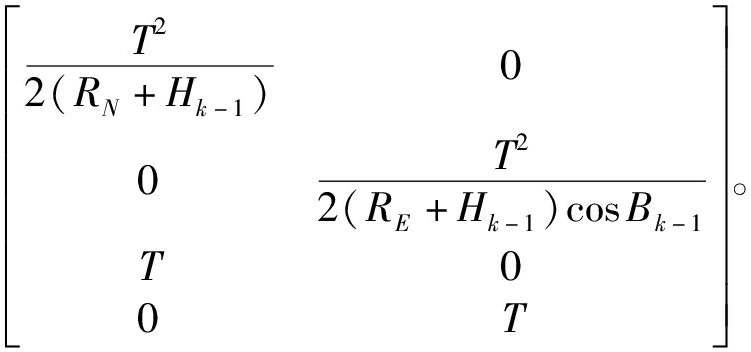
对于![]() 其中uk=[xk,yk,zk]T为k时刻在地固坐标系下辐射源的位置,
其中uk=[xk,yk,zk]T为k时刻在地固坐标系下辐射源的位置,![]() 为k时刻在地固坐标系下辐射源的速度,将k时刻下在地固坐标系的一组观测方程表示如下:
为k时刻在地固坐标系下辐射源的速度,将k时刻下在地固坐标系的一组观测方程表示如下:
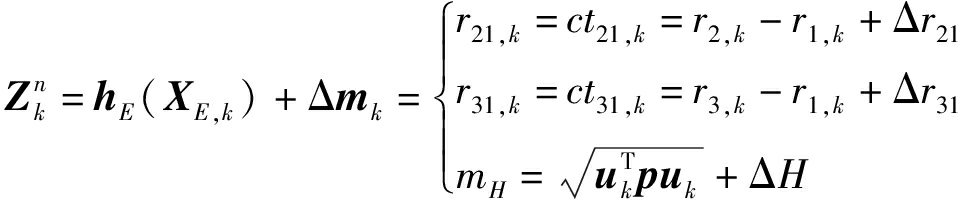
(9)
上式中,ri1,k(i=2,3)为k时刻卫星1与卫星2、3的距离差,ti1,k(i=2,3)为卫星1与卫星2、3的时间差,ri,k(i=1,2,3)为卫星1,2,3与辐射源的距离,c为信号传播速度,mH为高程量测,p=![]() 距离差误差Δr21和Δr31为均值为零,方差为(c·σt)2的高斯随机变量,高程误差ΔH为均值为零,方差为
距离差误差Δr21和Δr31为均值为零,方差为(c·σt)2的高斯随机变量,高程误差ΔH为均值为零,方差为![]() 的高斯随机变量,观测噪声协方差阵
的高斯随机变量,观测噪声协方差阵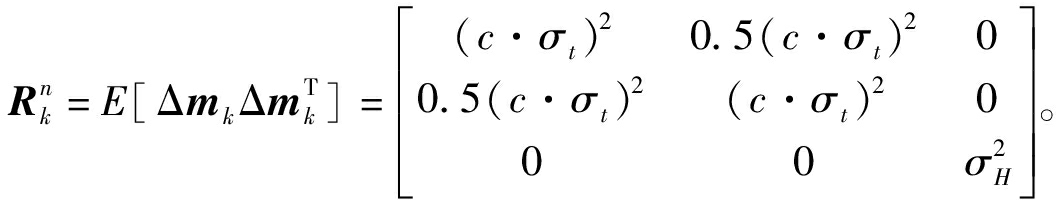 这里要注意上式中为真实时差的表达方式,模糊时差可在真实时差基础上加上整数倍的PRI。参照文献[18]可将地固坐标系下的观测方程(9)转换成经纬高大地坐标系下的观测方程(10):
这里要注意上式中为真实时差的表达方式,模糊时差可在真实时差基础上加上整数倍的PRI。参照文献[18]可将地固坐标系下的观测方程(9)转换成经纬高大地坐标系下的观测方程(10):
(10)
4 CKF结合高斯和滤波算法
本节利用CKF结合高斯和滤波算法对运动高重频辐射源进行跟踪,算法详细过程如下。
Step 1 确定滤波初始值。初始时刻利用2.2节方法得到模糊时差量测,结合高程量测使用三星时差定位[19]得到可视范围内的所有模糊定位点及其相应的克拉美罗下界(Cramer-Rao Lower Bound, CRLB)作为滤波初始值![]() 和
和![]() 其中m=1,...,M0。这里需注意滤波初始值的速度分量设为零,初始速度协方差分量设为
其中m=1,...,M0。这里需注意滤波初始值的速度分量设为零,初始速度协方差分量设为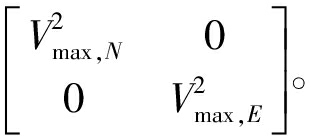 其中
其中![]() 和
和![]() 为纬度方向和经度方向速度的理论最大值,初始分量的权值
为纬度方向和经度方向速度的理论最大值,初始分量的权值![]()
Step 2 设k-1时刻共有Mk-1组滤波结果为![]() 和
和![]() 其中m=1,...,Mk-1,则k时刻的预测为:
其中m=1,...,Mk-1,则k时刻的预测为:
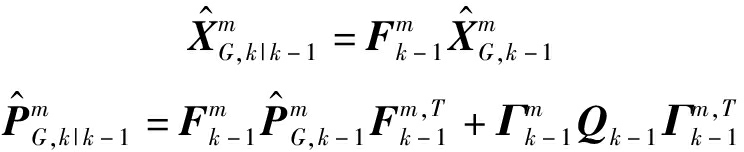
(11)
Step 3 利用预测值构造sigma点并带入观测方程:
(12)
![]() (n表示状态维数)
(n表示状态维数)
(13)
(14)
(15)
再计算sigma点的预测均值![]() 预测协方差
预测协方差![]() 以及状态和观测之间的互协方差
以及状态和观测之间的互协方差![]()

(16)
Step 4 结合k时刻得到的Nk组量测![]() 计算滤波增益Kk,滤波状态
计算滤波增益Kk,滤波状态![]() 协方差矩阵
协方差矩阵![]() 和相应的权值。状态更新如下:
和相应的权值。状态更新如下:
(17)
(18)
(19)
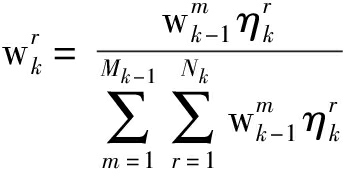
(20)
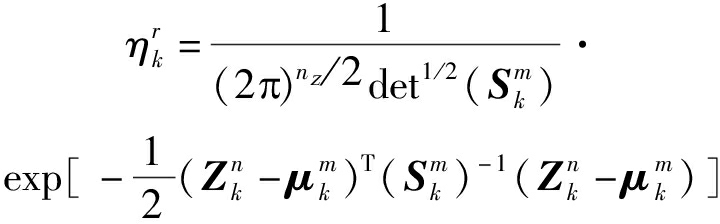
(21)
式中,nz为量测的维数,r=(m-1)Nk+n。
Step 5 设置门限λ,删除![]() 的高斯成分,将剩下的高斯成分
的高斯成分,将剩下的高斯成分![]() 代入下一次滤波,取加权平均结果
代入下一次滤波,取加权平均结果
(22)
作为最终结果。
门限设置规则如下:如上文所述,滤波开始前真实的辐射源定位点和所有模糊定位点权值相同,为![]() 随着滤波次数的增加,真实定位点的权值将会逐渐增大,哪怕仅滤波一次,其权值也将大于初始权值
随着滤波次数的增加,真实定位点的权值将会逐渐增大,哪怕仅滤波一次,其权值也将大于初始权值![]() 因此将门限范围设置为
因此将门限范围设置为![]() 即可保留住真实定位点的信息又能大幅减少计算量。
即可保留住真实定位点的信息又能大幅减少计算量。
5 BCRLB
针对CKF这类动态估计系统,衡量其滤波估计性能的标准为贝叶斯克拉美罗下界(Bayesian Cramer-Rao Lower Bound,BCRLB),因此本节通过计算无模糊条件下的BCRLB作为评价本文解模糊算法优劣的标准,其详细推导过程如下。
若k-1时刻的BCRLB表示为Bk-1,则定义k-1时刻的费舍尔信息(Fisher)矩阵Jk-1为
(23)
由文献[20]可得k时刻的Fisher矩阵Jk为
(24)
上式中,
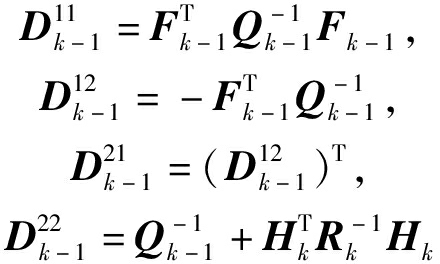
(25)
将公式(25)代入到公式(24)中可得Jk为
(26)
为避免Qk-1是奇异矩阵导致上式无法求解,则采用求逆引理将上式转化为
(27)
式中,Qk-1为k-1时刻的系统扰动噪声协方差阵,Fk-1为k-1时刻的状态转移矩阵,![]() 为k时刻的观测噪声协方差阵。将Jk求逆即可得到k时刻的BCRLB,B0由第4节Step1中的初始化决定,需注意这里是无模糊情况下的初始化。
为k时刻的观测噪声协方差阵。将Jk求逆即可得到k时刻的BCRLB,B0由第4节Step1中的初始化决定,需注意这里是无模糊情况下的初始化。
6 实验分析
6.1 低速目标(船只)解时差模糊
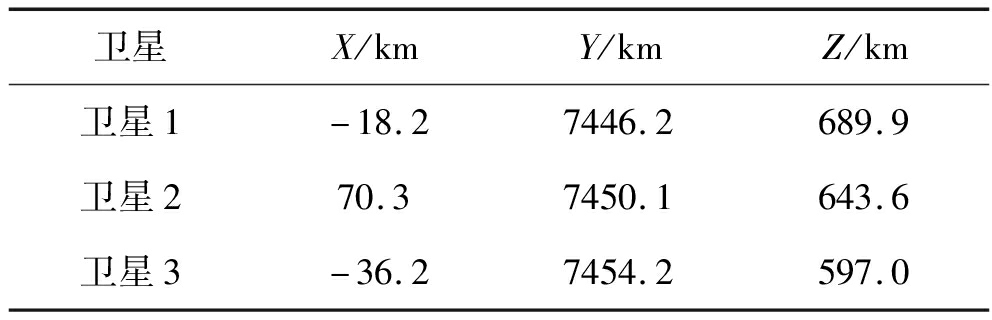
阶段一 在解时差模糊之前首先通过实验分析初始时差模糊定位点的分布情况。假设辐射源位置的经度和纬度分别为110.0°E和15.0°N,高程为零。用于实验仿真的卫星星历点数据基于STK软件生成,三星的轨道高度设为1100 km,轨道倾角为63.4°,星间距为50~110 km,轨道历元时刻从2020年8月29日4时开始,将采样间隔设为1 s。起始时刻三星星历点数据如表1所示。
表1 三星星历点数据
Tab.1 Triple satellites ephemeris point data
卫星X/kmY/kmZ/km卫星1-18.27446.2689.9卫星270.37450.1643.6卫星3-36.27454.2597.0
令时差测量误差σt=100 ns,卫星位置误差σs=25 m,高程误差σH=500 m,之后利用初始时刻三星星历点数据对高重频辐射源定位。此场景下利用2.2节方法求得时差窗为0.5686 ms,因此对于PRI大于3.5 kHz的辐射源都会产生时差模糊现象,设高重频辐射源脉冲重复频率为20 kHz,则初始时刻的三星时差模糊定位点分布如图4所示。
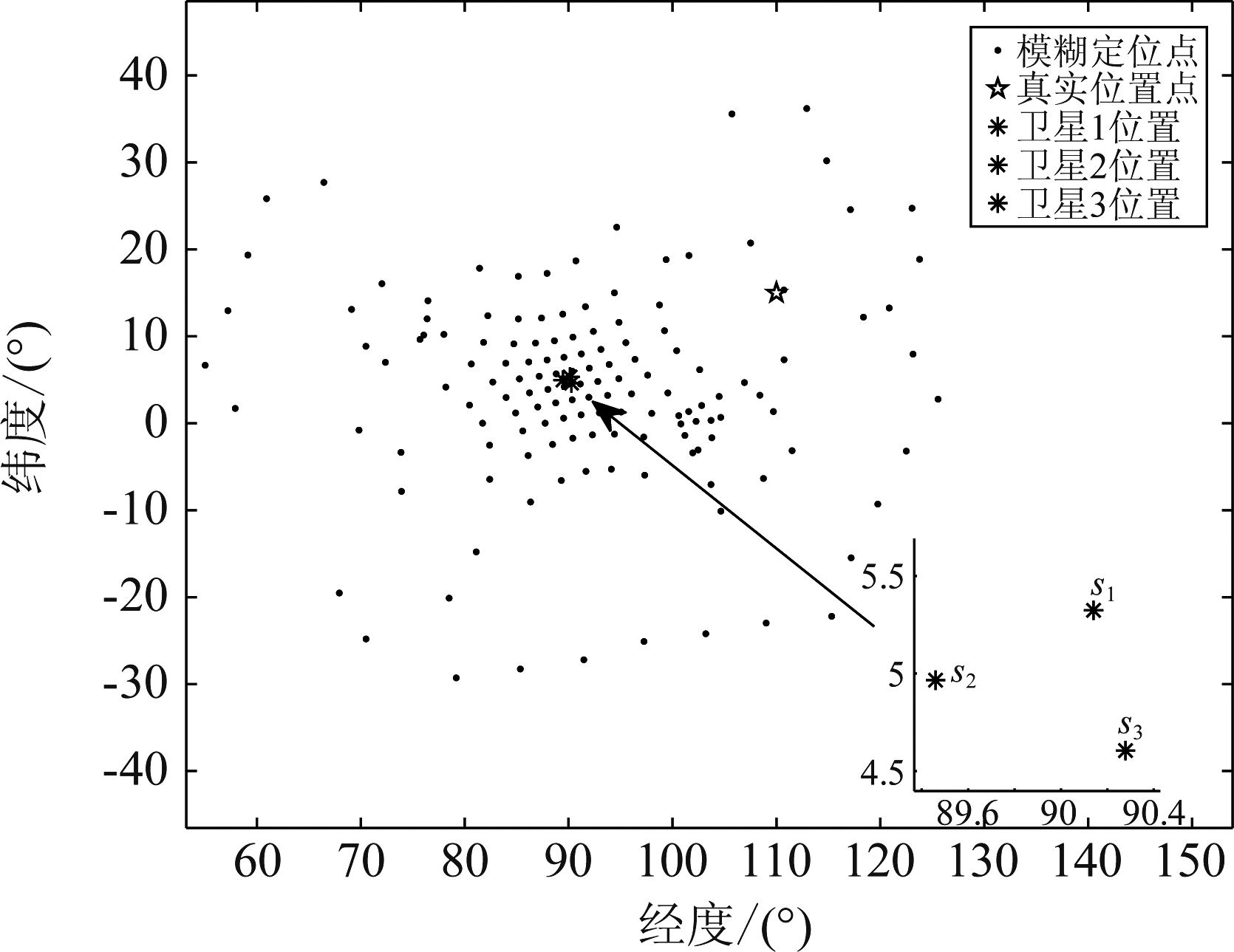
图4 初始模糊定位点分布
Fig.4 Initial localization ambiguity point distribution
从图4中可以看出三星时差定位模糊点数量较多,几乎布满三星的可视范围,其中只有一个定位点位置接近辐射源真实位置,此定位点即利用真实时差定位所得结果。在阶段二中,将初始定位的所有模糊点作为滤波初始值代入到高斯和滤波系统中。
阶段二 本小节通过实验验证低速目标跟踪解模糊算法。假设阶段一中辐射源以20 m/s的速度做等高程巡航运动,其高程为零,即在海平面航行的船只,航向角与纬度方向的夹角θ为北偏东45°。令Vmax,N=Vmax·sin(θ),Vmax,E=Vmax·cos(θ),Vmax为辐射源理论最大速度,这里设为20 m/s。令σN=σE=0.001 m/s,求得初始模糊定位点数量M0=132,因此将权值门限设置为λ=1/M0=1/132。用于仿真的卫星星历点数据同阶段一,设置滤波观测间隔为15 s,观测次数为50次。将本文算法与文献[3]和文献[13]的算法进行对比,文献[3]算法通过结合测向进行解时差模糊,分别设置测角误差0.1°和0.5°的对比实验,文献[13]利用扩展卡尔曼滤波结合高斯混合模型(Gaussian mixed model-extended Kalman filter, GMM-EKF)算法进行解模糊,比较本文算法与文献[3]算法和文献[13]的GMM-EKF算法的位置估计均方根误差(root mean square error, RMSE)和速度估计均方根误差,其数学表达如下:
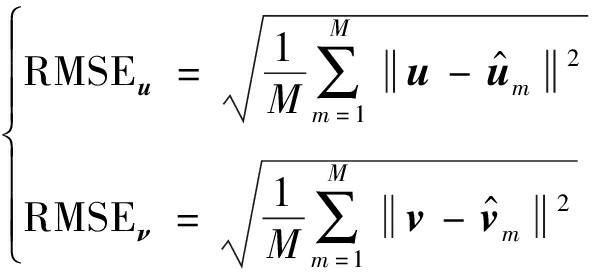
(28)
上式中,u和v分别为辐射源的真实位置和速度,![]() 和
和![]() 为第m次蒙特卡罗实验的估计值,蒙特卡罗仿真次数M为300次。算法跟踪场景及跟踪性能比较如图5~图6所示。
为第m次蒙特卡罗实验的估计值,蒙特卡罗仿真次数M为300次。算法跟踪场景及跟踪性能比较如图5~图6所示。
6.2 高速目标(飞机)解时差模糊
高速目标初始时差模糊定位点分布情况同低速目标一致,只是将辐射源高程改为5000 m,这里不再过多赘述。本小节通过实验验证高速目标跟踪解模糊算法。假设辐射源以300 m/s的速度做等高程巡航运动,Vmax设为300 m/s。其余实验参数与低速目标场景相同,算法跟踪场景及跟踪性能比较如图7~图8所示。
从图5和图7中分析得出,不论低速目标还是高速目标,本文算法随着观测时间的增加,其跟踪航迹与目标真实航迹基本吻合,文献[13]的GMM-EKF算法航迹也与真实航迹大致吻合,而文献[3]的两种情况到跟踪后期均发散,当测向误差为0.5°时,文献[3]算法从一开始就完全偏离真实航迹。从图6和图8中可以分析得出本文算法性能随着观测时间的增加逐渐可以达到无模糊情况下的BCRLB。GMM-EKF算法较本文算法而言,跟踪性能略偏离BCRLB。而文献[3]算法在测角误差0.1°的情况下一开始跟踪性能可以达到BCRLB,随着观测时间的增长其性能逐渐远离BCRLB,当测角误差增大到0.5°时,滤波结果发散的时间则更加提前,由此可见文献[3]算法受测向精度影响较大,低速目标尤为显著。GMM-EKF算法由于EKF的泰勒展开线性化过程会带来高阶项的损失误差,因此其性能略差于本文算法。而本文算法在不施加任何辅助方法的情况下,通过三星仅测时差即可对运动高重频辐射源进行有效地解时差模糊。
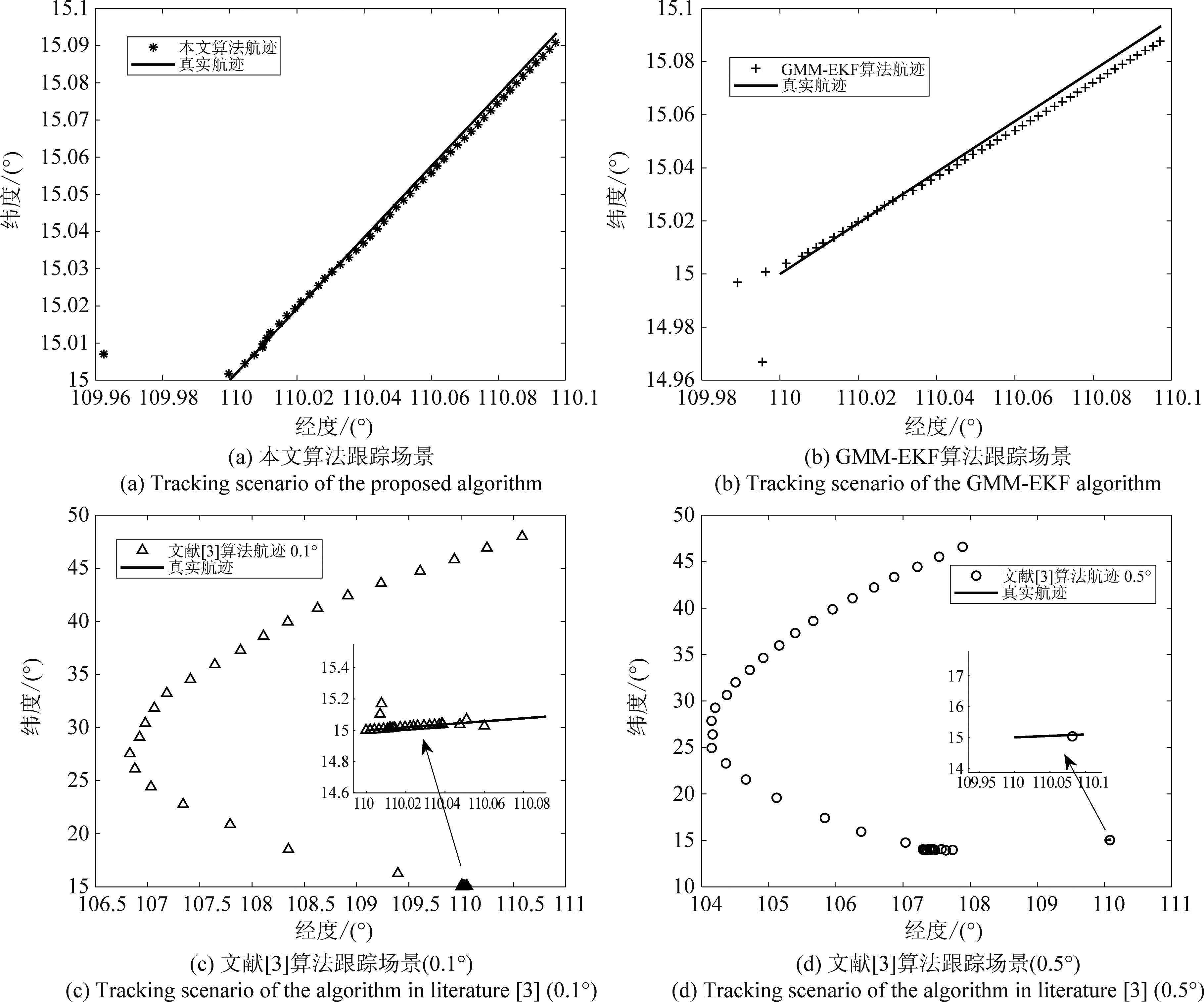
图5 低速目标跟踪场景
Fig.5 Tracking scenario of low speed target
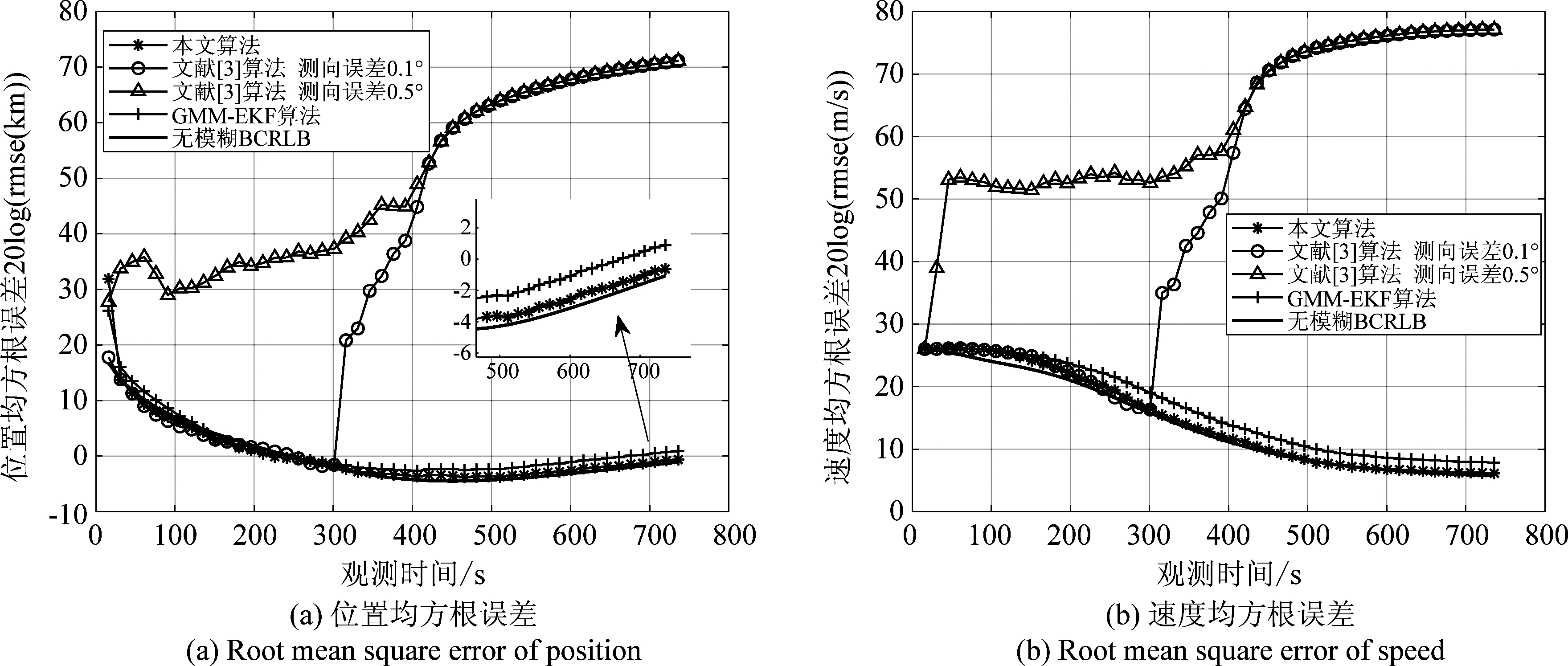
图6 低速目标跟踪性能比较
Fig.6 Low speed target tracking performance comparison
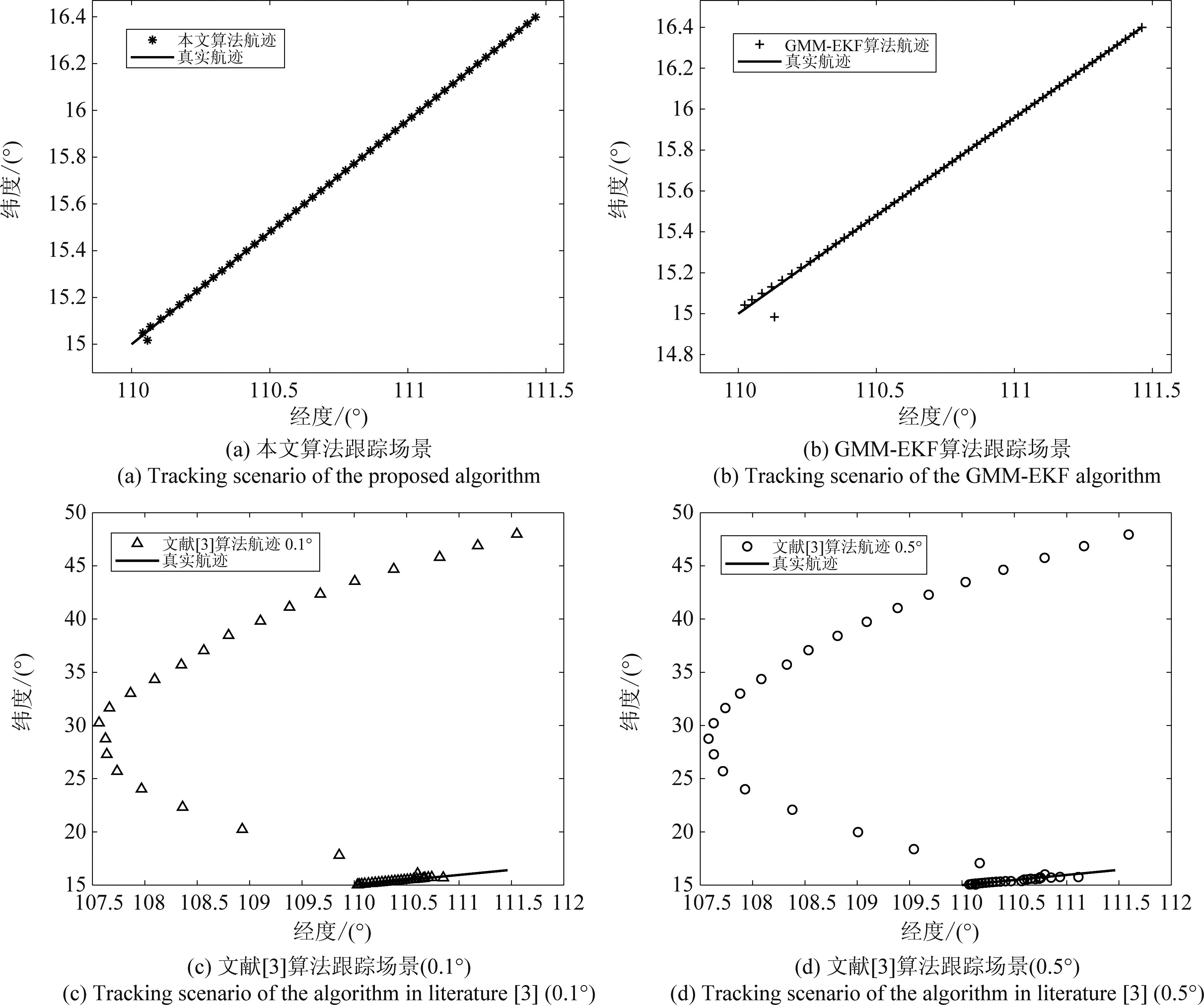
图7 高速目标跟踪场景
Fig.7 Tracking scenario of high speed target
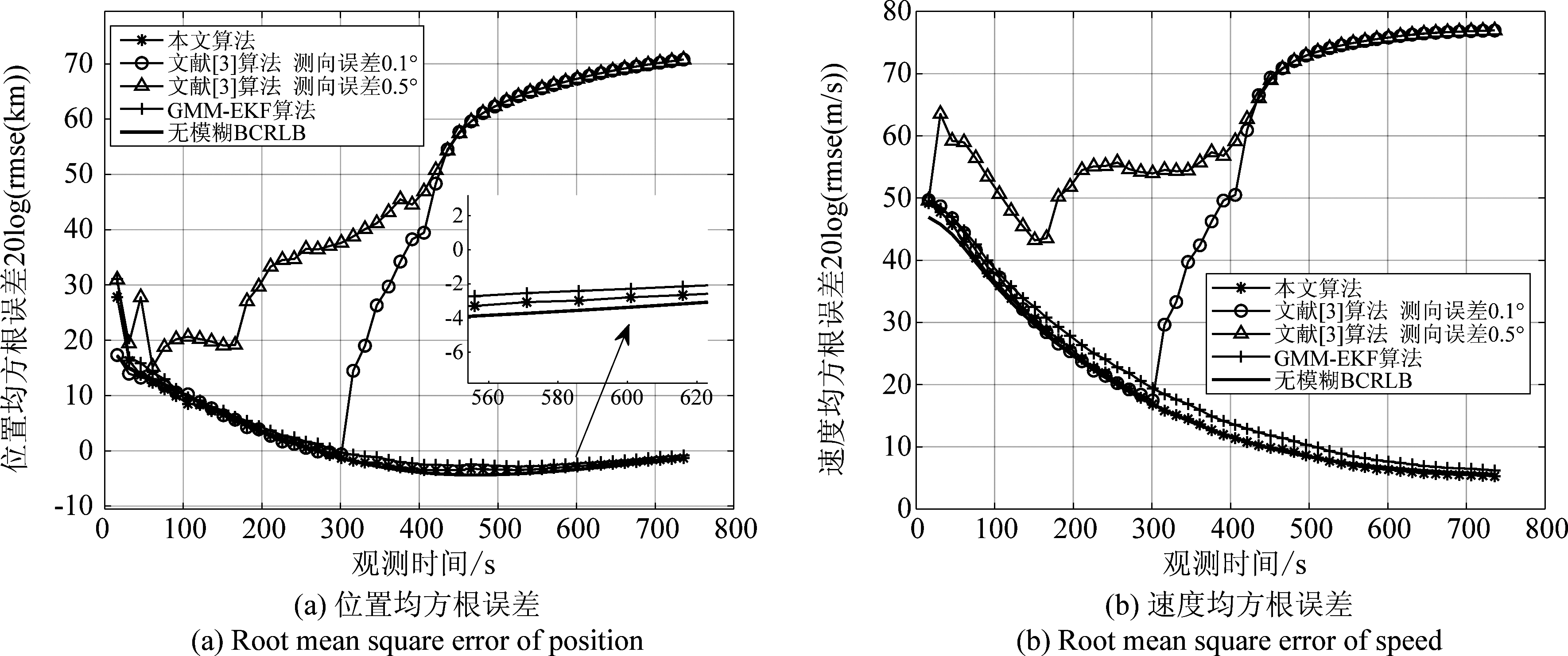
图8 高速目标跟踪性能比较
Fig.8 High speed target tracking performance comparison
6.3 计算复杂度比较
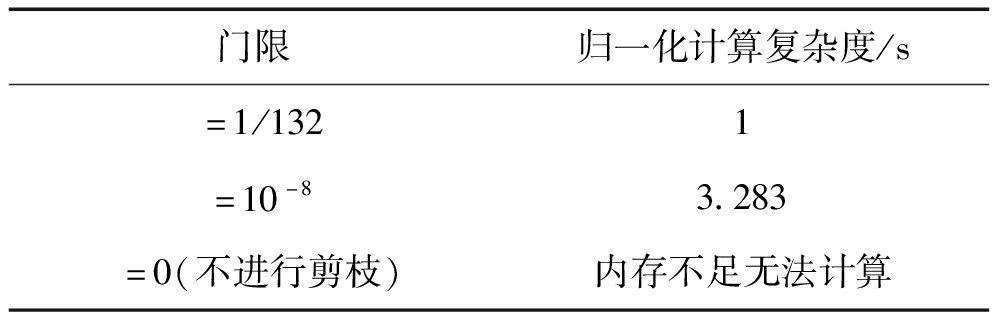
以低速目标为例,分别设置权值门限为λ=1/M0=1/132、λ=10-8和λ=0,其中λ=0为不进行剪枝处理的情况,通过实验分析三种情况下本文算法完成解时差模糊所需的计算复杂度,实验场景及参数设置同6.1节,其归一化计算复杂度如表2所示。
表2 三种情况下的归一化计算复杂度
Tab.2 Normalized computational complexity in three cases
门限归一化计算复杂度/s吠=1/1321吠=10-83.283吠=0(不进行剪枝)内存不足无法计算
通过上表可以得出,若不进行剪枝,则每次滤波的计算复杂度呈指数式增长,最终导致计算机内存不足无法计算。通过设置门限删除权值较小的高斯成分相较于不进行剪枝的情况可以大幅度减少计算复杂度,即使将门限λ设置成无限接近于0也可实现解时差模糊的计算,其中将门限设置为λ=1/132所需的计算复杂度最小。
7 结论
本文提出了一种基于CKF结合高斯和滤波的三星时差跟踪解模糊算法,该算法无需结合测向或者测频差等辅助手段,仅通过测时差即可对运动高重频辐射源有效地解时差模糊并跟踪,在工程应用中操作简单,成本较低。另外针对卫星时差定位场景出现的时差模糊数量比地面观测站或者无人机系统更加繁多而导致计算量增大的问题,通过设置门限删除掉每次滤波权值较小的高斯成分来减小计算量。在实验分析中,分别设置低速目标和高速目标两种场景对本文算法、文献[3]算法和文献[13]的GMM-EKF算法进行了比较,文献[3]的算法在测向误差较大时会出现发散的问题,GMM-EKF算法由于EKF本身存在的缺陷导致其性能略差于本文算法。本文算法在相同条件下仅利用模糊时差观测即可对做巡航运动的高重频辐射源进行有效地跟踪并且其性能达到了无模糊条件下的BCRLB。
[1] 李涛, 姜文利, 周一宇.高重频信号三星座时差定位研究[J].电子对抗技术, 2004, 19(4): 7-11.
LI Tao, JIANG Wenli, ZHOU Yiyu.TDOA location with high PRF signals based on three satellites[J].Electronic Warfare Technology, 2004, 19(4): 7-11.(in Chinese)
[2] 梁景修.高重频雷达精确快速定位的方法[J].电子对抗技术, 2005, 20(5): 19-22.
LIANG Jingxiu.Quick and accurate location of high PRF radar[J].Electronic Warfare Technology, 2005, 20(5): 19-22.(in Chinese)
[3] 任文娟, 胡东辉, 丁赤飚, 等.利用测向信息消除高重复频率信号的时差定位模糊[J].电子与信息学报, 2010, 32(12): 3003-3007.
REN Wenjuan, HU Donghui, DING Chibiao, et al.Eliminating TDOA location ambiguity of high PRF signal based on direction information acquired[J].Journal of Electronics & Information Technology, 2010, 32(12): 3003-3007.(in Chinese)
[4] 姚山峰, 欧阳鑫信, 贺青.窄带跳频信号的无模糊时差估计算法[J].电子学报, 2019, 47(4): 798-805.
YAO Shanfeng, OUYANG Xinxin, HE Qing.Unambiguous TDOA estimation algorithm of narrowband frequency hopping signal[J].Acta Electronica Sinica, 2019, 47(4): 798-805.(in Chinese)
[5] 丛迅超.基于频差和频差变化率的动目标定位反演解时差模糊算法[J].信息技术与信息化, 2019(9): 94-96.
CONG Xunchao.Tdoa ambiguity elimination for moving emitter by FDOA and FDOA-rate localization inversion[J].Information Technology and Informatization, 2019(9): 94-96.(in Chinese)
[6] 姚山峰, 贺青, 欧阳鑫信, 等.一种低轨双星高脉冲重复频率雷达信号的定位模糊消除算法[J].电子与信息学报, 2021, 43(3): 598-605.
YAO Shanfeng, HE Qing, OUYANG Xinxin, et al.A novel method for location ambiguity mitigation of high pulse repetition frequency radar signal in low earth orbit dual-satellite geolocation system[J].Journal of Electronics & Information Technology, 2021, 43(3): 598-605.(in Chinese)
[7] SUNDAR H, SREENIVAS T V, SEELAMANTULA C S.TDOA-based multiple acoustic source localization without association ambiguity[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(11): 1976-1990.
[8] VIVONE G, BRACA P, GRANSTROM K, et al.Multistatic Bayesian extended target tracking[J].IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(6): 2626-2643.
[9] OKELLO N, MUSICKI D.Measurement Association for emitter geolocation with two UAVs[C]∥2007 10th International Conference on Information Fusion.Quebec, QC, Canada.IEEE, 2007: 1-8.
[10] PANTA Kusha, CLARK D E, VO B N.Data association and track management for the Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1003-1016.
[11] SALMOND D J.Mixture reduction algorithms for point and extended object tracking in clutter[J].IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 667-686.
[12] RUNNALLS A R.Kullback-leibler approach to Gaussian mixture reduction[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 989-999.
[13] 张敏, 郭福成, 周一宇, 等.运动单站干涉仪相位差直接定位方法[J].航空学报, 2013, 34(9): 2185-2193.
ZHANG Min, GUO Fucheng, ZHOU Yiyu, et al.A single moving observer direct position determination method using interferometer phase difference[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2185-2193.(in Chinese)
[14] ALSPACH D, SORENSON H.Nonlinear Bayesian estimation using Gaussian sum approximations[J].IEEE Transactions on Automatic Control, 1972, 17(4): 439-448.
[15] GARCIA R V, PARDAL P C P M, KUGA H K, et al.Nonlinear filtering for sequential spacecraft attitude estimation with real data: Cubature Kalman Filter, Unscented Kalman Filter and Extended Kalman Filter[J].Advances in Space Research, 2019, 63(2): 1038-1050.
[16] DAID A, BUSVELLE E, AIDENE M.On the convergence of the unscented Kalman filter[J].European Journal of Control, 2021, 57: 125-134.
[17] ARASARATNAM I, HAYKIN S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.
[18] 李华, 郭福成.等高程运动假设的单星角度融合多普勒变化率跟踪方法[J].空间电子技术, 2018, 15(4): 41-48.
LI Hua, GUO Fucheng.A fusion of angle and Doppler rate-of-changing based tracking method forconstant altitude moving target by single satellite[J].Space Electronic Technology, 2018, 15(4): 41-48.(in Chinese)
[19] HO K C, CHAN Y T.Geolocation of a known altitude object from TDOA and FDOA measurements[J].IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770-783.
[20] TICHAVSKY P, MURAVCHIK C H, NEHORAI A.Posterior Cramer-Rao bounds for discrete-time nonlinear filtering[J].IEEE Transactions on Signal Processing, 1998, 46(5): 1386-1396.




