1 引言
宽带雷达具有高距离分辨力,其回波携带更多目标信息,在杂波抑制、目标识别、目标参数精密测量等领域具有独特的优势[1-2]。但宽带雷达目标能量被分散到多个距离单元,传统窄带检测方法不再适用于宽带雷达。因此许多学者对宽带雷达扩展目标检测方法进行了大量研究,目前已有积分检测器、SSD-GLRT检测器、MN检测器、基于能量积累的双门限检测器、序贯检测器、ESS-GLRT检测器[3-9]等宽带雷达检测器。
此类宽带雷达检测器通过某种判决准则将多个距离单元的能量累积作为检验统计量,将检验统计量与门限比较得到判决结果。对于某一给定判决准则的宽带雷达检测器,其判决门限由虚警概率决定。求解虚警概率对应的门限在本质上也是一个求H0(只有噪声)情况下检验统计量分位数的过程。然而宽带雷达的判决准则往往较为复杂,难以求得检验统计量服从的分布,因此门限的计算是宽带检测领域的难点。
对于SSD-GLRT检测器、序贯检测器等无法或难以求得解析门限的宽带检测器,可用传统的排序插值方法确定给定虚警概率对应的门限。具体地,按环境噪声的概率分布生成大量H0情况下的回波样本,输入检测器算得检验统计量,将其存储并按从小到大的顺序排序,绘制样本累积分布曲线并对其线性插值得到关注虚警概率对应的门限。传统排序插值方法需生成大量样本并存储排序,消耗了大量计算机资源,给实际实现带来困难。受计算机内存限制,有必要采用空间复杂度低的分位数估计方法[10-14]。其中R.Jain and I.Chlamtac[14]提出的经典P2(Piecewise-Parabolic)分位数更新算法在样本累积分布曲线上设置几个标志位,根据输入数据用抛物线分段插值算法对各标志位进行更新、迭代,从而实现在有限内存下估计待求分位数。然而雷达检测器常设有极低虚警概率,例如10-6,这种极端分位数需从稀有事件中估计,上述分位数估计方法存在较大的估计方差。
因此本文提出通过重要性采样[15],使采样能够更多地采到对计算期望分位数有利的样本,减少准确绘制关注虚警概率附近的样本累积分布曲线所需生成样本的数量,使门限的计算更加高效。本文第2节描述了宽带检测器门限设置的难题,第3节介绍了基于重要性采样的宽带雷达检测器门限设置方法,第4节以已有的积分检测器、难以求得解析门限的SSD-GLRT检测器两种宽带检测器为例,通过比较实验对所提方法进行性能分析,第5节小结。
2 问题描述
在宽带雷达检测领域的相关研究中,常假设H0(只有噪声)情况下的回波样本x=[x1,x2,…,xL]T,xi,i=1,2,…,L独立且服从参数为
的复高斯分布,L是检测窗长,
是噪声功率。记x的概率密度函数为p(x),宽带检测器的检验统计量Λ(x),检测门限T,则有虚警概率PFA与检测门限T的关系为
[I{Λ(x)>T}]
(1)
其中Pr{·}表示事件发生的概率,判决过程
往往是x的复杂函数,上式难以求得闭式解。为计算给定虚警概率对应的门限,传统方法由大数定律,生成大量H0情况下的回波样本,计算I{Λ(x)>T}的经验均值
以近似期望,即
[I{Λ(x)>T}]=PFA
(2)
其中N为样本数,
表示依概率收敛。上式的含义是可通过统计过门限样本在总样本中的比例来近似门限对应的虚警。换句话说,将Λ(xi),i=1,2,…,N存储并按从小到大的顺序排序,可近似绘制虚警与门限的关系曲线,对该曲线插值即可得到给定虚警概率对应的检测门限。
I{Λ(x)>T}服从期望μb=PFA,方差
的伯努利分布。设其期望的估计偏差为
置信概率为α,根据中心极限定理,所需样本数满足关系
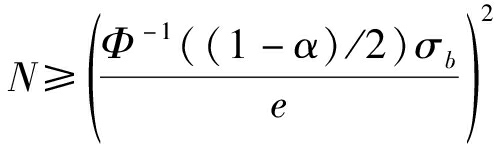
(3)
其中Φ-1(·)表示标准高斯分布的累积分布函数的反函数。相比于窄带检测,宽带检测面临着以下两个问题:
A.对于窗长为L个距离单元的宽带检测器,仿真N个样本需生成N·L个服从高斯分布的随机数;
B.宽带检测常做滑窗处理[16],每次判决的虚警概率往往相对于窄带较低。
因此带宽的增大会使准确估计虚警概率所需生成的随机数个数呈爆炸性增长。分别用带宽为5 MHz的窄带信号、1 GHz的宽带信号观测大小为24 m的目标,目标一维成像结果分别占据1个、160个距离单元。设估计偏差为PFA/10,宽带、窄带信号需生成的随机数个数与置信概率、虚警概率的关系如下图。可见为达到置信概率的要求,用传统排序插值做法绘制宽带检测器虚警概率与门限的关系曲线需要生成大量随机数,特别是对于低虚警概率的情况,亟需采用更高效的采样方法。
图1 传统排序插值方法需生成的随机数个数与置信概率的关系曲线
Fig.1 The relationship curves between the number of random numbers to be generated and the confidence probability obtained by the traditional sorting and interpolating method
3 基于重要性采样的宽带雷达检测门限设置原理
3.1 重要性采样
重要性采样算法的核心思想是按提议分布采样,使采样能够更多地采到对计算期望分位数有利的样本,使原稀有样本不再“稀有”,从而大幅减小仿真样本数,缩短运行时间。
设随机变量z的概率密度函数为p(z),则函数f(z)的期望可表示为
(4)
也可写作
(5)
其中q(z)是提议分布的概率密度函数。由z在q(z)上采样{z1,z2,…,zN}也可估计f(z)的期望,即
(6)
定义样本权重
(7)
文献给出了提议分布的选取方法和优化方法[17-19],若p(z)已知,则可选取合适的q(z),由式(7)计算每个样本的权重,代入式(6)即可计算f(z)的期望。
3.2 宽带雷达检测器虚警概率与门限的关系
如图2,宽带检测器判决结果I{Λ(x)>T}是检验统计量Λ(x)的阶跃函数,在H0情况下,将按原概率密度函数p(x)采样获得回波样本输入检测器,只有极少数检验统计量可以过门限以统计虚警。因此考虑增大噪声功率,用图示提议分布q(x)进行重要性采样。即设原分布和与提议分布的概率密度函数分别为
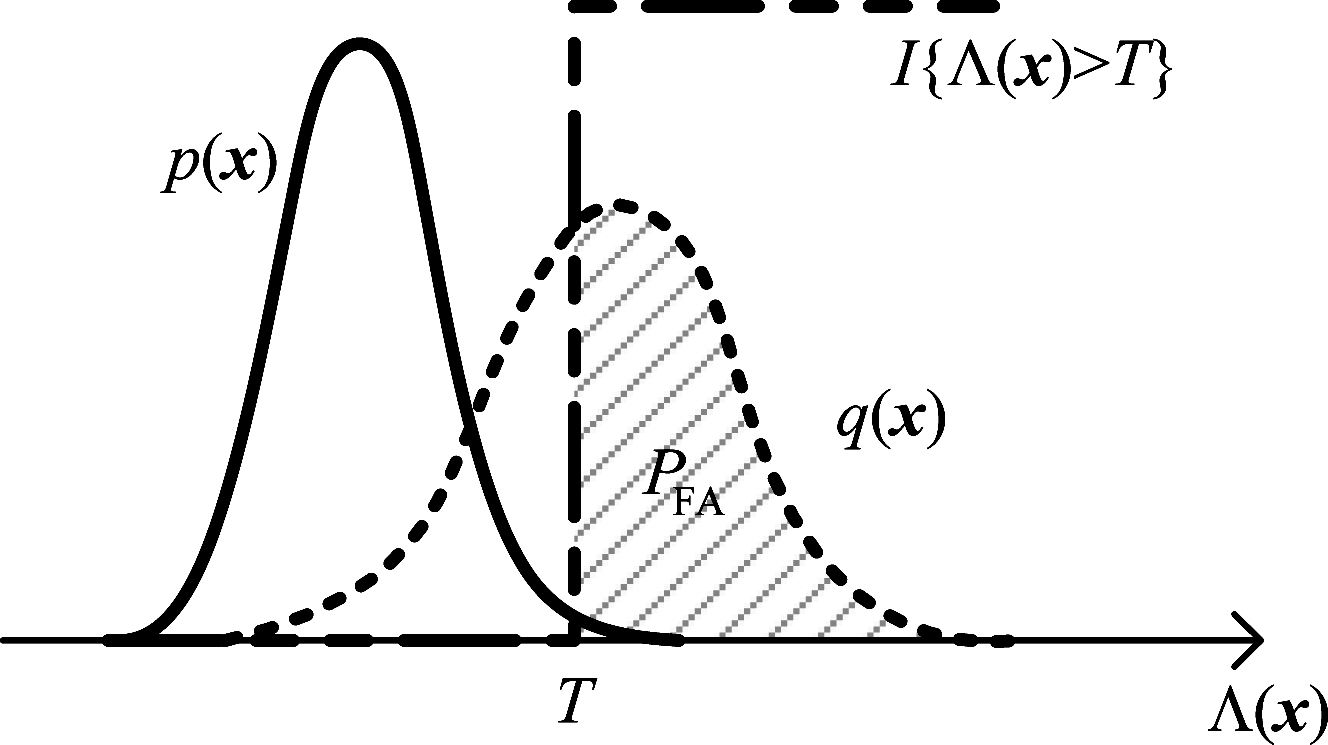
图2 引入重要性采样后检验统计量概率密度函数示意图
Fig.2 The schematic diagram of the probability density function of test statistics after importance sampling
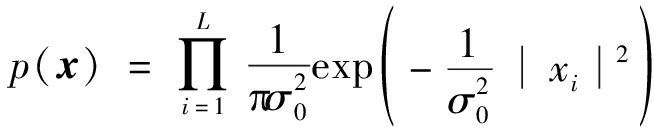
(8)
(9)
提议分布方差
应略大于
这样虚警概率对应的关注区间内的样本不再是稀有样本,样本效率得以提高。按提议分布采样后虚警与门限的关系可表示为
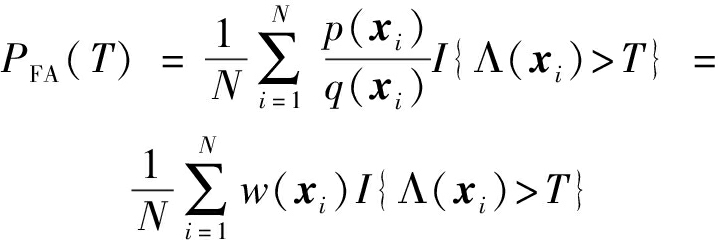
(10)
由此,可绘制引入重要性采样后的宽带雷达检测器虚警概率与门限的关系曲线,用线性插值的方法确定虚警概率对应的待求门限。
3.3 实现方法
基于重要性采样的宽带雷达检测门限设置方法的具体步骤如下:
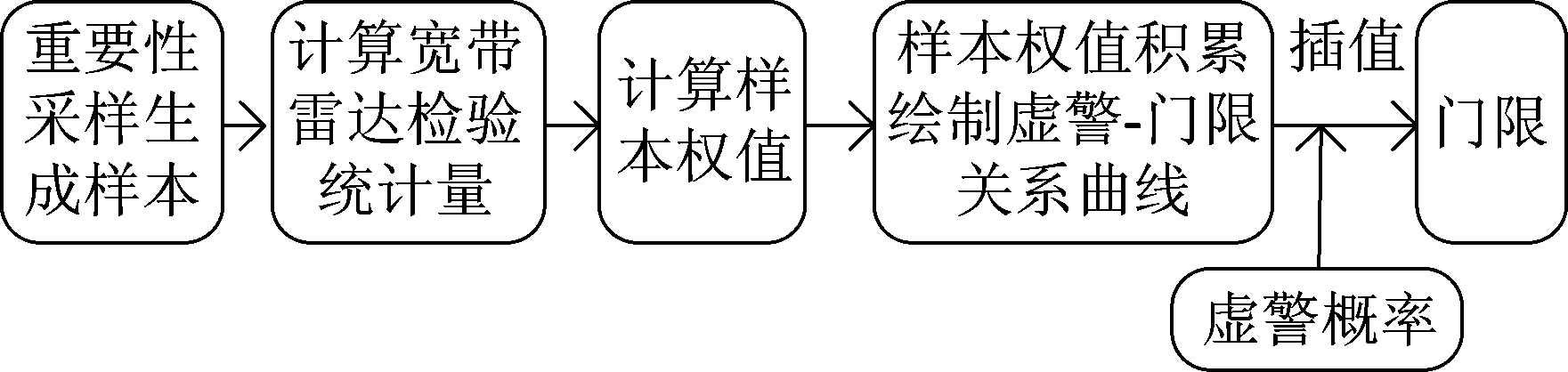
图3 基于重要性采样的宽带雷达检测门限设置流程图
Fig.3 The flow chart of wideband radar detection threshold calculation based on importance sampling
A.设置提议分布q(x),按q(x)生成N个噪声样本
B.将噪声样本输入宽带雷达检验统计量生成器,得到检验统计量Λ(xi),i=1,2,…,N;
C.计算权值
D.由式(10)积累样本权值计算虚警,绘得虚警与门限的关系曲线;
E.对上述曲线线性插值得到给定虚警概率对应的门限。
4 仿真结果分析
4.1 积分检测器
为验证所提方法的正确性,本节以具有解析解的积分检测器为例进行仿真分析。积分检测器将检测窗内所有距离单元的能量进行累积,再将累积结果与门限比较,从而判断有无目标,其检验统计量计算方法为
(11)
在H0情况下,样本的原概率分布和提议分布分别具有式(8)和式(9)的形式,仿真设置两分布的参数
检测窗长L=160,样本数N=105,将两种分布的噪声样本分别输入检测器,所得检验统计量的统计直方图如图4。
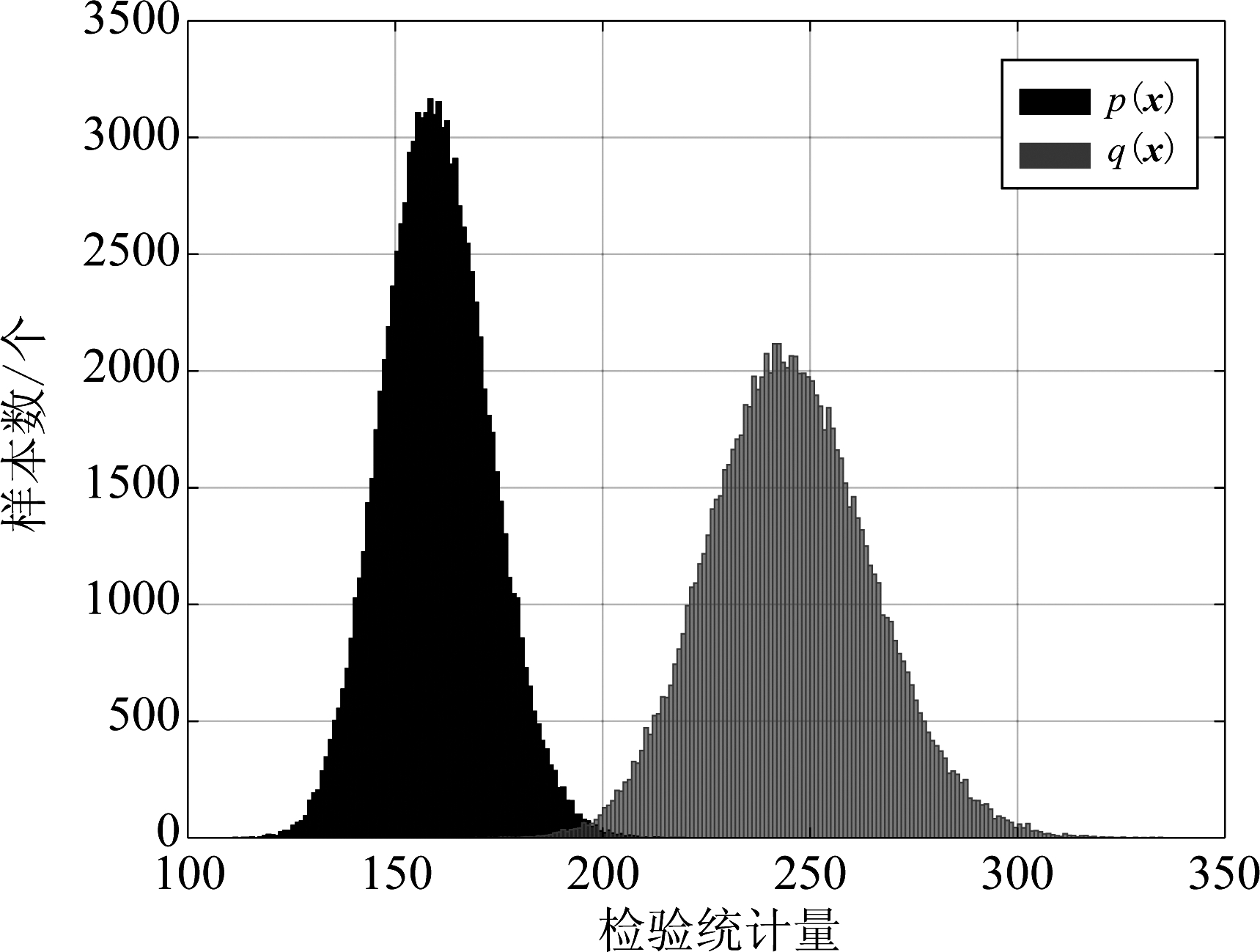
图4 检验统计量直方图
Fig.4 Histogram of test statistics
4.1.1 有效性分析
分别用传统排序插值、P2算法和本文所提的重要性采样三种方法绘制积分检测器虚警概率与门限的关系曲线,结果如图5。可见当虚警概率在10-1至10-10范围内时,重要性采样方法绘得的曲线与理论值近似,可验证所提方法的有效性;然而当虚警概率小于10-4时,排序插值方法和 P2 算法受样本数量限制而失效。
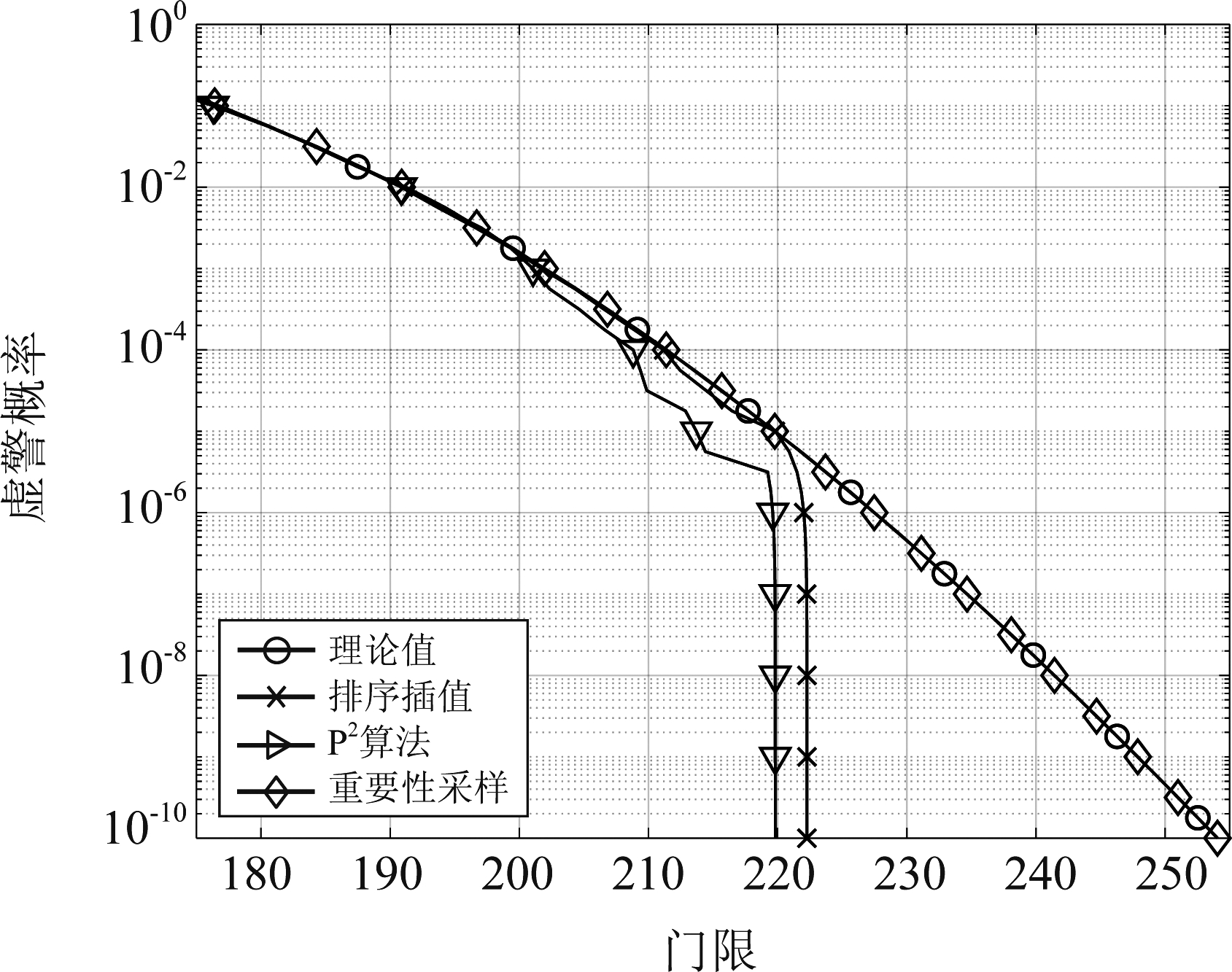
图5 积分检测器虚警与门限关系曲线
Fig.5 False alarm-threshold relationship curve of the integral detector
4.1.2 精度与用时分析
进行1000次蒙特卡洛仿真,三种方法计算10-3虚警概率对应门限的箱线图如图6。可见重要性采样方法的结果分布相对更集中,离群值更少,结果更稳定。
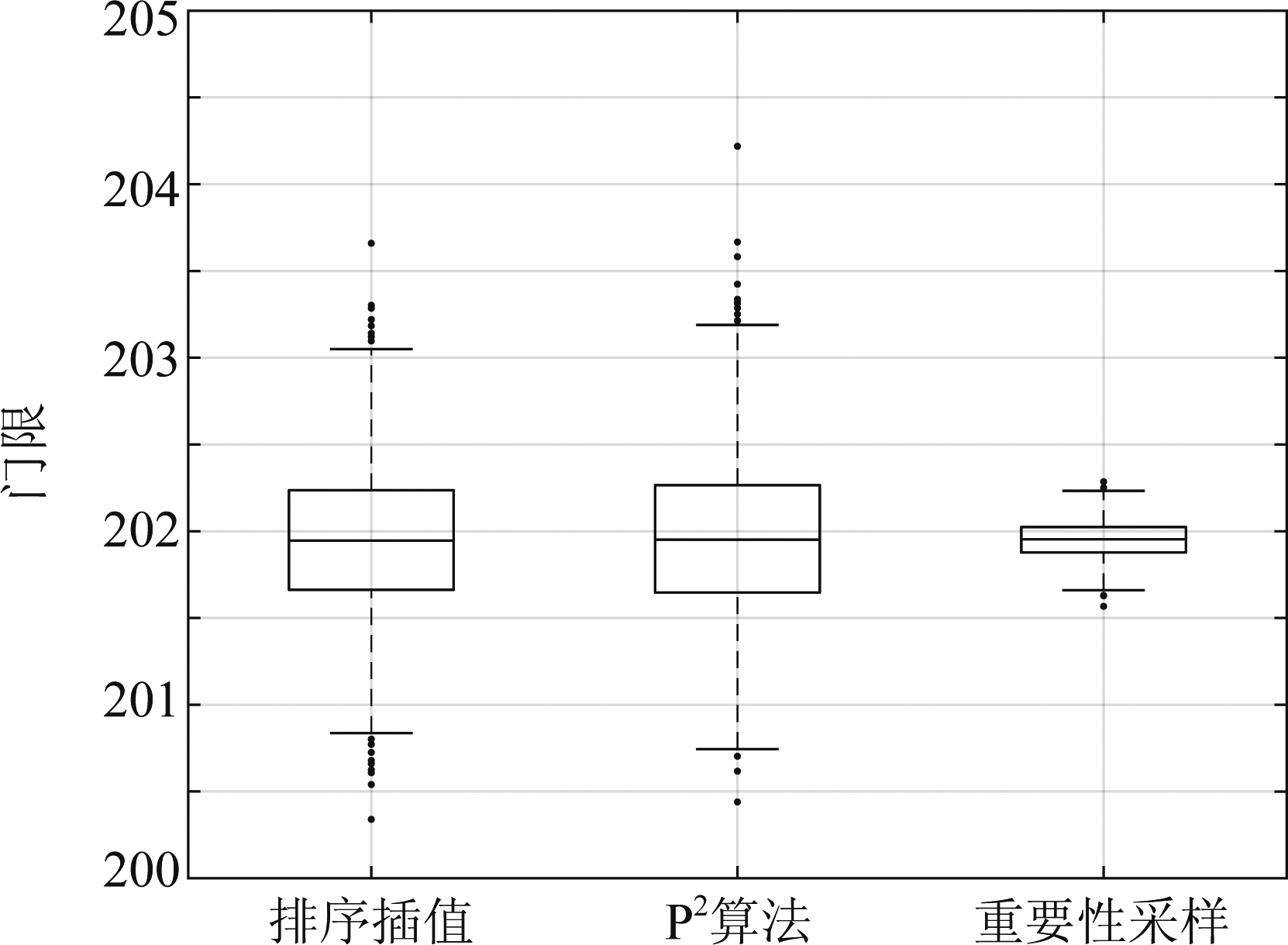
图6 排序插值、P2算法、重要性采样方法箱线图
Fig.6 The box plots obtained by sorting and interpolating method, P2 algorithm, importance sampling method
三种方法所得门限的均方误差与样本数的关系如图7所示。图中横坐标是样本数,纵坐标是1000次蒙特卡洛仿真所得门限的均方误差。可见所提方法的门限计算精度相比于排序插值、P2算法的计算精度更高。若达到图示相同的均方误差,排序插值、P2算法、重要性采样三种方法分别用时37.53 s、23.61 s、19.33 s,重要性采样方法用时最少。
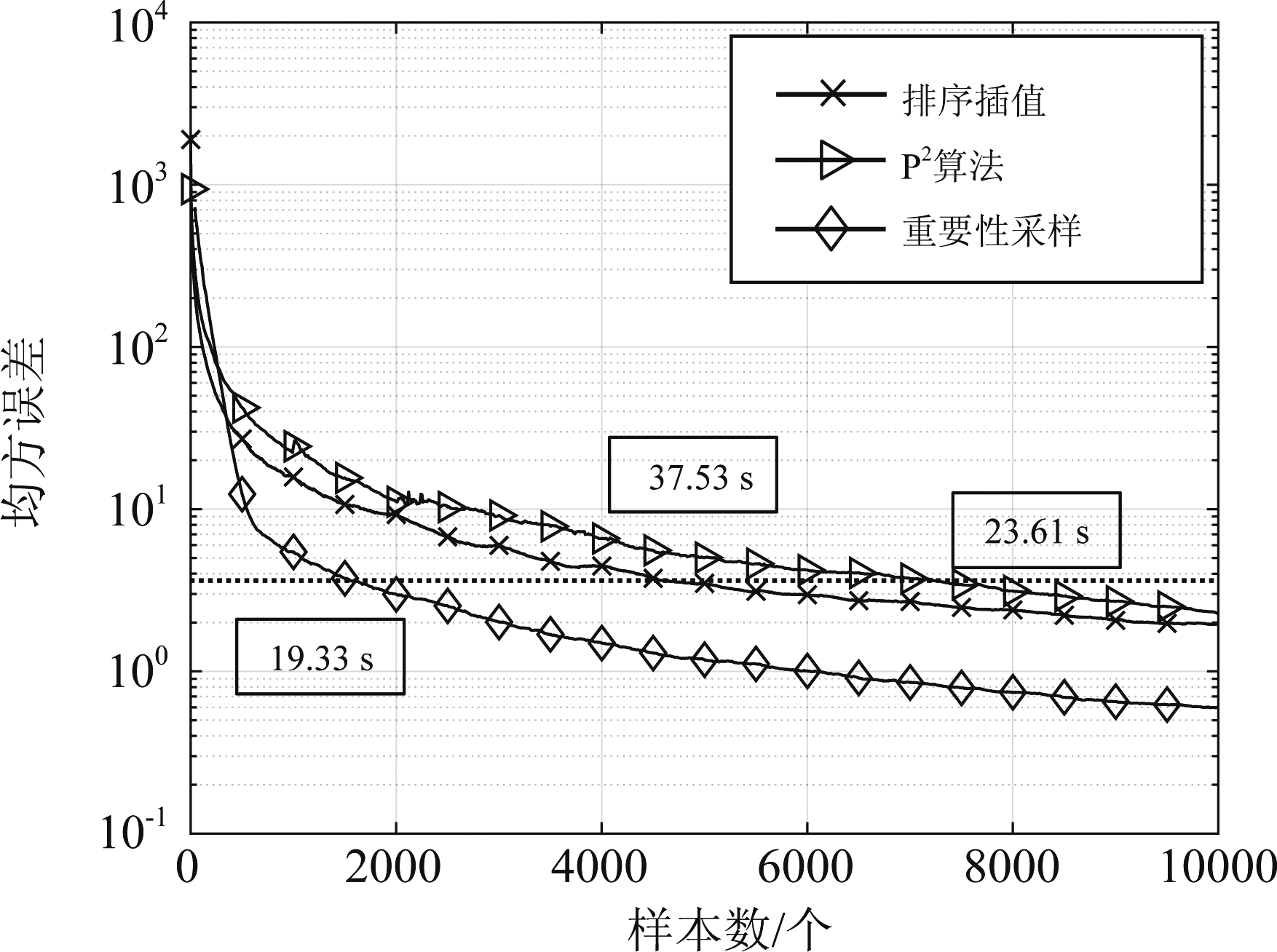
图7 排序插值、P2算法、重要性采样方法均方误差
Fig.7 The mean square error obtained by sorting and interpolating method, P2 algorithm, importance sampling method
三种方法具体用时如表1。
表1 排序插值、P2算法、重要性采样方法用时比较
Tab.1 Time comparisons of sorting and interpolating method, P2 algorithm, importance sampling method
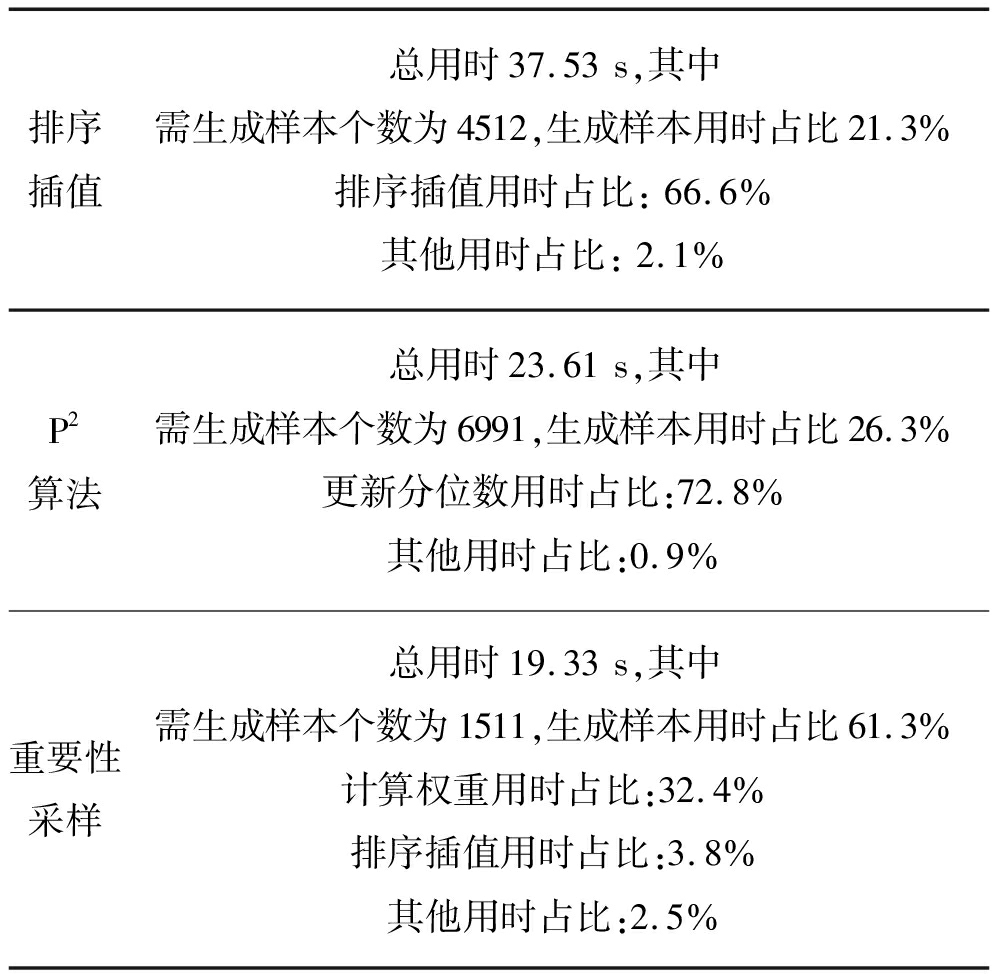
排序插值总用时37.53s,其中需生成样本个数为4512,生成样本用时占比21.3%排序插值用时占比:66.6%其他用时占比:2.1%P2算法总用时23.61s,其中需生成样本个数为6991,生成样本用时占比26.3%更新分位数用时占比:72.8%其他用时占比:0.9%重要性采样总用时19.33s,其中需生成样本个数为1511,生成样本用时占比61.3%计算权重用时占比:32.4%排序插值用时占比:3.8%其他用时占比:2.5%
4.2 SSD-GLRT检测器
以难以求得解析门限的SSD-GLRT检测器为例,SSD-GLRT检测器通过对检测窗内各距离单元回波能量加权来减小含有弱散射点或无散射点的距离单元回波对宽带检测器检测性能的影响。设检测窗内目标散射点密度为α,则有SSD-GLRT检测器检验统计量的计算方法为
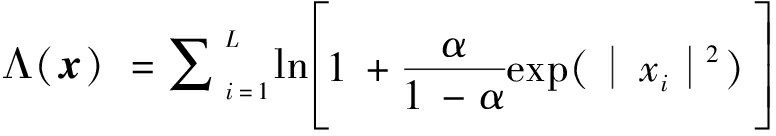
(12)
仿真设α=0.1,检测窗长L=10,提议分布
样本数N=105或N=107,分别统计传统排序插值方法、原P2算法和重要性采样三种方法得到的门限与虚警关系曲线如图8。可见样本数为105相比于样本数为107的情况,排序插值、P2算法两种方法受样本数量的限制而无法准确获得相对较低虚警概率对应的曲线。在有限样本下,所提方法相比于排序插值、P2算法的计算规模更大,解决了SSD-GLRT宽带检测器门限求解的难题。
图8 SSD-GLRT检测器虚警与门限关系曲线
Fig.8 False alarm-threshold relationship curve of the SSD-GLRT detector
5 结论
本文对宽带雷达检测门限设置方法展开了研究,针对某些无法或难以求得解析门限的宽带检测器,给出了基于重要性采样的宽带雷达检测器门限设置方法。通过仿真实验,得到所提方法相比于传统排序插值、经典P2算法计算规模更大、精度更高、速度更快的结论。同时所提方法也可用于低虚警宽带雷达检测器虚警概率的评估。
[1] LONG Teng, ZENG Tao, HU Cheng, et al.High resolution radar real-time signal and information processing[J].China Communications, 2019, 16(2): 105-133.
[2] LONG Teng, LIANG Zhennan, LIU Quanhua.Advanced technology of high-resolution radar: Target detection, tracking, imaging, and recognition[J].Science China Information Sciences, 2019, 62(4): 1-26.
[3] VAN DER SPEK G A.Detection of a distributed target[J].IEEE Transactions on Aerospace and Electronic Systems, 1971, AES-7(5): 922-931.
[4] GERLACH K, STEINER M, LIN F C.Detection of a spatially distributed target in white noise[J].IEEE Signal Processing Letters, 1997, 4(7): 198-200.
[5] HUGHES P K.A high-resolution radar detection strategy[J].IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(5): 663-667.
[6] LONG Teng, ZHENG Le, LI Yang, et al.Improved double threshold detector for spatially distributed target[J].IEICE Transactions on Communications, 2012, E95-B(4): 1475-1478.
[7] 陈新亮, 王丽, 柳树林, 等.高分辨雷达扩展目标检测算法研究[J].中国科学: 信息科学, 2012, 42(8): 1007-1018.
CHEN Xinliang, WANG Li, LIU Shulin, et al.Research on extended target detection for high resolution radar[J].Scientia Sinica(Informationis), 2012, 42(8): 1007-1018.(in Chinese)
[8] 戴奉周, 刘宏伟, 吴顺君.一种基于顺序统计量的距离扩展目标检测器[J].电子与信息学报, 2009, 31(10): 2488-2492.
DAI Fengzhou, LIU Hongwei, WU Shunjun.Order-statistic-based detector for range spread target[J].Journal of Electronics & Information Technology, 2009, 31(10): 2488-2492.(in Chinese)
[9] QU Kuiyu, YANG Xiaopeng, LIU Quanhua, et al.Improved generalized likelihood ratio detector for range-spread target[C]∥2019 IEEE International Conference on Signal, Information and Data Processing(ICSIDP).Chongqing, China.IEEE, 2019: 1-5.
[10] MUNRO J I, PATERSON M S.Selection and sorting with limited storage[J].Theoretical Computer Science, 1980, 12(3): 315-323.
[11] MANKU G S, RAJAGOPALAN S, LINDSAY B G.Approximate medians and other quantiles in one pass and with limited memory[J].ACM SIGMOD Record, 1998, 27(2): 426-435.
[12] JOSEPH A G, BHATNAGAR S.An adaptive and incremental approach to quantile estimation[C]∥2019 IEEE 58th Conference on Decision and Control(CDC).Nice, France.IEEE, 2019: 6025-6031.
[13] DUNNING T.The t-digest: Efficient estimates of distributions[J].Software Impacts, 2021, 7(100049).
[14] JAIN R, CHLAMTAC I.The P2 algorithm for dynamic calculation of quantiles and histograms without storing observations[J].Communications of the ACM, 1985, 28(10): 1076-1085.
[15] BISHOP C.Pattern recognition & machine learning[M].Amsterdam: Elsevier, 1992.
[16] 黄巍, 贺知明, 石云江, 等.滑窗检测在宽带雷达信号处理中的应用研究[J].信号处理, 2003, 19(5): 494-497.
HUANG Wei, HE Zhiming, SHI Yunjiang, et al.The study of sliding window detection method in broadband radar signal processing[J].Signal Processing, 2003, 19(5): 494-497.(in Chinese)
[17] BUGALLO M F, ELVIRA V, MARTINO L, et al.Adaptive Importance Sampling: The past, the present, and the future[J].IEEE Signal Processing Magazine, 2017, 34(4): 60-79.
[18] DOWLING M, NASSAR J, DJURIC P M, et al.Improved adaptive importance sampling based on variational inference[C]∥2018 26th European Signal Processing Conference(EUSIPCO).Rome.IEEE, 2018: 1632-1636.
[19] WANG Hechuan, BUGALLO M F, 
P M.Adaptive importance sampling supported by a variational auto-encoder[C]∥2019 IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing(CAMSAP).Le Gosier, Guadeloupe.IEEE, 2019: 619-623.
