1 引言
自适应滤波算法已经广泛应用到了许多信号处理的应用中,比如主动噪声控制、信道估计、回声消除等[1]。经典的最小均方算法(least mean square algorithms,LMS)、归一化最小均方算法(normalized least mean square algorithms,NLMS)由于其简洁性和适用性得到广泛的应用。最小均方自适应滤波算法是基于最小均方误差准则提出的,该算法输入信号没有被噪声污染,可以精确地估计未知系统的参数,从而达到较好的收敛性能。然而,在实际应用中,由于人工误差、采样误差以及仪器误差等的存在,自适应滤波器的输入信号通常会被噪声污染,在此情况下最小均方算法就会产生有偏估计,其收敛性能就会恶化。因此针对此问题,研究者们提出了含误差变量模型,其假设输入信号与输出信号中的所有变量被噪声污染[2-3]。对于上述EIV模型的一个较好的解决方法是总体最小二乘估计方法[4],即通过减少输入与输出信号中的扰动来寻找所需的最优解。研究者们也基于总体最小二乘估计方法提出了一些自适应滤波算法,例如总体最小均方算法(total least mean square,TLMS)[5]、梯度下降总体最小二乘算法(gradient-descent total least-squares,GDTLS)[6]以及递归总体最小二乘算法(recursive total least-squares,RTLS)[7]等。
然而,在许多实际应用中,由于脉冲噪声或者较大的异常值的存在,以上提及的算法的收敛性能就会严重恶化。为了提高算法在非高斯环境下的鲁棒性和增强其抑制脉冲噪声的能力,基于总体最小二乘算法已经提出了一些改进的鲁棒算法。在信息理论学习中,熵对于异常值有较好的鲁棒性,因此提出了最小误差熵准则,与此同时也提出了一些基于最小误差熵准则的自适应滤波算法。其中,当EIV模型的输出端被非高斯噪声污染时,作为最小误差熵准则的拓展,沈鹏程等提出了最小总体误差熵(minimum total error entropy,MTEE)自适应滤波算法[8],它在含误差变量模型的非高斯噪声环境下体现了较好的鲁棒性。但是,基于最小误差熵准则改进的算法在每次迭代时采用Parzen窗的方法估计误差分布,特别是当滑动窗的长度较大时,计算复杂度就会特别高。如前所述,由于复杂的数学表达式,对该算法进行严格的理论性能分析和算法改进也是十分困难和复杂的。
相比最小误差熵准则,另一种信息理论学习准则——最大相关熵准则由于其计算简单、易于实现等优点,受到了很大关注。相关熵是通过引入一个核函数来进行广义相关度量,最大相关熵准则采用的是高斯核函数,在高斯核中,相关性涉及到误差的所有二阶矩,并且它对异常值有着较好的抑制作用[9]。基于最大相关熵准则,提出了多种改进的自适应滤波算法[10-11],所提出的算法在非高斯噪声下的线性回归模型中具有较好的鲁棒性。然而,提出的这些基于最大相关熵准则的自适应滤波算法都假设输入端不被噪声污染,其仍然不能很好地应用到含误差变量模型中。为了处理这个问题,王飞等提出了最大总体相关熵自适应滤波算法[12],它是将最大相关熵准则和总体最小二乘估计的方法结合起来实现的,在非高斯噪声环境下的EIV模型中展现了较好的鲁棒性。在相关熵准则中,高斯核函数并不总是最优的选择[13-14]。在此基础上,陈霸东等提出了以广义高斯密度函数(generalized Gaussian density,GGD)为核的广义最大相关熵准则,分析了算法的多种性质,并在其基础上提出了广义最大相关熵准则(generalized maximum correntropy criterion,GMCC)自适应滤波算法[14]。广义最大相关熵准则涉及到误差信号的高阶(含二阶)绝对矩,与最大相关熵准则相比,所提出的广义最大相关熵准则是非常普遍和灵活的,因此可以比最大相关熵算法展现更好的鲁棒性能。然而,在含误差变量模型中,广义最大相关熵准则自适应滤波算法也会产生偏差估计。为解决此问题,受到最大总体相关熵(maximum total correntropy,MTC)算法的启发,将广义最大相关熵准则与总体最小二乘方法结合起来,利用它们两者的优势,提出广义最大总体相关熵自适应滤波算法。相比最大总体相关熵算法的高斯核,所提出这种应用广义高斯核函数的算法更加的普遍和灵活。同时,在高斯输入与相关输入两种情况下,对该算法与已有的算法进行了系统辨识下的算法比较仿真,经过不同噪声下的仿真结果得出,所提出的广义最大总体相关熵自适应滤波算法有着较好的收敛性能和鲁棒性。
本文其余部分的内容安排如下:在第二部分回顾了含误差变量模型和梯度下降总体最小二乘算法。第三部分详细推导了广义最大总体相关熵算法。第四部分在系统辨识场景下,进行了不同噪声条件下的仿真。最后一部分给出了结论。
2 含误差变量模型及总体最小二乘算法
2.1 含误差变量模型
在实际环境中,系统输入与输出信号都可能被噪声污染,为了能够准确描述这一模型,研究者们在原有的系统辨识模型上加入了输入噪声带来的干扰,这一模型也被叫做含误差变量(EIV)模型[15]。
假设一个未知系统为L阶的线性系统满足
d(n)=hTx(n)
(1)
其中,x(n)表示未知系统在n时刻的输入信号,h表示所需要寻找的未知系统的权值向量,d(n)表示未知系统在相应时刻下的输出信号。
在EIV模型中,输入信号与输出信号都是假设被噪声污染的,分别表示为
(2)
(3)
其中,
表示在时刻n含有输入噪声的输入信号,
表示为对应时刻的含有噪声的输出信号,u(n)表示自协方差矩阵为
的输入噪声,ν(n)表示输出噪声,它是由方差为
的背景噪声νA(n)和方差为
的脉冲噪声νB(n)组成的。
2.2 总体最小二乘算法的回顾
总体最小二乘(TLS)估计方法是通过最小化输入与输出信号之间的扰动来寻找最优解,梯度下降总体最小二乘(GDTLS)自适应滤波算法是通过定义式(4)的最小化问题,它是使用瑞利熵作为代价函数计算出来的[6,16]。
(4)
其中,
表示为输出信号噪声与输入信号噪声方差的比值。
将式(4)中的样本均值计算替换为期望计算,梯度下降总体最小二乘算法的代价函数表示为
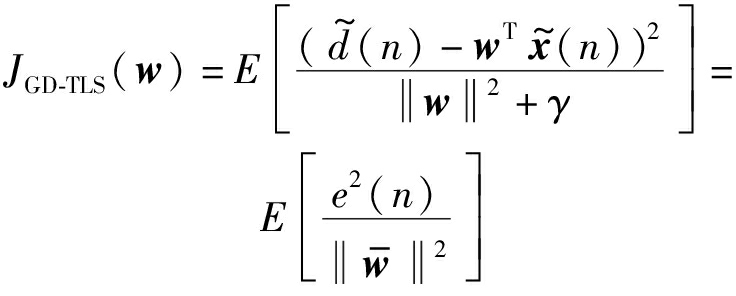
(5)
其中,
表示为修正后的增广权值向量,
表示为输出误差信号。
3 广义最大总体相关熵算法的推导
给定两个随机变量X和Y,两个随机变量的相关熵定义为如下
(6)
其中E表示为期望运算,κ(·,·)是位移不变默瑟核,FXY(x,y)表示为随机变量(X,Y)的联合分布函数。
在广义最大相关熵准则(GMCC)中,将广义高斯密度函数作为相关熵的核函数,表示如下
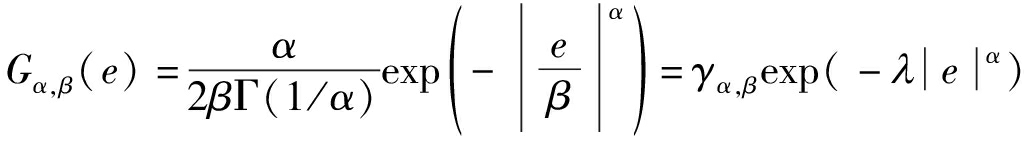
(7)
其中,Γ(·)是伽马函数,α>0是形状参数,β>0是规模参数,λ=1/βα是核参数,γα,β=α/2βΓ(1/α)是归一化常数。
因此广义最大相关熵准则可以定义为
Vα,β(X,Y)=E[Gα,β(X-Y)]
(8)
广义最大相关熵算法的最优解是通过最大化如下的代价函数来获得
JGMCC(w)=E[Gα,β(e(n))]=
E[γα,βexp(-λ|e(n)|α)]
(9)
结合总体最小二乘估计和广义最大相关熵准则两者的优势,提出了一种鲁棒的广义最大总体相关熵自适应滤波算法,其通过最大化以下的代价函数来获得最优解
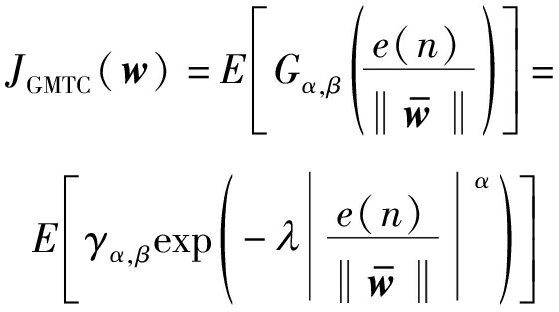
(10)
通过对式(10)中的代价函数JGMTC(w)对w求导,可以得到梯度为
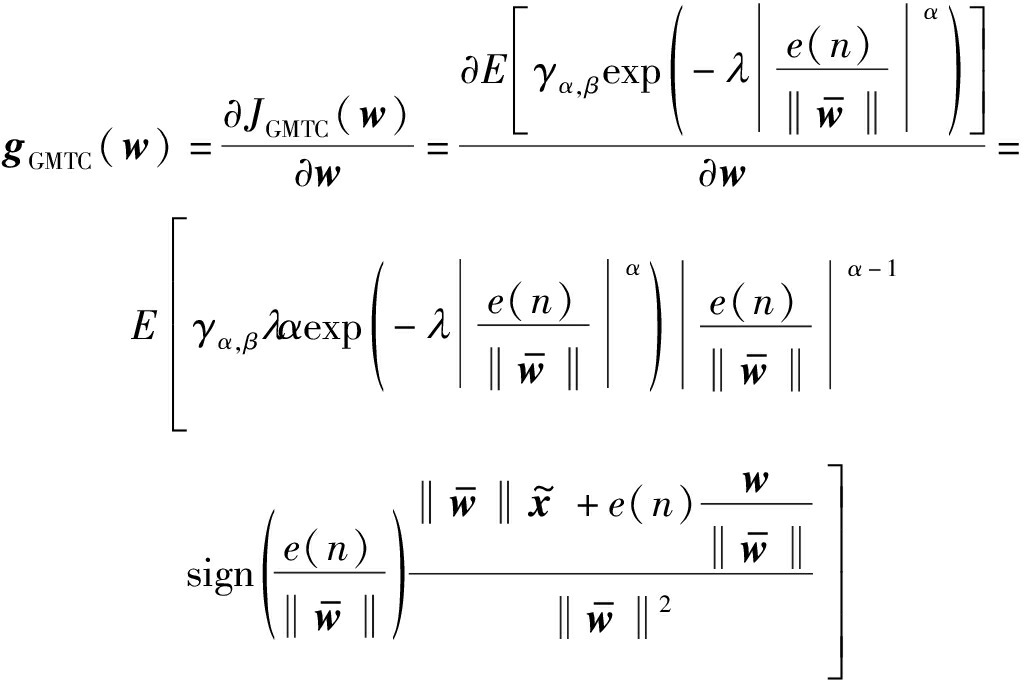
(11)
在基于梯度下降的自适应滤波算法中,通常使用梯度的瞬时值来代替梯度。通过去掉式(11)中的期望运算,可以得到近似的瞬时梯度为
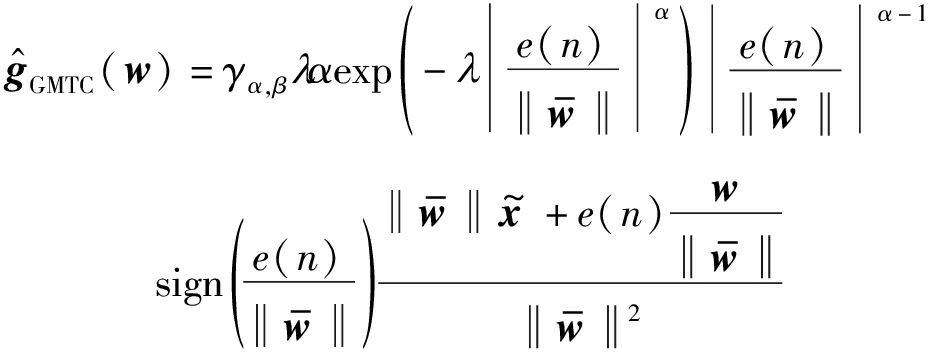
(12)
因此基于梯度下降的广义最大总体相关熵自适应滤波算法在时刻n的权值向量更新公式为
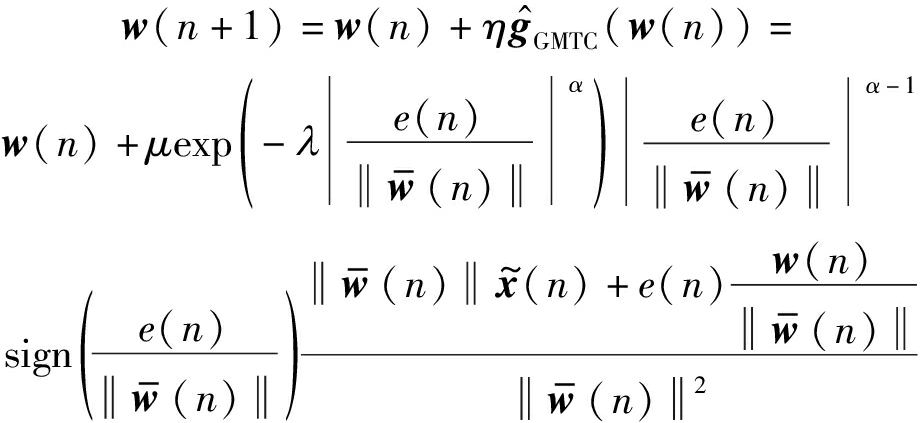
(13)
其中,μ=ηγα,βλα是步长参数并且η>0。
广义最大总体相关熵自适应滤波算法的伪代码总结在表1中。
表1 GMTC算法伪代码
Tab.1 The pseudo code of the GMTC algorithm
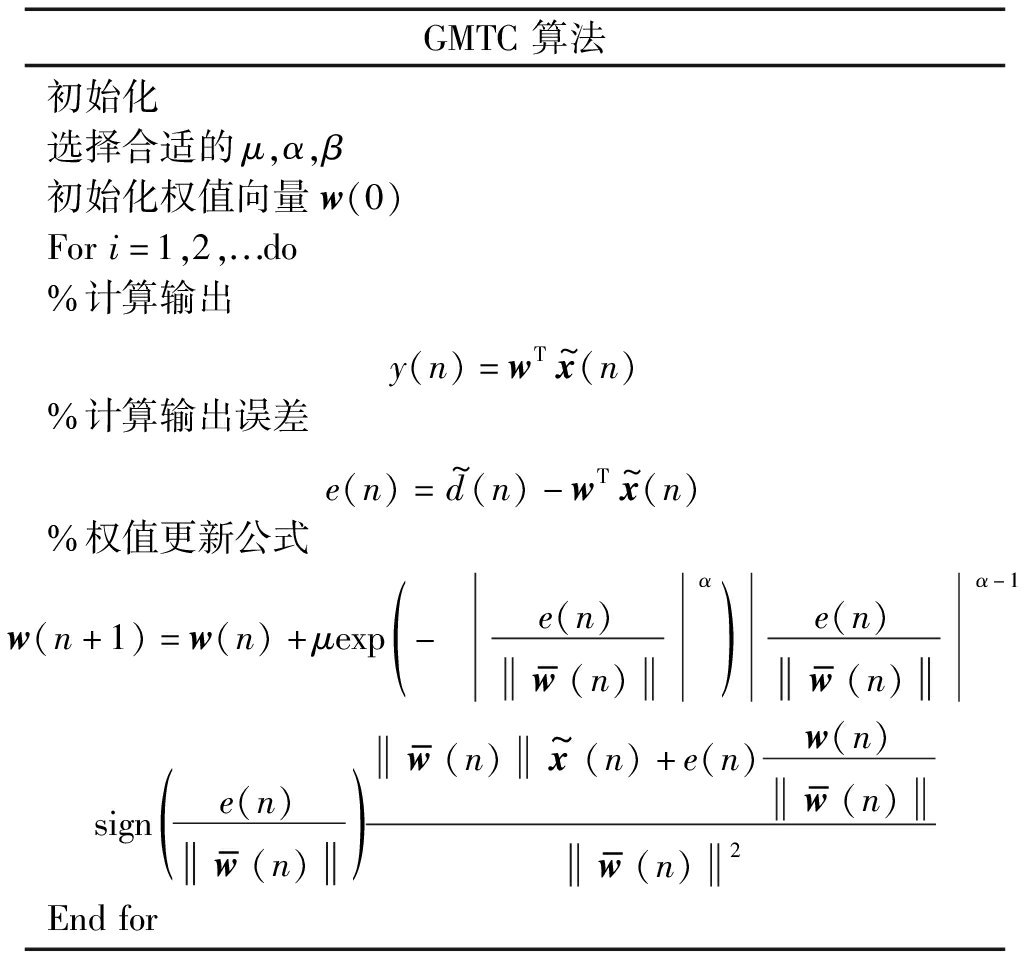
GMTC算法初始化选择合适的μ,α,β初始化权值向量w(0)Fori=1,2,...do%计算输出y(n)=wTx^(n)%计算输出误差e(n)=d^(n)-wTx^(n)%权值更新公式w(n+1)=w(n)+μexp -吠e(n)w-(n)α()e(n)w-(n)α-1sign e(n)w-(n)()w-(n)x^(n)+e(n)w(n)w-(n)w-(n)2Endfor
当α=2时,上面的权值向量更新公式就变成如下的式(14)
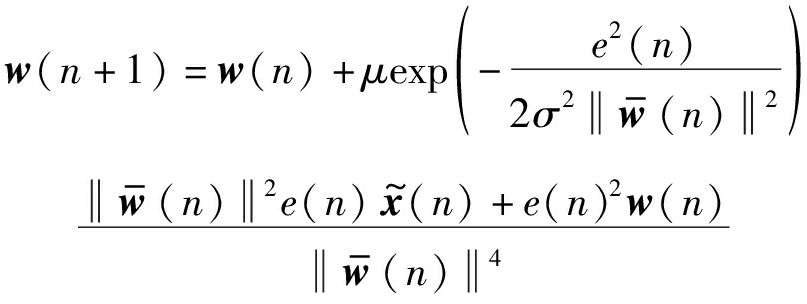
(14)
可以看出,当α=2时,广义最大总体相关熵算法就转化成为了最大总体相关熵算法。其中的广义高斯核函数就变成了高斯核函数。
4 算法仿真
在这一小节中,使用MATLAB软件仿真来验证所提出的算法的性能。未知系统的权值向量h是由-0.5到0.5均匀分布生成的长度为1,维度为9的向量。输入噪声和输出背景噪声分别是方差为
和
的零均值高斯噪声。输出信号脉冲噪声是由伯努利高斯过程产生的,如νB(n)=b(n)p(n),其中b(n)是伯努利过程,它的概率密度函数为P(b(n)=1)=Pr和P(b(n)=0)=1-Pr,Pr是异常值发生的概率,p(n)是方差为
的零均值高斯过程。选择合适的步长值确保所比较的算法有相同的初始收敛速度。用归一化稳态均方偏差NMSD=10log(‖w(n)-h‖2/‖h‖2)来衡量算法的收敛性能。最后所有的结果是由500次独立的蒙特卡罗运行下的取平均值生成的。
4.1 高斯输入情况下的仿真
在这一小节中,输入信号是由单位方差的零均值高斯信号生成的。在算法比较中,比较了最大相关熵(MCC)算法[10]、广义最大相关熵(GMCC)算法[14]、梯度下降总体最小二乘(GDTLS)算法[6]、最大总体相关熵(MTC)算法[12]、总体最小均值M估计(TLMM)算法[16]以及所提出的广义最大总体相关熵(GMTC)算法。选择不同的脉冲噪声发生概率以及不同的输出噪声与输入噪声方差比的情况下比较了不同算法的收敛性能。
图1和图2为不同算法在高斯输入条件下的比较结果,在表2中给出了高斯输入时两种脉冲噪声发生概率下的算法的仿真参数。通过上面两图的比较结果可以得出,GDTLS算法在脉冲噪声收敛性能变差,甚至当脉冲噪声发生概率变大时会发散,而所提出的鲁棒算法在脉冲噪声环境下能够很好的收敛,在脉冲噪声发生概率越大时,相比GDTLS算法的鲁棒性能就越好。而且通过比较也可以得出,所提出的广义最大总体相关熵算法相比最大总体相关熵算法、总体最小均值M估计算法有着更低的稳态均方偏差,鲁棒性更好。
表2 高斯输入下的仿真参数
Tab.2 Simulation parameters under Gaussian input
算法图1参数值图2参数值文献[6]算法μ=0.015μ=0.015文献[10]算法σ=0.8,μ=0.04σ=0.8,μ=0.04文献[12]算法σ=0.8,μ=0.03σ=1,μ=0.03文献[14]算法α=3,β=1.2,μ=0.04α=3,β=1.2,μ=0.04文献[16]算法μ=0.023μ=0.027本文算法α=3,β=1.3,μ=0.038α=2.8,β=1.2,μ=0.042
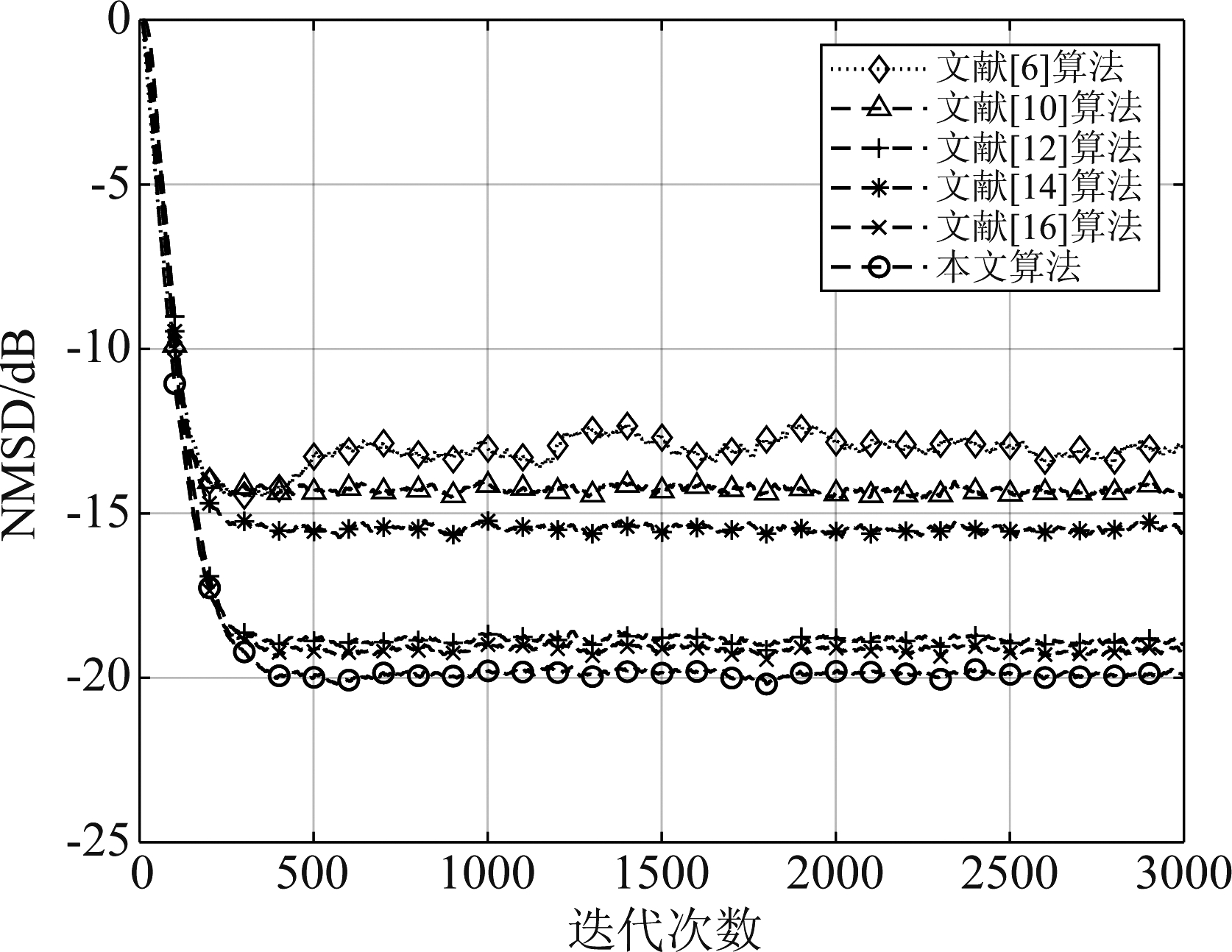
图1 在
下的平均NMSD学习曲线
Fig.1 Average NMSD learning curves with 
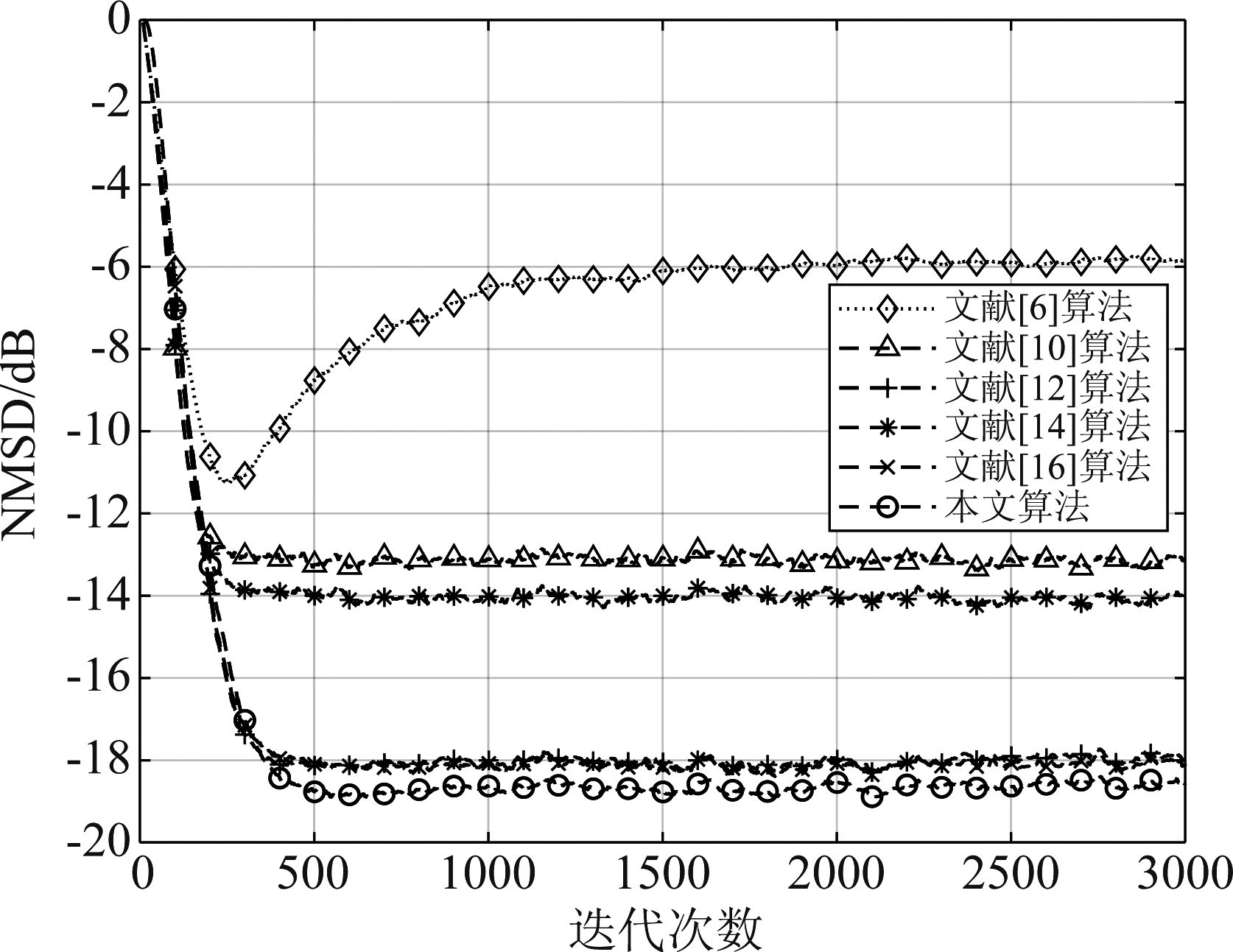
图2 在
Pr=0.05下的平均NMSD学习曲线
Fig.2 Average NMSD learning curves with 
4.1 相关输入的情况
在这一小节中,输入信号使用的是相关输入信号,它是通过一个一阶系统过滤一个零均值单位方差信号产生的,一阶自回归模型为G(z)=1/(1-0.8z-1)[16]。同样是选择两种不同的脉冲噪声发生概率以及不同的输出噪声与输入噪声方差比的情况下进行算法比较仿真。
图3和图4为在上述描述的相关输入信号下的不同算法比较结果,在表3中给出了相关输入下两种脉冲发生概率下的算法仿真时的参数。通过观察也可以得出所提出的鲁棒算法可以显著提高GDTLS算法在脉冲噪声环境下的鲁棒性,这种提升在脉冲噪声发生概率越大时比较效果越明显。而且在相关输入信号下所提出的广义最大总体相关熵算法也有着比最大总体相关熵、总体最小均值M估计算法较为出色的收敛性能。
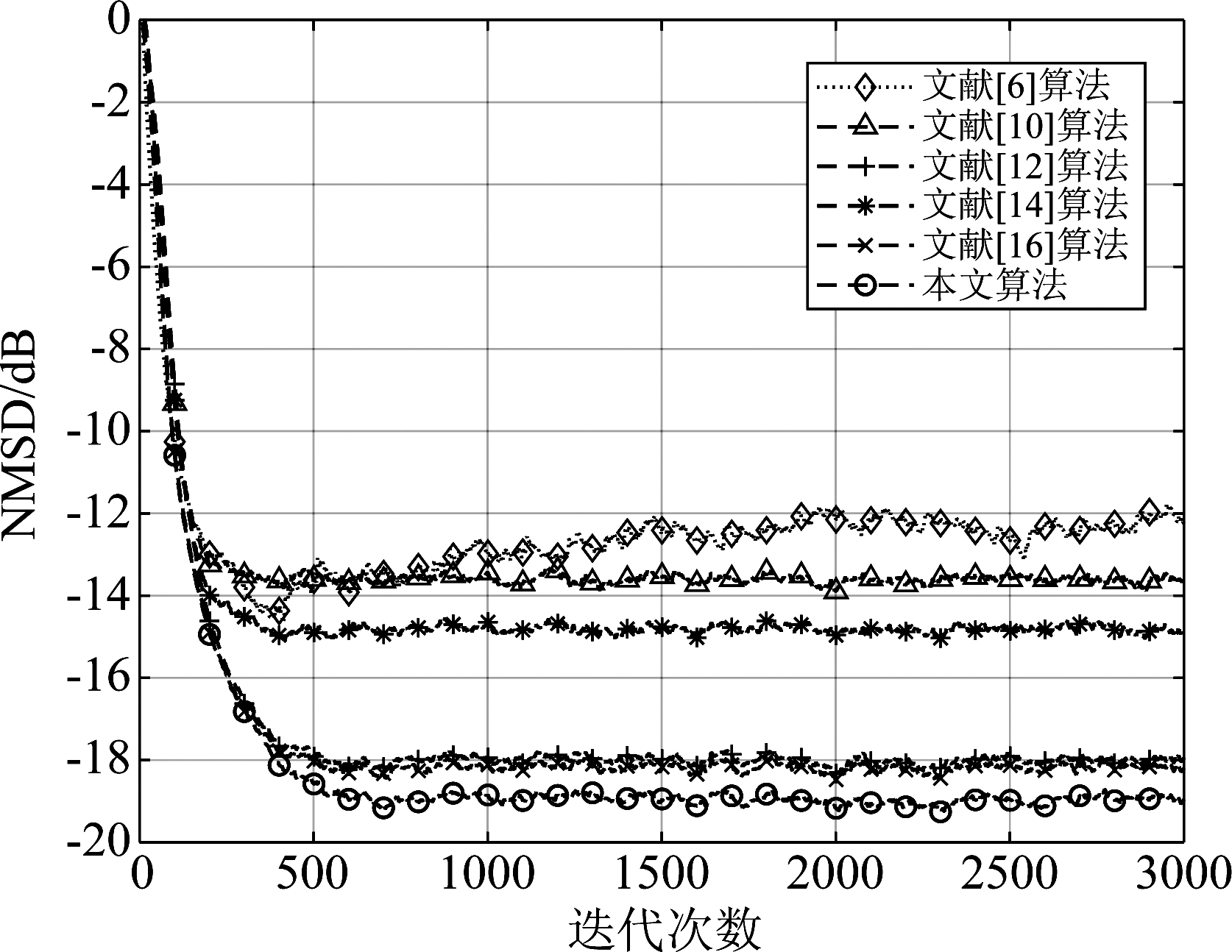
图3 在下的平均NMSD学习曲线
Fig.3 Average NMSD learning curves with
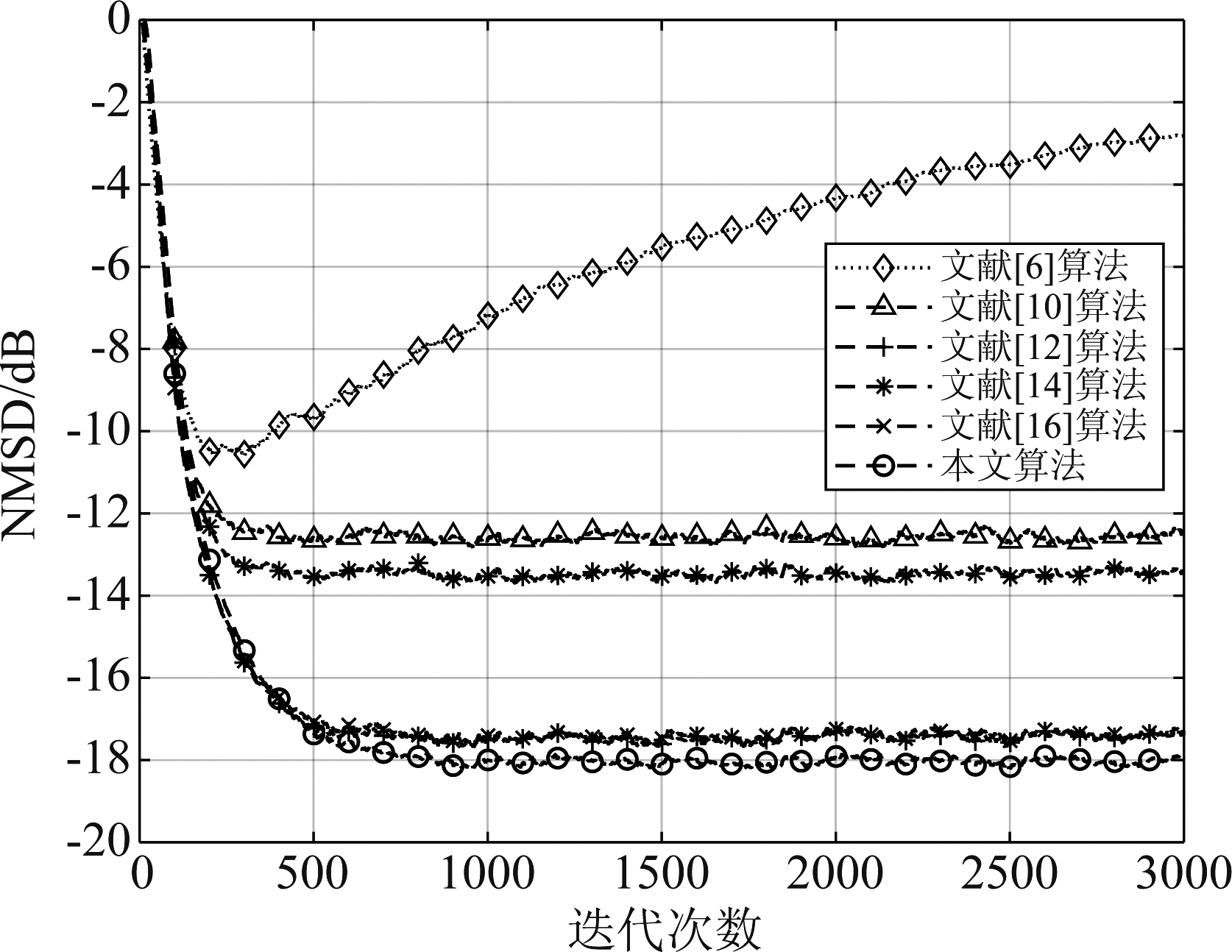
图4 在
下的平均NMSD学习曲线
Fig.4 Average NMSD learning curves with
表3 相关输入下的仿真参数
Tab.3 Simulation parameters under correlated input
算法图3参数值图4参数值文献[6]算法μ=0.015μ=0.015文献[10]算法σ=0.8,μ=0.04σ=0.8,μ=0.04文献[12]算法σ=0.8,μ=0.03σ=1,μ=0.03文献[14]算法α=3,β=1.2,μ=0.04α=3,β=1.2,μ=0.04文献[16]算法μ=0.023μ=0.027本文算法α=3,β=1.3,μ=0.038α=2.8,β=1.2,μ=0.043
5 结论
在本文中,针对含有脉冲噪声的EIV模型,通过利用广义最大相关熵准则以及总体最小二乘估计方法的优点,提出了一种能够抑制脉冲噪声的广义最大总体相关熵(GMTC)自适应滤波算法。所提出的算法不仅可以在输入含有噪声的情况下实现无偏估计,也可以更好的抑制脉冲噪声的干扰。分别针对高斯输入和相关输入进行了算法比较仿真,仿真结果表明,所提出的算法提高了GDTLS算法的鲁棒性,其次相比最大总体相关熵(MTC)算法、总体最小均值M估计(TLMM)算法,该算法的收敛性能更好。在接下来的研究工作中,将对所提出的算法进行理论性能分析和改进。
[1] SAYED A H.Fundamentals of adaptive filtering[M].John Wiley & Sons, 2003.
[2] SÖDERSTRÖM T.Errors-in-variables methods in system identification[J].Automatica, 2007, 43(6): 939-958.
[3] MARKOVSKY I, VAN HUFFEL S.Overview of total least-squares methods[J].Signal Processing, 2007, 87(10): 2283-2302.
[4] GOLUB G H, VAN LOAN C F.An analysis of the total least squares problem[J].SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893.
[5] FENG Dazheng, BAO Zheng, JIAO Licheng.Total least mean squares algorithm[J].IEEE Transactions on Signal Processing, 1998, 46(8): 2122-2130.
[6] ARABLOUEI R, WERNER S, 
K.Analysis of the gradient-descent total least-squares adaptive filtering algorithm[J].IEEE Transactions on Signal Processing, 2014, 62(5): 1256-1264.
[7] ARABLOUEI R, 
K, WERNER S.Recursive total least-squares algorithm based on inverse power method and dichotomous coordinate-descent iterations[J].IEEE Transactions on Signal Processing, 2015, 63(8): 1941-1949.
[8] SHEN Pengcheng, LI Chunguang.Minimum total error entropy method for parameter estimation[J].IEEE Transactions on Signal Processing, 2015, 63(15): 4079-4090.
[9] WANG Wenyuan, ZHAO Haiquan, K, et al.Robust adaptive filtering algorithm based on maximum correntropy criteria for censored regression[J].Signal Processing, 2019, 160: 88-98.
[10] SINGH A, PRINCIPE J C.Using Correntropy as a cost function in linear adaptive filters[C]∥2009 International Joint Conference on Neural Networks.Atlanta, GA, USA.IEEE, 2009: 2950-2955.
[11] 宋普查, 赵海全.基于最大混合相关熵准则的主动噪声控制算法[J].信号处理, 2020, 36(6): 942-947.
SONG Pucha, ZHAO Haiquan.Active noise control algorithm based on maximum mixture correntropy criterion[J].Journal of Signal Processing, 2020, 36(6): 942-947.(in Chinese)
[12] WANG Fei, HE Yicong, WANG Shiyuan, et al.Maximum total correntropy adaptive filtering against heavy-tailed noises[J].Signal Processing, 2017, 141: 84-95.
[13] ZHU Yingying, ZHAO Haiquan, ZENG Xiangping, et al.Robust generalized maximum correntropy criterion algorithms for active noise control[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28: 1282-1292.
[14] CHEN Badong, XING Lei, ZHAO Haiquan, et al.Generalized correntropy for robust adaptive filtering[J].IEEE Transactions on Signal Processing, 2016, 64(13): 3376-3387.
[15] 赵海全, 李磊.一种抗冲击噪声的对数总体最小二乘自适应滤波算法[J].电子与信息学报, 2021, 43(2): 284-288.
ZHAO Haiquan, LI Lei.A logarithmic total least squares adaptive filtering algorithm for impulsive noise suppression[J].Journal of Electronics & Information Technology, 2021, 43(2): 284-288.(in Chinese)
[16] LI Lei, ZHAO Haiquan.A robust total least mean M-estimate adaptive algorithm for impulsive noise suppression[J].IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(4): 800-804.
