1 引言
利用机器学习设计无线通信系统是第六代移动通信的重要研究方向。作为一种分布式训练方法,联邦学习[1]可以有效降低集中式训练机器学习模型时存在的数据隐私风险,相对于集中式学习在降低通信开销方面也有潜力[2],是在无线边缘实现人工智能的主流技术之一,在无线网络中有广阔的应用前景[3-4]。最近,联邦学习已经被用于各种无线任务。文献[5]提出了一种基于分布式训练的自动调制分类方法。文献[6]和文献[7]利用联邦学习预测文件流行度,以实现在基站端或在雾无线接入网中的主动缓存。文献[8]提出了基于联邦强化学习的联合协作边缘缓存方法,以减小延迟、提高缓存命中率。
然而,在付诸实际应用之前,联邦学习还面临多方面的挑战,其中一个来自于用户数据集的非独立同分布(Independent and identically distributed,IID)[9],即用户本地所记录的数据分布往往无法反映所有用户数据的全局分布。文献[10-11]发现用户数据集非IID会导致联邦学习精度下降,甚至使训练过程不收敛。文献[10]进一步发现联邦学习得到的模型参数与集中式训练得到的模型间的偏移与数据非IID的程度有关,且模型参数的偏移导致了联邦学习精度的下降。针对数据非IID带来的问题,已有不少文献提出了提高联邦学习性能的措施。文献[10]提出可以通过在所有用户间共享一个小的全局数据集来使数据集趋于IID,实验结果表明,通过共享5%的全局数据,可以使联邦平均[1]在CIFAR-10数据集上的准确率提高约30%。文献[12]在用户训练模型的损失函数上加入了一个本地模型与全局模型的差异项,仿真结果表明,这种方法在异质数据环境中具有更强的鲁棒性和更高的稳态精度。文献[13]通过在服务器端采用动量更新的方式来提高联邦平均在数据非IID时的准确率。文献[14]利用模型权重和数据分布之间的隐式联系,主动选择特定用户参与分布式训练从而平衡非IID引入的偏差。然而,共享数据会带来额外的通信开销,用户选择会减少能参加训练的用户数,限制了在移动性强、各小区中用户数有限的蜂窝网络中应用联邦学习。
大部分现有文献只针对MNIST、CIFAR-10等图像分类任务以及文本字符预测等任务提高联邦学习在数据非IID时的性能[12-15],而未解释是哪些因素导致用户数据非IID使联邦学习的性能下降。然而,当参与联邦学习的用户数据集非IID时,分布式训练的性能一定会下降吗？如果下降,原因是什么？正是因为不了解数据非IID为什么导致联邦学习性能下降,一些文献所提出的解决数据集非IID的方法在一些数据集(如MNIST)上性能提升不大[16]。为了回答上述问题,本文用神经网络进行平均信道增益预测和正交幅度调制(Quadrature Amplitude Modulation,QAM)信号解调,通过这两个无线通信任务以及两个图像分类任务,研究数据非 IID 对联邦学习分类和回归性能的影响,通过比较模型参数偏移量和损失函数曲面形状,尝试解释对于不同分类任务数据非 IID、及在回归问题中不同因素导致的数据非IID对联邦学习性能影响的程度及其原因。
本文第2节介绍基于联邦学习的两个无线任务,以及定量描述数据集非IID程度的方法、损失函数的可视化方法以及模型匹配原理。第3节比较对于多个任务当非IID程度不同时联邦学习的性能,从模型权重偏移和损失函数曲面形状的角度解释对于不同的任务联邦学习对数据非 IID敏感程度不同的原因。
2 基于联邦学习的无线任务及分析方法
2.1 基于联邦学习的平均信道增益预测
考虑在一个多基站覆盖区域内移动的用户的平均信道增益预测问题。各基站通过回传链路连接到一个边缘服务器。为了高效地分配通信资源,当有服务需求时,用户根据过去一段时间(称为观测窗)内记录的平均信道增益、利用本地训练的神经网络模型预测未来一段时间(称为预测窗)内每帧的平均信道增益,其中帧的时间长度为大尺度信道(包括路径损耗和阴影衰落)的相干时间。服务器可以通过基站收集基站与用户间的平均信道,通过集中式训练得到神经网络模型,也可以对用户上传的本地神经网络模型进行平均得到全局模型。
我们采用文献[17]中的多输入单输出神经网络结构完成上述预测任务。若用户在第t帧需要进行信道预测,则每隔一帧依次输入信道增益观测向量[xt-To+i,...,xt-Tp+i],神经网络依次输出在时刻t+i上的信道预测值xt+i, i=1,2,…,Tp,直至完成整个预测窗内信道增益的预测,其中To为观测窗中的观测数、Tp为预测窗中待预测的平均信道增益个数。神经网络的输入为To-Tp+1维向量,输出为一个实数。
共有K个移动用户参与联邦学习,对上述神经网络进行训练。当每个用户进入这个区域时,都开始记录每帧与所接入基站间的信道增益直至离开这个区域,从而形成一条记录。
本文采用联邦学习框架下最常用的算法:联邦平均[1]。在第t轮通信中,各用户从服务器下载第t帧的全局模型Wt,把全局模型作为初值利用所记录的数据集通过多次迭代进行训练,而后把更新后的模型参数上传到服务器。服务器对来自各个用户的模型参数进行加权平均,即
从而得到下一轮的全局模型Wt+1,其中
为第k个用户通过第t轮本地训练得到的模型参数,nk为第k个用户记录的信道增益条数,
经过多轮用户本地训练和通信,最终完成对神经网络的训练。
2.2 基于联邦学习的QAM解调
考虑基于神经网络的MQAM解调问题。把M个星座点分别编号为数字1～M。神经网络的输入节点数为2,分别对应于星座点的实部xr和虚部xi;输出节点数为M,对应于M个星座点的概率向量。
K个用户参与联邦学习,各用户都保存一个包含若干类星座点的数据集:
其中Dk是第k个用户的数据集,(xj,yj)是Dk中的第j个样本,xj包括一个星座点的实部xjr和虚部xji,yj是标签、为该星座点对应的数字,|·|表示集合中元素的个数。
在每一轮通信中,用户下载当前的全局模型参数,并在本地数据集上经多次迭代训练后把模型参数上传至服务器,直至完成训练。
2.3 描述数据集非IID程度的指标
对于分类问题,用户数据集非IID表现为每个用户所存数据的类别数少于所有用户数据的总类别数,即用户本地训练集中数据的分布与所有用户训练集组成的全局数据分布不同。文献[10]借用文献[18]中用于衡量图像间相似性的搬土距离(earth mover’s distance,EMD)来定量描述用户数据集非IID的程度。第k个用户数据集的搬土距离为:
(1)
其中
为总类别数,
为第k个用户数据集中各个类别数据的概率分布向量,p=[p1,...,pC]为全局数据分布向量。
若所有用户数据集的EMD值相同、即EMD1=...=EMDK=EMD,则EMD=0时对应于数据集IID的情况,且EMD越大用户数据集非IID的程度越高;若在全局数据中各类数据服从均匀分布,则EMD可达到如下的最大值:
对于回归问题,数据集非IID表现为用户所存数据的特征偏斜,即各用户本地训练集中的特征分布与所有用户训练集组成的全局数据集的特征分布不同。若特征是离散随机变量,则依然可以由EMD描述非IID程度;若特征是连续随机量(例如信道预测问题中用户的运动速度),则不能用EMD描述这些特征导致的数据非IID程度。我们借鉴文献[19]用颜色直方图间的欧式距度量图像间相似度的方式来定量描述连续特征所导致的非IID程度。令f为表示某个特征的连续变量,将其取值范围均匀分为Nf个区间,在全局数据集中特征f对应的直方图用向量
表示,其中h=[h1,...,hNf],hj是该特征分布在第j个区间内的样本数。则第k个用户数据集与全局数据集特征直方图的欧式距离为:
(2)
其中
表示第k个用户数据集关于特征f的直方图。
2.4 损失函数可视化
给定数据集D和神经网络结构,则损失函数为神经网络模型参数W的函数,L(W)。在分类问题中,我们采用交叉熵为损失函数,即:
其中N为样本数,xi为网络的输入,
为输入xi时神经网络输出的概率向量,y(xi)=[y1(xi),...,yC(xi)]为xi对应标签的独热编码向量。在回归问题中,我们采用经验均方误差为损失函数,即:
其中
为输入为xi时神经网络的预测输出,y(xi)为xi对应的标签。
可视化是解决神经网络事后可解释性、即对训练后的模型进行解释的一种有效手段,其中观察训练后得到的损失函数L(
)的几何形状是理解神经网络泛化能力的重要手段之一。然而,考虑到W包含了几百、上千、甚至上千万个模型参数,无法在构成的高维自变量空间上观察L(),文献[20]提出了如下方法对损失函数在二维或三维空间进行可视化。以已经训练好的模型参数W*作为中心点、再选择两个观察方向,即可得到损失函数L()在两个方向上的向量x、y构成的超平面上的值:
f(α,β)=L(W*+αx+βy)
(3)
其中α、β为从W*出发分别沿向量x和y移动的步长。
为了观察用集中式训练方式后得到的模型WSGD和用联邦学习训练后得到的模型WFed之间的关系,本文选择W*=WSGD为中心点,选择x′=WFed-WSGD、y′=WInit-WSGD(分别由权重矩阵和偏置向量之差拼接构成一个向量)为观察方向,其中WInit为集中式学习和联邦学习共同采用的初始模型参数。
2.5 神经网络的匹配与比较
为了分析非IID对联邦学习造成的影响,一种直观的方法是比较集中式训练得到的神经网络模型(记为WSGD)与通过联邦学习训练得到的模型(记为WFed)间的差异[10]。然而,如果在参与比较的两个神经网络中的一个网络任意层中的任一个神经元都能在另一网络的同一层中找到与其对应(权重和偏置近似相等)的神经元,而这两个网络的这一层仅仅是神经元的排列顺序有所不同,那么原本相似的两个模型也会被误判为两个差异较大的模型,所以在比较模型时需要考虑神经网络置换不变性[21]的影响。
以单隐层全连接神经网络(Fully Connected Deep Neural Network,FC-DNN)为例,设输入层到隐藏层的权重矩阵为W1,隐藏层到输出层的权重矩阵为W2,隐藏层的激活函数为σ,输入向量为x。为简化表示,忽略偏置向量,则网络的输出为
神经网络的置换不变性可以表示为:
其中Π是一个置换矩阵。换言之,若两个神经网络仅仅在神经元的排列顺序上有所不同,那么虽然它们的权重矩阵不同,但二者在输入相同时会产生相同的输出。
考虑到置换不变性的影响,在我们判断某两个模型之间的差异前,需要对模型进行匹配,即通过调整神经元的排列顺序,使得模型尽可能接近。同样以FC-DNN为例,令
表示第n个神经网络第k层的权重矩阵,其中
表示连接至第l个神经元的权重向量。文献[21]提出的联邦匹配平均是在服务器端对模型进行平均之前先对各个用户上传的模型进行匹配,以使用户模型与平均后的全局模型间的差异尽可能小;而本文的目的是比较集中式学习和联邦学习模型之间的差异,所以只需对WFed与WSGD进行匹配。为此,保持集中式学习模型中神经元的排列顺序不变,只改变联邦学习模型中神经元的排列顺序,便可以对该文献中的匹配方法进行简化。我们采用逐层匹配[21]的方法对神经网络进行匹配。设
和
分别为集中式训练和联邦学习得到的神经网络第一层的权重矩阵,从如下的优化问题中求解置换矩阵Π中的元素πi, j、即可对与进行匹配:
πi, j∈{0,1}, ∀i, j
(4)
其中L为第一个隐藏层的神经元数,
为相似度函数,我们采用向量的二范数作为相似度函数:
求解上述优化问题得到置换矩阵Π,则
即为完成匹配后联邦学习得到的神经网络第一层的权重矩阵。完成第一层匹配后,将
作为WFed第二层的权重矩阵,继续与WSGD第二层的权重
进行匹配,以此类推,直至完成整个联邦学习模型的匹配。
除置换不变性外,我们注意到当FC-DNN的激活函数是Relu时,若使某一层的权重和偏置同时变为原来的m(m>0)倍、后一层的权重相应变为原来的1/m倍,则在相同输入下,经参数缩放后的神经网络与未经缩放的神经网络有相同的输出。为了消除模型参数缩放带来的影响,需要对参与比较的模型参数进行缩放。同样以和为例,
即为完成缩放后联邦学习模型第一层的权重矩阵;然后取
作为WFed第二层的权重,继续根据集中式学习模型对第二层的权重进行缩放,以此类推,最终完成对联邦学习整个模型矩阵WFed的缩放。
虽然以上分析均以FC-DNN为例,但卷积神经网络(Convolutional Neural Networks, CNN)同样也具有这些性质[21]。不同的是对于FC-DNN置换不变的对象是神经元,而对于CNN置换不变的对象则是卷积层的通道。
文献[10]用权重偏移值对由联邦学习和集中式训练得到的神经网络的差异进行定量分析。考虑到神经网络具有置换不变性以及参数缩放的不变性,本文在联邦学习和集中式训练初始值相同的前提下,在比较差异之前首先把联邦学习模型逐层进行缩放(若激活函数是Relu才进行缩放),并与集中式学习模型进行匹配。由于对整体模型进行比较时仍会受到相邻层参数缩放等影响、且模型的偏移值会被参数量更多的层所主导,所以我们分层计算两个网络之间的权重偏移值。第k层权重偏移为[10]:
(5)
其中
和
分别是联邦学习和集中式训练得到的神经网络模型的第k层权重矩阵,‖·‖F指矩阵的Frobenius范数。
3 数据集非IID影响的分析及解释
本节首先评估当用户数据集非IID程度不同时联邦学习对于不同分类任务的性能,而后通过损失函数可视化技术解释用户数据集非IID对不同任务影响不同的原因,最后针对信道预测这个回归问题,分析由不同因素造成的非IID对预测性能的影响。
3.1 数据集生成及超参数
在信道增益预测问题中,仿真场景为三条长度均为8 km的直线道路,在道路一侧有16个服务半径为250 m的基站。第一条道路距基站100 m,在距离道路左端起点4 km处有一处红绿灯;第二条道路距基站50 m,无红绿灯;第三条道路距基站150 m,在距离左端道路起点2.5 km和5.5 km处各有一处红绿灯,如图1所示。每条轨迹包括用户从道路左端进入、从右端离开的移动过程中每帧记录的位置,不同轨迹的平均速度服从15～25 m/s间的均匀分布,不同轨迹的加速度为零均值、方差在0.5～1.5 m/s2间均匀分布的白高斯随机过程,用户的最低和最高运动速度为10 m/s和30 m/s。用户在红绿灯处减速和启动的加速度为2 m/s2,停车时间服从5～75 s间的均匀分布。每帧的时间长度为1 s。为了根据用户轨迹得到大尺度信道增益,需要生成信道地图、即各个位置处对应的平均信道增益;对于不同的移动轨迹,在相同位置处的平均信道增益相同。为此,考虑路径损耗模型为α+βlog10(d),其中α=36.8,β为路径损耗因子,d为用户与最近基站间的距离;阴影衰落服从对数正态分布;每个小区的β在36.6～36.8内随机选取,阴影衰落的相关距离在40～70 m范围内随机选取、标准差在7～9 dB间随机选取,从而反映各小区传播环境的差异。根据以上设置,首先随机生成在三条道路上移动的用户轨迹,对每条道路上移动的用户生成1500条运动轨迹,共4500条;再根据信道地图,把一条运动轨迹转换为一条时变大尺度信道的记录。取其中的2/3条信道记录作为总训练集,1/3作为总测试集。参与联邦学习的用户数为15,把总训练集按照记录数等分给各用户,则每个用户的本地训练集有200条时变信道增益记录。由于预测误差随预测窗长Tp的减小而降低,随观测窗长To的减小而升高;而当To-Tp> 60 s时继续加长观测窗难以进一步降低预测误差,因此考虑To=100 s,Tp=40 s。联邦学习的单轮通信迭代次数E=1,批大小B=128,固定学习率μ=0.1,此时对这个预测任务具有较高的收敛速度和精度。
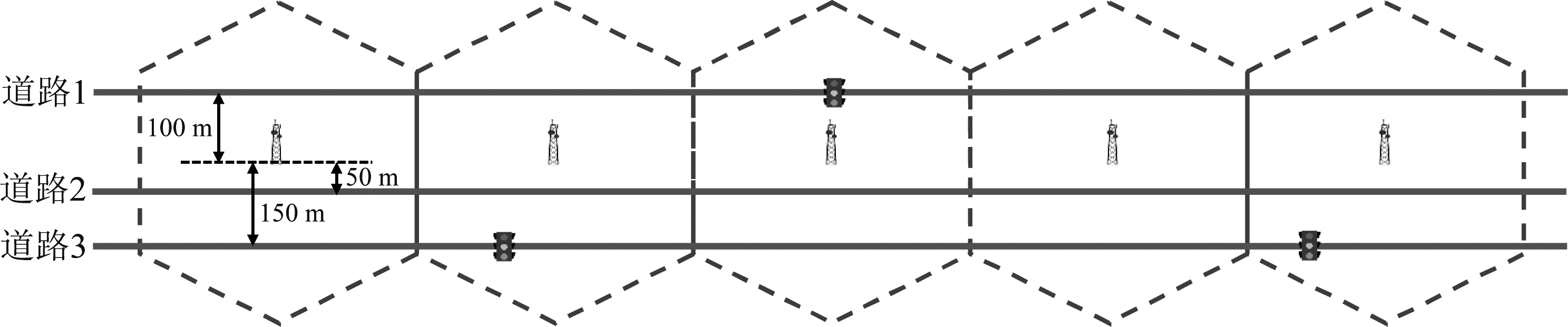
图1 仿真场景示意图
Fig.1 Simulation setups
对于QAM分类问题,我们以16QAM为例进行分析。当星座点数更多(如64QAM)时,利用非IID数据进行联邦学习的性能略差于16QAM,但不影响分析结果。生成1.6×104个16QAM星座点作为训练集,其中每个星座点上有加性高斯白噪声,由于在5～30 dB的范围内改变信噪比对最终的学习性能影响不大,选择SNR=15 dB进行分析。测试集包含104个在复平面上均匀分布的星座点,每个星座点的标签yj为与其距离最近的无噪声原始星座点对应的数字。参与联邦学习的用户数为16,每个用户的训练集都包含1000个样本。在联邦学习中选择批大小B=100、学习率μ=3、衰减率rd=0.998,此时学习这个分类任务的准确率高;选择E=20,此时可以在不降低收敛精度的前提下提高收敛速度。
由于现有分析非IID数据集影响的文献主要考虑图像分类问题,为与现有工作进行比较,我们考虑MNIST[22]和CIFAR-10这两个图像分类任务作为参照,二者均为10分类问题。其中,MNIST数据集包含了0～9的手写数字灰度图片,每张图片的大小为28×28;CIFAR-10数据集包含了飞机、汽车等10类物体的图片,每张图片的大小为32×32×3。在两个任务中参与联邦学习的用户数都为10。在MNIST问题中,训练集中有60000张图片,测试集中有10000张图片,每个用户的本地数据集中包含6000张图片。在CIFAR-10问题中,训练集中有50000张图片,测试集中有10000张图片,每个用户的本地数据集中包含5000张图片。进行联邦学习时的超参数采用文献[10]中的设置:在MNIST任务中E=1,B=100,μ=0.01,rd=0.995;在CIFAR-10任务中E=1,B=100,μ=0.1,rd=0.992。
尽管循环神经网络更适于预测任务,本文以FC-DNN为例对信道增益预测问题进行分析;16QAM是一个简单的分类任务,同样考虑FC-DNN。而对于两个图像分类任务,均考虑CNN。学习算法都采用随机梯度下降。各个任务的神经网络结构和精调后的超参数如表1所示。
表1 神经网络超参数
Tab.1 Hyper-parameters of neural networks
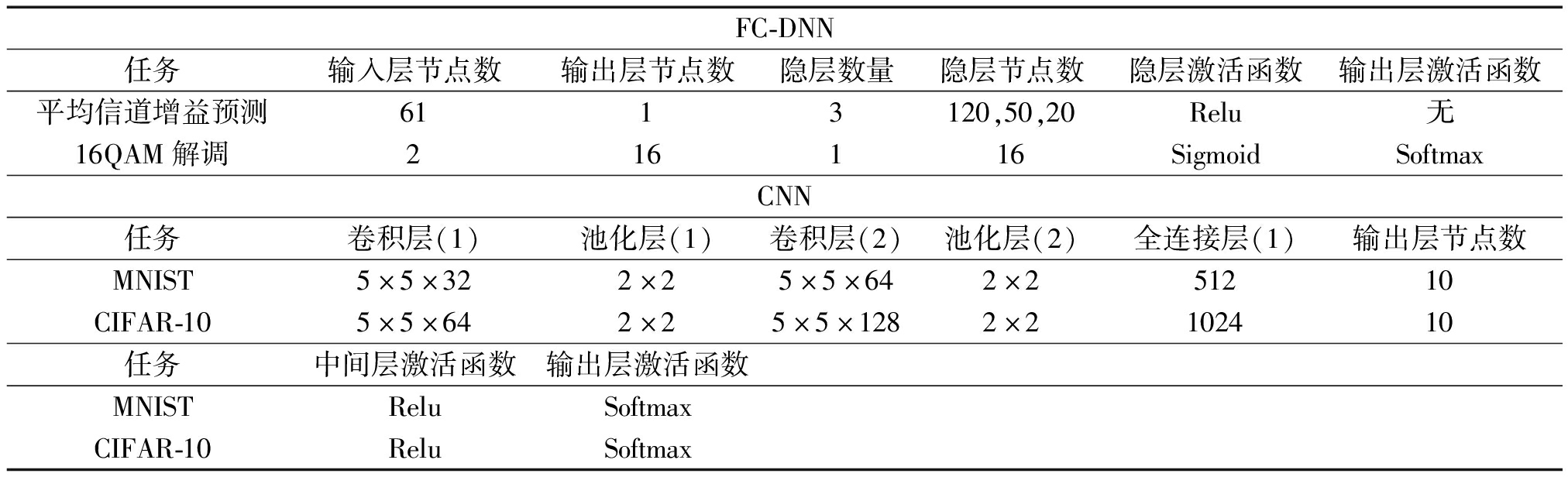
FC-DNN任务输入层节点数输出层节点数隐层数量隐层节点数隐层激活函数输出层激活函数平均信道增益预测6113120,50,20Relu无16QAM解调216116SigmoidSoftmaxCNN任务卷积层(1)池化层(1)卷积层(2)池化层(2)全连接层(1)输出层节点数MNIST5×5×322×25×5×642×251210CIFAR-105×5×642×25×5×1282×2102410任务中间层激活函数输出层激活函数MNISTReluSoftmaxCIFAR-10ReluSoftmax
3.2 分类问题
为了观察对于不同的任务用户数据集非IID对联邦学习的影响,首先给出当EMD取不同值时,联邦学习在16QAM解调、MNIST以及CIFAR-10数据集上的预测准确率随通信轮次的变化,如图2和表2所示。当非IID程度最大(每个用户只有一类数据)时,在16QAM和MNSIT(CIFAR-10)数据集上EMD分别达到最大值1.875和1.8。由于当EMD较小时联邦学习收敛较快,所以模型收敛后即停止训练;而当EMD较大时,训练至收敛所需的通信轮次也相应增加。
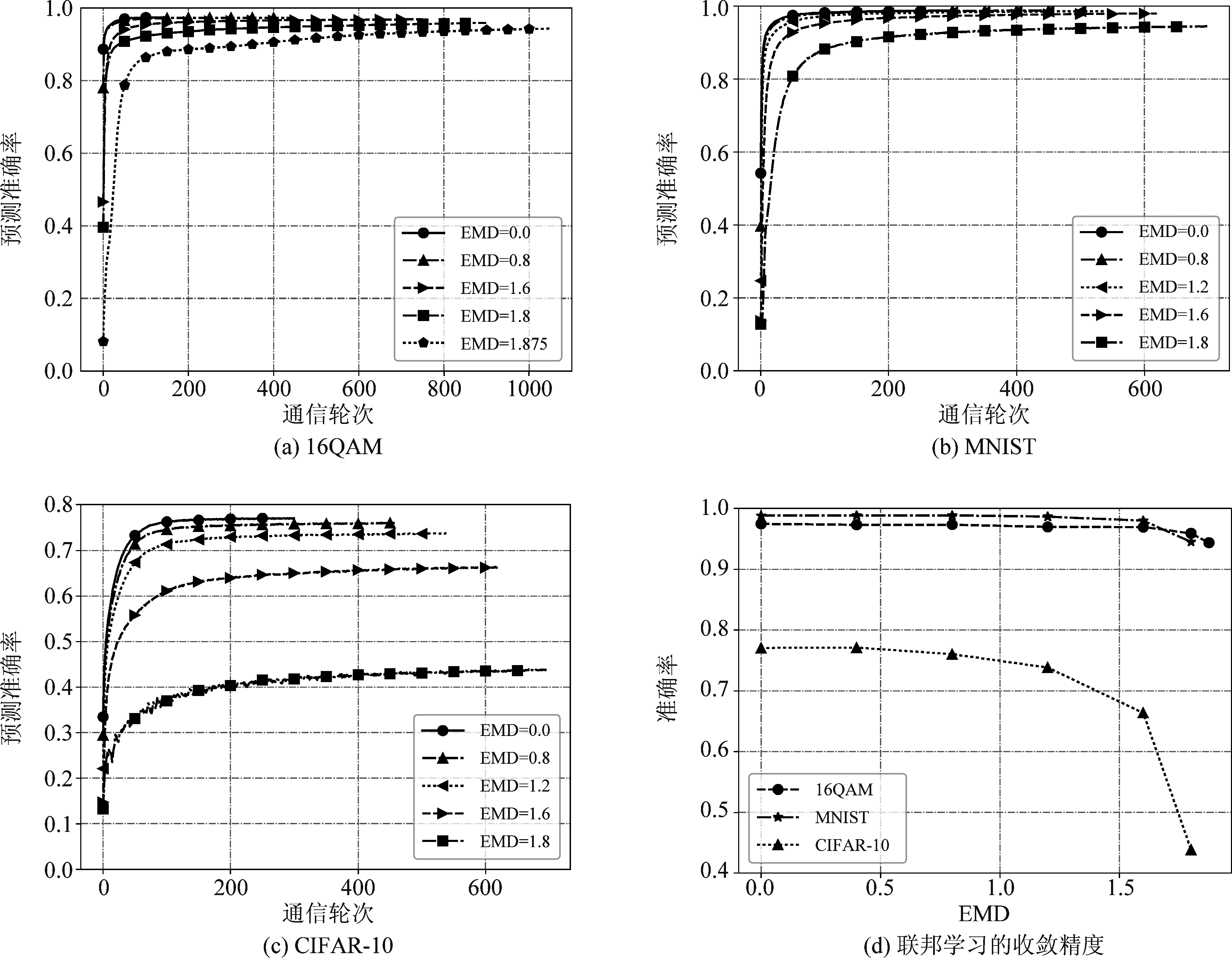
图2 联邦学习预测准确率随EMD的变化
Fig.2 Prediction accuracy of federated learning with different EMD
表2 联邦学习的预测准确率
Tab.2 Prediction accuracy of federated learning
EMD数据集 00.40.81.21.61.81.87516QAM0.9750.9730.9730.9700.9700.9600.944MNIST0.9890.9890.9890.9870.9800.945CIFAR-100.7710.7710.7600.7380.6640.439
由图2可以看出联邦学习的收敛速度和稳态准确率都随EMD的增加而降低,但在不同数据集上收敛速度和稳态准确率的下降程度差异很大。由表2可见,在16QAM、MNIST、CIFAR-10数据集上的稳态准确率分别下降了3.1%、4.4%和33.2%。
为了解释不同任务对非IID敏感程度的差异,下面首先用每层的权重偏移值定量分析联邦学习与集中式学习得到的神经网络模型之间差异。由于神经网络具有置换不变性以及参数缩放的不变性,所以在计算模型差异前已经对激活函数是Relu的联邦学习模型逐层进行了缩放、且与集中式学习模型进行了匹配。
文献[10]发现在给定相同的初始模型参数时,经过一轮通信后联邦学习模型各层相对于集中式学习模型的偏移程度随EMD的增加而增加。然而,对于联邦学习应该评估收敛后的性能,所以我们分析从相同初值出发集中式和联邦学习训练收敛后的模型参数WSGD和WFed(在16QAM数据集上经过约700轮通信、MNIST以及CIFAR-10数据集上经过约400轮通信),如图3所示,图标“全连接层1”表示神经网络的第一个全连接层、“卷积层1”表示第一个卷积层,以此类推。
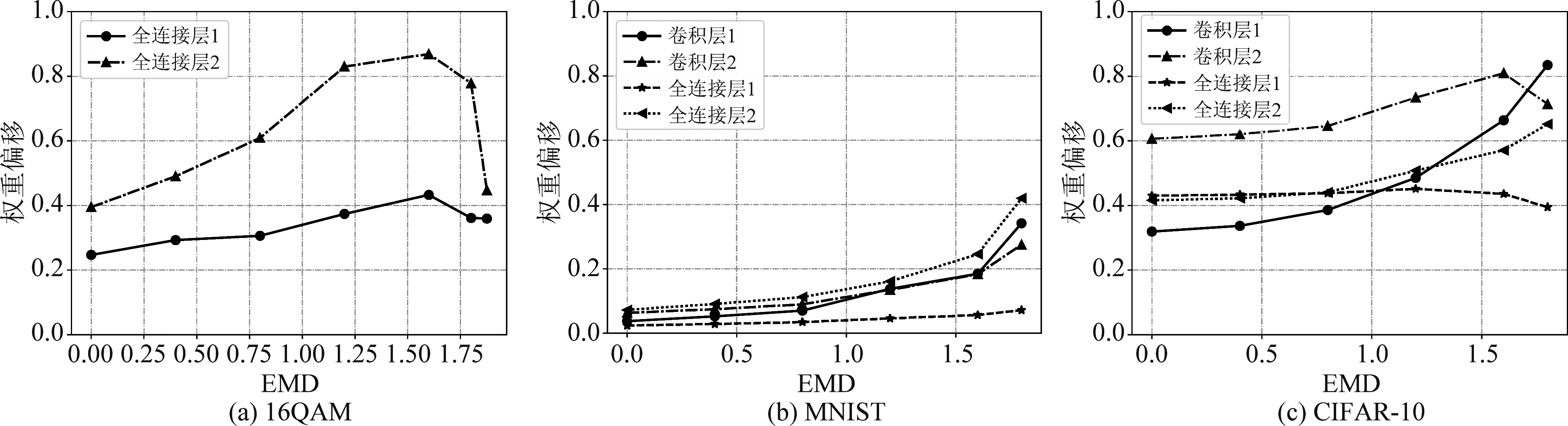
图3 权重偏移随EMD的变化
Fig.3 Weight divergence of federated learning model with different EMD
由图3可以看出,除MNIST数据集以外,在其他两个数据集上训练收敛后联邦学习模型的各层权重偏移量并非总是随EMD单调增加(若不先经过匹配和缩放,各数据集上权重偏移的变化趋势与此相似)。比较图3(a)和3(b)可以看出,在EMD值相同时,在16QAM数据集上不同层网络的权重偏移值普遍高于MNIST,但16QAM受非IID影响的程度却接近甚至略低于MNIST(见表2)。另外,对于MNIST数据集,当用户数据集IID(即横坐标EMD=0)时,联邦学习与集中式学习模型间的差异较小;而对于16QAM和CIFAR-10两个数据集,即使当数据集IID时,联邦学习的模型参数也与集中式学习的模型参数间存在一定的差异。可见,权重偏移值的大小并不能反映联邦学习受数据集非IID影响的程度。
为了解释联邦学习不同任务时对非IID数据集敏感程度不同的原因,我们用损失函数可视化方法给出在三个数据集上损失函数的二维等值线和三维曲面,如图4所示。为了观察不同模型间偏移的大小,我们对2.4节中的观察方向进行如下的归一化处理:x=x′/‖x′‖,y=y′/‖y′‖,其中,由于x′或y′包含了若干个权重矩阵和偏置向量,所以我们把这些矩阵和向量拼接为一个向量然后再计算其范数。图中两个箭头代表方向x和y,由于进行了归一化,两个箭头的长短分别表示了WSGD与WInit或WFed间差异的大小。图中曲线(曲面)的颜色越接近于黑色表示损失函数的值越小,越接近白色表示损失函数值越大。为了观察极小点附近的损失函数,只给出了损失函数值小于2时的几何形状。
从图3和图4可见,是模型偏移程度和损失函数几何形状的不同共同导致了联邦学习在学习不同任务时对数据集非IID的敏感程度不同。对于MNIST数据集,当数据集非IID时模型参数的偏移程度最小(从图4可见联邦学习与集中式学习模型间的距离很小),联邦学习和集中式模型收敛到同一个极小点附近,所以MNIST受非IID的影响较小。对于16QAM和CIFAR-10两个数据集,联邦学习模型参数的偏移程度都较大,但二者的损失函数呈现出了不同的特点。对于16QAM数据集,当EMD≤1.6时,随着EMD的增加联邦学习模型的偏移程度升高、逐渐落入了与集中式学习不同的另一极小点中,但两个极小点的损失值接近;当EMD=1.875时,联邦学习模型的偏移程度有所降低、未能完全收敛到与集中式学习不同的另一极小点中,但因此时联邦学习的损失值与集中式学习仍相差不大,所以当非IID程度上升时联邦学习仍能保持较好的学习性能。对于CIFAR-10数据集,随着EMD的增加联邦学习模型的偏移程度呈现先升高后降低的趋势(见图3),虽然偏移程度减小,但联邦学习模型却收敛到损失值较大的“边缘”处,导致其学习性能明显下降。
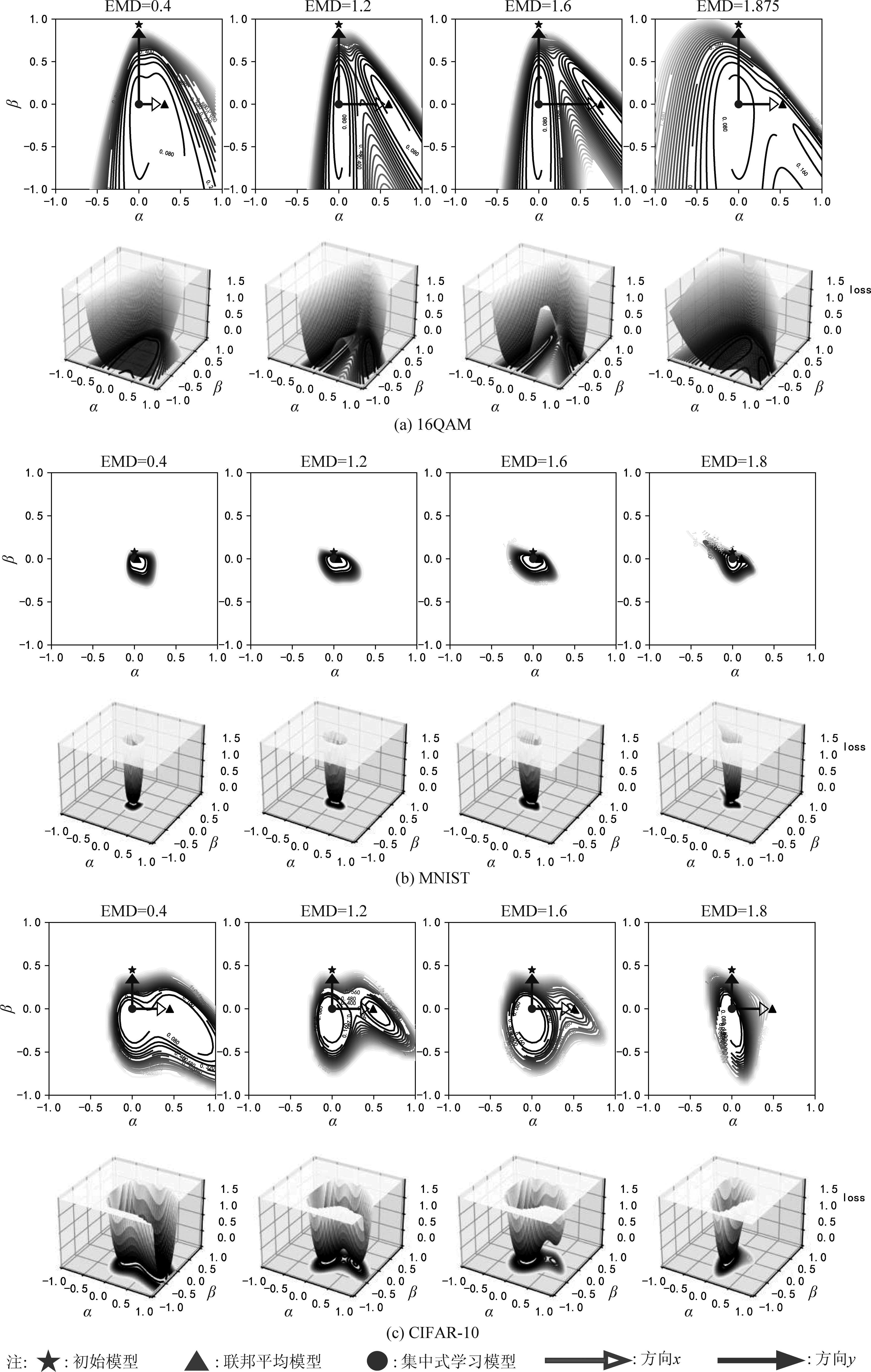
图4 损失函数的可视化
Fig.4 2D and 3D loss surface on different datasets
3.3 回归问题
与分类问题不同,信道预测这个回归问题的用户数据集非IID可以表现为用户的运动参数非IID(如不同用户数据集中记录的平均速度不同),也可以表现为不同用户经过各条道路(路径损耗、阴影衰落及红绿灯设置不同)的概率不同。
由于运动速度是连续变量,我们采用不同用户数据集关于速度直方图之间的欧式距离来描述速度导致的数据非IID程度。取直方图子区间数Nf=15,则根据用户的最低和最高平均速度,落在第j个子区间内的平均速度范围是
当每个用户数据集中记录的平均速度只分布在直方图中的一个子区间内时,直方图欧式距离dhist达到最大值,为0.9661。为了分析速度不同所导致的数据集非IID,图5给出当关于速度的非IID程度不同时信道预测误差随通信轮次的变化。可以看出速度非IID对预测性能的影响不大,稳态精度随直方图欧式距离的增加略有下降,当dhist取最大值时的稳态预测误差(为6.356 dB)相对与数据IID时的误差(为6.341 dB)只上升了0.19%。
图5 运动速度非IID对信道预测的影响
Fig.5 Impact of average velocity non-IID
为了分析由在不同道路移动用户的大尺度信道时变特性差异引起的用户数据集非IID对联邦学习造成的影响,当数据集非IID时,每个用户的信道增益记录不再等概率来自于三条不同的道路。我们采用概率向量
反映用户数据集的分布,其中
表示第k个用户数据集中的数据来自于第i条道路的概率(i=1,2,3)。当EMD为不同值时平均信道增益预测误差随通信轮次的变化如图6所示,联邦学习的收敛精度如表3所示。以6.5 dB(比IID时的收敛误差高2.5%)作为期望的误差值,表3还给出了EMD值不同时联邦学习达到期望误差所需的通信轮次。
结合图6和表3可以看出,道路特性不同导致的数据集非IID对联邦学习的预测性能有较大的影响。当EMD≤1时,联邦学习的收敛速度和稳态精度随EMD的增加略有下降;当EMD取最大值4/3时非IID程度最大(每个用户的数据集只来自于其中一条道路),此时稳态预测误差为7.639 dB,比数据集IID时上升了20.5%。另外,当EMD=11/9(此时各用户数据集中94.4%的数据都来自于三条道路中的一条、只有5.6%的数据来自其他两条)时,尽管EMD值很接近于非IID程度最高的EMD值(即4/3),但联邦学习的预测性能与EMD=4/3时相比有较大的提升,这说明在这个回归问题中,只要用户数据集中有少量包含不同特征的数据(来自不同道路的数据),联邦学习的预测误差受数据集非IID的影响就较小。
表3 信道特性非IID时联邦学习的预测误差和所需通信轮次
Tab.3 Prediction error and required communication round of federated learning when channel characteristics not IID
EMD01/32/311/94/3平均信道增益预测误差/dB6.3416.3486.3786.4617.639低于目标误差(6.5 dB)所需通信轮次485071245-
注:“-”表示不能收敛至期望的误差值
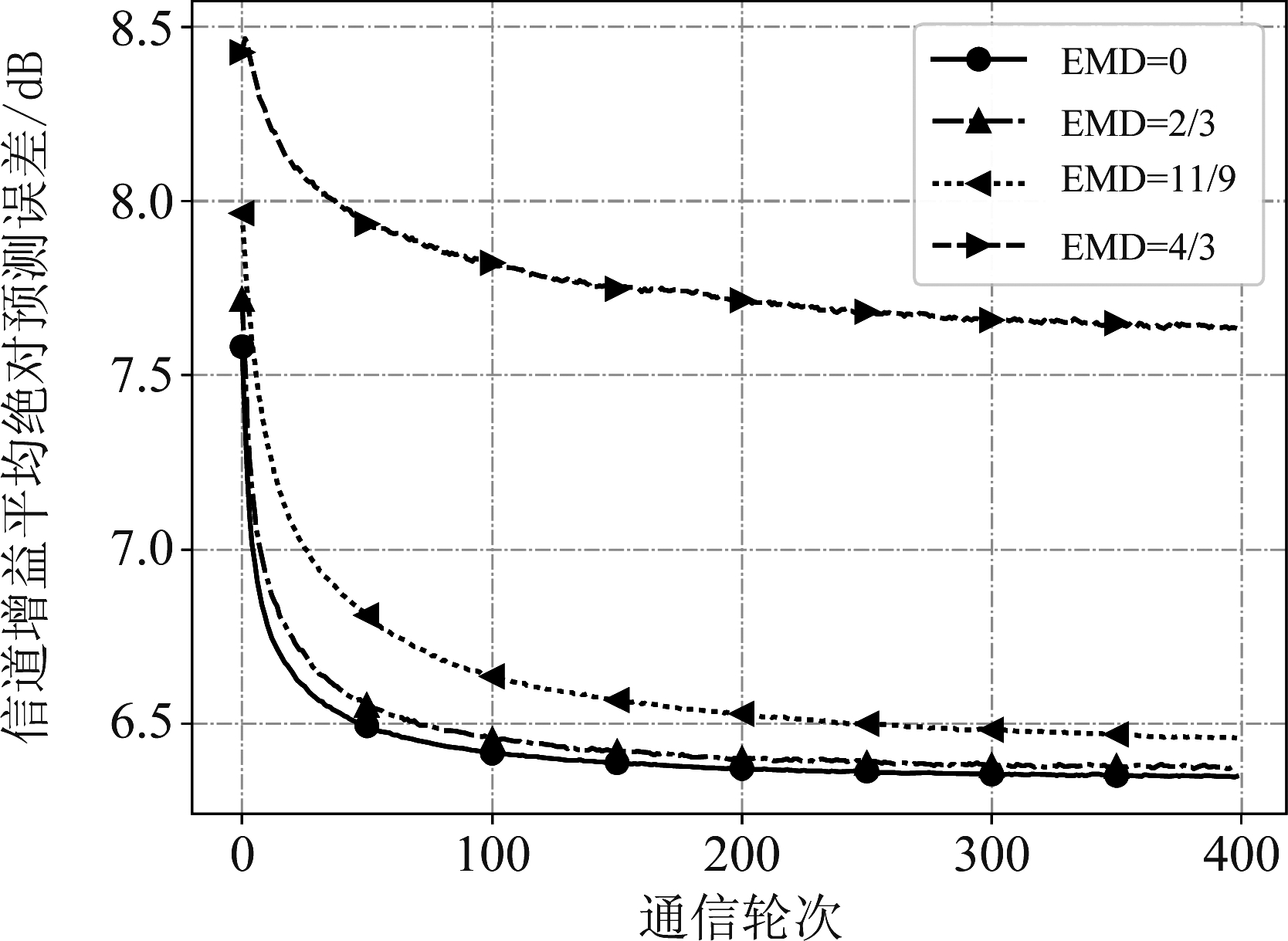
图6 道路特性非IID对信道预测的影响
Fig.6 Impact of road characteristic non-IID
图7给出了当速度和道路特性非IID时联邦学习相对于集中式学习模型的权重偏移与非IID程度的关系(联邦学习模型事先经过缩放和匹配)。可以看出,当速度非IID时,联邦学习模型各层的权重偏移基本不随dhist的增加而上升;当道路特性非IID时,随着EMD的增加,四个全连接层的权重偏移有不同程度的上升。然而,即使在数据集IID(dhist=0和EMD=0)时,联邦学习模型和集中式学习的模型间也存在不小的权重差异,这说明两种训练方式得到的模型参数差异并不完全是数据集非IID造成的。
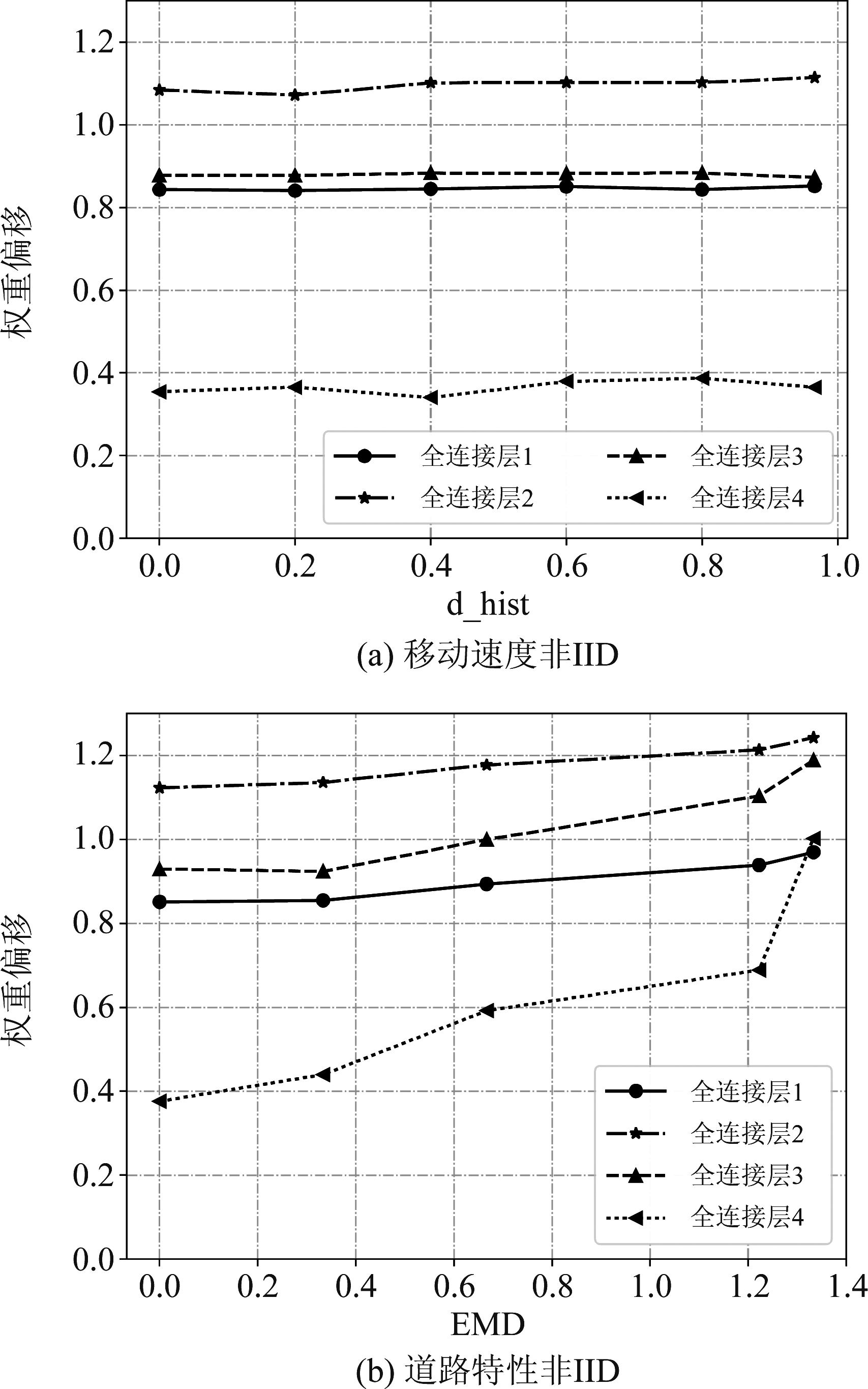
图7 联邦学习模型在信道预测问题中的权重偏移
Fig.7 Weight divergence of federated learning for average channel gain prediction
在平均信道增益数据集上训练神经网络的损失函数如图8所示,可以看出从dhist=0或EMD=0(数据集IID)开始,联邦学习和集中式学习模型就达到了两个不同的极小点,与图7的结果相吻合(即存在权重偏移)。当移动速度非IID时,随着dhist的增加,联邦学习模型偏移的程度基本不变,联邦学习模型所在极小点周围损失函数的形状也接近,导致联邦学习模型受非IID影响小。当道路特性非IID时,随着EMD的增加,联邦学习模型偏移的程度缓慢上升,同时联邦学习模型也落入了损失值更高的极小点中,导致收敛后的预测误差也有所升高。
图8 数据集非IID时平均信道增益损失函数曲面图
Fig.8 2D and 3D loss surface on average channel gain dataset when dataset non-IID
可见,在信道预测问题中造成数据集非IID的原因不同,对联邦学习预测性能的影响也不同。
由于时变信道增益的特性取决于用户的运动特性和大尺度信道,为了进一步分析当道路特性非IID时造成联邦学习性能下降的原因,下面在3.1节仿真场景的基础上保持信道地图不变、但取消三条道路上的红绿灯,此时在三条道路上移动的用户运动特性相同、只有包含阴影衰落和路径损耗的大尺度信道的时变规律不同。当EMD值不同时联邦学习的预测误差随通信轮次的变化如图9所示。可以看出,与图6类似,当EMD=4/3时预测误差同样有较大程度的上升,可见大尺度信道的非IID对大尺度信道增益预测性能的影响较大。
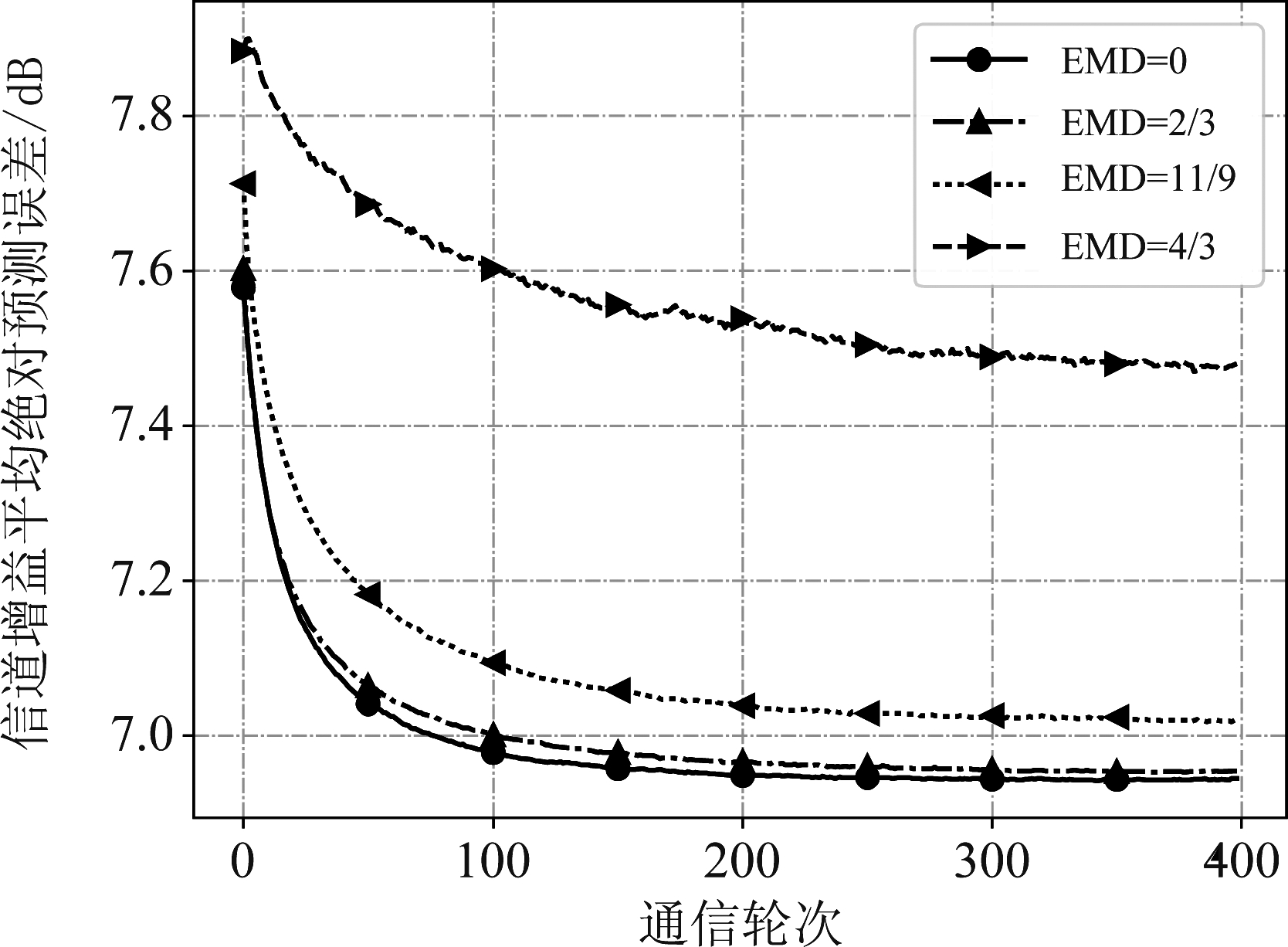
图9 信道特性非IID对信道预测的影响
Fig.9 Impact of channel characteristic non-IID
4 结论
本文以MQAM信号解调和平均信道增益预测问题为例,分析了利用联邦学习解决无线通信任务时参加训练的用户数据集非IID对学习过程的收敛速度和稳态精度的影响;通过损失函数可视化和对模型参数偏移进行比较,寻找了在非IID的用户数据集上分布式训练的性能下降的原因。研究结果表明,数据集非IID未必使联邦学习的性能下降,联邦学习与集中式训练得到的模型间的差异大小与数据非IID导致的分布式训练性能损失之间并没有一一对应的关系。损失函数的几何形状和联邦学习的模型参数偏移程度共同导致了学习不同任务时对数据非IID的敏感程度不同。对于分类问题,非IID数据集不一定导致联邦学习性能下降;对于平均信道增益预测这个回归问题,当引起数据集非IID的因素不同时,联邦学习预测性能对数据非IID的敏感程度也有很大的差异。尽管本文工作针对非IID数据的影响只进行了初步的探讨,但研究结果有助于确定某个任务是否需要考虑非IID问题、以及需要采取什么措施减轻数据非IID的影响。
[1] MCMAHAN H B, MOORE E, RAMAGE D, et al.Communication-efficient learning of deep networks from decentralized data[C]∥International Conference on Artificial Intelligence and Statistics, 2017.
[2] SAMARAKOON S, BENNIS M, SAAD W, et al.Distributed federated learning for ultra-reliable low-latency vehicular communications[J].IEEE Transactions on Communications, 2020, 68(2): 1146-1159.
[3] NIKNAM S, DHILLON H S, REED J H.Federated learning for wireless communications: Motivation, opportunities, and challenges[J].IEEE Communications Magazine, 2020, 58(6): 46-51.
[4] 刘婷婷, 杨晨阳, 索士强, 等.无线通信中的边缘智能[J].信号处理, 2020, 36(11): 1789-1803.
LIU Tingting, YANG Chenyang, SUO Shiqiang, et al.Edge intelligence for wireless communication[J].Journal of Signal Processing, 2020, 36(11): 1789-1803.(in Chinese)
[5] WANG Yu, GUO Liang, ZHAO Yu, et al.Distributed learning for automatic modulation classification in edge devices[J].IEEE Wireless Communications Letters, 2020, 9(12): 2177-2181.
[6] QI Kaiqiang, YANG Chenyang.Popularity prediction with federated learning for proactive caching at wireless edge[C]∥2020 IEEE Wireless Communications and Networking Conference(WCNC).Seoul, Korea(South).IEEE, 2020: 1-6.
[7] WU Yuting, JIANG Yanxiang, BENNIS M, et al.Content popularity prediction in fog radio access networks: A federated learning based approach[C]∥ICC 2020-2020 IEEE International Conference on Communications(ICC).Dublin, Ireland.IEEE, 2020: 1-6.
[8] WANG Xiaofei, WANG Chenyang, LI Xiuhua, et al.Federated deep reinforcement learning for Internet of Things with decentralized cooperative edge caching[J].IEEE Internet of Things Journal, 2020, 7(10): 9441-9455.
[9] LIM W Y B, LUONG N C, HOANG D T, et al.Federated learning in mobile edge networks: A comprehensive survey[J].IEEE Communications Surveys & Tutorials, 2020, 22(3): 2031-2063.
[10] ZHAO Yue, LI Meng, LAI Liangzhen, et al.Federated learning with non-IID data[EB/OL].https:∥arxiv.org/abs/1806.00582v1, 2018.
[11] HSIEH K, PHANISHAYEE A, MUTLU O, et al.The non-IID data quagmire of decentralized machine learning[EB/OL].https:∥arxiv.org/abs/1910.00189v1, 2019.
[12] LI Tian, SAHU A K, ZAHEER M, et al.Federated optimization in heterogeneous networks[EB/OL].2018: arXiv: 1812.06127[cs.LG].https:∥arxiv.org/abs/1812.06127.
[13] OZDAYI M S, KANTARCIOGLU M, IYER R.Improving accuracy of federated learning in non-IID settings[EB/OL].https:∥arxiv.org/abs/2010.15582,2020.
[14] WANG Hao, KAPLAN Z, NIU Di, et al.Optimizing federated learning on non-IID data with reinforcement learning[C]∥IEEE INFOCOM 2020-IEEE Conference on Computer Communications.Toronto, ON, Canada.IEEE, 2020: 1698-1707.
[15] MAO Zhicheng, DAI Wenrui, LI Chenglin, et al.FedExg: federated learning with model exchange[C]∥2020 IEEE International Symposium on Circuits and Systems(ISCAS).Seville, Spain.IEEE, 2020: 1-5.
[16] TONG Qianqian, LIANG Guannan, BI Jinbo.Effective federated adaptive gradient methods with non-IID decentralized data[EB/OL].https:∥arxiv.org/abs/2009.06557, 2020.
[17] ZHANG Wenjing, LIU Yuan, LIU Tingting, et al.Trajectory prediction with recurrent neural networks for predictive resource allocation[C]∥2018 14th IEEE International Conference on Signal Processing(ICSP).Beijing, China.IEEE, 2018: 634-639.
[18] RUBNER Y, TOMASI C, GUIBAS L J.The earth mover’s distance as a metric for image retrieval[J].International Journal of Computer Vision, 2000, 40(2): 99-121.
[19] HAFNER J, SAWHNEY H S, EQUITZ W, et al.Efficient color histogram indexing for quadratic form distance functions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(7): 729-736.
[20] LI Hao, XU Zheng, TAYLOR G, et al.Visualizing the loss landscape of neural nets[EB/OL].https:∥arxiv.org/abs/1712.09913, 2017.
[21] WANG Hongyi, YUROCHKIN M, SUN Yuekai, et al.Federated learning with matched averaging[C]∥International Conference on Learning Representations, 2020.
[22] LECUN Y.The mnist database of handwritten digits[EB/OL].Http:∥Yann.Lecun.Com/Exdb/Mnist/, 1998.
