1 引言
在实际雷达系统中,雷达接收到的回波信号通常会受到噪声干扰,所以雷达对目标的探测能力很大程度上取决于接收回波的输出信噪比。当雷达波形具有较大的时宽带宽积时,使用基于匹配滤波器(Matched Filter, MF)的脉冲压缩技术可以在不提高雷达发射功率的前提下有效提高雷达接收回波的输出信噪比[1]。但是,对于常用的线性调频(Linear Frequency Modulation, LFM)信号,由于其频谱形状类似于矩形,所以LFM信号的匹配滤波器输出具有类似sinc形状的旁瓣结构,其归一化峰值旁瓣值(Peak Sidelobe Level, PSL)约为-13.2 dB[2]。在实际应用中,较高的距离维旁瓣易产生目标遮蔽效应,即弱目标易被附近强目标的旁瓣淹没,严重影响雷达的目标探测性能。对于LFM信号而言,类矩形频谱的上升沿是造成高距离维旁瓣的关键因素,通常可以使用频域加窗(如Hamming、Kaiser窗等)的方法来平滑LFM信号频谱,从而抑制高距离维旁瓣。然而,现有窗函数相对固定且可调参数的数量和范围较小,无法根据设计者需求灵活、有效均衡距离维旁瓣抑制、信噪比损失(Loss of SNR, LSNR)、主瓣展宽等因素[3]。
另外,对于越来越受到关注和使用的非线性调频(Non-Linear Frequency Modulation, NLFM)波形、相位编码波形、频率编码波形等新体制波形,其频谱可呈现为任意形状,甚至会类似于噪声频谱,此时传统加窗法抑制距离维旁瓣也会失效。那么,需要针对特定的雷达波形优化设计失配滤波器(Mismatched Filter, MMF)来抑制距离维旁瓣。一种经典和常用的失配滤波器就是最小二乘失配滤波器(Least-Squares MMF, LS-MMF),其将最小化积分旁瓣值(Integrated Sidelobe Level, ISL)问题等效为基于L2范数的逼近问题,从而获得具有最优ISL的失配滤波器闭式解[4];Levanon等在传统LS-MMF基础上给出了一种基于对角加权的LS-MMF(Weighted LS-MMF, WLS-MMF)设计方法,通过引入适当的加权系数,在指定的局部区域获得了低旁瓣[5-6];Baden在WLS-MMF基础上给出了一种基于迭代递归的WLS-MMF(Iterative WLS-MMF, IWLS-MMF)设计算法[7-8],通过对WLS-MMF滤波输出结果进行迭代计算,可以获得具有最优PSL输出的失配滤波器。除了上述算法,通过改变目标函数与约束条件,利用不同的优化方法,可以实现对具有不同主、旁瓣输出特性的失配滤波器的高效求解,如循环迭代法[2]、凸优化方法[9-10]等。
为了更好地降低和分散距离维旁瓣能量,失配滤波器长度通常会设计为雷达波形有效长度的4～8倍。然而,就目前作者调研所知,现有失配滤波器设计算法,包括LS-MMF及其各种改进的算法、循环迭代法、凸优化方法等,算法过程中一般都会涉及到矩阵求逆的计算,且矩阵规模与所设计的失配滤波器长度一致。在实际应用中,由于常常需要对系统失真进行周期性标校,在失配滤波器长度较大时,这些算法的计算复杂度会极高,带来很大的计算开销,不利于雷达系统的硬件实现。针对这一问题,受到IWLS-MMF设计算法和交替投影算法(Method of Alternating Projection, MAP)两种算法的启发,本文提出一种基于动态交替投影(Dynamic Alternating Projection, DAP)的失配滤波器快速设计算法,可实现在最小PSL、ISL、Weighted ISL(WISL)等准则下的距离维旁瓣抑制,且信噪比损失、主瓣展宽可控。本文所提算法结合了两种算法各自的优势,即MAP算法的计算简单性和有效性以及IWLS-MMF设计算法对PSL的优化能力,而摒弃了传统IWLS-MMF算法的劣势,即需要在迭代过程中对矩阵进行求逆计算。本算法适用于多种脉冲压缩波形,算法实现过程仅用到了一些简单计算及快速傅里叶(Fast Fourier Transform, FFT)变换,适用于硬件的高效率设计与实现。
2 算法设计
2.1 失配滤波器模型
考虑雷达波形时域为s(t),在采样率fs的采样下,其离散形式可表示为向量形式如下
(1)
其中N为采样点数,(·)T表示转置。若考虑设计一个M点(M≥N)长度的失配滤波器,则考虑引入一个M点的离散傅里叶变换(Discrete Fourier Transform, DFT)矩阵F,此时s的频域可表示为
(2)
其中,0代表一个(M-N)×1的全零向量,其表示DFT前的补零过程,
则代表矩阵F的前N列。根据经典匹配滤波理论推导可知,匹配滤波器的频域形式可以表示为对应波形频域S的共轭,即
HMF=S*
(3)
其中,(·)*代表取共轭计算。
本文考虑对匹配滤波器优化设计一个由实数构成的修正系数向量K,进而得到失配滤波器频域的向量形式如下
HMMF=K⊙HMF=K⊙S*
(4)
其中,⊙为矩阵/向量对应元素的乘积,修正系数向量K的各个元素即为对匹配滤波器频域向量HMF各个系数的修正权值,记作
(5)
此时,失配滤波器时域输出的向量形式yMMF可表示为
yMMF=FH(HMMF⊙S)=FH(K⊙S*⊙S)=
FH(K⊙|S|2)
(6)
其中,(·)H表示矩阵/向量的共轭转置计算。特殊地,当K为全1向量时,此时匹配滤波器输出为
yMF=FH|S|2
(7)
需要注意的是,在评估失配滤波器的信噪比损失时,应提前对匹配滤波器和失配滤波器的能量进行归一化。以失配滤波器为例,其第m个系数在能量归一化后应为
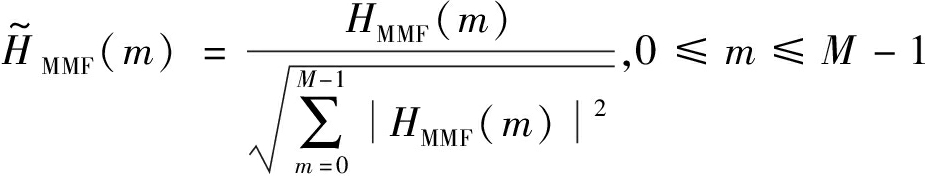
(8)
同理,可以得到能量归一化的匹配滤波器系数。此时,定义失配滤波器信噪比损失LSNR为
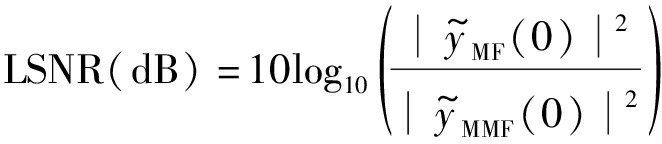
(9)
其中,
和
分别为归一化滤波器能量后匹配滤波器和失配滤波器输出的最大值。
根据不同的雷达应用场景,距离维旁瓣抑制通常会考虑优化以下三种准则,包括PSL准则,ISL准则以及WISL准则。对于PSL准则,其最优化问题可表示为
(10)
其中,Ω表示距离维旁瓣区域,ε为对LSNR的约束。类似地,对于ISL准则,其最优化问题可表示为
(11)
另外,在某些具有一定先验信息的应用中,有时仅需要抑制局部区域的旁瓣值。在这种情况下,可以定义加权积分旁瓣值(Weighted ISL, WISL),其最优化问题可表示为
s.t.LSNR≤ε 0≤w(m)≤1
(12)
其中,{w(m)|m∈Ω}表示对不同区域距离维旁瓣抑制程度的权重。根据先验信息,对于不需要抑制旁瓣的区域,令该区域的w(m)=0即可;对于需要抑制旁瓣的区域,可以根据需求设置该区域对应的权重w(m)。由(12)易知,当{w(m)≡1|m∈Ω}时,WISL准则等价于ISL准则,即ISL准则可以看作WISL准则的一种特殊情况。为了简便起见,后文对动态交替投影算法的推导中,两种准则统一使用式(12)作为算法推导的基础。
2.2 动态交替投影算法
交替投影是一种简单而有效的解决在有限制条件情况下最优化问题的算法。在解决优化问题时仅需要考虑“正投影”过程、“逆投影”过程以及添加限制三个步骤,即可以在交替投影的迭代过程中解决优化问题,避免了传统优化算法中的复杂计算,交替投影算法也被广泛应用于诸多领域[11]。为了解决上述优化问题,本节提出一种基于动态交替投影的失配滤波器设计算法。
当初始化K为全1向量时,此时满足yMMF=yMF。对于当前yMMF,考虑设计一组加权系数来获得理想失配滤波器输出如下
(13)
其中
0≤μ(m)≤1
(14)
代表加权系数。此时可根据不同的优化准则来设计对应的加权系数向量μ。如对于PSL优化准则,可以考虑设计μ为
s.t.yMMF(m0)=max{yMMF(m)},m∈Ω
(15)
即对旁瓣区域的最高值进行加权抑制,而其他区域保持不变。类似地,对于WISL优化准则,可以设计μ为
(16)
即对距离维旁瓣区域的所有旁瓣进行加权抑制。
以上可以看作交替投影的“正投影”过程,即确定理想失配滤波器输出。为了求解所构造的理想失配滤波器输出
对应的修正系数向量K′,则需要计算对应的“逆投影”过程。考虑式(6),其“逆投影”过程可表示为
(17)
式中除法为矩阵/向量对应元素除法。接着,为了实现交替投影过程,需要进一步添加相关限制条件。可以注意到,此时所求的K′并不能作为下次投影过程的修正系数向量,其原因有以下两点:
1)匹配滤波器在某种意义上可以看作是一种特殊的带通滤波器,其带外的低权值可以在一定程度上抑制带外噪声。而在设计失配滤波器时,在抑制距离维旁瓣的同时同样不希望产生较大的信噪比损失,所以也需要控制失配滤波器带外的权值。为方便起见,本文中考虑将失配滤波器带外的权值控制为与匹配滤波器相同,由于本文中失配滤波器是由匹配滤波器与修正系数向量K相乘得到的,所以修正系数向量K需要满足
K(m)≡1,∀m∉bandwidth
(18)
2)对于修正系数向量K的带外修正系数置1后,带内修正系数在某些情况下仍需要考虑进行限制。如随机相位编码信号,由于码片间相位调制可由设计者任意优化选择,所以其信号对应的带内频谱起伏通常较大,甚至有可能出现零点。考虑式(17)中的除法计算过程,当位于分母中的信号频谱出现极小值或零点时,其倒数计算会出现极大值或INF值。在这种情况下,失配滤波器的信噪比损失会变的极大甚至不可控制。为了解决这一问题,此处需要设定一个阈值δ来限制失配滤波器带内修正系数的最大值,即需对K′限制为
m∈bandwidth
(19)
此处需要注意,较大的阈值δ可为修正系数提供较大的设计自由度,但是,较大的阈值δ同样会有可能造成更大的信噪比损失,设计者需根据实际情况和工程经验灵活选择,通常δ可设定为2≤δ≤10。
综合式(18)和(19)可知,需要对K′进行以下限制以得到下次交替投影所需的修正系数向量K,即
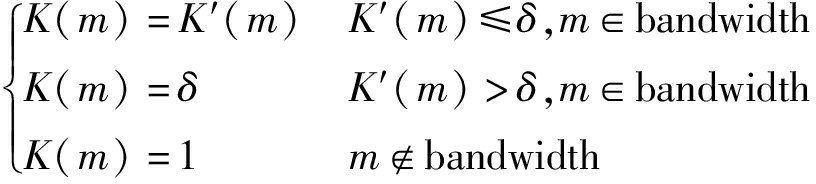
(20)
经过式(20)处理后,此时用限制过后的修正系数向量K得到的失配滤波器,其输出已不同于所构造的理想输出
但仍在一定程度上逼近于
为了逐步加强这一过程,利用多次动态交替投影迭代过程来完成对修正系数向量K的优化设计。综上,整体算法流程总结如下:
Step 1 初始化修正系数向量K为全1向量;
Step 2 根据式(6),由当前修正系数向量K计算得到当前失配滤波器输出yMMF;
Step 3 根据式(13)及优化准则,由当前失配滤波器输出yMMF得到理想失配滤波器输出
Step 4 根据式(17),计算修正系数向量K′;
Step 5 根据式(20),对K′进行约束限制得到新的修正系数向量K;
Step 6 重复Step 2～5直到满足迭代停止条件。
根据2.1节中的最优化问题设计,迭代停止条件可以由以下条件经过排列组合后组成
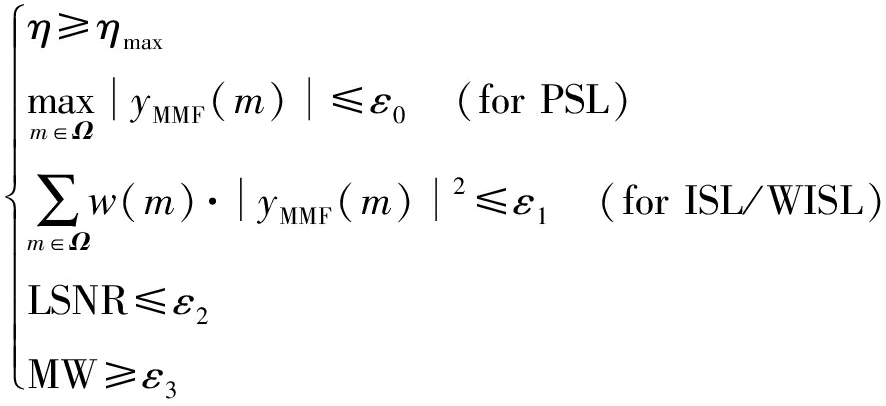
(21)
其中,η和ηmax分别表示算法当前迭代次数和允许的最大迭代次数,ε0到ε3表示对不同指标的约束条件,MW则表示主瓣宽度指标。这里需要说明的是,失配滤波器在抑制距离旁瓣的同时,除了会带来一定的信噪比损失,还会引起一定的主瓣展宽。设计者可根据实际需要对式(21)中的迭代停止条件进行灵活的组合和设计以获得最优的失配滤波器。典型地,ηmax为允许的最大迭代次数,通常可取103到106量级;ε0为对PSL指标的约束,以主瓣峰值归一化后通常可取-30 dB到-60 dB;ε1为对ISL/WISL指标的约束,以主瓣峰值归一化后通常可取-20 dB到-40 dB;ε2为对LSNR指标的约束,通常可取1 dB到3 dB;ε3为对主瓣展宽指标的约束,通常设定为原匹配滤波器输出主瓣宽度的1.2倍到1.5倍。
根据上述算法流程可知,本算法通过设计加权系数μ,动态调整每次交替投影迭代中的理想失配滤波器输出即本次迭代中理想失配滤波器输出由上次交替投影迭代中实际滤波器输出得到。通过对修正系数向量K′进行限制,使其对应的失配滤波器输出逐步逼近理想失配滤波器输出,而在下次交替投影迭代中算法又根据当前输出设置了新的理想失配滤波器输出,即通过动态设置理想输出的方法,让失配滤波器输出的距离旁瓣值不断降低。在这个过程中,信噪比损失和主瓣展宽也会随着距离维旁瓣降低而逐步严重,而设计者可根据需要设定对应的迭代停止限制条件。另外,本算法适用性强,可适用于PSL、ISL、WISL多种优化准则及多种脉冲压缩雷达波形。除此之外,整个算法流程中并不涉及任何矩阵求逆等复杂计算操作,其中的DFT变换在实际应用中也可以用FFT替换,所以本算法十分适用于硬件的高效率设计与实现。
3 仿真与分析
本节给出几种典型的最小二乘失配滤波器设计方法,并与本文所提算法进行对比仿真。仿真中所基于的雷达波形是由CAN算法[12]生成的128位最优ISL相位编码信号,且每个码片采样1个点,即设置采样率等于信号带宽。另外,在以下仿真中失配滤波器长度均设置为信号长度的4倍。
对于ISL准则,使用本文所提的基于动态交替投影法的失配滤波器(DAP-MMF)设计算法对比经典最小二乘失配滤波器(LS-MMF)设计算法;对于WISL准则,使用本文DAP-MMF设计算法对比加权最小二乘失配滤波器(WLS-MMF)设计算法,抑制区间设定为主瓣前后采样点区间[40,80];对于PSL准则,使用本文DAP-MMF算法对比迭代加权最小二乘失配滤波器(IWLS-MMF)设计算法,各组仿真对比结果如下。
由图 1和表 1可知,本文所提的DAP算法可以在更小的信噪比损失条件下实现更低的ISL;在WISL准则下,本文所提的DAP算法可以仅抑制感兴趣区域旁瓣而保持其他区域旁瓣不变,其好处是这样设计的失配滤波器可以在最大程度上接近匹配滤波器,对应的信噪比损失也比较小。从修正系数向量K的设计结果也可以获得相同的结论,由图 2可见修正系数向量K仅在1上下小幅度振动,即DAP设计的失配滤波器在匹配滤波器基础上修正程度并不大;对于PSL优化准则,由图 3和表 1可知,本文所提的DAP算法同样可以在更小的信噪比损失下实现更低的PSL值。
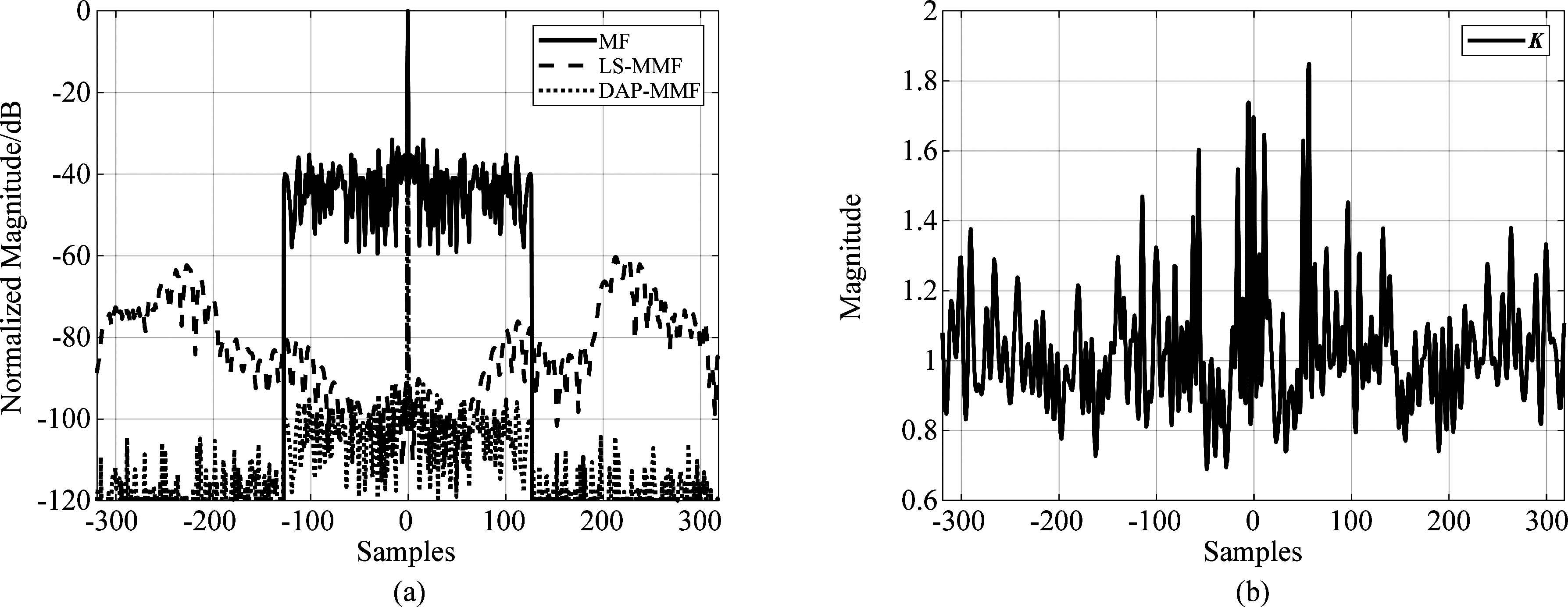
图1 (a)匹配滤波器(MF)、基于最小二乘法的失配滤波器(LS-MMF)和基于动态交替投影法的失配滤波器(DAP-MMF)输出结果；(b)基于动态交替投影法的失配滤波器(DAP-MMF)对应的修正系数向量K计算结果
Fig.1 (a)Filter outputs based on MF, LS-MMF and DAP-MMF, and(b)the corresponding correction factor vector K of DAP-MMF
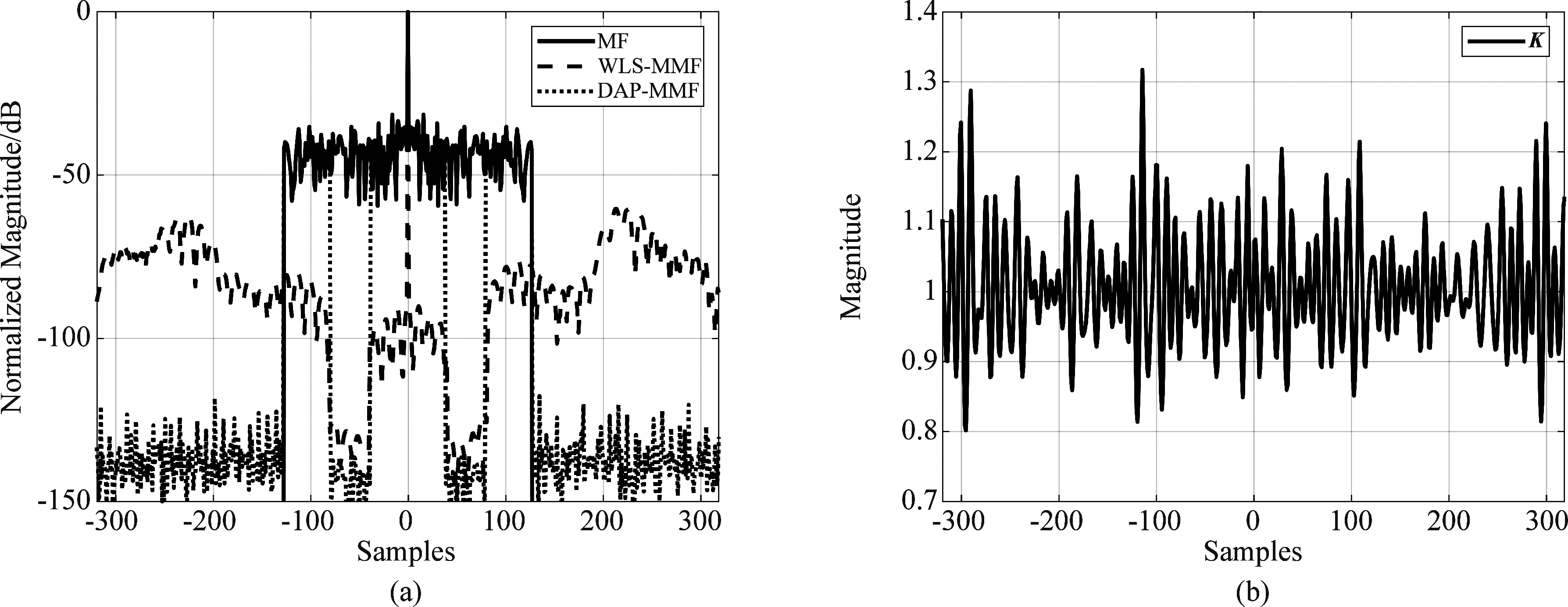
图2 (a)匹配滤波器(MF)、基于加权最小二乘法的失配滤波器(WLS-MMF)和基于动态交替投影法的失配滤波器(DAP-MMF)输出结果；(b)基于动态交替投影法的失配滤波器(DAP-MMF)对应的修正系数向量K计算结果
Fig.2 (a)Filter outputs based on MF, WLS-MMF and DAP-MMF, and(b)the corresponding correction factor vector K of DAP-MMF
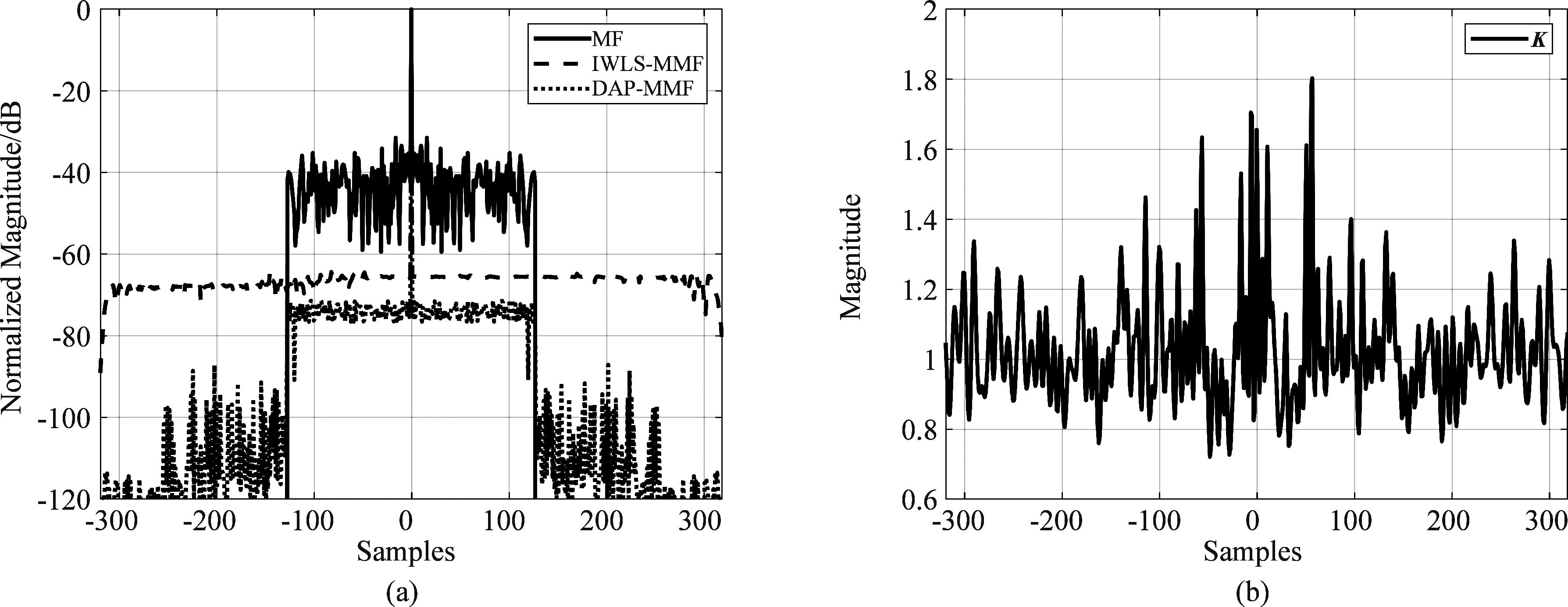
图3 (a)匹配滤波器(MF)、基于迭代加权最小二乘法的失配滤波器(IWLS-MMF)和基于动态交替投影法的失配滤波器(DAP-MMF)输出结果；(b)基于动态交替投影法的失配滤波器(DAP-MMF)对应的修正系数向量K计算结果
Fig.3 (a)Filter outputs based on MF, IWLS-MMF and DAP-MMF, and(b)the corresponding correction factor vector K of DAP-MMF
表1 各算法信噪比损失分析对比
Tab.1 LSNR of different algorithms
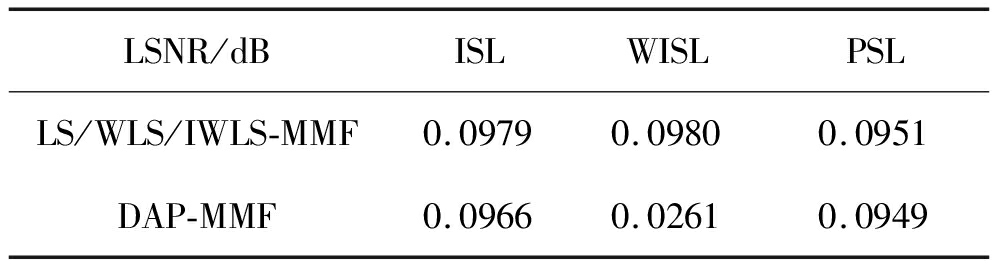
LSNR/dBISLWISLPSLLS/WLS/IWLS-MMF0.09790.09800.0951DAP-MMF0.09660.02610.0949
最小二乘系列算法及其他现有算法一般是将单位冲激响应函数作为理想失配滤波输出,通常会让目标输出过于“理想”,从而难以实现且会付出较高信噪比的代价;而本文所提的DAP算法的理想失配滤波输出是由匹配滤波器输出一步一步动态调整而来,通过对匹配滤波器修正来达到优化失配滤波器的目的,因此本文DAP算法可以在信噪比损失较小的条件下实现更好的旁瓣抑制效果。最后由表 2的计算复杂度分析对比可知,最小二乘系列算法及其他本文未列举的现有算法一般都涉及到矩阵求逆等复杂计算操作,其计算复杂度一般正比于滤波器长度的立方,在所求滤波器长度较大时,较高的计算复杂度并不利于实际系统的实现。而本文所提DAP算法的计算复杂度仅取决于过程中计算复杂度最高的FFT计算及迭代次数,所以计算复杂度远远小于现有算法,十分适用于硬件的高效率设计与实现。
表2 各算法计算复杂度分析对比
Tab.2 Computation complexity of different algorithms
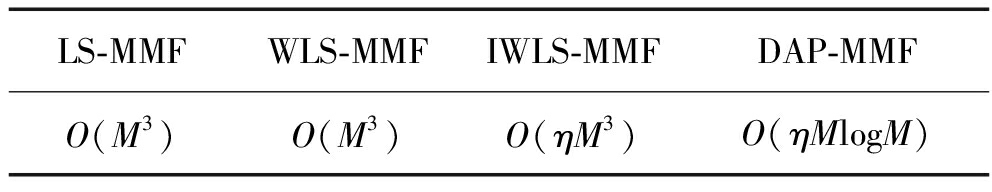
LS-MMFWLS-MMFIWLS-MMFDAP-MMFO(M3)O(M3)O(ηM3)O(ηMlogM)
4 结论
本文提出一种基于动态交替投影的失配滤波器快速设计算法,在算法中动态调整每次交替投影迭代中的理想失配滤波器输出,即通过动态设置目标输出的方法,让失配滤波器输出的距离旁瓣值不断降低。可实现在最优PSL、ISL、WISL等准则下的距离维旁瓣抑制,且信噪比损失、主瓣展宽可由设计者通过设计迭代停止条件来进行灵活控制。另外,本算法适用性强,可应用于多种脉冲压缩雷达波形。除此之外,整个算法流程中并不涉及任何矩阵求逆等复杂计算操作,其中的DFT变换在实际应用中也可以用FFT替换,所以本算法十分适用于硬件的高效率设计与实现。最后,基于CAN优化的128位相位编码信号仿真实现了几种典型的最小二乘失配滤波器设计方法,并与本文所提算法进行了对比仿真。由仿真结果可知,本文所提的DAP算法可以在更小的信噪比损失条件下实现更低的距离维旁瓣,且计算复杂度最低。
需要说明的是,由于仿真中采用相位编码信号且采样率等于带宽,所以本仿真中没有考虑主瓣展宽问题且并不存在带外权值限制的问题;同样地,本文仿真中用CAN算法优化的相位编码信号频谱相对较为平滑,带内并不存在极小值或零点,所以仿真中并未对修正系数向量K进行相关的限制,如读者有兴趣仿真高采样率或随机相位编码信号等情况,则需要考虑上文所述限制,本文不再进行赘述。另外需要注意,本文算法目前仅局限于零多普勒频移回波的失配滤波器设计,对于含多普勒频移回波的失配滤波器设计将在作者未来的工作中进一步考虑。
[1] LEVANON N, MOZESON E.Radar signals[M].Hoboken, NJ, USA: John Wiley & Sons, Inc., 2004.
[2] SUN Yinghao, LIU Quanhua, CAI Jinjian, et al.A novel weighted mismatched filter for reducing range sidelobes[J].IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(3): 1450-1460.
[3] SUN Yinghao, LIU Quanhua, CAI Jinjian, et al.A novel method for designing general window functions with flexible spectral characteristics[J].Sensors, 2018, 18(9): 3081.
[4] ACKROYD M H, GHANI F.Optimum mismatched filters for sidelobe suppression[J].IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 214-218.
[5] LEVANON N, SCHARF A.Range sidelobes blanking using contrasting mismatched filters[C]∥2009 16th International Conference on Digital Signal Processing.Santorini, Greece.IEEE, 2009: 1-6.
[6] HE Peng, CHEN Baixiao, YANG Minglei.A novel sidelobe suppression method based on the CLEAN algorithm for bi-phase codes pulse compression[C]∥2016 CIE International Conference on Radar(RADAR).Guangzhou, China.IEEE, 2016: 1-4.
[7] BADEN J M, COHEN M N.Optimal peak sidelobe filters for biphase pulse compression[C]∥IEEE International Conference on Radar.Arlington, VA, USA.IEEE, 1990: 249-252.
[8] GRIEP K R, RITCEY J A, BURLINGAME J J.Poly-phase codes and optimal filters for multiple user ranging[J].IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 752-767.
[9] RABASTE O, SAVY L.Mismatched filter optimization for radar applications using quadratically constrained quadratic programs[J].IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3107-3122.
[10] KAJENSKI P J.Mismatch filter design via convex optimization[J].IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1587-1591.
[11] ESCALANTE R, RAYDAN M.Alternating projection methods[M].Philadelphia, PA: Society for Industrial and Applied Mathematics, 2011.
[12] STOICA P, HE Hao, LI Jian.New algorithms for designing unimodular sequences with good correlation properties[J].IEEE Transactions on Signal Processing, 2009, 57(4): 1415-1425.
