1 引言
频谱设备的多样化应用带来了日益复杂的电磁环境,同时也给担负重要军事任务的机动作战平台带来一定的挑战。为了更好的适应以及应对复杂多变的电磁对抗,机动作战平台需要装备大量的电子设备。例如美国F-22战机装备的电子设备已超过了14个[1]。电子设备的增多必然导致机动作战平台空间、能耗的紧张。雷达和通信作为机动作战平台执行任务不可缺少的重要功能,对其天线进行一体化设计成为提升机动作战平台性能的一种有效方式。
与线性阵列相比,平面阵列天线可以在两个方向上控制波束指向,应用场景更加广泛。稀疏布阵和子阵交错技术的出现为天线共享设计提供了新的解决方案。稀疏布阵是在满阵列的基础上对阵列进行稀疏化,即采用较少的阵元便可在主要指标上达到原阵列的性能。子阵交错技术是在稀疏阵列的基础上,将多个阵列交错放置,使得天线阵列在同一孔径可以实现多功能。随着计算机技术的发展,快速算法和智能优化算法逐渐应用到平面阵列的共享设计上。文献[2-3]利用粒子群算法探讨了圆形阵列的阵列优化方法,得到的优化阵列旁瓣电平较低;文献[4]在保证旁瓣电平较低的基础上,对粒子群权重赋值方法进行改进,加快了算法的收敛速度。文献[5]构造l范数优化模型对圆形阵列进行了优化,有效减少了阵元数量。文献[6-7]利用阵元激励与阵列因子之间存在傅里叶变换关系提出了迭代快速傅里叶算法,与差集算法相比实现了更低的旁瓣电平。文献[8-10]利用遗传算法对平面阵列进行了优化设计,在保证阵列旁瓣电平较低的条件下有效减少了阵元数量。文献[11]利用矩阵映射函数确定阵元位置并提出了一种矩阵映射的方法。然而,在雷达-通信天线共享孔径领域,交错稀疏阵仍然属于较新的概念。文献[12]利用循环差集确定阵元位置从而实现雷达-通信一体化阵列设计,但是不能根据雷达通信需要实时改变阵列结构。
本文提出了一种基于遗传算法的雷达-通信共享孔径研究方法。首先介绍了雷达阵列和通信阵列的优化目标函数,在平面阵列的基础上建立了多目标优化模型;其次,基于遗传算法设计了算法流程,初步解决了多目标优化问题,能够在一定程度上调整阵列结构满足不同的雷达-通信功能需求;最后进行了仿真实验,实验结果表明,根据需求调整权系数改变阵列结构可使雷达和通信均达到相应的工作要求。
2 共享孔径模型
进行雷达和通信天线共享设计是在稀疏阵和子阵交错的基础上分析雷达和通信阵元分布对天线性能的影响。与单一工作阵列相比,共享阵列实际可划分为同时工作的雷达和通信两个阵列。考虑一个阵元数为M×N,栅格间距为
的平面阵列如图1所示。
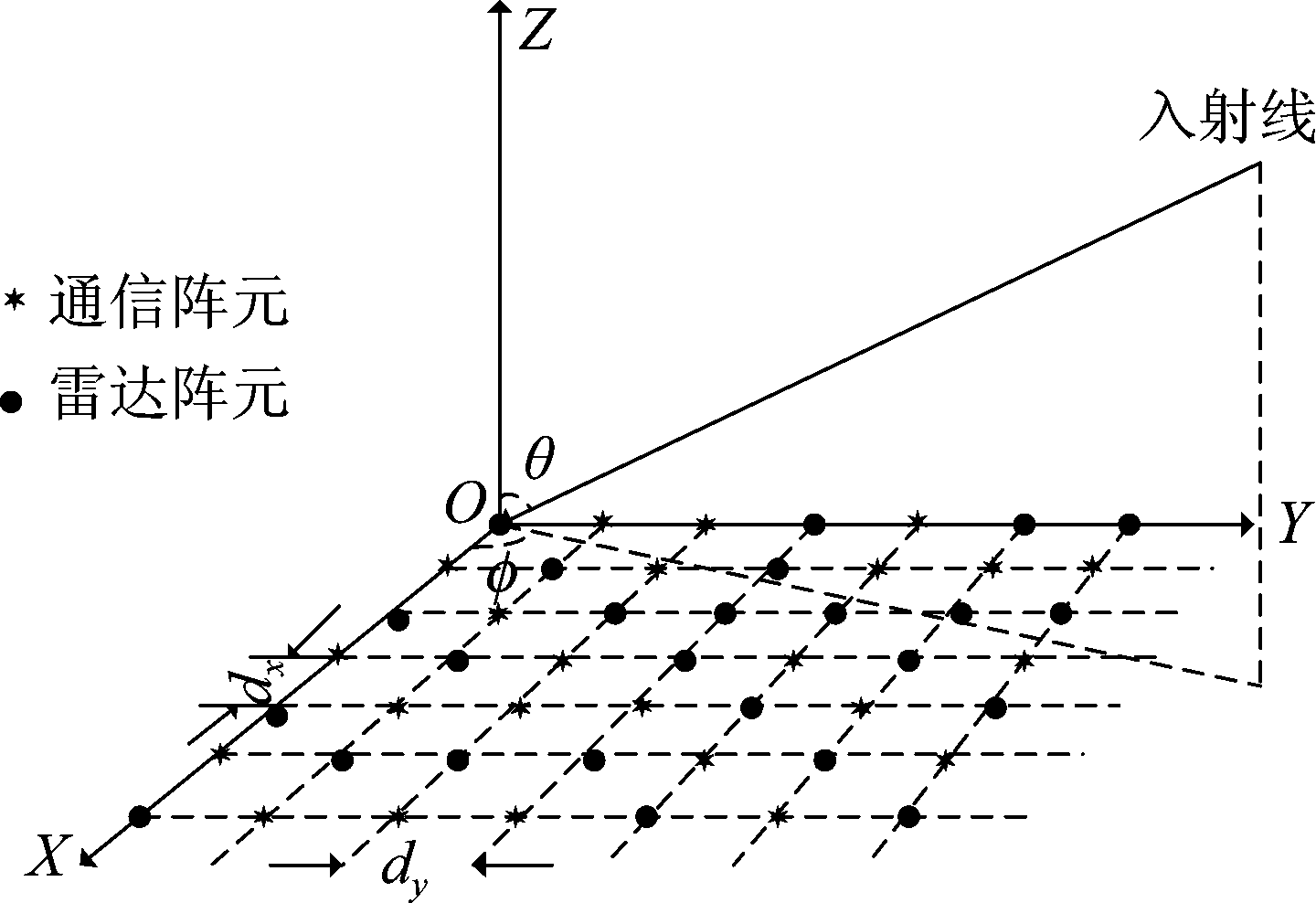
图1 平面阵列共享设计模型
Fig.1 Planar array sharing design model
此时天线阵元可工作在两种状态,并可实时调整。
对于雷达阵列来说,入射俯仰角为θ,方位角为φ,假设各阵元均为理想的全方向性阵元且主波束指向阵列法线方向,则其方向图可表示为:
jkndysin θsin φ)
(1)
其中,Im,n为第(m,n)个阵元的激励幅度,k=2π/λ,0≤m≤M-1,0≤n≤N-1,θ∈(0,π/2),φ∈(-π/2,π/2)。
用xmn表示在不同状态工作阵元。其中,xmn=1表示阵元处于雷达工作状态,xmn=0表示阵元处于通信工作状态。此时,工作在雷达状态的阵元形成的方向图函数可表示为:
jkndysin θsin φ)·xmn
(2)
对于雷达阵列来说,较为关键的性能指标有主瓣宽度和最大旁瓣电平等。若边界点位置的阵元工作在雷达状态,则能确保共享阵列的雷达方向图主瓣宽度基本不变。此时,选取最大旁瓣电平(Max Side-lobe Level)作为雷达阵列优化设计的指标,其计算公式可表示为:
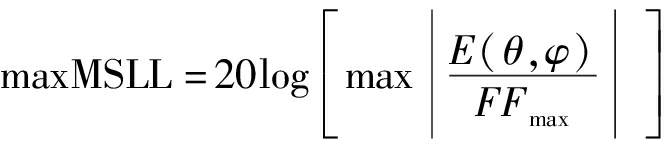
(3)
其中,FFmax是主瓣峰值,θ、φ的取值与公式(1)相同,不过要排除主瓣区间。
通信对天线的要求与雷达不同,主要关注信道容量和信噪比等指标。考虑到平面阵列为多输入多输出(MIMO)系统,与单一阵列相比,在一定的发射功率和带宽的条件下,MIMO通信系统的信道容量会有较大提高。一种典型的通信信道容量模型[13]为:
y=Hx+v
(4)
式中,x为NT×1发射信号矢量,y为NR×1接收信号矢量,v为接收端NR×1零均值高斯白噪声矩阵,H为NR×NT传输信道衰落矩阵。假设通信接收端已知信道矩阵H,信道容量C可以表示为
(5)
式中,I为单位阵,(·)H表示矩阵的共轭转置,ρ为信噪比,NT为通信阵元的数量。
由公式(5)可知,信道容量与信道传输矩阵相关,而信道传输矩阵又会受到天线之间空间相关性的影响。文献[14]的研究表明,在不考虑发射端天线相关性的前提下,平面天线中阵元的相关性可用二维指数相关模型近似
(6)
其中,i、j表示接收端的阵元序号,μx、μy分别表示水平方向和垂直方向的相关系数,且|μx|≤1,|μy|≤1。需要注意的是这里i、j表示的阵元实际上是一维的序号,是将二维阵列进行“先横后纵”重新整理成一维序列后获得的。在计算R(i, j)时,需要先将i、j还原为原二维阵列中的序号进行。
具体到平面阵列,此时R(i, j)变为R[(mi,ni),(mj,nj)],其中(mi,ni)(mj,nj)分别表示i、j对应矩阵元素的二维坐标(mi,ni)和(mj,nj)。二者的变换关系为i=mi×N+ni, j=mj×N+nj;则
表示向下取整数,ni=i%N,nj=j%N,%表示取余数。处理过程参考图2所示。
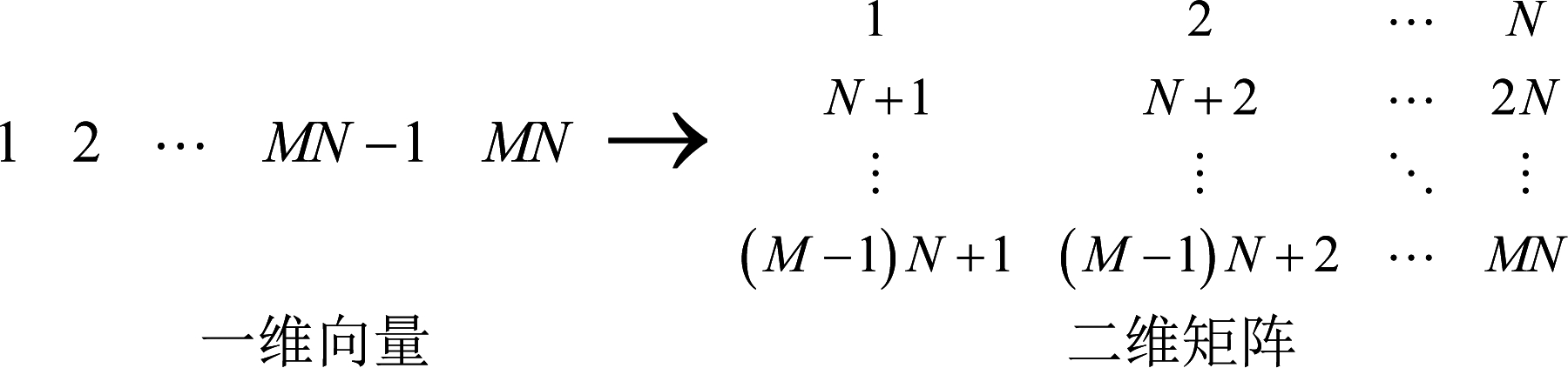
图2 阵元位置转换模型
Fig.2 Array element position conversion model
在上述基础上,公式(5)可进一步推导为[15]
(7)
式中,Qr为R特征值分解得到的对角阵,nr为接收信道选择后的天线阵元数,Hw表示均值为0、方差为1的随机矩阵。在功率有限的条件下,合理选择通信阵元会提高通信的信道容量[14]。
在分别确定了雷达和通信的天线性能与阵元位置关系后,考虑多目标优化问题
max f(x)=(f1(x), f2(x))
s.t.x=(x1,x2,...,xM)
(8)
其中，x为决策向量,xmn=1表示阵元处于雷达工作状态,xmn=0表示阵元处于通信工作状态。
f1(x)表示天线阵列合成的雷达波束具备的最大旁瓣电平
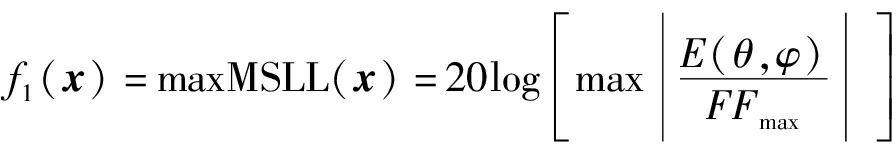
(9)
其中参数定义与公式(3)相同。
f2(x)表示天线阵列中通信阵元的信道容量,由文献[15]可知,通信阵列的信道容量公式(7)可进一步表示为:
(10)
其中,g(x)为平面阵列转换的一维向量,NZ(·)表示统计向量中的非零个数,T(·)代表一种运算方式即T(a,b)=a·b·aH,其余参数与公式(7)保持一致。
从公式(8)中可知,雷达阵列的旁瓣电平f1(x)和MIMO通信系统的信道容量f2(x)作为优化目标,目的是使旁瓣电平和信道容量的取值同时达到最优。这是一个二元优化问题,不存在一个同时满足两个目标函数的最优解。这一类问题的优化解称为帕累托最优解,它由一系列的解集组成[16]。为了简化问题,此处本文采用了加权的方法将多目标问题转化为如下单目标问题:
max f(x)=αf1(x)+(1-α)f2(x)
(11)
其中,0<α<1表示权系数,α越大则优化目标越接近f1(x),反之则接近f2(x)。已经证明公式(11)的一个全局最优解必为帕累托解集里的一个解[16]。
3 遗传算法及设计流程
由于式(11)中的f1(x)和f2(x)是非线性函数,经常需要采用一些启发式算法进行求解。遗传算法在解决非线性寻优问题上具有简单、通用和防止陷入局部最优的特点。因此选择其作为寻优求解方法。算法流程如下:
步骤1 适应度函数选择。以公式(11)中的目标函数f(x)作为适应度函数,由于在遗传算法的一般表达式中f1(x)要取极小值,所以需要将f1(x)前加负号,此时适应度函数为:
f(x)=(1-α)f2(x)-αf1(x)
(12)
在实验中要事先确定好偏好度α,α的取值与公式(11)一致。
步骤2 初始化和编码操作。采用一组数量为Np的二进制向量x形成一个种群。每个x向量作为种群的个体,其长度为L=M×N。x的每个元素从0和1随机选择,使其均符合0～1伯努利分布。将每一个长为L的一维向量x作为初始值带入公式(10),进行通信信道容量的计算;然后按照升维变换使其变形为M×N阶的矩阵,带入公式(9)计算雷达旁瓣电平;最后利用式(12)计算每个个体的适应度,得到f(x)的初始值。
步骤3 选择操作。这里采用“轮盘赌”的选择法,计算每个个体适应度f(x)i,则该个体被选取的概率为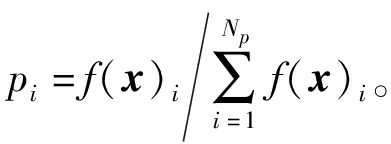
对于每个个体来说,其适应度越大,则其被选择的机会也越大;反之亦然。进行Np-1次轮盘赌,取出每轮得到的个体作为新种群的初始个体。
步骤4 交叉操作。首先,根据步骤3的选择结果取出一对个体,作为交配的父母;然后分别在父体和母体的长度L的向量中随机选取k个基因;最后,根据交叉概率pc进行交叉操作,即配对的个体在交叉点位置互换基因,从而形成一对新个体。
步骤5 变异操作。产生一个0到1均匀分布的随机数r,设变异概率为pm。如果r<pm,在经过步骤4后的种群中随机选择一个个体j(j=1～Np),并从该个体上随机选择一个基因i(i=1～L)进行变异。变异时,基因其向量值若为1,则变为0;若向量值为0,则变为1。
步骤6 算法终止。若达到循环次数G后,遗传算法终止,输出最优个体的适应度f(x)和对应的向量xbest,分别计算雷达最高旁瓣电平f1(x)和通信信道容量f2(x);否则,转向步骤2。
4 实验仿真
下面通过计算机仿真实验来验证本文所提方法的有效性。
实验参数如下:天线参数,方位向阵元和俯仰向阵元数量M=N=16;波长λ=0.03 m;通信阵元相关系数μx=μy=0.5,信噪比ρ=20 dB;遗传算法中,初始化种群数目Np=50;交叉概率pc=0.8;变异概率pm=0.05;迭代次数G=200。
(1)α取值对算法执行结果的影响
算法执行结果如图3～图6所示。
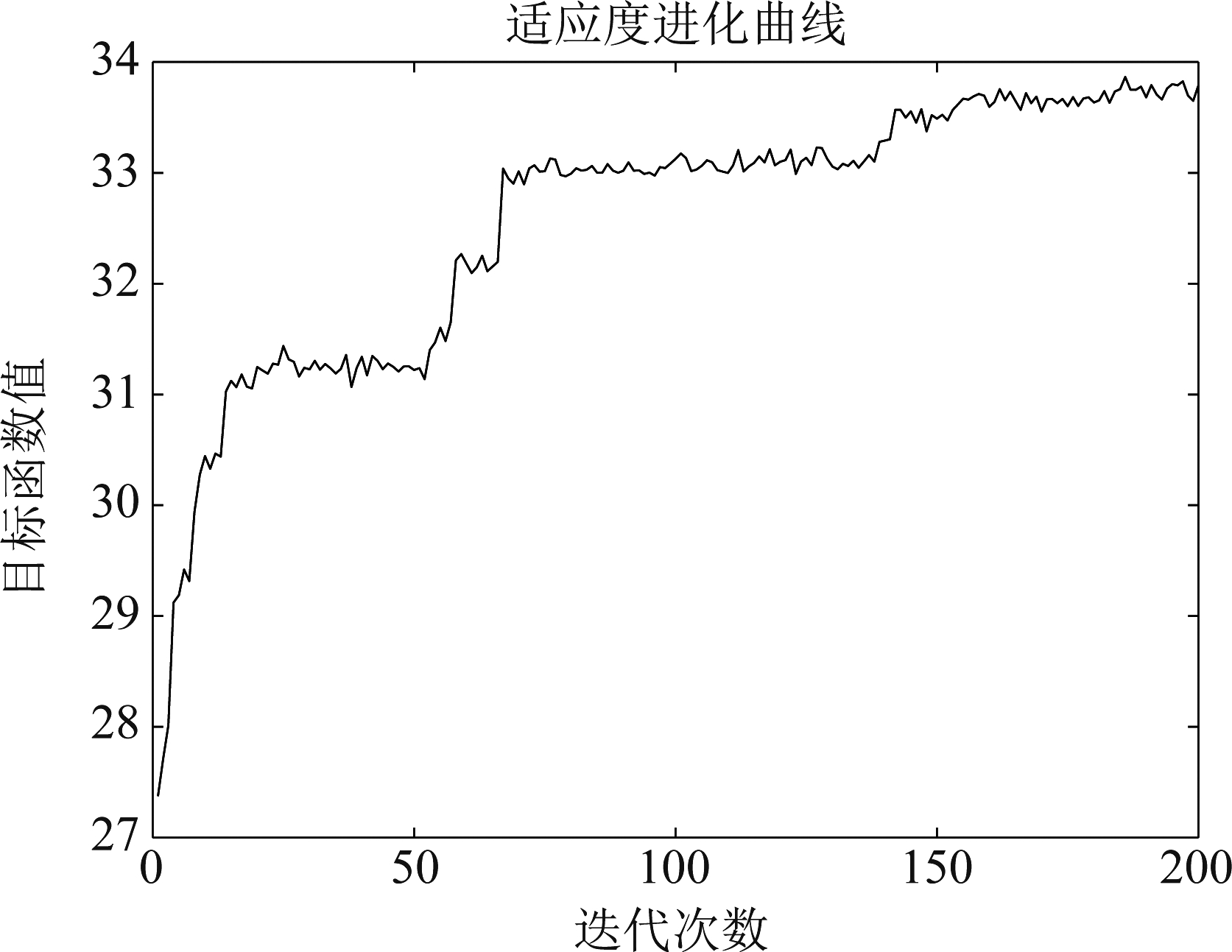
图3 适应度变化曲线
Fig.3 Fitness variation curve
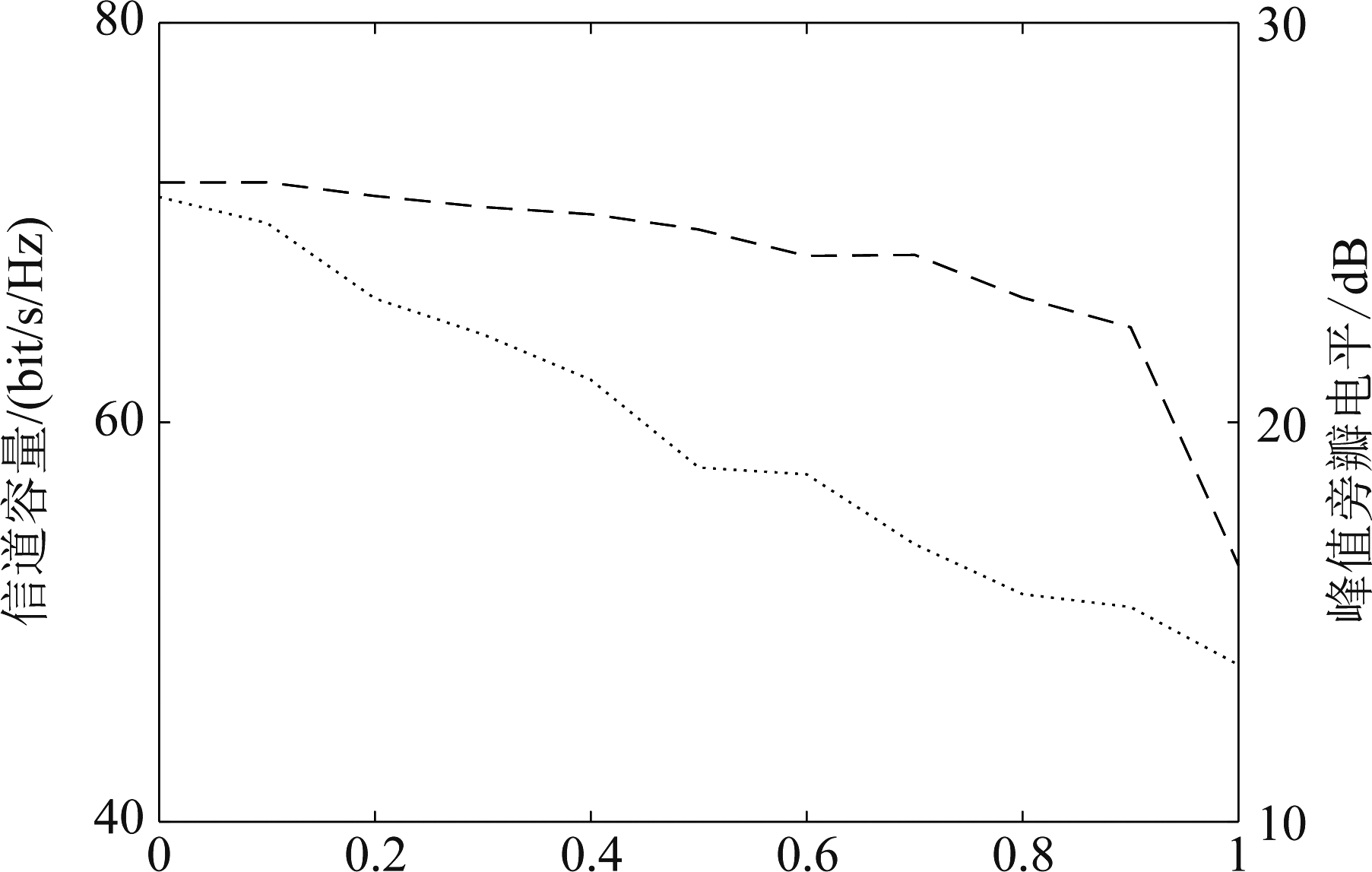
图4 α不同时目标函数变化曲线
Fig.4 The change curve of the objective function at different times
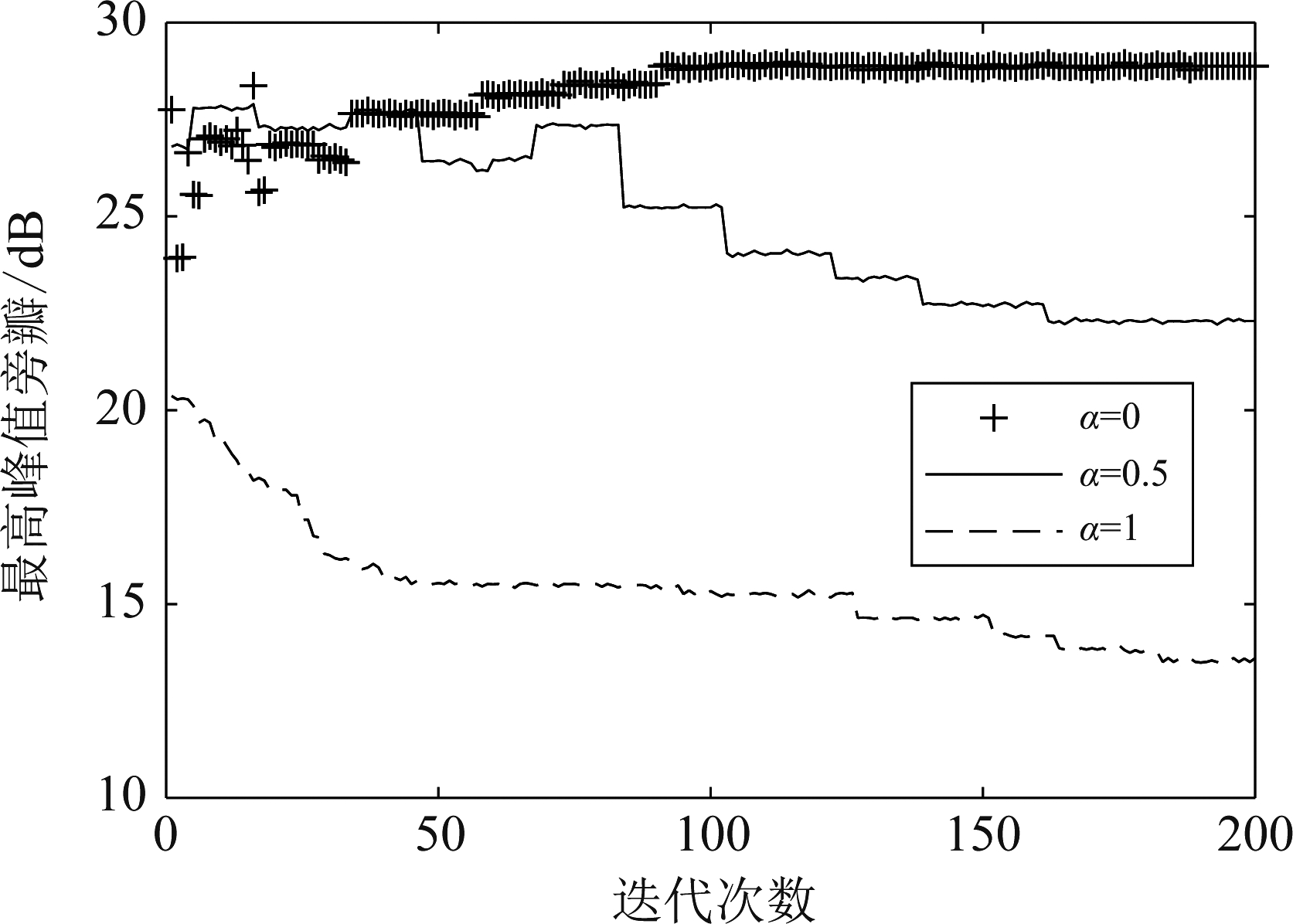
图5 α不同值时最大旁瓣电平变化曲线
Fig.5 Variation curve of maximum side lobe level at different values of α
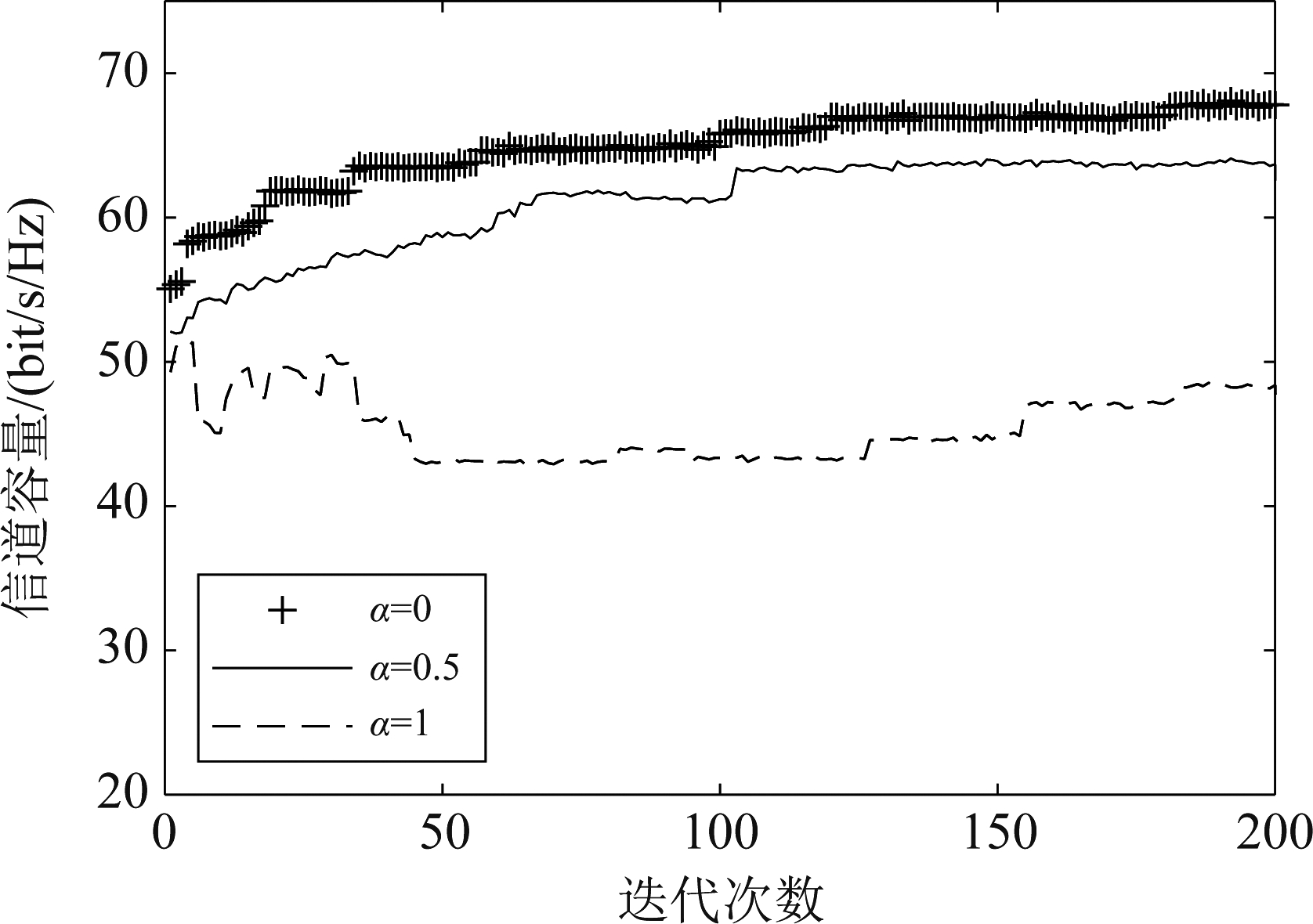
图6 α不同值时信道容量变化曲线
Fig.6 Channel capacity change curve at different values of α
图3给出了当α=0.5时,随着迭代次数的增加,适应度f(x)的变化曲线。可以看出适应度函数f(x)逐渐达到收敛状态且趋于平稳状态。
图4表示α在0到1范围内取值时,通信信道容量f2(x)与雷达最高旁瓣电平f1(x)的变化。其中虚线代表通信信道容量f2(x)的变化,点线代表的是雷达最高旁瓣电平f1(x)的变化。随着α的增大适应度函数f(x)偏向雷达最高旁瓣电平f1(x),即整体侧重于雷达性能。
从图5和图6中可以看出:当α=0时,此时约束条件中只有通信信道容量f2(x)起作用,相当于只对通信作了优化,所以雷达的最高旁瓣电平f1(x)优化效果很差;当α=0.5时,此时雷达和通信的约束力度相同,从图中可以看出最高旁瓣电平f1(x)与通信信道容量f2(x)都有一定程度的优化;当α=1时,约束条件中只有最高旁瓣电平f1(x)起作用,因此雷达性能上升而通信性能下降。显然在阵元数有限的条件下,不存在一个能够同时满足雷达和通信最优性能最优分配方案,需要根据要求适当选择α。
当α=0.5时,优化后的雷达阵列最高旁瓣电平为-14.67 dB,通信信道容量可达653 bit/s,可同时满足雷达和通信的工作要求。
(2)当α=0.5时雷达阵列方向图分析
当α=0.5时,经算法优化后各阵元排列如图7所示。其中*号代表的为通信阵元;圆圈为雷达阵元。
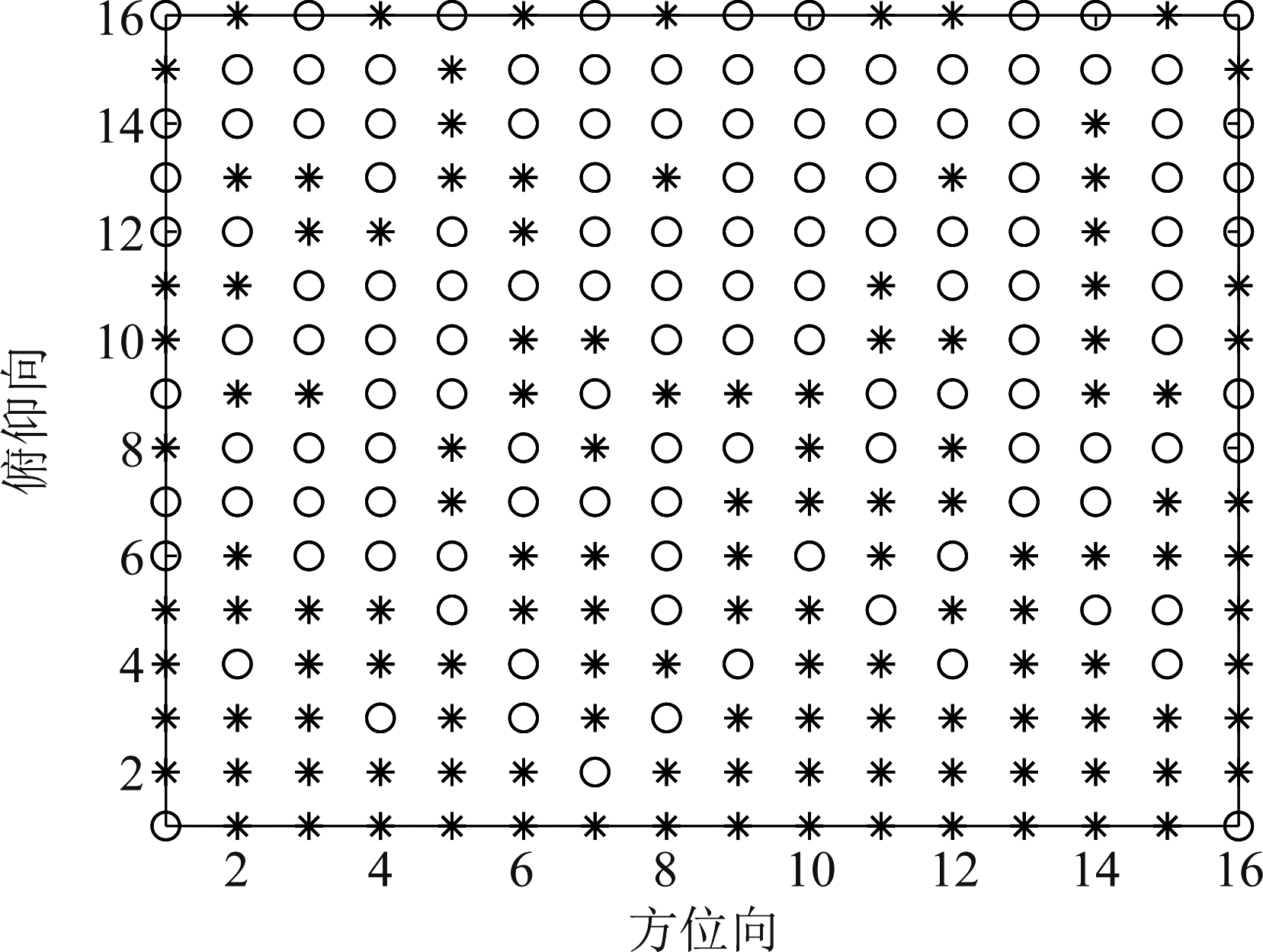
图7 优化后的阵元标识位置
Fig.7 Optimized array element identification position
在该优化模型下的雷达阵列方向图如图8～图11所示。
图8 优化后的阵列方向图三维图
Fig.8 Three-dimensional diagram of the optimized array pattern
如图10和图11所示,虚线为满阵列时的方向图,实线为一体化优化后的雷达阵列方向图。经对比可知,本文优化后的雷达阵列方向图旁瓣电平更低。
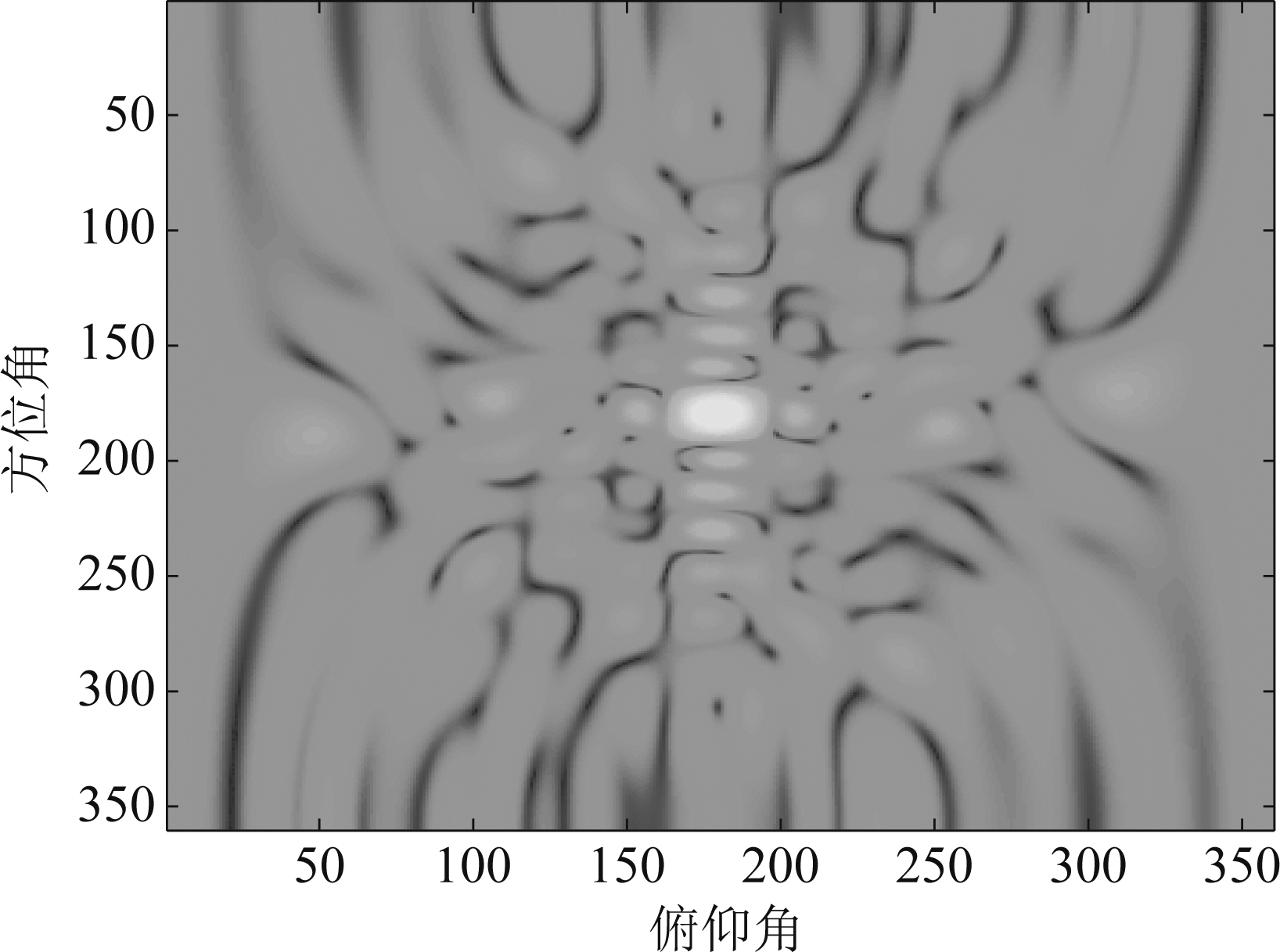
图9 三维图俯视图
Fig.9 Three-dimensional top view
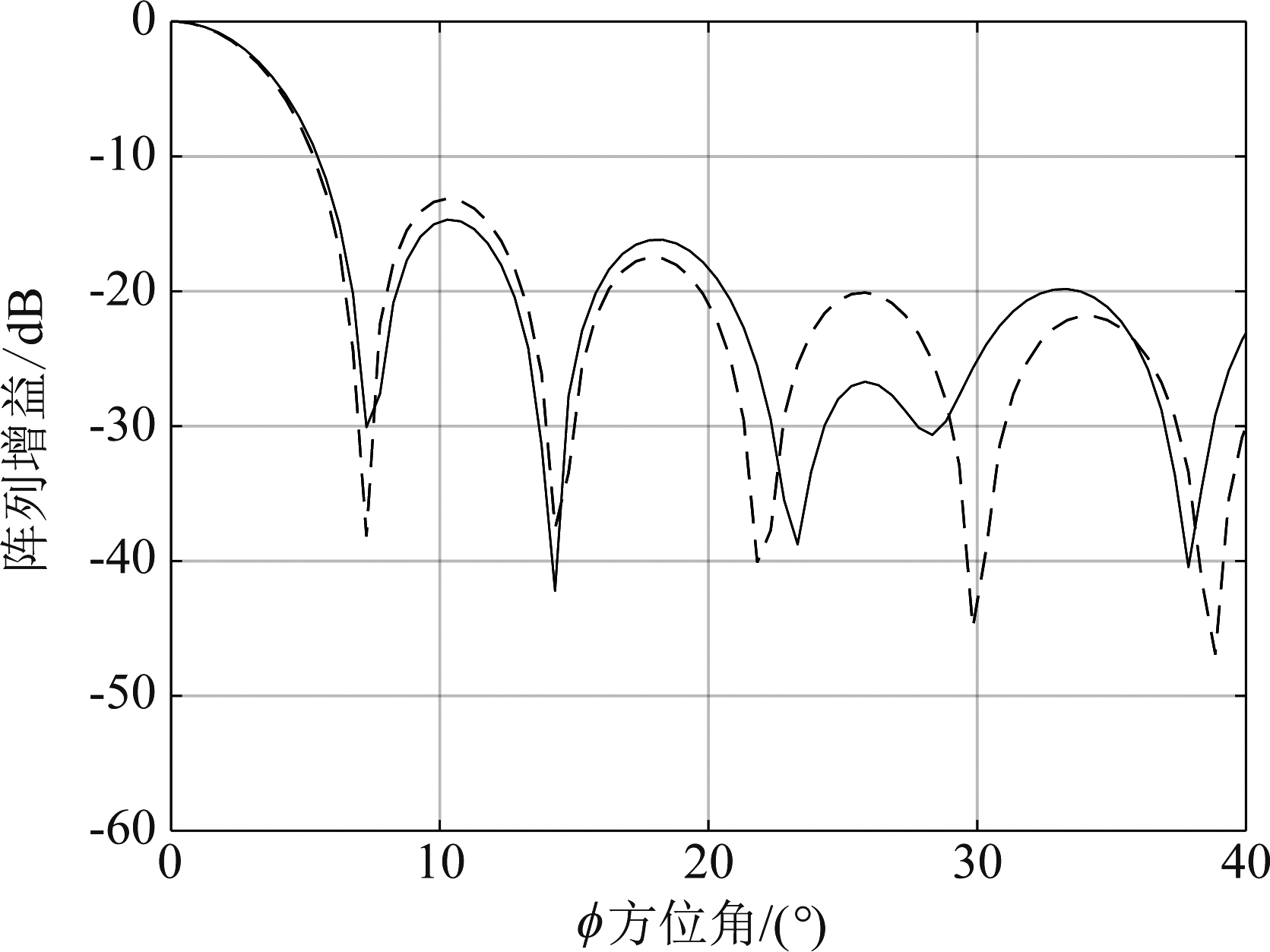
图10 方位向对比图
Fig.10 Comparison of azimuth
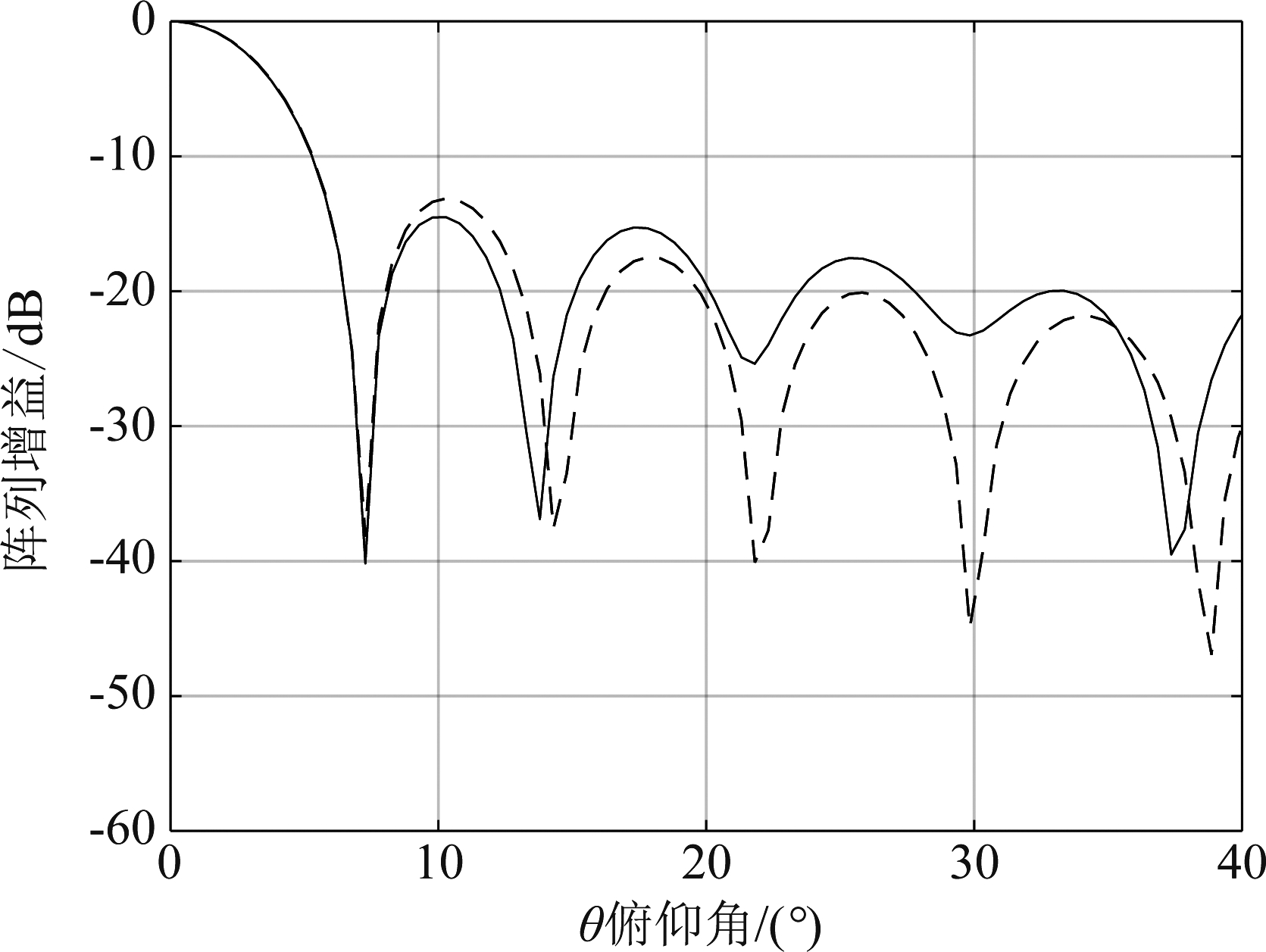
图11 俯仰向对比图
Fig.11 Comparison of pitch
5 结论
本文以雷达最高旁瓣电平和通信信道容量作为优化指标进行了共享阵列设计的研究。首先在平面阵列的基础上建立了相关的模型;其次,用改进的遗传算法对模型进行了优化并做了仿真分析,结果表明雷达最高旁瓣电平和通信信道容量能同时达到较好的工作能力。在下一步的工作中将进一步优化算法以达到更好的工作性能以及针对动态分配孔径问题做相关研究。
[1] 蒲小勃.现代航空电子系统与综合[M].航空工业出版, 2013.
PU Xiaobo.Modern avionics system and integration[M].Aviation Industry Press, 2013.(in Chinese)
[2] PATHAK N, MAHANTI G K, SINGH S K, et al.Synthesis of thinned planar circular array antennas using modified particle swarm optimization[J].Progress in Electromagnetics Research Letters, 2009, 12: 87-97.
[3] 张伟, 曲智国, 王晶晶, 等.基于模拟退火算法的大规模稀疏圆形阵列设计方法[J].信息系统工程, 2020(10): 88-89.
ZHANG Wei, QU Zhiguo, WANG Jingjing, et al.Design method of large-scale sparse circular array based on simulated annealing algorithm[J].Information Systems Engineering, 2020(10): 88-89.(in Chinese)
[4] 丛雯珊, 余岚, 杜鹏飞, 等.基于粒子群算法的宽带真延时平面阵列方向图综合[J].国防科技大学学报, 2020, 42(5): 31-36.
CONG Wenshan, YU Lan, DU Pengfei, et al.Planar array pattern synthesis of wideband real time delay based on particle swarm optimization algorithm[J].Journal of National University of Defense Technology, 2020, 42(5): 31-36.(in Chinese)
[5] 黄中瑞, 郑志东, 刘春生.约束阵元最少化的圆阵列方向图综合[J].信号处理, 2013, 29(7): 846-856.
HUANG Zhongrui, ZHENG Zhidong, LIU Chunsheng.Pattern synthesis of the circular array with the constraint of minimal arrays[J].Journal of Signal Processing, 2013, 29(7): 846-856(in Chinese)
[6] 曾伟一, 梁颖, 黄伟.基于迭代FFT算法的平面稀疏阵列优化方法[J].电讯技术, 2011, 51(11): 99-102.
ZENG Weiyi, LIANG Ying, HUANG Wei.An optimum method for thinned planar array based on iterative FFT algorithm[J].Telecommunication Engineering, 2011, 51(11): 99-102.(in Chinese)
[7] 李龙军, 王布宏, 夏春和.基于迭代FFT算法的平面阵列交错稀疏布阵方法[J].电波科学学报, 2016, 31(2): 387-393.
LI Longjun, WANG Buhong, XIA Chunhe.Thinned and interleaved planar array antenna based on iterative FFT techniques[J].Chinese Journal of Radio Science, 2016, 31(2): 387-393.(in Chinese)
[8] 马鹏鹏, 屈世伟, 杨仕文.基于遗传算法的非周期子阵排布的平面阵列综合[C]∥2019年全国天线年会论文集.昆明, 2019: 546-549.
MA Pengpeng, QU Shiwei, YANG Shiwen.Planar array synthesis of aperiodic sub-array arrangement based on genetic algorithm[C]∥Proceedings of the 2019 National Antenna Conference.Kunming, 2019: 546-549.(in Chinese)
[9] 王铮, 孙雨泽, 杨小鹏, 等.分布式雷达节点位置优化的多约束遗传算法研究[J].信号处理, 2019, 35(6): 979-985.
WANG Zheng, SUN Yuze, YANG Xiaopeng, et al.Research on multi-constrained genetic algorithm for distributed radar elements position optimization[J].Journal of Signal Processing, 2019, 35(6): 979-985.(in Chinese)
[10] 程乃平, 潘点飞.大型阵列天线子阵划分及栅瓣抑制方法[J].信号处理, 2014, 30(5): 535-543.
CHENG Naiping, PAN Dianfei.Subarray partition method and grating lobe suppression for large array antenna[J].Journal of Signal Processing, 2014, 30(5): 535-543.(in Chinese)
[11] 戴定成, 姚敏立, 贾维敏, 等.多约束稀布矩形平面阵列天线的方向图综合[J].电子与信息学报, 2019, 41(1): 107-114.
DAI Dingcheng, YAO Minli, JIA Weimin, et al.Synthesis of multi-constrained sparse rectangular arrays[J].Journal of Electronics & Information Technology, 2019, 41(1): 107-114.(in Chinese)
[12] 娄昊, 张群, 王恺, 等.面向雷达和通信一体化应用的阵列天线设计[J].电光与控制, 2017, 24(9): 54.
LOU Hao, ZHANG Qun, WANG Kai, et al.Antenna array design for integrated radar and communication system[J].Electronics Optics & Control, 2017, 24(9): 54.(in Chinese)
[13] TELATAR E.Capacity of multi-antenna Gaussian channels[J].European Transactions on Telecommunications, 1999, 10(6): 585-595.
[14] AALO V A.Performance of maximal-ratio diversity systems in a correlated Nakagami-fading environment[J].IEEE Transactions on Communications, 1995, 43(8): 2360-2369.
[15] 娄昊,张群,朱丰,等.基于交错稀疏阵列优化的雷达-通信共享孔径方法[J].电光与控制,2018,25(2): 83-87.
LOU Hao, ZHANG Qun, ZHU Feng, et al.Radar-communication shared aperture method based on staggered sparse array optimization[J].Electro-Optics and Control, 2018, 25(2): 83-87.(in Chinese)
[16] 石长安, 刘一民, 王希勤, 等.基于帕累托最优的雷达-通信共享孔径研究[J].电子与信息学报, 2016, 38(9): 2351-2357.
SHI Changan,LIU Yimin,WANG Xiqin, et al.Optimal allocation of shared aperture in radar-communication integrated system based on Pareto optimality[J].Journal of Electronics & Information Technology, 2016, 38(9): 2351-2357.(in Chinese)
