1 引言
随着我国航空运输业的快速发展,空中交通流量也在不断上升,空域资源日益紧张,飞行航路正面临着严重的饱和。受雷暴天气影响,当雷暴发生时常会伴随着湍流、冰雹、强降雨等多种危险气象发生,在这种情况下就容易造成航路失效[1],改航是解决航路失效的主要办法,高效的改航策略可以充分利用空域资源,确保飞行安全[2]。因此,改航路径规划一直是空中交通管理领域的热点研究问题之一。
目前,国内外对改航的研究已有较多的研究成果。文献[3]提出了一种基于非分时建模的航迹规划方法,通过准确地捕获航班的到达和起飞时刻,并考虑燃油消耗与速度的关系来规划航迹。文献[4]提出了一种对流天气背景下的多目标改航规划模型,并在空中交通管制战术层面上进行了更为精确的改航。文献[5]通过分析改航航班的到达时间,以评估改航路径的净效果。文献[6-8]通过蚁群算法、自适应蚁群算法、改进退火算法、元胞自动机等进行改航策略的优化。文献[9]通过航路网络模型来研究改航规划。文献[10]通过分析不同航班的到达时间,可以有效减少总航班延误。文献[11]在航线网络模型中,利用空中交通管理对航线流量进行实时预测,对改航规划具有一定的参考意义。文献[12]提出了一种不确定天气条件下空中交通改航的风险对冲方法。文献[13]通过对所有航线进行连续性分析并提供实时更新的航线变更报告,从而提出了相应的改航策略。
综上所述,目前的改航策略往往都是在静态单一层面航线网络环境下,把改航研究简化成求解最短路径问题,而在宏观层面上未作深入分析。主要有以下三点:第一,未能考虑雷暴天气下多种危险气象同时存在和不同危险气象类型影响的范围不同,以及仅考虑在单一层面上进行改航规划,当危险气象在单一层面上大面积覆盖空域时,这就容易造成规划的航迹在单一层面上产生大面积的冗余绕飞距离,降低了空域利用率,导致航班流量的汇聚,出现拥堵;第二,未能考虑航空器的运动学模型,这就容易造成规划的航迹可能不符合航空器的实际飞行情况;第三,未能考虑雷暴天气下飞行航路上临时出现的动态危险气象情况,这就需要进行二次改航规划,降低了改航决策效率,增加了管制员和飞行员的工作负荷。
针对上述问题,本文提出了一种考虑多种危险气象的分层航迹动态规划策略。该方法主要分为两步:第一步,改航空域分层规划。根据雷达回波图对改航空域进行分层规划。第二步,分层航迹动态规划。首先,基于改航起点和改航终点利用稀疏A*算法结合改航约束条件对分层规划空域进行全局航迹规划,并利用关键点选取策略以确定全局关键航迹点;然后,根据关键航迹点对全局航迹进行分段处理,并将每段航迹所涉及的气象信息沿该分段航迹所在的平面进行二维投影;最后,利用动态窗口法在投影的二维平面内基于分段航迹两端点(关键航迹点)进行实时航迹动态规划。实验结果表明所提方法具备良好的实时航迹动态规划性能,并且优于稀疏A*算法、动态窗口法和现行策略,而且所提方法能够提供在规避危险气象过程中关于航空器的航速和航向的变化情况供飞行员参考。
2 改航空域分层规划
危险气象在空域的分布具有多样性和无规则性,合理的规划改航空域是进行改航路径规划的前提和基础。本文以雷暴天气为例进行分析,当雷暴发生时常会伴随着湍流、结冰、冰雹、强降雨、对流风暴等多种危险气象发生[14]。然而,这些危险气象类型所影响的垂直高度范围和水平范围都是不一样的[15],例如强对流风暴影响的垂直高度范围很大,但水平范围却有限;而湍流、结冰等影响的水平范围很大,但垂直高度范围有限。因此,本文根据不同危险气象所影响的垂直高度范围和水平范围不同,对改航空域进行分层处理。为进行改航空域分层规划,本文采用了三维凸多边形柱的危险气象分层规划方法。假设某时刻航空器的计划航迹受雷暴天气的影响,航空气象部门获得的雷达回波图结果如图1所示。
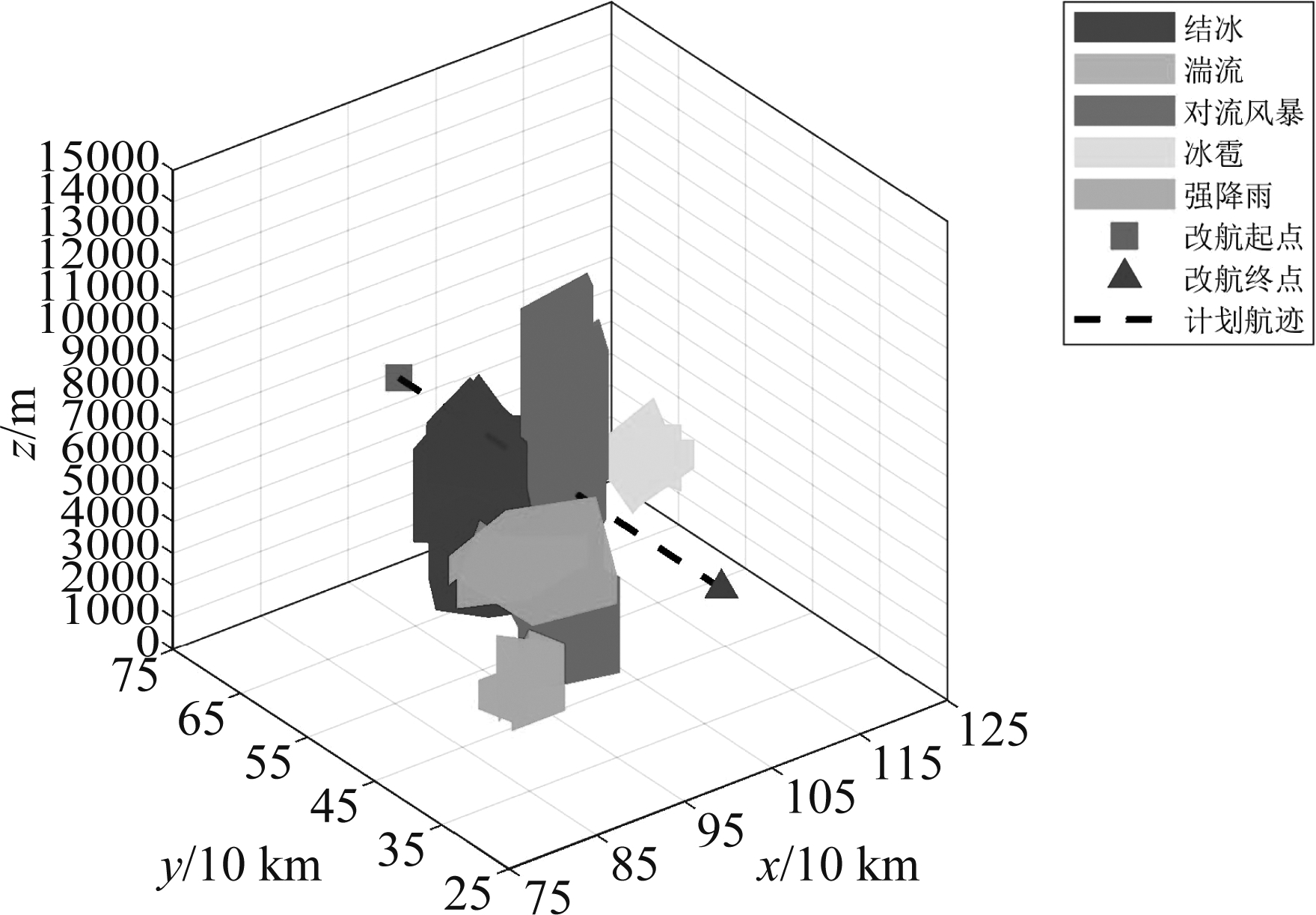
图1 雷达探测结果
Fig.1 Radar detection results
为满足飞行航迹实时动态规划的要求,本文利用得到的雷达实测数据对空域进行实时规划。从图1中的雷达探测结果可以看出危险气象的空域分布特征是不规则的,为避免规划的航迹进入“凹”型区域,需要对其进行进一步的处理,本文采用了三维凸多边形柱的危险气象分层规划方法,具体步骤如下:
(1)确定危险气象的垂直影响高度层。根据雷达探测结果确定不同危险气象类型影响的垂直高度层,设影响的最高高度为Hmax,影响的最低高度为Hmin,则垂直影响的高度层范围为H=Hmax-Hmin。
(2)确定危险气象的水平影响范围。根据获得的雷达探测结果,为方便起见,我们对图1中危险气象区域某点的坐标用s(x, y, z)表示。然后,将危险气象整体投影到x、y平面,如图2所示,从而可以确定危险气象区域范围(雷达回波≥41 dBZ的区域)的最外围边界点集合,设得到的危险气象区域最外围边界点集合为R={sk(xk,yk)|k=0,1,2,…,K}。
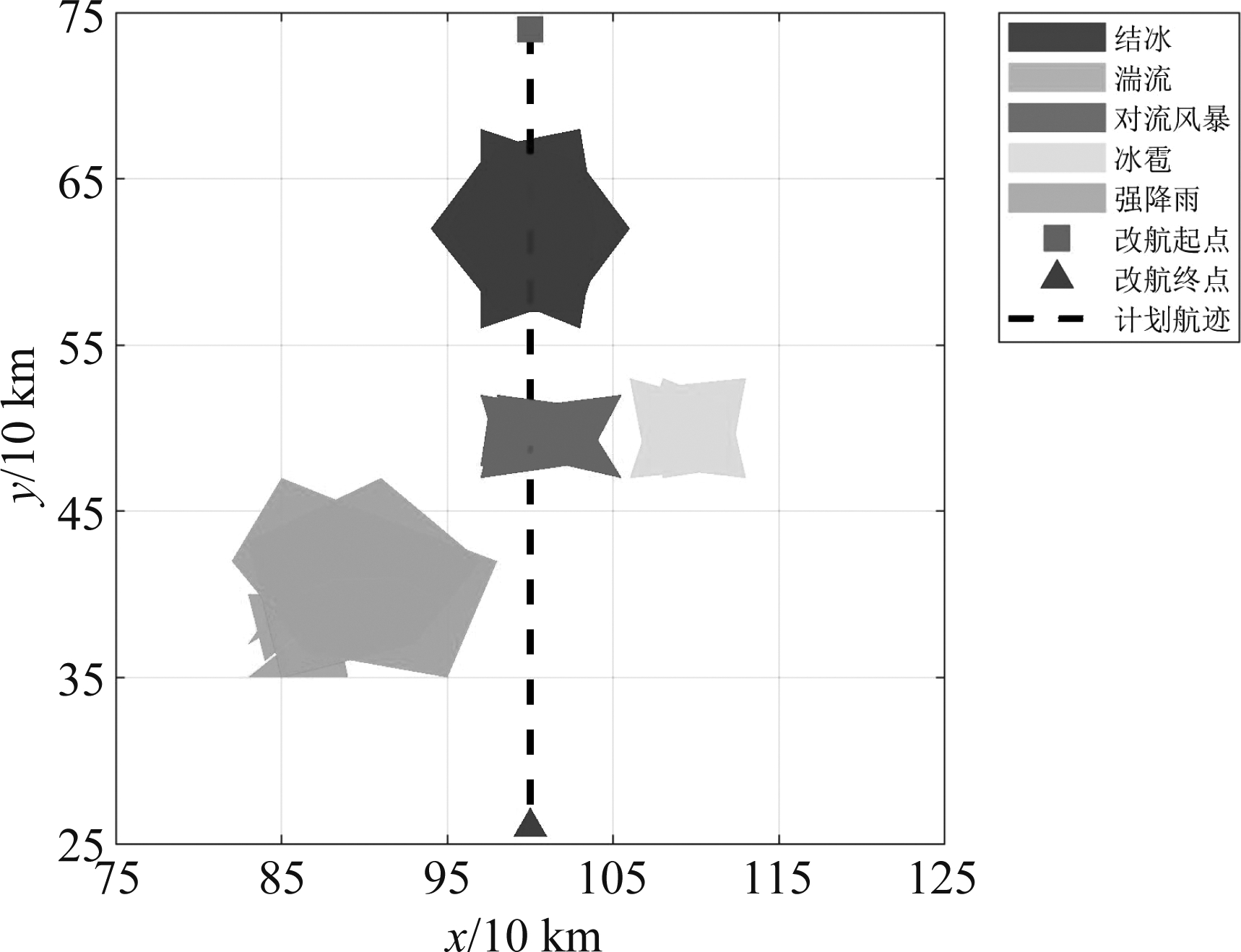
图2 危险气象二维投影结果
Fig.2 Two dimensional projection results of hazardous weather
(3)二维凸多边形规划。对步骤(2)中得到的边界点集合R,利用Graham(格雷厄姆)算法[16]确定危险气象凸多边形的边界点,设利用Graham算法处理得到的二维凸多边形危险气象区域边界点集合为R′={sj(xj,yj)|j=0,1,2,…,J(J≤K)}。
(4)三维凸多边形柱分层规划。根据步骤(3)中得到的边界点集合R′可确定危险气象二维凸多边形区域,并根据步骤(1)中确定的垂直影响高度范围H,将其向三维空域拓展得到凸多边形柱。以图1为例,对图1中全部危险气象的分层规划如图3所示,其二维凸多边形如图3(a)所示,三维凸多边形柱如图3(b)所示。
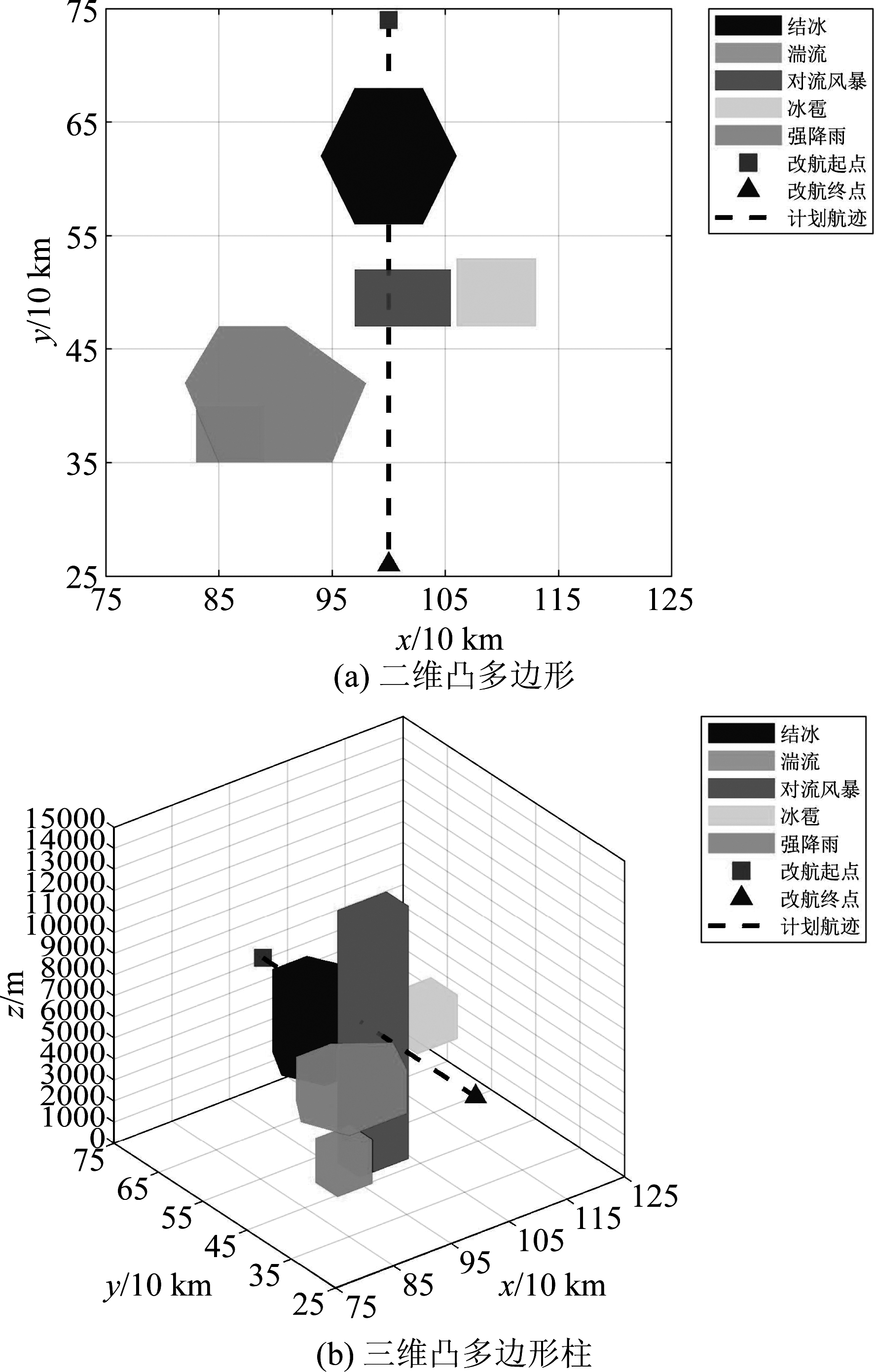
图3 危险气象分层模型
Fig.3 Hazardous weather stratification model
从图3中可知不同的危险气象类型对航路的影响是不一样的,如图3中对流风暴影响的垂直高度范围很大,但水平范围有限;结冰和湍流影响的水平范围很大,但垂直高度范围有限;强降雨和冰雹影响的垂直高度范围和水平范围都有限。因此,针对不同危险气象采取的规避策略也不同,像结冰和湍流这类危险气象区域,如果在单一层面采取规避策略势必会产生大面积偏离计划航迹的飞行计划,这就容易造成在单一层面出现航班汇聚拥堵的情况,降低了空域利用率和整体航线网络流量。在这种情况下,为提高空域利用率和整体航线网络流量,通常都是在保证飞行安全的情况下适当采取一定的激进策略[17],通过管制调度选择在垂直平面上采取改变飞行高度层的规避策略。因此,采取改变飞行高度层的规避策略需要对建立的危险气象分层模型划分飞行高度层,根据图3得到的危险气象分层模型,并结合我国民航局实施的RVSM(Reduced Vertical Separation Minimum)方案对规划空域进行分层,海拔高度在600 m至8400 m,每隔300 m为一个飞行高度层;海拔高度在8400 m至8900 m,隔500 m为一个飞行高度层;海拔高度在8900 m至12500 m,每隔300 m为一个飞行高度层;海拔高度在12500 m以上,每隔600 m为一个飞行高度层。改航空域分层规划结果如图4所示。
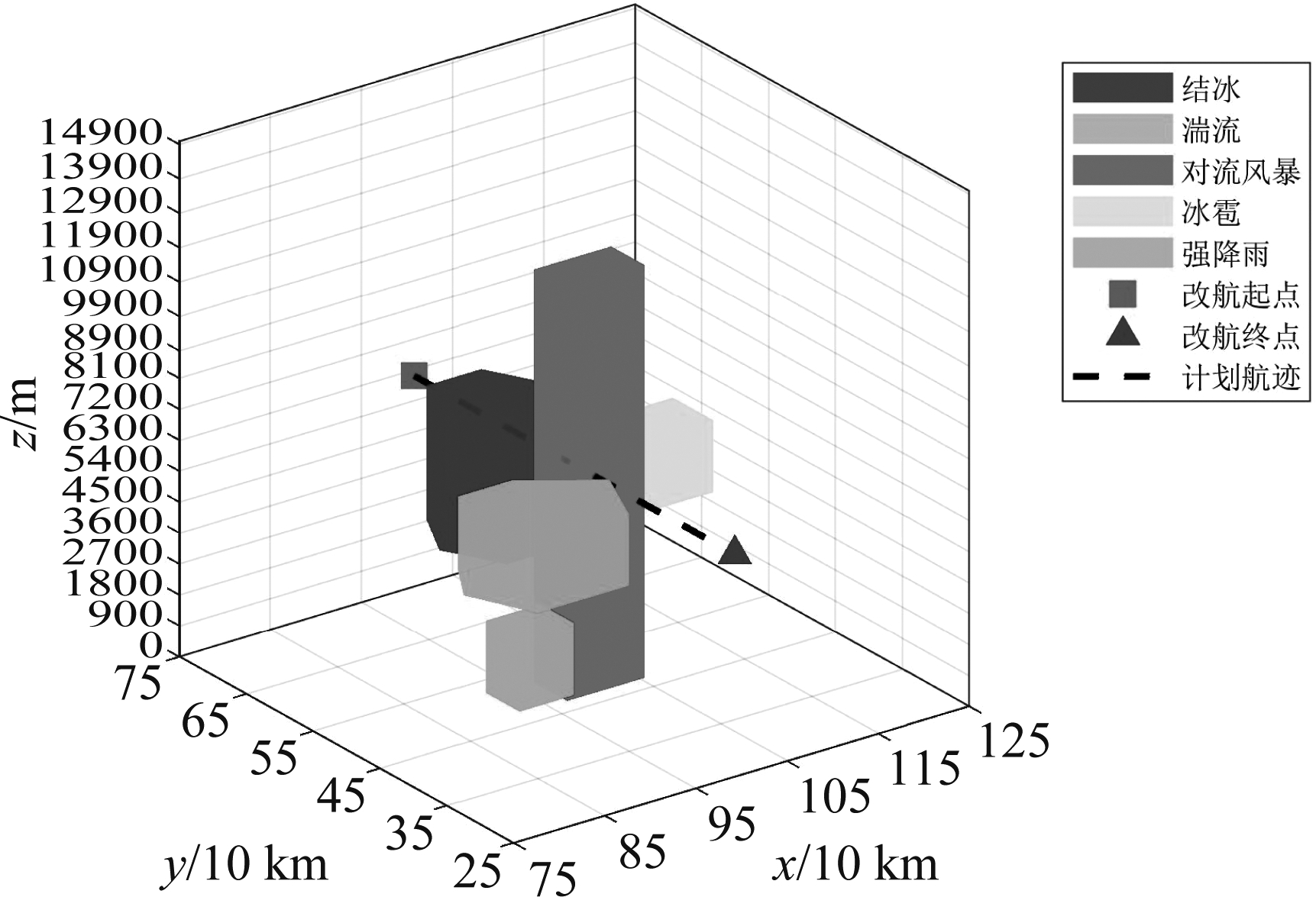
图4 改航空域分层规划模型
Fig.4 Stratified planning model of rerouting airspace
3 分层航迹动态规划
稀疏A*算法是将约束条件结合到算法搜索当中以减少算法搜索时间和空间,因此在静态环境中搜索效率非常高,而且能够很好地兼顾全局最优,但该算法并不具备动态规划性能。而动态窗口法能够在线实时规划路径,通过检测窗口滚动前进,具有良好的局部动态规划能力,但该方法在全局环境下无法保证规划的路径全局最优的要求[18]。在此,针对全局环境下分层航迹动态规划的需求,我们利用稀疏A*算法进行全局航迹规划,并融合动态窗口法进行局部实时动态规划。在这个过程,先利用稀疏A*算法进行全局航迹规划并结合关键点选取策略以确定全局关键航迹点,随后根据全局关键航迹点将全局航迹分成若干段,并利用动态窗口法基于分段航迹两端点(关键航迹点)进行实时航迹动态规划。需要说明的是:利用稀疏A*算法搜索处理得到的全局关键航迹点在无特殊情况下固定不变,随后利用动态窗口法在每两个最关键航迹点之间进行实时航迹动态规划,在这个过程只需要更新雷达探测气象信息即可。所提方法的具体步骤如下:
(1)根据规划的改航空域分层规划模型,建立稀疏A*算法搜索约束条件(即改航约束条件);
(2)利用稀疏A*算法结合约束条件对分层空域进行全局航迹规划,并利用关键点选取策略以确定全局关键航迹点;
(3)根据全局关键航迹点将全局规划航迹进行分段处理,并对分段航迹存在的两种情况采取不同的投影方式。即,同一飞行高度层的分段航迹采取二维水平面投影;跨越飞行高度层的分段航迹采取二维斜平面投影;
(4)利用动态窗口法在步骤(3)中得到的二维投影平面内基于分段航迹两端点进行实时航迹动态规划。
分层航迹动态规划方法的整体框图如图5所示。
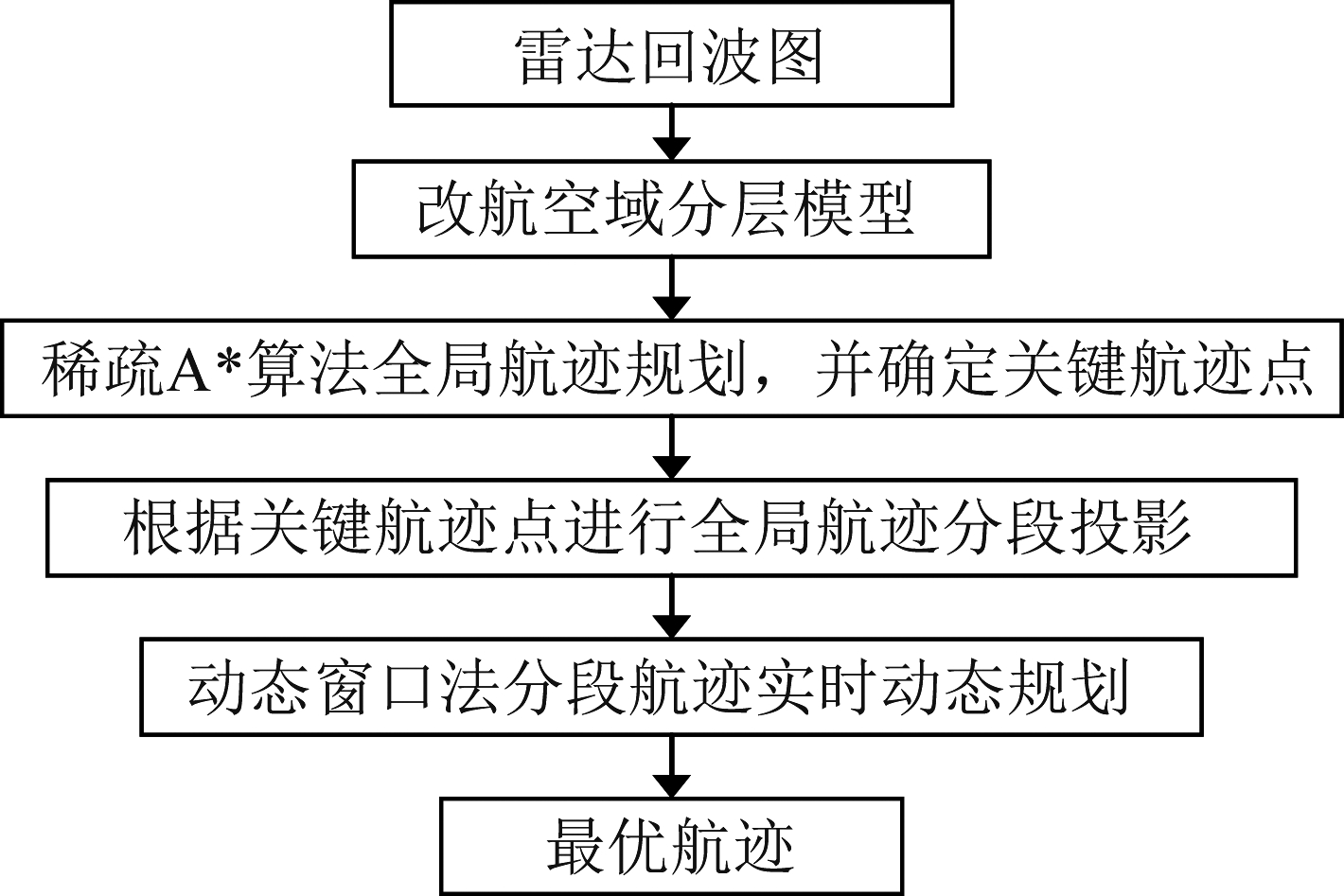
图5 分层航迹动态规划方法框图
Fig.5 Block diagram of stratified trajectory dynamic planning method
3.1 约束条件
稀疏A*算法是将约束条件结合到算法搜索当中以减少算法搜索时间和空间,因此需要事先建立算法搜索约束条件,即改航约束条件。在此,从航空器的飞行性能和飞行安全,以及航空管制约束的角度出发,建立的改航约束条件有以下几个:
1)最小航段距离约束
最小航段距离是指两个转弯点(改航点或航路点)之间的距离,其长度应满足在该距离内航空器可顺利完成2次转弯,假设该航段距离为D,最小航段距离为Dmin,通常Dmin≥7.4 km。根据不同的机型,则需满足:
D=τ·Dmin
(1)
式(1)中,τ为不同机型对应的转弯距离系数。
2)转弯角度约束
转弯角度指飞行过程中航空器航向的改变量,航向指的是航空器纵轴所指的方向,如图6所示,假设航空器从A向B飞行,途中经过转弯点O进行转弯。出于飞行安全考虑,转弯角度通常不小于90°,即∠AOB≧90°。
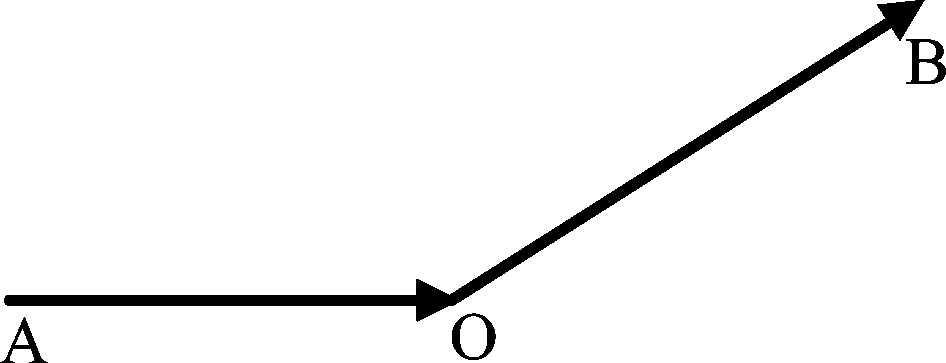
图6 转弯角示意图
Fig.6 Diagram of turning angle
3)危险区域约束
通常情况对于航空器来说,当雷达回波强度大于等于41 dBZ的危险区域,不允许航空器穿越飞行,必须采取规避策略。
4)安全距离约束
根据美国航空局和中国民用航空局的建议,在执行规避战术过程中需远离危险气象边界飞行至少25 km(6000 m以下为20 km)。假设最小安全距离为Lmin:
(2)
5)飞行高度约束
对于短程航线的航空器,其最高飞行高度为9600 m;对于长程洲际航线的航空器,其最高飞行高度为12600 m;对于一些公务机,其飞行高度可以达到15000 m。
6)俯仰角约束
运输航空为保证飞行的舒适性和安全性,一般允许的最大俯仰角为30°。
3.2 稀疏A*算法
3.2.1 代价函数设计
稀疏A*算法是在A*算法的基础上通过扩展搜索领域,并将约束条件结合到算法搜索当中,可以有效地减小搜索空间,缩短搜索时间。为综合考虑多方面影响因素,使得稀疏A*算法规划的全局航迹尽可能最优,需要构造一个综合的代价函数,并基于该代价函数进行全局航迹规划。构造的综合代价函数包括实际代价、管制代价和预估代价(即启发函数),如公式(3)所示:
f(s)=g(s)+c(s)+u(s)
(3)
式(3)中,g(s)表示改航起点到航迹点s的实际代价;c(s)表示航迹点s处的管制代价;u(s)表示航迹点s到改航终点的预估代价。
1)实际代价。实际代价需要综合考虑影响航迹规划的各项指标因素,故对公式(3)中的实际代价定义如下:
g(s)=w1l(s)+w2h(s)+w3φ(s)
(4)
式(4)中,l(s)表示从改航起点到航迹点s的航程;h(s)表示航迹点s处的海拔高度;φ(s)表示航迹点s处的威胁指数;w1、w2、w3为相应的权系数。
在此,对于公式(4)中的l(s)、h(s)和f(s)的具体计算如下:
(5)
式(5)中,x、y、z表示航迹点s的横、纵和竖坐标;X1、Y1和Z1表示改航起点的横、纵和竖坐标。
h(s)=|z-Z1|
(6)
(7)
式(7)中,Ks为一个参数,它反映航迹点s处受危险气象的威胁程度;βs为一个乘数因子,当航迹点s处没有收到预警信息时,βs=1,否则βs>1;Ls表示航迹点s到危险气象区域中心的距离。
2)管制代价。在航迹规划的过程中需要考虑管制员的调度指令,管制员可以综合评估航路网中航班的容量和分布情况,并给出相应的调度指令,故对公式(3)中的管制代价定义如下:
c(s)=λs
(8)
式(8)中,λs表示航迹点s处管制员发出的管制代价值,一旦管制员发出管制命令,λs值就非常大,可以一票否决这条路径。
3)预估代价。常见的启发函数有曼哈顿距离、欧式距离、切比雪夫距离和Octile距离这四种。在此,为考虑改航中新增转弯点数指标,并尽可能减少转弯点,对公式(3)中的启发函数,我们采用欧式距离。同时,为考虑朝不同方向飞行的代价不同。其公式如下:
(9)
式(9)中,α表示转移代价;X2、Y2和Z2表示改航终点的横、纵和竖坐标。
3.2.2 关键点选取策略
假设通过稀疏A*算法搜索得到的航迹点序列为E={si(xi,yi,zi)|i=0,1,2,…,N},在序列E中可能还会存在冗余航迹点和转弯点情况,因此需要对航迹点序列E提取转弯点进行优化处理,去除冗余航迹点和转弯点,保留关键转弯点(即关键航迹点),设提取的转弯点集合为{P(i)(i=1,2,3,…,I)}。关键航迹点选取策略如图7所示,假设I=10,提取的转弯点如图7(a)所示。首先连P1P2,若P1P2不经过危险气象区域,则继续连接P1P3,直到P1P(i)(i=2,3,…,I)连线经过危险气象区域,则把P(i-1)与P1连接起来,同时删除中间的冗余转弯点,更新航迹;然后,从P2重复上述操作,直到航迹中没有冗余转弯点;最后,得到去除冗余转弯点的结果如图7(b)所示。经过上述处理后,设得到的关键航迹点序列为E′={si(xi,yi,zi)|i=0,1,2,…,M(M≤N)}。

图7 关键航迹点选取策略
Fig.7 Key track point selection strategy
比较图7(a)和图7(b)的结果可知,采取关键航迹点选取策略后,全局航迹的航程从22.82 km减少到22.17 km,优化了2.85%;转弯点数从8个减少到5个,优化了37.50%;航迹累积的转弯角度从1098.40°减少到746.57°,优化了32.03%。因此,采取关键点选取策略在一定程度上可以进一步优化稀疏A*算法规划的全局航迹。
3.3 动态窗口法
根据3.2.2处理得到的关键航迹点序列E′={si(xi,yi,zi)|i=0,1,2,…,M(M≤N)},为实现实时航迹动态规划的需求,利用动态窗口法依次在每两个关键航迹点之间进行实时航迹动态规划。以图7(b)的关键航迹点为例,则依次在P1P2;P2P3;……;P6P7之间利用动态窗口法进行实时航迹动态规划。因此,在这个过程,首先需要根据关键航迹点将全局航迹进行分段二维投影;其次,建立航空器运动学模型;然后,进行速度采样,并结合建立的航空器运动学模型进行轨迹模拟;最后,设计一个综合的评价函数对不同采样速度所对应的模拟轨迹进行评价,以选出最优的模拟轨迹。
3.3.1 航迹分段投影
利用动态窗口法依次在每两个关键航迹点之间进行实时航迹动态规划,但由于动态窗口法是属于二维规划方法,因此需要根据关键航迹点将全局规划航迹进行分段二维投影。首先,根据3.2.2得到的关键航迹点序列E′={si(xi,yi,zi)|i=0,1,2,…,M(M≤N)}将全局航迹分成M段,并将分成的M段航迹依次编号为Pi(i=1,2,3,…,M)。其次,将分段航迹进行二维投影,对于分段的航迹存在两种情况。第一种:同一飞行高度层的分段航迹,直接将该分段航迹所涉及的气象信息向二维水平面投影;第二种:跨越飞行高度层的分段航迹,沿分段航迹所在的斜平面,将该分段航迹所涉及的气象信息向二维斜平面投影。然后,为方便后续建模,设在二维投影平面内每一段航迹Pi(i=1,2,3,…,M)的起始点都设为ps(xs,ys),目标点都设为pg(xg,yg)。最后,利用动态窗口法在投影的二维平面内基于起始点和目标点进行实时航迹动态规划。
在此,由于经过稀疏A*算法处理得到的全局关键航迹点在无特殊情况下固定不变,只需要更新雷达探测气象信息即可。因此,利用动态窗口法进行分段航迹实时动态规划的过程中存在一种特殊情况,即分段航迹的目标点被更新的危险气象覆盖。针对这种情况,我们只需直接抛弃该关键航迹点作为目标点,选择关键航迹点序列E′中的下一个关键航迹点作为目标点,并以此类推,直到选择的目标航迹点不被危险气象覆盖为止。然后,根据起始点和目标点所确定的二维投影平面,利用动态窗口法基于起始点和目标点进行实时航迹动态规划。
3.3.2 航空器运动学模型
动态窗口法是通过速度采样来模拟航空器的运动轨迹,因此需要事先建立航空器的运动学模型。在空间内线速度和角速度的变化反映了航空器的运动变化,而在一次速度采样中可以获得多组采样速度对(νi,ωi),其中一组采样速度对(νi,ωi)则表征了一段轨迹。为简化航空器的运动学模型,假设航空器在时间间隔Δt内作匀速直线运动,采样轨迹点为pt(xt,yt),则航空器的运动模型如下所示:
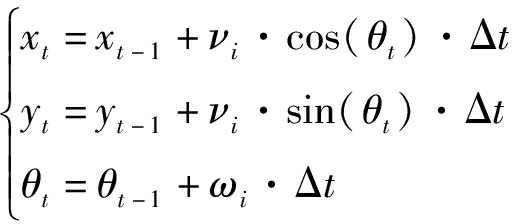
(10)
式(10)中,θt表示航向角;t表示时刻;νi表示采样线速度;ωi表示采样角速度;i表示下标。
3.3.3 速度采样
在速度二维空间中存在多组速度对(νi,ωi),但在时间间隔Δt内会受到航空器性能的限制需要对采样速度范围进行约束。
(1)航空器最大、最小速度约束:
Vm={ν∈[νmin,νmax]∧ω∈[ωmin,ωmax]}
(11)
式(11)中,νmax和νmin分别表示最大和最小线速度;ωmax和ωmin分别表示最大和最小角速度。
(2)航空器加减速约束:
(12)
式(12)中,νd和ωd分别表示当前的线速度和角速度;![]() 和
和![]() 分别表示最大线加速度和最大线减速度;
分别表示最大线加速度和最大线减速度;![]() 和
和![]() 分别表示最大角加速度和最大角减速度。
分别表示最大角加速度和最大角减速度。
(3)制动距离约束:为了保证航空器在进入危险气象区域前能够最大限度的进行规避绕飞,保证航空器不进入危险气象区域。因此,在最大减速的条件下有一个速度范围。
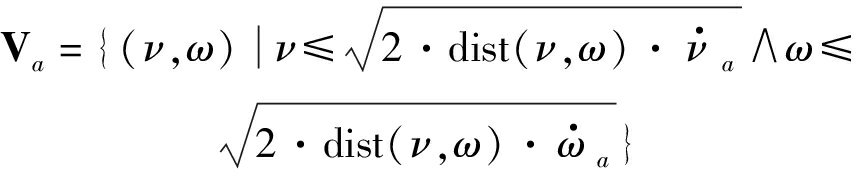
(13)
式(13)中,dist(ν,ω)为采样速度(νi,ωi)对应轨迹离危险气象区域的最近距离。
根据上述建立的速度约束条件进行速度采样,并结合航空器运动学模型进行轨迹模拟。本文仿真实验中采样速度模拟轨迹如图8所示。
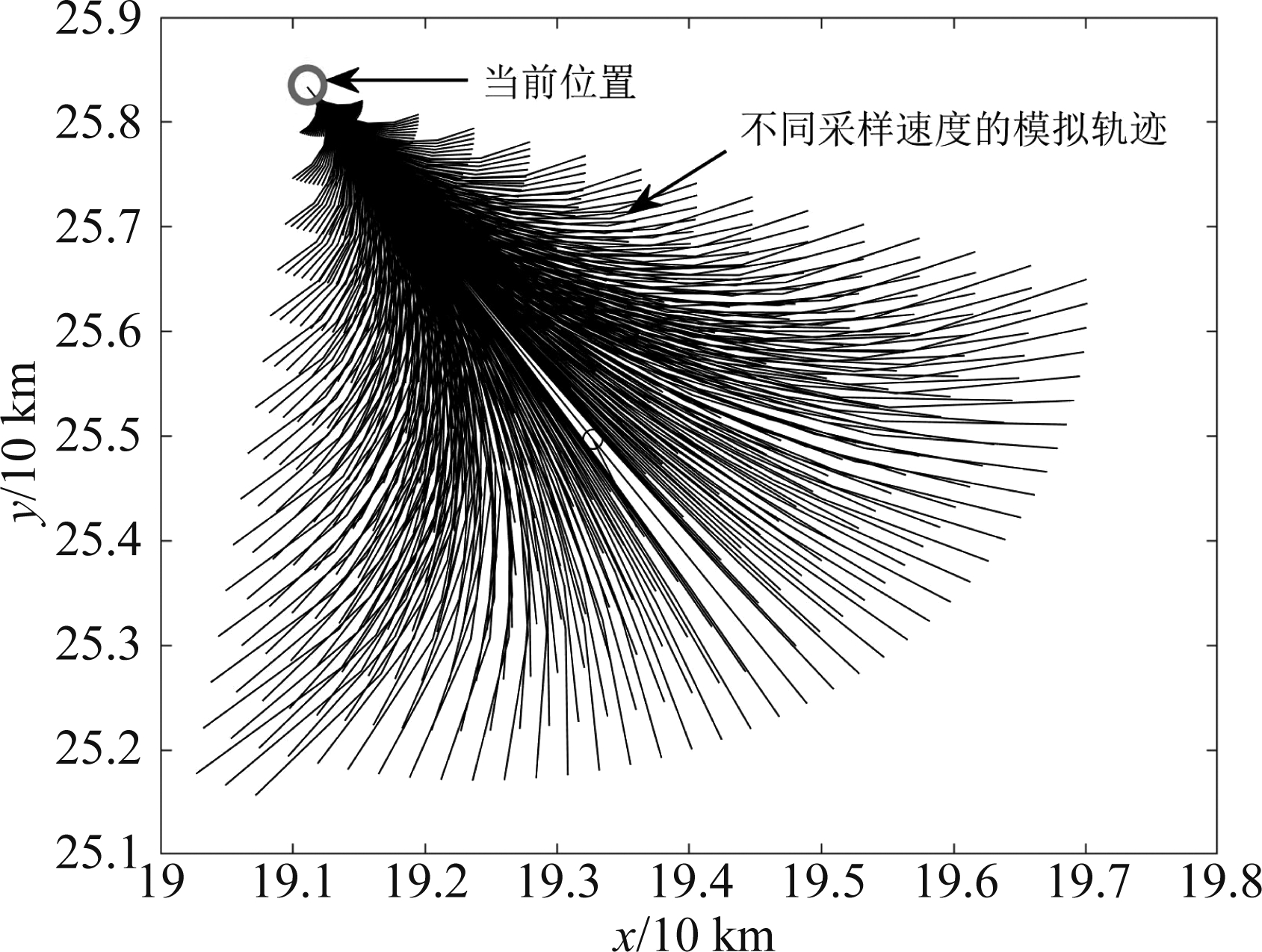
图8 速度采样结果
Fig.8 Speed sampling results
3.3.4 评价函数
在上述的速度采样结果中,不同的采样速度对(νi,ωi)所对应的模拟轨迹不同。因此,需要设计一个综合的评价函数对模拟轨迹进行评价以选出最优的轨迹,同时需要保证最优轨迹尽可能靠近稀疏A*算法规划的全局航迹,并完成动态避障任务,朝向目标快速运动。在此,根据文献[19]、文献[20]中对方位角评价函数、距离评价函数、路径评价函数、避障评价函数进行的定义和图解说明,以及文献[21]中对速度采样函数的定义,结合公式(10),本文中设计的综合评价函数定义如下所示:
G(ν,ω,θt,xt,yt,xa,ya,xc,yc,xg,yg)=
σ[γ1·Head(θt)+γ2·Vel(ν,ω)+γ3·
Goal(xt,yt,xg,yg)+γ4·Path(xt,yt,xc,yc)+
γ5·Obs(xt,yt,xa,ya)]
(14)
式(14)中,σ表示平滑函数;Head(θt)为方位角评价函数;Vel(ν,ω)为速度采样函数;Goal(xt,yt,xg,yg)为距离评价函数;Path(xt,yt,xc,yc)为路径评价函数;Obs(xt,yt,xa,ya)为避障评价函数;γ1,γ2,γ3,γ4,γ5为相应的权系数;ν表示采样的线速度;ω表示采样的角速度;θt表示航向角;xt、yt表示采样航迹点pt的横坐标和纵坐标;xa、ya表示二维投影平面内危险气象区域的横坐标和纵坐标;xc、yc表示二维投影平面内全局航迹上航迹点的横坐标和纵坐标;xg、yg表示目标点pg的横坐标和纵坐标。
1)方位角评价函数:Head(θt)主要是评价航空器到目标点之间的方位角函数,其目的是使得航空器的朝向不断趋向目标点方向,保证航空器朝目标点运动。在航空器朝目标点飞行时,航空器的航速方向沿航迹的切线方向成180°,而在速度采样过程中因采样角速度的不同而存在一定的航向角θt偏差,θt的值越小,则说明与目标点的方位角越大[19],其示意图如图9所示,其公式定义[20]如下所示:
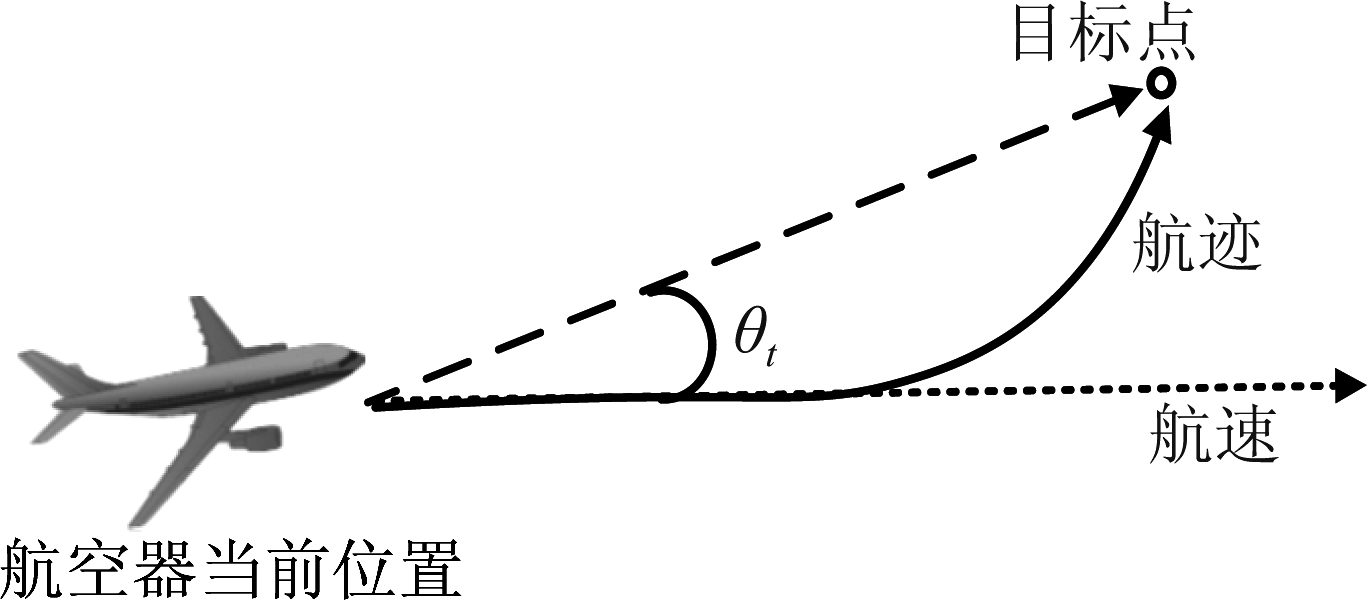
图9 方位角评价函数示意图
Fig.9 Schematic of azimuth evaluation function
Head(θt)=180°-θt
(15)
2)速度采样函数:Vel(ν,ω)主要是获取采样速度对(νi,ωi)的数值函数,其目的是保证航空器尽可能减少飞行姿态的变化,确保运输航空的舒适性和安全性。在采样速度空间内,存在多组采样速度对(νi,ωi),而这些采样速度对中的线速度νi和角速度ωi的大小是不一样的,因此需要通过速度采样函数获得每一组采样速度对(νi,ωi)的线速度值和角速度值带入到综合评价函数中,从而选取出最优的一组速度对(νi,ωi)。在此,对Vel(ν,ω)的定义[21]如下所示:
Vel(ν,ω)=Vi
(16)
式(16)中,Vi={νi,ωi}表示获得采样速度对(νi,ωi)的线速度值和角速度值。
3)距离评价函数:Goal(xt,yt,xg,yg)主要是评价航空器当前位置到目标点的距离函数,其目的是不断缩短与目标点的距离。在速度采样结果中,不同的采样速度对(νi,ωi)所对应的采样轨迹是不同的,而航空器当前位置到目标点之间的最短距离则为直线距离,故采用欧式距离[20]进行距离评价函数的定义,其示意图如图10所示,其公式定义如下所示:

图10 距离评价函数示意图
Fig.10 Schematic of distance evaluation function
(17)
4)路径评价函数:Path(xt,yt,xc,yc)主要是评价规划航迹与全局航迹之间的偏离距离函数,其目的是尽可能保证规划的航迹以最小的偏离度到达目标点,从而降低规划航迹的偏离度,提高空域利用率,减少管制员的工作量。在速度采样结果中,存在多组采样轨迹,而这些采样轨迹与全局航迹之间存在一定的距离偏差,即横向距离偏差和纵向距离偏差,故采用曼哈顿距离[22]进行路径评价函数的定义,其公式如下所示:
Path(xt,yt,xc,yc)=|xt-xc|+|yt-yc|
(18)
5)避障评价函数:Obs(xt,yt,xa,ya)主要是评价规划航迹到危险气象的距离函数,其目的是保证规划的航迹远离危险气象区域。对于避障评价函数的定义同距离评价函数的定义一样,采用欧式距离[20]进行距离定义,与距离评价函数不同的是,避障评价函数需要保证一个最小安全距离Lmin(数值常量)。如果规划航迹大于最小安全距离Lmin,即避障评价函数值大于0,则说明这条航迹安全;反之,则说明有碰撞危险,舍弃这条航迹。其公式如下所示:
(19)
式(19)中,Lmin表示约束条件(4)中的最小安全距离。
4 仿真分析
本文的仿真环境为PIV 3.4 GHz PC,运行环境为Windows 10,编译环境为MATLAB R2018b。以图4中改航空域分层规划模型为例,在全局环境下采用本文方法、动态稀疏A*算法、动态窗口法,以及现行的沿扩展飞行受限区边界绕飞的改航方法[23]进行了对比仿真实验。本文方法的主要仿真参数如下所示:
(1)稀疏A*算法的实际代价函数权系数w1=w2=w3=1/3;
(2)动态窗口法综合评估函数权系数γ1=0.1;γ2=0.2;γ3=0.3;γ4=0.3;γ5=0.3;
(3)巡航速度为800 km/h,即最大线速度;最大转弯角速度60°/s;最大线加速度20 m/s2;最大角加速度50°/s2;巡航高度为6000 m。
仿真结果如图11所示,其中图12和图13分别为图11的水平投影图和垂直剖面图。
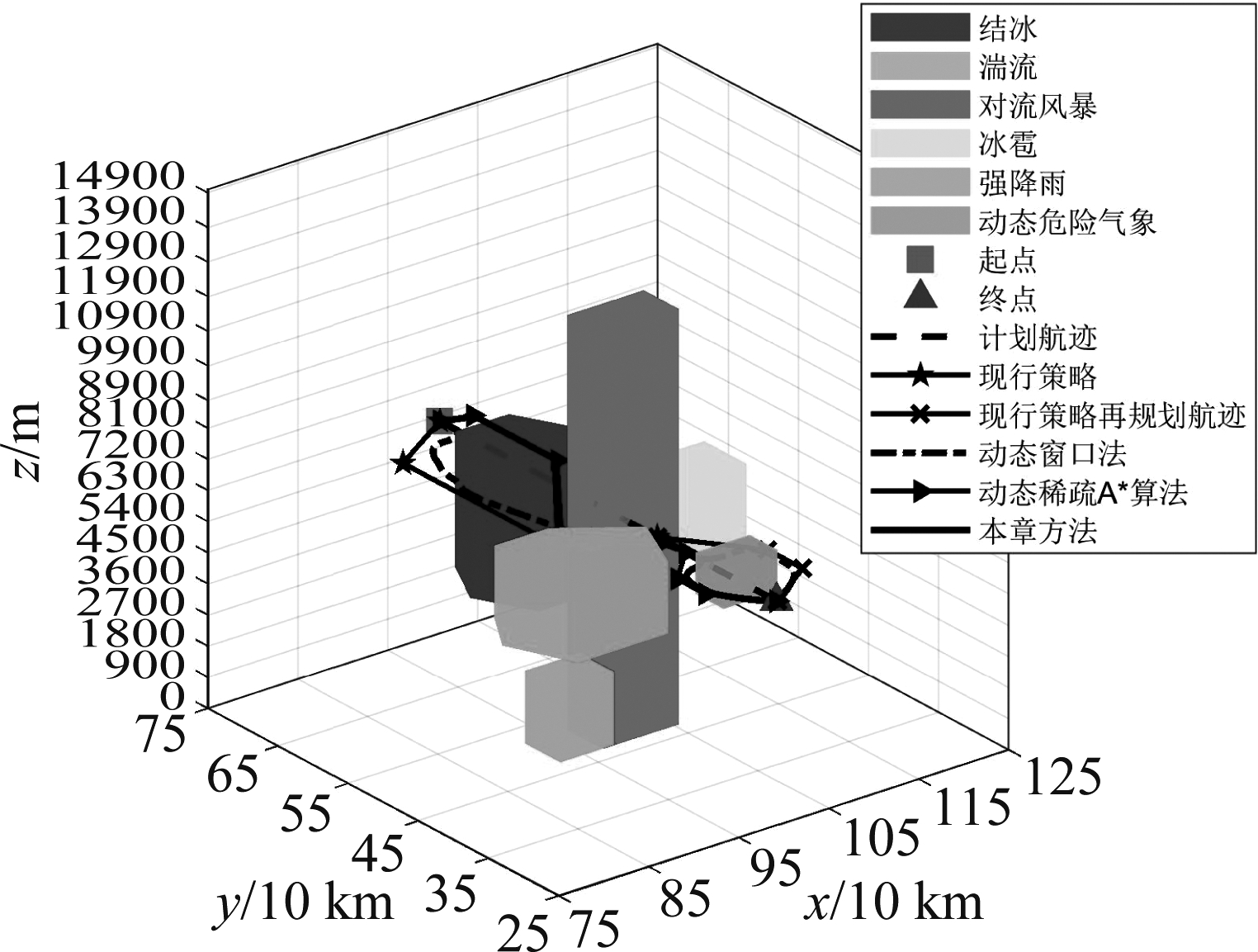
图11 四种策略的仿真结果对比图
Fig.11 Comparison of simulation results of four strategies
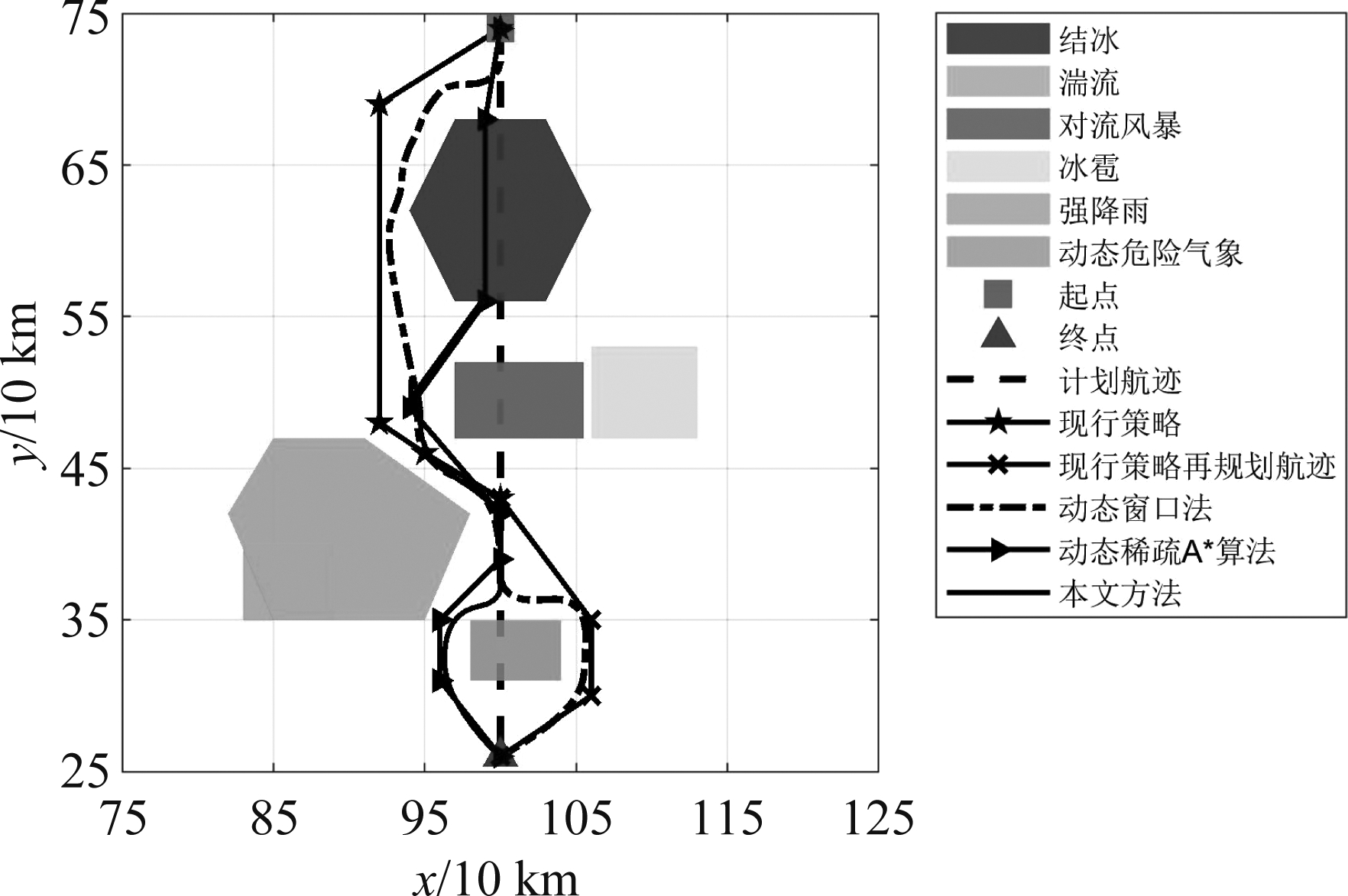
图12 四种策略的水平投影图
Fig.12 Horizontal projection of four strategies
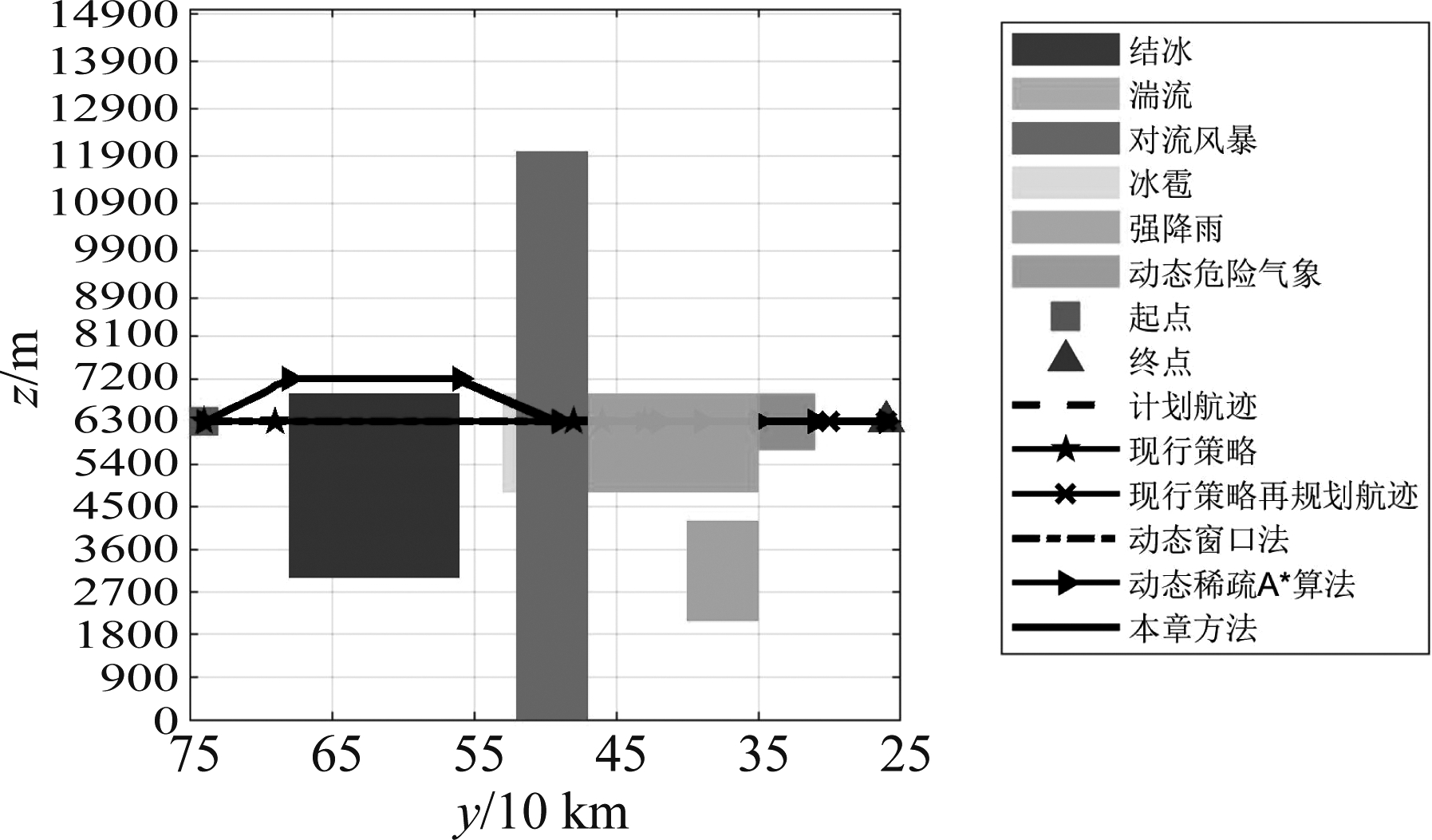
图13 四种策略的垂直剖面图
Fig.13 Vertical profile of four strategies
为定量评估四种策略仿真结果的优劣性,分别通过规划航迹总代价、航程、转弯点数、侧向偏离距离和算法运行时间来对仿真结果进行评估,表1为四种策略的评估指标对比。
通过表1的实验评估结果可知,在动态环境下,本文方法与动态稀疏A*算法相比,在转弯点个数上两者相等,在算法进行时间上动态稀疏A*算法优于本文方法,但是本文方法在航迹总代价、航程和侧向偏离距离上优于动态稀疏A*算法的优势;本文方法与动态窗口法相比,本文方法各项指标都要优于动态窗口法;本文方法与现行策略相比,在转弯点个数和算法运行时间上现行策略优于本文方法,但是本文方法在航迹总代价、航程和侧向偏离距离上优于现行策略的优势。综上所述,本文方法的综合性价最高。
在表1各项评估指标的基础上为更加全面对四种策略仿真结果进行评价,利用3.3.4中定义的5种评价函数进行仿真结果评估,表2为四种策略的5个评价函数指标对比。
表1 四种策略的评估指标对比
Tab.1 Comparison of evaluation indexes of six strategies

航迹总代价航程/km转弯点数/个侧向偏离距离/km算法运行时间/s动态稀疏A∗算法375.49724.877305.45106.68动态窗口法431.33759.4610647.30254.02现行策略417.81747.135785.6358.51本文方法352.12703.067252.91169.19
在表2中各项评价值越小越好,并且最大值为1。通过表2的实验评估结果可知,在动态环境下,本文方法与动态稀疏A*算法相比,本文方法在距离评价值和路径评价值上小于动态稀疏A*算法,在避障评价值上两者相等;本文方法与动态窗口法相比,本文方法各种评估值都要小于动态窗口法,故本文方法要优于动态窗口法;本文方法与现行策略相比,在避障评价值上现行策略小于本文方法,在距离评价值和路径评价值上本文方法小于现行策略,故综合而言本文方法优于现行策略。综上所述,本文方法的综合性价最高。
表2 四种策略的5个评价函数指标对比
Tab.2 Comparison of five evaluation functions of four strategies

综合评价方位角评价速度采样评价距离评价路径评价避障评价动态稀疏A∗算法---0.290.140.31动态窗口法0.390.410.280.310.290.35现行策略---0.290.360.29本文方法0.300.360.240.280.120.31
注:表2中由于稀疏A*算法和现行策略都无法提供航速和航向的参考,所以方位角评价值和速度采样评价值无法得到。
最后,为辅助飞行员进行危险气象的规避,本文方法还可以提供在规避过程中关于航空器的航速和航向的变化情况供飞行员参考。以本文实验为例,我们给出了本文方法在航迹规划过程中关于航空器的航速和航向的变化情况,分别如图14和图15所示。
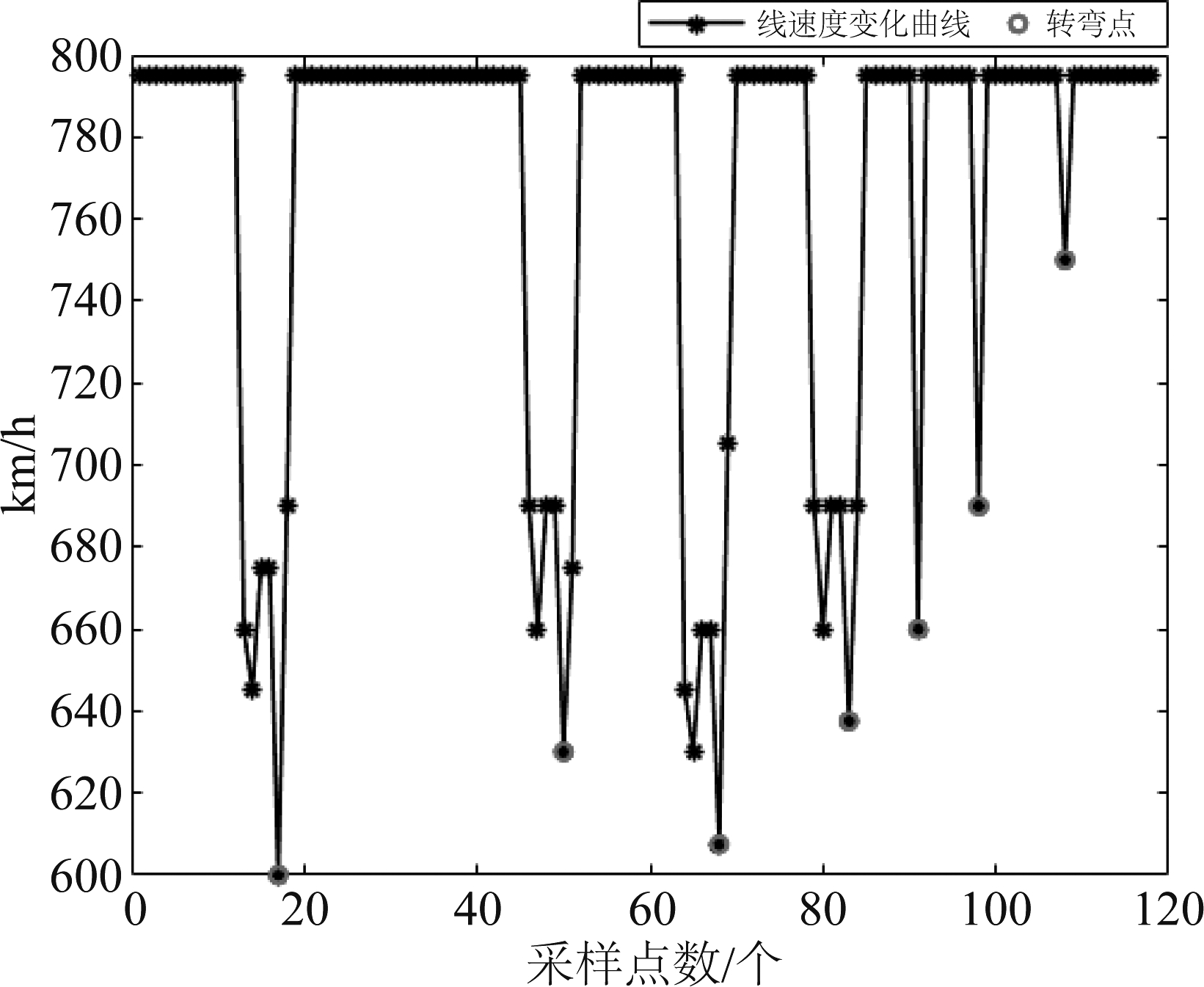
图14 航速变化情况
Fig.14 Change of speed
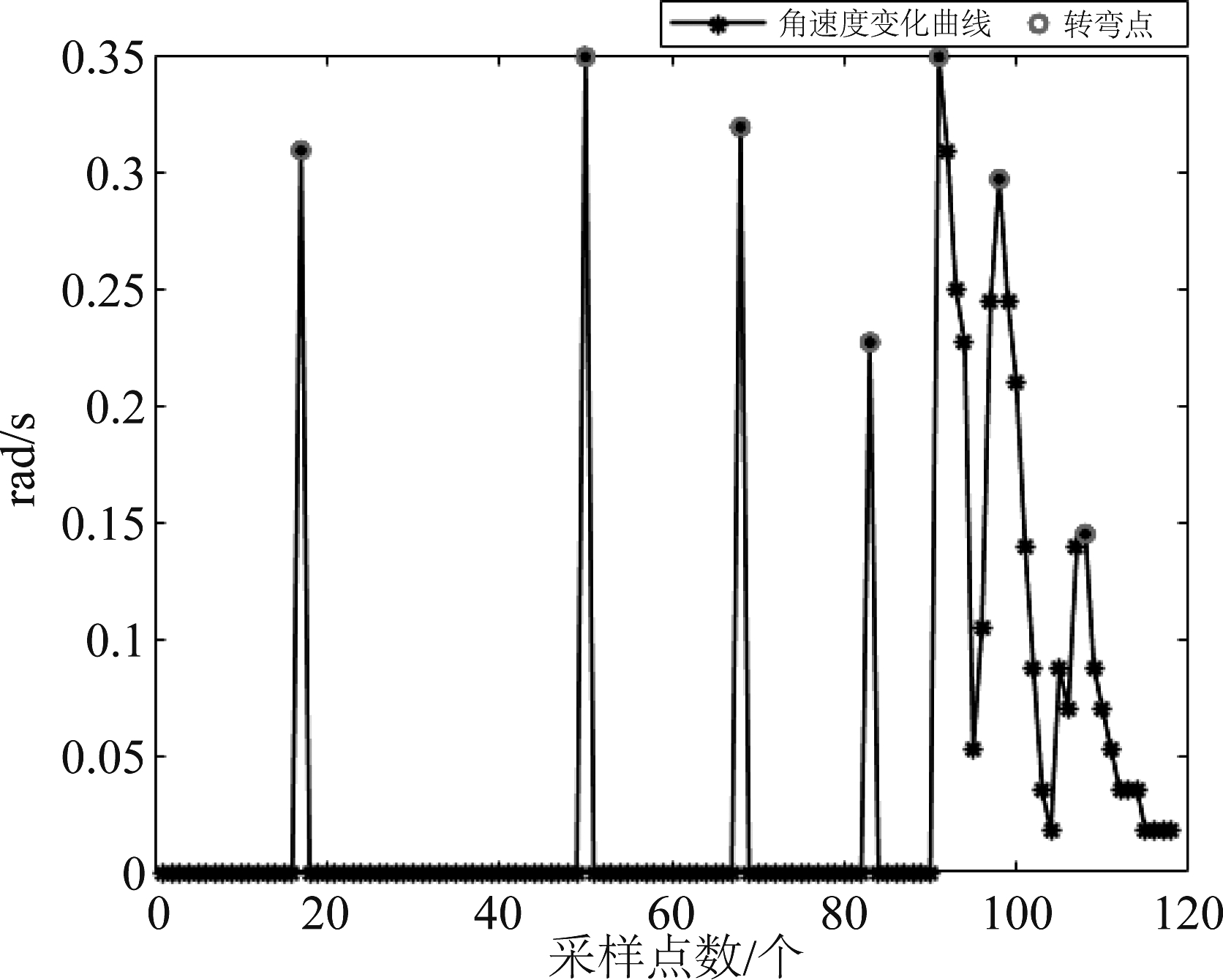
图15 航向变化情况
Fig.15 Change of course
在图14和图15中,绿色圆圈分别对应本文方法规划航迹中的转弯点。本文方法规划航迹中总共有7个转弯点,分别对应图14和图15中的7个圆圈。
5 结论
本文给出一种考虑多种危险气象的分层航迹动态规划策略,该方法主要用于航空器在飞行过程中的实时航迹动态规划,为飞行员在实际飞行过程中提供一条安全可靠的最佳航迹进行危险气象的规避,并且还提供了在规避危险气象过程中关于航空器的航速和航向的变化情况供飞行员参考,以辅助飞行员进行规避策略的执行。同时,本文方法在针对雷暴天气下的实时航迹动态规划需求,从宏观层面上作了深入分析,考虑了雷暴天气下多危险气象类型同时存在和不同危险气象类型产生的高度和影响范围不同,对改航空域进行分层规划。考虑了航空器的飞行性能和飞行航迹上临时可能出现的动态危险气象情况,在改航空域分层规划的基础上进行分层航迹动态规划。实验结果表明本文方法具备良好的实时航迹动态规划性能,并且优于动态稀疏A*算法、动态窗口法和现行策略。
[1] 何光勤, 鲁力, 胡敬玉, 等.基于最小二乘法的雷暴天气下飞行改航决策研究[J].安全与环境工程, 2019, 26(4): 171-176.
HE Guangqin, LU Li, HU Jingyu, et al.Flight track change decision in thunderstorm based on least square method[J].Safety and Environmental Engineering, 2019, 26(4): 171-176.(in Chinese)
[2] CHEN Dan, HU Minghua, ZHANG Honghai, et al.A network based dynamic air traffic flow model for en route airspace system traffic flow optimization[J].Transportation Research Part E: Logistics and Transportation Review, 2017, 106: 1-19.
[3] AKGUNDUZ A, KAZEROONI H.A non-time segmented modeling for air-traffic flow management problem with speed dependent fuel consumption formulation[J].Computers & Industrial Engineering, 2018, 122: 181-188.
[4] ZHANG Ming, KONG Xianglu, LIU Kai, et al.A novel rerouting planning model for the terminal arrival routes under the influence of convective weather[J].Journal of Advanced Transportation, 2018, 2018: 1-21.
[5] DING Wenzhe, ZHANG Yu, HANSEN M.Downstream impact of flight rerouting[J].Transportation Research Part C: Emerging Technologies, 2018, 88: 176-186.
[6] 李宪强, 马戎, 张伸, 等.蚁群算法的改进设计及在航迹规划中的应用[J].航空学报, 2020, 41(S2): 724381.
LI Xianqiang, MA Rong, ZHANG Shen, et al.Improved design of ant colony algorithm and its application in path planning[J].Acta Aeronautica et Astronautica Sinica, 2020, 41(S2): 724381.(in Chinese)
[7] WANG Shijin, LI Qingyun, CAO Xi, et al.Optimization of air route network nodes to avoid “Three areas” based on an adaptive ant colony algorithm[J].Transactions of Nanjing University of Aeronautics and Astronautics, 2016, 33(4): 469-478.
[8] WANG Shijin, CAO Xi, LI Haiyun, et al.Air route network optimization in fragmented airspace based on cellular automata[J].Chinese Journal of Aeronautics, 2017, 30(3): 1184-1195.
[9] 任广建, 朱金福, 卢朝阳.基于复杂网络的北京管制区航路网络特性分析[J].武汉理工大学学报(交通科学与工程版), 2021, 45(1): 33-37.
REN Guangjian, ZHU Jinfu, LU Chaoyang.Analysis of route network characteristics in Beijing control area based on complex network[J].Journal of Wuhan University of Technology(Transportation Science & Engineering), 2021, 45(1): 33-37.(in Chinese)
[10] CHEN Jun, DELAURENTIS D, SUN Dengfeng.Dynamic stochastic model for converging inbound air traffic[J].Journal of Guidance, Control, and Dynamics, 2015, 39(10): 2273-2283.
[11] CHEN Dan, HU Minghua, MA Yuanyuan, et al.A network-based dynamic air traffic flow model for short-term en route traffic prediction[J].Journal of Advanced Transportation, 2016, 50(8): 2174-2192.
[12] SADOVSKY A V, BILIMORIA K D.Risk-hedged approach for Re-routing air traffic under weather uncertainty[C]∥16th AIAA Aviation Technology, Integration, and Operations Conference.Washington, D.C..Reston, Virginia: AIAA, 2016.
[13] SHETH K S,MCNALLY B D, ERZBERGER H, et al.Method and system for air traffic rerouting for airspace constraint resolution[J].Nasa Tech Briefs,2017,41(3):34-36.
[14] 向征, 张文奇, 张文军.雷暴天气下基于多航空器冲突避让的路径规划[J].中国安全科学学报, 2019, 29(8): 151-156.
XIANG Zheng, ZHANG Wenqi, ZHANG Wenjun.Route planning based on multi-aircraft conflict avoidance under thunderstorm weather[J].China Safety Science Journal, 2019, 29(8): 151-156.(in Chinese)
[15] SAUER M, STEINER M, SHARMAN R D, et al.Tradeoffs for routing flights in view of multiple weather hazards[J].Journal of Air Transportation, 2019, 27(2): 70-80.
[16] 李雄.飞行危险天气下的航班改航路径规划研究[D].南京: 南京航空航天大学, 2009.
LI Xiong.Flight rerouting path planning in severe weather[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.(in Chinese)
[17] MARCONNET D, NORDEN C, VIDAL L.Optimum Use of Weather Radar[J].Safety First, 2016, 22:22-43.
[18] ZHU Zeya, XIE Jun, WANG Zhi.Global dynamic path planning based on fusion of A* algorithm and dynamic window approach[C]∥2019 Chinese Automation Congress(CAC).Hangzhou, China.IEEE, 2019: 5572-5576.
[19] MOON J, LEE B Y, TAHK M J.A hybrid dynamic window approach for collision avoidance of VTOL UAVs[J].International Journal of Aeronautical and Space Sciences, 2018, 19(4): 889-903.
[20] 劳彩莲, 李鹏, 冯宇.基于改进A*与DWA算法融合的温室机器人路径规划[J].农业机械学报, 2021, 52(1): 14-22.
LAO Cailian, LI Peng, FENG Yu.Path planning of greenhouse robot based on fusion of improved A* algorithm and dynamic window approach[J].Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(1): 14-22.(in Chinese)
[21] JI Xianyou, FENG Shuo, HAN Qidong, et al.Improvement and fusion of A* algorithm and dynamic window approach considering complex environmental information[J].Arabian Journal for Science and Engineering, 2021: 1-15.
[22] 李浩君, 张鹏威, 郭海东.基于种群曼哈顿距离的自适应多目标粒子群优化算法[J].计算机集成制造系统, 2020, 26(4): 1019-1032.
LI Haojun, ZHANG Pengwei, GUO Haidong.Adaptive multi-objective particle swarm optimization algorithm based on population Manhattan distance[J].Computer Integrated Manufacturing Systems, 2020, 26(4): 1019-1032.(in Chinese)
[23] 徐肖豪, 李成功, 赵嶷飞, 等.基于人工势场算法的改航路径规划[J].交通运输工程学报, 2009, 9(6): 64-68.
XU Xiaohao, LI Chenggong, ZHAO Yifei, et al.Rerouting path planning based on artificial potential field algorithm[J].Journal of Traffic and Transportation Engineering, 2009, 9(6): 64-68.(in Chinese)


