1 引言
盲源分离能在混合系统和源信号未知的情况下估计出源信号[1],在无线通信、语音处理、图像处理、生物医学、雷达及经济数据分析等领域有着广泛的应用[2-7],一直以来都是研究热点。除常见的非欠定盲源分离问题(传感器的数量大于或等于源信号的数量)[8-10],传感器的数量小于源信号的数量的欠定盲源分离(Underdetermined Blind Source Separation, UBSS)在实际应用中也非常普遍[11-13],大部分相关研究都是假设源信号数目已知,本文研究更具挑战性的源信号数目未知的UBSS问题。
根据以往的研究,利用信号在时频(Time frequency, TF)域的稀疏性可以有效解决UBSS问题[14-16],一般分为两步:第一步估计混合矩阵,第二步恢复源信号。针对混合矩阵估计,文献[17]提出基于势函数(Potential Function, PF)的混合矩阵估计方法, 该方法仅适用于两个传感器的情况。文献[18]提出了基于聚类中心引导的粒子群优化算法(Cluster Guide Particle Swarm Optimization, CGPSO)用于混合矩阵估计,该方法易陷入局部最优。文献[19]直接使用K-means实现矩阵估计,由于K均值对初始聚类点敏感,因此准确性较低。文献[20]提出将仿射传播(Affinity Propagation, AP)聚类算法与K-means相结合,先使用仿射传播聚类算法确定初始聚类点及源信号的数量,再使用K-means实现混合矩阵估计,解决了K-means对初始聚类点敏感的问题。文献[21]提出了结合具有噪声的基于密度的聚类方法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)和霍夫变换的混合矩阵估计方法,先通过DBSCAN确定源信号的数量并进行初步聚类,再使用霍夫变换的方法在DBSCAN聚类的基础上实现高精度的混合矩阵估计,但这种方法的时间消耗非常大。文献[22]提出了方向性C-均值模糊(Directional Fuzzy C-Means, DFCM)聚类方法,先估计源信号的数量再实现混合矩阵估计。由于UBSS是对方向的估计所以相较于传统的模糊C-means(Fuzzy C-means, FCM)[23],DFCM对于盲源分离问题具有更强的鲁棒性。上述方法虽然具有不错的盲分离效果,但仍然存在如下问题:1)病态条件下(某些混合向量的方向接近)不能正确估计信源数目,无法有效解决信源数未知的UBSS问题;2)易受离群点的干扰,导致混合矩阵估计精度较低。
针对以上不足,本文提出了一种基于DFCM与K-means(DFCMK)的混合矩阵估计方法。DFCMK先通过DFCM对观测信号进行预聚类,通过预聚类可以达到以下目的:1)根据聚类有效性指标值的收敛点确定信源数目;2)根据隶属度矩阵排除掉离群点;3)确定K-means的初始聚类点。因为预聚类排除了离群点并为K-means确定了可靠的初始聚类点,所以最后通过K-means可以实现高精度的混合矩阵估计。仿真结果表明提出的方法具有较优的混合矩阵估计性能。
2 瞬时混合UBSS模型
令
和
分别表示N个观测信号和K个源信号向量,其中(·)T表示转置,K>N。在无噪条件下,瞬时混合UBSS的数学模型可以表示为:
x(t)=As(t)
(1)
其中,A=[a1,...,aK]为N×K的混合矩阵。对式(1)进行短时傅里叶变换(Short-time Fourier Transform, STFT)可以得到:
(2)
其中,
和
分别代表观测信号和源信号在时频点(t, f)的STFT系数。为了进一步增强信号在时频域的稀疏性,采用单源检测方法对数据进行预处理[24],仅保留满足以下条件的观测点进行下一步处理:
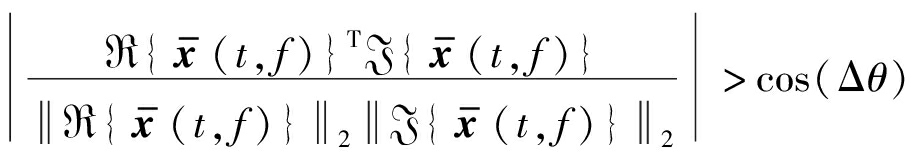
(3)
其中,R{·}和J{·}分别代表取复值的实部和虚部,‖·‖2为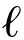
2范数。Δθ是角度参数,取值范围为(0°,90°],其取值越小,单源点的识别精度将增加,但容易导致单源点样本不足。反之,如果Δθ取值过大,则会导致异常值被误认为单源点,本文取经验值0.5°。理想情况下,经过单源检测后,观测到的时频点
会呈明显的线性分布,且直线的方向对应混合矩阵的列向量。最后通过正则化将数据转换为方向性数据的多维表示:
(4)
其中,m为有效(t, f)的序列索引。
可以视为聚类问题的样本集,下面将通过DFCM算法和K-means算法对进行聚类以实现混合矩阵估计。
3 基于DFCMK的混合矩阵估计方法
3.1 基于DFCM的预聚类
DFCM由Sgouros和Mitianoudis于2020年提出[22],在该文中已经证明DFCM比传统的FCM更适合方向性数据的聚类,所以更适合混合矩阵估计问题。假设有M个观测点
个类簇,第i个类簇的中心表示为ci,DFCM的代价函数为:
(5)
其中:
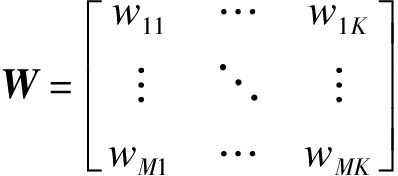
为隶属度矩阵,wmi代表观测点属于第i类的隶属度。对任意m=1,…,M,i=1,…,K,wmi满足
为超参数用于确定聚类的模糊度,q越大聚类的模糊度越高。通过交替优化ci和wmi获得最小的代价函数值,得到最终的聚类结果。根据文献[22],ci的更新公式为:
(6)
α为优化步长。wmi的更新公式为:
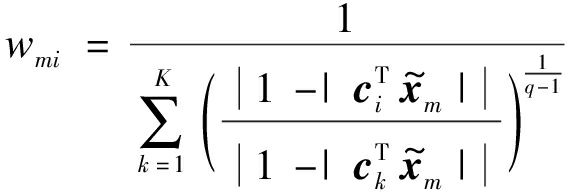
(7)
3.1.1 基于DFCM的信源数估计
针对聚类簇数量的估计问题,2004年文献[25]提出了基于FCM的簇数目估计算法。2010年文献[26]直接将该方法应用于盲源分离问题中源信号数量的估计。2020年文献[22]将该方法改进后进行源信号数量估计,使其在盲源分离问题中有更好的鲁棒性,其中最主要的改进是采用DFCM替换FCM。这几个方法核心思想一致,在此介绍文献[22]中的方法。
给定l=2,…,lmax代表可能的源信号数目,lmax代表最大可能的源信号数目。将不同的l作为输入,使用DFCM算法评价聚类的有效性,聚类有效性指标定义为:
(8)
W为隶属度矩阵,
为l个簇的集合,其对应的簇中心构成的矩阵为C=[c1,...,cl],ci代表第i个簇,ci代表第i个簇的中心,将样本集表示为
用来评估第l个簇的紧凑性,其定义为:
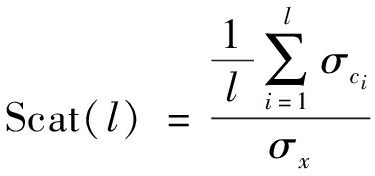
(9)
其中
(10)
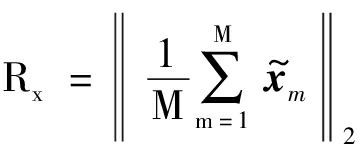
(11)
σx=1-Rx
(12)
Scat(l)的范围为[0,1],Scat(l)越小簇越紧凑。簇之间的分散性采用Sep(l)评估,其定义为:
(13)
其中
(14)
(15)
簇之间的间隔越大,Sep(l)的值越小。当式(8)的值最小时,簇内紧凑性强,簇之间间隔大,可以实现最佳聚类,令(8)最小的l值即为确定的信源的数目。为了进一步增强鲁棒性,引入了文献[27]的有效性评价指标
其定义为:
(16)
其中,
为正则化后簇数目过少的惩罚项,当簇的数目越少该项越大,
为正则化后簇数目过多的惩罚项,簇的数目越多该项越大,它们的定义分别为:
(17)
(18)
正则化方式为:
(19)
z代表u或者o,νz,min和νz,max分别为最小的vz和最大的vz。最终的聚类有效性评价指标定义为:
(20)
常规条件下(各混合向量的方法都不接近),采用式(20)能正确估计源信号的数量,但是在病态条件(某些混合向量的方向接近)下,式(20)中包含的项dmin会变得很小,导致Sep(l)和
偏大,最终VDFCM偏大并造成对源信号数量的欠估计(估计出的源信号数量小于实际的源信号数量)。以N=2,K=4为例,常规条件和病态条件下的观测信号散点图如图1所示,病态条件下有两条线的方向比较接近。在病态条件下,采用式(20)计算的有效性指标值如图2(a)所示,此时估计出的源信号数量为3,为欠估计。
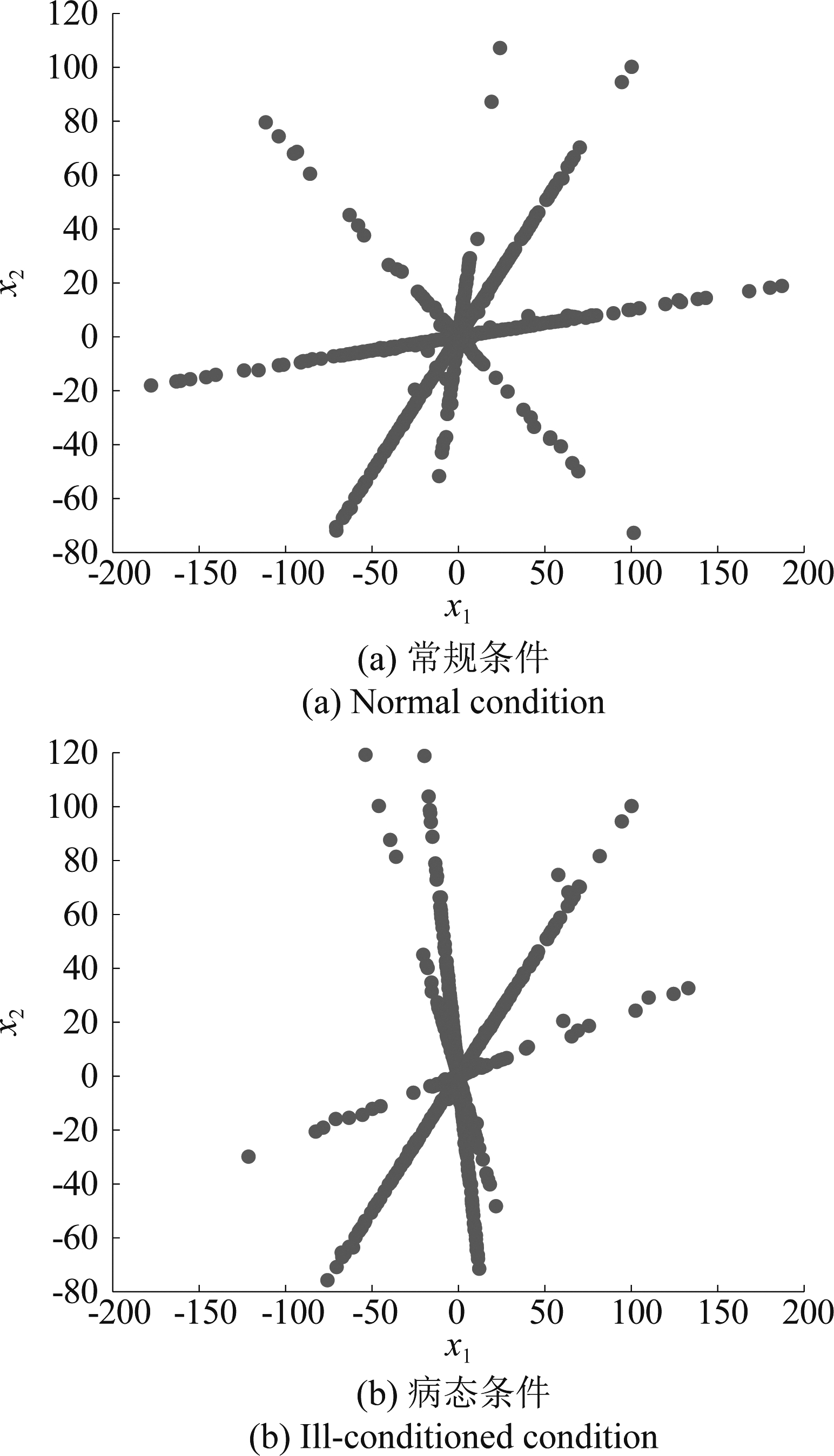
图1 常规条件和病态条件观测信号散点图
Fig.1 Observation signal scatter plot of normal and ill-conditioned conditions
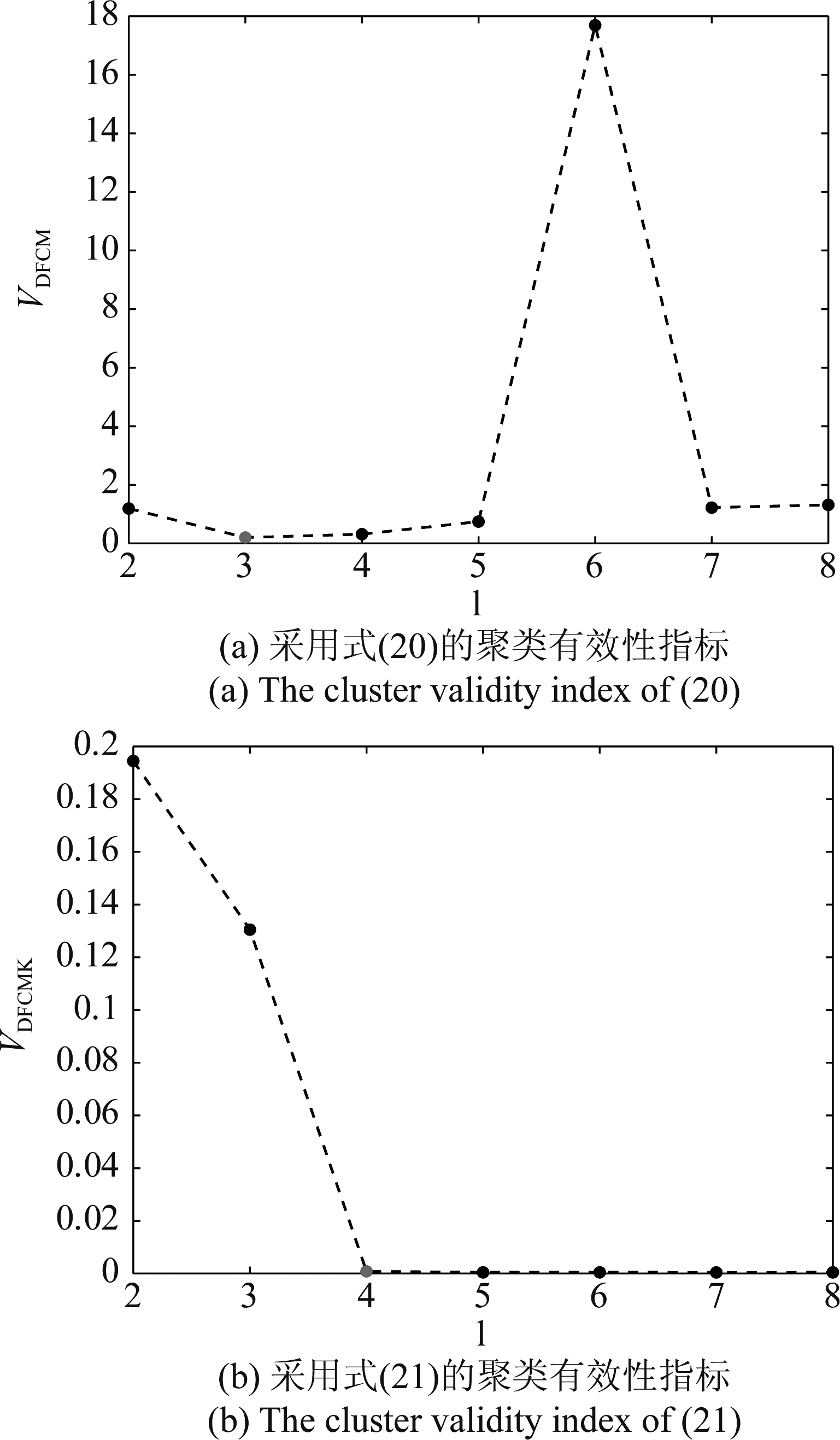
图2 聚类有效性指标曲线图
Fig.2 Graph of cluster validity index
针对上述问题,若考虑簇间的间隔很容易导致欠估计,因此DFCMK采用式(9)作为聚类有效性评价指标,即:
VDFCMK=Scat(l)
(21)
采用式(21)计算的有效性指标值如图2(b)所示,可以通过查找图中的收敛点以判断源信号的数量。因为式(9)考虑的是簇内的紧凑程度,随着l的增大VDFCMK的值会越来越小,当VDFCMK的变化不再明显(收敛)时,说明当前的簇无需再细分,收敛的点即为源信号的数量估计值。DFCMK通过参数β判断收敛点,当l满足:
Scat(l)-Scat(l+1)≤β, 2≤l<lmax
(22)
l即为收敛点,估计的源信号数量为l。
3.1.2 初始聚类点确定及离群点排除
在确定源信号数量l的同时,可以获得对应的簇中心矩阵C=[c1,...,cl]和隶属度矩阵
C将作为下一步中K-means的初始点,以提高K-means的聚类精度。由于离群点会严重影响混合矩阵估计的效果,在采用K-means聚类前,根据隶属度矩阵删除离群点。离群点的示意图如图3所示,红色的观测点为部分离群点,它们的方向偏离正确方向,会影响混合矩阵的估计精度。离群点在隶属度矩阵中的表现为归属不明确,假设第i个样本的归属度向量为Wi=[wi1,...,wiK],wi1,...,wiK的最大值wi,max,wi,max值越大,样本i的归属越明确,因此满足下面公式的样本被判定为离群点。
图3 离群点示意图
Fig.3 Schematic diagram of outliers
wi,max≤wmean
(23)
其中
(24)
经过筛选,归属不明显的离群点将从样本集中排除。
3.2 基于K-means的混合矩阵估计
经过基于DFCM的预聚类,获得了信源的数量、K-means的初始聚类点C=[c1,...,cl]、排除了观测信号中的离群点,将信源的数量、C=[c1,...,cl]、排除离群点后的观测信号作为输入,使用K-means进行聚类,得出的聚类中心即为估计的混合矩阵。因为有可靠的初始聚类点C=[c1,...,cl]且排除了离群点的干扰,K-means能够实现高精度的混合矩阵估计。DFCMK方法的流程图如图4所示。
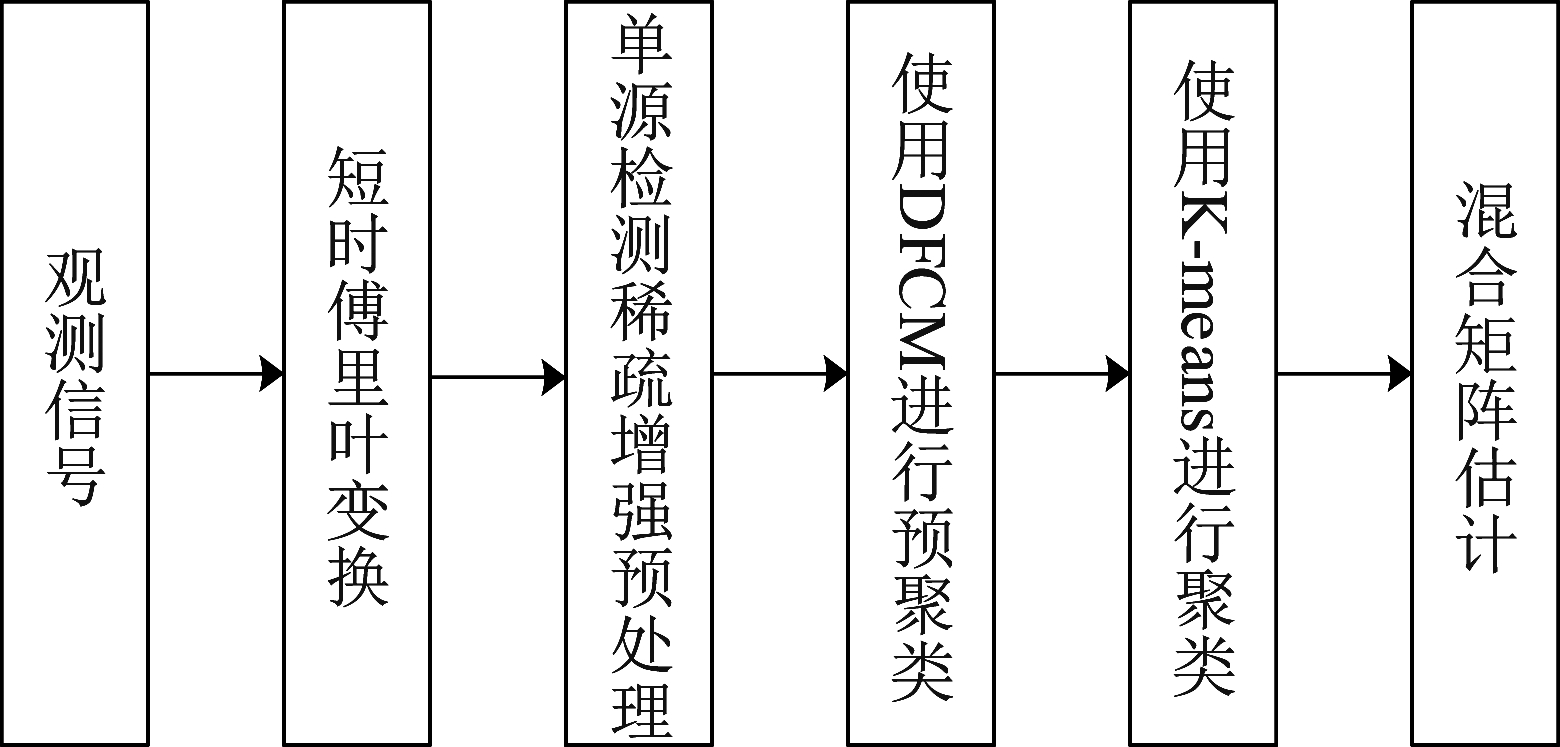
图4 DFCMK的流程图
Fig.4 Flowchart of DFCMK
4 仿真与分析
4.1 实验设置与评价标准
实验采用5段音频信号,每段音频的长度为105,STFT窗口大小为2048,窗与窗之间50%的重叠,窗函数使用Hanning窗。本文使用角度偏差来评估混合矩阵的估计精度,其定义为:
(25)
ak和
分别表示正确的混合向量和估计的混合向量,〈·,·〉代表向量积,平均角度偏差可以通过
计算得到。最终实验结果为20次独立实验结果的平均值。
本章将比较欠定盲源分离中混合矩阵估计效果,对比的算法有基于势函数的方法PF[17],K-means方法[19],FCM方法[23],CGPSO方法[18],AP-K-means方法[20],DFCM方法[22]及本文提出的DFCMK方法。其中,PF方法、K-means方法、FCM方法需要预先给出源信号的数量,而其他方法可以估计源信号的数量。PF方法和CGPSO方法仅适用于两个传感器的情况,其他方法可以直接应用于多个传感器的情况。
实验设置如下:在PF方法中,网格比例为720,调整所需角度宽度的参数为55;在CGPSO方法中,设置σ为
为0.8,β为1,PD为0.8;DFCMK方法β为0.01,模糊度q为2。算法的其他设置保持默认。文献[24]的单源点检测方法被用来增强混合信号的稀疏性,其参数Δθ设置为0.5°。此外,仅保留能量超过最大能量的10%的观测点。
4.2 实验结果
实验1 本实验考虑了2个传感器处于良态的情况,其2×3的混合矩阵如下:
观测信号的散点图如图5所示,不同线之间的角度差距较大,存在少量的离群点。实验结果如表1所示,可以看出,K-means、AP-K-means的实验结果相同,原因是可以获得相同的聚类中心。由于排除了离群点的干扰,本文提出的DFCMK估计的角度偏差最小,远优于其他对比算法。该实验中,DFCMK方法的聚类有效性指标收敛图如图6所示,收敛的位置恰好是源信号的数量。实验对应的时间消耗如表2所示,无需信源数目估计的PF、K-means和FCM效率较高。在需要估计信源数目的算法中,AP-K-means时间消耗最大,DFCM和DFCMK效率较高。
表2 实验1的时间消耗
Tab.2 The time consumption of experiment 1
算法PFK-meansFCMCGPSOAP-K-meansDFCMDFCMK时间消耗0.03630.00180.00720.84814.72940.45130.4457
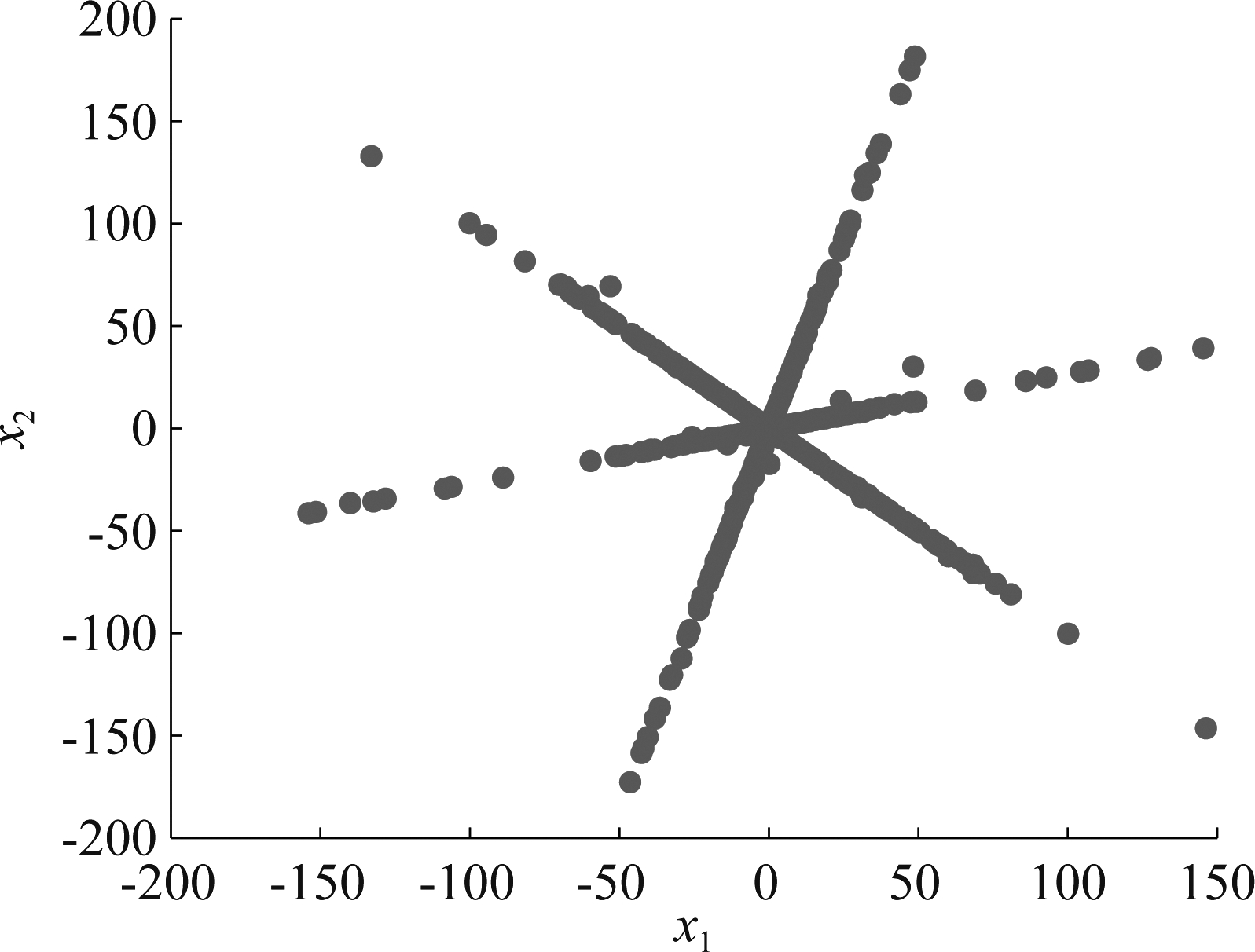
图5 N=2,K=3,良态时观测信号散点图
Fig.5 Observation signal scatter plot in the well condition case of N=2, K=3
表1 实验1的角度偏差
Tab.1 The deviation angles of experiment 1
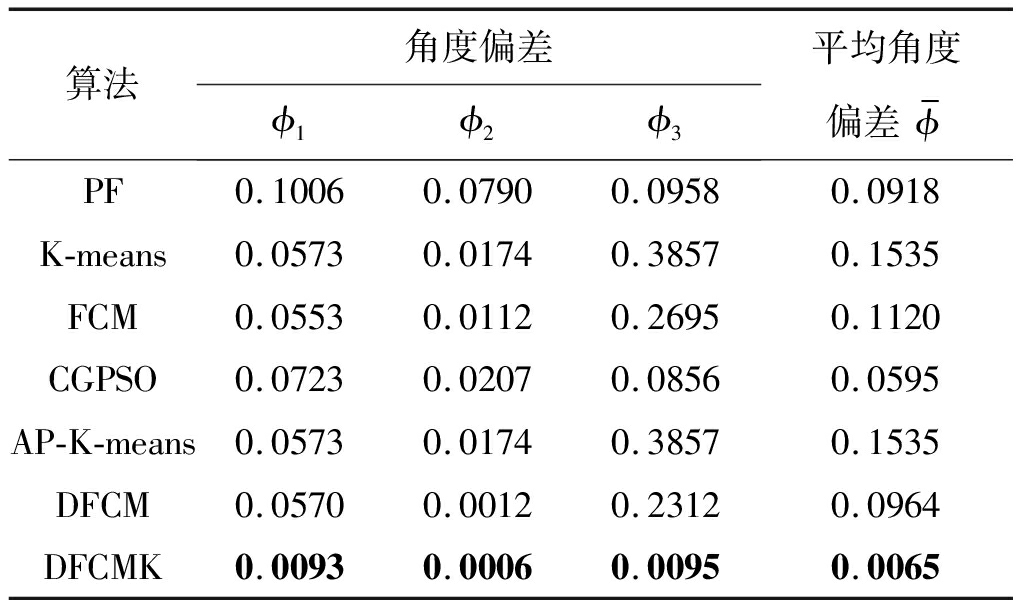
算法角度偏差ϕ1ϕ2ϕ3平均角度偏差ϕ-PF0.10060.07900.09580.0918K-means0.05730.01740.38570.1535FCM0.05530.01120.26950.1120CGPSO0.07230.02070.08560.0595AP-K-means0.05730.01740.38570.1535DFCM0.05700.00120.23120.0964DFCMK0.00930.00060.00950.0065
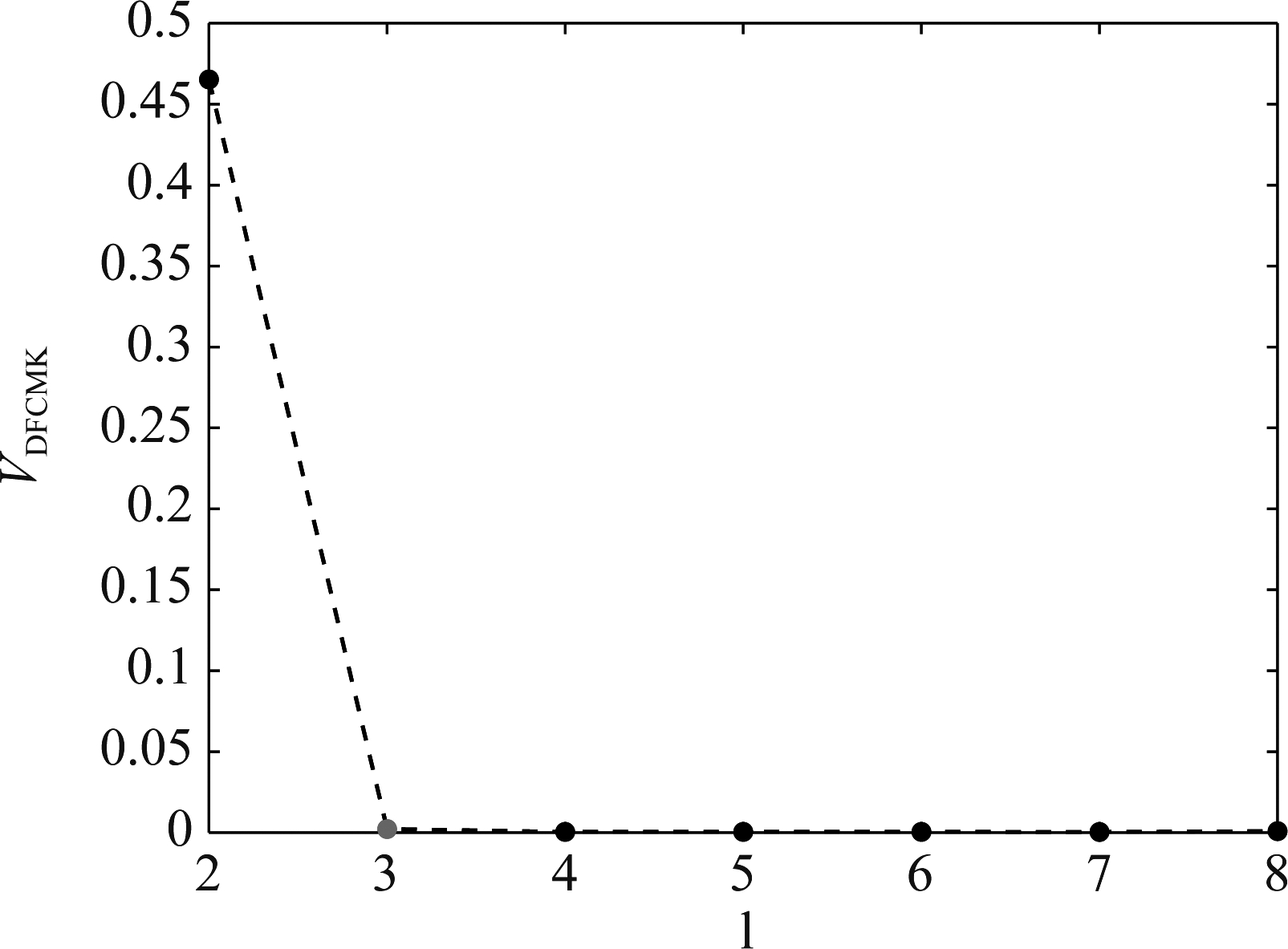
图6 实验1中DFCMK聚类有效性指标收敛图
Fig.6 Convergence graph of VDFCMK in experiment 1
实验2 在本实验中,我们考虑病态条件下2个传感器的情况,2×4的混合矩阵如下:
其中A的第3列和第4列方向相近。观测信号的散点图如图7示,其中两条线的角度差距很小,存在少量的离群点。实验结果如表3所示,对应的时间消耗如表4所示。可以看出,在这种病态的情况下,DFCM错误地将源信号的数量估计为3个,角度相近的2个方向被估计为1个方向,出现了欠估计问题。DFCMK、CGPSO和AP-K-means能正确估计源信号的数量,DFCMK的效率较高。DFCMK具有最优的估计精度。该实验中,DFCMK方法的聚类有效性指标收敛图如图8示,当l>4时VDFCMK的变化不再明显,说明源信号的数量为4。
表4 实验2的时间消耗
Tab.4 The time consumption of experiment 2
算法PFK-meansFCMCGPSOAP-K-meansDFCMDFCMK时间消耗0.02850.00200.00570.67641.6434-0.3281
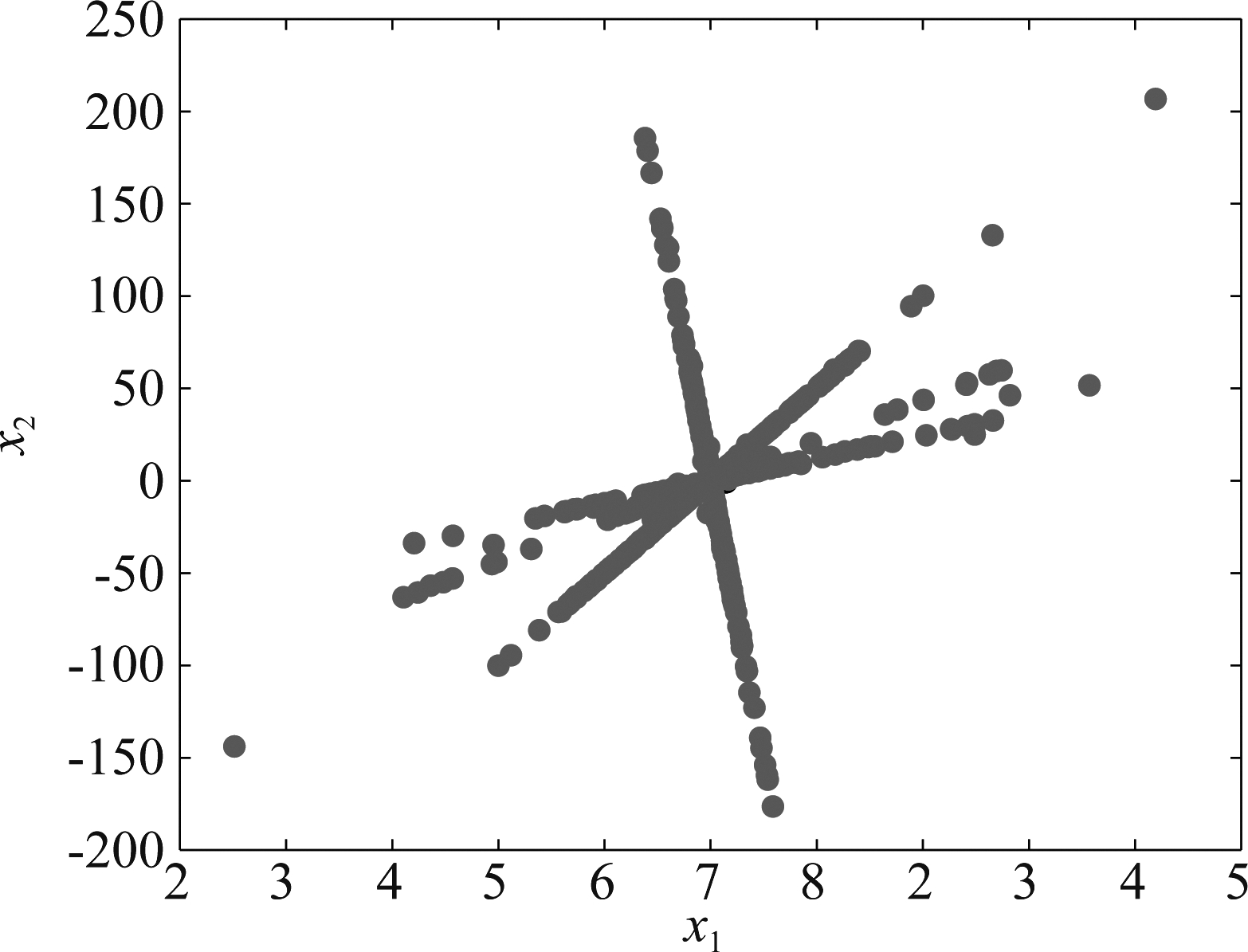
图7 N=2,K=4,病态条件下观测信号散点图
Fig.7 Observation signal scatter plot in the ill-conditioned case of N=2, K=4
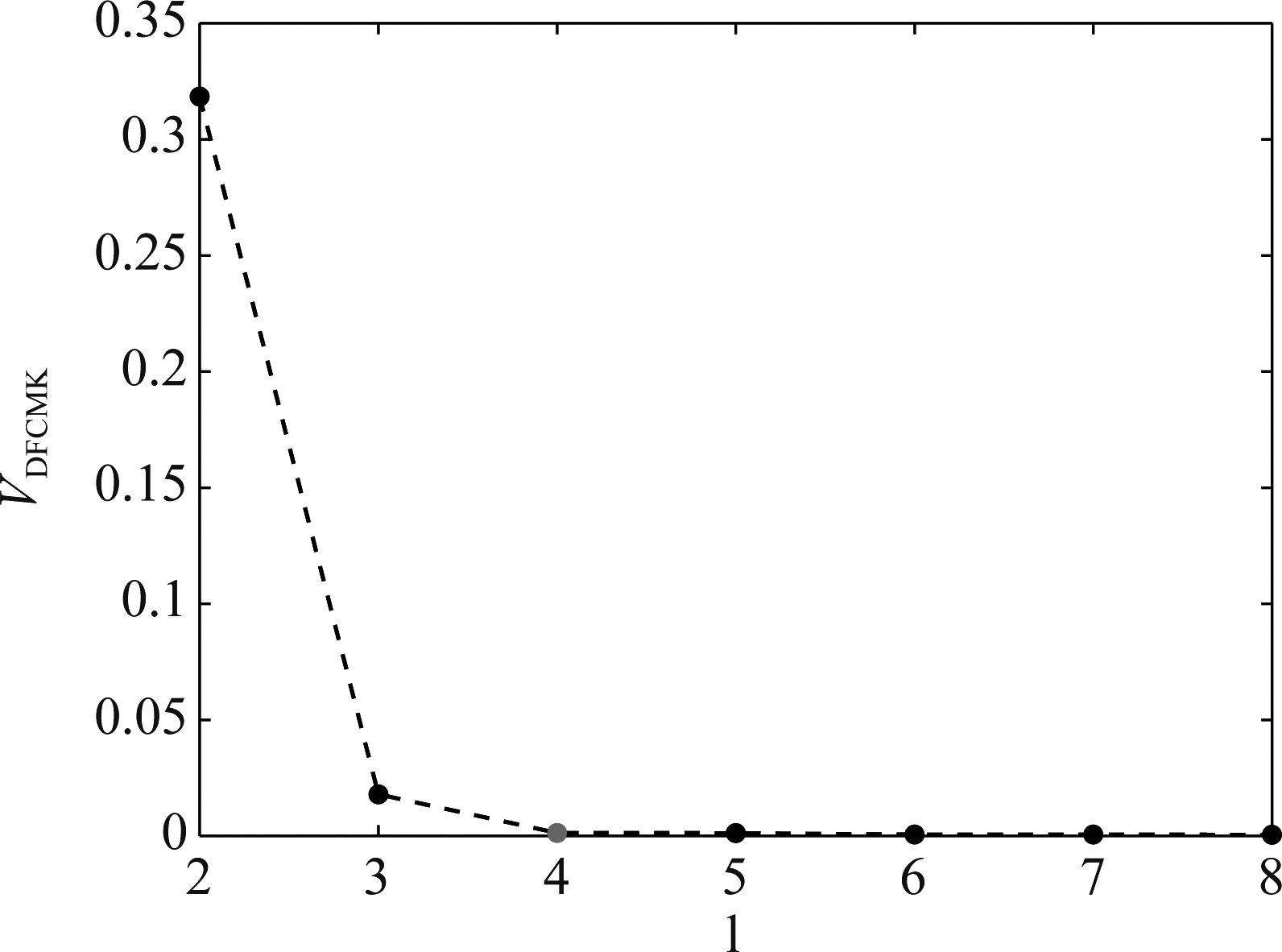
图8 实验2中DFCMK聚类有效性指标收敛图
Fig.8 Convergence graph of VDFCMK in experiment 2
表3 实验2的角度偏差
Tab.3 The deviation angles of experiment 2
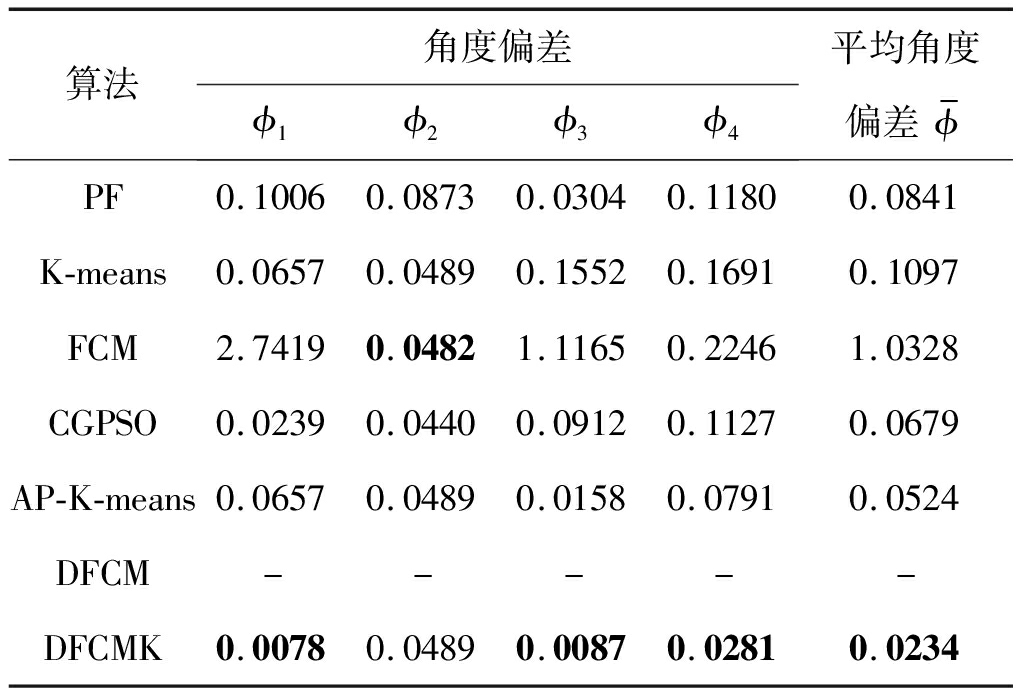
算法角度偏差ϕ1ϕ2ϕ3ϕ4平均角度偏差ϕ-PF0.10060.08730.03040.11800.0841K-means0.06570.04890.15520.16910.1097FCM2.74190.04821.11650.22461.0328CGPSO0.02390.04400.09120.11270.0679AP-K-means0.06570.04890.01580.07910.0524DFCM-----DFCMK0.00780.04890.00870.02810.0234
实验3 在本实验中,我们考虑了3个传感器处于良态的情况,其3×5的混合矩阵如下:
实验结果如表5所示。可以看出,FCM、AP-K-means、DFCM算法的估计精度几乎相同。AP-K-means、DFCMK方法的角度偏差小优于K-means,其主要原因是AP-K-means采用AP聚类算法确定K-means的初始点,DFCMK采用DFCM预聚类确定K-means的初始点,两种方法均有效解决了K-means对初始点敏感的问题。此外,DFCMK排除了离群点的干扰,能有效提高混合矩阵估计的精度。
表5 实验3的角度偏差
Tab.5 The deviation angles of experiment 3
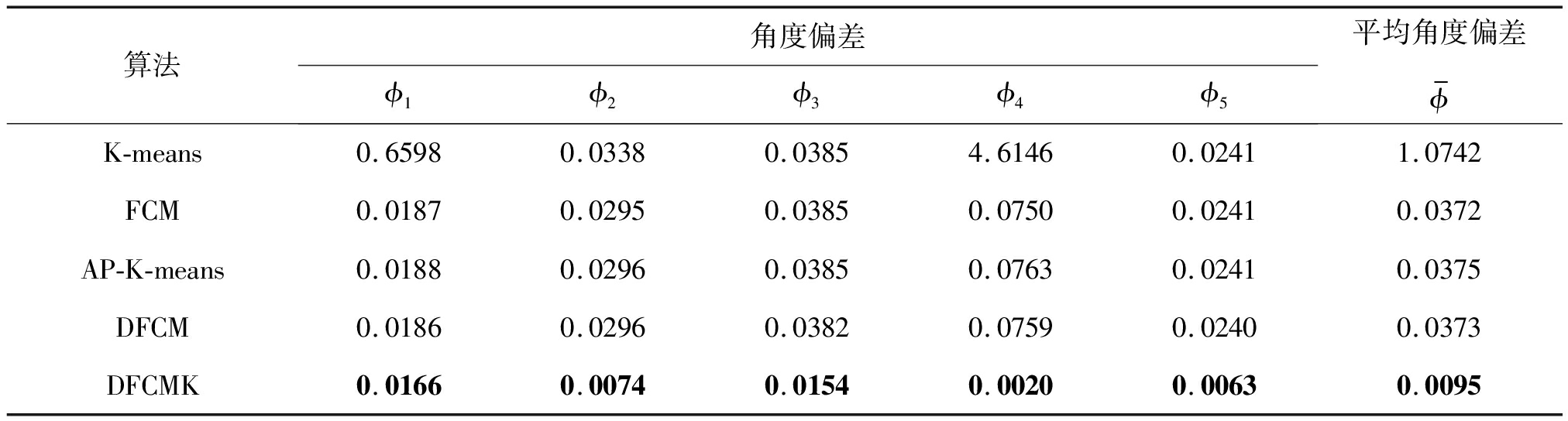
算法角度偏差ϕ1ϕ2ϕ3ϕ4ϕ5平均角度偏差ϕ-K-means0.65980.03380.03854.61460.02411.0742FCM0.01870.02950.03850.07500.02410.0372AP-K-means0.01880.02960.03850.07630.02410.0375DFCM0.01860.02960.03820.07590.02400.0373DFCMK0.01660.00740.01540.00200.00630.0095
实验4 在本实验中,我们考虑3个传感器处于病态的情况,其3×5的混合矩阵如下:
其中A的第4列和第5列方向相近。实验结果如表6所示。由于K-means对初始点较敏感,其估计精度偏低。FCM、AP-K-means的估计精度几乎相同,但FCM需要提前知道源信号的数量而AP-K-means可以估计源信号的数量。DFCM会将源信号的数量估计为3个或4个。DFCMK和AP-K-means能正确估计源信号的数,DFCMK的估计精度优于AP-K-means。
表6 实验4的角度偏差
Tab.6 The deviation angles of experiment 4
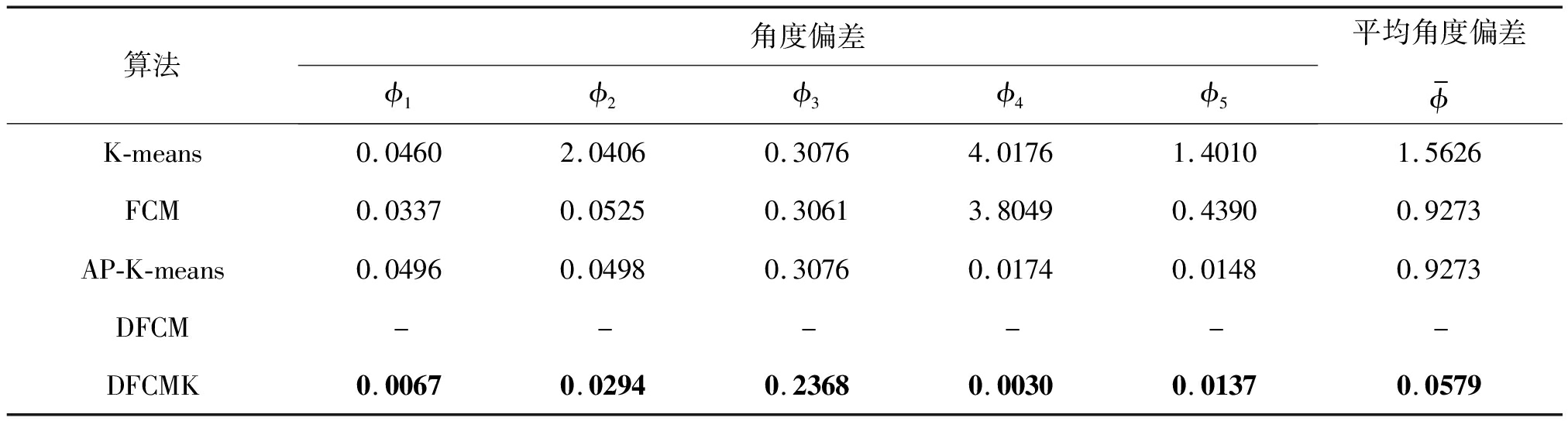
算法角度偏差ϕ1ϕ2ϕ3ϕ4ϕ5平均角度偏差ϕ-K-means0.04602.04060.30764.01761.40101.5626FCM0.03370.05250.30613.80490.43900.9273AP-K-means0.04960.04980.30760.01740.01480.9273DFCM------DFCMK0.00670.02940.23680.00300.01370.0579
5 结论
针对信源数目未知的欠定盲源分离问题,本文提出了一种基于DFCM与K-means的混合矩阵估计方法,即DFCMK。DFCMK先通过DFCM对观测信号进行预聚类,通过预聚类确定信源数目、排除掉离群点、确定K-means的初始聚类点。最后使用K-means预聚类确定的信源数目和得到的初始聚类点实现混合矩阵估计。仿真结果表明DFCMK在病态条件(某些混合向量的方向接近)能正确估计信源数目,比现有方法具有更佳的估计精度和鲁棒性。
[1] YILMAZ O, RICKARD S.Blind separation of speech mixtures via time-frequency masking[J].IEEE Transactions on Signal Processing, 2004, 52(7): 1830-1847.
[2] FENG Fangchen, KOWALSKI M.Underdetermined reverberant blind source separation: sparse approaches for multiplicative and convolutive narrowband approximation[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(2): 442-456.
[3] ABOLGHASEMI V, FERDOWSI S, SANEI S.Blind separation of image sources via adaptive dictionary learning[J].IEEE Transactions on Image Processing, 2012, 21(6): 2921-2930.
[4] 于欣永, 郭英, 张坤峰, 等.基于盲源分离的多跳频信号网台分选算法[J].信号处理, 2017, 33(8): 1082-1089.
YU Xinyong, GUO Ying, ZHANG Kunfeng, et al.A network sorting algorithm based on blind source separation of multi-FH signal[J].Journal of Signal Processing, 2017, 33(8): 1082-1089.(in Chinese)
[5] VIGARIO R, SARELA J, JOUSMIKI V, et al.Independent component approach to the analysis of EEG and MEG recordings[J].IEEE Transactions on Biomedical Engineering, 2000, 47(5): 589-593.
[6] 李红光, 郭英, 张东伟, 等.基于欠定盲源分离的同步跳频信号网台分选[J].电子与信息学报, 2021, 43(2): 319-328.
LI Hongguang, GUO Ying, ZHANG Dongwei, et al.Synchronous frequency hopping signal network station sorting based on underdetermined blind source separation[J].Journal of Electronics & Information Technology, 2021, 43(2): 319-328.(in Chinese)
[7] 李帅, 刘宏清, 彭鹏,等.混响环境下基于卷积模型的欠定盲源分离[J].信号处理: 2021,37(4), 624-632.
LI Shuai, LIU Hongqing, PENG Peng, et al.Underdetermined blind source separation based on convolution model in reverberant environment[J].Journal of Signal Processing, 2021,37(4), 624-632.(in Chinese)
[8] COMON P.Independent component analysis, A new concept?[J].Signal Processing, 1994, 36(3): 287-314.
[9] HYVARINEN A.A family of fixed-point algorithms for independent component analysis[C]∥1997 IEEE International Conference on Acoustics, Speech, and Signal Processing.Munich, Germany.IEEE, 1997: 3917-3920.
[10] FU Xiao, MA W K, HUANG Kejun, et al.Blind Separation of quasi-stationary sources: exploiting convex geometry in covariance domain[J].IEEE Transactions on Signal Processing, 2015, 63(9):2306-2320.
[11] 任喜顺, 沈越泓, 高猛, 等.基于时频分析的混合矩阵估计方法[J].信号处理, 2012, 28(4): 545-553.
REN Xishun, SHEN Yuehong, GAO Meng, et al.Algorithm for mixing matrix estimation based on time-frequency analysis[J].Signal Processing, 2012, 28(4): 545-553.(in Chinese)
[12] AISSA-EL-BEY A, LINH-TRUNG N, ABED-MERAIM K, et al.Underdetermined blind separation of nondisjoint sources in the time-frequency domain[J].IEEE Transactions on Signal Processing, 2007, 55(3): 897-907.
[13] KIM S, YOO C D.Underdetermined blind source separation based on subspace representation[J].IEEE Transactions on Signal Processing, 2009, 57(7): 2604-2614.
[14] LI Yuanqing, AMARI S, CICHOCKI A, et al.Underdetermined blind source separation based on sparse representation[J].IEEE Transactions on Signal Processing, 2006, 54(2): 423-437.
[15] XIE Shengli, YANG Liu, YANG Junmei, et al.Time-frequency approach to underdetermined blind source separation[J].IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 306-316.
[16] ZHEN Liangli, PENG Dezhong, YI Zhang, et al.Underdetermined blind source separation using sparse coding[J].IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 3102-3108.
[17] BOFILL P, ZIBULEVSKY M.Underdetermined blind source separation using sparse representations[J].Signal Processing, 2001, 81(11): 2353-2362.
[18] SUN T Y, LIU Chancheng, TSAI S J, et al.Cluster guide particle swarm optimization(CGPSO)for underdetermined blind source separation with advanced conditions[J].IEEE Transactions on Evolutionary Computation, 2011, 15(6): 798-811.
[19] XIE Yuan, XIE Kan, WU Zongze, et al.Underdetermined blind source separation of speech mixtures based on K-means clustering[C]∥2019 Chinese Control Conference(CCC).Guangzhou, China.IEEE, 2019: 42-46.
[20] HE Xuansen, HE Fan, CAI Weihua.Underdetermined BSS based on K-means and AP clustering[J].Circuits Systems & Signal Processing, 2016, 35(8):2881-2913.
[21] SUN Jiedi, LI Yuxia, WEN Jiangtao, et al.Novel mixing matrix estimation approach in underdetermined blind source separation[J].Neurocomputing, 2016, 173: 623-632.
[22] SGOUROS T, MITIANOUDIS N.A novel directional framework for source counting and source separation in instantaneous underdetermined audio mixtures[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28: 2025-2035.
[23] BEZDEK J C, EHRLICH R, FULL W.FCM: The fuzzy c-means clustering algorithm[J].Computers & Geosciences, 1984, 10(2/3): 191-203.
[24] REJU V G, KOH S N, SOON I Y.An algorithm for mixing matrix estimation in instantaneous blind source separation[J].Signal Processing, 2009, 89(9): 1762-1773.
[25] SUN Haojun, WANG Shengrui, JIANG Qingshan.FCM-based model selection algorithms for determining the number of clusters[J].Pattern Recognition, 2004, 37(10): 2027-2037.
[26] REJU V G, KOH S N, SOON I Y.Underdetermined convolutive blind source separation via time-frequency masking[J].IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(1): 101-116.
[27] KIM D J, PARK Y W, PARK D J.A novel validity index for determination of the optimal number of clusters[J].IEICE Transactions on Information and Systems, 2001, 84(2):281-285.
