1 引言
近年随着高功率微波技术的快速发展,高功率微波武器已成为电子战中抢夺作战先机的有力武器。因其所辐射的高功率电磁波可掩盖真实目标所发射信号,可干扰雷达对真实目标的探测[1-2]。尤其是现代电子战的战场环境中,强干扰信号与弱真实信号交织在一起,导致战场的电磁环境异常复杂[3-4]。研究不同功率的信号同时入射到雷达接收天线阵列时,入射信号的功率对波达方向(DOA)估计的影响,对雷达的辐射源定位具有重要意义。
复杂电磁环境中普遍存在强信号与弱信号同时入射到天线接收阵列的情形,强信号会淹没弱信号从而导致弱信号波达方向(DOA)估计性能下降。当前针对不同功率入射信号DOA估计问题的研究大致可分为两类:一类集中于研究如何提高DOA估计算法对弱信号的分辨率。如文献[5]提出了SSMUSIC算法,该方法通过建立标准子空间与信号-干扰模型下子空间的关系,利用信号空间的信息构造基于MUSIC方法的谱估计函数,可同时对入射的强信号与弱信号进行DOA估计。文献[6]等研究了基于特征空间干扰相消的方法,该方法利用阻塞矩阵来剔除信号协方差矩阵中的强干扰。文献[7-8]利用噪声子空间对入射信号功率不变这一性质,提出了有效的不同功率入射信号的DOA算法。此类算法利用噪声子空间的不变性,可对不同功率的入射信号进行DOA估计,与利用信号空间的DOA算法相比具有较高的分辨率。文献[9]提出将强信号对应的特征向量纳入噪声空间,然后利用与MUSIC算法类似的谱估计对不同功率入射信号进行DOA估计。文献[10]提出基于特征波束 mCapon方法,通过简单的门限比较和子空间处理,提高了大功率差异下空间临近入射信号的参数估计性能。上述研究均不同程度的提高了DOA估计算法对弱信号的分辨性能;另外一类研究集中于分析强信号对算法DOA估计性能的影响。通常此类研究以MUSIC算法作为研究对象,这是由于MUSIC算法是十分具有代表性的空间谱估计算法,在通信、雷达、声呐等领域获得广泛而深入的研究[11-13]。文献[14]采用渐进统计分析的方法对MUSIC算法的估计性能进行了研究,得到强信号功率远远高于弱信号功率时,弱信号零谱的数学期望谱表达式。文献[15]提出了针对不同功率入射信号的平均信噪比分辨门限,给出了MUSIC算法平均信噪比分辨门限表达式,并得到入射信号功率差异越大,平均信噪比分辨门限越高的结论。文献[16]给出了MUSIC算法对相关信源的平均信噪比分辨门限表达式,并讨论了信源功率差异对MUSIC算法分辨性能的影响。上述两类研究均针对具体的DOA估计算法进行研究,未注意到信号功率对入射信号DOA估计算法评价准则的影响,未从更普遍的意义上证明强信号功率对弱信号DOA估计的影响。
本文首先从克拉美罗界的角度证明了强信号功率会影响弱信号DOA估计性能,由于克拉美罗界是任何无偏估计算法均方根误差的最下界,因此分析强信号对弱信号DOA估计CRB的影响更具有普遍意义;然后分析了DOA估计算法经典评价准则在分辨不同功率入射信号时存在的局限性,评价准则是评价算法性能的依据,通过蒙特卡洛实验验证了当弱信号信噪比低于5 dB时,经典评价准则对分辨不同功率入射信号其误判率较大;最后提出了针对不同功率入射信号的新评价准则,并证明了新准则较经典准则更适用于评价DOA估计算法对不同功率入射信号的分辨性能。
2 接收信号阵列模型
假设自由空间中有P个相互独立且波长为λ0的窄带信号,入射到如图1所示均匀直线接收天线阵列中。该均匀线阵各阵元间距为d,阵元总数为M,第一个阵元位于坐标原点处。θi为第i个入射信号的DOA与y轴的夹角,则均匀线阵所接收到的入射信号可表示为:
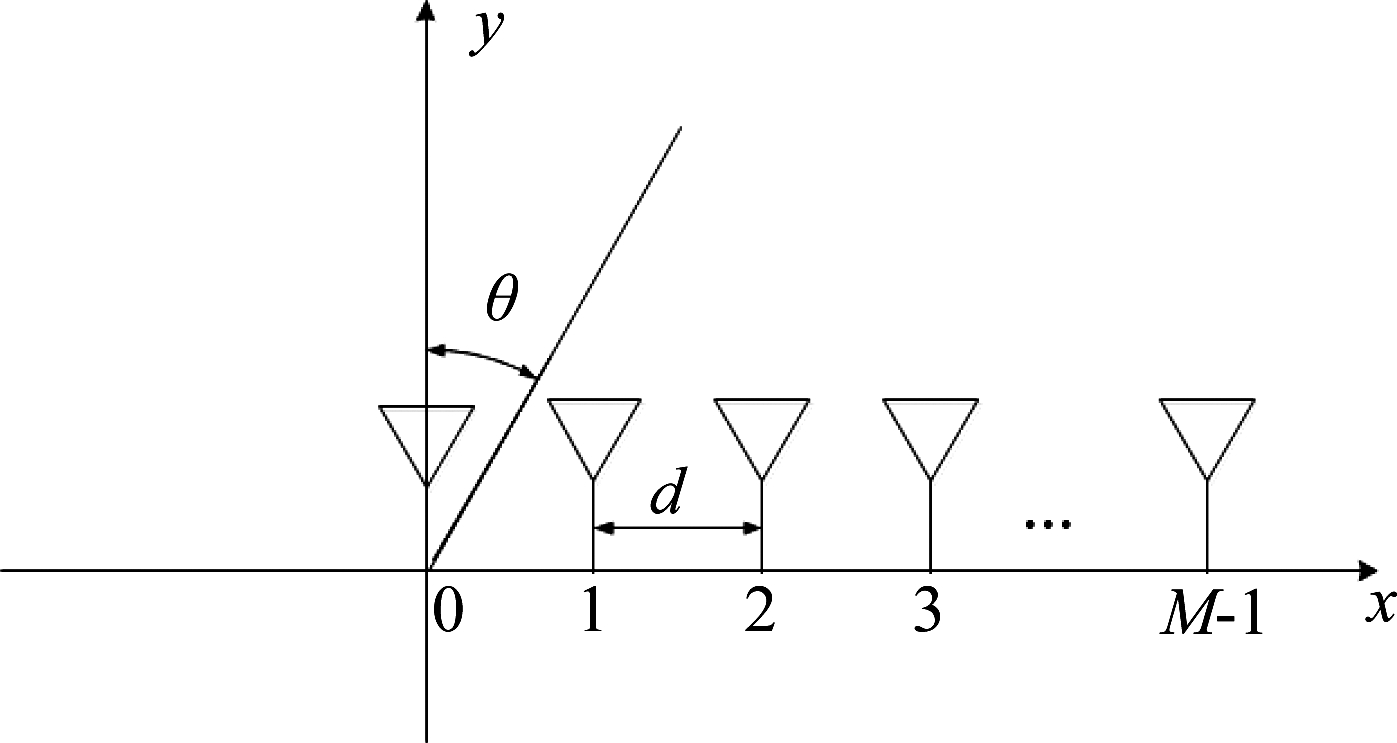
图1 均匀直线接收天线阵列示意图
Fig.1 Configuration of uniform linear receiving antenna array
X(t)=A(θ)S(t)+N(t)
(1)
式中
为t时刻均匀直线阵列所接收到的入射信号的数据矢量,
与
分别为入射信号复振幅矢量与加性高斯白噪声矢量,信号与噪声不相关,各阵元所接收的噪声独立同分布,协方差为
为阵列流形矩阵:
A(θ)=[a(θ1),a(θ2),…,a(θi),…a(θp)]
(2)
其中a(θi)=[1,e-jωi,…,e-j(M-1)ωi]T,ωi=k0dsin θi,k0为入射信号自由空间波数。则接收信号X(t)的协方差矩阵为:
(3)
其中Rs为入射信号协方差矩阵。接收信号X(t)的样本协方差矩阵为:
(4)
其中K为采样的快拍数。对
进行经特征值分解得:
(5)
其中
为特征值,
为特征向量。
3 强信号功率对弱信号DOA估计克拉美罗界的影响
CRB为任何无偏估计子提供了估计均方误差的最下界,因此研究信号功率对入射信号DOA估计CRB的影响,对其他DOA估计算法分析信号功率对算法性能的影响具有重要借鉴意义。本节将分析入射信号中其中一个信号入射功率的提高,对其他信号DOA估计CRB的影响。信号DOA估计的CRB,可利用Fisher信息矩阵求逆得到。对于图1所示的直线阵列,P个入射信号的角度分别为θ1,θ2,…θP,此时Fisher信息矩阵为:
(6)
其中Fisher信息矩阵中的每个元素
(7)
当入射信号相互独立时,Rs=diag(ρ1,ρ2,…,ρP)为对角阵,其中ρi代表第i个入射信号的功率。此时Rx可简化为
(8)
则阵列协方差矩阵对θi的偏导∂a(θi)/∂θi为
(9)
其中导向矢量a(θi)对θi的偏导∂a(θi)/∂θi为
(10)
其中q(θi)=e-jk0dsin θi,相移因子q(θi)对θi的导数为
=(m-1)q(θi)m-2·q(θi)·(-jk0dcos θi)=
-j(m-1)k0dcos θi·q(θi)m-1,m=1,2,…,M
(11)
当阵元间距d=λ0/2时,相移因子q(θi)可简化为q(θi)=exp(-jπsin θi)。将式(11)、(10)、(9)代入式(7),便可得到Fisher信息矩阵中的每个元素。进而对式(6)求逆便可得入射信号θ=[θ1,θ2,…,θP]估计的CRB为
θCRB=diag(F-1)
(12)
假设有两个功率不相等的信号从正上方入射到如图1所示的均匀线阵上,其中阵元数M=9,阵元间距d=λ0/2,噪声功率
两入射信号夹角为Δ=10°,其中信号1入射角为θ1=-5°,信号2入射角θ2=5°。本节将重点考察当信号1与信号2的功率不同时,即信噪比(SNR)不同时,功率较大的信号对功率较小的信号DOA估计CRB的影响。在此设信号1为强信号,信号2为弱信号,强信号与弱信号功率的比值为强弱信号比(Strong Weak Ratio, SWR)。
当强信号功率提高时,弱信号DOA估计的CRB如图2所示。由图2可知,在不同强信号功率下随着弱信号SNR2的提高,弱信号DOA估计的CRB均不断降低,即DOA估计的均方根误差不断减小。当SWR=0 dB时,两入射信号功率相等。对比SWR=0 dB与SWR=5 dB可得,当强信号功率增加5 dB,而弱信号功率不变时,弱信号DOA估计的CRB有所上升,即估计的均方根误差增加。同样可得当SWR=10 dB、15 dB、20 dB时,弱信号DOA估计的CRB均有所上升。因此可知,对于均匀线阵当其中一个入射信号功率增加时,会导致另外一个入射信号DOA估计的最小均方根误差增加。不同的弱信号信噪比下,强信号功率提高导致弱信号DOA估计CRB上升的百分比如图3所示。由图3可知,强信号功率提高均会导致弱信号DOA估计CRB上升。随着强信号功率的进一步提高,弱信号DOA估计的CRB上升幅度有所减小。随着弱信号SNR2的提高,强信号功率的提高对弱信号DOA估计CRB的影响降低,这说明当弱信号SNR较高时,强信号功率对其影响较小。
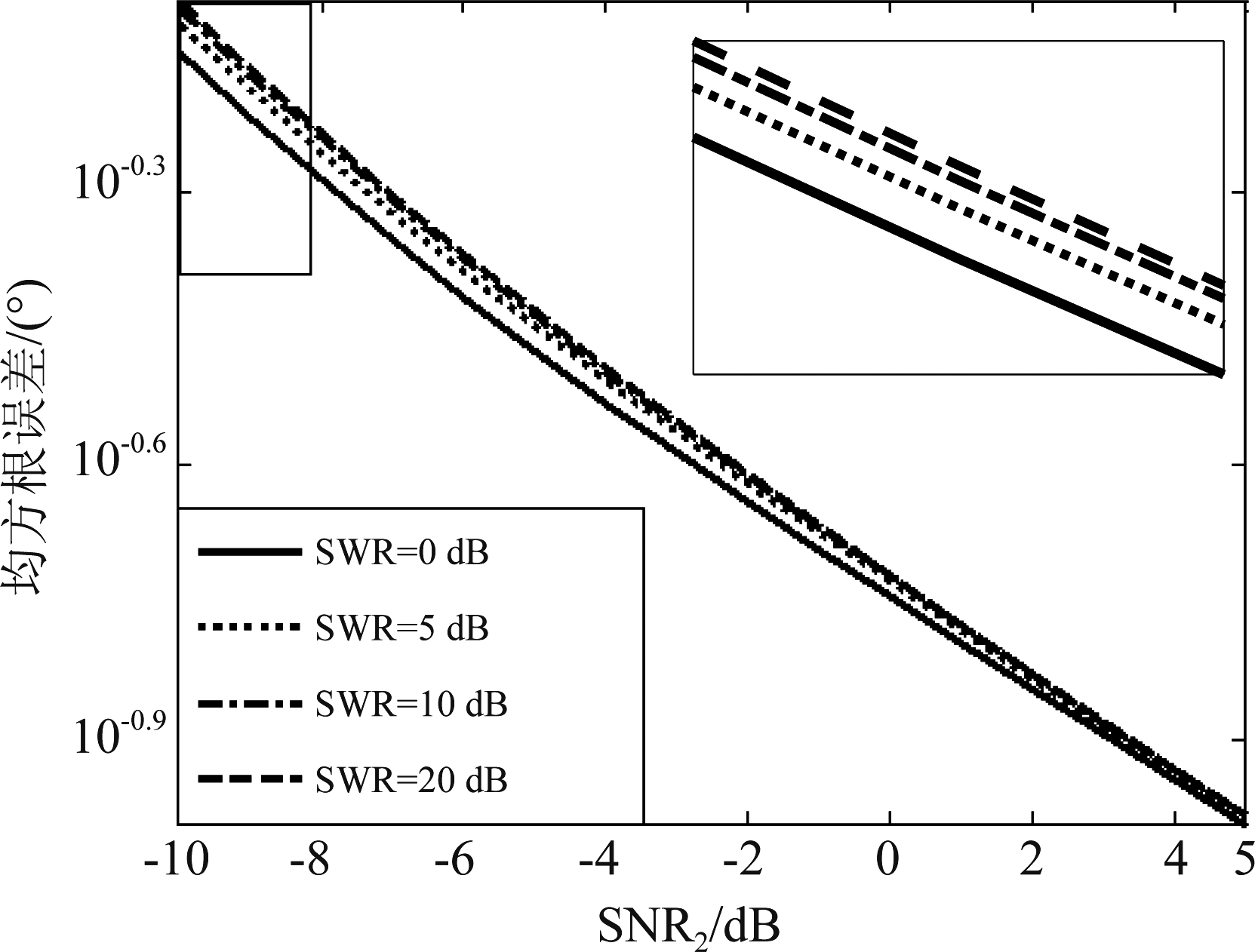
图2 不同SWR下弱信号DOA估计的CRB随弱SNR2的变化
Fig.2 The CRB of DOA estimation for weak signal against different SNR2 under different SWR
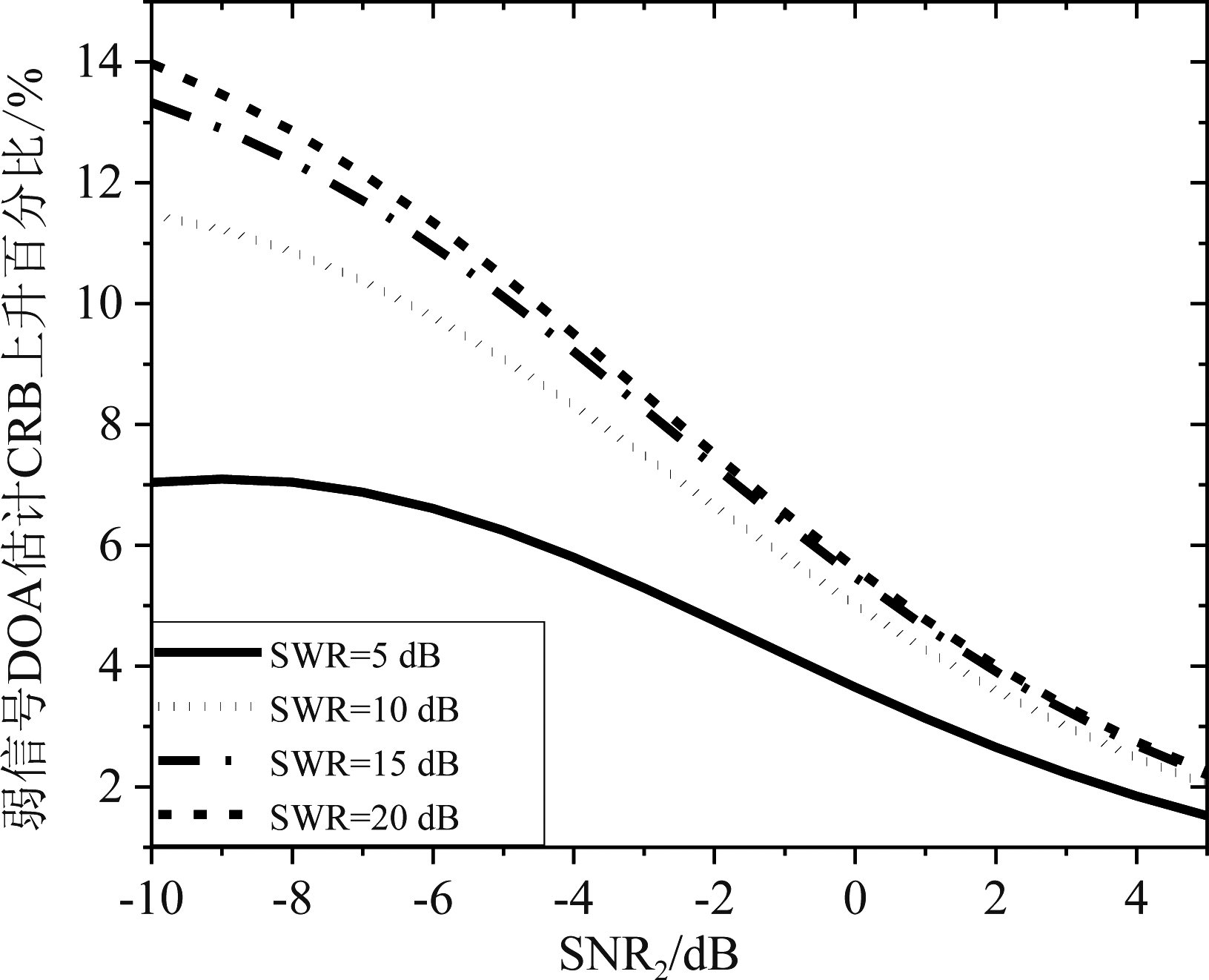
图3 不同SWR下弱信号DOA估计CRB上升百分比随弱SNR2的变化
Fig.3 The rising percentage of CRB for weak signal DOA estimation against different SNR2 under different SWR
通过本节分析可知,强信号功率增加会影响弱信号DOA估计的CRB,强信号功率增加导致弱信号CRB上升,即均方根误差增加。这种影响在弱信号信噪比较低时体现尤其明显,伴随着强功率信号进一步增加,此影响最终趋于稳定。
4 DOA估计算法经典评价准则局限性分析
DOA估计算法对入射信号的理论分辨性能依赖于评价准则,评价准则是计算算法理论分辨性能的前提。对利用空间谱进行DOA估计的算法而言,经典的判定两入射信号分辨成功的准则为[17]:对于两个相邻的入射信号θ1与θ2,其中θm=(θ1+θ2)/2,若满足
(13)
则认为算法可以成功分辨两个入射信号,其中
为算法的零谱估计。通常式(13)被用作评价算法对入射信号理论分辨率的准则。然而在复杂电磁环境中式(13)的评价准则存在一定局限性,当入射信号功率不同时,应用此准则会导致部分误判。下面以经典的空间谱估计算法MUSIC算法为例,说明式(13)经典评价准则的局限性。
4.1 MUSIC算法期望谱
MUSIC算法是基于空间谱进行入射信号DOA估计的经典方法,获得了广泛而深入的研究[11-13]。因此以MUSIC算法为例说明式(13)经典评价准则存在局限性具有一定代表性。本文通过分析MUSIC算法零谱的数学期望(期望谱),来分析式(13)经典评价准则存在的局限性。
MUSIC算法的零谱
在入射信号到达角θ邻近区域内的统计特性,可通过分析的统计均值
与方差
获得,进而可获得MUSIC算法在入射角θ处对入射信号的分辨性能。当有两个入射信号同时入射到如图1所示的均匀线阵上时,MUSIC算法的期望谱为[14]:
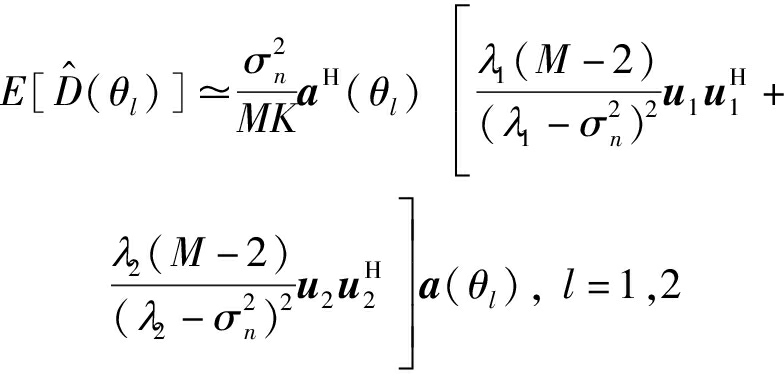
(14)
其中λ1、λ2与u1、u2分别为Rx特征值分解后所得特征值与特征向量。由于MUSIC算法零谱的方差
与期望谱
的比值≪1,因此通过分析MUSIC算法期望谱可获得MUSIC算法的分辨性能。
若有两个不相关的信号入射到如图1所示的天线阵列上,两入射信号波达方向分别为θ1,θ2,功率分别为P1,P2。则入射信号的协方差矩阵可记为:
(15)
此时式(3)中第一项:
ARsAH=P1a(θ1)aH(θ1)+P2a(θ2)aH(θ2)
(16)
由于θ1≠θ2,对方阵ARsAH进行特征值分解可得两个非零特征值分别记为λ1、λ2,相应的特征向量记为u1、u2。则有[18]
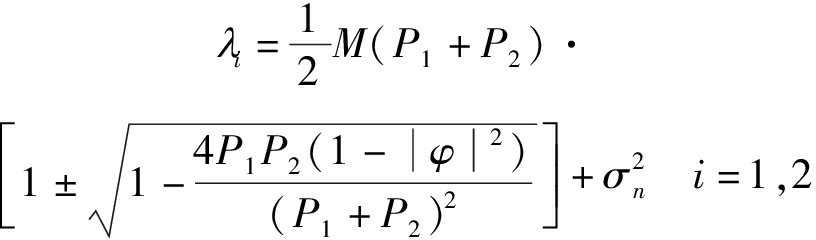
(17)
(18)
其中
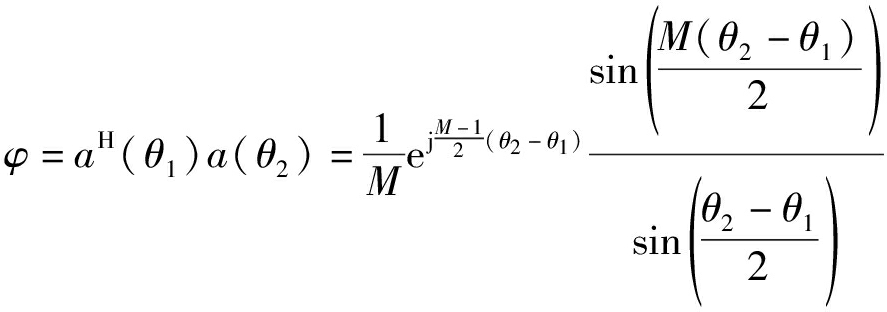
(19)
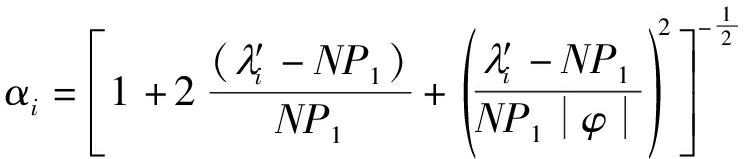
(20)
(21)
将式(17)、(18)所求得的特征值与特征向量代入式(14),便可得MUSIC算法的期望谱。
为了验证式(14)所得MUSIC算法期望谱的有效性,下面将对比蒙特卡洛实验所得MUSIC算法零谱的平均值与式(14)所得MUSIC算法的期望谱,其中蒙特卡洛实验的次数为1000次。假设两个相互独立的信号入射到如图1所示的均匀阵列上,其中阵元数M=9,阵元间距d=λ0/2,噪声功率两入射信号夹角为Δ=6°,信号1入射角为θ1=3°,信号2入射角θ2=-3°,设信号1为强信号,信号2为弱信号,信噪比为SNR2=7 dB。不同的入射信号强弱信号比SWR下,计算式(14)中MUSIC算法的期望谱和蒙特卡洛实验所得MUSIC算法零谱的均值。为了方便对比,在此将MUSIC的期望谱与蒙特卡洛实验的零谱均值二者均取倒数,取倒数后分别命名为极值期望谱与极值平均谱,如图4所示。由图4可知,强信号功率提高时,其极值期望谱与极值平均谱均在增加。两信号功率相等即SWR=0 dB(见图4(a))与两信号功率不同时(见图4(b)、(c)、(d)),MUSIC算法的极值期望谱与极值平均谱基本相同。因此可得,MUSIC算法的期望谱与采用蒙特卡洛实验所得零谱均值具有良好的一致性,验证了式(14)的正确性,并说明MUSIC算法的期望谱可作为分析MUSIC算法对入射信号理论分辨性能的依据。因此下文将借助MUSIC算法的期望谱,分析经典评价准则对评价MUSIC算法对不同功率入射信号分辨性能的局限性。
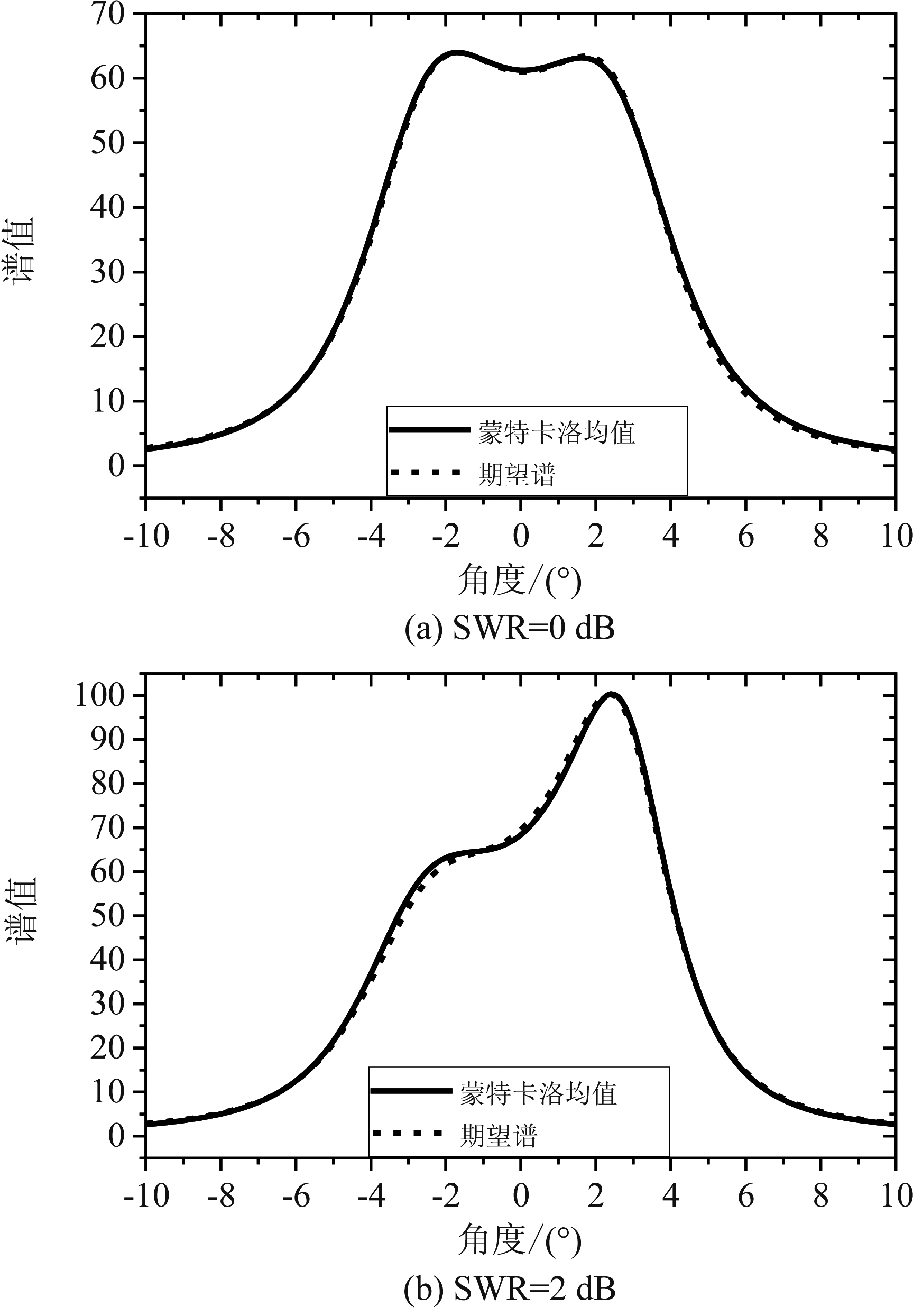
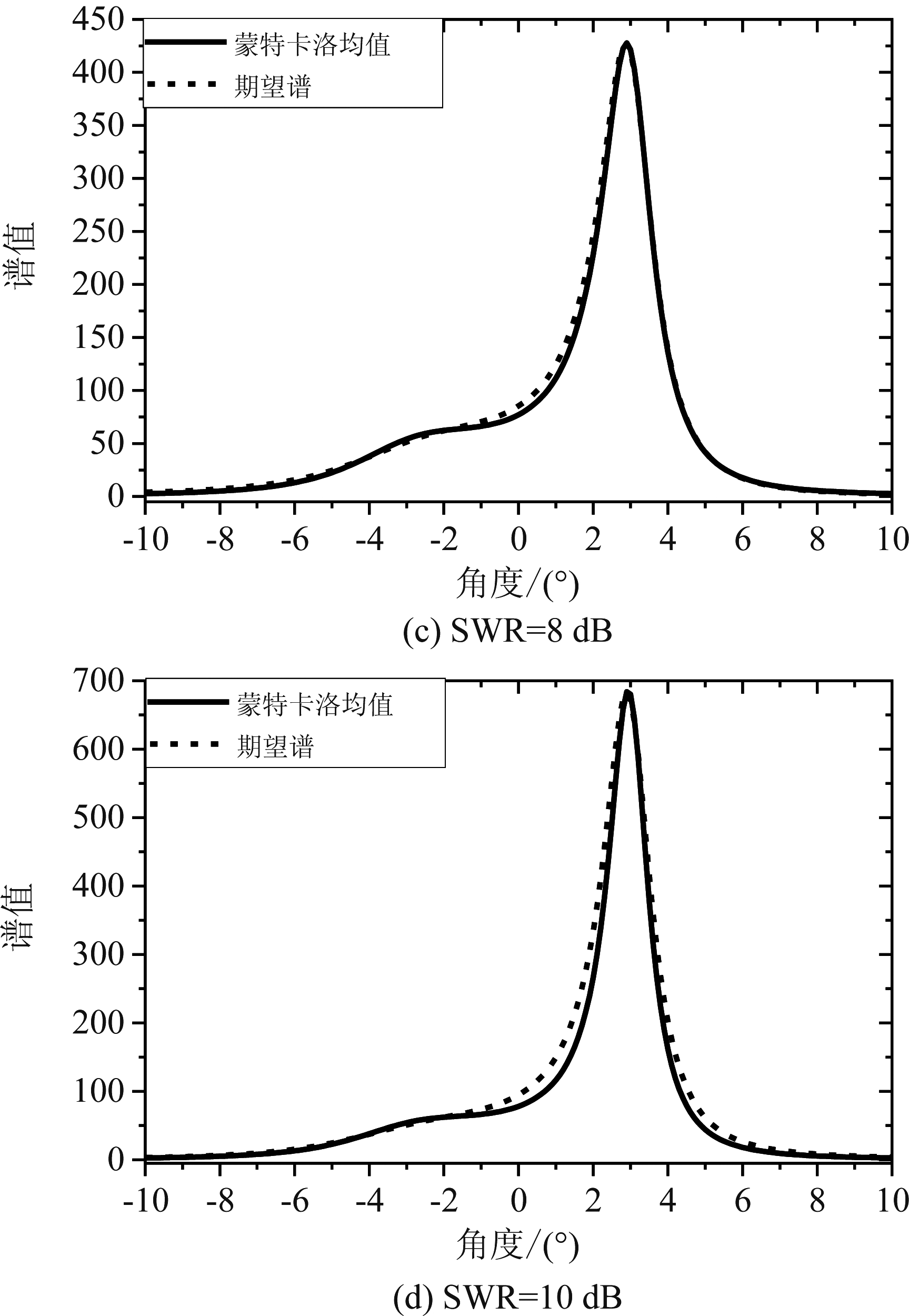
图4 不同强弱信号比下极值期望谱与极值平均谱
Fig.4 The extremum expectation spectrum and extremum average spectrum under different SWR
4.2 经典评价准则的局限性
根据4.1节中式(14),可计算不同入射信号功率下MUSIC算法的期望谱。与MUSIC算法单次DOA估计所得零谱相比,期望谱为零谱的数学期望,更具代表性。下面借助于MUSIC算法的期望谱分析经典评价准则的局限性。
实验1 设两个相互独立的信号入射到如图1所示的均匀阵列上,其中阵元数M=9,阵元间距d=λ0/2,噪声功率两入射信号夹角为6°,入射信号1的入射角度θ1=3°,信噪比为SNR1=10 dB,入射信号2的入射角度θ2=-3°,信噪比为SNR2=8 dB。由式(14)所得到的MUSIC算法的极值期望谱如图5所示。
图5 入射信号的极值期望谱
Fig.5 The extremum expectation spectrum of input signals
由图5可知,此时MUSIC算法无法成功分辨两入射信号。然而此时极值期望谱满足
其中
为极值期望谱在θ1、θ2、θm处的谱值。即对于期望谱而言仍然满足式(13)所示的准则
也即依据式(13)仍然判定两入射信号分辨成功。显然以式(13)作为DOA估计算法的评价准则,来评价算法对两个不同功率入射信号的分辨率有一定局限性。
下面将通过对MUSIC算法进行蒙特卡洛实验进一步验证式(13)经典评价准则存在的局限性。首先根据式(13)判断MUSIC算法每次蒙特卡洛实验可否分辨两个不同功率的入射信号。然后利用每次蒙特卡洛实验所得MUSIC算法空间谱,实际统计该次实验下是否出现两个入射信号的谱峰,如果出现则认为此次实验MUSIC算法实际能成功分辨两入射信号,反之则认为不能分辨两入射信号。最后对比依据式(13)得到的分辨成功次数与实际分辨成功概率,其中分辨成功概率定义为:成功分辨两入射信号的次数与蒙特卡洛实验总次数的比值。
实验2 设有两个相互独立的信号入射到如图1所示的均匀阵列上,其中阵元数M=9,阵元间距d=λ0/2,噪声功率设入射信号1为强信号,入射信号2为弱信号,两入射信号夹角为6°,入射信号1的入射角度θ1=3°,入射信号2的入射角度θ2=-3°。如上所述,不同强弱信号比SWR与弱信号信噪比SNR2条件下,进行1000次蒙特卡洛实验。由经典评价准则得到的分辨成功概率(简称经典准则)与实际分辨成功概率(简称实际)如图6所示。
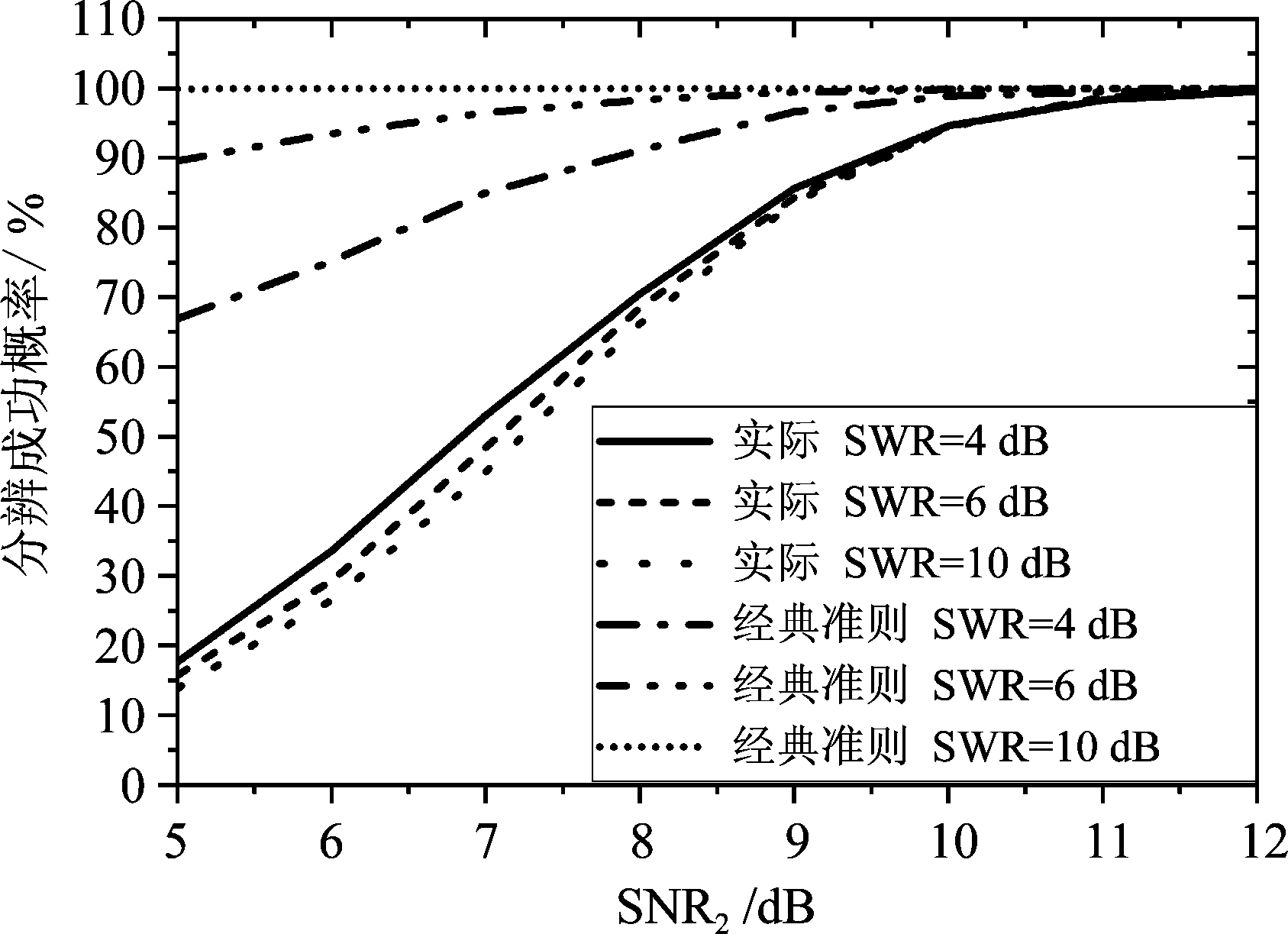
图6 1000次蒙特卡洛实验中经典准则与实际分辨成功概率
Fig.6 The actual probability of success and that based on the classical criterion in 1000 Monte Carlo experiments
由图6可知,随着弱信号信噪比的增加,基于经典准则的分辨成功概率与实际分辨概率均增加。在相同的弱信号信噪比SNR2条件下,随着强信号功率的提高,实际分辨成功概率逐步降低,而基于经典准则的分辨成功概率却增加,显然经典准则发生误判。经典准则与实际分辨成功概率的差值即为误判率,误判率如图7所示,在相同的弱信号信噪比SNR2条件下,当强信号功率提高时,经典准则的误判率增加。
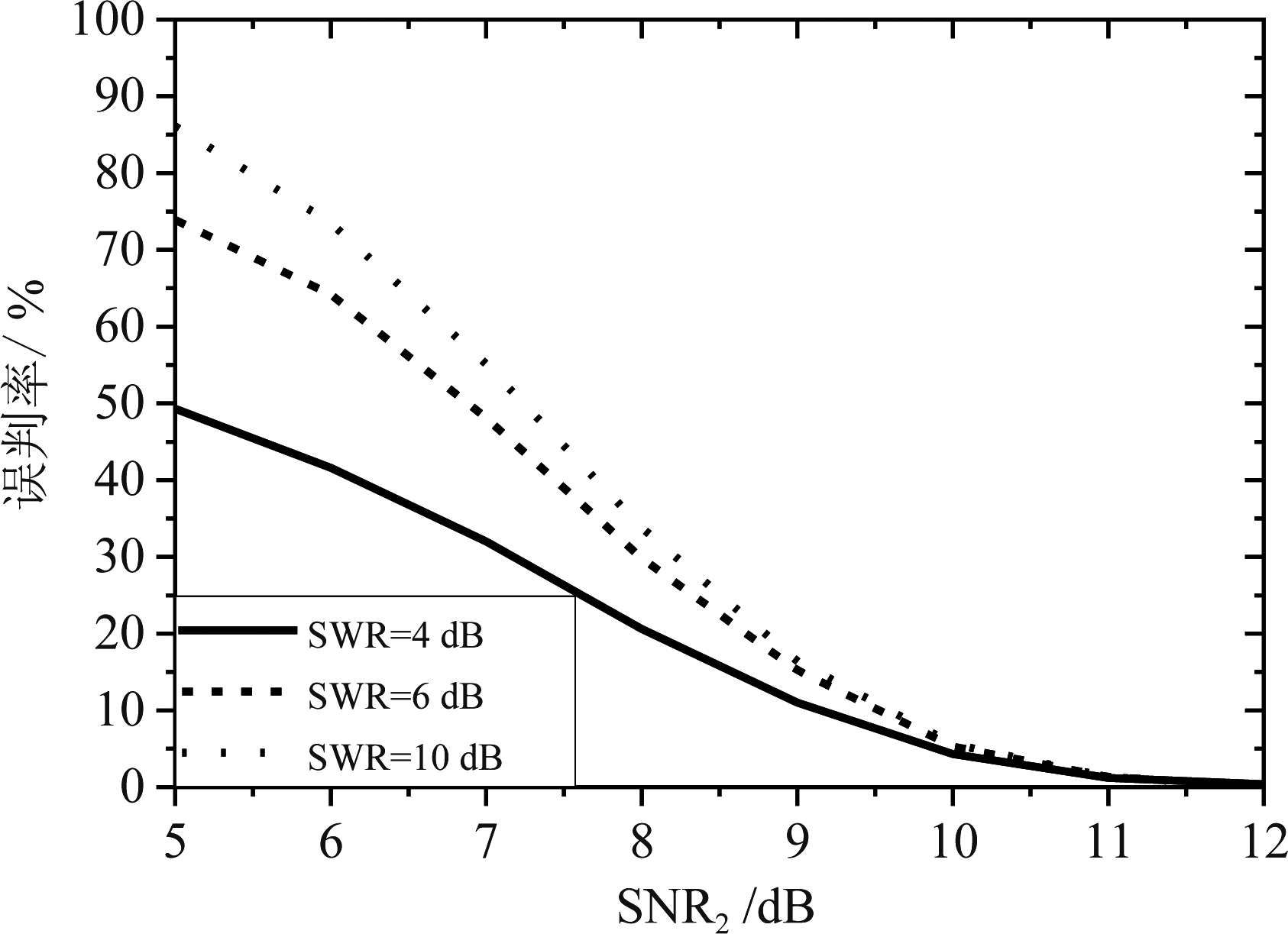
图7 经典准则的误判率
Fig.7 Misjudgment rate of classical criterion
由图6、图7可知,当实际分辨成功概率小于50%时,经典准则的误判率高于30%,并随强信号功率的增加误判率增加,尤其当SWR=10 dB时,误判率高于50%。当SNR2=5 dB时,不同强弱信号比下经典准则的误判率均高于50%。这说明经典准则不适用于评价算法对不同功率入射信号的分辨性能,尤其当算法实际分辨成功率小于50%时,经典准则误判率较高。由图7可知,随着弱信号信噪比的变化,不同的强弱信号比下多条误判率曲线各不同,这进一步说明经典准则不适用于评价算法对不同功率入射信号的分辨性能。
5 DOA估计算法新的评价准则
复杂电磁环境中入射信号功率通常是不同的,由第4节的分析可知,采用经典评价准则评价DOA估计算法对不同功率入射信号的分辨率存在局限性。因此本文针对不同功率入射信号提出新的算法评价准则。
5.1 新的评价准则
对于两个相邻的入射信号θ1与θ2,其中θm=(θ1+θ2)/2。若满足
(22)
则认为算法可以成功分辨两个入射信号,其中
为算法的零谱估计。因此对于极值谱,若满足
(23)
则认为算法可以成功分辨两个入射信号,其中
为算法的极值谱估计。
实验3 此实验条件设置与实验2相同,由新的评价准则得到的分辨成功概率(简称新准则)与实际分辨成功概率(简称实际)如图8所示。由图8可知,随着弱信号信噪比的增加,新准则分辨成功概率与实际分辨成功概率均增加。在相同的弱信号SNR2条件下,强信号功率增加时,实际分辨成功概率与新准则分辨成功概率均有所减少。
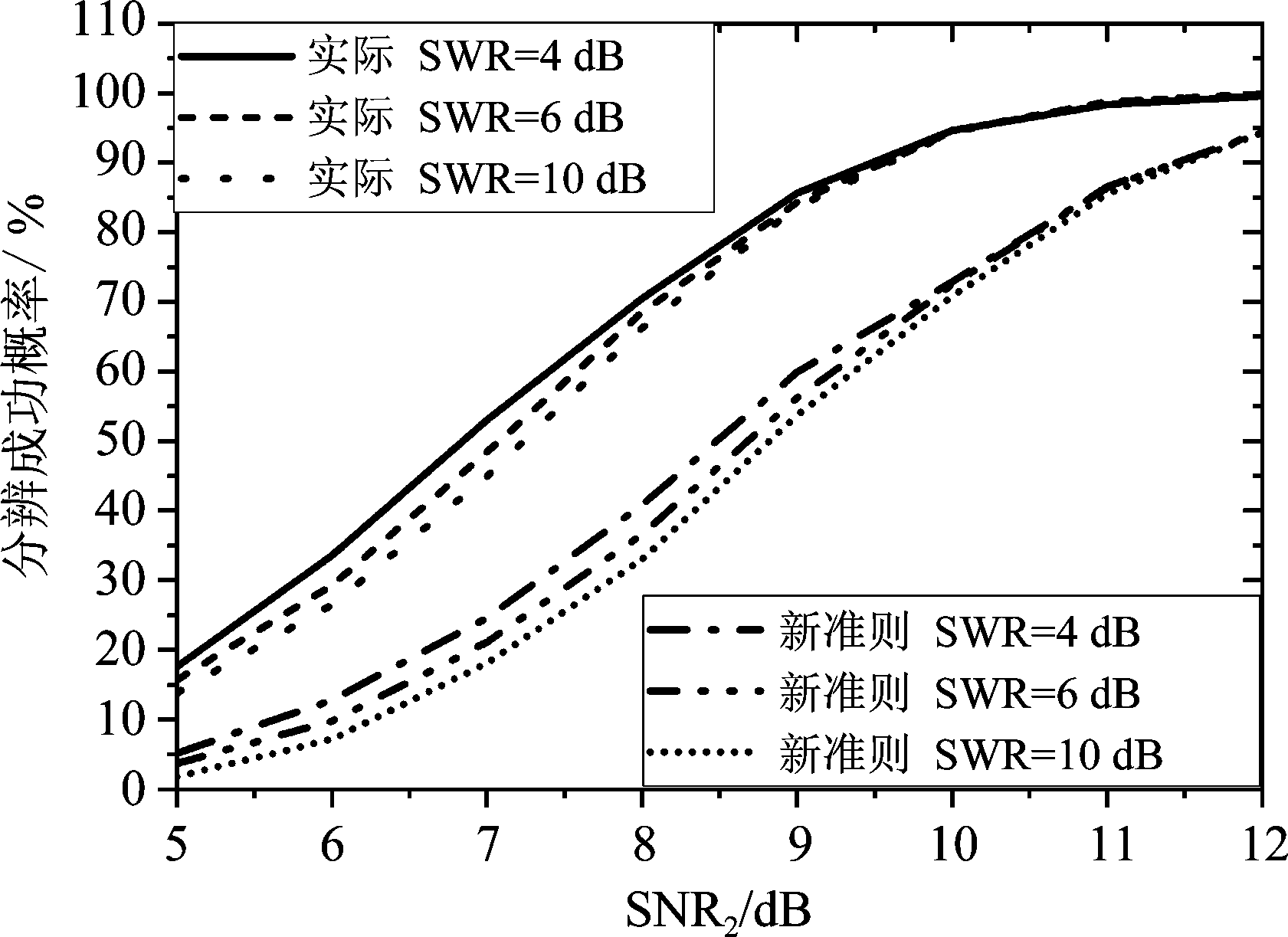
图8 1000次蒙特卡洛实验中新准则与实际分辨成功概率
Fig.8 The actual probability of success and that based on the new criterion in 1000 Monte Carlo experiments
总体而言在不同的弱信号信噪比SNR2条件下,新准则分辨成功概率小于实际分辨成功概率。这说明新准则较苛刻,即实际上MUSIC算法已经成功分辨了两入射信号,而依据新准则依然判断MUSIC算法无法分辨两入射信号。在此定义实际分辨成功概率与新准则分辨成功概率的差值为漏判率,则新准则的漏判率如图9所示。
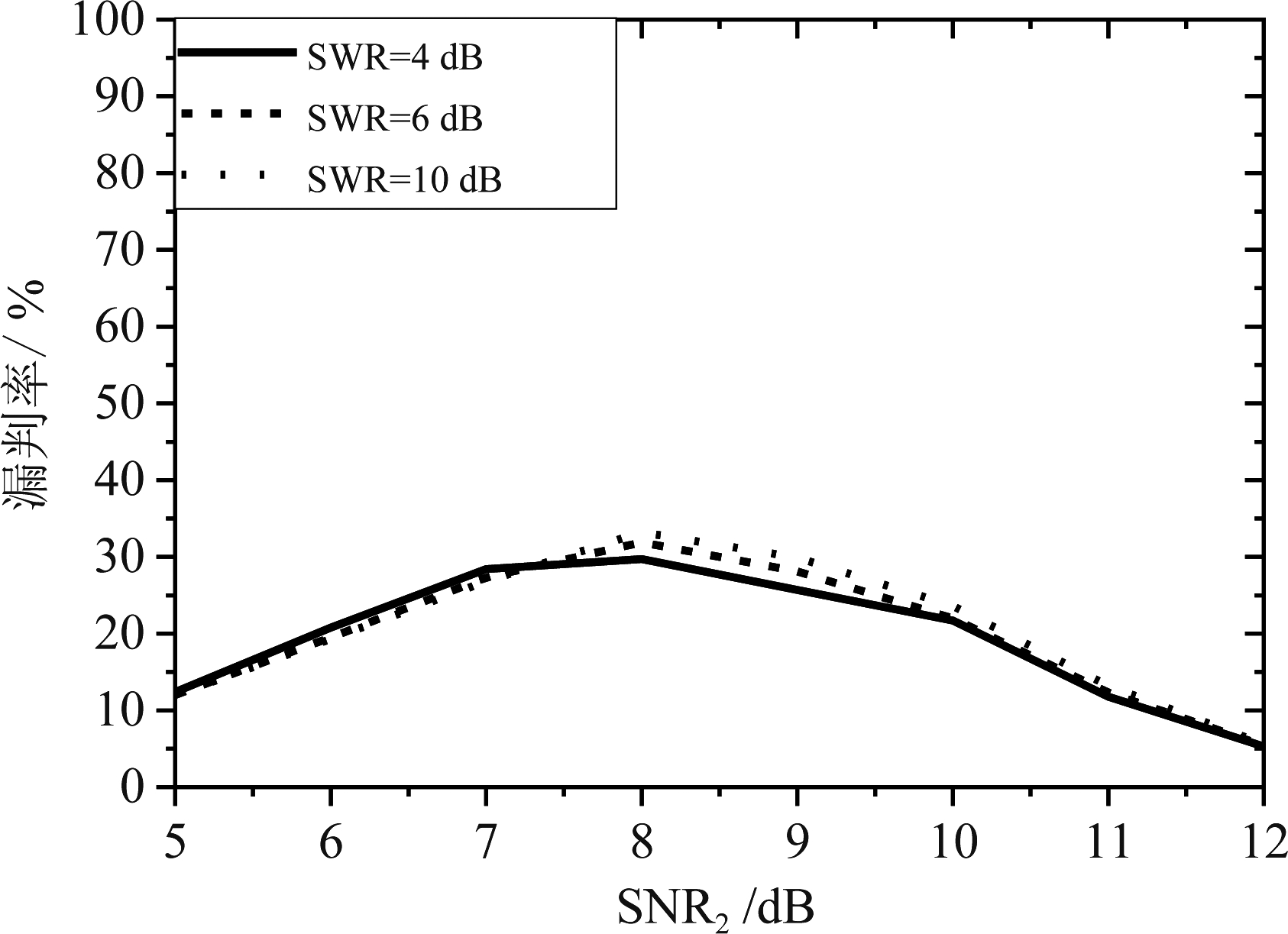
图9 新准则的漏判率
Fig.9 Misjudgment rate of new criterion
由图9可知,不同的强弱信号比下,新准则的漏判率基本一致,这说明新准则对不同功率的入射信号鲁棒性较强。不同弱信号信噪比SNR2条件下,新准则的漏判率基本都在30%以下。对比图9与图7可知,新准则与经典准则相比,新准则判定结果具有较高的可信性。当算法实际分辨成功率小于40%时,对不同功率入射信号新准则漏判率小于25%,而经典准则对SWR=10 dB不同功率入射信号,误判率高于65%。同时本文所提出的新评价准则对不同功率入射信号的漏判率基本一致,具有较好的鲁棒性。因此本文所提的新准则与经典准则相比,更适用于评价算法对不同功率入射信号的分辨性能。
为了评价经典准则与新准则的适用性,下面将进一步对比分析经典准则与新准则的性能。为此需定义几个新的参量以更精细的区分不同准则对两入射信号的分辨性能。此处定义判断准确概率ps为:ps=ccc/cm+cff/cm,其中ccc为根据判定准则与空间谱的谱峰均判断两入射信号分辨成功的次数,cff为通过判定准则与空间谱的谱峰均判断两入射信号未分辨成功的次数,cm为蒙特卡洛实验的总次数;定义虚警概率pcf为:pcf=ccf/cm,其中ccf为通过判定准则判断两入射信号分辨成功,但根据空间谱的谱峰判断两入射信号未分辨成功。定义漏警概率pfc为:pfc=cfc/cm,其中cfc为通过判定准则判断两入射信号未分辨成功,但根据空间谱的谱峰判断两入射信号分辨成功。则由实验2 和实验3可得经典准则与新准则的虚警概率如图10所示,漏警概率如图11所示,判断准确概率如图12所示。
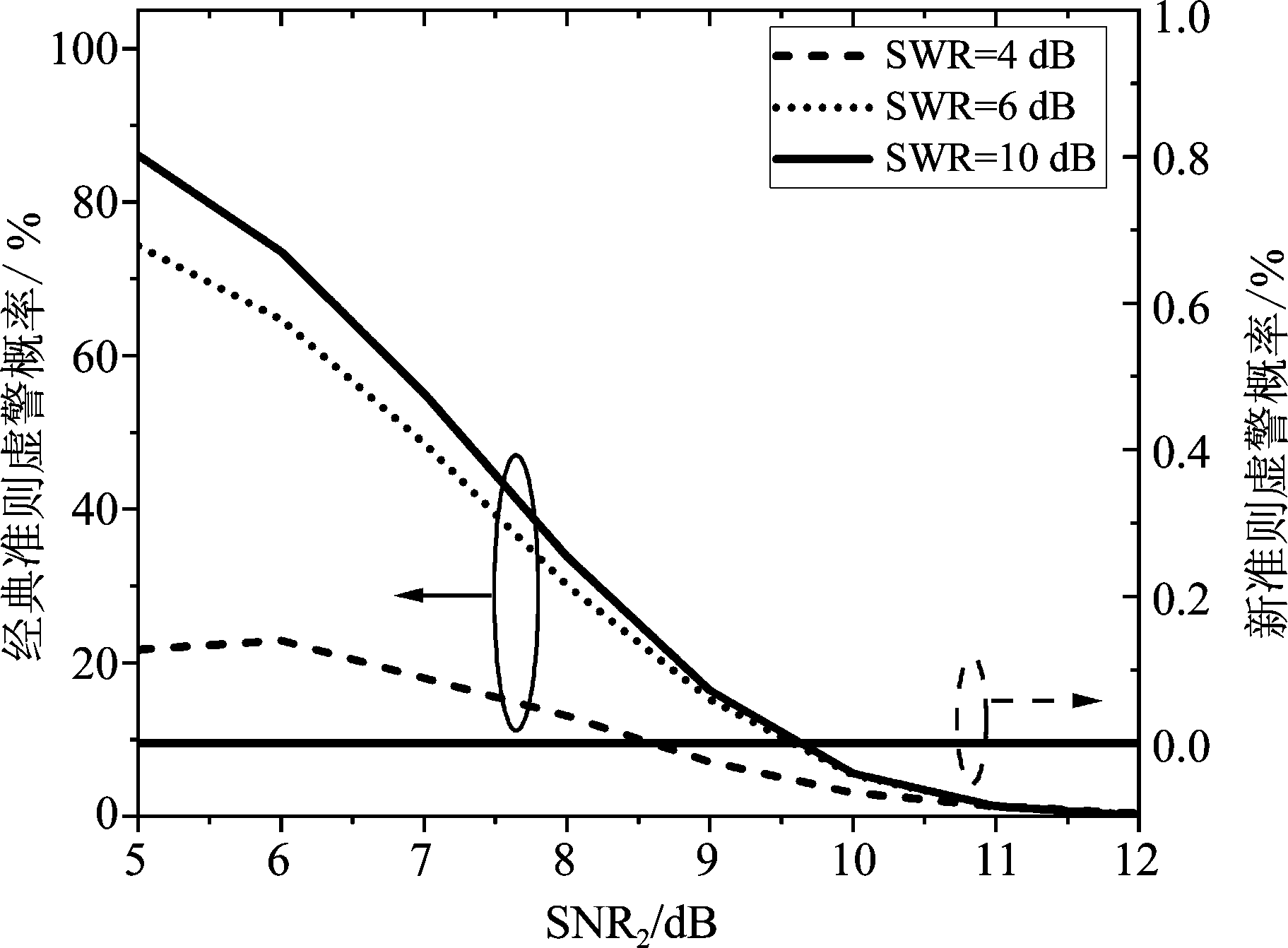
图10 经典准则与新准则的虚警概率
Fig.10 The false alarm probability of classical criterion and new criterion
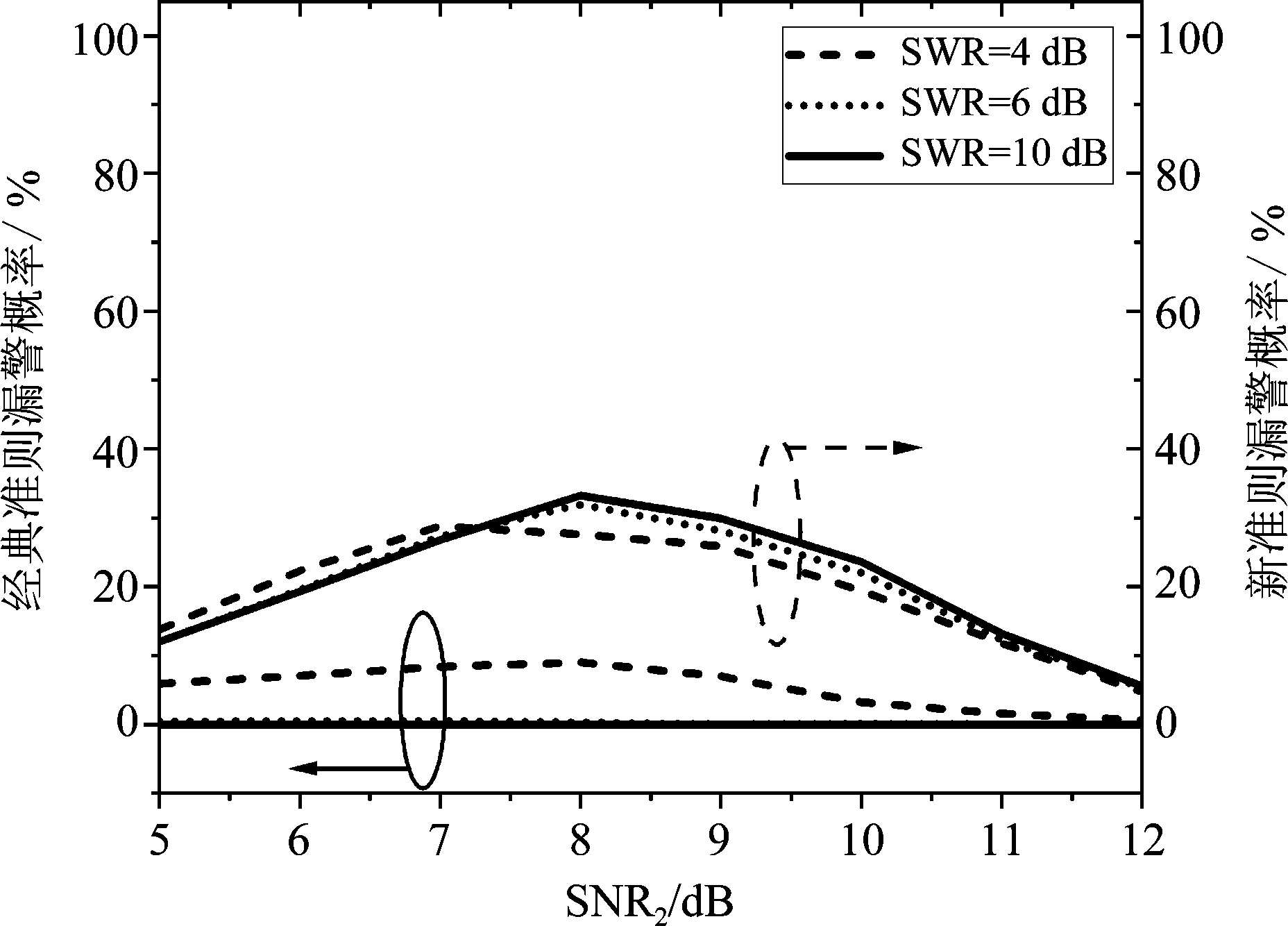
图11 经典准则与新准则的漏警概率
Fig.11 The missed alarm probability of classical criterion and new criterion
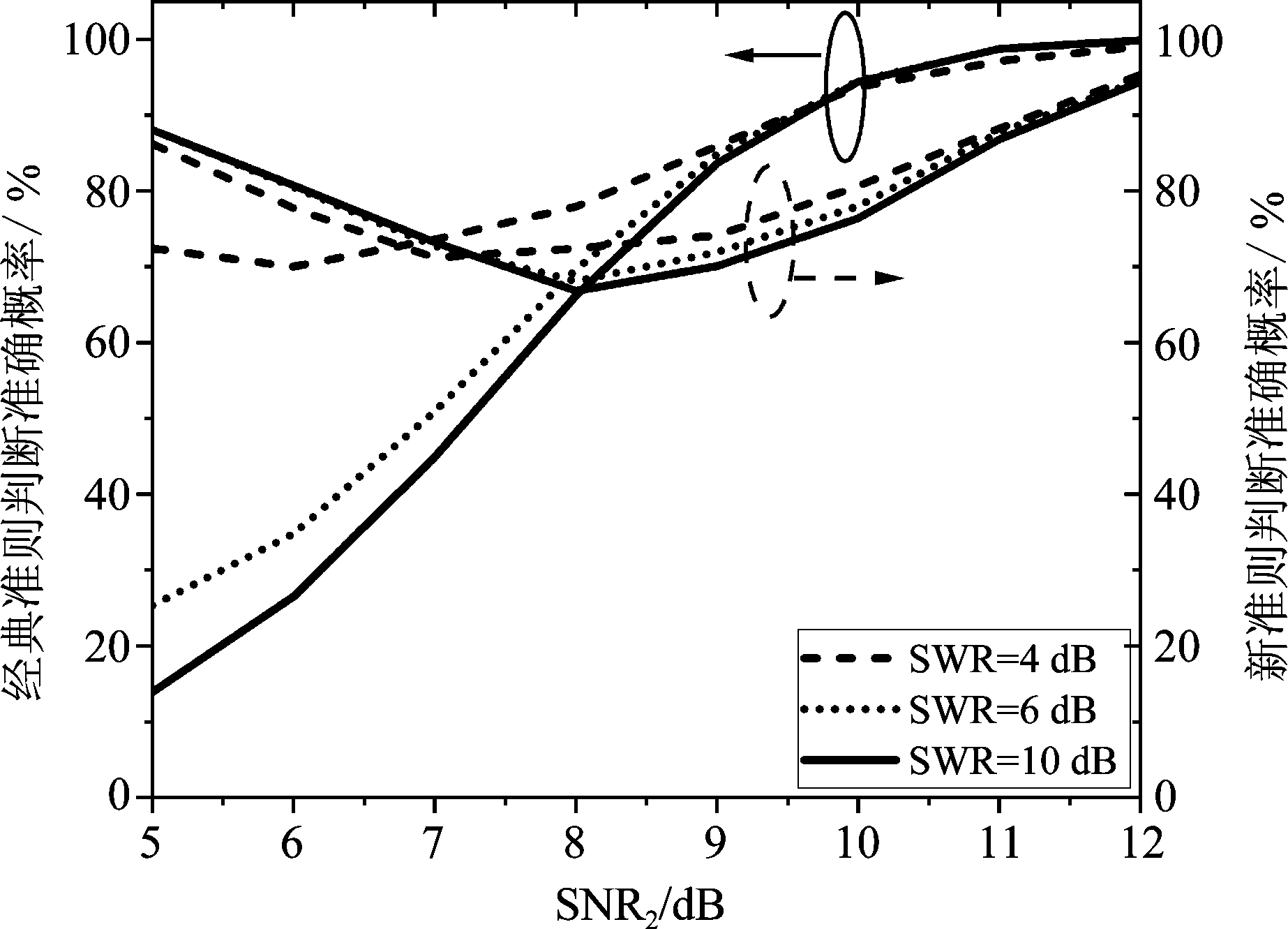
图12 经典准则与新准则的判断准确概率
Fig.12 The accurate probability of classical criterion and new criterion
由图10可知,经典准则在不同强弱信号比下的虚警概率均高于新准则。当强弱信号比SWR=10 dB时,相对于SWR=4 dB时来说,经典准则的虚警概率有明显的升高,尤其当SNR2=5 dB时,经典准则的虚警概率升高了65%。这说明针对于强弱信号比较大的两入射信号,经典准则存在局限性,新准则很好的改善了经典准则的虚警概率。由图11可知,新准则的漏警概率高于经典准则,当SNR2=8 dB时,新准则的漏警概率为33%。不同强弱信号比下新准则的漏警概率均低于33%,而不同强弱信号比下经典准则的漏警概率均低于10%。由图12可知,当SNR2<8 dB时,新准则具有较好的判断准确概率,尤其当SNR2=5 dB、SWR=10 dB时,新准则的判断准确概率较经典准则提高了74%。当SNR2>8 dB时,经典准则具有较好的判断准确概率。对比分析图10与图11可得,当弱信号信噪比SNR2>9 dB时,经典准则的漏判概率与虚警概率均低于16%;当弱信号信噪比SNR2<7 dB时,新准则的虚警概率为0,漏判率低于29%,而经典准则的虚警概率高于55%;当弱信号信噪比SNR2为7 dB～9 dB之间时,经典准则的虚警概率为16%～55%高于新准则,新准则的漏警概率为29%～33%高于经典准则。因此可得,经典准则适用于弱信号信噪比SNR2高于9 dB的情况,新准则适用于信噪比SNR2低于5 dB的情况。当信噪比处于7 dB～9 dB之间时,两种准则各有优缺点,但新准则的漏警概率要低于经典准则的虚警概率,且新准则的鲁棒性较好。
6 结论
通过本文研究得到以下结论:
(1)复杂电磁环境中强信号功率会影响弱信号DOA估计的克拉美罗界。随着强信号功率的增加弱信号DOA估计的CRB不断恶化,即弱信号DOA估计的均方根误差增加,并随着强信号功率的进一步增加此影响最终趋于稳定。
(2)经典评价准则对评价DOA算法对不同功率入射信号的分辨性能具有局限性。经典评价准则对分辨功率差别大的入射信号误判率较高,尤其当弱信号信噪比低于5 dB时,其误判率大于50%,且不同的强弱信号比(SWR)下经典评价准则的误判率不一致。
(3)本文提出的新评价准则很好的改善了经典评价准则的虚警概率,当弱信号信噪比较低时更适于分辨不同功率的入射信号,尤其SNR2=5 dB、SWR=10 dB时新准则的判断准确概率较经典准则提高了74%,且新准则与经典准则相比的其鲁棒性较高。
本文的研究可为复杂电磁环境中评价不同DOA估计算法的分辨性能提供参考依据。
[1] CHEN X, SHU T, YU K B, et al.Joint adaptive beamforming techniques for distributed array radars in multiple mainlobe and sidelobe jammings[J].IEEE Antennas and Wireless Propagation Letters, 2020, 19(2): 248-252.
[2] 刘尚合,刘卫东.电磁兼容与电磁防护相关研究进展[J].高电压技术,2014,40(6):1605-1613.
LIU Shanghe, LIU Weidong.Progress of relevant research on electromagnetic compatibility and electromagnetic protection[J].High Voltage Engineering, 2014, 40(6): 1605-1613.(in Chinese)
[3] DAWOOD H S, HUSSEIN A H, GEMEAY E, et al.DOA/MoM-based ABF algorithm for SINR enhancement[J].IET Communications, 2019, 13(11): 1565-1572.
[4] SCHOENECKER S, WILLETT P, BAR-SHALOM Y.Resolution limits for tracking closely spaced targets[J].IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(6): 2900-2910.
[5] MCCLOUD M L, SCHARF L.A new subspace identification algorithm for high-resolution DOA estimation[J].IEEE Transactions on Antennas & Propagation, 2002, 50(10): 1382-1390.
[6] LEE J H, LEE C C.Analysis of the performance and sensitivity of an eigenspace-based interference canceler[J].IEEE Transactions on Antennas & Propagation, 2000, 48(5): 826-835.
[7] HAN Y, FANG Q, YAN F, et al.Joint DOA and polarization estimation for unequal power sources based on reconstructed noise subspace[J].Journal of Systems Engineering and Electronics, 2016, 27(3): 501-513.
[8] 方庆园,韩勇,金铭,等.基于噪声子空间特征值重构的DOA估计算法[J].电子与信息学报,2014,36(12):2876-2881.
FANG Qingyuan, HAN Yong, JIN Ming, et al.DOA estimation based on eigenvalue reconstruction of noise subspace[J].Journal of Electronics & Information Technology, 2014,36(12): 2876-2881.(in Chinese)
[9] 徐亮,曾操,廖桂生,等.基于特征波束形成的强弱信号波达方向与信源数估计方法[J].电子与信息学报,2011,33(2):321-325.
XU Liang, ZENG Cao, LIAO Guisheng, et al.DOA and source number estimation method for strong and weak signals based on eigen beamforming[J].Journal of Electronics & Information Technology, 2011, 33(2): 321-325.(in Chinese)
[10] GAO Y, XU J, JIA X.Joint number and DOA estimation via the eigen-beam mCapon method for closely spaced sources[J].Science China Information Sciences, 2015, 58(12): 1-3.
[11] CHEN L, QI W, LIU P, et al.Low-complexity joint 2-D DOA and TOA estimation for multipath OFDM signals[J].IEEE Signal Processing Letters, 2019, 26(11): 1583-1587.
[12] ZHANG X, CHEN W, ZHENG W, et al.Localization of near-field sources: A reduced-dimension MUSIC algorithm[J].IEEE Communications Letters, 2018, 22(7): 1422-1425.
[13] CLAUDIOE D, PARISI R, JACOVITTI G.Space time MUSIC: Consistent signal subspace estimation for wideband sensor arrays[J].IEEE Transactions on Signal Processing, 2018, 66(10): 2685-2699.
[14] KAVEH M, BARABELL A.The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise[J].IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(2): 331-341.
[15] 程正东,罗景青,樊祥,等.信号源功率不一致对MUSIC算法分辨性能的影响[J].电子与信息学报,2008,30(5):1088-1091.
CHENG Zhengdong, LUO Jingqing, FAN Xiang, et al.Effect of power difference of two signal sources on resolving performance of MUSIC algorithm[J].Journal of Electronics & Information Technology, 2008, 30(5): 1088-1091.(in Chinese)
[16] 樊祥,程正东,马东辉,等.两信号源的相关性对MUSIC算法分辨性能的影响[J].电子学报,2008,36(12):2315-2318.
FAN Xiang, CHENG Zhengdong, MA Donghui, et al.Effect of correlation of two signal sources on resolution performance of MUSIC algorithm[J].Acta Electronica Sinica, 2008, 36(12): 2315-2318.(in Chinese)
[17] ZHANG Q T.Probability of resolution of the MUSIC algorithm[J].IEEE Transactions on Signal Processing, 1995, 43(4): 978-987.
[18] 刘德树.空间谱估计及应用[M].合肥:中国科学技术,1997:205-206.
LIU Deshu.Spatial spectrum estimation and its applications[M].Hefei: China Science and Technology Press, 1997: 205-206.(in Chinese)
