1 引言
机载雷达与其他类型雷达相比,具有可视范围广、体积小等特点,因此得到了广泛的应用[1]。机载雷达一般工作在空中,接收的地杂波信号种类多、强度大,造成有用目标信息难以提取,严重影响了动目标的检测性能,因此需要对杂波进行有效抑制[2]。空时自适应处理(Space Time Adaptive Processing, STAP)将接收信号进行空间域和时间域处理,实现了与复杂环境的有效匹配,且补偿了雷达系统误差,可以有效抑制杂波[3]。然而,空时自适应处理技术在实际使用中有计算量太大、样本数量和质量要求高、非理想因素广泛存在等问题,导致其实现受到诸多限制[4]。
压缩感知理论的提出为STAP技术的实现提供了新的思路和方法。研究者发现一般雷达信号在特定条件下具有稀疏性,故将压缩感知理论与STAP方法相结合,提出了基于稀疏恢复的空时自适应处理方法(Sparse Recovery Space Time Adaptive Processing,SR-STAP)[5]。该方法降低了STAP对样本数量的要求,可在有少量样本的情况下恢复出比较准确的杂波协方差矩阵。因此,SR-STAP算法引起了国内外学者的广泛关注,提出了多种不同应用场合的具体算法[6-11]。例如,孙珂等人将稀疏表示与直接数据域方法相结合,提出了基于凸优化的杂波抑制方法[12]。段克清等人通过将稀疏性与STAP算法结合,提出了提取近距杂波的新方法,有效消除了非平稳杂波[13]。高志奇等人提出了机载雷达稳健STAP算法,消除了非均匀杂波中离群点使协方差矩阵估计出现的偏差[14]。
虽然SR-STAP算法提升了机载雷达抑制杂波的性能,但此类方法也存在一定的不足。比较突出的问题是,雷达信号稀疏恢复过程需要使用冗余基向量构成的字典,当字典的划分不准确时会带来格子对不准问题[15],称为离网效应[16-17]。所谓离网效应是指当杂波点没有准确匹配到离散化空时平面网格点上时,引起稀疏恢复的结果不准确的现象。当出现离网效应时,SR-STAP算法的性能会受到严重影响[18]。有研究指出可增加网格构建的密集度来增大杂波点准确附着的概率,但网格点太紧凑会降低稀疏恢复性能[19],所以目前网格校正方法主要从知识辅助[20]、贝叶斯学习[21-22]、正交匹配追踪[23]等方面入手。其中,袁华东等人通过将稀疏贝叶斯学习与SBL自适应处理相结合,通过构造小规模的互补字典来校正离网字典[22]。文献[23]中提出的正交匹配追踪法通过参数搜索找到与杂波子空间配合度最高的原子,但没有考虑运算量问题,且算法性能还有待提升。文献[24]通过构建降维字典减少了运算量,并通过构建局部字典提高了搜索杂波子空间的精准度[24],但局部搜索范围划分不够恰当,运算量没有得到大的改善。
本文提出了离网误差迭代自校正的STAP算法(STAP Algorithm Based on Iterative Self-calibrated method for Off-Grid,IT-LESCA-STAP)以实现在低运算量的基础上校正离网误差。贝叶斯方法近几年被广泛应用于目标搜索问题中,基于贝叶斯搜索算法与其他搜索方法相比有很强的实用性和有效性[25-27]。因此本方法将贝叶斯搜索算法应用于局部搜索范围划分,在解决离网问题的前提下,减少了运算量,获得了正侧视阵情况下的高分辨率杂波空时谱,有效提高了杂波抑制性能。本文分为5节,第2节为正侧视信号模型的介绍,第3节为所提算法的原理分析,第4节为相关算法的仿真分析,第5节对本文内容进行总结。
2 信号模型
本文以机载正侧视均匀线性阵列雷达为研究对象,不考虑距离模糊的影响。机载雷达阵列的工作模型见图1所示。其中,飞机平台高度和速度分别表示为Ha和Va,方位角、空间锥角和俯仰角分别由θ、φ、ψ来表示,载机沿x轴正方向飞行。雷达阵列在一个相干处理间隔内雷达发射M个脉冲,阵元数为N,阵元间隔为d,发射信号波长为λ。
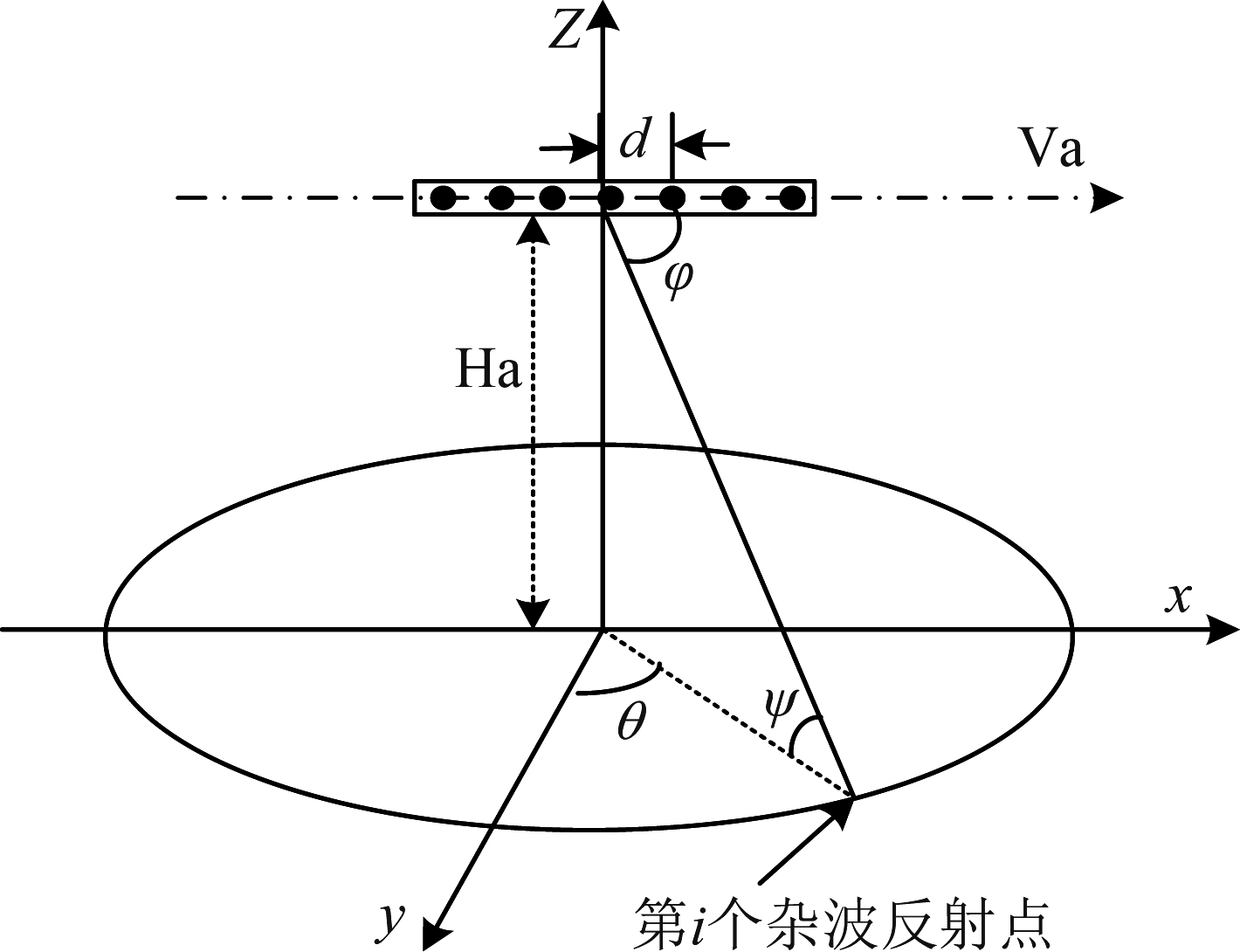
图1 机载雷达模型
Fig.1 Airborne radar model
阵列接收到的某个距离单元的杂波信号可建模为:
(1)
G(fd,i, fs,i)=Gt(fd,i)⊗Gs(fs,i)
(2)
其中,X为雷达接收样本快拍,NC指雷达接收的热噪声,εi代表反射点的强度,G代表地面反射点的空时导向矢量,Gt(fd,i)和Gs(fs,i)分别指时间导向矢量和空间导向矢量,可表示为:
Gt(fd,i)=[1,exp(j 2πfd,i),...,exp(j 2π(M-1)fd,i)]T
(3)
Gs(fs,i)=[1,exp(j 2πfs,i),...,exp(j 2π(N-1)fs,i)]T
(4)
其中,(·)T表示转置运算,fs,i为第i个杂波反射点的空间频率,fd,i为第i个杂波反射点的多普勒频率,即:
(5)
(6)
其中,φi指的是第i个杂波反射点的空间锥角,fr指脉冲重复频率。在杂波服从高斯分布的环境下,最优STAP滤波器权矢量W为[28]:
W=μR-1Gt
(7)
其中,μ为常数,Gt为目标导向矢量,R为所估计的自相关协方差矩阵,计算公式如下:
(8)
其中,Xl表示第l个距离单元的快拍数据,(·)H表示共轭转置运算。
在SR-STAP算法中,空时导向字典的构造是关键,一般的空时导向字典是对角度-多普勒平面进行离散化得到,整个归一化的空间平面沿空间频率轴和多普勒轴均匀地离散为Ts×Tr个网格点,其中Ts=ηsN, Tr=ηrM,并且ηs、ηr>1,离散化的空间频率间隔和多普勒频率间隔可以分别表示为Δfs=1/Ts、Δfd=1/Tr, 离散后形成的网格点对应于空时导向字典中的导向矢量。假设所有的杂波点都恰好位于网格点上,则可以将式(1)中的快拍表示为:
X=Ψα+Nc
(9)
其中,Ψ指的是稀疏恢复字典,维度为NM×TsTr;α为稀疏恢复系数向量。分别可用公式表示为:
Ψ=[G(fd,1, fs,1),G(fd,2, fs,2),...,G(fd,Tr, fs,Ts)]
(10)
α=[α1,α2,...,αTrTs]T
(11)
3 离网误差迭代自校正算法
在SR-STAP方法中,可使用尽可能少的样本来估计杂波协方差矩阵。然而,均匀离散化空时平面获得的固定字典极易带来离网误差,导致估计得到的协方差矩阵并不准确。为了克服此问题,本部分提出了利用全局选优和局域搜索的方法进行最优原子的筛选。
3.1 全局选优
首先,设Qc表示杂波子空间上的正交投影矩阵,设Qn表示噪声子空间上与杂波子空间正交的正交投影矩阵。按照SR-STAP算法,构造传统字典Ψ,再对Ψ中每个原子按式(12)进行计算。
(12)
然后,将结果降序排列,取出前k个coup值对应的导向矢量构造全局字典ΨW=[g1,g2,…,gk],其中W指包含全局字典原子序号的集合。该步骤实际是将位于杂波脊上的杂波点对应的导向矢量挑选出来,可保证取出的原子位于网格点上的可能性较大。杂波脊上的部分空时导向矢量分布情况如图2所示。
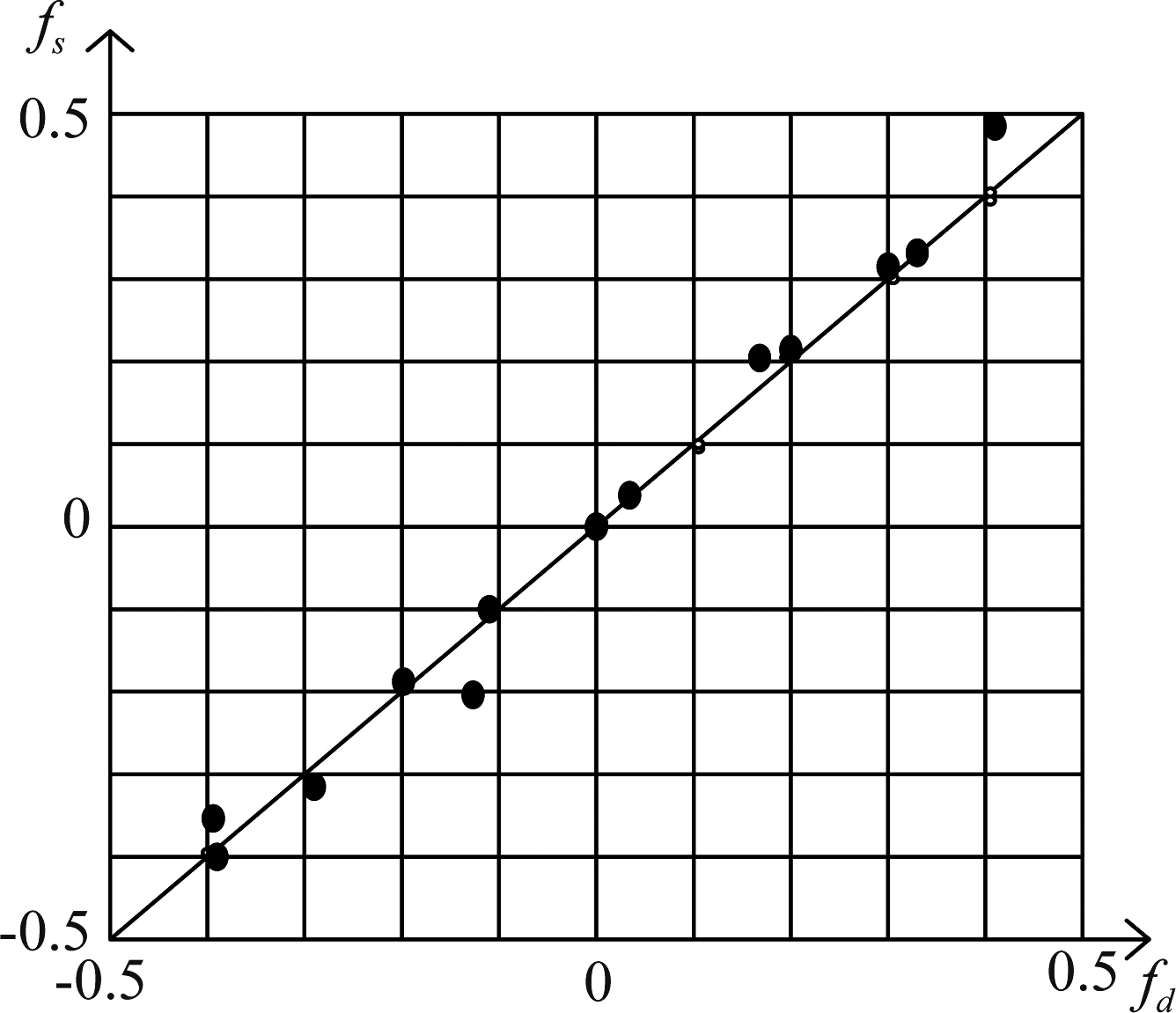
图2 杂波脊表示
Fig.2 Clutter ridge representation
一般离网状态下的杂波脊并不能完全与网格点相交,因此ΨW中的原子并不能保证全部落于空时平面网格点上,故需对ΨW中的原子进一步筛选。
首先,构建空集合W0、ΨW1,分别用于存放所需全局原子对应编号和最优局部原子。将全局字典ΨW中的原子取出按式(13)和(14)进行迭代计算(其中L指的是全局字典对应的有限快拍数);然后,将运算结果降序排列,得到计算结果最大的原子,记其序号为![]()
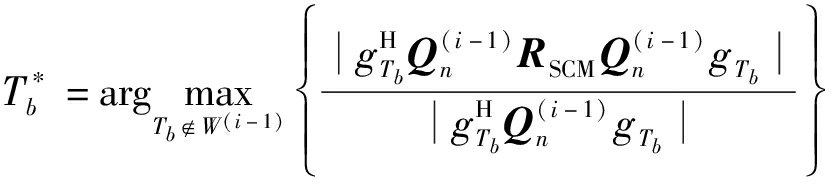
i∈{1,2,…,k}
(13)
(14)
找到最大的原子后,对该原子进行局域搜索操作。然后将该原子从ΨW中移除,对应序号放于W0中。再对ΨW按上述过程迭代运算,找到下一个最大原子。
3.2 局域搜索
通过全局字典ΨW的构建以及迭代更新,杂波子空间可以较为精确地进行确定。然而网格失配的问题仍然存在,需要进一步更新字典以消除因网格失配造成的稀疏恢复误差。全局字典ΨW中相关导向矢量对应的全局原子不一定是真实杂波点,在其周围杂波点附着的可能性也比较大,故在第i次迭代中,选择一个最大原子,以它为中心,以离散化的空间频率间隔ΔfS和多普勒频率间隔Δfd为尺度,构建网格点数为Tl,s×Tl,r的局部字典ΨL,如图3所示。其中大圆点代表选定的全局原子,小网格代表局部字典的划分。局部字典的规范化空间频率和多普勒频率的数目分别用Tl,s和Tl,r表示,局部字典ΨL可以通过式(15)表示。对ΨL中的原子按式(16)运算。
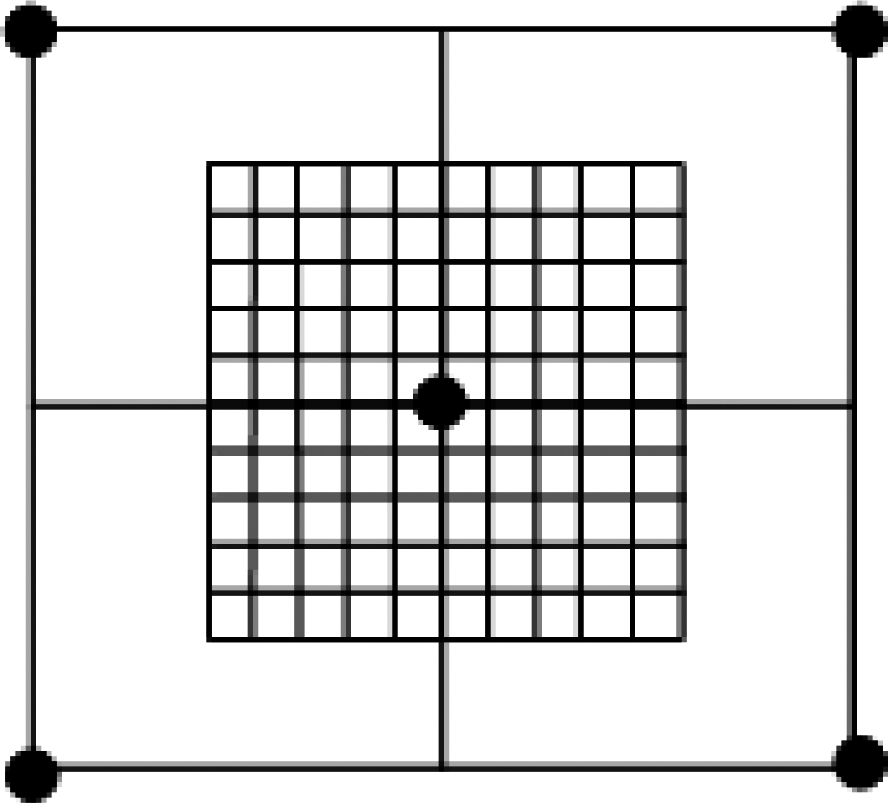
图3 局部字典构建
Fig.3 Local dictionary construction
ΨL=[ν1,ν2,…,νTl,sTl,r]
(15)
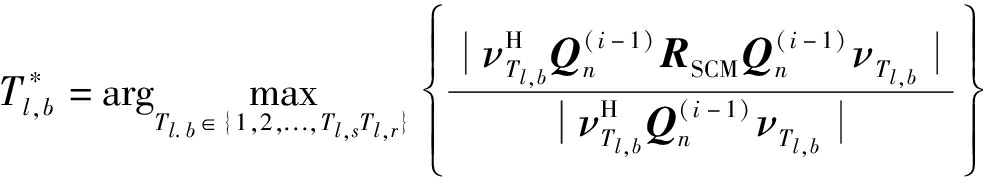
(16)
其中![]() 指计算结果最大的局部原子序号。对第i个局部字典完成搜索后,
指计算结果最大的局部原子序号。对第i个局部字典完成搜索后,![]() 对应局部原子放于ΨW1中。杂波子空间上的正交投影矩阵更新为
对应局部原子放于ΨW1中。杂波子空间上的正交投影矩阵更新为![]() 这里[·]†指的是广义逆算子。此外,噪声子空间上的正交投影矩阵被更新为
这里[·]†指的是广义逆算子。此外,噪声子空间上的正交投影矩阵被更新为![]()
值得注意的是,在进行局部迭代时,为了减少运算量,迭代原子的选取步骤与全局原子的选取参考了贝叶斯后验概率最大的思想,将待搜索的局部字典中的原子看作随机变量,对这些原子进行初步筛选,得到真实杂波点最有可能出现的区域,然后在该区域进行进一步搜索,就可以得到后验概率最大的杂波位置。故先假定局部字典在顶点处与杂波点的匹配度较高,对顶点位置进行相关操作,再将结果进行比较。在这里假设点b处的原子运算值最大进行图形演示,如图4所示。
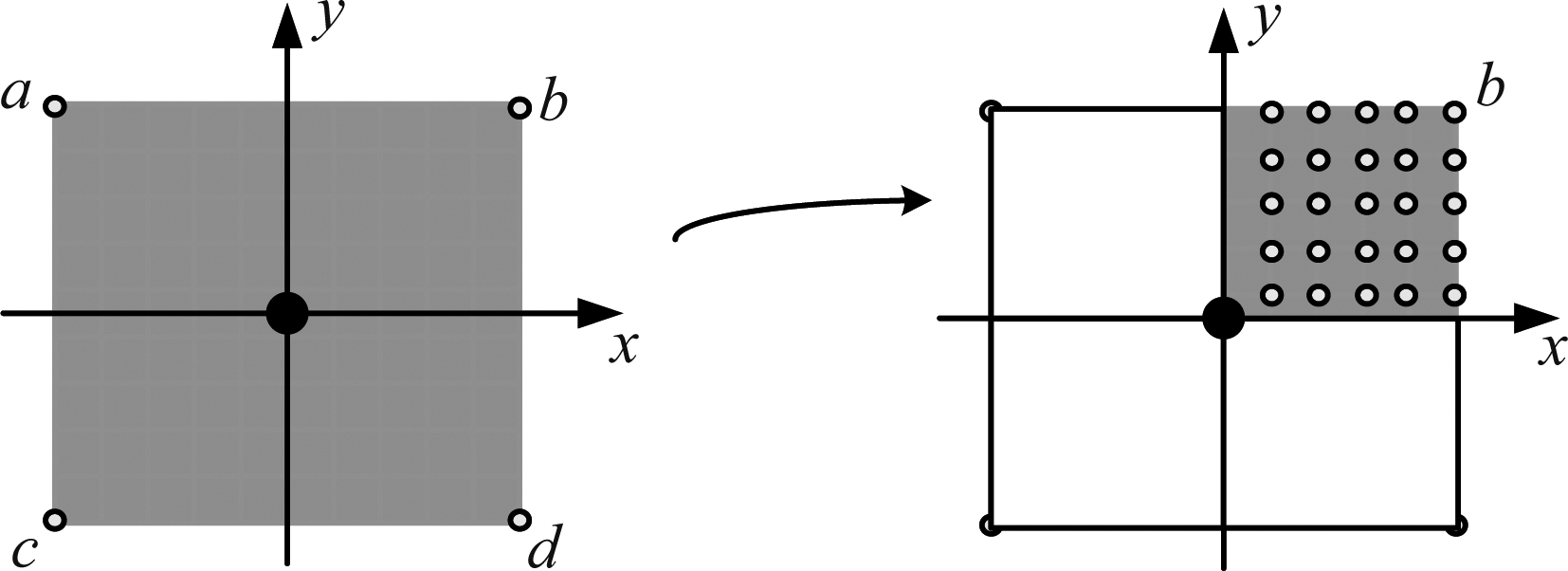
图4 局部原子搜索
Fig.4 Local atom search
图4中以选定的全局原子为中心将局部字典划分为四个象限,即先取Tl,b={a,b,c,d}(以构建的局部字典维度10×10为例)进行迭代,然后对所得运算结果进行比较,得到对应最大值的顶点原子;接着再对该顶点所在象限的原子按照式(16)进行迭代运算,得到结果最大的局部原子,以此找到真正杂波点对应位置。在保证恢复杂波子空间足够准确的情况下,减少了计算复杂度。
第i次迭代结束后,当满足式(17)和(18)时(其中tr(·)指求迹运算,η为预先设定的阈值),迭代终止。综合以上分析,得到比较准确的网格失配STAP权重向量如式(19)所示。所提算法流程见表1所示。
表1 算法流程
Tab.1 Algorithm flow

(17)
E(i)<η
(18)
(19)
3.3 计算复杂度分析
表2为文献[24]所提RD-LSCSE-STAP算法和本文所提IT-LESCA-STAP的算法单个样本的平均计算复杂度对比,分别统计了从全局搜索到局部搜索一次迭代复加和复乘次数。从表中可以看出,与RD-LSCSE-STAP算法相对比,IT-LESCA-STAP算法由于借助了贝叶斯后验概率思想,优先找到了与杂波点相邻的网格点,减少了原子搜索范围。在一次迭代中,复加法数可比RD-LSCSE-STAP算法少(0.75NM-4)(NM-1)(3NM+2)次,复乘法数可比RD-LSCSE-STAP算法少[3(NM)2+2NM+1](0.75NM-4)次,且保证了算法的精确度。
表2 单个样本平均复杂度对比
Tab.2 Comparison of average complexity of single sample
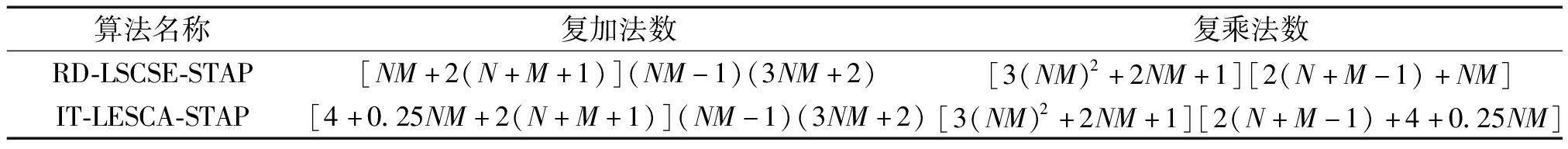
算法名称复加法数复乘法数RD-LSCSE-STAP[NM+2(N+M+1)](NM-1)(3NM+2)[3(NM)2+2NM+1][2(N+M-1)+NM]IT-LESCA-STAP[4+0.25NM+2(N+M+1)](NM-1)(3NM+2)[3(NM)2+2NM+1][2(N+M-1)+4+0.25NM]
4 仿真分析
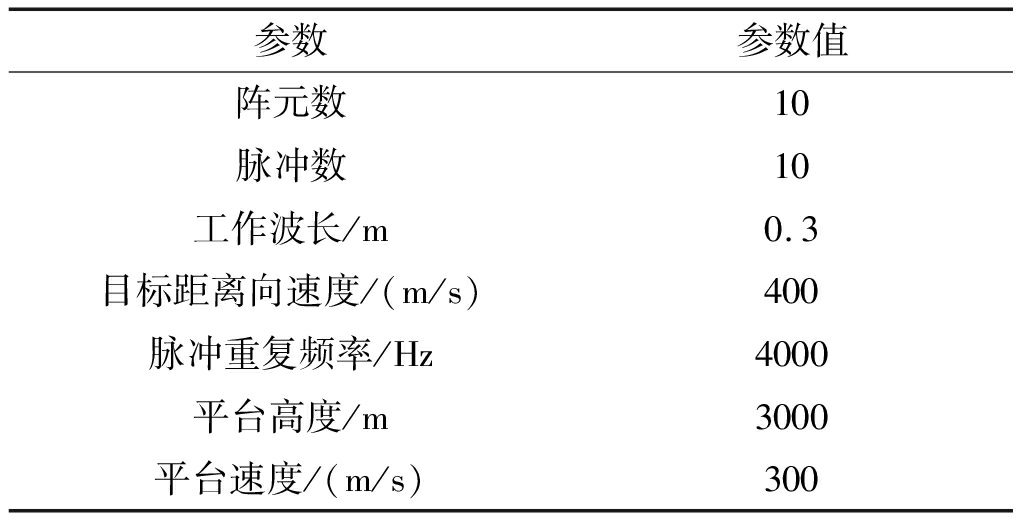
本节通过仿真分析IT-LESCA-STAP算法的性能,并与SR-STAP算法、文献[24]所提RD-LSCSE-STAP算法进行对比验证。从文献[24]可知,局部字典的构建同时考虑SINR损失和平均计算时间,其空间频率或多普勒频率的数目设置为10~15比较合理。且文献[24]中RD-LSCSE-STAP算法局部字典构建维度为10×10。故为了更准确的对比,本文选取局部字典维度与RD-LSCSE-STAP算法相同。雷达系统参数见表3所示。
表3 雷达系统参数
Tab.3 Radar system parameters
参数参数值阵元数10脉冲数10工作波长/m0.3目标距离向速度/(m/s)400脉冲重复频率/Hz4000平台高度/m3000平台速度/(m/s)300
第一个实验分析了SR-STAP算法、RD-LSCSE-STAP算法、IT-LESCA-STAP算法的杂波功率谱。其中三种算法的传统STAP字典大小设置ηs=4,ηr=4;RD-LSCSE-STAP算法、IT-LESCA-STAP算法全局STAP字典设置为k=76,局部STAP字典大小设置为Tl,s=10,Tl,r=10;迭代终止阈值η=10-15。实验中三种算法都采用了20个快拍进行实验,实验结果见图5所示。从图5(a)中可看出杂波脊在离网状态下展宽;图5(b)中RD-LSCSE-STAP算法和图5(c)中IT-LESCA-STAP算法功率谱上的杂波点几乎都分布在杂波脊上,杂波脊没有展宽现象,这是因为两种算法都通过全局搜索和局部搜索迭代找到了杂波真正对应的点,故稀疏恢复后得到的滤波权较精确,选取的网格点与杂波点配合度高。

图5 功率谱对比图
Fig.5 Power spectrum comparison diagram
第二个实验分析SR-STAP算法、RD-LSCSE-STAP算法和IT-LESCA-STAP算法的改善因子,实验结果见图6所示。可以看出,RD-LSCSE-STAP和IT-LESCA-STAP在旁瓣杂波区可以获得接近最优的性能,且图形平滑度较高,在两种情况下都优于SR-STAP。此外,在主瓣杂波区,所提IT-LESCA-STAP算法可以获得与RD-LSCSE-STAP算法相同的杂波抑制性能。比较而言,所提IT-LESCA-STAP算法减少了局部搜索范围,降低了运算量的同时可以达到与RD-LSCSE-STAP相同的杂波抑制性能。
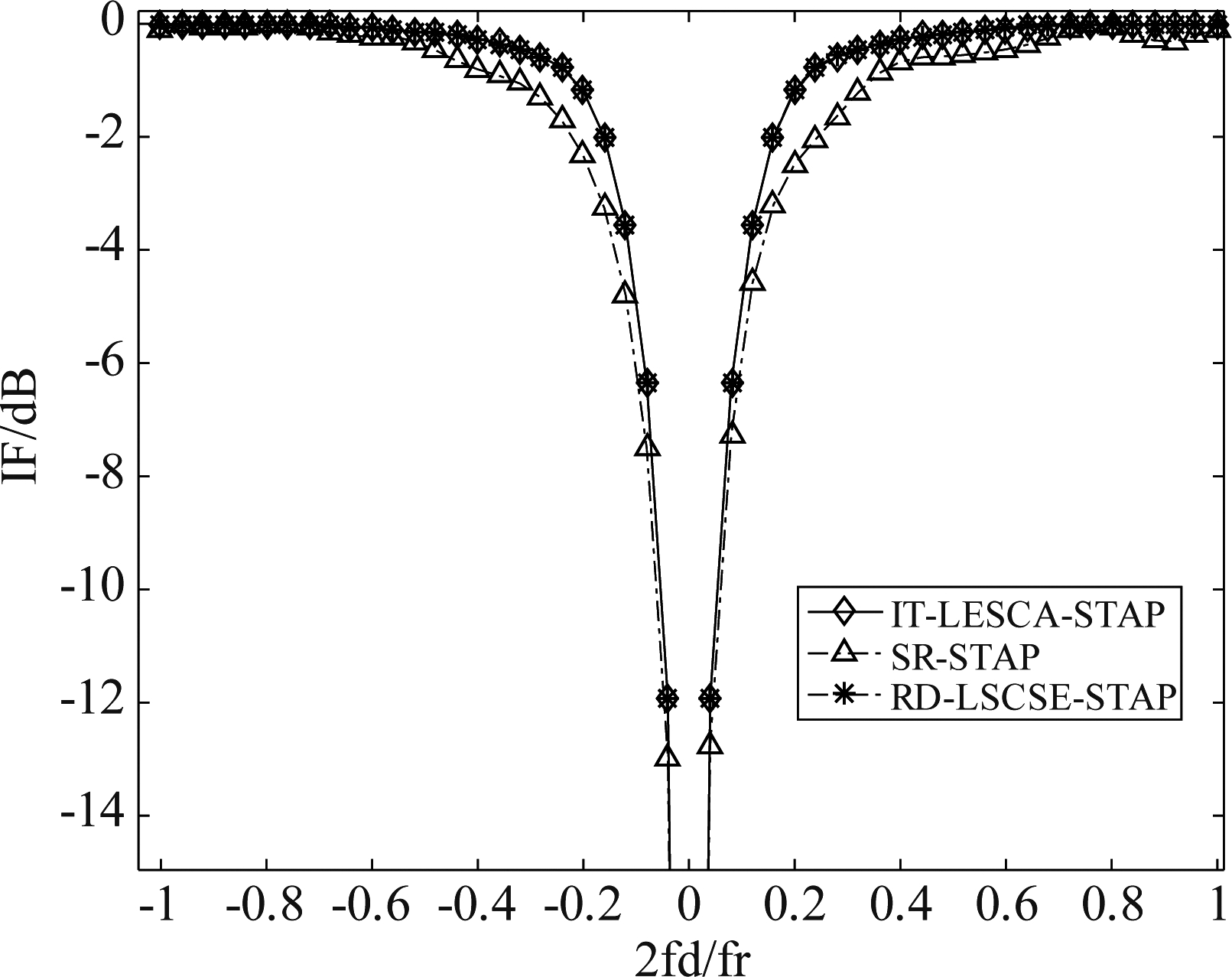
图6 IF性能对比图
Fig.6 IF performance comparison chart
第三个实验分别使用SR-STAP算法、RD-LSCSE-STAP算法和IT-LESCA-STAP算法对测试样本进行滤波,计算输出功率,实验结果见图7所示。可以看出,三种算法都可以有效地检测出位于第51号距离单元的目标。比较而言,RD-LSCSE-STAP算法和IT-LESCA-STAP算法的动目标检测性能优于SR-STAP算法。

图7 输出功率结果图
Fig.7 Output power result diagram
第四个实验对SR-STAP算法、RD-LSCSE-STAP算法和IT-LESCA-STAP算法进行150次蒙特卡罗仿真实验运行时间对比,其他所用参数与上述三个实验相同,所用计算机CPU系统为i5-4210M,64位操作系统,内存8 GB。实验结果见表4所示。从表中可看出,IT-LESCA-STAP算法通过选择适当的局部搜索范围,在进行150次蒙特卡罗实验的情况下,运行时间比RD-LSCSE-STAP算法减少44.65 s,可验证IT-LESCA-STAP算法有效降低了运算量,实时性较好。
表4 运行时间对比
Tab.4 Comparison of operation time

算法名称运行时间/sSR-STAP4550.48RD-LSCSE-STAP375.26IT-LESCA-STAP330.61
5 结论
针对因离网问题造成的SR-STAP杂波抑制性能下降的问题,本文提出一种离网误差迭代自校正STAP算法。该算法通过对传统STAP字典的原子筛选构造全局字典,对全局字典中的原子迭代选优,最后对局部字典的原子小范围搜索,得到了比较准确的杂波子空间估计值。在局部搜索时,通过缩小搜索范围,减少了运算复杂度。实验证明,本文所提算法能够选择与真正杂波点更匹配的原子,改善了因离网问题所引起的误差,在较低运算复杂度的条件下保证了STAP的性能不低于现有方法。
[1] 保铮, 张玉洪, 廖桂生, 等.机载雷达空时二维信号处理[J].现代雷达, 1994,16(1): 38-48.
BAO Zheng, ZHANG Yuhong, LIAO Guisheng, et al.Space-time signal processing for airborne radars[J].Modern Radar, 1994, 16(1): 38-48.(in Chinese)
[2] 杜鹏飞, 王永良, 孙文峰.机载监视雷达地杂波背景中的CFAR检测方法[J].系统工程与电子技术, 2004, 26(3): 321-324.
DU Pengfei, WANG Yongliang, SUN Wenfeng.Study of CFAR detection for airborne surveillance radar in ground clutters[J].Systems Engineering and Electronics, 2004, 26(3): 321-324.(in Chinese)
[3] KLEMM R.Introduction to space-time adaptive processing[J].Electronics&Communication Engineering Journal, 1999, 11(1): 5-12.
[4] REED I S, MALLETT J D, BRENNAN L E.Rapid convergence rate in adaptive arrays[J].IEEE Transactions on Aerospace and Electronic Systems,1974,AES-10(6): 853-863.
[5] 阳召成, 黎湘, 王宏强.基于空时功率谱稀疏性的空时自适应处理技术研究进展[J].电子学报, 2014, 42(6): 1194-1204.
YANG Zhaocheng, LI Xiang, WANG Hongqiang.An overview of space-time adaptive processing technology based on sparsity of space-time power spectrum[J].Acta Electronica Sinica, 2014, 42(6): 1194-1204.(in Chinese)
[6] ENDER J H G.On compressive sensing applied to radar[J].Signal Processing, 2010, 90(5): 1402-1414.
[7] ZHANG Tong.Sparse recovery with orthogonal matching pursuit under RIP[J].IEEE Transactions on Information Theory, 2011, 57(9): 6215-6221.
[8] ZAKHAROV Y V, NASCIMENTO V H.DCD-RLS adaptive filters with penalties for sparse identification[J].IEEE Transactions on Signal Processing, 2013, 61(12): 3198-3213.
[9] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al.On clutter sparsity analysis in space-time adaptive processing airborne radar[J].IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1214-1218.
[10] 孙珂, 张颢, 李刚, 等.基于杂波谱稀疏恢复的空时自适应处理[J].电子学报, 2011, 39(6): 1389-1393.
SUN Ke, ZHANG Hao, LI Gang, et al.STAP via sparse recovery of clutter spectrum[J].Acta Electronica Sinica, 2011, 39(6): 1389-1393.(in Chinese)
[11] WU Honglin, WANG Shu.Adaptive sparsity matching pursuit algorithm for sparse reconstruction[J].IEEE Signal Processing Letters, 2012, 19(8): 471-474.
[12] 段克清, 袁华东, 许红, 等.稀疏恢复空时自适应处理技术研究综述[J].电子学报, 2019, 47(3): 748-756.
DUAN Keqing, YUAN Huadong, XU Hong, et al.An overview on sparse recovery space-time adaptive processing technique[J].Acta Electronica Sinica, 2019, 47(3): 748-756.(in Chinese)
[13] DUAN Keqing, YUAN Huadong, XU Hong, et al.Sparsity-based non-stationary clutter suppression technique for airborne radar[J].IEEE Access, 2018,6: 56162-56169.
[14] 高志奇, 陶海红, 赵继超.基于联合稀疏功率谱恢复的机载雷达稳健STAP算法研究[J].电子学报, 2016, 44(11): 2796-2801.
GAO Zhiqi, TAO Haihong, ZHAO Jichao.Robust STAP algorithm based on joint sparse recovery of clutter spectrum for airborne radar[J].Acta Electronica Sinica, 2016, 44(11): 2796-2801.(in Chinese)
[15] 张海龙, 陆广华, 于慧, 等.基于压缩感知的分布式MIMO成像雷达网格失配问题研究[J].现代雷达, 2015, 37(12): 49-53.
ZHANG Hailong, LU Guanghua, YU Hui, et al.A study on off-grid problem for distributed MIMO imaging radar based on compressive sensing[J].Modern Radar, 2015,37(12): 49-53.(in Chinese)
[16] HE Pengyuan, HE Shun, YANG Zhiwei, et al.An off-grid STAP algorithm based on local mesh splitting with bistatic radar system[J].IEEE Signal Processing Letters, 2020, 27:1355-1359.
[17] SU Yuyu, WANG Tong, TAO Fuyu, et al.A grid-less total variation minimization-based space-time adaptive processing for airborne radar[J].IEEE Access, 2020,8: 29334-29343.
[18] CHI Yuejie, SCHARF L L, PEZESHKI A, et al.Sensitivity to basis mismatch in compressed sensing[J].IEEE Transactions on Signal Processing, 2011, 59(5): 2182-2195.
[19] HE Xuezhi, LIU Changchang, LIU Bo, et al.Sparse frequency diverse MIMO radar imaging for off-grid target based on adaptive iterative MAP[J].Remote Sensing, 2013, 5(2): 631-647.
[20] DUAN Keqing, LIU Weijian, DUAN Guangqing, et al.Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP[J].IET Radar,Sonar&Navigation, 2018, 12(5): 557-564.
[21] DUAN Keqing, WANG Zetao, XIE Wenchong, et al.Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J].IET Signal Processing, 2017, 11(5): 544-553.
[22] YUAN Huadong, XU Hong, DUAN Keqing, et al.Sparse Bayesian learning-based space-time adaptive processing with off-grid self-calibration for airborne radar[J].IEEE Access, 2018, 6: 47296-47307.
[23] 李志汇, 张永顺, 高乾, 等.基于局部搜索OMP的网格失配STAP算法[J].系统工程与电子技术, 2018, 40(6): 1221-1226.
LI Zhihui, ZHANG Yongshun, GAO Qian, et al.Off-grid STAP algorithm based on local search orthogonal matching pursuit[J].Systems Engineering and Electronics, 2018, 40(6): 1221-1226.(in Chinese)
[24] LI Zhihui, ZHANG Yongshun, HE Xingyu, et al.Low-complexity off-grid STAP algorithm based on local search clutter subspace estimation[J].IEEE Geoscience and Remote Sensing Letters, 2018, 15(12): 1862-1866.
[25] 于美, 徐子健.基于贝叶斯方法的失踪目标优化搜索算法[J].计算机与现代化, 2016(10): 21-24,29.
YU Mei, XU Zijian.Optimal search algorithm for missing target based on Bayesian approach[J].Computer and Modernization, 2016(10): 21-24,29.(in Chinese)
[26] 余亮, 刘永春, 林达.基于贝叶斯的概率搜索决策框架[J].电光与控制, 2020, 27(9): 50-54,65.
YU Liang, LIU Yongchun, LIN Da.A probabilistic search decision-making framework based on Bayesian method[J].Electronics Optics&Control, 2020, 27(9): 50-54,65.(in Chinese)
[27] 施皓晨, 肖海鹏, 周建江.一种双线性分段二分网格搜索SVM最优参数方法[J].计算机与数字工程, 2020, 48(9): 2179-2184.
SHI Haochen, XIAO Haipeng, ZHOU Jianjiang.A bilinear segmented dichotomy grid searching SVM optimal parameters method[J].Computer&Digital Engineering, 2020, 48(9): 2179-2184.(in Chinese)
[28] TEKE O, GURBUZ A C, ARIKAN O.Perturbed orthogonal matching pursuit[J].IEEE Transactions on Signal Processing, 2013, 61(24): 6220-6231.


