1 引言
多输入多输出(MIMO)技术在无线通信领域得到广泛应用。受此启发,Fishler等人于2004年首次提出MIMO雷达概念[1]。与传统单发单收体制雷达和相控阵雷达相比,MIMO雷达在检测性能、参数估计等方面具有独特的优势,近年来受到了国内外学者和研究人员的广泛关注[2-4]。
根据MIMO雷达发射站与接收站的位置分布关系,MIMO雷达可分为两种类型[5]。第一种称为统计MIMO雷达,其发射阵元、接收阵元间距很大,每个发射接收阵元间形成的探测通道具有一定的统计分布特性。统计MIMO雷达可以克服目标RCS起伏,实现系统性能的改善。第二种称为相参MIMO雷达,其发射天线阵元之间,以及接收天线阵元之间的间距较小,每个发射接收阵元间形成的探测通道是相参的。相参MIMO雷达又可以根据收发站是否放置在同一位置,进一步分为分布式相参MIMO和集中式相参MIMO。
相参MIMO雷达与常规相控阵雷达的本质区别是,相参MIMO雷达的发射阵元发射多组不同的正交波形,而常规相控阵雷达的发射阵元发射相同的波形,不同阵元之间只存在时延差和相位差。随着数字阵技术的发展,先进体制的雷达系统可以将常规相控阵雷达和相参MIMO雷达分别作为不同的工作模式,从而根据不同作战场景需求进行工作模式选择。由于相参MIMO雷达与传统相控阵雷达的相似性,分析它们在目标检测、目标参数测量、杂波抑制以及抗干扰等不同方面的能力,从而作为工作模式选择的依据,具有重要的理论指导意义和工程应用价值。
MIMO雷达抗干扰能力的分析与研究受到了广泛关注。文献[6]对MIMO雷达抗干扰性能分析,包括被截获概率和抗无源/有源干扰能力等。针对集中式MIMO雷达与传统相控阵雷达的抗干扰能力的不同,文献[7]提出集中式MIMO雷达通过提升信干噪比输出增强干扰抑制能力,但是由于未考虑发射天线增益引起的信号回波差异,其分析结果有待进一步优化。MIMO雷达可以同时利用发射端和接收端的系统自由度,文献[8]对基于自适应波束形成方法的MIMO雷达抗干扰性能开展了研究。同时,由于MIMO雷达的系统自由度与收发阵列的构型决定,为提升其抗有源干扰能力,文献[9]对MIMO雷达的阵列设计方法进行了分析和论证。
本文针对集中式相参MIMO雷达的抗干扰能力进行了分析,包括雷达发射信号的抗截获能力、抗侦察分选能力以及抗副瓣干扰能力,并与传统相控阵雷达的抗干扰能力进行了对比。通过分析可以发现,MIMO雷达的抗截获能力优于相控阵雷达的主瓣,但劣于相控阵雷达的副瓣。MIMO雷达发射的正交波形,在空间、时间叠加合成后信号幅度起伏,具有时空伪随机特征,增加了干扰机的参数测量和信号分选难度。MIMO雷达抗副瓣干扰能力不仅与阵列构型有关,还受到不同干扰类型的影响,对抗噪声干扰的能力与传统相控阵相同,但是对抗转发式干扰具有一定优势。
2 信号模型
如图1所示,为不同类型的MIMO雷达系统。

图1 不同类型的MIMO雷达系统
Fig.1 Different type of MIMO radar system
假设MIMO雷达的发射阵元个数为M,接收阵元个数为N。假设第m个阵元的发射信号表示为φm(t)。为便于分析,对脉冲的发射能量进行归一化处理,使其满足
(1)
发射信号照射到目标后,将M个发射波形反射回来。N个接收阵元对每个回波进行接收。
为简化分析,假设MIMO雷达工作在窄带模式,目标处于雷达远场,即阵元之间的发射或接收信号只是相差一个相位。阵元间的相位关系可以利用导向矢量进行表示,导向矢量与阵列构型、工作频率以及观测角度等因素相关。对于集中式相参MIMO雷达而言,发射和接收角度相同,表示为θ,则存在发射和接收两个导向矢量:发射导向矢量a(θ),维度为M×1;接收导向矢量b(θ),维度为N×1。假设导向矢量只存在相位加权不存在幅度加权,即导向矢量每个元素的模值为1。因此,
‖a‖2=M,‖b‖2=N
(2)
基于点目标构建MIMO雷达的信号模型,第n个接收机接收到的信号为
(3)
其中,γ表示目标回波的信号幅度,它与雷达发射功率、目标的径向距离以及电磁散射特性等因素相关;Ψ表示发射接收传输过程中路径长度造成的回波信号整体相移;am(θ)、bn(θ)分别表示导向矢量a(θ)、b(θ)的第m、n个元素;ηn(t)表示接收机噪声。
将每个发射阵元的发射波形写成向量形式,可表示为
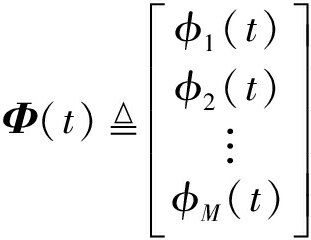
(4)
MIMO雷达的发射波形要求具有优异的正交性。用Rφ表示M个发射信号的相关矩阵,矩阵维度为M×M
Rφ
![]() Φ(t)Φ(t)Hdt
Φ(t)Φ(t)Hdt
(5)
矩阵的积分是逐元素进行计算的。矩阵的每个元素表示对应两个发射信号的相关性。矩阵中的第m行第m′列的元素表示第m个发射信号经过第m′个波形对应的匹配滤波器后的输出相应。该元素可以表示为
(6)
相关矩阵Rφ描述了发射信号波形之间的自相关和互相关特性,是表征MIMO雷达性能的关键参量。此处假设Rφ=IM,IM为M维单位阵,即假设每个发射阵元的发射波形之间彼此正交,这在实际工程应用中很难实现,但在理论上便于开展后续分析。
公式(3)的接收信号,可以利用向量和矩阵形式重新表示为
y(t)=γejΨb(θ)a(θ)TΦ(t)+η(t)
(7)
η(t)为向量形式的接收机噪声,并且假设为满足独立同分布的复高斯白噪声,其协方差为N维单位阵
E[η(t)η(t)H]=IN
(8)
定义MIMO雷达的信道传输矩阵为
A(θ) b(θ)a(θ)T
b(θ)a(θ)T
(9)
该矩阵维度为N×M,表示在角度θ的目标对每一对发射-接收阵元造成的相位偏移。
考虑雷达远场存在有源干扰的场景,假设干扰源的角度为θJ。干扰机接收到雷达的发射信号后,按照一定的准则和策略辐射干扰信号J(t)。此时,接收阵元接收到的信号向量变为
y(t)=γejΨb(θ)a(θ)TΦ(t)+b(θJ)J(t)+η(t)
(10)
MIMO雷达的N个接收阵元,分别输出一路接收信号。每一路信号各自进行匹配滤波处理。每一路接收信号中都包含了M个发射信号,因此需要在每一路接收信号后设置M路对应的匹配滤波器,接收端的处理如图2所示。

图2 MIMO雷达接收端的信号处理示意图
Fig.2 The signal processing diagram of MIMO radar receiver
每一路信号经过匹配滤波后,变为M路数据。第n个接收阵元接收到的信号,即y(t)的第n个信号yn(t),经过匹配滤波器组后输出信号定义为:
zn(t)=[z1n(t),z2n(t),…,zMn(t)]T
(11)
其中,zmn(t)为yn(t)经过第m个发射波形对应的匹配滤波器的输出结果,即
zn(t)=![]() yn(t)Φ(t)Hdt=
yn(t)Φ(t)Hdt=
γejΨbn(θ)a(θ)d(t-τ0)+bn(θJ)g(t)+en(t)
(12)
其中,d(t-τ0)表示发射信号的自相关函数波形(即每个发射信号经过各自波形进行脉冲压缩后的信号),且在目标对应的时延τ0处取最大值。此处假设所有发射波形的自相互函数波形是相同的,这在信号自相关函数的主瓣是成立的。g(t)=[g1(t),…,gM(t)]T为干扰信号经过匹配滤波器组后的输出,其元素gm(t)为干扰信号经过第m个发射波形对应滤波器的输出结果。en(t)为第n个阵元接收噪声经过匹配滤波组的输出噪声。
将公式(12)中表示的所有接收阵元的输出向量重新表示为列向量形式
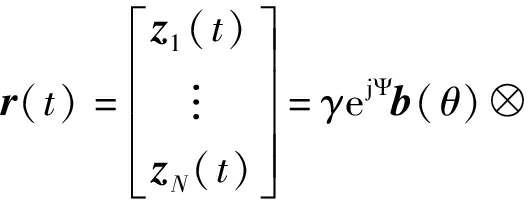
a(θ)d(t-τ0)+b(θJ)⊗g(t)+e(t)
(13)
其中,e(t)为将en(t)沿列方向堆叠后重新生成的噪声矢量,⊗表示Kronecker积。
3 抗有源干扰能力分析
随着现代战场电磁环境的日益恶化,抗有源干扰能力成为雷达系统的重要考核指标。雷达系统与电子战干扰机双方的对抗是贯穿全系统全流程的,干扰机对雷达释放干扰时,需要首先进行雷达侦察,即利用侦察设备获取雷达发射信号的信息,包括雷达信号截获、雷达信号参数测量、雷达信号分选等。因此雷达系统的抗干扰能力需要从多个不同的方面分别进行阐述。本文对相参MIMO雷达抗有源干扰的能力分析主要从以下几个方面展开,包括抗侦察截获、抗信号分选以及抗副瓣干扰能力。
3.1 抗侦察截获能力分析
雷达信号截获是指干扰机侦察设备对敌方雷达发射信号的检测,此步骤是干扰机能否进行后续参数测量、信号分选的基础,是干扰机能否有效释放干扰的先决条件。
干扰机侦察设备可以看作一个多维“滤波器”,侦察接收机为了有效截获雷达信号,需要在时域、频域、空域、极化域等满足以下条件:
1)时域:雷达发射信号到达侦察接收机的脉冲时间段,与干扰机接收开窗时间段存在重合;
2)频域:雷达发射信号的频谱需落入侦察接收机的接收带宽内;
3)空域:侦察接收机的接收波束覆盖范围需与雷达的发射波束范围有一定重合,截获性能随连线角度上增益的乘积相关;
4)极化域:信号的极化应位于侦察接收机接收天线的极化测量范围内。
在满足以上条件的基础上,干扰机接收的雷达发射信号功率应高于接收机灵敏度,以保证信号被正确检测和接收。
干扰机侦察设备接收到雷达发射信号的SNR为

(14)
其中,PT为雷达发射峰值功率,GT为指向干扰机方向的雷达天线发射增益,GE为指向雷达方向的干扰机天线接收增益,λ为信号波长,LE为干扰机的接收损耗,τE为干扰机接收时间长度,BE为干扰接收带宽,γ为有效截获因子,k为玻尔兹曼常数,T0为侦察机噪声温度,Fe为侦察机噪声系数。
将与干扰机相关的参数联合表示为α,且该参数取值保持不变,则公式(14)可重新表示为
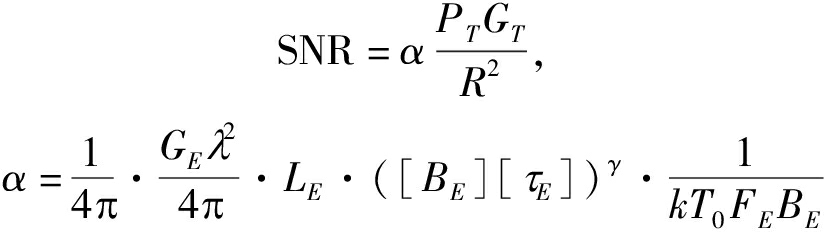
(15)
干扰机的最大侦察截获距离指的是在一定的检测概率和虚警概率条件下,正确检测雷达发射信号的距离。将SNR超过一定阈值δ时,干扰机所处的距离定义为截获距离。阈值δ与干扰机灵敏度和信号检测门限值等参数相关。
以一个发射单元发射信号的干扰机接收SNR和截获距离为参考,对比M个发射单元分别以相控阵雷达模式和MIMO雷达时的干扰机截获距离,如表1所示。其中,GT(θ|θ0)为相控阵雷达主瓣波束指向角度θ0时,θ方向上的发射增益。
表1 干扰机截获距离对比
Tab.1 The comparison of jammer receiver interception range

干扰机接收信号SNR干扰机截获距离一个发射单元SNR1=αPTR2R1=αδPT相控阵雷达(M个发射单元)SNRPA=αPTR2·MGT(θ|θ0)RPA=MGT(θ|θ0)·R1MIMO雷达(M个发射单元)SNRMIMO=αPTR2·MRMIMO=M·R1
通过分析可以发现,若干扰机对一个发射单元的截获距离为R1,则M个阵元组成的相控阵雷达与MIMO雷达的截获距离具有不同特性:
1)相控阵雷达,不仅发射功率增加了M倍,同时,由于发射信号在空间中相参叠加形成发射波束的主瓣和副瓣,因此,干扰机的截获距离与发射天线波束指向θ0及干扰机所处角度θ有关,相较于单个发射阵元的截获距离提升了![]() 倍;
倍;
2)MIMO雷达,发射功率增加了M倍,但是各个发射单元之间的发射信号彼此正交,因此,可以认为MIMO雷达相较于单个发射阵元的截获距离提升了![]() 倍。
倍。
以发射阵元数M=16的天线阵列为例,以MIMO雷达相比,相控阵雷达的发射增益在主瓣和副瓣存在明显的差异:相控阵雷达的副瓣增益GSide_PA小于MIMO雷达的发射增益GMIMO;相控阵雷达的主瓣增益GMain_PA大于MIMO雷达的发射增益GMIMO。这意味着MIMO雷达与相控阵雷达主/副瓣的抗截获性能是不同的,以θ0=0的情况,及相控阵主瓣波束指向0°为例。
若θ=0,即干扰机位于相控阵主瓣波束指向,则:![]()
若θ≠0,且GSide_PA<GMIMO,干扰机位于相控阵副瓣波束,并且增益小于MIMO雷达时,RMain_PA<RMIMO。
通过以上分析可知,MIMO雷达的截获距离小于相控阵主瓣,但大于相控阵雷达副瓣。
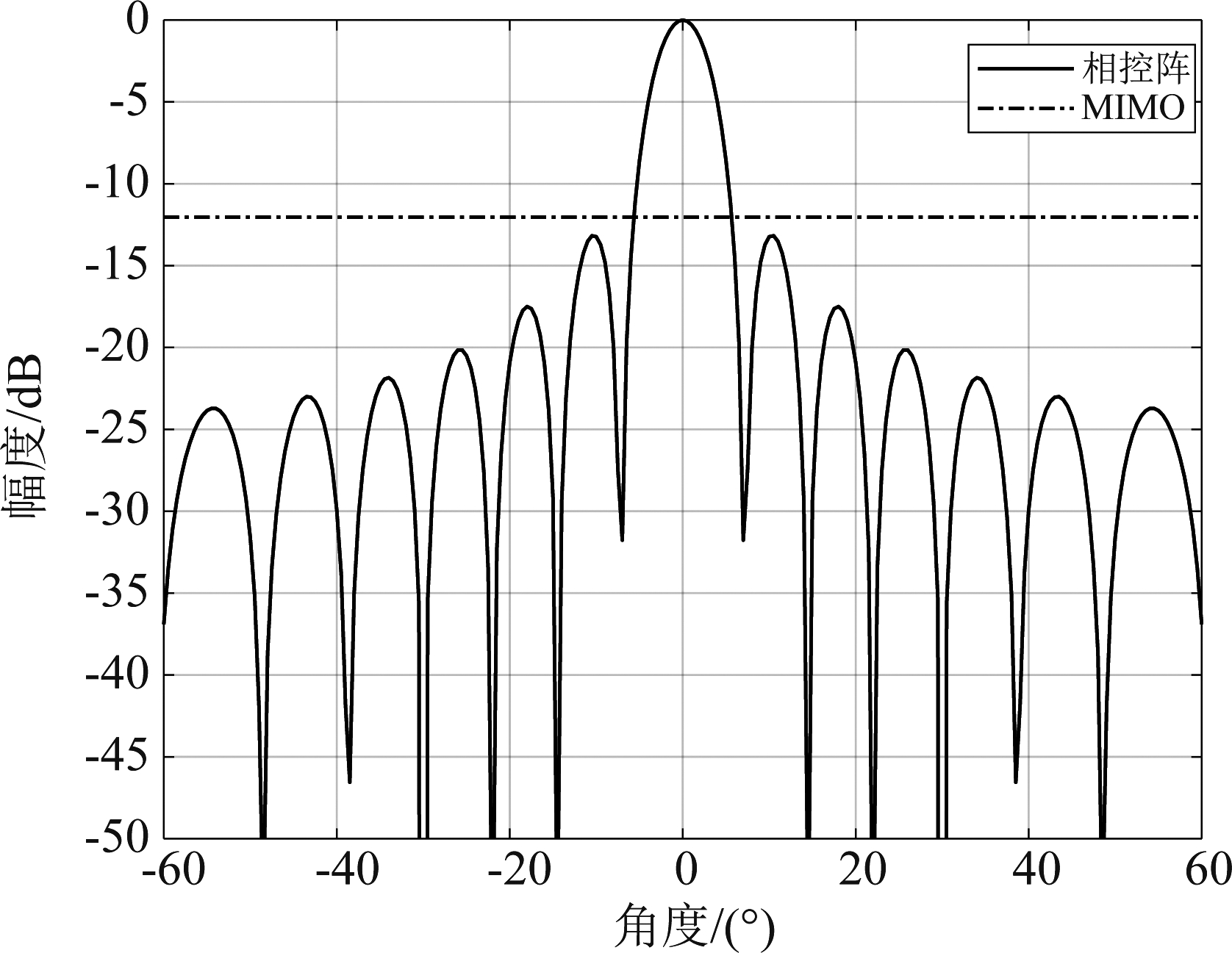
图3 天线阵列发射增益对比
Fig.3 The comparison of antenna array transmit gain
3.2 抗信号分选能力分析
干扰机信号分选,是指干扰机侦察接收设备对截获的雷达脉冲信号进行参数测量,例如(载频RF、脉冲达到时间TOA、脉冲宽度PW、脉冲幅度PA等),或者进行脉内调制类型的识别。在此基础上,干扰机的侦察设备对截获的多部雷达混合脉冲串进行分离,从而分别获取各部雷达的发射信号。只有准确分选出各部雷达的脉冲串,才能正确评估雷达的工作模式、威胁度等相关信息,从而引导干扰机对雷达进行有效干扰,否则,会造成干扰资源的浪费,降低干扰效果。
MIMO雷达发射的多个波形具有良好的正交性,频分正交波形可以实现发射信号的频谱展宽,具有更低的功率谱密度;码分正交波形,则利用信号调制的正交性,在空间、时间叠加合成后的发射信号幅度起伏,具有时空伪随机特征,可以增加干扰机的参数测量和信号分选难度。下面以采用Gold码的多个发射波形在时间、空间上信号叠加的结果进行分析。
Gold码是R.Gold为了克服m序列个数受限于1967年提出的一种伪随机编码[10]。Gold码具有优良的自相关和互相关特性,相关函数副瓣较为平坦,且Gold序列中“0”的个数与“1”的个数最多相差一个。Gold码被广泛应用于移动通信和雷达等系统中。Gold码的产生原理如图4所示,是由两个码长相等的m序列优选对进行位移模2加构成的。其中,m序列产生器1和2生成的序列m1和m2必须为满足一定关系的优选对,即其互相关函数值满足
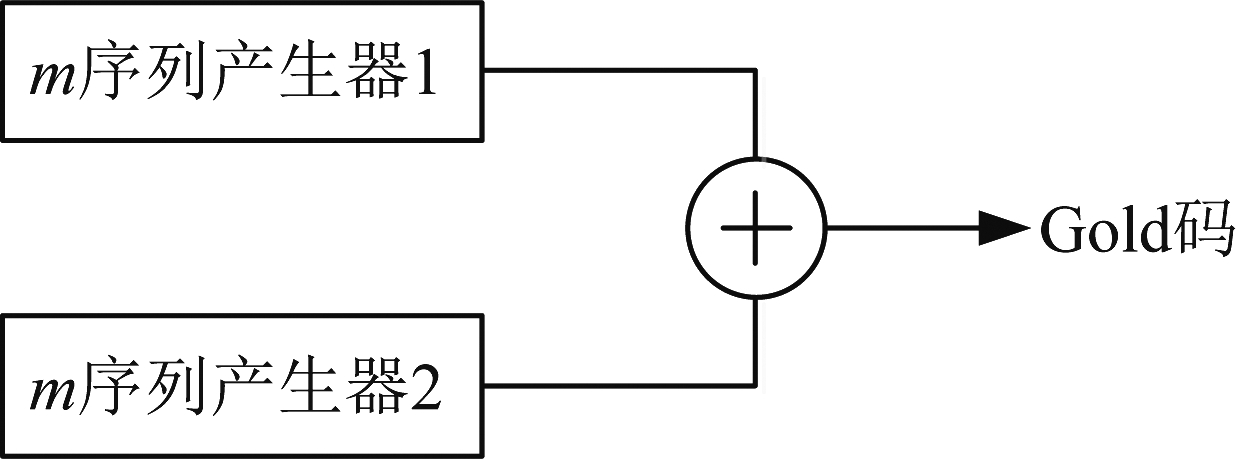
图4 Gold码产生示意图
Fig.4 The diagram of Gold sequence generation
![]()
(16)
其中,r为m序列的移位寄存器级数。
以r=7码元长度为27=128的Gold码为例,分析M=16的MIMO雷达发射波形的时空伪随机特性。
通过图5分析可以发现,MIMO雷达发射的多个码分正交波形,在空间、时间叠加合成后幅度起伏,具有时空伪随机特征,从而增加干扰机的截获、分选难度。
如图5(d)所示,两个不同角度干扰机接收到的信号波形完全不同,对该信号脉宽、到达时间、脉冲功率等估计可能存在不同结果。这种现象,还会对双站时差定位等无源定位方法造成性能恶化,甚至失效。

图5 多组Gold码叠加后的时空伪随机性
Fig.5 Time-Space pseudo-random character after addition of multiple Gold sequences
3.3 抗副瓣干扰能力分析
副瓣干扰是雷达探测目标时最常面临的威胁。相控阵雷达通过自适应波束形成技术可以实现对副瓣干扰的有效抑制。下面通过分析和对比相控阵雷达以及MIMO雷达的抑制副瓣干扰自由度的区别,说明MIMO雷达在对抗副瓣干扰方面的优势。如图6所示,为MIMO雷达与相控阵雷达的自适应处理示意图。

图6 两种雷达系统自适应处理流程对比
Fig.6 The comparison of two different radar system adaptive processing
相控阵雷达,所有发射阵元辐射的信号具有相同的波形,通过发射阵元间进行幅度、相位(收发为窄带信号)或时延(收发为宽带信号)的调整在空间实现信号干涉叠加,从而形成发射主瓣波束和副瓣波束。相控阵的接收端,通过对多个接收阵列的自适应波束合成,在副瓣干扰方向自适应形成波束零点,从而实现副瓣干扰的抑制。相控阵的波束形成方式可以表示:
(17)
其中,WT和WR分别表示发射和接收的加权矢量,φ(t)为相控阵的发射信号波形。因此,相控阵只能通过改变接收端加权系数调整天线方向图,即WPA=WR,维度为N×1。因此,相控阵的自适应处理自由度N,理论上最多可以对消N-1个干扰。
第2节分析了MIMO雷达的信号模型,其波束形成方式可以表示为:
![]()
a(θ)d(t-τ0)+b(θJ)⊗g(t)+e(t)]
(18)
其中,WMIMO为MIMO接收信号的加权矢量,维度为MN×1。由于MIMO雷达的发射波形正交,可以在接收端恢复出发射端的信号,从而实现收发端联合自适应加权处理。
相同收发阵列的相控阵雷达与MIMO雷达相比,接收端自适应波束合成时的加权系数WPA和WMIMO的维度分别为N和MN。这是否意味着MIMIO雷达比相控阵雷达的自由度更多,从而可以对消更多副瓣干扰呢?
对于有源干扰而言,按照发射干扰的性质可以分为噪声干扰与转发干扰。噪声干扰覆盖雷达发射信号的带宽,实现压制的效果;转发干扰,则通过对接收信号进行调制(包括幅相、时延等参数),实现欺骗的效果。实际上,MIMO雷达对副瓣的噪声干扰与转发干扰的抑制能力是不同的。
如公式(12)中,为干扰信号经过匹配滤波器组后的输出。
当干扰信号分别为噪声干扰和转发干扰时,g(t)具有不同的特性。
(1)若干扰信号为噪声干扰JNoise(t),由于噪声信号与MIMO的各个发射信号均不相关,经过发射信号的匹配滤波之后,gNoise(t)=[gNoise_1(t),…,gNoise_M(t)]T的每个元素之间不相关。这意味着,1个噪声干扰经过匹配滤波器组后,变成了M个不相关的干扰信号。因此,对于噪声干扰而言,MIMO雷达的实际自由度仍然是N,理论上最多可以对消N-1个噪声干扰。
(2)若干扰信号为转发干扰JDRFM(t),由于干扰信号是干扰机接收到的雷达发射信号的调制,经过发射信号的匹配滤波之后,gDRFM(t)=[gDRFM_1(t),…,gDRFM_M(t)]T=a(θJ)dJ(t)的每个元素之间是相关的,其中dJ(t)为干扰信号经过匹配滤波后的输出,其结果与干扰机对雷达发射信号的调制方式有关。因此,对于转发干扰而言,MIMO雷达的实际自由度是发射端与接收端自由的组合f(M,N),其取值与收发端阵列的排布方式有关。
为了验证上述分析的结论,假设MIMO发射/接收阵列为阵元数M=N=4的均匀线阵,阵列构型包括以下两种。阵型1收发阵元的阵元间距均为λ/2,阵型2发射阵元间距为2λ,接收阵元间距为λ/2。为了验证不同构型阵列对不同类型干扰的抑制能力,假设存在多个干扰机位于不同的方位角度,释放不同类型的干扰信号,通过分析接收信号阵列的协方差矩阵大特征值数目,验证对消不同干扰数量所需的自由度。
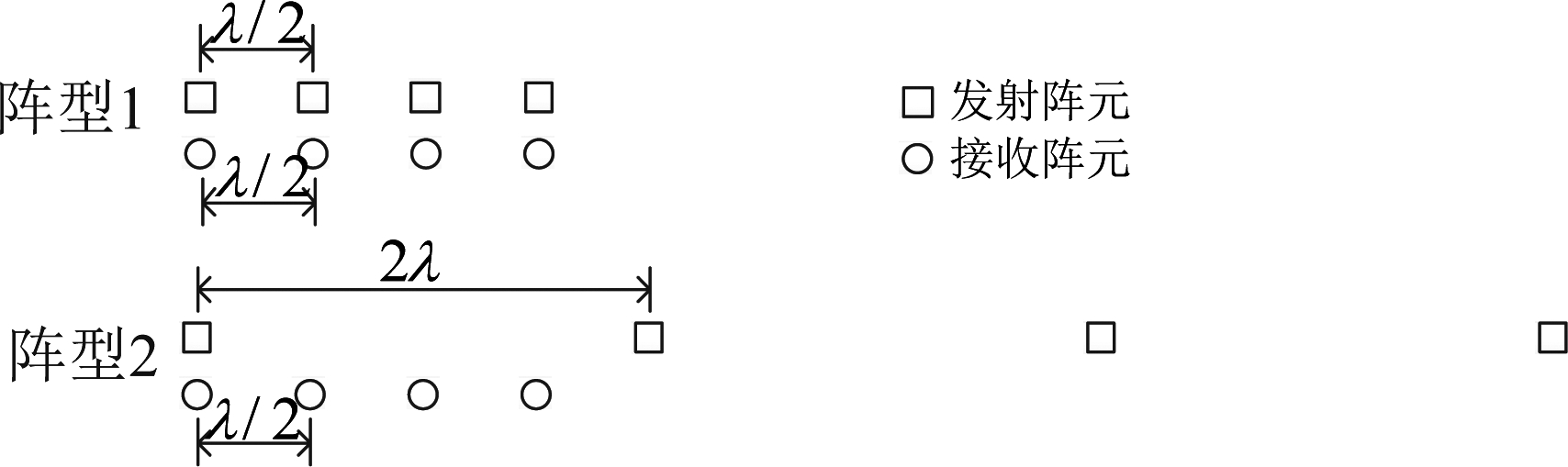
图7 两种不同的MIMO雷达阵列结构
Fig.7 Two different MIMO Radar array structure
仿真试验1 假设MIMO发射/接收阵列为阵元数的线阵,阵元间距为半波长分别存在1/2/3个干扰机位于方位角[-20,10,40]°,期望目标角度为0°。干扰机均释放噪声干扰。对接收信号进行匹配滤波后,分析M×N=16维接收信号的协方差矩阵的特征值分布情况,如图8所示。由于阵型1与阵型2的接收阵列相同,因此,特征值分布情况是相同的结果。可见n个压制干扰,消耗了M×n个自由度。因此,噪声干扰与发射导向矢量解耦,MIMO雷达对消噪声干扰时的自由度并未增加。
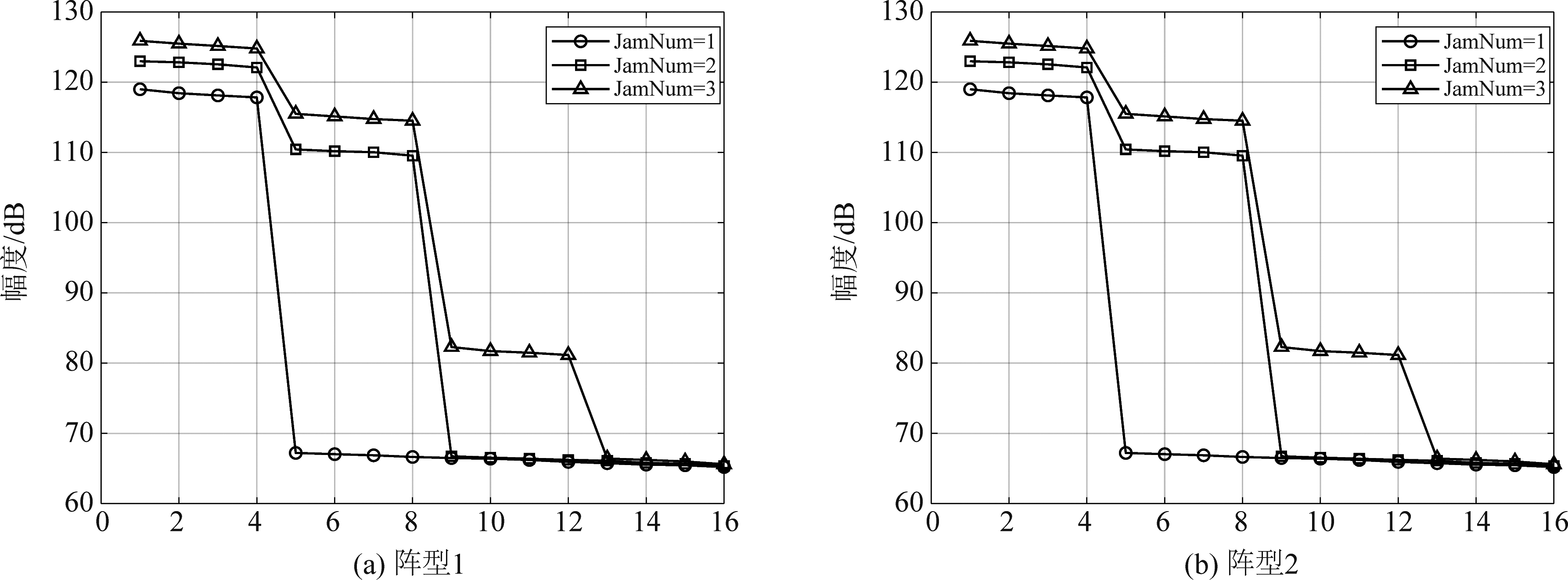
图8 噪声干扰情况下协方差矩阵的特征值
Fig.8 Eigenvalues of the covariance matrix with the noise jamming
仿真试验2 假设存在5个干扰机位于方位角[-50,-30,-10,20,40]°,期望目标角度为0°。干扰机释放转发干扰。对接收信号进行匹配滤波后,分析M×N=16维接收信号的协方差矩阵的特征值分布情况,如图9所示。可见n个转发干扰,消耗n个自由度。这是由于,转发干扰包含了发射导向矢量的信息,MIMO雷达可以利用发射端自由度,从而增加了对消转发干扰时的系统自由度。
如图9(a)所示,阵型1的系统自由度为M+N=8,这意味着其最多可抑制7个转发干扰;如图(b)所示,阵型2的系统自由度为M×N=16,这意味着其最多可抑制15个转发干扰。阵型1与阵型2的系统自由度不同,其本质为不同阵型的有效虚拟阵元数不同。
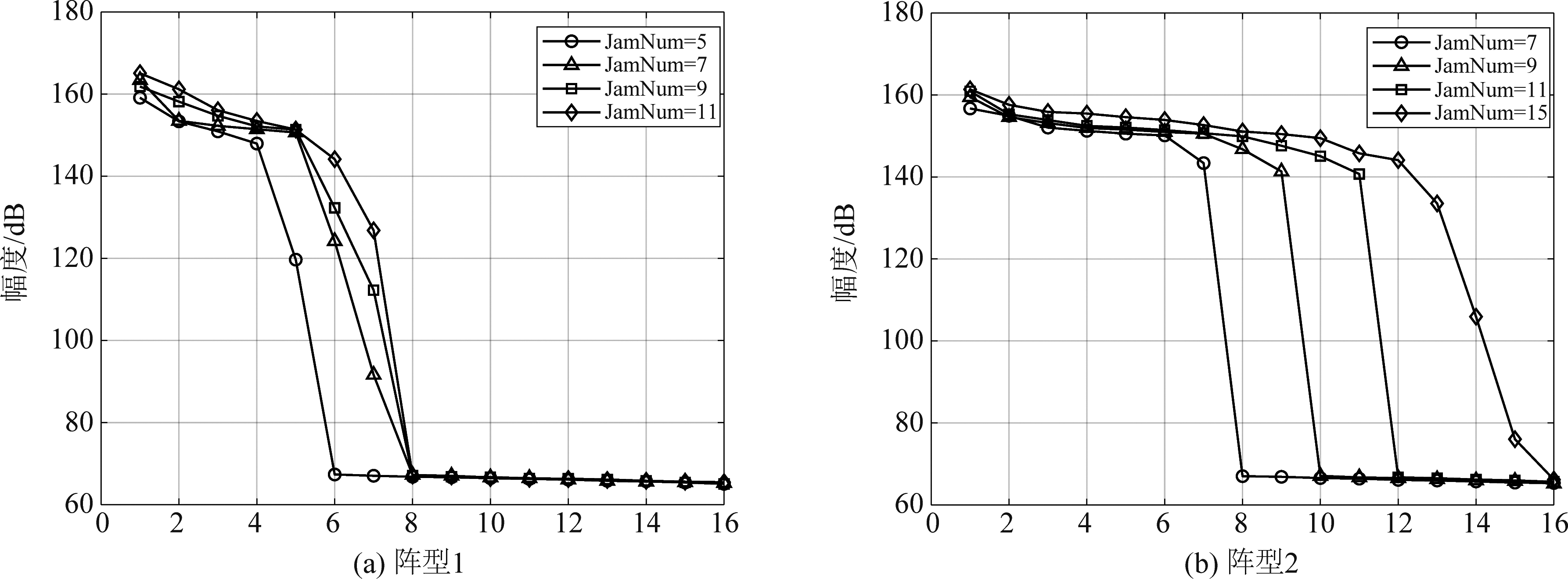
图9 转发干扰情况下协方差矩阵的特征值
Fig.9 Eigenvalues of the covariance matrix with the DRFM jamming
3.4 抗干扰能力对比总结
由于不同战场环境下的不同雷达系统的工作任务和功能不同,对于雷达系统的抗有源干扰能力尚未形成统一的综合抗干扰能力评估指标。为了对比同样干扰条件下的MIMO雷达和相控阵雷达的抗干扰性能,采用定性的方式描述两种不同体制雷达系统的抗干扰能力。
表2 两种不同体制系统抗干扰能力对比
Tab.2 The comparison of anti-jamming capability of different type radar system

抗干扰能力相控阵雷达MIMO雷达能力对比抗侦察截获能力干扰机高灵敏度可侦收主瓣/副瓣可侦收MIMO雷达相当干扰机低灵敏度仅侦收主瓣不能侦收MIMO雷达MIMO更优抗信号分选能力仅在时间维实现复杂波形在时间-空间二维实现复杂波形MIMO更优抗副瓣干扰能力干扰机发射压制干扰仅依赖接收自由度仅依赖接收自由度相当干扰机发射假目标干扰仅依赖接收自由度依赖接收和发射联合自由度MIMO更优
通过以上分析可知,在抗侦察截获、抗信号分选、抗副瓣干扰能力方面,MIMO雷达与相控阵雷达相比,均具有相当或更优的性能。这说明在抗有源干扰能力方面,MIMO雷达具有更大的优势。
4 结论
针对集中式相参MIMO雷达的抗有源干扰的能力开展了研究。首先,分析了相参MIMO雷达的发射、接收和处理的回波信号模型。然后,对相参MIMO雷达抗有源干扰时的抗侦察截获、抗信号分选以及抗副瓣干扰能力分别进行了分析。相参MIMO雷达的截获距离,与相控阵雷达主副瓣的抗截获距离相比各有优劣。相参MIMO雷达发射的正交波形,在时域/空域叠加合成波形的调制方式更复杂,具有幅度伪随机特性,可以增加干扰机的信号分选能力。在抗副瓣干扰能力方面,相参MIMO雷达抗噪声干扰的自由度与相控阵相同,抗转发干扰时则具有一定的优势。相参MIMO雷达抗有源干扰的能力均通过仿真试验进行了分析,验证了本文结论的正确性。
[1] FISHLER E, HAIMOVICH A, BLUM R, et al.MIMO radar: An idea whose time has come[C]∥Proceedings of the 2004 IEEE Radar Conference(IEEE Cat.No.04CH37509).Philadelphia, PA, USA.IEEE, 2004: 71-78.
[2] LI J, STOICA P.MIMO Radar Signal Processing[M].Wiley-IEEE Press, New York, 2008.
[3] MONZINGO R A, MILLER T W.Introduction to Adaptive Arrays[M].SciTech, Raleigh, NC, 2011.
[4] MELVIN W L, SCHEER J A.Principles of modern radar: Advanced techniques[M].SciTech Publishing, Edison, NJ, 2013.
[5] 王宁, 陈翼, 于俊朋, 等.基于MIMO雷达信号模型的天线方向图研究[J].现代雷达, 2017, 39(11): 85-89.
WANG Ning, CHEN Yi, YU Junpeng, et al.A study on antenna pattern based on MIMO radar signal model[J].Modern Radar, 2017, 39(11): 85-89.(in Chinese)
[6] 王建明, 吴道庆.MI MO雷达抗干扰性能分析[J].航天电子对抗, 2006, 22(5): 48-50.
WANG Jianming, WU Daoqing.Anti-jamming performance analysis of MIMO radar[J].Aerospace Electronic Warfare, 2006, 22(5): 48-50.(in Chinese)
[7] 李涛.集中式MIMO雷达与相控阵雷达干扰抑制性能对比[J].电讯技术, 2016, 56(8): 894-899.
LI Tao.Interference suppression performance comparison between colocated MIMO radar and phased array radar[J].Telecommunication Engineering, 2016, 56(8): 894-899.(in Chinese)
[8] 张艺乐.MIMO雷达抗干扰性能研究[D].成都: 电子科技大学, 2017.
ZHANG Yile.Research on performance of anti-jamming for MIMO radar[D].Chengdu: University of Electronic Science and Technology of China, 2017.(in Chinese)
[9] 王洁.MIMO雷达抗有源干扰阵列设计方法[D].西安: 西安电子科技大学, 2018.
WANG Jie.Array design of MIMO radar anti-active jamming[D].Xi’an: Xidian University, 2018.(in Chinese)
[10] 蒋青, 于秀兰, 范馨月.通信原理[M].3版.北京: 人民邮电出版社, 2011: 298-300.
JIANG Qing, YU Xiulan, FAN Xinyue.Communication principles[M].Third edition.Beijing: Posts & Telecom Press, 2011: 298-300.(in Chinese)




