1 引言
空时自适应处理(Space Time Adaptive Processing, STAP)可以抑制机载雷达中的杂波,进而检测出运动目标[1-2]。STAP性能的好坏与被测距离单元中杂波协方差矩阵(Clutter Covariance Matrix,CCM)的估计准确性有关。传统STAP方法通常是利用训练样本的极大似然估计来计算CCM。根据RMB(Reed-Mallett-Brennan)准则,估计CCM所需要的独立同分布训练样本数量要达到系统自由度(System Degree Of Freedom, DOF)的两倍,才能保证STAP输出信噪比损失不超过3 dB[3]。因此,传统的STAP算法通常需要从均匀杂波环境中来获得足够的训练样本。但在实际场景中,尤其是在非同质杂波环境下,很难满足这一要求,导致了传统STAP方法性能下降[4]。
针对STAP方法中所需样本数太多的问题,研究者提出了降维与降秩STAP方法。虽然这两种算法都可以减少估计CCM所需要的样本数量,但是会带来DOF损失和STAP性能下降的问题[3]。直接数据域(Direct Data Domain, D3)方法只利用来自CUT中的数据,避免了训练样本的异质性,解决了所需样本量大的问题[5]。但是,D3方法是建立在降低DOF的基础上,将导致STAP性能的较大损失。随着雷达电子行业的快速发展,知识辅助(Knowledge-Aided,KA)的STAP技术因其在非同质杂波环境下利用先验知识来提高检测性能而备受关注[6-7]。然而,先验环境知识的确切存在形式难以确定,因此知识辅助STAP方法在实际中的应用较为困难。
稀疏恢复(Sparse Recovery, SR)技术利用过完备稀疏字典中最小数目的向量来表示目标信号[8-10]。近年来,稀疏恢复技术被成功地应用于提高STAP算法的收敛性[11-12],利用杂波谱的内在稀疏性和基于范数最小化的方法,可以在少量甚至单个训练样本的情况下提高CCM的估计精度。现有的SR-STAP算法中,稀疏恢复方法和字典构造方法对CCM估计的精度影响较大。目前,关于SR-STAP的研究主要集中在提高SR算法的恢复精度[13-17],对空时导向字典的构造方法关注较少。
现有的SR-STAP算法用空时平面上离散网格对应的空时导向矢量来构建稀疏恢复字典。通常情况下,这些导向矢量由角度和多普勒平面上的均匀采样得到。然而,由于阵列流形、雷达参数等因素的影响,杂波在空时平面的实际分布与人为划分的均匀网格点并不匹配。此时,实际的杂波分量大多不再位于均匀离散化的空时网格上,将导致稀疏恢复误差和STAP性能下降,这种现象称为字典失配或离网效应(Off-Grid)。Off-Grid问题也在压缩感知成像[18]和波达方向(Direction Of Arrival, DOA)估计[19-20]等应用中存在。
目前,对于SR-STAP算法中的字典失配问题,学者们提出了一些修正方法。文献[21]使用输出误差功率最小来校正网格失配字典。文献[22]提出了一种基于降维局部搜索正交匹配追踪的离网STAP算法,利用训练样本估计的CCM构造一个字典,然后从字典中挑选与杂波信号匹配的全局原子。文献[23]提出了利用稀疏贝叶斯方法来估计杂波加噪声协方差矩阵,可以有效缓解离网效应,但是增加了计算量。文献[24]提出了一种杂波脊匹配STAP算法,根据雷达系统参数计算杂波脊来重构杂波脊匹配字典,但是该算法仅对非侧视阵列适用。文献[25]提出了一种局部网格分割(Local Mesh Splitting, LMS)算法,根据子空间投影选择与残差最相关的时空矢量原子进行迭代局部网格分割来匹配真实杂波点,但是系统参数的测量误差会导致杂波抑制能力下降。文献[26]提出了一种直接增加网格数量的方法,但是网格划分的太密集会增加空时导向矢量的列相关性,大大增加了计算量。文献[27]首先通过雷达先验知识预先估算杂波脊,接着对多普勒频率间隔进行自适应调整来缓解离网效应,但该办法仅仅考虑了调整多普勒频率间隔,没有调整空间频率间隔,对离网效应改进不全面。针对这一问题,本文提出了一种基于知识辅助的机载雷达SR-STAP稀疏字典构造方法。该方法首先利用雷达参数等先验信息获取多普勒频率并且自适应调整多普勒频率间隔,然后根据多普勒频率和空间频率的关系调整空间频率间隔,最后构建超完备稀疏字典。仿真结果表明,与传统字典构造方法相比,该算法克服了离网效应的影响,改善了机载雷达的杂波抑制和目标检测性能。
2 信号模型
本文考虑采用由N个阵元组成的均匀线性阵列(Uniform Linear Array, ULA)的机载雷达。雷达的工作波长为λ,阵元间距为λ/2。几何模型见图1所示,载机高度为H,以恒定速度V运动。角θ、φ和ψ分别表示雷达天线发射波束指向的方位角、俯仰角和空间锥角。θα为阵列轴线与飞行方向的夹角。K个脉冲在每个相干处理间隔内以恒定的脉冲重复频率(Pulse Repetition Frequency, PRF)进行传输。
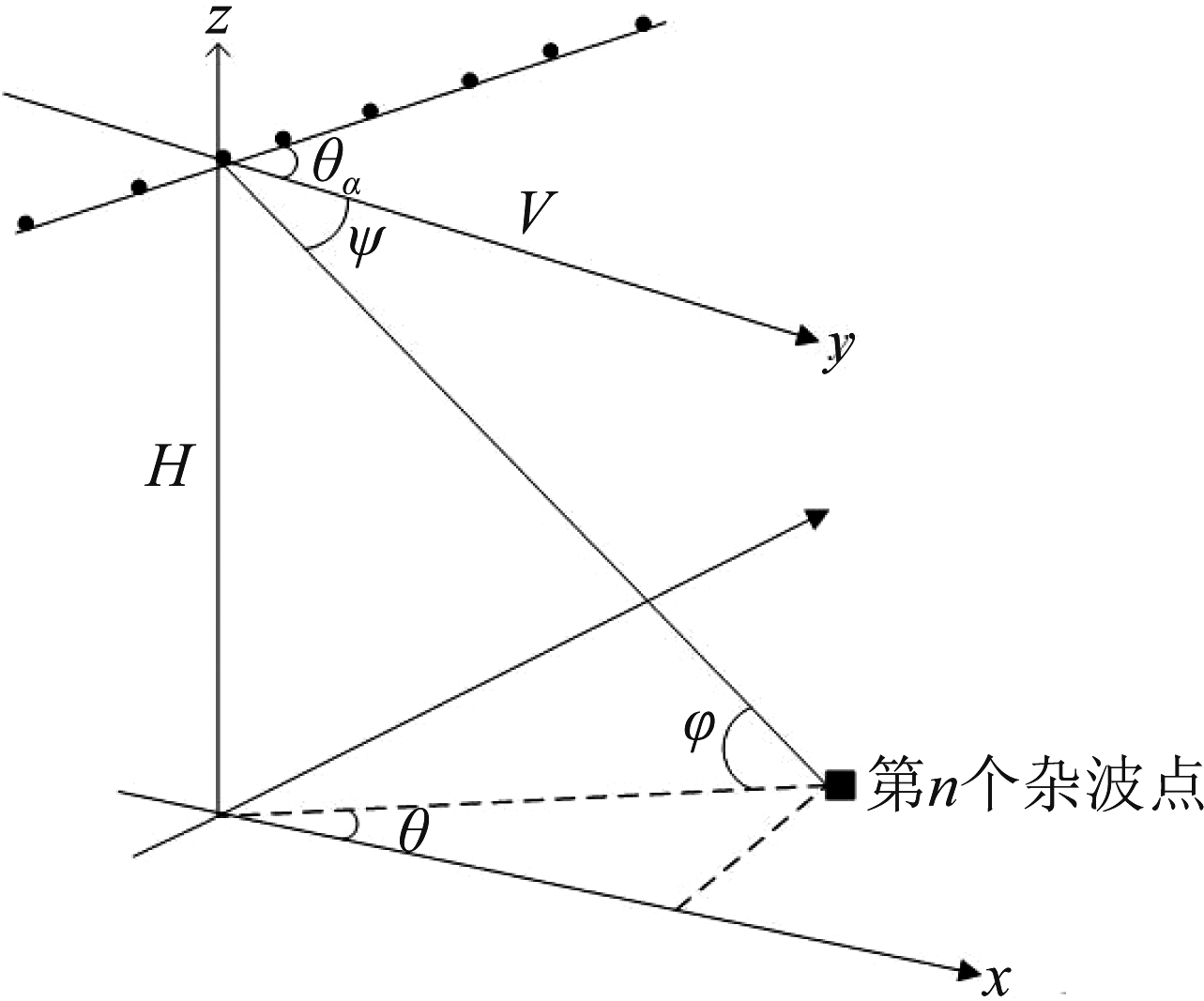
图1 ULA机载雷达模型图
Fig.1 An airborne radar model of ULA
单个距离环内的空时快拍数据
可以表示为:
x=xc+n
(1)
其中,xc和n分别表示空时杂波分量和噪声分量。通常,检测距离单元根据方位角被均匀的分为Nc个杂波反射点,则xc可以建模为Nc个独立杂波信号的和[21],即:
(2)
其中εn、fd,n和fs,n分别为第n个杂波点的复振幅、多普勒频率和空间频率,s(fd,n, fs,n)为空时导向矢量,可以表示为:
s(fd,n, fs,n)=st(fd,n)⊗ss(fs,n)
(3)
其中,时间导向矢量为st(fd,n)=[1,exp(j 2πfd,n),...,exp(j 2π(K-1)fd,n)]T,空间导向矢量为ss(fs,n)=[1,exp(j 2πfs,n),...,exp(j 2π(N-1)fs,n)]T,⊗表示矩阵克罗内克积运算,(·)T为矩阵转置运算。
杂波信号的多普勒频率为:
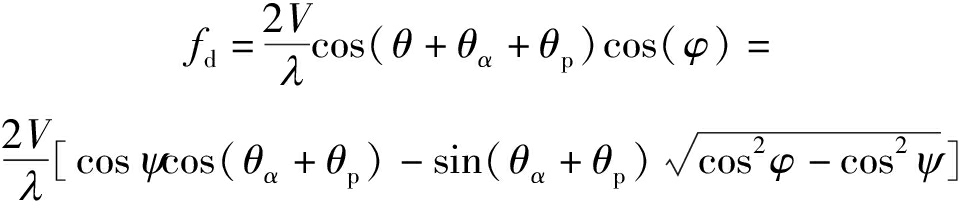
(4)
其中θp为载机偏航角。
杂波信号的归一化空间频率为:
fs=cos ψ
(5)
则式(4)可以改写为归一化多普勒频率形式:
(6)
其中β为杂波脊线的斜率:
β=2V/λ
(7)
假设各距离单元的快拍数据相互独立,则杂波协方差矩阵可以表示为:
R=E[xxH]
(8)
根据线性约束最小方差准则,最优STAP权向量可以表示为:
(9)
其中s0=st(fd,0)⊗ss(fs,0)是目标的空时导向矢量。通常,由于实际应用环境中CCM是未知的,因此用满足IID条件的训练样本通过最大似然估计来计算未知杂波协方差矩阵,即:
(10)
其中,L为训练样本的数量,至少为NK的2倍才能达到稳定性能,但是在非均匀杂波环境中很难获得足够的IID训练样本[3]。
3 基于知识辅助的字典构造方法
3.1 稀疏恢复原理
相比于传统的STAP算法,SR-STAP算法提高了空时分辨率,在训练样本数量不足的情况下可以体现出更好的性能[11]。SR-STAP算法首先需要构造字典,将空时平面沿着空间频率轴和多普勒频率轴均匀离散为Ns×Nd个网格,其中Ns=ρs×N, Nd=ρd×K,参数ρs和ρd分别为沿空间频率轴和多普勒频率轴的网格划分系数,且满足ρs>1和ρd>1。离散网格所对应的空时导向矢量字典Ф为:
Φ=[s(fd,1, fs,1),...,s(fd,1, fNs),...,
s(fd,Nd, fs,Ns)]NK×NdNs
(11)
当NsNd≫NK时,字典Ф具有冗余性,可以对快拍数据进行稀疏化表示,则式(1)可表示为:
x=Φγ+n
(12)
其中γ=[γ1,γ2,...,γNdNs]T为稀疏恢复的系数向量。根据杂波分布特性的分析结论,杂波通常只占据空时平面的少量位置,具有分布的稀疏性。另外,由于字典Ф具有冗余性,向量γ中只有少数不为0的元素,即为稀疏向量。如果已知Ф,则稀疏向量γ可以通过如下最优化问题进行求解[16]。
min‖γ‖0subject to ‖x-Φγ
≤ε
(13)
其中,‖.‖0代表在一个向量中非零元素的数量,‖.‖2代表2-范数,ε代表噪声误差允许量。
3.2 字典失配问题
现有的SR-STAP算法中的字典是由空时平面上均匀超采样网格对应的导向矢量构成的[13-17]。网格划分系数ρs和ρd需要设置合适的值。当网格划分系数设置较小时,网格间距会变宽,导致杂波分量估计误差增大;当网格划分系数设置较大时,会增大字典的列相干性,增加运算复杂度。所以,设置合适的网格划分系数对于构造字典至关重要,根据经验通常设置为4,5或6[13-17]。在正侧视ULA阵列情况下,当杂波脊线斜率值与Ns和Nd的比值相等且为1时,杂波分量可以落在均匀离散网格点上。在实际环境中,杂波脊斜率通常不等于整数,因此当Ns和Nd的比值设置不当时,就会出现网格失配效应。此外,在非正侧视阵列情形时,杂波脊呈非线性形式。此时,传统的字典构造方法会导致离网效应,杂波空时功率谱的估计精度严重下降。图2(a)为没有离网效应时的正侧视阵列杂波分布示意图,此时杂波脊的斜率等于Ns和Nd的比值且为1,杂波脊可以准确落在离散网格上。图2(b)为存在离网效应时的正侧视阵列杂波分布示意图,此时杂波脊的斜率设置为1.6,Ns和Nd的比值仍然设置为1,则大部分杂波分量没有准确落在空时平面的对角线上。
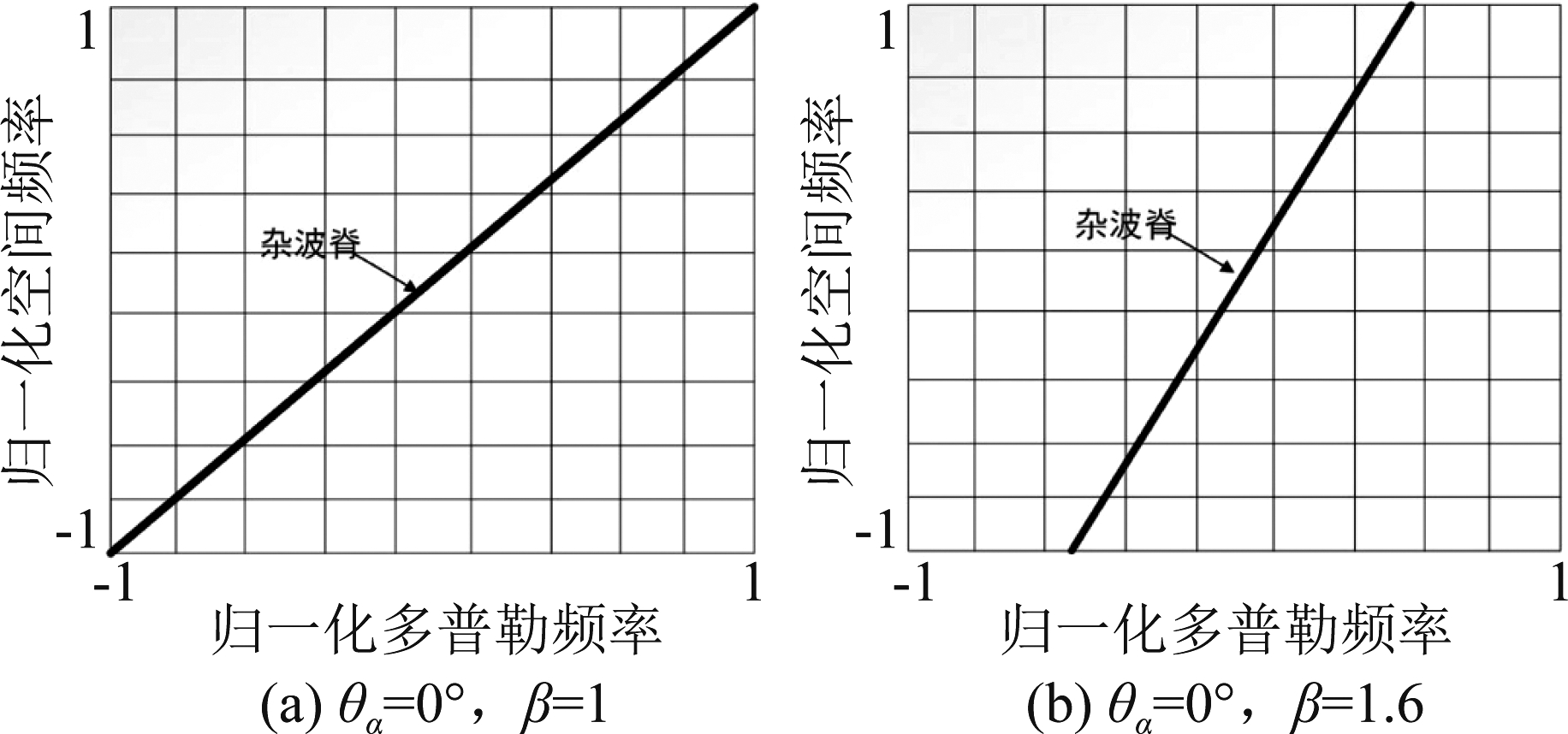
图2 离散空时平面杂波分布图
Fig.2 Discrete space-time plane clutter layout
3.3 字典构造方法
为了解决均匀划分的固定字典带来的离网问题,本文利用雷达系统参数、导航信息等先验知识来预先计算空时平面上的杂波分布,根据杂波分布的规律进行字典校正。在式(4)中,飞机速度V和偏航角θp的值可以从导航系统中获得,而λ、θα和φ可以通过雷达系统参数获得。
首先根据式(4)将归一化后的空间频率均匀离散化为Ns个网格点,构成集合{fs,i}。将空间频率中的网格间隔长度定义为:
(14)
然后根据离散化的空间频率集合来确定离散多普勒频率,式(6)可以写为:
i=1,...,Ns
(15)
且-1≤fd,min≤fd,i≤fd,max≤1, i=1,…,Ns,其中fd,min和fd,max分别为离散后多普勒网格点组的上界和下界。同理,将多普勒频率间隔长度组定义为:
Δd,i=|fd,i+1-fd,i|, i=1,...,Ns-1
(16)
对于正侧视阵列情形,当β<1时,多普勒频率间隔长度组{Δd,i}将会变大;当β>1时,{Δd,i}会变小。对于非正侧视阵列情形(θα或θp不等于0°),{Δd,i}是非均匀的,多普勒频率网格间距大小不一。较大的网格间距意味着低分辨率的多普勒频率,离网效应会更严重;而较小的网格间距会增强字典的列相关性,降低稀疏恢复的性能。因此,多普勒频率间隔应该满足αΔs<Δd,i<Δs。下面对原始多普勒频率间隔的大小展开讨论,其中定义
为fd,min和fd,max之间的一组新的多普勒频率,α为调整参数。
1)当原始的多普勒频率间隔大于空间频率间隔,即Δd,i>Δs,此时将这个间隔均匀离散为P个小区间,可以保证空时杂波谱的高分辨率。更新的多普勒频率和对应的间隔如下:
(17)
(18)
其中P=ceil(Δd,i/Δs)为将Δd,i/Δs的值四舍五入到不小于P的最小整数。
2)当原始的多普勒频率间隔小于空间频率间隔,即Δd,i<αΔs,此时将相邻的两个多普勒频率间隔合并为一个,这样可以减小字典的列相干性。更新的多普勒频率和对应的间隔如下:
(19)
(20)
(21)
3)当原始的多普勒频率间隔大小正好位于空间频率间隔和定义的间隔之间,即αΔs<Δd,i<Δs。此时多普勒频率和间隔不变,即:
(22)
(23)
通过上述分析,离散的多普勒频率组{fd,i}在区间[-1,-1+Δs,…, fd,min]和[fd,max, fd,max+Δs,…,1]之间调整后,得到一组新的离散化多普勒频率组
然后根据公式:
(24)
调整空间频率,得到一组新的离散化空间频率组
最后,用
和
来离散空时平面,对传统字典进行校正,构造式(11)中的过完备字典Ф,提高SR-STAP算法的性能。
因此,本文所提的字典构建方法具体步骤为:
1)根据式(5)将归一化后的空间频率均匀离散为Ns个网格点集合{fs,i};
2)根据式(15)得到相应的离散多普勒频率网格点集合{fd,i};
3)根据式(17)细化多普勒频率间隔,确保原始多普勒频率间隔不大于Δs;
4)根据式(18)合并相邻的多普勒频率间隔,确保原始多普勒频率间隔大于αΔs;
5)用间隔Δs离散符合αΔs<Δd,i<Δs条件的多普勒频率,并将步骤3)和4)得到新的多普勒频率合并起来得到一组新的多普勒频率组
6)根据式(24)调整空间频率,得到一组新的离散化空间频率组
7)根据离散化的
和
对应的空时导向矢量来构建空时过完备字典。
3.4 参数α的理论分析
机载雷达工作时会对接收到的数据进行采样,此时θm是第m个采样点的方位角,定义为:
θm=θ0+mΔθ, m=0,...,Nθ
(25)
其中θ0=0°,Δθ为方位角采样间隔,Nθ=180°/Δθ且θm∈[0°, 180°]。采样数据的回波信号多普勒频率定义为:
(26)
则此时的回波信号的多普勒频率间隔长度组为:
Δd1,m=|fd1,m+1-fd1,m|, m=0,...,Nθ-1
(27)
在STAP方法中,若空时离散化后的多普勒网格可以对应上采样数据中的多普勒频率间隔,回波信号的多普勒间隔需满足:
≤Δd,i≤Δd1,m
(28)
且Δd1,m取最小值。又因为Δd,i<αΔs,所以α最优取值区间应该为:
(29)
4 仿真实验
在机载正侧视ULA雷达中,将本文所提字典构造方法、传统字典构造方法、文献[27]所提调整多普勒频率字典构造方法进行对比分析,三种方法都用于稀疏恢复STAP算法中,主要考查各种方法在杂波空时谱估计、杂波抑制性能和运动目标检测性能三个方面的表现。在下文中将文献[27]所提方法命名为KASR-STAP,传统字典构造的稀疏STAP方法命名为SR-STAP。网格划分系数ρs设置为4,ρd设置为6。所有实验结果都是进行了100次独立蒙特卡洛运算的平均值。表1为仿真实验数据。
表1 仿真数据
Tab.1 Simulation data
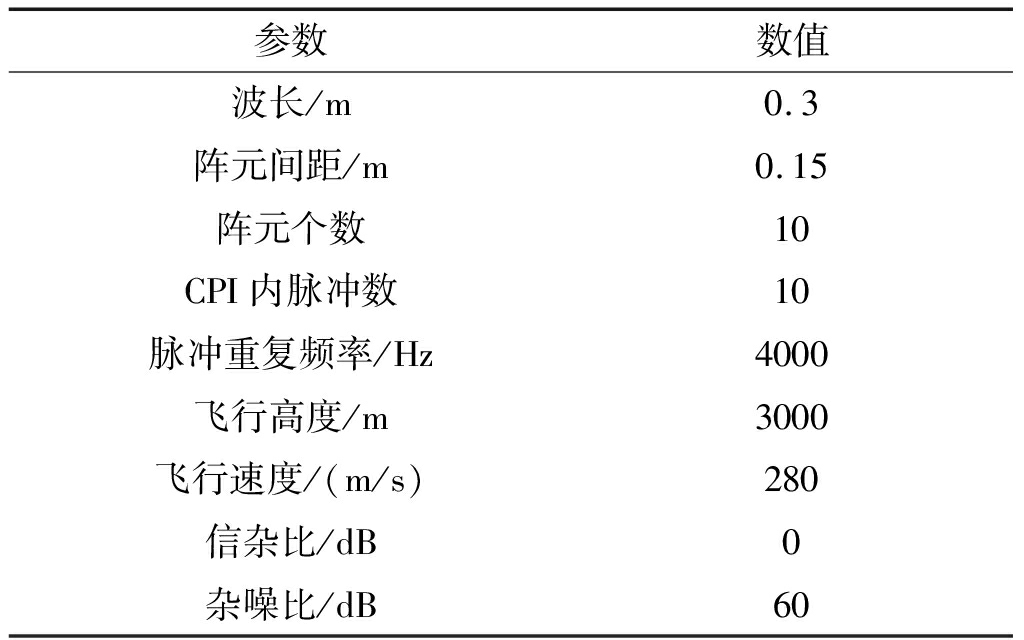
参数数值波长/m0.3阵元间距/m0.15阵元个数10CPI内脉冲数10脉冲重复频率/Hz4000飞行高度/m3000飞行速度/(m/s)280信杂比/dB0杂噪比/dB60
4.1 参数α的设定
第一个实验讨论参数α的不同取值对本文算法信杂噪比损失(Signal to Clutter plus Noise Ratio Loss, SCNRLoss)的影响。SCNRLoss定义为:
(30)
其中
为噪声的功率,μ为非零常数,
为检测范围内精确估计的CCM。用本文算法所构造的字典对SCNRLoss的评估结果见图3所示。在α最优取值区间内取0.1、0.2、0.3和0.4四个值,由仿真对比结果图可以得出,当α的取值为0.2时,SCNRLoss的性能最优。因此在以下实验中将α设置为0.2。
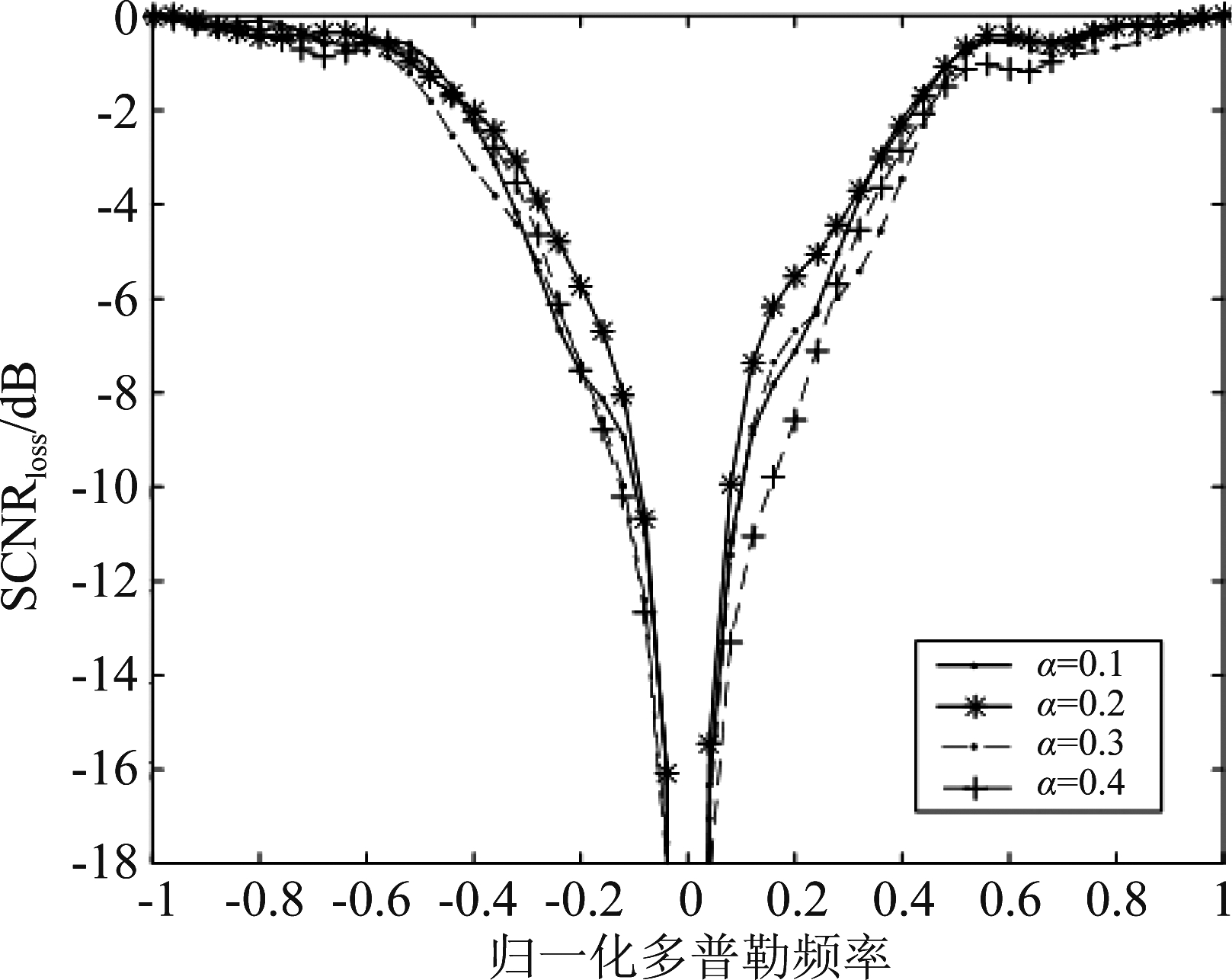
图3 参数α与SCNRLoss关系图
Fig.3 The relationship between factor α and SCNRLoss
4.2 杂波空时功率谱分析
第二个实验对本文所提算法与SR-STAP、KASR-STAP算法估计得到的杂波空时功率谱进行对比。图4(a)～(c)依次为SR-STAP、KASR-STAP和本文方法估计得到的杂波空时功率谱。由图4(a)和(b)可以看出,传统SR-STAP方法和KASR-STAP方法构造的字典估计的杂波功率谱虽然集中在杂波脊线上,但是有一定的展宽,这是由于离网效应导致杂波功率谱估计产生误差,会影响杂波抑制性能。由图4(c)可以看出,使用本文方法构造字典估计的杂波功率谱完全集中在杂波脊线上,有利于杂波抑制,验证了本文所提算法的有效性。
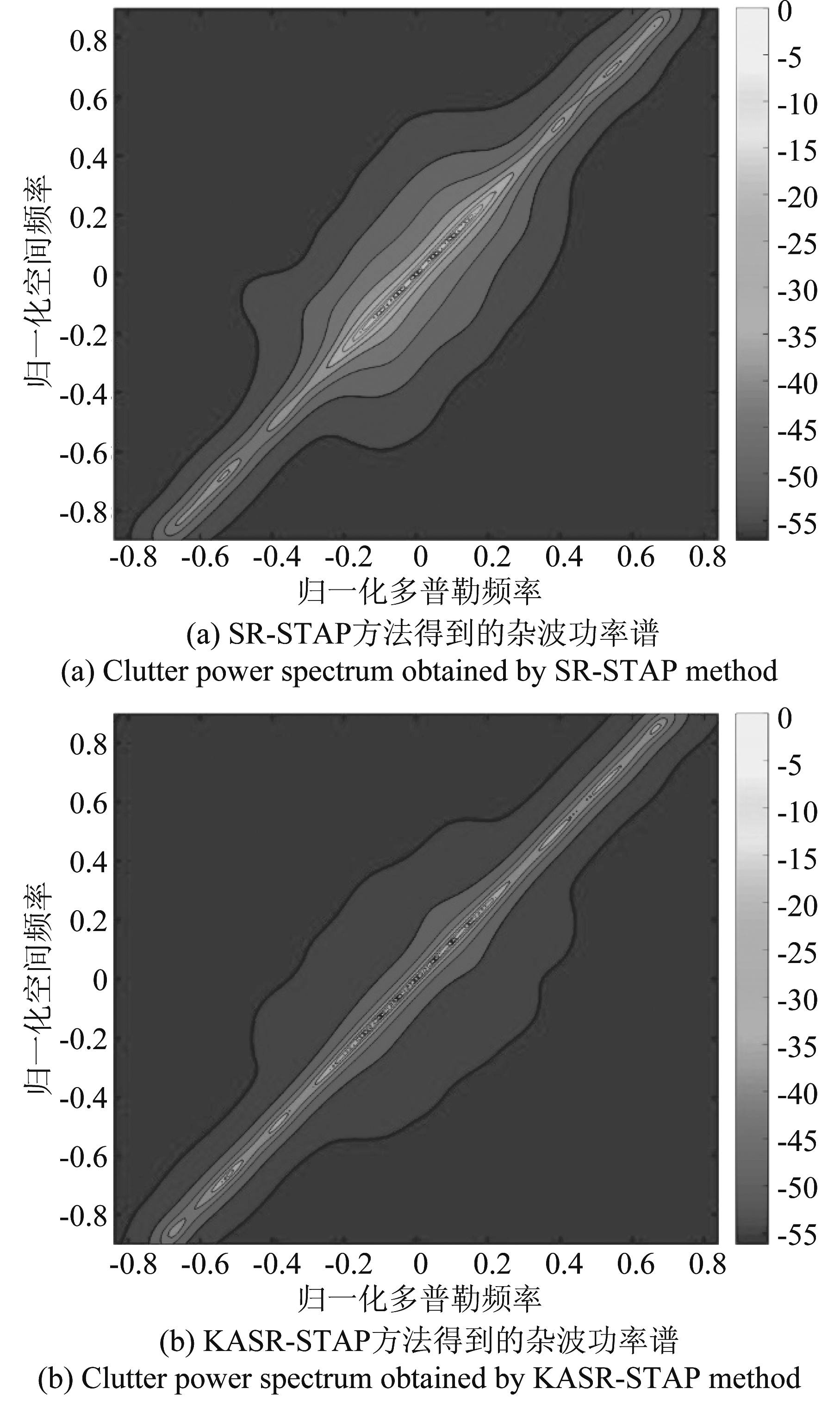
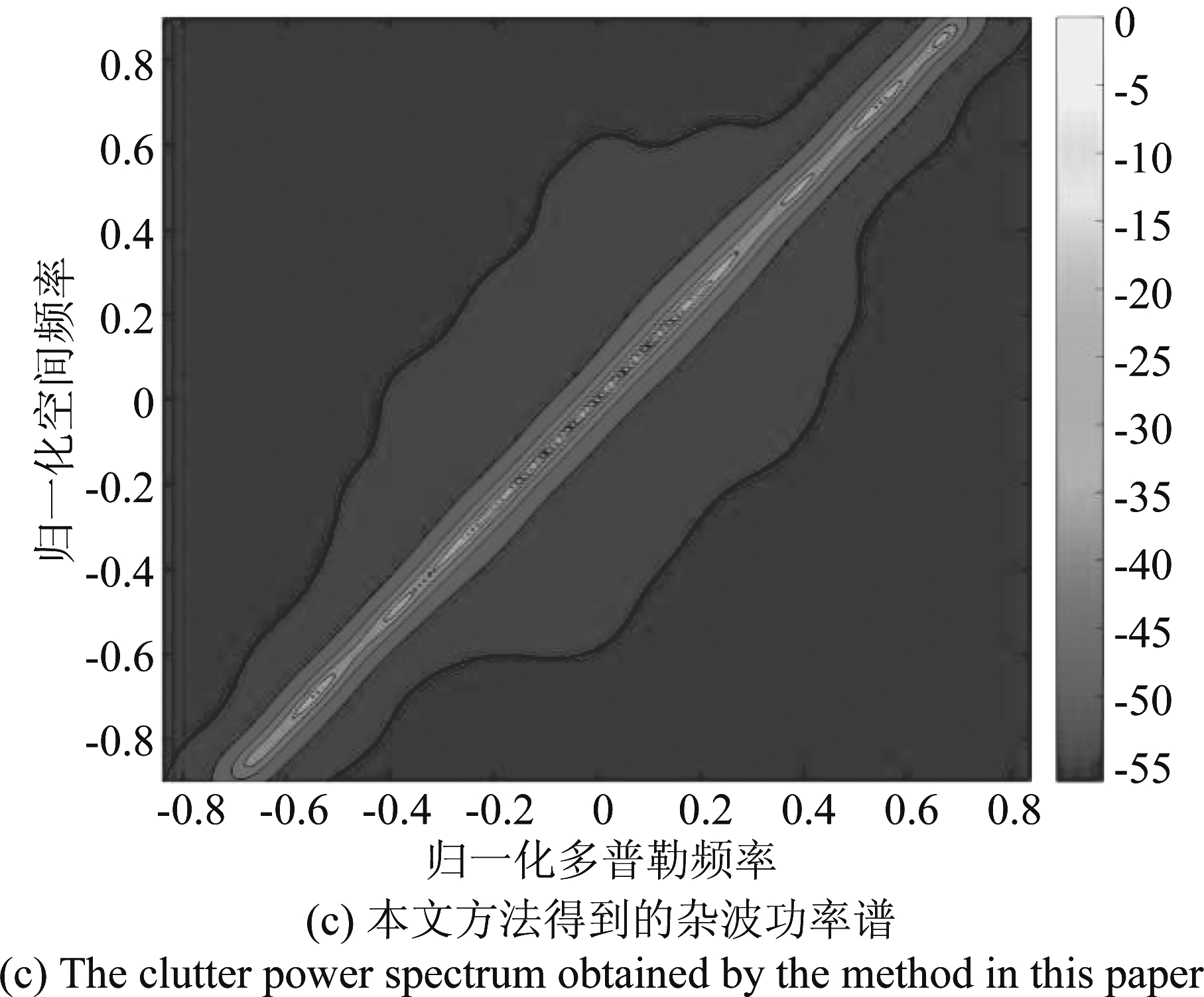
图4 杂波功率谱
Fig.4 Clutter power spectrum
4.3 杂波抑制性能分析
第三个实验对比分析了SR-STAP、KASR-STAP和本文所提算法的杂波抑制性能。图5为三种算法的SCNRLoss与归一化多普勒频率之间的关系曲线。可以看出,SR-STAP算法和KASR-STAP算法的SCNRLoss曲线与本文所提算法相比,在主杂波域内的凹陷深度较浅且凹口较宽,主要是由于离网效应导致对CCM的估计不准确,降低了杂波抑制性能。相比于其他两种算法,本文所提算法的SCNRLoss曲线在主杂波域内形成了更深的凹陷,相较于KASR-STAP算法大约加深了2 dB,且凹口变窄,因此可以更加有效地抑制杂波且有利于检测出动目标。
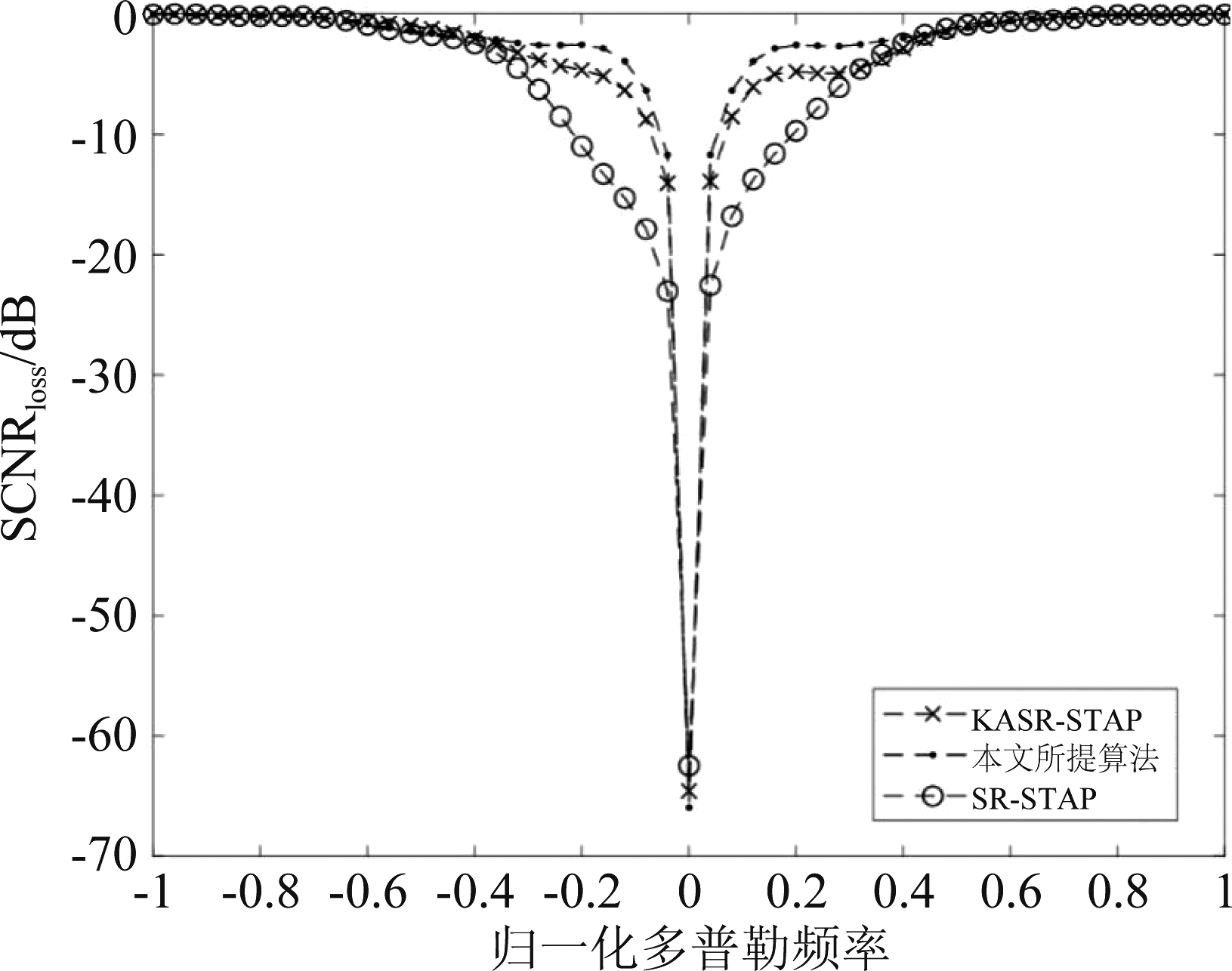
图5 信杂噪比损失
Fig.5 The signal to clutter plus noise ratio loss
4.4 运动目标检测性能分析
第四个实验对SR-STAP、KASR-STAP和本文所提算法针对距离单元样本中动目标的检测能力进行对比。分别使用三种算法对样本数据进行滤波,图6为距离向输出功率。由图可知,三种算法构成的自适应滤波权都可以检测出第51号距离单元处的运动目标,但是本文所提算法的剩余杂波功率小于另外两种算法。因此,本文算法的输出信杂噪比高于其他两种算法,对杂波的抑制能力更好,体现了较强的运动目标检测能力。
图6 距离向输出功率
Fig.6 The output power of range gate
5 结论
针对机载雷达稀疏恢复STAP中存在的离网效应问题,本文提出了一种网格失配下稀疏恢复STAP字典校正方法。该方法首先根据雷达参数等先验知识预先获得杂波脊,接着自适应调整空间频率和多普勒频率间隔,最后根据更新后的离散化空间频率和多普勒频率计算空时导向矢量,并构建超完备稀疏字典。仿真结果表明,与仅调整多普勒频率来校正字典的算法相比,本文方法校正的字典进一步克服了网格失配问题,使离网效应引起的杂波脊扩展得到了明显缓解,杂波的抑制和运动目标检测性能得到显著提升。
[1] MELVIN W L.A STAP overview[J].IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19-35.
[2] 毕权杨, 李旦, 张建秋.空时自适应处理张量波束成形器的外积合成法[J].航空学报, 2019, 40(10): 322939.
BI Quanyang, LI Dan, ZHANG Jianqiu.An outer product synthesis approach to tensor beamformer for space-time adaptive processing[J].Acta Aeronautica et Astronautica Sinica, 2019, 40(10): 322939.(in Chinese)
[3] REED I S, MALLETT J D, BRENNAN L E.Rapid convergence rate in adaptive arrays[J].IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853-863.
[4] DUAN Keqing, YUAN Huadong, XU Hong, et al.Sparsity-based non-stationary clutter suppression technique for airborne radar[J].IEEE Access, 2018, 6: 56162-56169.
[5] SARKAR T K, WANG Hong, PARK S, et al.A deterministic least-squares approach to space-time adaptive processing(STAP)[J].IEEE Transactions on Antennas and Propagation, 2001, 49(1): 91-103.
[6] CHEN Hongmeng, LIU Jing, SUN Hanwei, et al.Knowledge-aided space time adaptive processing for airborne radar in heterogeneous environments[C]∥2019 IEEE International Conference on Signal, Information and Data Processing(ICSIDP).Chongqing, China.IEEE, 2019: 1-5.
[7] SUN Guohao, HE Zishu, TONG Jun, et al.Knowledge-aided covariance matrix estimation via kronecker product expansions for airborne STAP[J].IEEE Geoscience and Remote Sensing Letters, 2018, 15(4): 527-531.
[8] DONOHO D L, ELAD M, TEMLYAKOV V N.Stable recovery of sparse overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory, 2006, 52(1): 6-18.
[9] CAND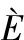
S E J, ROMBERG J K, TAO T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics, 2006, 59(8):1207-1223.
[10] COTTER S F, RAO B D, ENGAN K, et al.Sparse solutions to linear inverse problems with multiple measurement vectors[J].IEEE Transactions on Signal Processing, 2005, 53(7): 2477-2488.
[11] 马泽强, 王希勤, 刘一民,等.基于稀疏恢复的空时二维自适应处理技术研究现状[J].雷达学报, 2014, 3(2): 217-228.
MA Zeqiang, WANG Xiqin, LIU Yimin, et al.An overview on sparse recovery-based STAP[J].Journal of Radars, 2014, 3(2): 217-228.(in Chinese)
[12] 阳召成, 黎湘, 王宏强.基于空时功率谱稀疏性的空时自适应处理技术研究进展[J].电子学报, 2014, 42(6): 1194-1204.
YANG Zhaocheng, LI Xiang, WANG Hongqiang.An overview of space-time adaptive processing technology based on sparsity of space-time power spectrum[J].Acta Electronica Sinica, 2014, 42(6): 1194-1204.(in Chinese)
[13] SELESNICK I W, PILLAI S U, LI Keyong, et al.Angle-Doppler processing using sparse regularization[C]∥2010 IEEE International Conference on Acoustics, Speech and Signal Processing.Dallas, TX, USA.IEEE, 2010: 2750-2753.
[14] SUN Ke, MENG Huadong, WANG Yongliang, et al.Direct data domain STAP using sparse representation of clutter spectrum[J].Signal Processing, 2011, 91(9): 2222-2236.
[15] YANG Zhaocheng, DE LAMARE R C, LI Xiang.L1_regularized STAP algorithms with a generalized sidelobe canceler architecture for airborne radar[J].IEEE Transactions on Signal Processing, 2012, 60(2): 674-686.
[16] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al.Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J].Signal Processing, 2013, 93(12): 3567-3577.
[17] YANG Xiaopeng, SUN Yuze, ZENG Tao, et al.Fast STAP method based on PAST with sparse constraint for airborne phased array radar[J].IEEE Transactions on Signal Processing, 2016, 64(17): 4550-4561.
[18] HE Xuezhi, LIU Changchang, LIU Bo, et al.Sparse frequency diverse MIMO radar imaging for off-grid target based on adaptive iterative MAP[J].Remote Sensing, 2013, 5(2): 631-647.
[19] ZHANG Yi, YE Zhongfu, XU Xu, et al.Off-grid DOA estimation using array covariance matrix and block-sparse Bayesian learning[J].Signal Processing, 2014, 98: 197-201.
[20] TAN Zhao, NEHORAI A.Sparse direction of arrival estimation using co-prime arrays with off-grid targets[J].IEEE Signal Processing Letters, 2014, 21(1): 26-29.
[21] 高志奇.机载雷达的稳健稀疏空时自适应处理方法研究[D].西安: 西安电子科技大学, 2016.
GAO Zhiqi.Robust sparseness space-time adaptive processing algorithms for airborne radar[D].Xi’an: Xidian University, 2016.(in Chinese)
[22] LI Zhihui, ZHANG Yongshun, GE Qichao, et al.Off-grid STAP algorithm based on reduced-dimension local search orthogonal matching pursuit[C]∥2019 IEEE 4th International Conference on Signal and Image Processing(ICSIP).Wuxi, China.IEEE, 2019: 187-191.
[23] YUAN Huadong, XU Hong, DUAN Keqing, et al.Sparse Bayesian learning-based space-time adaptive processing with off-grid self-calibration for airborne radar[J].IEEE Access, 2018, 6: 47296-47307.
[24] YE Hongda, LI Zhongyu, LIU Zhutian, et al.Clutter-ridge matched SR-STAP technique for non-stationary clutter suppression[C]∥2020 IEEE Radar Conference(RadarConf20).Florence, Italy.IEEE, 2020: 1-4.
[25] HE Pengyuan, HE Shun, Yang Zhiwei, et al.An off-grid STAP algorithm based on local mesh splitting with bistatic radar system[J].IEEE Signal Processing Letters, 2020, 27: 1355-1359.
[26] CHI Yuejie, SCHARF L L, PEZESHKI A, et al.Sensitivity to basis mismatch in compressed sensing[J].IEEE Transactions on Signal Processing, 2011, 59(5): 2182-2195.
[27] DUAN Keqing, LIU Weijian, DUAN Guangqing, et al.Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP[J].IET Radar, Sonar & Navigation, 2018, 12(5): 557-564.
