1 引言
信道是无线通信系统的重要组成部分。信道模型通过模拟实际通信场景中的衰落、多径和多普勒效应可以为无线通信系统的性能评估、优化设计提供重要技术支撑,而多普勒谱建模在移动无线通信场景下引起了广泛的关注。因此设计准确、高效的多普勒谱建模算法具有重要意义。
在移动通信中,莱斯信道和瑞利信道是最重要的信道,这些信道可以相对容易的物理解释,并且易于描述,且能通过数据测量验证。根据多径效应,接收天线处接收到的电磁波相互叠加,会根据相位关系体现加性或者减性的相互作用。在移动通信场景中,根据发射机和接收机的相对移动会导致频率偏移或者散射体导致的频率偏移,我们称为多普勒频移[1],其取决于一部分波的到达角,产生不同的多普勒频移,对于所有波的和可以得到一个关于多普勒频率的连续谱,称为多普勒功率谱密度。
在移动无线信道建模时,经典的方法是将问题做简化,认为电磁波传播是在二维平面中传播的,且在到达角均匀分布在0到2π区间上的,天线是全向天线,这时候的多普勒功率谱为经典的Jakes功率谱[1-2]。如果不考虑简化方案,将垂直分量也考虑在内就会得到参考文献[3]中推导的三维传播模型。
为了准确的反应复杂的城区和山区的无线信道特性,我们针对山东省青岛市的城区和山区的无线信道进行了外场测量,并对其信道特征值进行提取建模,初步工作在文献[4]中有所展现,但是在后续的数据分析中,我们通过对于山区模型的分析并提取其特征值以后,得到的功率谱往往不是如上文献中提到的经典功率谱,最为常见的就是受限的Jakes功率谱,其出现的原因是由于不同的障碍物导致到达角不是均匀分布的,或者天线不是全向天线而是扇形天线[2,5],在此类情况下,功率谱不再如经典Jakes功率谱一般具有偶函数的性质,实际呈现的功率谱是非对称的,我们称为受限Jakes功率谱。信道建模较新的文献[6-8],基本都仅仅考虑经典的功率谱模型或者忽视了对于功率谱模型的考量,依旧停留在经典的Jakes功率谱、高斯谱和双高斯谱这类功率谱上,对于受限功率谱模型鲜有涉及。为了更真实的反映信道环境,对于受限多普勒功率谱的信道建模及其仿真工作变得尤为重要。本文将使用两种传统的经典多普勒功率谱仿真方法和一种针对非对称多普勒功率谱仿真方法对受限Jakes功率谱进行仿真,从建模准确度和复杂度两个方面进行了对比研究。
本文结构如下,第2节介绍两种经典的确定性信道建模原理,后文将在这两种方法的基础上进行具有受限多普勒功率谱的信道建模。第3节对于经典的Jakes功率谱和受限Jakes功率谱的功率谱密度函数及其自相关函数进行展开,后续建模将基于受限Jakes功率谱的功率谱密度函数和自相关函数进行仿真来评估仿真效果。第4节介绍三种具有受限多普勒谱的信道仿真模型,详细介绍了三种模型的仿真原理。第5节给出三种模型对于受限Jakes功率谱的仿真结果,并对比其自相关函数与理论自相关函数的均方根误差的均值和算法复杂度,评价模型优劣。第6节总结。
2 确定性信道建模原理
根据确定性信道建模原理,常用的多普勒谱的仿真方法基本分为两种:滤波法和正弦波叠加法。
2.1 滤波法
使用滤波法时,如下图1所示其中νi(t)为高斯白噪声,作为一个输入,再通过图中具有传递函数Hi(f)的多普勒滤波器,假设滤波器是理想的且可以拟合到任何给定的频率响应。当νi(t)～N(0,1)即,在滤波器的输出处得到的μi(t)是一个零均值的高斯随机过程,其功率谱密度Sμi μi(f)等于传递函数的绝对值的二次方,即Sμi μi(f)=|Hi(f)|2。所以,我们将一个有色高斯随机过程μi(t)看作高斯白噪声νi(t)滤波后的结果。
图1 滤波法参考模型
Fig.1 Filter method
2.2 正弦波叠加法
正弦波叠加法(Sum-of-Sinusoids,SoS)如图2所示,其依据是,将具有恒定增益、等距频率和随机相位的无穷数量正弦曲线进行叠加可以得到一个随机的高斯过程。根据这个原理,随机高斯过程μi(t)可以由无穷多个正弦曲线求和来描述,如下式
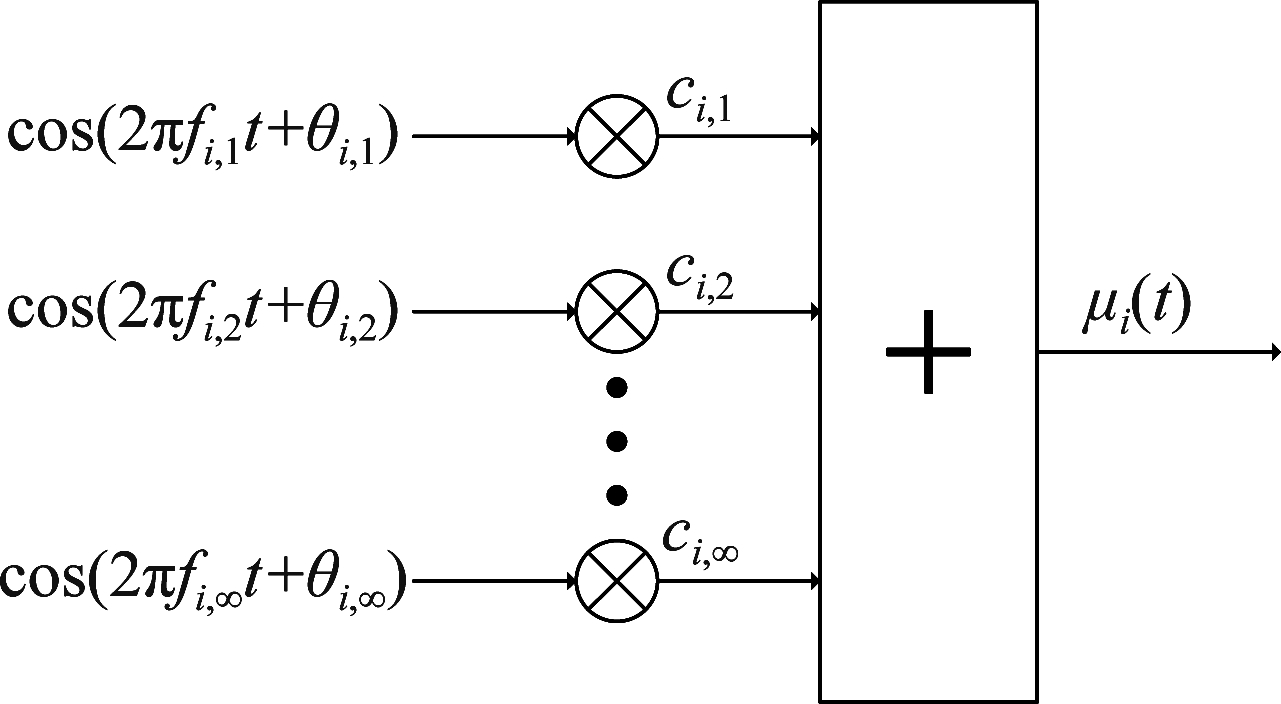
图2 正弦波叠加法参考模型
Fig.2 SoS method
(1)
式中,相位θi,n(n=1,2,...,Ni)是独立同分布的随机变量,在(0,2π]上均匀分布。Ni表示谐波分量数目,增益ci,n和频率fi,n由下式计算
(2)
fi,n=n·Δfi
(3)
由式(3)可以看出,当Ni→∞,Δf→0时,可以覆盖整个频率范围。
对于以上三个参数,目前已有各种方法进行确定。在此我们主要给出精确多普勒频散法(MEDS)。
精确多普勒频散法是由文献[11]首次引入,是专门针对Jakes功率谱密度开发而成的,其增益ci,n和频率fi,n分别表示为
(4)
(5)
其中均值功率为
表示最大多普勒频移。
3 多普勒功率谱
3.1 Jakes功率谱
假设电磁波是在二维平面发生的,到达角a0是均匀的分布在[0,2π)区间上,对于全向天线,可以计算到散射分量μ(t)的功率谱服从经典的Jakes多普勒多普勒功率谱Sμμ(f)[2]:
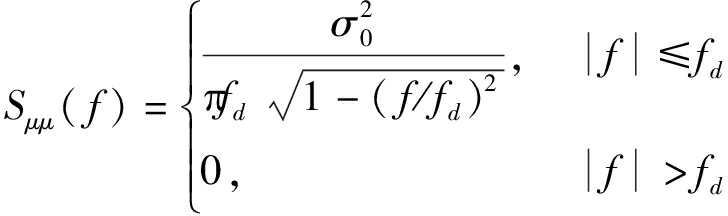
(6)
其中fd表示最大多普勒频移。
通过对Jakes功率谱密度Sμμ(f)的傅里叶反变换得到自相关函数
(7)
其中,J0(·)表示第一类零阶Bessel函数。
3.2 受限Jakes功率谱
Jakes功率谱认为到达波其到达角是均匀分布在区间[0,2π)上的,且天线是全向。在此条件下Jakes功率谱是一个对称的U型谱。但是Jakes谱的假设条件在实际中很难完全满足,因为实际空间的障碍物的随机分布特性,导致到达角a0可能被限制在[a0,2π-a0)区间不能到达接收器,或者使用的天线是扇形天线和定向天线,这个假设也成立。此时可以得到受限Jakes功率密度函数如式(8)。
(8)
式中, fd表示非受限时Jakes功率谱的最大多普勒频率,且fmin和fmax是受限Jakes功率谱的最小多普勒频率和最大多普勒频率,且落在区间0≤fmin≤fmax≤fd内。可以看出, fmin=fmax时,得到对称Jakes功率谱密度。因此,经典Jakes谱可以认为是受限谱的一种特殊情况。
通过对受限Jakes功率谱密度Sμμ(f)的傅里叶反变换得到自相关函数
(9)
4 受限多普勒功率谱仿真模型
通常可以使用一个复数高斯随机过程模拟一个窄带信号在非频率选择信道上的传输,该过程为
μ(t)=μ1(t)+jμ2(t)
(10)
其中μ1(t)和μ2(t)是实数高斯随机过程,分别为窄带过程的同相分量和正交分量。
4.1 双路滤波法
在使用滤波法仿真时,文献[9]在对于经典Jakes功率谱建模时,使用了两条路滤波的仿真方法,分别产生两条有色复高斯随机信号,分别表示I路和Q路,仿真模型如下图3所示。
图3 双路滤波法仿真模型
Fig.3 Dual-path filtering method
该方法首先生成两个高斯随机过程,然后通过快速傅里叶变换,将高斯随机过程转换到频域,接着进行频域滤波,滤波后在转换到时域,再将I路和Q路的随机过程相加,即可生成具有相应多普勒功率谱的随机过程。我们将这种方法使用在受限多普勒谱的仿真当中,将多普勒滤波器中的Jakes功率谱替换成受限Jakes多普勒功率谱,即可完成仿真。
4.2 单路滤波法
单路滤波法与双路滤波法不同的地方在于,直接产生一个复高斯随机过程,直接在频域进行滤波,再转换回时域,也可以生成具有相应多普勒功率谱的随机过程。
图4 单路滤波法仿真模型
Fig.4 Single-path filtering method
4.3 拼接法
此方法是由文献[10]在扩展的Suzuki过程建模中提出的,并将其于正弦波叠加法结合做出了改进。根据式(8)可以通过由两个功率谱进行拼接,得到想要的功率谱形状。首先,由于考虑的功率谱是非对称的,这使得实数值高斯随机过程μ1(t)和μ2(t)是互相关的,因此给出了如下交叉相关的模型,如图5所示。
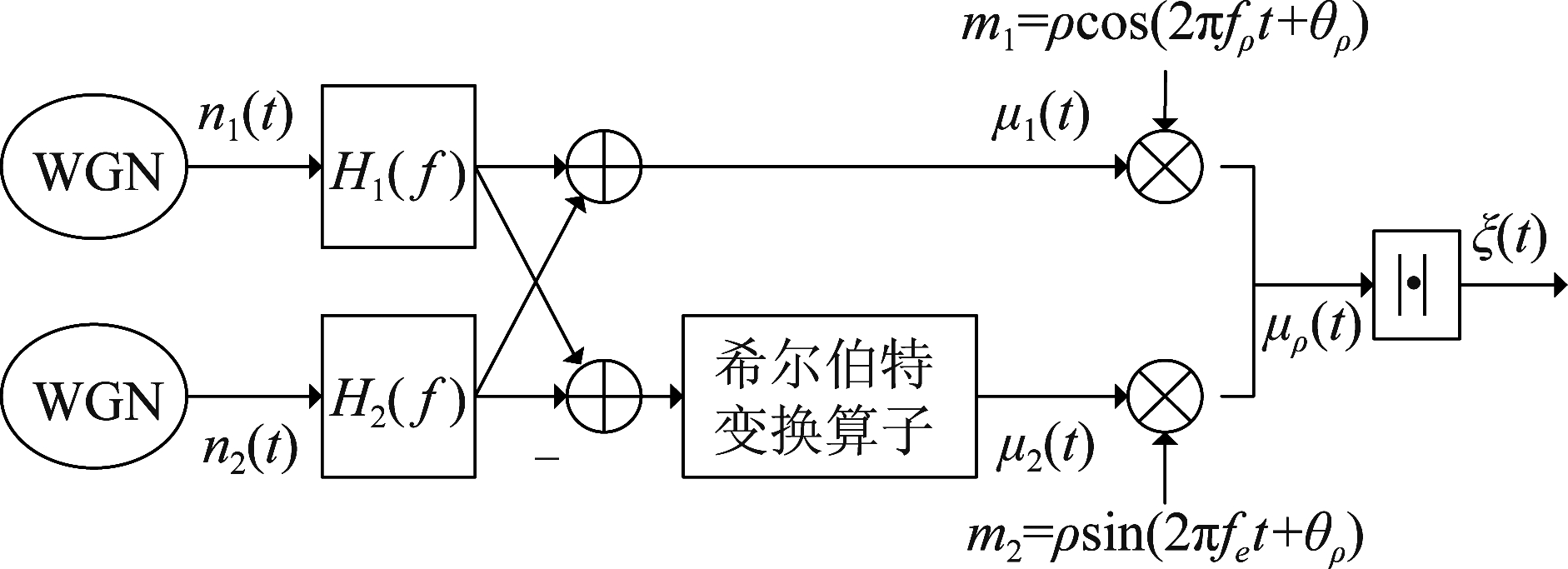
图5 具有交叉相关的高斯随机过程μ1(t)和μ2(t)的莱斯过程ξ(t)的参考模型
Fig.5 Reference model for Rice processes ξ(t)with cross-correlated underlying Gaussian random processes μ1(t)and μ2(t)
由图5可以得出以下关系
μ1(t)=ν1(t)+ν2(t)
(11)
(12)
式(11)中,νi(t)表示一个有色高斯随机过程,式(12)中的
表示其希尔伯特变换。νi(t)的谱形状是由传递函数为
的理想滤波器对于高斯白噪声ni(t)～N(0,1)滤波得到的。假定n1(t)和n2(t)是不相关的。μ(t)=μ1(t)+jμ2(t),μ1(t)和μ2(t)的自相关函数和交叉相关函数可以表示为
rμμ(τ)=rμ1μ1(τ)+rμ2μ2(τ)+j(rμ1μ2(τ)-rμ2 μ1(τ))
(13)
可以推出
rμ1μ1=rν1ν1+rν2ν2+rν1ν2+rν2ν1
(14)
(15)
(16)
(17)
通过知道关系式
和
可推出
rμ1μ1(τ)=rμ2μ2(τ)
(18)
rμ1μ2(τ)=-rμ2 μ1(τ)
(19)
rμ1μ1(τ)=rν1ν1(τ)+rν2ν2(τ)=rμ2μ2(τ)
(20)
(21)
所以式(13)又可以表示为
(22)
对式(13)和式(22)做傅里叶变换后,得到多普勒功率谱密度表达式
Sμμ(f)=Sμ1μ1(f)+Sμ2μ2(f)+j[Sμ1μ2(f)-Sμ2 μ1(f)]
(23)
(24)
于是对于多普勒功率谱密度Sνiνi(f)和
以及其自相关函数rνiνi(τ)和
有如下关系式
(25)
(26)
Sν2ν2(f)=rect(f/fmin)·Sν1ν1(f)
(27)
(28)
(29)
(30)
(31)
(32)
式中,J0(·)和H0(·)分别表示第一类零阶Bessel函数和零阶Struve函数。将式(25)和式(31)代入式(24),则用Sνiνi(f)表示Sμμ(f)为
Sμμ(f)=2[(1+sgn(f))·Sν1ν1(f)+
(1-sgn(f))·Sν2ν2(f)]
(33)
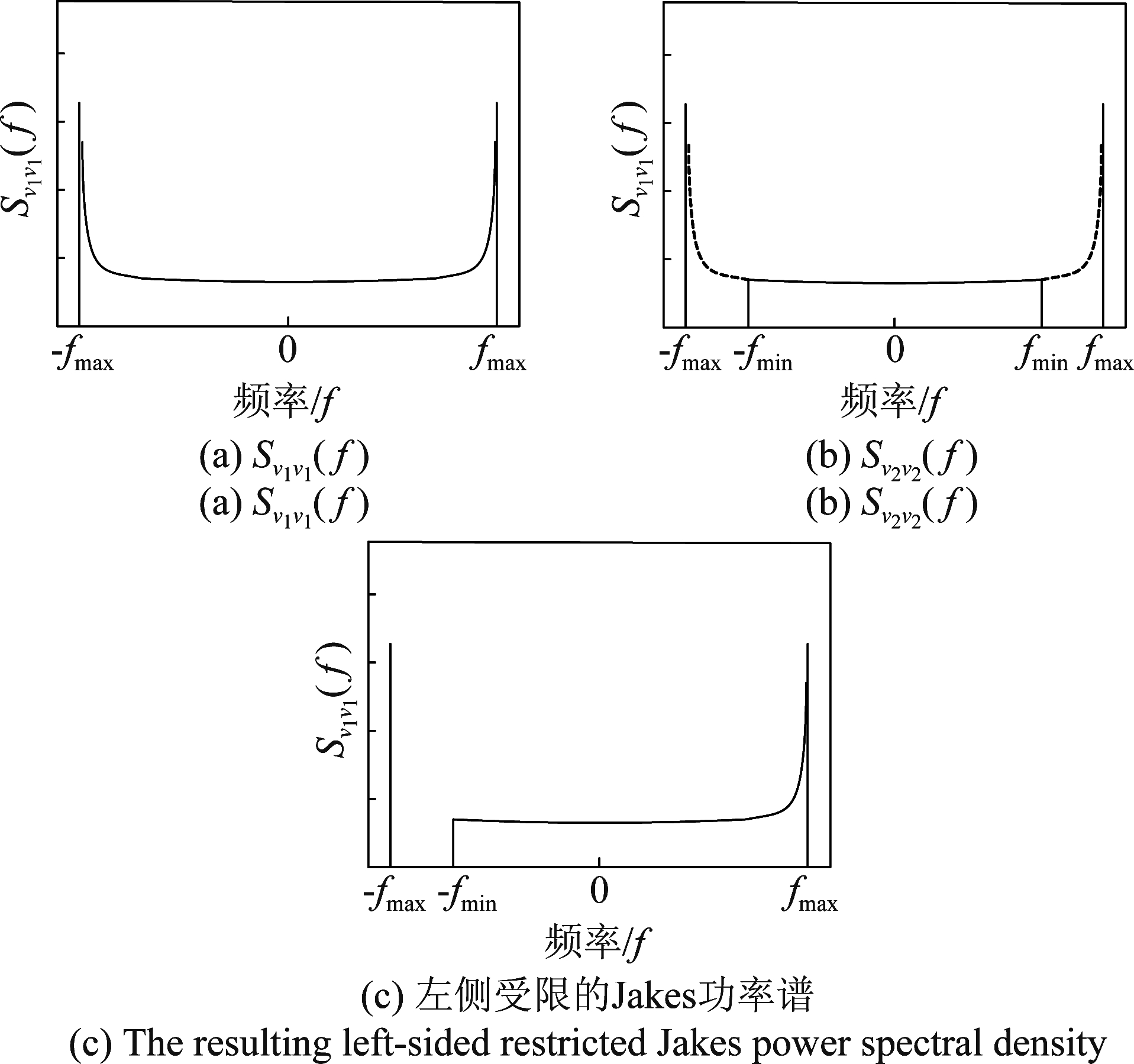
图6 拼接法拼接过程示意图
Fig.6 Doppler power spectral densities
4.3.1 改进拼接法仿真模型
4.3节给出的拼接法,其主要核心结构是通过数字滤波器和希尔伯特变化器达到仿真效果。
为了避免设计数字滤波器和希尔伯特变换器,可以结合正弦波叠加法得出拼接法下的正弦波叠加法仿真模型(本文统称为改进拼接法模型),根据图5的模型,将其行修改如图7的仿真模型。
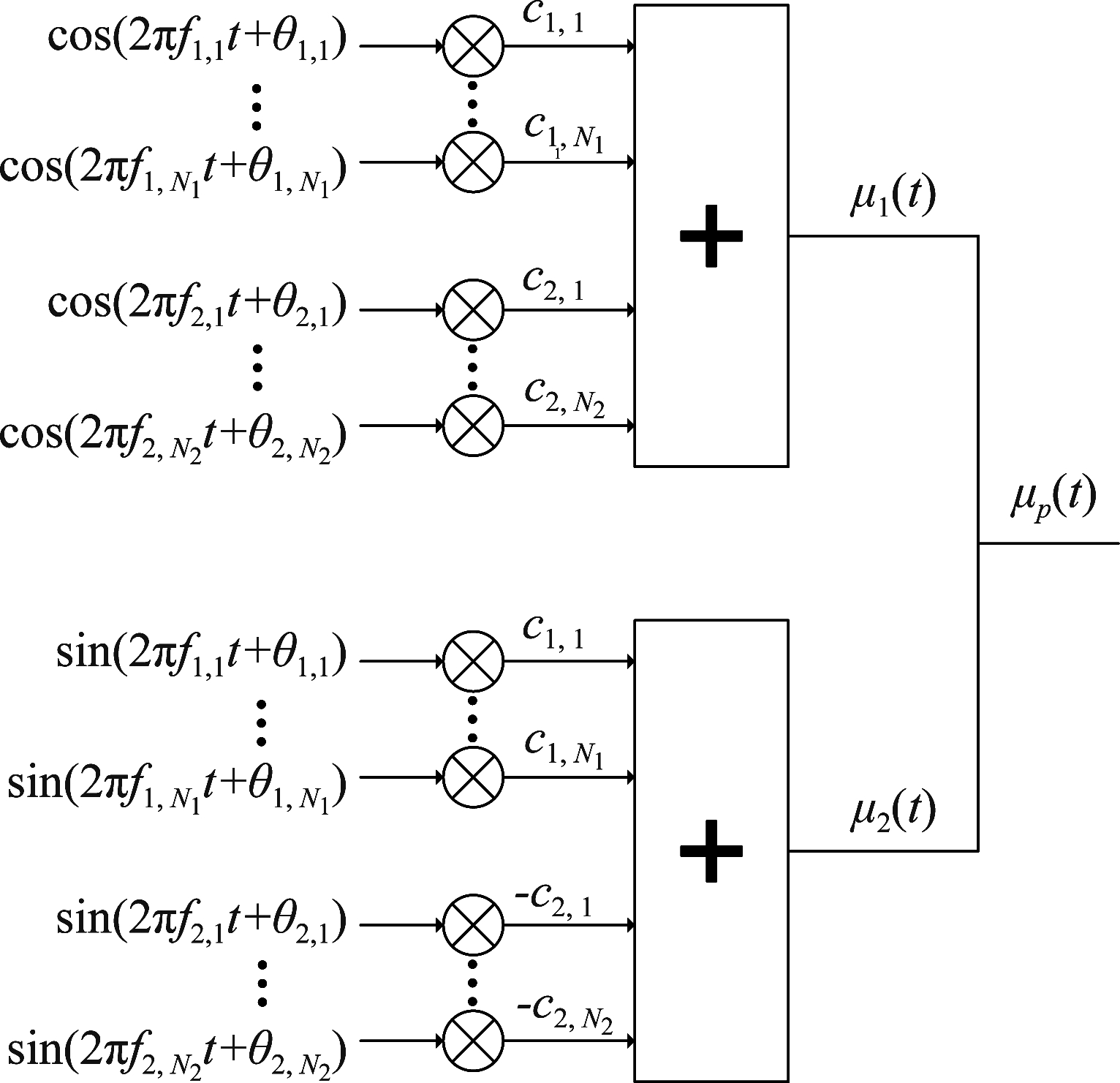
图7 改进拼接法仿真模型
Fig.7 Improved splicing method
根据图7的模型,重新针对精确多普勒频散法的参数进行计算,在此需要引入一个辅助变量k0=fmin/fmax,表示频率比,经典Jakes功率谱k0=1,对于受限Jakes功率谱k0≤1,有如下关系式
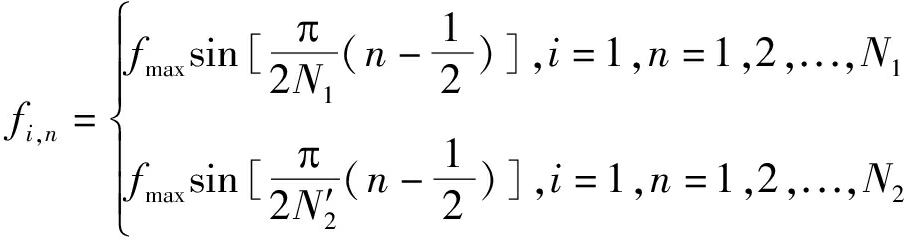
(34)
式中
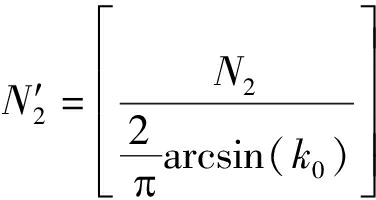
(35)
对于式(34)中N2是将离散多普勒频率f2,n限制在区间(0, fmin]。对于正弦曲线数量N2(≤N2)仍需要根据实际需求自己定义。路径增益ci,n也需要经过修正,如下式
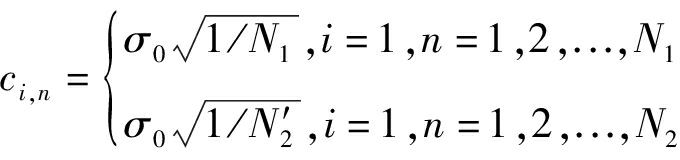
(36)
5 仿真结果
在这一节中,使用matlab的.periodogram和PSD函数计算仿真信号的功率谱,使用xcov函数计算自相关函数,并绘制了仿真信号的幅度分布特性,将其与理论的功率谱、自相关函数和幅度分布进行比较,最后运行100次,计算其自相关函数与理论自相关函数的均方根误差的均值来衡量三种仿真模型的效果。其中统一设置, fmax=33.333 Hz、fmin=5 Hz分别为最大、最小多普勒频移,改进拼接法的正弦波数量N2=25。
5.1 多普勒谱及自相关函数
图8、图9、图10分别为使用单路滤波法、改进拼接法和双路滤波法仿真的信道的功率谱。图 11、图12、图13分别为使用单路滤波法、改进拼接法和双路滤波法仿真的自相关函数。
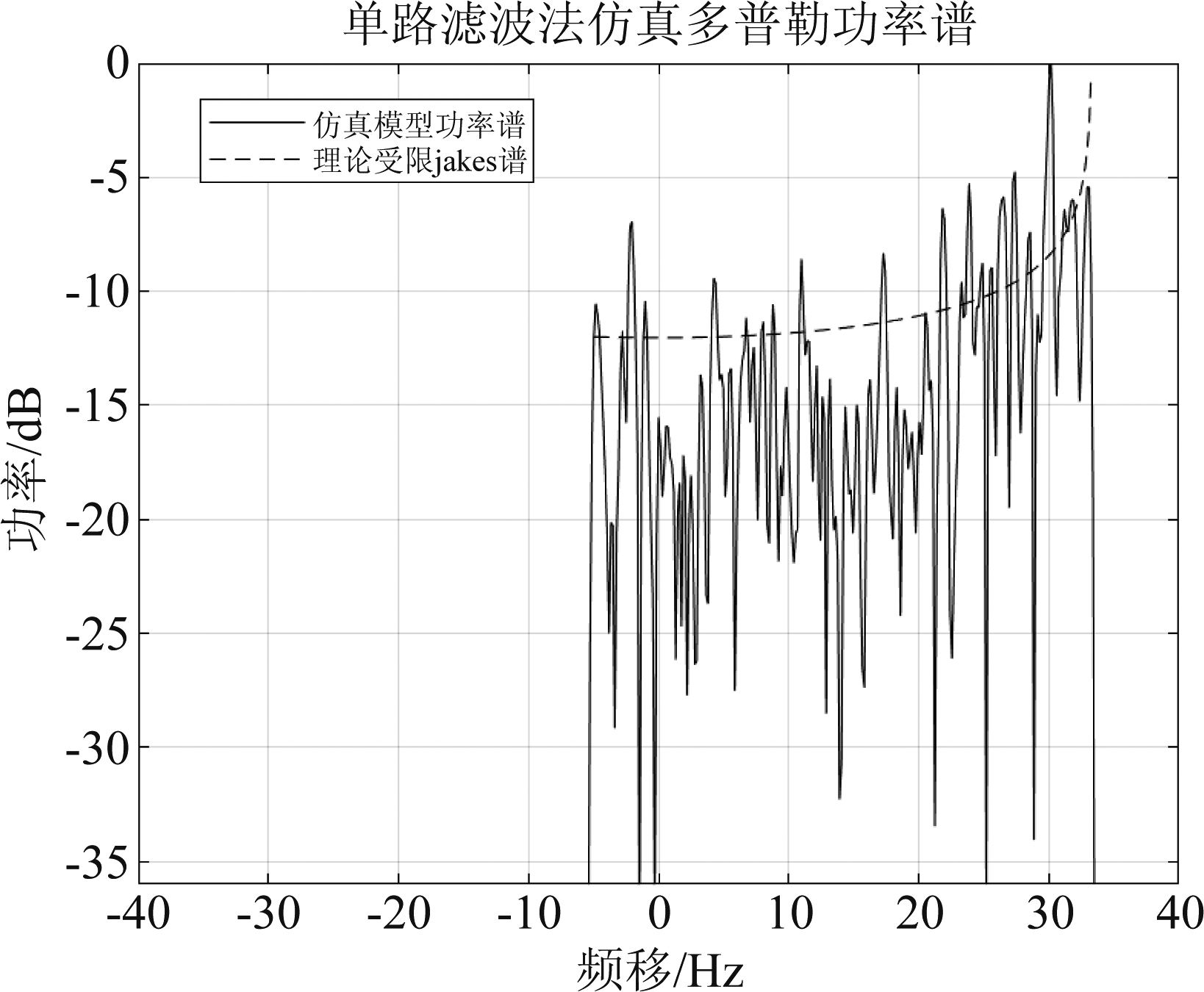
图8 单路滤波法仿真功率谱
Fig.8 Simulation of power spectra by single-path filtering
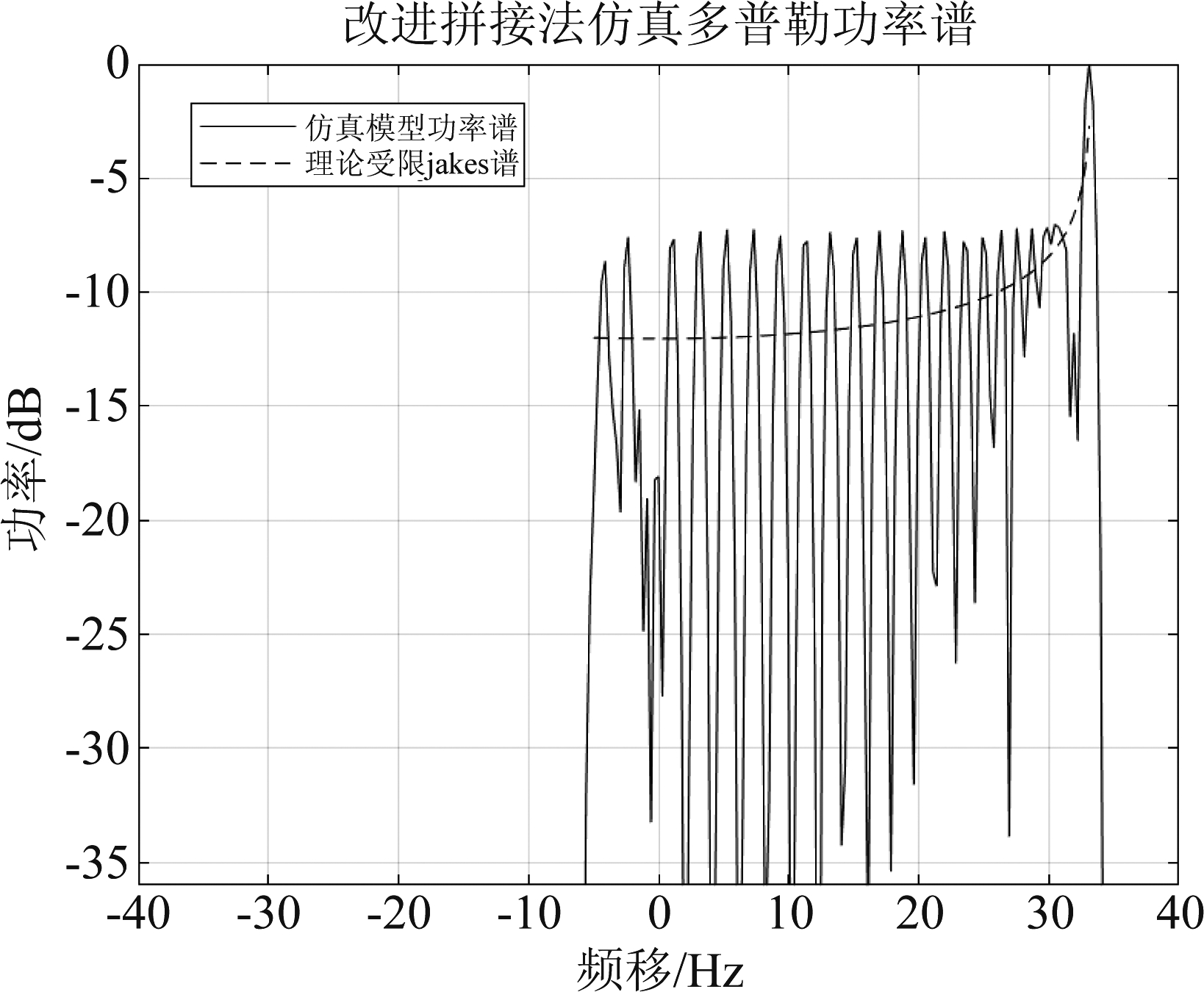
图9 改进拼接法仿真功率谱
Fig.9 Simulation of power spectra by improved splicing method
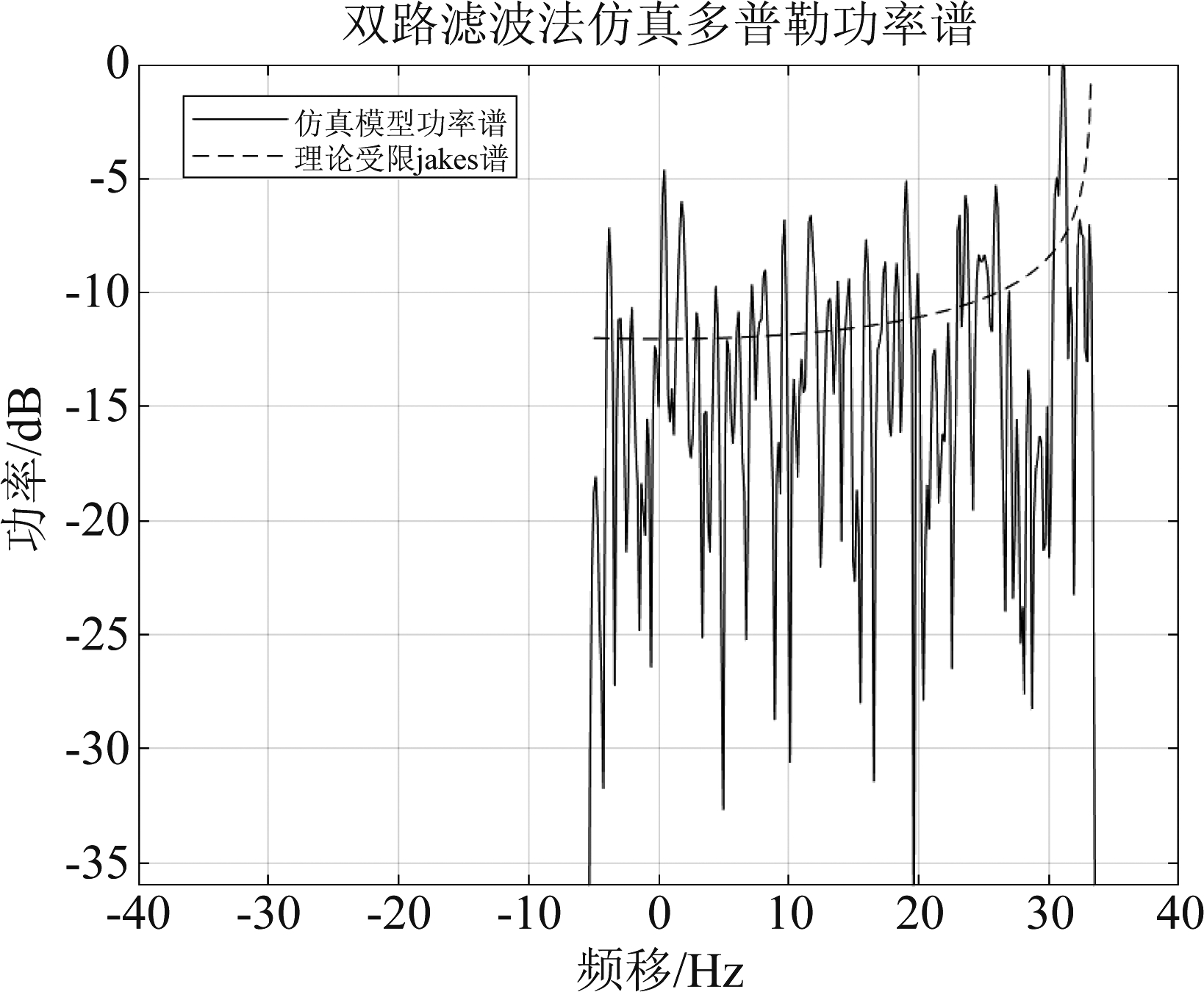
图10 双路滤波法仿真功率谱
Fig.10 Simulation of power spectra by dual-path filtering
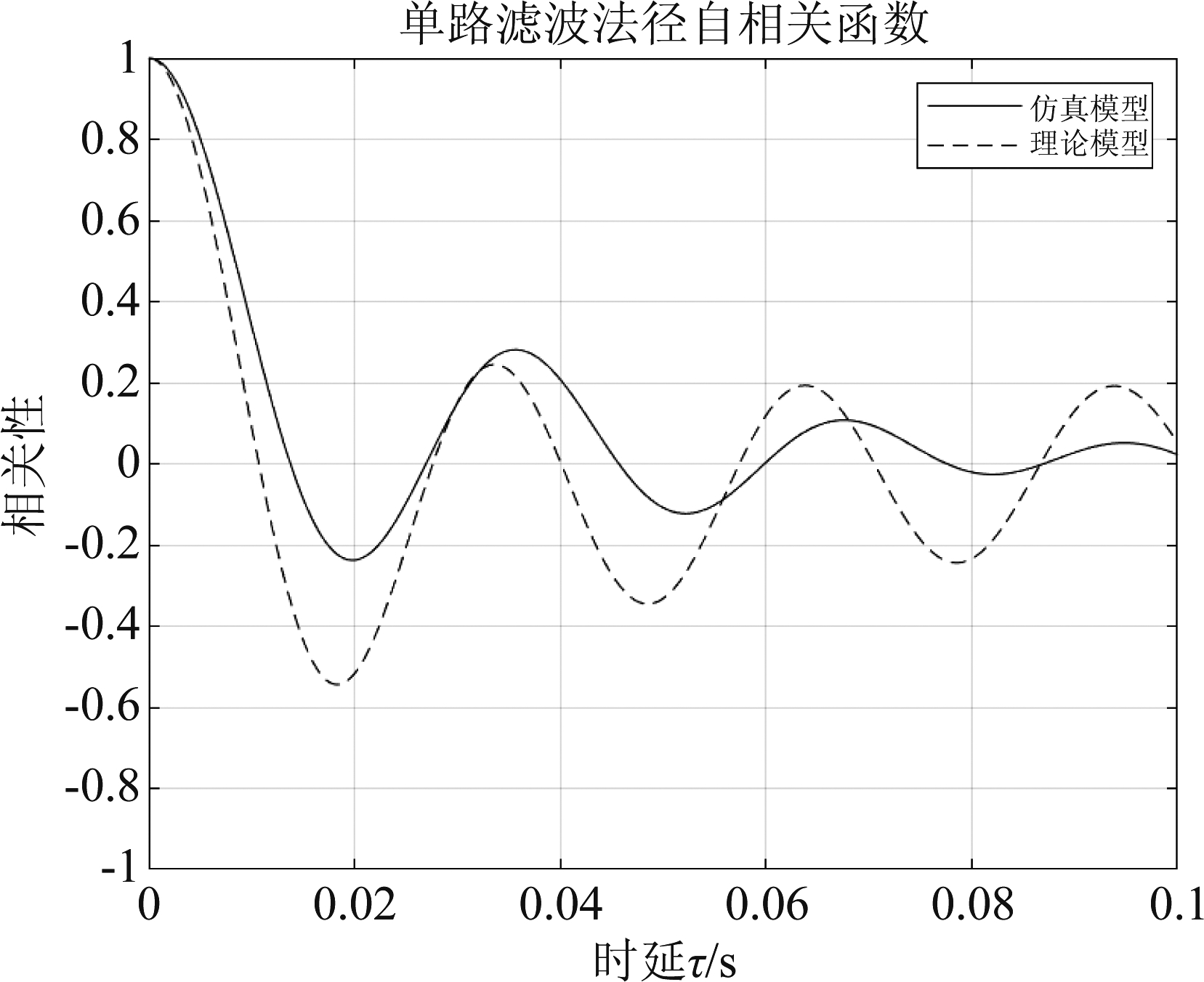
图11 单路滤波法仿真自相关函数
Fig.11 Simulation of autocorrelation function by single-path filtering
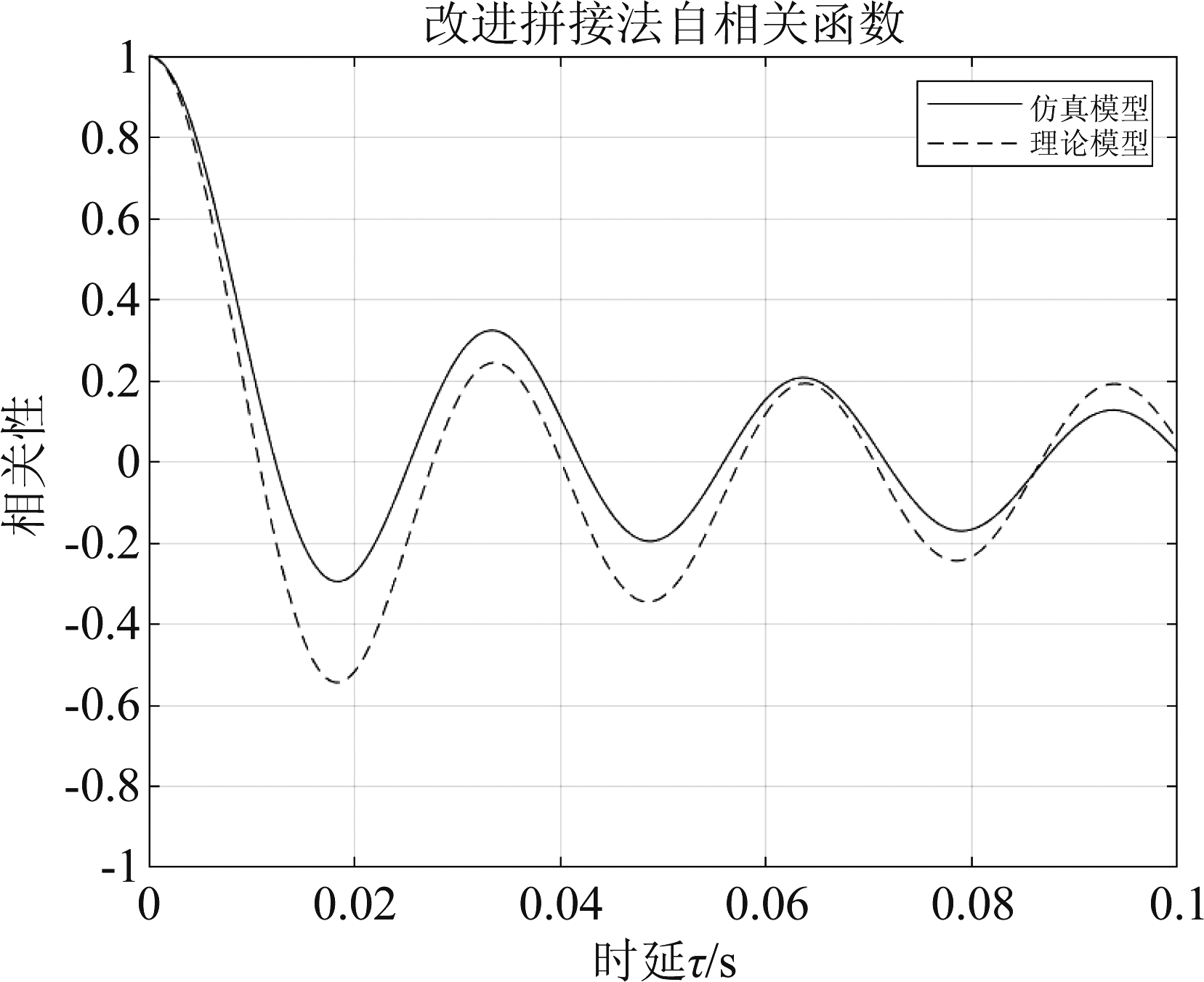
图12 改进拼接法仿真自相关函数
Fig.12 Simulation of autocorrelation function by improved splicing method
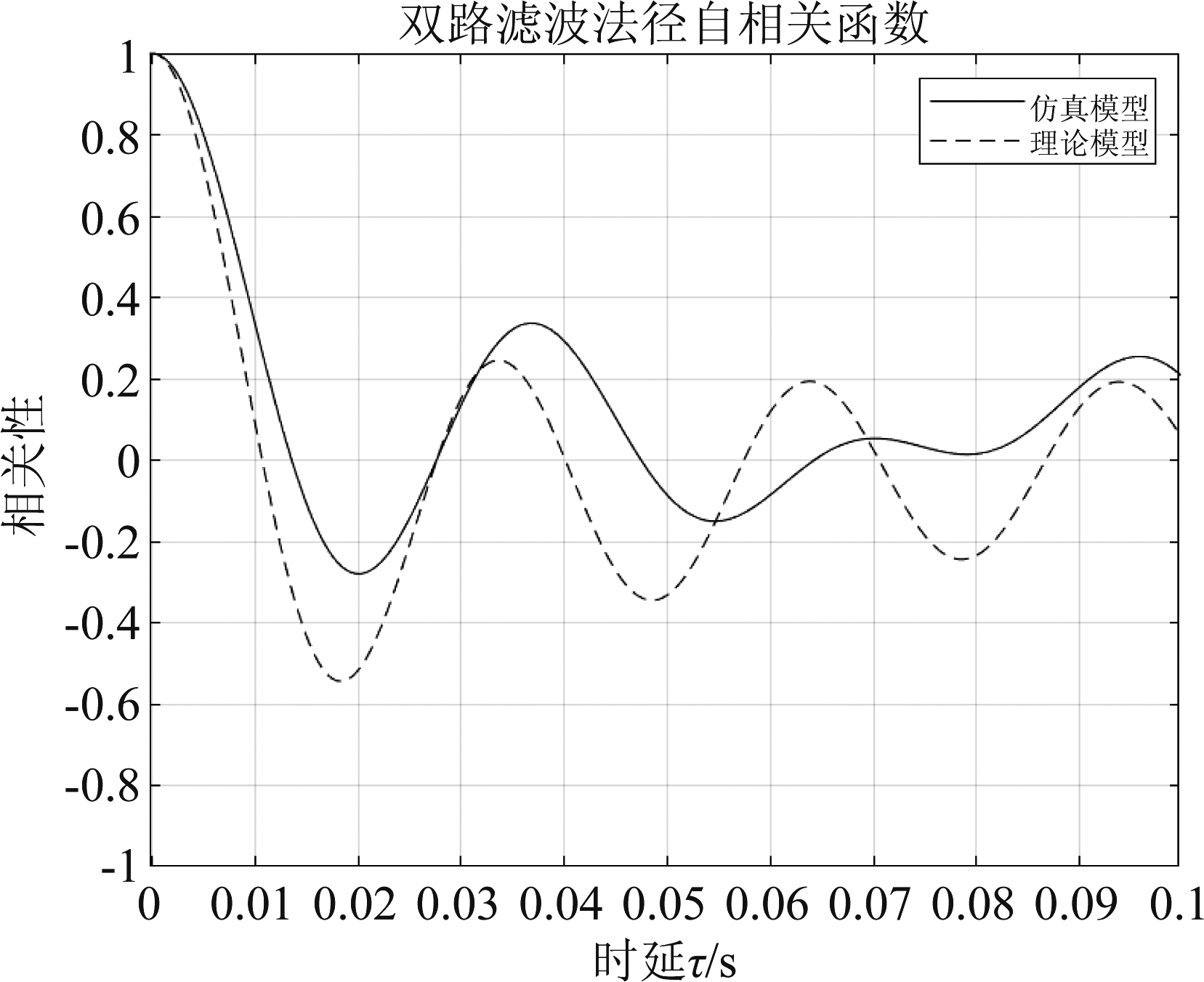
图13 双路滤波法仿真自相关函数
Fig.13 Simulation of autocorrelation function by dual-path filtering
其中理论受限Jakes功率谱为式(8),理论自相关函数为式(9)。
根据仿真结果和理论值进行比较,可以从以上图中直观得看出,三种方法都能较好的仿真具有受限Jakes功率谱的信道。通过比较其自相关函数,能明显看出改进拼接法的自相关函数更加接近于理论自相关函数。为了更好地提现三种方法的效果,通过多次循环计算取其自相关函数仿真与理论值的均方误差均值,具体如表1所示。
表1 模型性能对比
Tab.1 Model performance comparison
仿真方法单路滤波法双路滤波法改进拼接法均方根误差1.24781.16290.1512
5.2 幅度分布特性
图14、图15、图16分别为使用单路滤波法、改进拼接法和双路滤波法仿真的信道的幅度分布特性,其中纵坐标单位为万次。
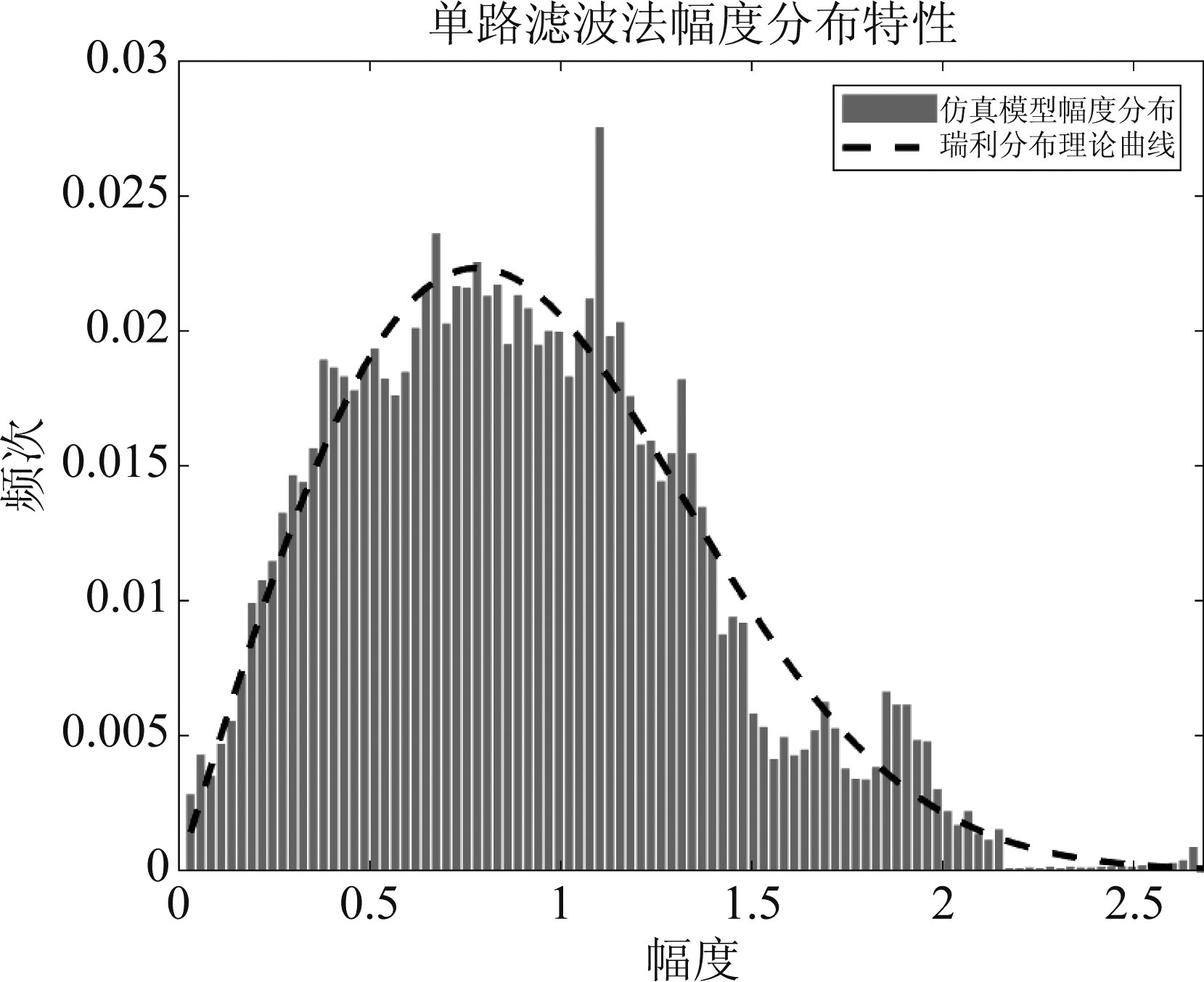
图14 单路滤波法仿真信道
Fig.14 Simulation of distribution of magnitude by single-path filtering
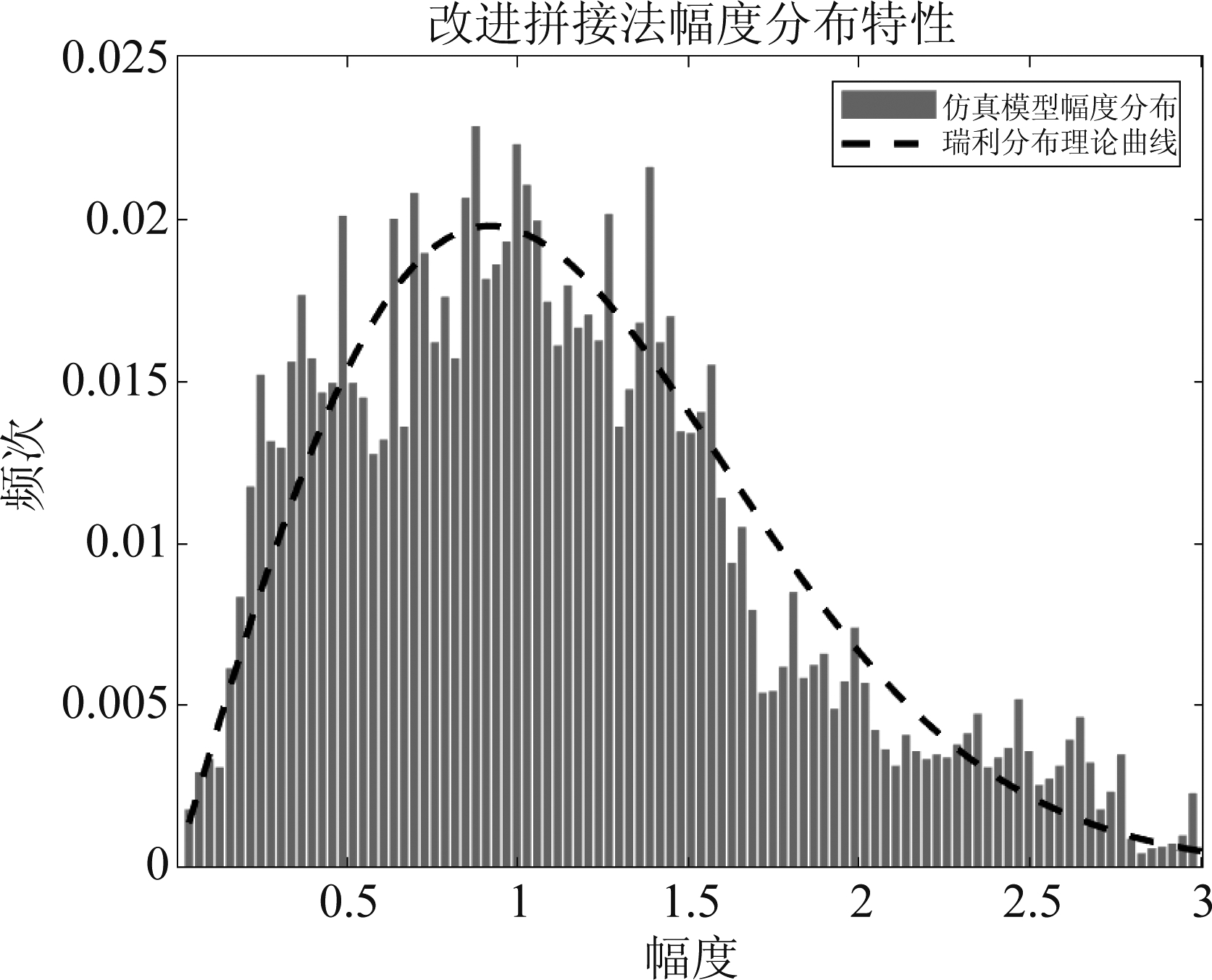
图15 改进拼接法仿真信道幅度分布特性
Fig.15 Simulation of distribution of magnitude by improved splicing method
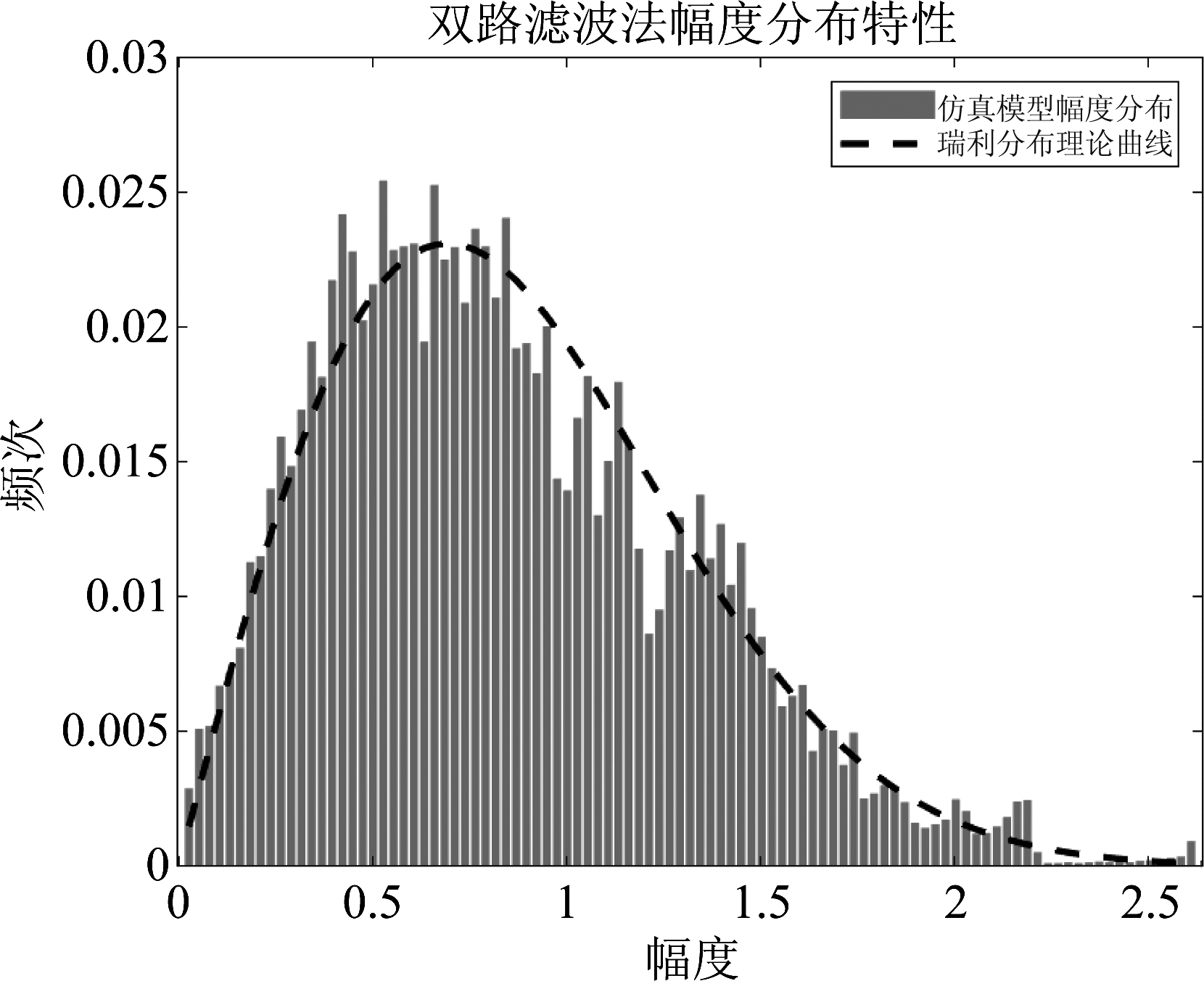
图16 双路滤波法仿真信道幅度分布特性
Fig.16 Simulation of distribution of magnitude by dual-path filtering
从以上仿真结果图中可以看出,三个模型仿真的信道幅度分布特性都基本吻合瑞利分布曲线。
5.3 算法复杂度
除了对于仿真结果的比较之外,我们还需要对于三种模型的算法的时间复杂度进行比较。对于三种模型我们列出其算法操作和其对应算法时间复杂度。
表2为单路滤波法的算法操作和对应的时间复杂度,其中按照时间复杂度表述原则,常量级的时间复杂度用常数1表示。所以单路滤波法的基本操作次数为TS(n)=3,所以根据大O表示法转化为时间复杂度为TS(n)=O(1)。
表2 单路滤波法算法操作
Tab.2 Single-path filtering algorithm operation
操作名称基本操作次数产生复高斯随机信号1生成多普勒序列1随机信号添加多普勒分量1
表3为双路滤波法的算法操作和对应的时间复杂度,双路滤波法的基本操作次数为TD(n)=6,转化为时间复杂度为TD(n)=O(1)。
表3 双路滤波法算法操作
Tab.3 Dual-path filtering algorithm operation
操作名称基本操作次数产生两段高斯随机信号2生成多普勒序列1正交分量添加多普勒分量1同相分量添加多普勒分量1正交同相分量相加1
表4为改进拼接法的算法操作和对应的时间复杂度,n表示此问题的规模,在本文中主要与正弦波叠加数量和仿真实现的分辨率相关,其基本操作次数为TI(n)=6n+7,转化为时间复杂度为TI(n)=O(n)。
表4 改进拼接法算法操作
Tab.4 Improved splicing method algorithm operation
操作名称基本操作次数产生非受限多普勒谱路径增益、离散多普勒分量和相位分量3生成非受限多普勒谱分量正弦波2n产生受限多普勒谱路径增益、离散多普勒分量和相位分量3生成非受限多普勒谱分量正弦波2n正交同相分量相加1
由大O表示法的运行时间规则可知,上述O(1)和O(n)分别表示为常数时间和线性时间,在同等规模下O(1)<O(n),所以改进拼接法的算法复杂度大于单路滤波法和双路滤波法,又由上表计算的操作次数可知,双路滤波法大于单路滤波法。
对于上述理论推导我们通过统计每种方法对于浮点数的计算次数可以直观的比较出三种算法的时间复杂度的差别。算法占用的内存和仿真设备的物理内存可以通过matlab自带的memory函数查看,本文仿真设备的物理内存为16263 MB,分别运行三个模型比较其使用内存作为其复杂度的另一个参考值。
三种方法的算法复杂度比较如表5所示。
表5 算法复杂度对比
Tab.5 Algorithm Complexity Comparison
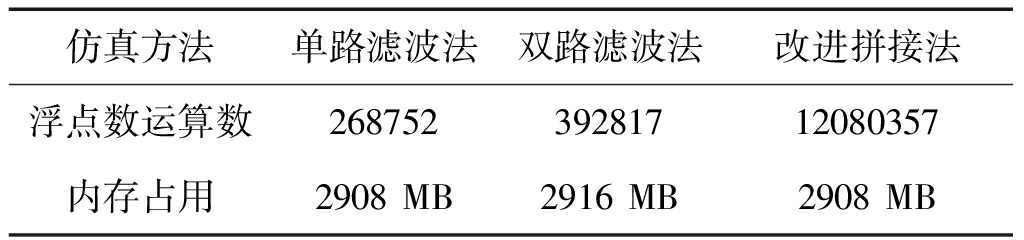
仿真方法单路滤波法双路滤波法改进拼接法浮点数运算数26875239281712080357内存占用2908MB2916MB2908MB
通过仿真结果表明,改进拼接法的仿真效果远远要好于另外两种方法,同时此种方法还可以有效的避免设计数字滤波器和希尔伯特变换器。在复杂度方面,改进拼接法的算法时间复杂度远远大于其他两种算法,单路滤波法的算法时间复杂度最低,双路滤波法的算法复杂度接近单路滤波法要远远好于改进拼接法。内存占用情况上来看,单路滤波法和改进拼接法的占用内存相当,双路滤波法稍大。所以通过以上比较,在不考虑算法时间复杂度和占用内存的情况下,为了对于受限多普勒谱的仿真具有更好地精度,选用改进拼接法是最好的选择,在设备受限或者对于时间复杂度有要求的情况下,可以选择单路滤波法或者双路滤波法,对于只对内存占用有要求的情况下改进拼接法是很好的选择。
6 结论
本文以受限Jakes功率谱为例汇总了三种受限多普勒功率谱的仿真模型,并对三种模型在多普勒功率谱、自相关函数、幅度分布特性、算法时间复杂度和算法占用内存五个方面比较了三种模型的优劣,对于受限的功率谱的建模与仿真有一定参考作用。
[1] JAKES W C.Microwave mobile communications[M].IEEE Press, 1993.
[2] CLARK R H.A statistical theory of mobile radio reception[J].The Bell System Technical Journal, 1968, 47(6): 957-1000.
[3] AULIN T.A modified model for the fading signal at a mobile radio channel[J].Vehicular Technology IEEE Transactions on, 1979, 28(3):182-203.
[4] 孔凌劲, 刘月玲, 张校晨，等.超短波频段复杂城区场景的信道测量与建模[J].电波科学学报, 2020, 35(4):542-550.
KONG Lingjin,LIU Yueling,ZHANG Xiaochen,et al.Channel measurement and modeling for VHF bands in typical urban scenarios[J].Chinese Journal of Radio Science,2020,35(4):542-550.(in Chinese)
[5] GANS, M.J A power-spectral theory of propagation in the mobile radio environment[J].IEEE Transactions on Vehicular Technology, 1972, 21(1):27-38.
[6] 何睿斯.移动场景下无线信道测量与建模:理论与应用[J].电信科学,2018,34(9):193.
HE Ruisi.Wireless channel measurement and modeling in mobile communication scenario: Theory and application[J].Telecommunications Science, 2018, 34(9): 193.(in Chinese)
[7] TANG Denghong, SHAO Genfu, ZHOU Jie, et al.A novel MIMO channel model for vehicle-to-vehicle communication system on narrow curved-road environment[J].Wireless Personal Communications, 2018, 98(4): 3409-3430.
[8] CHA B, YUN T S, NOH S K.Doppler effect using the TDL channel model for V2V communications[C]∥2019 International Conference on Information and Communication Technology Convergence(ICTC).Jeju, Korea(South).IEEE, 2019: 1400-1403.
[9] CHO Y S, KIM J, YANG W Y, et al.MIMO channel models[M].MIMO-OFDM Wireless Communications With MATLAB®, 2013, 5894: 71-109.
[10] P
TZOLD M.Mobile fading channels[M].Chichester, UK: John Wiley & Sons, Ltd, 2002.
[11] RICE S O.Mathematical analysis of random noise[J].Bell System Technical Journal, 1944, 23(3): 282-332.
