1 引言
煤炭是工业生产的基石,是我国的主导能源。目前我国煤炭消费量占能源消费总量的50%以上,由此可见煤炭开采对我国工业发展的重大意义。然而,煤炭开采行业风险较大,一旦发生重大煤矿事故,就会破坏开采设备、伤害开采人员、造成巨大经济损失。因此,在煤矿生产中必须高度重视安全问题。在各类安全事故中,瓦斯事故(如瓦斯突出、瓦斯爆炸等)尤为严重,又十分常见。因此,对煤矿内的瓦斯安全状态进行评估,对于煤矿安全生产非常重要。瓦斯安全状态可用于指导实际生产,在较为安全时可将工作重点集中在煤炭开采上,在提出预警时则应暂停开采工作,保证煤矿安全。
近年来,我国加强了采矿人员的培训与监管,部署了各类数据监测系统,煤矿事故发生率和造成的损失得到了一定的控制。特别地,在矿井内的关键位置设有瓦斯浓度传感器,能够实时监测瓦斯浓度的变化。然而,目前还存在两个仍亟待解决问题。其一,瓦斯浓度记录具有滞后性。当记录中瓦斯浓度过高时,往往瓦斯事故已经发生了,起不到事先预警的作用。其二,某一时刻的瓦斯浓度并不足以反映当时的安全状态,评估某一时刻的瓦斯安全状态还需要结合近段时间以来瓦斯浓度的变化规律。因此,虽然瓦斯浓度实时监测系统提供了大量的原始数据,但如何利用这些原始数据来指导实际生产仍需要做深入的探索。
随着机器学习与人工智能的发展,涌现出了许多从数据中提取有效信息并用于指导生产实践的模型和算法。高斯过程[1](Gaussian Process,GP)是一种非参数贝叶斯方法,与传统机器学习方法相比,不再需要假设样本之间是相互独立的,且可以有效地利用样本之间的相关性,因此被广泛地应用在时间序列预测任务中。高斯过程混合模型[2-3](Mixture of Gaussian Processes,MGP)是以高斯过程为分量的线性混合结构,增强了模型的表达能力,能够有效建模来自非平稳信源的数据,挖掘出时间序列数据中的内在结构。高斯过程混合模型具有表达能力强、解释性强、预测精度高等特点,在实际应用中也表现出良好的性能[4]。本文基于高斯过程混合模型,通过构造瓦斯浓度数据的时序特征,将不同的高斯过程分量对应到不同安全状态下的瓦斯浓度数据,提出了一种非监督的(Unsupervised)瓦斯安全状态分类的算法,在进行瓦斯浓度预测的同时对瓦斯安全状态做评估。
2 相关研究综述
许多学者在瓦斯安全状态识别与预测方面做过深入的分析和探索。具体来说,这些研究主要集中在两个方面:(1)瓦斯浓度预测;(2)瓦斯安全状态估计。
瓦斯浓度的精准预测对煤矿安全管理具有重要的指导意义。在实际中,影响瓦斯浓度的因素较多,瓦斯浓度变化趋势较为复杂,但具有显著的时序特征。因此,瓦斯浓度预测模型往往要利用好样本点之间的相关性,通过时序结构来预测。韩婷婷等人针对灰色神经网络预测瓦斯浓度时部分预测值精度不高的问题,提出了用马尔科夫残差修正来提高精度[5],说明了在瓦斯浓度预测模型中时序信息的重要性。吴兆法等人提出了基于插值梯形模糊信息粒化的瓦斯浓度趋势预测方法[6]。杨丽等人提出了基于多元分布滞后模型的瓦斯浓度动态预测[7],在自回归模型中引入了变量选择的思想。马莉等人提出了基于门控循环单元(Gated Recurrent Unit,GRU)的瓦斯浓度预测模型[8],并使用粒子群算法和Adam算法来进行参数优化。这一模型考虑了瓦斯浓度数据的时序特征,并利用这一特征结合循环神经网络(Recurrent Neural Network,RNN)来进行预测。
相对于瓦斯浓度预测,瓦斯安全状态评估对实际生产意义更加显著,难度也更高。崔迎迎综合人为原因、机器原因、环境原因、管理原因这四方面的因素,通过层次分析法(Analytic Hierarchy Process,AHP)建立了安全状态评价指标体系,并利用灰色预测模型(Grey Prediction Model,GM)来预测瓦斯安全状态[9]。这一方法具有较强的可解释性,但其相对重要性矩阵的构造具有一定的主观性。王建提出了一种基于支持向量机(Support Vector Machine,SVM)的煤与瓦斯突出预测模型[10],分别利用粒子群算法(Particle Swarm Optimization,PSO)及遗传算法(Genetic Algorithm,GA)进行参数优化,在小样本数据中显示出了较好的性能。李爽等人提出了基于贝叶斯网络(Bayesian Networks,BN)和极限学习机(Extreme Learning Machine,ELM)的瓦斯安全态势预测方法[11]。极限学习机在预测任务上具有精度高、速度快的特点,而贝叶斯网络可以集成专家知识,并具有较强的可解释性[12]。
3 高斯过程模型
高斯过程是一种传统的随机过程模型,现在已被引入到机器学习领域中,成为数据分析和预测的有效工具。设有输入x,输出为y,它们之间的关系可以用等式y=f(x)+ε来表示,其中ε是噪声, f是一个函数。传统的线性回归模型假设f是一个线性函数,而高斯过程模型则假设f是一个受x驱动的高斯过程,也就是说f本身的任意有限维分布都是一个多元正态分布。具体地说,给定样本{(xi,yi),i=1,2,…,n},那么f的有限维分布(f(x1), f(x2),…, f(xn))服从正态分布
其中C是n×n的协方差矩阵。一般我们还假设噪声是独立的高斯随机变量,均值为0,方差为σ2,那么根据多元正态分布的性质,可将f消去,直接得到(y1,y2,…,yn)的联合分布为
其中I为n阶单位矩阵。
在数学上,高斯过程的定义只要求该过程的任意有限维分布服从多元正态分布,对协方差矩阵C的形式没有特殊限制。但在机器学习中,为了便于学习和预测,往往假设C由一个协方差函数c来决定。具体地,Cij=c(xi,xj;θ),其中θ是模型的参数。在实际应用中,往往选取如下的协方差函数:
(1)
在上式中,d为输入数据的维数,{θ0,θ1,…,θd}为参数,xi,l表示第i个样本的输入在第l个维度上的取值。虽然在数学上“过程”这一概念一般是对时间来定义的,但机器学习中的高斯过程模型其输入不一定要是时间,可以是多维的输入,只要能合理地定义协方差函数即可,这大大拓宽了高斯过程的应用场景。
给定训练数据后,我们通过极大似然估计(Maximum Likelihood Estimation)来学习高斯过程中的参数:θ0,θ1,…,θd,σ。记y=(y1,y2,…,yn)T,对数似然函数则为
(2)
式中,C依赖于样本x1,x2,…,xn和参数θ0,θ1,…,θd。以对数似然函数为目标函数,采用梯度上升算法(Gradient Ascent Algorithm),即可得到对参数的极大似然估计。在训练过程中,由于涉及到n×n协方差矩阵的求逆,每步迭代的复杂度为O(n3)。
在预测时,给定一个输入x*,希望得到系统在该点的输出。根据高斯过程的定义可知,(y1,y2,…,yn, f(x*))仍然服从高斯分布。记c*=(c(x1,x*;θ),…,c(xn,x*;θ))T,c*,*=c(x*,x*;θ),则该高斯分布的均值为0,协方差矩阵为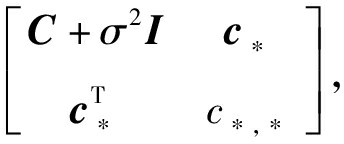
再根据多元正态分布的性质,可得到条件分布f(x*)|y1,y2,…,yn服从高斯分布
(3)
即在x*处的预测为
方差为
由这一公式可以看出,高斯过程在做预测时通过C利用了样本之间的相关性,最终的预测结果也显式地依赖于训练集中的输出y。在完成训练后,可以预先计算好(C+σ2I)-1,这样在预测时只需计算n×n矩阵与n维向量的乘法,每个预测样本需要O(n2)的时间复杂度。
在图1中,我们展示了高斯过程的例子。左图中,没有训练样本,高斯过程的参数随机设置,不同的线型代表不同的参数,对每一组参数展示三条样本曲线。由图可见,高斯过程的参数对曲线形态有很大影响,某些参数设置下样本曲线较为平滑,而另一些参数设置下样本曲线抖动较剧烈,不同组的样本曲线变化的幅度也不同。在右图中,给定了一些训练样本,经过训练后,所得到的参数对应的后验曲线能很好地拟合样本变化趋势。
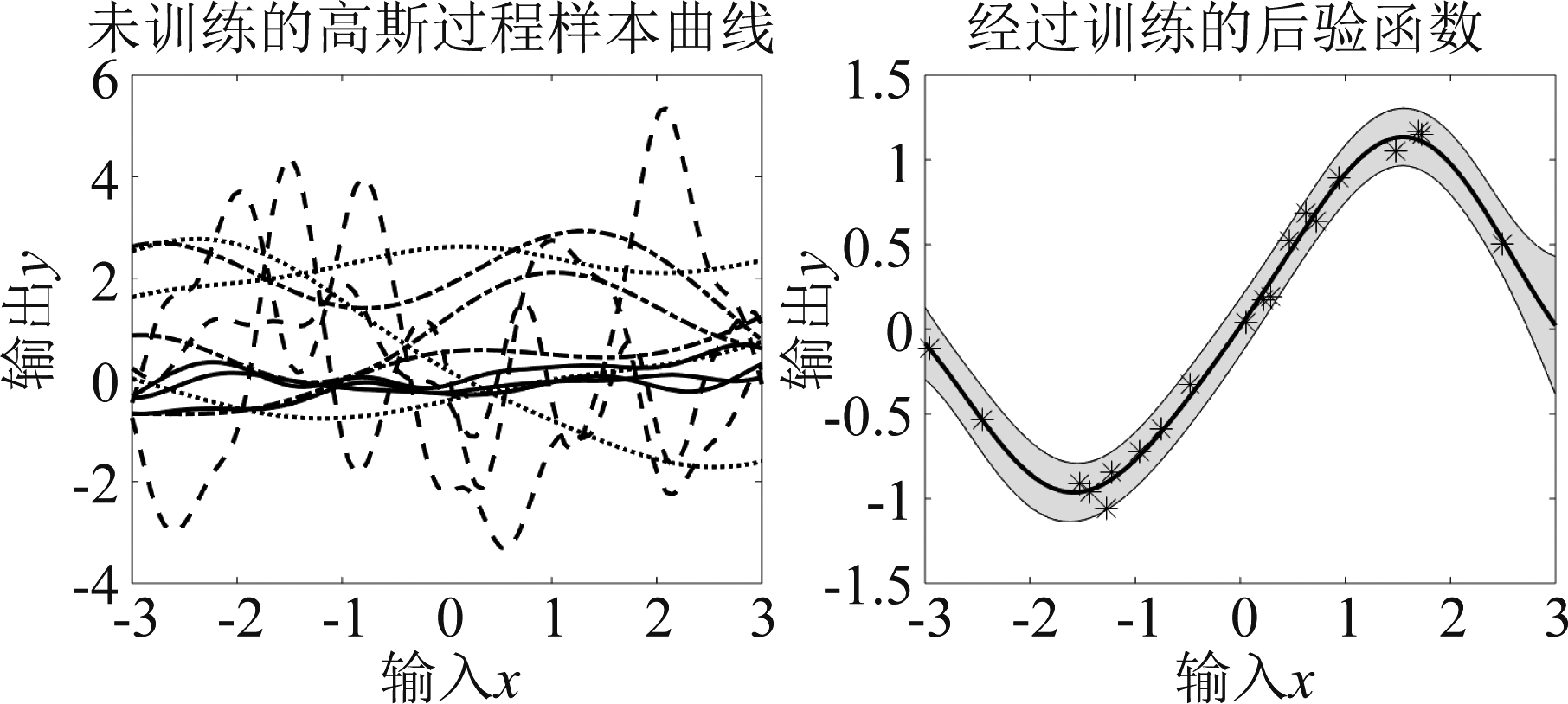
图1 高斯过程的例子
Fig.1 An example of Gaussian Processes
4 高斯过程混合模型及其学习算法
虽然高斯过程模型在非线性回归中表现较好,但仍存在一些缺陷。高斯过程的参数能刻画样本曲线的形态,训练后的高斯过程总是平稳的,样本曲线的统计性质不随时间而变化,曲线的变化趋势保持不变。在实际问题中,数据可能来自不同的信源,每个信源的样本曲线具有不同的变化趋势,单个高斯过程无法有效建模这样的复杂数据。
为解决这一问题,我们引入高斯过程混合模型,不再假设数据来源于一个高斯过程,而是假设它们来自K个不同的高斯过程。对于一个样本(xi,yi),假设有对应的隐变量zi∈{1,2,…,K},表示它们来自于第zi个高斯过程,且zi=k的先验概率为πi。在高斯过程模型中,对于输入x未做概率假设。在高斯过程混合模型中,我们假设当zi=k时,xi来自于高斯分布
其中μk,Σk分别代表均值向量和协方差矩阵。如图2所示,整个模型的结构为z→x→y,由隐变量zi决定第i个样本来自哪一个高斯过程,在第k个高斯过程中,输入x又服从高斯分布输出y和x的关系如前一节中所述。
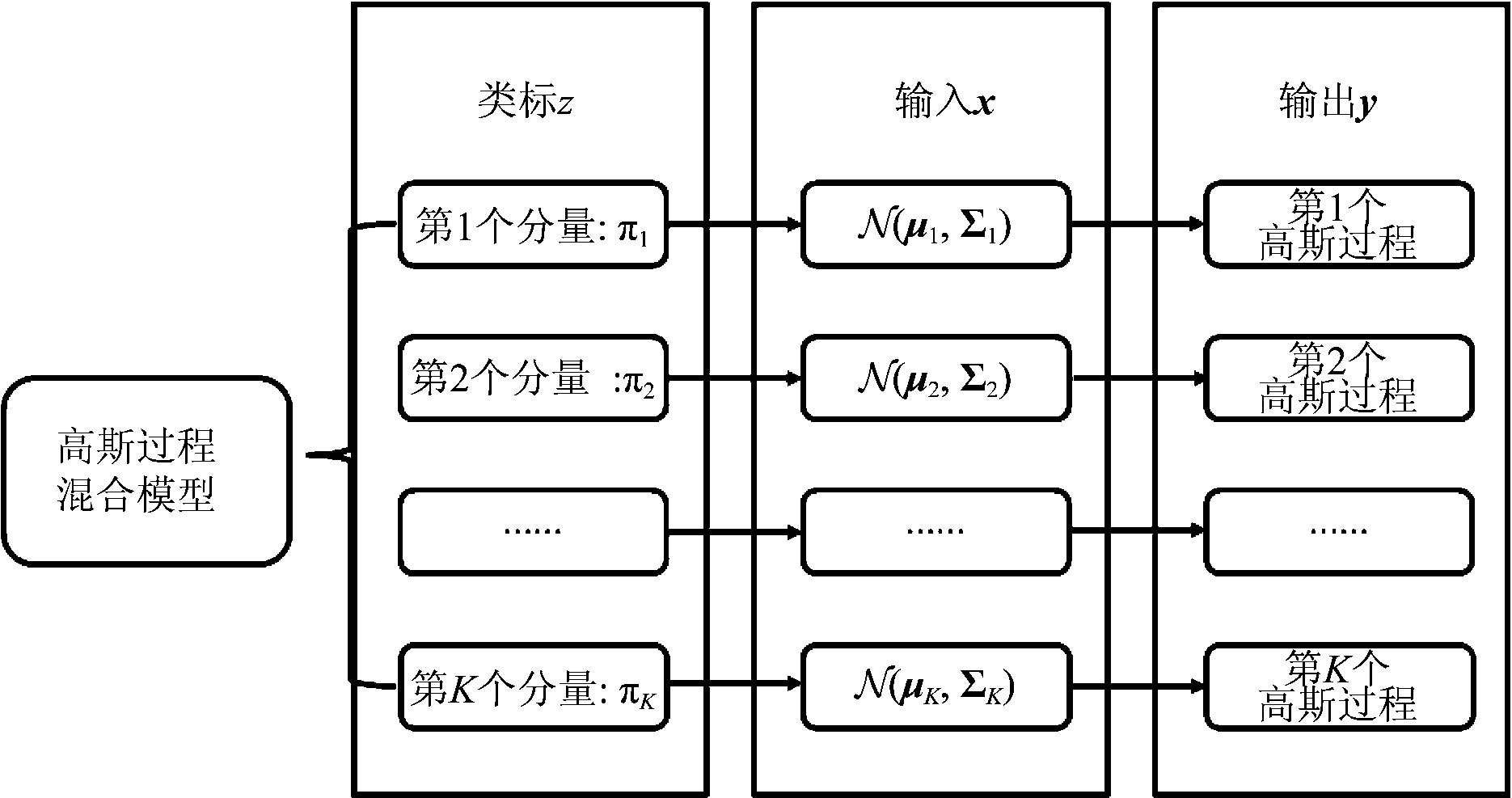
图2 高斯过程混合模型结构示意图
Fig.2 An illustration of the mixture of Gaussian processes model
在实际应用中,隐变量zi无法观测到,需要学习。此外,除了要学习K个高斯过程的参数之外,还要学习K个高斯分布的参数μ1,μ2,…,μK,Σ1,Σ2,…,ΣK,以及K个分量的混合比例π1,π2,…,πK。相比单个高斯过程,高斯过程混合模型表达能力更强,能建模具有复杂结构的数据,但其参数学习更加困难。EM(Expectation Maximization,期望极大化)算法[13]是处理缺失数据与混合模型参数估计问题的有效方法。在高斯过程混合模型中,我们可利用EM算法的框架来进行参数学习。EM算法为解决似然函数难以计算的问题,先对缺失数据(即隐变量)进行估计,再计算完全数据似然函数(即Q-函数)并优化模型参数。具体地,为解决Q-函数计算时指数多项求和的问题,我们采用硬分类EM算法[14]。EM算法总体来说可分为两步:E步和M步。在E步,根据上一步学习的参数,计算每个样本属于每一个分量的概率,并取zi为概率最高的那一类。在M步,根据E步的分类结果,每一个分量内分别学习高斯过程的参数、高斯分布的参数μk,Σk以及混合比例。算法不断迭代E步和M步,直至收敛。在实际中,一般将Q-函数的相对变化率小于某阈值作为迭代收敛的判定标准。算法伪代码见图3。由于难以事先估计每个分量中含有多少样本,故高斯过程混合模型的算法复杂度无法精确分析。但若假设样本在各个成分中等概分布,每步迭代所需的复杂度近似为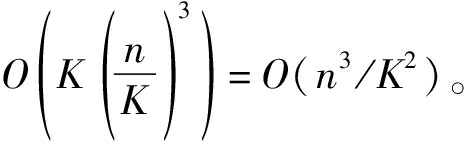
图3 高斯过程混合模型参数学习的硬分类EM算法
Fig.3 The hard-cut EM algorithm for learning the parameters of the mixture of Gaussian processes model
在预测时,给定一个输入x*,先在K个高斯过程中分别独立地进行预测,再根据x*隶属于每个高斯过程的概率对这K个预测结果进行加权平均。其中,x*隶属于第k个高斯过程的概率正比于x*来自高斯分布
的概率。同样地,预测的复杂度依赖于混合比例系数,若假设样本在各个成分中等概分布,预测的复杂度为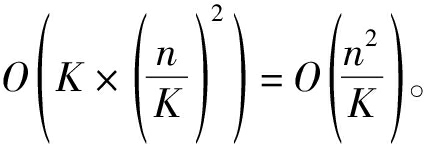
在图4中,我们对比了高斯过程混合模型与单个高斯过程模型。首先,我们生成了一个具有三个组成成分的非平稳数据,每个分量的样本用不同的标识符表示。由图可见,这三个分量内时间序列的变化趋势不同,第二个分量变化频率较快而另外两个分量变化频率较慢。使用单个高斯过程来拟合曲线,发现受第一个和第三个分量影响严重,在第二个分量上过于平滑,不能精准地刻画曲线变化趋势。而使用高斯过程混合模型进行拟合,能够自适应地将样本分为三类,在每一类里可根据该分量的变化趋势自适应地调整预测曲线形态。
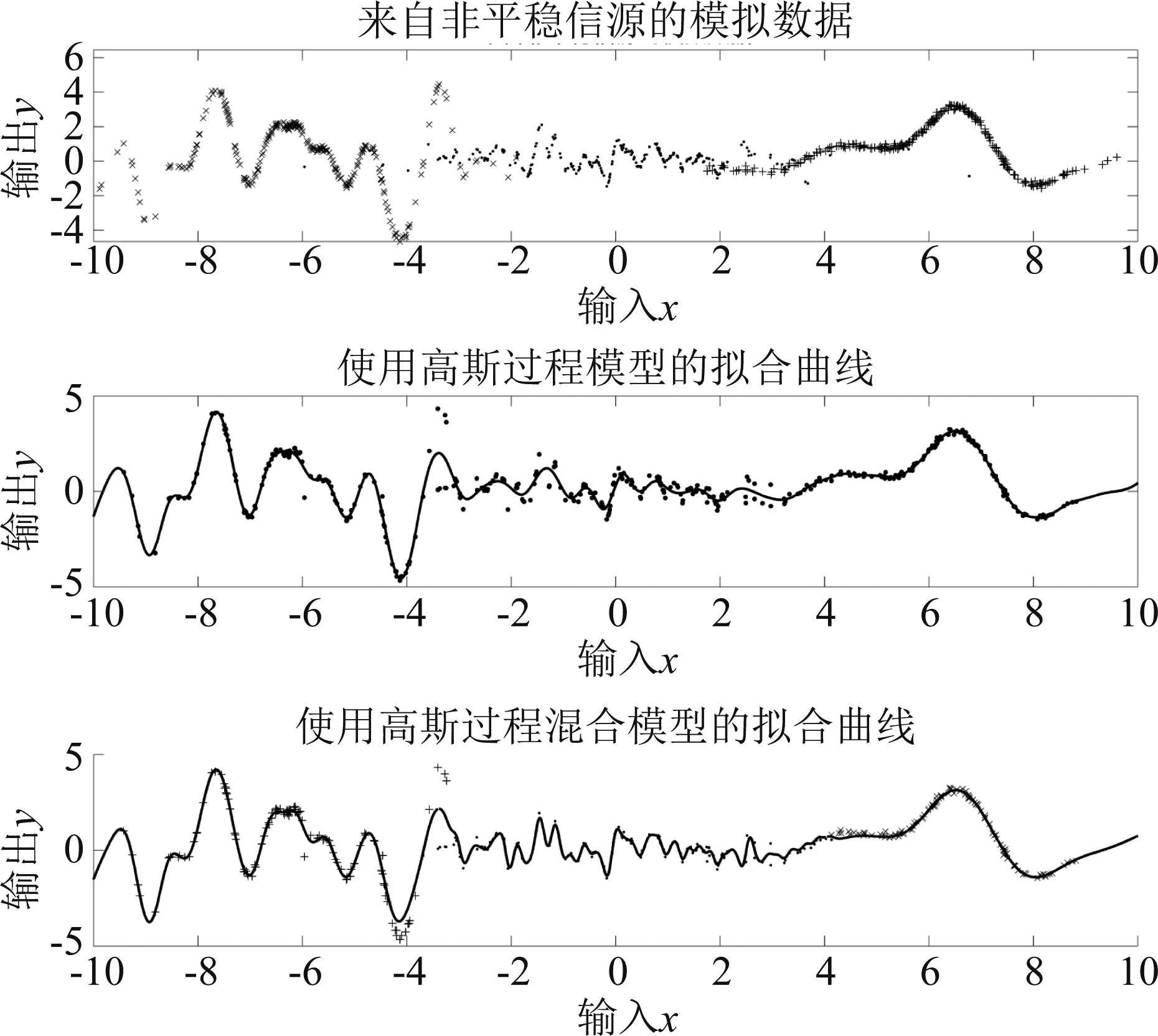
图4 高斯过程混合模型与单个高斯过程模型的对比
Fig.4 Comparison between the mixture of Gaussian processes model and a single Gaussian process
5 瓦斯浓度预测与安全状态分类模型
我们现将高斯过程混合模型应用于瓦斯浓度预测与瓦斯安全状态分类。首先来讨论如何设置与构造输入变量或特征。假设在过去一段时间的瓦斯浓度记录ct,t=1,2,…,T,基本想法是下一时刻的瓦斯浓度不仅仅取决于当前时刻的瓦斯浓度,还取决于近期一段时间的瓦斯浓度。因此,设置时间窗口长度为l,在预测cT+1时应用到cT+1-l,cT+2-l,…,cT,以及当前的时间T,将这两方面特征串联,即可得到用于预测cT+1的特征(T,cT+1-l,cT+2-l,…,cT)。为训练预测模型,我们将这种特征构造方式应用于历史数据,可得到如下的训练集:
xi=(i+l-1,ci,ci+1,…,ci+l-1),yi=ci+l
(4)
通过这种设置,原先长度为T的瓦斯浓度记录转化为了包含T-l-1个样本的训练集。在图5中,我们以l=3为例展示了训练集构造的过程。训练集构造完成后,我们可用一个高斯过程来描述xi和yi之间的关系。在这个训练集上学习参数后,即可预测在x*=(T,cT+1-l,cT+2-l,…,cT)的输出,即为T+1时刻的瓦斯浓度预测值。若后续又测得T+1时刻的瓦斯浓度cT+1,希望预测T+2时刻的瓦斯浓度,可直接输入特征(T+1,cT+2-l,cT+3-l,…,cT+1)做预测,无需对模型参数再进行调整。
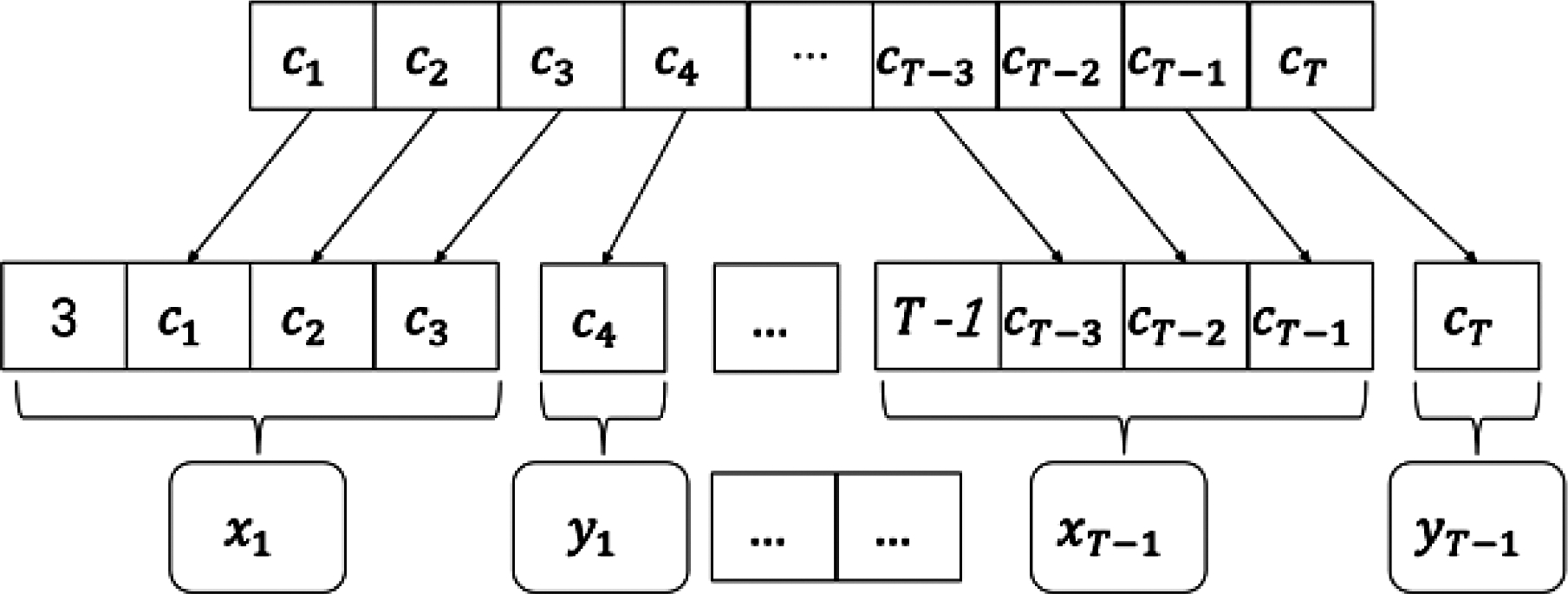
图5 训练集构造过程图示
Fig.5 An illustration of constructing the training set
上述过程只进行了瓦斯浓度预测,而未涉及瓦斯安全状态的分类。显然,在不同的安全状态下,瓦斯浓度的变化应遵循不同的规律,使用单个高斯过程来描述所有安全状态下的规律不够精确。因此,我们进一步用高斯过程混合模型来建模瓦斯浓度数据,不同安全状态下瓦斯浓度变化规律对应不同的高斯过程。这样,在学习的过程中,我们可以自适应地得到每个样本点对应于哪个分量,也就是它对应的安全状态。在预测时,还可根据x*隶属于每个高斯过程的概率得到下一时刻瓦斯安全状态的分布。综上所述,基于高斯过程混合模型,我们可以同时做到瓦斯浓度预测与瓦斯安全状态分类。
在图6中,我们展示了基于高斯过程混合模型的瓦斯安全状态分类方法的完整流程。整个算法框架可分为三部分:预处理过程,高斯过程混合模型的参数学习过程,预测与结果解释。
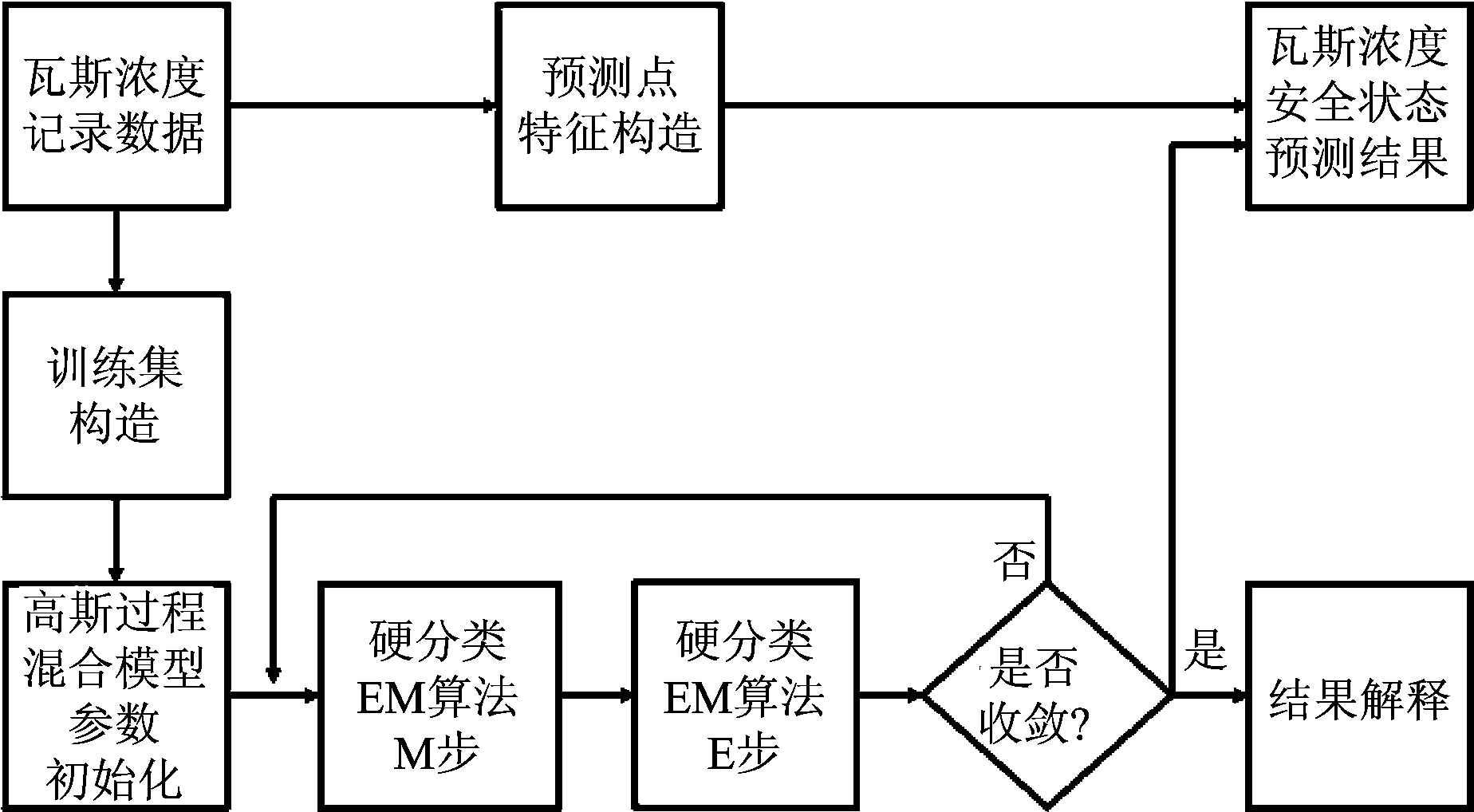
图6 基于高斯过程混合模型的瓦斯安全状态分类流程图
Fig.6 The flow chart of gas safety state classification based on the mixture of Gaussian processes model
在实际问题中,有一些参数需要设定,比如时间窗口的长度l,以及高斯过程混合模型中混合成分的数量。时间窗口长度一般要取决于专家知识,l越大表示建模者认为下一时刻的瓦斯浓度与过去较长一段时间内的瓦斯浓度都有关,l越小则表示短期内的瓦斯浓度已足够预测下一时刻的瓦斯浓度。针对混合成分的数量K,应根据实际问题的背景来决定。在该应用场景中,我们可将瓦斯安全状态根据风险等级由高到低分为四档:红、橙、黄、蓝。因此,在高斯过程混合模型中我们设置K=4,每个分量对应一个安全状态。在实际应用时还需注意,由于安全状态分类是无监督的,模型虽然可以将瓦斯浓度数据根据风险状态自适应地分为四类,但具体每一个分量代表哪一个风险等级还需根据实际数据、结合专家知识来判定。
6 实验结果分析
我们使用松藻煤电集团打通一矿的瓦斯浓度数据进行实验分析。具体地,我们使用打通一矿S二区压风站从2017年8月28日至2018年11月9日瓦斯浓度数据。该数据集共包含439条记录,对应于每天的平均瓦斯浓度。在实验中,我们用含有4个分量的高斯过程混合模型来建模,时间窗口l分别取5、7、15、30,以探究时间窗口长度对实验结果的影响。在将原始数据根据图5的方式进行构造后,我们取后100个样本作为测试集,剩余的样本作为训练集。以l=5为例,训练集中的部分数据如表1所示。注意根据时间窗口长度设置不同,训练集的大小也不同。在实验中我们关注两方面,一方面是瓦斯浓度预测的准确度,另一方面是瓦斯安全状态的分类结果。为评测瓦斯浓度预测的效果,我们采用均方误差(Rooted mean square error, RMSE)来衡量,均方误差越小代表预测越准确。关于瓦斯安全状态分类,则需要结合实际意义进行分析。
表1 当l=5时训练集中的部分数据
Tab.1 Some of the training data when l=5
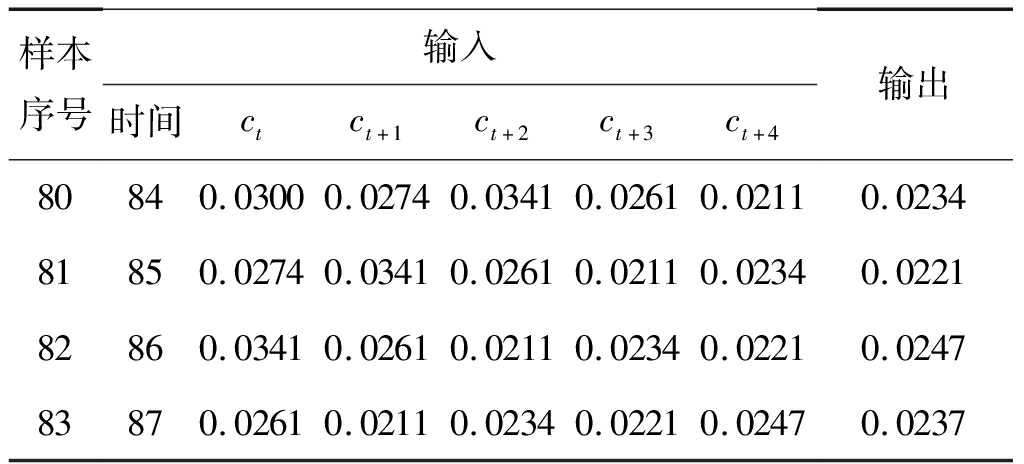
样本序号输入时间ctct+1ct+2ct+3ct+4输出80840.03000.02740.03410.02610.02110.023481850.02740.03410.02610.02110.02340.022182860.03410.02610.02110.02340.02210.024783870.02610.02110.02340.02210.02470.0237
瓦斯浓度预测的结果如图7和表2所示。从中可以看出,当时间窗口长度较短(为5或7)时,瓦斯浓度预测的效果较好,预测值与真实值较为接近。当考虑过去半个月或过去一个月的浓度信息来预测时,效果反而会变差,这有两方面原因。一方面,不同时间点的瓦斯浓度有依赖关系,但随着间隔变大这种依赖关系会减弱,时间窗口长度过长反而会引入噪声,降低信噪比,从而对预测带来不良影响。另一方面,时间窗口越长,构造的特征维数就越高,而高维数据往往会给参数学习造成困难。特别地,在EM算法的M步需要估计高斯分布的均值和协方差矩阵,在相近的样本量下,特征的维数越高,越难以准确估计。从表格中还可以看出,当时间窗口长度增加时,训练时间有缩短的趋势。根据我们的特征构造方式,当时间窗口长度为l时,训练集中有T-l+1个样本,因此时间窗口长度越大,样本数越少,而高斯过程混合模型的学习复杂度随着样本数n时呈n3的量级增长的,因此增大时间窗口长度反而缩短训练时间。此外,我们看到在不同的时间窗口长度设置下,随着迭代进行Q-函数总呈现上升的趋势,这说明了使用硬分类EM算法来学习高斯过程混合模型参数的有效性。由于我们在算法中用了“硬分类”近似,在某些迭代中可能出现暂时下降的情况,但总体趋势是单调上升的。我们也将高斯过程混合模型与其他经典的非线性回归算法(如支持向量回归、单个高斯过程模型)进行了对比,实验结果表明,高斯过程混合模型在瓦斯浓度预测任务上效果更好。从训练时间来看,由于要进行迭代,高斯过程混合模型相比其他算法需要更长的时间,但仍可以在较短时间内完成训练。
表2 高斯过程混合模型及其他算法在瓦斯浓度预测任务上的均方误差及时间(单位:秒)
Tab.2 The rooted mean square errors and running times of the mixture of Gaussian processes model and other algorithms on the gas concentration prediction task
时间窗口长度l5RMSE时间7RMSE时间15RMSE时间30RMSE时间支持向量回归0.00540.020.00520.010.00580.020.01710.01高斯过程0.00580.640.00550.690.00590.780.01770.71高斯过程混合模型0.00478.720.00508.070.00595.350.01645.16
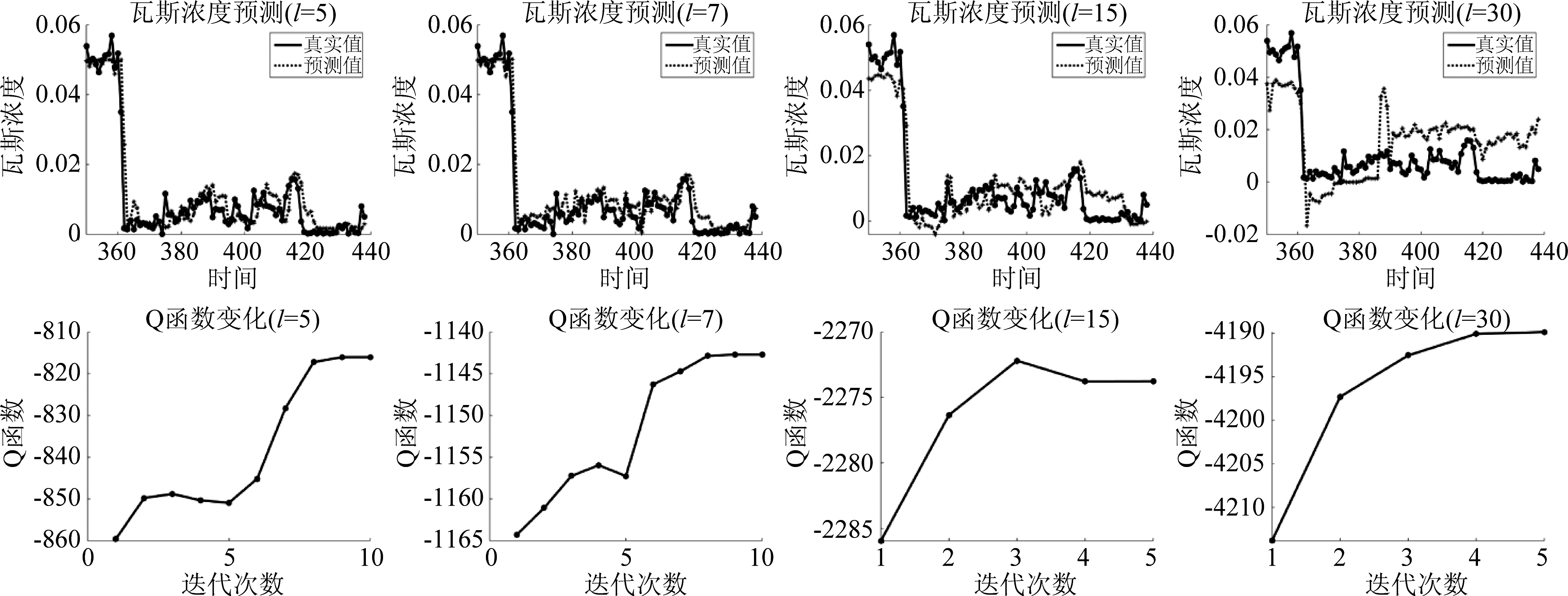
图7 高斯过程混合模型在瓦斯浓度数据上的预测结果与Q-函数随着迭代的变化
Fig.7 The prediction results of the mixture of Gaussian processes model on gas concentration dataset and the variation of Q-function with respect to iteration steps
瓦斯安全状态分类的结果如图8所示,图中将每个时刻对应的风险状态等级用不同的标识符标注。注意每张图中后100个时刻的风险状态是在高斯过程混合模型中预测的过程中得到的,而前面用于训练的样本点对应的风险状态是在高斯过程混合模型的参数学习过程中得到的。从图中可以看出,红色风险等级一般对应瓦斯浓度较高的时刻。橙色次之,代表瓦斯浓度相对较高的时刻。黄色风险等级一般体现了瓦斯浓度具有上升趋势的时段,而蓝色风险等级瓦斯浓度较低,相对较安全。此外,由于风险等级是由历史数据来推测的,当红色风险等级下瓦斯浓度得到控制开始骤降时,警报不会立即解除,估测的风险等级仍是红色。直到瓦斯浓度得到控制并持续一段时间风险等级才会降低。此外,我们注意到当时间窗口长度取为30时效果较差,原因与瓦斯浓度预测时类似。在其他三组参数下,得到的安全状态估计基本一致。
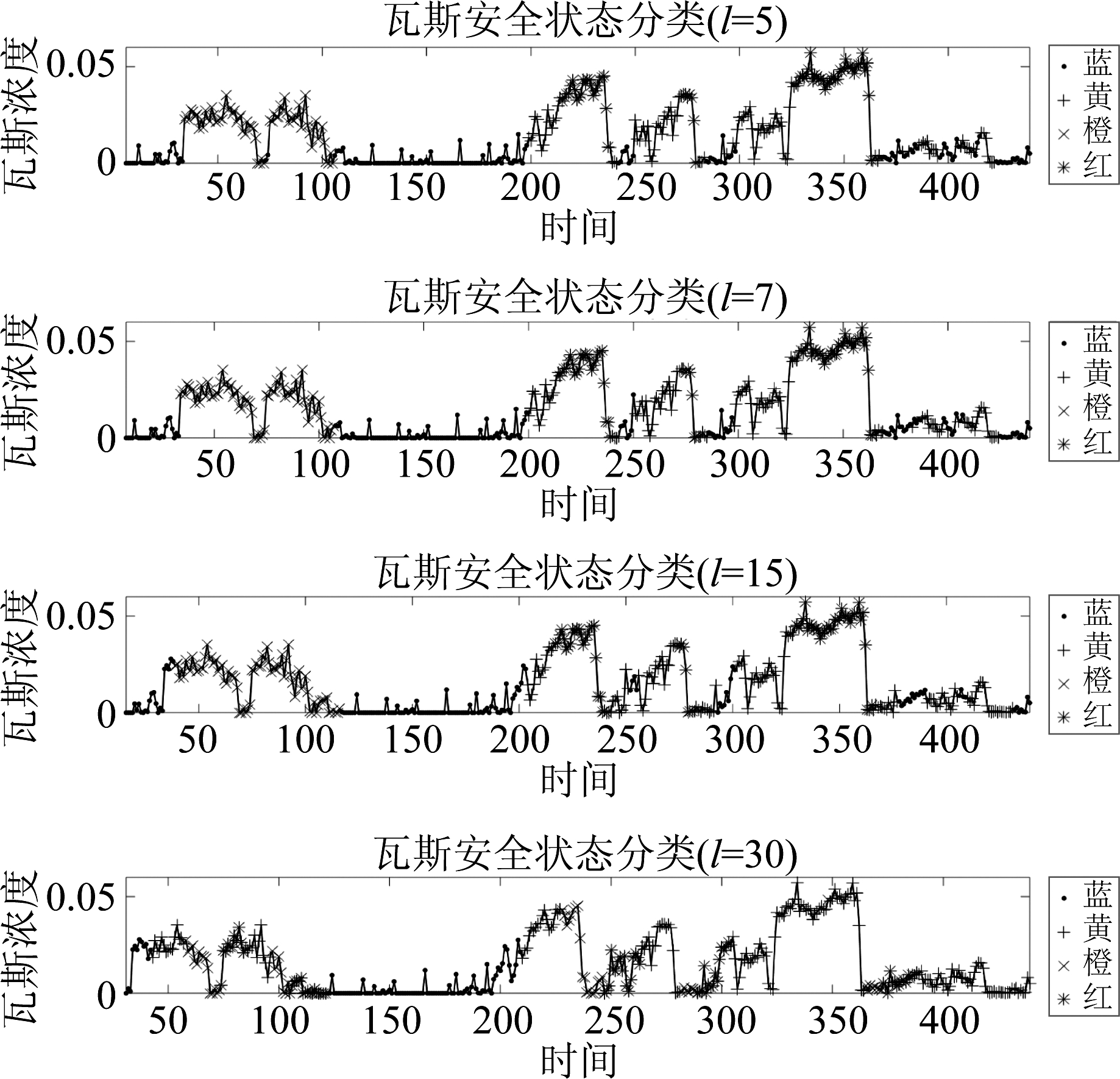
图8 不同窗口长度设置下瓦斯浓度安全状态分类结果
Fig.8 The results of gas safety state classification under different settings of window lengths
7 结论
针对煤矿安全生产中的瓦斯浓度预测与瓦斯安全状态分类问题,我们提出了使用高斯过程混合模型来建模瓦斯浓度数据。我们详细地介绍了高斯过程与高斯过程混合模型的理论基础及学习算法,并通过时序特征构造将其应用于瓦斯浓度数据,提出了一个用于瓦斯浓度预测和安全状态评估的框架。最后,我们在松藻煤电集团打通一矿的瓦斯浓度监测数据中进行了实验分析,验证了高斯混合模型的有效性,并就模型中的超参数设置对结果的影响进行了讨论。
本文的创新点主要在于将高斯过程混合模型应用于瓦斯浓度数据,通过我们提出的特征构造方式,在进行瓦斯浓度预测的同时,可根据模型的混合结构识别出瓦斯浓度的安全状态。这一方法具有坚实的理论基础和较强的可解释性,实验结果也证实了其有效性,对于实际生产工作具有重要的意义。
[1] RASMUSSEN C E, WILLIAMS C K I.Gaussian processes for machine learning[M].Cambridge: MIT Press, 2006.
[2] TRESP V.Mixtures of Gaussian processes[C].Advances in Neural Information Processing, 2001: 654-660.
[3] 周亚同,陈子一,马尽文.从高斯过程到高斯过程混合模型:研究与展望[J].信号处理,2016,32(8):960-972.
ZHOU Yatong, CHEN Ziyi, MA Jinwen.From Gaussian processes to the mixture of Gaussian processes: a survey[J].Journal of Signal Processing, 2016, 32(8):960-972.(in Chinese)
[4] 曾鑫,赵龙波,马尽文.基于高斯过程混合模型的国债收益率预测[J].信号处理,2019,35(5):831-836.
ZENG Xin, ZHAO Longbo, MA Jinwen.Gaussian process mixture based prediction of treasury bond yield rate[J].Journal of Signal Processing, 2019, 35(5):831-836.(in Chinese)
[5] 韩婷婷,吴世跃,王鹏军.基于马尔科夫残差修正的瓦斯浓度预测[J].工矿自动化,2014,40(3):28-31.
HAN Tingting, WU Shiyue, WANG Pengjun.Prediction of gas concentration based on residual correction of Markov chain[J].Industry and Mine Automation, 2014, 40(3): 28-31.(in Chinese)
[6] 吴兆法,吴响,钱建生.基于插值梯形模糊信息粒化的瓦斯浓度趋势预测[J].工矿自动化, 2014,40(12): 31-36.
WU Zhaofa, WU Xiang, QIAN Jiansheng.Trend prediction of gas concentration based on interpolation trapezoidal fuzzy information granulation[J].Industry and Mine Automation, 2014, 40(12): 31-36.(in Chinese)
[7] 杨丽,刘晖,毛善君, 等.基于多元分布滞后模型的瓦斯浓度动态预测[J].中国矿业大学学报, 2016, 45(3):455-461.
YANG Li, LIU Hui, MAO Shanjun, et al.Dynamic prediction of gas concentration based on multivariate distribution lag model[J].Journal of China University of Mining & Technology, 2016, 45(3):455-461.(in Chinese)
[8] 马莉,潘少波,代新冠, 等.基于 PSO-Adam-GRU的煤矿瓦斯浓度预测模型[J].西安科技大学学报,2020,40(2): 363-368.
MA Li, PAN Shaobo, DAI Xinguan, et al.Gas concentration prediction model of working face based on PSO-Adam-GRU[J].Journal of Xi’an University of Science and Technology, 2020, 40(2): 363-368.(in Chinese)
[9] 崔迎迎.基于AHP和GM(1,N)的煤矿瓦斯安全状态的识别和预测[J].科技创业月刊, 2016(6): 102-104.
CUI Yingying.Coal gas safety state identification and prediction based on AHP and GM(1,N)[J].Pioneering with Science & Technology Monthly, 2016(6):102-104.(in Chinese)
[10] 王建.基于SVM的煤与瓦斯突出预测模型及应用[J].陕西煤炭,2020,39(2):109-113.
WANG Jian.Prediction model and application of coal and gas outburst based on SVM[J].Shaanxi Coal, 2020, 39(2):109-113.(in Chinese)
[11] 李爽,李丁炜,犹梦洁, 等.基于BN-ELM的煤矿瓦斯安全态势预测方法研究[J].系统工程,2020, 38(3):132-141.
LI Shuang, LI Dingwei, YOU Mengjie, et al.Study on coal mine gas security situation forecasting method[J].Systems Engineering, 2020,38(3): 132-141.(in Chinese)
[12] 张宁,盛武.基于贝叶斯网络的煤矿瓦斯爆炸事故致因分析[J].工矿自动化,2019,45(7):53-58.
ZHANG Ning, SHENG Wu.Causes analysis of coal mine gas explosion accidents based on Bayesian network[J].Industry and Mine Automation, 2019,45(7):53-58.(in Chinese)
[13] DEMPSTER A P, LAIRD N M, RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm[J].Journal of the Royal Statistical Society.Series B(Methodological),1977,39(1).
[14] CHEN Z, MA J, ZHOU Y.A precise hard-cut EM algorithm for mixtures of Gaussian processes[C].Lecture Notes in Computer Science, 2014, 8589:68-75.
