1 引言
近年来,随着航天航空科技的发展,高速机动目标大量涌现,此类目标速度快,并且具有一定的机动能力(加速度)。同时,隐身技术的发展与大量应用,导致高速机动目标回波微弱(信噪比低),给雷达探测带来了巨大的挑战[1-2]。
长时间相参/非相参积累是提升信噪比(Signal to Noise Ratio,SNR)和雷达的探测性能[3-4]的有效途径,如Hough Transform(HT)等[5-6]非相参积累算法不利用回波的相位信息,实现简单,但增益受限;相对而言,相参积累算法同时考虑时延和相位,有更高的SNR增益。然而,在相参积累过程中,高速机动目标可以短时间内在距离向上产生走动(Range Migration, RM),并且在多普勒上发生变化(Doppler Spread, DS)。如何解决上述RM和DS问题成为当下国内外相参积累领域的前沿课题。
为了校正距离走动,国内外学者先后提出了Keystone Transform(KT)[7]和Radon傅里叶变换(Radon-Fourier Transform,RFT)[8]两类方法,但是,KT和RFT仅能校正距离向的一阶走动,无法对距离向的高阶走动进行校正,也不能补偿加速度带来的多普勒变化。为此,北京理工大学许稼提出了名为Generalized Radon-Fourier Transform(GRFT)[13]的积累检测算法,通过搜索目标的多维参数,实现了回波的相位补偿并进行积累。此外,海军航空大学的陈小龙和电子科技大学的李小龙在GRFT算法的基础上,分别研究了Radon分数阶傅里叶变换(Radon-Fractional Fourier Transform,RFRFT)[10]和Radon-Lv’s Distribution(RLVD)[12]相参积累方法。GRFT、RFRFT、RLVD通过多维参数搜索对机动目标的回波进行有效积累,但是上述方法搜索参数维度高,计算量较大。
为此,北京理工大学许稼等人又提出了一种基于MTD+GRT的积累算法[14-15],在保证在子片段内不会出现跨距离单元和多普勒走动的前提下,对积累时间进行分段,随后对子片段内的回波信号进行MTD操作,最后通过GRT完成各片段间的积累。与GRFT方法相比,MTD+GRT方法的计算量能够有所下降。然而,由于片段之间非相参叠加,其积累检测性能会遭受较大损失。此外,每个片段内都要求目标不发生距离走动和多普勒走动,因此片段内的积累时间与积累脉冲数受限,不利于回波SNR的提升。随后,北京理工大学丁泽刚等人提出在逆合成孔径雷达成像中利用Sub-aperture GRFT(SAGRFT)进行积累[16],该算法在MTD-GRT的基础上通过子孔径间相参积累的方式进一步抑制了噪声得到更高的信噪比增益,然而,与MTD-GRT算法类似,SAGRFT算法要求子孔径内不发生由速度造成的RM,这将制约子孔径内所允许的积累时间以及相应的积累脉冲数。
本文针对高速机动目标的长时间相参积累处理问题,提出了一种基于RFT和积累时间分段的积累算法。首先,对目标回波信号进行分段,致使子片段内目标加速度引起的RM和DS可忽略(不用考虑);其次,通过RFT实现每个子片段内回波信号的相参积累,进而分析了各片段输出峰值的分布特性,在此基础上,提出了距离-速度(多普勒)域的多片段RFT结果相参叠加方法,以进一步提升SNR与目标检测性能。相比于MTD+GRT,本文在噪声抑制和正确检测上性能更优。
2 回波建模及分段预处理
2.1 目标回波建模
探测雷达采用脉冲多普勒体制,其发射信号为:
(1)
其中,![]() 为脉冲宽度,μ=B/TP为调频斜率,B为带宽。
为脉冲宽度,μ=B/TP为调频斜率,B为带宽。
假设雷达观测时间为T,脉冲重复周期为Tr,那么在观测期间内雷达共接收到Na=T/Tr个脉冲,其基带回波可以表示为:
![]()
exp(-j2πfcτ(k))
(2)
其中,k=1,2,…,Na为积累脉冲数,Ar为目标的回波复幅度,τ(k)=2R(k)/c为目标和雷达间的间距造成的回波时延, fc为雷达载频。
基带回波经过匹配压缩后为:
src(t,k)=Armsinc[πB(t-τ(k))]exp(-j2πfcτ(k))
(3)
其中,Arm为经过匹配滤波器后的信号复幅度。
假设观测区域内有一匀加速运动目标(速度为a1,加速度为a2),其径向距离为:
(4)
其中,k=1,2,3,…,Na为脉冲数,a0为初始距离,由于目标的回波时延与r间存在的确定关系r=ct/2,式(3)可以改写为:
src(r,k)=
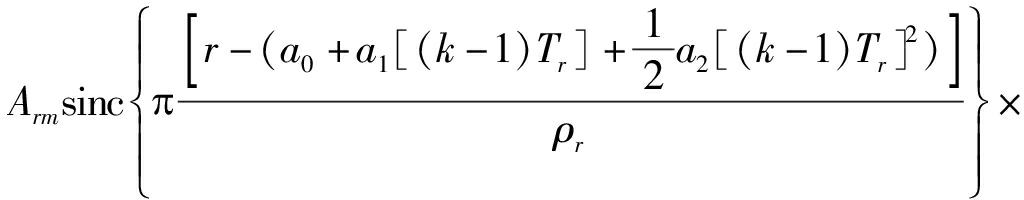
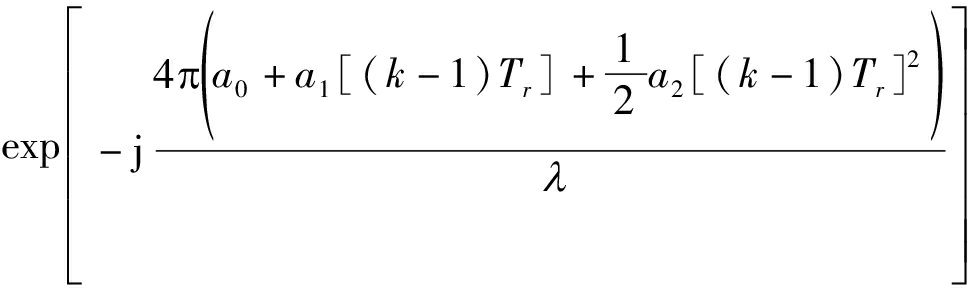
(5)
其中,ρr=c/2B为雷达的距离分辨率,λ=c/fc为雷达的信号波长。
2.2 目标回波分段处理
将接收到的回波每Nsub个脉冲划分为一个子片段,则观测时间内的回波可以分为Nc个子片段,其中Nc=Na/Nsub,经过分段后第m个子片段的脉冲压缩信号可以表示为:
![]()
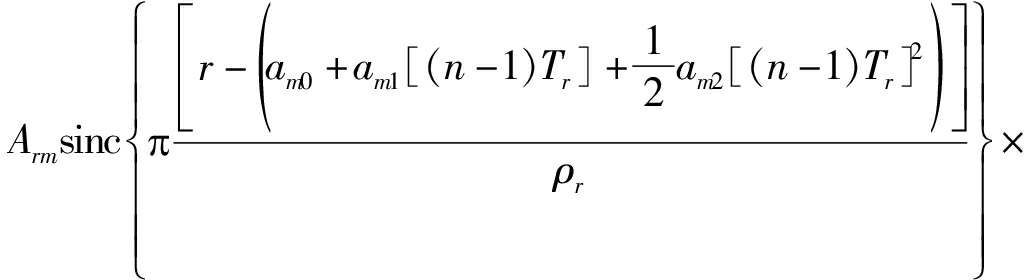
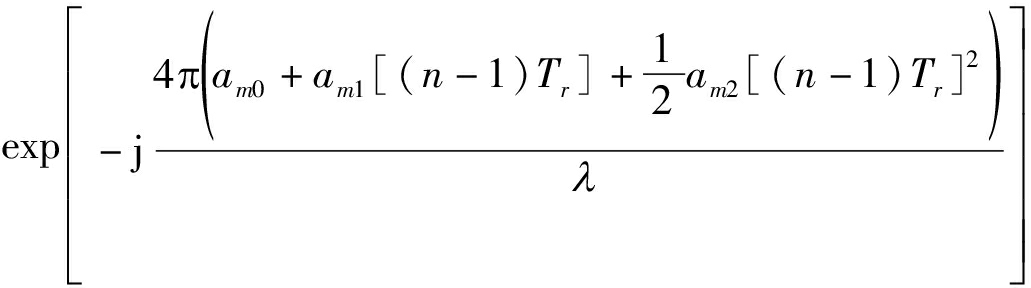
(6)
其中,n=1,2,…,Nsub为子片段内的脉冲数,m=1,2,…,Nc为子片段数,am0、am1和am2表示目标在第m个子片段内的初始运动参数;其具体表达式为:
(7)
am1=a1+a2[(m-1)Tsub]2
(8)
am2=a2
(9)
为了保证子片段内,目标加速度造成的距离变化不会跨越距离单元,并且多普勒频率变化量可以忽略,则在每个子片段的时长需要满足:
(10)
(11)
相应的有:
(12)
(13)
其中,Tsub为子片段的时长, fs为快时间(距离项)的采样率,amax为目标可能的最大加速度。
因此子片段的时长应该满足:
(14)
若目标可能的最大加速度为amax,通过上式(14)我们可以确定子片段的相参积累时间Tsub,得到子片段内的脉冲数为:
(15)
且由总脉冲数和子片段积累的脉冲数我们可以得到子片段数:
(16)
通过上述约束条件进行子片段划分后,每个子片段的回波信号可以近似为:
![]()
![]()
(17)
3 目标回波分段积累算法
3.1 子片段相参积累算法
经过分段处理后,目标回波信号可以近似表示为(17),从该式我们可以看出:目标在子片段内只发生由径向速度产生的线性距离走动,因此我们通过RFT实现子片段内目标回波信号的相参积累,其计算公式如下[8]:
![]()
![]()
![]()
![]()
(18)
其中,rsm为第m个子片段内的搜索径向距离,νsm为第m个子片段的搜索径向速度,经过RFT处理后的信号近似为[9]:
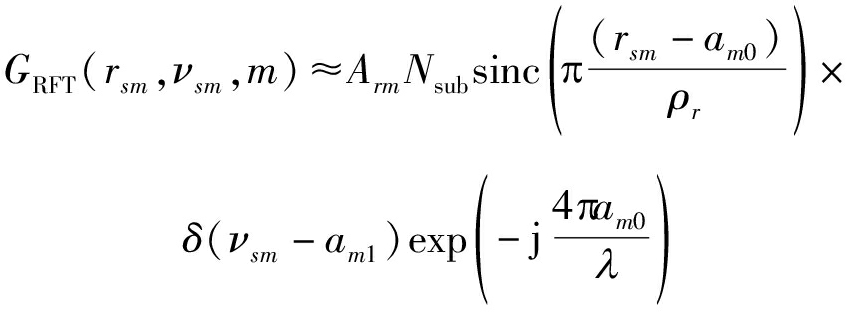
(19)
其中,am0为第m个子片段的距离,am1为第m个子片段的速度,Nsub为子片段的积累脉冲数,exp(-j4πam0/λ)为RFT处理后由子片段初始径向距离造成的余留相位。
3.2 子片段间积累
由式(19),第m个子片段经过RFT积累后,该片段的多脉冲回波信号能量在距离-速度域形成峰值,其峰值位置为(am0,am1),对应第m个子片段对应的距离和速度。通过式(7)和式(8)的递推关系可知:每个子片段RFT输出位置都是由a0、a1和a2以及片段参数m所决定。同时,注意到子片段m的回波信号经过RFT处理后,峰值相位包含φm=exp(-j4πam0/λ)项,该相位项由子片段m的初始径向距离am0决定。根据公式(7)可得,相位φm可以改写为:
![]()
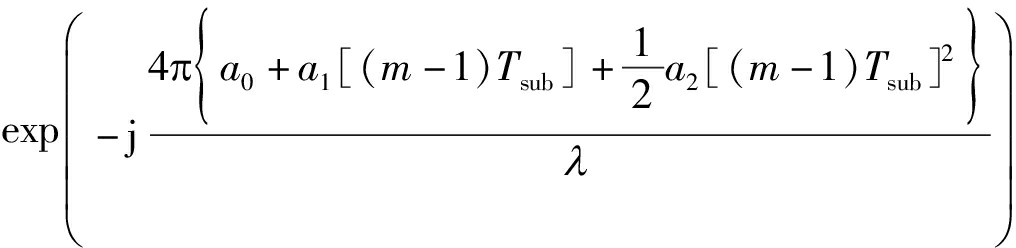
(20)
基于以上分析,本文通过设计距离-速度域的片段间能量积累方案,以实现各片段RFT积累幅值的能量积累,其计算公式如下:
![]()
![]()
![]()
(21)
其中,as0、as1和as2为搜索目标运动参数,Hθ(as1,as2,m)为相位补偿函数:
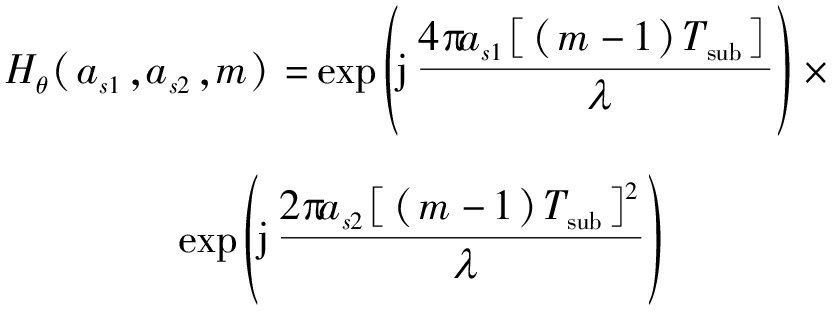
(22)
如式(21)所示,当搜索参数(as0、as1和as2)分别与目标实际参数(a0、a1和a2)相等时,不同子片段间的RFT的输出峰值可以同向叠加,形成最大输出峰值。随后,基于积累输出,可以完成目标检测[11]。
本文算法如图1所示,其主要步骤有:
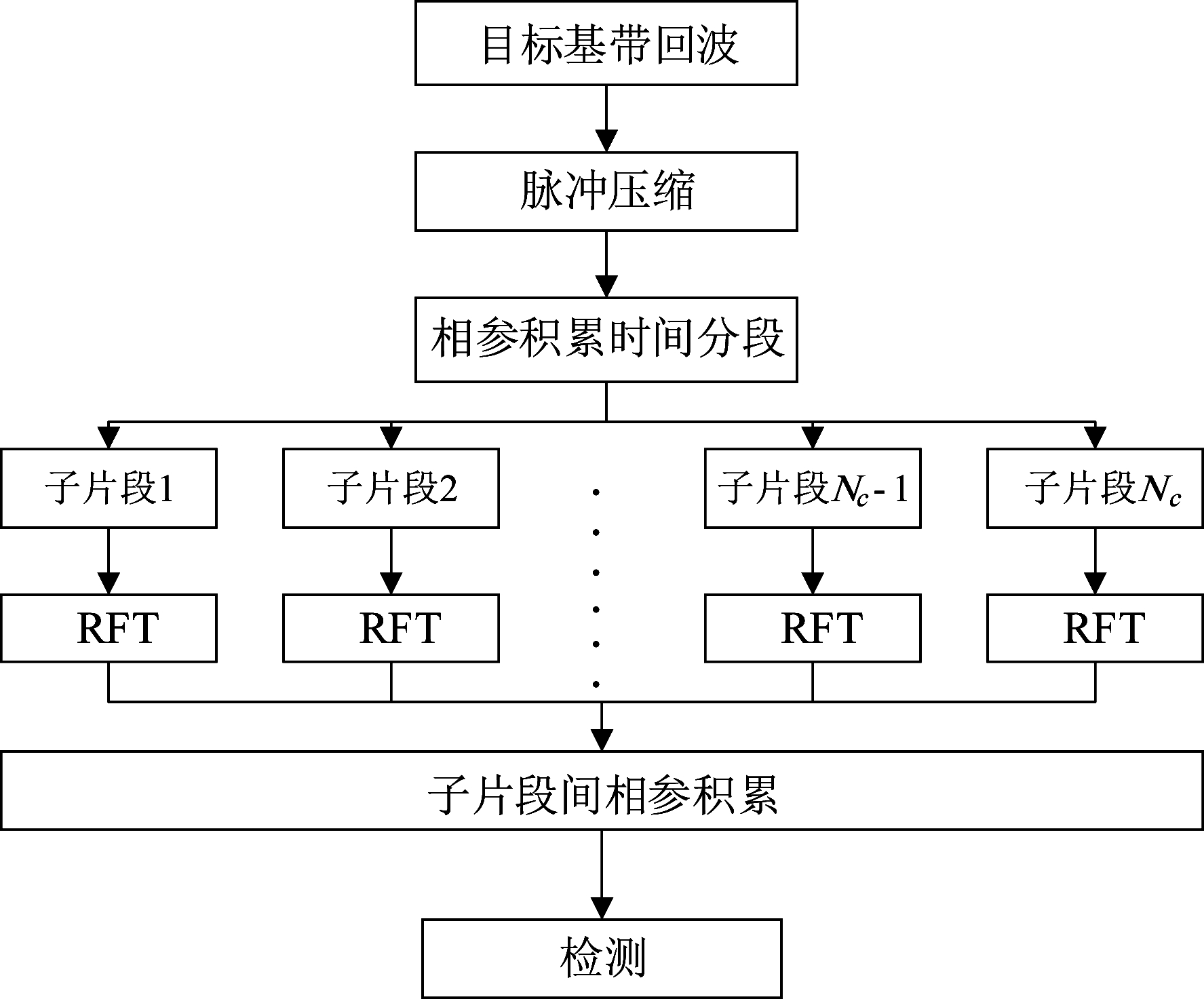
图1 处理流程图
Fig.1 Flow chart
(1)对接收到的雷达基带回波sr(t,k)进行匹配滤波,得到脉压信号src(t,k);
(2)对脉压信号src(t,k)进行分段,通过式(14)的约束条件将相参积累时间分为Nc个子片段得到分段后的信号![]()
(3)对每个子片段回波信号![]() 进行RFT积累处理,得到相应的子片段积累输出GRFT(rsm,νsm,m);
进行RFT积累处理,得到相应的子片段积累输出GRFT(rsm,νsm,m);
(4)利用式(21)对多个子片段的RFT输出进行积累处理,进而得到所有子片段回波信号的相参积累结果GRFT+RDCI(as0,as1,as2);
(5)基于积累输出GRFT+RDCI(as0,as1,as2),完成目标检测。
4 计算量分析
假设目标距离搜索Nr个单元,径向速度参数搜索单元数为Nν,加速度参数搜索单元数为Na,本文算法处理过程中,子片段脉冲数和子片段数分别为Nsub和Nc,MTD+GRT的子片段脉冲数和子片段数分别为![]() 和
和![]() 的多普勒模糊数搜索数为Nk。
的多普勒模糊数搜索数为Nk。
本文所提算法主要包含子片段内相参处理和子片段间相参处理,其中每个子片段内需要的复乘运算次数为NrNνNsub,需要的复加运算次数为NrNν(Nsub-1),所有子片段共需要复乘NcNrNνNsub次,复加NcNrNν(Nsub-1)次。另外,子片段间的复乘运算为NrNνNaNc次,复加运算次数为NrNνNa(Nc-1)。因此,本文算法所需复乘运算为NcNrNνNsub+NrNνNaNc次,复数加法运算为NcNrNν(Nsub-1)+NrNνNa(Nc-1)次。此外,GRFT算法所需的复乘,复加运算次数分别为[14]:NrNνNaNsum和NrNνNa(Nsum-1)。
MTD+GRT主要包含子片段内MTD处理和子片段间GRT处理,MTD处理可以通过快速傅里叶变换实现,那么所有子片段的复乘运算和复加运算分别为![]() 和
和![]() 次,另外子片段间GRT的实数加法次数为
次,另外子片段间GRT的实数加法次数为![]()
用Icm,Ica,Irm和Ira分别表示复乘,复加,实乘和实加的计算复杂度。GRFT、MTD+GRT以及本文算法的对比结果如表1所示。采用表2中的雷达参数,三种算法的计算量随积累脉冲数的变化曲线如图2所示,可以看到,本文提出的方法的计算量小于GRFT,当脉冲数为3000时,GRFT的计算量约为本文算法的10倍。
表1 计算复杂度
Tab.1 Computation complexity

方法计算量GRFTNrNνNa(NsumIcm+(Nsum-1)Ica)MTD+GRTN′cNr(N′sublog2(N′sub)Ica+N′sub2log2(N′sub)Icm)+NrNνNaNk(N′c-1)Ira本文方法NcNrNν(NsubIcm+(Nsub-1)Ica)+NrNνNa(Nc-1)Ica+NrNνNaNcIcm
表2 仿真参数
Tab.2 Simulation parameters

参数参数值雷达载频/MHz150信号带宽/MHz5脉冲重复频率/Hz500采样率/MHz5脉冲宽度/μs20
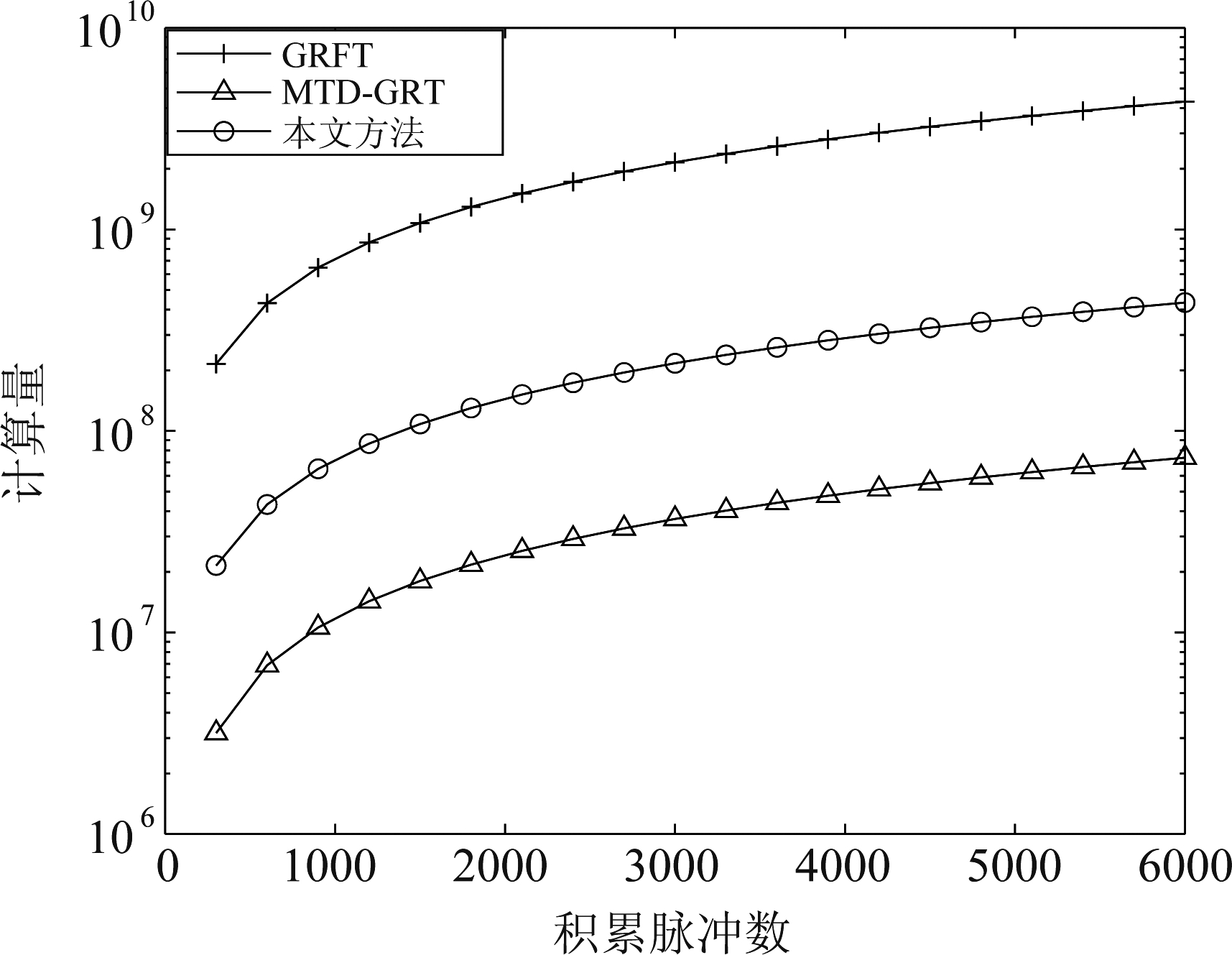
图2 计算复杂度比较
Fig.2 Computational complexity comparison
5 仿真验证与分析
为了验证本文提出的基于分段处理的相参积累算法的有效性,在本节对算法进行仿真实验,雷达系统参数如表2所示。目标的初始径向距离a0=200 km,初始径向速度a1=200 m/s,初始径向加速度a2=25 m/s2,相参积累时间为6 s。
首先,仿真分析了本文提出的算法原理。图3(a)为目标3000个脉冲回波信号的脉压结果,可以看到目标发生了距离弯曲,能量分布在多个距离单元内。如图3(b)所示,目标跨越了55个距离单元:其中由速度引起距离单元走动为a1T/ρr=40,由加速度造成的距离单元走动为0.5a2T2/ρr=15。基于公式(14)中的分段准则,将3000个脉冲进行分段处理,总共分成了30个子片段,每个子片段内有100个脉冲回波。其中,第6个子片段的首尾脉冲如图3(c)所示。可以看到,子片段6内目标的距离走动量降为1(由片段6内目标的速度引起:fix(225*0.2/30)=1)。第28个子片段的首尾脉冲如图3(d)所示,可以看到该子片段内目标的距离走动量降为2(由片段28内目标的速度引起:fix(335*0.2/30)=2)。图3(e)和图3(f)分别给出了第6个子片段和第28个子片段的RFT输出。最后,利用公式(21)对30个子片段间的处理结果如图3(g)所示。可以看到,子片段间的能量被有效积累。

图3 所提算法处理仿真
Fig.3 The proposed algorithm processes simulation
图4对高斯白噪声背景下的算法性能进行了对比分析,其中脉压后的SNR设置为0 dB。图4(a)为脉压结果,此时难以对信号进行有效检测。图4(b)、(c)、(d)和(e)分别为MTD、RFT、MTD+GRT和本文方法的回波积累结果。可以看出:MTD和RFT无法实现回波信号的有效积累,原因在于:高速机动目标可以在短时间内发生DS效应,且MTD/RFT均不能补偿DS。与MTD+GRT相比,本文算法在噪声抑制性上更好,能够获得更高的积累增益,如图4(d)和图4(e)所示,原因在于:本文算法子片段内和子片段间都采用相参处理,而MTD+GRT的片段间积累方式为非相参处理;此外,本文所提算法的子片段脉内的脉冲允许个数更多,有利于子片段内回波SNR的提升。
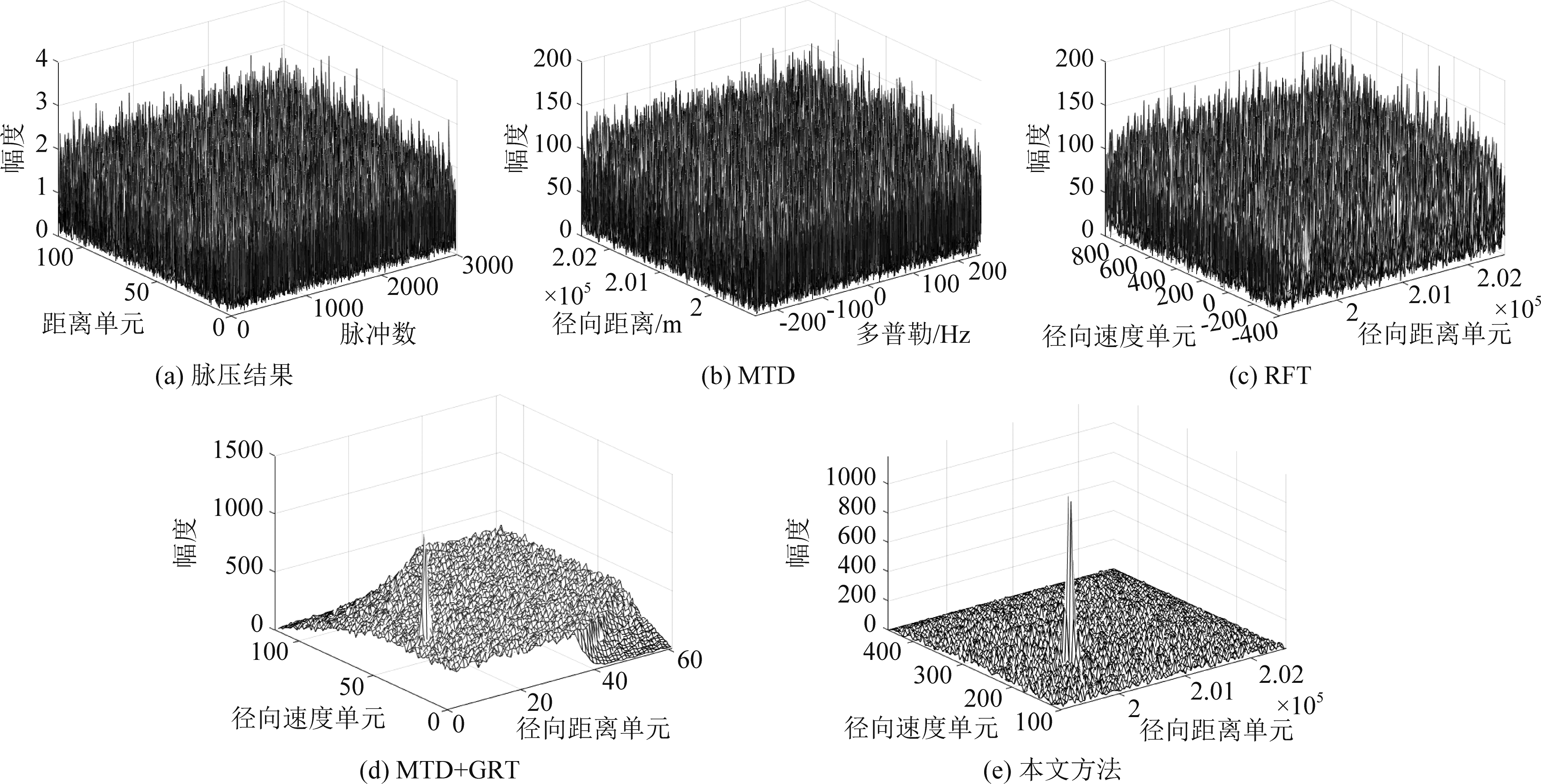
图4 积累结果对比(0 dB)
Fig.4 Comparison of accumulated results(0 dB)
图5给出了本文算法在多目标场景下的仿真实验(脉压后SNR=0 dB),目标参数由表3给出。图5(a)为脉压信号,可以看到目标A与目标B均发生了距离弯曲,且能量分布在多个距离单元内。图5(b)、(c)分别给出了MTD与RFT的积累结果,可以看出:MTD和RFT无法实现回波信号的有效积累,原因在于:MTD无法对目标的RM和DS进行补偿,而RFT无法补偿由加速度造成的RM和DS,图5(d)给出了本文算法的积累结果可以看出目标A和目标B均被有效地积累并且峰值位置与实际参数相吻合。
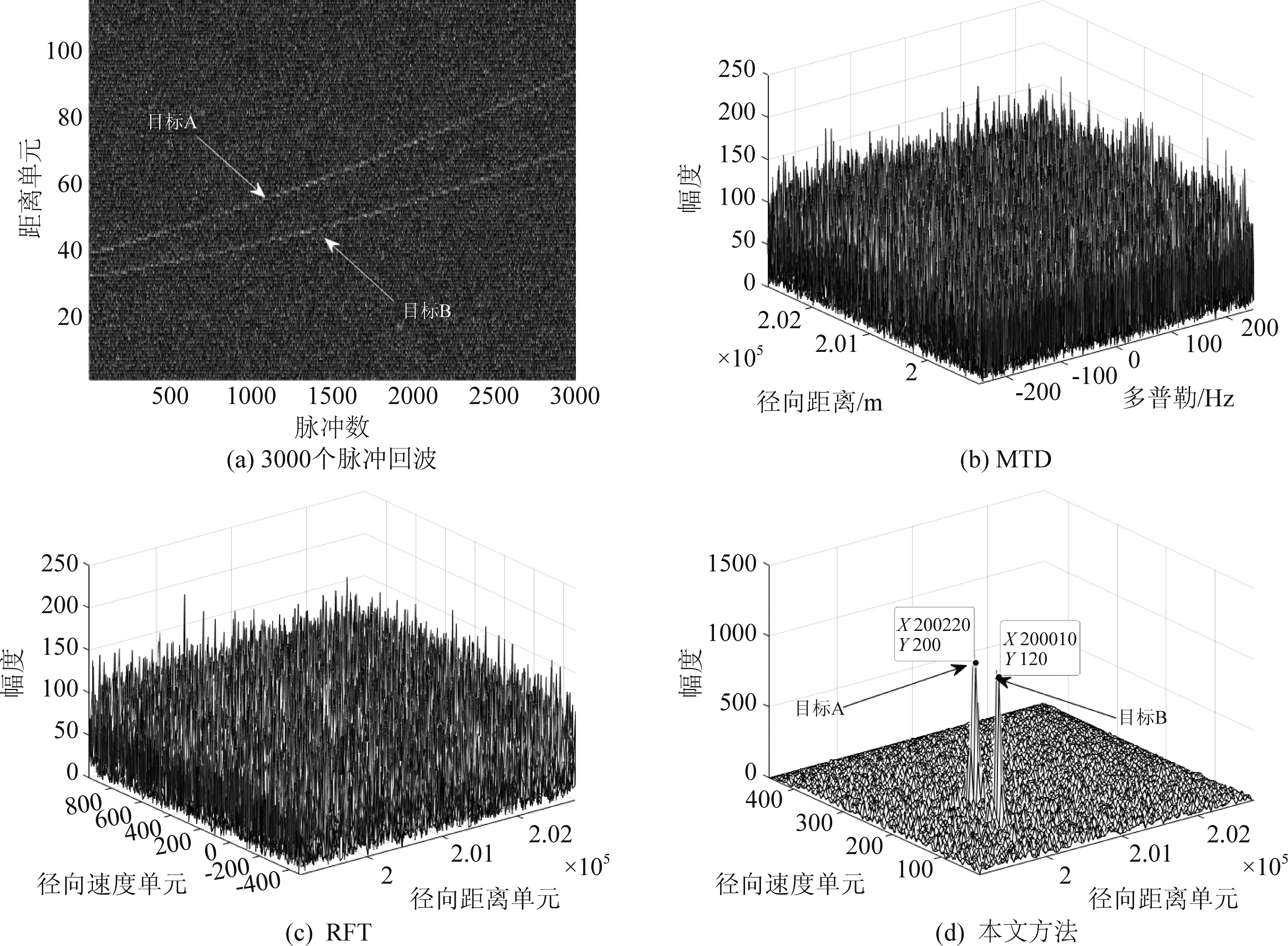
图5 多目标实验
Fig.5 Multiple-target experiment
表3 目标参数
Tab.3 Target parameters

参数目标A目标B初始径向距离/m200220200010初始径向速度/(m/s)200120初始径向加速度/(m/s2)2525
最后,图6给出了与图3相同仿真参数与目标参数下,在虚警率pfa=10-3时,本文算法与GRFT、RFT和MTD+GRT检测概率曲线(1000次蒙特卡洛)。由于RFT无法对加速度在距离和多普勒上造成的走动进行补偿,因此,仅在信噪比较高时才能对目标进行正确稳定的检测;MTD+GRT虽然由于子片段间采用了非相参积累,因此在积累检测性能上略差于本文方法。
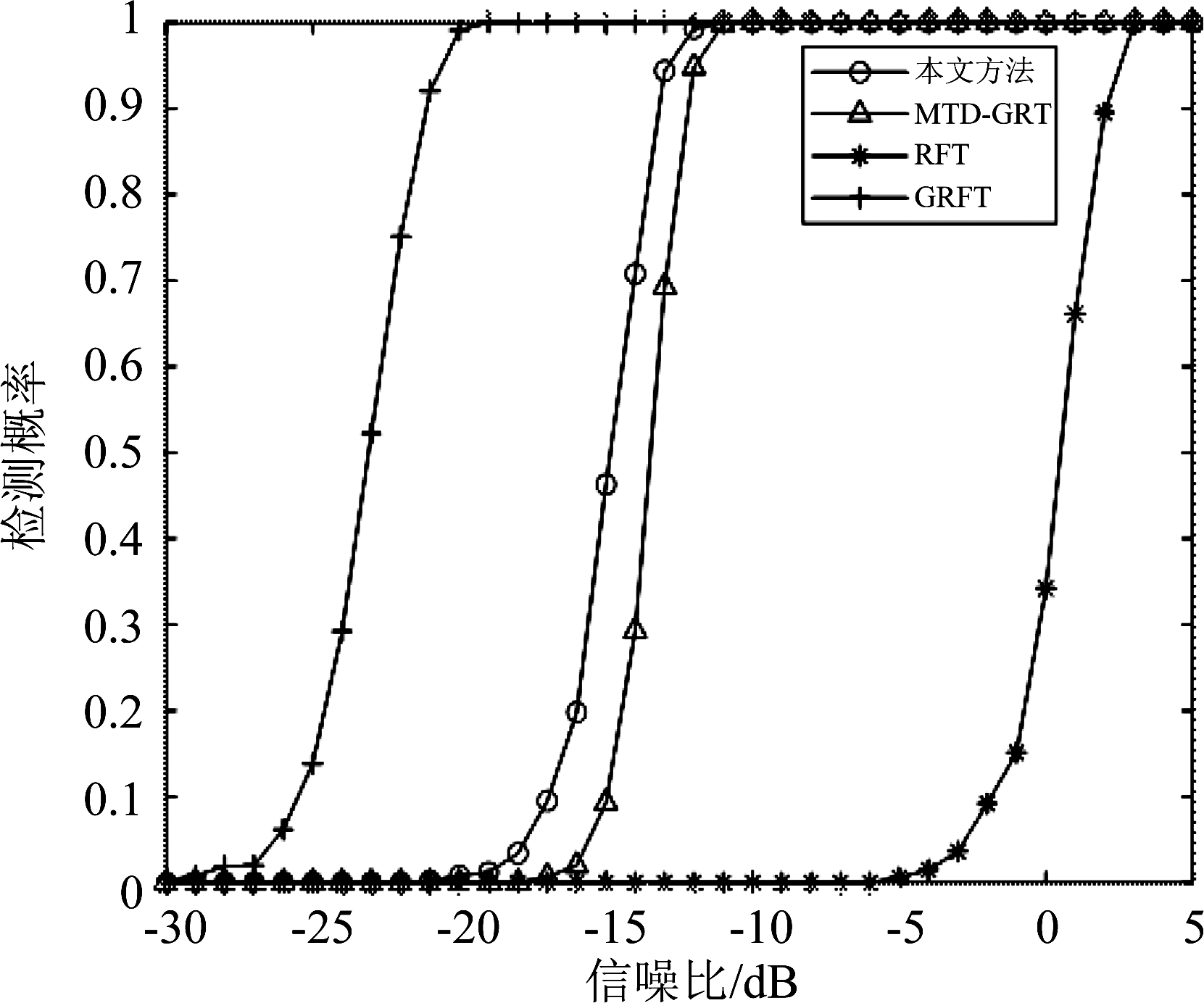
图6 检测概率曲线
Fig.6 Detection probability curve
6 结论
本文方法首先通过将相参积累时间分为若干个子片段,使得子片段内由加速度造成的RM和DS可以忽略,进而通过RFT积累目标子片段内的回波信号;随后分析了各子片段RFT积累后的峰值分布特性,并提出了基于距离-速度域的子片段间RFT输出幅值的相参积累处理方法,提高了检测概率。与GRFT和MTD+GRT相比,本文算法能够在计算代价与积累增益之间取得平衡。最后,通过数值实验对本文算法进行了分析验证。
[1] 赵彦君.雷达低空微弱目标检测技术研究[D].成都:电子科技大学,2019.
ZHAO Yanjun.Research on radar low-altitude weak target detection technology[D].Chengdu: University of Electronic Science and Technology of China, 2019.(in Chinese)
[2] 黄响.高速微弱目标检测算法研究[D].西安:西安电子科技大学,2019.
HUANG Xiang.Study on high-speed low-observable target detection[D].Xi’an: Xidian University, 2019.(in Chinese)
[3] 陈小龙, 黄勇, 关键, 等.MIMO雷达微弱目标长时积累技术综述[J].信号处理, 2020, 36(12): 1947-1964.
CHEN Xiaolong, HUANG Yong, GUAN Jian, et al.Review of long-time integration techniques for weak targets using MIMO radar[J].Journal of Signal Processing, 2020, 36(12): 1947-1964.(in Chinese)
[4] 杨宇超.高速目标的长时间相参积累算法研究[D].哈尔滨:哈尔滨工业大学,2020.
YANG Yuchao.Research on long time coherent integration algorithm for high speed target[D].Harbin: Harbin Institute of Technology, 2020.(in Chinese)
[5] CARLSON B D, EVANS E D, WILSON S L.Search radar detection and track with the Hough transform.I.system concept[J].IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102-108.
[6] 王宁,孟晋丽,刘国庆,等.机载雷达微弱目标帧间非相参积累与检测技术[J].信号处理, 2021, 37(2): 248-257.
WANG Ning, MENG Jinli, LIU Guoqing, et al.Airborne radar weak target interframe noncoherent integration and detection method[J].Journal of Signal Processing, 2021, 37(2): 248-257.(in Chinese)
[7] ZHANG Shunsheng, ZENG Tao, LONG Teng, et al.Dim target detection based on keystone transform[C]∥IEEE International Radar Conference, 2005.Arlington, VA, USA.IEEE, 2005: 889-894.
[8] XU Jia, YU Ji, PENG Yingning, et al.Radon-Fourier transform for radar target detection, I: Generalized Doppler filter bank[J].IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1186-1202.
[9] XU Jia, YU Ji, PENG Yingning, et al.Radon-Fourier transform for radar target detection(II): Blind speed sidelobe suppression[J].IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2473-2489.
[10] CHEN Xiaolong, GUAN Jian, LIU Ningbo, et al.Maneuvering target detection via radon-fractional Fourier transform-based long-time coherent integration[J].IEEE Transactions on Signal Processing, 2014, 62(4): 939-953.
[11] 关键,陈小龙,于晓涵.雷达高速高机动目标长时间相参积累检测方法[J].信号处理, 2017, 33(3A): 1-8.
GUAN Jian, CHEN Xiaolong, YU Xiaohan.Long-time coherent integration-based detection method for high-speed and highly maneuvering radar target[J].Journal of Signal Processing, 2017, 33(3A): 1-8.(in Chinese)
[12] LI Xiaolong, CUI Guolong, YI Wei, et al.Coherent integration for maneuvering target detection based on radon-lv’s distribution[J].IEEE Signal Processing Letters, 2015, 22(9): 1467-1471.
[13] XU Jia, XIA Xianggen, PENG Shibao, et al.Radar maneuvering target motion estimation based on generalized radon-Fourier transform[J].IEEE Transactions on Signal Processing, 2012, 60(12): 6190-6201.
[14] XU Jia, ZHOU Xu, QIAN Lichang, et al.Hybrid integration for highly maneuvering radar target detection based on generalized radon-Fourier transform[J].IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(5): 2554-2561.
[15] 周煦, 许稼, 钱李昌, 等.高机动雷达目标快速长时间混合积累算法[J].信号处理, 2015,31(12): 1547-1553.
ZHOU Xu, XU Jia, QIAN Lichang, et al.Fast algorithm of long-time hybrid integration for highly maneuvering radar target detection[J].Journal of Signal Processing, 2015, 31(12): 1547-1553.(in Chinese)
[16] DING Zegang, LIU Siyuan, LI Yinchuan, et al.Parametric translational compensation for ISAR imaging based on cascaded subaperture integration with application to asteroid imaging[J].IEEE Transactions on Geoscience and Remote Sensing, 2020,PP(99):1-17.doi: 10.1109/TGRS.2020.3043028.


