1 引言
随着水下资源勘探、海洋科学研究和国防安全等领域的需求增加,其对水下信息高速传输的要求也不断提高。由于水声信道是带宽受限信道,提高水声信道频谱利用率能够提高水下信息传输的效率。正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术具有频谱利用率高、结构简单和抗多径干扰等优点,被广泛的用于无线通信标准中[1]。近些年来,该技术被引入到水声通信之中,成为了水下高速通信的热点研究方向[2-3]。
由于水下环境复杂多变的特性,水声信道往往呈现明显的多径现象、强时变、空变特性和大多普勒效应,这些因素也使得水声信道成为目前最复杂无线信道之一[2]。在进行OFDM水声通信时,水声信道的多径现象和快变特性使得接收端存在严重的码间干扰(Inter-Symbols Interference, ISI)和数据块间干扰(Inter-Blocks Interference, IBI);多普勒频移会破坏OFDM子载波间的正交性,产生载波间干扰(Inter-Carrier Interference, ICI)[4]。这些干扰的存在严重影响了OFDM通信系统的可靠性,且当信道为深度衰落信道时,某些子信道响应可能会被噪声淹没,传统的信道估计和信道均衡技术并不能完全消除以上的干扰。
针对以上问题,水声通信系统还需要结合信道编码技术进一步纠正复杂信道所造成的随机错误。常用的信道编码方法主要有LDPC码、Turbo码、卷积码、BCH码和RS码等。其中LDPC码和Turbo码都具备接近香农极限的译码性能,被广泛的用于水声通信系统之中[5]。但LDPC码和Turbo码译码过程需要进行多次迭代,具有较高的译码复杂度,解码实时性较差,且存在错误平层的问题[6]。
针对LDPC码和Turbo码译码复杂度高和错误平层问题,还需要进一步研究其他高效的编码方法。2009年Erdal Arikan正式提出了信道极化和极化码(Polar code)的概念[7],并在二进制输入离散无记忆信道(Binary-input Discrete Memoryless Channels, B-DMC)背景下证明了该码具备达到香农极限的能力。同时,Arikan给出了极化码的连续消除(Successive Cancellation, SC)译码方法,但该方法存在误码传递和译码时延问题。为了改善这一现象,文献[8]提出了列表连续消除(Successive Cancellation List, SCL)译码方法。之后又有学者将循环校验与极化码进行级联,提出了CRC-SCL译码方法,进一步提高了极化码的译码性能[9-10]。实验仿真表明CRC-SCL译码方法在高斯白噪声信道下具有比LDPC码更好的译码性能,且不存在误码平层现象。需要说明的是,极化码性能取决于信道极化的状况,只有准确实现信道极化才能充分发挥极化码优良的译码特性。现阶段信道极化方法主要是针对B-DMC信道展开的,且依赖于信道参数和码长,不适用于实际传输信道[11]。为了解决这一问题,华为提出了一种独立于信道特性的极化权重PW(Polarization Weight, PW)子信道可靠性评估方法[12-13],但该方法仅依赖一个参数进行信道极化,且未考虑不同极化层极化程度的差异,因此极化性能依旧有待提高。
针对上述问题,本文提出了一种基对称扩展PW信道极化方法,并将该方法用于OFDM水声通信中的信道编码。本文方法扩展了原始PW方法中扩展基单一的情况,分层考虑了不同极化层子信道可靠性的程度,实现了更准确的信道极化。实验仿真结果表明,本文提出的信道极化方法具有更强的信道极化稳健性,且不存在误码平层,能够用于OFDM水声通信系统的纠错检错。
2 信道极化
2.1 信道极化原理
信道极化是极化编码的核心过程,Arikan在B-DMC信道条件下对信道进行如图1所示的合并和分裂操作,使得等效的分裂子信道容量呈现两极分化的现象。假设极化层度足够大,极化后的信道部分呈现无噪声特性,部分呈现全噪声特性,这就是信道极化的基本概念。
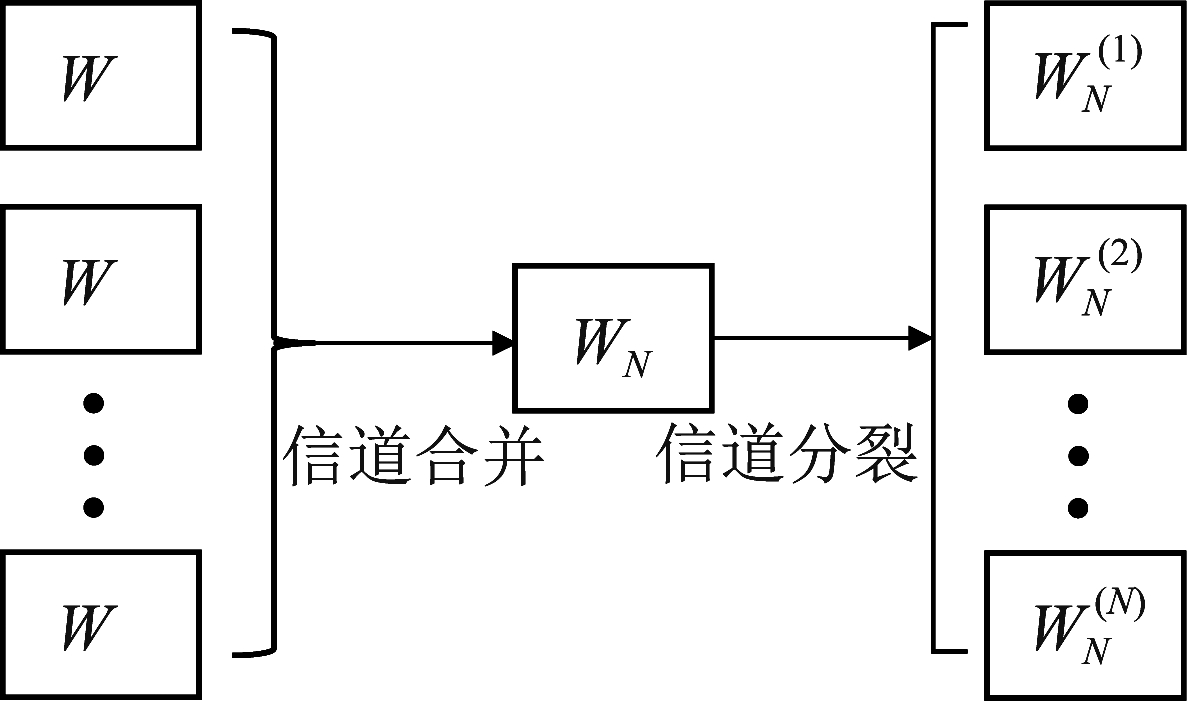
图1 信道极化变换
Fig.1 Channel polarization transformation
图2所示是信道极化的基础结构,下面以此为例说明信道极化的过程。
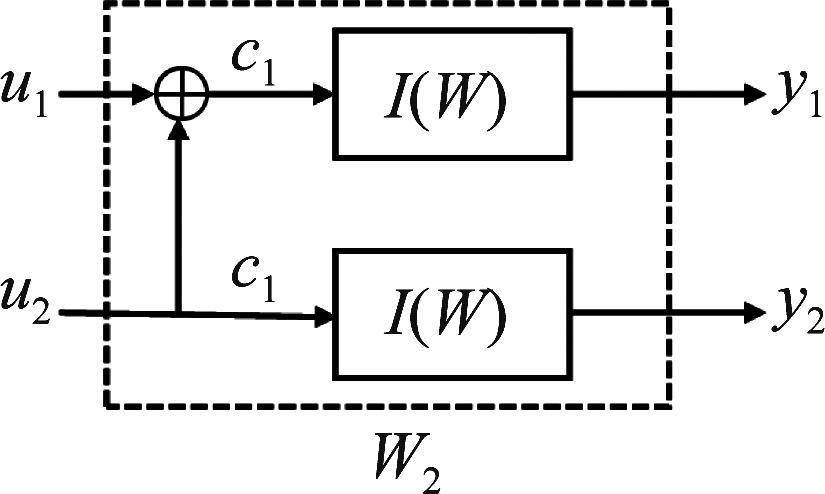
图2 码长为2的信道极化结构
Fig.2 Channel polarization structure of N=2
在图2中，u1和u2是输入信息比特，y1和y2是经过信道W后的输出，I(W)表示信道W的信道容量。在这种背景下，u1和u2通过信道W后，对应的互信息可表示为
I(u1,u2;y1,y2)=I(c1,c2;y1,y2)=
I(u1;y1,y2)+I(u2;y1,y2|u1)=2I(W)
(1)
将I(u1;y1,y2)记为
将I(u2;y1,y2|u1)记为
其中
和
表示信道W分裂后的分裂信道。假设输入信息比特u1和u2间是相互独立的，则
可写作
I(u2;y1,u1|y2)=I(W)+I(u2;y1,u1|y2)≥I(W)
(2)
可以看出经过信道合并和分裂操作后,两个极化子信道的信道容量发生了改变。图3是信道传输错误概率为0.5,码长为256和2048时信道极化的情况。从图中可以看出随着码长的增加,信道极化程度也随之增加。可以预见当码长足够长时,部分极化子信道将接近无噪声信道,其余子信道接近于全噪声信道,此时可在无噪声信道上传输信息比特,在噪声信道上传输双方已知的冻结信息比特[14],一般为0。
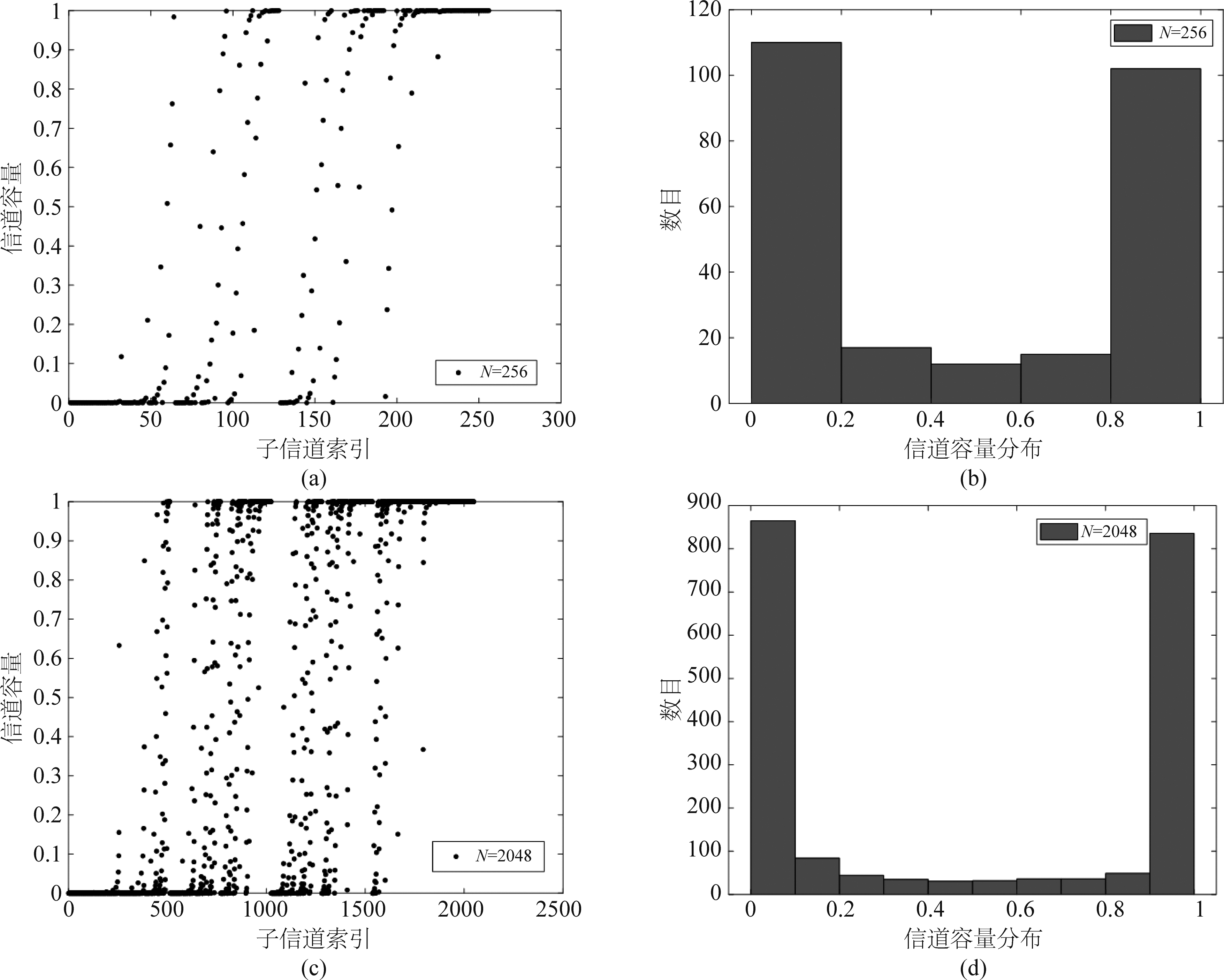
图3 码长256和2048的BEC信道极化分布
Fig.3 BEC channel polarization distribution, N=256 and 2048
在极化码的实际应用中,码长都是有限的,此时信道极化不彻底,不同信息子信道的选取将对极化码的译码性能产生较大影响。为了提高极化码编码系统的传输可靠性,还需要研究极化子信道可靠性的评估方法。
2.2 极化子信道可靠性评估方法
极化子信道的可靠性可以通过其信道容量的大小进行衡量,但子信道容量难以提前获知。因此常用巴氏参数法(Bhattacharyya Parameter)、密度进化法(Density Evolution)、高斯近似法(Gaussian Approximation, GA)、蒙特卡洛法(Monto Carlo)进行信道可靠性的评估[11, 15]。
Bhattacharyya参数是一种评估信道可靠程度的参数,它是由信道转移概率定义的,其表达式为
(3)
式中，W(y|0)和W(y|1)是信道转移概率。Z(W)越大表明该信道可靠性越低，且Z(W)与原始信道容量I(W)之间满足式(4)的关系
(4)
Bhattacharyya参数只有在二进制擦除信道条件下才能获得极化子信道可靠性的准确值,而对于其他类型的信道只能获得大概的范围。密度进化法需要计算和存储概率密度函数,计算复杂度高。蒙特卡洛法是通过多次仿真实验求得各个子信道误码率,以此表征子信道的可靠性,存在复杂度高和精度有限的问题。现阶段,低复杂度的极化码构造方法主要有GA法,与密度进化法不同的是,GA法将多维的概率密度函数转换为简单的一维均值计算,在求得各个子信道的概率密度函数后,通过式(5)求得信道的错误传输概率,以此评估子信道的传输可靠性。
(5)
式中，
是第i个子信道概率密度函数的均值。
以上介绍的信道极化方法在进行信道极化时都与信道参数相关,如信噪比和码长。不同信道参数对应着不同的信道极化结果,因此不适合于实际通信系统。
2.3 基对称扩展信道极化方法
为了增强极化码在实际系统中的可用性和极化信道的稳健性,华为提出了基于极化权重(Polarization Weight, PW)的信道极化方法,该方法采用固定化的信道可靠性排序方法,能够独立于信道状态实现精确的信道极化,且对不同码长的信道极化具有更强的稳定性[12]。
考虑一个长度为N=2n的极化信道，并用二进制表示第i个子信道对应的编号i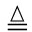
(bn-1,bn-2,…,b0)，定义第i个子信道PW值为
(6)
式中，β是展开式基，经过3GPP RAN 87会议研讨，最终将其定为β=21/4。此时，第i个子信道PW值Wi为
(7)
从式(7)可知，基于PW法的信道极化结果具有较强的稳健性，即当新的极化码长N1<N时，可以直接采用长度为N的信道极化结果中前N1个PW值进行信道评估。如图4所示为码长N=512、1024、2048时子信道PW值分布图，可以发现，长码PW法信道极化结果可以直接用于短码信道极化，即短码是长码的一个子集。PW方法实现了独立于信道状态的信道极化，且具有极低的计算复杂度。但是由于PW法展开式仅仅与单个基相关，并未考虑不同极化层的权重，因此不能精确地评价各个子信道的可靠性。为了改善这一现象，文献[13]将不同二进制位的贡献纳入极化信道的考量中，描述每个通道间细微的变化，形成修正的PW信道极化法
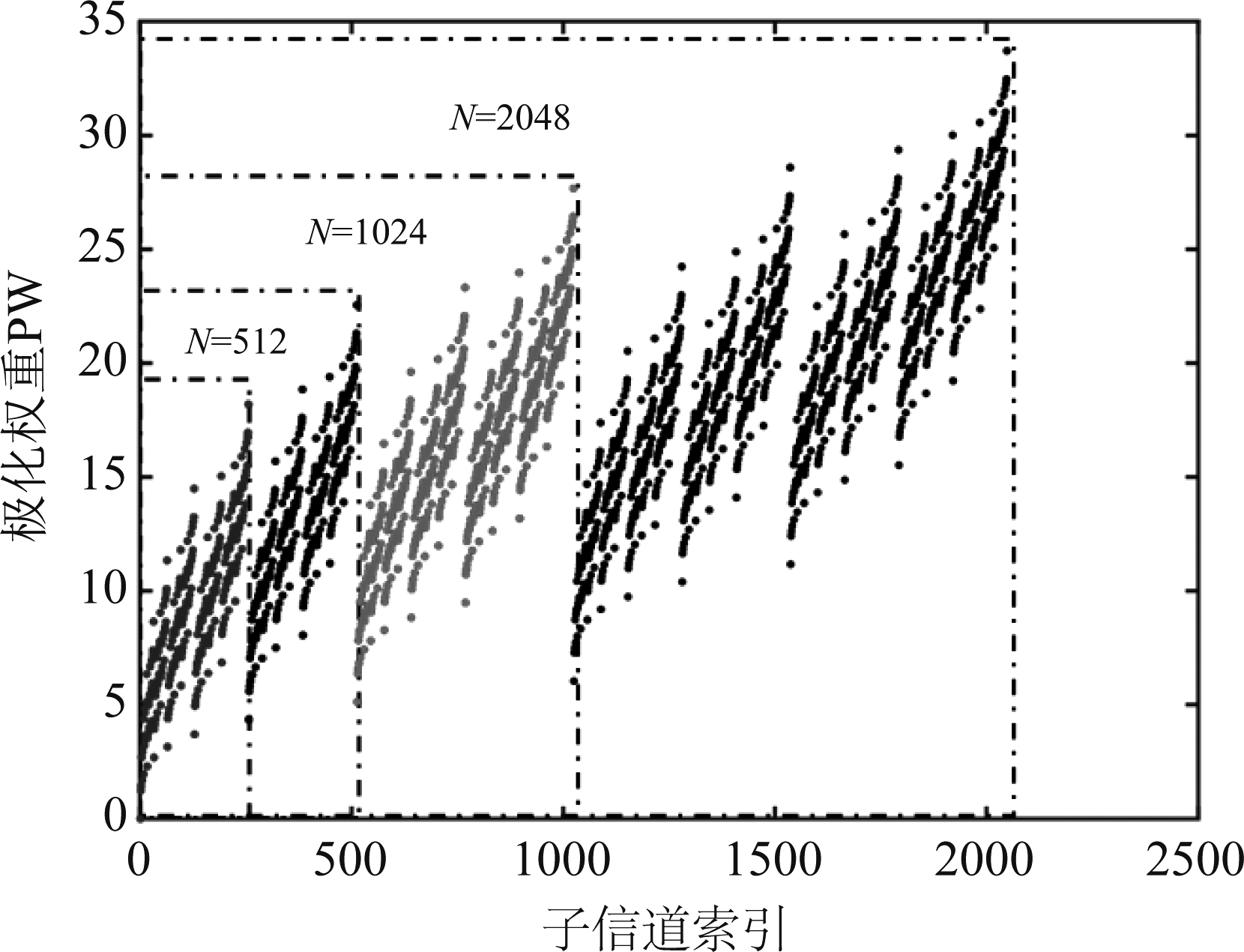
图4 不同码长下极化子信道PW值
Fig.4 Sub-channel PW of different code length
(8)
在保证算法简便性的前提下，对式(8)进行2阶展开，即
(9)
上式进一步细化了不同极化子信道间的差异。但这种极化方法也存在极化结果的对称性，即前半部分子信道偏序顺序与后半部分相同，极化结果依旧存在偏差。为了进一步改善这一现象，本文将对称反馈变量引入到基扩展中，以此改变极化结果的对称性，提出了基对称扩展PW信道极化法
(10)
式中，bf是对称点位置，a是权重因子，c是扩展基。本文中，c为式(8)的多阶扩展，a为多阶扩展系数。引入扩展基的多阶展开，改变了原始极化结构中内部对称的特性，实现了更精确的信道极化。之后将通过仿真实验验证该PW信道极化法的有效性。
3 极化编码与译码
在完成信道极化后，可根据极化子信道PW值进行可靠性排序，完成极化码的编解码过程。这里将信息比特对应信道位置的集合记作A，剩余信道位置集合记作Ac，并在这些位置上传输已知的固定比特0，简记为冻结比特。在实际传输过程中，信息比特往往是选取极化分裂信道中信道容量最大的前K个分裂子信道对应的位置，因此极化码可以简记为(N,K,A,uAc)[14]。图2所示的信道极化过程是极化码最小的结构单元，信源比特
与编码比特
间满足
(11)
式中，生成矩阵
当码长为N时，信源比特
于编码比特
间满足
GN=BNF⊗n
(12)
式中，
表示n次Kronecker运算。Kronecker运算定义为
(13)
BN是一个比特置换矩阵，BN=RN(I2⊗BN/2)，B2=I2，RN的作用如下
(u1,u2,u3,…,uN)RN=
(u1,u3,u5,…,uN-1，u2,u4,u6,…,uN)
(14)
从极化码的编码过程可以看出，极化码具有线性编码的特性，但Polar码的构造过程并未考虑最大化码距的问题，因此也具有概率码的特点。在完成极化编码后，信号经过调制等过程，通过信道后被接收端接收。Arikan最早提出了SC译码方法，该方法在码长足够长时，能够达到香农极限，且译码复杂度仅为O(Nlog(N))。考虑第i个比特的译码过程，采用软判决译码，将其对应的分裂信道
转移概率对数比LLR表示为
(15)
式中，
是接收信号，
是
的估计值。当前时刻
判决规则如下
(16)
式中，
是判决函数
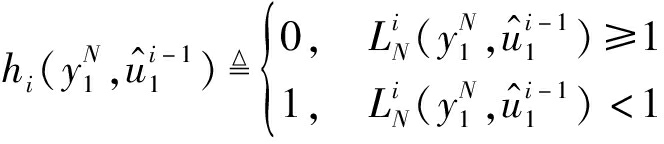
(17)
从SC译码的过程可以看出，SC译码是一种顺序译码。因此，可以通过分裂子信道间的递归关系简化译码过程
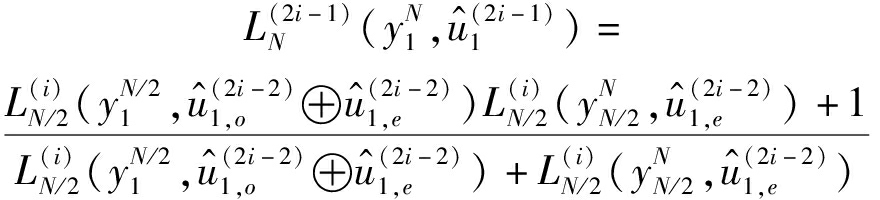
(18)
(19)
由于SC译码是连续译码,若某一比特译码错误将导致错误传递。为了增强极化码译码的可靠性,之后学者们又提出了串行抵消列表SCL译码方法。与SC译码方法每次译码时仅有一个译码路径不同的是,SCL译码是在译码时保留L个路径度量值最大的译码路径,并最终选择一个最佳的译码路径作为最后的译码结果,该方法有效地避免了错误传递。SCL译码随着列表长度的增加译码能力不断提高,但也存在路径模糊的情况。针对现有译码方法的缺陷,之后出现了很多改进的方法,如采用RS码、Turbo码等组成级联码,也有将循环校验CRC引入到SCL译码中[9, 16]。这些改进方法进一步增强了Polar码的译码能力。本文将采用CRC-SCL方法作为译码方案,研究该方法在OFDM系统中的译码性能。
4 Polar-OFDM水声通信系统模型
OFDM是一种多载波调制技术,它是将串行的数据分配到若干个相互正交的子载波上并行传输,因此具有传输效率和频谱利用率高、抗多径干扰等优点。由于水声信道是带宽受限信道,提高信道频谱利用率对于高速水声通信具有重要意义,因此OFDM技术被引入到水声通信系统中来[2-4, 17-18]。为了研究极化码在水声多径信道条件下的性能,本节搭建如图5所示的Polar-OFDM水声通信系统模型。
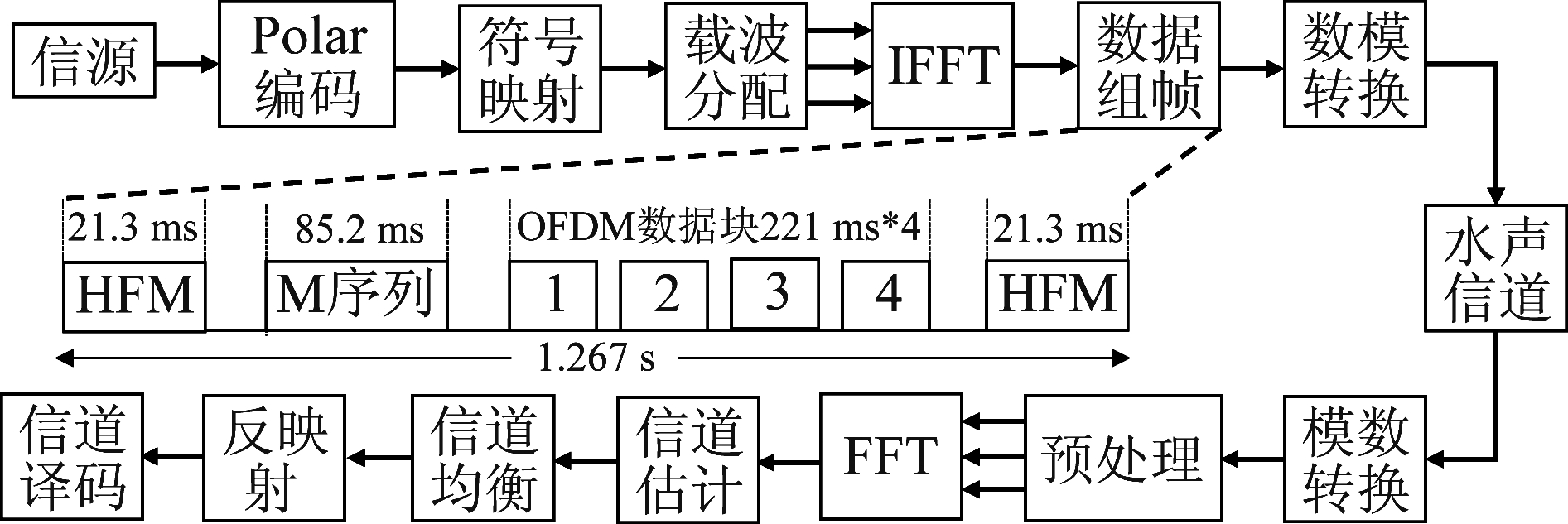
图5 水声OFDM通信系统结构
Fig.5 Structure of OFDM underwater acoustic communication system
水声通信中水声信道大多具有强多径、大多普勒频移现象。此时,可将水声信道建模为时延-多普勒双扩展信道,即
(20)
式中，Npa是多径数目，Ap是第p条路径的幅度，τp(t)是第p条路径的时延，a是多普勒频移因子。这里假设所有信道是慢变的，即在一个数据块内信道响应不变。实际中OFDM调制可通过快速傅里叶变换FFT/IFFT实现，结构简单，工程中易于实现。
本文以零后缀(Zeros Padded, ZP)OFDM系统为例进行研究。假单个数据块内ZP和OFDM符号持续时间分别为TZP和T，则数据块中第m个OFDM符号基带信号是
(21)
式中，sm(k)和g(t)分别是第k个子载波上的符号和升余弦窗。之后，ZP-OFDM信号经过通带变换在水声信道中传输。接收端接收到发射信号后，再经过基带变换和同步等预处理，得到接收端信号ym(t)
ym(t)=xm(t)*hm(t)+nm(t)
(22)
式中，*是卷积运算符号，nm(t)是加性噪声。此时，在对ym(t)进行FFT操作，得到OFDM频域信号
Ym(k)=Xm(k)Hm(k)+Nm(k)
(23)
本文采用频域信道估计和MMSE均衡算法估计原始符号，MMSE均衡器Wm(k)为
(24)
式中，N0是平均噪声功率。得到原始信号的估计值之后，经过反映射进行信道译码过程，就完成了OFDM通信系统的全过程。下文的仿真就是基于这个模型进行的，为了进一步简化分析，假设ZP长度大于信道多径时延。
5 实验仿真与分析
本节首先通过实验仿真验证所提出的基对称扩展PW信道极化法的编译码性能,并在实际信道环境下对比不同信道极化程度、不同编码效率和不同译码算法的编译码性能。
5.1 不同信道极化方法性能对比
本节仿真巴氏参数法、高斯近似法GA、Monto Carlo和PW类方法信道极化的性能。由于巴氏参数法、高斯近似法只适用于高斯白噪声信道,因此本节仿真将在该信道环境下进行,并采用通信系统误码率作为对比参数,结果如图6所示。
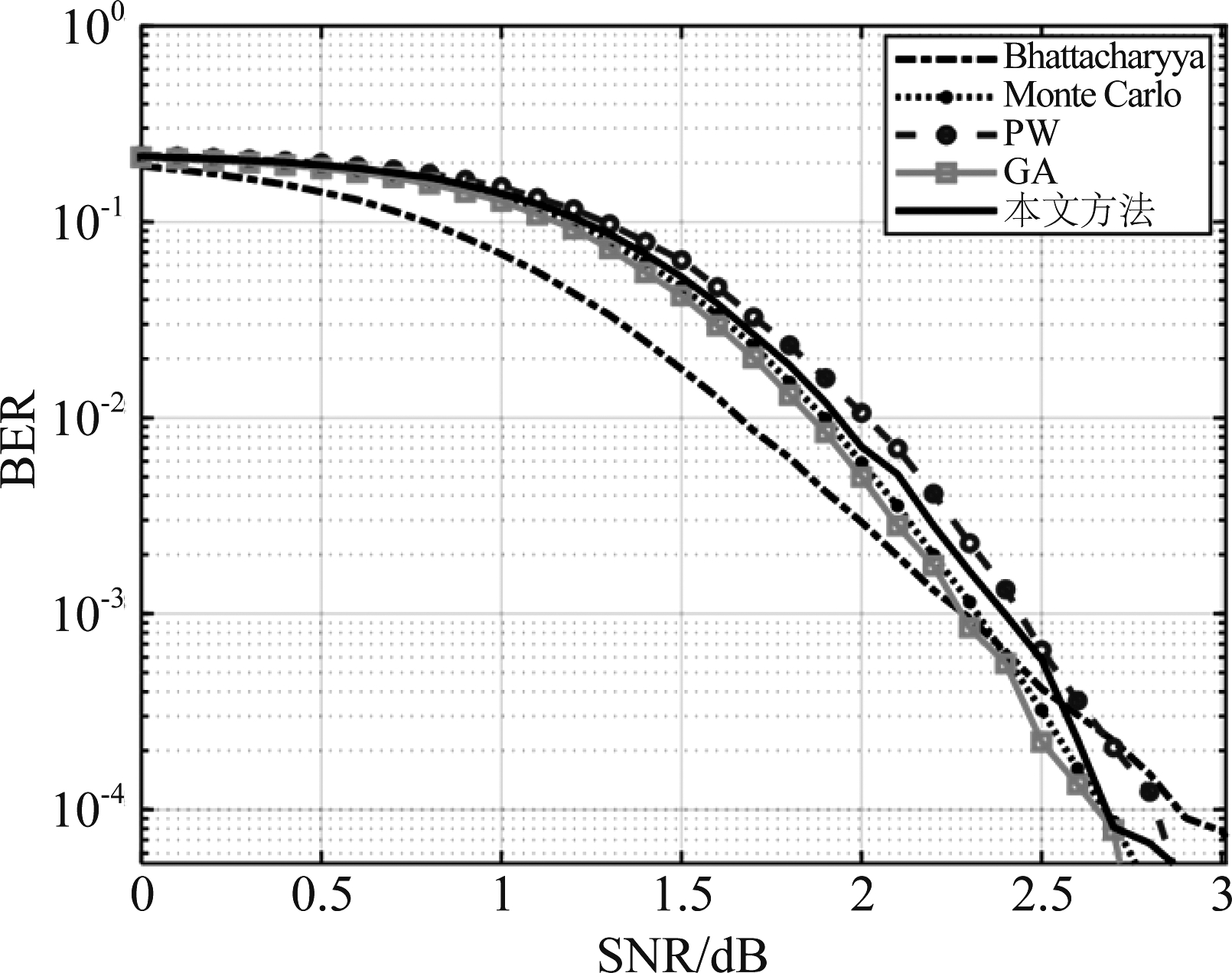
图6 不同信道极化方法误码曲线
Fig.6 Different channel polarization BER curve
图6是4种常见的信道极化方法和修正PW信道极化方法误码率结果对比。从中可知,如果提前准确获知信道的参数特性,巴氏参数法和高斯近似法GA就能够较为精确地极化信道,但实际中信道是变化的,且准确获知信道特性也是困难的。因此,只能研究接近这两中极化性能的信道极化方法。本文提出的修正PW信道极化方法相比于传统PW方法在高信噪比处性能提升约0.5 dB,且更接近于GA信道极化法,这也验证了该算法的有效性,后文的仿真实验都将基于该方法进行。
5.2 Polar-OFDM码在水声多径信道中的译码性能
本节将修正的PW信道极化方法引入到水声OFDM系统中,并在实测水声信道条件下仿真不同码率R、不同码长N和不同译码方法的译码性能。首先设置OFDM通信系统参数,如表1所示。
表1 OFDM系统参数设置
Tab.1 OFDM system parameters
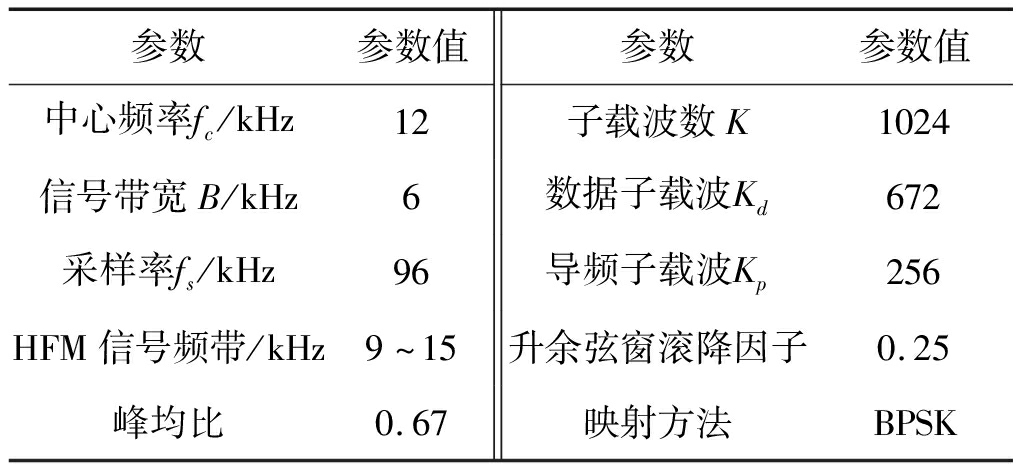
参数参数值参数参数值中心频率fc/kHz12子载波数K1024信号带宽B/kHz6数据子载波Kd672采样率fs/kHz96导频子载波Kp256HFM信号频带/kHz9～15升余弦窗滚降因子0.25峰均比0.67映射方法BPSK
仿真所采用的信道为本团队2020年12月千岛湖实测信道,发射距离500 m,接收换能器与发射换能器均放置在水下5 m,结构如图7所示,噪声为加性高斯噪声。
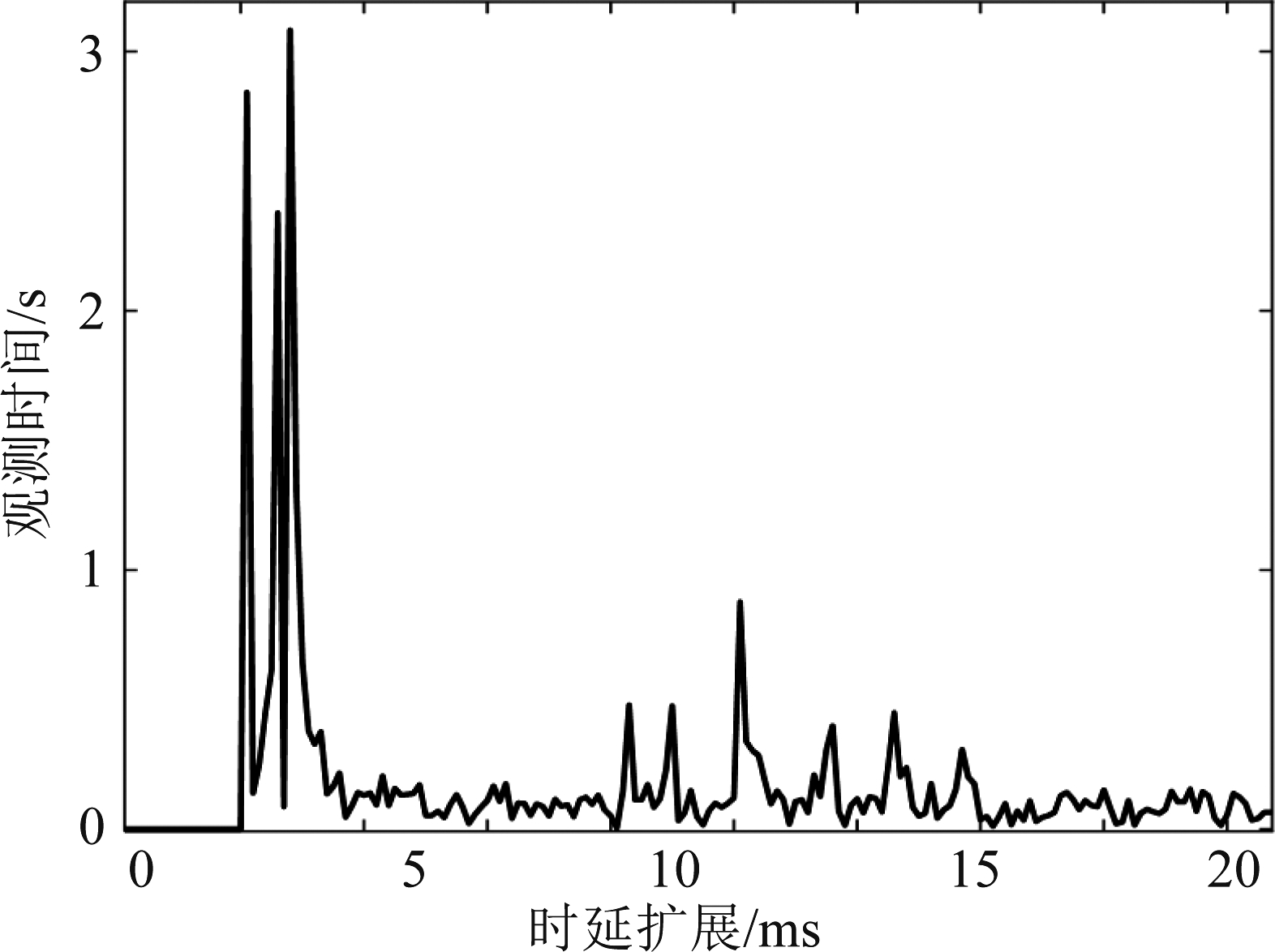
图7 信道冲激响应
Fig.7 Channel impulse response
当接收端信噪比为0 dB时,发射信号和接收信号如图8所示。
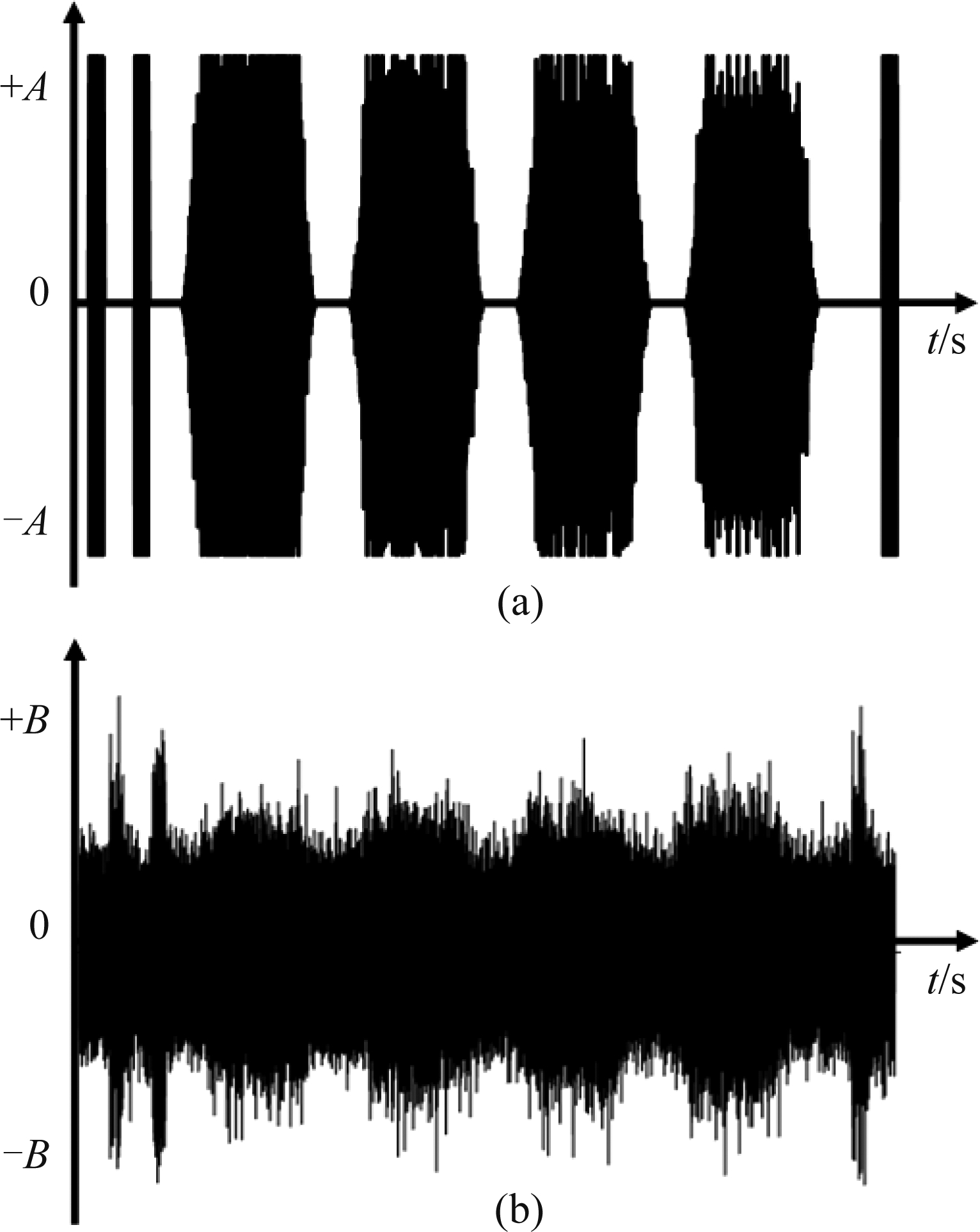
图8 发射信号、接收信号时域波形图
Fig.8 Waveform of transmitted and received signal
为了研究信道不同极化程度下的系统译码性能，仿真码率R=0.5，码长N=256、512、1024和2048时，Polar-OFDM系统译码的性能，结果如图9所示。从仿真结果来看，Polar码在短码条件下信道并未充分极化，因此译码能力较差。随着码长的增加，信道极划程度也随之增加，基扩展信道极化算法的译码能力也逐渐提高。
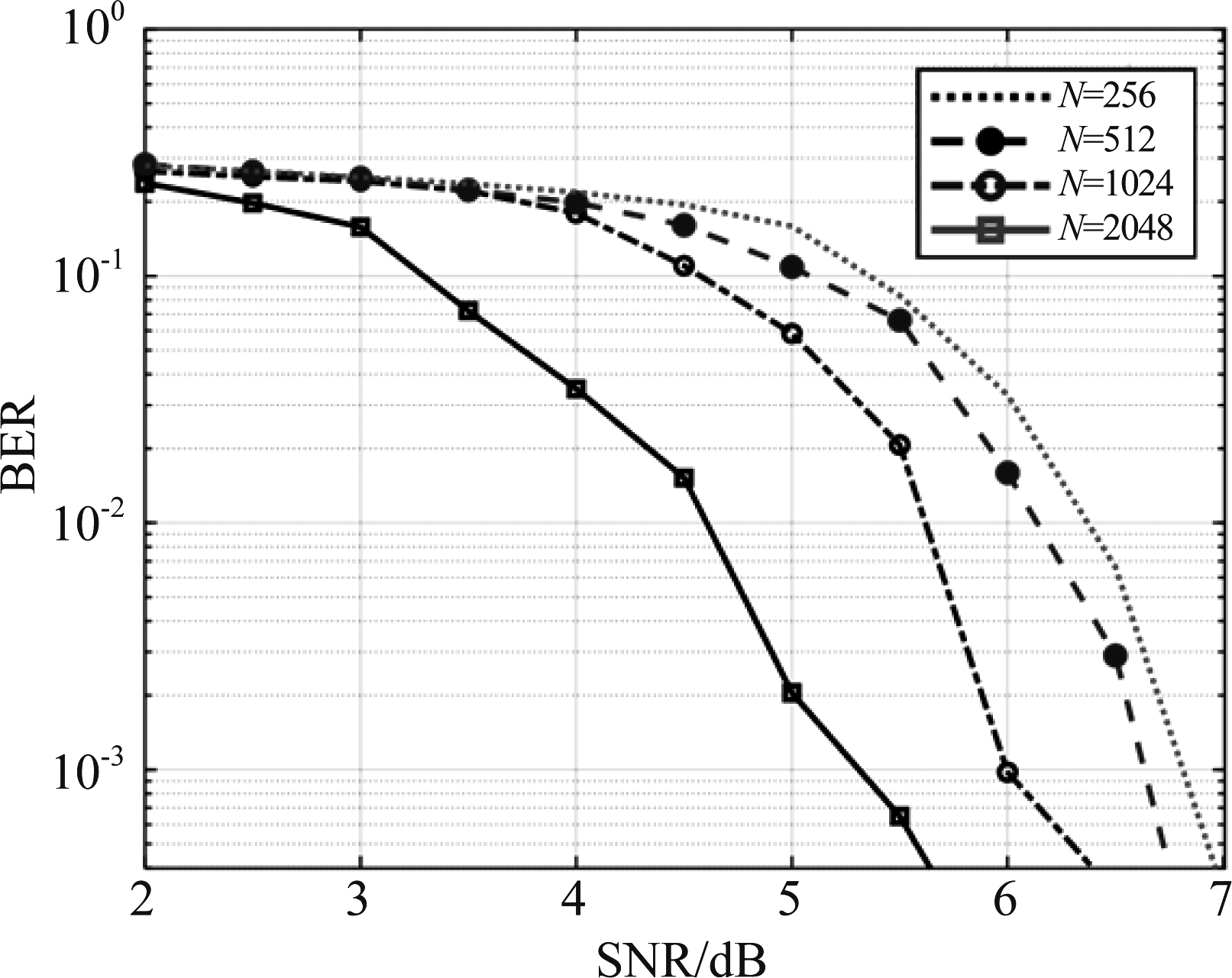
图9 不同码长N时误码率曲线
Fig.9 BER curve of different N
信道编码的核心思想是在原始信息序列中可控的加入冗余信息，以此进行纠错检错。因此，不同的编码效率R将影响编码系统的抗噪声性能。下面仿真码长N=2048，码率R=0.125、0.25、0.5和0.75时，Polar-OFDM系统SC译码的性能，结果如图10所示。从仿真结果来看，极化码具有很强的译码性能，且不存在LDPC编码中的错误平层问题，因此适合于水下可靠通信的编码，且编码率越低，系统误码率越低。
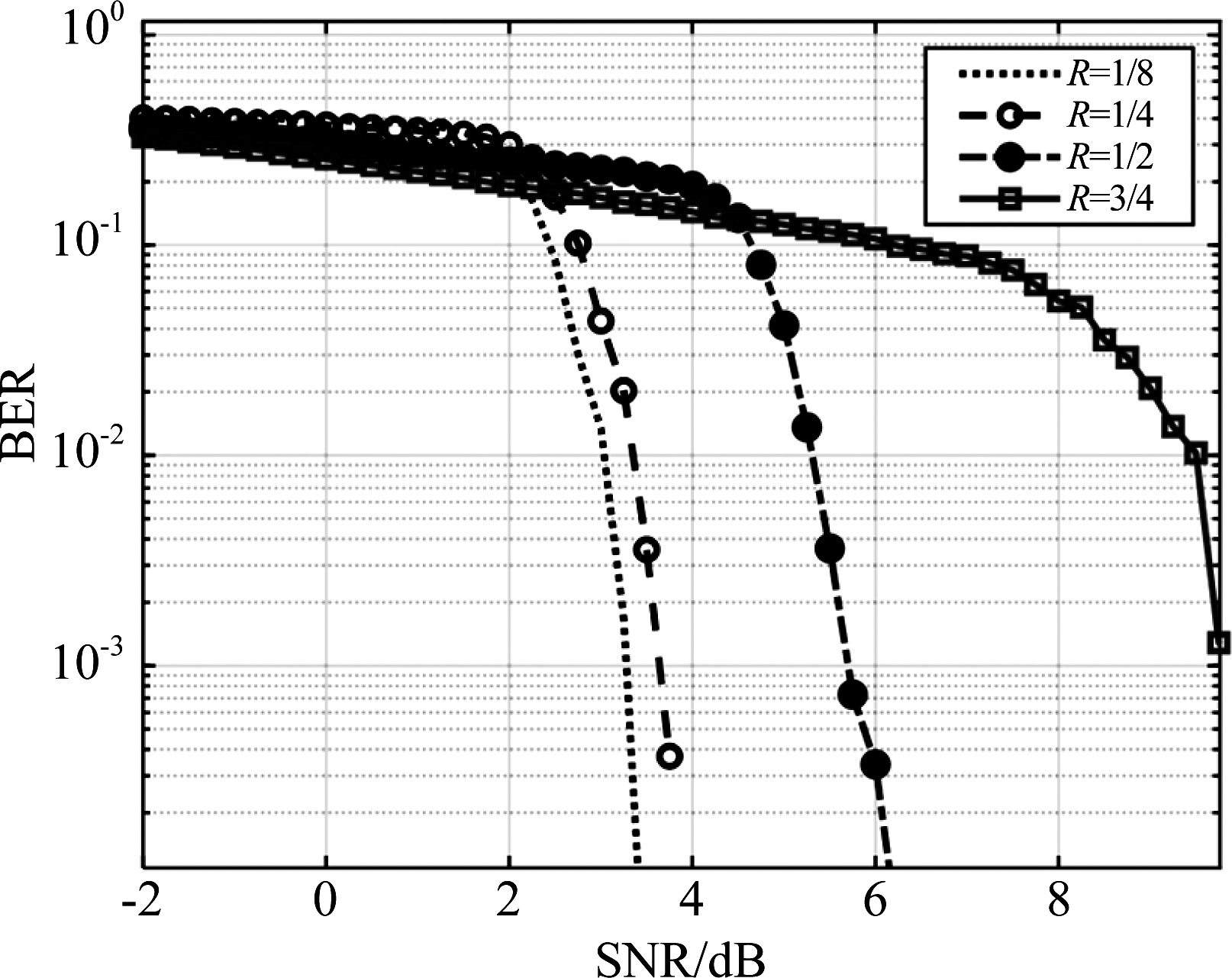
图10 不同码率R时误码率曲线
Fig.10 BER curve of different R
以上的仿真都是基于单一的译码方法进行的,没有对比不同译码方法的译码性能。SC译码方法译码能力有限,且存在错误传递现象,SCL译码方法相比于SC方法具有更高的译码精度。为了对比CRC-SCL译码方法与SC译码方法的性能差异,接下来仿真码长为2048,码率为0.5,SCL译码列表长度L=1、L=4、L=8和L=32条件下的性能差异。结果如图11所示。当SCL译码列表长度L=1时,SCL算法退化为SC算法,随着列表长度的增加,Polar-OFDM系统的译码性能也随之增加,但计算复杂度也随着列表的长度线性增加。
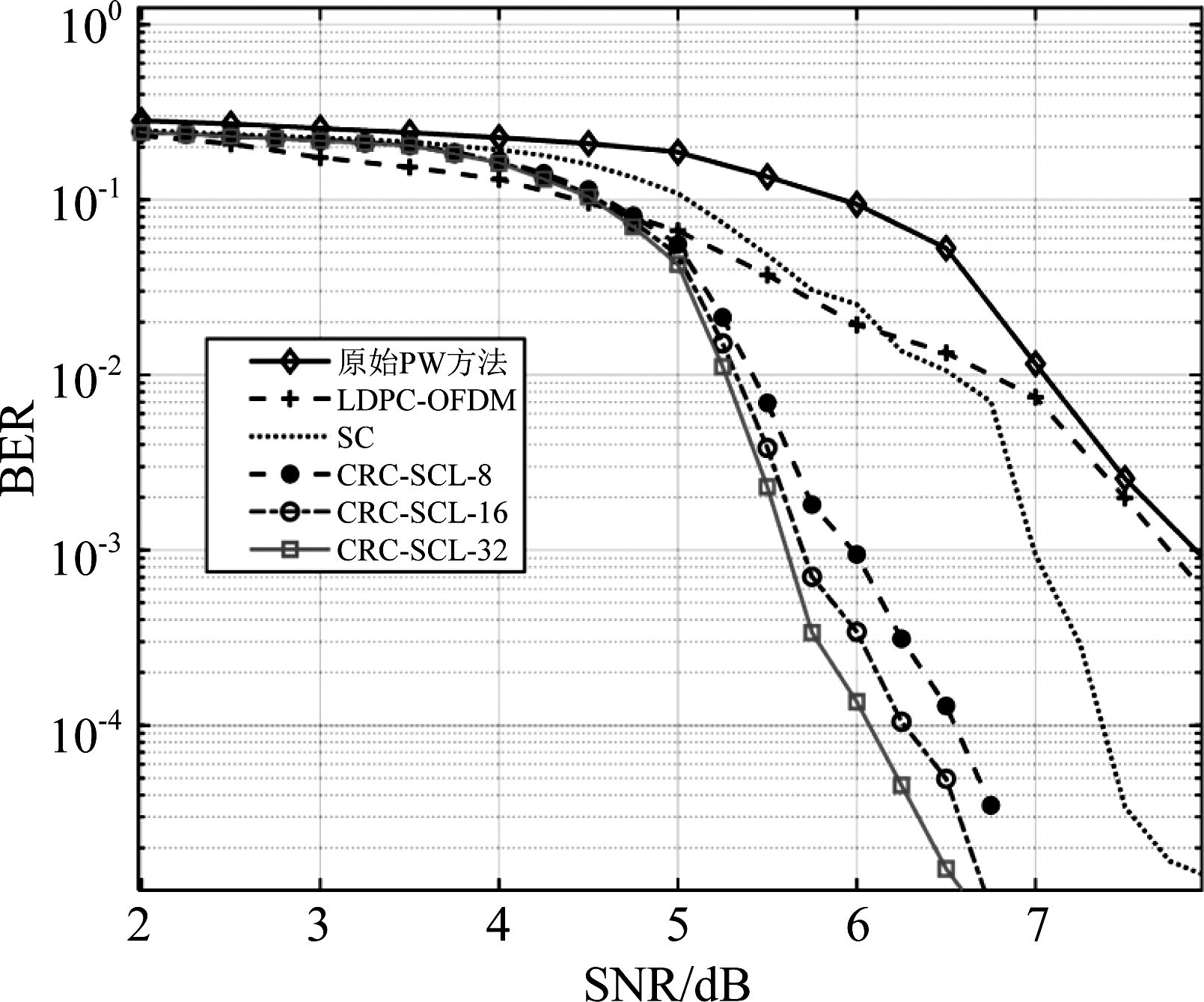
图11 水声多径信道下系统误码率曲线
Fig.11 BER performance under underwater multipath Channel
从图11中可以看出,基于修正的PW信道极化方法能够用于实际OFDM水声通信系统中,相比较与传统信道极化编码方法具有更低的误码率,更适合于实际水声信道的极化,这也进一步证实了本文算法的有效性;当采用CRC-SCL译码时,系统误码率相比于SC译码方案降低了约1.5 dB,即基于CRC校验的极化编码方案具有更强的稳定性;相比于LDPC编码方案,本文算法具有更好的纠错检错性能,且误码平层现象也得到了改善,这进一步验证了本文设计的Polar-OFDM系统的可靠性。
6 结论
本文提出了一种新的基对称扩展信道极化方法,实现了更为精确且不依赖于信道参数的信道极化,并设计了基于该信道极化方法的Polar-OFDM水声通信系统,改善了LDPC等编码方法存在的错误平层和译码复杂度高的问题,提高了OFDM水声通信系统的可靠性。仿真结果也证明了该系统在水声多径信道下的有效性。本文工作有效地验证了Polar码在水声通信应用方面的可行性,对水下编码和水声可靠通信研究具有重要的补充作用。
[1] BELLALTA B.IEEE 802.11ax: High-efficiency WLANS[J].IEEE Wireless Communications, 2016, 23(1): 38-46.
[2] WEN Miaowen, CHENG Xiang, YANG Liuqing, et al.Index modulated OFDM for underwater acoustic communications[J].IEEE Communications Magazine, 2016, 54(5): 132-137.
[3] LI Baosheng, ZHOU Shengli, STOJANOVIC M, et al.Pilot-tone based ZP-OFDM demodulation for an underwater acoustic channel[C]∥OCEANS 2006.Boston, MA, USA.IEEE, 2006: 1-5.
[4] LI Baosheng, ZHOU Shengli, STOJANOVIC M, et al.Multicarrier communication over underwater acoustic channels with nonuniform Doppler shifts[J].IEEE Journal of Oceanic Engineering, 2008, 33(2): 198-209.
[5] MOUNIKA B, PRIYA B K.Analysis and comparison of different channel coding techniques for underwater channel using AWGN and acoustic channel[C]∥2018 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques(ICEECCOT).Msyuru, India.IEEE, 2018: 1664-1669.
[6] CHEN Qiwang, LAU F C M, WU Huihui, et al.Analysis and improvement of error-floor performance for JSCC scheme based on double protograph LDPC codes[J].IEEE Transactions on Vehicular Technology, 2020, 69(12): 14316-14329.
[7] ARIKAN E.Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J].IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073.
[8] TAL I, VARDY A.List decoding of polar codes[J].IEEE Transactions on Information Theory, 2015, 61(5): 2213-2226.
[9] NIU Kai, CHEN Kai.CRC-aided decoding of polar codes[J].IEEE Communications Letters, 2012, 16(10): 1668-1671.
[10] 石旭, 周林, 张树颖, 等.改进交织的单层极化码高阶编码调制系统[J].信号处理, 2020, 36(2): 210-216.
SHI Xu, ZHOU Lin, ZHANG Shuying, et al.Single-layer high-order polar-coded modulation system with improved interleaver[J].Journal of Signal Processing, 2020, 36(2): 210-216.(in Chinese)
[11] 刘荣科, 孙贺, 冯宝平, 等.极化码研究综述[J].遥测遥控, 2020, 41(4): 2-17.
LIU Rongke, SUN He, FENG Baoping, et al.A survey of polar code research[J].Journal of Telemetry,Tracking and Command, 2020, 41(4): 2-17.(in Chinese)
[12] HE Gaoning, BELFIORE J C, LAND I, et al.Beta-expansion: A theoretical framework for fast and recursive construction of polar codes[C]∥GLOBECOM 2017-2017 IEEE Global Communications Conference.Singapore.IEEE, 2017: 1-6.
[13] ZHOU Yue, LI Rong, ZHANG Huazi, et al.Polarization weight family methods for polar code construction[C]∥2018 IEEE 87th Vehicular Technology Conference(VTC Spring).Porto, Portugal.IEEE, 2018: 1-5.
[14] TAL I, VARDY A.How to construct polar codes[J].IEEE Transactions on Information Theory, 2013, 59(10): 6562-6582.
[15] TRIFONOV P.Efficient design and decoding of polar codes[J].IEEE Transactions on Communications, 2012, 60(11): 3221-3227.
[16] CHAKI P, KAMIYA N.A novel design of CRC-concatenated polar codes[C]∥ICC 2019-2019 IEEE International Conference on Communications(ICC).Shanghai, China.IEEE, 2019: 1-6.
[17] PATIL V S, PATIL K S.Performance analysis of polar coded OFDM with different frequency offsets and code rates[C]∥2019 International Conference on Intelligent Sustainable Systems(ICISS).Palladam, India.IEEE, 2019: 71-75.
[18] DENG Xiangyun, SHA Jin, ZHOU Xiaotian, et al.Joint detection and decoding of polar-coded OFDM-IDMA systems[J].IEEE Transactions on Circuits and Systems I: Regular Papers, 2019, 66(10): 4005-4017.
