1 引言
随着雷达技术的不断发展,人们对精确测量提出了更高的要求[1]。提高雷达精确测速能力可以提高雷达对目标精细运动的刻画能力,进而可以提取目标的微动特征[2-3]。
由于能够实现半波长量级的测量精度,基于回波相位的测量方法引起人们的广泛关注。该方法起源于美国在上个世纪七十年代提出的基于窄带回波相位的游标测距技术。随后,两篇专利[4-5]进一步论证了采用相推测距方法实现微动参数估计的可行性。基于宽带脉冲多普勒雷达,文献[6]介绍了利用宽带回波相位测距的基本模型,即相推测距方法。相应地,对相邻帧距离增量除以一帧时间可以得到目标的速度,即相推测速方法。文献[7]介绍了步进频信号的相推测速方法,并将其应用于微动特征提取。
相推测速方法对回波信噪比要求比较高。传统的方法采用基于包络测速结果解相位模糊的方法,该方法利用包络测速的粗速度估计值作为后续解模糊处理的参考速度,其单帧解模糊的方法对信噪比要求较高。文献[8-9]分别介绍了基于宽带线性调频信号的去斜处理和匹配脉压处理的相推测量模型,但是其主要分析的是静止目标,当目标有速度时,其方法要求较高的速度补偿精度。此外,该方法对信噪比的要求比较高,很难满足实际应用需求。文献[10]虽然对信噪比要求比较低,但是其方法要求相邻帧距离变化小于四分之一波长,实际中目标运动很难满足该要求。
文献[11]介绍了基于宽带步进频信号的相推测距和测速技术,可以较好的适用于实际场景,并提出了联合多帧解相位模糊的方法,该方法联合多帧回波相位共同求解模糊数,能够显著降低相推测速对信噪比的要求。该方法可以适用于脉压后信噪比大于10 dB的情况。鉴于此,本文进一步研究更低信噪比下的相推测速方法。
低信噪比对于相推测速的影响主要体现在提取回波相位和解相位模糊[12]。当信噪比比较低时,信号能量比较弱,甚至于完全湮没在噪声里,无法准确地提取相位信息。此外,当信噪比比较低时,包络测量的结果误差很大,不能用于解相位模糊。本文提出了对距离像互相关结果进行积累的低信噪比下相推测速方法。该方法可以重新提取峰值点相位,并进行解模糊,可以有效的解决上述两大问题。此外,本文还提出设计滤波器对相位滤波,进一步提高相推测速精度。
本文主要安排如下:首先,建立了宽带线性调频信号去斜处理的回波模型,并介绍了距离像互相关方法。然后,基于距离像互相关结果,提出了沿慢时间维积累并进行相位滤波的低信噪比下相推测速方法,并给出了算法步骤和处理流程图。最后,通过仿真实验验证了本文所提方法的有效性。
2 回波模型
雷达发射的大带宽线性调频信号可以表示为:
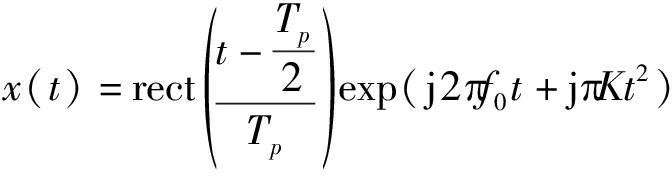
(1)
其中,
为脉冲宽度,K为线性调频信号的调频率,B=KTp为信号带宽, f0为载频。此外,令Tr表示信号的脉冲重复周期。
假设目标沿着雷达视线方向运动,初始距离为R0,运动速度为ν,远离雷达为正,靠近雷达为负。则目标相对雷达的距离和速度可以分别表示为:
R(t)=R0+νt
(2)
忽略干扰和噪声的影响,雷达接收到的回波信号为:
(3)
其中,σb为后向散射系数。
去斜处理是处理大带宽线性调频信号常用的处理方法。去斜信号可以表示为:
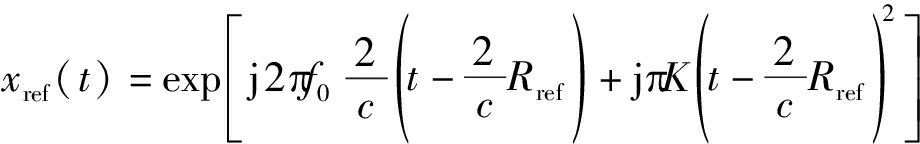
(4)
其中Rref为参考距离。
对回波信号做去斜处理,可以得到:
(5)
其中:
(6)
(7)
式(5)中存在二次相位项2π
R2(t),需要对其进行粗补偿。假设距离补偿精度近似认为
则补偿后残留的相位误差为π
。考虑线性调频信号的脉冲宽度为0.1 ms,带宽为300 MHz,则调频率K=3×1012,补偿后残留的相位误差约为1.05×10-4 rad,该量级误差可以忽略。后续第3节考虑距离像互相关处理时即认为已经对二次相位项做过补偿处理。对式(5)的二次相位项补偿后,对其做傅里叶变换即可得到高分辨一维距离像。
3 距离像互相关
距离像互相关通过对相邻帧的一维距离像做互相关运算,可以得到目标多普勒重心处的速度估计。相邻两帧的距离像互相关运算可表示如下:
(8)
其中Ym(l)表示第m帧的一维距离像。
根据相关定理,两个信号的时域相关求和可以等效为它们相应的频域响应共轭相乘的逆傅里叶变换,即:
Rm,m+1(τ)=IFT{FT {Ym+1(l)}·FT {Ym(l)}*}
(9)
其中FT {·}和IFT {·}表示傅里叶变换和逆傅里叶变换。
由傅里叶变换与逆傅里叶变换的对偶性质,去斜处理的一维距离像的互相关结果可以按下式计算:
(10)
忽略包络的影响,假设目标匀速运动且去斜参考距离相同,则进一步计算可得:
exp[j 2π(fν,m+1-fν,m)t]=
(11)
则距离像互相关的结果为:
(12)
分析式(12),距离像互相关结果的包络为sinc形状,峰值位置与目标速度有关,其相位项也包含目标的速度信息。通过提取距离像互相关峰值点处的相位,进而可以进行相推测速,获得高精度的速度估计结果。
4 低信噪比下相推测速方法
传统的相推测速方法适用于高信噪比情况。当回波信噪比较低时,相推方法的测量精度会急剧恶化。低信噪比对相推测速处理的影响主要体现在提取回波相位和解相位模糊。
一方面,考虑到受噪声影响最小的因素,相推测速方法要求提取回波峰值点处的相位信息。当信噪比比较低时,距离像互相关峰值位置湮没在噪声里,无法准确的提取到峰值点的相位。本文提出采用沿慢时间维积累的方法,可以准确的估计出峰值点的位置,进而可以重新提取到峰值点的相位。
另一方面,由于电磁波的周期性,提取到的回波相位存在以2π周期的模糊,需要对其进行解模糊处理。而解相位模糊需要获得目标参考速度作为辅助信息。传统的方法采用包络测量的结果作为参考速度。当信噪比比较低时,包络测量结果误差很大,不能用于解相位模糊。本文提出对距离像互相关结果沿慢时间维积累的方法可以估计出目标的粗速度,用于辅助后续的解相位模糊。
此外,噪声本身对相位信息的影响也会降低测量精度。本文提出根据目标运动参数的粗估计值设计带通滤波器,通过在频域滤波进一步滤除噪声对相位的影响,提高相推测速精度。假设目标速度可以近似表示为ν(t)=V0+at,则提取的峰值点相位为
其中λ为波长,Tr为脉冲重复周期。该信号可近似认为是载频为
的单频信号,因此可以设计滤波器滤除噪声。滤波器的中心频率设置可以采用基于距离像互相关结果沿慢时间维积累所得到的峰值点位置的粗估计值。
假设得到的距离像互相关结果的离散形式为:R(n,l),n=1,2,…,N,l=1,2,…,L,其中n表示距离像互相关后的速度分辨单元,N表示速度分辨单元总数,l表示不同的相邻帧距离像互相关后的慢时间分辨单元,L表示慢时间分辨单元总数。由式(12),沿着慢时间维度,其相位信息包含目标的速度信息,因此可以对其进行相参积累,进而可以在低信噪比条件下找到峰值点的位置。
本文所提低信噪比条件下的相推测速方法处理流程图如图1所示。其具体实现步骤如下:
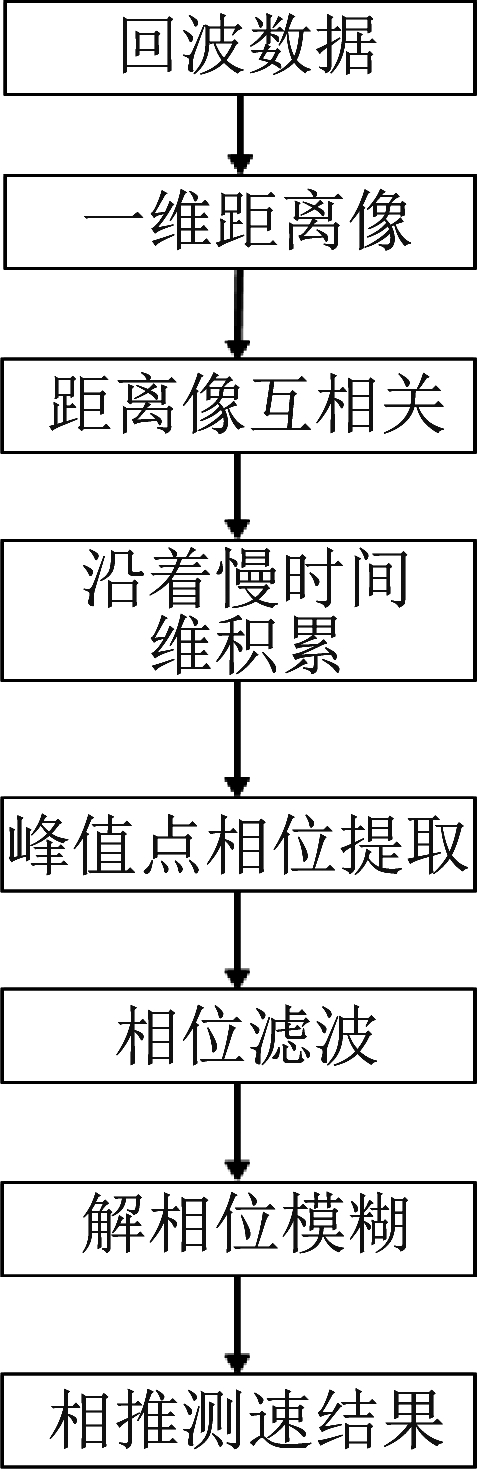
图1 低信噪比下的相推测速流程图
Fig.1 Flow chart of phase-derived velocity measurement method under low SNR
1)对R(n,l)沿着l所在的维度做FFT,得到:
2)寻找Y的峰值点,假设峰值点位置沿着n所在维度记为nmax,沿着l所在维度记为lmax。
3)根据nmax可以得到基于距离像互相关包络测量结果的速度粗估计值,即νcoarse=nmax·δν,其中δν为速度分辨率。
4)重新提取距离像互相关的峰值点相位,得到:ψ=angle{R(nmax,l)}。
5)设计滤波器对提取的峰值点相位进行滤波。滤波器的截止频率为:
其中ξ为约束因子,限制滤波器带宽中心到截止频率的宽度,根据实际的积累脉冲数以及设计的滤波器的陡峭程度决定。假设滤波后的相位记为ψ*。
6)根据目标速度的参考估计值νcoarse和滤波后的相位ψ*采用文献[6-7]中的方法解相位模糊,得到解模糊后的相位,记为ψ ′。
7)目标高精度的相推测速结果为:
假设沿慢时间积累L个脉冲,则信噪比会提升10lgL dB。在恒虚警检测的情况下,假设虚警率要求为Pf=10-6,若距离像互相关结果的信噪比为0 dB,采用传统的包络法的检测概率近似为0。而采用本文所提方法,若L=10,则信噪比提高10 dB,检测概率为0.06,若L=20,则信噪比提高13 dB,检测概率为90%。因此,采用本文所提方法可以有效的提取到峰值点相位,以及获得目标速度的粗估计值进而辅助后续的解相位模糊。
假设信号带宽为300 MHz, 脉冲重复周期为1 ms。积累100个脉冲,即积累时间为0.1 s。若直接对回波一维距离像沿慢时间维进行积累,即脉冲多普勒(Pulse Doppler, PD)处理,要使不产生距离走动现象,则对目标速度的限制条件为:
m/s。该条件在实际应用中很难满足。但是,若采用本文所提的对距离像互相关结果沿慢时间维进行积累的方法,要保证距离像互相关峰值位于同一速度分辨单元,即实现能量积累,则对目标加速度的限制条件为:
m/s2。该条件在实际应用中很容易满足。因此,本文所提方法相比于PD处理适用性更强。
滤波器可以提高提取相位的信噪比,获得更高精度相推测速结果。因此滤波器对相推测速精度的改善可以近似通过信噪比的变化来表征。假设滤波前后的信噪比分别记为SNR1和SNR2。由文献[6],相推测速的CRLB为
则滤波后的相推测速精度相比滤波前的改善可以表示为:
5 仿真验证
下面通过仿真验证本文所提方法在低信噪比条件下的高精度测速性能。假设目标沿着雷达径向匀速运动。目标初始距离为1 km,速度为20 m/s。雷达采用线性调频信号,载频为3 GHz,脉宽100 μs,带宽为300 MHz,脉冲重复周期为1 ms,采样频率为30 MHz。
仿真产生200帧回波,其脉压后的信噪比为5 dB。由于信噪比较低,距离像互相关的峰值位置完全淹没在噪声里。图2给出了基于距离像互相关的包络测速结果。在此信噪比条件下,包络测速结果偏差很大。此时更不能利用传统的方法直接提取回波相位进行相推测速。
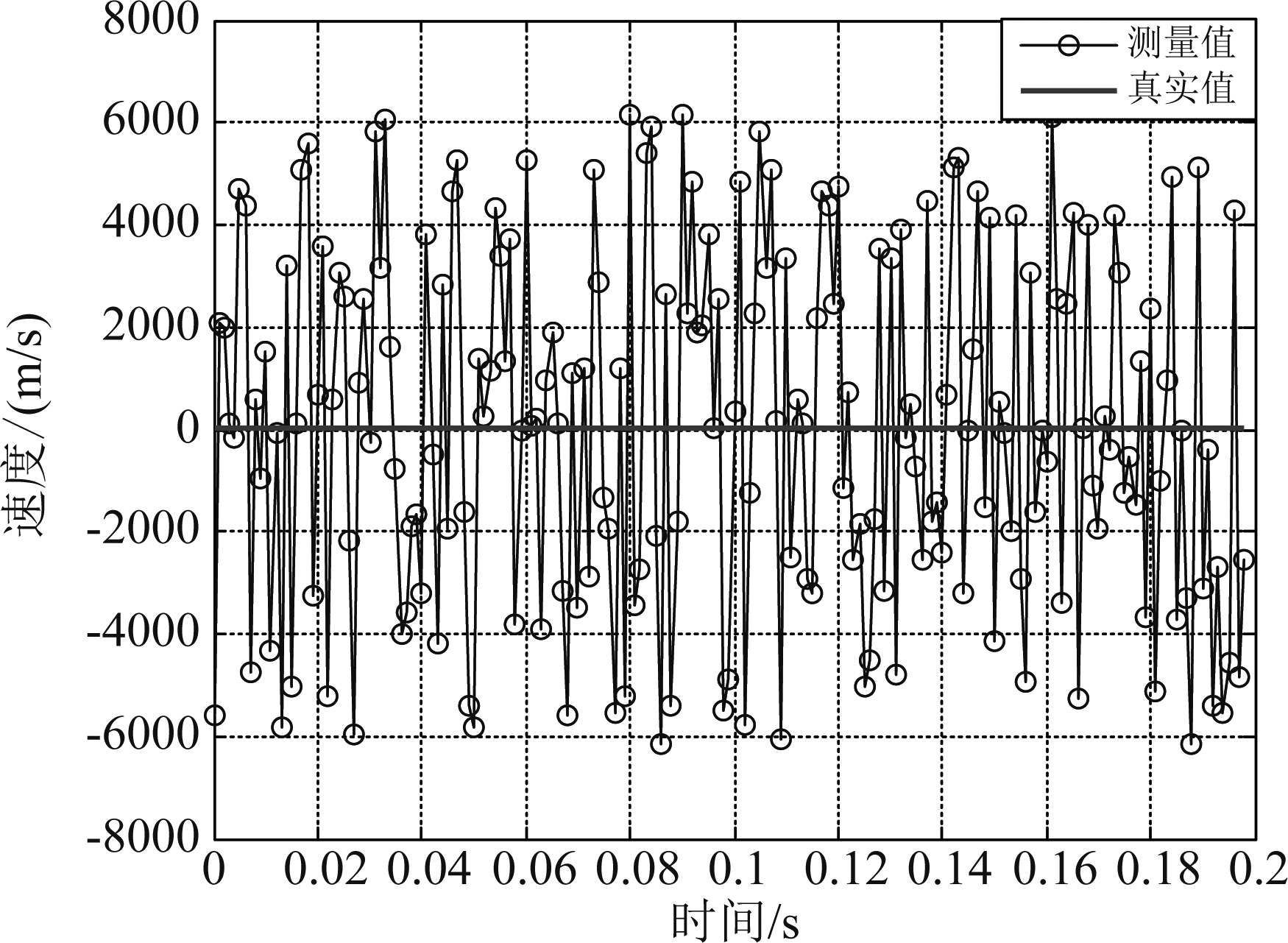
图2 基于距离像互相关的包络测速结果
Fig.2 Envelope velocity measurement results based on range profile cross correlation
图3给出了对距离像互相关结果沿慢时间维积累的结果。由于距离像互相关结果的相位中包含目标的运动信息,因此可以进行相参积累。通过分析峰值点的位置,采用本文所提的方法,可以重新提取回波相位,并得到目标速度的粗估计结果辅助后续的解相位模糊。
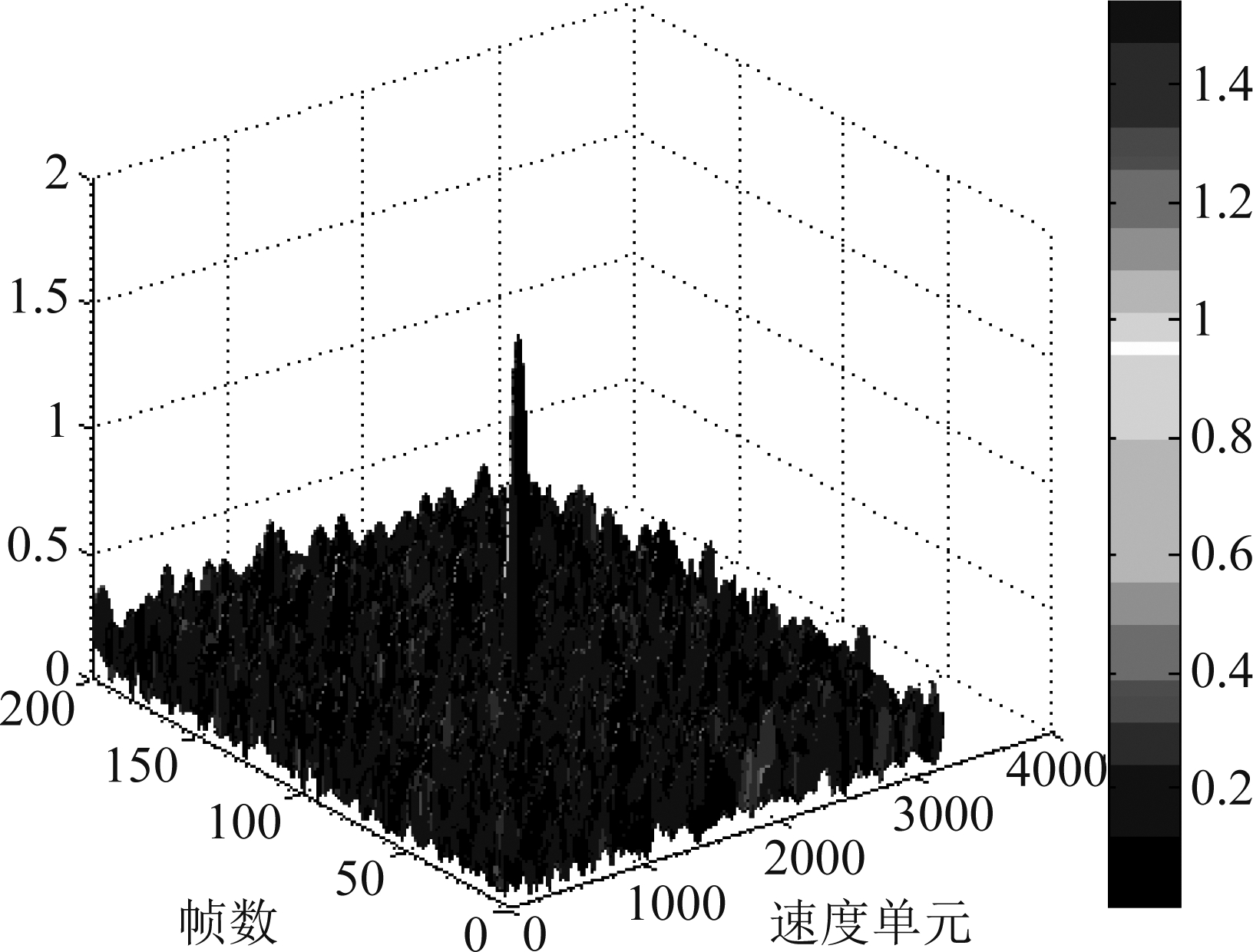
图3 沿慢时间维积累结果
Fig.3 Accumulation results along the slow time dimension
重新提取峰值点的回波相位,并采用本文所提的方法设计滤波器,图4给出了滤波前的相位和滤波器的频谱。通过对相位滤波可以进一步抑制噪声对相位的影响。图5给出了滤波后的相位与真实的相位的对比。在此基础上,解相位模糊并得到相推测速结果,其速度误差如图6所示。在脉压后信噪比为5 dB的条件下,测速误差最大不超过6 m/s,验证了本文所提算法在低信噪比条件下的高精度测速性能。
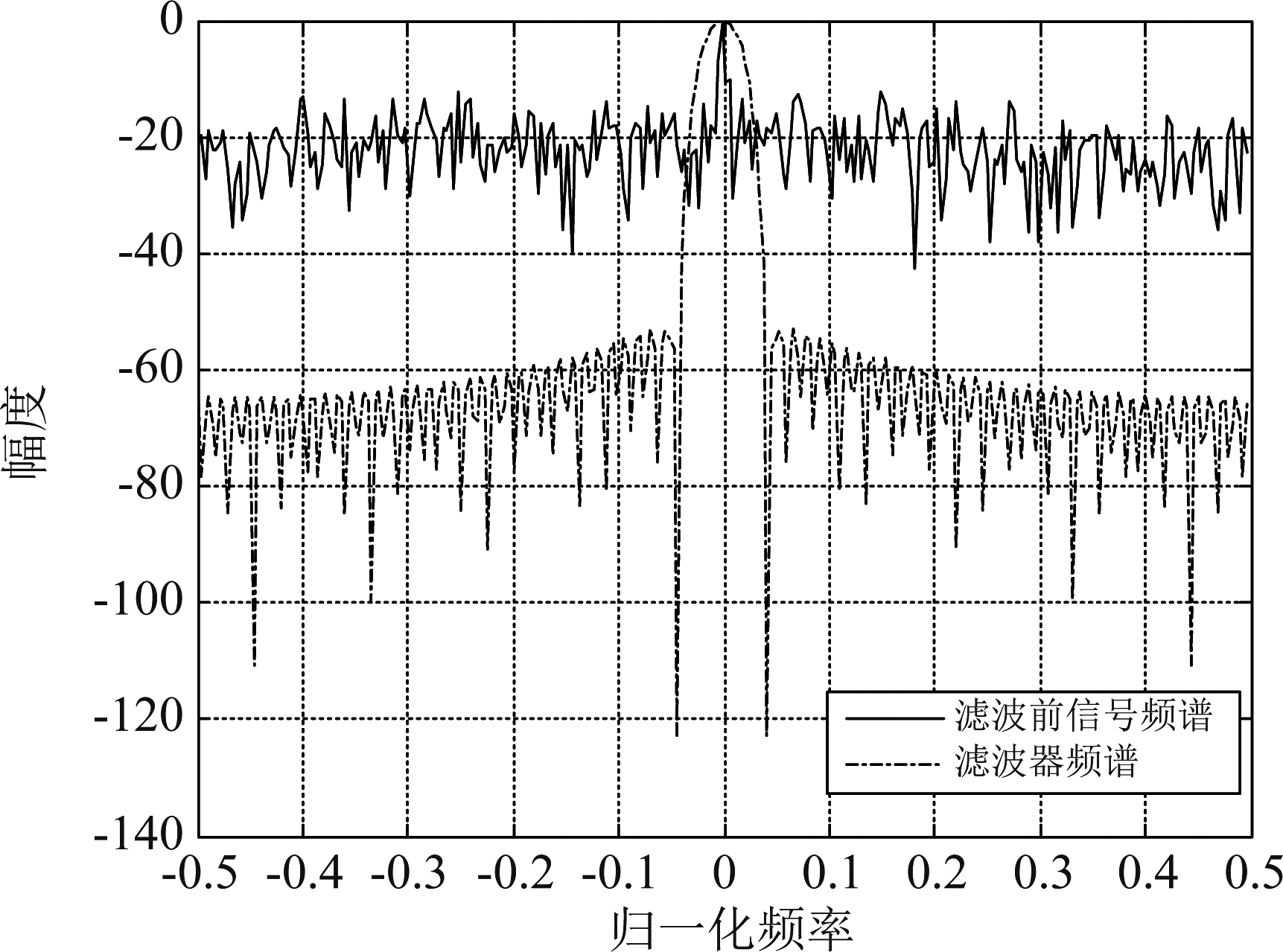
图4 峰值点相位频谱分析
Fig.4 Spectrum analysis of peak position phase
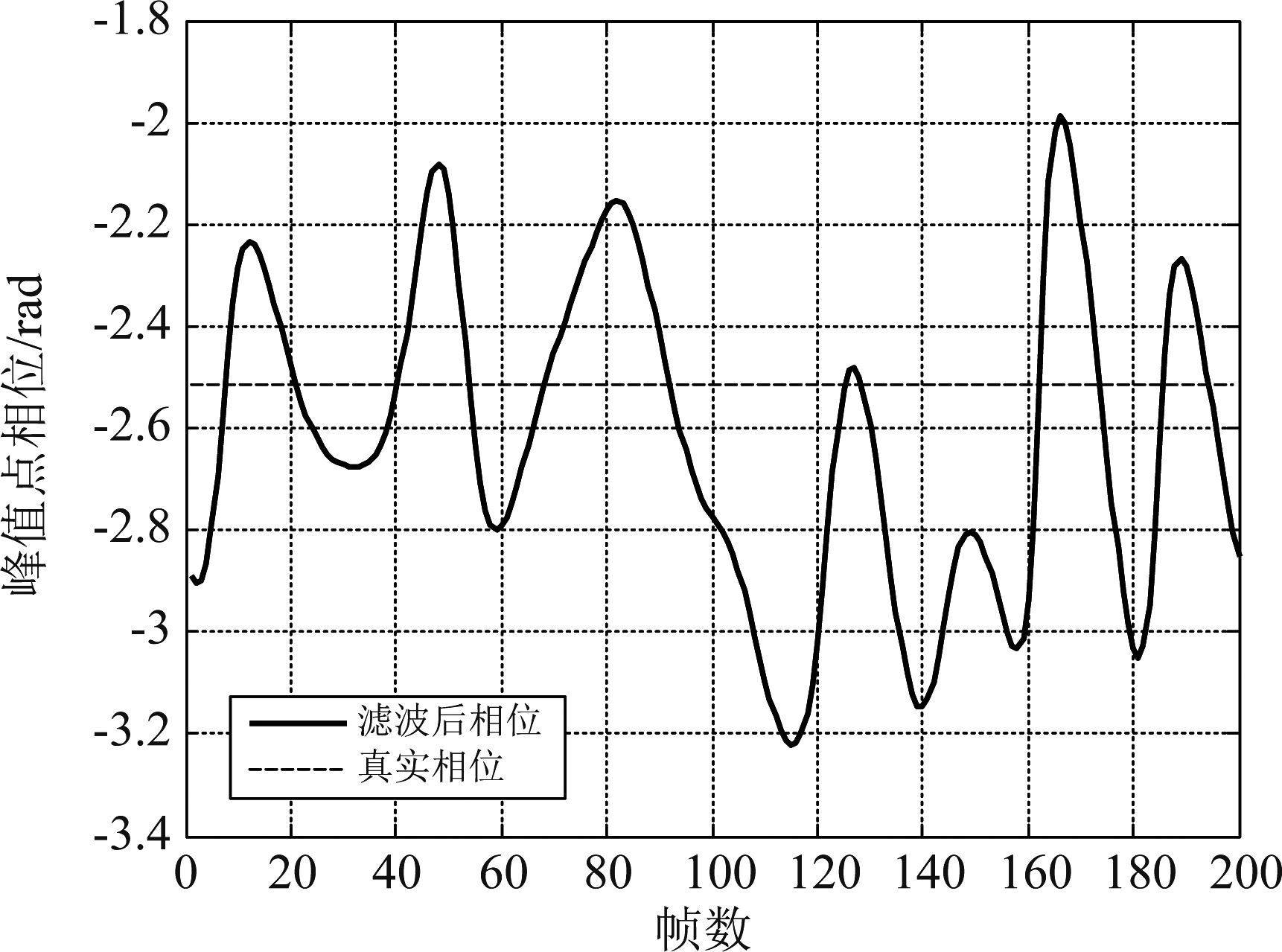
图5 峰值点相位滤波结果
Fig.5 Peak position phase filtering results
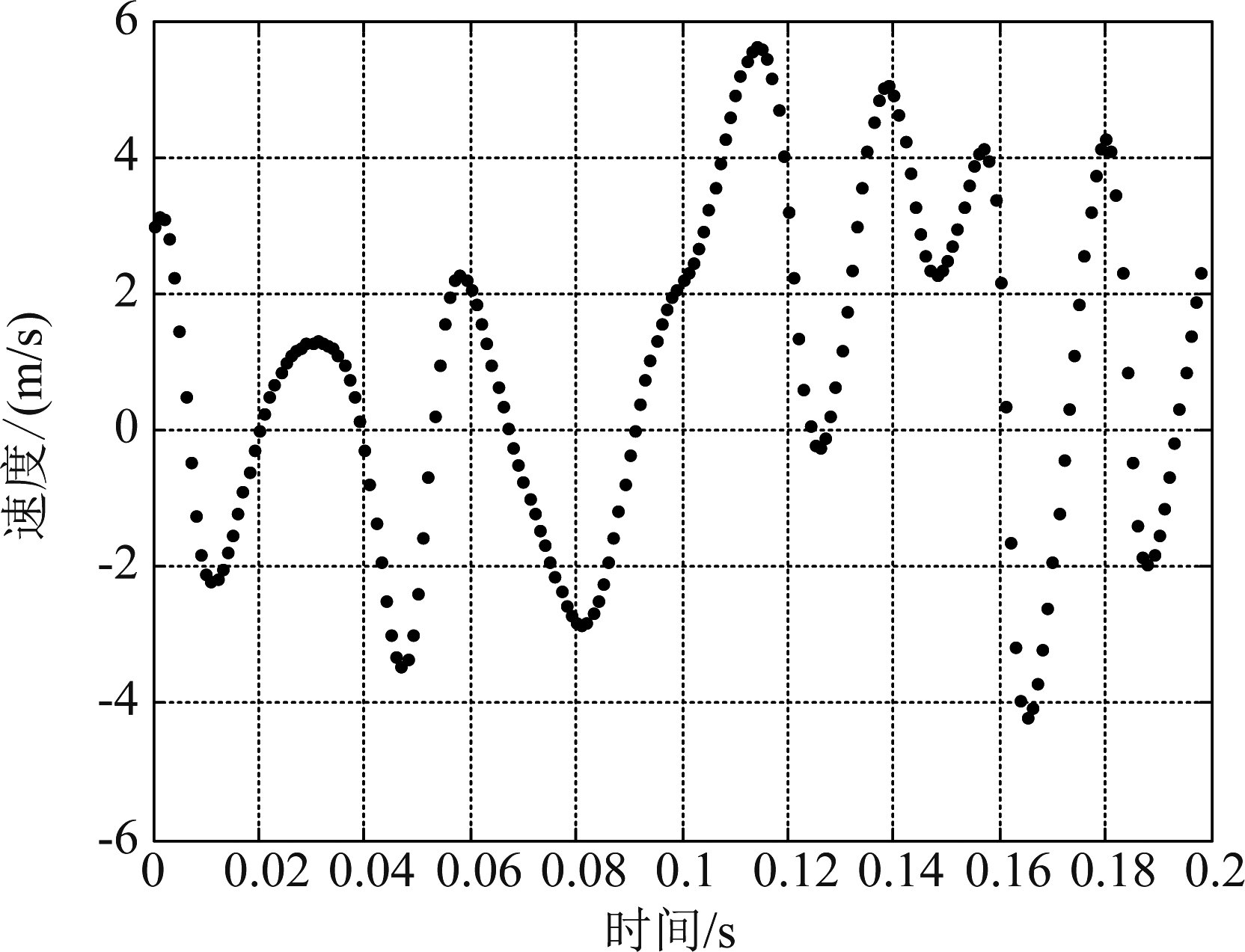
图6 相推测速误差
Fig.6 Phase-derived velocity measurement error
下面进一步比较不同积累脉冲数对积累结果的影响。由文献[10],距离像互相关会使信噪比降低3 dB,而积累L个脉冲,则信噪比会提升10lgL dB。因此,一维距离像信噪比为5 dB时,采用本文所提方法,当积累10个、20个、50个脉冲时,信噪比会提升12 dB、15 dB、19 dB。由文献[11],相推测速要求单帧信噪比高于15 dB。因此当一维距离像信噪比为5 dB时,应至少积累20个脉冲才能进行相推测速处理。图7分别给出了积累10个、20个、50个脉冲的积累结果。由图7可知,当积累20个、50个脉冲时可以看到较为明显的峰值点,而积累10个脉冲时,其峰值点淹没在噪声里,无法进行后续的相推测速处理。
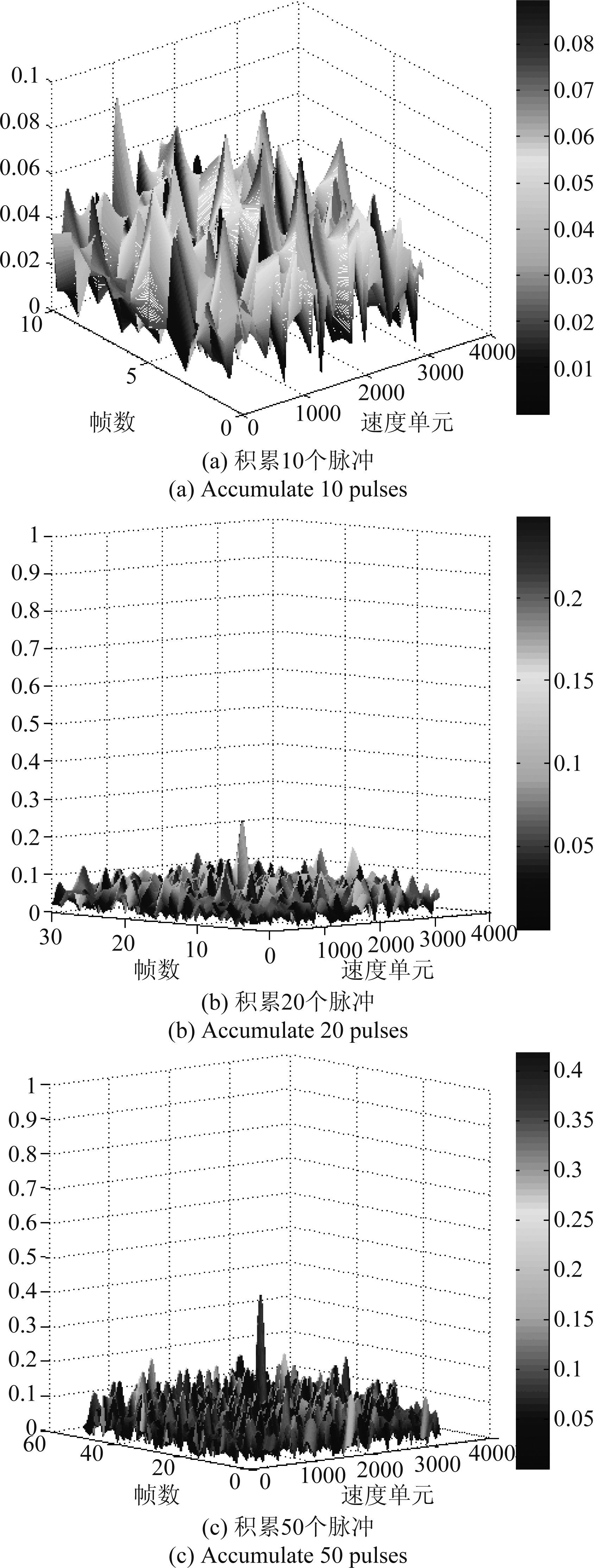
图7 不同脉冲数的积累结果
Fig.7 Accumulation results of different pulse numbers
为比较不同信噪比条件下,本文所提方法的性能,进行蒙特卡洛仿真1000次。比较直接提取峰值点相位进行相推测速的方法、对提取峰值点相位拟合后进行相推测速的方法和本文所提对相位滤波的方法这三种方法的测速均方根误差。为比较方便,假设仿真中可以准确提取到峰值点位置。三种方法的测速均方根误差结果图8所示。图9为图8中本文所提方法的测量结果的放大图。
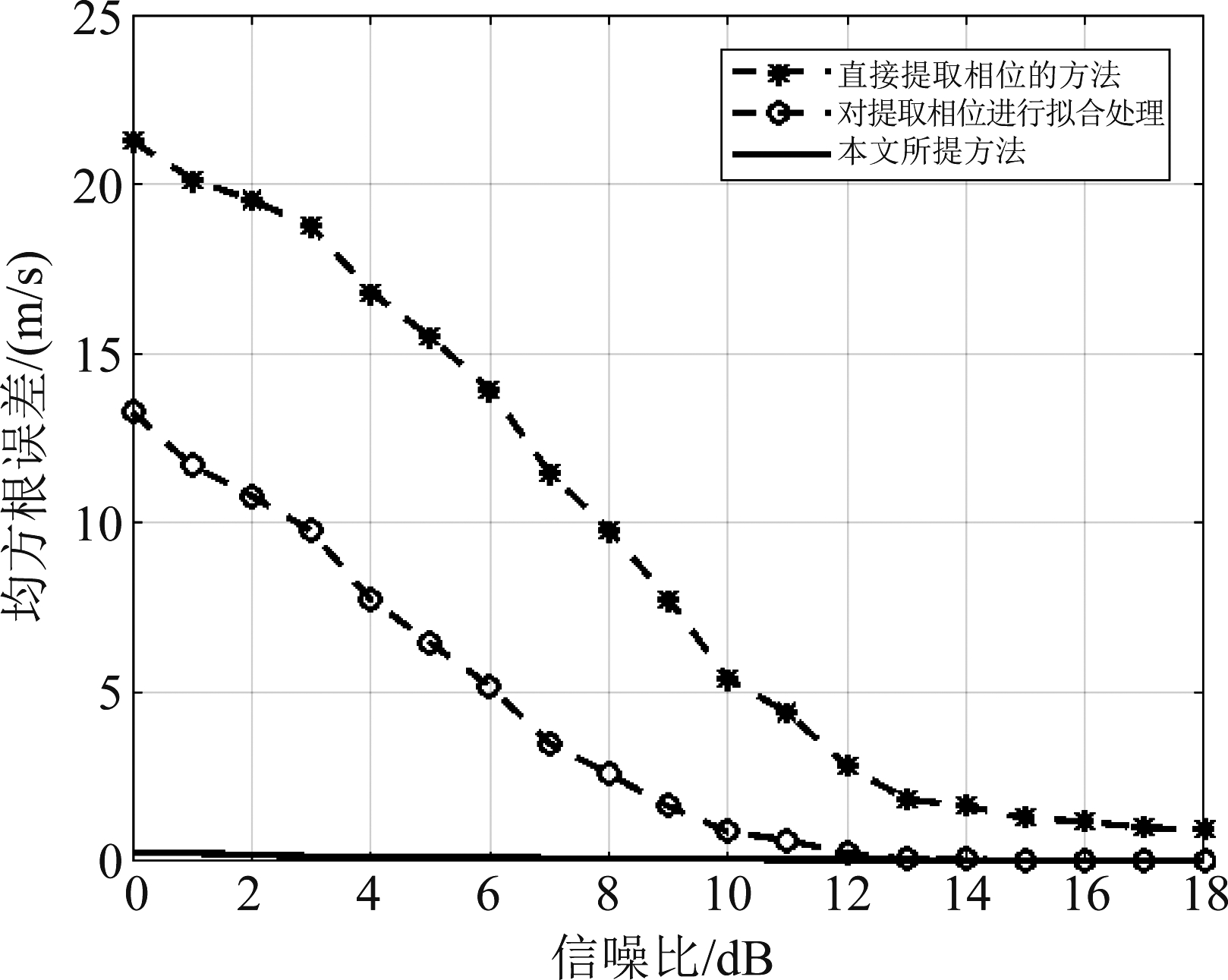
图8 不同方法的测速均方根误差
Fig.8 Root mean square error of velocity measurement by different methods
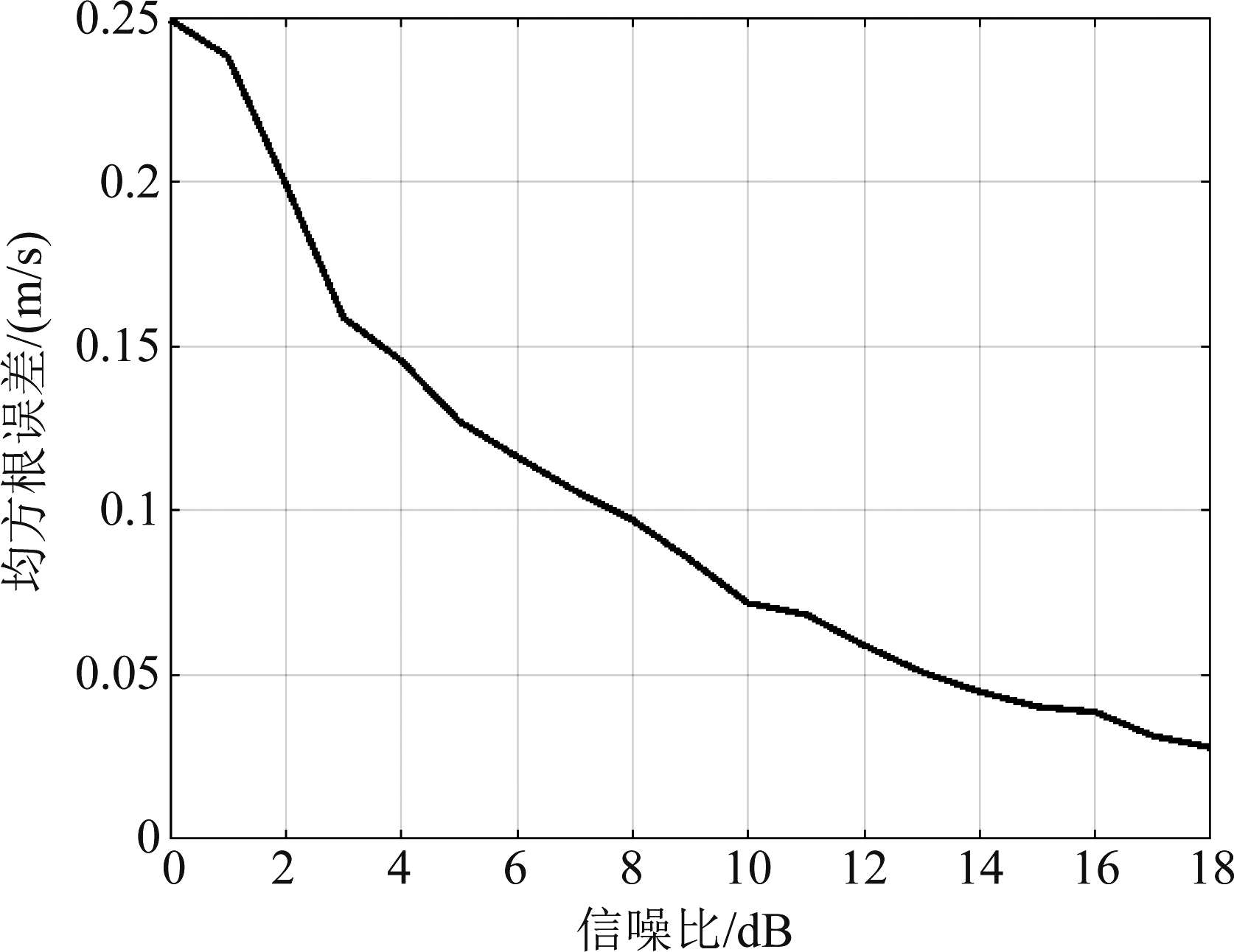
图9 图8的局部放大图
Fig.9 A partial enlargement of Fig.8
由于噪声的影响,在信噪比较低时,直接提取峰值点相位进行相推测速的结果精度很差。相应地,对相位拟合后进行相推测速的结果也比较差。在信噪比比较高时,对相位拟合后进行相推测速的方法的测速均方根误差和本文所提方法基本一致。而本文所提方法在0 dB到18 dB的信噪比范围均可以获得高精度的测速均方根误差,验证了本文所提方法在低信噪比条件下的高精度测速性能。
基于地基S波段雷达,开展民航飞机实验,验证本文所提方法。选取其中一段信噪比约为0 dB的实测数据,采用所提方法进行相推测速处理。由于信噪比较低,从距离像和距离像互相关结果上无法看到目标所在的位置。因此基于距离像互相关的包络测速方法失效,其测量结果偏差很大。采用本文所提的方法,积累50个脉冲,对距离像互相关结果沿慢时间维积累的结果如图10所示。图中可以看到明显的峰值位置。重新提取相位,并设计滤波器,对相位进行滤波。最终得到的相推测速结果如图11所示。由图中可以看出,飞机速度约为71 m/s,最大测速误差不超过0.8 m/s。
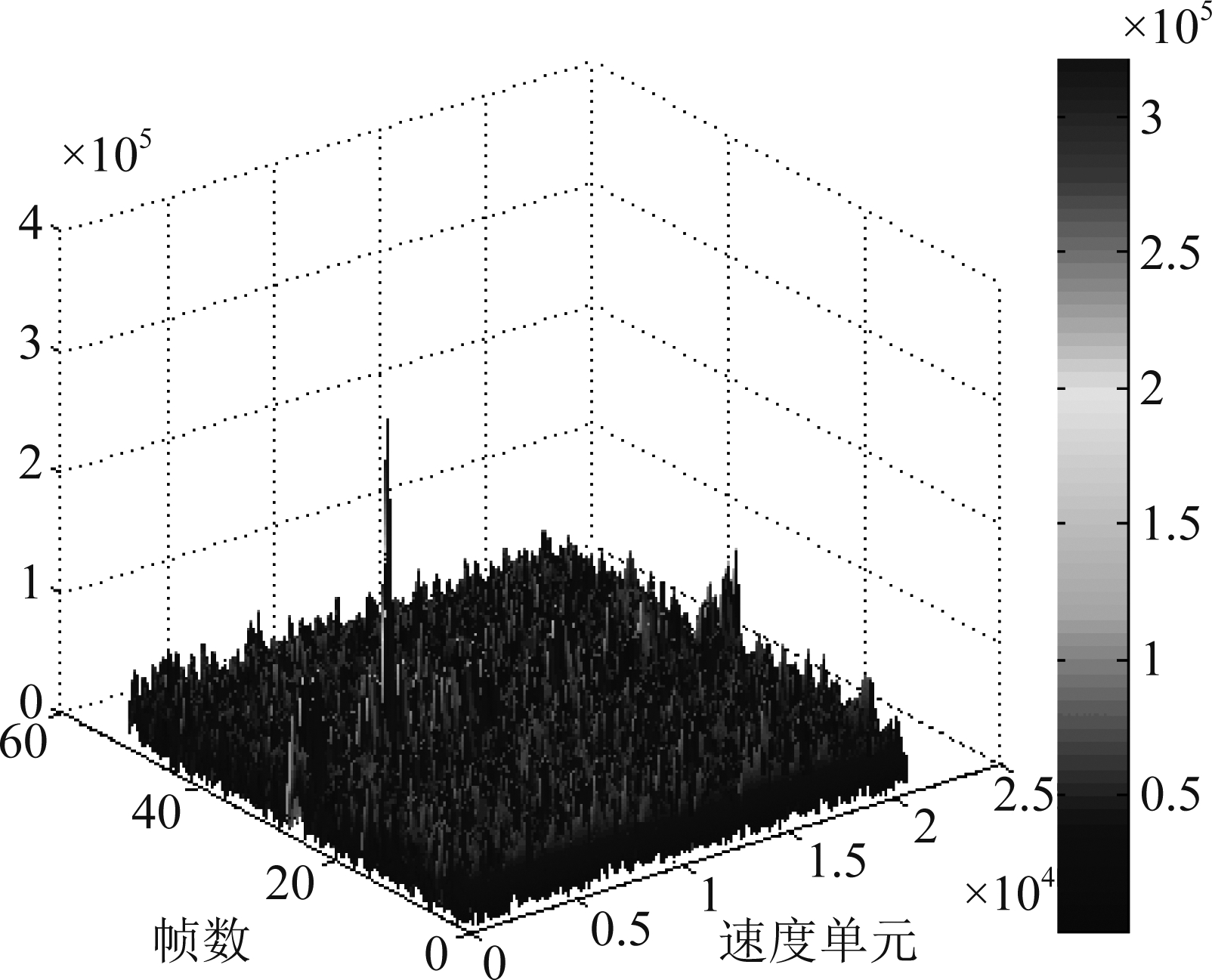
图10 积累结果
Fig.10 Accumulation results
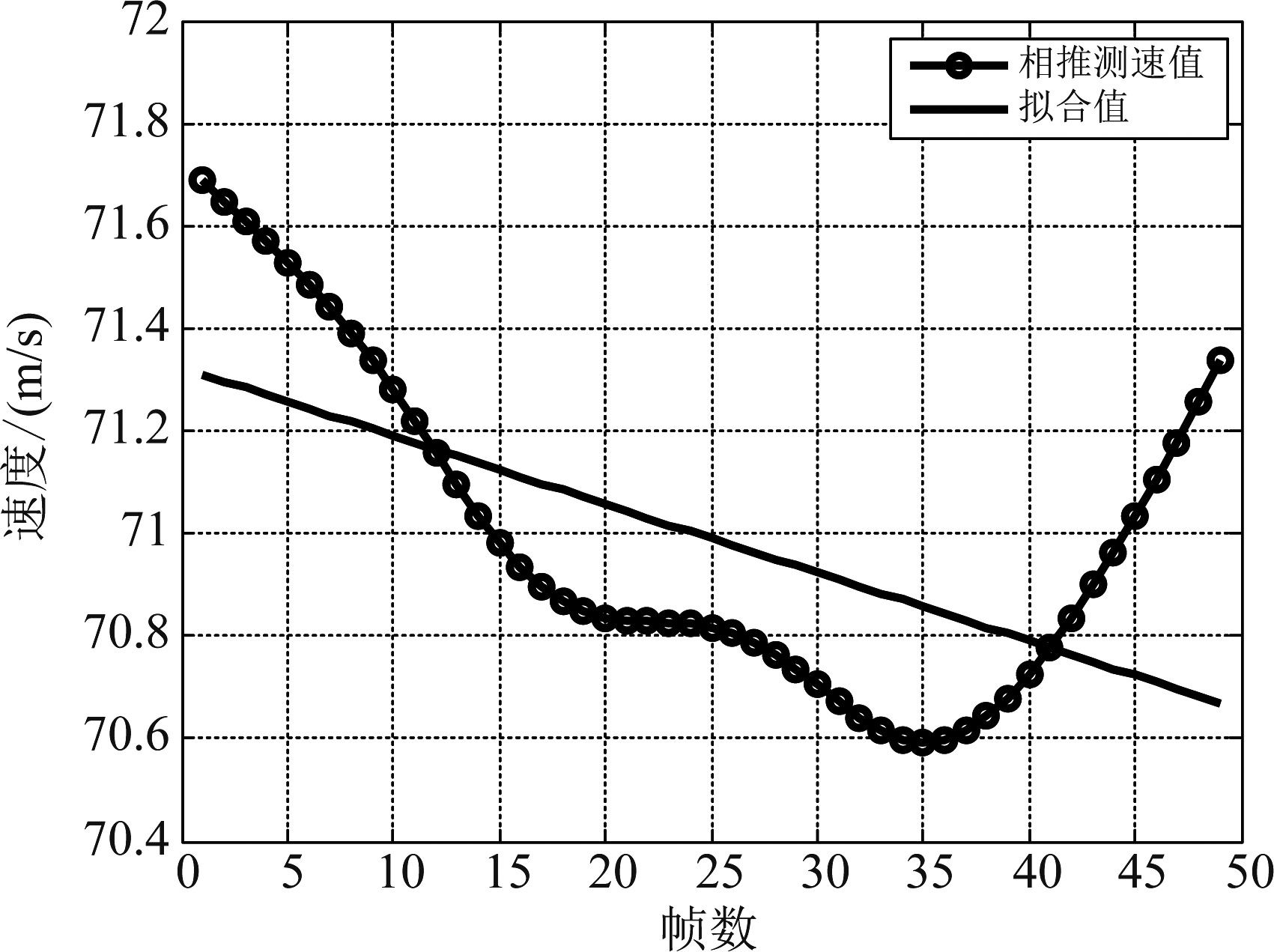
图11 相推测速结果
Fig.11 Phase-derived velocity measurement results
6 结论
本文介绍了基于距离像互相关的低信噪比条件下相推测速方法。首先,基于宽带线性调频信号的去斜处理回波模型,推导了相邻帧距离像互相关结果;然后,针对相推测速在低信噪比条件下的提取回波相位和解相位模糊的难点,提出了基于距离像互相关结果沿慢时间维积累重新提取回波相位的方法,以及利用积累结果得到速度的粗估计值进而辅助后续解相位模糊处理。此外,还可以根据相位的频谱特性设计滤波器进一步滤除噪声对相位的影响。因此能够有效降低相推测速对信噪比的要求。最后通过仿真和实验验证了本文所提方法在低信噪比条件下的有效性。
[1] LONG Teng, LIANG Zhennan, LIU Quanhua.Advanced technology of high-resolution radar: Target detection, tracking, imaging, and recognition[J].Science China Information Sciences, 2019, 62(4): 1-26.
[2] CHEN V C, LI F, HO S S, et al.Micro-Doppler effect in radar: Phenomenon, model, and simulation study[J].IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2-21.
[3] 朱得糠, 刘永祥, 李康乐, 等.基于雷达相位测距的微动特征获取[J].宇航学报, 2013, 34(4): 574-582.
ZHU Dekang, LIU Yongxiang, LI Kangle, et al.Feature extraction for target with micro-motion based on radar phase derived range[J].Journal of Astronautics, 2013, 34(4): 574-582.(in Chinese)
[4] STEUDEL F.An improved process for phase-derived-range measurements.World intellectual property organization patent, 1651978, 2005-2-24.
[5] STEUDEL F.Process for phase-derived-range measurements.U.S.patent, 7046190, 2005-2-10.
[6] FAN Huayu, REN Lixiang, LONG Teng, et al.A high-precision phase-derived range and velocity measurement method based on synthetic wideband pulse Doppler radar[J].Science China Information Sciences, 2016, 60(8): 1-12.
[7] LI Wenji, FAN Huayu, REN Lixiang, et al.Micromotion feature extraction based on phase-derived range and velocity measurement[J].IEEE Access, 2019, 7: 114167-114182.
[8] LIU Yongxiang, ZHU Dekang, LI Xiang, et al.Micromotion characteristic acquisition based on wideband radar phase[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3650-3657.
[9] ZHU Dekang, LIU Yongxiang, HUO Kai, et al.A novel high-precision phase-derived-range method for direct sampling LFM radar[J].IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1131-1141.
[10] XIONG Xiangyu, DENG Zhenmiao, QI Wei, et al.A novel high-precision range estimation method based on phase of wideband radar echo[J].IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3392-3403.
[11] FAN Huayu, REN Lixiang, MAO Erke, et al.A high-precision method of phase-derived velocity measurement and its application in motion compensation of ISAR imaging[J].IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 60-77.
[12] 许邦建, 皇甫堪.噪扰条件下相位测距中的解模糊问题[J].国防科技大学学报, 2001, 23(3): 73-76.
XU Bangjian, HUANGFU Kan.Problem in the measurement of range by phases in noisy circumstance[J].Journal of National University of Defense Technology, 2001, 23(3): 73-76.(in Chinese)
