1 引言
在雷达数据处理过程中,跟踪波门内由杂波产生的虚警增加了量测来源的不确定性,需要利用数据关联算法进行关联决策,进而实现复杂环境中的多目标跟踪[1-2]。常用的数据关联算法有概率数据关联[3](Probabilistic Data Association, PDA)、综合概率数据关联[4](Integrated Probabilistic Data Association, IPDA)和多假设跟踪[5-7](Multiple Hypothesis Tracking, MHT)算法。在上述数据关联算法中,杂波强度作为一个重要参数用于计算航迹的存在概率及数据关联概率,且通常会假定其先验已知。在未知杂波强度的观测场景中,时变的杂波密度将增大杂波强度误差进而导致算法跟踪性能下降。因此,杂波强度估计成为未知杂波强度场景下多目标跟踪算法的一个重要问题。
为了改善未知观测场景下跟踪算法的稳定性与准确性,研究人员提出了多种杂波强度估计方法。一种是基于杂波数的杂波强度估计算法。Li等人采用条件均值和最大似然估计等方法估计波门内的杂波数[8-9],并在杂波密度均匀分布的前提下计算杂波强度。Song等人提出了一种空间稀疏性估计算法[10]。该算法根据量测相对目标预测位置的距离及该量测距离波门内的量测数求解出杂波的空间稀疏性,并估计出该空间内的杂波强度。文献[11]在空间稀疏估计算法的基础上通过增加量测距离波门的体积,减小了杂波强度估计误差,改善了未知杂波场景下多目标跟踪算法的性能。另一种是基于模型的杂波强度估计方法。Raftery在文献[12]中提出了一种基于高斯混合模型(Gaussian Mixture Model, GMM)的杂波强度估计算法。该算法利用贝叶斯信息准则(Bayesian Information Criterion, BIC)和期望最大化(Expectation Maximum, EM)算法对杂波空间分布进行估计,计算出波门内的杂波强度。Lian等人在文献[13]中提出采用有限混合模型(Finite Mixture Model, FMM)对未知观测场景中的杂波空间分布进行拟合,并将得到的杂波强度估计结果应用于随机有限集滤波器中,获得了较好的跟踪性能。上述方法可在一定程度上改善未知杂波场景下目标的跟踪性能,但在时变杂波的观测场景中,这些方法将无法准确估计杂波强度,导致数据关联准确性降低。
为解决该问题,本文在面向航迹的MHT(Track-Oriented MHT, TOMHT)框架下,提出一种基于高斯核密度的在线杂波估计MHT算法(MHT-KDE)。该算法利用基于渐进平均平方误差积分准则(Asymptotic Mean Integrated Squared Error, AMISE)的直接插入法和每一时刻量测的特征信息自适应地计算出核函数的带宽,并估计出波门内位置自适应的杂波强度,然后利用得到的杂波强度计算出未知杂波场景下的航迹得分及全局最优假设。仿真结果表明,MHT-KDE算法改善了未知杂波观测场景下数据关联的准确性,并获得了较好的跟踪性能。
2 问题描述
2.1 TOMHT框架
MHT算法的实现方案一般分为面向假设的多假设跟踪(Hypothesis-Oriented MHT, HOMHT)[5- 6]和面向航迹的多假设跟踪(Track-Oriented MHT, TOMHT)[7]两种。TOMHT作为一种经典的MHT算法,具有储存量小,可以直接输出航迹等优点。图1为TOMHT算法流程图,TOMHT算法主要由航迹得分计算模块及全局假设生成模块组成。首先,在航迹得分计算模块中利用波门内量测的特征信息,如新生目标密度、杂波强度等计算出各量测的存在概率,并求解出该时刻的航迹得分。然后,进行基于航迹得分的航迹删减、合并等操作以减少虚假航迹数。在全局假设生成模块中,利用优化算法求解出该时刻最优的全局假设,并计算出航迹全局概率。最后,进行N回扫剪枝和基于全局概率的航迹剪枝,得到该时刻最优的全局假设。
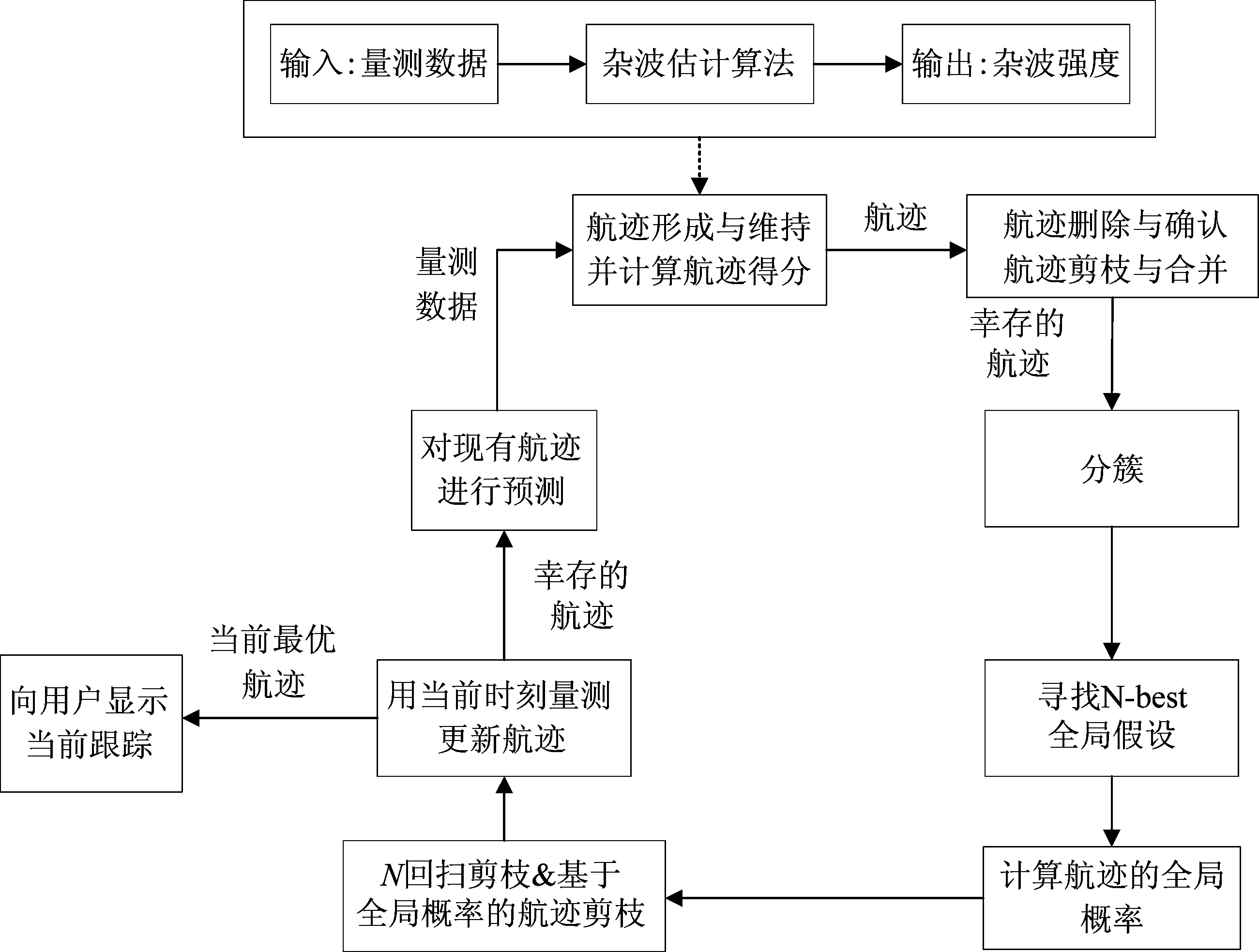
图1 TOMHT处理流程
Fig.1 The flowchart of the TOMHT
(1)航迹得分
多假设跟踪算法是一种基于延迟决策的数据关联算法,该算法对每一时刻波门内的量测进行数据关联处理,形成假设航迹分支。然后利用多帧量测数据计算出每个分支的航迹得分,并根据航迹得分的大小对航迹可能性大小进行判断。航迹是由同一目标产生的一组量测序列。假设在k时刻存在N条假设航迹Tj(k-1), j=1,...,N,且在航迹Tj(k-1)的波门内存在M个量测zm(k),m=1,...,M。当量测数据中运动信息与相关信号信息之间相互独立,且相关信号只包含探测信息时,得分函数计算如下
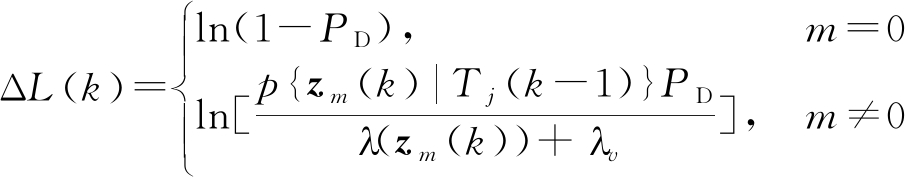
(1)
式中,m=0表示波门内没有量测,PD为检测概率,ln(1-PD)表示k时刻波门内没有量测时的得分增量。λ(zm(k))表示杂波强度,λv表示新目标的空间密度。p{zm(k)|Tj(k-1)}表示k时刻量测zm(k)与航迹Tj(k-1)的似然函数。k时刻航迹得分的递归表达式可写为
L(k)=L(k-1)+ΔL(k)
(2)
接着,对k时刻存在的假设航迹进行序贯概率比检验,以减少虚假航迹的数量。并对幸存的航迹进行分簇处理,以降低假设组合的复杂度。
(2)全局假设
全局假设由一组相互兼容的航迹组成,即在同一个全局假设中航迹之间没有共享量测。在TOMHT算法中,可通过优化算法寻找最优全局假设。求解最优假设h*的过程相当于求解条件概率分布P(h|z)上的最大后验概率解,即
(3)
式中,h表示一组全局假设,z为传感器接收到的量测。假设k时刻存在J个全局假设,则全局假设hi的条件概率分布的对数形式可表示为
(4)
其中,L(Tj(k))表示航迹Tj(k)的得分。然后对幸存的航迹进行N回扫剪枝和基于全局概率的航迹剪枝。最终求解出该时刻最优的全局假设。
2.2 杂波估计问题
本节我们首先介绍了杂波强度估计问题,并给出了基本的杂波强度估计方法。通常而言,为获得更好的跟踪性能,波门内杂波强度参数误差越小越好。由式(1)可以看出,当杂波强度参数值越准确,假设航迹得分的计算越准确,进而可以获得较优的数据关联结果。然而，许多实际跟踪场景中的杂波都具有时变和空变特性，这将增加杂波强度估计误差，降低数据关联的准确性。为提高杂波估计的准确性,本文提出了一种基于核密度估计的杂波密度估计方法。下面对核密度估计算法的基本原理进行介绍。
(1)杂波强度估计
本文假设杂波数服从泊松分布[14],则波门内由杂波产生虚警数为l的概率质量函数可表示为
(5)
式中,M表示波门内的杂波数。
杂波强度估计问题一般可分解为杂波数估计问题和杂波密度估计问题[13],即
λ(z)=Mc(z)
(6)
式中,λ(z)为单位体积内的平均杂波数,即杂波强度,c(z)表示杂波密度函数,z为传感器接收到的量测。
在传统的多目标跟踪算法中,通常假定杂波密度函数为均匀分布函数,即c(z)=1/V。由文献[3]可知,k时刻波门内杂波数估计为
(7)
式中,mk为波门中的量测数,PD为检测概率,PG为真实目标量测落入波门的概率,
为预测目标的存在概率。结合式(6)可得波门内的杂波强度为
(8)
(2)核密度估计
核密度估计算法是一种非参数检验方法,该算法根据给定的样本点集合计算出自适应核函数带宽,进而求解出样本分布的概率密度函数[15-17]。该方法仅利用给定样本数据本身的特征,不需要对数据分布附加任何先验假定,提高了概率密度函数估计的准确性和鲁棒性。
核密度估计是将每个数据点(假设存在Ntotal个数据点)及带宽作为核函数(如高斯核函数)的参数求解得到Ntotal个核函数,然后经过线性叠加及归一化处理计算出该数据的概率密度函数。假设k时刻存在随机样本Z=(z1,...,zNtotal),每个样本是由d维随机向量组成即z=(x1,...,xd)T,且概率密度函数可表示为f(z)=f(x1,...,xd),带宽为b=(b1,...,bd)T。假设样本每个分量对应的带宽相同,即b1=b2=…=bd。则带宽固定为b时的核密度估计
可表示为
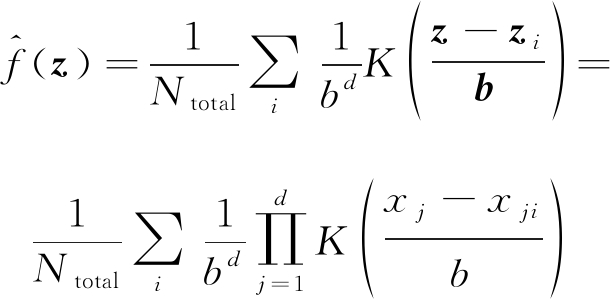
(9)
式中,K(·)为多维核函数,b={b1,…,bd}为核密度带宽。当不同分量的带宽不同时,多维核密度估计为
(10)
由于概率密度函数在定义域区间内的积分为1,故核密度函数的参数之间存在以下约束[15]
(11)
(12)
(13)
3 采用核密度杂波估计的多假设跟踪算法
本文提出的MHT-KDE算法采用核密度杂波估计方法计算出波门内杂波分布的概率密度函数,并将杂波强度估计结果应用于TOMHT算法中,获得最优假设航迹。在本节中,我们首先给出了基于高斯核函数的杂波空间密度函数。然后介绍了基于AMISE算法的带宽优化、自适应杂波密度估计的具体推导过程。最后求解出非均匀杂波场景下的杂波强度及航迹得分。
根据杂波的随机分布特性,本文利用高斯核函数对杂波空间密度进行拟合,结合式(9)可得高斯核密度函数为
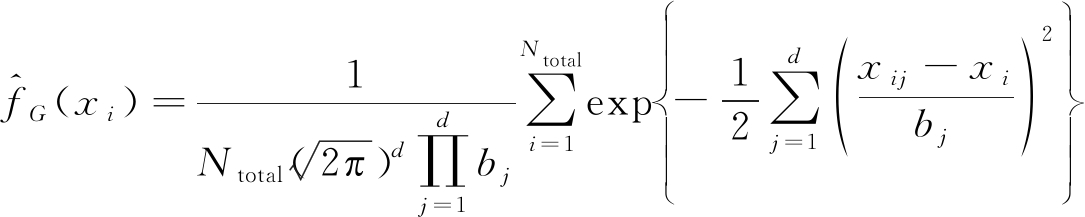
(14)
(1)基于AMISE的自适应核密度带宽
核密度函数的带宽参数b决定了估计结果的平滑程度,参数b过大时,会导致核密度函数过平滑,损失过多的局部特征;参数b过小时,将过多地体现样本的局部特征,导致估计结果的尾部误差增大。为降低核密度估计误差,研究人员提出了平均平方误差积分准则(Mean Integrated Squared Error, MISE)和渐进平均平方误差积分准则(Asymptotic MISE, AMISE)等带宽优化准则[16]。相比MISE准则,AMISE准则利用基于泰勒公式的近似计算方式,简化了样本方差和误差的计算过程,降低了带宽优化的计算量。因此,本文采用AMISE准则对核密度函数的带宽进行优化,
AMISE=MISE-o((nb)-1+b4)
(15)
其中,o((nb)-1+b4)是一个无穷小量[16]。
(16)
因此,
(17)
式中,
文献[16]中介绍了直接插入(Direct Plug In, DPI)带宽优化器,即将式(17)中的R(f ″)替换为
避免了二阶导数求解带来的计算量,简化了带宽计算过程。DPI带宽优化器可写为
(18)
式中,
因此,分量xj的优化带宽可写为
(19)
当核密度函数为均值为0,方差为δ2的高斯函数时,
(2)自适应带宽因子
由式(14)可以计算出自适应局部带宽因子[18]为
(20)
式中,0≤α≤1为灵敏因子。通常α取0.5,当α=0时,自适应带宽核密度估计就变成了固定带宽核密度估计。式(20)中几何均值参数q为
(21)
结合式(19)和式(20),可得自适应带宽为
(22)
(3)自适应杂波空间密度函数及自适应航迹得分
将式(22)自适应带宽参数Bi替换式(14)中的固定带宽参数bj,可以计算出自适应杂波空间密度函数为
(23)
结合式(1)、(6)、(7)和(23)可分别计算出杂波强度及得分函数,
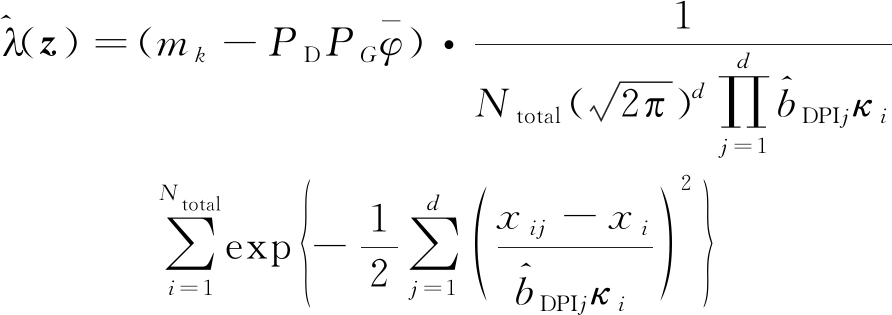
(24)
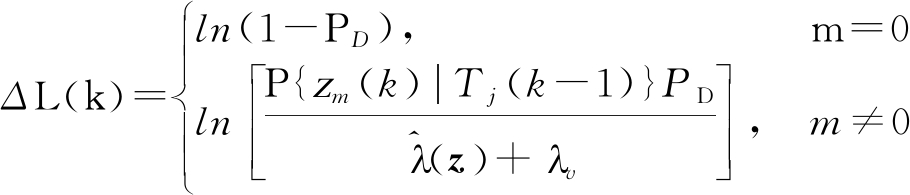
(25)
4 仿真与分析
本节通过非均匀杂波场景对基于自适应高斯混合模型估计未知杂波的改进MHT算法(MHT-AGMM)和MHT-KDE算法进行仿真,并利用文献[19-21]中的性能评价指标,最优子模式分配距离(Optimal sub-Pattern Assignment, OSPA)、势估计、数据关联正确率(Rcc)、关联错误率(Rmc)、航迹断续率(Rfg)以及算法平均一帧运行时间(Tavg),对两种算法的跟踪性能进行比较。最后给出基于实测数据的验证结果。
假设目标在X-Y平面作匀速运动,目标的运动状态可写为
其中x,y分别表示目标位置,
表示速度。目标的运动模型可写为
x(k)=Fx(k-1)+v(k)
(26)
式中,F为状态转移矩阵,v(k)表示协方差矩阵为Q(k)的零均值高斯过程噪声。
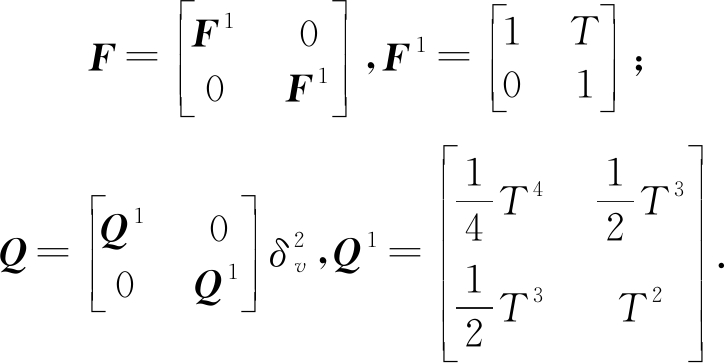
式中,δv为过程噪声标准差。目标的观测模型可写为
z(k)=Hx(k)+w(k)
(27)
其中,H为观测矩阵,w(k)表示协方差矩阵为R(k)的零均值高斯量测噪声。
式中,δε为量测噪声标准差。
(1)仿真数据验证
跟踪场景中设置6个交叉运动的目标,目标分布在二维空间[-4000 m, 4000 m]×[-4000 m, 4000 m]中,并在该空间中加入非均匀分布杂波。由式(6)可知,观测区域内非均匀杂波强度可写为λ(z)=Mc(z)。本小节设置平均每帧杂波数为M,其中M为1～100范围内的随机数。杂波密度函数为
其中n为2～4范围内的随机整数,Pi是均值为ui,方差为
的高斯分布
目标的运动参数如表1所示,非均匀杂波空间密度函数的参数设置如表2所示。表2中ε是0～100范围内的随机数。diag(·)表示对角矩阵。图2为真实目标航迹,图3为加入杂波后的量测分布图。图中“x”表示航迹的终点,“o”表示航迹的起点。
表1 目标运动参数
Tab.1 The motion parameters of targets
目标初始状态存活时间[0 m,30 m/s,-2000 m,50 m/s]1～100 s[1500 m,40 m/s,-500 m,30 m/s]1～90 s[3500 m,-49 m/s,2800 m,-42 m/s]1～100 s[-3000 m,30 m/s,-3000 m,50 m/s]1～100 s[-2000 m,80 m/s,2000 m,-100 m/s]40～90 s[2000 m,-20 m/s,-3000 m,120 m/s]30～80 s
表2 杂波空间密度参数
Tab.2 Parameters of the clutter spatial density
分布函数均值和方差P1～(u1,δ21)u1=[-2000,1000]T+ε1,δ21=diag{800,800}+ε1P2～(u2,δ22)u2=[2000,500]T+ε2,δ22=diag{700,700}+ε2P3～(u3,δ23)u3=[-500,1500]T+ε3,δ23=diag{400,600}+ε3P4～(u4,δ24)u4=[100,-400]T+ε4,δ24=diag{500,600}+ε4
图2 目标航迹
Fig.2 The target trajectories
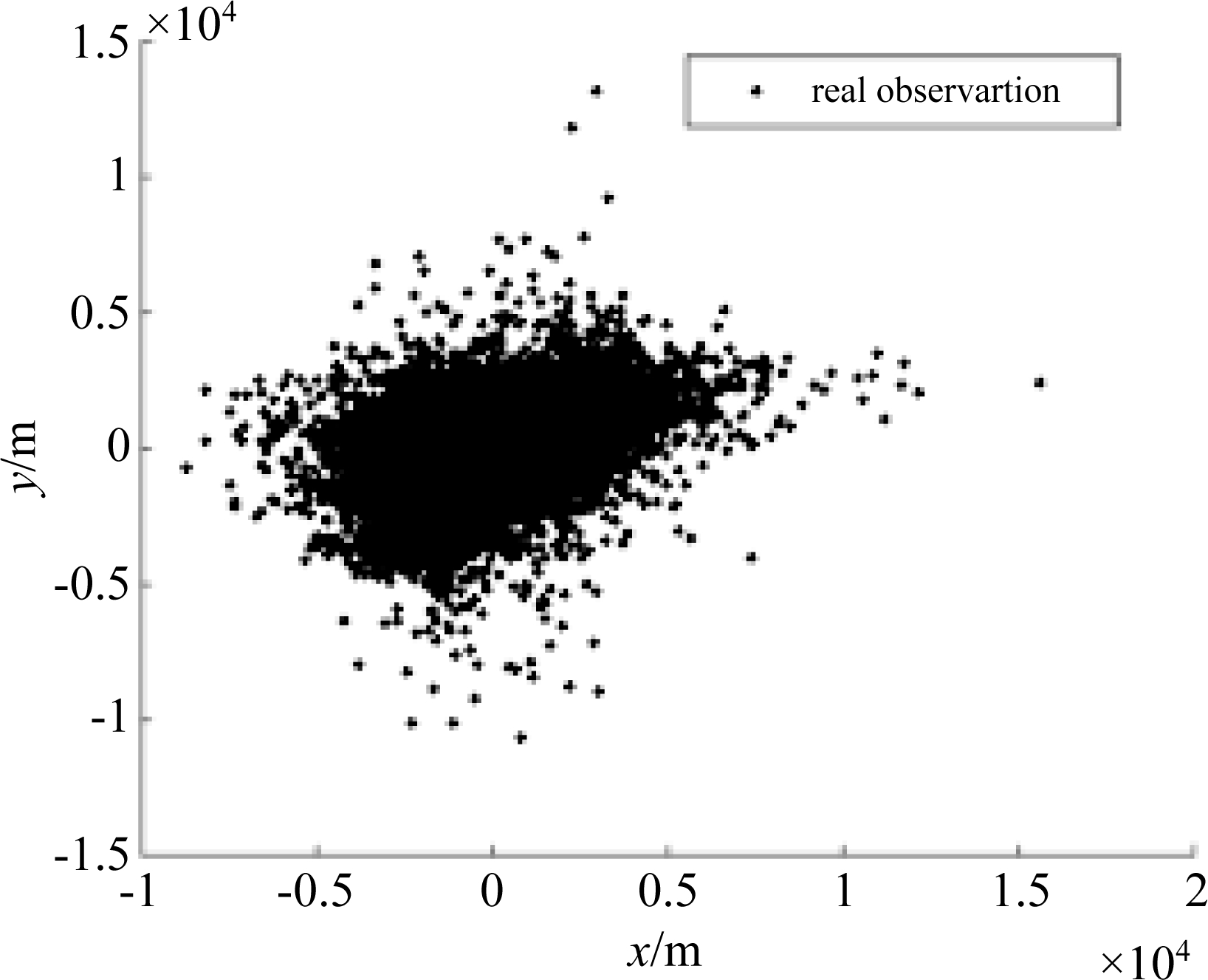
图3 量测分布图
Fig.3 The distribution diagram of measurements
跟踪处理参数设置如下:检测概率为0.9,新生目标密度为10-7,杂波强度为10-9,量测噪声标准差为δv=6 m/s,过程噪声标准差为δε=10 m,MHT剪枝深度为3。在仿真场景中,如果量测数较多,则利用核密度估计可以得到较准确杂波估计结果。但对量测数较少的仿真场景,核密度估计方法估计结果误差增大,将降低数据关联准确性。为此,本实验设置量测数门限为20。当量测数小于20时,假设杂波密度为均匀分布,当量测数大于20时,利用核密度估计方法进行杂波密度估计。图4为MHT-AGMM算法的跟踪结果,图5为MHT-KDE算法的跟踪结果,图6为OSPA结果对比图,图7为势估计结果对比图,表3为100次蒙特卡洛仿真下两种算法的性能对比。
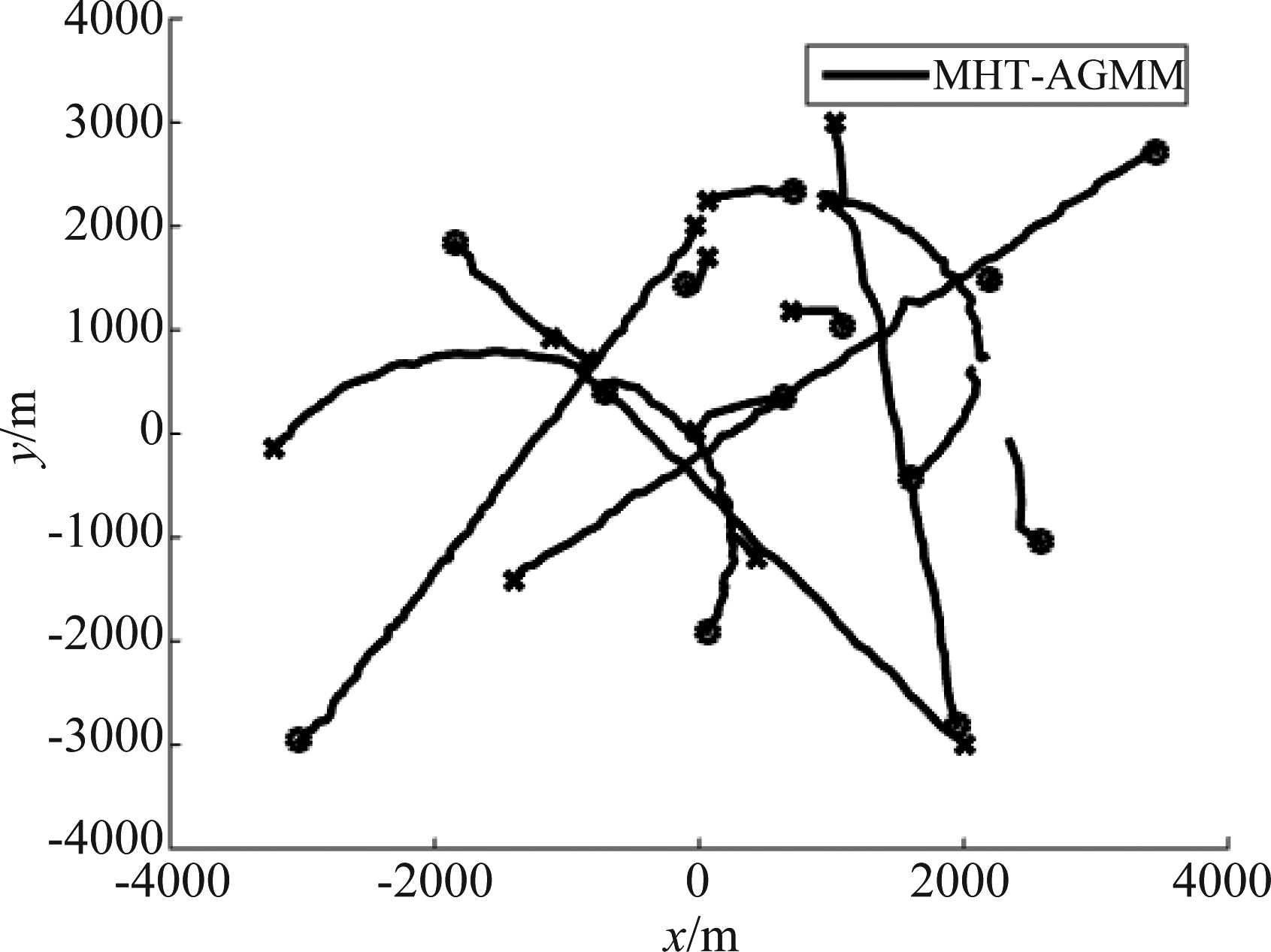
图4 MHT-AGMM算法跟踪结果
Fig.4 The estimated trajectories of the MHT-AGMM
图5 MHT-KDE算法跟踪结果
Fig.5 The estimated trajectories of the MHT-KDE
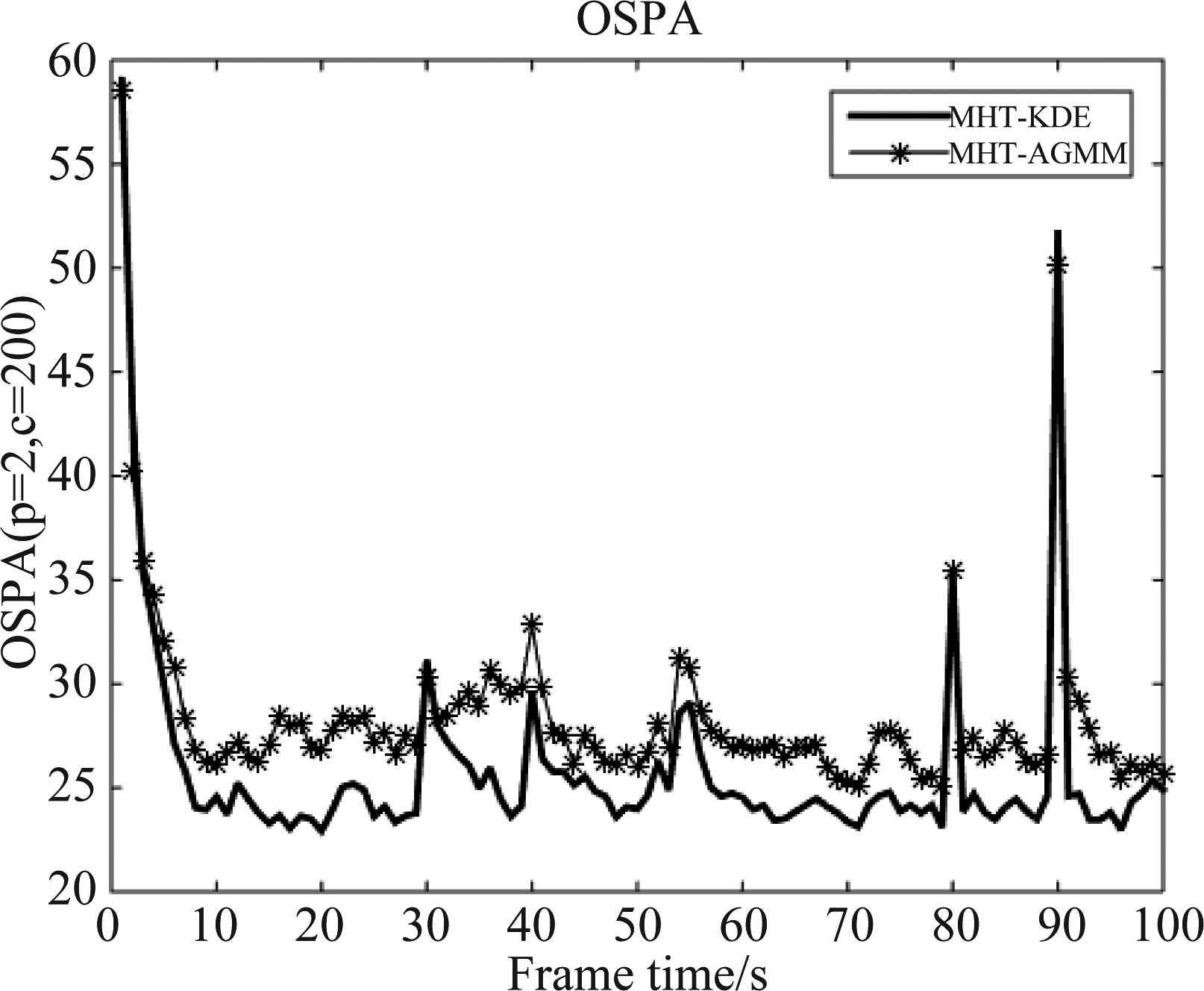
图6 OSPA结果对比图
Fig.6 The OSPA distance of two algorithms
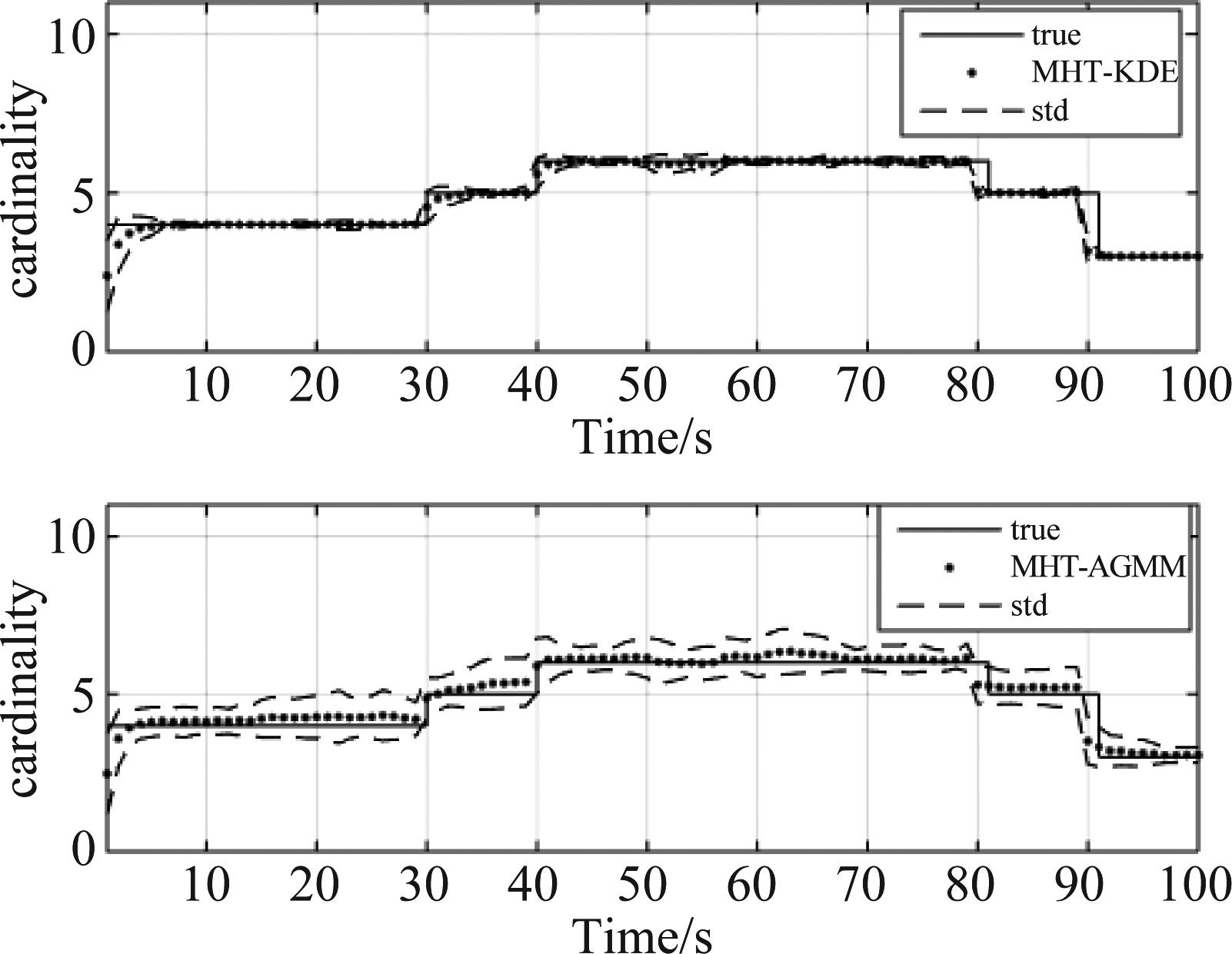
图7 势估计结果对比图
Fig.7 The cardinality estimation of two algorithms
本小节使用MHT-KDE和MHT-AGMM算法分别对非均匀杂波场景进行多目标跟踪处理。由图4、图5两种算法的跟踪结果可以看出,核密度估计方法实现了更好的数据关联性能,得到了更优的跟踪轨迹。接着,使用OSPA距离曲线和势估计分别对两种算法的数据关联性能进行验证,由图6、图7可以看出,MHT-KDE算法具有更小的OSPA距离,且势估计精度更准确。为了更好地对比两算法的跟踪性能,表3中分别利用数据关联正确率(Rcc),关联错误率(Rmc),航迹断续率(Rfg)以及算法平均一帧运行时间(Tavg)等评价指标对两种算法跟踪性能进行比较。可以看出,MHT-KDE算法具有较优的数据关联准确性和航迹维持性能并且具有较小的运算量。
表3 两种算法的性能对比
Tal.3 The performance metrics of two algorithms
RccRmcRfgTavgMHT-KDE0.97610.01760.10600.7487 sMHT-AGMM0.94780.03910.18501.8327 s
(2)实测数据验证
采用一部X波段对海探测雷达所录取点迹数据对算法的有效性进行验证。图8为点迹数据的量测图,可以看出,实际海杂波跟踪场景具有明显的非均匀特性。
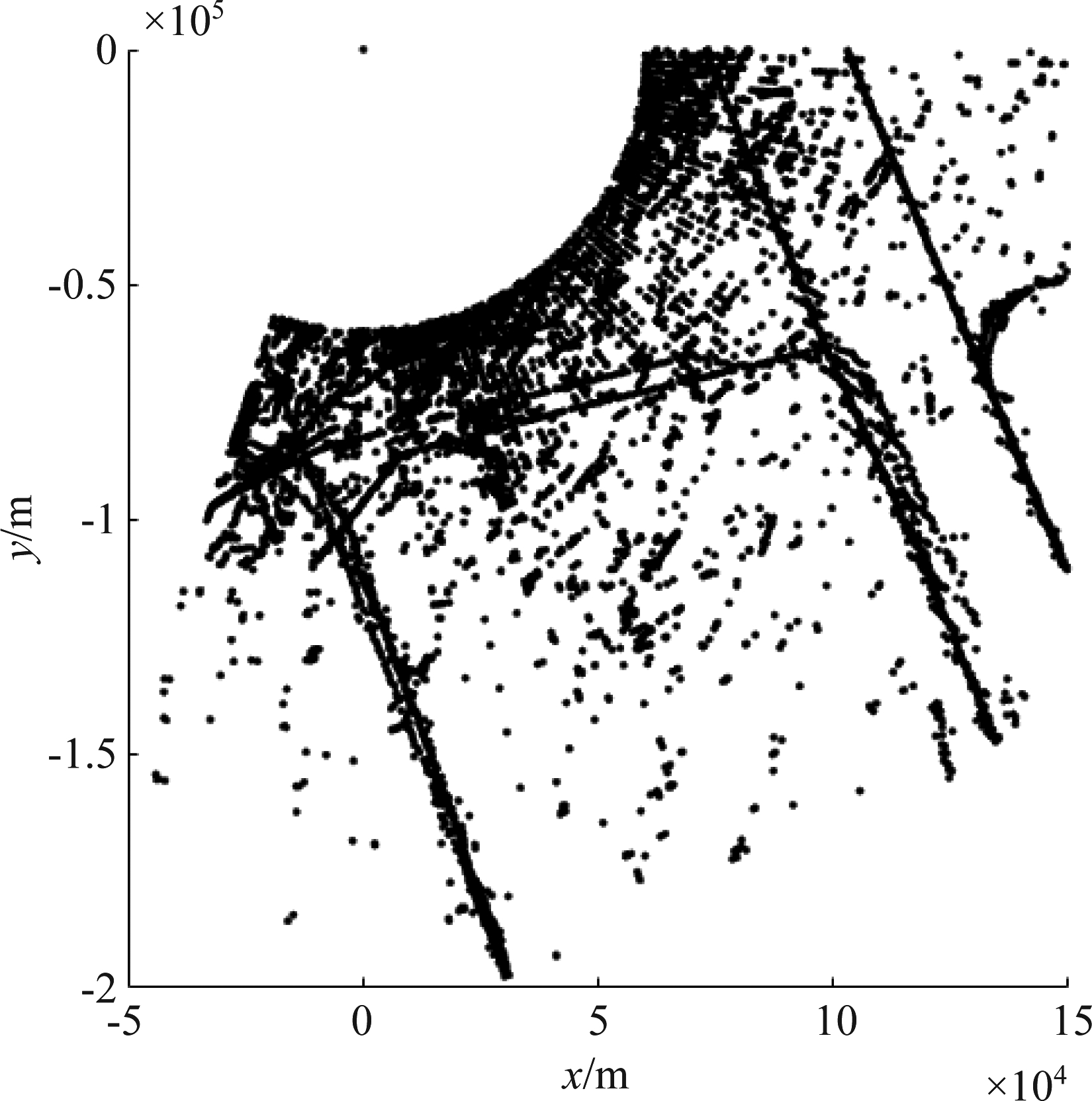
图8 实测数据量测图
Fig.8 The observations of real data
跟踪处理参数设置如下:检测概率为0.95,新生目标密度为10-14,杂波强度为10-15,量测噪声标准差为δν=6 m/s,过程噪声标准差为δε=40 m,MHT剪枝深度为6。图9为MHT-AGMM算法的跟踪结果,图10为MHT-KDE算法的跟踪结果。图中“x”表示航迹的终点,“o”表示航迹的起点。
为了更好地对比跟踪结果,将跟踪结果中的两条航迹提取出来。由图9和图10可以看出,当杂波的空间分布时变时,MHT-AGMM算法无法准确进行数据关联处理,出现航迹断续、关联错误等现象。本文所提MHT-KDE算法利用核密度估计方法得到较准确的杂波强度及数据关联结果,仍可实现较好的跟踪效果。在同一仿真参数设置下,MHT-KDE算法和MHT-AGMM算法的运行时间分别为127.91 s和218.813 s,可以看出,MHT-KDE算法在降低运算复杂度的同时获得了更好的跟踪性能。
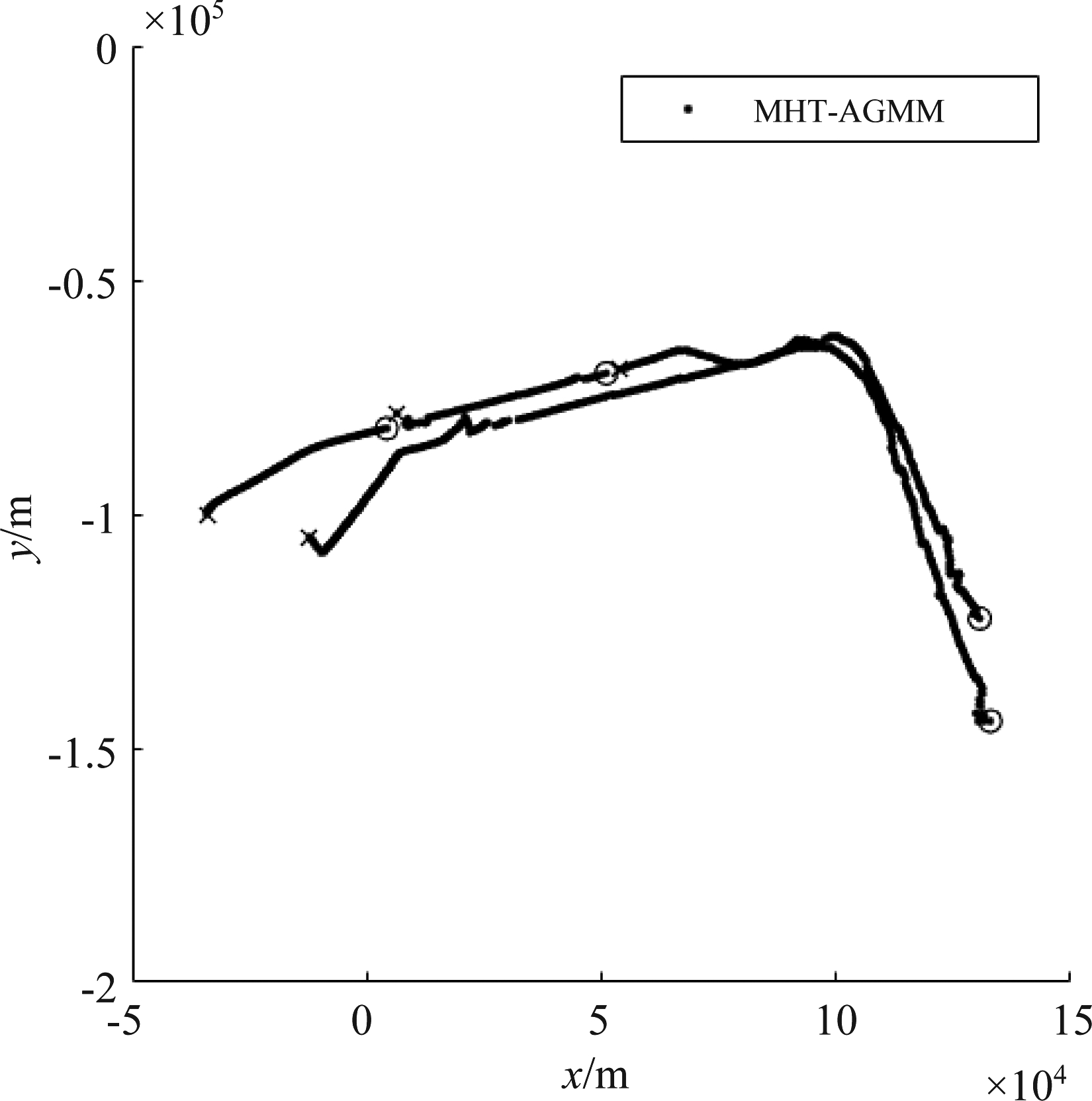
图9 MHT-AGMM算法实测数据跟踪结果
Fig.9 The estimated trajectories of the MHT-AGMM with real data
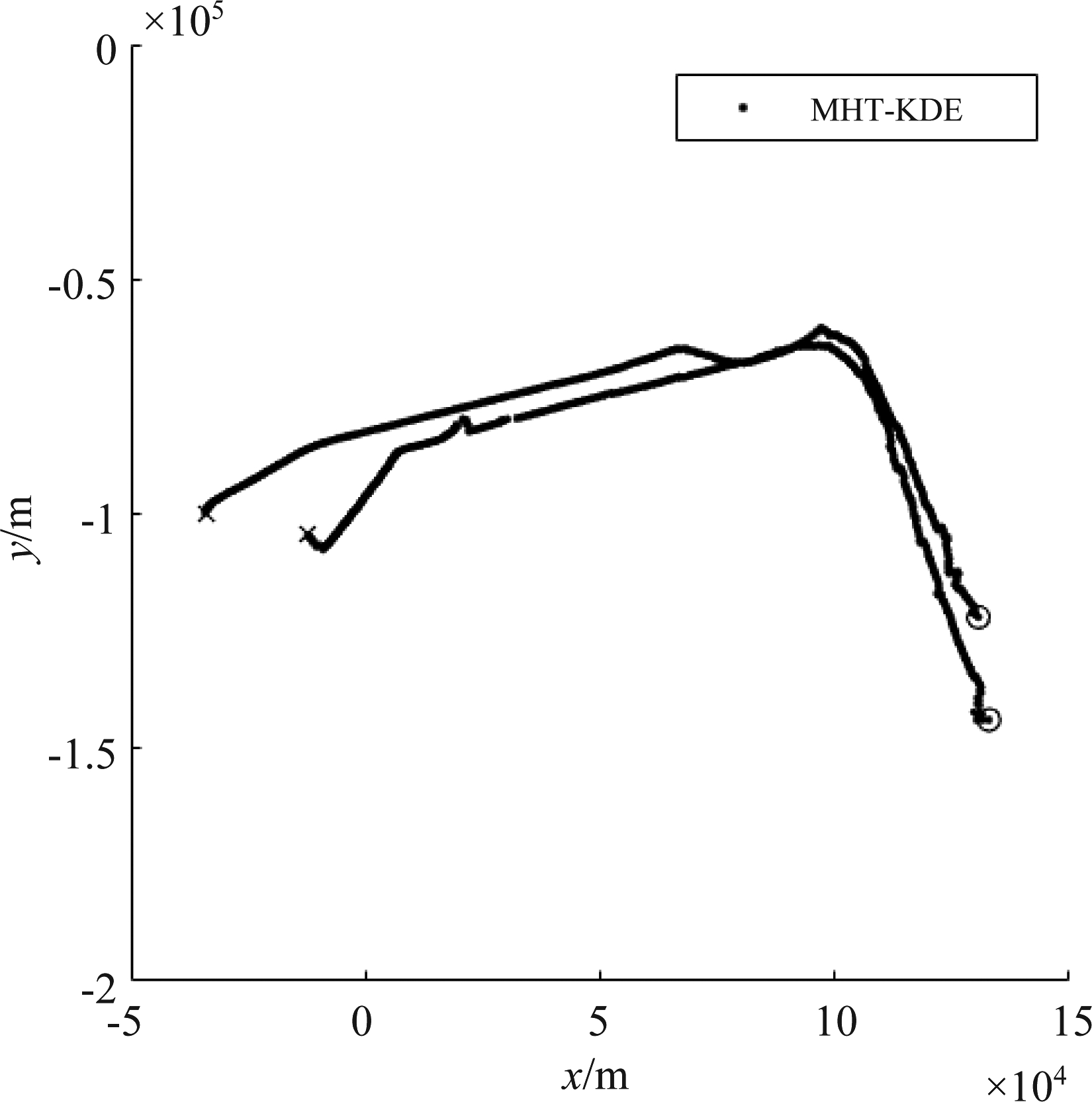
图10 MHT-KDE算法实测数据跟踪结果
Fig.10 The estimated trajectories of the MHT-KDE with real data
5 结论
本文提出了一种基于核密度估计的在线杂波估计MHT算法。与传统MHT算法假设杂波强度先验已知不同,MHT-KDE算法在TOMHT逻辑框架下,利用核密度函数自适应地估计出波门内的杂波强度,并计算得到未知杂波场景下的最优全局假设。为了证明该方法的有效性,本文通过仿真数据验证和实测数据验证,对比了MHT-KDE与MHT-AGMM算法的跟踪性能。实验结果表明,所提算法能够准确估计波门内的杂波强度,在数据关联准确性、航迹连续性等性能指标上优于MHT-AGMM算法,并在一定程度上降低了算法的复杂度。
[1] BAR-SHALOM Y,FORTMANN T E,CABLE P G.Tracking and data association[J]. The Journal of the Acoustical Society of America, 1990, 87(2): 918-919.
[2] BLACKMAN S S,ROBERT P.Design and Analysis of Modem Tracking System.Norwood,Artech House,1999.
[3] BAR-SHALOM Y, TSE E. Tracking in a cluttered environment with probabilistic data association[J]. Automatica, 1975, 11(5): 451- 460.
[4] MUSICKI D,EVANS R,STANKOVIC S.Integrated probabilistic data association[J]. IEEE Transactions on Automatic Control, 1994, 39(6): 1237-1241.
[5] REID D. An algorithm for tracking multiple targets[J]. IEEE Transactions on Automatic Control, 1979, 24(6): 843- 854.
[6] COX I J, HINGORANI S L. An efficient implementation of Reid′s multiple hypothesis tracking algorithm and its evaluation for the purpose of visual tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(2): 138-150.
[7] DEMOS G C, RIBAS R A, BROIDA T J, et al. Applications of MHT to Dim Moving Targets[J]. Proceedings of SPIE-The International Society for Optical Engineering, 1990, 1305: 297-309.
[8] LI Ning, LI X R. Target perceivability and its applications[J]. IEEE Transactions on Signal Processing, 2001, 49(11): 2588-2604.
[9] LI X R, LI Ning. Integrated real-time estimation of clutter density for tracking[J]. IEEE Transactions on Signal Processing, 2000, 48(10): 2797-2805.
[10] SONG T L, MUSICKI D. Adaptive clutter measurement density estimation for improved target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1457-1466.
[11] PARK S H, CHONG Sayong, KIM H J, et al. Adaptive estimation of spatial clutter measurement density using clutter measurement probability for enhanced multi-target tracking[J]. Sensors, 2020, 20(1): 114-141.
[12] DASGUPTA A, RAFTERY A E. Detecting features in spatial point processes with clutter via model-based clustering[J]. Journal of the American Statistical Association, 1998, 93(441): 294-302.
[13] LIAN Feng, HAN Chongzhao, LIU Weifeng. Estimating unknown clutter intensity for PHD filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 2066-2078.
[14] ROY L.Streit.Poisson Point Processes:Imaging,Tracking,and Sensing[M]. London,Springer US, 2010, 1:273-280.
[15] WAND M P,JONES M C.Kernel Smoothing[M]. London,New York, Springer US, 1994:1-222.
[16] SILVERMAN B W.Density Estimation for Statistics and Data Analysis[M]. US, Chapman and Hall, 1998:1-186.
[17] 夏婷, 谢维信, 陈富健. 基于核相关滤波器的颜色自适应目标跟踪算法[J]. 信号处理, 2020, 36(7): 1107-1117.
XIA Ting, XIE Weixin, CHEN Fujian. Color-adaptive object tracking algorithm based on kernel correlation filter[J]. Journal of Signal Processing, 2020, 36(7): 1107-1117.(in Chinese)
[18] NOSRATABADI H,MOHAMMADI M,KARGARIAN A.Nonparametric probabilistic unbalanced power flow with adaptive kernel density estimator[J]. IEEE Transactions on Smart Grid, 2018, 10(3): 3292-3300.
[19] SUN Jinping, LI Qing, ZHANG Xuwang, et al. An efficient implementation of track-oriented multiple hypothesis tracker using graphical model approaches[J]. Mathematical Problems in Engineering, 2017, 2017: 1-11.
[20] 盛涛, 夏海宝, 杨永建, 等. 密集杂波环境下的简化JPDA多目标跟踪算法[J]. 信号处理, 2020, 36(8): 1280-1287.
SHENG Tao, XIA Haibao, YANG Yongjian, et al. A simplified JPDA multi-target tracking algorithm for dense clutter environment[J]. Journal of Signal Processing, 2020, 36(8): 1280-1287.(in Chinese)
[21] 孙进平, 付福其, 付锦斌, 等. 应用超图匹配的多假设群目标跟踪方法[J]. 信号处理, 2017, 33(11): 1497-1504.
SUN Jinping, FU Fuqi, FU Jinbin, et al. Multiple hypothesis group target tracking using hypergraph matching[J]. Journal of Signal Processing, 2017, 33(11): 1497-1504.(in Chinese)
