1 引言
随着低可观测目标技术的快速发展和应用,对该类目标的高精度和远距离探测给传统相控阵雷达带来了巨大挑战。为了弥补大孔径、高功率相控阵雷达制造成本高昂、机动性差的缺点,多输入多输出(Multiple-input Multiple-output, MIMO)雷达作为一种新体制雷达,被提出以来就受到了研究人员的广泛关注。分布式MIMO雷达系统具有单元雷达成本低、易实现等优点,在预警探测中通过多节点雷达回波信号的相参积累,可大幅提高系统的预警能力[1-2]。
美国麻省理工学院林肯实验室率先开展了MIMO雷达的理论研究、性能分析和试验验证等工作[3- 4]。MIMO雷达不同于传统相控阵雷达的显著特点是不同单元雷达采用波形分集技术,发射正交信号。借助正交波形回波的可分离特点,各单元雷达进行时延差和相位差补偿操作,可实现信号级相参积累合成。利用幅度和相位信息的多通道相参积累操作可显著提高目标回波信噪比(Signal to Noise Ratio, SNR),达到提高雷达系统威力的目的。但分布式MIMO雷达系统中,各单元雷达分布放置,单元雷达间的同步误差、基线长短、相参参数估计都会导致信号的相位差异,严重影响回波信号的相参积累性能[5]。
为此,针对分布式MIMO雷达,现有文献从同步误差分析、基线选择、相参参数估计等方面开展了较多研究。同步误差方面,文献[6]、[7]采用频率步进信号,分析了时间同步误差对系统相参性能的影响。文献[8]借助外部设备惯性导航系统(Inertial Navigation System,INS),利用MIMO直达波估计了各单元雷达的时间同步误差、位置误差和本振初相,但相位估计精度和稳定度均需要较高SNR为前提。基线选择方面,文献[9]从回波相关、信号相参等方面给出了雷达基线选择准则,提供了单元雷达布站的理论指导。文献[10]从单元雷达位置对信号相参合成影响的角度出发,提出了保证信号相参合成性能约束下的单元雷达位置策略。相参参数估计方面,文献[11]、[12]在考虑时延差异和相位同步误差下,推导了MIMO雷达相参参数估计的克拉美罗界,然而并未给出相关的估计方法。文献[6]基于正交信号分析了静止目标相参参数估计问题,利用匹配滤波的相关接收技术,从峰值处提取回波时延和相位进行相参参数估计,并推导了相关的克拉美罗界,但在低信噪比下,该方法并不适用。文献[13]在非理想正交信号互相关能量泄露情形下,提出了基于信号重建的相参参数估计方法,然而该方法信号处理过程复杂,计算复杂度较高。文献[14]进一步研究了动目标场景下双基地MIMO雷达相参合成问题。文献[15]针对滤波器网格失配问题,利用搜索和稀疏傅里叶变换技术估计了目标参数,文献[16]研究了OFDM-MIMO雷达运动目标回波相参积累方法,但均忽略了时间和相位同步误差等影响因素。
不同于上述研究,本文针对分布式MIMO雷达预警探测中的回波积累问题,将分布式MIMO多节点回波相位补偿问题看作对优化问题的求解,构建了基于信息熵的积累代价函数,实现了回波能量的相参积累。具体地,由于实际分布式MIMO雷达工作时,各单元雷达在同步误差影响下,回波信号会携带有不同发射节点通道的附加相位,此外,采用的OFDM-LFM信号因为单元发射雷达间的步进频不同,也会导致相位差异。为此,本文提出的基于信息熵的回波相位补偿与相参积累方法,首先对距离对齐后的回波数据进行频移操作,然后通过回波数据相参积累后的信息熵值,调整补偿各节点回波的相位差异,进而得到多节点回波的相参积累结果。最后,仿真实验结果验证了本文相位补偿和相参积累方法的有效性。
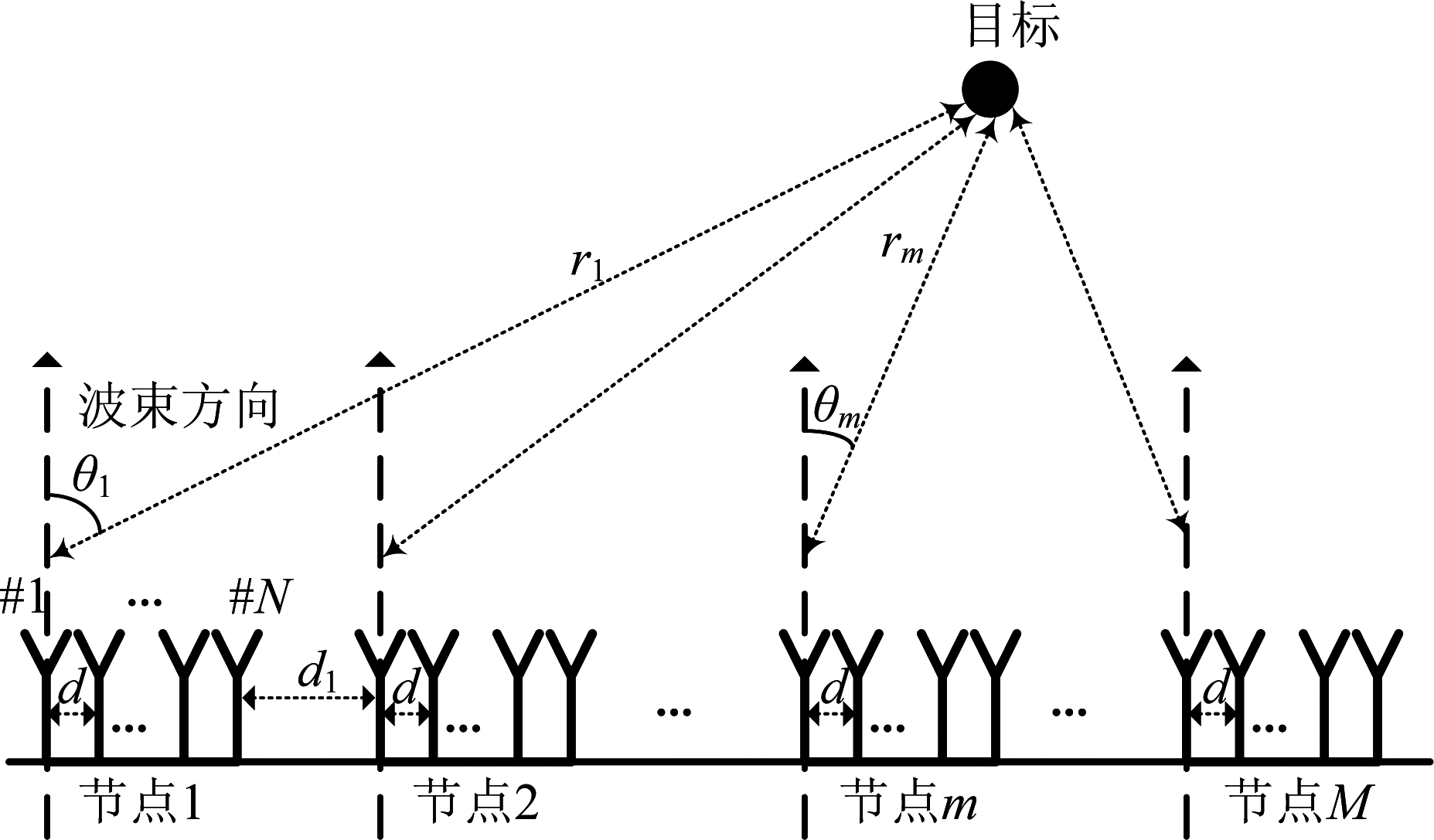
图1 系统模型
Fig.1 System model
2 信号模型
2.1 发射信号
假设分布式MIMO雷达系统有M个发射节点,L个接收节点(M=L收发共用),单个节点为具有N个阵元的相控阵雷达,第m个节点的发射信号为um(t),不同节点的发射波形相互正交,各雷达节点分布在一条直线,节点m和节点m+1的间距为dm。
发射信号采用正交多载频线性调频信号,第m个节点发射的单脉冲信号sm(t)可写为
(1)
其中,t表示快时间,(·)H表示共轭转置,wm,t=[ej2πφm,1,ej2πφm,2,...,ej2πφm,N]T为第m个发射节点的阵元相位加权矢量,(·)T表示转置,φm,n表示第m个节点第n个阵元的相位加权值。Am,t=[a1(θm),a2(θm),...,aN(θm)]T为第m个发射节点的发射导向矢量,an(θ)=ej2πndsin(θm)/λ,n=1,2,...,N,θm为第m发射节点的波束方向,d=λ/2表示阵元间距,节点内阵元等距排列。um(t)表示第m个节点的发射信号
(2)
其中,rect(·)为矩形脉冲调制函数,表示为
(3)
其中, fm为第m个发射节点发射信号的载频, fm=f0+(m-1)·Δf, f0为初始载频,Δf为频率间隔,μ=B/T为线性调频信号的调频斜率,B为信号的带宽,T为脉宽长度。φm为第m发射节点的附加通道相位,由同步误差造成。
2.2 回波信号
针对单个点目标,第m个发射节点发射的信号经过目标反射后,第l个节点接收的回波可以写为
(4)
其中,γl,m为m发l收路径下的目标雷达散射面积(Radar Cross Section,RCS)值,wl,r=[ej2πφ1,ej2πφ2,...,ej2πφN]T为第l个接收节点的阵元相位加权矢量,Al,r=[β1(θl),β2(θl),...,βN(θl)]T为第l个接收节点的接收导向矢量,βn(θl)=ej2πndsin(θl)/λ,n=1,2,...,N,θl为第l接收节点的波束方向。nl,m为该收发路径下的高斯白噪声。τl,m=(Rl+Rm)/c表示m节点发,l节点收路径的时延。
同理,第l个节点同时也会接收其他节点的回波信号,即
(5)
其中,为简化幅度表示,记
针对式(5),下变频处理后,快时间进行傅里叶变换操作,在频域的表达式为
P1(f-(m-1)Δf)+Nl,m]
(6)
其中,
m=1,2,...,M
(7)
FFT(·)表示快速傅里叶变换;将m=1带入式(7)即可得到式(6)中的P1( f ),P1( f )表示基带发射线性调频信号的傅里叶变换,Pm( f )表示步进频系数为m时的发射信号的傅里叶变换;Nl,m表示经过傅里叶变换的频域高斯白噪声。
观察式(6)可知,在时域上混合的信号,在频域上可以利用发射信号的正交性进行分离。以分离发射节点m的回波为例,式(6)乘以频域脉冲压缩系数
表示取共轭操作,得到
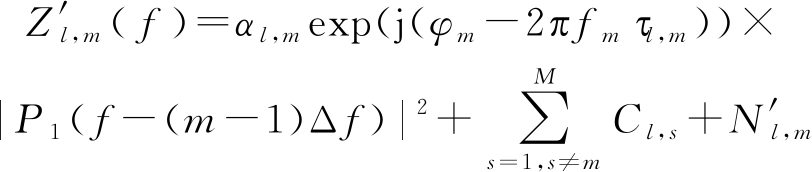
(8)
Cl,s表示频域匹配滤波过程中,第s节点的发射信号与Pm( f )产生的交叉项,
表示经过匹配滤波后的高斯白噪声。耦合回波经过分离,可以得到L×M路观测回波。
将式(8)进行傅里叶逆变换,时域表达式为
sinc(πB(t-τl,m))exp(j 2πt(m-1)Δf)+
(9)
其中,sinc(x)=sin(x)/x,cl,s为交叉项的时域表达形式,
为高斯白噪声。
3 基于信息熵的相位补偿与信号积累
观察式(9)可知,不同节点回波信号相参积累的困难在于以下两点的不同:1)包络未对齐,由于回波的空间路径不同造成;2)回波间相位的差异:步进频不同导致的快时间相位差异、时延不同和节点通道附加相位造成的慢时间相位差异。为了利用信息熵函数完成相位补偿,首先进行多节点回波信号距离对齐和频移操作的预处理步骤,然后针对回波信号构建信息熵函数,利用得到的估计相位,补偿回波间的相位差异,完成多节点回波信号的相参积累输出。
3.1 回波预处理
距离对齐:借助外部设备信息,例如导航卫星等,可以实现回波间的距离对齐[17-18]。以m发l收路径的时延为参考,a收b发路径下的回波
经过包络对齐表示为
sinc(πB(t-τl,m))exp(j 2πt(b-1)Δf)+
(10)
观察式(10)可知,a收b发路径下的回波经过距离对齐后,其回波包络位置与m发l收路径的回波包络位置相同,然而,回波信号间仍存在相位差异。
频移操作:节点间的快时间相位差异,可以通过频移操作消除。耦合回波经过信号分离操作时,其步进频通过对应的匹配滤波器确定,因此利用匹配滤波的信息在频域进行频移操作完成不同节点间快时间相位的调整。式(10)的快时间相位对齐过程表示为
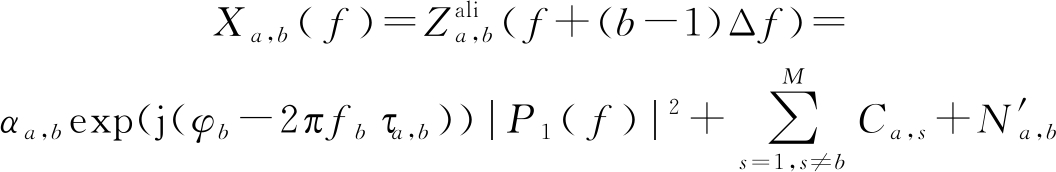
(11)
其中,
表示距离对齐后回波的快时间傅里叶变换形式,将(11)进行傅里叶逆变换,可得频移操作后的时域表达式为
xa,b(t)=αa,bexp(j(φb-2πfbτa,b))×
(12)
观察式(12)可知,距离对齐后的回波存在时延相位和通道附加相位的不同,注意到此时不同节点间的相位差异表现为常数相位项的不同。
3.2 信息熵代价函数建立
回波间的时延相位受限于外部定位信息精度和相位模糊问题,无法做到精确补偿。此外,不同节点间的通道附加相位由硬件造成,误差随机产生,不存在相关性,因此是难以解决的。受逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)图像相位补偿技术启发[19-20],本文利用回波相参积累后的熵函数特性,对回波间的常数相位项差异进行补偿。
为了便于分析,将式(12)离散化,离散形式写作
xa,b(k)=αa,bexp(j(φb-2πfbτa,b))×
sinc(πB(k·Δt-τl,m))+
(13)
其中,k表示快时间采样索引,K表示快时间采样点数,Δt=1/(2fs)。
将快时间离散回波表示为向量形式
可得
(14)
将L×M路回波数据拼接,构建离散回波矩阵
(15)
其中,H=L×M。
不同节点的回波数据能够相参积累,实质是可以同相叠加。同时调整不同节点的回波相位,消除相位差异,进行累加可得
(16)
其中,
为累加后的行向量,h表示行索引,k表示列索引,G(h,k)是矩阵G第h行第k列的元素,φ(h)是将要求解的未知补偿相位。
|g(k)|2的信息熵被定义为
(17)
其中,S为常数,定义为
(18)
式(17)又可以写为
(19)
忽略常数S,式(19)可以写为
(20)
因此,多节点回波的相位补偿,可以转化为对目标函数(20)极值点的求解。
3.3 补偿相位优化问题求解
φ(m)使得E′取极值时,满足
=0
(21)
E′的一阶导可以表示为
(22)
又因为|g(k)|2=g(k)g*(k)
(23)
将式(23)带入到(22)中,可以得到
(24)
可以通过式(16)得到,并且注意到φ(h)之间是相互独立的,即有
=jG(h,k)exp[jφ(h)]
(25)
结合式(24)、(25)可以得到
=2Im{exp[jφ(h)]ψ*(h)}
(26)
其中,
(27)
式(26)带入到(21),可以得到
φ(h)=Jπ+angle(ψ(h))
(28)
其中,J可以取任意整数,angle(·)表示取角操作。
通过对补偿相位的求解,各节点回波对应的补偿相位表示为φ★(h),补偿后的回波经过累加,得到最终多节点回波的相参积累结果
g★
(29)
相参积累后得到的回波(29),通过雷达目标检测算法验证所提方法性能[21]。
4 仿真验证与分析
为了验证本文所提出的积累方法的有效性,进行仿真实验与分析。考虑分布式MIMO雷达系统节点数为4,4个节点雷达同时发射、同时接收,发射波形为OFDM-LFM信号,雷达仿真参数如表1所示。
表1 雷达参数
Tab.1 Radar parameters
参数参数值中心频率/MHz5000信号带宽/MHz1步进频率/MHz1采样率/MHz8脉宽/μs100
4节点到目标的距离依次为R1=8438 m、R2=5625 m、R3=3000 m、R4=1875 m,角度依次为θ1=100、θ2=150、θ3=290、θ4=510。c=3.0×108 m /s为电磁波传播速度,单节点通道回波信号脉压前SNR为0 dB,节点通道相位误差在00到3600内随机产生。
图2给出了匹配滤波后,节点1接收到的4路回波信号处理结果,图3给出了节点1接收到的4路回波信号距离对齐后的结果,可以看出节点1回波信号的距离均已对齐。
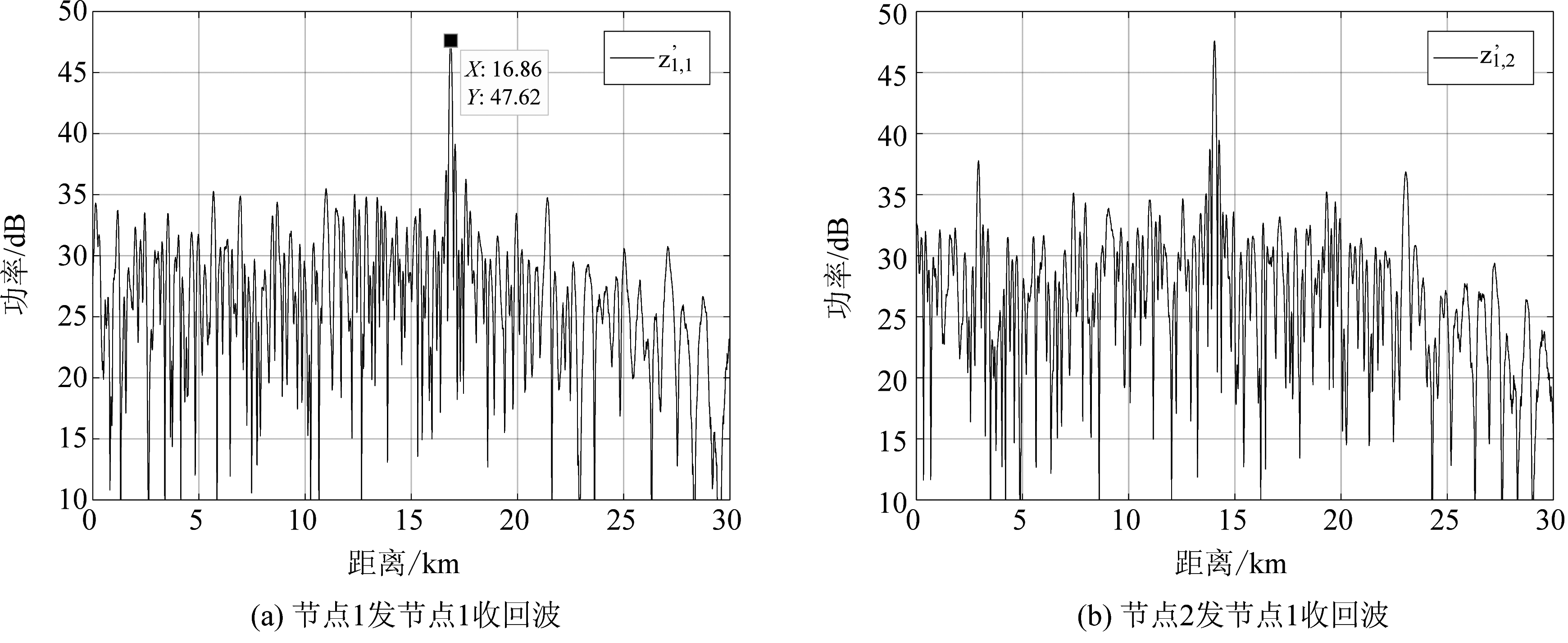
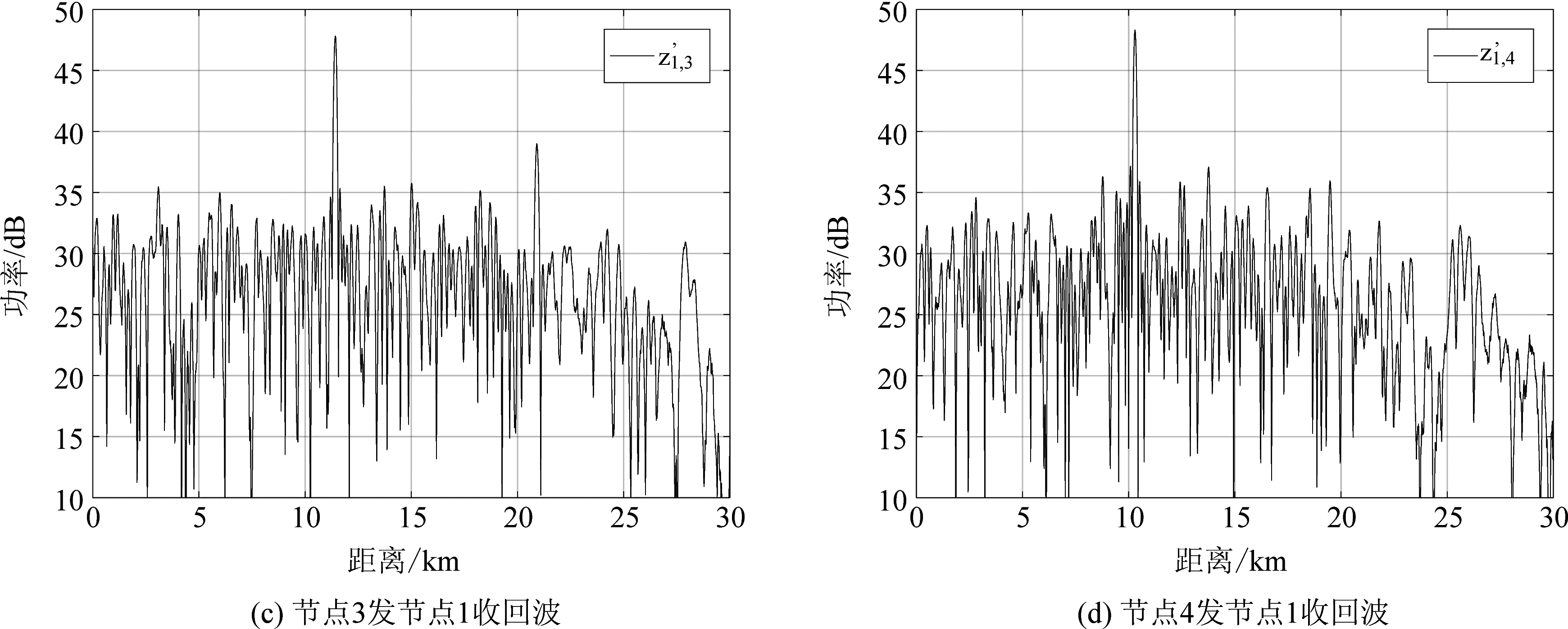
图2 节点1回波分离结果
Fig.2 Echo separation results of 1st node
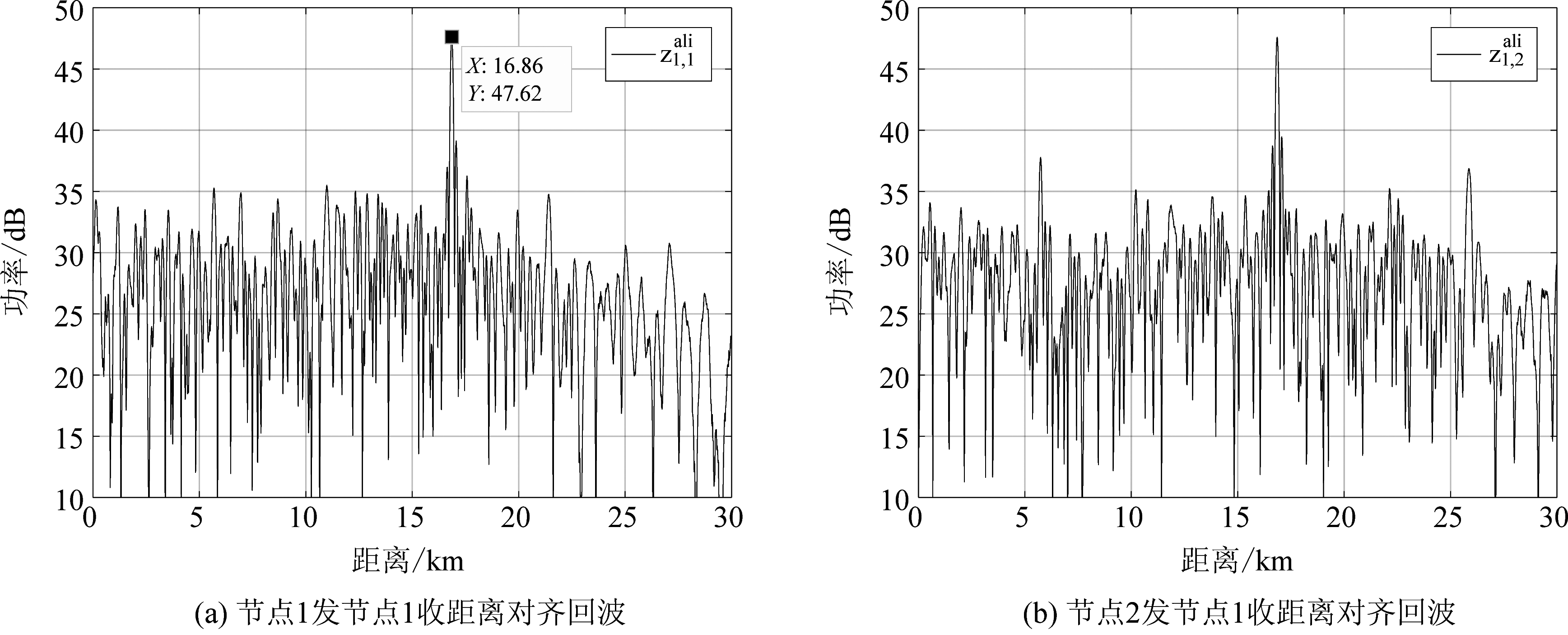
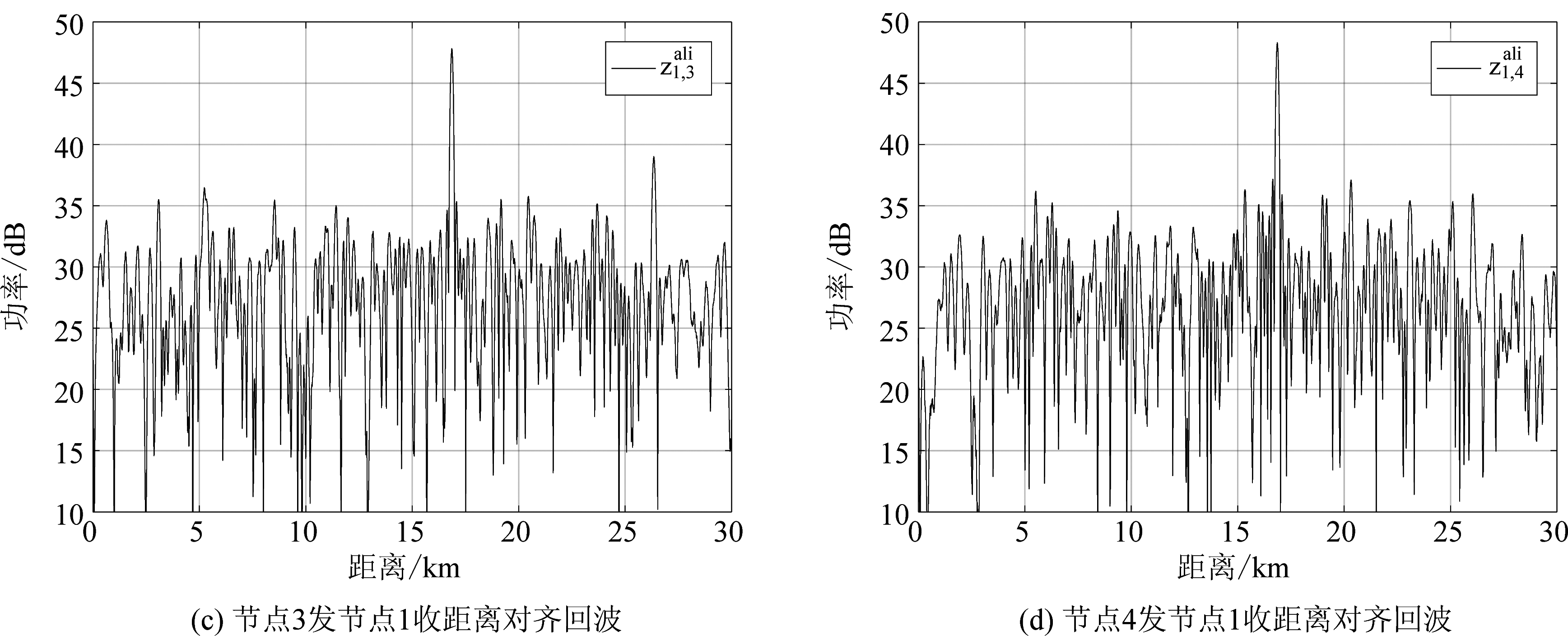
图3 节点1回波距离对齐结果
Fig.3 Echo range alignment result of 1st node
距离对齐后,为了实现信号的相参积累,本文方法利用信息熵估计对齐后各路信号的相位差异,进而补偿相位差异。利用式(12)和上述的仿真参数,可以计算出节点1接收的不同发射节点的回波峰值相位,注意到分布式MIMO雷达间的距离差异会引起相位出现相位模糊问题,表2给出了节点1补偿前4路回波峰值的真实相位值(真实值)和真实相位对2π取余后的相位值(补偿前),以及补偿后的相位(补偿后)。从表中可以看到距离对齐后,节点1接收的不同发射节点回波峰值相位不同,无法进行同相叠加,经过基于熵函数的相位补偿方法处理后,回波的峰值相位达到同相,能够进行相参积累。图4给出了节点1内分离出的4路回波信号相参积累结果,峰值功率提升了11.79 dB,与理论值20log10(4)≈12.04 dB一致。
表2 相位参数
Tab.2 Phase parameters
峰值相位1发1收2发1收3发1收4发1收真实值-63674940.000-59299447.500-55822290.000-54707841.000补偿前60.000112.50030.000279.000补偿后63.89064.03063.82063.970
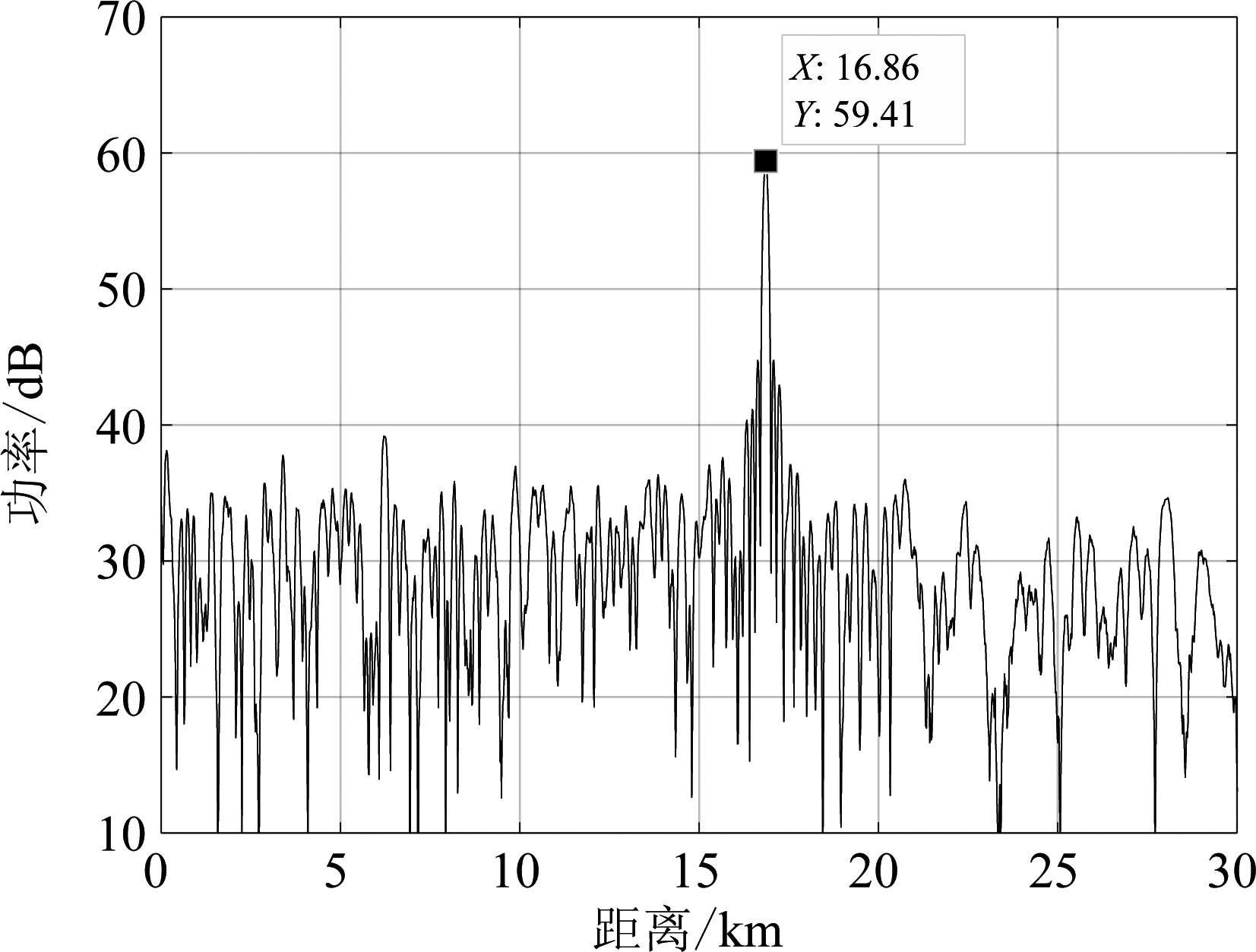
图4 节点1内4路回波相参积累结果
Fig.4 Coherent integration result of the 1st node
4发4收场景下,匹配处理后共获得16路回波信号,相参积累后峰值功率增益的理论值为
20log10(M·L)=20log10(16)=24.08 dB
(30)
利用所提方法,图5给出了16路回波信号相参积累后的结果,比较积累前后的仿真结果可以看出,在当前信噪比下,利用所提方法回波信号峰值功率提升了23.75 dB,与理论值24.08 dB相符合。
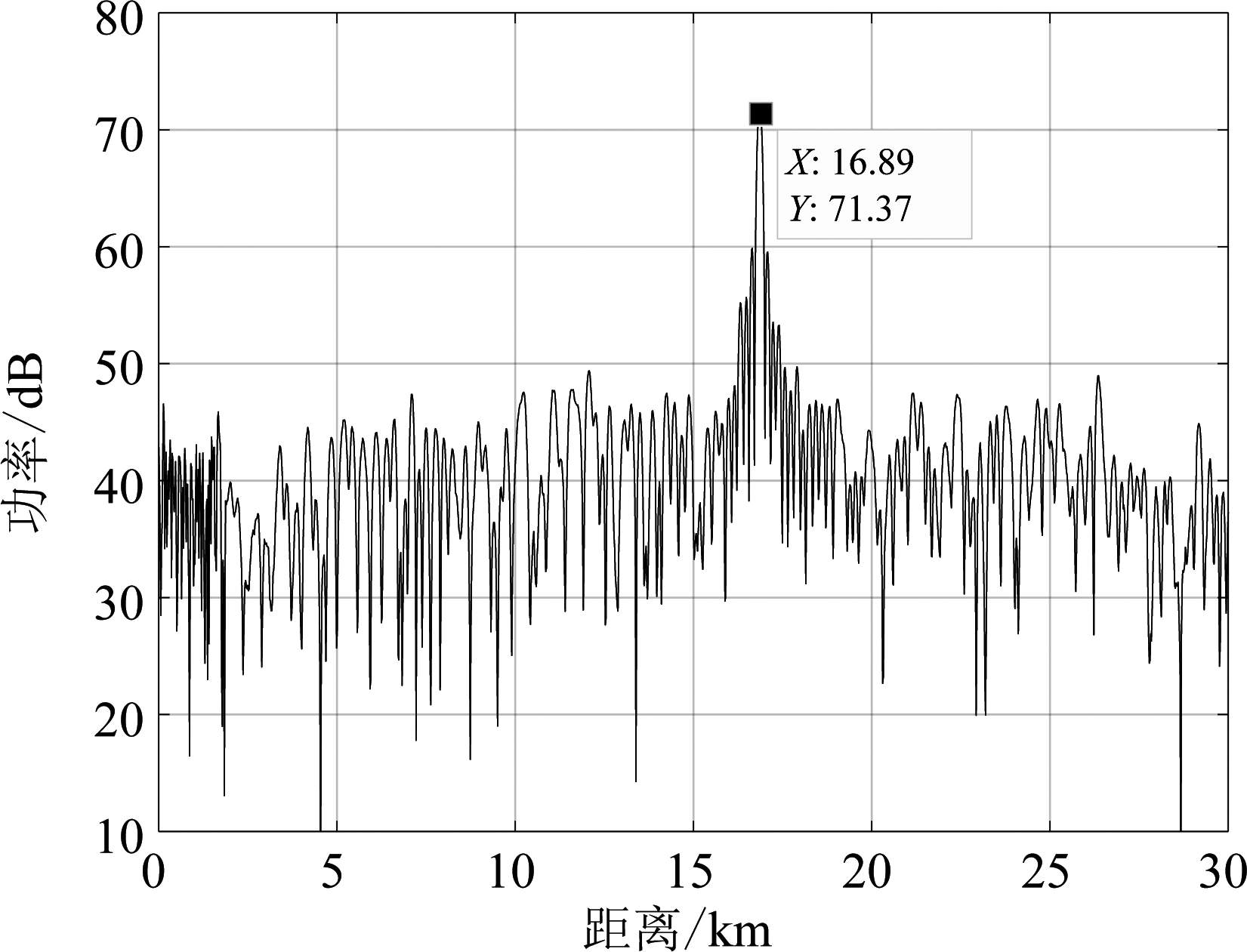
图5 相参积累结果
Fig.5 Coherent integration result
相位的补偿精度在很大程度上影响了回波信号的相参积累性能,文献[22]指出相参参数的精确估计是实现系统良好相参性能的前提和核心,并采用互相关法给出了参数的估计性能。图6给出了脉压前SNR在-40 dB到0 dB时,利用本文方法和互相关方法对补偿相位进行估计时的均方根误差曲线,从仿真结果可以看出:1)当输入信噪比高于-30 dB时,随着SNR的增大,本文方法的估计性能逐渐提升;2)当脉压前输入SNR高于-15 dB时,本文方法的相位估计误差接近于0,此时可获得较好的相位估计精度;3)在-40 dB到0 dB范围内,本文方法的估计误差都小于互相关法。表明所提方法具有比互相关更好的相位估计精度。
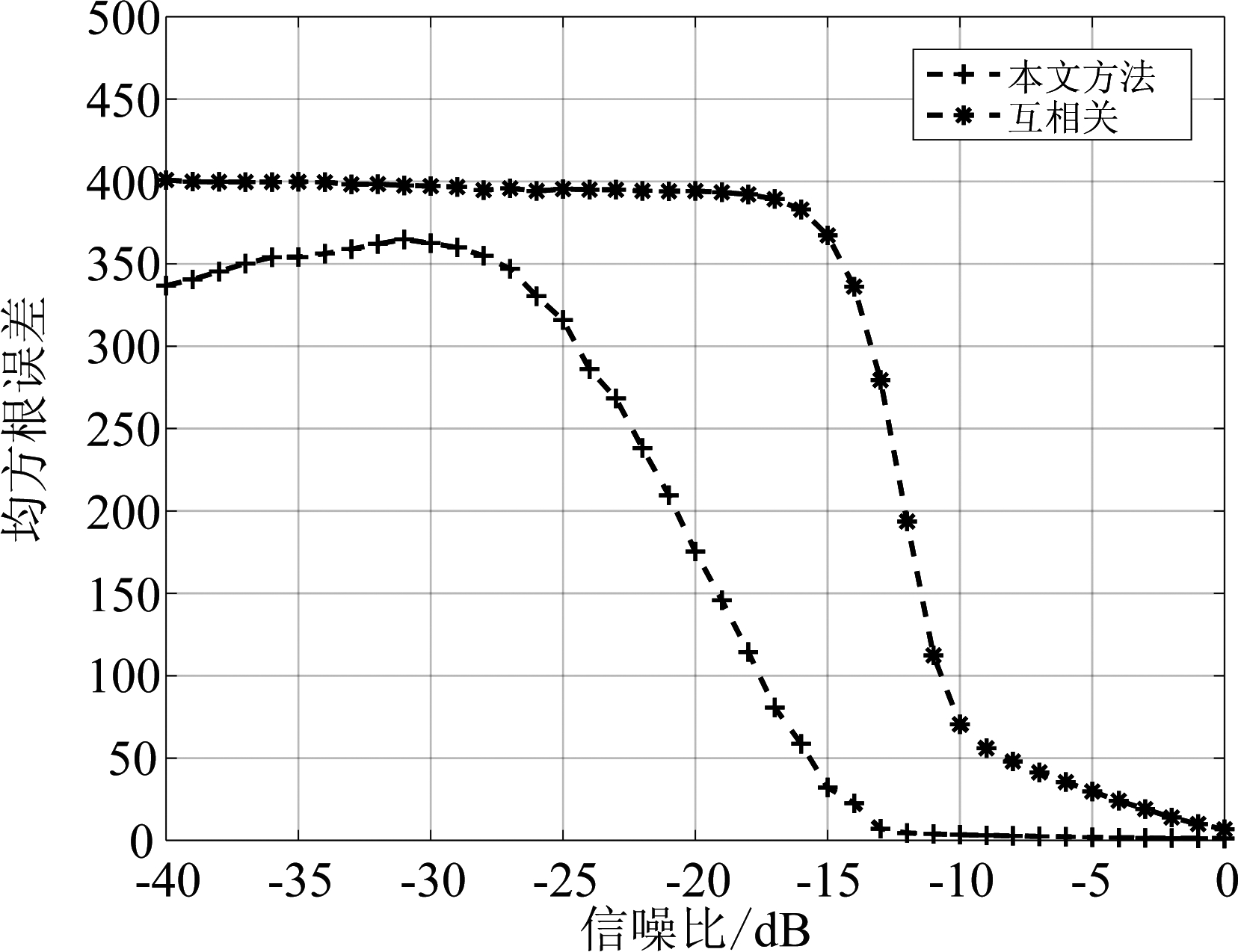
图6 不同信噪比下相位估计的均方根误差
Fig.6 Root mean square error of phase estimation in different SNR
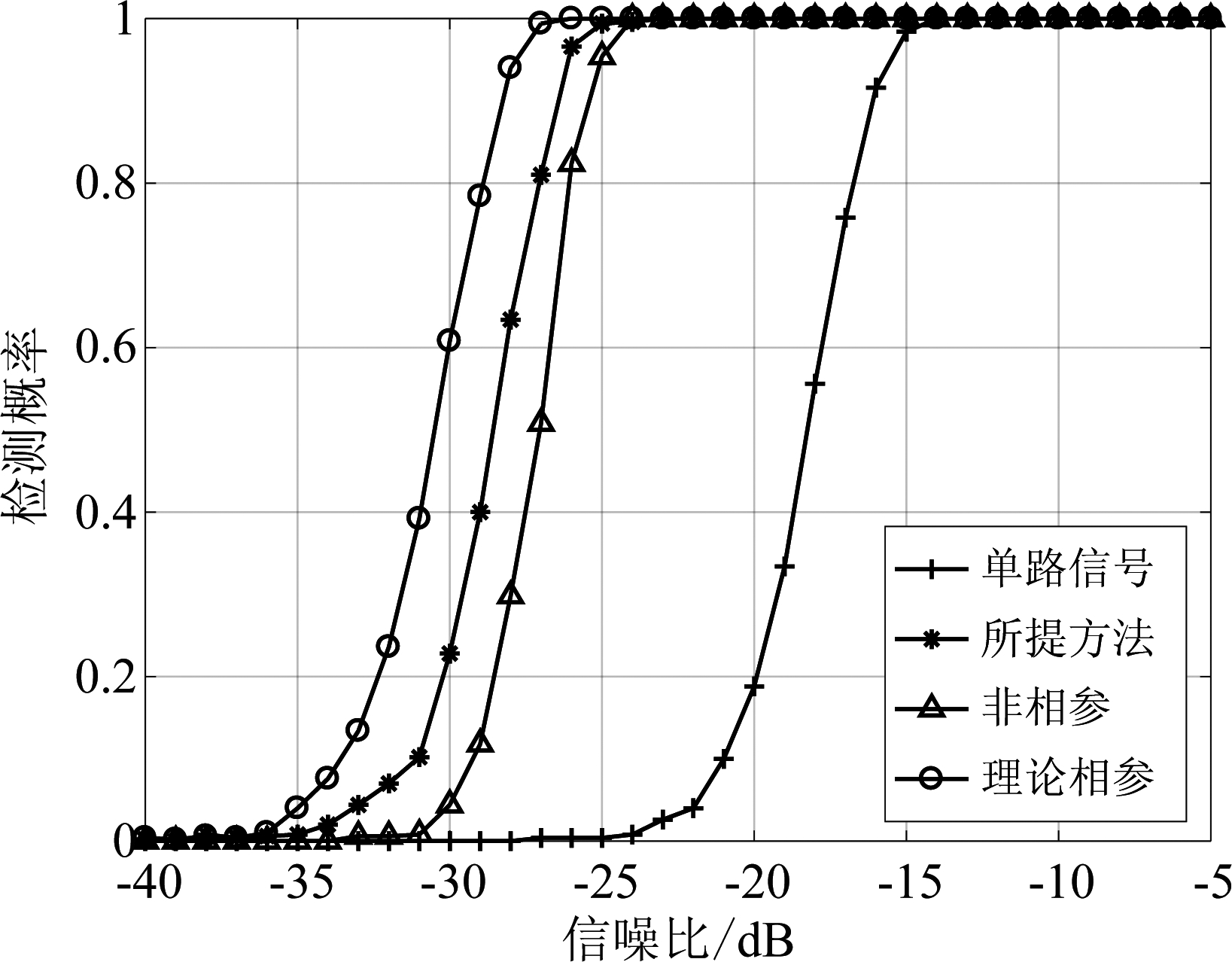
图7 4节点下不同检测方法的检测概率性能对比
Fig.7 Detection probability comparsion of different methods for 4 nodes
图7给出了单路信号、非相参积累、所提积累方法和理论相参积累的检测性能曲线,虚警概率为10-3,脉压前输入SNR范围为-40 dB到-5 dB,从图中可以看出,本文所提相参积累方法的检测性能要优于单路信号检测方法以及多路信号非相参积累方法。例如,当检测概率为0.8时,本文方法所需SNR分别比单独信号检测方法以及多路信号非相参积累方法低10.0 dB、1.5 dB。
图8给出了不同雷达节点个数下,本文方法的积累检测性能曲线。可以看出:1)随着节点个数的增加,本文方法的积累检测性能也在逐步提升;2)相比于节点数为3时,节点数为4、5、6、7、8时,本文方法提出的积累检测性能分别提升1.5 dB、3.0 dB、5.0 dB、6.0 dB、7.0 dB。
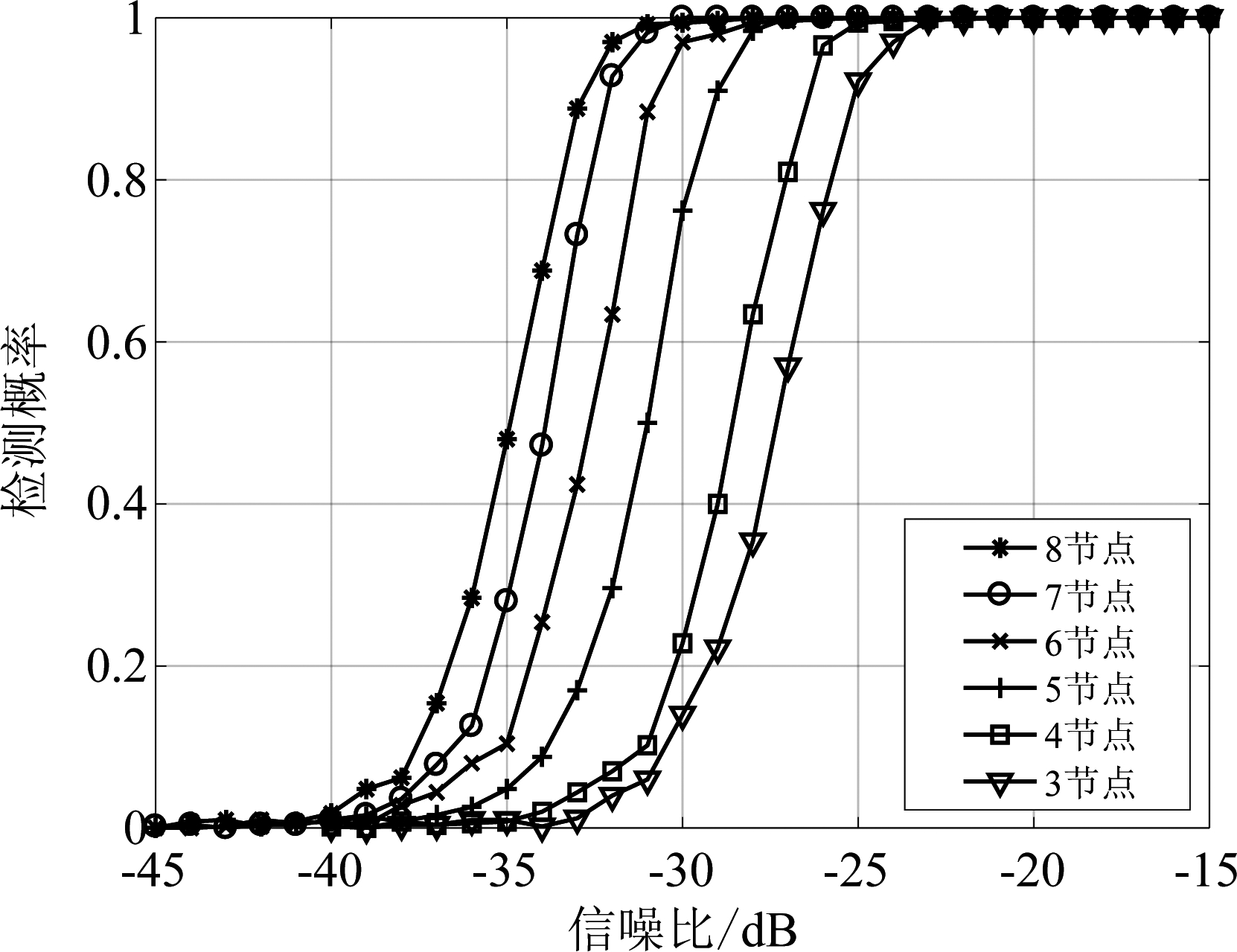
图8 不同节点下所提方法的检测概率性能
Fig.8 Detection probability of the proposed method for different node numbers
5 结论
本文提出了一种基于熵的分布式MIMO雷达回波信号相位补偿和相参积累方法。首先利用匹配滤波分离耦合信号,然后针对距离对齐回波构建熵函数,推导了补偿相位的表达式,对回波相位差异进行了补偿,得到了多路回波的相参积累结果,数值仿真验证了所提方法的检测性能优于单路信号和非相参积累的检测性能。但本文的结论是在高斯白噪声和单脉冲条件下针对单目标给出的,后续工作可以考虑杂波背景或者多目标运动目标场景。
[1] 陈小龙, 黄勇, 关键, 等. MIMO雷达微弱目标长时积累技术综述[J]. 信号处理, 2020, 36(12): 1947-1964.
CHEN Xiaolong, HUANG Yong, GUAN Jian, et al. Review of long-time integration techniques for weak targets using MIMO radar[J]. Journal of Signal Processing, 2020, 36(12): 1947-1964.(in Chinese)
[2] 周宝亮, 雷子健, 周东明, 等. 分布式孔径相参雷达预警探测技术[J]. 信号处理, 2018, 34(11): 1330-1338.
ZHOU Baoliang, LEI Zijian, ZHOU Dongming, et al. Early-warning detection technology of distributed aperture coherent radar[J]. Journal of Signal Processing, 2018, 34(11): 1330-1338.(in Chinese)
[3] AHLGREN G W. Next generation radar concept definition team final report[R]. MIT Lincoln Laboratory, 2003.
[4] CUOMO K M, COUTTS S D, MCHARG J C, et al. Wideband aperture coherence processing for next generation radar (NexGen)[R]. Defense Technical Information Center, 2004.
[5] 袁海锋, 江朝抒. OFDM-MIMO雷达体制的多径抑制性能分析[J]. 信号处理, 2012, 28(7): 1000-1005.
YUAN Haifeng, JIANG Chaoshu. Performance of OFDM-MIMO radar for mulpath suppression[J]. Signal Processing, 2012, 28(7): 1000-1005.(in Chinese)
[6] ZENG Tao, YIN Pilei, LIU Quanhua. Wideband distributed coherent aperture radar based on stepped frequency signal: Theory and experimental results[J]. IET Radar, Sonar & Navigation, 2016, 10(4): 672- 688.
[7] 殷丕磊,闫路,张宗傲,等. 基于频率步进的宽带分布式全相参雷达[J].北京理工大学学报,2016,36(7):749-754.
YIN Pilei, YAN Lu, ZHANG Zongao, et al. Wideband distributed coherent aperture radar based on step frequency signal[J].Transaction of Beijing Institute of Technology,2016,36(7):749-754.(in Chinese)
[8] 刘晓瑜, 王彤, 吴建新, 等. 基于MIMO直达波的无人机分布式相参雷达相位同步方法[J]. 系统工程与电子技术, 2020, 42(5): 1014-1025.
LIU Xiaoyu, WANG Tong, WU Jianxin, et al. Phase synchronization method based on MIMO direct path wave for UAV distributed coherent aperture radar[J]. Systems Engineering and Electronics, 2020, 42(5): 1014-1025.(in Chinese)
[9] 周宝亮, 高红卫, 文树梁, 等. 分布式相参雷达基线选择与标定误差分析[J]. 系统工程与电子技术, 2018, 40(11): 2438-2443.
ZHOU Baoliang, GAO Hongwei, WEN Shuliang, et al. Distributed coherent radar baseline selection and calibration error analysis[J]. Systems Engineering and Electronics, 2018, 40(11): 2438-2443.(in Chinese)
[10] 刘兴华, 徐振海, 肖顺平. 分布式相参雷达几何布置约束条件[J]. 系统工程与电子技术, 2017, 39(8): 1723-1731.
LIU Xinghua, XU Zhenhai, XIAO Shunping. Geometric arrangement constraints of distributed coherent aperture radar[J]. Systems Engineering and Electronics, 2017, 39(8): 1723-1731.(in Chinese)
[11] SUN Palin, TANG Jun, HE Qian, et al. Cramer-Rao bound of parameters estimation and coherence performance for next generation radar[J]. IET Radar, Sonar & Navigation, 2013, 7(5): 553-567.
[12] TANG Xiaowei, TANG Jun, HE Qian, et al. Cramer-Rao bounds and coherence performance analysis for next generation radar with pulse trains[J]. Sensors (Basel, Switzerland), 2013, 13(4): 5347-5367.
[13] 刘兴华, 徐振海, 王罗胜斌, 等. 基于信号重建的分布式相参雷达相参参数估计算法[J]. 系统工程与电子技术, 2018, 40(9): 1931-1938.
LIU Xinghua, XU Zhenhai, WANG Luoshengbin, et al. Coherent parameters estimation algorithm for distributed coherent aperture radar based on signal reconstruction[J]. Systems Engineering and Electronics, 2018, 40(9): 1931-1938.(in Chinese)
[14] LIU Xinghua, XU Zhenhai, WANG Luoshengbin, et al. Dual-radar coherently combining: Generalised paradigm and verification example[J]. IET Radar, Sonar & Navigation, 2019, 13(5): 689- 699.
[15] 陈金铭, 王彤, 吴建新, 等. 基于滤波器网格失配的分布式相参雷达目标参数估计方法[J]. 系统工程与电子技术, 2019, 41(11): 2460-2470.
CHEN Jinming, WANG Tong, WU Jianxin, et al. Target parameter estimation method for distributed coherent aperture radar based on grid mismatch filtering[J]. Systems Engineering and Electronics, 2019, 41(11): 2460-2470.(in Chinese)
[16] 刘京然, 王星, 王党卫. OFDM-MIMO雷达运动目标回波相参积累方法[J]. 现代雷达, 2014, 36(12): 43- 47,53.
LIU Jingran, WANG Xing, WANG Dangwei. Conherent integral mehod of the movement-target echoes of OFDM-MIMO radar[J]. Modern Radar, 2014, 36(12): 43- 47,53.(in Chinese)
[17] 杨生, 孙付平, 陈坡, 等. 基于惯导/天文高精度定姿方法[J]. 测绘科学技术学报, 2009, 26(2): 82- 85.
YANG Sheng, SUN Fuping, CHEN Po, et al. Precise attitude determination based on INS/CNS[J]. Journal of Geomatics Science and Technology, 2009, 26(2): 82- 85.(in Chinese)
[18] 吴志华. 基于星敏感器/陀螺组合定姿系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
WU Zhihua. Research on attitude detemination based on star sensor/gyro integrated system[D]. Harbin: Harbin Institute of Technology, 2011.(in Chinese)
[19] WANG J, LIU X, ZHOU Z. Minimum-entropy phase adjustment for ISAR[J]. IET Radar, Sonar and Navigation, 2004, 151(4):203-209.
[20] USTUN D, TOKTAS A. Translational motion compensation for ISAR images through a multicriteria decision using surrogate-based optimization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 4365- 4374.
[21] 何友, 关键, 孟祥伟, 等. 雷达目标检测与恒虚警处理[M]. 2版. 北京: 清华大学出版社, 2011: 36- 40.
HE You, GUAN Jian, MENG Xiangwei, et al. Radar Target Detection and CFAR Processing[M]. 2nd ed. Beijing:Tsinghua University Press, 2011: 36-40.(in Chinese)
[22] 王雪琦, 涂刚毅, 吴少鹏. 分布式相参雷达多脉冲积累相参参数估计方法[J]. 太赫兹科学与电子信息学报, 2020, 18(6): 1003-1009.
WANG Xueqi, TU Gangyi, WU Shaopeng. Coherent parameters estimation method for distributed coherent radar based on multi-pulse accumulation[J]. Journal of Terahertz Science and Electronic Information Technology, 2020, 18(6): 1003-1009.(in Chinese)
