1 引言
随着我国国力和国际地位的不断增强,所面临的海洋争端和安全威胁日益严峻。此时,可靠的海面目标识别方法对探寻敌对目标战略意图、制定正确应对方案和进行先敌打击等环节都十分的重要。目前,高分辨宽带雷达技术已经广泛应用于目标识别领域,高分辨一维距离像(High Resolution Range Profile,HRRP)表征了散射中心沿雷达视线方向的分布情况,包含了目标的结构特征,而且因其易于获取和处理等优势,在雷达目标识别领域中有着重要作用[1]。
现有海面目标HRRP识别算法主要针对高信噪比条件进行设计,如基于t-分布概率主成分分析模型的目标识别算法[2],基于自适应进化粒子群和支持向量机的HRRP目标识别算法[3],基于卷积稀疏编码与多分类器融合的HRRP识别算法[4]等,信噪比(signal-to-noise ratio,SNR)变化时分类识别率的稳定性和鲁棒性难以保证,特别是低SNR条件下的识别正确率远远低于高SNR条件下的识别正确率。文献[5]提出了一种基于深度生成网络的HRRP数据生成方法,但该方法并没有考虑低SNR条件下HRRP识别正确率低的问题。
在对海远距离探测场景下,相比于近海杂波,远海杂波幅度起伏较为平坦,其影响可能低于接收机内部噪声[6],因此,对海远距离探测时主要需考虑噪声的不利影响。为此,本文主要研究了噪声影响下的海面目标识别问题。在卷积神经网络(convolutional neural network,CNN)的基础上,结合HRRP的特性,设计了一个包含降噪模块的分类识别模型,模型首先分析了HRRP图像和二维图像的相似特性,并从理论上分析了HRRP降噪和图像降噪的互通性。其次,利用深层次卷积层和批归一化(batch normalization,BN)层,增大网络感受域,提取深层次的噪声特征。此外,利用残差学习网络,减轻网络学习负担的同时重构图像,实现信噪比的提升。最后通过实验,在不同SNR条件下,对降噪模块的降噪性能和模型的分类识别能力进行分析,再对比CNN分类识别模型的识别能力,实验证明了该模型具有更良好的分类识别能力和鲁棒性。
2 基于去噪卷积神经网络的海面目标分类识别模型设计
CNN是深度学习的典型算法之一,是一种包括卷积运算的前馈神经网络,主要由输入层、卷积层、池化层、全连接层和输出层组成[7]。本文将在CNN结构上进行海面目标分类识别模型的设计。
2.1 模块框架设计
CNN的输入层可以处理多种维度的数据,根据数据维度的不同,CNN可以划分成一维、二维或三维。考虑到本文利用的是高分辨雷达的一维距离像进行海面目标的识别,鉴于距离像的一维特性,本文将模型输入层的维度设定为一维,并选用了一维卷积神经网络作为基本网络结构。本文设计的模型共分为三个模块,分别为一维降噪模块、特征降维提取模块以及全连接分类输出模块,模型框架如图1所示。
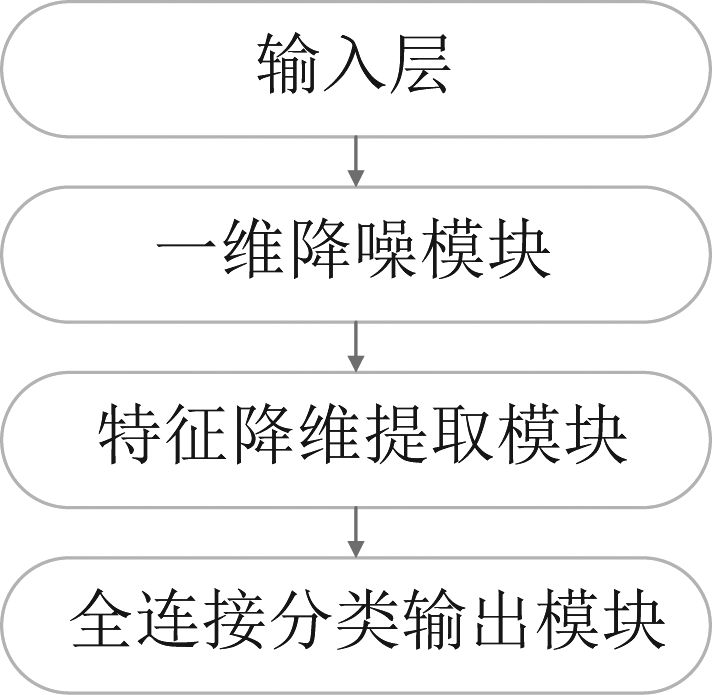
图1 模型框架结构图
Fig.1 Model frame structure diagram
2.2 降噪模块设计
HRRP在横轴上的物理意义是距离,在竖轴上的物理意义是散射点的强度。而一幅二维图像在XY轴上物理意义也是距离,在Z轴上的物理意义则是该像素点的灰度值,也可看成是一种强度单位。因此一维距离图像可以近似的看成是一副X轴维度为1的二维图像,从原理分析来看,HRRP可以当成二维图像进行降噪处理。因此,本节设计了一种基于去噪卷积神经网络(Denoising convolutional neural network,DnCNN)的降噪模块。
DnCNN是一种二维的卷积神经网络,由卷积层、BN层和激活函数组成,通常用于二维或者三维图像的降噪处理,相比于传统的信号降噪技术具有盲去噪和不需手动进行参数设计等优点[8]。本节根据HRRP的一维特性,降低了DnCNN网络的适应维度,将其网络中的卷积层从二维卷积层变换成一维卷积层,卷积核的维度也从二维降成一维。设计了一种适用于HRRP的一维降噪模块,降噪模块结构如图2所示。
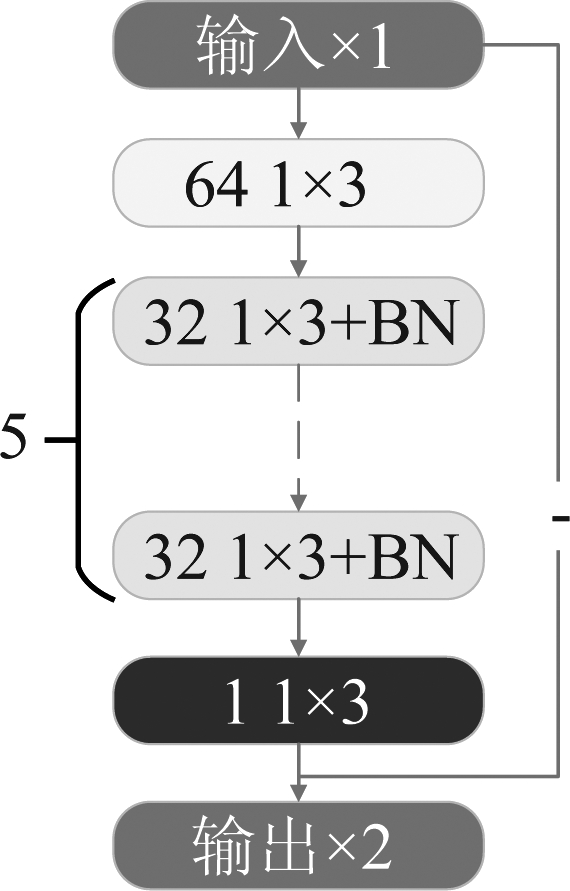
图2 降噪模块结构示意图
Fig.2 Structure diagram of noise reduction module
模块结构主要分为三部分,第一部分由一层卷积层构成,卷积核个数为64个,大小为1×3,激活函数选用RELU函数[9],该部分主要利用卷积层生成一定数量的特征图传递给下一部分。第二部分是整个模块的主体部分,该部分在卷积层和RELU之间添加了BN层,三者构成了一个标准化卷积层。标准化卷积层通过BN层对每层激活函数的输入值进行校正,将输入值拉回到均值为0方差为1的标准正态分布,以提升激活函数输出的灵敏性,解决内部协变量移位问题[10],从而加大了损失函数的梯度变化,避免了梯度消失的问题,提高识别精度。此外,根据网络降噪效果,该部分的网络深度设定为5层结构,卷积核个数32个,大小为1×3。第三部分为一个卷积层,卷积核个数为1,大小1×3,用于特征图重建。
由于降噪模块具有较深的层次结构,为了避免梯度消失问题,降噪模块在整体上采用了残差学习技术。残差学习是针对层数过深的网络所带来的退化问题而提出的一种减轻网络训练负担的学习技术[11]。残差网络通过支路直接将输入信息传递到输出,减少了信息传递过程中的损失。同时,因为输入信息的传递,学习目标由原本的输出变成了输入与输出之间的差值,降低了学习目标的难度,加大了反向传播过程中对参数的调整作用,避免了梯度消失的问题。此外,在残差学习过程中,要求两者相加减时的维度要相同,因此,本节利用zero padding方法来增加两者的维度,即对特征图进行补零操作,保证了在维度增加的同时也不会影响到学习的最终结果。
2.3 特征降维提取模块设计
卷积层是CNN特有的网络层结构,其功能是为了自动提取目标特征,主要参数有卷积核大小、步长以及填充。池化层是对卷积层提取的特征进行特征选择和信息过滤,常用的池化方法有均值池化和最大池化,分别是在池化区域内取均值或者最大值[12]。
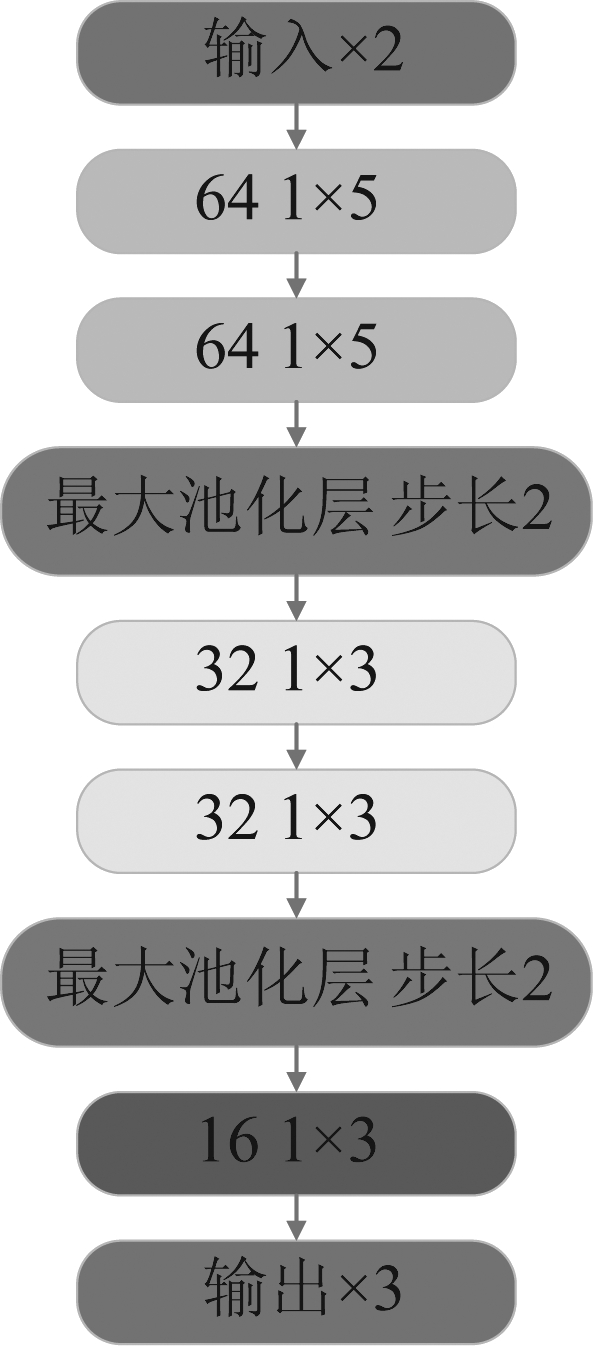
图3 特征降维提取模块结构示意图
Fig.3 Schematic diagram of feature reduction extraction module structure
本节将利用多层次卷积层进行特征提取,所用卷积层的步长均为1,填充方式为相同填充,即输入输出的维度相同。同时,利用最大池化层进行特征降维,剔除多余信息,保留有效信息。模块结构如图3所示,模块采取卷积层和池化层交替连接的方式,首先是两层卷积层,卷积核个数为64个,大小为1×5,其后接一层最大池化层,步长为2,使输出维度降为输入维度的1/2;之后,再接两层卷积层,卷积核个数为32个,大小为1×3,后面同样接一层步长为2的最大池化层进行特征降维;最后是一层卷积层,本层将卷积核的个数减少至16个,大小仍为1×3,因为如果本层卷积核个数过多,会形成大量的特征,不方便后面的特征拼接。这种结构设计可以使浅层次的卷积层运用较大的卷积核提取目标的大致轮廓特征,深层次的卷积层运用较小的卷积核提取深层次的细微特征。
2.4 全连接分类输出模块设计
全连接分类输出模块主要进行特征的拼接和类别输出,模块结构如图4所示。首先,利用FLatten函数将经过卷积层和池化层提取出来的特征拼接层一维数组;之后,连接两个神经元个数分别为200和5的全连接层,由于本文进行的是五类舰船目标的分类识别,故第二个全连接层的神经元个数设为5。最后,将第二个全连接层的输出和类别标签一同传送至中心损失函数和softmax分类器。
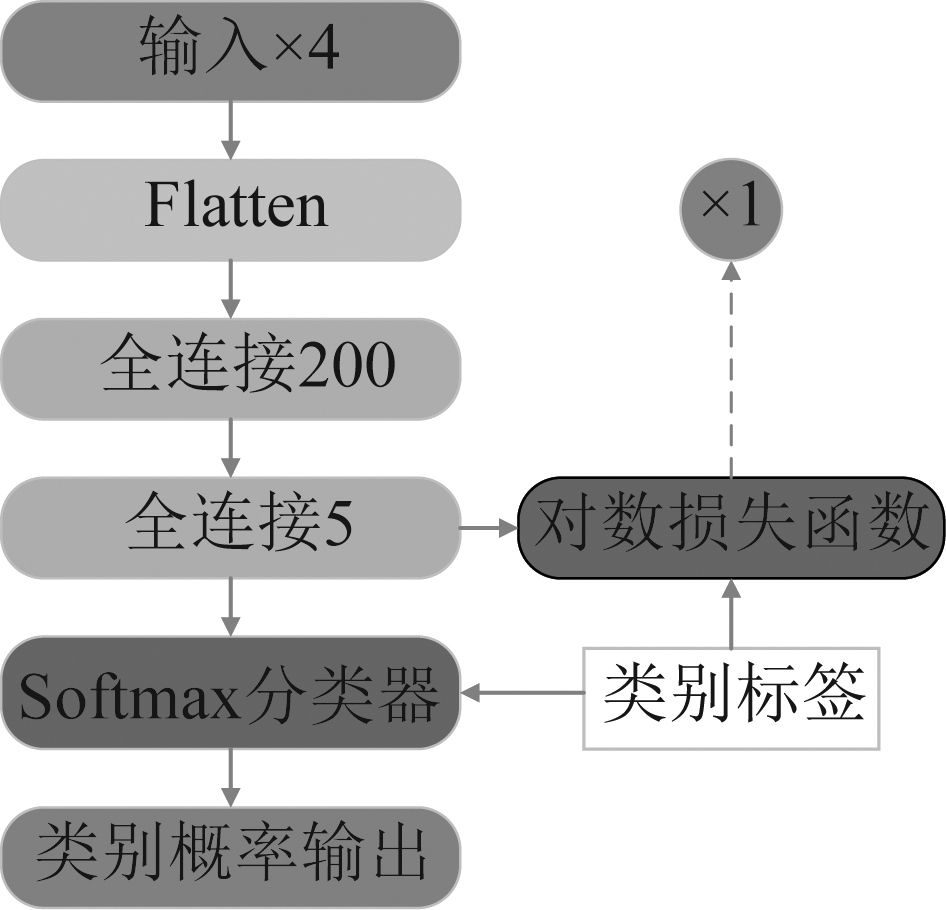
图4 全连接分类输出模块结构示意图
Fig.4 Structure diagram of fully connected classification output module
损失函数是正向传播的终点,也是反向传播的起点。在网络训练过程中,网络每轮训练都在不断地寻求中心损失函数最小化的方向,并回馈给整个网络,使得网络参数不断地向中心损失函数最小化的方向变化,直至中心损失函数收敛。由于本文是多分类问题,所以选取多分类对数损失作为中心损失函数,其分类交叉熵如式(1)[13]
(1)
式中,yi, j为目标真实类别,pi, j为预测类别。
而softmax分类器是将第二层全连接层的输出进行概率划分,分类器输出的结果就相当于每个样本被分到每个类别标签的概率分布,从而实现目标的分类识别[14]。类别概率的计算过程如式(2)
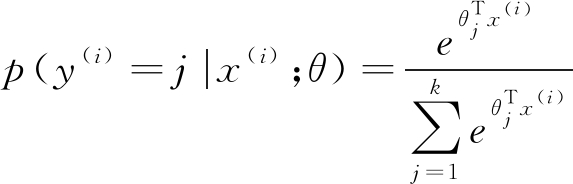
(2)
式中,p(y(i)=j|x(i);θ)表示在第i个样本输入为x(i)的条件下,分类器判别其属于第j类的概率,其中,T表示矩阵的转置,k表示总类别数,θ是分类器参数,θ通过dJ(θ)/θ=0求得,J(θ)为代价函数,其表达式如式(3)
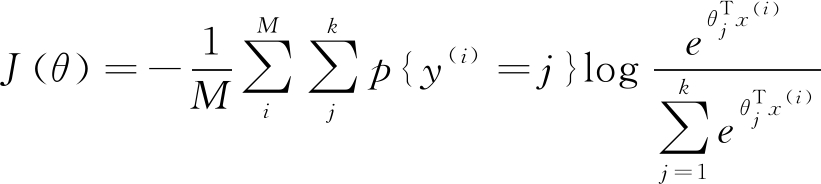
(3)
其中,T、k、i、j等参数与上面含义相同,M表示总样本数。
3 实验及分析
3.1 数据集构建
实验所采用的数据是利用计算机仿真软件所得的五类目标的一维距离像,某舰船的仿真模型如图5所示。仿真参数设置如下:雷达中心频率10 GHz,带宽80 MHz,方位角范围为0°~360°,间隔1°,200个距离单元,分辨率1.875 m。最终得到,每类目标360个方位角的样本数据,每个方位角的数据长度为200。目标类型及结构参数如表1所示。
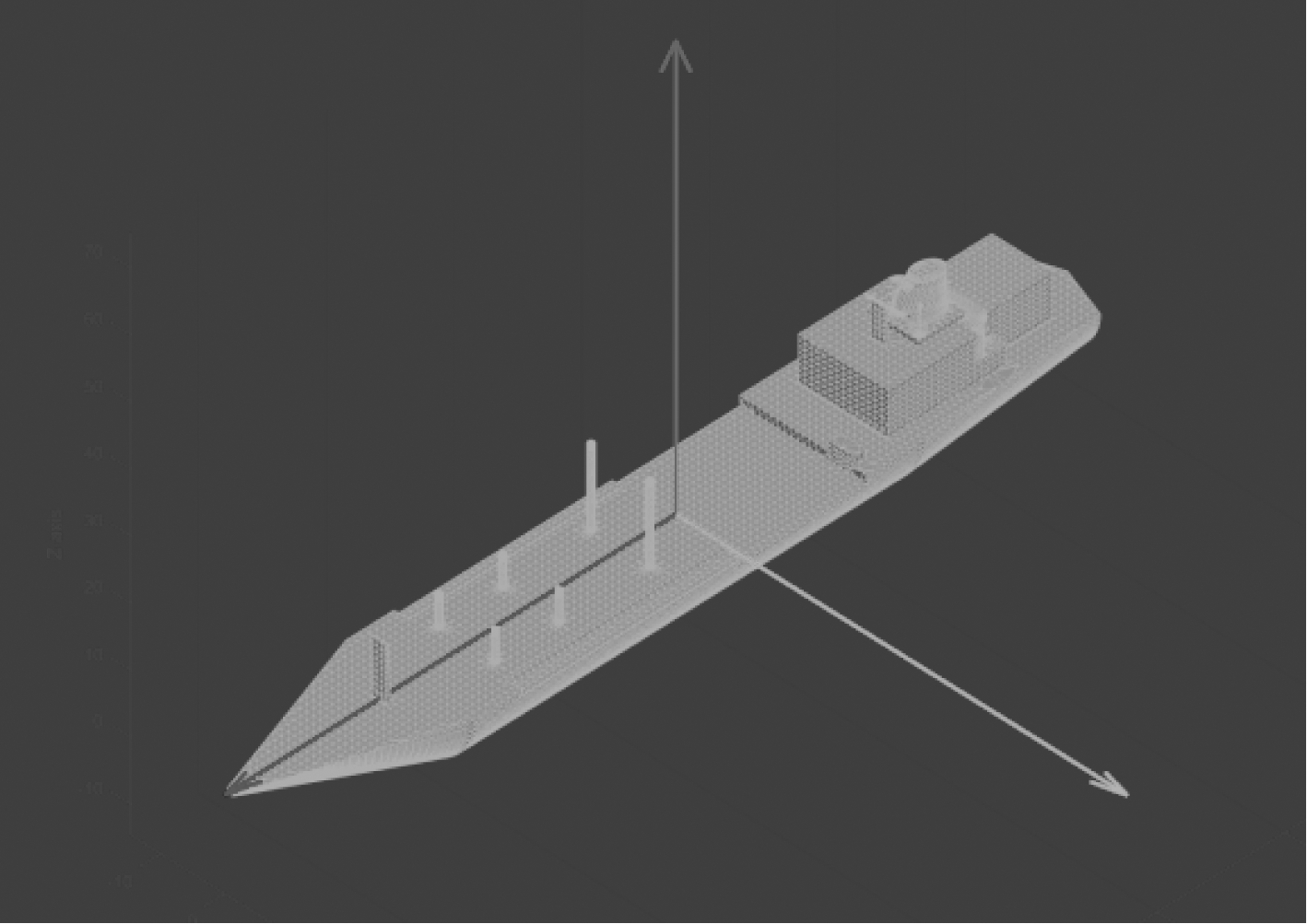
图5 舰船1仿真模型示意图
Fig.5 Schematic diagram of ship 1 simulation model
表1 五类海面目标类型及参数
Tab.1 Five types of sea targets and parameters
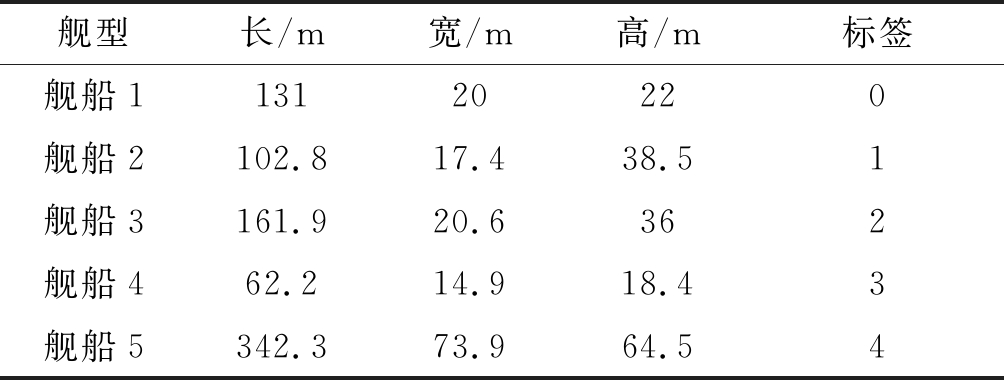
舰型长/m宽/m高/m标签舰船113120220舰船2102.817.438.51舰船3161.920.6362舰船462.214.918.43舰船5342.373.964.54
在构建数据集时,首先对HRRP数据进行加噪处理。本节添加的噪声选定为额定SNR的随机噪声,SNR的计算通过信号的有效功率求得,即信号幅度的平方,具体计算过程如式(4)
SNR=10lg(PS/PN)
(4)
式中,PS表示信号的有效功率,PN表示噪声的有效功率,有效功率power的计算公式如式(5)所示。
power=sum(x.*x)/size(x)
(5)
其中,x表示所需计算的信号。
在本节中,我们已经通过仿真软件获得了干净的HRRP信号,可求得HRRP信号的有效功率PS,通过添加的额定SNR和SNR计算公式(4),反求出噪声的有效功率PN;再通过有效功率的计算公式(5),反求出噪声信号;最后将噪声和距离像相叠加得到带噪HRRP,实现HRRP数据的加噪处理。
其次,本文的模型具有较深的层次结构,如果数据集匮乏,会导致网络训练过拟合,为避免此类现象发生,需要对已有的HRRP数据集进行扩充。本节选用了两种扩充的方法:
方法1 通过加噪处理对原始数据进行扩充,利用前面提到的加噪处理方式,对原始数据进行5次噪声的添加,每次添加的SNR相同;
方法2 通过HRRP信号搬移对数据集进行扩充,将加噪处理后的数据进行距离方向的平移,每次平移10个距离单位,共进行了21次平移。
最后,对扩充后的数据集按照每类目标8∶2的比例划分成训练集和测试集,由于本文采取的是监督学习的方式,故在数据集划分的过程中,同时要构建数据的类别标签,将每个标签与每组数据一一对应。此外,为确保网络模型分类识别性能的真实有效性,还需将整组数据集随机打乱重组后进行划分。
3.2 降噪模块性能分析
本节将对降噪模块进行性能分析,对比分析不同SNR条件下的降噪性能。降噪模块直接上连输入层,下接输出层,仿真数据采用带噪的HRRP数据集,标签集采用干净的HRRP数据集。为验证不同SNR条件下的降噪性能,共进行了六组实验,每组实验输入数据的SNR分别为0.1 dB、0.5 dB、1 dB、5 dB、10 dB和15 dB。表2体现了不同SNR条件下,降噪前后的各带噪HRRP的SNR变化。图6(a)、(b)、(c)分别为1 dB下的HRRP信号降噪前后的对比图。
表2 不同SNR条件下,降噪前后各带噪HRRP的SNR变化
Tab.2 Under different SNR conditions, the SNR change of each noisy HRRP before and after noise reduction

实验序号123456降噪前的SNR/dB0.10.5151015降噪后的SNR/dB9.29.329.6412.2714.5616.22
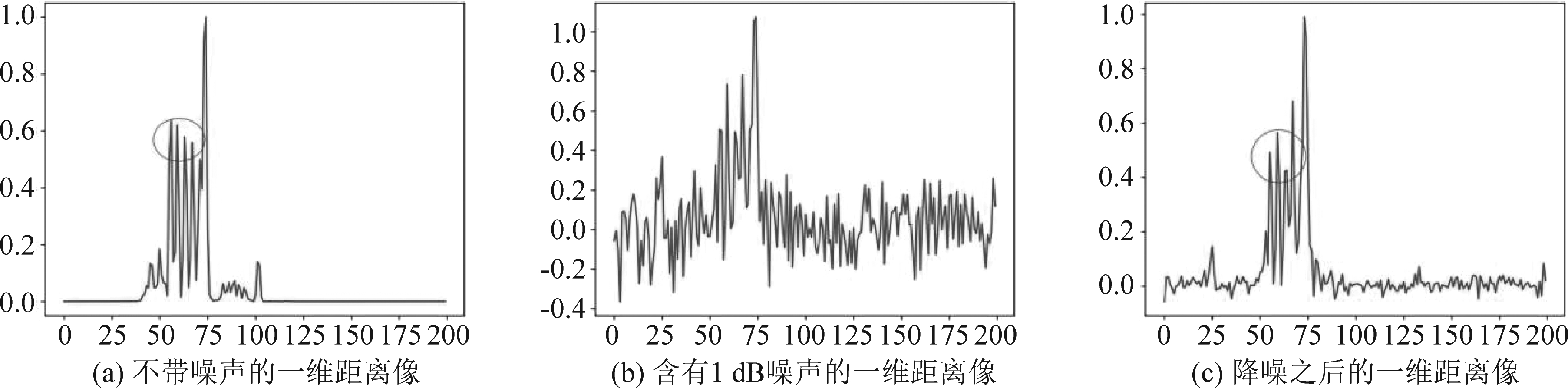
图6 SNR=1 dB条件下HRRP信号降噪前后对比图
Fig.6 Comparison of HRRP signal before and after noise reduction under SNR =1 dB
从下列图表可以明显看出,降噪之后的HRRP相比原始带噪图像,其SNR明显提高,且目标部分也更加地清晰可见,由此可以说明所设计的降噪模块具有良好的降噪效果,但其降噪性能存在上限,随着SNR不断增大,SNR的提升越来越不显著,且在降噪过程中,目标信号会丢失部分细节信息,如图6(a)、(c)中的圆圈标记处,可能会对整个模型的分类识别性能造成影响。
3.3 识别性能分析
本节主要对本文模型的识别性能进行仿真分析,仿真数据采取第一节所划分的数据集,根据SNR的不同,共分成七组数据,其SNR分别为0.1 dB、0.5 dB、1 dB、5 dB、10 dB、15 dB和20 dB。下列图7、图8分别展现了低SNR条件下(≤1 dB),本文模型与经典CNN模型的分类混淆矩阵,表3则体现了其每类目标的具体分类情况。
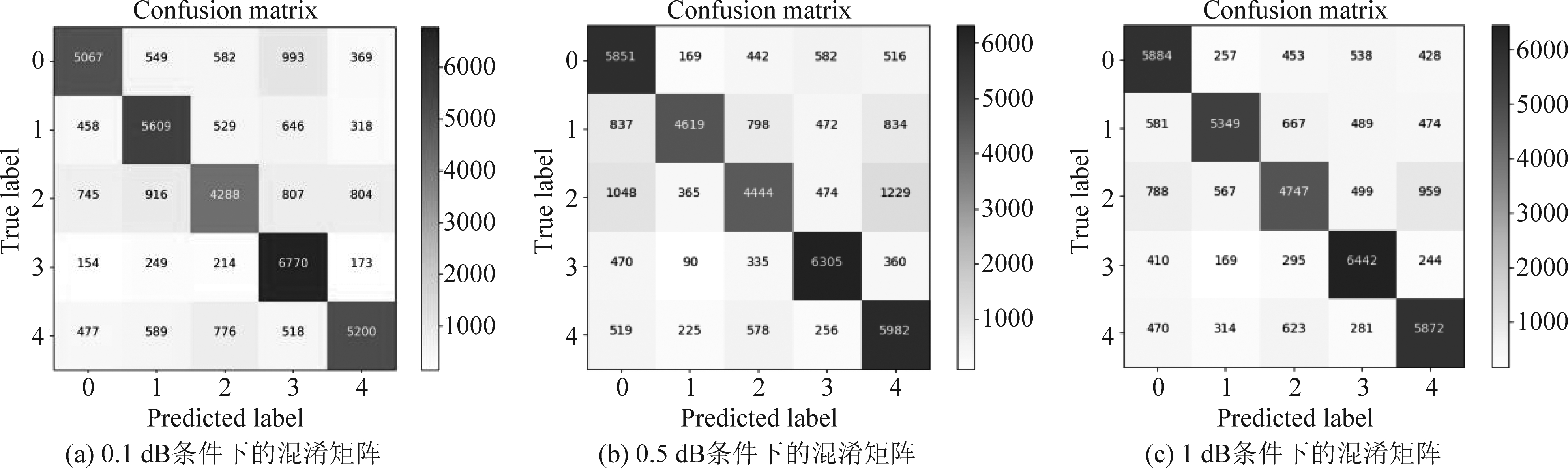
图7 不同SNR条件下,经典CNN模型的识别混淆矩阵
Fig.7 Under different SNR conditions, the recognition confusion matrix of the classic CNN model
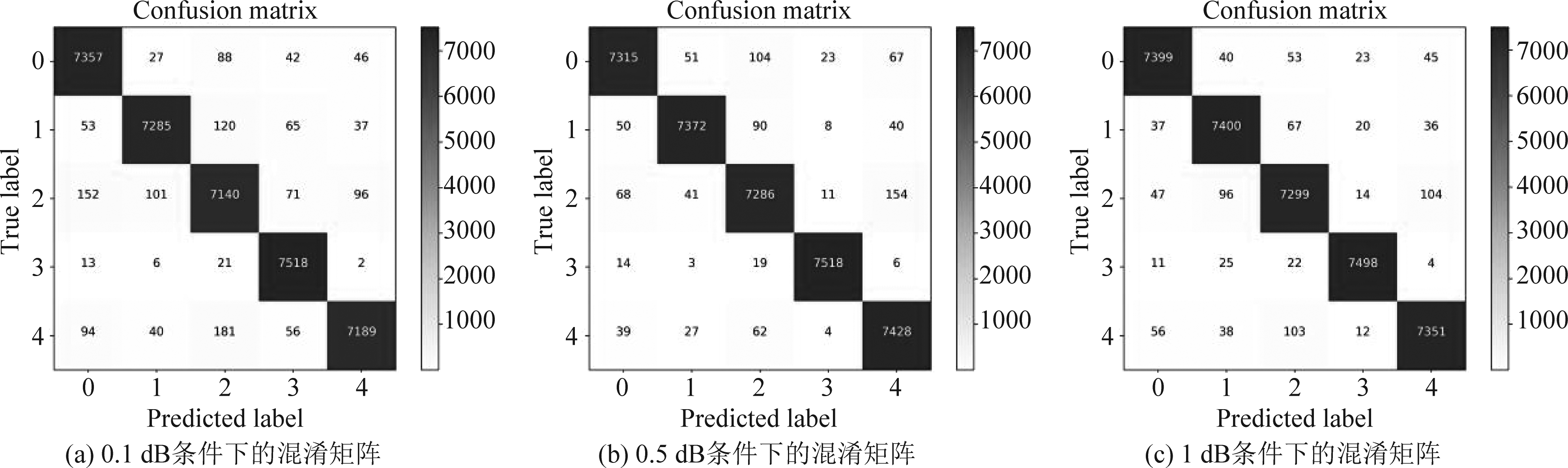
图8 不同SNR条件下,本文模型的识别混淆矩阵
Fig.8 Under different SNR conditions, the recognition confusion matrix of this model
表3 不同SNR条件下,每类目标的识别正确率(%)
Tab.3 Under different SNR conditions, the recognition accuracy of each type of target (%)

SNR/dB模型舰船1舰船2舰船3舰船4舰船5平均识别率提升效果0.1CNN67.0274.1956.7289.5568.7871.2525.28本文模型97.3196.3694.4499.4495.0996.530.5CNN77.3961.1058.7883.4079.1371.9625.71本文模型96.7697.5196.3899.4498.2397.671.0CNN77.8370.7562.7985.1977.6774.8522.82本文模型97.8797.8896.5599.1897.2497.74
从中可以细致地看到,在低SNR条件下,本文模型每类目标的分类正确率均大于对比模型。相比经典CNN模型,本文模型可以大幅度提升低SNR条件下的分类正确率,且提升效果均超过了20%,说明了本文模型在低SNR条件下具有更良好的识别性能。
图9展现了两种模型在各SNR条件下的平均分类识别正确率,从图中可以看出,两种模型的平均识别正确率均随SNR的提升而不断升高。不过,本文模型在不同SNR条件下均能保持较高的识别率,具备良好的鲁棒性,而经典CNN模型在低SNR(≤1 dB)条件下,其识别正确率要远远低于本文模型,因此本文模型的整体识别性能要优于经典的CNN模型。
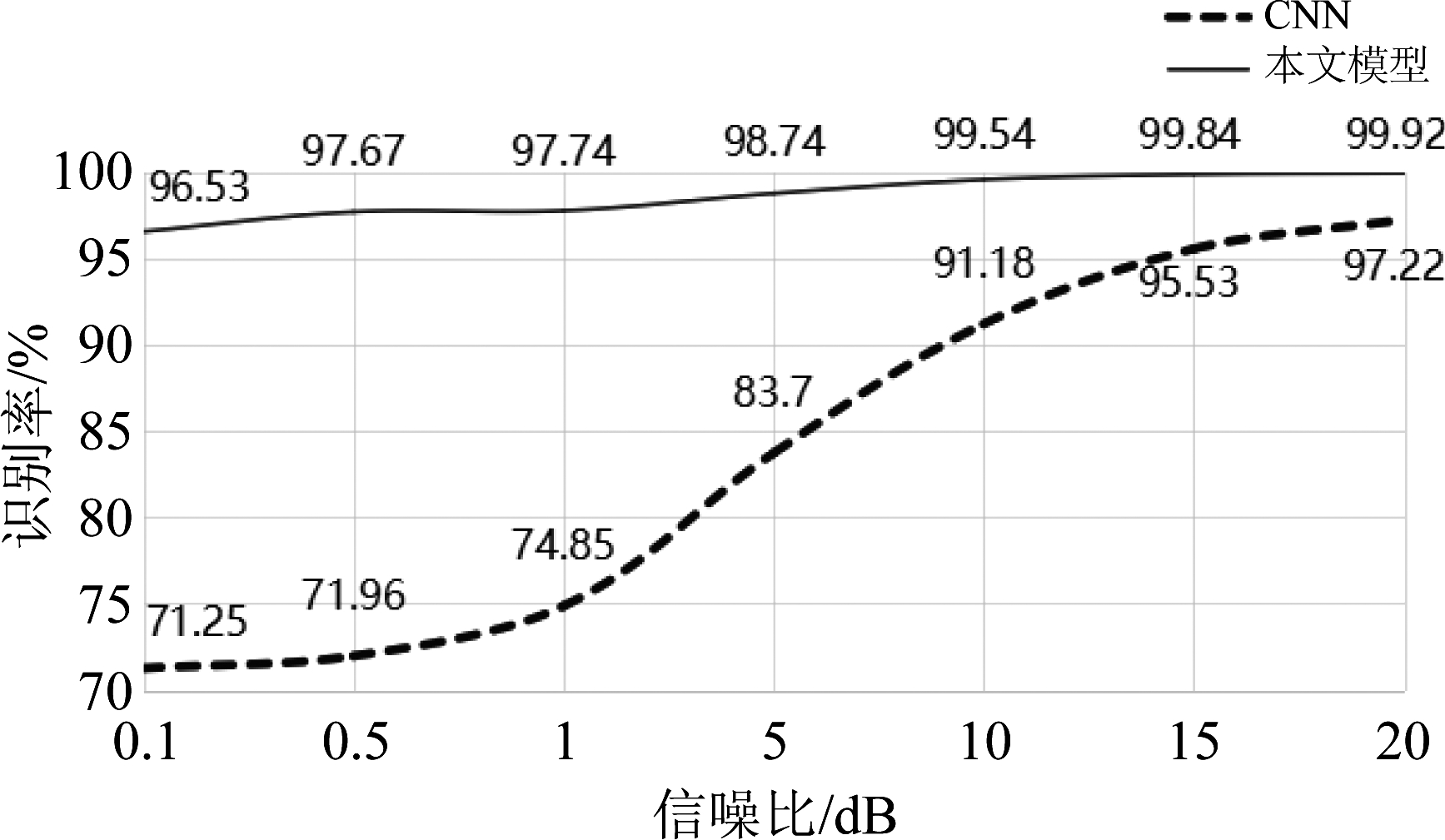
图9 不同SNR条件下,两种模型的平均识别正确率折线图
Fig.9 Line graph of the average recognition accuracy of the two models under different SNR conditions
并且随着SNR的增加,两种模型的识别性能越来越接近,差异性越来越小。可以预见随着SNR的增加,带噪信号会无限接近于干净的无噪声信号。根据上一节的分析,降噪模块在降噪的同时会造成图像细节信息的丢失,从而影响识别精度,这种问题在高SNR条件下应显得尤为严重,但根据图8中显示,高SNR条件下,本文模型的识别正确率仍然高于经典的CNN模型,原因在于本文采用了BN层结构,解决了内部协变量移位问题的同时,也提高了网络的识别性能,弥补了因细节信息丢失所带来的损失。
为进一步验证本文模型的识别性能,使用实测数据进行方法验证,实验采用三类舰船的实测HRRP数据,该数据利用某型X波段雷达对海探测获得。三类实测目标中每类目标舰船的长度分别为105.2 m、98.8 m和102.7 m,宽度均约为20 m左右,距离像个数约为2030个,但由于探测角度的影响,所获得的数据均为小角度范围内的数据,并非全方位角360°的数据。图10为两种模型的实测混淆矩阵,表4则展现了本文模型的实测结果,实验结果表明,在实测环境中,本文模型相比于经典的CNN模型仍具备较高的识别率,在识别性能方面仍具有一定的优越性。虽然每类实测目标均有较多的实测数据,但由于小角度数据的影响,实测数据间的类内相似性很大,类间相似性较小。由于多角度实测数据的缺失,导致两种模型的识别结果差异性不大,因此还有待进一步积累实测数据开展方法验证。
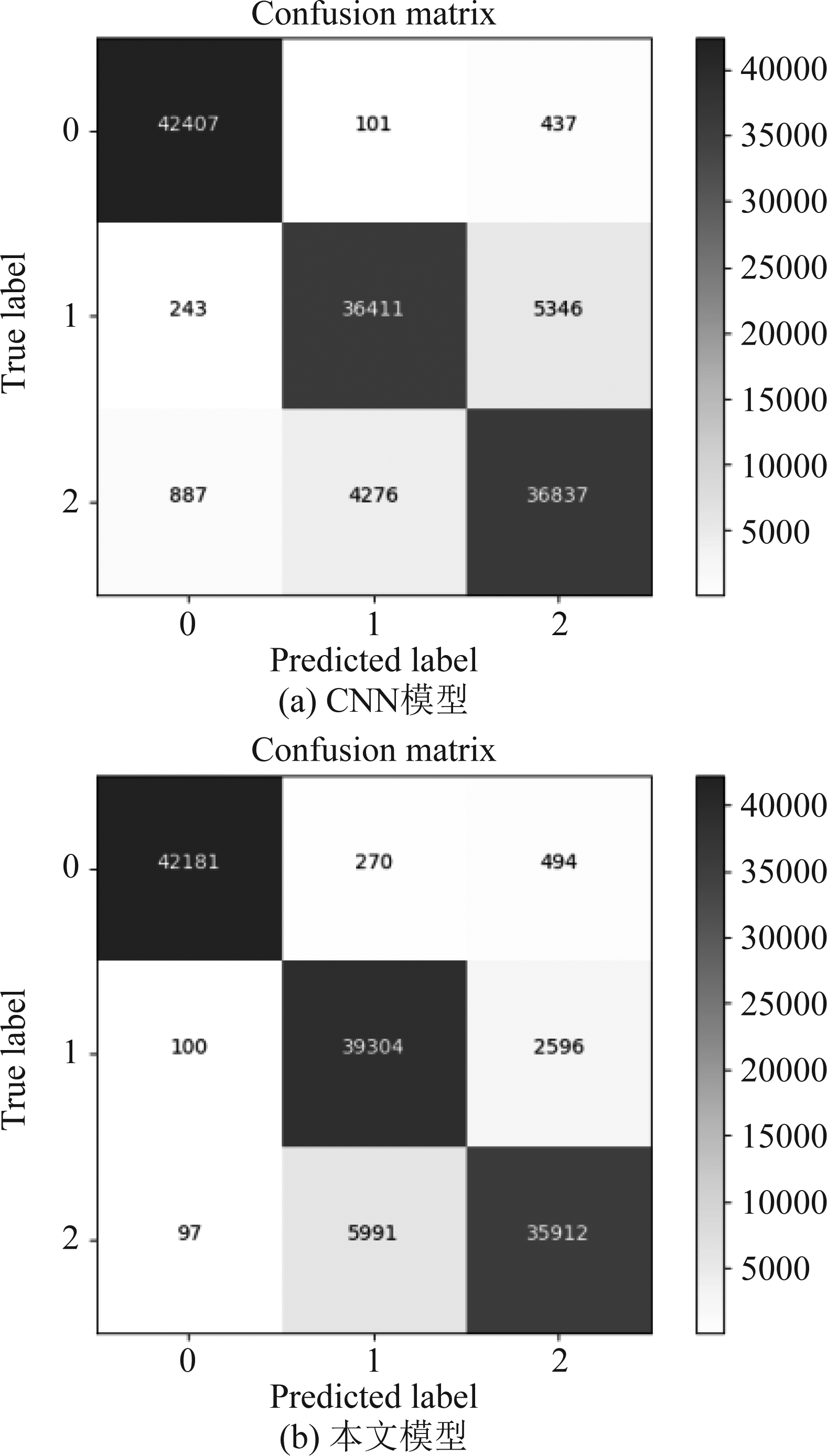
图10 两种模型实测数据的混淆矩阵
Fig.10 The confusion matrix of the measured data of two models
表4 两种模型实测数据的识别结果(%)
Tab.4 Experimental results of two models (%)
CNN本文模型识别率91.0693.08
此外,表5展现了模型的训练时间。从中可以看出,本文模型的训练时间较经典CNN模型有所延长。由于为了获得更佳的识别率和稳定性,本文模型在结构上比经典的CNN模型更为复杂,网络参数数量也更多,总体来说,本文模型的训练时间平均增加一倍左右,但在较低信噪比情况下识别率提升20%以上。
表5 不同SNR条件下,两种模型每次迭代的时间(s)
Tab.5 Under different SNR conditions, the time of each iteration of the two models (s)
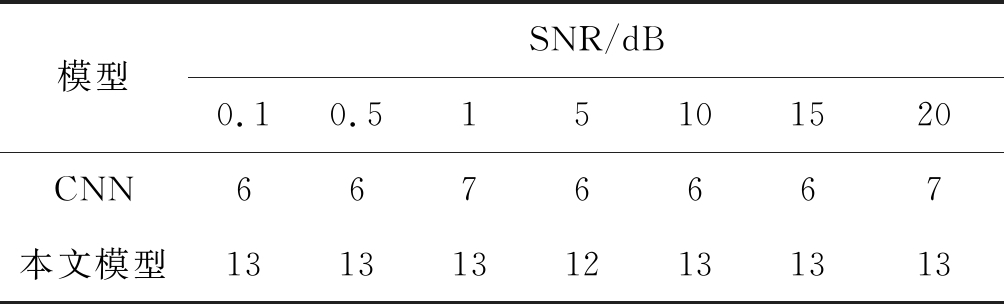
模型SNR/dB0.10.515101520CNN6676667本文模型13131312131313
综上所述,在低SNR条件下,对比经典CNN模型,本文模型可大幅度提升多类海面目标的分类识别正确率,具有更佳的识别性能,但这种提升效果会随SNR的增加而逐渐减弱。此外,在不同SNR条件下,本文模型均可保持较高的识别正确率,因此具有良好的鲁棒性,但模型训练时间会因模型结构复杂有所延长。
4 结论
本文提出了一种基于DnCNN的海面目标分类识别方法。利用DnCNN的降噪性能和CNN网络的分类识别能力,设计了一个基于DnCNN的海面目标分类识别模型,模型采用了残差学习技术和BN解决梯度消失问题,提升识别精度。通过仿真结果表明,模型中的降噪模块具有良好的降噪性能,可以有效的提高低SNR条件下的HRRP质量。同时,对比经典CNN模型,本文模型在低SNR条件下仍具备较高分类识别正确率,具有更良好的鲁棒性和分类识别能力。为了更好的验证本文模型的性能,下一步将重点研究海杂波影响下本文模型的目标识别性能,并注重实测数据积累的完备性和多样性,加强方法的实测验证研究,提升模型的适用性。
[1] 汪钰,姜元,王彦华,等.基于原子范数最小化的高分辨距离像散射中心估计[J].信号处理,2017,33(4):511-515.
WANG Yu,JIANG Yuan,WANG Yanhua,et al.Scattering center estimation of HRRP via atomic norm minimization[J]. Journal of Signal Processing,2017,33(4):511-515.(in Chinese)
[2] 李彬,李辉,郭淞云.基于t分布扩展概率主成分分析模型的一维距离像识别方法[J].电子与信息学报,2017,39(8):1857-1864.
LI Bin,LI Hui,GUO Songyun.Using t-distribution based probabilistic principal component analysis model for high resolution range profile recognition[J]. Journal of Electronics & Information Technology, 2017,39(8): 1857-1864.(in Chinese)
[3] 王彩云,黄盼盼,李晓飞,等.基于AEPSO-SVM算法的雷达HRRP目标识别[J].系统工程与电子技术,2019,41(9):1984-1989.
WANG Caiyun,HUANG Panpan,LI Xiaofei,et al. Radar HRRP target recognition based on AEPSO-SVM algorithm [J]. Systems Engineering and Electronics,2019,41(9):1984-1989.(in Chinese)
[4] 王彩云,胡允侃,李晓飞,等.基于卷积稀疏编码与多分类器融合的雷达HRRP目标识别方法[J].系统工程与电子技术,2018,40(11):2433-2437.
WANG Caiyun,HU Yunkan,LI Xiaofei,et al.Radar HRRP target recognition method based on convolutional sparse coding and multi-classifier fusion [J]. Systems Engineering and Electronics, 2018,40(11): 2433-2437.(in Chinese)
[5] 宋益恒,王彦华,李阳,等.基于深度生成网络的雷达HRRP生成技术[J].信号处理,2019,35(6):1118-1122.
SONG Yiheng,WANG Yanhua,LI Yang,et al.Radar HRRP generation using deep generative networks[J]. Journal of Signal Processing,2019,35(6):1118-1122.(in Chinese)
[6] 黄晓刚,徐佳龙.海杂波与噪声分界分析[J].现代雷达,2013,35(2):11-12,17.
HUANG Xiaogang,XU Jialong.Analysis of the division of sea clutter and noise[J].Modern Radar,2013,35(2):11-12,17.(in Chinese)
[7] 楼奇哲,刘乐,姚元.采用卷积神经网络的海面多目标检测研究[J].信号处理,2018,34(9):1053-1059.
LOU Qizhe,LIU Le,YAO Yuan.Multi-target detection in sea clutter with convolutional neural network[J]. Journal of Signal Processing,2018,34(9):1053-1059.(in Chinese)
[8] ZHANG Kai, ZUO Wangmeng, CHEN Yunjin.Beyond a Gaussian denoiser:Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing,2017,26(7):3142-3155.
[9] 杨真真,匡楠,范露,等.基于卷积神经网络的图像分类算法综述[J].信号处理,2018,34(12):1474-1489.
YANG Zhenzhen,KUANG Nan,FAN Lu,et al.Review of image classification algorithms based on convolutional neural networks[J]. Journal of Signal Processing,2018,34(12):1474-1489.(in Chinese)
[10] KALAYEH M M, SHAH M.Training faster by separating modes of variation in batch-normalized models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2020,42(6):1483-1500.
[11] XIA Haiying, ZHU Fuyu, LI Haisheng,et al.Combination of multi-scale and residual learning in deep CNN for image denoising[J]. IET Image Processing,2020,14(10):2013-2019.
[12] 周飞燕,金林鹏,董军.卷积神经网络研究综述[J].计算机学报,2017,40(6):1229-1251.
ZHOU Feiyan,JIN Linpeng,DONG Jun.Review of convolutional neural network[J]. Chinese Journal of Computers,2017,40(6):1229-1251.(in Chinese)
[13] 邓建国,张素兰,张继福,等.监督学习中的损失函数及应用研究[J].大数据,2020,6(1):60- 80.
DENG Jianguo,ZHANG Sulan,ZHANG Jifu,et al.Loss function and application research in supervised learning[J].Big Data Research,2020,6(1):60- 80.(in Chinese)
[14] 斋藤康毅.深度学习入门:基于Python的理论与实现[M]. 陆宇杰, 译. 北京:人民邮电出版社,2018:63- 67.
Saito Yasuyoshi.Introduction to Deep Learning:Theory and Experiments Based on Python [M].LU Yujie Translated.Beijing: Posts&Telecom Press,2018:63- 67.(in Chinese)

