1 引言
单载波频域均衡(Single-Carrier Frequency-Domain Equalization,SC-FDE)和正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是两种能够克服因多径传播引起的频率选择性衰落的传输体制[1]。与OFDM通信系统相比,SC-FDE通信系统具有对载波频偏不敏感、峰均功率比低以及发射机结构简单等优点[1],因此SC-FDE在功率受限平台上得到了广泛的应用,例如长期演进(Long Time Evolution,LTE)上行链路[2]、无人机通信链路[3]和航空器通信链路[4]等。
SC-FDE算法主要分为两类:线性算法和非线性算法。非线性SC-FDE算法虽然具有比线性SC-FDE算法更优的误码率(Bit Error Rate,BER)性能,但是其复杂度较高且处理时延较大[5]。线性SC-FDE算法主要包含三个模块:信道估计、噪声功率估计和信道均衡。传统信道估计算法有最小二乘(Least Square,LS)信道估计算法、最小均方误差(Minimum Mean-Square Error,MMSE)信道估计算法以及线性MMSE(Linear MMSE,LMMSE)信道估计算法等[6]。相比于MMSE信道估计算法和LMMSE信道估计算法,LS信道估计算法不需要信号和信道的统计特性,算法简单,计算复杂度低,因此得到了广泛地应用。传统信道均衡算法包括迫零(Zero-Forcing,ZF)均衡和MMSE均衡。MMSE均衡不会放大深衰落频点处的噪声,因而性能优于ZF均衡[7]。传统算法通过独立地优化单个模块以提高SC-FDE通信系统的BER性能。然而,经过多年的发展,通过单独优化每个模块来进一步提高BER性能变得越来越困难。
近年来,深度学习已经显示出联合优化通信系统物理层模块的能力[8]。文献[9]设计了一种用于OFDM通信系统信道估计和信号检测的深度全连接神经网络。当无线信道受到严重失真和干扰时,该网络取得了比LS信道估计和MMSE信道估计更好的性能。文献[10]提出了一种基于深度学习的端到端单载波通信系统,其发送机和接收机都由全连接神经网络构成,通过端到端的训练优化,实现了优于传统算法的性能。在文献[11]中,Amer等提出了一种针对单载波通信系统符号检测的深度全连接神经网络。上述基于深度学习的算法虽然展示出了优于传统算法的性能,但是其仍然存在一定的缺陷。首先是训练数据维度爆炸问题,当全连接神经网络单次处理的数据包含n个比特信息时,为了遍历所有组合,需要至少2n个训练数据[8];然后是信道泛化问题,现有基于深度学习的算法仅能在已训练的信道下正常工作,当实际信道与训练信道不同时,其性能较差。
本文提出了一种基于深度学习的SC-FDE (Deep Learning-based SC-FDE,DL-SC-FDE)算法来联合优化信道估计、噪声功率估计和信道均衡。为了减少网络收敛所需的训练数据量,所提算法针对三个不同模块设计了三个不同的子网络。此外,通过在训练中平等地对待每条路径的重要性,解决了信道估计的泛化问题。数值结果表明,与基于LS信道估计和MMSE信道均衡的算法相比,DL-SC-FDE具有更好的误码率性能,并且在各种信道条件下保持鲁棒性。本文内容安排如下:第2节描述SC-FDE通信系统模型;第3节详细阐述了所提出的DL-SC-FDE算法;第4节对DL-SC-FDE进行了性能仿真与分析,并与现有SC-FDE算法进行了性能对比;最后总结全文。
2 系统模型
一个简化的SC-FDE通信系统如图1所示。在发射机中,调制模块的任务是将每a个比特映射为一个符号,组帧模块为每b个符号添加独特字(Unique Word,UW)序列,其中a和b都是正整数。由于同步模块可能同步到任意一条路径,为了消除码间干扰(Inter-Symbol Interference,ISI),UW序列的长度应大于最大多径延迟的两倍。均衡模块采用信道状态估计值和噪声功率估计值来均衡接收到的均衡序列。
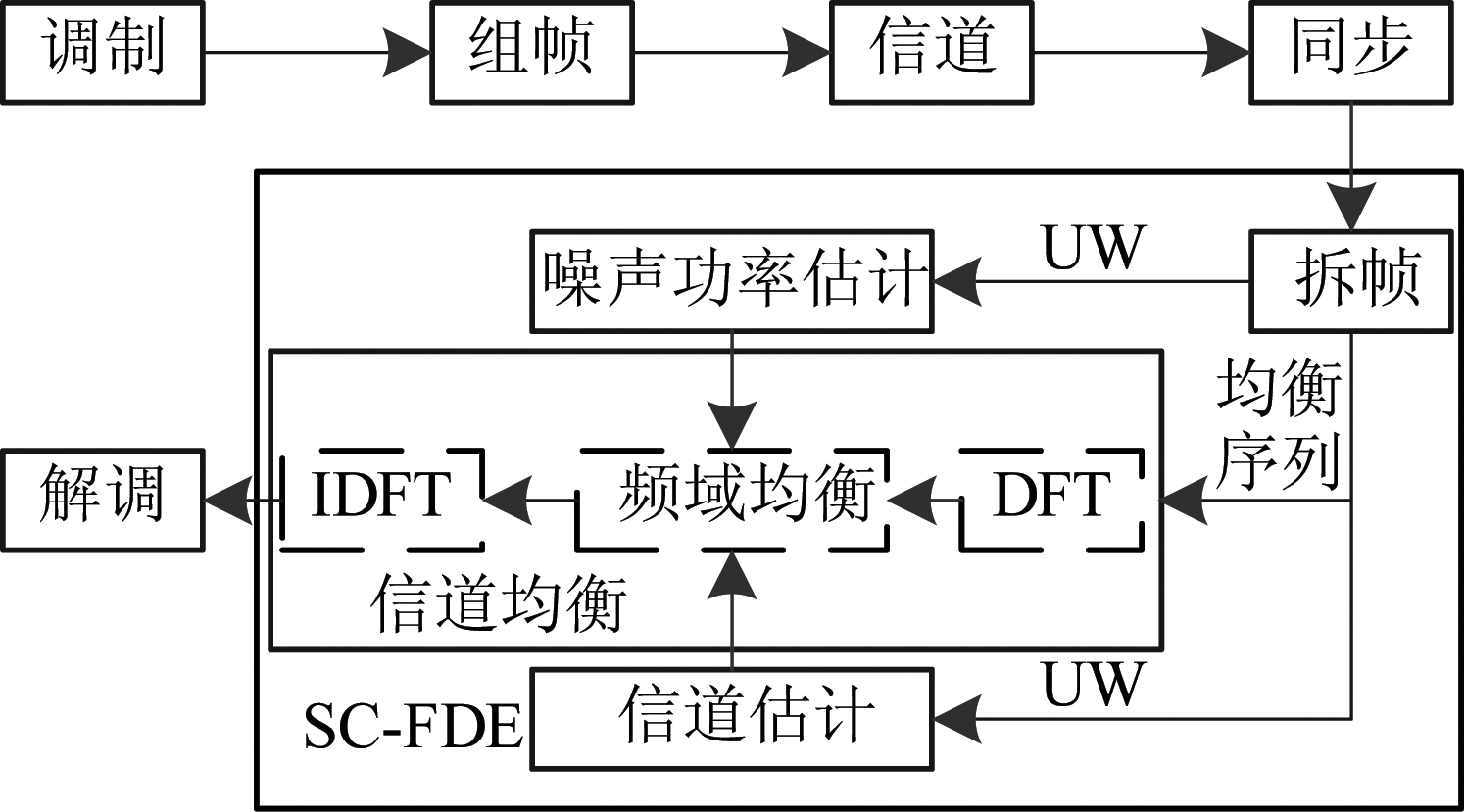
图1 简化的SC-FDE通信系统结构
Fig.1 A simplified structure of SC-FDE communication systems
一种典型的SC-FDE通信系统的帧格式如图2所示。数据序列s含有b个调制符号,s的左右两边分别有c个UW序列,每个UW序列的长度都为e,且e为偶数。这样,均衡序列可以表示为
(1)
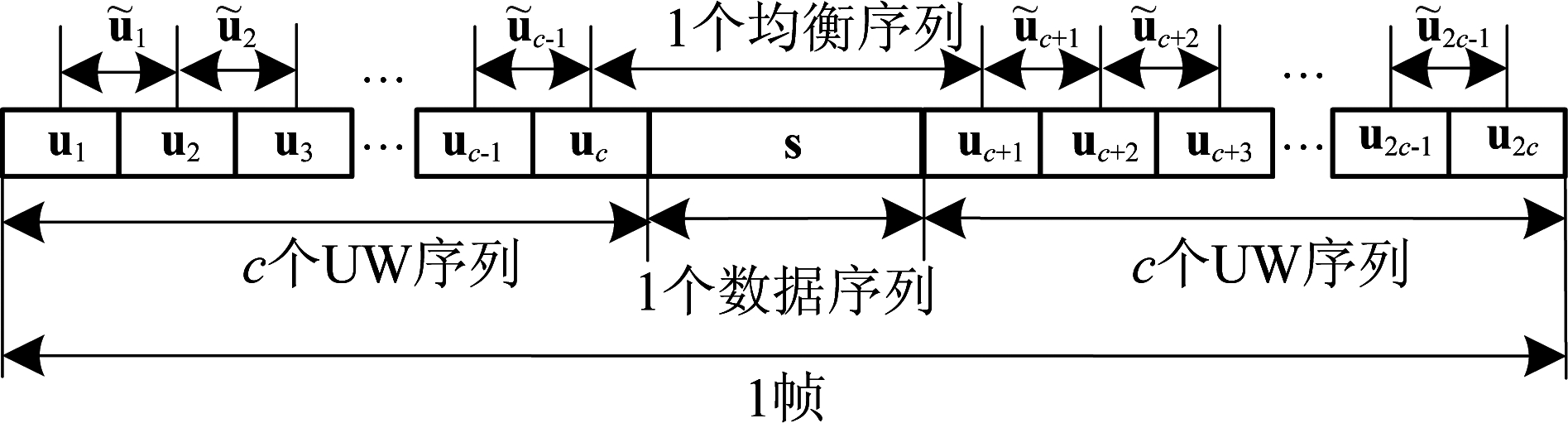
图2 SC-FDE通信系统典型帧结构
Fig.2 A typical frame structure of SC-FDE communication systems
其中
和uc+1[n]分别代表s、uc和uc+1的第n个元素。通常,各个UW序列是相同的,即ui=ui′,其中1≤i,i′≤2c。这样,均衡序列内部的最后e′个符号与其外部前方的e′个符号相同,都为一个UW序列的前e′个符号,即UW序列完成了循环前缀的功能。
通常一个均衡序列的持续时间是远小于信道相干时间的,因此本文假设多径信道的时域冲击响应在一帧内是不变的,且最大多径时延为τ,则e应该大于2(τRs+Ls),Rs为符号率,Ls为成型滤波中根升余弦滤波器所包含的符号数。这样,接收到的均衡序列可以表示为
y[n]=x[n]⊗h[n]+w[n]
(2)
其中⊗代表循环卷积, w[n]为加性高斯噪声且w[n]～CN(0,Pn),Pn为噪声功率,h[n]为符号级等效多径信道的时域冲击响应且可以被表示为
(3)
(4)
其中hn为采样级信道冲击响应,Lu为上采倍数, fn为根升余弦滤波器系数且长度为LuLs+1。注意,y[n]、x[n]、h[n]和w[n]都是复数。根据式(2)可知,多径会引起码间串扰,为了消除这种串扰,需对y[n]进行均衡。根据循环卷积的性质可得
Y[k]=H[k]X[k]+W[k]
(5)
其中k=0,1,…,N-1,Y[k]、H[k]、X[k]和W[k]分别为y[n]、h[n]、x[n]和w[n]的N点离散傅里叶变换(Discrete Fourier Transform,DFT)的结果。
因为e′大于(τRs+Ls),所以仅u1内部的前e′个符号、uc内部的后e′个符号、uc+1内部的前e′个符号和u2c内部的后e′个符号在经过信道后不能被用于信道估计和噪声功率估计,为了充分利用UW序列,定义
(6)
其中
为序列
的第n个元素。根据图2可知,内部的后e′个符号与其外部前方的e′个符号相同,都为一个UW序列的前e′个符号。这样,接收到的UW序列可以表示为
(7)
其中wl[n]为加性高斯噪声且wl[n]～CN(0,Pn)。
类似地,
的频域信号可以表示为
(8)
其中
和Wl[k]分别为
和wl[n]的e点DFT变换。需要注意的是,l的取值并不包含c,这是因为uc和uc+1并不相邻。
在接收机,
是已知的,因此噪声功率估计模块可以利用估计Pn,且信道估计模块也可利用估计H′[k]。然后,h[n]的估计值
可以通过对H′[k]的估计值
进行e点的反离散傅里叶变换(Inverse DFT,IDFT)得到。H[k]的估计值
可以通过或得到。最后,信道均衡模块根据和Pn的估计值
对x[n]进行均衡并得到均衡后的调制符号
3 本文提出的DL-SC-FDE算法
为了联合优化SC-FDE中的信道估计、噪声功率估计和信道均衡,本文提出了一种DL-SC-FDE算法。根据式(5)可知,每一个Y[k]都可以被独立地均衡,为了将这个特性引入网络中以降低网络规模并提高均衡性能,所提算法采用了卷积神经网络(Convolutional Neural Network,CNN),其网络结构如图3所示。
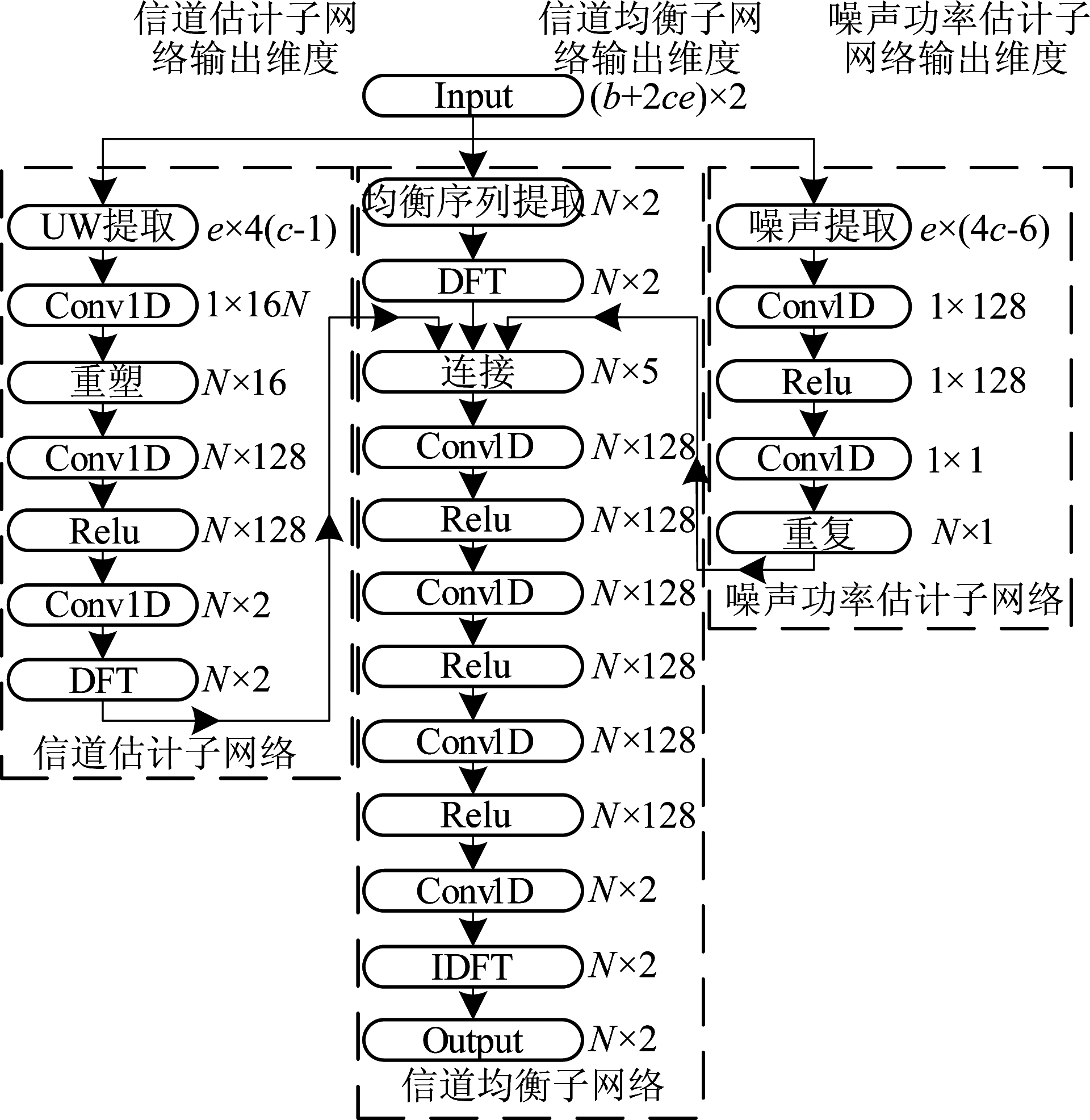
图3 所提网络的结构
Fig.3 The structure of the proposed network
在图3中,所提网络包含了3个子网络:信道估计子网络、噪声功率估计子网络和信道均衡子网络。所提网络的输入可以表示为
rn,0=R{r[n]},rn,1=I{r[n]}
(9)
其中n=0,1,…,b+2ce-1,r[n]为接收到的一个完整的帧。因为神经网络采用实数运算,所以网络输入为r[n]的实部和虚部。
SC-FDE通信系统通常采用正交振幅调制(Quadrature Amplitude Modulation,QAM),根据QAM的原理可知,QAM调制符号的实部和虚部分别包含了不同比特的信息,因此其实部和虚部是相互独立的。为了独立地处理输入信号的实部和虚部,所提网络采用了一维卷积神经(1-dimensional convolutional,Conv1D)层,设其输入为dn1,n2,其中n1=0,1,…,N1-1,n2=0,1,…,N2-1,N1为输入长度,N2为输入通道数,则该层的输出可以表示为
(10)
其中
为输出长度且
为卷积核尺寸,N4为步长,N5为填充长度,
为输出通道数,
为卷积核权重,
为卷积核偏置;
为Conv1D层的超参数,
和
为Conv1D层的可学习参数。在Conv1D层中,不同的输入通道对应着不同的
根据式(10)可知,Conv1D层同步地处理I、Q两路以保持数据的正交性,并且两路是独立处理的。
在信道估计子网络中,UW提取层的任务是从r[n]中提取
因此其输出可以表示为
(11)
其中n=0,1,…,e-1,l′=1,2,…,2c-2,
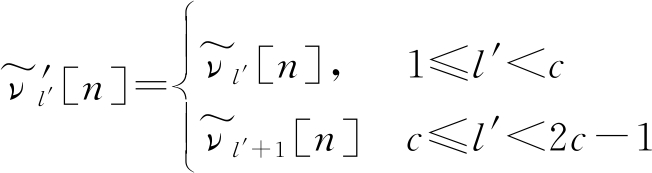
(12)
信道估计子网络采用了3个Conv1D层。这3个Conv1D层的卷积核大小分别为e、1和1,卷积核数量分别为16N、128和2,步长分别为e、1和1,填充长度都为0。注意,每个层的输入数据都是二维的,其第二维代表通道数。根据第一个Conv1D层的参数可知,其输出的维度为1×16N。重塑层用于重塑第一个Conv1D层的输出维度。设第一个Conv1D层的输出为p0,η,其中η=0,1,…,16N-1,则重塑层的输出可以表示为
(13)
其中n=0,1,…,N-1,λ=0,1,…,15。
DFT层被用于产生频域信号,其输出可以表示为
(14)
(15)
其中k=0,1,…,N-1,qn,m为DFT层的输入且m=0,1。
根据式(7)和式(12)可知,
因此,在噪声功率估计子网络中,噪声提取层的输出可以表示为
(16)
其中n=0,1,…,e-1,l′=1,2,…,2c-3。由于噪声功率估计需要平方运算,该子网络包含2个Conv1D层,且第一个Conv1D层的激活函数为非线性的Relu函数。当输入不小于0时,Relu函数直接将其输出;当输入小于0时,Relu函数输出0。第一个Conv1D层的卷积核大小为e,卷积核数量为128,步长为e,填充长度为0;第二个Conv1D层的卷积核大小为1,卷积核数量为1,步长为1,填充长度为0。根据第二个Conv1D层的参数可知,该层的输出的维度为1×1。重复层用于重复第二个Conv1D层的输出,因此该层的输出可以表示为
(17)
其中n=0,1,…,N-1,g0,0为第二个Conv1D层的输出。
在信道均衡子网络中,均衡序列提取层从r[n]中提取y[n],因此其输出可以表示为
yn,0=R{y[n]},yn,1=I{y[n]}
(18)
其中n=0,1,…,N-1。然后,DFT层将时域信号变换为频域信号。连接层将频域信号、信道估计值和噪声功率估计值在第二维进行连接,因此该层的输出维度为N×5。信道均衡子网络含有4个Conv1D层,这4个Conv1D层的卷积核大小都为1,步长也都为1,填充长度都为0,前3个Conv1D层的卷积核数量为128,最后一个Conv1D层的卷积核数量为2。根据第4个Conv1D层的参数可知,该层的输出维度为N×2。类似地,IDFT层将均衡后的频域信号变换为时域信号,因此其输出可以表示为
(19)
(20)
其中
为IDFT层的输入。
本文采用L2损失函数,
(21)
需要注意的是,三个子网络是一起训练的。L2损失函数不仅用于信道均衡子网络,同时也用于其他两个子网络。在误差反向传播的过程中,连接层将维度为N×5的误差矩阵在第二维分解,得到维度分别为N×2、N×2和N×1的3个误差矩阵,并将这3个误差矩阵分别送入信道均衡子网络的DFT层、信道估计子网络的DFT层和噪声功率估计子网络的重复层。
为了防止噪声功率估计失去泛化能力,所提网络在两个不同的信噪比(Signal-to-Noise Ratio,SNR)下进行训练。较小的SNR等于α dB,较大的SNR等于β dB。对应于较小SNR的训练帧数为γB,对应较大SNR的训练帧数为(1-γ)B,其中0<γ<1,B为总训练帧数。根据式(21)可知,训练的损失近似反比于SNR。为了平衡两个SNR下的训练损失,式(22)应被满足。
(22)
对式(22)进行简化,可得
(23)
如果在训练阶段将多径信道参数设得比较特定,当实际信道参数与训练所用的信道参数不匹配时,系统传输性能会显著下降,而实际信道是未知的,为了更好地适应各种不同类型的无线信道,提高所提网络的信道泛化能力,本文在训练阶段将每一条径同等对待,基于此,本文提出了一种新的训练机制,具体而言,本文将用于训练的多径时延向量设置为[0,1,…,e′-Ls-1]/Rs,且每条径的相对功率都设置为0 dB,此外,在训练时,每个帧随机同步到任意一条径。这样,所提算法可以支持最大多径时延满足τ<(e′-Ls)/Rs的所有信道。
4 性能仿真分析
本节仿真对比了本文所提的DL-SC-FDE算法和传统SC-FDE算法在各种信道下的BER性能。仿真参数如下:符号率Rs=3.84 MBaud,a=2,调制方式为正交相移键控(Quadrature Phase Shift Keying,QPSK),b=448,c=2,e=64,UW序列为根等于1的ZC序列,N=512,Ls=8,Lu=4,滚降系数为0.3,优化器为Adam,初始学习率为0.001,训练周期为3,学习率下降周期为1,下降因子为0.1,测试数据集和训练数据集是分别随机产生的,且每帧都独立地经过信道,小批量(mini-batch)大小为
在产生训练数据时,每帧信道冲击响应保持恒定,产生测试数据时,最大多普勒频移被设置为70 Hz。在仿真中,传统SC-FDE算法采用MMSE信道均衡以及结合DFT插值算法的LS或MMSE信道估计,DFT插值算法可以表示为
(24)
其中
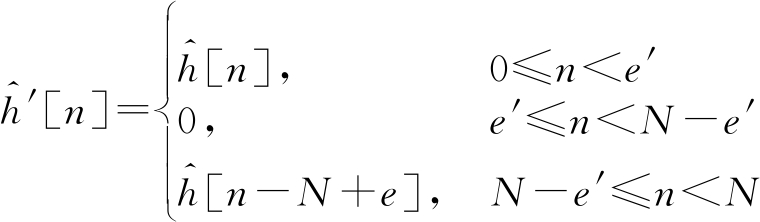
(25)
同步模块可能同步到第一条径也可能同步到最后一条径,因此在DFT插值算法中补零的位置在中部。
在传统SC-FDE算法中,Pn被估计为
(26)
根据网络参数可知,网络的计算量约为44.2 MFLOPs。仿真采用的软件平台为MATLAB 2019b,GPU为NVIDIA GeForce GTX 1660 Ti,CPU为i7- 8700K,在此平台上,DL-SC-FDE的训练时间约为190 s。
4.1 传统训练机制
传统训练机制指用于训练的信道与用于测试的信道相同。在本小节中,训练数据集包含131072个不同的帧,信道被设置为LTE中的扩展车辆A(Extended Vehicular A,EVA)模型,其多径时延向量为[0,30,150,310,370,710,1090,1730,2510]ns,相对路径功率为[0,-1.5,-1.4,-3.6,-0.6,-9.1,-7,-12,-16.9]dB,采用理想同步,且总是同步到第一条径。
注意,Eb/N0与SNR的关系为
(27)
图4给出了采用传统训练机制的DL-SC-FDE与传统SC-FDE算法在EVA模型下的BER性能;可以看出,采用LS信道估计的SC-FDE算法性能最差;DL-SC-FDE具有与采用MMSE信道估计的SC-FDE算法几乎相同的BER性能,这是因为用于训练的信道和用于测试的信道是相同且不变的,DL-SC-FDE可以通过训练学习到信道的统计特性。
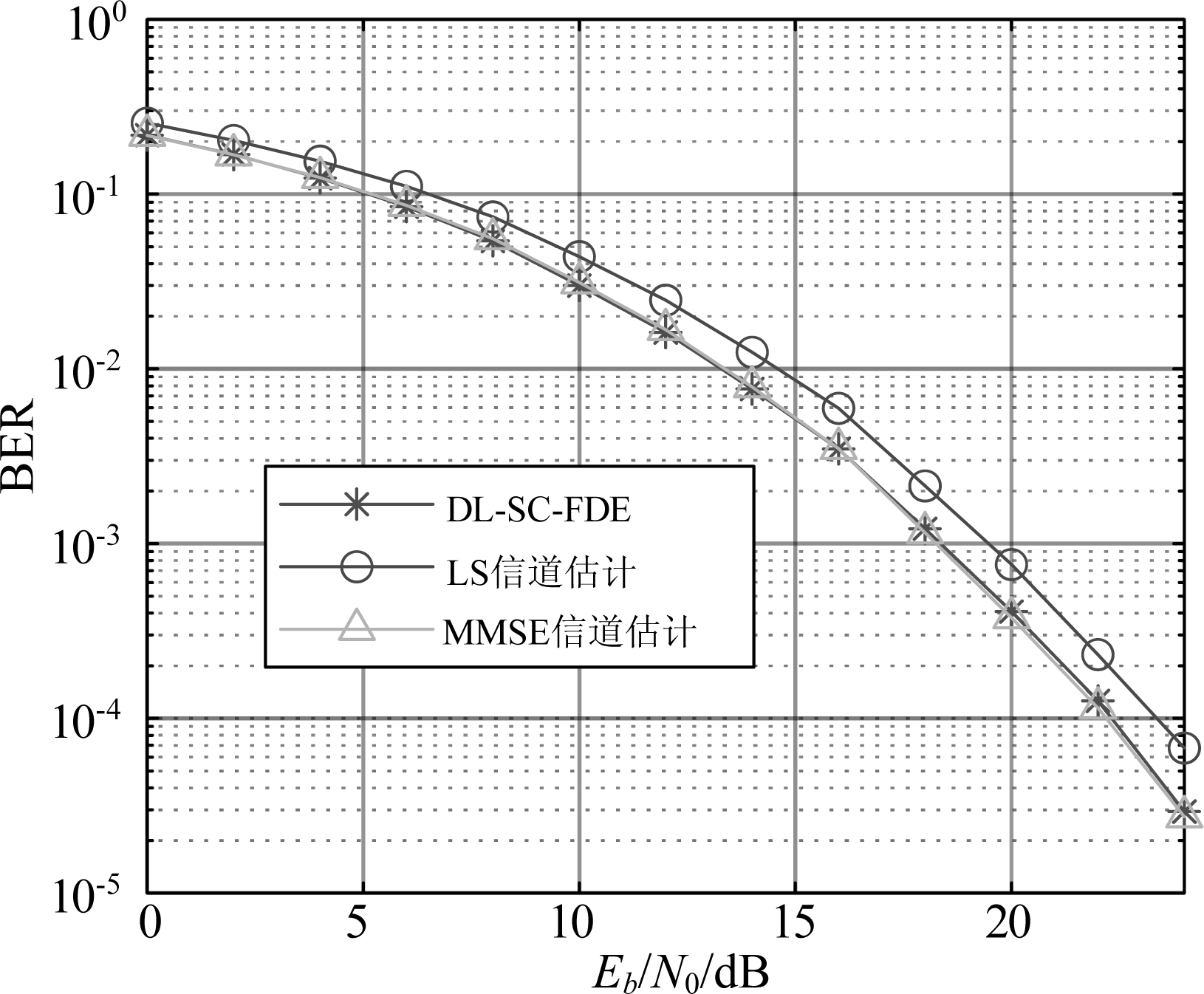
图4 采用传统训练机制的DL-SC-FDE与传统SC-FDE算法在EVA模型下的BER性能
Fig.4 BER performances of traditional SC-FDE algorithms and DL-SC-FDE with the conventional training mechanism under EVA
图5给出了在EVA模型下训练但在扩展典型城市(Extended Typical Urban,ETU)模型下测试的DL-SC-FDE的BER性能。ETU的多径时延向量为[0,50,120,200,230,500,1600,2300,5000]ns,相对路径功率为[-1,-1,-1,0,0,0,-3,-5,-7]dB。从图中可以看出,DL-SC-FDE的BER性能极差,这是因为DL-SC-FDE仅在EVA信道下训练,且已根据EVA信道的统计特性进行了网络参数的优化,当测试信道不是EVA信道时,这些优化反而会使网络不能正常工作。对比图4和图5的结果可知,传统训练机制存在信道泛化问题。
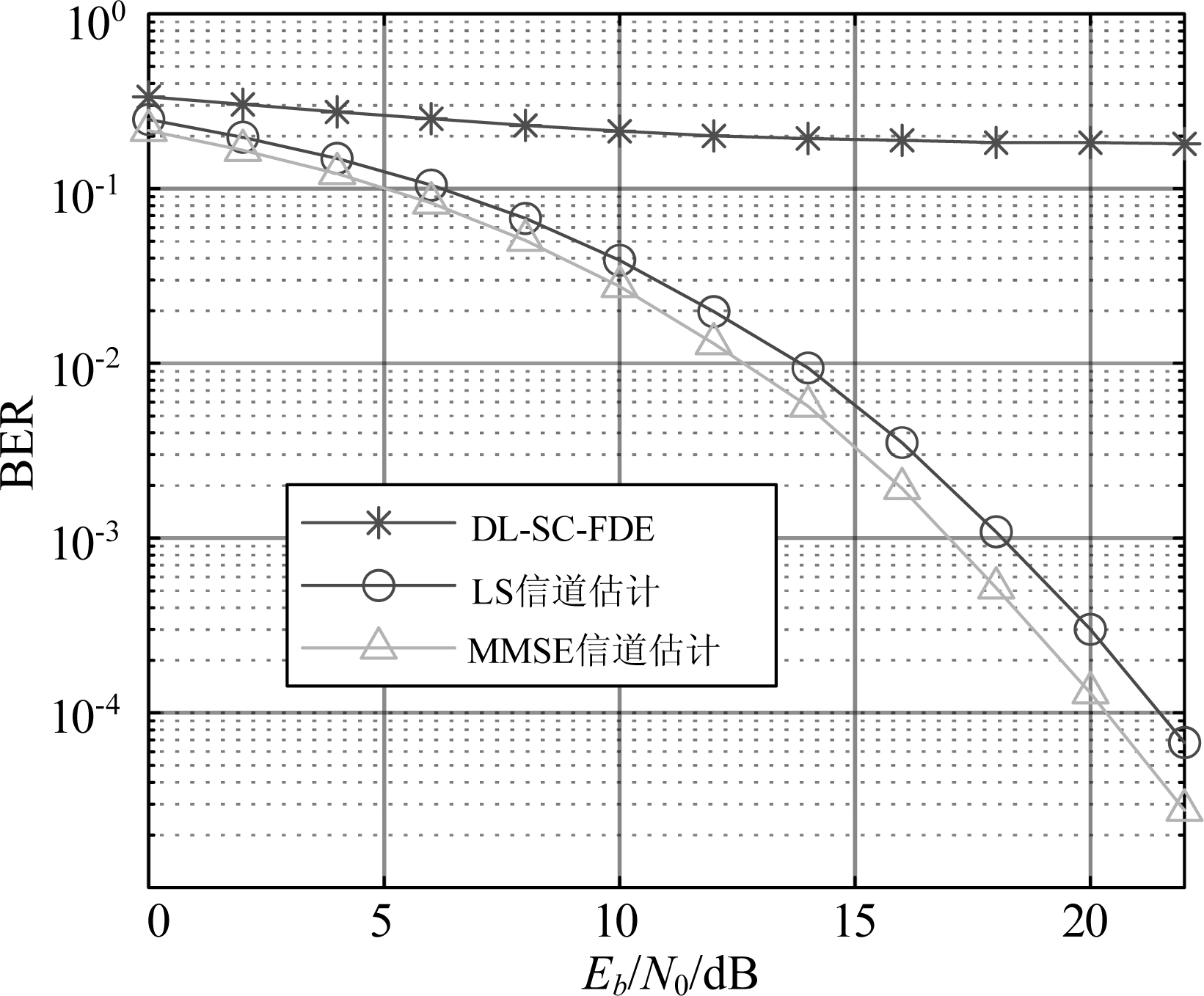
图5 EVA模型下训练并在ETU模型下测试的DL-SC-FDE的BER性能
Fig.5 BER performances of DL-SC-FDE when the training channel model is EVA and the testing channel model is ETU
4.2 新训练机制
在新训练机制中,用于训练的多径时延向量被设置为[0,1,…,e′-Ls-1]Ts,每条径的相对功率都被设置为0 dB,每帧随机同步到任意一条径。在测试阶段,本小节采用了EVA模型和ETU模型,且每帧也随机同步到任意一条径。根据EVA和ETU的多径参数可知其相干带宽分别约为0.45 MHz和0.16 MHz,由于Rs=3.84 MBaud,仿真信道都为频率选择性衰落信道。
图6仿真了不同训练数据量下DL-SC-FDE的BER性能,信道为EVA。从图中可以看出,随着B的增大,DL-SC-FDE的BER性能逐渐提升,当B≥131072时,继续增大B则不能再带来明显的BER性能增益,因此当B=131072时,DL-SC-FDE就已基本收敛。由于131072≪2896,所提算法极大地降低了网络收敛所需的训练数据量。后续的仿真都采用了B=131072所对应的已训练网络。
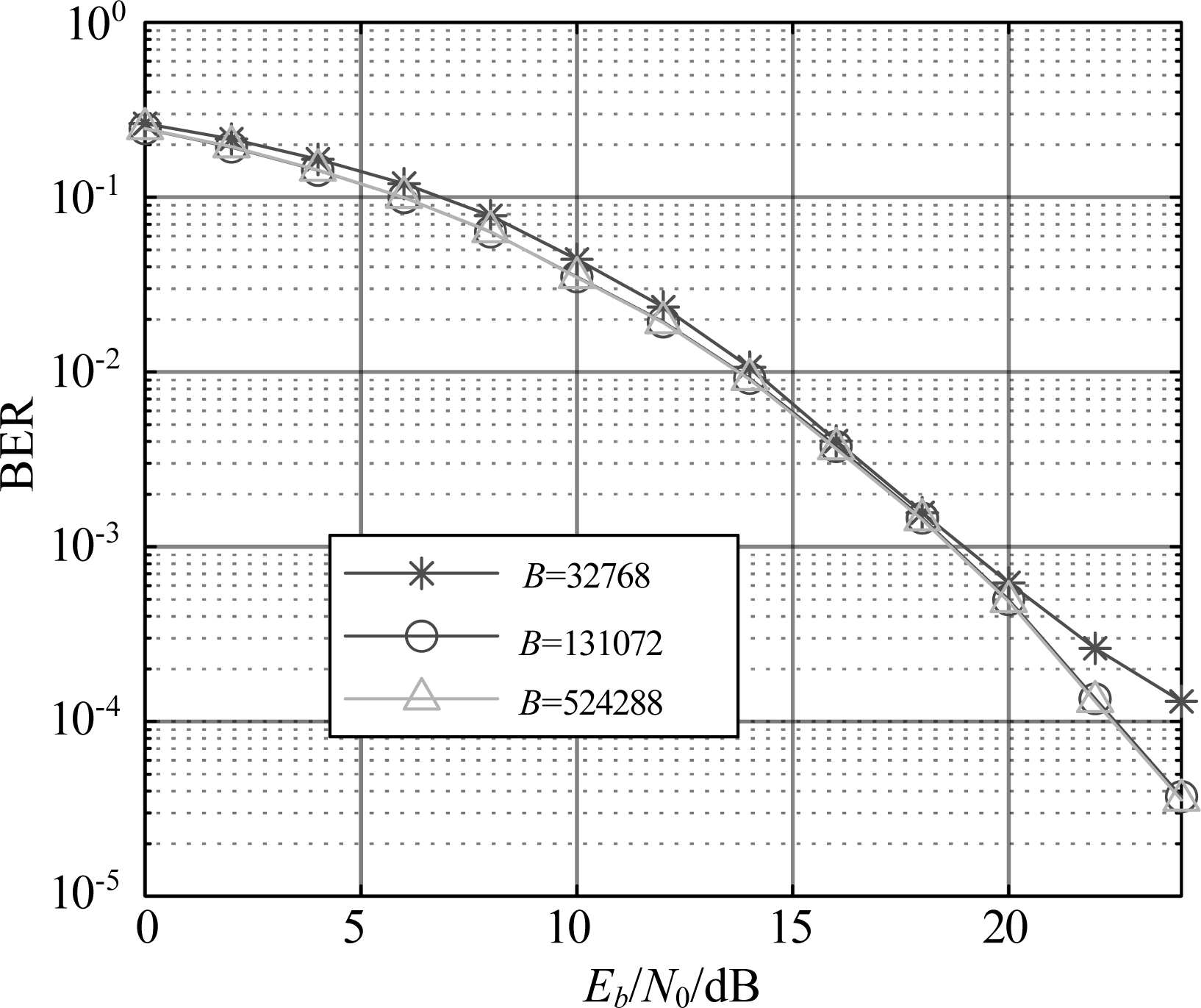
图6 不同训练数据量下DL-SC-FDE的BER性能
Fig.6 BER performances of DL-SC-FDE under different amounts of training date
图7为EVA信道模型下DL-SC-FDE与传统SC-FDE算法的BER性能。采用MMSE信道均衡的SC-FDE算法的BER性能最优;DL-SC-FDE的BER性能优于采用LS信道估计的SC-FDE算法;当Eb/N0≥18 dB时,DL-SC-FDE几乎具有与采用MMSE信道估计的SC-FDE算法相同的BER性能;MMSE信道估计需要信道的统计特性,而DL-SC-FDE并不需要信道的统计特性,因此DL-SC-FDE更具有实用性。
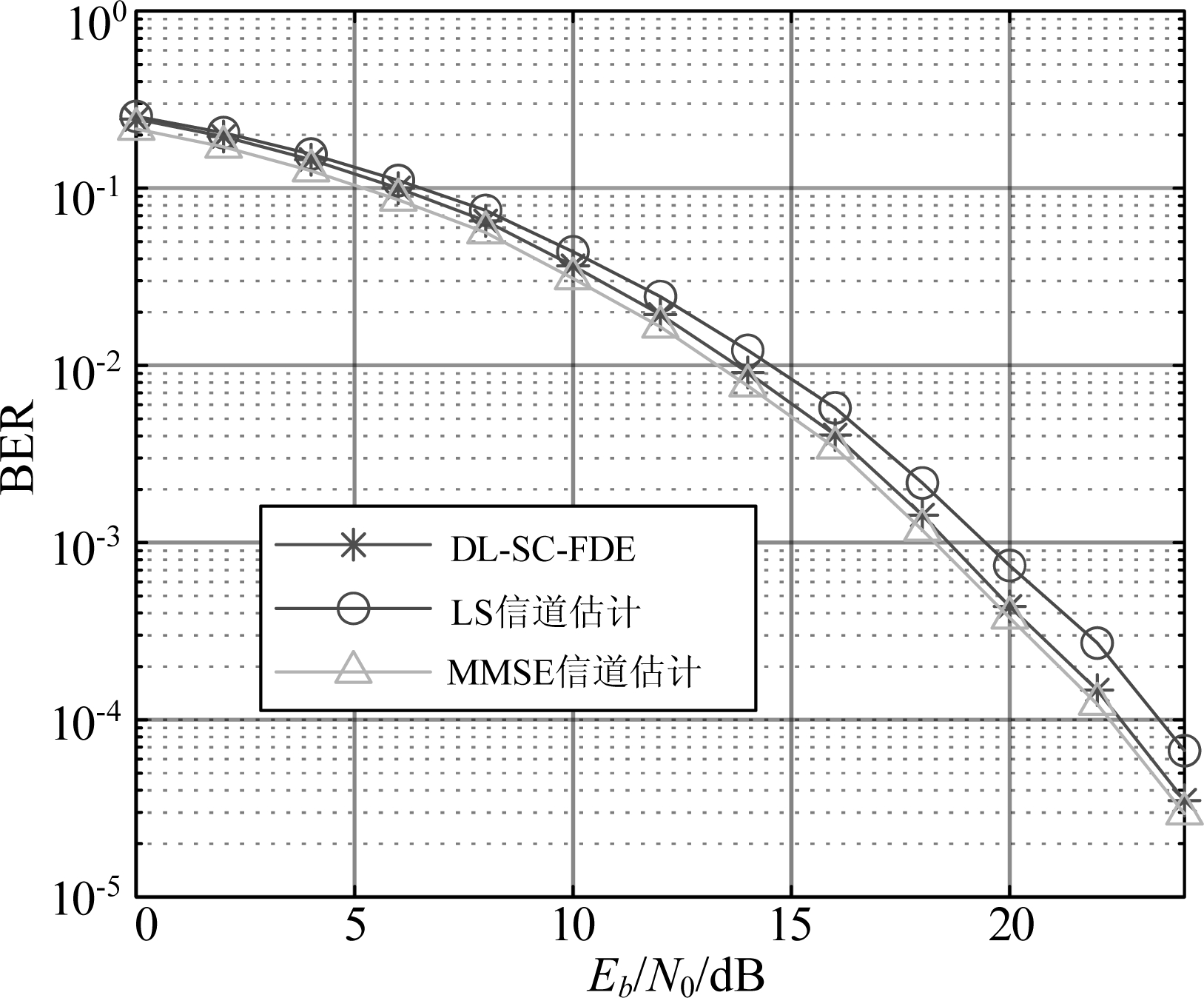
图7 采用新训练机制的DL-SC-FDE与传统SC-FDE算法在EVA模型下的BER性能
Fig.7 BER performances of traditional SC-FDE algorithms and DL-SC-FDE with the new training mechanism under EVA
图8为ETU信道模型下DL-SC-FDE与传统SC-FDE算法的BER性能。DL-SC-FDE仍然具有比采用LS信道估计的SC-FDE算法更优的BER性能,这说明当采用新的训练机制时,DL-SC-FDE不仅可以在EVA信道下正常工作,也可以在ETU信道下正常工作。
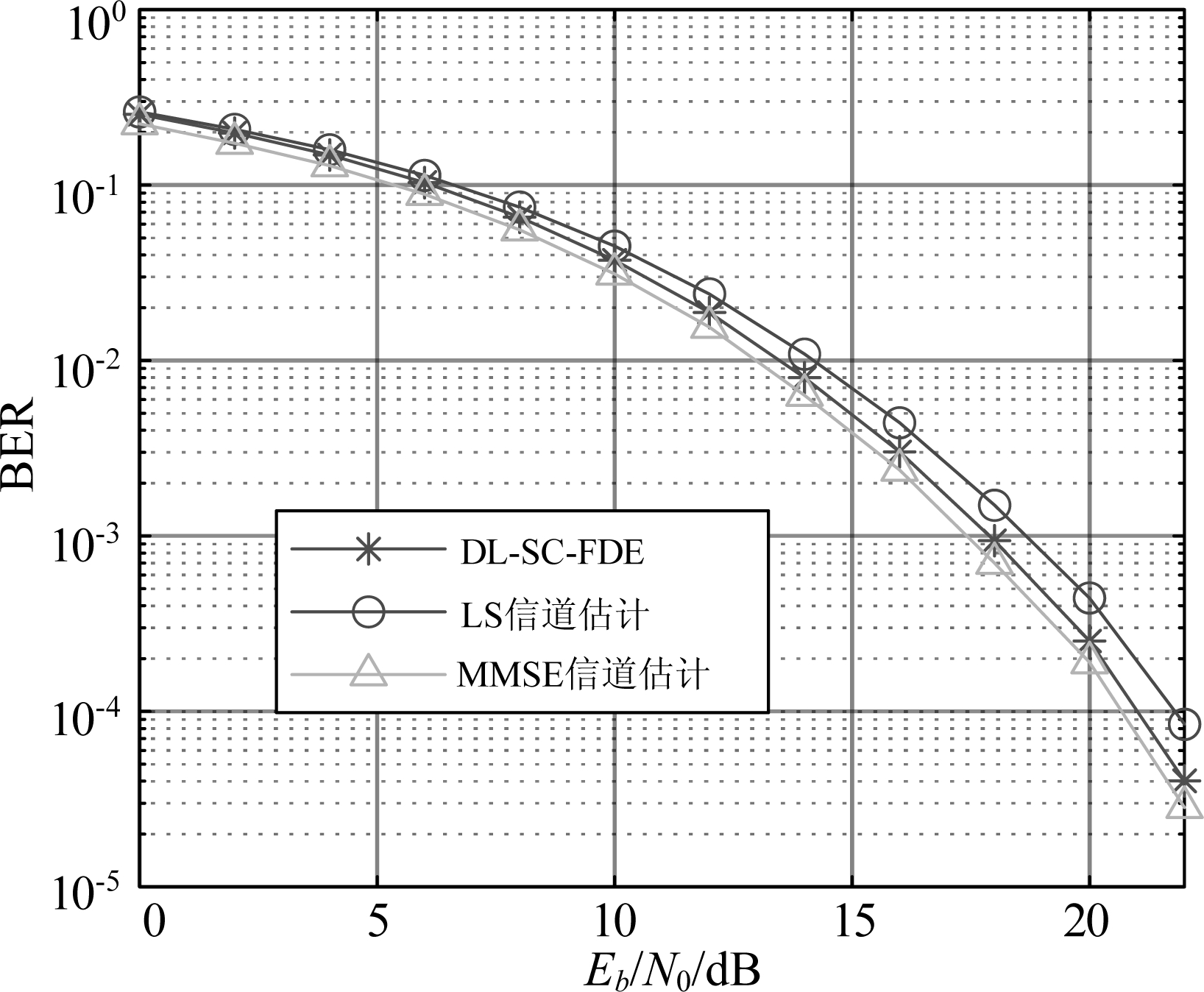
图8 采用新训练机制的DL-SC-FDE与传统SC-FDE算法在ETU模型下的BER性能
Fig.8 BER performances of traditional SC-FDE algorithms and DL-SC-FDE with the new training mechanism under ETU
为了探究DL-SC-FDE优于采用LS信道估计的SC-FDE算法的原因,图9给出了EVA模型下DL-SC-FDE的信道估计性能。DL-SC-FDE的信道估计值由信道估计子网络产生。可以看出,DL-SC-FDE的信道估计性能优于LS信道估计,且当Eb/N0≥18 dB时能达到接近MMSE信道估计的性能,这与图7中的结果一致。
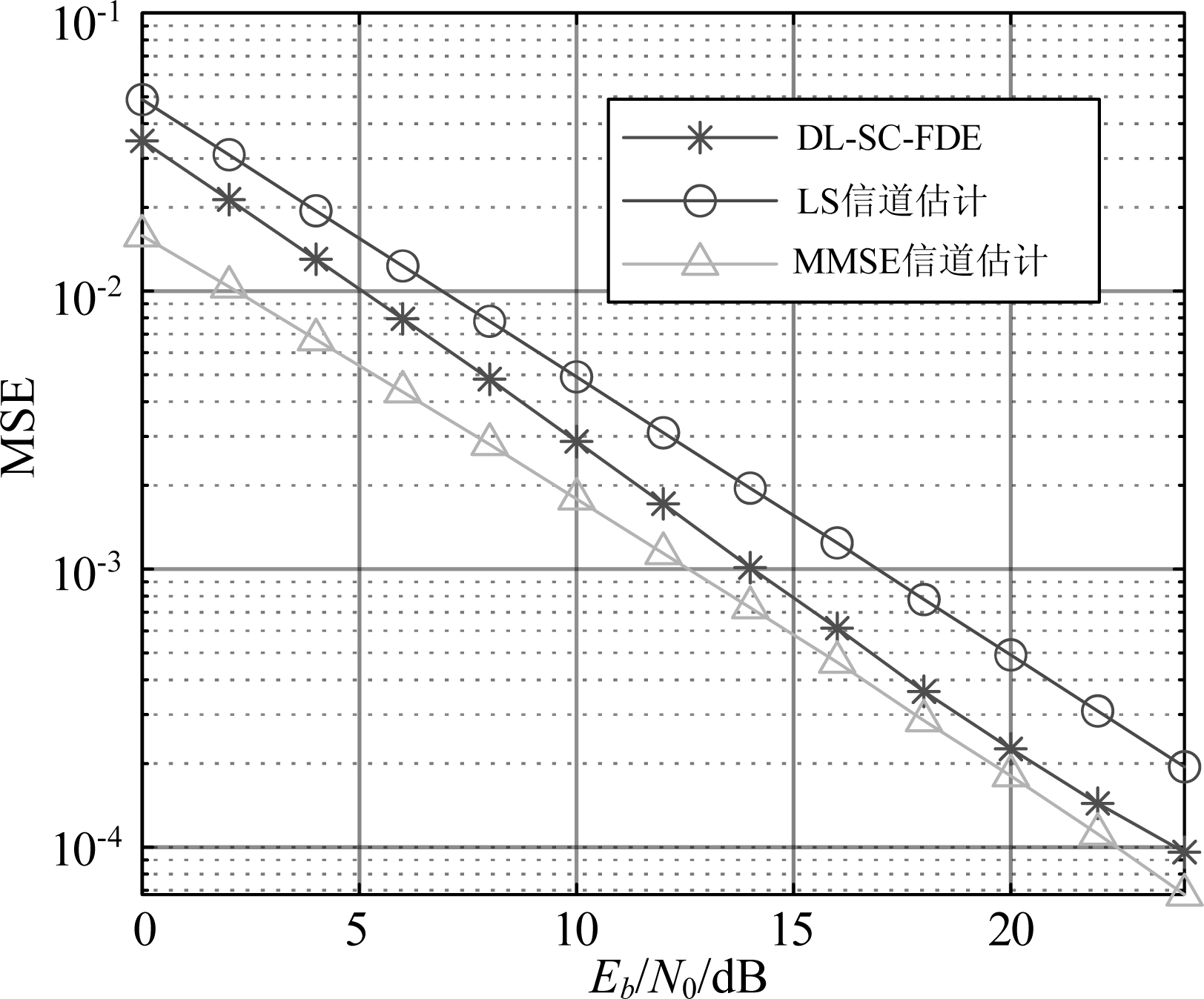
图9 采用新训练机制的DL-SC-FDE与传统SC-FDE算法在EVA模型下的信道估计性能
Fig.9 Channel estimation performances of traditional SC-FDE algorithms and DL-SC-FDE with the new training mechanism under EVA
因为本文提出了一种新的训练机制可以支持最大多径时延满足τ<(e′-Ls)/Rs的不同信道,具有较好的信道泛化能力,所以为了模拟更加真实的信道场景,图10的仿真对EVA模型增加了随机扰动,具体而言,将原EVA多径时延向量中除第一个元素外的所有元素都加上了一个随机扰动δi,δi相互独立且服从区间为(-15 ns,15 ns)的均匀分布,i=1,2,…,8,并将原EVA相对路径功率向量中所有元素也都加上了一个随机扰动
其中
相互独立且服从区间为(-0.5 dB,0.5 dB)的均匀分布,i=0,1,…,8。可以看出,DL-SC-FDE在有随机扰动的EVA模型下仍能正常工作,且其BER性能仍然优于采用LS信道估计的SC-FDE算法,接近采用MMSE信道估计的SC-FDE算法。DL-SC-FDE在信道模型有扰动的情形下也能正常工作。
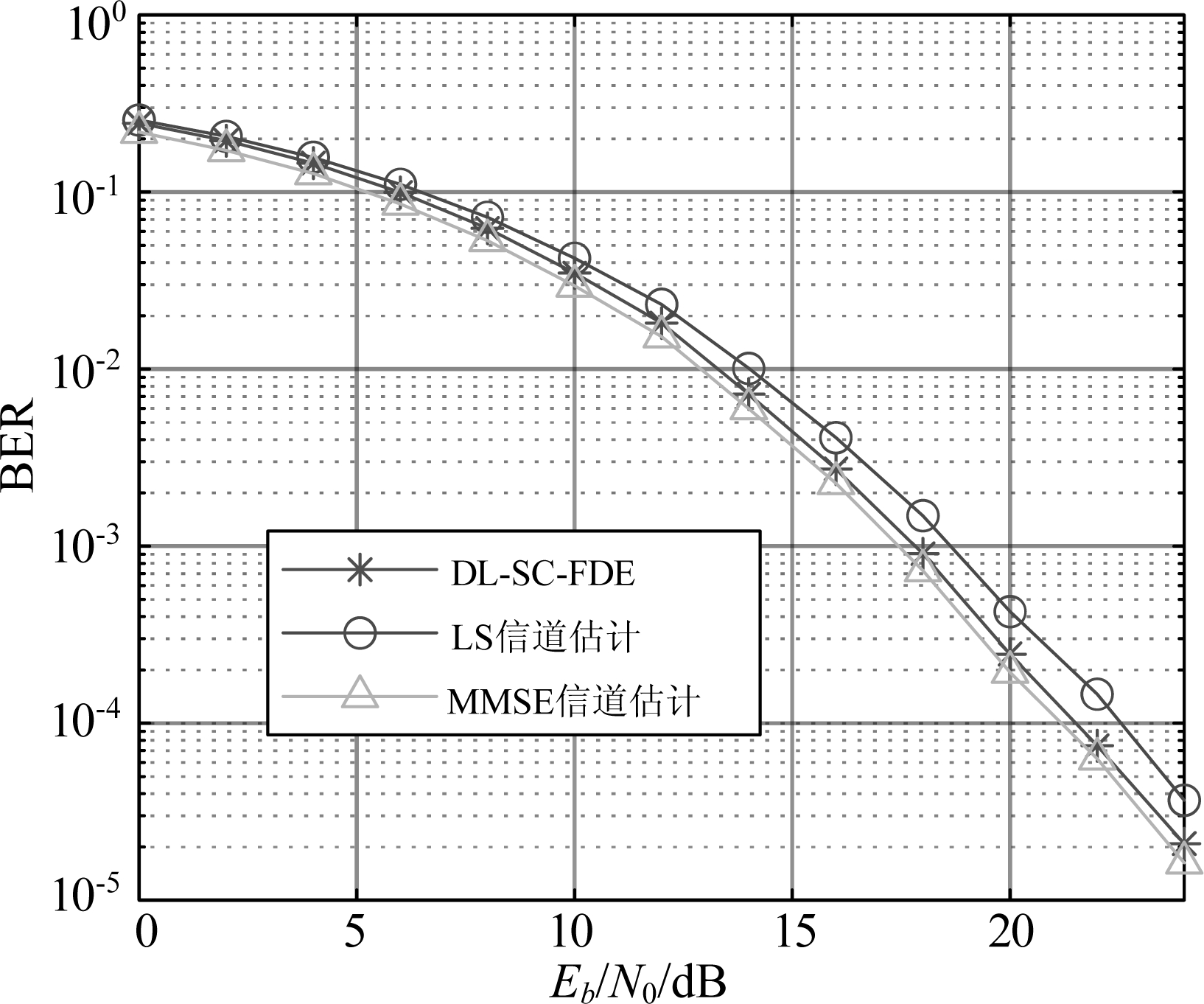
图10 有随机扰动的EVA模型下DL-SC-FDE与传统SC-FDE算法的BER性能
Fig.10 BER performances of DL-SC-FDE and traditional SC-FDE algorithms under EVA model with stochastic disturbance
图11与图12进一步探究了当τ>e′/Rs时DL-SC-FDE与传统SC-FDE算法的BER性能和信道估计性能。在图11和图12中,信道的多径时延向量被设置为[0,50,120,200,230,500,1600,2300,5000,10000]ns,且相对路径功率被设置为[-1,-1,-1,0,0,0,-3,-5,-7,-10]dB。从图11中可以看出,由于最后一条径的时延大于半个UW序列的持续时间,所有SC-FDE算法都出现了BER平层;然而,当Eb/N0≥14 dB时,DL-SC-FDE实现了优于采用MMSE信道估计的SC-FDE算法的BER性能,且其BER平层约为8×10-3,小于其他两种SC-FDE算法的BER平层。而在图12中,DL-SC-FDE的信道估计性能仅优于LS信道估计,没有优于MMSE信道估计。结合图11和图12的结果可知,DL-SC-FDE通过联合优化学习到了一种更稳健的信道均衡方式。
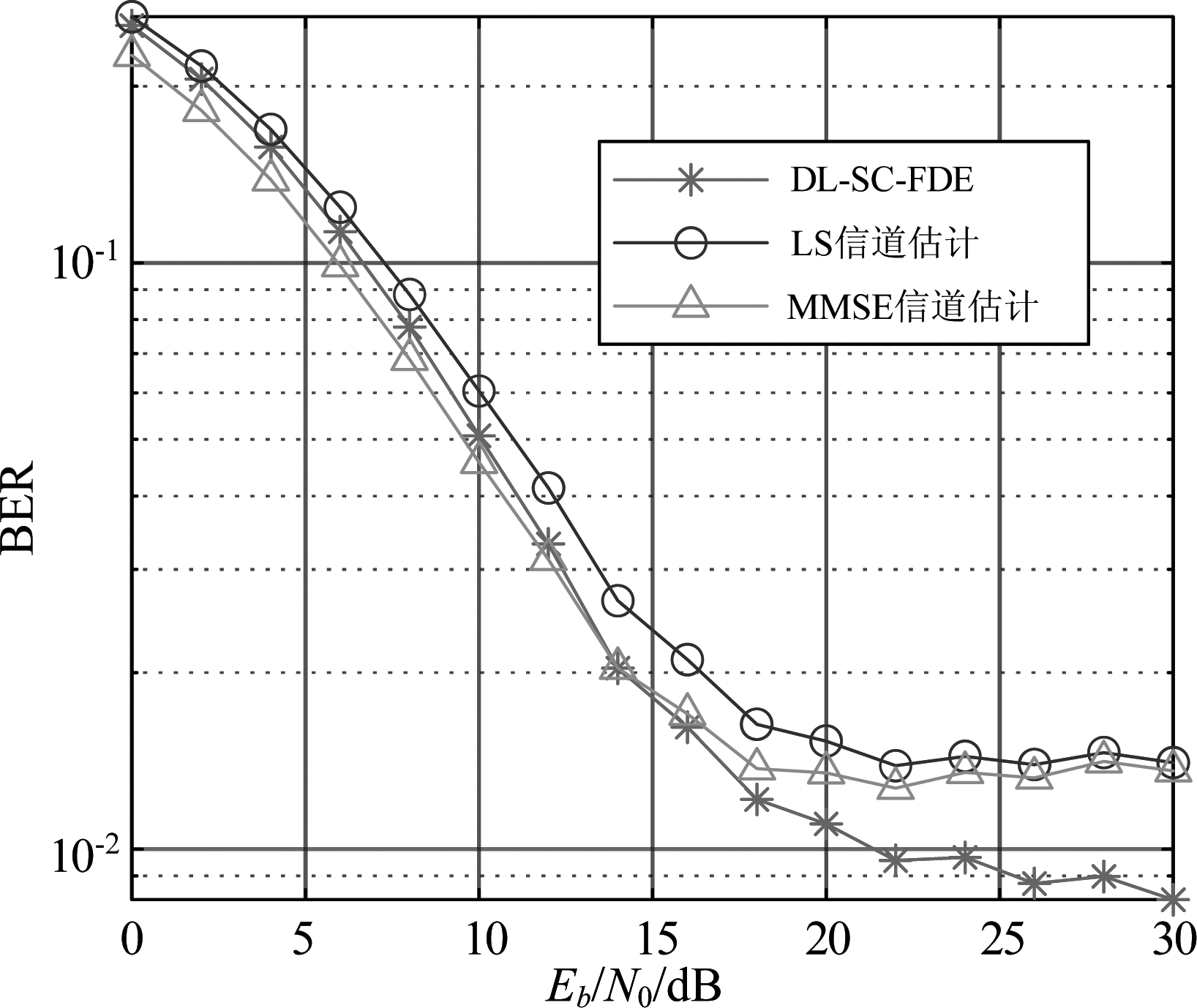
图11 当
时DL-SC-FDE与传统SC-FDE算法的BER性能
Fig.11 BER performances of traditional SC-FDE algorithms and DL-SC-FDE when
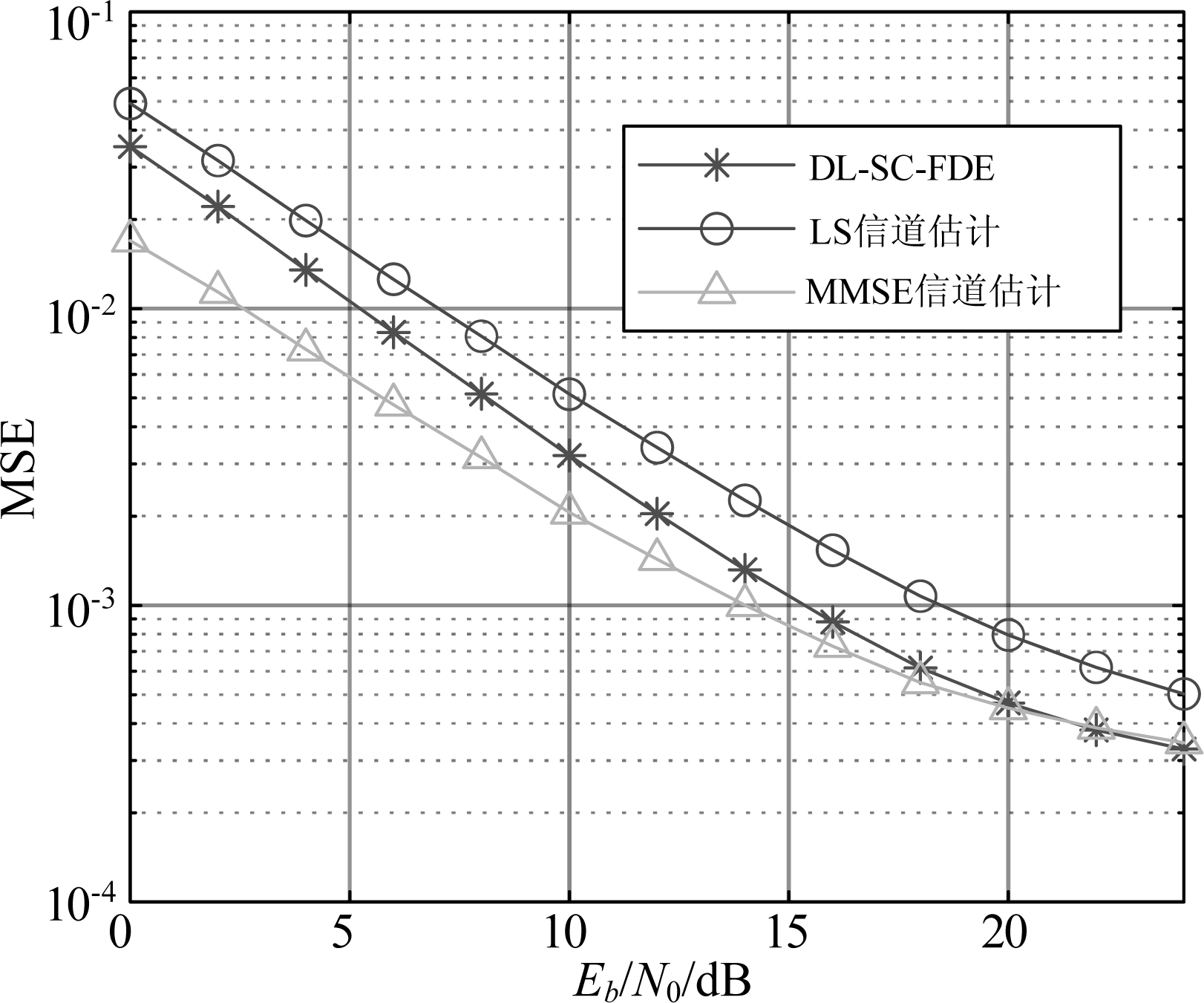
图12 当时DL-SC-FDE与传统SC-FDE算法的信道估计性能
Fig.12 Channel estimation performances of traditional SC-FDE algorithms and DL-SC-FDE when
图13给出了DL-SC-FDE在符号率Rs=3.84 MBaud下训练并在符号率
下测试的BER性能,测试信道为EVA信道。可以看出,虽然DL-SC-FDE在符号率Rs=3.84 MBaud下进行训练,但是由于
在符号率
下仍能正常工作,并得到接近采用MMSE信道估计的SC-FDE技术的BER性能。对于任意的码速率Rs,只要其满足τ<(e′-Ls)/Rs,DL-SC-FDE都可以支持。
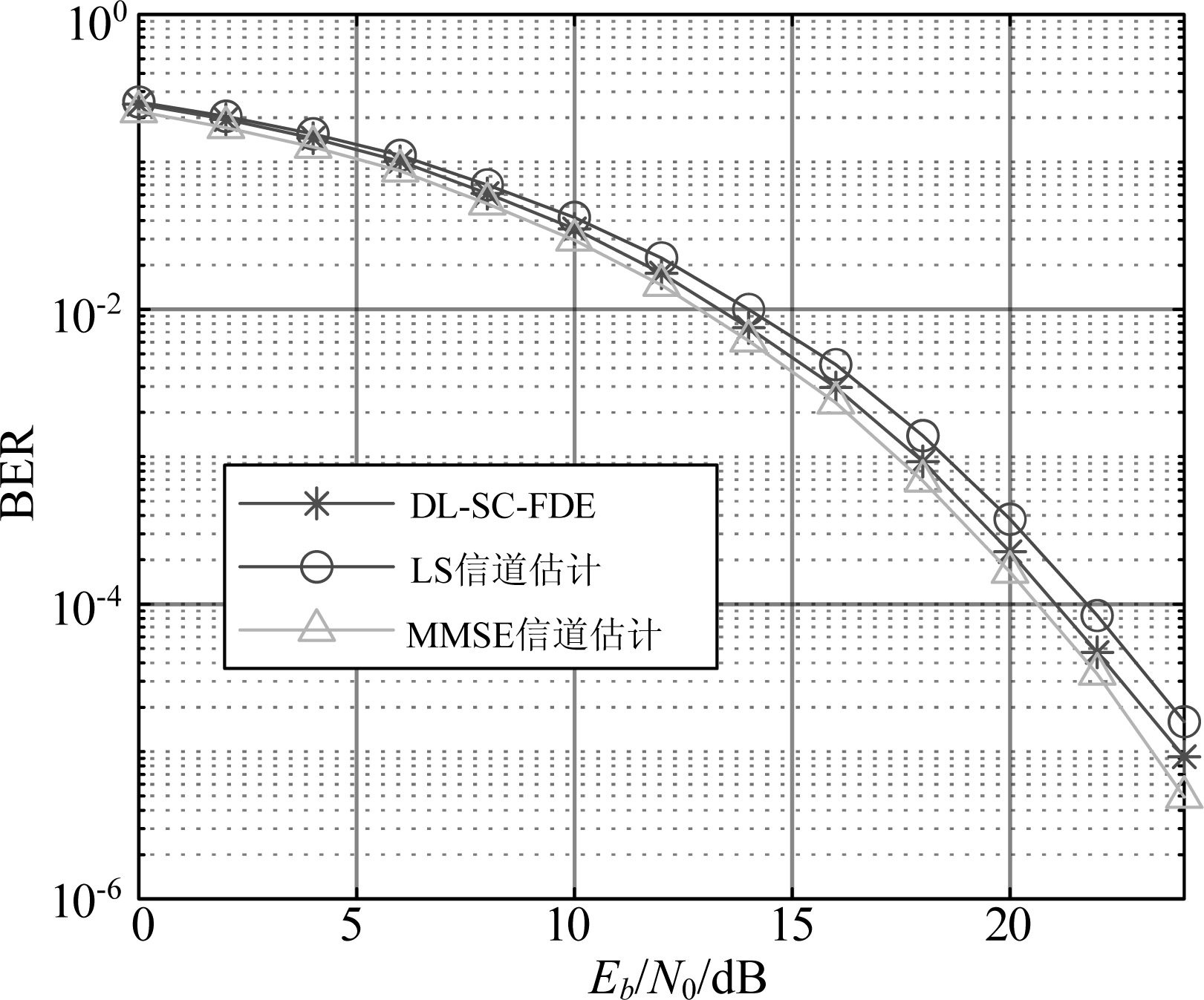
图13 在Rs=3.84 MBaud下训练并在
下测试的DL-SC-FDE的BER性能
Fig.13 BER performances of DL-SC-FDE when the training symbol rate is 3.84 MBaud and the testing symbol rate is 8 MBaud
图14给出不同滚降系数下DL-SC-FDE的BER性能,信道模型为EVA,注意,网络仅在滚降系数为0.3的条件下进行训练。从图中可以发现,不同滚降系数下DL-SC-FDE的BER性能大致相同,这说明DL-SC-FDE可以适应不同的滚降系数。
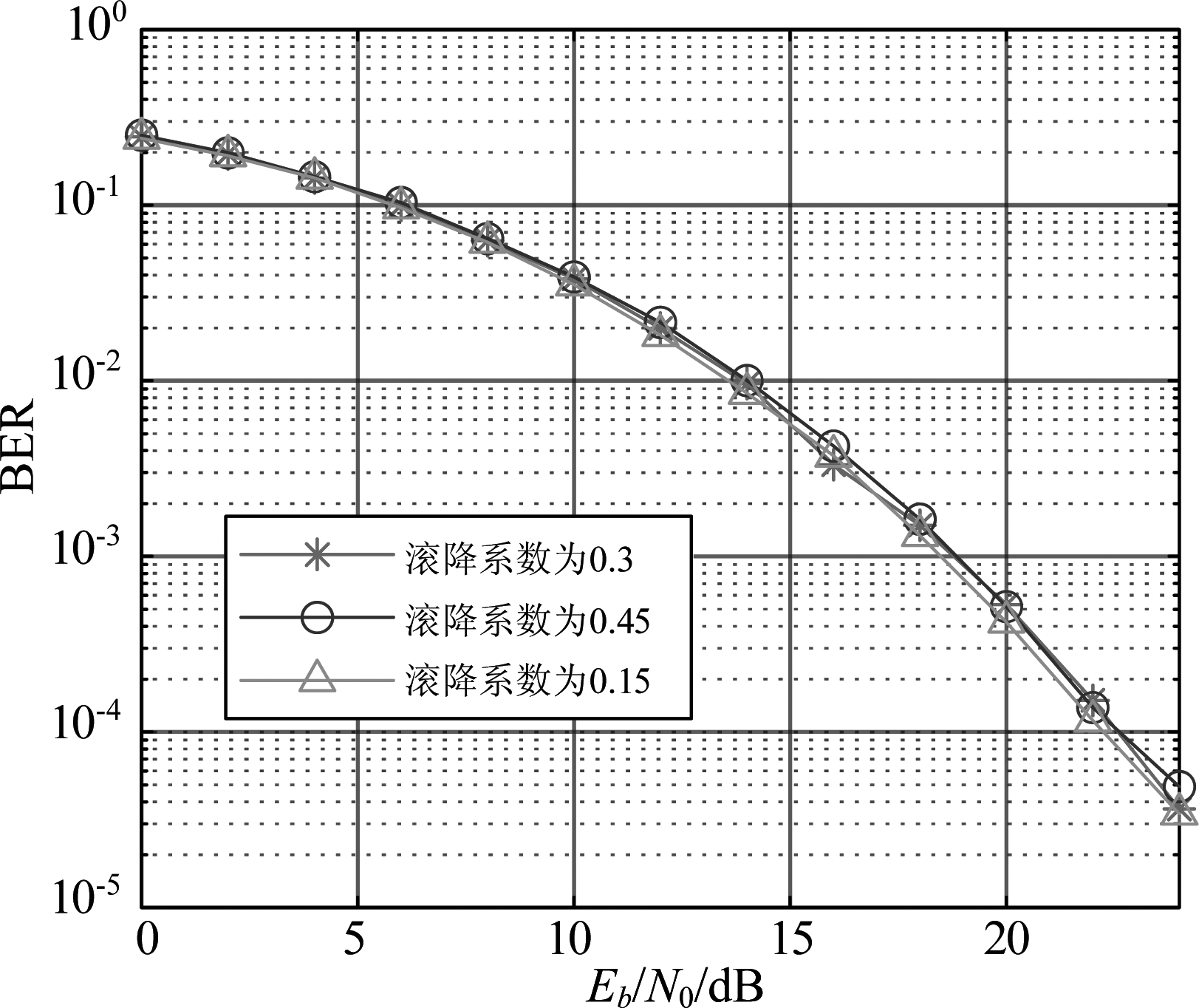
图14 不同滚降系数下DL-SC-FDE的BER性能
Fig.14 BER performances of DL-SC-FDE under different roll-off factors
在图15中,c被更改为3,因此每帧的开销由原来的约1.96 dB升高到了约2.69 dB,此时DL-SC-FDE的BER性能仍然接近采用MMSE信道估计的SC-FDE算法,对比图15和图7可知,当c被更改为3时,所有SC-FDE算法的BER性能都出现了少量的退化,这说明,虽然将c增大到3时信道估计和噪声功率估计的性能会提升,但这些提升对BER性能的改善仍然小于增大c所带来的开销提升。
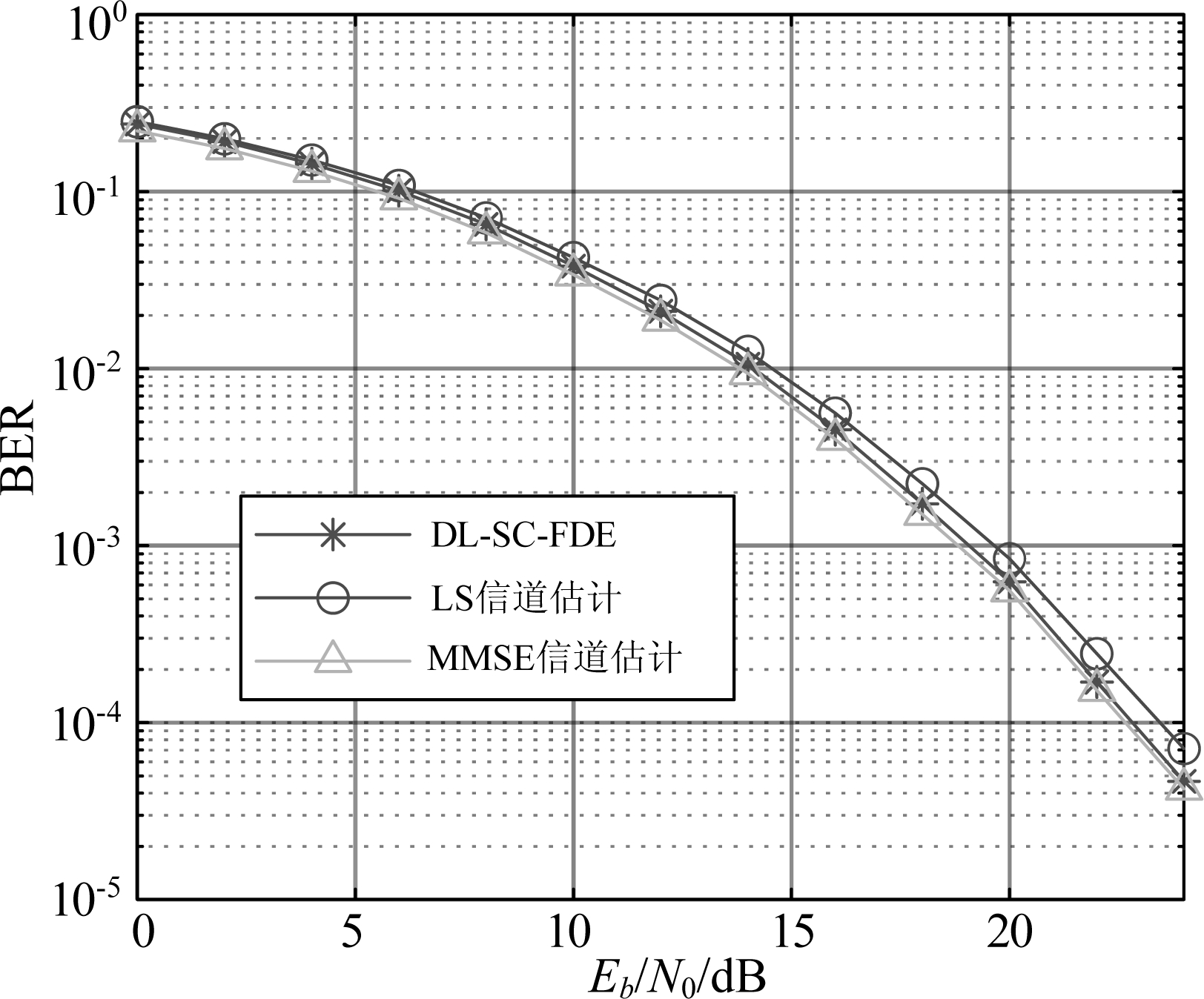
图15 c=3时EVA模型下DL-SC-FDE
与传统SC-FDE算法的BER性能
Fig.15 BER performances of DL-SC-FDE and traditional SC-FDE algorithms under EVA model when c=3
DL-SC-FDE虽然具有更高的复杂度,但是其主要包含的运算仅为乘加运算和Relu函数的非线性运算,这些运算在深度学习专用芯片上可以得到非常高效的执行,其运行时延并不大。此外,DL-SC-FDE的BER性能优于采用LS信道估计的SC-FDE算法,接近采用MMSE信道估计的SC-FDE算法,而MMSE信道估计需要信道统计特性,实际无线信道一般是不断变化的,稳定的统计特性难以获得,因此MMSE信道估计的实用性较低,多被用于仿真中的性能对比分析。本文通过仿真展示出了DL-SC-FDE具有较高的适应能力,经过一次训练后,支持不同的信道、不同的符号率、不同的成型滤波滚降系数、含有扰动的信道模型等,且DL-SC-FDE不需要信道统计特性。
5 结论
本文提出了一种基于深度学习的SC-FDE算法,实现了对信道均衡、信道估计和噪声功率估计的联合优化,通过对每一个模块设计一个子网络,所提算法极大地降低了网络收敛所需的训练数据量,此外,本文提出了一种新的训练机制,通过平等地对待每一条径,提高了网络的信道泛化能力,仿真结果表明,所提算法具有比基于LS信道估计和MMSE信道均衡的SC-FDE算法更优的BER性能,且所提算法不需要信道统计特性,具有较高的应用价值。
[1] CHENG Xiantao, YANG Ying, LI Shaoqian. Joint compensation of transmitter and receiver I/Q imbalances for SC-FDE systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(8): 8483- 8498.
[2] 顾晨阳, 李丁山, 李含辉. 单载波频域均衡系统信道估计的粒子滤波方法[J]. 信号处理, 2014, 30(4): 483- 488.
GU Chenyang, LI Dingshan, LI Hanhui. Channel estimation of single carrier frequency domain equalization system using particle filter method[J]. Journal of Signal Processing, 2014, 30(4): 483- 488.(in Chinese)
[3] LIM K, KIM H, HONG T C, et al. Wideband transmission for unmanned aircraft systems[C]∥2018 International Conference on Information and Communication Technology Convergence (ICTC). Jeju, Korea (South). IEEE, 2018: 1518-1520.
[4] 杨大龙, 陈大海, 邝文, 等. SC-FDE宽带航空数传接收机的设计与实现[J]. 电讯技术, 2017, 57(12): 1408-1414.
YANG Dalong, CHEN Dahai, KUANG Wen, et al. Design and implementation of a broadband aeronautical high data rate receiver using SC-FDE[J]. Telecommunication Engineering, 2017, 57(12): 1408-1414.(in Chinese)
[5] 刘梦, 刘威, 周志刚. 基于线性因子更新的频域迭代判决反馈均衡[J]. 信号处理, 2019, 35(10): 1739-1746.
LIU Meng, LIU Wei, ZHOU Zhigang. Frequency domain iterative decision feedback equalization based on linearization factor update[J]. Journal of Signal Processing, 2019, 35(10): 1739-1746.(in Chinese)
[6] DUAN Hao, YU Xinle, HOU Yahui. Efficient channel parameters estimation design for SC-FDE in HF wireless communications[C]∥2015 8th International Congress on Image and Signal Processing (CISP). Shenyang, China. IEEE, 2015: 1338-1342.
[7] 张晟歌. 单载波频域均衡系统分析及MATLAB仿真[J]. 软件, 2017, 38(10): 152-157.
ZHANG Shengge. Analysis and MATLAB simulation of single carrier frequency domain equalization system[J]. Computer Engineering & Software, 2017, 38(10): 152-157.(in Chinese)
[8] O’SHEA T, HOYDIS J. An introduction to deep learning for the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 563-575.
[9] YE Hao, LI G Y, JUANG B H. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114-117.
[10] GANESH S, SAYEE SUNDER V, THAKRE A. Performance improvement in Rayleigh faded channel using deep learning[C]∥2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI). Bangalore, India. IEEE, 2018: 1307-1312.
[11] AL-BAIDHANI A, FAN H H. Learning for detection: A deep learning wireless communication receiver over Rayleigh fading channels[C]∥2019 International Conference on Computing, Networking and Communications (ICNC). Honolulu, HI, USA. IEEE, 2019: 6-10.
