1 引言
低轨道(Low Earth Orbit, LEO)卫星星座通信系统因其巨大的发展潜力和广阔的应用前景成为世界各国争相研究的热点之一,近几年各个国家分别在LEO星座建设领域进行了竞争,同时也带来了频率资源紧缺的问题。目前,国际电信联盟(International Telecommunication Union, ITU)负责对空间网络频率资源根据业务类型以及地理区域进行统一的划分,L/S等移动业务的黄金频段早已被瓜分殆尽,Ku/Ka等固定宽带业务的频段也即将耗尽,呈现出用频紧张的局面[1]。相比较而言,地面无线通信系统的频谱共享技术已经发展的较为成熟。如文献[2]中提出的次级用户功率优化的方法、文献[3]中提出了波形设计的方法以及文献[4]中次级用户采用多天线收发的方法等。然而针对卫星通信领域日益增长的通信服务需求,传统的、静态的、单一的频率分配模式不再适用,因此当前空间信息领域亟需解决的问题之一就是探索更加高效并且可靠的频率分配方式。
将认知无线电技术与卫星通信相结合被认为是解决未来空间信息网络频谱资源供需矛盾的一大有效途径[5]。通过多个系统共享同一频率,充分发掘并利用空闲的频谱资源,来改善频谱资源利用效率,同时缓解卫星通信网络中频谱资源紧缺的现状。双卫星共存网络是指两个卫星网络共用一个频率对各自用户进行服务。由于近年来互联网星座发展趋势甚好,未来将会有愈来愈多的非静止轨道(Non-geostationary orbit, NGSO)星被发射至太空,实现全球范围覆盖[6]。因此在地球同步轨道(Geostationary Earth Orbit)和NGSO卫星系统之间探寻适用的频谱共享策略显得尤为重要。对于固定宽带业务而言,用频频率较高,卫星和用户的天线均具有较强的指向性。NGSO卫星处于高速在轨运动状态,因此NGSO和GEO系统之间的相互干扰会随着卫星的运动时变。经分析,干扰最为恶劣的情况即GEO卫星、NGSO卫星和地面站在一条直线上,此时产生的干扰极为严重,一般称为共线(In-line)干扰。共线干扰时,频率共享的卫星系统的通信性能将急剧下降甚至瘫痪无法正常进行工作。针对共视干扰场景,OneWeb系统中引进了一种“渐进倾斜”技术,当卫星运行到赤道附近时,调整卫星姿态,逐渐倾斜卫星来避免与GEO卫星系统之间的相互干扰[7]。但是,该种技术需要消耗一定的燃料,对卫星的寿命造成一定的损害;文献[8]中针对GEO卫星系统和MEO卫星系统的共存,提出了一种自适应功率控制的技术。然而,采用自适应功率控制技术时,通常为了确保主用户正常工作,会牺牲掉一些次级用户的性能,造成次级用户频谱效率的损失;文献[9]中出现共视干扰时NGSO 地面站在可视范围内选择另一个可用的NGSO卫星进行通信。但是采用该种方法需要保证有足够多的卫星数目来提供多重覆盖;文献[10]中共视干扰发生时,主动停止次级用户的工作,有限保证主用户的工作。但是该种情况下,系统需要能够容忍链路临时中断带来的影响。
针对GEO卫星通信系统与LEO卫星通信系统频谱共存场景中存在的共视干扰问题,本文采用低轨分布式编队卫星系统通过组阵的方式联合处理电磁信号,类似于地面5G网络研究中多基站的协调传输[11]。本文将卫星编队波束成形技术与频谱共享相结合,综合考虑卫星通信系统长传播时延导致的阵列导向矢量存在一定误差,基于分布式卫星编队联合处理的思想提出了一种鲁棒波束成形算法,从空间域功率隔离角度解决了高低轨卫星通信系统上行链路频谱共享时的共视线干扰问题。对已有频谱感知技术进行适应性修正和补充,以适配卫星动态场景下的频谱共享。
2 GEO/LEO频谱共享模型
如图1所示,主要考虑地面用频设备与卫星通信系统之间的上行链路传输,整个通信系统工作在Ku频段。在双卫星通信系统中,GEO卫星系统充当主用户,LEO卫星通信系统为次级用户,双卫星系统在上行链路传输时共用同一频段。与卫星进行通信的地面用户均采用定向天线,时刻指向各自系统的卫星。LEO卫星编队在整个运行过程中对GEO用户方位是未知的。
空间信息网络中卫星分布在立体多层的空间内,低轨编队卫星的位置会随着时间运动而发生变化,因此使用同一频率的各卫星系统之间容易发生频谱混叠。干扰最为恶劣的情况即GEO卫星、NGSO卫星和地面站在同一条直线上,此时产生的干扰极为严重,称为共线(In-line)干扰[8],如图2所示。共视干扰会对低轨卫星通信系统产生极大的干扰,严重时甚至会导致低轨卫星通信系统的瘫痪。
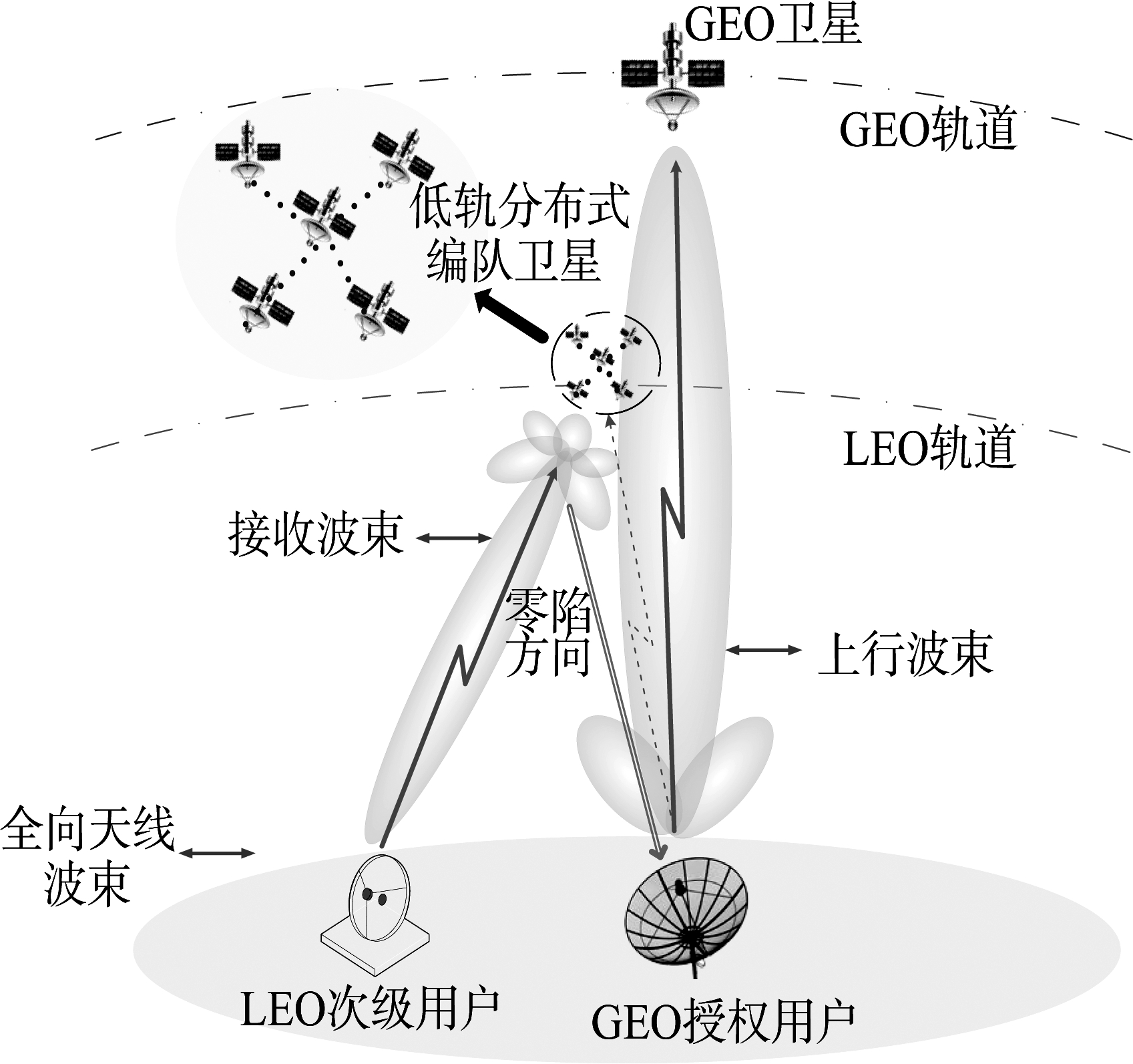
图1 LEO卫星和GEO卫星频率共存示意图
Fig.1 Illustration of spectrum sharing between LEO and GEO satellites
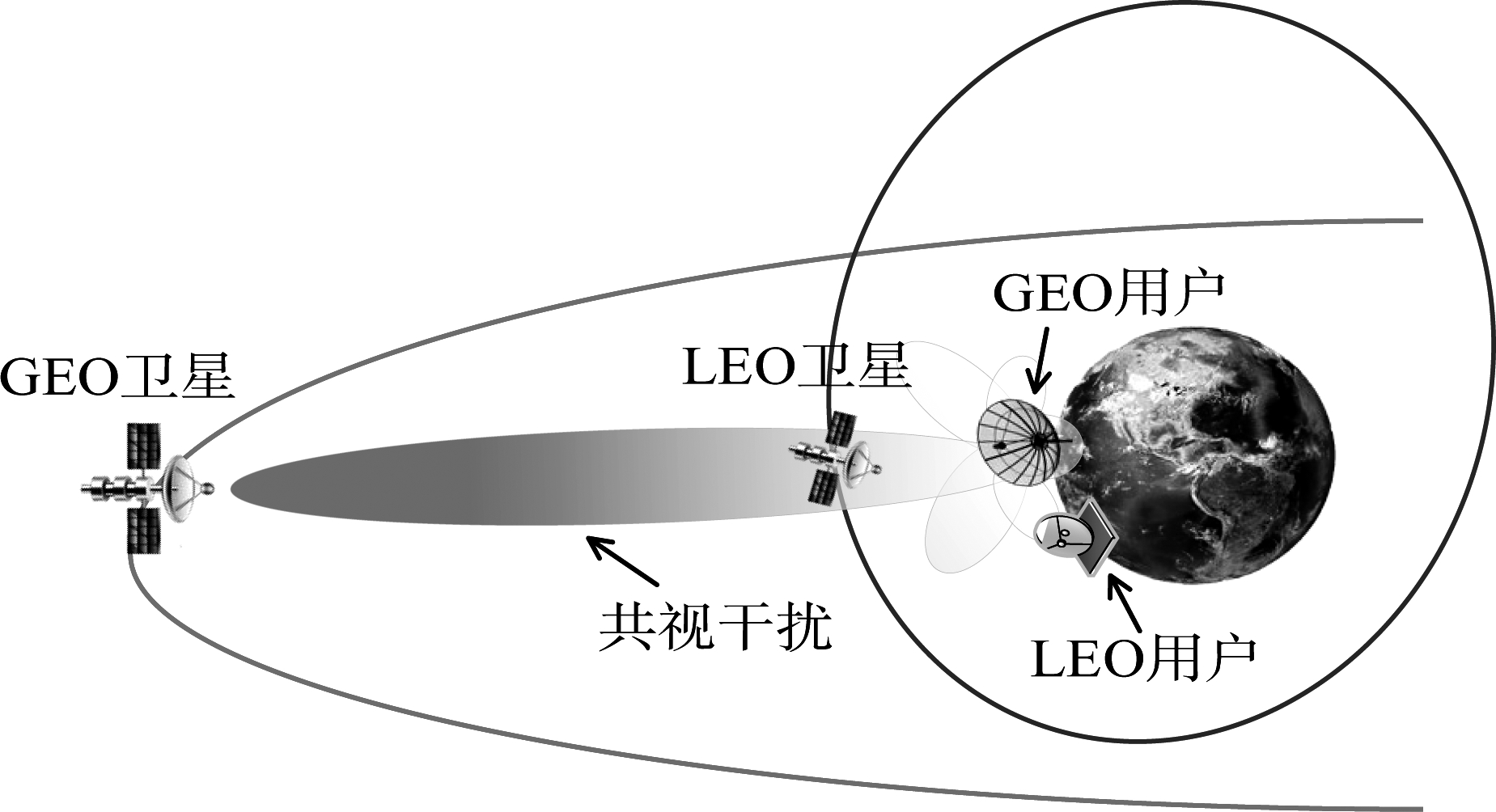
图2 共视线干扰产生示意图
Fig.2 Illustration of In-line Interference
以接收信号质量作为衡量标准,由于LEO卫星的运动特性,当LEO编队卫星簇逐渐运动到GEO卫星通信系统主用户上行波束范围内时,低轨卫星编队在接收到正常通信信号的同时,也会受到GEO用户较强的上行干扰,从而对正常信号的质量造成影响。为了保证低轨卫星的正常工作,其接收信号质量Q应当不小于卫星所需的信号质量门限Qth。如图3所示,卫星簇A在某一时刻位于某一位置上,其接收到某一频率的信号,信号的质量大于该时刻卫星簇A正常解调所需的门限,因此此时A卫星通信系统能够正常工作;而对于B卫星簇来说,接收到的信号质量小于所需的门限,因此B卫星通信系统无法正常工作。在空间信息网络中,应当避免B中情况的出现,才能保证低轨卫星通信系统正常运行。
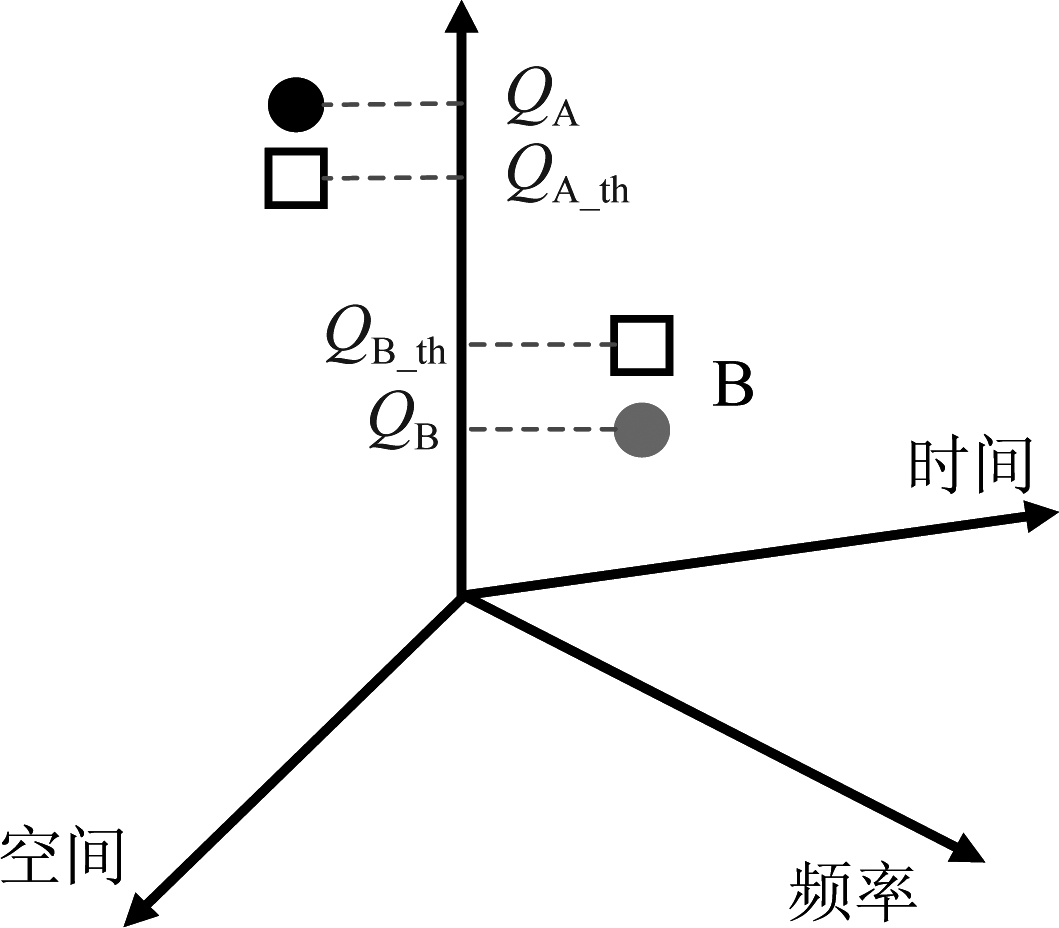
图3 卫星通信系统信号质量模型
Fig.3 Signal quality model of satellite communication system
本文评估信号质量的指标为低轨编队卫星的接收信干噪比(Signal to Interference plus Noise Ratio, SINR),依据信号质量门限阈值,建立模型如下:
∀t∈T,s∈S, f∈F,
s.t.γ(t,s, f)≥γth(t,s, f)
(1)
上式中,T表示运行时间,S表示分布式卫星簇位置集合,F表示网络中的频率集合,t表示某一时刻,s表示当前时刻分布式卫星簇的位置, f表示当前使用的频率,γ(t,s, f)表示当前低轨通信系统接收信号质量,γth(t,s, f)表示当前时刻对应频率所需的最低解调门限。本文中高低轨卫星通信系统均工作在Ku频段,所以信号质量计算公式可表达为:
(2)
其中,C(t,s)为分布式卫星簇正常通信时接收到的有用信号功率,表达式为:
(3)
其中,PTleo表示低轨用户发射信号功率,GTleo为低轨用户发射天线增益。GRleo表示LEO卫星编队接收波束偏移角为φ时的接收天线增益,Lf为自由空间传输损耗:
(4)
d为通信距离;N=kTnB为系统噪声功率,其中k为玻尔磁曼常数,Tn为等效噪声温度,B为带宽。I为低轨卫星编队接收到来自GEO用户的干扰信号功率,表达式为:
(5)
其中,PTgeo表示高轨用户发射信号功率,GTgeo为高轨用户发射天线增益。表达式为[12]:
GTgeo(ϑ)[dB]=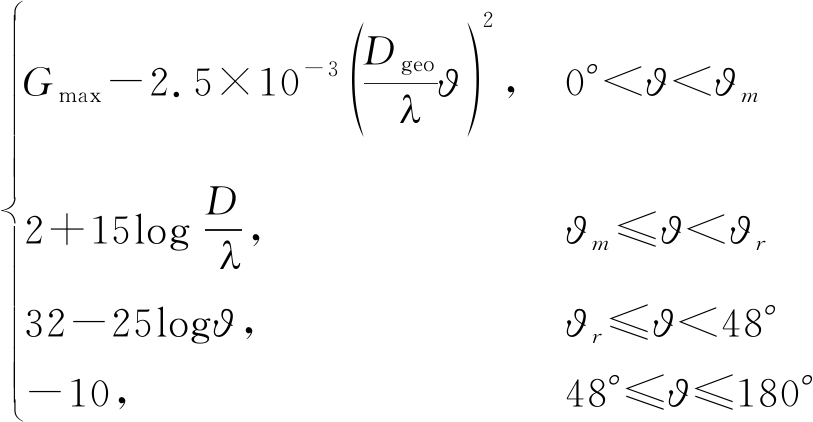
(6)
其中,Gmax表示GEO用户天线的最大增益,ϑ为波束偏移角度,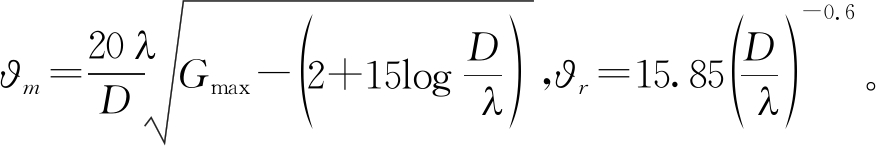
如图4所示,φ为低轨编队卫星波束中心的指向和GEO用户之间的夹角,ϑ为GEO用户波束中心的指向和低轨编队卫星之间的夹角,d为两者之间的距离。随着低轨编队的运动,两者之间相对位置会发生变化,因此ϑ,φ,d都是关于时间t的因变量。
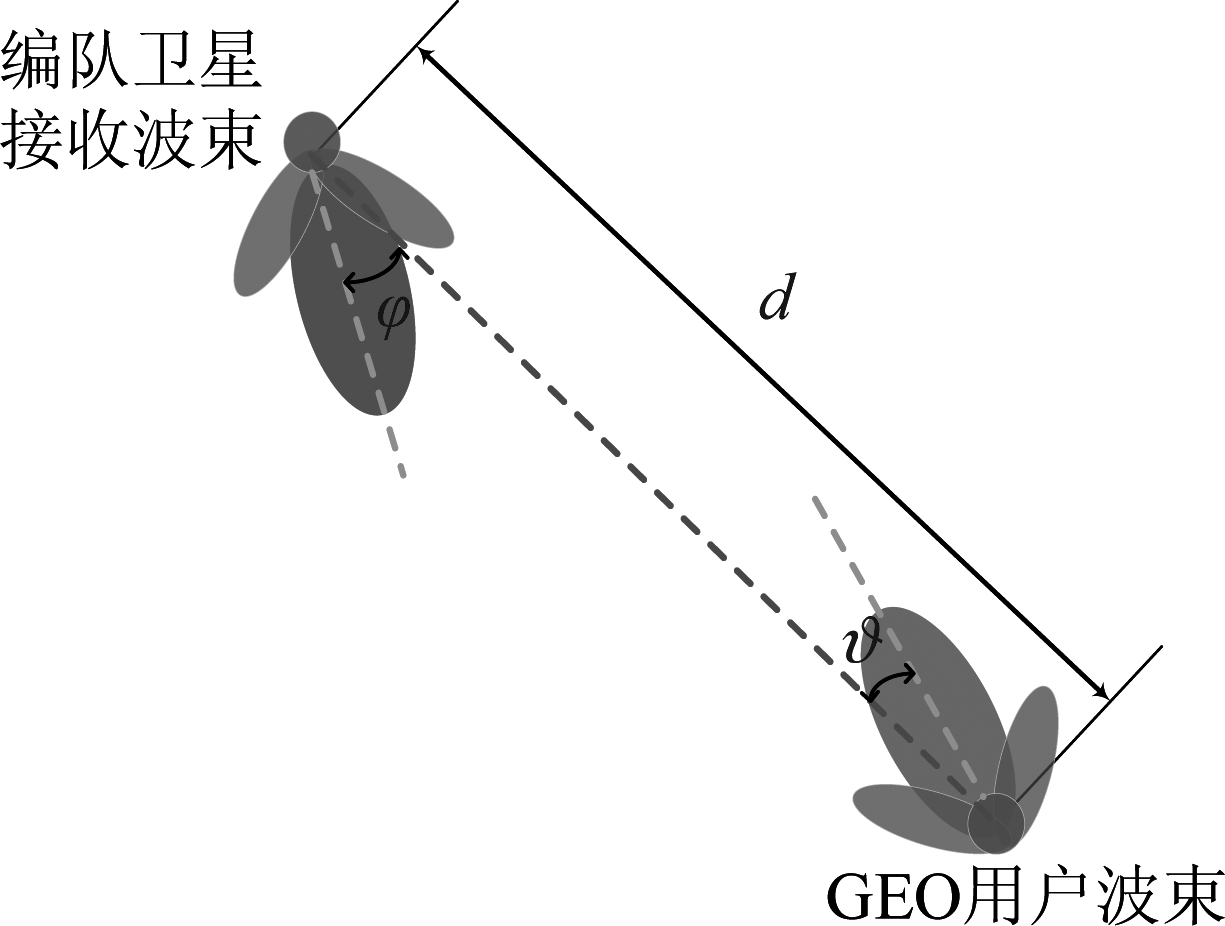
图4 发送端与接收端之间天线指向的相对位置关系
Fig.4 The relative position of the antenna pointing between the sender and receiver
因此,式(1)可以表示为:
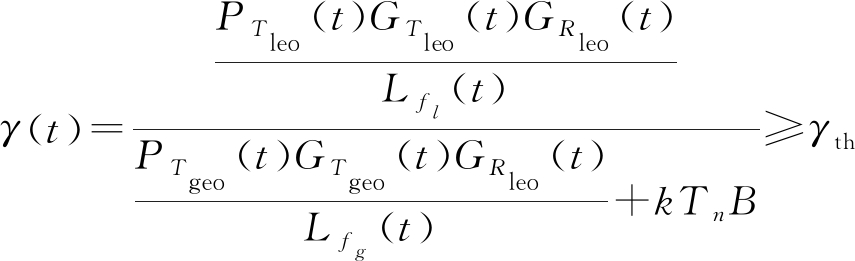
(7)
3 GEO/LEO频谱共享方法
本文基于分布式卫星编队联合处理的思想,从空间域功率隔离角度解决了高低轨卫星通信系统上行链路共用频谱GEO用户对于LEO卫星共线干扰问题。通过调整编队卫星的接收方向图指向,使其波束主瓣指向与其通信的低轨卫星通信系统次级用户,波束零陷方向对准GEO卫星通信系统主用户,主动抑制GEO卫星通信系统主用户对于LEO卫星通信系统次级用户的干扰,确保LEO次级用户的通信性能。流程框图如图5所示,具体步骤如下:
图5 GEO/LEO卫星系统频谱共享流程图
Fig.5 The flow chart of GEO/LEO satellite system for spectrum sharing
步骤1 低轨编队卫星进行信号数据采集。
步骤2 低轨编队卫星接收端对接收到的数据报头中的独特码进行检测,判断独特码能否被正确解调,来判断系统是否正确接收信号。如果独特码能够被正确解调,则进入步骤3;否则,进入步骤4。
步骤3 最大比合并接收:若低轨卫星接收信号中独特码能够被正确解调,说明此时信号被正确捕获并且信号可以同步,此时认为不存在干扰。低轨卫星编队采用最大比合并的方式对LEO用户信号进行接收,直接进入步骤6。
步骤4 低轨编队卫星协作波束成形:采用鲁棒波束成形算法来调整编队卫星的权值,从而调整编队卫星的接收方向图指向。使其波束主瓣指向与其通信的低轨卫星通信系统次级用户,波束零陷方向对准GEO卫星通信系统主用户。进入步骤5。
步骤5 接收端判断LEO用户信号能否被正确解调,如果接收到的LEO用户信号能被正确解调,则说明在GEO/LEO频率共享情况下采用该算法能够有效降低GEO用户的干扰,进入步骤6;如果未能成功解调,随着低轨卫星编队的运动,时间进入下一帧,回到步骤4,采用鲁棒自适应波束成形算法重新调整编队卫星的权值。
步骤6 低轨卫星通信系统与LEO用户建立通信。
3.1 最大比合并多星协作接收
若低轨卫星接收信号中独特码能够被正确解调,说明此时信号被正确捕获并且信号可以同步,此时认为不存在干扰,低轨卫星编队采用最大比合并(maximum ratio combining, MRC)多星协作接收的方式对LEO用户信号进行接收。图6为由M颗卫星组成的分布式编队卫星的组阵模型,记第m颗卫星确定的轨道位置信息为Pm(rm,θm,φm),俯仰角和方位角分别满足θm∈[0,π]和φm∈[0,2π)。假设由于摄动力的影响,卫星的瞬时实际位置在一个半径为B的球内服从随机分布。
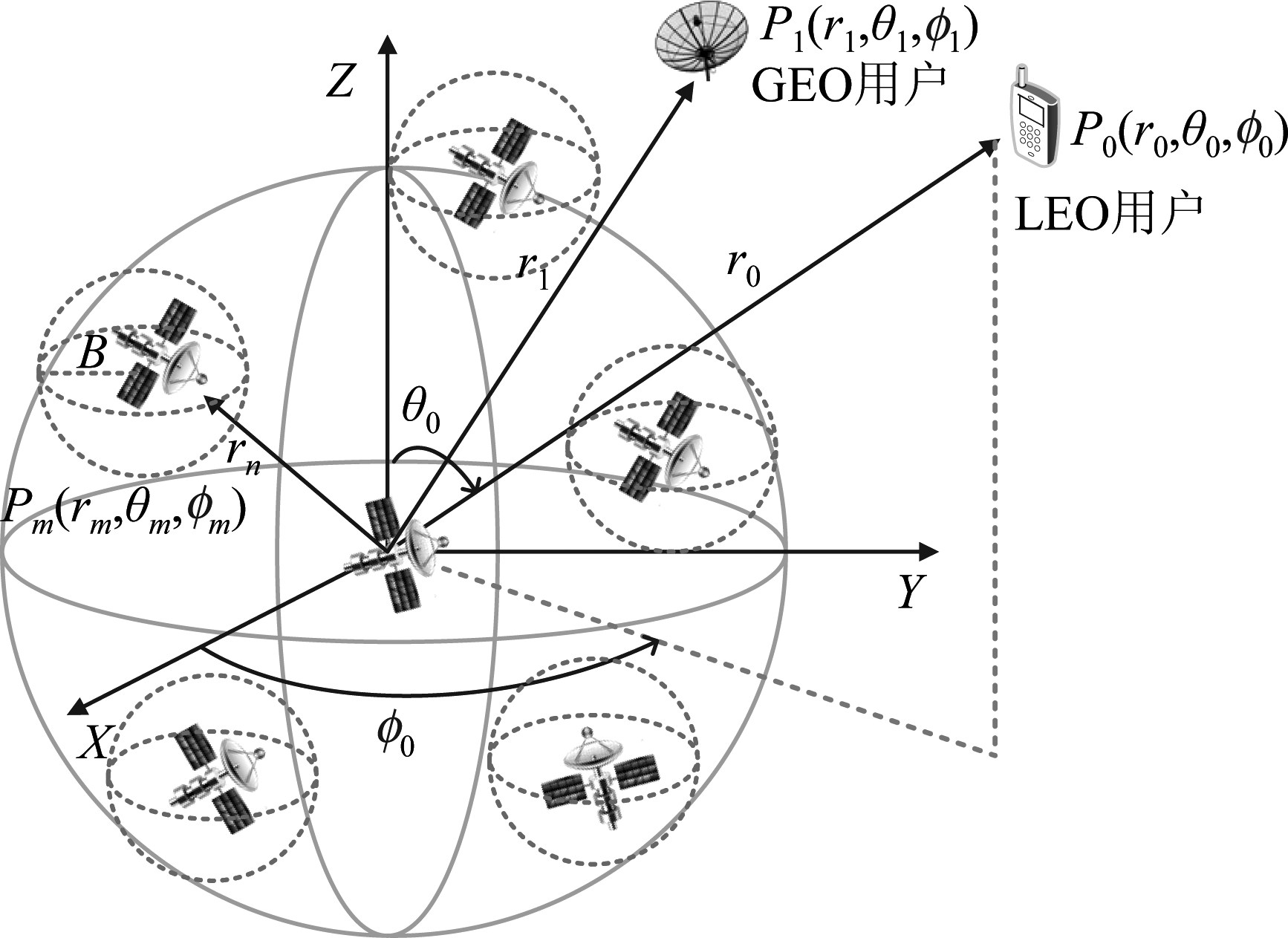
图6 分布式编队卫星组阵模型
Fig.6 Array model of distributed formation satellite
考虑如下的组阵条件:
(1)低轨分布式卫星簇中组阵阵元间的距离远远小于组阵卫星距离地面的高度。这样不同的编队卫星之间的电磁信号路径衰减近似相同。
(2)文献[13-16]针对分布式节点同步问题提出了反馈信息闭环方法、主从式开环方法以及盲估计开环方法等节点同步方案。本文中假设编队卫星在载波频率、相位和时间上完美同步,在同步方法研究的基础上展开方向图综合性能分析。
(3)分布式编队卫星采用相同类型的喇叭口天线,组阵卫星的方向图函数满足方向图乘积定理。卫星天线增益表示为[17]:
(8)
其中,J1和J3为第一类1阶和3阶贝塞尔函数,μ=2.07123sin(α)/sin(α3 dB),α为卫星与用户的连线与波束中心的夹角,α3 dB为相对于最大增益3 dB衰减处对应的角度。G0为α=0°时对应的最大增益值。计算公式为:
(9)
式中,η为天线效率,D为天线的口径,c为光速, f为载波频率。以中心卫星为坐标原点建立坐标系,则第m颗组阵卫星的导向矢量可表示为如下形式[18]:
a(θ,φ|rm(k),θm(k),φk(k))=
ejκrm(k)cos ψm(k), m=1,2,...,M
(10)
其中,
为波长,rm为各编队卫星到中心卫星的距离。
cos ψm(k)=sin θsin θm(k)cos(φ-φm(k))+
cos θcos θm(k)
(11)
采用最大比合并接收时,分布式编队卫星中每颗协作小卫星接收到的信号加权转发至中心卫星,k时刻下加权项可表示为下式[18]:
wm(k)=e-jκrm(k)(sin θsin θm(k)cos(φ-φm(k))+cos θcos θm(k))
(12)
通过上式的加权,编队卫星信号矢量在期望方位上同相叠加形成期望的主瓣。最大比合并下,各颗编队卫星等幅度加权,不考虑星间链路损耗下,卫星编队无功率损失。
3.2 基于LCMV准则的多星协作波束成形
由第一节GEO/LEO频谱共享模型分析可知,当LEO编队卫星簇逐渐运动到GEO卫星通信系统主用户上行波束范围内时,会受到GEO用户较强的上行干扰,严重影响LEO卫星通信系统的性能。针对高低轨卫星通信系统之间频谱共享的场景,考虑GEO卫星通信系统主用户和LEO卫星通信系统次级用户共用同一频率,采用基于LCMV准则的编队卫星分布式自适应波束成形算法,完成对低轨卫星编队加权值的优化设计。随着编队卫星运动逐渐调整编队卫星的接收方向图指向,调整波束主瓣指向与其通信的低轨卫星通信系统次级用户,同时波束零陷方向对准GEO卫星通信系统主用户,从空域维度上来缓解高低轨卫星系统频率共享时存在的同频干扰问题。
如图7所示,由M颗低轨卫星组成的LEO编队卫星簇逐渐运动到GEO卫星通信系统主用户上行波束范围内时,各颗分布式编队卫星作为中继,将接收到的地面用户信号加权转发到中心卫星进行合并,假设各颗编队卫星精确同步,星间链路信号无损传输。
图7 分布式编队卫星波束成形模型图
Fig.7 Beamforming model of distributed satellite cluster
由于卫星编队不仅接收到低轨用户的发送信号,同时还会接收到来自GEO主用户的同频信号。卫星通信系统主用户对LEO卫星通信系统次级用户产生一定的干扰。假设k时刻下LEO用户信号和GEO用户信号的俯仰角和方位角分别表示为(θ0(k),φ0(k))和(θ1(k),φ1(k))。对编队卫星接收信号进行采样,则第k次采样信号可以表示为:
(13)
其中:s0(k)为期望接收到的LEO次用户的发送信号,s1(k)为编队卫星运行过程中接收到来自GEO主用户的上行信号,i表示第i个地面用户信号,a(θi(k),φi(k))为第i个信号导向矢量:
a(θi(k),φi(k))=[ejωτ1(θi(k),φi(k)),
ejωτ2(θi(k),φi(k)),...,ejωτM(θi(k),φi(k))]T
(14)
τ1(θi(k),φi(k)),τ2(θi(k),φi(k)),...,τM(θi(k),φi(k))表示第i个信号到各颗卫星的时延。N(k)为编队卫星的噪声矢量。低轨编队卫星接收信号的自相关矩阵可以表示为:
Rxx=E[x(k)xH(k)]=
Rs+R1+RN
(15)
其中:
和
分别表示LEO用户发送信号功率和GEO用户发送信号功率。Rs,R1,RN分别表示LEO用户发送信号、GEO用户发送信号以及噪声的相关矩阵。对编队卫星接收信号进行加权合并,则接收信号可以表示为:
y(k)=wHx(k)
(16)
其中w=[w1(k),w2(k),...,wM(k)]为编队卫星接收信号的加权矢量。加权合并后输出信号功率表示为:
P=E[|y(k)|2]=E[wHx(k)(wHx(k))*]=
wHRxxw
(17)
采用基于LCMV准则的编队卫星自适应波束成形算法建立优化问题如下:
s.t. wHa(θ0(k),φ0(k))=1
(18)
构建拉格朗日代价函数:
L(w,λ)=wHRxxw+λ(wHa(θ0(k),φ0(k))-1)
(19)
求解得到最优加权:
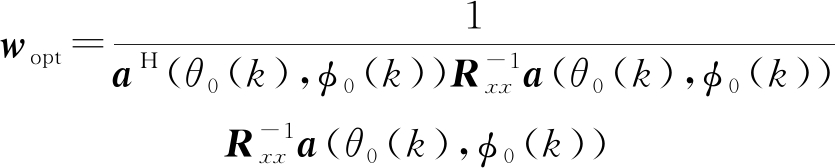
(20)
根据公式(20)得到的加权矢量,则卫星组阵接收到的LEO用户信号功率的计算公式可以表示为:
(21)
其中,EIRPleo=PTleo·GTleo为发射天线的等效全向辐射功率,GR,leo表示单颗LEO卫星的接收增益,
表示卫星阵列辐射增益,Lfleo为LEO链路的自由空间损耗,下标中的leo表示LEO信号链路。LCMV自适应波束成形可以在不损失LEO用户发送信号接收增益的同时,抑制来自其他方向的同频干扰,使得在产生同频干扰的情况下,通过该算法自适应地调整编队卫星的接收波束指向,使LEO用户始终处于接收波束的主瓣范围内,而零陷对准GEO用户,从而尽可能减小低轨编队卫星受到的上行干扰。
3.3 鲁棒波束成形算法
在实际卫星通信系统中,由于卫星的长距离传输导致的过时信道信息,使得来波方向存在一定的误差。由于卫星轨道的实际位置是先验已知的,卫星轨道可等效为无数个卫星位置的集合。当卫星初始轨道信息确定的情况下,结合卫星轨道方程,可以计算出来波方向偏离的角度。图8为卫星运动过程与地面站之间的几何关系图。
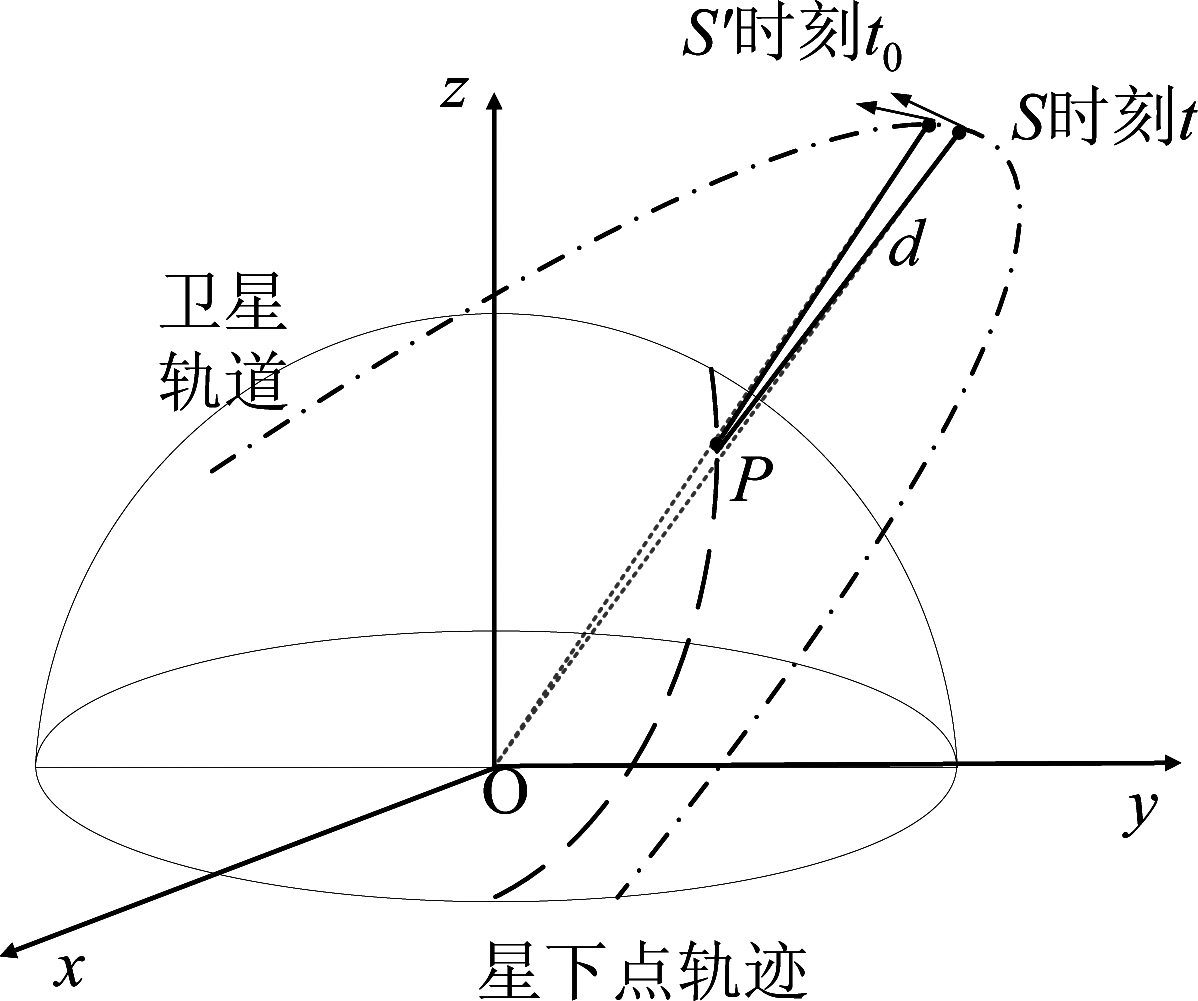
图8 卫星与地面站之间几何关系图
Fig.8 Geometric relationship between satellite and ground station
卫星轨道半长轴为a,卫星相对于地心的角速度
其中μ为地球引力常数,μ=3.986005×1014m3/s2,假设LEO地面站恰好位于卫星星下点位置P,到卫星距离为d。此时卫星相对于地面站P的角速度ωs与卫星相对于地心的角速度ωe之间满足以下关系:
(22)
LEO地面站信号传播时延
为光速。因此,由于卫星长距离传输导致的来波方向角度误差为:
ζ=Δt·ωs
(23)
然而,传统的LCMV自适应波束成形算法对信号来波方向是非常敏感的,由于信号传输环境的不确定性可能会导致波束成形器输出信噪比急剧下降,卫星系统的通信性能变得十分恶劣。本文采用一种基于导向矢量不确定集的鲁棒自适应波束成形技术(Robust Adaptive Beamformer with Uncertainty Set, RAB_us)来提高自适应波束成形器在导向矢量失配条件下的稳健性。在传统的LCMV准则中,我们认为LEO用户的来波方向精确已知,该方向上编队卫星的参考导向矢量为a0,由于卫星的长距离传输导致的过时信道信息,实际LEO用户信号的导向矢量as与a0之间存在一定误差。鲁棒波束成形算法中假设导向矢量的误差范围在一个球体内。以理想情况下的导向矢量作为参考,即为球体内的中心向量。该球体的半径的平方为误差的上界ζ。假设实际情况下LEO用户信号的导向矢量位于如下所示的球体不确定集合当中:
ε={Au+a0|||u||≤1}
(24)
其中,矩阵A决定了椭球的大小和形状,将A设置为A=ζI,得到ε如下:
ε={e+a0|||e||≤ζ}, e=ζu
(25)
当导向矢量不确定集是椭球集时,优化问题可以转化为如下形式:
subject to |wHa0|≥ζ||w||+1
(26)
然而,由于式(26)约束条件中,不等式左边为绝对值函数,所以式(26)中非线性约束条件是非凸的。实际上,当w经过任意相位旋转之后,(26)中的代价函数是不变的。因此可另:
Re{wHa0}≥0
(27)
Im{wHa0}=0
(28)
将式(27)和式(28)代入(26)中,可以将(26)中的优化问题转换为如下凸问题:
subject to wHa0≥ζ||w||+1
(29)
(29)中的约束称为二阶锥约束(second-order cone constraints, SOCP)。采用拉格朗日方法求解式(29)中的最优加权向量w,首先形成下面的拉格朗日函数:
J(w,λ)=wHRxxw-λ t(wHa0-ζ||w||-1)
(30)
其中,t(·)为阶梯函数,用来确保wHa0≥ζ||w||+1和λ为拉格朗日乘数。当式(30)中的代价函数最小,便可以满足式(29)中的不等式约束。对式(30)进行微分,令微分的结果为0,得到:
(31)
求解得到w:
(32)
式(32)的求解存在以下难点:权向量范数的估计、拉格朗日乘子的估计、以及对样本协方差矩阵求逆的计算量。下面将通过泰勒级数逼近法,对wWC进行求解。由于wWC乘上任意常数不会影响波束成形器的性能,因此,可以得到wWC如下形式:
(33)
将式(33)用泰勒级数展开:
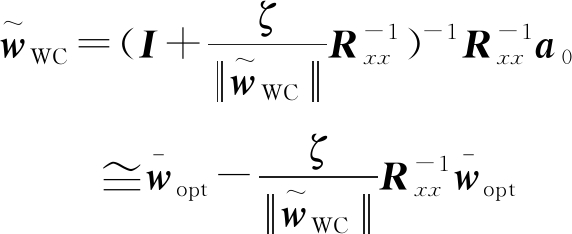
(34)
其中,
为标准的LCMV波束成形器的另一种写法。引入一个新的向量
将其代入式(34)中:
(35)
其中,
是与权值向量范数有关的参数,可以通过将(35)代入(29)中进行估计。采用该方法可以求解出满足频谱共享任务需求下的编队卫星的最优权向量。
4 频谱共享仿真分析
为了评估本文算法性能,设置卫星与地面用户的具体仿真参数如下:
表1 GEO和LEO仿真场景参数
Tab.1 Simulation parameters of the satellite system
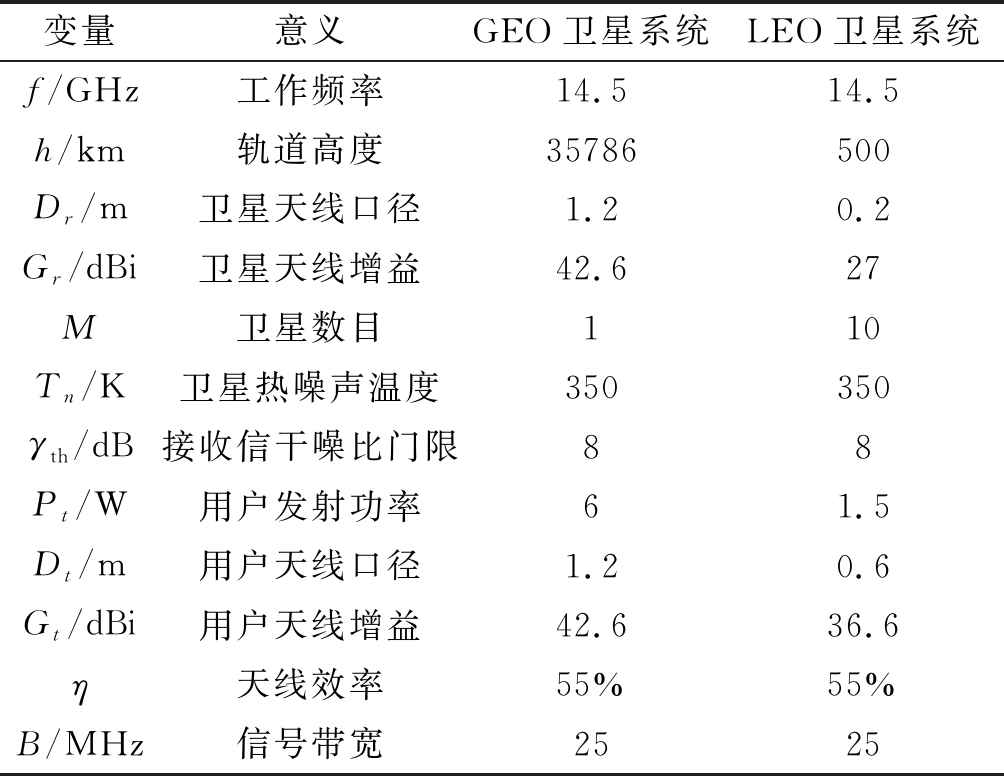
变量意义GEO卫星系统LEO卫星系统f/GHz工作频率14.514.5h/km轨道高度35786500Dr/m卫星天线口径1.20.2Gr/dBi卫星天线增益42.627M卫星数目110Tn/K卫星热噪声温度350350γth/dB接收信干噪比门限88Pt/W用户发射功率61.5Dt/m用户天线口径1.20.6Gt/dBi用户天线增益42.636.6η天线效率55%55%B/MHz信号带宽2525
十颗低轨卫星采用一种典型的星形编队队形,仿真初始时刻在图6极坐标系下的确定轨道信息依次为:
r=[0, 50, 50, 50, 50, 50, 50, 50, 50, 50]
θ=[0, 69, 63, 92, 47, 142, 57, 51, 76, 27]
φ=[0, 42, 337, 111, 54, 127, 234, 345, 57, 39]
分布式卫星簇采用具有鲁棒性的RAB_us方法进行波束成形,结合卫星轨道运动方程联合计算,设置导向矢量不确定集上界ζ=0.5,图9(a)和图9(b)分别给出了仿真时刻t=0 s时,以上编队队形下的三维接收信号增益方向图及其俯视图(为了更直观地理解,基于角信息的坐标系被转换为地理坐标系)。可以看到该卫星编队的接收信号增益方向图在LEO用户方向上形成了主瓣且获得了最大增益,并且在GEO用户来波方向上形成了较深的零陷,零陷角度归一化增益为-38 dB,将表1中的参数代入计算,此时LEO卫星编队的接收端信干噪比SINR=13.5 dB,达到了信号正确解调的信干噪比阈值,此时可以有效降低GEO用户对低轨卫星编队的同频干扰。
图9 t=0 s时刻三维接收增益方向图及其俯视图
Fig.9 Receiving beam pattern and its top view at t=0 s
经第1节内容分析,由于LEO卫星相对于地面处于高速运动状态,因而地面LEO用户以及GEO用户相对于编队卫星的方位是时刻变化的,且卫星编队队形也会随着卫星在轨运动而动态变化。图10(a)和图10(b)给出了仿真时刻t=30 s时,该卫星编队的三维接收增益方向图以及俯视图,可以看到随着低轨卫星在轨运动,编队卫星的接收增益方
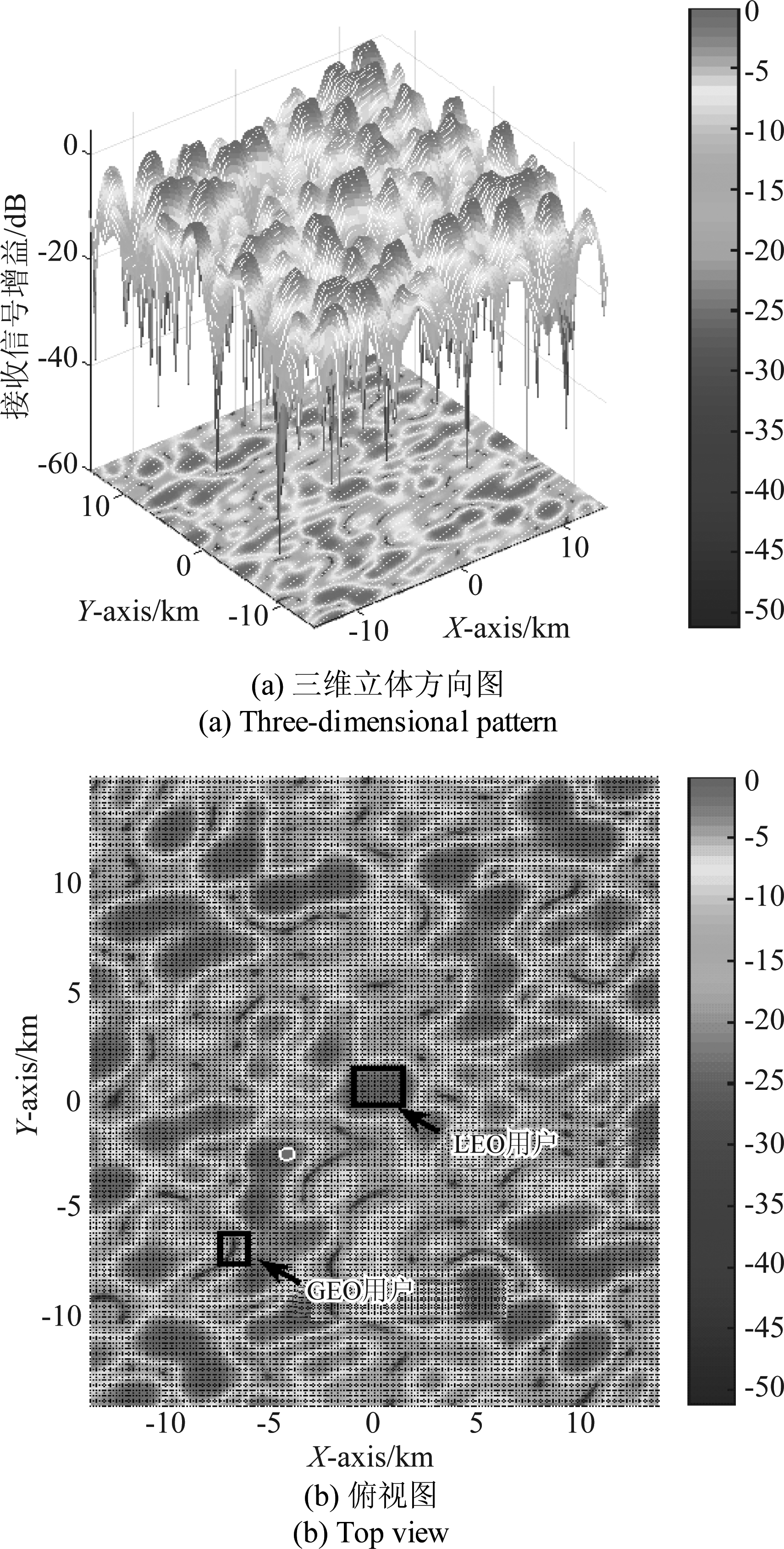
图10 t=30 s时刻三维接收增益方向图及其俯视图
Fig.10 Receiving beam pattern and its top view at t=30 s
向图发生了变化,但是接收信号波束主瓣仍然指向与其通信的低轨卫星通信系统次级用户,同时波束零陷方向对准了GEO卫星通信系统主用户,低轨卫星通信系统的接收信干噪比大于接收信干噪比阈值。因而随着编队卫星在轨运动,通过RAB_us算法可以动态调整各编队卫星的加权值,时刻调整接收波束方向图的指向。
不失一般性,我们取方位角平面(即θ=90°)观察分布式编队卫星组阵的接收增益方向图。以上述编队队形形成分布式编队卫星组阵,在组阵卫星数目、卫星俯仰角和方位角不变的条件下,改变其他卫星离中心卫星的距离。图11给出了不同rm下组阵的接收增益方向图。可以看出接收信号方向图均在LEO用户方向获得了最大增益,并且在GEO用户方向上形成了较深的零陷。且随着组阵卫星离主星的距离增加,方向图的主瓣逐渐变窄,这是由于增加距离相当于增大了阵列的虚拟天线口径。
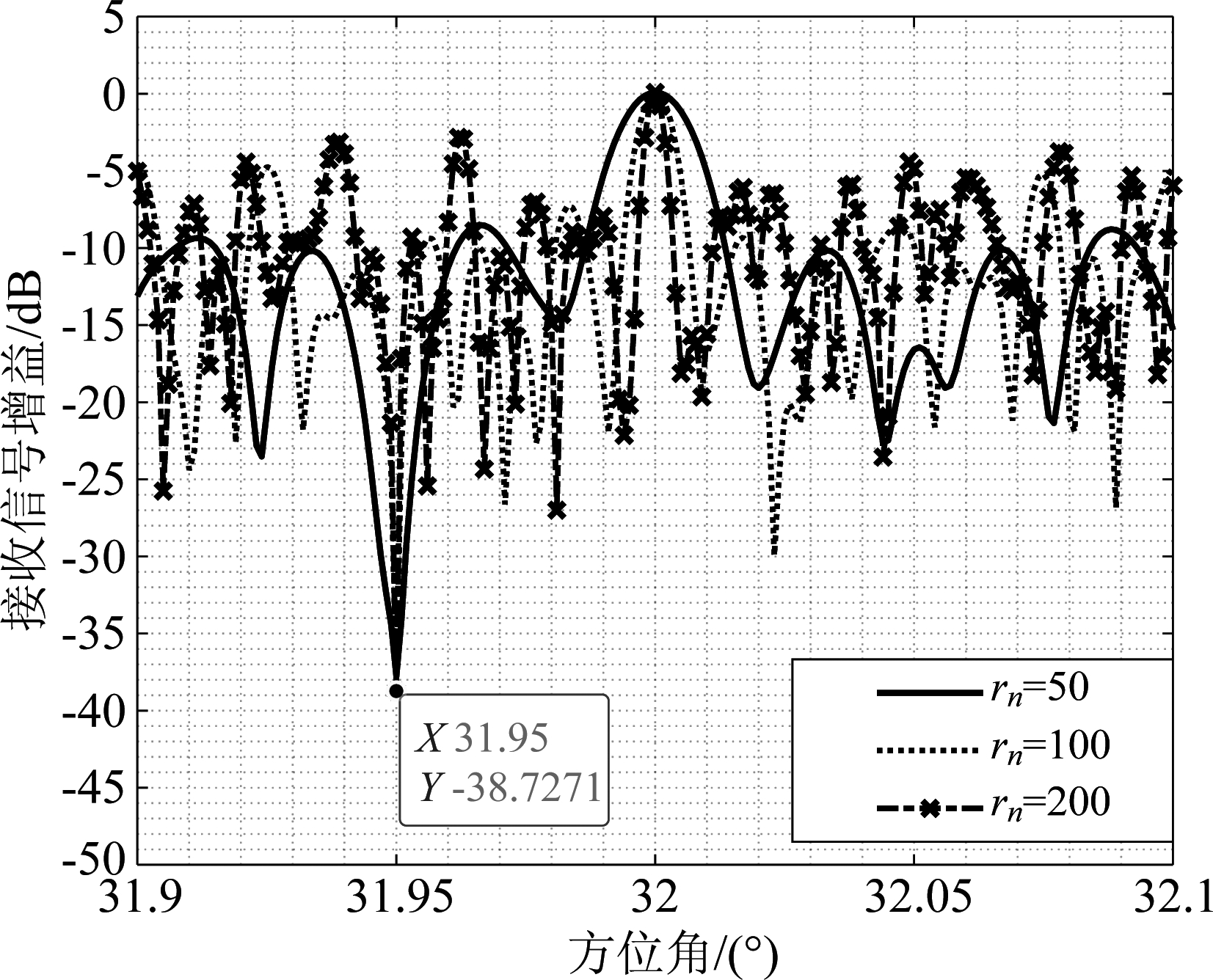
图11 不同组阵半径下的接收增益方向图
Fig.11 Receiving beam pattern under different array radius
取编队卫星在轨运动过程中的三个时刻,得到如表地面用户相对于卫星编队的位置信息:
表2 不同时刻地面用户的位置信息
Tab.2 Positions of Users at different times
观察时刻LEO用户位置GEO用户位置t=0 sϕ0=32°ϕ1=31.95°t=30 sϕ0=31.6°ϕ1=31.53°t=60 sϕ0=31.15°ϕ1=31.06°
由图12验证可知,随着低轨编队卫星在轨运动,各编队卫星通过对加权值的调整,可以自适应地调整接收波束的指向。使LEO用户方向增益最大的同时,极大地抑制GEO卫星通信系统主用户对LEO卫星通信系统次级用户的干扰,从空域维度上缓解了高低轨卫星通信系统频谱资源紧缺的问题。
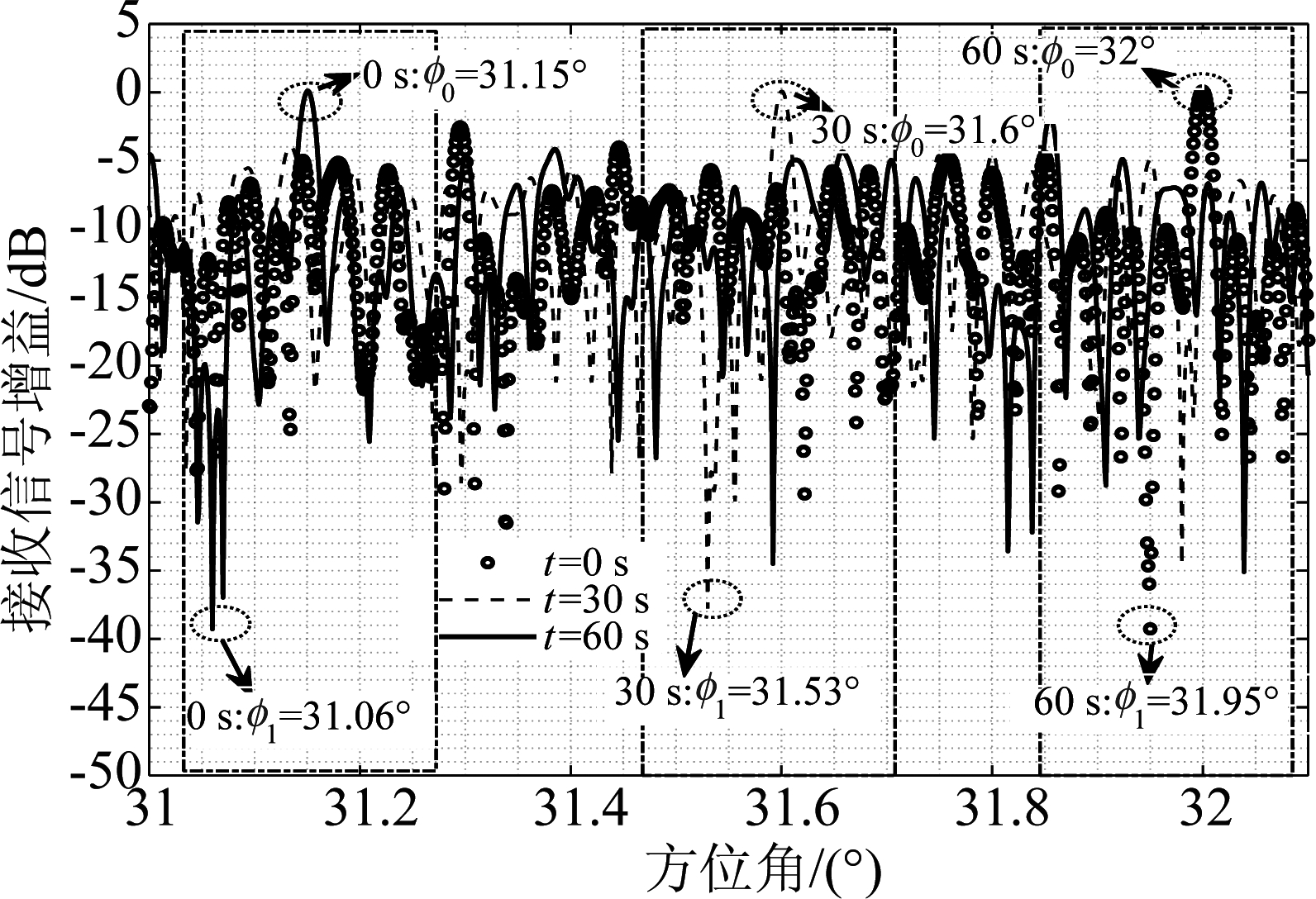
图12 不同时刻下的接收波束方向图
Fig.12 Receiving beam pattern at different times
图13为观测时间10分钟内,GEO用户方向的接收增益。可以看到,在卫星编队飞行过程中,GEO用户方向的接收增益始终在-39 dB左右,经计算编队卫星的信干噪比约等于15 dB,超过了系统接收信干噪比的门限值。低轨卫星通信系统在受到GEO主用户较强的干扰时,仍然能够正确解调出LEO用户信号。也验证了采用鲁棒自适应波束成形技术,可以大大降低上行链路中GEO用户对LEO卫星系统的同频干扰,实现频谱资源的高效利用。
图13 GEO用户方向增益变化曲线图
Fig.13 Graph of the receiving gain versus time In the direction of GEO users
当组成卫星编队的卫星数目不同时,编队卫星波束成形输出性能也会有一定差异。图14两条曲线分别为编队卫星数目M=10和M=6时对应的接收增益曲线。当编队卫星数目越多时,波束方向图的指向性更强,在GEO用户方向的零陷更深,整体输出性能更佳。
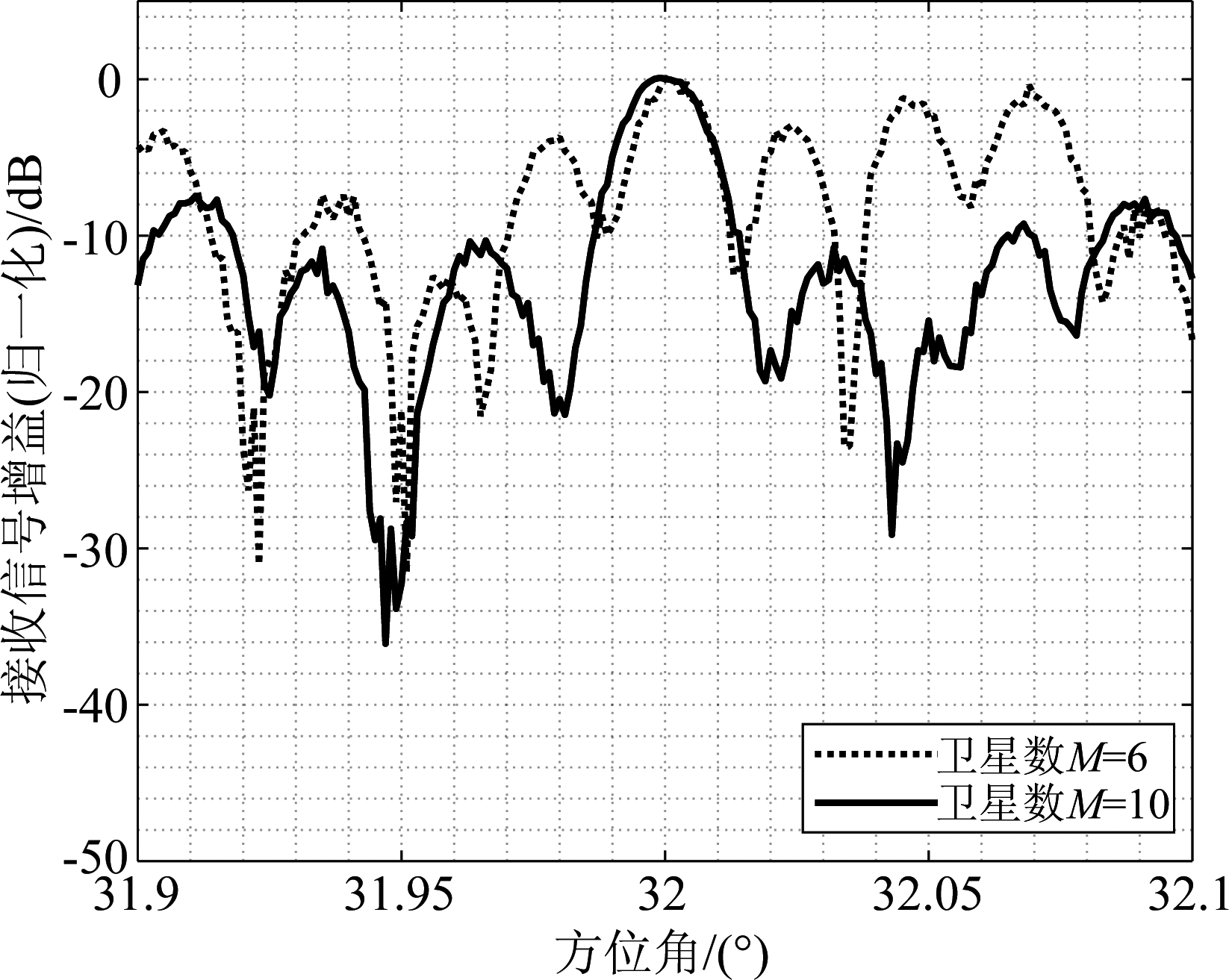
图14 不同卫星数目下的接收波束方向图
Fig.14 Receiving beam pattern at different number of satellites
为了验证相比于传统的LCMV算法,RAB_us方法具有更好的鲁棒性,图15给出了两种算法下的接收波束方向图。从图15可以看出,当考虑卫星的长距离传输导致的过时信道信息时,传统的LCMV算法性能急剧恶化,方向图整体旁瓣上升,且零陷方向明显偏离了GEO用户方向;而采用RAB_us方法,具有较好的鲁棒性,波束方向图只有轻微抖动,仍然能够在GEO用户方向上形成较深的零陷,系统具有较高的SINR,接收性能良好。
图15 两种算法的鲁棒性对比
Fig.15 The robustness of the two algorithms
进行1000次蒙特卡罗仿真,进一步对鲁棒自适应波束成形算法性能进行验证。图16中分别给出了存在/不存在干扰情况下,低轨卫星编队采用最大比合并方式接收信号的SINR曲线、传统LCMV算法下的SINR曲线以及采用鲁棒波束成形算法下的SINR曲线进行对比验证。当系统环境中无干扰信号时,采用MRC方式可以在不损失次用户信号功率的情况下,使系统性能达到最佳,可达到26 dB左右。但是,当低轨卫星编队与GEO卫星系统出现共视干扰情况,在MRC方式下低轨卫星系统的性能将急剧下降,信干噪比下降至-12 dB左右。采用传统的LCMV算法,SINR波动较大,大部分情况都低于解调阈值,SINR偶尔出现高于门限值的情况。这是卫星的长距离传输导致的过时信道信息,使得来波方向存在一定的误差,导致接收性能的不稳定性。而采用鲁棒自适应波束成形算法后低轨卫星编队接收信干噪比在15 dB左右波动,始终大于解调门限值。与传统的LCMV算法相比,本文提出的鲁棒波束成形算法在高低轨卫星频率共存系统适应度更高,性能更加稳定,具有较好的鲁棒性。
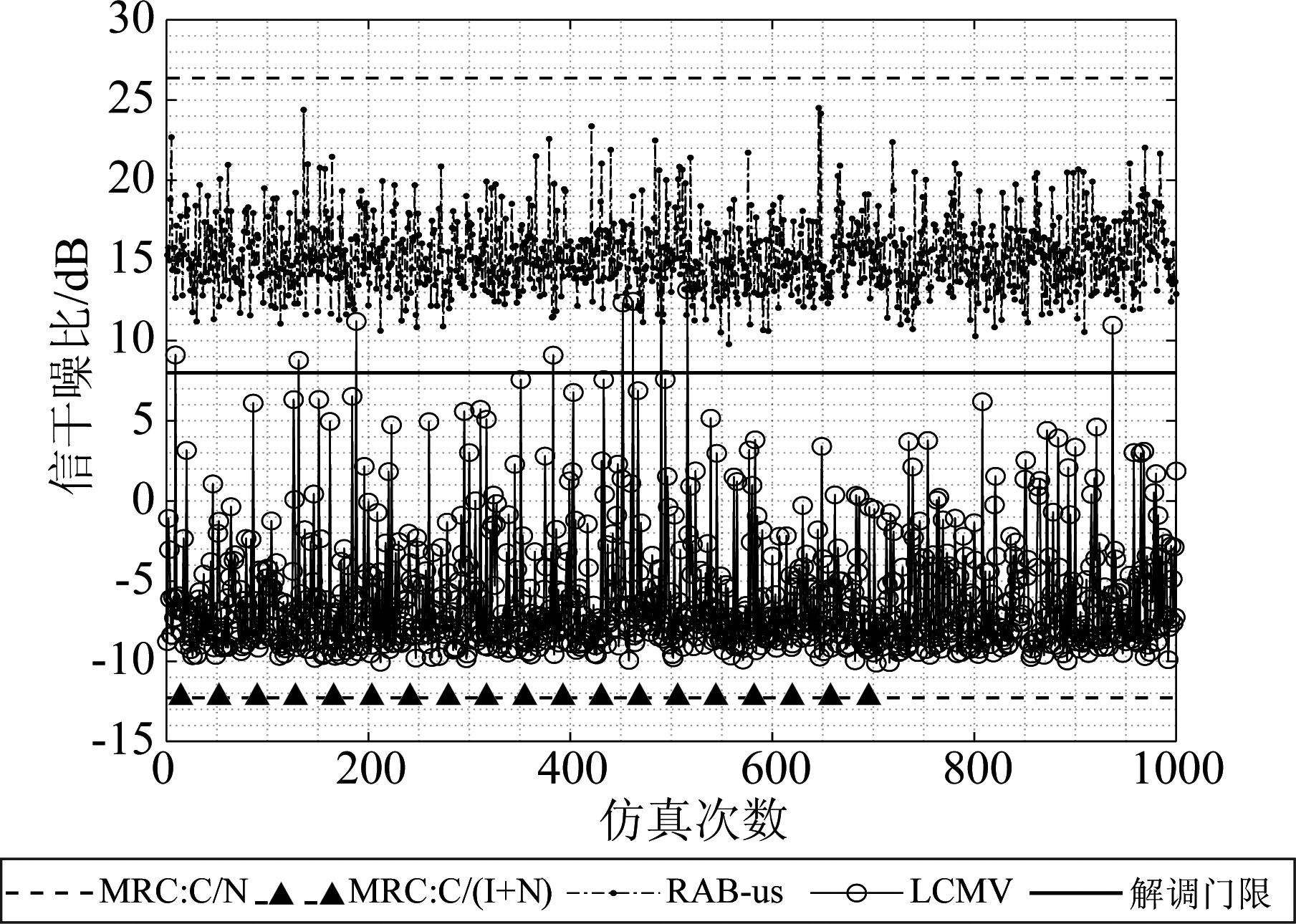
图16 LEO卫星编队信号质量变化曲线
Fig.16 Signal quality curve of LEO satellite formation
5 结论
本文针对传统的固定的静态的频率分配方式难以满足空间信息网络日益增长的频率需求这一问题,从空间信息网络的体系架构出发,对静止轨道卫星通信系统和低轨道卫星通信系统上行链路频谱共享场景进行了干扰分析。考虑到卫星通信系统实际应用中,卫星的长距离传输导致的过时信道信息,使得来波方向存在一定的误差,本文提出了一种基于鲁棒LCMV算法的编队卫星分布式自适应波束成形方法,完成对低轨卫星编队加权值的优化设计,提高了低轨卫星通信系统的稳健性。本文通过多个系统共用同一频率,充分发掘并利用空闲的频谱资源,从空域维度上缓解了空间网络用频紧张的问题,一定程度上改善了频谱资源利用效率。针对编队卫星之间的星间同步方法、一定的同步误差条件下鲁棒性波束成形算法、不同电磁收发任务编队卫星最优的编队队形设计和队形重构问题需要进行下一步研究。
[1] CLEGG A, WEISSHAAR A. Future radio spectrum access[J]. Proceedings of the IEEE, 2014, 102(3): 239-241.
[2] 岳文静, 武聪, 陈志, 等. 感知频谱共享下的多天线功率优化分配算法研究[J]. 信号处理, 2014, 30(11): 1298-1302.
YUE Wenjing, WU Cong, CHEN Zhi, et al. Optimal power allocation algorithm with multi-antenna in sensing-based spectrum sharing networks[J]. Journal of Signal Processing, 2014, 30(11): 1298-1302.(in Chinese)
[3] 张令浩, 张剑云, 周青松. 杂波环境下共享频谱恒模波形设计[J]. 信号处理, 2020, 36(2): 257-264.
ZHANG Linghao, ZHANG Jianyun, ZHOU Qingsong. Design of unimodular waveform for spectrum sharing in clutter environment[J]. Journal of Signal Processing, 2020, 36(2): 257-264.(in Chinese)
[4] ZHENG Lizhong, TSE D N C. Diversity and multiplexing: A fundamental tradeoff in multiple-antenna channels[J]. IEEE Transactions on Information Theory, 2003, 49(5): 1073-1096.
[5] LIOLIS K, SCHLUETER G, KRAUSE J, et al. Cognitive radio scenarios for satellite communications: The CoRaSat approach[C]∥2013 Future Network & Mobile Summit. Lisboa, Portugal. IEEE, 2013: 1-10.
[6] S
NCHEZ A H, SOARES T, WOLAHAN A. Reliability aspects of mega-constellation satellites and their impact on the space debris environment[C]∥2017 Annual Reliability and Maintainability Symposium (RAMS). Orlando, FL, USA. IEEE, 2017: 1-5.
[7] HANSON W A. In their own words: OneWeb′s Internet constellation as described in their FCC form 312 application[J]. New Space, 2016, 4(3): 153-167.
[8] SHARMA S K, CHATZINOTAS S, OTTERSTEN, et al. Inline interference mitigation techniques for spectral coexistence of GEO and NGEO satellites[J]. International Journal of Satellite Communications & Networking, 2016, 34(1):11-39.
[9] KIRTAY S. Broadband satellite system technologies for effective use of the 12-30 GHz radio spectrum[J]. Electronics & Communication Engineering Journal, 2002, 14(2): 79- 88.
[10] Interference Mitigation Techniques to Facilitate Coordination Between Non-Geostationary-Satellite Orbit Mobile-Satellite Service Feeder Links and Geostationary-Satellite Orbit Fixed-Satellite Service Networks in the Bands 19.3～19.7 GHz and 29.1～29.5 GHz, Document ITU-R S.1419, Nov. 1999.
[11] YANG Peng, XI Xing, FU Yaru, et al. Multicast eMBB and bursty URLLC service multiplexing in a CoMP-enabled RAN[J]. IEEE Transactions on Wireless Communications, 2020.
[12] Guidelines for Evaluation of Radio Interface Technologies for IMTAdvanced, Document ITU-R M.2135, 2008.
[13] LEE J, LEE S, PARK J. Fast phase synchronization with clustering and one-bit feedback for distributed beamforming in a wireless sensor network[C]∥2018 IEEE 87th Vehicular Technology Conference (VTC Spring). Porto, Portugal. IEEE, 2018: 1- 4.
[14] BROWN III D R, POOR H V. Time-slotted round-trip carrier synchronization for distributed beamforming[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5630-5643.
[15] QUITIN F, UR RAHMAN M M, MUDUMBAI R, et al. Distributed beamforming with software-defined radios: Frequency synchronization and digital feedback[C]∥2012 IEEE Global Communications Conference (GLOBECOM). Anaheim, CA, USA. IEEE, 2012: 4787- 4792.
[16] BLETSAS A, LIPPMAN A, SAHALOS J N. Zero-feedback, collaborative beamforming for emergency radio: Asymptotic analysis[J]. Mobile Networks and Applications, 2011, 16(5): 589-599.
[17] DIAZ M A, COURVILLE N, MOSQUERA C, et al. Non-linear interference mitigation for broadband multimedia satellite systems[C]∥2007 International Workshop on Satellite and Space Communications. Salzburg, Austria. IEEE, 2007: 61- 65.
[18] BUCHANAN K, HUFF G H. A stochastic mathematical framework for the analysis of spherically-bound random arrays[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(6): 3002-3011.
