1 引言
受支持超可靠低延迟(ultra-reliable and low latency communication, URLLC)等5G应用场景的推动,设计URLLC无线系统的一个主要挑战是满足超高可靠性和低延迟之间的固有冲突,其中低延迟场景需要较短的块长度,而高可靠性通常采用高效的编码技术。近年来,人们对短块编码的兴趣再度升温,基于现有编码方案的短块编码的设计和分析工作层出不穷[1- 4]。在短块长度的情况下,传统的译码算法与迭代译码算法相比具有较好的性能优势,且复杂度相对较低。咬尾卷积码(tail-biting convolutional codes,TBCC)作为URLLC场景下短码的备选编码方案,通过咬尾网格译码来消除传统归零卷积码带来的速率损失。研究表明,在非常低的延迟情况下,基于维特比(Viterbi algorithm, VA)译码的TBCC提供了最佳的性能[5],因此对TBCC的深入研究有着重要的意义。
卷积码由有限状态机生成,它的状态依赖于当前和过去的输入。如果编码器的起始状态和结束状态都是为零,则译码过程更有效,但结尾补零会导致码率损失。在长块长度的情况下,码率损失可以忽略,但在短块长度的情况下,速率损失通常是不可接受的。咬尾卷积码是一种用咬尾符号约束代替固定的零尾卷积码,可以克服补零带来的速率损失,保证编码器的起始状态和结束状态相同,消除全零状态特性所带来的性能损失。通过在咬尾网格上进行循环译码,获得比传统卷积码更好的译码性能。咬尾网格表示使得基于网格的最大似然(Maximum likelihood, ML)译码器得以实现。ML译码器通过软判决信息序列的最大累积度量来获得最大似然路径。同理,将该算法运用要咬尾网格中,从每个状态依次查找,最终选择首尾状态相同且度量最大的路径作为输出。无疑这种方法是最佳的,但开销巨大,计算复杂度高,让人难以接受。
Y.Shao等人总结前人工作,提出了一种切实可行的TBCC译码算法——绕维特比译码算法(wrap-around Viterbi algorithm, WAVA)[6],它是通过对咬尾网格进行迭代处理,每次迭代检查网格边界处的咬尾情况,确保连续探索传输序列的初始状态。随后,Wang等人指出,这种基于迭代的方法寻找咬尾路径是有缺陷的,即会存在循环陷阱[7]导致咬尾路径达不到收敛状态,造成译码性能下降。随后提出两种解决循环陷阱的方法,但停止规则过于繁琐,迭代次数不能根据通信质量的变化而变化。为解决复杂度和收敛性的问题,提出一种算法,能够避开圆形陷阱,并且每次迭代后只需做一次运算就能判断咬尾路径是否收敛,减少了计算量。
文章的结构组织如下,第2部分介绍TBCC相关概念和已有算法的不足;第3部分详细描述提出的算法;第4部分针对TBCC在码长极短的情况下,给出了已有算法和本文算法性能比较的实验仿真;第5部分为全文的总结。
2 TBCC的循环VA算法分析
2.1 咬尾路径
TBCC和一般的归零卷积码有着相同的基本参数,通常是由(n,k,m)来表示。其中n表示编码后的输出码长,k表示输入信息位的数量,m表示约束长度,其码率为k/n。TBCC译码通常用网格图表示,在网格上具有相同初始和结束状态的路径称为咬尾路径。设Γ为(n,1,m)的二进制TBCC,输入的信息比特长度为L,则通过编码器后产生的码字长度为nL,在每个时刻k都会产生2m个状态,k满足0≤k≤L。其中在网格图中含有N个子网格,每个子网格开始和结束于N中任意一种状态。
如图1所示,描述了一个四状态,信息长度为8的咬尾编码网格。每个时刻状态分支按一定规律交错连接构成了所有可能的路径,但只有一条是原始信息的编码路径。它可以开始于所有状态中的任一状态,因为需要构成咬尾路径,所以结束状态和开始状态相等。要保证成功正确译码,必须满足两点:首先,需要正确找到起始状态,其次,保证每次迭代的相同时刻状态转移分支完全相同。WAVA也可以看作是在原有译码网格上的拓展,即将相同的接收块进行拼接,经过多次迭代,使译码路径收敛到最佳。
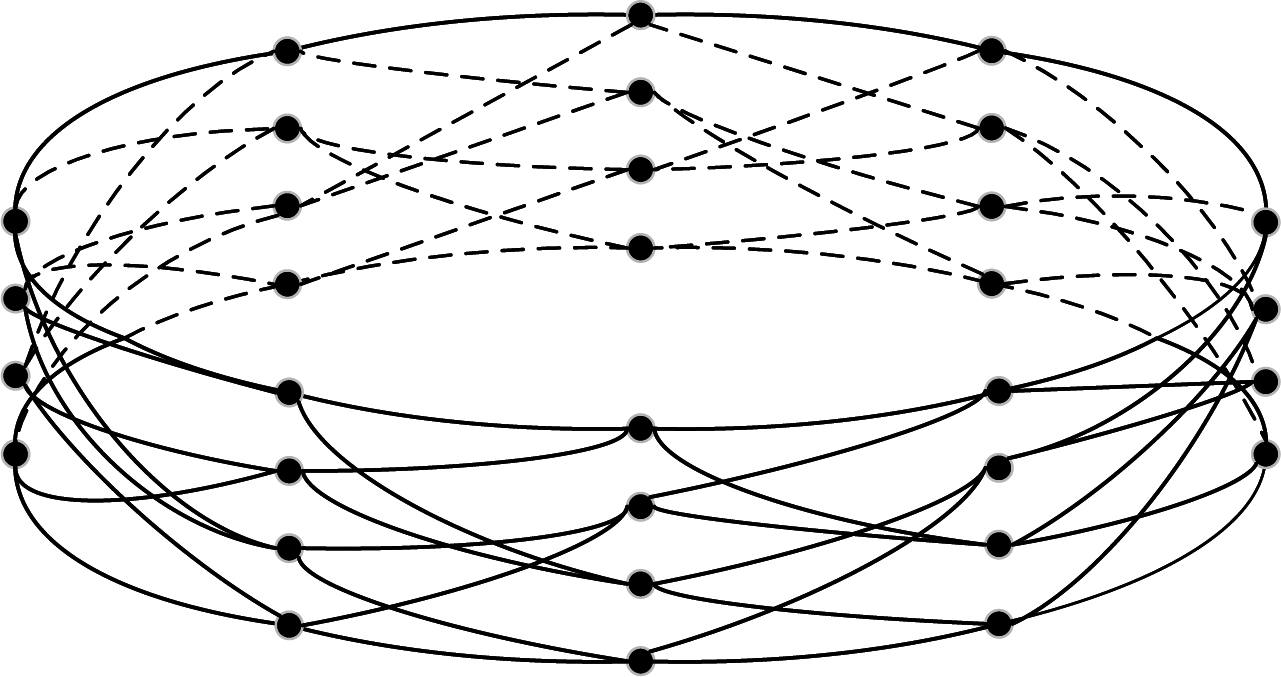
图1 TBCC的四状态咬尾网格
Fig.1 The tail-biting trellis of four states for TBCC
在网格图中,第i次迭代,经过译码存留下来的路径称为幸存路径,可以表示为Pi(βi(s),s),βi(s)表示从状态s开始回溯到该路径0时刻所在的状态,其中s∈{0,...,2m-1}。其路径对应的净路径度量为
定义如下:
(1)
它表示当前迭代下,该路径分支度量的累积。
是定义在第i次迭代时刻k所对应的幸存路径度量的累积。在所有幸存路径中,净路径度量最大的路径定义为最佳幸存路径,表示为
其净路径度量等于
若最佳幸存路径恰好为咬尾路径,则称为最佳咬尾路径,路径和度量可以分别表示为
和
另外,规定净状态度量为Mstate,net(s),定义如下:
(2)
即等于不同迭代次数下,相同首尾状态度量的差值的最小值。
2.2 WAVA算法
算法流程总结如下:
步骤1 初始化STB=
,SNTB=,
步骤2 执行VA译码,结束后对每个状态进行回溯。
步骤3 计算每个状态的净路径度量
并将咬尾路径储存于STB中,非咬尾路径储存于SNTB中,每次迭代更新STB和SNTB中路径的度量值。
步骤4 判断最佳幸存路径是否为咬尾路径。是,将该序列
作为译码输出;否则,执行步骤5。
步骤5 i=i+1,用上次迭代得到的所有状态的最后度量作为下一次迭代的起始值,
重复执行步骤2。当达到最大迭代次数I停止时,执行步骤6。
步骤6 找到STB中净路径度量最大的路径作为译码输出;如果STB=,则将SNTB中最佳幸存路径
作为译码输出。
该算法的核心在于每次准确计算每个状态的净路径度量。由于TBCC的译码网格是由2m个子网格构成,每条路径的首尾状态是未知的,因此需要对每个状态逐一回溯,这必然会造成极大的开销。另外,最大迭代次数I都是需要预先设置的,设置的过小,会造成一定的性能损失;设置的过大,可能会产生无效迭代。
2.3 简化陷阱检测算法
在文献[7]中,证明了三个定理。其中定理2和3指出,对于循环迭代的译码方法,如果最佳咬尾路径等于最佳幸存路径,只能在第一次迭代中满足,并且第一次迭代得到的最佳幸存路径净路径度量值最大。因此,提出了简化陷阱检测算法。
算法设置了一个全局参数
和
表示全局最佳咬尾路径,每次搜索当前迭代下的最佳咬尾路径的净路径度量,判断是否大于该全局参数,如果大于的话,更新其度量值和路径;否则将继续迭代,最后输出全局最佳咬尾路径。
简化陷阱检测算法的缺陷在于停止迭代的方式。虽然设计了有效检验循环陷阱的规则,但最大迭代次数的设置会对复杂度造成很大影响。假设在译码过程中,第一次迭代找出的最佳咬尾路径不是最佳幸存路径,根据定理2,那迭代只会在达到最大迭代次数时停止,如果每个状态的幸存路径已经不再变化,那之后的迭代就是无效的,并且无效迭代在高信噪比下表现地更明显。
3 自适应循环VA译码算法
3.1 迭代停止准则修正
在总结上述两种算法的不足后。因此,改进算法具体步骤总结如下:
停止规则1:译码最后时刻,最佳幸存路径等于最佳咬尾路径。
停止规则2:当前迭代的最后时刻的所有状态的前继状态与上一迭代最后时刻的所有状态的前继状态相同[8]。
步骤1 i=1,将所有状态的初始度量设置为0,即
进行传统VA译码。检测停止规则1,是,执行步骤4;否,记录最佳幸存路径PMLP(β(s′),s′)和度量MMLP,net(β(s′),s′),并执行步骤2。
步骤2 i>2,将上次迭代得到的所有状态的净状态度量作为下一次迭代的起始值,执行VA译码,检测停止规则1,是,执行步骤4;否则,执行步骤3。
步骤3 检测停止规则2,是,找出所有咬尾路径,取净状态度量值最大的路径作为最佳咬尾路径PMLTBP(s′,s′),执行步骤4;否,重复步骤2。
步骤4 将最佳咬尾路径PMLTBP(s′,s′)作为译码输出;如果没有,则将最佳幸存路径PMLP(β(s′),s′)作为译码输出。
详细算法流程如图2所示。
图2 改进算法流程图
Fig.2 Flow diagram of improved algorithms
3.2 收敛性能分析
在以往的停止迭代的规则中,都是搜索当前迭代中的最佳咬尾路径,那必然需要对每条路径进行回溯再比较其净路径度量[9],这一系列操作的计算量必然不小。改进算法不再从度量值的角度设计停止规则,而是从咬尾路径本身进行考虑。译码网格中的所有路径经过有限次迭代达到收敛,考察每条路径和上次迭代的路径是否相同是一个很好的选择。但逐一比较每条路径的每个分支确实会增加计算的复杂度。因此本文提出了一种简化方法,即每次迭代判断最后时刻的前继状态是否与上一次迭代的前继状态相同。因为如果每个状态对m个连续符号做出了相同的分支判定,m表示编码器的记忆长度,这意味着从任何状态回溯到它的m个先前符号将是相同的。对于(n,1,m)的二进制TBCC,每个状态只有只能选择两条支路,这里定义选择0表示上分支,选择1表示下分支,因此判定结束迭代的规则就简化为相同状态间的异或操作,大大减低了计算的复杂度。具体操作如下,图3中,显示了四状态的路径回溯图,其中,只有P1是咬尾路径,每个状态的前继状态分支选择在图中已标出,将上一次迭代的分支选择放入寄存器中,与下一次迭代结束时的分支选择进行对比,连续两次分支选择相同,则认定所有路径收敛完毕,无需再次迭代,输出此刻最佳的咬尾路径即能达到最佳效果。
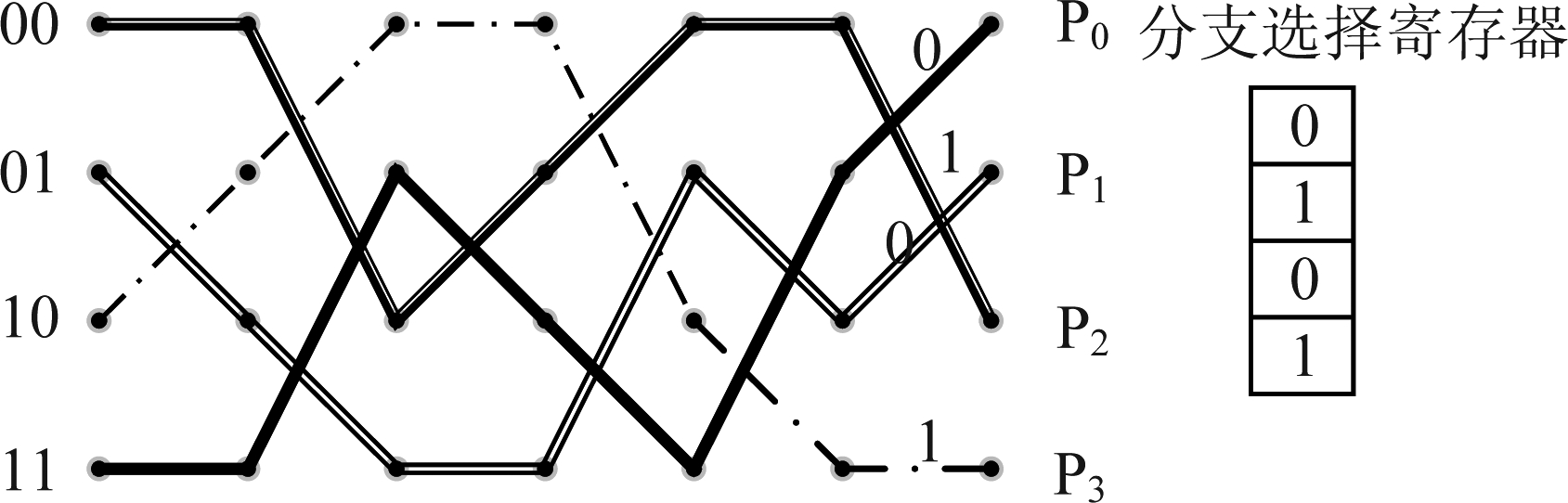
图3 改进算法路径回溯图
Fig.3 Path traceback diagram of improved algorithms
仅仅使用这个简化方法,在仿真中会发现,不是每次都能成功译码,有时候会陷入一个死循环,即永远也找不到相邻两次迭代分支选择相同的情况,并且每隔一定周期相同的分支选择会再次出现。这就是文献[7]中提到的循环陷阱在路径回溯中的体现。
为了避免上述问题,改进方法引入了净状态度量的计算,该参数与净路径度量的区别在于,不用知道每条路径的具体的初始状态,就能很好的反映出咬尾路径的真实度量。每个状态取全局的净路径度量的最小值,如果某条路径为咬尾路径,则它的净状态度量就等于净路径度量;如果不是,每个状态的净路径度量将收敛到最小值。这时,咬尾路径和非咬尾路径之间会出现两级分化现象,不可靠的路径将逐步从咬尾路径中分离,可靠路径净度量值不会发生改变。由此增强了译码路径判决的准确性。
3.3 复杂度分析
设最大迭代次数为I,一次VA运算的计算量为δ,回溯的计算量为σ,排序计算量为ε,净路径(状态)度量的计算量为q,异或计算量为p, n表示小于等于2m的有限回溯次数。各算法的复杂度如表1所示。
表1 不同算法的复杂度比较
Tab.1 Comparison of complexity of different algorithms
算法最小复杂度最大复杂度WAVA算法δ+σIδ+2mIσ+Iq+ε简化陷阱检测算法δ+σIδ+nIσ+Iε改进算法δ+σIδ+nσ+Ip+Iq+ε
从表中可以看出,当信道条件良好时,所列算法的最小复杂度输出所用开销相同。在信道恶劣的条件下,WAVA算法需要对每个状态进行回溯,计算量不容忽视;同样,简化陷阱检测算法,每次迭代都要对每个状态最后时刻的累积度量值进行排序,当约束长度很大时,复杂度会成指数上升。改进算法主要执行的是加法和异或运算,仅仅在译码满足停止规则后,进行一次排序和有限次回溯即可找到最佳路径,这是其他两种算法无法比拟的。
4 仿真实验与分析
在短块传输中,一般用块长n来描述其信息序列编码后的长度,用k来表示原始信息序列的大小尺寸,简写为(n,k),编码性能用块错误率(codeword error rate, CER)来表示。在本节中,我们将展示在AWGN信道下,不同约束长度的TBCC的性能以及不同块长下的最低信噪比要求,最后统计本文算法的平均的迭代次数与已有的WAVA算法进行比较,得出结论。
首先,我们分别选择约束长度m=8,11,14的TBCC作为性能分析的研究对象。图4仿真了(128,64)的TBCC 在不同信噪比下的误码率(bit error rate, BER),同时选取了工业上最常用m=6的卷积码与相同约束长度的TBCC进行比较。可以看出在短码下,归零卷积码的性能急剧下降,在BER等于10-5时,比相同约束长度的TBCC损失了约1 dB增益,显然TBCC更适合短块传输。
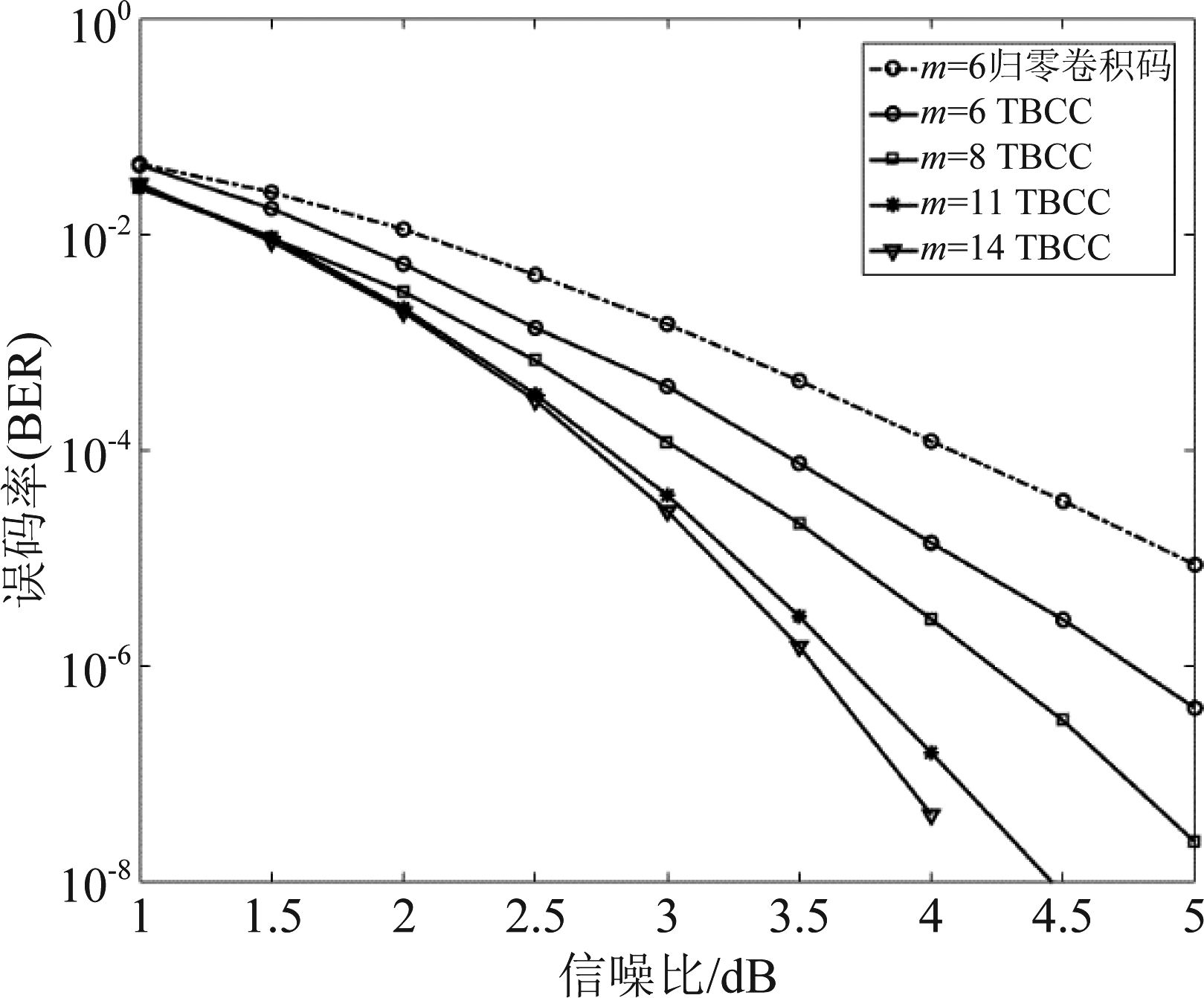
图4 TBCC与卷积码BER比较
Fig.4 Comparison of BER between TBCCs and convolutional codes
由于在块传输的应用中,更注重考查信息传递的准确性,因此分析CER比BER更具有实际意义。图5仿真了(128,64)的TBCC在不同信噪比下,错50帧时两种译码算法的CER。从图中可以看出,随着约束长度的增大,两种译码算法的CER不断降低。并且本文算法的CER非常接近于WAVA算法。同时可以发现,由于约束长度的增大,译码的复杂度会呈指数级增加,实际性能的增长幅度却越来越小。并且当约束长度从8增加到11时,CER的减少量有着大幅度降低,但当m再次增大到14后,m=14相比m=11的CER的间增益已经非常小。
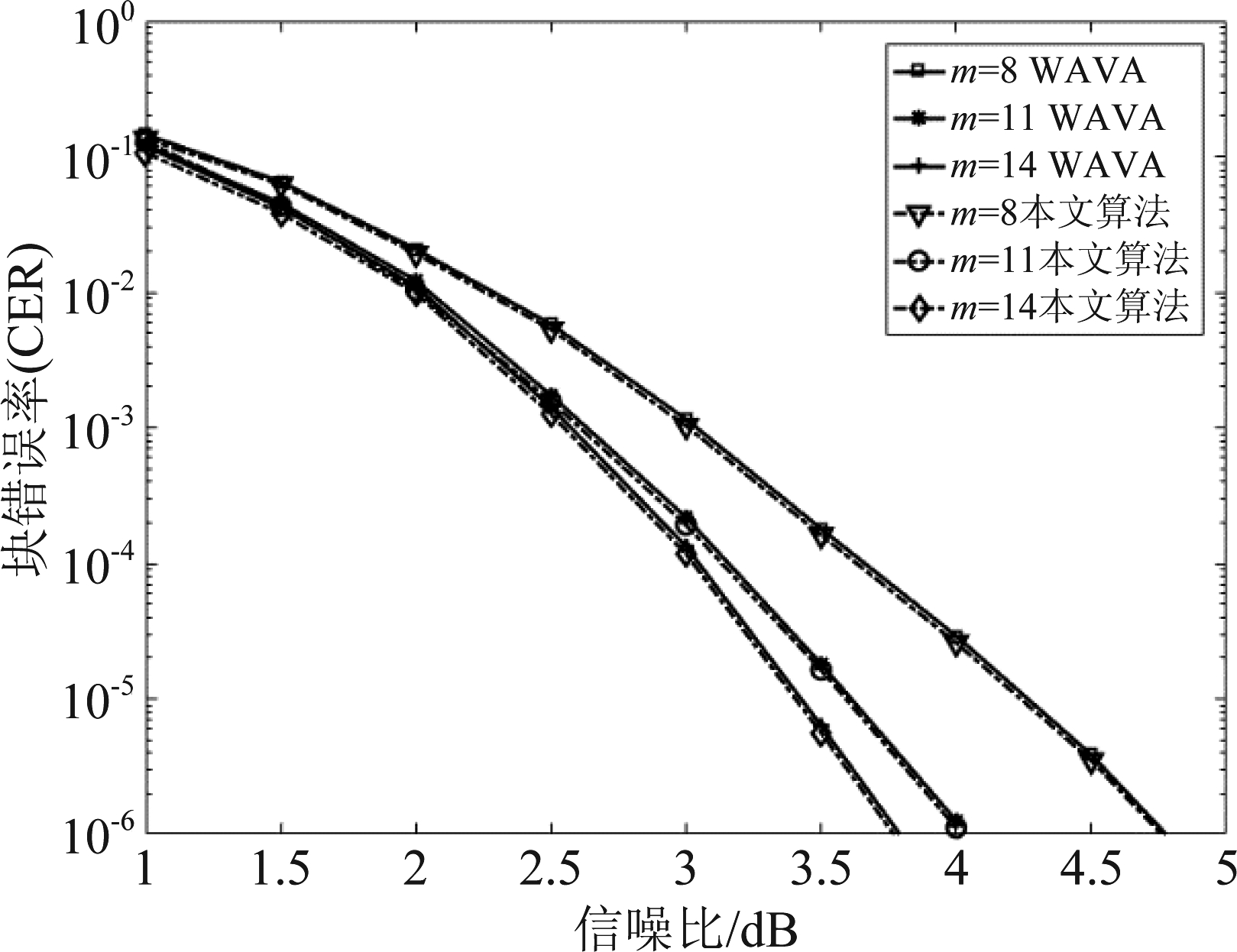
图5 (128,64) TBCC的两种算法性能比较
Fig.5 Performance comparison of the two algorithms for (128,64) TBCCs
为了探究在更短块长下TBCC的性能,在图6中仿真了(64,32) TBCC译码算法错50帧时的CER。可以看出,增加约束长度获得的增益已经微乎其微,甚至当约束长度m=11和14后,其性能出现了恶化,没有m=8时表现优越。并且当原始信息序列变短后,相同信噪比下CER会增加,这与文献[10-11]所提到的短块传输理论结果相吻合,块长越短,相应的可达信道容量就会降低。而TBCC可以看作是一种循环编码方式,自身循环的特性在空间上等于增加了码字的长度,在一定程度上能够缓解块长变短带来的损失,这也是TBCC运用到短码上的原因。
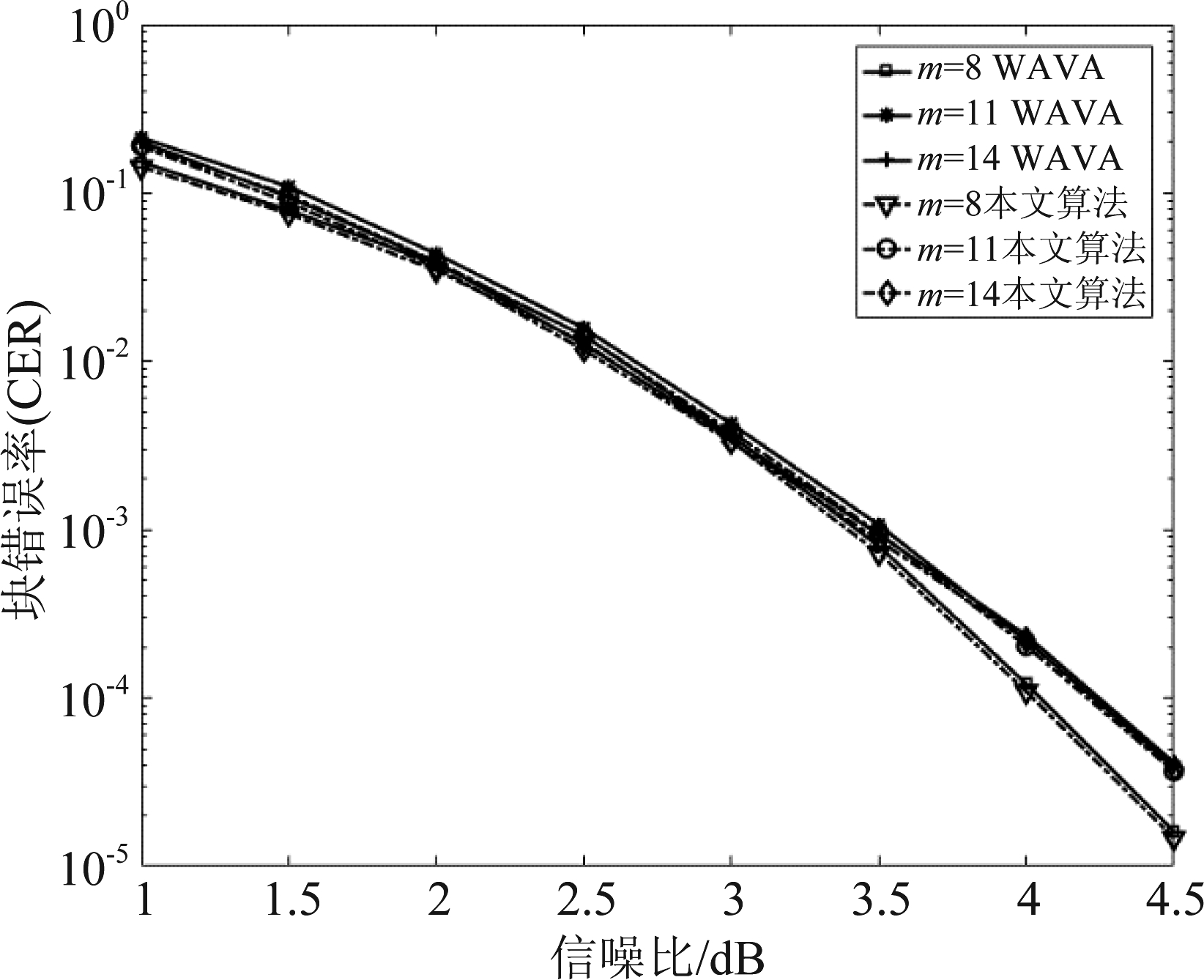
图6 (64,32) TBCC的两种算法性能比较
Fig.6 Performance comparison of the two algorithms for (64,32) TBCCs
前面已经通过仿真验证了本文算法与已有算法性能接近。图7给出了在不同信噪比下,约束长度m=8时三种算法完成一次译码所需要的平均迭代次数。可以看到WAVA(I=10)算法所需迭代次数最多,并且信噪比越低,所需迭代次数增大的越明显。相比于WAVA算法,另外两种算法在低信噪比下迭代次数大幅减少,并且本文算法有着比简化陷阱检测算法更少的迭代次数,在译码时间上的优势更明显。
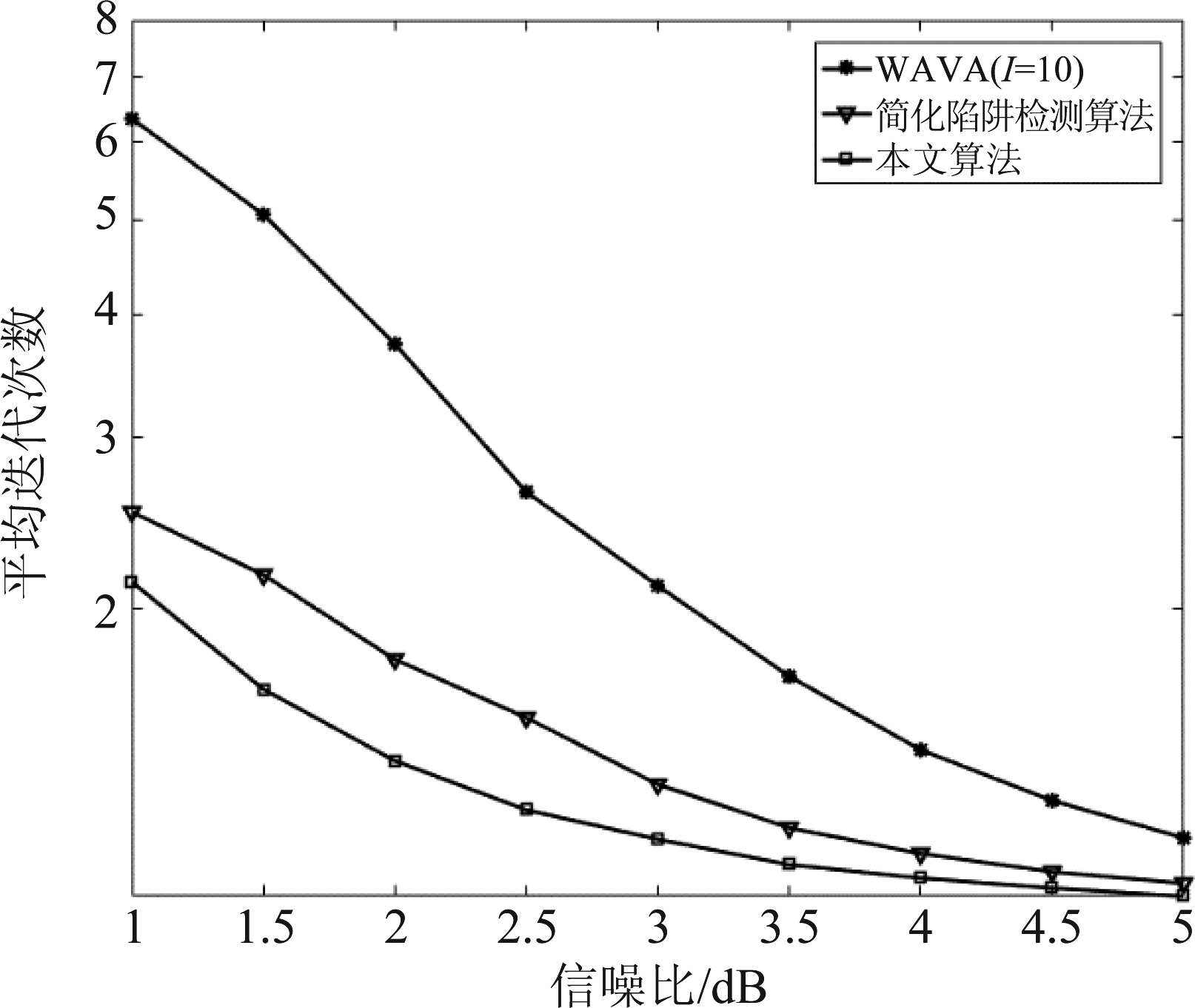
图7 (128,64) TBCC的三种译码算法平均迭代次数比较
Fig.7 Average number of iterations comparison of the third algorithms for (128,64) TBCCs
图8 1/2码率TBCC的CER满足10-4时所需信噪比
Fig.8 SNR required to achieve a CER of 10-4 for rate-1/2 TBCCs
经过对大量短TBCC性能的仿真,得出了块长对性能影响的一般规律。图8展示了码率为1/2,CER到达10-4时,采用本文算法译码所需的最低信噪比。我们观察到块长比较长时,所需的最低信噪比稳定在一个值,变化不太大,当块长继续缩短,所需的信噪比会急剧上升,说明此刻译码性能已发生严重恶化,这可能与回溯深度有关,一般归零卷积码回溯深度是约束长度的5～7倍,我们发现产生恶化的块长,TBCC的信息长度小于了回溯深度。例如, 图中约束长度m=8,块长为64,其信息码长为32,小于回溯深度5×8=40。因此可以得出,在短码场景中,TBCC在信息码长大于回溯深度时,性能是可控的。
5 结论
本文重点关注在短块传输下的高效信道编码,特别是信息位小于100比特的短码。针对TBCC已有算法存在的问题,提出了自适应循环VA算法,在不降低CER的前提下,平均迭代次数大幅下降。 从实验及分析中观察到,TBCC性能明显好于归零卷积码,可以看出随着约束长度的增加,性能的增幅会逐渐下降。并且在满足相同错误率的情况下,块长极短时性能会有明显恶化,随着块长的增加,所需信噪比会逐渐趋于稳定。因此在实际应用中,应该折中考虑复杂度和性能,选择合适的约束长度。
[1] TAJIMA M. Characteristic matrices and trellis reduction for tail-biting convolutional codes[J]. ArXiv Preprint ArXiv:1705.03982, 2017.
[2] GAUDIO L, NINACS T, JERKOVITS T, et al. On the performance of short tail-biting convolutional codes for ultra-reliable communications[C]∥11th International ITG Conference on Systems, Communications and Coding. Hamburg, Germany. VDE, 2017: 1- 6.
[3] LIANG E, YANG Hengjie, DIVSALAR D, et al. List-decoded tail-biting convolutional codes with distance-spectrum optimal CRCS for 5G[C]∥2019 IEEE Global Communications Conference (GLOBECOM). Waikoloa, HI, USA. IEEE, 2019: 1- 6.
[4] VAN WONTERGHEM J, ALLOUM A, BOUTROS J J, et al. Performance comparison of short-length error-correcting codes[C]∥2016 Symposium on Communications and Vehicular Technologies (SCVT). Mons, Belgium. IEEE, 2016: 1- 6.
[5] SHIRVANIMOGHADDAM M, MOHAMMADI M S, ABBAS R, et al. Short block-length codes for ultra-reliable low latency communications[J]. IEEE Communications Magazine, 2019, 57(2): 130-137.
[6] SHAO R Y, LIN Shu, FOSSORIER M P C. Two decoding algorithms for tailbiting codes[J]. IEEE Transactions on Communications, 2003, 51(10): 1658-1665.
[7] WANG Xiaotao, QIAN Hua, XIANG Weidong, et al. An efficient ML decoder for tail-biting codes based on circular trap detection[J]. IEEE Transactions on Communications, 2013, 61(4): 1212-1221.
[8] COX R V, SUNDBERG C E W. An efficient adaptive circular Viterbi algorithm for decoding generalized tailbiting convolutional codes[J]. IEEE Transactions on Vehicular Technology, 1994, 43(1): 57- 68.
[9] HAN Y S, WU Tingyi Y, CHEN Poning, et al. A low-complexity maximum-likelihood decoder for tail-biting convolutional codes[J]. IEEE Transactions on Communications, 2018, 66(5): 1859-1870.
[10] POLYANSKIY Y, POOR H V, VERDU S. Channel coding rate in the finite blocklength regime[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2307-2359.
[11] ERSEGHE T. Coding in the finite-blocklength regime: Bounds based on Laplace integrals and their asymptotic approximations[J]. IEEE Transactions on Information Theory, 2016, 62(12): 6854- 6883.
