1 引言
跳频通信技术具有很强的抗干扰、抗衰落、抗截获能力以及可多址组网等优点,在现代军事通信、民用移动通信中获得了广泛的应用。其中跳频序列的好坏将直接影响跳频通信系统的抗干扰能力,其主要研究包括两个方面:一是探寻受参数限制所设计的跳频序列能达到的理论界限;二是如何设计出达到或者接近理论界限的跳频序列。目前跳频序列的理论界限研究已相对成熟,如Lempel-Greenberger界,Peng-Fan界等;构造跳频序列所使用的方法主要有代数构造和组合构造两种:Zhou等人将m序列的部分状态序列作为基序列,使用交织技术构造了最优跳频序列[1];Yang等人建立起循环码(Reed-Solomon codes, RS)与跳频序列之间的联系,进而构造出了最优跳频序列[2];Zhou等人[3]利用笛卡尔积提出三种最优跳频序列的通用构造方法;Ren等人[4]利用有限域上的分圆和中国剩余定理给出了一个最优跳频序列的构造方法。
上述跳频序列的构造拥有完备的理论体系,可以通过数学推导证明其构造的跳频序列能够达到或接近理论界限;但其构造方法也存在一定的限制条件,如跳频序列的频点数为素数或奇素数等;另外上述方法都没有考虑干扰的影响,抗干扰性能有待提升。为此有学者提出宽间隔跳频的方法[5],将相邻两跳的频点保持一定的频率间隔,以降低被截获或干扰的概率,常用对偶频带法对跳频序列进行宽间隔处理,但存在遗漏满足宽间隔的频率对的问题。文献[6]为解决上述问题提出一种改进对偶频带法,构造的跳频序列具有较好的汉明相关性,但其属于盲抗干扰的方式,抗干扰能力有待提升且所能应对的干扰类型单一。未来电磁环境日益复杂,往往会存在多种干扰,跳频序列的设计需要具有更强的针对性以保证系统的正常通信。目前频谱感知技术研究已经相对成熟,这意味着通信方可以获得更加详细的干扰信息,如何充分利用这些干扰信息将是抗干扰通信的研究热点之一。
跳频序列实质是频点的排列组合,抗干扰跳频序列的设计则可以利用干扰信息对频点的组合进行优化,从而得到相应的跳频序列,对于组合优化问题[7]常采用启发式优化算法进行求解。灰狼优化算法(Grey Wolf Optimizer,GWO)[8]是由澳大利亚学者Mirjalili提出的,通过模仿自然界中灰狼群体的等级制度和捕食过程实现算法优化搜索的目的。GWO具有原理简单、参数少、易于实现等优点,已广泛应用于路径规划[9]、支持向量机[10]、文本聚类[11]等领域。金星等[12]通过灰狼算法与差分进化算法(Differential Evolution Algorithm, DE)结合以增强种群的多样性,该算法有较好的全局收敛性,但计算的时间复杂度高且易早熟。黄晨晨等[13]对狼群中最差位置的灰狼进行随机蛙跳搜索有助于算法跳出局部最优,使用logistic映射初始化狼群提高种群多样性;刘彬等[14]将单种群划分为多种群,引入竞争策略动态更新各种群的决策层个体,上述两种方法都提高了算法的全局寻优能力,但收敛速度较慢。
本文首先对抗干扰跳频序列设计进行问题建模,得到优化目标函数。然后对灰狼算法进行改进:提出反向学习策略和个体信息交流机制,其中反向学习策略用于加快算法的收敛速度,而个体信息交流机制则可以减少算法陷入局部最优的概率。最后使用灰狼算法优化设计抗干扰跳频序列,在多种干扰环境中大大提升跳频通信系统的抗干扰容限。
2 问题建模
在实际通信系统中收发双方之间存在时延,为减少时延对信号接收的影响,跳频通信系统希望使用的跳频序列具有良好的汉明相关性。设F={f1, f2,..., fq}为通信系统所能使用的频点集,S={s0,s1,...,sl-1}为使用频点集F中的频点所组成的跳频序列,l为跳频序列S的周期或长度。跳频序列性能的测度最常用的是汉明自相关,它表征了跳频序列在一定时延下一个周期内频率碰撞的次数,其汉明自相关HS(τ)和最大汉明自相关H(S)定义为:
(1)
式中:i+τ为模l运算;si,si+τ∈F且![]()
H(S)=max{HS(τ)},1≤τ<l
(2)
Lempel和Greenberger在1974年给出了跳频序列S的最大汉明自相关值H(S)的一个下界,由定理1所述。
定理1 (Lempel-Greenberger界)设S是F上的周期为l的跳频序列,则
(3)
式中:q为跳频序列使用的频点个数;b为l模q的最小非负整数;「x⎤表示大于或等于x的最小整数。
面对复杂电磁环境中的各种干扰,单纯提高发射功率带来的系统收益极低。跳频通信作为一种载频可变的通信方式,可灵活躲避干扰,从而间接提高接收端信噪比,所以跳频信号被干扰的概率是评价跳频序列在不同干扰下性能的另一指标。对干扰信号使用短时傅里叶变换(short-time Fourier transform, STFT)进行时频分析,得到干扰信号的时频谱:
(4)
STFTu(t, f)=![]() u(τ)h*(τ-t)exp(-j 2πfτ)dτ
u(τ)h*(τ-t)exp(-j 2πfτ)dτ
(5)
式中:h*(t)为窗函数的共轭形式;u(t)为干扰信号;M为窗函数的长度。通过干扰信号的时频谱可直观的看出跳频信号被干扰信号影响的程度。
在通信过程中可能存在新干扰出现的情况,跳频序列中频点应分布均匀,降低信号被干扰的概率,从而减弱新干扰对跳频信号的影响程度。跳频序列的均匀性可表示为:
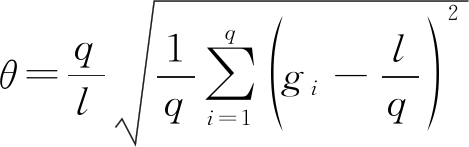
(6)
式中:gi表示频点fi在一个周期内出现的次数。θ越接近0说明在一个周期内频点分布越均匀,跳频序列的均匀性越好。
本文在评判跳频序列时考虑以下四个性能指标:
(1)跳频信号在当前干扰下被干扰的概率,其可使用跳频信号频点处所对应的平均干扰功率Y来间接表示:
(7)
(2)跳频序列的最大汉明自相关值H(S)。
(3)根据香农定理,通过增加带宽可获得更大的信道容量,所以跳频序列应具有较高的跳频增益Gp:
(8)
式中:W为跳频系统所使用的总带宽;B为每跳信号带宽。
(4)跳频序列的均匀性θ。
因此可以将抗干扰跳频序列设计建模如下:
(9)
式中:![]() 表示平均干扰功率的归一化值;
表示平均干扰功率的归一化值;![]() 表示跳频序列的最大汉明自相关值的归一化值;
表示跳频序列的最大汉明自相关值的归一化值;![]() 表示最小化跳频增益的归一化值。可以看出跳频序列S所对应的f(S)值越小,其性能就越好。对于式(9)中的权重系数,本文使用层次分析法[18](Analytic Hierarchy Process, AHP)求得权重系数分别为:0.6411、0.2242、0.0799、0.0548。
表示最小化跳频增益的归一化值。可以看出跳频序列S所对应的f(S)值越小,其性能就越好。对于式(9)中的权重系数,本文使用层次分析法[18](Analytic Hierarchy Process, AHP)求得权重系数分别为:0.6411、0.2242、0.0799、0.0548。
由以上讨论可以得出,抗干扰跳频序列设计是一个组合优化问题。使用穷举搜索(Exhaustive Searching,ES)可以找到最优的频点排列组合,但算法计算复杂度为O(ql),计算开销巨大。启发式优化算法可以求解组合优化问题,它的计算复杂度要远远小于穷举算法,所以本文使用启发式优化算法进行抗干扰跳频序列优化设计。
3 灰狼算法的改进
3.1 标准灰狼算法
灰狼算法通过模拟自然界中灰狼的捕食行为和种群等级制度来进行优化搜索,算法将狼群分为4个社会等级:α狼、β狼、δ狼以及ω狼。其中α狼、β狼、δ狼为狼群的决策层负责指导狼群中的ω狼对猎物进行跟踪围捕,其分别对应狼群中适应度排前三的灰狼。灰狼跟踪包围猎物的数学描述如下:
D=|C·Xp(t)-X(t)|
(10)
X(t+1)=X(t)-A·D
(11)
A=(2r1-1)a
(12)
C=2r2
(13)
式中:Xp为猎物的位置;X为灰狼个体的位置;t为当前迭代次数;C为摆动因子矢量;A为收敛因子矢量;r1、r2为在区间[0,1]内均匀分布的随机向量;a为控制参数,其值随迭代次数从2线性递减到0,计算方式如下:
a=2-2t/Tmax
(14)
式中,Tmax为最大迭代次数。
狼群中ω狼在α狼、β狼、δ狼的指导下对猎物进行捕食,其行为用数学描述如下:
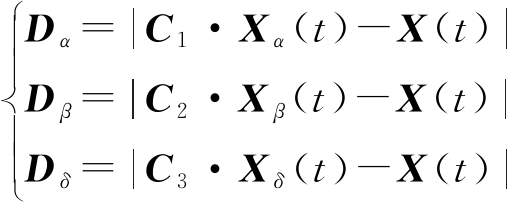
(15)

(16)
(17)
3.2 控制参数
在灰狼算法中,算法的全局搜索与局部搜索是由A决定的,当|A|>1时,灰狼会放弃当前猎物转而寻找更好的猎物,此时算法进行全局搜索;当|A|<1时,灰狼向当前猎物靠近,此时算法进行局部搜索。收敛因子A由控制参数a决定,在标准GWO算法中,a由2到0线性减少,这会导致算法的搜索能力不强。本文改进控制参数为:
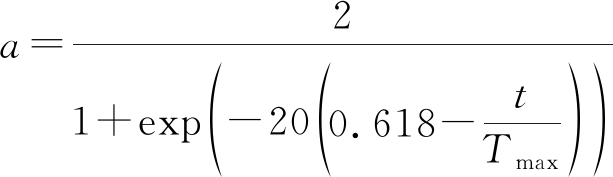
(18)
改进控制参数a后能够更好的平衡算法全局搜索与局部搜索。在算法迭代前期收敛因子能够保持较大的数值,且变化缓慢,扩大算法的搜索范围,提高全局搜索能力;在算法迭代后期,收敛因子保持较小的数值,可保证灰狼算法以较小的步长进行探索,提高算法局部搜索能力。
3.3 反向学习策略
反向学习策略是计算机智能领域出现的一种新技术[19],其主要思想是对于一个可行解,同时计算并评估其反向解,从中选择较优的解作为下一代个体。为了提高算法的收敛速度和求解精度,本文改进的反向学习过程如下:
X*=(m+n)-X
(19)
X′=X*+r3·((m+n)/2-X*)
(20)
式中:X为灰狼个体;X*为传统反向学习的反向解;n和m分别为求解区域的最大值和最小值;r3为在区间[0,1]内均匀分布的随机向量;X′为本文改进反向学习的反向解。
使用本文的反向学习策略比传统反向学习具有更高的概率找到全局最优解,所以此策略可加快算法的收敛速度。下面证明使用本文反向学习策略得到的反向解X′比传统反向学习策略的X*更接近最优解。
首先对一维情况进行证明,令d(x′)表示本文方法的反向解x′与最优解xbest的距离,d(x*)表示传统反向解x*与最优解xbest的距离,即证明P(d(x′)≤d(x*))≥1/2。假设x的取值范围为[m,n],最优解记为xbest且在区间内均匀分布,o=(m+n)/2。对于不同的x取值,分为以下两种情况考虑:x≤o和x>o。
当x≤o时,由式(19)可得x*≥o,进而由式(20)得:
x′≤x*
(21)
将区间划分为[m,o]、[o,x*]、[x*,n],分别讨论最优解位于以上3个区间的情况:
(1)当最优解xbest在区间[m,o]内时,由式(21)可得x′比x*更接近于最优解,即P(d(x′)≤d(x*)|xbest∈[m,o])=1;
(2)当最优解xbest在区间[o,x*]内时,因为最优解xbest与x′都在该区间内均匀分布,所以x′和x*接近最优解的概率相等,即P(d(x′)≤d(x*)|xbest∈[o,x*])=1/2;
(3)当最优解xbest在区间[x*,n]内时,由式(21)可得x*更接近最优解,即P(d(x′)≤d(x*)|xbest∈[x*,n])=0。
因为最优解在区间[m,n]内均匀分布,所以最优解位于区间的概率与该区间的长度成正比,即P(xbest∈[m,o])=1/2。当x≤o时,可以得到以下结论:
P(d(x′)≤d(x*))=1/2(1+P(xbest∈[o,x*]))≥1/2
(22)
同理,当x>o也可得到以上结论。以上为一维情况下的证明过程,当求解问题为高维时,证明思路相同,也可得到相同结果,证毕。
所以使用本文改进反向学习策略拥有更高的概率找到最优解,使得算法收敛速度加快。
3.4 信息交流机制
标准GWO算法中,狼群中的个体始终由种群中排名前三的个体领导,若当前领导层的灰狼位于局部最优区域,则会导致狼群向局部最优区域靠拢,使得算法最终收敛于局部最优。狼群中其他个体之间并没有信息交流,信息利用率可进一步提高,本文提出一种个体信息交流机制,其数学描述如下:
(23)
式中:Xi为狼群中第i个灰狼;Xk为随机选取的第k个灰狼且k≠i;Xbest为当前最优秀的灰狼个体;r4为在区间[0.5,1]内均匀分布的随机向量,取值的大小代表Xi对于Xk所提供信息的接受程度,取值为1时代表完全接受;Rlevy(λ)表示一个服从莱维分布的随机向量,决定了灰狼的行进步长,本文使用Mantegna算法产生莱维分布的随机步长。
当行进步长的取值服从莱维分布时,该运动轨迹是一种短距离与偶尔长距离相间的随机路径,它符合自然界中许多昆虫的觅食轨迹。将其应用于灰狼个体的信息交流,使得灰狼个体在搜索过程中偶尔会出现较大步长的搜索路径,该方式可有效提高种群的多样性,扩大搜索范围,在提高算法搜索能力的同时避免陷入局部最优。为保证算法的收敛速度,该步骤执行贪婪准测,最终保留适应度靠前的灰狼个体。
4 抗干扰跳频序列设计流程
在当前干扰环境下,综合考虑跳频序列的最大汉明自相关性、均匀性、跳频增益和抗干扰能力,本文提出的利用灰狼优化算法设计抗干扰跳频序列算法具体步骤如下:
(1)确定跳频序列长度l、频点数目q、以及使用式(4)、(5)计算干扰信号的时频谱,将以上参数作为算法的输入;
(2)初始化算法参数:灰狼种群数目N、最大迭代次数Tmax;
(3)初始化狼群X1,X2,...,XN,每个灰狼个体代表不同的跳频序列;
(4)使用式(9)计算每个灰狼个体的适应度,确定α狼、β狼、δ狼,分别使用式(18)、式(12)、式(13)更新参数a、A、C;
(5)使用式(15)~(17)完成领导层灰狼指导灰狼种群的位置更新;
(6)使用式(19)~(20)执行反向学习策略,择优保留灰狼位置;
(7)使用式(23)完成灰狼个体之间的信息交流,将信息交流前后的灰狼种群合并比较,保留适应度前N的灰狼个体;
(8)判断迭代次数是否满足最大迭代次数要求,若满足要求,输出最优的灰狼个体,执行第(9)步;反之,则返回第(4)步继续执行;
(9)根据灰狼算法得到的优化结果构造跳频图案。
5 算法仿真与性能分析
5.1 改进灰狼算法性能
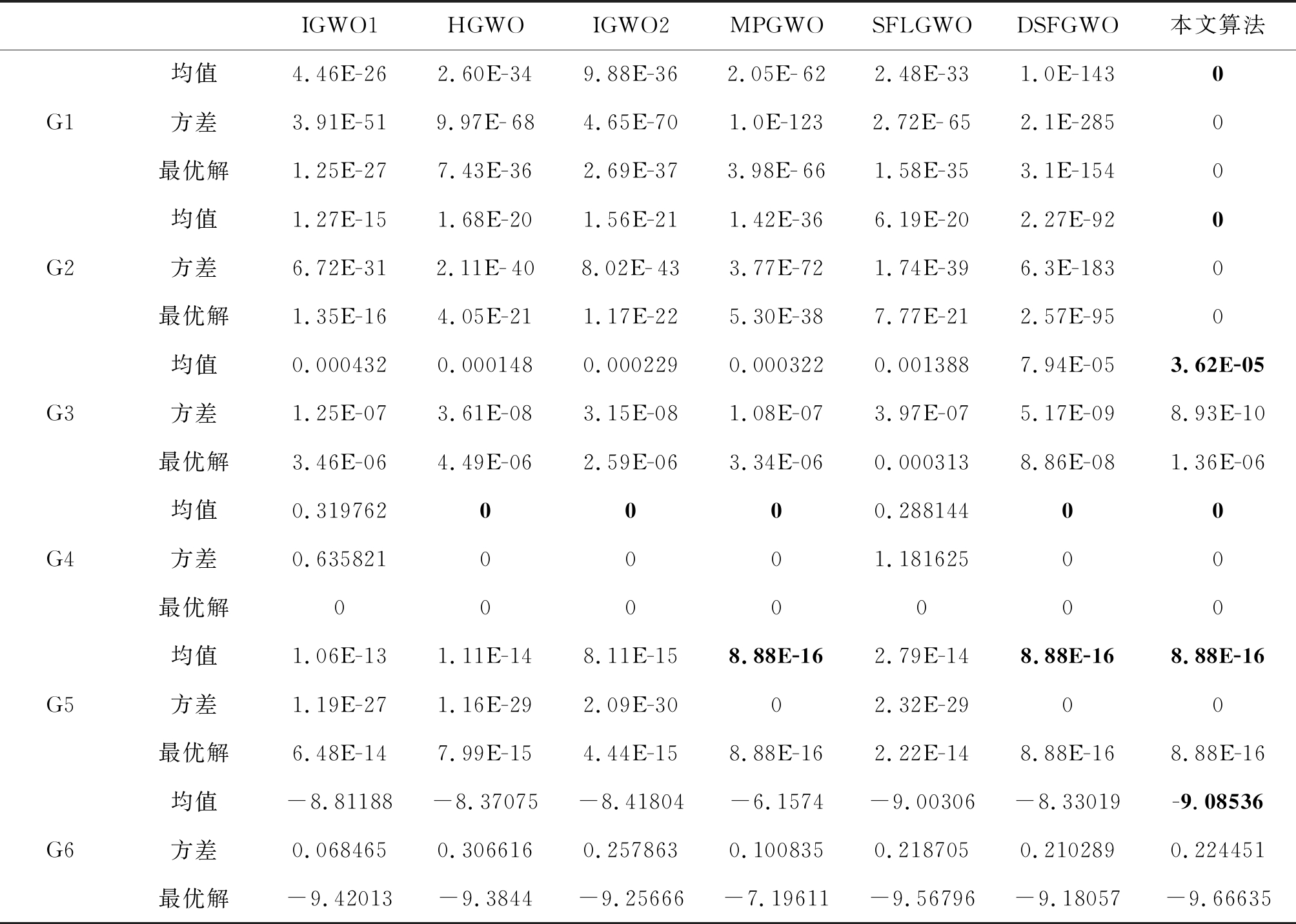
为验证本文改进灰狼算法的有效性,本文选取文献[8]中的F1、F2、F7、F9、F10、F14作为本文的测试函数进行测试,将其编号为G1-G6,对比算法分别为:IGWO1[15]、HGWO[12]、IGWO2[16]、MPGWO[14]、SFLGWO[13]、DSFGWO[17]。设置算法最大迭代次数为500次,种群规模为40,MPGWO算法中每个子种群的规模为10,对比算法的其他参数设置参考其对应参考文献。每种算法独立运行30次,每种算法30次优化结果的平均值、方差以及最优值结果如表1所示。
函数G1-G3为单峰函数,用于考察算法的收敛速度和求解精度;函数G4-G6为多峰函数,用于考察算法跳出局部最优的能力。由表1可以看出,本文算法在所有测试函数上都得到了比其他6种算法较为优异的结果,这表明本文所提出的改进策略的有效性。由单峰测试函数的结果表明本文算法的收敛速度比其他算法快得多,从多峰测试函数的结果可以看出其他算法易陷入局部最优。
表1 七种算法结果对比表
Tab.1 Comparison table of seven algorithm results
IGWO1HGWOIGWO2MPGWOSFLGWODSFGWO本文算法G1均值4.46E-262.60E-349.88E-362.05E-622.48E-331.0E-1430方差3.91E-519.97E-684.65E-701.0E-1232.72E-652.1E-2850最优解1.25E-277.43E-362.69E-373.98E-661.58E-353.1E-1540G2均值1.27E-151.68E-201.56E-211.42E-366.19E-202.27E-920方差6.72E-312.11E-408.02E-433.77E-721.74E-396.3E-1830最优解1.35E-164.05E-211.17E-225.30E-387.77E-212.57E-950G3均值0.0004320.0001480.0002290.0003220.0013887.94E-053.62E-05方差1.25E-073.61E-083.15E-081.08E-073.97E-075.17E-098.93E-10最优解3.46E-064.49E-062.59E-063.34E-060.0003138.86E-081.36E-06G4均值0.3197620000.28814400方差0.6358210001.18162500最优解0000000G5均值1.06E-131.11E-148.11E-158.88E-162.79E-148.88E-168.88E-16方差1.19E-271.16E-292.09E-3002.32E-2900最优解6.48E-147.99E-154.44E-158.88E-162.22E-148.88E-168.88E-16G6均值-8.81188-8.37075-8.41804-6.1574-9.00306-8.33019-9.08536方差0.0684650.3066160.2578630.1008350.2187050.2102890.224451最优解-9.42013-9.3844-9.25666-7.19611-9.56796-9.18057-9.66635
在函数G4、G5上七种算法收敛曲线如图1所示。由图1可以看出,虽然部分改进算法具有跳出局部最优的能力,但本文算法的收敛速度更快。本文提出的个体信息交流机制可以提高种群的信息利用率使得灰狼个体不只依赖于领导层的灰狼,同时使用莱维飞行模拟昆虫的觅食轨迹使得算法的搜索更有效率,这就使得算法具有跳出局部最优的能力;反向学习策略提高了灰狼个体找到最优解的概率,加快了灰狼的搜索速度。
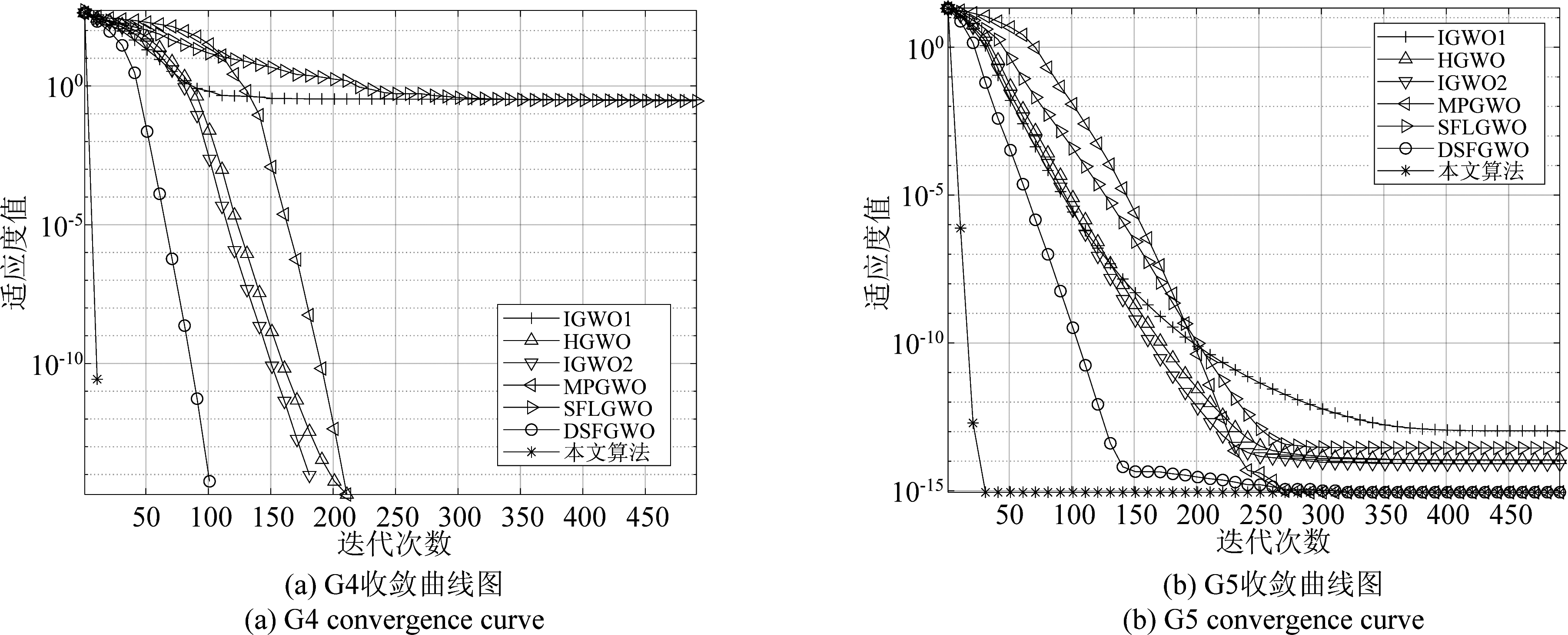
图1 算法收敛曲线图
Fig.1 Algorithm convergence curve
综上所述,相比于其他改进灰狼算法本文算法具有较高的收敛速度以及稳定性。
5.2 跳频序列抗干扰测试
本节将检验所设计跳频序列的抗干扰能力。设定跳频系统的通信频带范围为14 kHz~22 kHz,基带信号的带宽为0.5 kHz,故划分为16个频点,编号为1~16,跳速为10 Hop/s,跳频周期为6 s,故跳频序列的长度为60。4种人为干扰信号分别为:扫频干扰(记作干扰1),部分频带干扰(记作干扰2),部分频带干扰与扫频干扰的混合干扰(分别记作干扰3和干扰4)。
使用文献[6]方法构造的最小间隔为0的跳频序列记为跳频序列I,最小间隔为2的跳频序列记为跳频序列J,最小间隔为7的跳频序列记为跳频序列K,其中I为传统跳频序列, J和K为宽间隔跳频序列,都属于盲抗干扰跳频序列,它们与当前存在的干扰无关;使用本文方法在4种干扰背景下设计得到的跳频序列分别记为S1、S2、S3、S4。
计算得到它们在不同干扰下的被干扰概率和最大汉明自相关值、跳频增益以及均匀性分别如表2和表3所示。
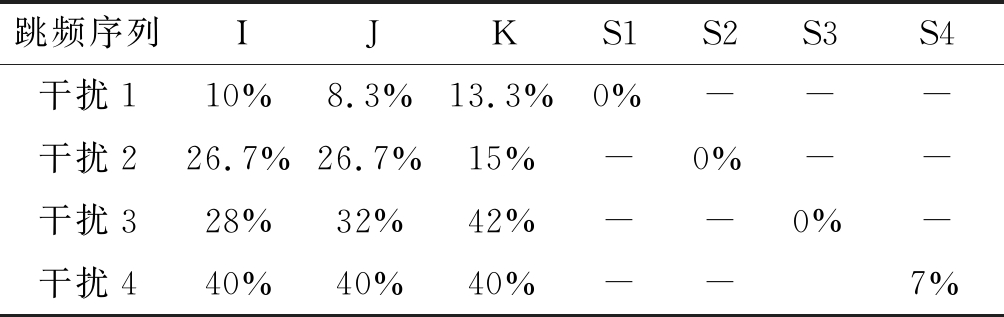
表2 四种干扰下7组跳频序列被干扰概率
Tab.2 Interference probability of 7 groups of frequency-hopping sequences under 4 kinds of jamming
跳频序列IJKS1S2S3S4干扰110%8.3%13.3%0%---干扰226.7%26.7%15%-0%--干扰328%32%42%--0%-干扰440%40%40%--7%
由表2可以看出,本文算法设计的跳频序列在单一干扰下,可以完全避开被干扰的频段,抗干扰能力明显优于其他三组跳频序列;在复杂混合干扰下,当干扰分布不是很密集时,跳频序列S3仍可以完全避开干扰频带;当干扰分布过于密集(如干扰4)时,跳频信号被干扰的概率为7%。而文献[6]方法在扫频干扰下设计的3组跳频序列的被干扰概率在10%左右,躲避干扰的能力相差不大;在部分频带干扰下,干扰信号包含了跳频通信的4个频点,跳频序列K可以保证在当前跳信号被干扰时下一跳信号可跳出干扰范围,但跳频序列I和J间隔过小,无法使信号跳出干扰范围,所以跳频序列K相比于其他两组跳频序列具有较高抗干扰能力;在复杂混合干扰下,因干扰信号在通信频带内分散分布,所以宽间隔跳频序列的抗干扰机制不再适用,被干扰概率超过30%,已严重影响通信双方的正常通信。
综上所述,本文算法所设计的跳频序列无论在单一干扰还是混合干扰下都比其他两种跳频序列具有更高的抗干扰能力。而宽间隔跳频序列只在部分频带干扰下比传统跳频序列具有较高的抗干扰能力,且抗干扰能力与其最小间隔相关,当部分频带干扰的带宽超过其最小间隔时,其抗干扰能力与传统跳频序列相当。
由表3可以看出:(1)本文方法设计的抗干扰跳频序列不仅抗干扰能力强,而且最大汉明相关值也较小,均匀性差于传统跳频序列,但仍好于宽间隔跳频序列,这是因为传统跳频序列在设计时没有考虑到干扰影响,而宽间隔跳频序列进行了宽间隔处理,本文跳频序列考虑了干扰的时频分布。(2)由定理1可以得到周期为60,频点数为16的跳频序列其L-G界为3,频点数为12的跳频序列其L-G界为5,频点数为14的跳频序列其L-G界为4。本文设计的抗干扰跳频序列S2、S4与其对应的L-G界相差1,属于次最优跳频序列。本文方法设计的抗干扰跳频序列在跳频增益方面要弱于传统跳频序列和宽间隔跳频序列,这是因为个别频点在整个跳频周期内一直处于被干扰的状态,为保证系统拥有良好的通信效果放弃使用这些频点。(3)文献[6]方法设计的跳频序列K虽在部分频带干扰下比跳频序列I和J具有较强的抗干扰能力,但其最大汉明自相关值以及均匀性都要差于后两者。该方法是基于m序列进行跳频序列设计,跳频序列的频点数只能为2的幂次方,无法根据频带宽度和基带信号带宽灵活划分频点,灵活性较差。
表3 跳频序列其他性能参数
Tab.3 Other performance parameters of frequency-hopping sequence

跳频序列IJKS1S2S3S4最大汉明自相关值67105685均匀性0.11550.27490.50330.22110.24490.34640.2848跳频增益16161616121214
以上实验结果表明,本文算法根据不同干扰构造不同跳频序列,可灵活应对各种干扰信号,设计出的跳频序列针对性强且拥有更强的抗干扰能力。
6 结论
本文为解决跳频通信抗干扰的问题,提出一种新的跳频序列设计方法,根据不同的干扰可设计出不同的跳频序列。首先对灰狼算法进行了改进,提出反向学习策略和信息交流机制提高算法的收敛速度、求解精度以及稳定性。测试函数上的性能对比验证了本文算法的优越性。然后使用灰狼算法设计抗干扰跳频序列。最后与其他跳频序列设计方法进行对比分析,结果表明本文构造的跳频序列可应对更复杂的干扰环境,具有更强的抗干扰能力。
[1] ZHOU Limengnan, PENG Daiyuan, LIANG Hongbin, et al. Constructions of optimal low-hit-zone frequency hopping sequence sets[J]. Designs, Codes and Cryptography, 2017, 85(2): 219-232.
[2] YANG Yang, TANG Xiaohu, PARAMPALLI U, et al. New bound on frequency hopping sequence sets and its optimal constructions[J]. IEEE Transactions on Information Theory, 2011, 57(11): 7605-7613.
[3] ZHOU Limengnan, PENG Daiyuan, LIANG Hongbin, et al. Generalized methods to construct low-hit-zone frequency-hopping sequence sets and optimal constructions[J]. Cryptography and Communications, 2017, 9(6): 707-728.
[4] REN Wenli, FU Fangwei, ZHOU Zhengchun. New sets of frequency-hopping sequences with optimal Hamming correlation[J]. Designs, Codes and Cryptography, 2014, 72(2): 423- 434.
[5] GUAN Lei, LI Zan, SI Jiangbo, et al. Generation and characteristics analysis of cognitive-based high-performance wide-gap FH sequences[J]. IEEE Transactions on Vehicular Technology, 2015, 64(11): 5056-5069.
[6] 牛强军, 孙会超. 一种生成宽间隔跳频序列的改进对偶频带法[J]. 电讯技术, 2019, 59(1): 50-55.
NIU Qiangjun, SUN Huichao. Wide-gap frequency-hopping sequences generated by improved dual sub-band method[J]. Telecommunication Engineering, 2019, 59(1): 50-55.(in Chinese)
[7] 徐华正,余金澳,朱诗兵.毫米波通信低复杂度波束选择和用户调度算法[J]. 信号处理, 2019, 35(11): 1853-1860.
XU Huazheng, YU Jinao, ZHU Shibing. Low-complexity beam selection and user scheduling algorithm for millimeter-wave communication[J]. Journal of Signal Processing, 2019, 35(11): 1853-1860.(in Chinese)
[8] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46- 61.
[9] 王永琦, 江潇潇. 基于混合灰狼算法的机器人路径规划[J]. 计算机工程与科学, 2020, 42(7): 1294-1301.
WANG Yongqi, JIANG Xiaoxiao. Robot path planning using a hybrid grey wolf optimization algorithm[J]. Computer Engineering & Science, 2020, 42(7): 1294-1301.(in Chinese)
[10] 周广悦, 李克文, 刘文英, 等. 灰狼优化的混合参数多分类孪生支持向量机[J]. 计算机科学与探索, 2020, 14(4): 628- 636.
ZHOU Guangyue, LI Kewen, LIU Wenying, et al. Grey wolf optimizes mixed parameter multi-classification twin support vector machine[J]. Journal of Frontiers of Computer Science and Technology, 2020, 14(4): 628- 636.(in Chinese)
[11] 潘成胜, 张斌, 吕亚娜, 等. 改进灰狼优化算法的K-Means文本聚类[J]. 计算机工程与应用, 2021, 57(1): 188-193.
PAN Chengsheng, ZHANG Bin, LYU Yana, et al. K-means text clustering based on improved gray wolf optimization algorithm[J]. Computer Engineering and Applications, 2021, 57(1): 188-193.(in Chinese)
[12] 金星, 邵珠超, 王盛慧. 一种基于差分进化和灰狼算法的混合优化算法[J]. 科学技术与工程, 2017, 17(16): 266-269.
JIN Xing, SHAO Zhuchao, WANG Shenghui. A hybrid optimization algorithm based on differential evolution and grey wolf optimizer[J]. Science Technology and Engineering, 2017, 17(16): 266-269.(in Chinese)
[13] 黄晨晨, 魏霞, 黄德启, 等. 求解高维复杂函数的混合蛙跳-灰狼优化算法[J]. 控制理论与应用, 2020, 37(7): 1655-1666.
HUANG Chenchen, WEI Xia, HUANG Deqi, et al. Shuffled frog leaping grey wolf algorithm for solving high dimensional complex functions[J]. Control Theory & Applications, 2020, 37(7): 1655-1666.(in Chinese)
[14] 刘彬, 刘泽仁, 李德健, 等. 多种群灰狼算法优化ELM网络参数的研究[J]. 燕山大学学报, 2020, 44(5): 508-518.
LIU Bin, LIU Zeren, LI Dejian, et al. Research on optimization of ELM network parameters by multi-population grey wolf algorithm[J]. Journal of Yanshan University, 2020, 44(5): 508-518.(in Chinese)
[15] 张增辉, 邓宇豪, 李春卫, 等. 基于改进灰狼优化算法的光伏MPPT方法[J/OL]. 电测与仪表: 1-7[2021-01-10]. http:∥kns.cnki.net/kcms/detail/23.1202.TH.20200905.1210.002.html.
ZHANG Zenghui, DENG Yuhao, LI Chunwei, et al. Photovoltaic MPPT method based on improved grey wolf optimization[J/OL]. Electrical Measurement and Instrumentation:1-7[2021-01-10]. http:∥kns.cnki.net/kcms/detail/23.1202.TH.20200905.1210.002.html.(in Chinese)
[16] 甄永琦, 蒋伟. 改进灰狼算法在配电网故障定位中的应用[J]. 计算机应用与软件, 2020, 37(11): 200-205.
ZHEN Yongqi, JIANG Wei. Application of improved grey wolf algorithm in fault location of distribution network[J]. Computer Applications and Software, 2020, 37(11): 200-205.(in Chinese)
[17] 王正通, 程凤芹, 尤文, 等. 基于翻筋斗觅食策略的灰狼优化算法[J/OL]. 计算机应用研究: 1-5[2021-01-10]. https:∥doi.org/10.19734/j.issn.1001-3695.2020.04.0102.
WANG Zhengtong, CHENG Fengqin, YOU Wen, et al. Grey wolf optimization algorithm based on somersault foraging strategy[J/OL]. Application Research of Computers: 1-5[2021-01-10]. https:∥doi.org/10.19734/j.issn.1001-3695.2020.04.0102. (in Chinese)
[18] 吴仁彪, 何理, 王晓亮, 等. 通用航空飞行计划评估方法综述[J]. 信号处理, 2019, 35(3): 426- 434.
WU Renbiao, HE Li, WANG Xiaoliang, et al. Review of general aviation flight plan evaluation method[J]. Journal of Signal Processing, 2019, 35(3): 426- 434.(in Chinese)
[19] AHANDANI M A.Opposition-based learning in the shuffled bidirectional differential evolution algorithm[J]. Swarm and Evolutionary Computation, 2016, 26: 64- 85.



