1 引言
在进行机械振动状态监测和减振降噪处理时,需要先获取各振动源的振动信号,而振动传感器接收的信号往往包含不同振动源的振动信号和环境噪声,这些振动源位于机械的不同位置,会从不同传递路径到达振动传感器[1-2]。在对设备特征及系统特性难以获取的条件下,为了从少量振动传感器的接收信号中识别信号源数和各频率分量,盲源分离成为了一种有效的解决方法,为振动信号的特征提取与识别提供了新的手段[3- 6]。这整个过程相当于从混合信号中识别出有哪些振动源,它们的振动特性、幅频特性是什么,强调的是从混合信号中辨识出有价值、可解释的特征和成分,所以称之为“识别”。在测量机械振动信号时,通常振动传感器的数量会少于机械振动源的个数,而机械振动源的传递路径是未知的,此时振动源识别问题变为了欠定盲源分离问题(Underdetermined Blind Source Separation,UBSS)。UBSS是一种从少量通道混合信号中分离多个源信号的新技术,具有广阔的应用前景[7-10]。
目前,解决欠定盲源分离问题通常基于稀疏分量分析(Sparse Component Analysis,SCA)[11-15]。2001年,Bofill[11]提出了SCA算法的经典思路“两步法”,即首先根据观测信号估计得到混合矩阵,然后结合混合信号与估计的混合矩阵,通过优化算法实现源信号的分离。然而源信号的稀疏性对于SCA类算法非常重要,特别是在有噪声的情况下。为了进一步增强信号的稀疏性,很多时域或时频域的源稀疏性扩展方法被提出来[16-19]。Jourjine等人提出了一种简并混合估计技术(The Degenerate Unmixing Estimation Technique,DUET)[20],该方法假设源信号在时频域是正交的,每个时频点只由一个源信号支配,通过信号时频变换后的比值来恢复源信号。Abrard等人进一步放松了时频正交约束,提出了混合时频比方法(The Time-frequency Ratio of Mixtures,TIFROM)和单源域(Single Source Region)概念[21],只要求在某些相邻的时频区域内有一个源信号处于激活状态。Li扩展了DUET和TIFROM方法,达到了放松稀疏性假设的目的,提出了适应性更强的Li-TIFROM方法[22]。Reju等人提出了一种通过比较混合信号的傅里叶变换系数向量的实部和虚部的绝对方向来检测单源点,然后对检测出的单源点进行聚类来估计混合矩阵[23-24]。Zhen等人发现混合信号的时频表示可以由单源点组成的子空间集合来表示,利用稀疏编码方法(UBSSC)检测单源点,并利用一系列最小二乘法实现了源信号的恢复[25]。Arberet等人提出了局部占优假设模型,假设在某一时频范围内只存在一个主要激活源,利用主成分分析(Principal Components Analysis,PCA)方法对混合矩阵的时频变换进行单源域检测,并提出了一种自动选择聚类簇数的聚类方法来估计混合矩阵[26]。
在提取出足够的单源点或者单源域之后,可以对这些特征数据进行聚类来估计出混合矩阵[23]。基于这一观点,许多聚类方法被用于估计混合矩阵,例如K-means方法[27-28]、K-means++方法[29]、模糊聚类(Fuzzy Clustering-means,FC-means)[19]、层次聚类方法[23]、密度聚类方法[30]、密度峰值聚类方法[31]等。K-means、FC-means方法的优点在于其精度高计算速度快,然后其聚类结果对初始聚类中心比较敏感,聚类个数需要人工输入。密度聚类方法可以自动判断聚类个数,但缺点是计算量较大,运行效率低。
为了解决时频比方法对噪声敏感的缺点,本文基于Arberet的局部占优模型[26],提出了一种考虑每个时频点周围邻域数据的局部主成分提取方法,筛选出单源域特征数据,进行归一化投影到单位圆上得到用方向角表示的特征数据。针对源数估计和混合矩阵估计问题,本文提出了余弦距离来改进聚类验证技术和F-C means聚类算法,对提取出的时频激活源区域进行源数估计和聚类参数更新,得到源信号的个数并精确估计出混合矩阵。最后通过求解一系列最小二乘问题从混合信号对应的时频点中抽取出源信号。仿真实验及实测数据验证了所提出分离算法的可行性,同等条件下该方法比经典的时频比方法(TIFROM方法和Reju方法)得到了更精确的分离结果,特别是在噪声环境下,可以精确识别振动源成分,有助于对机械振动源进行识别和定量评估,以方便后续进行机械状态监测和减振降噪处理。
2 问题描述与数学模型
2.1 欠定盲源分离模型
在对机械振动信号应用盲源分离进行源识别前,首先必须明确机械设备的振动信号中“源”的含义。在机械系统中,通常认为“源”是由激励力引起的机械系统的冲击强度随时间的变化,称之为“本底振源”[32]。本底振源是机械系统对激励力源的响应[33],它是统计意义上的源的概念,与激励力源存在物理相关性。本底振源包括常规振动,调幅振动,调频振动,附加冲击,随机振动等。
盲源分离是利用多个传感器的观测信号,在源信号形式未知、传输通道参数未知的条件下,仅由观测信号实现源信号的恢复。通常观测信号来自一组传感器的输出,其中每个传感器接收到的是多个源信号的混合信号。考虑传感器数量为N,源信号数量为M,在欠定情况下,传感器数量小于源信号数量,即N<M,源信号从不同传递路径到达传感器,不同传递路径会使得源信号有着不同的衰减和时延,则欠定盲源分离模型可表示为
(1)
其中x(t)=[x1(t),x2(t),...,xN(t)]T为观测的混合信号向量,s(t)=[s1(t),s2(t),...,sM(t)]T为源信号向量,anm为信号衰减系数,τnm为第m个源信号到达第n个传感器的时延,n(t)=[n1(t),n2(t),...,nN(t)]T为加性噪声向量。式中anm,s(t),n(t),τnm均为未知的。由于信号在频域或时频域稀疏性更强,通常将信号变换到频域或时频域进行处理,先不考虑噪声项
X(t, f)=A( f )S(t, f)
(2)
此时,混合矩阵A=[a1( f ),a2( f ),...,aM( f )],其中am=[a1me-i2πfτ1m,...,aNme-i2πfτNm]T。
2.2 稀疏分量分析
稀疏分量分析利用的是信号的稀疏性,当接收信号在时域、频域或时频域上是稀疏的,则只有少数点有非零值。对于某些采样点上充分稀疏的信号,如果仅有一个源信号有占主导地位的值,而其他源信号接近于零,这些采样点称为单源激活点。为充分利用信号的稀疏性,通常用短时傅里叶变换(Short-time Fourier Transform,STFT)变换将混合信号变换到时频域
X(t, f)=A( f )S(t, f)
(3)
其中X(t, f)=[X1(t, f),X2(t, f),...,XN(t, f)]T,S(t, f)=[S1(t, f),S2(t, f),...,SM(t, f)]T。以两传感器,四个源信号为例,某个时频域单源点处只有源信号Sm激活,接收信号可以近似表示为
X(t, f)≈amSm(t, f)
(4)
此时混合信号时频比
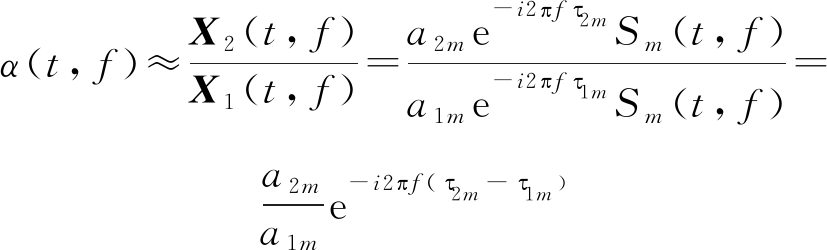
(5)
上式说明,单源点会沿着斜率为α的直线分布。而斜率α即为混合矩阵的列元素之比
以接收信号X1为横轴,X2为纵轴,得到的时域和时频域散点图如图1所示。在时频域中,信号有较强的稀疏性,呈现出明显的沿直线分布特性。
图1 混合信号时域和时频域分布散点图
Fig.1 Mixed signal time-domain and time-frequency domain distribution scatter plot
由于机械结构振动信号通过结构传递会产生延迟,机械系统的瞬态特征不会保持不变。但是当考虑一个刚度大体积小的结构,且传感器距离振源较近时,其振动的传递延迟可以忽略不计,可以近似为瞬态模型[3- 4]。此时时域时延项τnm为很小值,e-i2πfτnm近似为1,混合矩阵列元素变为am=[a1m,...,aNm]T,即混合矩阵A为实数矩阵,这使得瞬时混合模型在振动信号盲源分离领域应用广泛。
单源点假设过于严格,如果直接对数据点进行聚类来估计混合矩阵,则无法保证估计的准确性。一般而言,可以放宽稀疏性要求,通过混合时频比方法[21-23]筛选出近似满足公式(4)的特征数据,然后根据数据的沿直线分布特性公式(5),可以利用聚类算法将这些特征数据聚类为不同的簇,计算出这些簇的中心作为估计的混合矩阵的列,最后通过稀疏优化方法求解出源信号。
3 稀疏扩展模型与分离算法
3.1 稀疏特征提取
为了增强信号的稀疏性,利用STFT将混合信号变换到时频域,得到
X(t, f)=AS(t, f)+N(t, f)
(6)
将STFT变换后每个传感器接收数据X(t, f)展开称一维行向量,由于有N个传感器,可以将X(t, f)变换成N维行向量,方便后续特征提取。
由于盲源分离问题的双盲性,我们需要对源信号和混合矩阵提出先验假设,才能使得问题有解:
1.对于每一个源信号sm(t),在时频域存在一些时频点,使得Sm(t, f)占主导地位,幅值远大于其他源信号Sp(t, f),即
|Sm(t, f)≫Sp(t, f)|, ∀p≠m
(7)
2.混合矩阵A的任意M列向量是独立的。
3.在每一个时频点的邻域上,源信号的数量都小于混合信号的数量。
对于振动源信号而言,通常振动源的频率成分是不尽相同的,满足假设1和假设3,振动源所处的位置也不尽相同,传递路径也是不一样的,这就满足了条件2。
在时频域利用TIFROM[21]、Reju[23]等算法等单源点检测方法,利用混合信号时频比,对每个时频点进行比较筛选出单源点稀疏特征并进行聚类,得到混合矩阵的估计。这种经典时频比方法由于每次计算只考虑一个时频点的接收信号,由于噪声的存在,单源点的空间分布会偏离混合矩阵A对应的列方向,结果偏差较大,算法性能不稳健。在检测单源域时每次只考虑一个时频点是不够的,本文使用一种考虑时频点周围邻域Ω的单源域检测方法。该方法基于Arberet的局部占优模型[26],用多个数据进行筛选,增加信息量以提高筛选的准确性。利用一个当前时频点x(t, f)为中心的N×2N的滑动窗口,N为传感器个数,由于瞬时混合模型混合矩阵为实数,对每个元素取实部,每次滑动选取N×2N的实数矩阵X(Ω),利用PCA对矩阵X(Ω)提取区域置信度T(Ω)。当该区域为单源域时,即该区域只有一个激活源信号时,T(Ω)会得到一个较大的值,如果该区域为多源域或者无源域,则T(Ω)会得到一个较小的值。
(8)
其中λ1(Ω)>λ2(Ω)>...>λN(Ω)为X(Ω)的协方差矩阵的降序排列特征值,T(Ω)为局部置信度。使用所改进的单源域检测方法从混合信号中提取特征数据并存储进矩阵Z中,根据文献[23-24],特征数据占X(t, f)总数的20%～40%较为合适。由于零值附近有很多幅值较小的点,通过下式去除这些低能量的点,进一步减小混合矩阵估计误差
(9)
其中,
代表提取的特征数据中所有时频向量的l2范数的平均值,而ε是阈值系数。对数据进行归一化,此时第k个特征数据可用方向角β表示,即zk=(cos βk,sin βk),筛选之后的时频域特征数据散点图为图2,五角星表示混合矩阵的列元素的坐标。由于直线有正负两个方向,在后续处理中取方向绝对值。
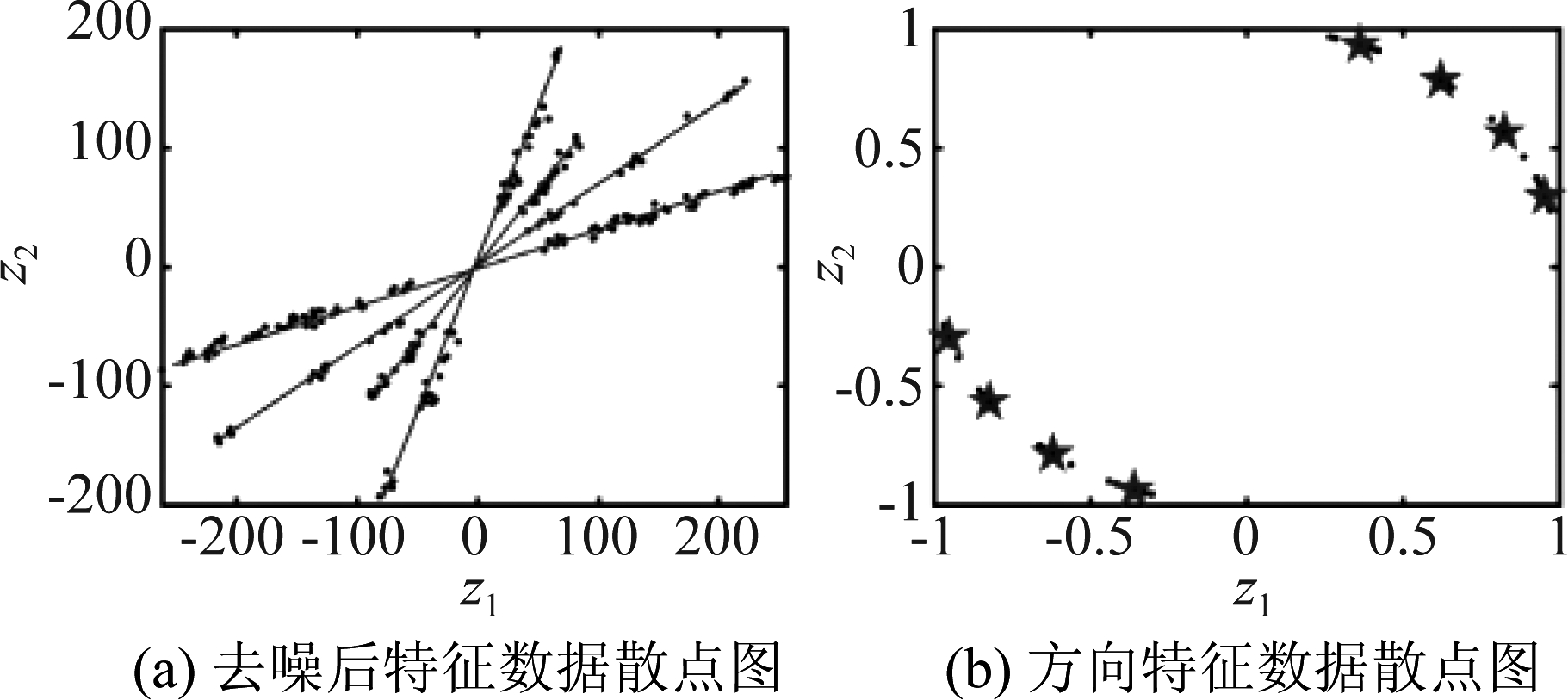
图2 去噪后的特征数据及用方向角表示的特征数据散点图
Fig.2 Feature data after denoising and scatter plot feature data expressed by direction angle
3.2 混合矩阵估计
在获得足够的单源域之后,可以通过聚类方法估计混合矩阵,聚类算法输出的聚类中心即混合矩阵的估计。由于特征数据只与角度β相关,可视其为方向数据,此时混合矩阵估计可以转化为角度聚类问题。假设聚类个数为L,聚类中心矩阵为C=[c1,c2,...,cL],第l(l=1,2,...,L)个聚类中心为cl(cl=(cos θl,sin θl)),则聚类中心cl与特征数据zk之间的夹角为φ,内积为
(10)
一般的聚类算法都采用欧式距离作为距离度量,由于3.1节中已使数据变为方向数据,对数据夹角取绝对值,以避免直线的正负方向的影响。则特征点与聚类中心的距离可用余弦距离来表示
(11)
余弦距离通过测量两个特征向量的夹角的余弦值来度量它们之间的相似性。由于特征数据呈现沿混合矩阵列元素方向上分布的特性,通过测量特征数据与聚类中心夹角的余弦值,相比于欧式距离,可以更好的求得特征数据与聚类中心的相似度关系,为后续聚类更新提供了更加精确的结果。
利用余弦距离计算公式,对FC-means聚类算法进行改进,利用拉格朗日乘子法,得到针对方向数据的FC-means参数更新公式。
FC-means聚类算法求解公式如下,ulk表示特征数据zk与聚类中心cl的隶属度,K为特征数据Z的列数,q为隶属度平滑参数(通常取2)
(12)
其中ulk为隶属度,||xmk-cl||为欧式距离,将余弦距离公式
代入,得到
(13)
利用拉格朗日乘子法,令
J(cl,ulk)=
(14)
求解得到隶属度更新公式和聚类中心更新公式
(15)
(16)
其中η为更新步长,
表示更新后的聚类中心。
在使用FC-means聚类方法时,必须事先知道源信号个数。为了自动识别源数并更新聚类结果,本文采用了余弦距离,对聚类验证技术理论[24]进行改进,根据不同的簇数L(L=2,...,Lmax)对数据进行聚类,其中Lmax是可能的最大聚类个数。对每次聚类结果用聚类验证技术进行验证,并将最佳聚类结果中的聚类个数作为源数估计结果,使用下式的损失函数来衡量L簇的聚类结果(对每个L进行一次聚类分析,共进行Lmax-2+1次聚类分析,后续分析选择损失函数最优的聚类结果)
(17)
其中U=[u1,u2,...,uL]T为隶属度矩阵,ul(l=1,2,...,L)表示特征数据Z与聚类中心cl的隶属度,C=[c1,c2,...,cL]T为聚类中心矩阵,Scat(L)表示当簇数为L时得到的簇的紧密度
(18)
(19)
(20)
其中,Scat(L)的取值在0到1之间,Scat(L)越小,簇的紧密度越大,表示类内距离越小。Sep(L)表示簇与簇的距离,即类间距离
(21)
(22)
(23)
一个好的聚类结果应该有尽量小的类内距离和尽量大类间距离,则式(17)取值越小,表示聚类效果越好。当ν(U,C,L)取得最小值时,对应的最佳的聚类个数Lopt,即可视为源信号的数目。将FC-means与聚类验证技术结合使用,可以在同时估计出源数和混合矩阵,算法最终输出的聚类中心矩阵C即为混合矩阵的估计
由于聚类算法是随机初始化的,求取出的聚类中心排列是不固定的,所以估计出的混合矩阵的列是随机排列的,这不影响最终的估计结果,因为在实际工程中,加性信号没有顺序性。
3.3 源信号恢复
估计出混合矩阵后,接下来需要进行源信号的恢复。源信号恢复是信号处理领域具有挑战性的热点问题,众多学者提出了不同的恢复算法[11,25],但目前来说源信号恢复仍然是一个困难的问题。本文采用求解一系列最小二乘问题来恢复源信号[25],文献[25,31]证明了这种最小二乘方法的计算效率和精度都比较高。根据假设2和假设3,通过选择估计出的混合矩阵
的最优N×(M-1)阶子矩阵
使误差函数式(27)最小,令包含所有子矩阵的集合为
(24)
其中
是不同子矩阵
的列,对于每个时频点(t, f),必然存在
满足
(25)
其中†为矩阵广义逆,然后通过下式对源信号进行估计
(26)
其中,
其中
通过下式得到
(27)
最后通过逆短时傅里叶变换将源信号变换到时域。
算法流程:(1)短时傅里叶变换到时频域X(t,f),并变换成N维行向量;(2)滑动窗口选取数据实部并进行主成分分析,比较局部置信度函数T(Ω)挑选出满足公式(4)的单源域特征数据;(3)去除低能量点‖Z‖2<ε‖Z-‖2,将特征数据归一化,得到方向角β表示的特征数据zk=(cosβk,sinβk);(4)设定聚类个数L,随机初始化聚类中心,用针对方向数据的FC-means参数更新公式(15)和(16)更新聚类中心和隶属度;(5)用余弦距离改进的聚类验证技术公式(17)计算聚类结果的损失函数;(6)聚类个数L+1,重复步骤(4)和(5),直到L取到设定最大聚类个数,输出使损失函数最小的一组聚类个数和聚类中心,作为源数和混合矩阵的估计A^;(7)对混合信号按公式(27)求取混合矩阵的最优子矩阵 *,并用最小二乘重建时频域源信号;(8)逆短时傅里叶变换到时域得到源信号S(t)。
4 仿真实验
4.1 仿真振动信号分离
本节通过数值仿真机械振动信号对所提出的欠定盲源分离算法性能进行验证。在仿真中设置了5个振动源信号,s1和s2为幅度调制周期信号,s3为齿轮箱振动信号,s4和s5为单频正弦波信号,设置2个传感器接收振动源信号,这5个振动源信号分别从5个不同传递路径到达传感器,混合矩阵A描述了这5个传递路径的参数,信号模型S和混合矩阵A如下
s1=(cos(2π·10t)+1)×sin(2π·50t)
s2=(cos(2π·10t)+1)×sin(2π·150t)
s3=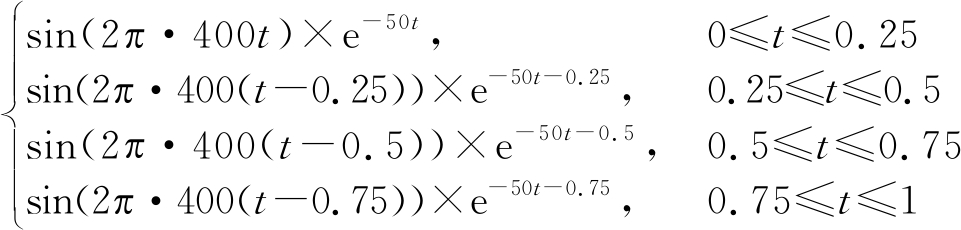
s4=sin(2π·200t)
s5=sin(2π·100t)
(28)
(29)
仿真信号采样率为1024 Hz,采样时间为1 s,信号波形和频谱如图3所示。混合信号由公式x(t)=As(t)产生,混合信号波形和频谱如图4所示,从图中可以看出,混合信号是不同传递路径振动源信号的线性叠加,不能直接从混合信号得到源信号。通过所提出的特征提取算法提取单源域特征,并通过所提出的方向聚类算法和聚类验证技术得到源数和混合矩阵的估计为
(30)
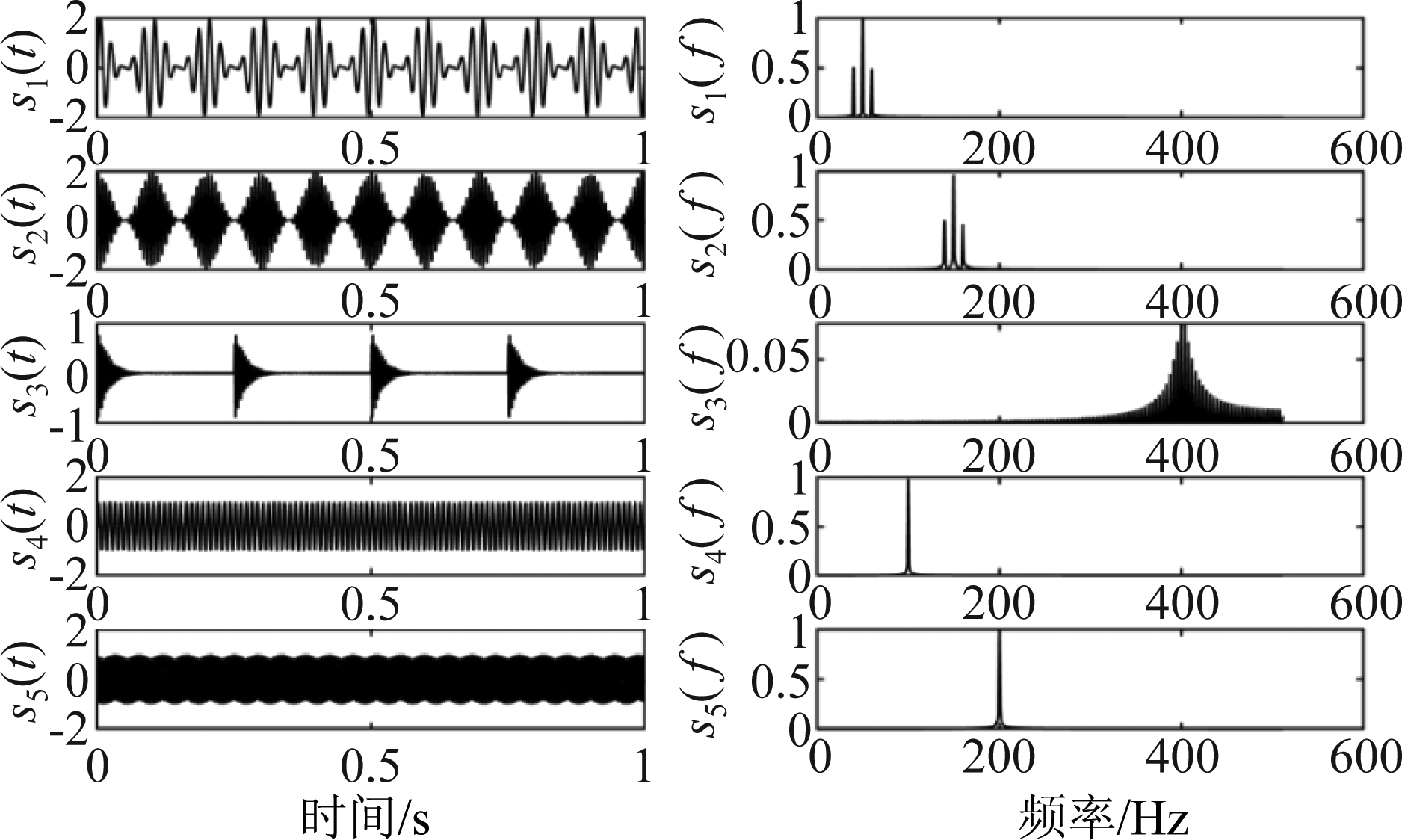
图3 仿真振动源信号时域波形及频域频谱图
Fig.3 Time-domain waveform and frequency-domain spectrogram of simulated vibration source signal
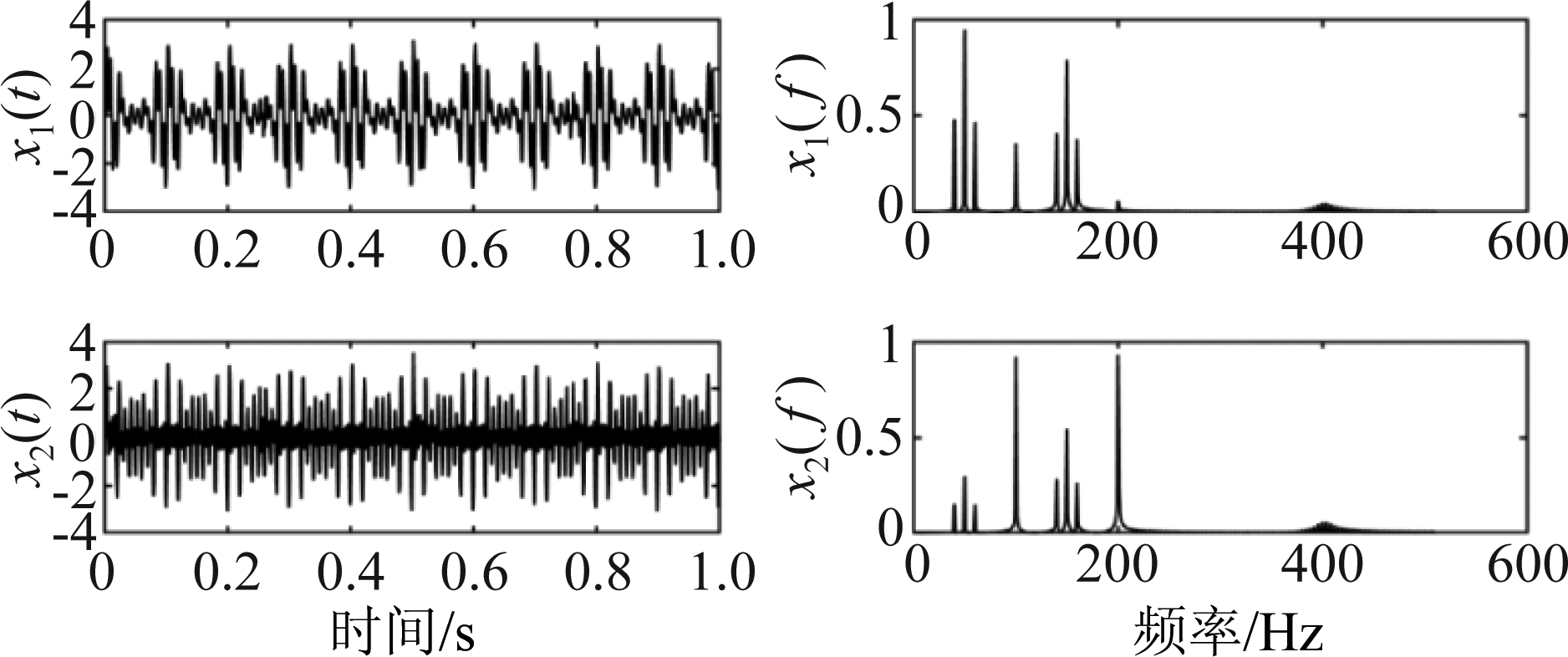
图4 混合信号时域波形及频域频谱图
Fig.4 Time-domain waveform and frequency-domain spectrogram of mixed signal
比较式(29)和(30),可以看到,所提出的算法可以精确的估计出源数和混合矩阵。最后通过源信号恢复方法恢复出振动源信号,如图5所示。可以看出,该方法可以很好的恢复源信号的波形和频率分布。这些结果可以说明本文所提出的方法的有效性。
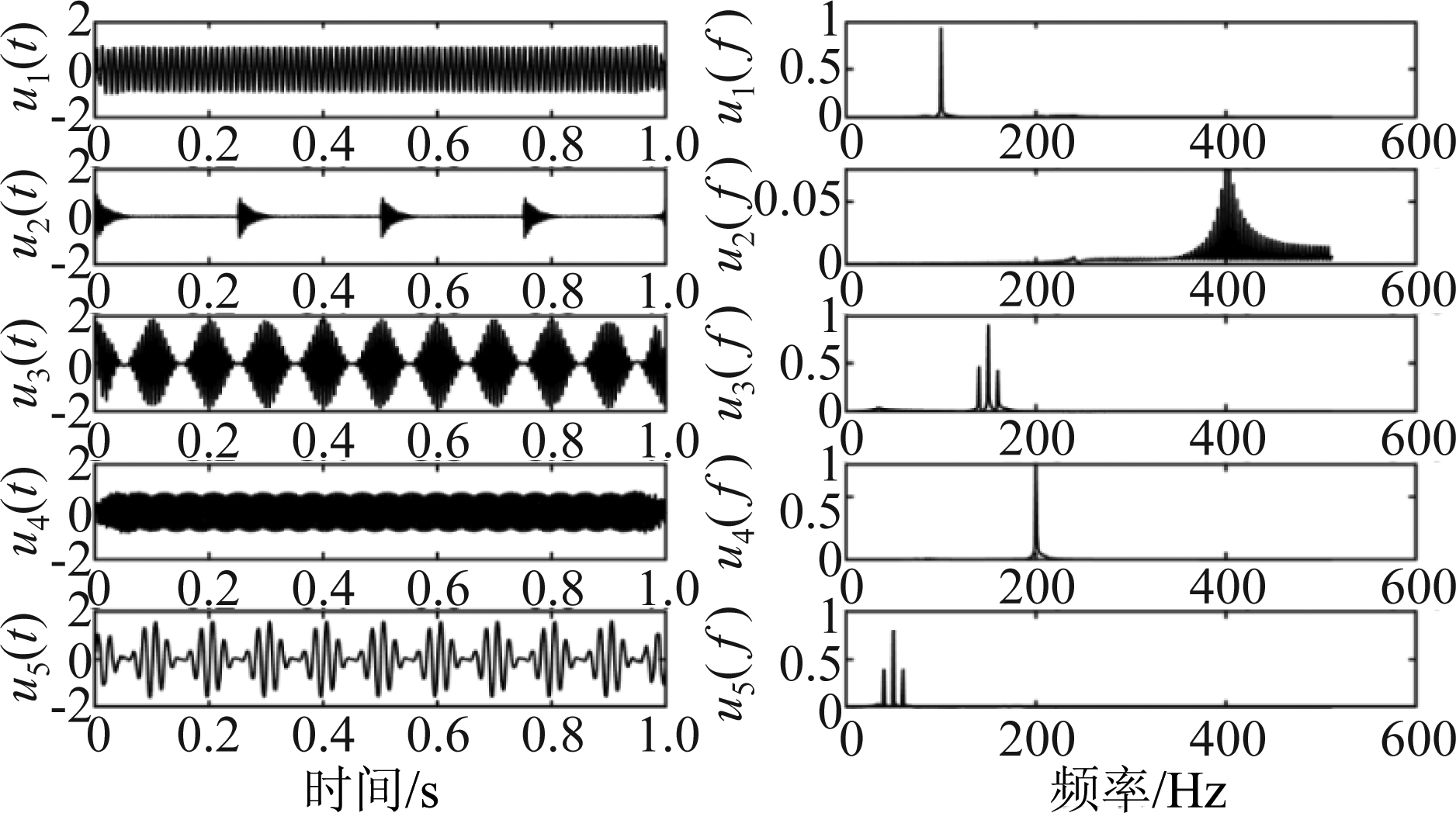
图5 恢复的振动信号时域波形和频域频谱图
Fig.5 Time-domain waveform and frequency-domain spectrogram of recovered vibration signal
4.2 噪声环境下的振动信号分离
设置4个不同的仿真振动源信号,s1是多分量信号,s2为单频正弦波信号,s3为调幅信号,s4为调频信号,设置2个传感器接收振动源信号,这4个振动源信号从4个不同传递路径到达传感器,混合矩阵A描述了这4个传递路径的参数,信号模型S和混合矩阵A如下
s1=0.5sin(2π·17t)+sin(2π·171t)+sin(2π·350t)
s2=sin(2π·200t)
s3=sin(2π·7t)cos(2π·80t)
s4=sin(2π·300t-cos(2π·10t))
(31)
(32)
设置采样率为4 kHz,采样时间为4 s,为了模拟强噪声环境,给源信号加入高斯白噪声并设置信噪比为0 dB,源信号波形和频谱如图6所示,混合信号由公式x(t)=As(t)产生,再加入高斯白噪声并设置信噪比为0 dB,混合信号波形和频谱如图7所示。通过所提出的特征提取算法提取单源域特征,并通过所提出的方向聚类算法和聚类验证技术得到源数和混合矩阵的估计
(33)
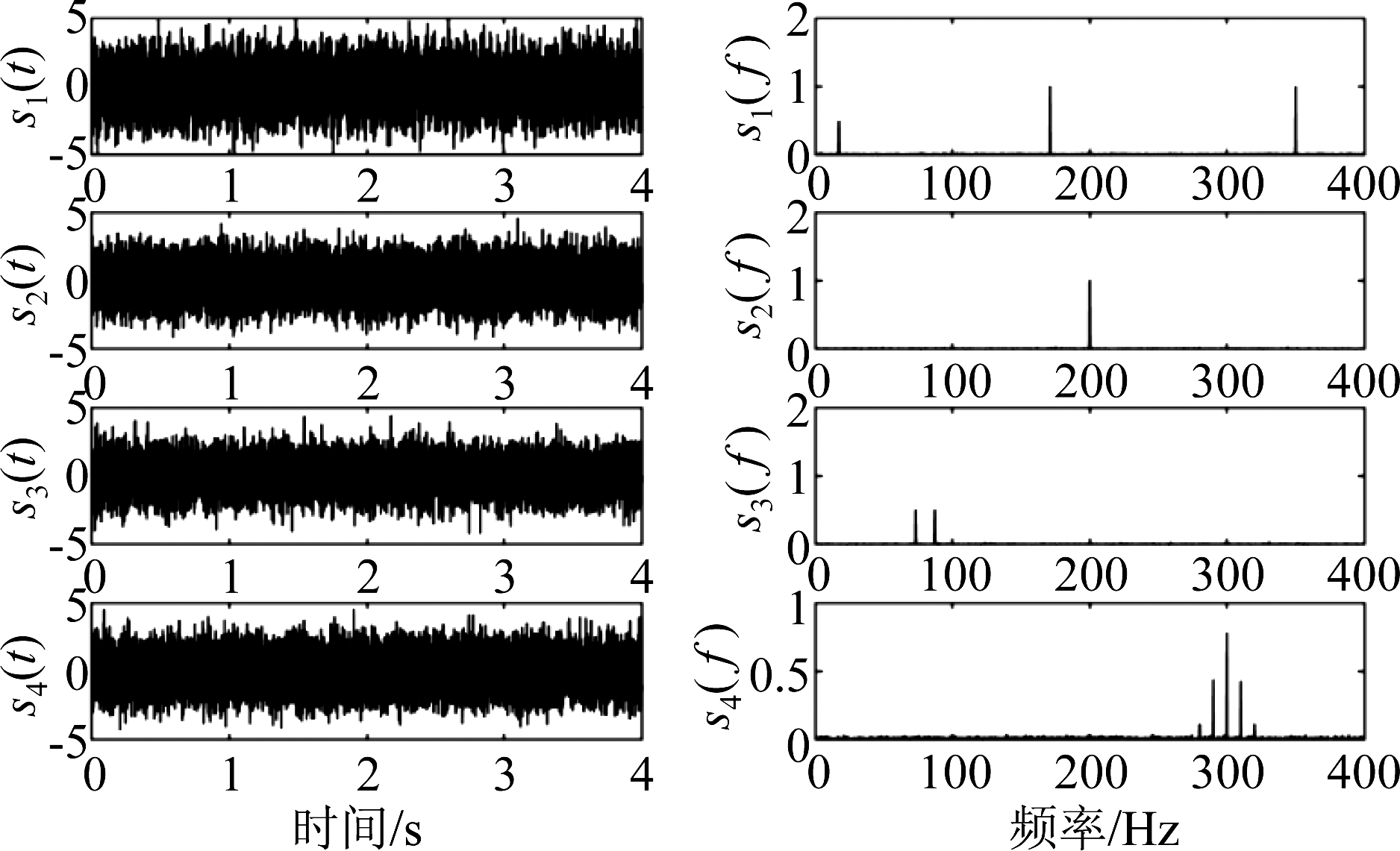
图6 仿真振动源信号时域波形及频域频谱图
Fig.6 Time-domain waveform and frequency-domain spectrogram of simulated vibration source signal
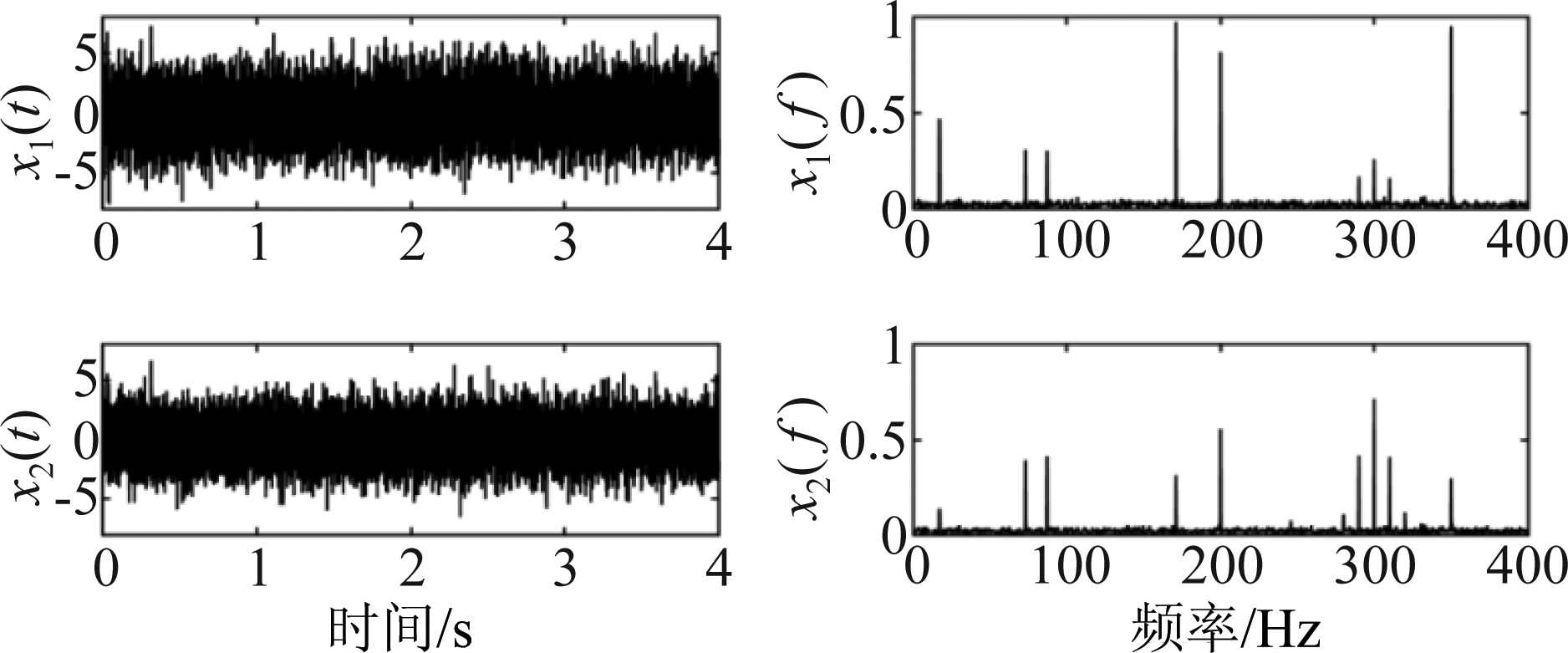
图7 混合信号时域波形及频域频谱图
Fig.7 Time-domain waveform and frequency-domain spectrogram of mixed signal
比较式(32)和(33),可以看到,所提出的算法可以在噪声环境下精确的估计出源数和混合矩阵。
最后通过源信号恢复方法恢复出源信号,如图8所示。可以看出,在强噪声环境下,所提出的算法可以精确提取出源信号的主要频率成分,这些结果可以说明本文所提出算法的稳健性。
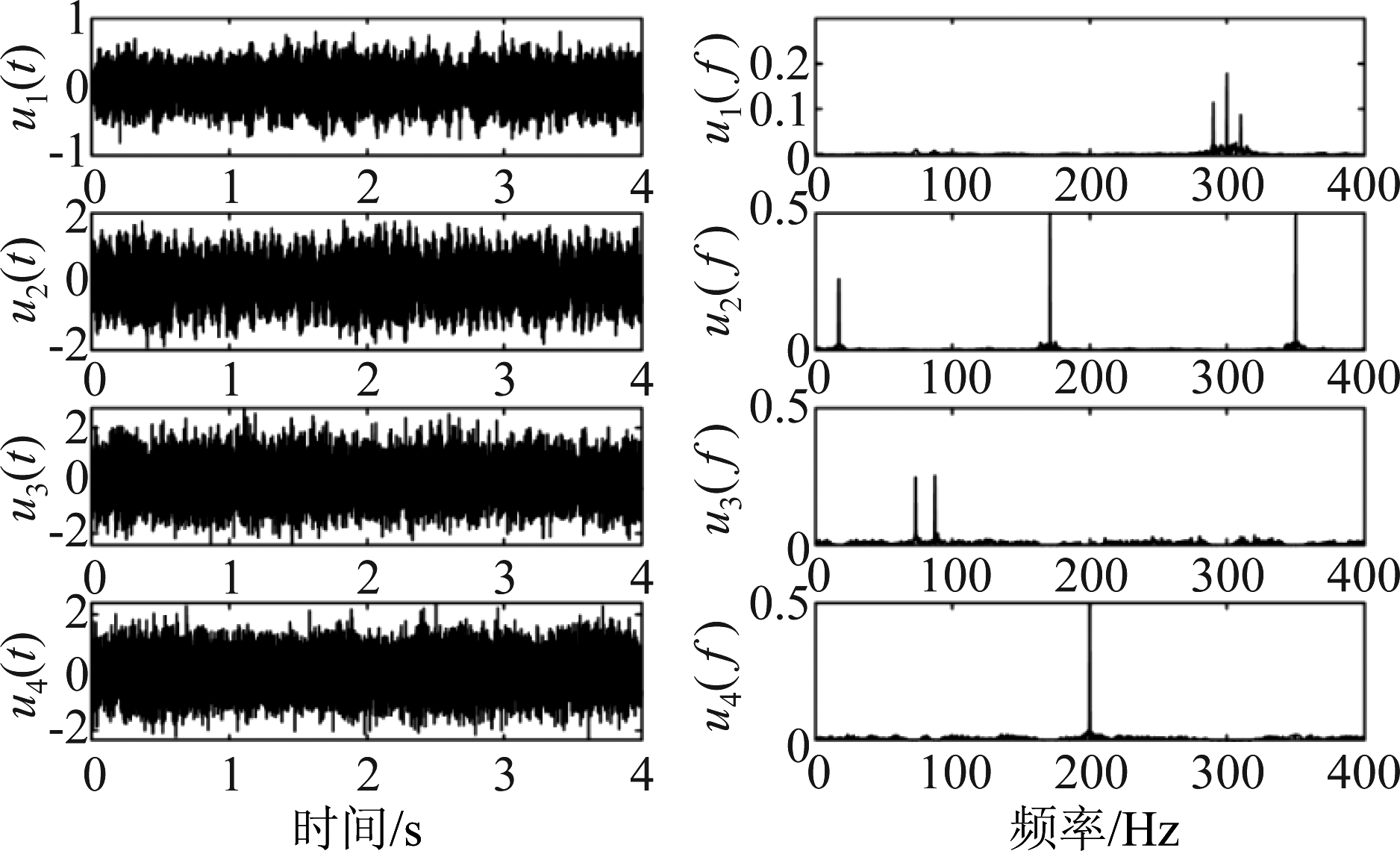
图8 恢复的振动信号时域波形和频域频谱图
Fig.8 Time-domain waveform and frequency-domain spectrogram of recovered vibration signal
4.3 Monte Carlo仿真实验
设置Monte Carlo仿真实验来评估所提出算法与其他算法的性能。振动源信号中加入高斯白噪声,并设置信噪比0 dB到30 dB,每次实验由100次Monte Carlo实验获得平均结果。所比较的算法为本文算法和TIFROM[21]、Reju[23]。源信号模型和混合矩阵与4.2节中的一致。
为了评估混合矩阵估计和振动源信号恢复的结果,采用平均信干比(Signal-to-interference,SIR),即源信号比上估计信号与源信号的差值来进行比较
(34)
(35)
式中,N表示传感器数量,ai表示混合矩阵第i列,
表示估计出的混合矩阵第i列,si表示第i个源信号,
表示恢复出的第i个信号,ξ是反映标量模糊性的一个标量。通过Monte Carlo仿真实验得到的混合矩阵和恢复信号SIR随源信号信噪比的变化图如图9所示。
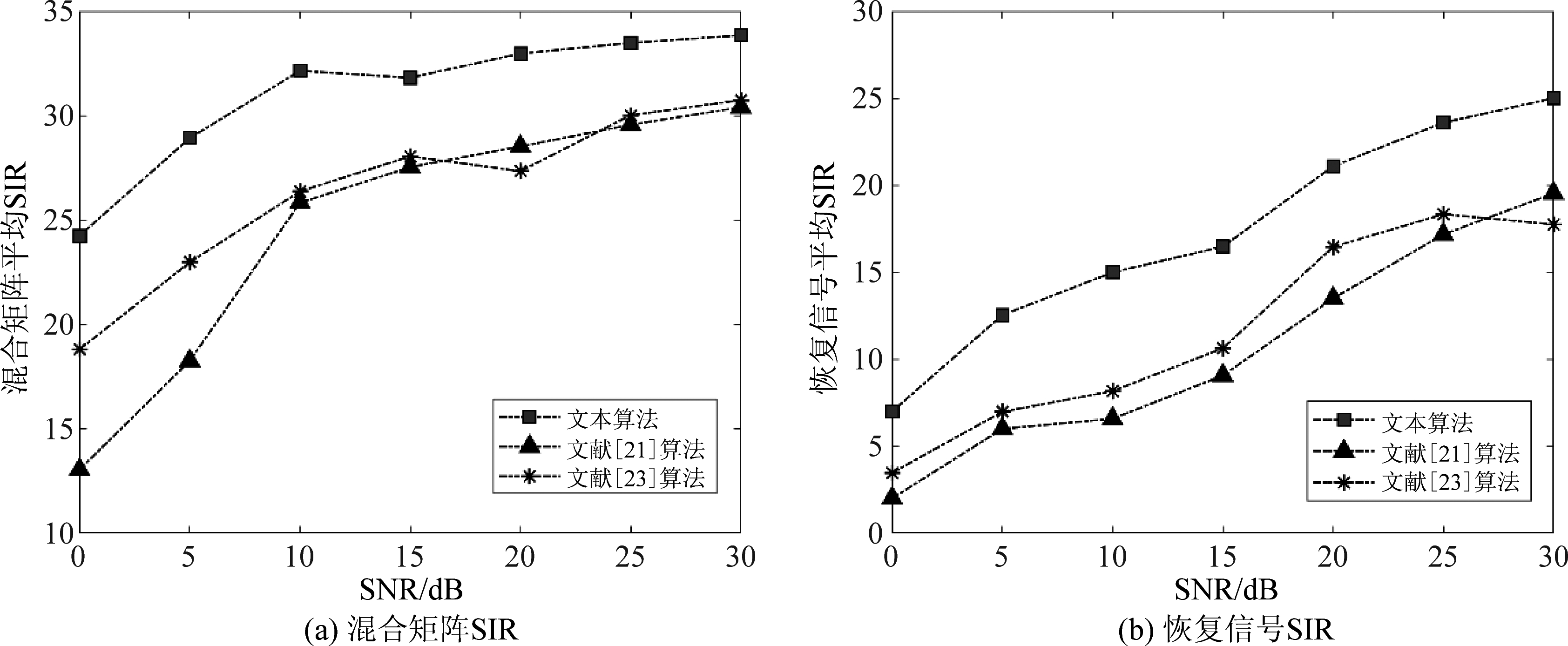
图9 估计混合矩阵平均SIR与恢复信号SIR
Fig.9 Estimate the average SIR of the mixed matrix and the recovered signal SIR
从图9(a)中可以看出,TIFROM方法和Reju方法性能较为接近,在低信噪比时Reju方法估计精确度更高一些,在高信噪比时两者相差无几。从图中结果看,在所有情况下本文方法的平均SIR都比上述两种方法高,可以说本文方法可以更精确估计混合矩阵。而且本文算法在低噪比下混合矩阵平均SIR明显高于其他两种方法,可以说明在本文算法抗噪性能优于其他两种方法。
从图9(b)中可以看出,其他两种方法在低信噪比时,恢复信号SIR都比较低,而在高信噪比时,TIFROM方法和Reju方法性能较为接近,而本文方法的SIR高于TIFROM方法和Reju方法。源信号的恢复结果很依赖于混合矩阵估计的精度,由于本文算法混合矩阵估计精度较高,在所有情况下平均SIR都比其他方法高,可以说明本文算法可以得到更加精确、更加稳健的结果。
5 试验验证
使用文献[34-35]提供的实测振动数据,如图所示,使用0.38×0.038×0.006 m3的均匀TC4钛合金柱作为测试对象,三个加速度传感器安装在横梁上,用于检测立柱受到冲击锤激励时的加速度响应。采样率为2560 Hz,使用0.5 s采样时间的数据用作分析,加速度相应波形和频谱如图11所示,可以看到有四个小于1280 Hz的主尖峰,它们表示响应中激发的四种频率成分,这四个频率的信号激励力激发的四种本底振源,所以可以看作是四个“源”,它们从不同传递路径到达传加速度计。使用本文算法和TIFROM[21]、Reju[23]、YGBSS[33]进行对比,本文算法分离结果如图所示,几种算法提取的频率成分如表1所示。
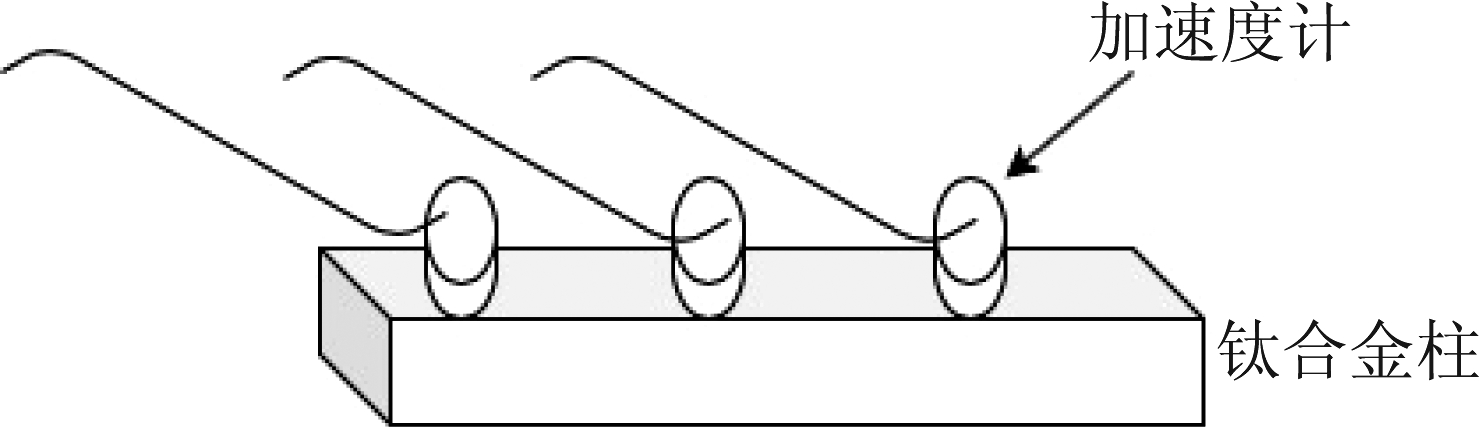
图10 TC4钛合金柱和三个加速度传感器
Fig.10 TC4 titanium alloy column and three acceleration sensors
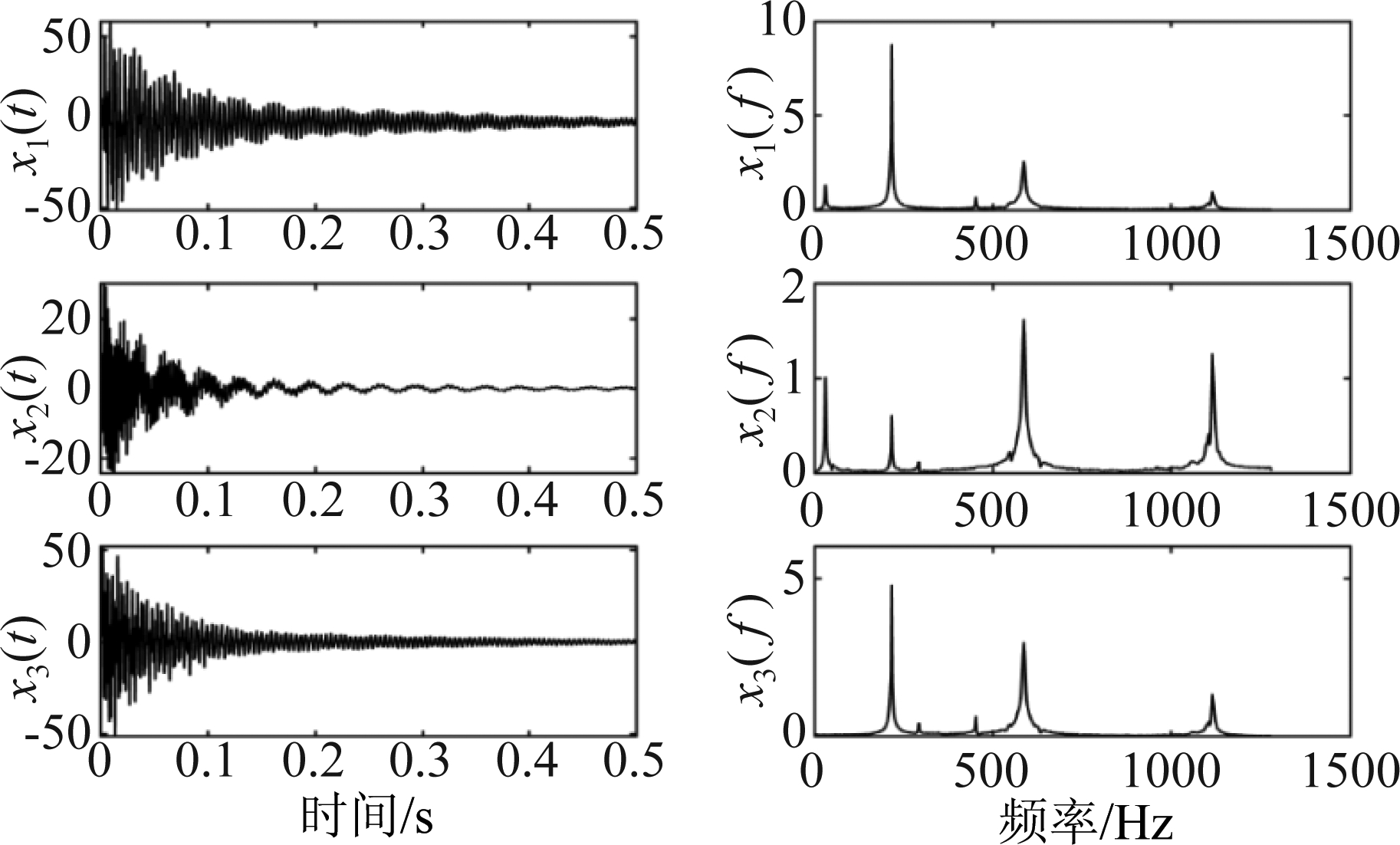
图11 实测振动信号时域波形和频域频谱图
Fig.11 Time domain waveform and frequency domain spectrogram of measured vibration signal
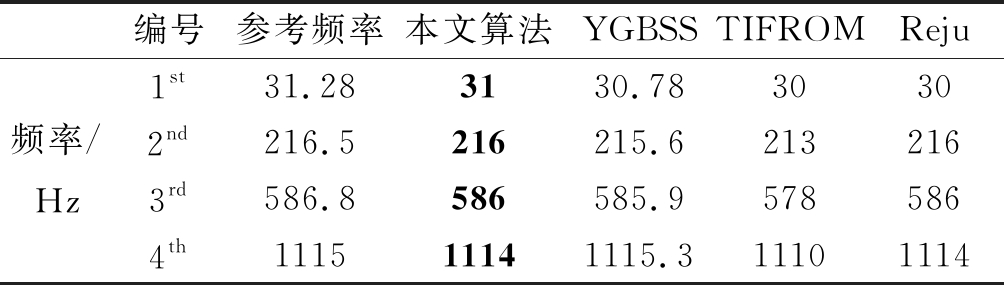
从图11可以看出,传感器接收的混合信号是由多个振动源振动信号混合在一起的,从混合信号中无法判断几种振源的频率成分,通过本文算法对混合信号进行处理,从图12可以看出,本文算法可以很好的分离出4个指数衰减振动信号,信号波形得到了准确的恢复,分离出的信号频率成分识别如表1所示。从表中来看,本文算法和YGBSS方法得到的结果最为接近理论参考频率,TIFROM方法得到的结果与理论参考频率相差较大。综合来看,在混合信号稀疏性较高时,4种方法都能准确分离出4个频率成分的信号,本文算法的精度相对较高。
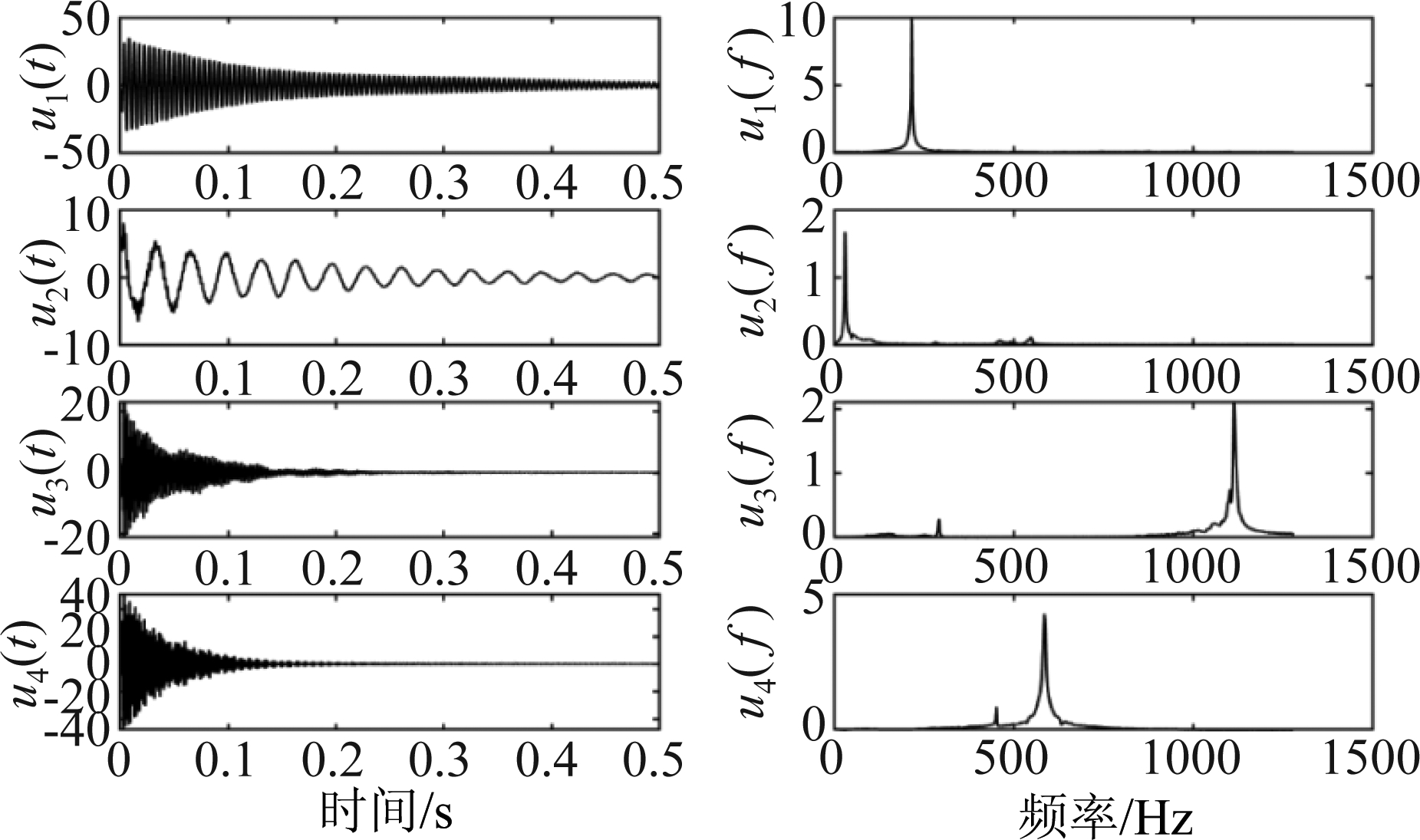
图12 所提出算法分离出的信号时域波形和频域频谱图
Fig.12 The time-domain waveform and frequency-domain spectrogram of the signal separated by the proposed algorithm
表1 TC4钛合金柱振源频率成分识别结果
Tab.1 Recognition results of frequency components of TC4 titanium alloy column vibration source
编号参考频率本文算法YGBSSTIFROMReju频率/Hz1st31.283130.7830302nd216.5216215.62132163rd586.8586585.95785864th111511141115.311101114
6 结论
本文提出了一种解决未知源数的振动信号欠定盲源分离方法,达到从少量振动传感器的接收信号中识别信号源数和各频率分量的目的。该方法根据信号从不同传递路径到达的特性,以时频域的每个混合信号点为中心,通过局部占优假设和主成分分析方法识别出单源域特征数据,然后将数据投影到单位圆上,得到数据的方向表示,接着采用方向余弦距离代替常规的欧氏距离,改进了聚类验证技术和FC-means方法,可以自动识别源数和聚类中心,从而得到振动源数和混合矩阵估计,最后利用得到的数据,利用混合矩阵列元素的线性不相关特性,使用一系列最小二乘优化算法从混合信号对应的时频点中抽取出源信号。仿真实验和实测数据实验表明本文方法在噪声环境下可以精确识别振动源数和各个源的频率成分,本文方法稳健性和精确度均优于对比的TIFROM方法和Reju方法。本文方法也有局限性,如本文方法需要利用多个传感器,不适用于单传感器的情况;本文建模使用的线性瞬时混合模型,对于卷积混合模型和非线性混合模型可能不适用,这是本文方法下一步研究的重点内容。
[1] SADHU A, NARASIMHAN S, ANTONI J. A review of output-only structural mode identification literature employing blind source separation methods[J]. Mechanical Systems and Signal Processing, 2017, 94: 415- 431.
[2] 张贤达, 保铮. 盲信号分离[J]. 电子学报, 2001, 29(S1): 1766-1771.
ZHANG Xianda, BAO Zheng. Blind source separation[J]. Acta Electronica Sinica, 2001, 29(S1): 1766-1771.(in Chinese)
[3] YPMA A, LESHEM A. Blind separation of machine vibration with bilinear forms[C]∥Proceedings of ICA-2000, Helsinki, 2000: 405- 410.
[4] 李舜酩. 振动信号的盲源分离技术及应用[M]. 北京:航空工业出版社, 2011.
LI Shunming. Blind source separation technology and application of vibration signal[M]. Beijing: Aviation Industry Press, 2011.(in Chinese)
[5] 骆刚刚. 旋转机械欠定盲源分离模态分析方法研究[D]. 北京: 北京化工大学, 2017.
LUO Ganggang. Research on mode analysis method for undetermined blind source separation of rotating machinery[D]. Beijing: Beijing University of Chemical Technology, 2017.(in Chinese)
[6] LI Guozheng, TANG Gang, LUO Ganggang, et al. Underdetermined blind separation of bearing faults in hyperplane space with variational mode decomposition[J]. Mechanical Systems and Signal Processing, 2019, 120: 83-97.
[7] XIE Yuan,XIE Kan,XIE Shengli.Underdetermined blind source separation for heart sound using higher-order statistics and sparse representation[J]. IEEE Access, 2019, 7: 87606- 87616.
[8] Zou L,Chen X,Ji X,et al.Underdetermined Joint Blind Source Separation for Two Datasets Based on Tensor Decomposition[J]. IEEE Signal Processing Letters, 2017, 5(99):7474-7487.
[9] 李志农, 刘卫兵, 易小兵. 基于局域均值分解的机械故障欠定盲源分离方法研究[J]. 机械工程学报, 2011, 47(7): 97-102.
LI Zhinong, LIU Weibing, YI Xiaobing. Underdetermined blind source separation method of machine faults based on local mean decomposition[J]. Journal of Mechanical Engineering, 2011, 47(7): 97-102.(in Chinese)
[10] 李豫川, 伍星, 迟毅林, 等. 基于形态滤波和稀疏分量分析的滚动轴承故障盲分离[J]. 振动与冲击, 2011, 30(12): 170-174.
LI Yuchuan, WU Xing, CHI Yilin, et al. Blind separation for rolling bearing faults based on morphological filtering and sparse component analysis[J]. Journal of Vibration and Shock, 2011, 30(12): 170-174.(in Chinese)
[11] BOFILL P, ZIBULEVSKY M. Underdetermined blind source separation using sparse representations[J]. Signal Processing, 2001, 81(11): 2353-2362.
[12] 王川川, 曾勇虎. 欠定盲源分离算法的研究现状及展望[J]. 北京邮电大学学报, 2018, 41(6): 103-109.
WANG Chuanchuan, ZENG Yonghu. Research status and prospects of underdetermined blind source separation algorithms[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(6): 103-109.(in Chinese)
[13] GEORGIEV P, THEIS F, CICHOCKI A. Sparse component analysis and blind source separation of underdetermined mixtures[J]. IEEE Transactions on Neural Networks, 2005, 16(4): 992-996.
[14] GUO Qiang, RUAN Guoqing, LIAO Yanping. A time-frequency domain underdetermined blind source separation algorithm for MIMO radar signals[J]. Symmetry, 2017, 9(7): 104.
[15] YANG Yongchao, NAGARAJAIAH S. Output-only modal identification with limited sensors using sparse component analysis[J]. Journal of Sound and Vibration, 2013, 332(19): 4741- 4765.
[16] LUO Yuhui, WANG Wenwu, CHAMBERS J A, et al. Exploitation of source nonstationarity in underdetermined blind source separation with advanced clustering techniques[J]. IEEE Transactions on Signal Processing, 2006, 54(6): 2198-2212.
[17] PENG Dezhong, XIANG Yong. Underdetermined blind source separation based on relaxed sparsity condition of sources[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 809- 814.
[18] BELOUCHRANI A, AMIN M G, THIRION-MOREAU N, et al. Source separation and localization using time-frequency distributions: An overview[J]. IEEE Signal Processing Magazine, 2013, 30(6): 97-107.
[19] XIE Shengli, YANG Liu, YANG Junmei, et al. Time-frequency approach to underdetermined blind source separation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 306-316.
[20] JOURJINE A, RICKARD S, YILMAZ O. Blind separation of disjoint orthogonal signals: Demixing N sources from 2 mixtures[C]∥2000 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No.00CH37100). Istanbul, Turkey. IEEE, 2000: 2985-2988.
[21] ABRARD F, DEVILLE Y. A time-frequency blind signal separation method applicable to underdetermined mixtures of dependent sources[J]. Signal Processing, 2005, 85(7): 1389-1403.
[22] LI Yuanqing, AMARI S, CICHOCKI A, et al. Underdetermined blind source separation based on sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(2): 423- 437.
[23] REJU V G, KOH S N, SOON I Y. An algorithm for mixing matrix estimation in instantaneous blind source separation[J]. Signal Processing, 2009, 89(9): 1762-1773.
[24] REJU V G, KOH S N, SOON I Y. Underdetermined convolutive blind source separation via time-frequency masking[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2009, 18(1): 101-116.
[25] ZHEN Liangli, PENG Dezhong, YI Zhang, et al. Underdetermined blind source separation using sparse coding[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 3102-3108.
[26] ARBERET S,GRIBONVAL R,BIMBOT F.A robust method to count and locate audio sources in a multichannel underdetermined mixture[J]. IEEE Transactions on Signal Processing, 2009, 58(1): 121-133.
[27] 谭北海, 谢胜利. 基于源信号数目估计的欠定盲分离[J]. 电子与信息学报, 2008, 30(4): 863- 867.
TAN Beihai, XIE Shengli. Underdetermlned blind separation based on source signals′ number estimation[J]. Journal of Electronics & Information Technology, 2008, 30(4): 863- 867.(in Chinese)
[28] 付卫红, 马丽芬, 李爱丽. 基于改进K-均值聚类的欠定混合矩阵盲估计[J]. 系统工程与电子技术, 2014, 36(11): 2143-2148.
FU Weihong, MA Lifen, LI Aili. Blind estimation of underdetermined mixing matrix based on improved K-means clustering[J]. Systems Engineering and Electronics, 2014, 36(11): 2143-2148.(in Chinese)
[29] HU J S, YANG C H, WANG Chengkang. Estimation of sound source number and directions under a multi-source environment[C]∥2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis, MO, USA. IEEE, 2009: 181-186.
[30] YANG Junjie, GUO Yi, YANG Zuyuan, et al. Estimating number of speakers via density-based clustering and classification decision[J]. IEEE Access, 2019, 7: 176541-176551.
[31] LU Jiantao, CHENG Wei, HE Dong, et al. A novel underdetermined blind source separation method with noise and unknown source number[J]. Journal of Sound and Vibration, 2019, 457: 67-91.
[32] 叶红仙. 机械系统振动源的盲分离方法研究[D]. 杭州: 浙江大学, 2008.
YE Hongxian. Research on blind source separation of the vibration signals of mechanical system[D]. Hangzhou: Zhejiang University, 2008.(in Chinese)
[33] LYON R H, SAUNDERS H. Machinery noise and diagnostics[J]. Journal of Vibration and Acoustics, 1989, 111(4): 495- 496.
[34] YU Kaiping,YANG Kai,BAI Yunhe.Estimation of modal parameters using the sparse component analysis based underdetermined blind source separation[J]. Mechanical Systems and Signal Processing, 2014, 45(2): 302-316.
[35] GANG Yu. An underdetermined blind source separation method with application to modal identification[J]. Shock and Vibration, 2019, 2019(7): 1-15.
