1 引言
动态纹理是根据事物表现出的“外观”和“运动”特性联合定义的一种空间中体现为“图像纹理”且随时间变化的视觉模式,作为图像序列中的基本属性,它为图像序列处理、分析和理解提供重要视觉线索[1]。动态纹理分类在过去十几年里引起了广泛的关注,在动态纹理的分类中,特征提取方法直接影响动态纹理分类的性能,根据动态纹理的“外观”和“运动”属性,可将动态纹理的特征提取方法主要分为两类,一类是基于运动分析的方法[2],另一类是将运动与外观结合的方法[3],其中基于变换的方法在第二类中应用最为广泛。
近年来,很多学者使用小波变换进行信号处理[4-5],它具有多分辨率以及对分段平滑的时间序列和图像进行稀疏表示的特点,因此小波变换被用于动态纹理分类。Smith等人[6]最先使用时空小波来表示动态纹理,随后,Qiao 等人[7]提出了一种空时复小波对动态纹理进行分类。但是传统小波变换的多尺度分解只能隐含的考虑动态纹理的局部结构,谱图小波变换在保留其多尺度分析特性的同时,还可明确表示信号样本之间的结构和关系。2011 年,Hammond[8]系统地提出图谱小波变换,及基于切比雪夫多项式近似的快速变换算法。2012 年,Narang[9]首次提出两通道完全重构图小波滤波器组。随后图小波变换和图多速率滤波器组基本理论得到信号处理领域学者的高度关注,目前已有很多研究人员将谱图小波应用于图像去噪以及纹理分类中。徐兴敏在[10]中应用谱图小波变换对图像进行去噪,赵玥[11]将谱图小波变换应用于纹理分类。
动态纹理表现出的“外观”可以看成是图像纹理,图像纹理是一种区域属性,通过空间中像素值和像素值的相对位置关系联合体现,动态纹理的“运动”则是通过某个区域或邻域内像素沿时间的变化来体现,因此,动态纹理在空间上将图像纹理模型为空间图信号,而时间上的“运动”信息则可认为图顶点上信号是时变信号,即时间—顶点图信号。动态纹理分类中的特征提取就是分析动态纹理的“外观”或(和)“运动”属性,即分析相应的时间—顶点图信号,从而提取有效的动态纹理特征。最近,Grassi等人[12]提出了时变图信号处理框架,并基于谱图理论,提出了时间—顶点谱图小波变换(Spectral Time-Vertex Wavelet Transform, STVWT)。因此本文将动态纹理模型为时间—顶点图信号,并利用STVWT提取动态纹理特征进行分类。
本文提出了一种基于STVWT和边缘分布协方差模型(Marginal distribution covariance model, MDCM)的动态纹理分类方法。该方法将动态纹理模型成时变图信号,利用STVWT得到动态纹理的谱图多尺度表示,在动态纹理特征提取过程中,根据其时变特性,设计3D滑动窗口取邻域构造观测矩阵,并将广义高斯分布(Generalized Gaussian Distribution, GDD)函数作为STVWT小波系数观测矩阵的边缘分布模型,最后使用MDCM模型获得基于累积分布函数(cumulative distribution function,CDF)空间的协方差矩阵作为动态纹理特征进行分类。
2 时间—顶点谱图小波变换
2.1 时间—顶点图信号表示
一般地,无向图可用G=(V,ε,WG)表示,其中V表示顶点集,ε表示边集,WG表示N×N的对称权重矩阵,
(1)
当w(i, j)=1时,该权重矩阵为邻接矩阵,相应的度矩阵为
(2)
图信号就是定义在图顶点上的函数:f:V→RN,一般用向量x∈RN表示图信号值,现有基于谱图理论的信号处理通常利用拉普拉斯矩阵LG=DG-WG(或归一化拉普拉斯矩阵)的特征值和特征向量,这是因为特征值具有类似于传统频率的物理意义[8]。
假设图G上定义的信号随着时间发生变化,我们用xt∈RN表示时刻t的图信号,则时变图信号可用矩阵X=[x1,x2,…,xT]∈RN×T表示,其中N为图的顶点数,T为信号的长度。在这里我们假设图上的信号是以单位长度T进行连续规则间隔采样的。图某个顶点上信号在时刻1到T的取值,可以看成是环图GT上的信号,因此信号X∈RN×T是时间—顶点图信号,该时间—顶点图是图G与环图GT的笛卡尔积。令图G的拉普拉斯矩阵为LG,环图GT的拉普拉斯矩阵为LT。则联合拉普拉斯算子定义为[12]:
(LT×LG)x=LGX+XLT
(3)
其中第二项是根据克罗内克积的性质
得到的。
根据图傅里叶变换,可得到联合时间—顶点图傅里叶变换(JFT)定义为[12],
(4)
其中ul是LG的特征向量,向量
为拉普拉斯矩阵LT的特征向量,由式(4)可知,该变换是在图域首先应用图傅里叶变换,再沿时间域应用传统离散傅里叶变换,写成矩阵形式:
(5)
如文献[8]所示,谱图域有助于定义图上的局部化函数,例如图小波。
2.2 谱图小波变换与时间—顶点谱图小波变换
与传统小波变换类似,可以在谱图域定义小波核函数[8],因此,在尺度t下,定义小波算子为
则在尺度t和顶点n处的谱图小波定义为:
(6)
其中g是小波生成函数,在谱图域中定义,通常表现为带通滤波器;χl和λl分别为图拉普拉斯算子的特征向量和特征值。小波系数由信号f和谱图小波基的内积Wf(t,n)=〈ψt,n, f〉表示[10]。
同理,谱图小波对应的尺度函数定义如下:
(7)
其中h是尺度函数生成算子,满足h(0)>0,且
相当于低通滤波器,可用来提取信号的低频成分。φn(m)系数由信号f与尺度函数的内积Sf(t,n)=〈φn, f〉表示[10]。
STVWT[12]是谱图小波变换在时间—顶点域的扩展,设szλ,zω(·,·)为广义图膨胀或缩放,在谱图域中定义为:
szλ,zw(λ,w)=[zλλ,zωω]
(8)
因此,已知谱图小波核为g(λ,ω),信号X的STVWT为:
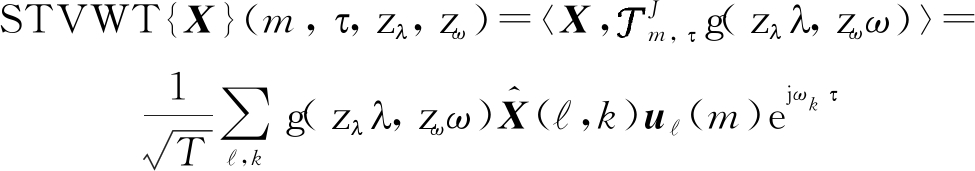
(9)
其中
是图上的联合局部化算子,它是图局部化算子[13]的推广,图局部化算子在顶点νm处的局部化核g(LG)可表示为
(10)
其中,δm是以顶点νm为中心的克罗内克函数。类似地,在联合域中,用二维克罗内克滤波函数定义联合时间—顶点局部化算子:
(11)
结果表明,联合时间—顶点局部化算子具有图局部化算子和传统平移算子的优点。在STVWT的定义中zλ,zω是时间和顶点域的尺度参数,通常对g(λ,ω)的要求为它有零直流分量,即g(0,0)=0。这里的STVWT比谱图小波的网络结构更加复杂。在动态纹理的分类中,为了捕捉到全部的纹理信息,一般可令m,τ选取到全部可取的N和T值。
3 动态纹理分类方法
动态纹理表现出的“外观”通过空间中像素值和像素值的相对位置关系联合体现,而“运动”则是通过某个区域或邻域内像素沿时间的变化来体现,动态纹理分类中的特征提取就是研究像素值及像素间的空时关系,分析动态纹理的“外观”或(和)“运动”属性,从而提取有效的动态纹理特征。因此,本文将动态纹理模型为时间—顶点图信号,首先对动态纹理的第一帧图像,利用K近邻法(K-nearest neighbor,KNN)构造图的拓扑结构,像素即为图的顶点,像素值是顶点上的信号值,图的边描述顶点的局部邻域关系,动态纹理沿时间的变化可看成是空间的图信号沿时间变化(时间—顶点图信号),再采用联合时间—顶点Meyer滤波器组将图信号分解为多尺度分量,获得不同尺度的L个小波子带。最后利用改进的MDCM用协方差矩阵描述局部邻域内小波系数的相关性,从而提取动态纹理特征。所提动态纹理分类方法如图1所示。
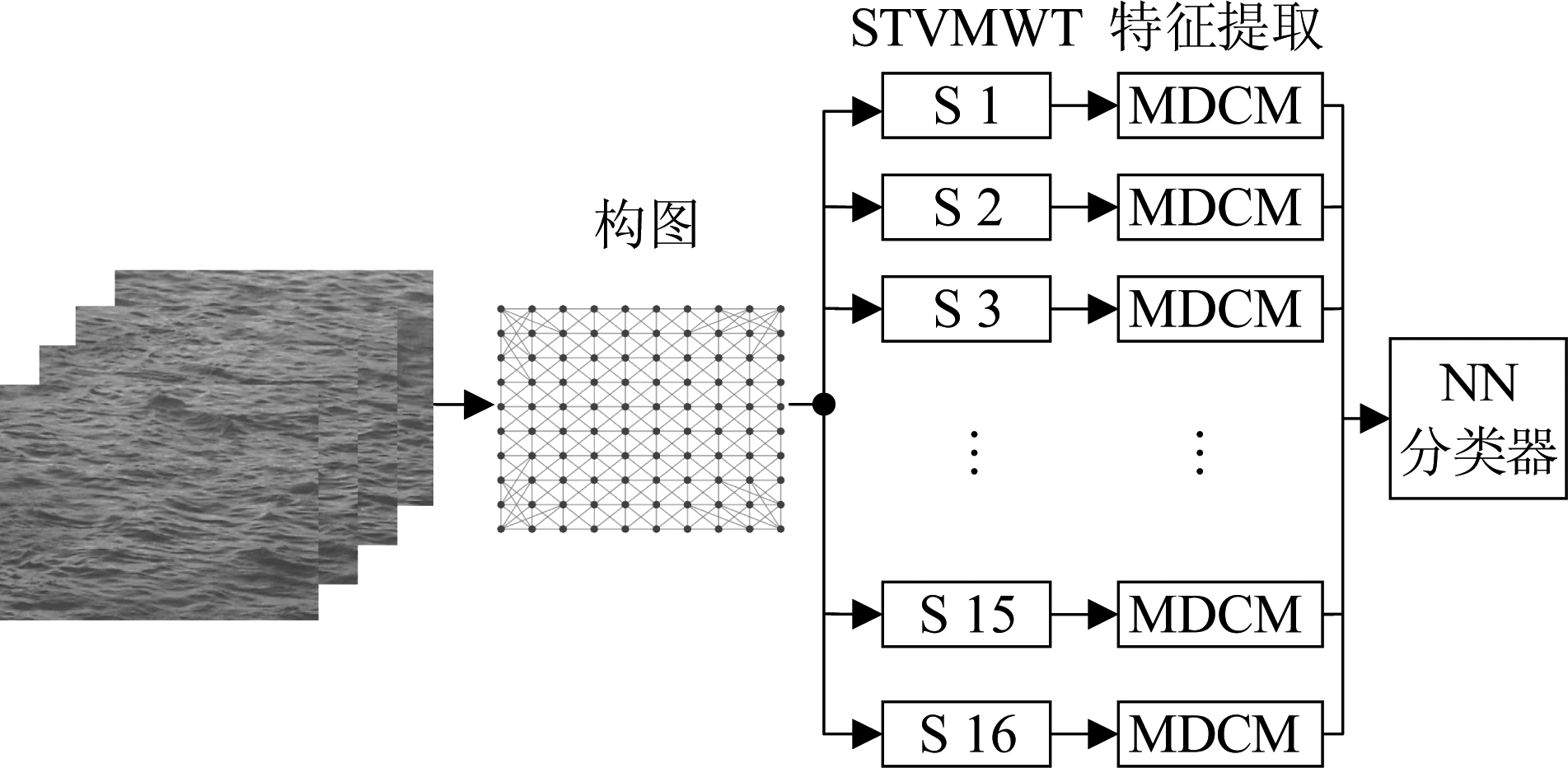
图1 动态纹理分类算法原理图
Fig.1 Schematic diagram of dynamic texture classification algorithm
3.1 动态纹理的时间—顶点图信号表示
假设动态纹理由矩阵X=[x1,x2,…,xT]∈RN×T表示,其中N为每帧的像素数,T为动态纹理的长度。如2.1节所示,如果动态纹理第一帧x1是图G上的信号在t=1时的取值,那么信号X∈RN×T是时间—顶点图信号,并且该信号(动态纹理)可以看成是图G与环图GT的笛卡尔积图上的信号,如图2所示。因此,本文首先利用KNN法[14]和动态纹理第一帧图像构造图G(V,ε,W),将图像中的像素点作为图的顶点,采用KNN法,使顶点与其周围最近的K个顶点相连,边的权值与顶点之间的距离相关,距离越近,则权值越大。
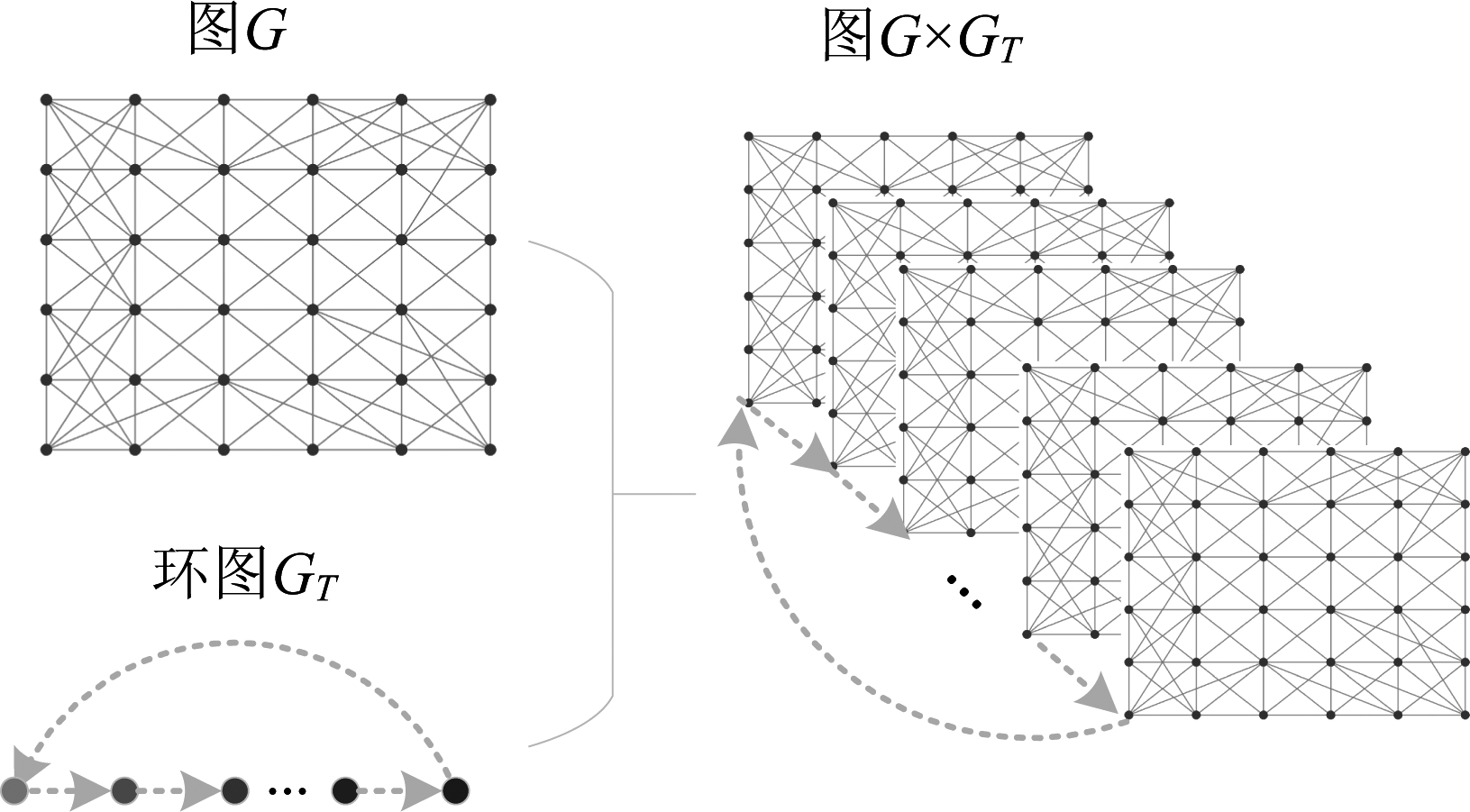
图2 动态纹理的时间—顶点图信号表示
Fig.2 Time-vertex graph signal representation of dynamic textures
3.2 时间—顶点谱图Meyer小波变换
Leonardi等人[15]基于传统Meyer小波设计了图谱域Meyer小波核函数,该谱图Meyer小波可以对图信号进行多尺度分解,捕获不同尺度上信号的特征。通过在UCLA数据集中动态纹理boiling-c-mid上的实验表明,经过时间—顶点谱图Meyer小波变换后,不同子带小波系数的分布近似服从广义高斯分布,系数分布如图3所示。针对小波系数进行广义高斯分布建模可获得动态纹理的特征,因此,本研究采用时间—顶点谱图Meyer小波描述动态纹理。
在图傅里叶域中Meyer小波的小波核g和尺度函数h的定义如下[15]:
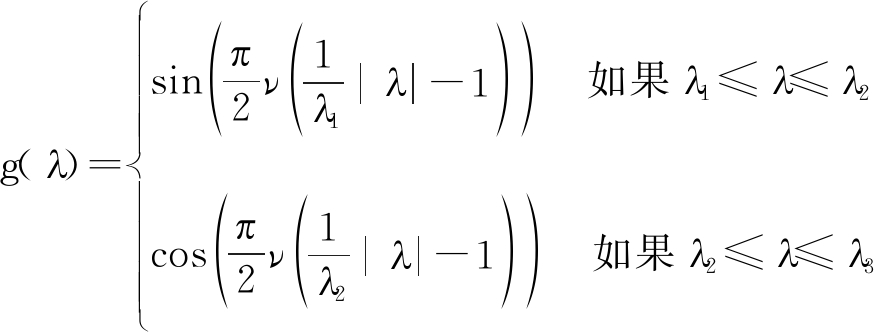
(12)
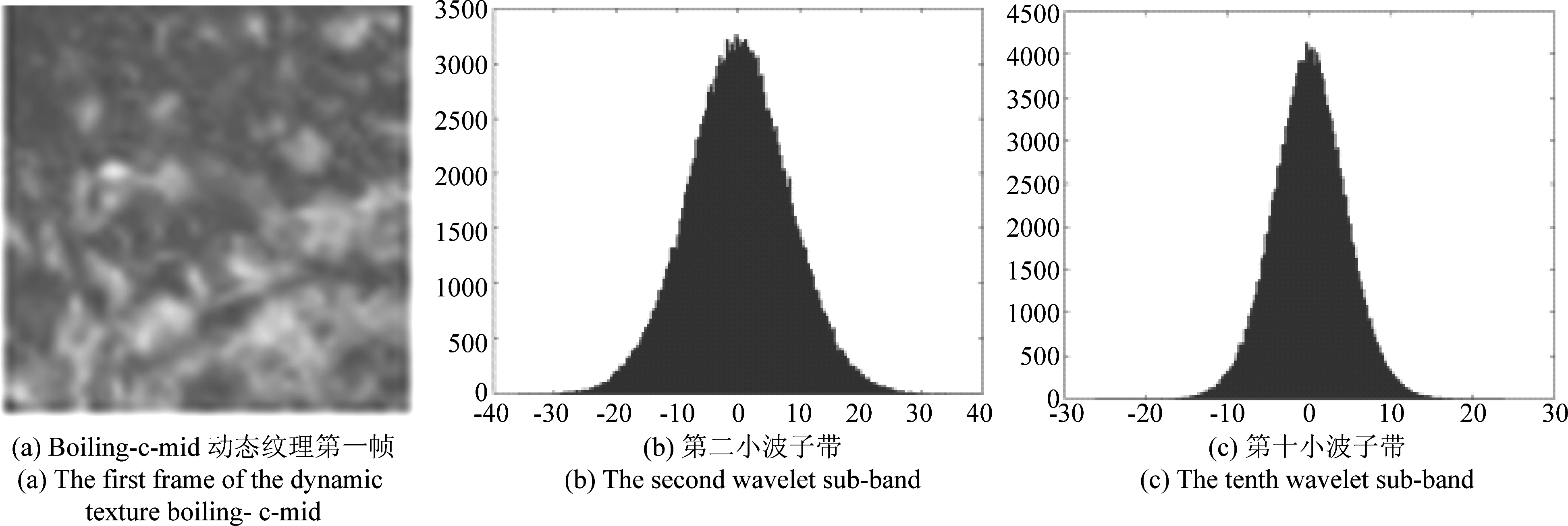
图3 小波子带系数分布图
Fig.3 Distributions of wavelet sub-band coefficients
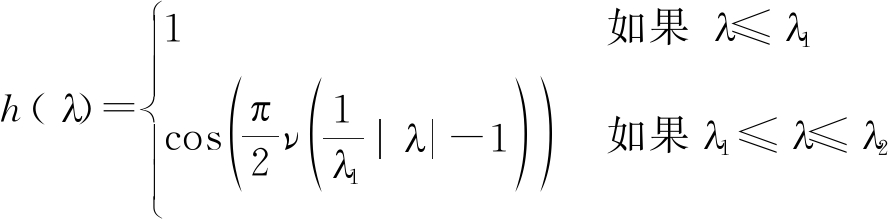
(13)
其中
并且λ2=2λ1,λ3=4λ1,第L个小波尺度定义为
本文中的时间—顶点Meyer小波核在此基础上加入了时间Meyer小波核,它的第L个小波尺度定义为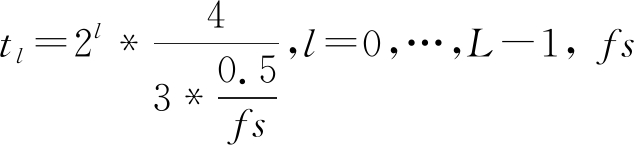
为采样频率[12]。联合时间—顶点Meyer小波核为时间核与谱图核的内积:
gJ(zλλ,zωω)=
(14)
得到Nf2个时间—顶点小波核,则时间—顶点谱图Meyer小波变换(Spectral Time-Vertex Meyer Wavelet Transform, STVMWT)为:
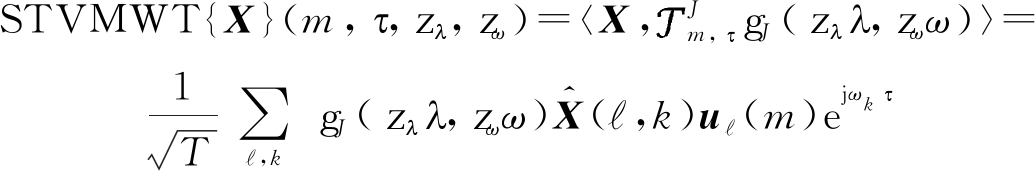
(15)
本文中将采样频率fs设为1,m,τ可取到所有的N和T值。最终,对每个动态纹理分解产生具有不同尺度的Nf2个小波子带。
3.3 基于MDCM模型的特征提取
在对动态纹理进行STVMWT后,得到Nf2个小波子带。通常来讲,可对小波系数使用数据统计分析或模型建模进行特征提取。在小波域现有的多变量模型中,copula是一种先进的、用于捕捉小波子带依赖结构的统计模型,[16]中指出高斯copula可以有效的对小波系数进行建模,并应用于图像检索。在高斯copula中,对称正定协方差矩阵是该模型的关键部分,它用来表示CDF空间中变量的依赖结构。同时,协方差矩阵广泛应用于图像分析。 Pang等人[17]利用协方差矩阵对局部区域的Gabor小波特征建模进行人脸识别,[16]中指出带内空间邻域的小波系数相关性最大,受以上思想的影响,Li等人[18]提出MDCM用于图像纹理分类,因此本文借鉴[18]中特征提取的方法,针对动态纹理的特点,设计有效的邻域系数提取方法,利用MDCM模型,在谱图小波子带内提取边缘分布的协方差矩阵作为动态纹理特征,具体步骤如图4所示:构造观测矩阵,将边缘观测值映射到累积分布函数(CDF)空间,计算协方差矩阵[18]。
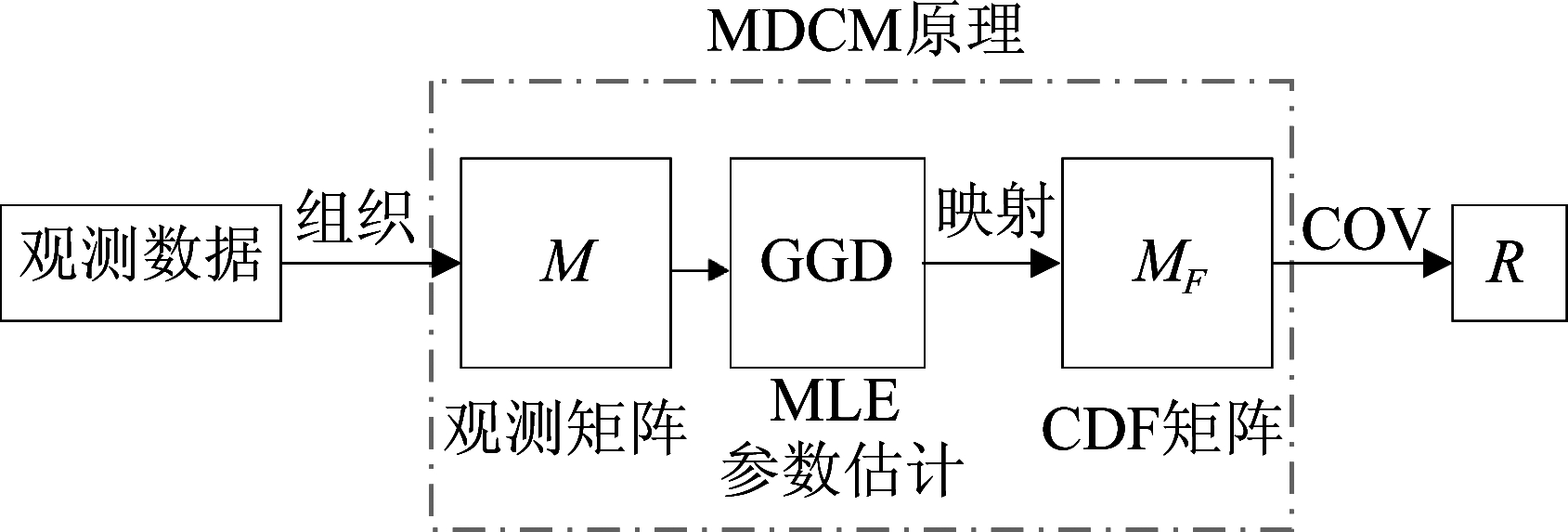
图4 MDCM算法的实现过程
Fig.4 The realization of MDCM algorithm
第一步:构造观测矩阵。文献[18]使用2D滑动窗口(如图5(b)所示)构造观测矩阵提取图像纹理特征,但是对于动态纹理,2D滑动窗口不能有效捕捉相邻两帧图像之间的动态信息,因此本文提出新的3D滑动窗口,如图5 (a)所示,该滑动窗口在相邻两帧之间取5+4交叉邻域,可较好描述动态纹理的动态变化过程。给定变量x1,…,xd,d为滑窗内的像素数,利用3D滑动窗口构造观测矩阵M∈Rd×n,M的每一行都是一个边缘变量xi的观测值。
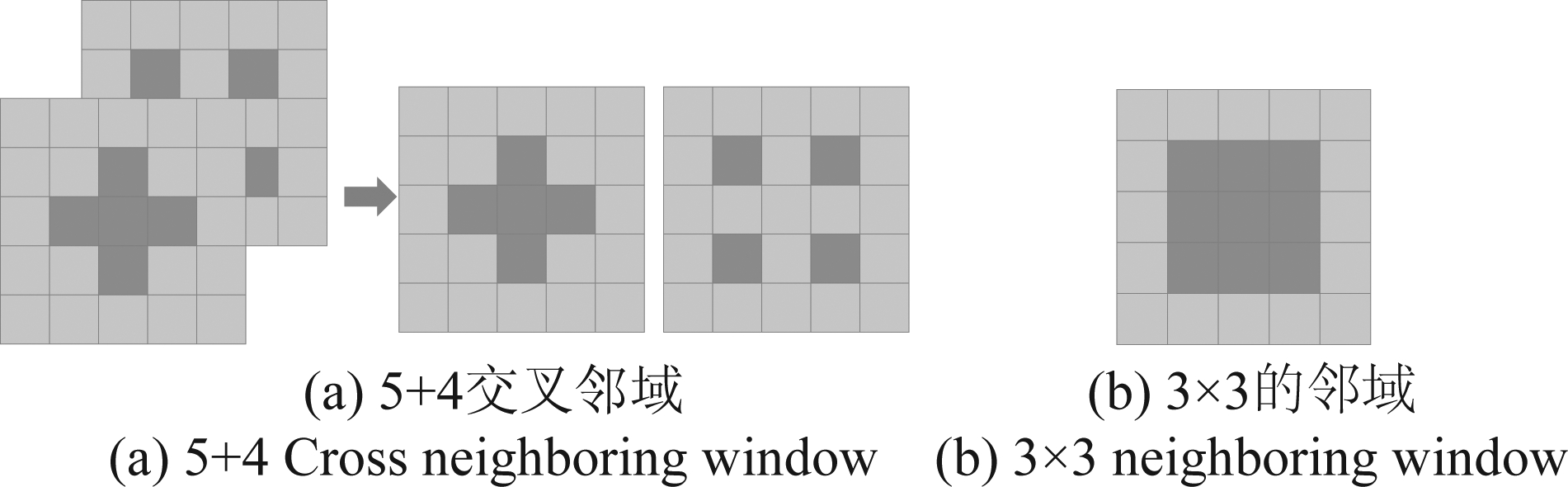
图5 滑动窗口
Fig.5 Sliding windows
第二步:将边缘观测值映射到CDF空间。本文将广义高斯分布(GGD)作为MDCM的边缘分布函数,GGD的概率密度函数为:
其中α和β分别为尺度和形状参数[18];Γ(z)=
e-ttz-1dt,z>0。对M的每一行ri,首先使用最大似然估计(MLE)估计GGD的参数
再将M第i行观测值映射到CDF空间[18],得到向量Fi=[F1,i,F2,i,…,Fn,i]。
第三步:计算协方差矩阵。对向量Fi(i=1,…,d),计算其协方差矩阵。对于任意两个向量Fi和Fj,其协方差为[18]
(16)
其中
是Fi的均值;n是观测值的数量,相应的协方差矩阵为[18]
R=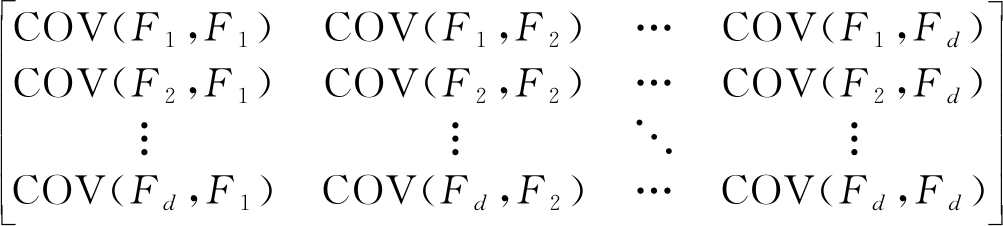
(17)
由于0≤Fi, j≤1,R中的元素满足-1≤Ri, j≤1。
3.4 相似性测距
文献[18]中使用的黎曼距离(Riemannian distance, RD)计算两个对称正定协方差矩阵的距离,从而衡量图像纹理间的相似性,因此本文采用黎曼距离作为测距函数来度量两个协方差矩阵Rl,1和Rl,2的相似性。由于多尺度分解形成不同小波子带,因此采用链式规则,在同一尺度分解下得到的小波系数计算相似性,将每个小波子带对应的相似性测距相加,最终得到两个动态纹理的相似性测度。设L为谱图小波子带个数,则动态纹理特征为DTR={R1,R2,…,RL},那么,衡量两个特征向量间相似性的距离函数为:
(18)
其中
是根据|λiRl,1-Rl,2|=0计算的Rl,1和Rl,2的广义特征值。
4 实验与仿真结果分析
为了评估本文所提算法(STVMWT-MDCM)的分类性能,本文选用标准测试动态纹理数据库UCLA[19]和DynTex[20],在进行STVMWT时,Nf=4,共得到L=Nf2=16个小波子带。为了验证所提动态纹理特征的有效性,同时便于与其他方法进行比较,本文所有实验均采用最近邻(Nearest Neighbor,NN)分类器。实验中所选择的对比方法分为三类,由于LBP在动态纹理分析中表现出优秀的性能,第一类对比方法为基于LBP的方法;同时,本文的时间—顶点谱图Meyer小波变换通过滤波器组实现,第二类对比方法为基于3D滤波的方法;另外,由于卷积神经网络在图像处理中得到广泛应用,所以,第三类为基于深度学习的方法。
4.1 实验数据集4.1.1 UCLA数据集
该数据集包含200个动态纹理,分为50类。每个视频的大小为48×48,共75帧。在该数据库上进行3种评估实验。
实验1 对50类视频进行四折交叉验证。每类动态纹理中三个用于训练,剩下的一个用于测试,为了确保每个视频都被测试一次,该实验重复四次。四次实验的平均正确率为最终结果。
实验2 将50类视频重新划分为9类,分别为烟(4),火(8),沸水(8),水(12),花(12),海(12),瀑布(16),植物(108)[24]。从每类中随机选择50%视频用于训练,其余用于测试。此实验重复20次,并以平均分类率为最终结果。
实验3 在实验2的基础上,将植物类去掉,对剩下的8类视频采取与实验2同样的方法进行实验。
4.1.2 DynTex-35数据集
该数据集[20]由DynTex数据库构造,共包含35类动态纹理,每个视频大小为400×300[21],共250帧。本文采用[22]中的实验方法,将每个视频分割为10个子视频,采用留一法进行动态纹理分类测试。
4.1.3 DynTex++数据集
该数据集将DynTex数据库中的345个视频裁剪为50×50×50大小的动态纹理,共36类,每类100个动态纹理[23-24]。实验中,我们和[23]一样每类随机选取50%的动态纹理用于测试,其余50%的样本用于训练,重读该实验10次, 以10次分类结果的平均值作为最终分类率。
4.1.4 Alpha、Beta数据集
Alpha数据集[24]包含DynTex数据库的60个动态纹理,分为3类:海、草和树;Beta数据集[24]由162个动态纹理组成,分为10类:海洋、植被、树木、旗帜、平静的水、喷泉、烟雾、自动扶梯、交通和旋转。对于这两个数据集,同样采用留一法进行实验。在特征提取时,将Alpha和Beta数据集的每个视频平均分割为250帧的16个子视频,将16个子视频的特征和作为动态纹理特征。
4.2 分类实验结果及分析
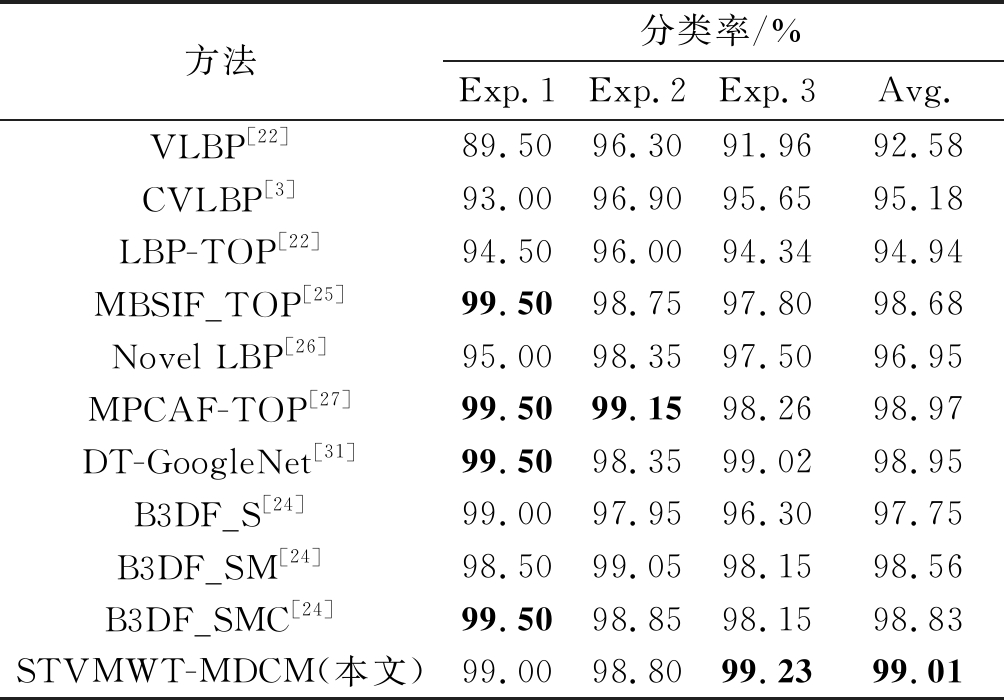
所提算法STVMWT-MDCM与比较方法在UCLA数据集上的性能如表1所示,其中Exp.1、Exp.2、Exp.3分别表示三种分类实验方式,Avg.表示分类正确率的平均值。在对比实验中,VLBP[22]、CVLBP[3]、LBP-TOP[22]和Novel LBP[26]均为基于局部二进制编码的方法,MBSIF_TOP[25]、MPCAF-TOP[27]和B3DF[24]是基于3D滤波的方法,DT-GoogleNet[31]是在三个正交平面上应用卷积神经网络的方法。在实验一中,STVMWT-MDCM方法的分类正确率为99.0%,比方法MBSIF_TOP、MPCAF-TOP和DT-GoogleNet的分类正确率低0.5%;在实验二中,STVMWT-MDCM方法的分类正确率为98.8%,比方法MBSIF_TOP、B3DF_SM和B3DF_SMC的分类正确率分别低0.35%、0.25%和0.05%;在实验三中,STVMWT-MDCM方法的分类正确率为99.23%,优于所有比较算法。观察数据可以发现,基于滤波学习的方法普遍分类效果较好,然而在实验三中,本文方法优于其他基于滤波学习的方法。并且从表1可以看出,本文所提算法的分类正确率平均值为99.01%,优于其他比较方法,说明了本文提出方法在UCLA数据集上具有较好的性能。
表1 UCLA数据集上动态纹理分类实验结果
Tab.1 Experimental results of dynamic texture classification on UCLA dataset
方法分类率/%Exp.1Exp.2Exp.3Avg.VLBP[22]89.5096.3091.9692.58CVLBP[3]93.0096.9095.6595.18LBP-TOP[22]94.5096.0094.3494.94MBSIF_TOP[25]99.5098.7597.8098.68Novel LBP[26]95.0098.3597.5096.95MPCAF-TOP[27]99.5099.1598.2698.97DT-GoogleNet[31]99.5098.3599.0298.95B3DF_S[24]99.0097.9596.3097.75B3DF_SM[24]98.5099.0598.1598.56B3DF_SMC[24]99.5098.8598.1598.83STVMWT-MDCM(本文)99.0098.8099.2399.01
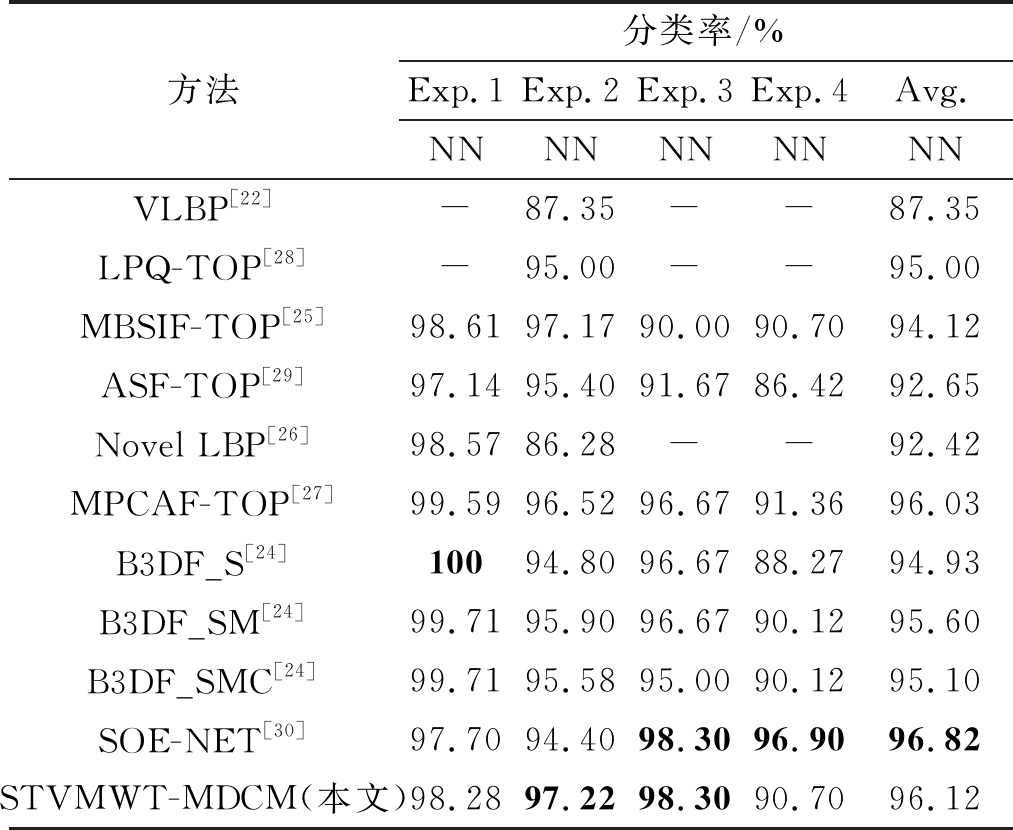
在表2中列出了所提算法和其他比较方法在4个DynTex数据集上的分类实验结果,其中,LPQ-TOP[28]方法对局部傅里叶变换的相位信息进行量化,得到动态纹理描述符;ASF-TOP[29]由LBP-TOP演化而来,在三个正交平面上聚集显著特征来描述动态纹理。SOE-NET[30]是基于时空卷积网络的动态纹理分类方法。由表中实验结果可以看出,所提算法STVMWT-MDCM在DynTex++和Alpha数据集上,分类正确率分别为97.22%和98.30%,高于所有其他比较方法;在数据集DynTex-35上,STVMWT-MDCM的分类正确率为98.28%,B3DF_S的分类效果最好,达到为100%;在数据集Beta上,分类正确率为90.70%,比方法MPCAF-TOP(91.36%)和SOE-NET(96.90%)低,主要原因是,该数据集中同一类别中的动态纹理差别过大,例如喷泉(Fountains)类中包含不同尺度下的动态纹理,植被类(Vegetation)中包含同一语义类别的动态纹理,视觉特性差别很大,很明显,仅从动态纹理特性角度来看,要将其分为同类动态纹理,存在较大困难,因此基于LBP、3D滤波的方法以及本文的方法在该数据库上分类性能较差。这也是后续研究的重点方向。整体上来看,方法MPCAF-TOP和基于B3DF的方法具有和所提算法类似的分类性能,然而所提算法在数据集DynTex++和Alpha上优于这两种方法,并且在4个DynTex数据集上的平均分类正确率也要稍优于这两种方法。
表2 DynTex四种数据集上的动态纹理分类实验结果
Tab.2 Experimental results of dynamic texture classification on four datasets of DynTex
方法分类率/%Exp.1Exp.2Exp.3Exp.4Avg.NNNNNNNNNNVLBP[22]-87.35--87.35LPQ-TOP[28]-95.00--95.00MBSIF-TOP[25]98.6197.1790.0090.7094.12ASF-TOP[29]97.1495.4091.6786.4292.65Novel LBP[26]98.5786.28--92.42MPCAF-TOP[27]99.5996.5296.6791.3696.03B3DF_S[24]10094.8096.6788.2794.93B3DF_SM[24]99.7195.9096.6790.1295.60B3DF_SMC[24]99.7195.5895.0090.1295.10SOE-NET[30]97.7094.4098.3096.9096.82STVMWT-MDCM(本文)98.2897.2298.3090.7096.12
5 结论
本文将动态纹理看成时间—顶点图信号,并利用STVWT,提出了一种基于STVWT与MDCM模型的动态纹理分类方法。该方法通过STVWT,得到动态纹理的多尺度表示,再利用MDCM模型提取动态纹理特征。在标准动态纹理数据集UCLA和DynTex上的分类结果表明,所提算法可以很好的刻画动态纹理的特性,达到较好的分类效果,同时也表明,STVWT在动态纹理分析中具有潜在的应用前景。
[1] FENG Jinwang, LIU Xinliang, DONG Yongsheng, et al. Structural difference histogram representation for texture image classification[J]. IET Image Processing, 2017, 11(2): 118-125.
[2] WANG Chen, LU Zongqing, LIAO Qingmin. Local texture based optical flow for complex brightness variations[C]∥2014 IEEE International Conference on Image Processing (ICIP). Paris, France. IEEE, 2014: 1972-1976.
[3] TIWARI D,TYAGI V.Dynamic texture recognition based on completed volume local binary pattern[J].Multidimensional Systems and Signal Processing, 2016, 27(2): 563-575.
[4] 梁淑芬, 刘银华, 李立琛. 小波变换和LBP对数域特征提取的人脸识别算法[J]. 信号处理, 2013, 29(9): 1227-1232.
LIANG Shufen, LIU Yinhua, LI Lichen. Face recognition based on wavelet transform and LBP in logarithm[J]. Journal of Signal Processing, 2013, 29(9): 1227-1232.(in Chinese)
[5] 彭自然, 王国军. 用小波变换对ECG信号进行去噪研究[J]. 信号处理, 2017,33(8): 1122-1131.
PENG Ziran, WANG Guojun. Denoising of ECG signal by wavelet transform[J]. Journal of Signal Processing, 2017, 33(8): 1122-1131.(in Chinese)
[6] SMITH J R, LIN C Y, NAPHADE M. Video texture indexing using spatio-temporal wavelets[C]∥IEEE International Conference on Image Processing, 2002: 437- 440.
[7] QIAO Yulong, SONG Chunyan, WANG Fushan. Wavelet-based dynamic texture classification using gumbel distribution[J]. Mathematical Problems in Engineering, 2014, 2013(11):583- 603.
[8] HAMMOND D K, VANDERGHEYNST P, GRIBONVAL R. Wavelets on graphs via spectral graph theory[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 129-150.
[9] NARANG S K, ORTEGA A. Perfect reconstruction two-channel wavelet filter banks for graph structured data[J]. IEEE Transactions on Signal Processing, 2012, 60(6): 2786-2799.
[10] 徐兴敏. 谱图小波变换在图像去噪中的应用研究[D]. 西安: 西安理工大学, 2018.
XU Xingmin. The application of spectral graph wavelet transform in image denoising[D]. Xi’an: Xi’an University of Technology, 2018.(in Chinese)
[11] 赵玥. 基于图小波变换的纹理分类与SAR图像识别[D]. 哈尔滨: 哈尔滨工程大学, 2019.
ZHAO Yue. Texture classification and SAR image recognition based graph wavelet transform[D]. Harbin: Harbin Engineering University, 2019.(in Chinese)
[12] GRASSI F,LOUKAS A,PERRAUDIN N,et al.A time-vertex signal processing framework: Scalable processing and meaningful representations for time-series on graphs[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 817- 829.
[13] PERRAUDIN N, VANDERGHEYNST P. Stationary signal processing on graphs[J]. IEEE Transactions on Signal Processing, 2017, 65(13): 3462-3477.
[14] SHAHID N, PERRAUDIN N, KALOFOLIAS V, et al. Fast robust PCA on graphs[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(4): 740-756.
[15] LEONARDI N, VAN DE VILLE D. Wavelet frames on graphs defined by fMRI functional connectivity[C]∥2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Chicago, IL, USA. IEEE, 2011: 2136-2139.
[16] LASMAR N E, BERTHOUMIEU Y. Gaussian copula multivariate modeling for texture image retrieval using wavelet transforms[J]. IEEE Transactions on Image Processing, 2014, 23(5): 2246-2261.
[17] PANG Yanwei, YUAN Yuan, LI Xuelong. Gabor-based region covariance matrices for face recognition[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2008, 18(7): 989-993.
[18] LI Chaorong, HUANG Yuanyuan, YANG Xingchun, et al. Marginal distribution covariance model in the multiple wavelet domain for texture representation[J]. Pattern Recognition, 2019, 92: 246-257.
[19] DORETTO G, CHIUSO A, WU Yingnian, et al. Dynamic textures[J]. International Journal of Computer Vision, 2003, 51(2): 91-109.
[20] PÉTERI R, FAZEKAS S, HUISKES M J. DynTex: A comprehensive database of dynamic textures[J]. Pattern Recognition Letters, 2010, 31(12): 1627-1632.
[21] XU Yong, QUAN Yuhui, LING Haibin, et al. Dynamic texture classification using dynamic fractal analysis[C]∥2011 International Conference on Computer Vision. Barcelona, Spain. IEEE, 2011: 1219-1226.
[22] ZHAO Guoying,PIETIKAINEN M.Dynamic texture recognition using local binary patterns with an application to facial expressions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(6):915-928.
[23] GHANEM B,AHUJA N.Maximum margin distance learning for dynamic texture recognition[M]∥Computer Vision-ECCV 2010.Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 223-236.
[24] ZHAO Xiaochao, LIN Yaping, LIU Li, et al. Dynamic texture classification using unsupervised 3D filter learning and local binary encoding[J]. IEEE Transactions on Multimedia, 2019, 21(7): 1694-1708.
[25] ARASHLOO S R, KITTLER J. Dynamic texture recognition using multiscale binarized statistical image features[J]. IEEE Transactions on Multimedia, 2014, 16(8): 2099-2109.
[26] TIWARI D,TYAGI V.A novel scheme based on local binary pattern for dynamic texture recognition[J].Computer Vision and Image Understanding,2016,150:58- 65.
[27] ZHAO Xiaochao, LIN Yaping, HEIKKILA J. Dynamic texture recognition using multiscale PCA-learned filters[C]∥2017 IEEE International Conference on Image Processing (ICIP). Beijing. IEEE, 2017: 4152-4156.
[28] RAHTU E,HEIKKIL
J,OJANSIVU V,et al.Local phase quantization for blur-insensitive image analysis[J].Image and Vision Computing,2012,30(8):501-512.
[29] HONG S, RYU J, YANG H S. Not all frames are equal: Aggregating salient features for dynamic texture classification[J]. Multidimensional Systems and Signal Processing, 2018, 29(1): 279-298.
[30] HADJI I, WILDES R P. A spatiotemporal oriented energy network for dynamic texture recognition[C]∥2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy. IEEE, 2017: 3085-3093.
[31] ANDREARCZYK V,WHELAN P F.Convolutional neural network on three orthogonal planes for dynamic texture classification[J]. Pattern Recognition, 2018, 76: 36- 49.
