1 引言
辐射源个体识别(Specific Emitter identification, SEI)是提取同类辐射源发送的信号中的细微特征来识别不同辐射源个体的过程[1]。这种能够区分不同辐射源的细微特征被称为射频指纹(Radio Frequency Fingerprint, RFF)。由于射频指纹来自于发射机模拟器件的固有缺陷,不可避免且难以伪造,SEI技术在军用和民用领域有着广阔的应用前景。在民用方面,SEI技术可以应用于频谱资源管控、无线网络安全和认知无线电等领域。在军事通信方面,SEI技术可以在复杂的战场环境中识别特定辐射源的信号,对于敌我识别和掌握战场态势具有重要意义。
一个典型的SEI流程可以分为三个主要步骤:(1)对接收到的信号进行预处理。(2)从处理后的信号中提取包含辐射源个体信息的射频指纹特征。(3)设计分类识别算法并对信号进行识别,确定发射该信号的特定辐射源。第一个步骤要求确保射频指纹特征不被破坏,同时尽可能少的引入噪声。第二个步骤针对暂态信号或稳态信号,采取相应的技术手段进行特征提取。对于暂态特征的提取通常使用分形理论[2]和小波变换[3]。而稳态特征的提取则多借助双谱分析[4]和时频分析[5]。第三个步骤则使用适当的分类器对辐射源进行分类。Reising等人使用了(MDA/ML)分类器对高维的射频指纹特征进行分类[6]。而brik等人则将支持向量机(Support Vector Machine, SVM)和KNN应用到SEI中,并指出了SVM更具优势[7]。
近年来,深度学习技术展示了其在SEI应用中的巨大潜力,与传统的手工提取特征的方法相比,性能得到了很大的提升[8-11]。待识别辐射源发送的信号的传输环境和接收机与用于训练的带标签信号完全相同时,神经网络借助其强大的非线性映射能力,可以实现对射频指纹特性的提取和抽象,达到较好的分类性能。但在实际通信场景下,由于传输环境和接收机内部噪声的变化,对于同一个辐射源而言,发送的信号被接收后的信噪比并不完全一样。当有标签训练信号与无标签待测信号的信噪比不同时,有监督的深度学习模型的识别性能将大打折扣。训练信号与待测信号的信噪比虽不一致,但携带的指纹信息是一致的,如何学习这种“不变”的指纹特征是问题的关键。本文利用了迁移学习领域的领域自适应思想,将神经网络从有标签训练信号学到的指纹特征迁移到无标签信号,降低了噪声干扰对识别性能的影响,解决了待识别信号与有标签训练信号信噪比不一致时的SEI问题。
本文内容安排如下:第2节描述信号模型与本文使用的相关技术;第3节介绍了本文提出的基于领域自适应的辐射源识别算法;第4节对算法的性能进行验证和分析;第5节总结全文。
2 问题描述与相关工作
2.1 信号建模
由于制造工艺和工作环境的差异,通信辐射源的模拟器件在工作过程中会表现出非线性,使得接收信号之间存在着细微的差异,利用这些差异可以辨别不同的辐射源个体。功放是发射机的主要模拟器件之一,当其进入饱和工作区域时,会产生非常严重的非线性畸变失真。对无记忆的窄带功放的非线性行为进行建模时,通常使用Taylor级数模型[12]。假设s0(t)表示基带信号, fc为载波频率,输入功放的射频信号为s(t)=Re{s0(t)ej2πfct},功放的输出信号为
(1)
其中L为多项式的阶数,{λ1,λ2,...,λR}为功放非线性系数,通常情况下λ1设置为1。考虑有K个发射机的通信系统,信号经过信道后到达接收机,第k个发射机发送的信号在接收端可以表示为
(2)
其中α是信道的衰落因子,n(t)为加性高斯白噪声,L为多项式的阶数。{λk,1λk,2,...,λk,L}为第k个发射机的非线性系数。本文考虑加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道场景,此时α设置为1。本文假设接机是理想的,不必考虑接收端的器件影响。
2.2 迁移学习与领域自适应
迁移学习是机器学习领域的一个重要分支。简单来说,给定源域Ds和目标域Dt,迁移学习的目的是将模型从Ds中学到的知识迁移到Dt。领域自适应(Domain Adaptation, DA)是迁移学习的重要研究方向,用于解决任务相同但分布不一致的问题。即给定一个有标签的源域
和一个无标签的目标域
假定他们的特征空间相同,即Xs=Xt,以及它们的类别空间也相同,即Ys=Yt,并且它们的条件概率分布也相同,即Qs(ys|xs)=Qt(yt|xt)。但这两个域的边缘分布不同,即Ps(xs)≠Pt(xt)。领域自适应的目标是:利用有标记的数据Ds去学习一个分类器f:xt→yt来预测Dt的标签yt∈Yt。本文基于领域自适应的原理,通过设计迁移学习模型将有标签单一信噪比下训练的神经网络迁移到无标签的其他信噪比下,达到模型可以实现有效识别不同信噪比信号的目的,打破由于噪声干扰造成的隔离,减弱传统辐射源识别算法对训练数据和测试数据的信道噪声条件一致的要求。
3 基于领域自适应的辐射源识别算法
动态信道噪声干扰下的辐射源个体识别问题可以视作领域自适应问题,其中有标签特定信噪比下的信号为源域,无标签的其他信噪比下的信号为目标域。特别地,由于目标域信号没有标签,这个问题也称为无监督领域自适应问题。受Tang等人[13]工作的启发,针对动态噪声干扰下的辐射源识别问题,做以下假设:
1)域内可聚类性假设。
假设源域和目标域都具有可区分的内在结构,可以根据共享标签空间进行聚类。当训练样本和测试样本的信噪比一致时,样本之间细微差异来自于不同发射机的辐射源指纹不同,此情况下训练神经网络模型可以得到较好的分类性能,佐证了这一假设的合理性。
2)类间紧密性假设。
假设不同领域内的同一类样本的簇在几何上应该是紧密的。对于同一个辐射源而言,即使发送的信号经历了不同的噪声环境,其所携带的射频指纹是不变的,因此对于各个信噪比下的同一个辐射源,它们形成的簇在几何上应该邻近的,直觉上这个假设是合理的。
图1形象地展示了这两种假设,基于第一个假设,本文算法在目标域实施无监督聚类,再基于第二个假设,使用源域标签的强约束将源域和目标域的特征进行对齐,实现无监督领域自适应的目的。
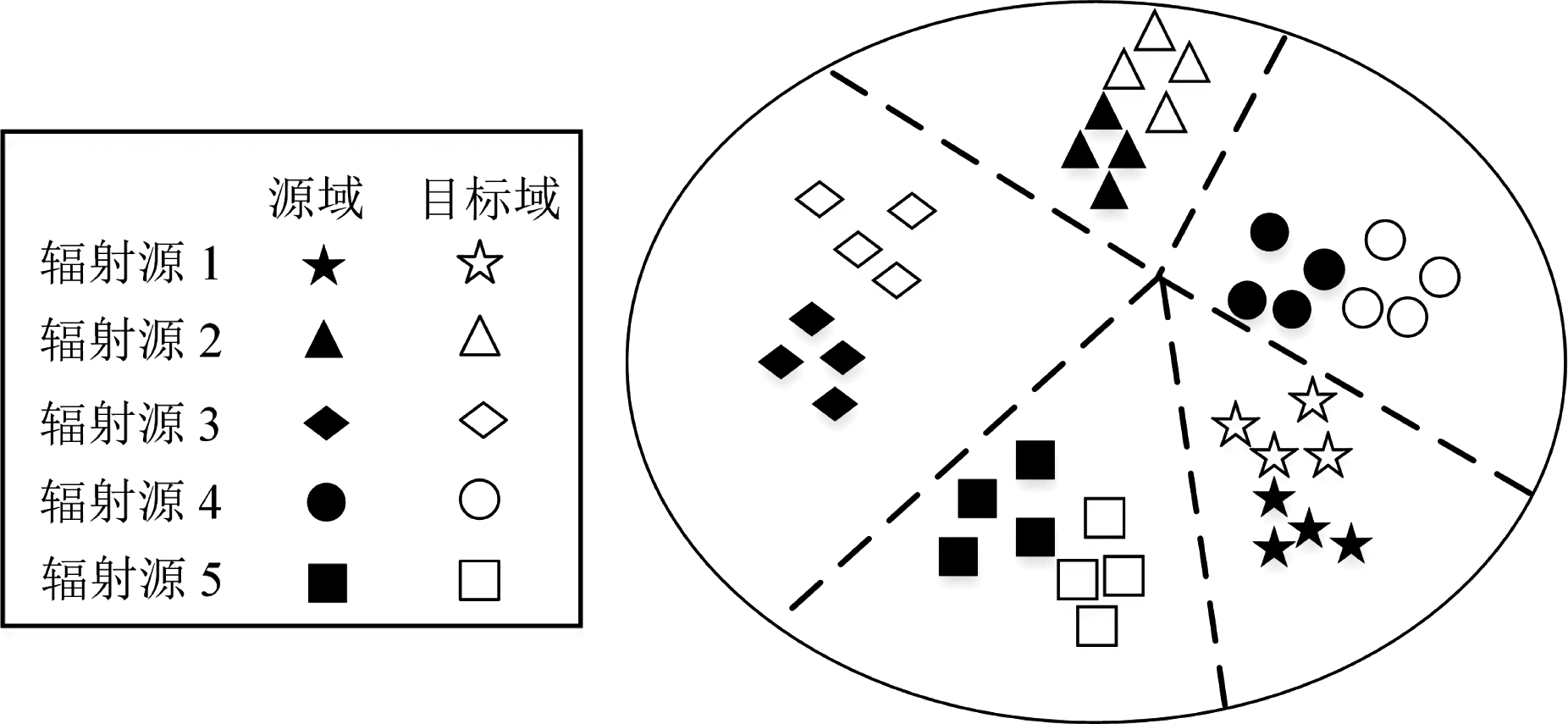
图1 域内可聚类性和类间紧密性示意图
Fig.1 Illustration of domain-wise clustering and class-wise closeness
3.1 信号表示
将信号样本输入神经网络前,需要将信号转换为适当的表示形式。文献[10-11]的工作表明,星座轨迹图能够在很大程度上保留射频指纹,是一种有效的信号表达形式。设星座轨迹图的表示范围为:{(I,Q)||I|≤S,|Q|≤S},预设图像矩阵H的大小为P×P,H的第(i, j)个元素Hi, j表示信号采样点落在区域
的次数,Hi, j的表达式如下
Hi, j=||Di, j||0
(3)
由于信号采样点在星座点附近较为密集,而其他区域相对较小,为了防止像素值出现极端分布,需要对矩阵H进行平坦化处理,处理方法由下式给出
H′=lg(H+1)
(4)
为了适应二维卷积神经网络的训练,进一步将星座轨迹图转换为灰度图像。给定图像量化位数ζ,灰度图的第(i, j)个像素Gi, j为
(5)
其中⎣·」表示向下取整。图2给出了信噪比0 dB和10 dB下的星座轨迹图灰度图像,可见由于信噪比的差异,两种星座轨迹图在视觉特上呈现了很大的差异,使用单一噪声条件下的样本训练的模型,很难学到统一的特征。
图2 不同信噪比下的星座轨迹图灰度图像
Fig.2 The grayscale constellation figures under different SNRs
3.2 领域自适应目标函数设计
本文将待识别的信号样本转换为星座轨迹图,作为神经网络的输入。一个标准的卷积神经网络(Convolutional Neural Network, CNN)可视作由特征提取器φ(·;θ)和分类器f(·;υ)组成,其卷积层为特征提取器,全连接层为分类器。对于一个有K个待识别辐射源的SEI问题,输入样本实例x,CNN的最后一个卷积层输出样本的特征表示z=φ(x),分类器的最后一层后输出一个概率矢量P=softmax( f(z))∈[0,1]K。基于前文提出的两个假设,分别定义以下两个约束。
3.2.1 目标域聚类约束
对于有nt个样本的无标签目标域
网络的预测结果为
统称为
为一个K维矢量,
为
的第k个元素,表示把输入网络的样本实例
识别为第k个辐射源的概率。与文献[14]中的无监督聚类算法相似,引入一个离散概率分布Qt作为辅助分布,交替执行两步操作:(a)更新辅助分布Qt,(b)把更新后的Qt视作伪标签,更新网络参数{θ,υ},损失函数如下
(6)
其中
式(6)的第二项鼓励伪标签分布
的熵最大化,即鼓励各个簇大小的平衡,防止出现聚类的简并,得到退化解。式(6)的第一项计算Qt和Pt的KL散度,由下式给出
(7)
目标函数(6)的优化按以下步骤交替进行:
步骤1 固定网络参数{θ,υ},更新Qt。通过将(6)的梯度设置为0,可以得到Qt的封闭解,用于更新Qt,其表达如下
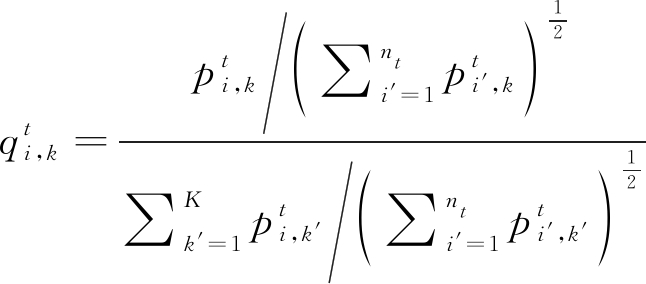
(8)
步骤2 固定Qt,更新网络参数{θ,υ}。此时式(6)等价于将Qt视作标签来训练网络的交叉熵(cross-entropy,CE)损失函数,如下式所示
(9)
对于输入样本实例x,最后一个卷积层输出的特征表示为z=φ(x),用Z表示特征空间。对Z施加类似的目标域聚类约束,在源域和目标域的共享特征空间Z中定义可学习的聚类中心
在特征空间上的分配概率定义为
它的第k个元素
表示该样本实例分配到第k个聚类中心的概率,表达式如下
(10)
将
统称为
引入相应的辅助分布
在嵌入特征空间Z上的深度可区分聚类目标函数为
(11)
其中
式(11)的推导过程与式(6)一致,且采用与(6)相同的交替优化方式,即交替更新辅助分布
和聚类中心
结合(6)和(11)可以得到目标域聚类约束,即本文算法的目标函数的第一项
(12)
3.2.2 类间紧密性约束
基于类间紧密性假设,本文使用了类间紧密性约束来实现源域和目标域的特征对齐。分类器f(·;υ)将特征空间Z划分为K个区域,每个区域代表一个待识别的辐射源。由于源域和目标域共享相同的标签空间,通过联合训练将两个域中的同一类样本推到Z中的相同区域中,也就实现了隐式的特征对齐。对于有ns个样本的无标签目标域
网络的预测结果为
统称为
为一个K维矢量,
为
的第k个元素,表示把输入网络的样本实例
识别为第k个辐射源的概率。将(6)中的辅助分布替换为真实标签,此时目标函数转换为了与有监督分类问题常用的交叉熵损失目标函数,如下式所示
(13)
其中
是网络对样本xj的预测向量
的第k个元素。
是样本的标签
的单热编码向量的第k个元素。同样需要在特征空间Z施加约束,如下式所示
(14)
其中,
的定义如下
(15)
合并(11)和(12),给出类间紧密性约束,即本文算法的目标函数的第二项
(16)
本文算法总的目标函数如下
(17)
其中λ为平衡系数,λ过大则不利于目标域的聚类,λ过小则会导致特征无法对齐,本文采取了动态的λ设置,将初始λ设置为0,并且在训练过程中逐步增加到1,在训练初期鼓励目标域聚类形成,随着训练的进行逐步将特征对齐。
3.3 网络构架和算法流程
本文使用ResNet-50[15]模型作为基本网络构架,它包括49个卷积层和1个1000个节点的全连接层。所有卷积层作为特征提取器,去除最后一个全连接层并新增一个两层的随机初始化的全连接网络作为分类器,节点数分别为1024和5。如图3所示。
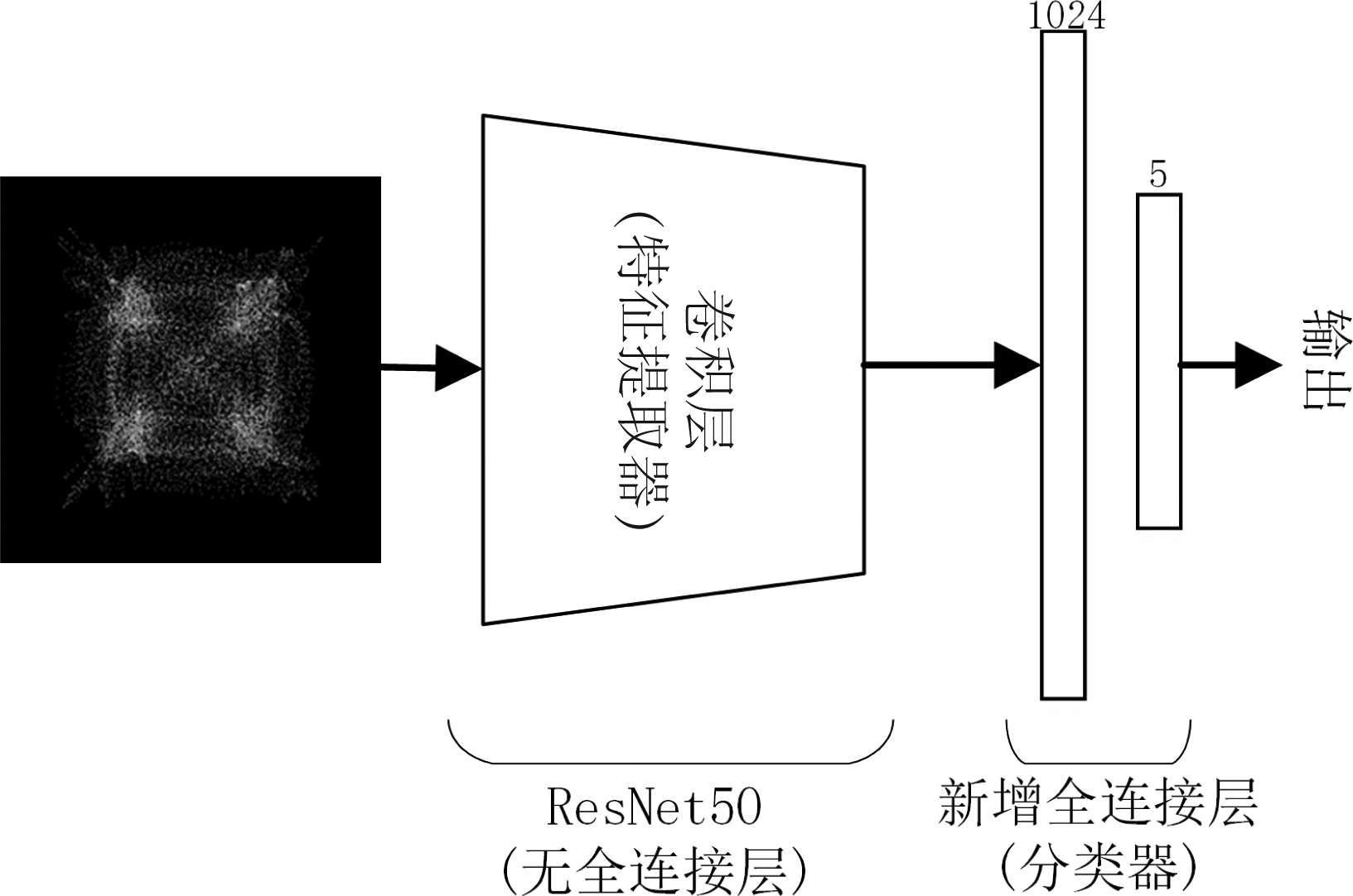
图3 网络结构示意图
Fig.3 The structure of the proposed neural network
本文算法通过最小化损失目标函数式(17)来学习网络参数{θ,υ}和聚类中心训练流程为如下:
(1) 将源域和目标域时域信号转换为星座轨迹图,得到带标签的源域样本集
和不带标签的目标域样本集
定义最大训练轮数E,每轮最大迭代次数I。
(2) 初始化
和
且
(3) 从S和T中采样一次迭代的所需的数据Bs和Bt。
(4) 通过在Bs和Bt上最小化损失函数式(17)来更新{θ,υ}和
(5) 利用式(9)计算
和
(6) 循环执行步骤(3)～(5),直到循环次数达到最大迭代次数I。
(7) 依据当前目标域特征
的聚类分配和源域特征
的标签重新初始化
(8) 循环执行步骤(6)和(7),直到模型收敛或循环次数达到最大训练轮数E。
当训练结束后,将待测无标签信号样本的星座轨迹图输入网络,分类器的输出即为分类结果。
4 实验分析
4.1 实验数据及参数配置
仿真实验的条件设置为:QPSK调制,信号观测时长为1000个符号周期,符号速率为100 KBaud,载频为420 kHz,采样率为1.6 MHz,基带成型采用滚降系数为0.35的升余弦脉冲。待识别辐射源个数为K=5,参考了文献[5,9]的设置,采用3阶Taylor级数模型来刻画功放非线性畸变,不同辐射源的各阶功放非线性系数如表1所示,射频信号依据式(2)仿真产生。在每个信噪比下,每个辐射源包含10000个信号样本,随机选择8000个样本用于训练,剩余2000个样本用于测试。将每个样本转化为8 bit量化的星座轨迹图灰度图,图片的大小统一为224×224。实验中使用ResNet-50作为分类网络,使用Adam优化器进行训练,学习率设置为0.001,每个训练批次的大小设置为128。式(17)中平衡系数λ的设置如下式所示
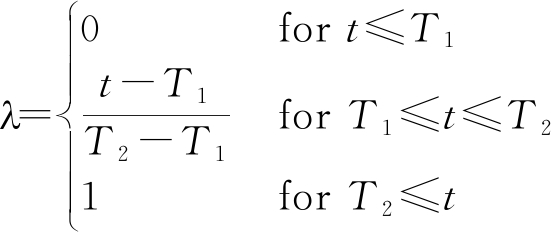
(18)
其中t表示当前训练的轮次,T1和T2分别设置为5和25。
表1 不同辐射源的功放非线性系数
Tab.1 Nonlinear coefficients of the emitters
参数辐射源1辐射源2辐射源3辐射源4辐射源5葜20.50.080.010.010.6葜30.30.60.010.40.8
4.2 不同信号表示下的识别性能
文献[10-11]证明了星座轨迹图的有效性,但其场景与本文场景略有不同,为了验证星座轨迹图在本文场景下的有效性,为后续实验奠定基础,将星座轨迹图作为输入与其他算法在不同信噪比下的识别性能进行对比。各种算法使用的输入包括:①星座轨迹图(本文所用输入),②Hilbert时频谱灰度图[9],③双谱灰度图[8],均使用ResNet-50训练100轮,实验结果如图4所示。
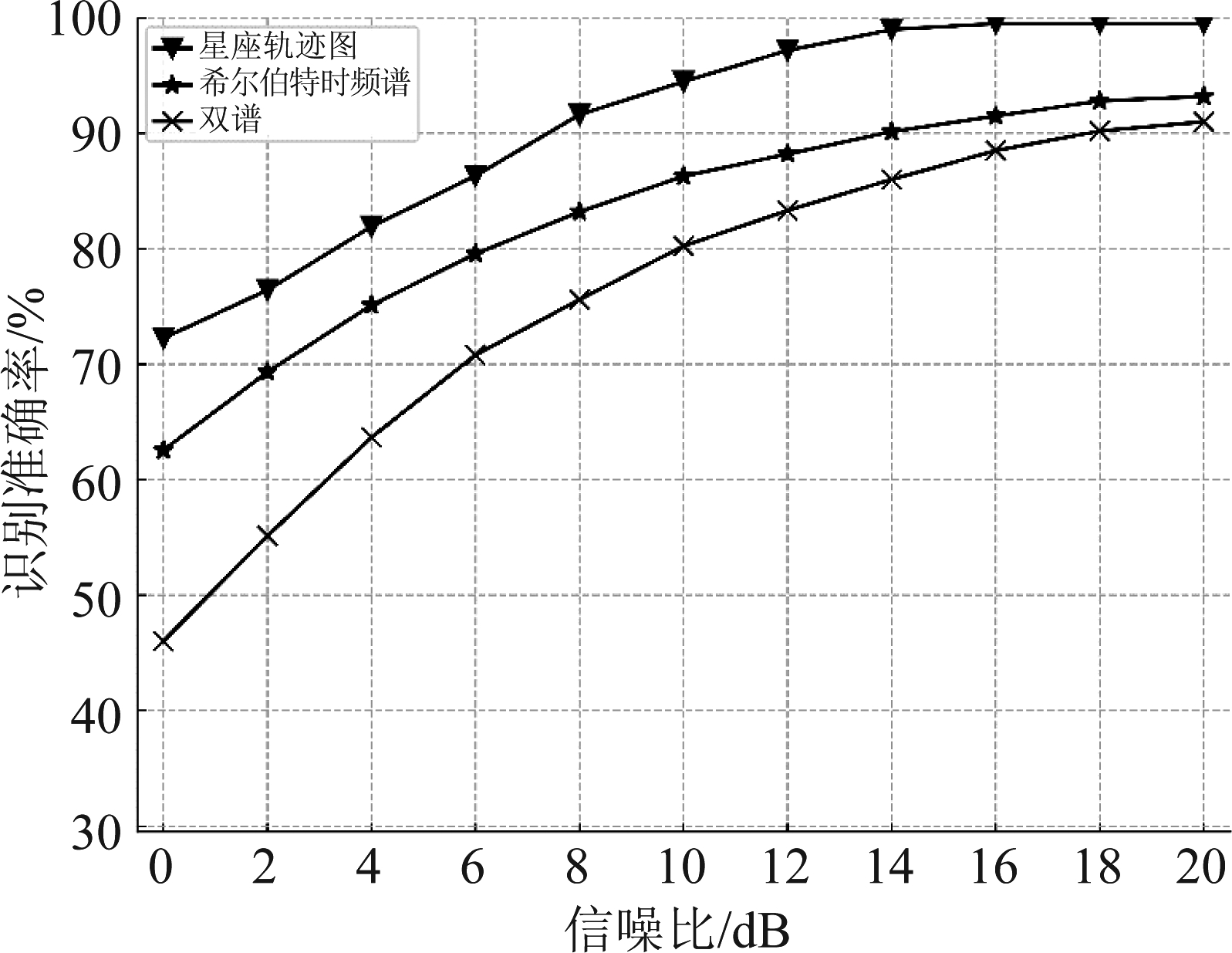
图4 3种不同种输入的识别性能
Fig.4 The identification accuracy of three different types of input
实验结果表明,使用星座轨迹图的方法在不同信噪比下性能衰减更小,并且识别准确率高于使用基于双谱和Hilbert时频谱的方法,表明了星座轨迹图是一种更有效的信号表示方法。
4.3 动态噪声条件下本文算法的性能
为了模拟动态噪声条件下的SEI场景,首先将带标签的信噪比为10 dB的信号作为源域,训练ResNet-50模型100轮,然后将不带标签的其他信噪比下的信号作为目标域,使用本文算法对模型进行优化,训练轮次为30轮,最后比较优化前后的模型对目标域信号的识别率。本实验拟将信号转换为星座轨迹图作为输入,但为了体现本文算法具备一般性,加入了使用Hilbert时频图灰度图和双谱灰度图作为输入的实验组,实验结果如图5所示,其中现有算法指未经本文算法优化直接测试模型在目标域的准确率。
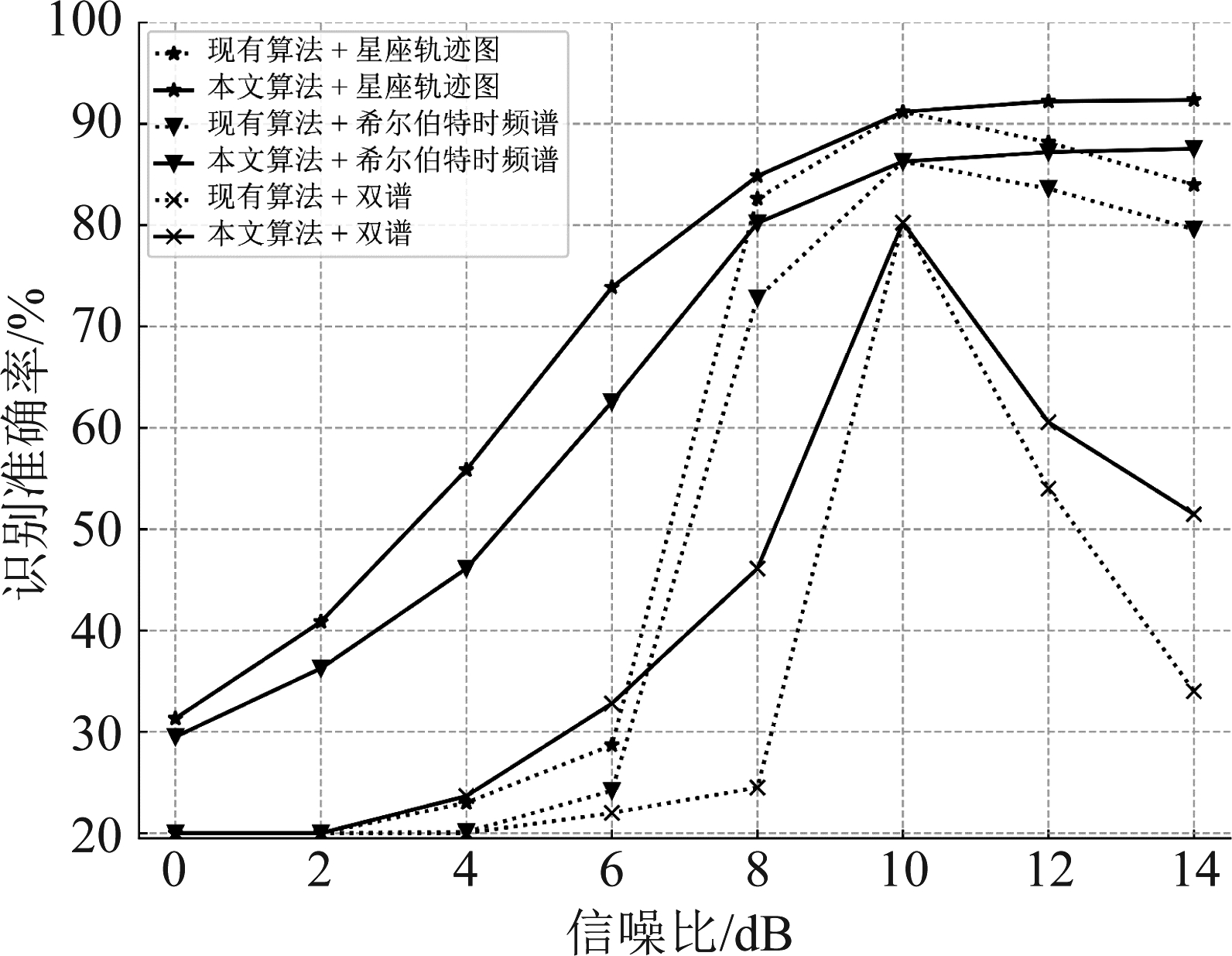
图5 目标域信号信噪比对识别性能的影响
Fig.5 The influence of SNRs of the target domain on identification accuracy
使用本文算法对模型进行优化前,模型的性能出现了劣化,这是由于噪声带来的隔离。特别是目标域信噪比低于源域时,识别率下降明显。当目标域信噪比低于4 dB时,模型准确率均下降到接近20%,此时高信噪比下训练的模型没有提取到有用的射频指纹特征,已经无法进行识别。使用本文算法对模型进行优化后,相较于未经优化的模型,识别性能明显改善。使用星座轨迹作为输入的情况下,当目标域信噪比为6 dB时,本文算法相比现有算法的增益最大,达到45.18%。使用Hilbert时频谱灰度图和双谱灰度图作为输入时,增益最大为38.37%和21.61%,分别在目标域信噪比为6 dB和8 dB的时候达到。
输入为星座轨迹图,源域信噪比为10 dB,目标域信噪比为6 dB,图6给出了使用本文优化前后,模型输出的混淆矩阵。本文算法优化前,模型的混淆矩阵存在比较明显的错误;而模型经过优化后,混淆矩阵明显更加接近于单位矩阵,体现了本文算法对分类结果带来的明显改善。
为了进一步理解本文算法的增益,使用t-SNE算法[16]将优化前后模型的第一个全连接层的输出降到二维,并进行可视化。输入为星座轨迹图,源域信噪比为10 dB,目标域信噪比为6 dB,可视化结果如图7所示。模型经过优化后,提取到的目标域特征可分性更好,体现在同一辐射源发送的信号的特征分布更紧密,不同辐射源发送的信号的特征分布边界更清晰。这是由于本文算法实现了模型迁移,使模型提取到了不同信噪比信号中“不变的”指纹特征。
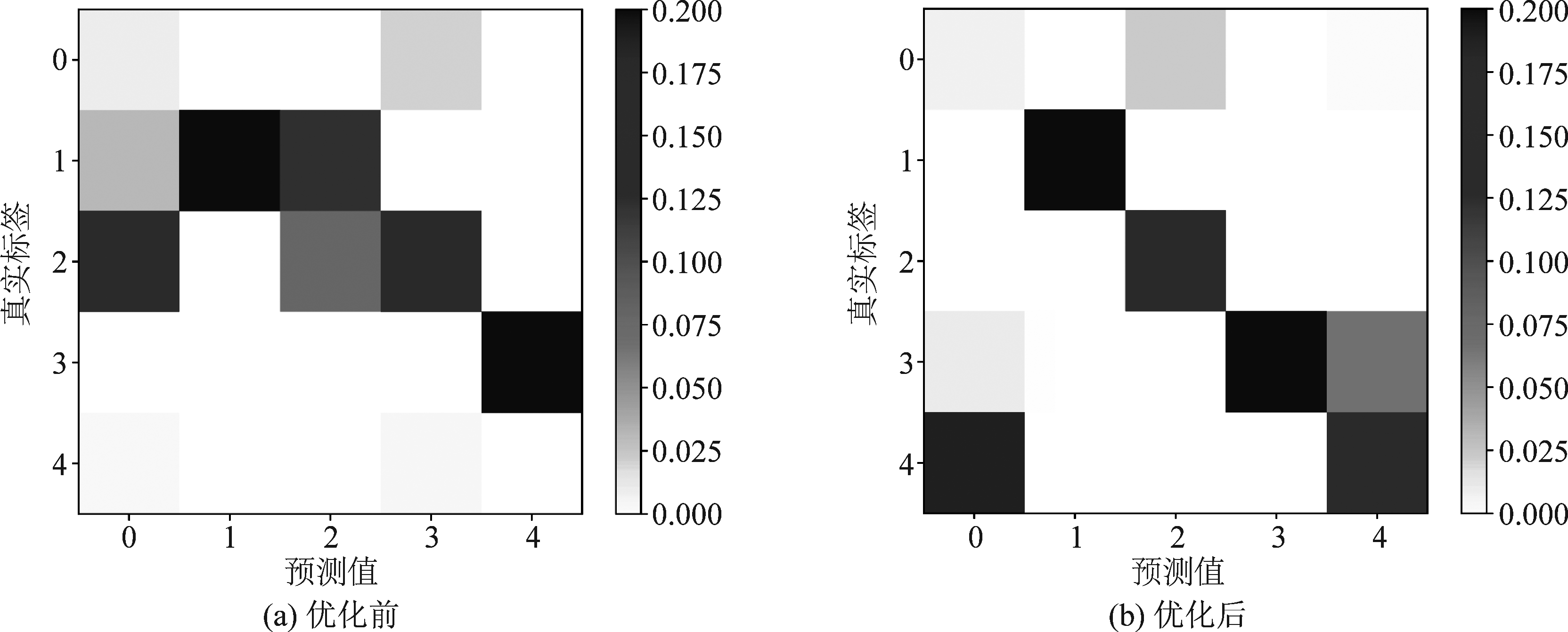
图6 本文算法优化前后的模型输出的混淆矩阵
Fig.6 The confusion matrixs of the output of the model before and after the proposed algorithm optimization
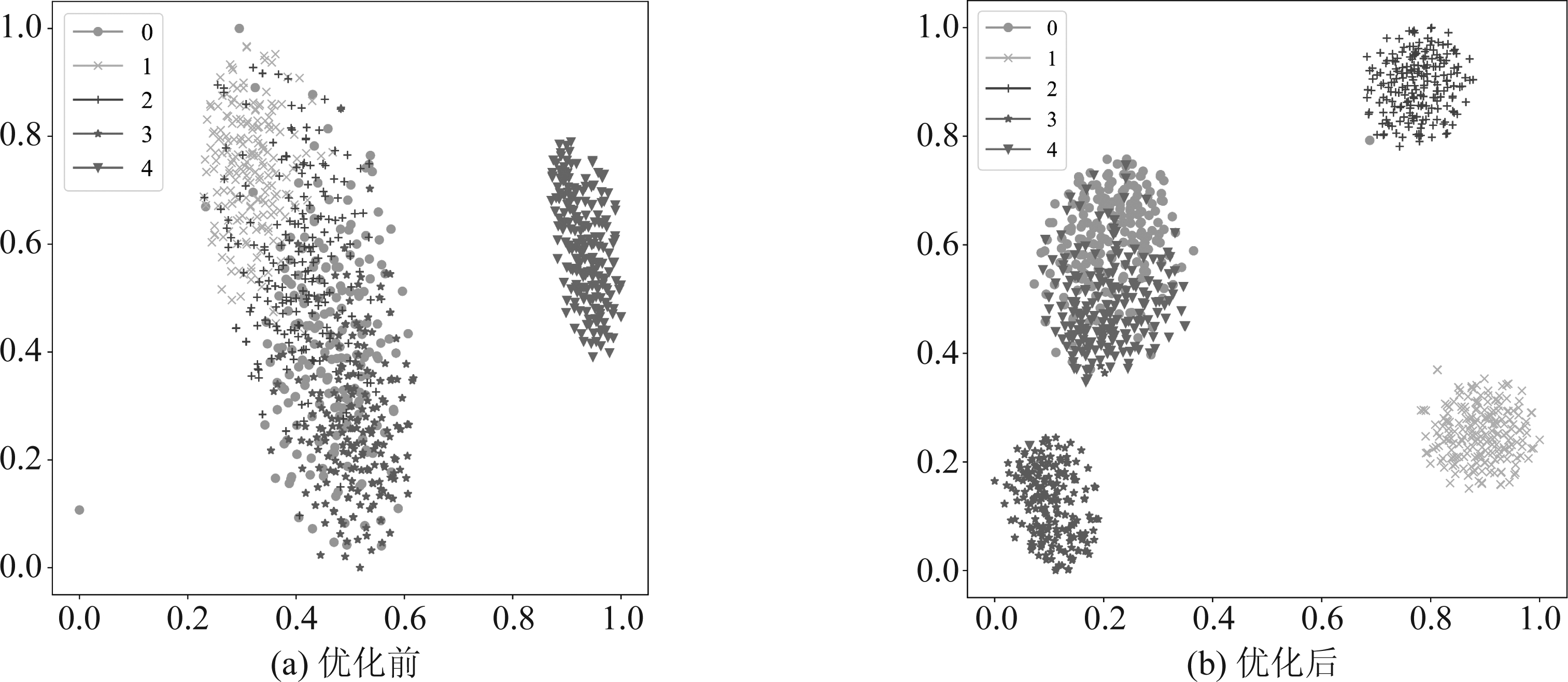
图7 本文算法优化前后的模型的第一个卷积层输出的特征分布
Fig.7 The output feature distribution of the first convolutional layer of the model before and after the proposed algorithm optimization
5 结论
针对训练信号和待测无标签信号信道噪声环境不一致导致辐射源个体识别算法性能劣化严重的问题,本文提出了一种基于领域自适应的动态噪声辐射源识别算法。该算法基于迁移学习中领域自适应的原理,同时使用有标签信号和其他信噪比下的无标签信号进行网络训练,使模型学习到不同信噪比下的信号的“不变”的射频指纹特征。仿真实验表明,本文提出的算法可以有效提升深度神经网络在动态信噪比条件下的识别准确率,对于复杂干扰场景下的辐射源个体识别算法的设计具有重要的参考价值。
[1] TALBOT K I, DULEY P R, HYATT M H. Specific emitter identification and verification [J]. Technology Review, 2003, 3: 113-133.
[2] 唐智灵, 杨小牛, 李建东. 调制无线电信号的分形特征研究[J]. 物理学报, 2011, 60(5): 556-562.
TANG Zhiling, YANG Xiaoniu, LI Jiandong. Study on fractal features of modulated radio signal[J]. Acta Physica Sinica, 2011, 60(5): 556-562.(in Chinese)
[3] HALL J, BARBEAU M, KRANAKIS E. Enhancing intrusion detection in wireless networks using radio frequency fingerprinting[C]∥Proceedings of the 3rd IASTED Conference on Communications, Internet and Information Technology, 2004. St. Thomas, USA, 2004: 201-206.
[4] ZHANG Guicai, DU Ruxu, SHI Tielin. Extracting gear fault features using integrated bispectrum[C]∥IEEE International Conference on Robotics, Intelligent Systems and Signal Processing, 2003. Proceedings. 2003. Changsha, China, IEEE, 2003: 548-553.
[5] ZHANG Jingwen, WANG Fanggang, DOBRE O A, et al. Specific emitter identification via Hilbert-Huang transform in single-hop and relaying scenarios[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(6): 1192-1205.
[6] REISING D R, TEMPLE M A, MENDENHALL M J. Improved wireless security for GMSK-based devices using RF fingerprinting[J]. International Journal of Electronic Security and Digital Forensics, 2010, 3(1): 41-59.
[7] BRIK V, BANERJEE S, GRUTESER M, et al. Wireless device identification with radiometric signatures[C]∥Proceedings of the 14th ACM International Conference on Mobile Computing and Networking-MobiCom′08. San Francisco, California, USA. New York: ACM Press, 2008: 116-127.
[8] DING Lida, WANG Shilian, WANG Fanggang, et al. Specific emitter identification via convolutional neural networks[J]. IEEE Communications Letters, 2018, 22(12): 2591-2594.
[9] PAN Yiwei, YANG Sihan, PENG Hua, et al. Specific emitter identification based on deep residual networks[J]. IEEE Access, 2019, 7: 54425-54434.
[10] PENG Linning, ZHANG Junqing, LIU Ming, et al. Deep learning based RF fingerprint identification using differential constellation trace figure[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 1091-1095.
[11] 潘一苇, 杨司韩, 彭华, 等. 基于矢量图的特定辐射源识别方法[J]. 电子与信息学报, 2020, 42(4): 941-949.
PAN Yiwei, YANG Sihan, PENG Hua, et al. Specific emitter identification using signal trajectory image[J]. Journal of Electronics & Information Technology, 2020, 42(4): 941-949.(in Chinese)
[12] 贾永强. 通信辐射源个体识别技术研究[D]. 成都:电子科技大学, 2017.
JIA Yongqiang. The research on communication emitters identification technology[D]. Chengdu: University of Electronic Science and Technology of China, 2017.(in Chinese)
[13] TANG Hui, CHEN Ke, JIA Kui. Unsupervised domain adaptation via structurally regularized deep clustering[C]∥2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle, WA, USA, IEEE, 2020: 8722- 8732.
[14] XIE Junyuan, GIRSHICK R, FARHADI A. Unsupervised deep embedding for clustering analysis[C]∥Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 2016: 478- 487.
[15] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA, IEEE, 2016: 770-778.
[16] VAN DER MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(11): 2579-2605.
