1 引言
在5G大规模物联网连接中,在任何给定时刻,只有一小部分(未知)设备处于活动状态[1];因此,提供大规模物联网连接的关键挑战之一是首先检测活动设备,然后以低延迟解码它们的数据[2]。非正交多址接入(Non-Orthogonal Multiple Access,NOMA)被认为是未来5G系统的关键技术之一。在上行链路无授权NOMA方案中,不需要动态调度,这可以显著降低信令开销和传输延迟[3- 4]。
当考虑大规模机器通信时,由于处于活动状态的设备数量少,大规模接入信道矩阵呈现出稀疏性[5- 6],我们可以利用压缩感知(Compressed Sensing,CS)理论来解决信道估计和活动用户检测问题。CS中,与输入信号的稀疏度成比例的测量值足以重建原始信号[7-9]。CS中有许多稀疏恢复算法,在文献[10]中作者提出了一种近似消息传递(Approximate Message Passing,AMP)算法,AMP是一种针对大规模压缩感知问题设计的有效迭代阈值方法,这使得它对大规模物联网连接场景具有吸引力。针对信道估计(Channel Estimation,CE)和活动用户检测(Active User Detection,AUD)问题,文献[11]的作者在反向散射通信系统采用AMP算法取得了良好的效果,但是性能仍有改进的空间;文献[5]中作者采用期望最大-贝叶斯AMP(Expectation Maximization Bayesian Approximate Message Passing,EM-B-AMP)算法,取得了优异的效果。这是因为期望最大(Expectation Maximization,EM)算法可以获得恢复量的先验知识[12],从而提高了AMP性能,但是这是以增加算法复杂度为代价的。
针对NOMA的联合信道估计和多用户检测问题,本文在文献[11]中采用的AMP算法基础上,提出一种新的压缩感知重建算法——阈值自适应-加约束重加权-近似消息传递算法(Threshold Adaptive Constrained Reweighted Approximate Message Passing,TA-CR-AMP)。该算法在合适的迭代终止准则下,对AMP加入了更新稀疏信号稀疏结构的操作;改进文献[13]中的重加权思想,在算法中引入加约束的重加权机制,并令阈值自适应变化。仿真结果表明,本文提出的TA-CR-AMP算法在复杂度占优的条件下,信道估计误差和活动用户检测成功率明显超过了文献[11]中的AMP算法;同样在复杂度明显占优的情况下,信道估计误差和活动用户检测成功率最终可以接近文献[5]中的EM-B-AMP算法。
2 NOMA系统的信道估计和多用户检测模型
在上行NOMA系统中,我们假设有一个基站和K个用户。为了简单但不失一般性,假设基站和所有用户都配备有单个天线。在信道编码和映射后,活跃用户的发送符号xk被调制到长度为N的扩频序列sk上。特别地,我们考虑N<K的情况,即过载系统。之后,来自所有活动用户扩频后的信号均在正交频分复用系统N个子载波上进行传输,即这些传输信号是重叠的。对于典型的大规模接入场景,在给定的时间间隔内,只有少数用户设备被激活并试图接入基站。本文假设一帧内含有L个时隙,用户在这L个时隙中保持同步,也就是一帧内用户的活动状态保持不变。每个活跃用户,在第1个时隙首先发送一个导频符号,接着在后面L-1个时隙发送数据符号。此外,我们假设系统为平坦瑞利衰落信道,也就是一帧内的信道状态保持不变。
本文考虑用户设备发送导频符号用于信道估计,我们假设用户设备活动指示符表示为αk,当第k个用户设备活动时等于1,否则等于0。同时,我们将活动用户设备集定义为A={k|αk=1,1≤k≤K},活动用户设备的总数量用Ka表示。则基站子载波n上的接收信号可以表示为:
(1)
其中,snk是扩频序列sk的第n个分量,根据独立同分布(Independent and identically distributed,iid)的标准复高斯分布产生,hnk是第k个用户在第n个子载波上的信道增益,νn是第n个子载波上的复高斯噪声。我们组合所有N个子载波上的接收信号,然后接收信号y=[y1,y2,...,yN]T∈CN×1可以表示为:
(2)
其中,sk=[s1,k,s2,k,...,sN,k]T∈CN×1是用户k对应的扩频序列,S=[s1,s2,...,sK]∈CN×K是扩频矩阵,h=[α1h1,α2h2,...,αkhK]T∈CK×1是信道系数向量,x=[x1,x2,...,xK]T∈CK×1是发送的导频符号向量,v∈CN×1是服从复高斯分布的噪声向量。
我们设导频符号向量x=[x1,x2,...,xK]T∈CK×1中的导频符号xk为1,则公式(2)可以继续化为:
y=Sdiag(h)x+v=Sh+v
(3)
其中y∈CN×1,S∈CN×K,h∈CK×1以及v∈CN×1。
由于在一定的时间内,仅有少量用户处于活动状态,向量h呈现稀疏特性,公式(3)中,系统的信道估计和活动用户检测的任务就是由已知接收信号y和扩频序列矩阵S来估计向量h,该问题可以转化为CS稀疏信号重建问题。
3 TA-CR-AMP算法的联合信道估计和多用户检测
传统的AMP是解决大规模压缩感知问题的有效方法,但在性能上具有很大的改进空间,而EM-B-AMP算法相较于传统AMP虽然在性能上有了很大提升,但EM算法的加入无疑大大增大了算法的复杂度。这时,文献[13]重加权的思想便起到了重要作用,本文首先在传统AMP基础上结合了重加权思想,结合后的算法可以称为重加权-近似消息传递(Reweighted Approximate Message Passing,R-AMP)算法。重加权的主要思想是“大值缓慢变化,小值快速衰减”,因为压缩感知的信号重构具有较大元素的重构概率和重构精度均高于较小元素的特点,因此重加权可以提高信号重构能力。重加权是对阈值进行重加权,借助传统AMP算法的软阈值函数定义式(传统AMP算法流程可见文献[10]),可以设计出对应的权值,从而使信号h中模值较大的元素缓慢变化,较小的元素快速衰减为0,实现更准确的CE和AUD。
重加权的思想对提升算法性能起了很大帮助,虽然它不会像EM-B-AMP算法一样明显的增大算法复杂度,但性能的提升总会带来复杂度的上升,因此本文接着对重加权进行恰当的改进来减少该副作用。重加权的主要思想是“大值缓慢变化,小值快速衰减”,但是当算法刚开始运行时,即重建精度比较低时,信号h模值中的“大值”可能还不是我们所需要的“大值”,同理“小值”也是如此。如果此时就进行重加权可能会适得其反,使算法性能会短暂恶化。因此,我们在重加权前加入了约束条件,当算法满足约束条件,即重建精度比较高时,才让算法执行重加权。本文称加了约束后的算法为加约束重加权-近似消息传递(Constrained Reweighted Approximate Message Passing,CR-AMP)算法。这样可以避免算法在重建精度比较低时而进行重加权而导致误差的短暂上升,从而在保证提升算法重建性能的前提下,可以使算法更快的收敛,一定程度上降低算法的复杂度。
为了进一步降低算法复杂度,本文又加入了阈值自适应,阈值自适应实际上是阈值控制参数自适应。根据传统AMP算法流程,当AMP算法不断迭代过程中,精度在不断提高,残差在不断减小,因此阈值在不断减小,但是阈值控制参数是不变的。因此,为了降低算法复杂度,本文使阈值控制参数在一定范围内随着迭代而逐渐上升,因此阈值也会上升,而阈值的上升会带来一定的性能恶化,这是为了降低算法复杂度而要付出的代价,但是这是可控的。本文借助传统AMP的软阈值函数定义式构造出一个变量,使它作用于阈值控制参数,使得阈值控制参数可以缓慢上升。因为阈值控制参数不断上升会降低算法重建精度,所以在进行阈值自适应前,也要加一个约束条件,这个约束条件与重加权的约束条件类似,区别在于,阈值自适应的约束条件是让算法一开始就进行阈值自适应,而当算法达到比较高的重建精度后,便停止阈值控制参数增大。因为越高的重建精度,需要越低的阈值,如果此时还让阈值控制参数上升,势必会恶化算法重建质量。
对传统AMP算法改进后,本文提出的TA-CR-AMP算法流程如下:
输入:接收矩阵y,扩频序列矩阵S,最大迭代次数num。
输出:重建稀疏信号h=[α1h1,α2h2,...,αkhK]T∈CK×1。
步骤:
(1)初始化参数:阈值控制参数λ=1;稀疏信号h0=0,残差Z0=y;
权值βk=1,归一化权值Bk=βk/〈β〉,〈·〉表示求平均数,其中k=1,2,...,K,β=[β1,β2,...,βK]T∈CK×1;
(2)开始迭代:令迭代次数m=0;
(3)更新稀疏信号:
其中k=1,2,...,K,n=1,2,...,N;λ σmBk整体称为阈值,
称为阈值函数,我们这里采用常见的软阈值函数表达式,即
其中
(4)更新残差:
其中k=1,2,...,K,n=1,2,...,N;B=[B1,B2,...,BK]T∈CK×1,δ称为欠采样率,
为ηm(·)的一阶导数,〈·〉表示求平均数;我们将更新的估计值hm+1代入更新残差的式子中,化简后更新残差的式子可以等效为
其中
(5)更新稀疏信号的稀疏结构:对于k=1,2,...,K,如果
则令
其中ω>0,且ω是一个接近于0的值;
(6)判断是否进入阈值自适应:当满足(||y-Shm+1
)2>μ(||y)2时,其中0<μ<1,进入第7步,执行阈值自适应;否则进入第8步,判断是否满足约束条件,从而判断是否进入重加权;
(7)阈值自适应:对于k=1,2,...,K,计算
其中p=[p1,p2,...,pK]T∈CK×1;更新阈值控制参数
可能会有0值,在计算的时候要消去;
(8)根据约束条件,判断是否进入重加权:当满足(||y-Shm+1)2<ε(||y)2时,其中0<ε<1,进入第9步,执行重加权,否则进入第10步;
(9)重加权:对于k=1,2,...,K,更新权值
更新归一化权值Bk=βk/〈β〉。其中β=[β1,β2,...,βK]T∈CK×1,〈·〉表示求平均数,τ是一个正的更新因子;
(10)判断迭代停止条件:如果满足||hm+1-hm/||hm+1<φ或m>num,则停止迭代,否则进入第11步;
(11)更新迭代次数:m=m+1,返回第(3)步。
算法步骤中参数ω,μ,ε,τ的具体取值可以根据信噪比的变化调试所得,我们仿真时发现随着信噪比的提高,这些参数的最佳取值会逐渐减小。
算法步骤中(1)、(2)、(3)、(4)、(10)、(11)等步骤可以组成传统的AMP算法流程,相关的推导可以从文献[10]得到。本文提出的TA-CR-AMP算法在其基础上主要增加了步骤(5)～ (9),其中(8)、(9)两步为改进的重加权,(6)、(7)两步为自适应阈值,另外本文还额外增加了第(5)步,来更新估计的稀疏信号的稀疏结构,根据ω的取值,可以将一些非常小的值直接归0,从而提高了用户活跃检测成功率和信道估计准确性。
由于h=[α1h1,α2h2,...,αkhK]T∈CK×1,利用TA-CR-AMP算法恢复出h后也就得到了信道状态信息hk和用户信息αk,所以本文提出的算法可以用来联合解决CE和AUD问题。
4 仿真结果和分析
本文使用Matlab2019a进行仿真实验,电脑配置如下:16 GB RAM、1.00 GHz 的I5-1035G1 CPU。我们假设扩频序列的长度为96,即N=96;潜在用户数为K=200;激活用户数Ka=24;扩频序列是独立同分布的复高斯序列;信道为平坦瑞利衰落信道;最大迭代次数num=30,以下仿真的所有算法根据误差准则||hm+1-hm/||hm+1<φ来停止迭代,其中φ=0.04,然后在不同的条件下每次仿真进行1000次,取平均值得出各个情况下的仿真结果。我们从信道估计均方误差(Mean Square Error,MSE)、成功活跃检测率(Successful Activity Detection Rate,SADR)、算法的复杂度等方面对不同算法进行比较。
MSE的计算表达式为:
(4)
I是仿真的次数,h为信道系数向量,
为估计的信道系数向量。
SADR的计算表达式为:
(5)
其中
的计算公式为:
(6)
I是仿真的次数,αk为用户设备活动指示符,
为估计的用户设备活动指示符。
下面比较本文提出的TA-CR-AMP算法与AMP以及EM-B-AMP算法进行稀疏信号重建的性能。在复杂度比较时,本文还加入了R-AMP与CR-AMP算法,来体现对重加权加约束的优势。比较时,除了本文提出的TA-CR-AMP算法, AMP、R-AMP、CR-AMP以及EM-B-AMP算法都加入了本文算法步骤中的第(5)步,即更新稀疏信号的稀疏结构,这样可以提高这几个算法的用户活跃检测成功率和信道估计准确性。
4.1 MSE性能分析
本节比较三种算法在不同参数下的信道估计MSE大小。
图1为不同信噪比下各种算法信道估计MSE性能曲线。由仿真曲线可知,EM-B-AMP算法在中高信噪比时,相较于AMP有较明显优势;而本文提出的TA-CR-AMP算法在信道估计的MSE性能上相较于AMP算法在各种信噪比上都有较明显的提升,并且在中高信噪比时可以接近EM-B-AMP算法。
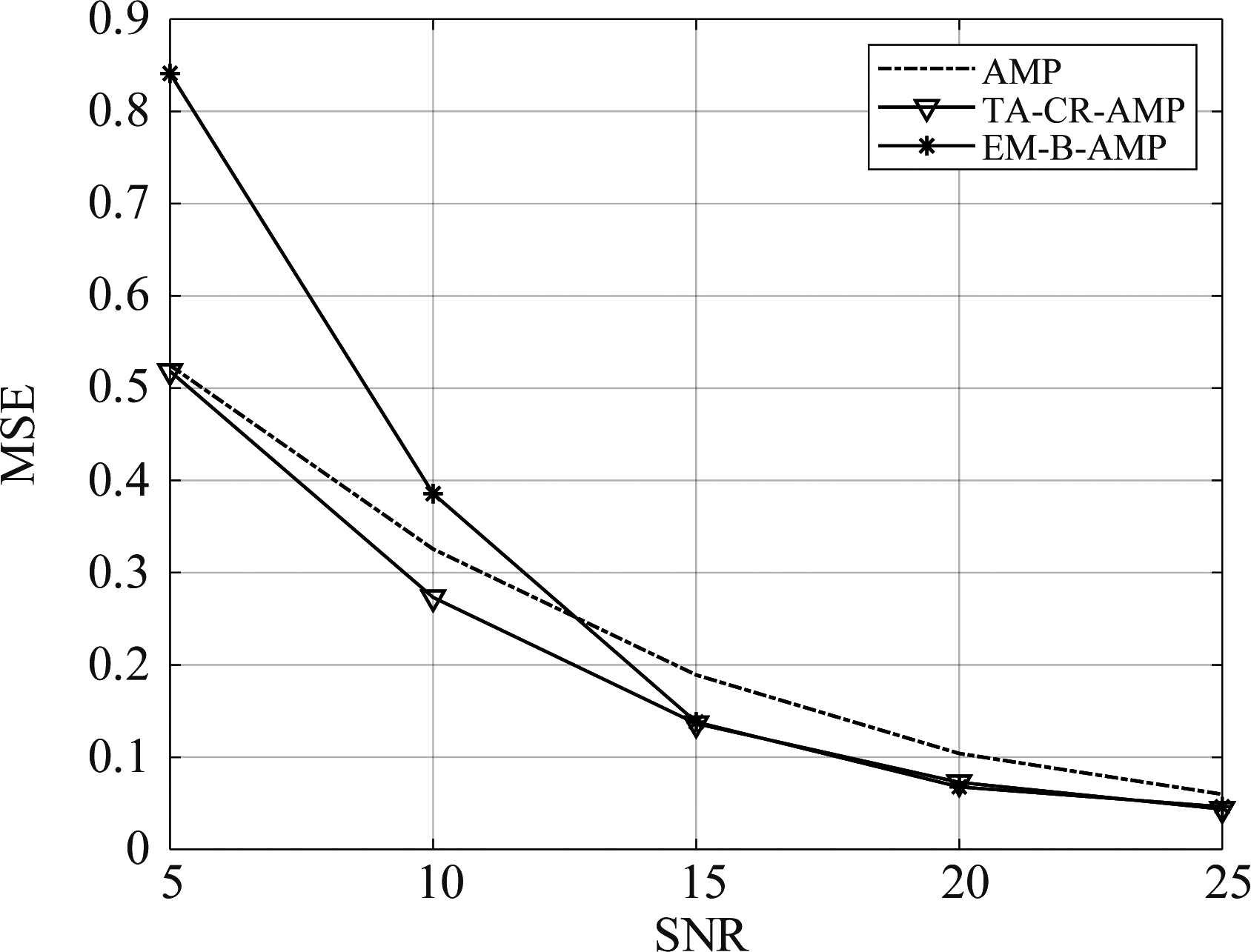
图1 不同信噪比下各种算法信道估计MSE性能比较
Fig.1 Comparison of MSE performance of various algorithms under different SNR
图2比较了15 dB时不同扩频序列长度下各种算法信道估计MSE性能。由仿真曲线可知,在各种扩频序列长度下,本文提出的TA-CR-AMP算法明显好于AMP,且在扩频序列长度较大情况下信道估计的MSE性能可以逼近EM-B-AMP。
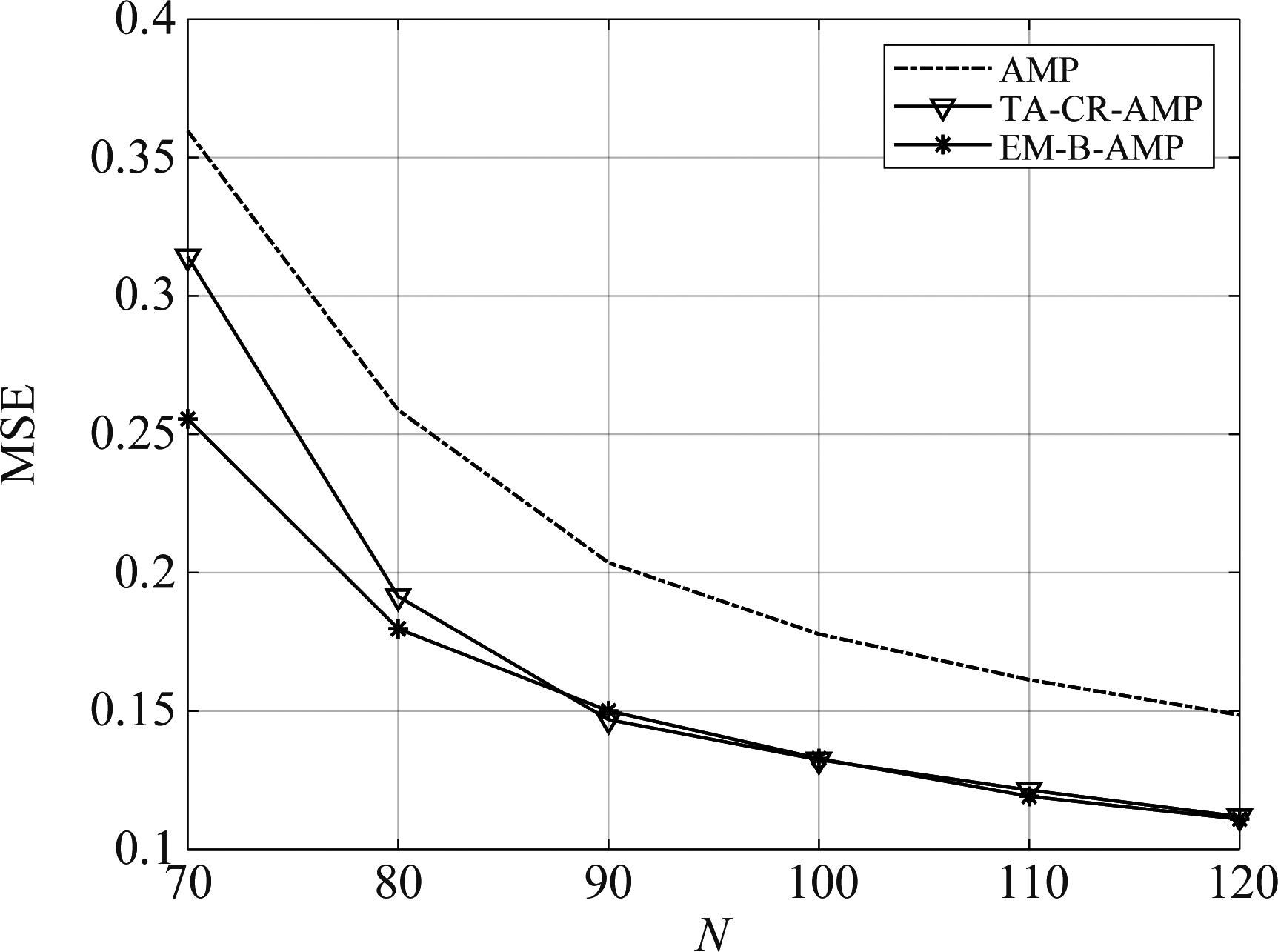
图2 15 dB时不同扩频序列长度下各种算法信道估计MSE性能比较
Fig.2 Comparison of MSE performance of various algorithms under different spreading sequence lengths at 15 dB
图3为15 dB时不同激活用户数下各种算法信道估计MSE性能比较图。由仿真曲线可知,在各种激活用户数下,本文提出的TA-CR-AMP算法的MSE性能会明显优于AMP;此外还发现大约在激活用户数为15时,TA-CR-AMP与EM-B-AMP两条曲线在此处相交,在此交点后TA-CR-AMP的MSE性能会略好于EM-B-AMP,可见在保证激活用户数少量的前提下,提高激活用户数对EM-B-AMP的影响较大。原因可能是EM-B-AMP算法通过EM算法估计了先验知识,而其中先验知识包括了稀疏率,稀疏率的定义为
其中Ka未知,因此稀疏率是未知的。利用EM算法估计稀疏率的公式见文献[6]的公式(37), 由这公式可以得出稀疏率主要由扩频长度与潜在用户数决定,当激活用户数Ka改变时,稀疏率依然不变,可见这是一个粗略的估计,因此这会对EM-B-AMP算法的性能带来一定影响。虽然文献[6]中EM-B-AMP算法的后部分,利用EM算法对稀疏率进行了更新,起到了一定矫正作用,但这粗略的初始化带来的影响是不能轻易消除的。
TA-CR-AMP算法获得较好性能的原因是它引入了重加权的思想,导致稀疏信号中较大的元素会变化缓慢,较小的元素会快速衰减为0,有效的降低了信道估计误差。
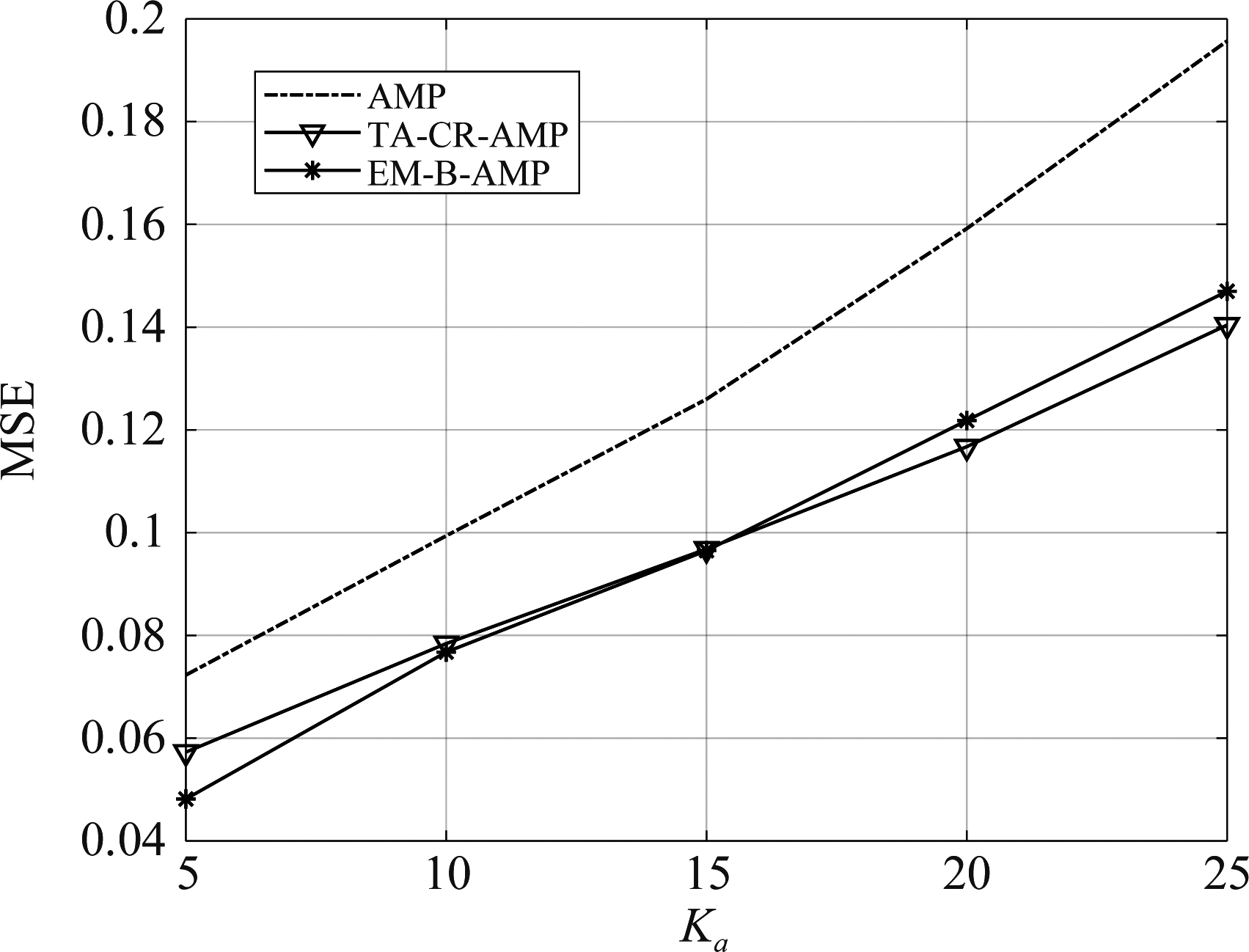
图3 15 dB时不同激活用户数下各种算法信道估计MSE性能比较
Fig.3 Comparison of MSE performance of various algorithms under different number of active users at 15 dB
4.2 SADR性能分析
本节比较不同算法在不同信噪比下SADR的仿真结果,如图4所示。仿真结果表明: EM-B-AMP算法在中高信噪比时,相较于AMP有较明显优势,而本文提出的TA-CR-AMP算法在SADR性能上相较于AMP算法在各种信噪比上都有较明显的提升,并且在中高信噪比时可以接近EM-B-AMP算法。
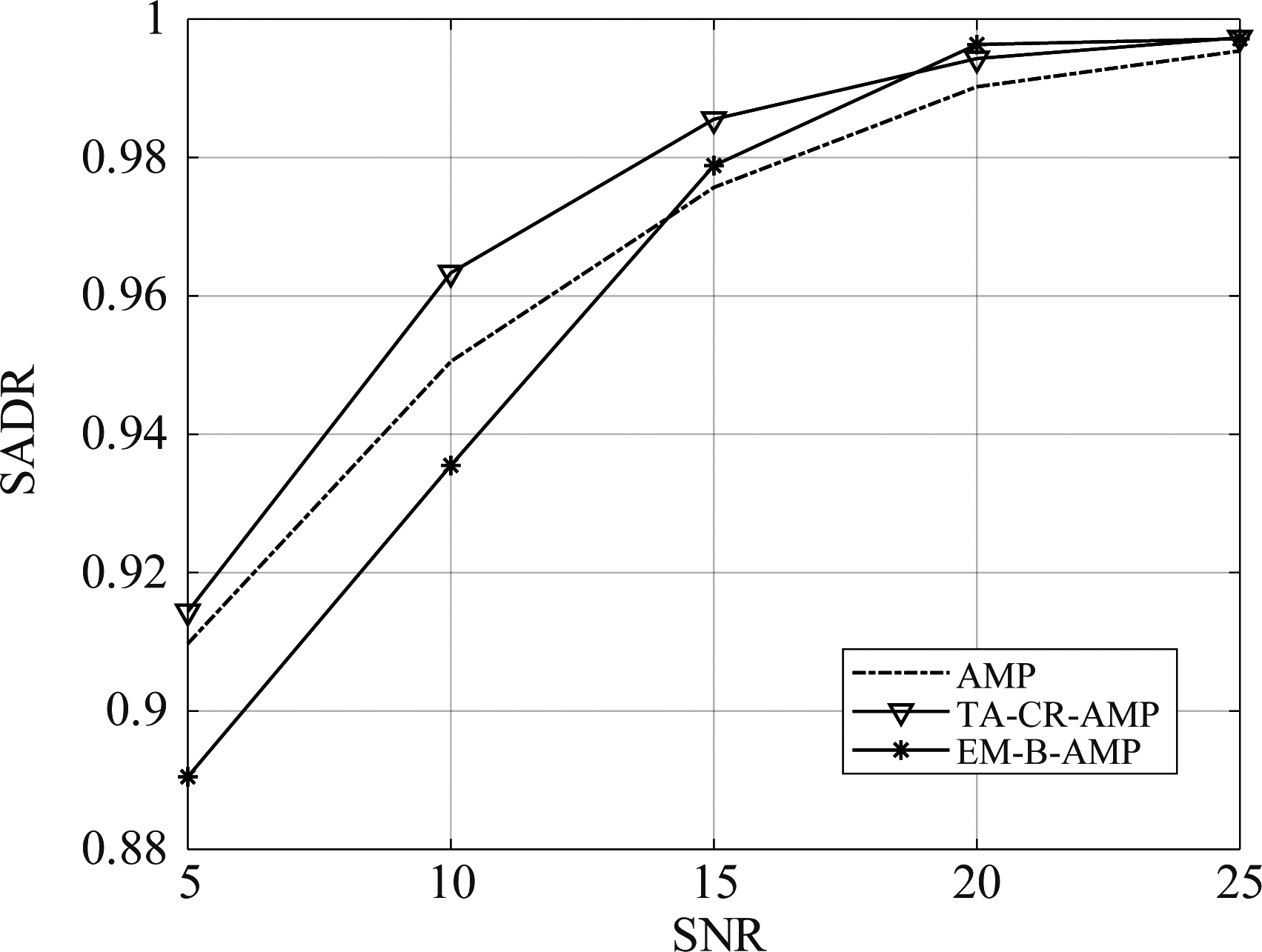
图4 不同信噪比下各种算法SADR性能比较
Fig.4 Comparison of SADR performance of various algorithms under different SNR
4.3 复杂度分析
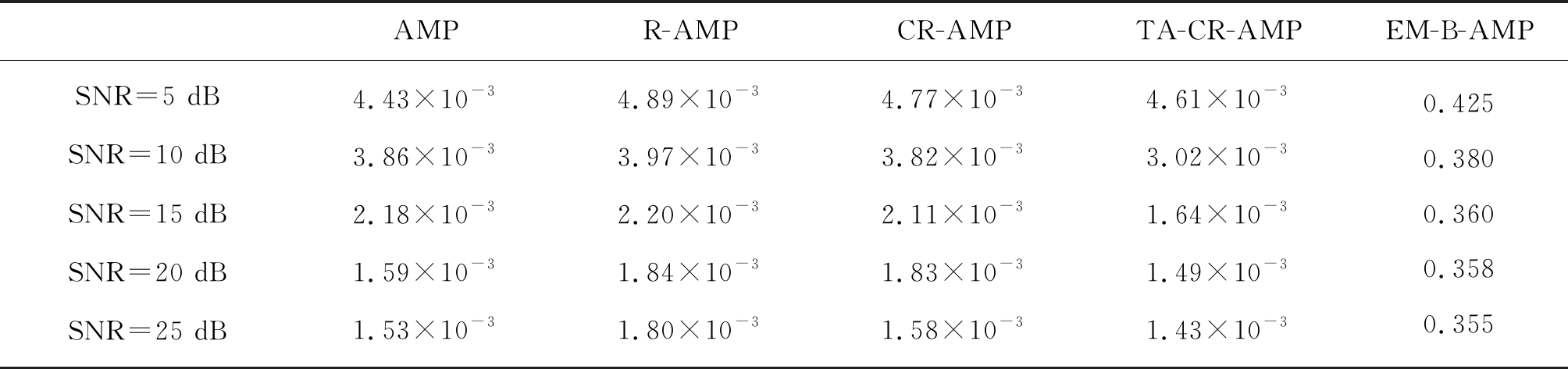
表1列出了不同信噪比下AMP、R-AMP、CR-AMP、TA-CR-AMP、EM-B-AMP五种算法单次运行的平均时间。我们可以看出R-AMP的运行时间较明显大于AMP,然而CR-AMP因为对重加权进行了约束,减少了运行时间,并与AMP相差不大。TA-CR-AMP 因为在CR-AMP基础上又引入了阈值自适应,使运行时间较明显小于AMP算法,此外TA-CR-AMP的运行时间明显小于EM-B-AMP算法。由此可见,在这五种算法中,TA-CR-AMP的复杂度是最低的。
表1 不同信噪比下三种算法的运行时间比较(单位:秒)
Tab.1 Comparison of the running time of the three algorithms under different SNR (unit: second)
AMPR-AMPCR-AMPTA-CR-AMPEM-B-AMPSNR=5 dBSNR=10 dBSNR=15 dBSNR=20 dBSNR=25 dB4.43×10-33.86×10-32.18×10-31.59×10-31.53×10-34.89×10-33.97×10-32.20×10-31.84×10-31.80×10-34.77×10-33.82×10-32.11×10-31.83×10-31.58×10-34.61×10-33.02×10-31.64×10-31.49×10-31.43×10-30.4250.3800.3600.3580.355
下面比较AMP、R-AMP、CR-AMP、TA-CR-AMP四种算法停止迭代的次数,进一步说明本文提出的TA-CR-AMP算法运行时间少的原因。我们分别在5 dB、15 dB、25 dB三个信噪比条件下比较了四种算法MSE随迭代次数的收敛情况,结果如图5、图6和图7所示。通过仿真可以发现,5 dB时,四种算法都达到了最大迭代次数30次,说明此时对重加权加约束的影响不大,并且为了防止算法性能恶化,算法并没有执行阈值自适应操作;15 dB时,AMP在迭代15次停止,R-AMP在迭代19次停止,CR-AMP在迭代15次停止,而TA-CR-AMP在迭代11次停止;25 dB时,AMP在迭代10次停止,R-AMP在迭代14次停止,CR-AMP在迭代11次停止,而TA-CR-AMP在迭代8次停止。此外,三幅图中都可以看出R-AMP会出现短暂的“尖峰”,CR-AMP因为对重加权加了约束削去了“尖峰”,减少了因误差短暂上升而花费的时间,这也是CR-AMP比R-AMP复杂度低的原因。从而可以得出结论:在中、高信噪比上,本文提出的TA-CR-AMP停止迭代次数较明显小于AMP算法,从而可以有效降低算法复杂度。这是因为本文的算法在重加权前加入了约束条件,同时阈值自适应发挥了主要作用,从而使算法更快收敛。
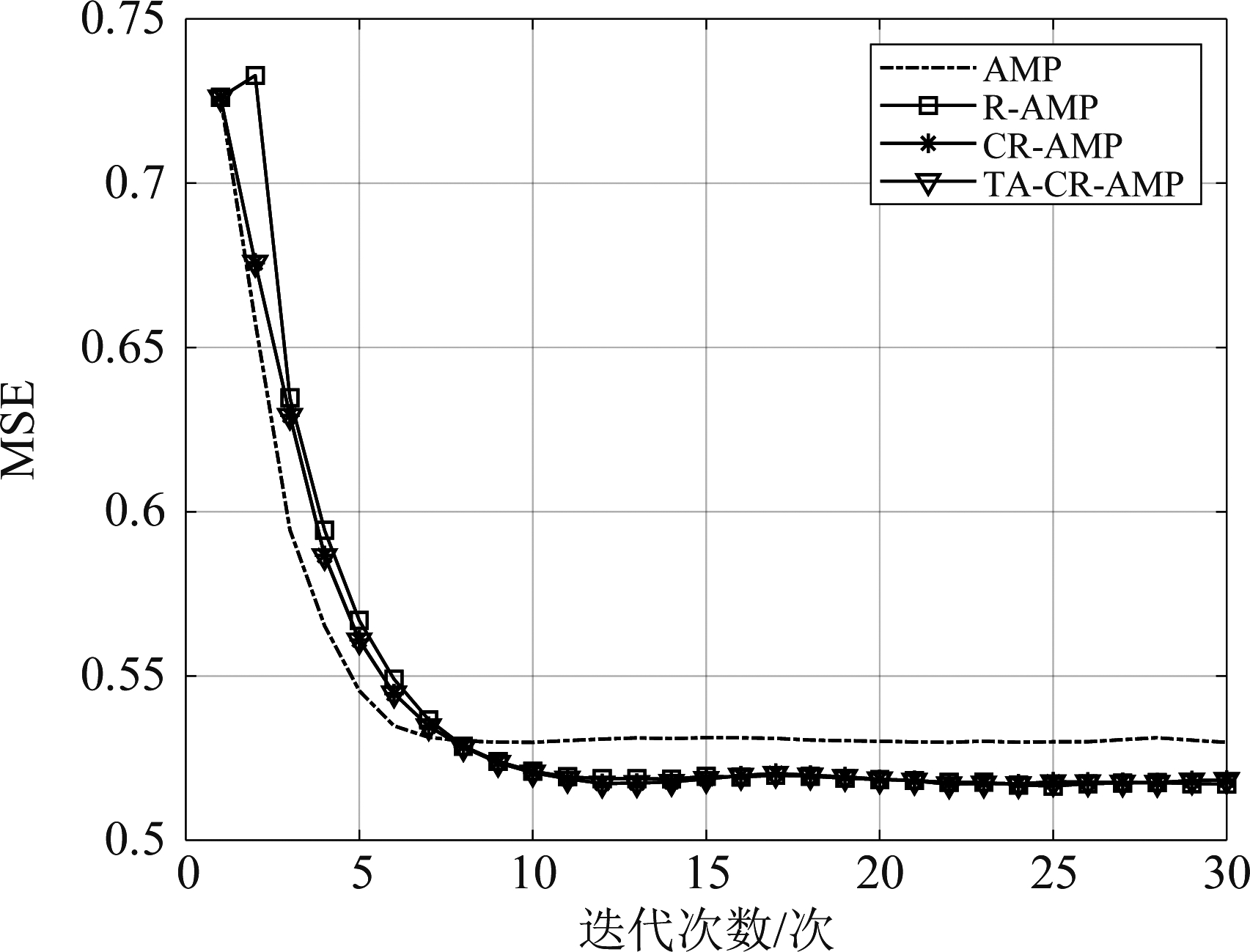
图5 5 dB时各种算法的收敛情况
Fig.5 Convergence of various algorithms at 5 dB
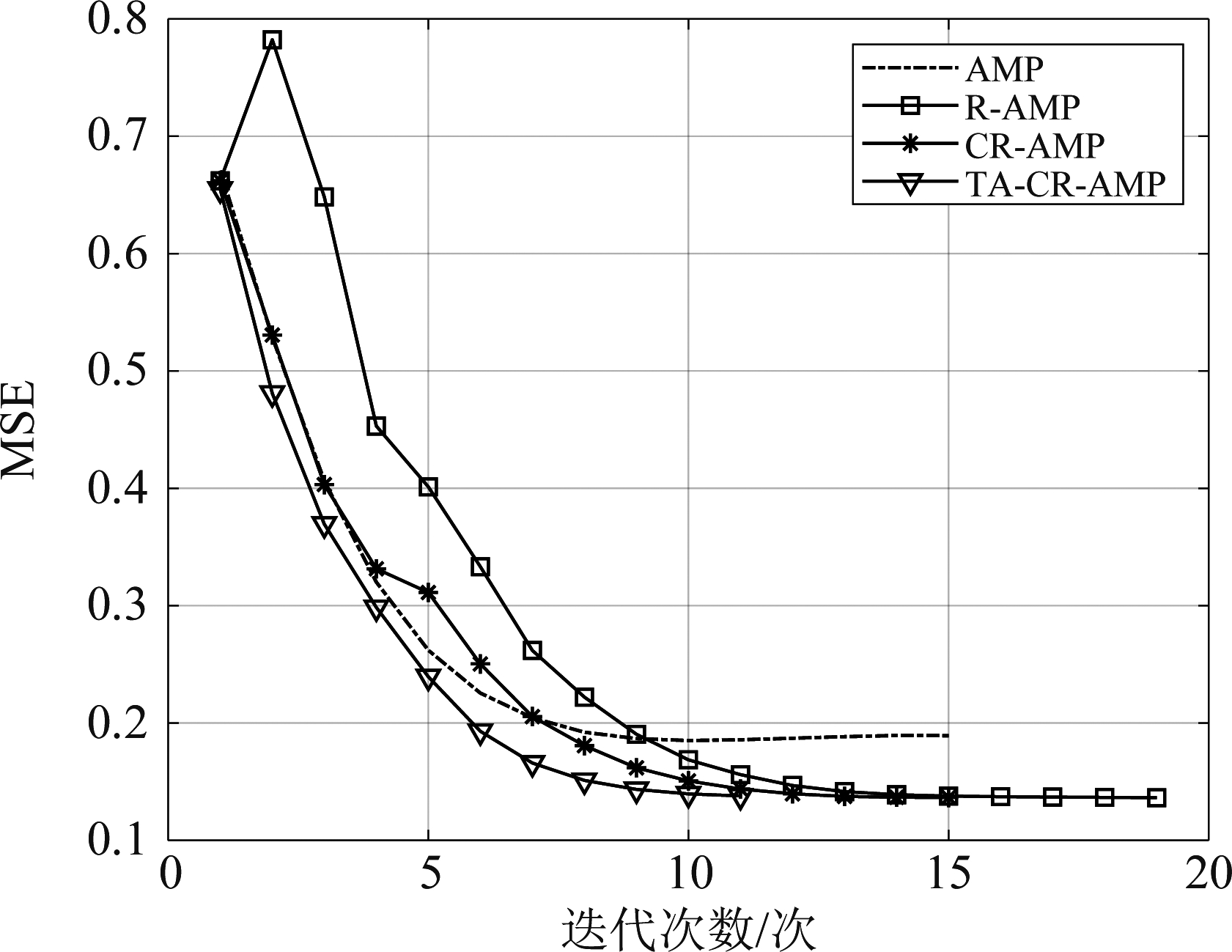
图6 15 dB时各种算法的收敛情况
Fig.6 Convergence of various algorithms at 15 dB
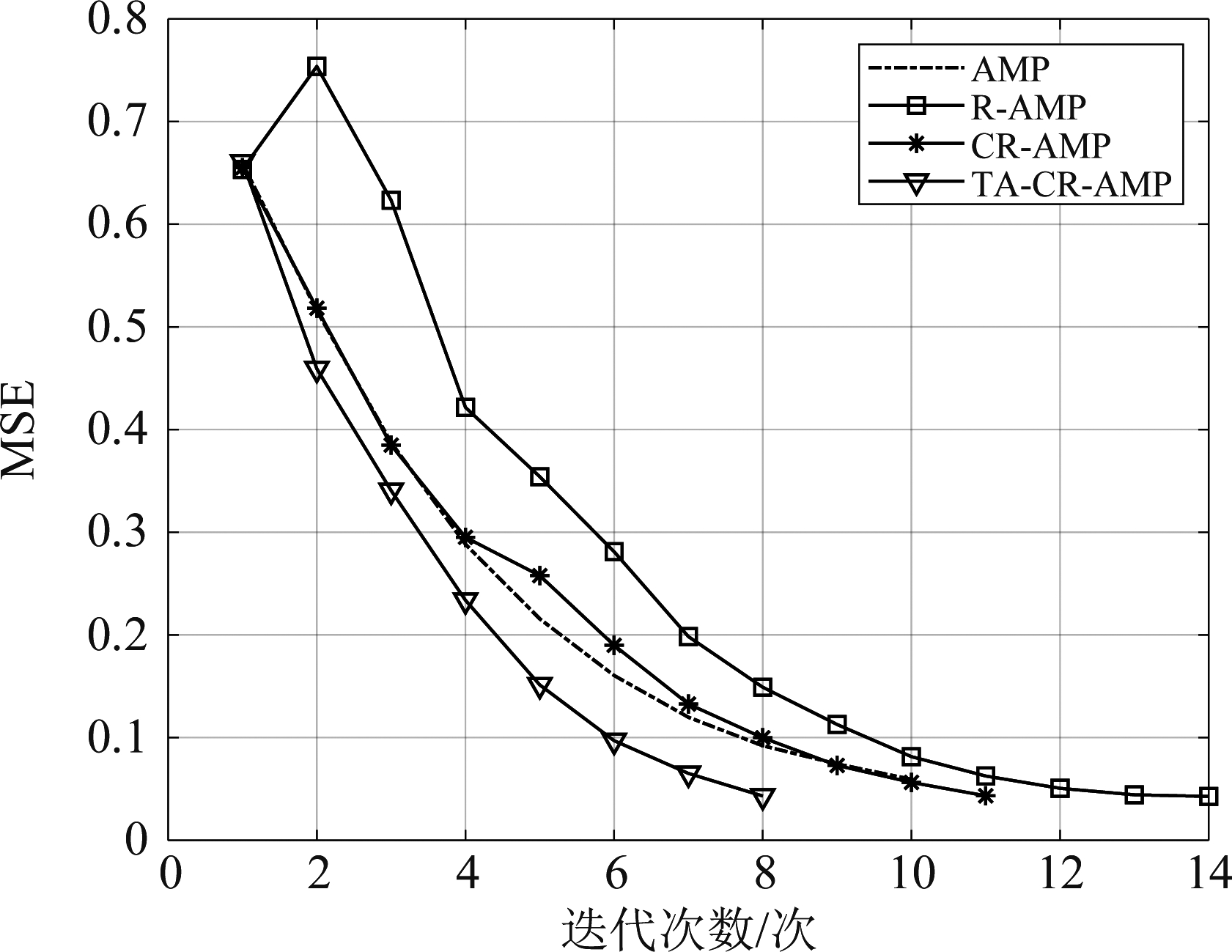
图7 25 dB时各种算法的收敛情况
Fig.7 Convergence of various algorithms at 25 dB
5 结论
本文针对免调度NOMA系统,提出了一种阈值自适应-加约束重加权-近似消息传递(TA-CR-AMP)算法联合进行信道估计和活动用户检测。本文提出的算法在AMP算法基础上加入了更新稀疏信号的稀疏结构的操作,在此基础上对算法引入了加约束的重加权,并令阈值自适应变化。对阈值进行重加权,提高了算法重建稀疏信号的性能;同时在重加权前加入约束条件,又引入了阈值自适应,使得阈值控制参数缓慢上升一段时间,从而减少算法停止迭代次数,降低了算法的复杂度。仿真结果表明,在上行免调度NOMA系统的联合CE和AUD问题中,TA-CR-AMP算法在运算复杂度占优的情况下,明显超过了AMP算法的性能;同时,它以极低的运算复杂度接近EM-B-AMP的信道估计误差和活动用户检测成功率。
本文提出的TA-CR-AMP算法是解决单一测量向量(single-measurement vector,SMV)问题的,这是因为本文是在解决SMV问题的AMP算法上进行改进的。但是只要在解决多重测量向量(Multiple-measurement vector,MMV)问题的AMP算法上,进行类似于本文的改进,就可以得到解决MMV问题的TA-CR-AMP算法,便可以应用到类似于多输入多输出(Multi Input Multi Output,MIMO)通信的系统中,进行联合活动用户检测与数据检测,这也是我们未来要进行的研究方向。
[1] SENEL K, LARSSON E G. Grant-free massive MTC-enabled massive MIMO: A compressive sensing approach[J]. IEEE Transactions on Communications, 2018, 66(12): 6164- 6175.
[2] LIU Liang, LARSSON E G, YU Wei, et al. Sparse signal processing for grant-free massive connectivity: A future paradigm for random access protocols in the Internet of Things[J]. IEEE Signal Processing Magazine, 2018, 35(5): 88-99.
[3] WANG Bichai, DAI Linglong, MIR T, et al. Joint user activity and data detection based on structured compressive sensing for NOMA[J]. IEEE Communications Letters, 2016, 20(7): 1473-1476.
[4] 凤丽丽, 何雪云, 孙林慧. NOMA系统基于自适应匹配追踪算法的联合信道估计与多用户检测新方法[J]. 信号处理, 2020, 36(7): 1136-1143.
FENG Lili, HE Xueyun, SUN Linhui. A new method of joint channel estimation and multiuser detection based on adaptive matching pursuit algorithm in NOMA system[J]. Journal of Signal Processing, 2020, 36(7): 1136-1143.(in Chinese)
[5] KE Malong, GAO Zhen, WU Yongpeng, et al. Compressive massive random access for massive machine-type communications (mMTC)[C]//2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP). Anaheim, CA, USA. IEEE, 2018: 156-160.
[6] KE Malong, GAO Zhen, WU Yongpeng, et al. Compressive sensing-based adaptive active user detection and channel estimation: Massive access meets massive MIMO[J]. IEEE Transactions on Signal Processing, 2020, 68: 764-779.
[7] KHOBAHI S, SOLTANALIAN M. Model-based deep learning for one-bit compressive sensing[J]. IEEE Transactions on Signal Processing, 2020, 68: 5292-5307.
[8] LOTFI M, VIDYASAGAR M. A fast noniterative algorithm for compressive sensing using binary measurement matrices[J]. IEEE Transactions on Signal Processing, 2018, 66(15): 4079- 4089.
[9] 李周, 崔琛. 压缩感知中观测矩阵的优化算法[J]. 信号处理, 2018, 34(2): 201-209.
LI Zhou, CUI Chen. An optimization algorithm for observation matrix in compressive sensing[J]. Journal of Signal Processing, 2018, 34(2): 201-209.(in Chinese)
[10]DONOHO D L, MALEKI A, MONTANARI A. Message-passing algorithms for compressed sensing[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(45): 18914-18919.
[11]马俊. 环境反向散射通信系统中的活跃用户检测和信道估计[D]. 成都: 电子科技大学, 2020.
MA Jun. Research on active device detection and channel estimation of ambient backscatter systems[D]. Chengdu: University of Electronic Science and Technology of China, 2020. (in Chinese)
[12]LIU Liang, YU Wei. Massive connectivity with massive MIMO—part I: Device activity detection and channel estimation[J]. IEEE Transactions on Signal Processing, 2018, 66(11): 2933-2946.
[13]ZEINALKHANI Z, HAGHIGHATPANAH N, BANIHASHEMI A H. On weighting/reweighting schemes for approximate message passing algorithms[C]//2016 IEEE International Conference on Communications (ICC). Kuala Lumpur, Malaysia. IEEE, 2016: 1-5.
