1 引言
现如今,物联网的高速发展使得人们迫切需要高精度的位置服务[1],传统的全球定位导航系统(Global Positioning System, GPS)技术因为建筑物的阻碍严重影响定位准确度,导致其无法成为室内定位的关键技术[2]。由于各行业的迫切需求,室内定位技术得到了快速发展的机会。现阶段的已知定位技术包括射频识别技术[3](Radio Frequency Identification, RFID)、蓝牙[4]、无线局域网[5](Wireless Local Area Networks, WLAN)、超宽带[6-7](Ultra-Wideband, UWB)等,但由于室内场景的复杂性和多样性,室内定位技术仍具有一些缺点与局限性。 当前的指纹定位技术中的指纹主要是使用RSSI和CSI特征。基于RSSI的指纹定位,指纹数据维度低、参数计算匹配复杂度低,由于室内环境因素导致RSSI值在同一参考点处波动较大[8]。基于CSI特征的指纹定位技术中指纹数据维度高,对应的匹配计算复杂度也会提高。文献[9]对比分析了两种指纹RSSI和CSI的特点,并选择将CSI应用到指纹定位,在建立CSI指纹数据库阶段时运用克里金插值法;文献[10]设计了基于CSI幅度相位指纹和卷积神经网络的主动定位方法,将相位与幅度结合,构建了特征更丰富的定位指纹矩阵;文献[11]采用高斯拟合-卡尔曼滤波算法来修正RSSI,并利用RSSI具有高斯分布的特性以对数据进行拟合,从而消除RSSI的不确定性;文献[12]首先动态确定分类算法—加权K近邻(weight K-nearest Neighbors, WKNN)算法的K值,以RSSI特征匹配结果辅助CSI进行定位,以提高定位精度;文献[13]提出在超宽带系统中以RSSI传播损耗公式测距采集指纹,实现定位。现有的CSI和RSSI指纹数据受环境影响大,使得指纹数据不确定性增大,降低了系统鲁棒性和减小了定位准确率,因此指纹数据的采集至关重要。
TOA测距是基于第一条直射路径的到达时间估计从而得出距离。现有关于TOA估计的研究如文献[14]提出了一种基于能量检测的最大似然TOA估计方法,该方法利用较长的积分窗口,克服了与接收机的实际硬件限制;文献[15]中提出一种基于匹配滤波的广义最大似然算法(Generalized Maximum Likelihood,GML),通过接收信号与发射信号模板的互相关运算,得出最大值其对应的时刻即为TOA估计值;文献[16]提出了一种利用RSSI协助TOA和AOA的优化算法,实现协同定位,以提高室内定位精度。但是室内多径的存在会使得TOA估计不准确,如何有效克服利用多径效应并准确估计出第一条路径的TOA成为一个重要的研究方向。1992年,M.Fink等人首次提出了TR技术,并将其应用于水声通信[17],时间反演技术在时域上对收到的信号进行时间翻转等同于频域上的相位共轭[18]。在复杂多径环境下,信号经时间反演处理后再发送,信号会呈现空时聚焦特性,能减少多径效应的影响,文献[19]提出了一种基于TR的抗多窃听者的物理层安全吞吐量优化方案,利用TR的空时聚焦特性,显著提高安全吞吐量;该空时聚焦特性使得其在室内定位中前景广泛。文献[20]对CSI指纹数据采用TR技术以减少室内多径对指纹收集的影响,实现了0.9 m×1 m区域的定位,并且误差仅有10 cm;文献[21]在超宽带系统中采集传播时间作为指纹联合角度进行定位,但其RP数量达到3个,并且时间的采集对仪器设备要求较高;文献[22]在文献[21]的基础上加入TR技术,并在MIMO系统中实现单个参考点(Reference Point, RP)定位;文献[23]将TR技术应用至TOA中,相较于传统的TOA定位,该方案定位精度更高。TR技术能有效克服多径的影响,其空时聚焦特性使得TOA估计准确率更高,将其作为获取新指纹的方法至关重要。
基于上述研究,本文提出了基于距离的指纹定位技术,该技术以RP至网格点(Grid Point, GP)的距离作为指纹,采集简单,数据维度低;然后通过TR技术估计出RP至目标点(Blind Point, BP)的TOA,进而得到距离,与构建的距离指纹库进行比对,实现了室内6 m区域内定位误差小于0.44 m的目标定位。
2 系统结构
整个系统设计在室内6 m的可视距(Line Of Sight, LOS)条件下,设置两个已知位置的RP,主要包括离线采集指纹数据、在线匹配定位两个阶段。离线采集指纹数据:在待测区域建立二维坐标系,采集RP至GP的距离作为指纹,并构建指纹数据库。在线匹配定位:对两个RP采用TOA方法并联合TR技术分别测量出不同RP至BP的距离,作为采集的指纹数据,与指纹数据库进行匹配,通过K近邻(K-nearest Neighbors, KNN)算法求出相似度高的样本,进而估计出BP的位置。如图1所示。
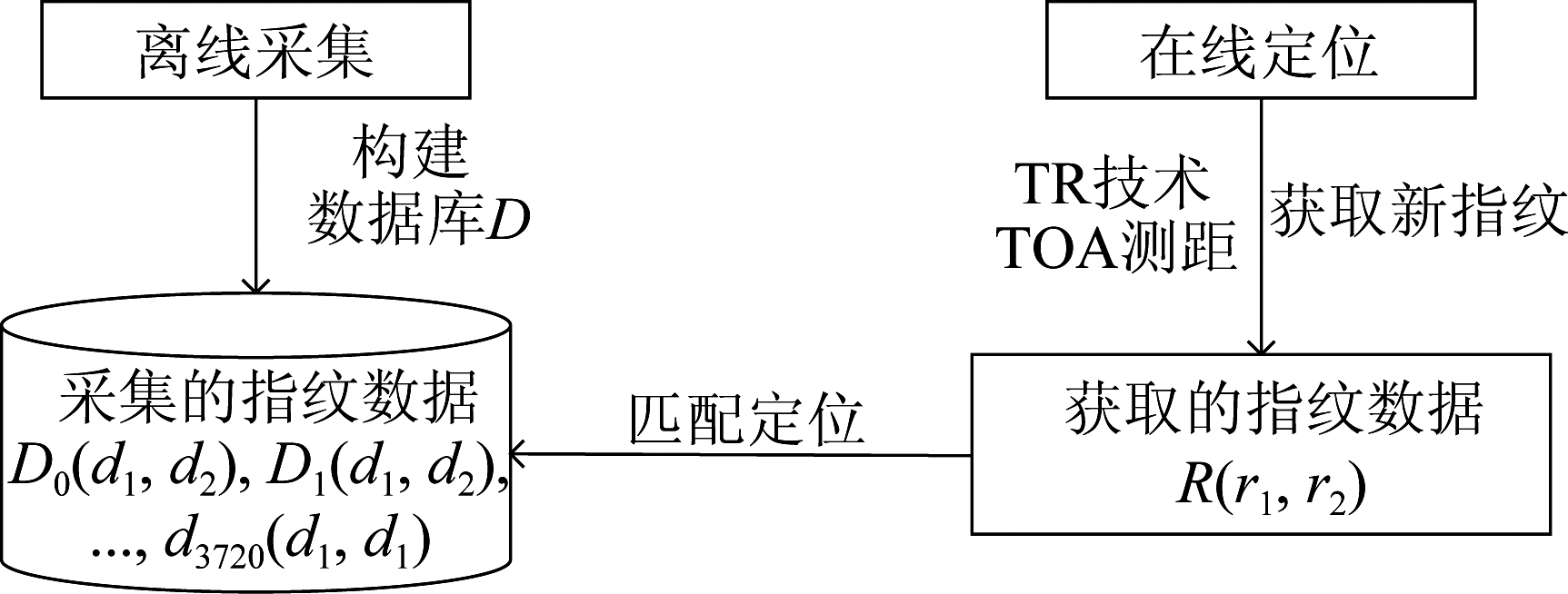
图1 距离指纹定位模型
Fig.1 Distance fingerprint location model
3 传统指纹定位技术
指纹定位技术中以CSI为指纹,整体可以分为两个阶段。其中离线训练过程产生特征训练集,在线定位通过匹配训练集来完成定位。定位过程如图2。
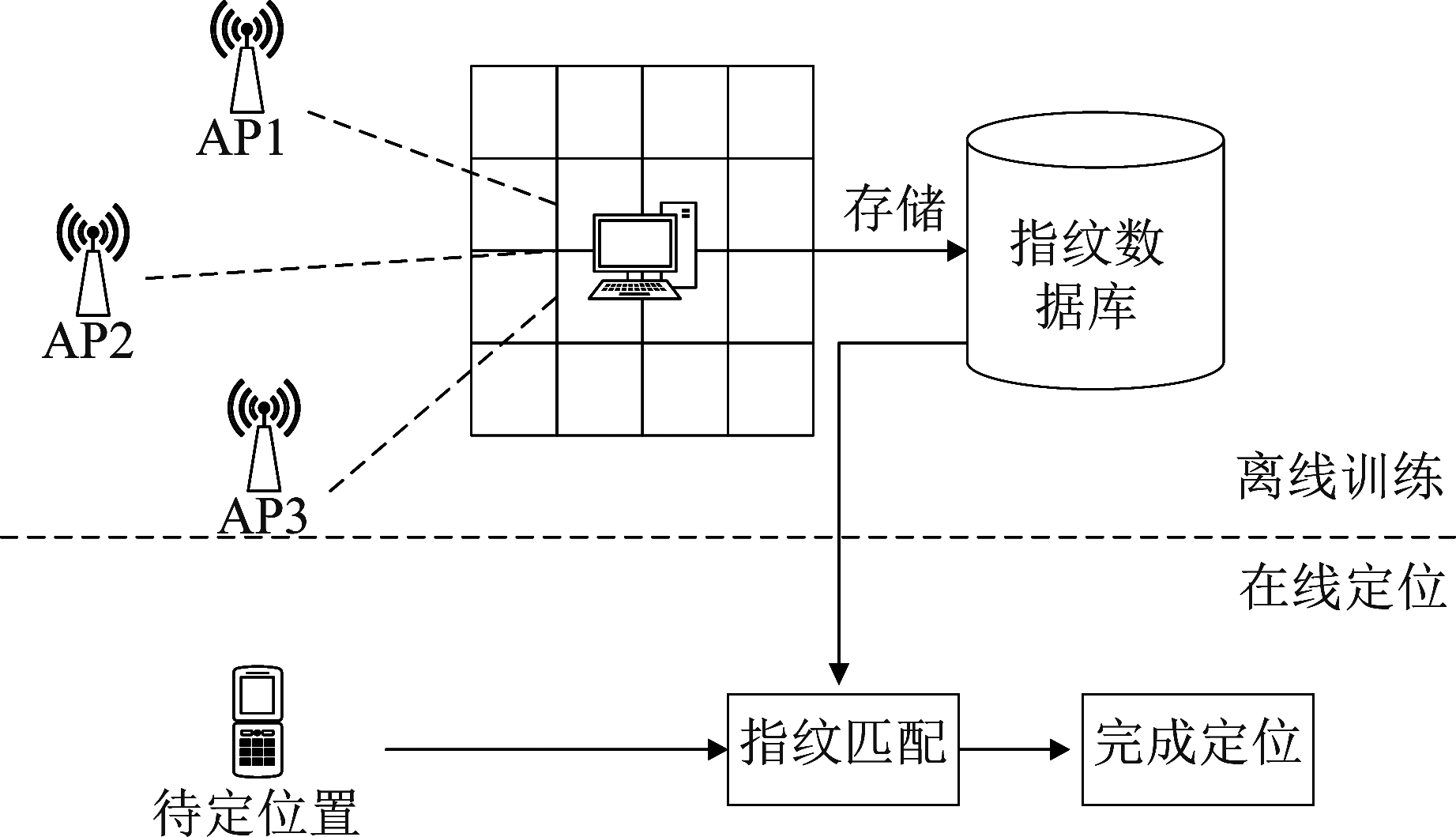
图2 指纹定位原理
Fig.2 Fingerprint location schematic
3.1 离线采集
将待定区域的物理地址和信号特征之间建立对应关系,对于每个点来说,都要采集其信号参数CSI,整个区域组成特征参数矩阵,构成训练集。由于环境的变换会导致CSI的不准确性,所以应该采集一段时间内的信号特征,构成一个特征向量,若干个特征向量构成了区域的整个训练集。如式(1)。
Di=(d1,d2,...,dN)
(1)
其中,N是网格点数,指纹数据如式(2)。
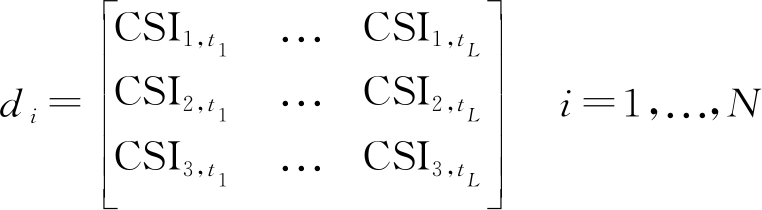
(2)
其中,CSI1,t1表示AP1在t1时刻对应的CSI,CSI2,t1表示AP2在t1时刻对应的CSI,CSI3,t1表示AP3在t1时刻对应的CSI。
3.2 在线定位
在线定位阶段就可以根据算法得出定位结果。首先收集BP的CSI,根据式(3),与构建的指纹数据库进行对比,得到相似度最高的匹配样本,其对应的点的位置即为BP的位置。
在现有的指纹定位技术中,定位算法有KNN算法、贝叶斯算法、和神经网络算法。其中KNN算法简单有效且训练代价低,适用于大量数据。KNN算法类似投票,选择前K个相似样本,决定新样本。其应用至匹配定位即是通过计算BP与数据样本中的点的相似度来判别BP所在的位置。其过程是在数据样本中遍历BP与所有AP的欧式距离,然后将最相近的K个样本取出,对其取平均以确定BP位置,欧式距离可以表示为:
(3)
其中,Disi为RP至BP的欧式距离,即相似度;CSIj表示BP点接收到的第j个RP对应的CSI,CSIij表示第i个网格点接收到的第j个RP信号对应的CSI,N为指纹点个数。
4 TR联合TOA测距的指纹定位技术
TR联合TOA测距的指纹定位原理如图3,在6 m定位区域内存在任意位置的BP,区域外部署两个已知位置的RP,整个定位流程可以分成两个步骤。离线采集阶段:根据已知坐标分别记录两个RP点至网格顶点的距离数据构建指纹数据库;在线定位匹配阶段:在TOA中加入TR技术进行估计测距,获取新距离指纹数据,与构建的距离指纹数据进行比对,根据KNN算法得出相似度最高的数据,从而对BP实行定位。
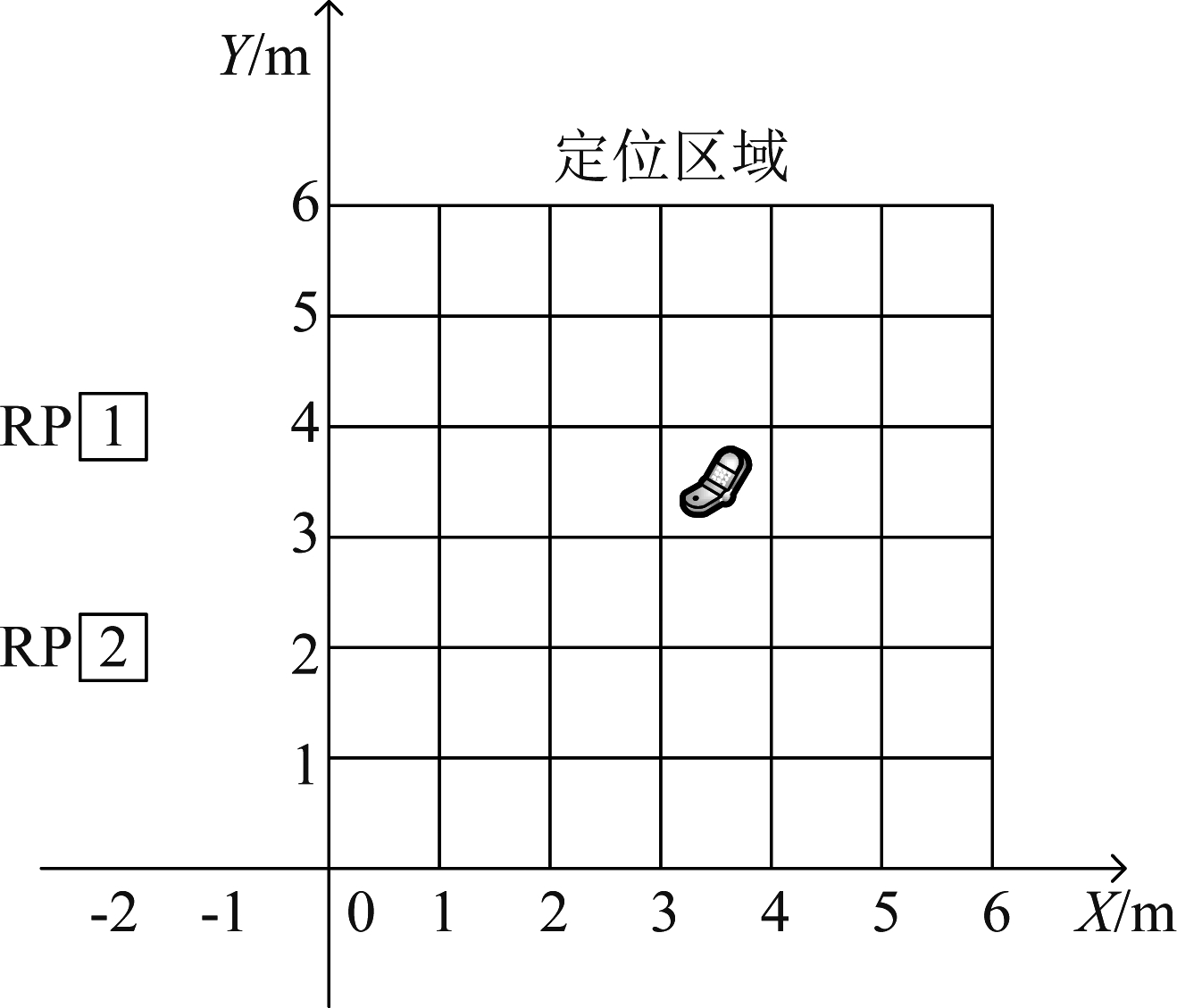
图3 距离指纹定位
Fig.3 Distance fingerprint
4.1 离线采集
在待测区域坐标系外,设置两个已知位置的参考点RP1=(X1,Y1)和RP2=(X2,Y2),将待测区域在划分成60×60的网格,每个GP坐标已知,GP=(xk,yk) k=0,1,...,3720。根据
(4)
(5)
构建距离指纹数据库:
D=(d1,d2)
(6)
其中,d1表示RP1到所有GP的距离,d2表示RP2到每一个GP的距离,指纹数据库D也可以表示为:
D=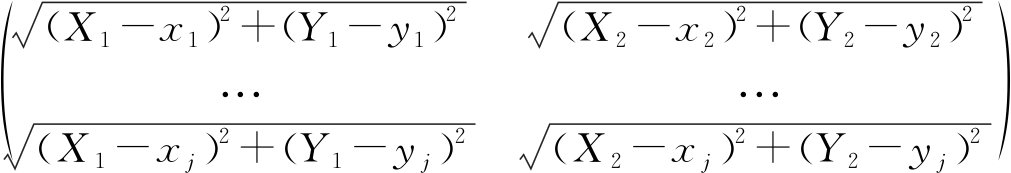
j=0,1,...,3720
(7)
其中(X1,Y1)表示第一个RP的坐标,(X2,Y2)表示第二个RP的坐标,(xk,yk) k=0,1,...,3720表示所有网格点的坐标。
4.2 在线定位
在线定位阶段可以两个过程,分别是获取新指纹以及目标位置估计。新指纹采集利用TR技术联合TOA测距进而得到RP至BP点的距离;位置估计是采用KNN分类算法,依据欧氏距离,得出最相近的数据,进而估计坐标。
4.2.1 获取新指纹
新指纹采集主要是基于时间反演技术的TOA测距,过程如图4。
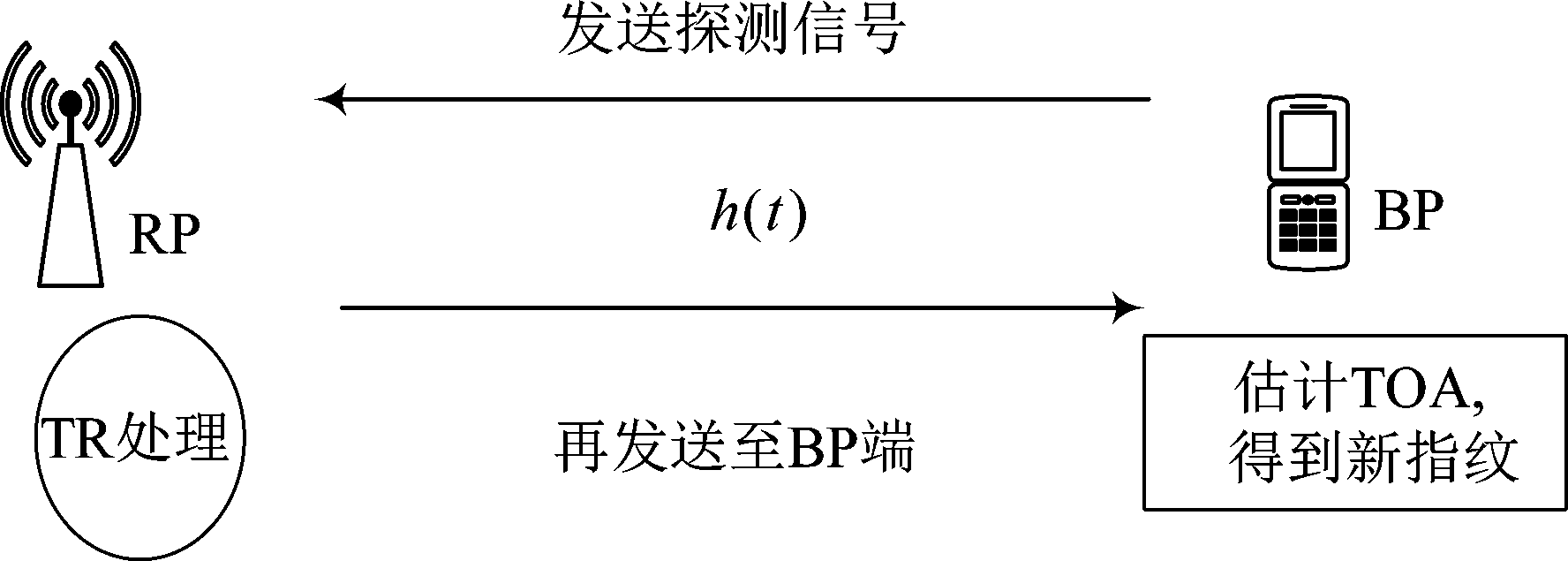
图4 新指纹采集过程
Fig.4 New fingerprint collection process
空时聚焦特性是TR在多径复杂条件下最明显的特性,经验证,TR技术对多径有着良好的抑制作用。基于此,本文提出了一种将TR技术与TOA相结合的测距方案。在超宽带信道中,利用TR的空时聚焦特性在接收端信号输出的最高峰准确估计TOA值,进而得出RP至BP的距离。
TR过程主要分为如下三个阶段。假设参考点RP向目标点BP发送消息,过程如下:
(1)探测阶段
接收端BP向发送端RP发射探测信号p(t),估计信道脉冲响应(Channel Impulse Response, CIR),得出探测信号经过超宽带信道后的输出。探测信号p(t)经过超宽带信道后的输出为:
y(t)=p(t)*h(t)+u(t)
(8)
其中,y(t)表示探测信号经过超宽带信道后的输出,p(t)表示探测信号,h(t)表示信道脉冲响应,u(t)表示零均值方差为
的高斯白噪声。
为确保信道脉冲响应h(t)不变,探测过程需要进行M次,得到第m次经过超宽带信道后的输出:
ym(t)=p(t)*h(t)+νm(t)
(9)
其中,ym(t)表示第m次探测时得到的信号,νm(t)表示第m次探测时的高斯白噪声,M表示总的探测次数。
根据M次经过超宽带信道后的输出,计算得出信道响应的最小均方误差:
p(t)*h(t)+ν(t)
(10)
其中,yε(t)表示信道响应的最小均方误差,ym(t)表示第m次经过超宽带信道后的输出,ν(t)表示均值为0方差
的高斯白噪声。
(2)反演阶段
发送端RP对接收信号yε(t)进行时间反演处理得到:
其中,
表示时间反演处理后的信号,yε(T0-t)表示信号yε(t)波形反转并经过T0时间后的信号,T0表示观察的时间长度。
(3)传输阶段
发送端RP将时间反演处理后的信号再发射至BP,BP收到的信号表示为:
(11)
其中,ytr(t)表示时间反演处理后的信号到达接收端的接收信号,w(t)表示均值为0方差
的加性高斯白噪声。
上述过程中探测信号p(t)为二阶高斯脉冲导函数,一个高斯脉冲可表示为如式:
(12)
则二阶高斯脉冲导函数可表示为如式:
(13)
其中,α2=4πσ2,σ2为方差,当减小α的值,脉冲宽度减小,传输信号的带宽随之增加,本文α采用的是0.4 ns。
对于实际的多径信道模型,其信道冲击响应的离散表达式h(t)如式:
(14)
其中,αl和 τl是第l条多径的幅度和时延,δ(t)为狄拉克函数。
式(11)中的等效信道冲激响应H(t)可表示为:
H(t)=h(-t)*h(t)=
(15)
将式(15)中第一部分设为自相关R(t)和互相关Q(t),可分别写成:
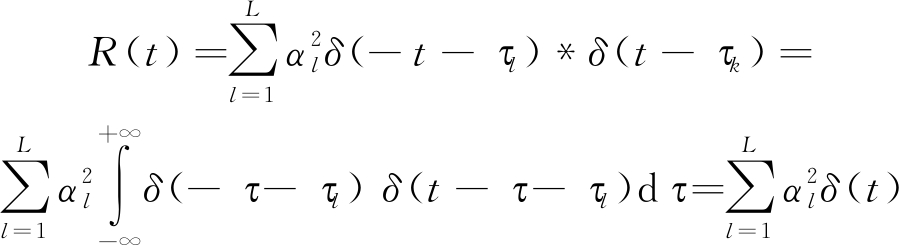
(16)
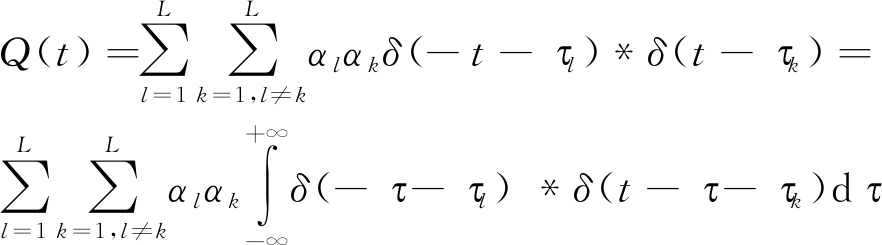
(17)
互相关函数Q(t)是各个不同传播路径的互相关函数,非相关多径信号卷积叠加后的结果是相互抵消的,而R(t)的大小和多径数目相关,多经数越多,自相关函数越大,所以Q(t)相比R(t)要小的多。则根据式(15),可以看作探测信号p(t)通过一个信道脉冲响应CIR的自相关输出,时间反演后的接收端接收的信号波形会有一个明显的波峰即最高点如图6,接收端接收信号输出波形的最高峰所对应的时间指标即为估计的TOA。
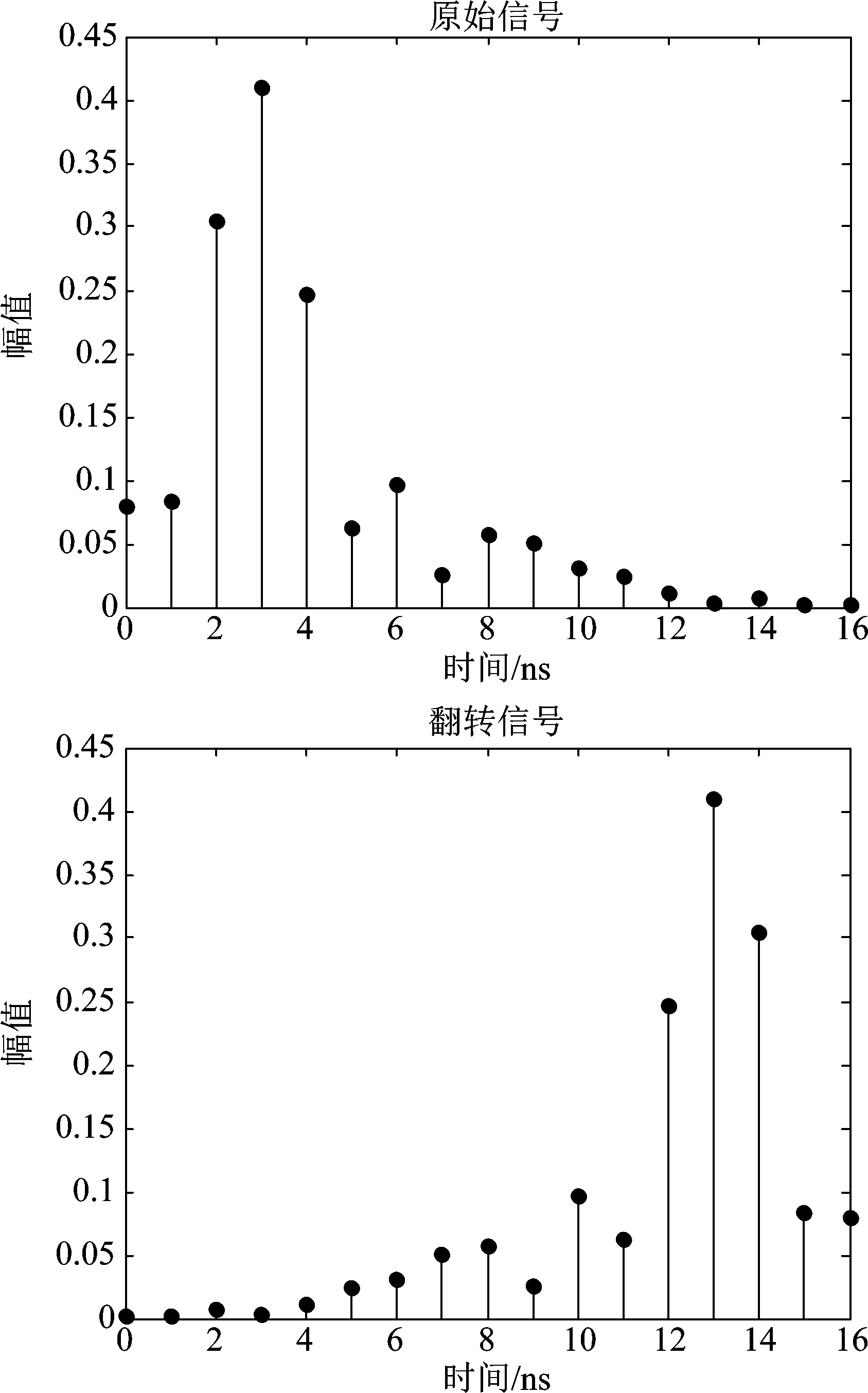
图5 信号幅值图
Fig.5 The signal amplitude
图6 时间反演聚焦图/TOA估计
Fig.6 TR focus graph/TOA estimation
得出到达时间t后,根据d=c×t计算出RP至BP的距离,作为在线定位阶段的新指纹数据,其中t为RP至BP的传播时延,c是电磁波传播速度3×108 m/s。
4.2.2 位置估计
为了保证基于距离指纹方法的有效性和普适性,更倾向于简单、基本和流行的匹配算法。本文将采用KNN分类算法进行位置估计,该算法主要依据最近邻的K个样本从而确定样本数据特征。其实KNN算法就是将所求得的近邻度进行排序,定义近邻度:
(18)
选取前面K个最相似的样本数据,计算其平均值,从而得到BP的位置。实际应用中,K值一般取一个比较小的值,采用交叉验证法本文选取K值11。
5 仿真分析
为了评估本方案的性能,本文在一个二维坐标系房间中选取6 m×6 m的区域作为实验场景,在区域外LOS环境下布置两个已知位置的RP,目标点随机出现在定位区域中如图7。
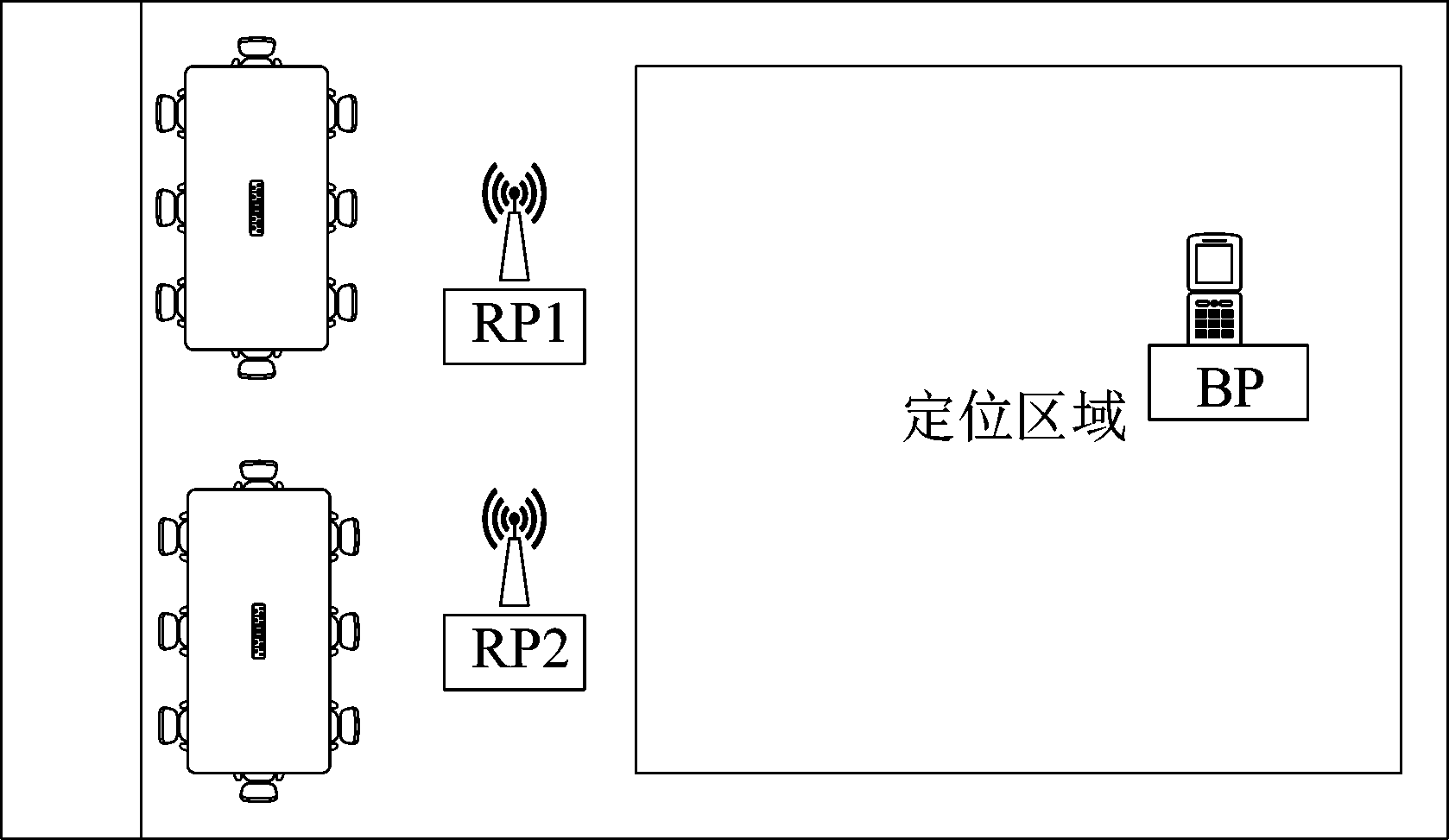
图7 实验场景
Fig.7 The experimental scene
通过MATLAB对本文提出的方案进行仿真验证。TR过程中的探测信号采用二阶高斯脉冲导函数,室内多径数设置为8,信号传输在5.4 GHz频段下,带宽为125 MHz。如图8,分别分析了以CSI、RSSI作为指纹和本方案的定位性能,在线定位时均使用KNN近邻算法估计BP位置,以误差累计分布函数作为评估标准。
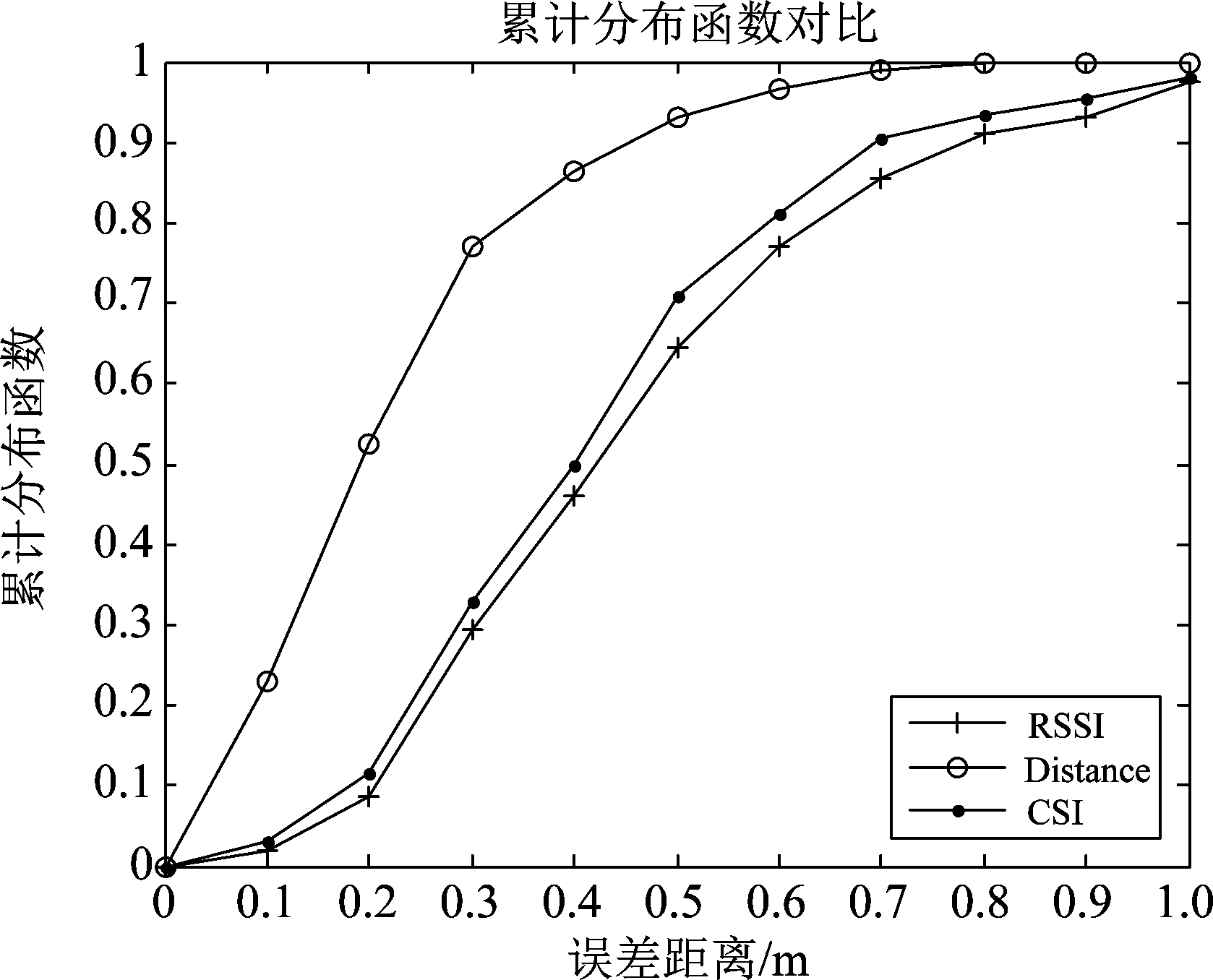
图8 不同指纹定位方案下的累积误差分布图
Fig.8 The cumulative error distribution under different fingerprint location schemes
由图8可知,本文提出的方案得到的定位误差有90%概率小于0.45,其累计误差分布图曲线位于以RSSI、CSI为指纹的定位方案曲线之上,这表明本方案有更快地收敛速度,且定位误差更小。
图9分别比较TR和GML 估计TOA的均方根误差,其中TR算法估计的均方根误差接近克拉美罗下界(Cramer-Rao Low Bound, CRLB),所以TR算法相对GML估计TOA更加精确。
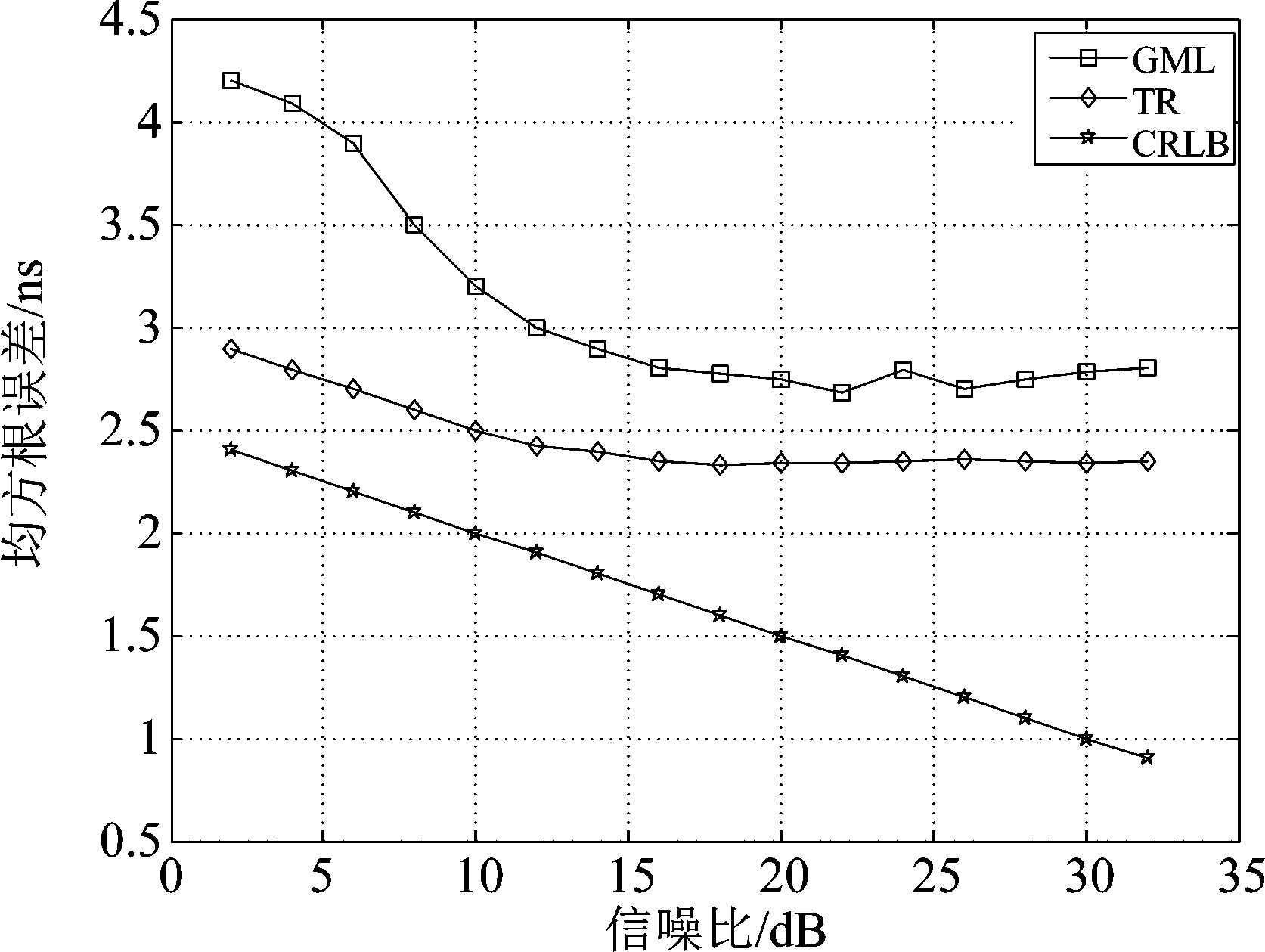
图9 TR与GML估计TOA的性能比较
Fig.9 Performance comparison of TR and GML to estimate TOA
由图10可得出,在以距离作为指纹的情况下,并将TR用于TOA进行测距,其累积分布图曲线在同等条件下使用GML 估计TOA进行测距的曲线之上,这也表明了TR技术良好的空时聚焦特性能提高TOA估计精度。
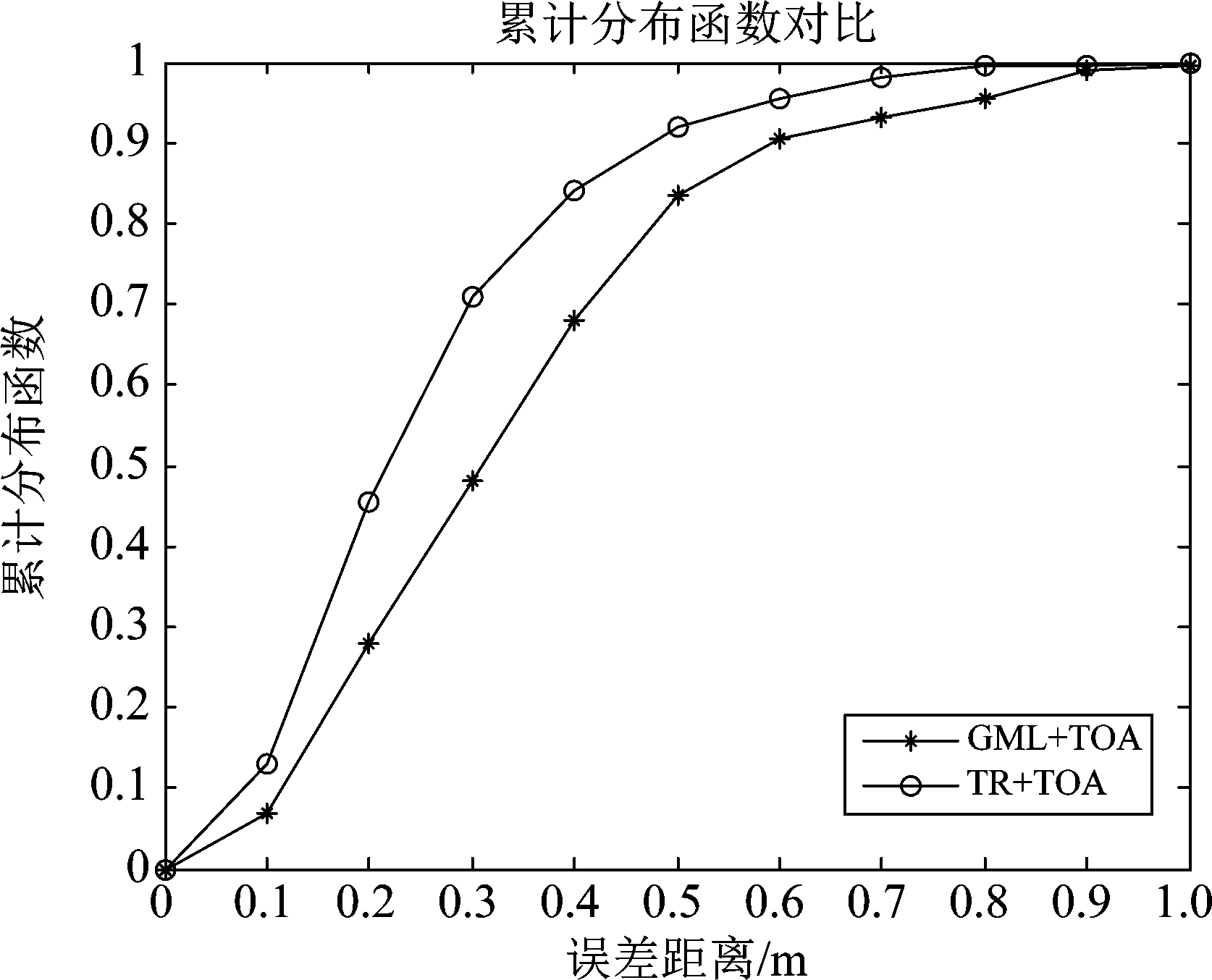
图10 本方案下采用TR测距与未采用TR测距的对比图
Fig.10 A comparison diagram of TR ranging and TR not used in this scheme
在定位区域内,共划分3600个网格,部署两个RP,以网格顶点作为指纹点,由于CSI和RSSI随环境变换,所以需采集在n个时间段内的CSI和RSSI,需要精密仪器的测量,开销大且过程繁琐。在MATLAB条件下,输入采集的指纹数据,创建数据库,本文提出的方案在200次仿真下,定位误差保证在0.44±0.1 m的情况下,准确率达到100%。以距离作为指纹不用考虑环境变化对离线阶段指纹数据采集的影响,系统的鲁棒性有所提高,复杂度降低,大大提高了定位效率和准确率。
表1 不同指纹下定位方案的复杂度和准确率的对比
Tab.1 Comparison of the complexity and accuracy of different fingerprint location schemes
定位方法复杂度定位准确率CSI61×61×2×n94%RSSI61×61×2×n95%Distance61×61×2100%
6 结论
针对室内环境指纹数据的采集具有不稳定性和不可靠性的问题,本文创新性的提出了以距离作为指纹,减小了成本并且降低了复杂度,再采用TR联合TOA测距的指纹定位方案,实现了6 m×6 m室内定位,定位准确率达到100%,且定位误差达到0.44 m。文章最后比较了本方案与其他方案的定位误差,有明显的减小。接下来的工作,可以考虑对指纹数据进行整理,新指纹采集方案进一步优化。
[1] 郑明洋. 基于富散射电磁环境信道特征的高精度室内定位技术研究[D]. 北京:北京邮电大学, 2019:10.
ZHENG Mingyang. Research on high-precision indoor positioning technology based on channel characteristics of rich scattering electromagnetic environment[D]. Beijing: Beijing University of Posts and Telecommunications, 2019:10. (in Chinese)
[2] 江小平, 王妙羽, 丁昊, 等. 基于信道状态信息幅值-相位的被动式室内指纹定位[J]. 电子与信息学报, 2020, 42(5): 1165-1171.
JIANG Xiaoping, WANG Miaoyu, DING Hao, et al. Passive fingerprint indoor positioning based on CSI amplitude-phase[J]. Journal of Electronics & Information Technology, 2020, 42(5): 1165-1171.(in Chinese)
[3] FLOAREA D, SG
RCIU V. Indoor positioning using RFID and REST[C]∥2019 11th International Symposium on Advanced Topics in Electrical Engineering (ATEE). Bucharest, Romania. IEEE, 2019: 1- 4.
[4] CHALLA N S R, KESARI P, AMMANA S R, et al. Design and implementation of bluetooth-beacon based indoor positioning system[C]∥2019 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE). Bangalore, India. IEEE, 2019: 1- 4.
[5] AIKAWA S, YAMAMOTO S, MORIMOTO M. WLAN finger print localization using deep learning[C]∥2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP). Auckland, New Zealand. IEEE, 2018: 541-542.
[6] FENG Daquan, WANG Chunqi, HE Chunlong, et al. Kalman-filter-based integration of IMU and UWB for high-accuracy indoor positioning and navigation[J]. IEEE Internet of Things Journal, 2020, 7(4): 3133-3146.
[7] CHENG Yun, ZHOU Taoyun. UWB indoor positioning algorithm based on TDOA technology[C]∥2019 10th International Conference on Information Technology in Medicine and Education (ITME). Qingdao, China. IEEE, 2019: 777-782.
[8] WU Chenshu, YANG Zheng, LIU Yunhao. Smartphones based crowdsourcing for indoor localization[J]. IEEE Transactions on Mobile Computing, 2015, 14(2): 444- 457.
[9] LI Xuhong, ZHU Jinhua. Improved indoor positioning method based on CSI[C]∥2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS). Changsha, China. IEEE, 2019: 274-277.
[10]CAI Chenwei, DENG Li, LI Shufang. CSI-based device-free indoor localization using convolutional neural networks[C]∥2018 IEEE 4th International Conference on Computer and Communications (ICCC). Chengdu, China. IEEE, 2018: 753-757.
[11]韩学法, 吴飞, 朱海, 等. 基于GF-KF修正RSSI的室内指纹定位方法[J]. 全球定位系统, 2020, 45(3): 54- 62.
HAN Xuefa, WU Fei, ZHU Hai, et al. Indoor fingerprint positioning method based on RSSI modified by GF-KF[J]. GNSS World of China, 2020, 45(3): 54- 62.(in Chinese)
[12]姚喆. 基于RSSI与CSI的定位技术研究[D]. 北京:北京邮电大学, 2019:25.
YAO Zhe. Research on positioning technology based on RSSI and CSI[D]. Beijing:Beijing University of Posts and Telecommunications, 2019:25. (in Chinese)
[13]ARIAS-DE-REYNA E, MENGALI U. Mapping techniques for UWB positioning[C]∥2009 IEEE International Conference on Communications. Dresden, Germany. IEEE, 2009: 1-5.
[14]SHANG Fang, CHAMPAGNE B, PSAROMILIGKOS I N. A ML-based framework for joint TOA/AOA estimation of UWB pulses in dense multipath environments[J]. IEEE Transactions on Wireless Communications, 2014, 13(10): 5305-5318.
[15]RABBACHIN A, OPPERMANN I, DENIS B. ML Time-of-Arrival estimation based on low complexity UWB energy detection[C]∥2006 IEEE International Conference on Ultra-Wideband. Waltham, MA, USA. IEEE, 2006: 599- 604.
[16]史云飞, 郝永生, 刘德亮, 等. RSS协助的Ray-tracing室内定位算法[J]. 信号处理, 2018, 34(10): 1259-1266.
SHI Yunfei, HAO Yongsheng, LIU Deliang, et al. RSS-assisted Ray-tracing indoor positioning algorithm[J]. Journal of Signal Processing, 2018, 34(10): 1259-1266.(in Chinese)
[17]黄海燕. 时间反演电磁波传播特性研究[D]. 成都: 电子科技大学, 2014: 18.
HUANG Haiyan. Researches on propagation characteristics of time reversal electromagnetic wave[D]. Chengdu: University of Electronic Science and Technology of China, 2014: 18.(in Chinese)
[18]冷建华. 傅里叶变换[M]. 清华大学出版社, 2004: 15-18.
LENG Jianhua. Fourier transform[M]. Tsinghua University Press, 2004: 15-18.(in Chinese)
[19]袁小扣, 朱江. 时间反演系统中抗多窃听者的物理层安全吞吐量优化方案[J]. 信号处理, 2021, 37(3): 437- 446.
YUAN Xiaokou, ZHU Jiang. Physical layer security throughput optimization scheme combate multiple eavesdroppers in time reversal system[J]. Journal of Signal Processing, 2021, 37(3): 437- 446.(in Chinese)
[20]WU Z H, HAN Yi, CHEN Yan, et al. A time-reversal paradigm for indoor positioning system[J]. IEEE Transactions on Vehicular Technology, 2015, 64(4): 1331-1339.
[21]BOGDANI E, VOUYIOUKAS D, NOMIKOS N, et al. Angle-based time Fingerprint positioning technique for indoor UWB systems[C]∥2015 IEEE International Conference on Communications (ICC). London, UK. IEEE, 2015: 6193- 6198.
[22]BOGDANI E, VOUYIOUKAS D, NOMIKOS N, et al. Single-point model of MIMO-UWB indoor systems using time-reversal transmission[C]∥2017 IEEE International Conference on Communications (ICC). Paris, France. IEEE, 2017: 1- 6.
[23]DING Hong, LIU Wenyan, ZHENG Linhua, et al. Application of time reversal for TOA estimation in UWB ranging under dense multipath channel[C]∥2013 IEEE International Conference on Ultra-Wideband (ICUWB). Sydney, NSW, Australia. IEEE, 2013: 61- 65.
