1 引言
数字水印技术是当前进行版权保护和信息隐藏的重要手段之一。目前大部分水印算法均是研究的二值水印图像或是灰度水印图像[1-2],由于彩色图像数据量较大,采取盲提取的方式鲁棒性不强,将彩色图像作为水印信息的算法较少,而生活中大部分图像都是彩色图像,所以提高彩色图像水印算法鲁棒性的研究是相当有必要的。常见的水印算法可以分为空间域算法和变换域算法,非盲提取算法和盲提取算法。其中盲水印算法是研究的重点,但大多数盲水印算法鲁棒性不强,水印信息尤其易受旋转、剪切等几何攻击破坏。
空间域算法是指直接修改载体图像的像素值,算法复杂度低,但是其抵抗攻击能力弱[3]。文献[4]将图像的像素块的奇偶性进行修改以达到嵌入水印的目的,该算法对顽健性很高的水印提取效果较好,但如果二维码水印信息过于紧凑,则提取效果不好。文献[5]提出一种新颖的彩色图像的量子水印算法,将图像量子化再修改图像的灰度值嵌入水印,可获得不错的视觉效果、良好的安全性,未对其受到攻击后的鲁棒性进行深入的研究。
变换域算法是替换变换域的系数,会使水印信息更加均匀嵌入在空间域上,更加具有视觉遮蔽特性和强鲁棒性。文献[6]在Contourlet域嵌入水印,对JPEG压缩攻击具有良好的效果,但是对旋转攻击效果较差。文献[7]提出了一种利用分形编码和离散余弦变换的非盲方法,具有良好的不可感知性,然而对高斯噪声攻击鲁棒性较低。文献[8]作者提出了一种利用Arnold置乱与冗余RDWT变换和离散余弦变换的盲水印方法。这种方法不易察觉,但它对均值和中值滤波攻击的鲁棒性较低,而且Arnold置乱只是打乱水印像素值的位置并未改变其像素值,使缺乏保密性。文献[9]提出了一种DCT域使用双峰结构和迭代选择过程的盲水印算法,对攻击具有很好的鲁棒性,但是其峰值信噪比(PSNR)很低。文献[10]提出一种Blob-Harris特征区域结合CT-SVD的鲁棒图像水印算法,对大部分攻击具有较强的鲁棒性,但未能实现水印的盲提取,对旋转攻击效果不佳,并且水印图像并非彩色图像。文献[11]在NSCT域利用BSVD分解嵌入水印,结合Radon变换校正攻击后的图像,该算法能有效抵抗旋转攻击,但并未能实现盲提取。文献[12]提出一种使用Schur分解的盲水印算法,它对众多攻击具有较强鲁棒性,不可感知性较差。文献[13]提出了一种使用LU分解的盲算法,其中水印信息被嵌入到下三角矩阵的第二和第三行的第一个元素中。该方法对攻击具有鲁棒性,它具有较低的不可感知性。文献[14]提出了一种基于快速沃尔什-哈达玛变换(FWHT)、奇异值分解、密钥映射和系数排序的盲技术,其不可感知性和对旋转、剪切等几何攻击效果较差。
从上面讨论中,可以得出结论,一些算法是低鲁棒性的,一些是不可觉察性低的,还有些是非盲的算法或者是非彩色水印。为克服这些缺点,进一步加强双彩色盲水印算法的鲁棒性,本文先结合Baker映射与时空混沌将水印加密,再将载体图像在Contourlet进行QR分解,把加密后的水印信息按嵌入规则嵌入到QR分解后的酉矩阵中,可实现水印信息的盲提取,实现不可感知性和鲁棒性的折中。水印提取之前,先利用Radon变换进行几何校正,再对提取出的RGB分量中的水印信息进行自适应中值滤波增强处理能显著提升水印系统抗旋转、剪切等几何攻击。
2 Baker映射和耦合映像格子(CML)模型
本文采用Baker映射和CML相结合的方法对水印信息进行加密处理,先采用Baker映射置乱水印图像像素之间的相关性,再通过耦合映像格子产生的混沌序列来对水印异或加密,使得水印信息具有良好的混淆和扩散特性。水印加密算法示意图如图1。
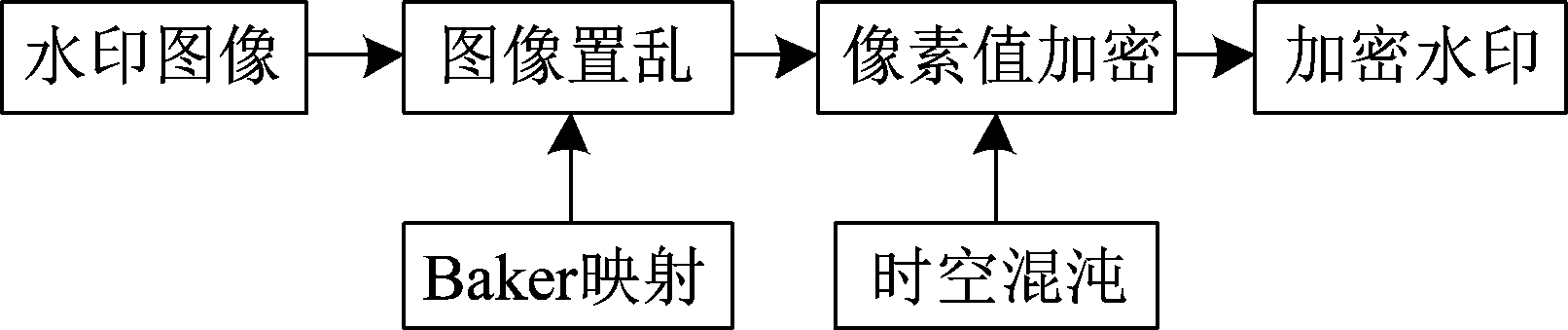
图1 加密算法示意图
Fig.1 Schematic diagram of encryption algorithm
2.1 Baker映射
Baker变换类似于Arnold置乱,是一种图像置乱的方法。相比Arnold置乱,Baker周期更长,只需要较少的置乱次数就可以达到很好的置乱效果,而且算法简单,保密性好。根据Pichler和Scharinger[15]的理论,将N×N的图像切分为t小的长方形,高分别为{n1,n2,…,nt},要保证n1+n2+…+nt=N。使N0=0,将原始图像的每一个像素点(r,s)(Ni-1≤r≤Ni,0≤s≤N)映射为(x,y):
(1)
其中qi=N/ni,1≤i≤t。
2.2 耦合映像格子模型
耦合映像格子(CML)模型[16-17]是一种时空混沌模型,在时间和空间上具有双重混沌行为,较低维的混沌系统具有更加复杂的行为和丰富的特征。CML模型既对初始条件敏感,又对边界条件敏感。其数学模型如下:
xn+1(i)=(1-ε)f(xn(i))+
(2)
其中耦合常数ε∈(0,1),n=1,2,3,…为时间索引,i=1,2,3,…为网格位置索引, f(·)为局部更新函数,此处选取Logistics映射f(y)=1-λy2,其中λ∈(0,2),y∈(0,1)。
图2为256×256的Lena图像采用Baker映射置乱5次与CML加密相结合的方式对图像进行加密的效果图。
图2 图像加密效果图
Fig.2 Effect of image encryption
3 Contourlet变换和QR分解
3.1 Contourlet变换
Do和 Vetterli[18]提出了一种多方向和多尺度变化的Contourlet变换,相比传统的小波变换可以有效地表示具有更多方向信息的图像。方法如图3所示,Contourlet变换主要包括两个阶段:子带分解和方向变换。拉普拉斯金字塔(LP)滤波器作用第一级,解析图像,获取奇异点,方向滤波器组(DFB)作用于第二级合并同方向的奇异点,得到各个方向子带。图像a0[n]经过Contourlet后得到J个带通方向子图bj[n], j=1,2,…, j和一个低通子带aj[n]。
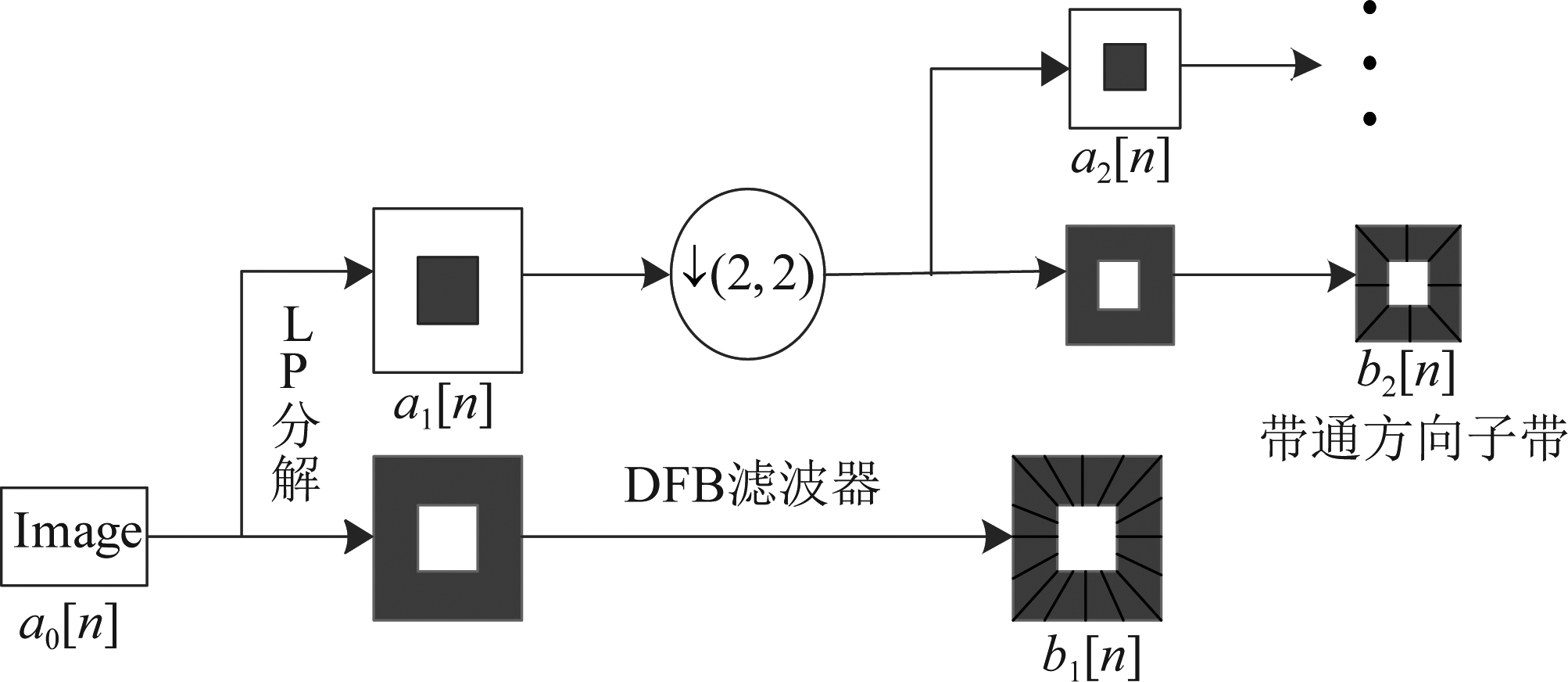
图3 Contourlet变换示意图
Fig.3 Schematic diagram of Contourlet transform
3.2 QR分解
QR[19-20]分解是一种常用的矩阵分解方式,其时间复杂度为O(N2),而SVD分解和Schur分解的复杂度分别为O(11N3)、O(8N3/3),能提高算法的效率。大小为m×m的矩阵A的QR分解定义如下:
[Q,R]=qr(A)
(3)
其中,Q代表大小为m×m的酉矩阵,R为m×m的上三角矩阵,使得A=Q×R。
4 Radon变换
本文在水印信息提取之前采用Radon变换[21]预处理的方法,先对受到几何攻击的图像校正处理。由Radon变换的性质,它是捕捉图像方向信息的有力工具。给定的一组角度,对图像f(x,y)进行Radon变换就是计算图像沿着给定角度的投影,得到的投影是每个方向上像素强度的总和,即线积分。像素矩阵f(x,y)Radon变换的定义为:
P(γ,θ)=R(γ,θ){f(x,y)}=
(4)
其中,γ为原点到直线的距离,θ为直线与坐标轴的夹角,δ为f(x,y)对γ-xcos θ-ysin θ的线积分。由此可以得到(γ,θ)处f(x,y)沿着该直线的投影。
校正步骤如下:
(1)提取载体图像R通道,计算参考向量R(0):对原始图像进行Radon变换。
(2)获取检测向量R(θ),θ∈[1°,2°,3°,…，180°]:对载体图像分别进行1°～180° Radon变换,获得180个检测向量,构成“角度-检测向量对”。
(3)计算旋转角度:对比R(0)和R(θ)的相关系数,相关系数最大者为其对应的角度。
(4)图像校正。将所求角度进行逆旋转,即可得到校正后图像。
5 水印的嵌入与提取
5.1 水印嵌入步骤
(a)水印预处理。将彩色水印图像分离成R、G、B分量形式的灰度图,按照图1方式对三个分量进行加密得到W。根据公式(5)将置乱后各灰度分量归一化矩阵W′,再按公式(6)将各分量进行二值化,得到的二值化矩阵Lg。
W′(i, j)=W(i, j)/255
(5)
(6)
(b)为了提高水印抗旋转攻击能力,先对宿主图像进行R、G、B分量分离,取出R分量进行Radon变换,获得参考矢量R(0),用于检测和校正旋转攻击。
(c)宿主图像预处理。对宿主图像进行R、G、B分量分离,分别对三种分量形式下的灰度图做3级Contourlet变换,取出低频子带,再对低频子带进行4×4分块,对每一子块进行QR分解得到每块的酉矩阵U。
(d)按式(7)嵌入规则将归一化后的水印W′嵌入到矩阵U中。
if Lg(i, j)=1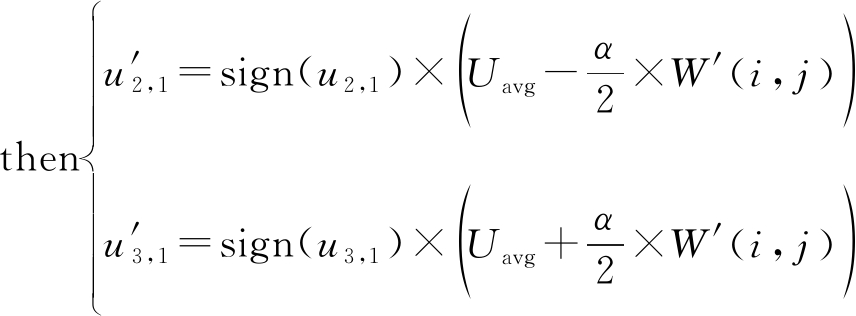 
if Lg(i, j)=0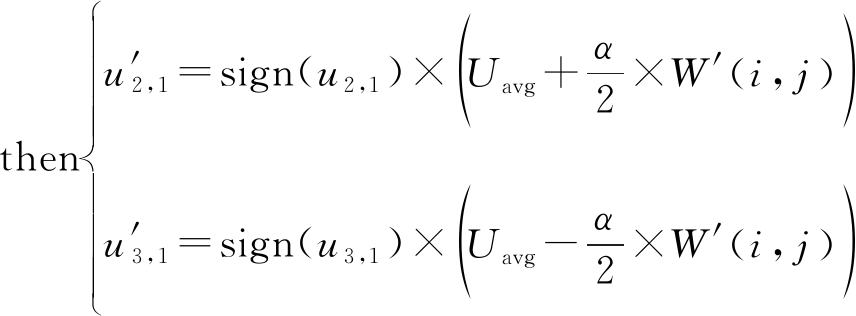 
(7)
其中,α为嵌入强度，u2,1,u3,1分别表示U中第2行第1列和第3行第1列的值。sign(u2,1)表示U中第2行第1列元素的符号,
为u2,1的绝对值。
(e)重构恢复得到含水印的图像。分通道分别进行QR逆变换和Contourlet逆变换,最后合并R、G、B分量得到嵌有彩色水印的彩色载体图像。水印的嵌入流程如图4(a)所示。
图4 水印嵌入与提取流程框图
Fig.4 Block diagram of watermark embedding and extraction
5.2 水印提取步骤
水印的提取流程如图4(b)所示。
(a)在水印提取之前先检测载体图像中R分量的旋转角度。计算出待测向量R(θ)与参考向量R(0)进行比对,检测的角度即为旋转攻击的角度,对图像进行校正。
(b)对载体图像的R、G、B分量分别进行3级Contourlet变换,再取出低通子带进行4×4分块,对子块进行QR分解得到每块的酉矩阵U′。
(c)根据提取公式(8)可得到加密的水印信息W″。
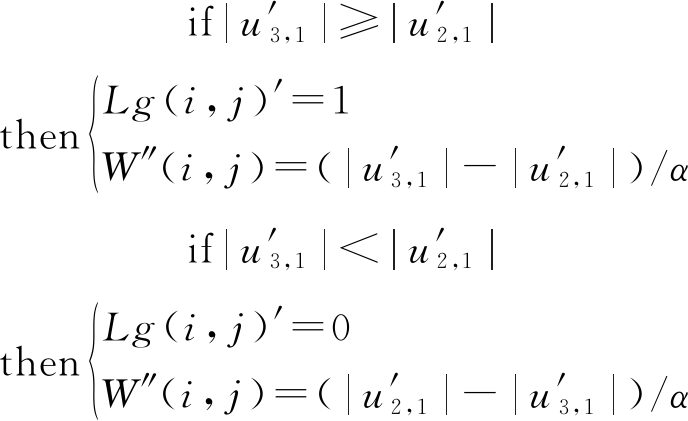
(8)
其中,
分别为U′中第2行第1列和第3行第1列的元素,Lg′为提取出来的二值矩阵。
(d)对R、G、B分量依次进行与CML产生的混沌序列异或解密,Baker映射解密,再对各分量应用自适应中值滤波增强处理,即可得到水印信息。
6 仿真结果与分析
本文在Matlab2017a进行仿真实验。载体图像选取CVG-UGR图像库中2048×2048的24位真彩色图像,若图像大小为512×512可用imresize设置尺寸。水印图像选取标志汽车64×64彩色logo。
6.1 不可见性分析
峰值信噪比(PSNR)来评价嵌入水印后的图像的不可见性,PSNR值越大越好。PSNR的定义式如下:
PSNR=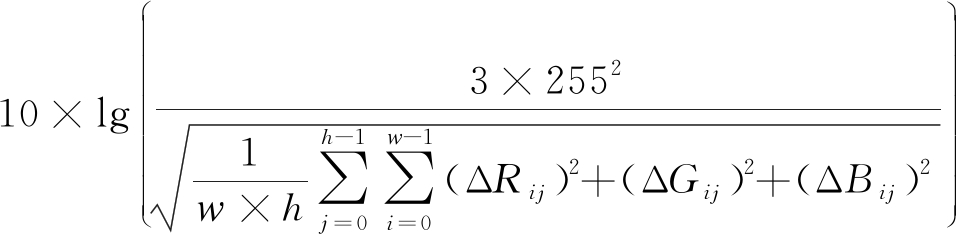
(9)
其中ΔRij,ΔGij,ΔBij分别载体图像和嵌入水印图像红、绿、蓝分量对应像素值的差值。w和h分别是图像的宽度和高度。
取嵌入强度α=0.03时,选取Lena,Peppers, Baboon图像进行实验,仿真结果如图5分别为载体图像和嵌入水印后的图像;图6为测试Lena图像与嵌入水印后的RGB分量直方图对比图;图7为未加攻击所提取出来的水印信息。
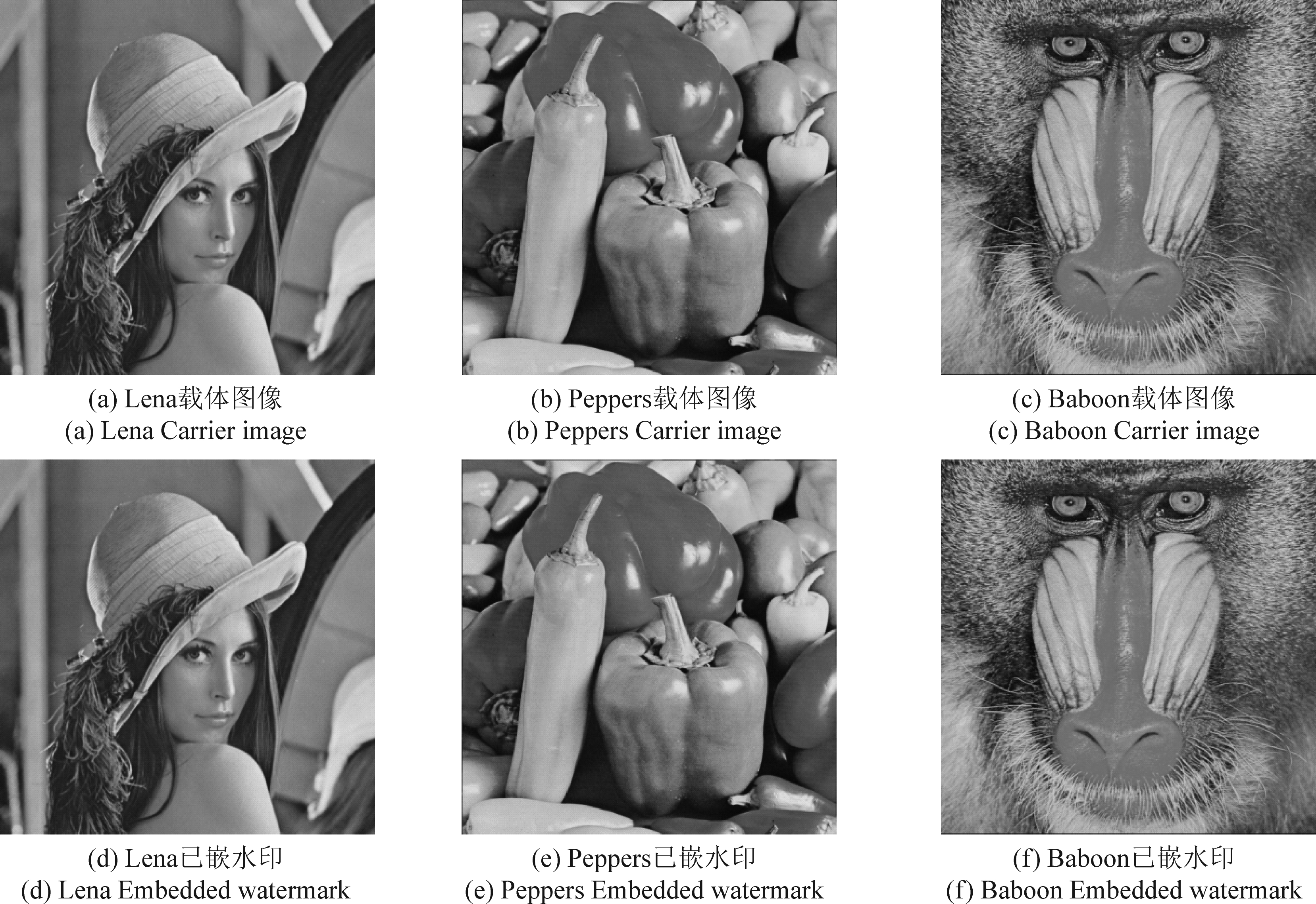
图5 载体图像与嵌入水印载体图像
Fig.5 Carrier image and embedded watermark carrier image
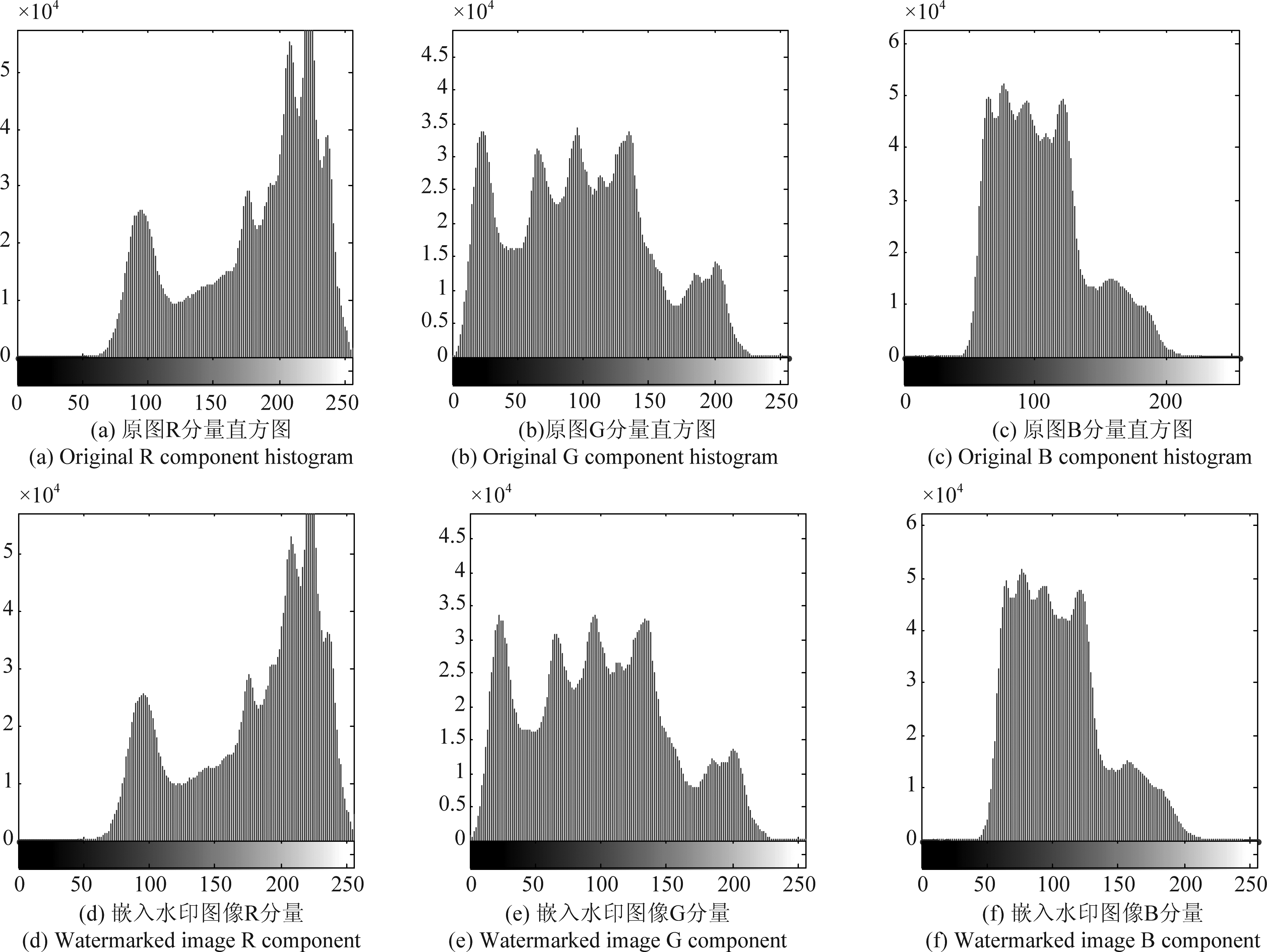
图6 载体图像与嵌入水印后图像各分量直方图
Fig.6 Histogram of each component of the carrier image and the watermarked image
图5中(a)、(b)、(c)为原始载体图像，(d)、(e)、(f)为嵌入水印后的图像，PSNR分别为40.4954，40.2618，39.6842。在视觉上几乎看不出差别，进一步对比原图与嵌入水印后的各分量直方图，仅有轻微的变化，这是因为修改变换域的系数后不可避免的影响，而本文选择Contourlet变换将水印嵌入到最优子带中，让算法获得很高的不可见性，此变化几乎可以忽略，所以本文算法达到了理想的信息隐藏和视觉隐藏效果。由图7可以看出，在未加攻击时，本文算法都能将水印信息完整的提取出来，且具有良好的不可见性。
图7 原始水印与提取的水印
Fig.7 Original watermark and extracted watermark
6.2 鲁棒性测试
提取水印与原始水印的归一化相关系数(NC)往往作为评价水印鲁棒性的标准。NC定义式如下：
NC=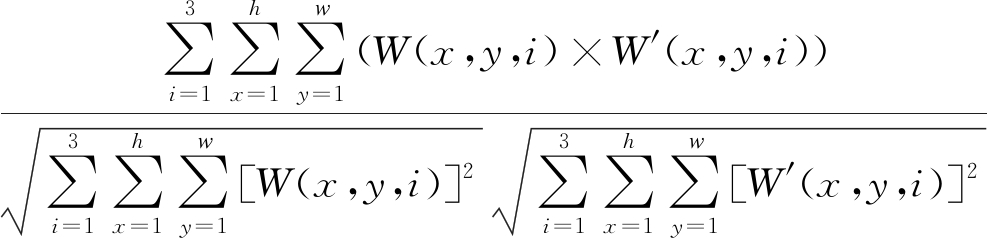
(10)
其中w和h分别是图像的宽度和高度，W和W′分别为原始水印图像和提取水印图像。
6.2.1 非几何攻击
非几何攻击即常见的信号处理攻击,是一种添加性的攻击方式,是对图像的像素值进行了修改。为测试本文算法在非几何攻击下的鲁棒性,取α=0.03,分别对Lena,Peppers,Baboon图像进行均值为0,方差为0.005,0.01的高斯噪声,椒盐噪声,斑纹噪声攻击;均值滤波,中值滤波,高斯低通滤波模板大小为3×3,5×5攻击;JPEG压缩因子为50,30攻击;对比度调整[0.2,0.8]、对比度增强0.2攻击。实验结果见表1。
表1 非几何攻击实验(NC)
Tab.1 Non-geometric attack experiment (NC)
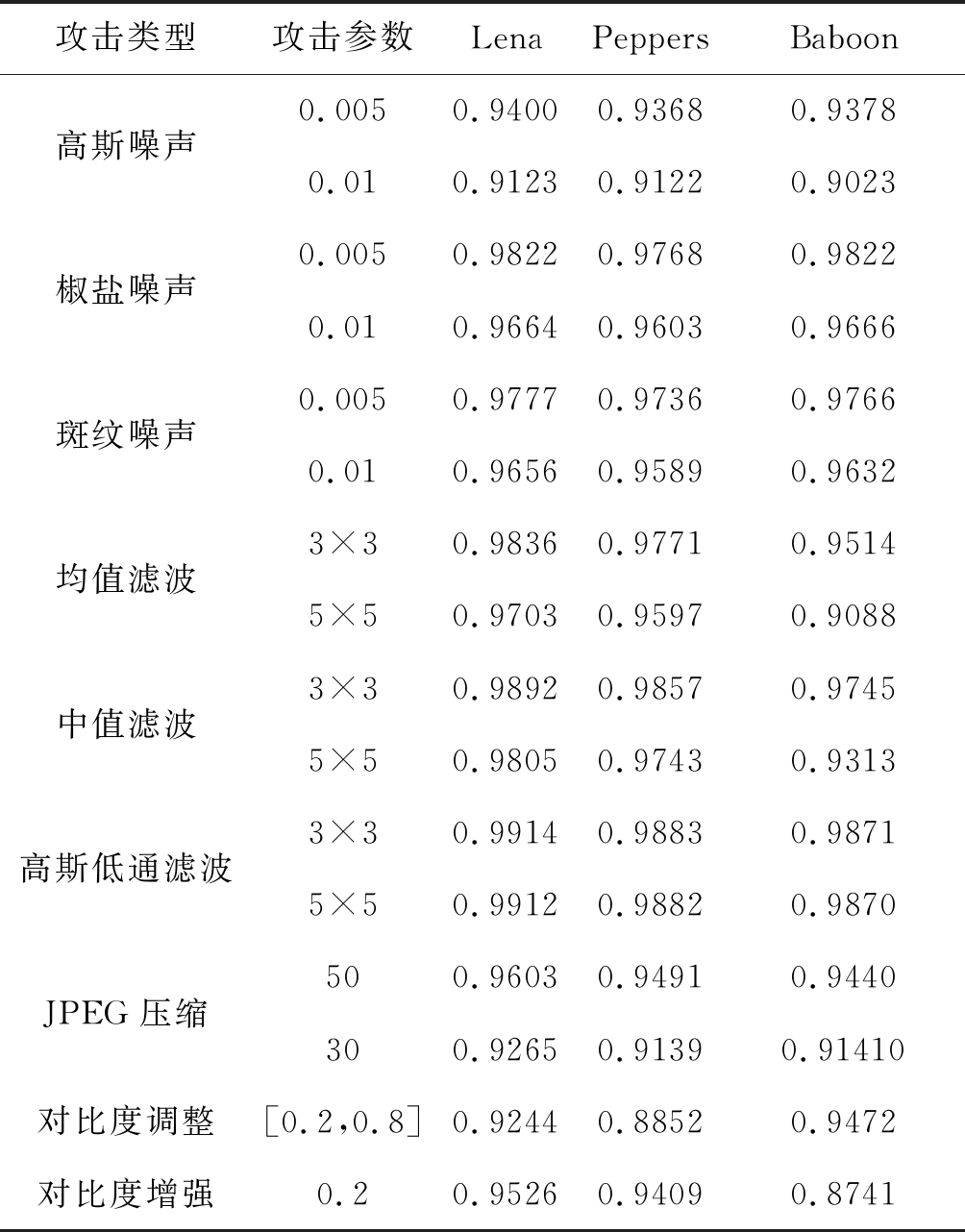
攻击类型攻击参数LenaPeppersBaboon高斯噪声0.0050.94000.93680.93780.010.91230.91220.9023椒盐噪声0.0050.98220.97680.98220.010.96640.96030.9666斑纹噪声0.0050.97770.97360.97660.010.96560.95890.9632均值滤波3×30.98360.97710.95145×50.97030.95970.9088中值滤波3×30.98920.98570.97455×50.98050.97430.9313高斯低通滤波3×30.99140.98830.98715×50.99120.98820.9870JPEG压缩500.96030.94910.9440300.92650.91390.91410对比度调整[0.2,0.8]0.92440.88520.9472对比度增强0.20.95260.94090.8741
由表1可知,三幅载体图像对于不同类型噪声攻击NC都达到0.9以上,对于滤波攻击,NC值均在0.95以上,表明本文算法能有效的抵抗滤波攻击。对于JPEG压缩,在压缩因子为30时,最低NC仍在0.91以上。在调整图像对比度情况下,会使图像像素值大面积改变,提取水印的NC也在0.87以上。本文算法在常见的信号处理攻击下,水印信息有不错的提取效果,是因为Contourlet变换具有良好的方向性,选择稳定的低频子带嵌入水印的同时采用QR分解,其中U矩阵第2行第1列元素与第三行第1列元素的差值具有很强的稳定性,即便在图像遭受常见的攻击时,对各子块U矩阵中两元素差值影响较小,在合并通道前进行滤波处理,使得算法具有良好的抗噪性能,故本文算法对噪声攻击和其他非几何攻击具有强鲁棒性。
6.2.2 几何攻击和其他攻击
为了进一步验证本文算法的鲁棒性,选取Lena,Butterfly,Peppers图像,对嵌入水印后的载体图像采用旋转,剪切等几何攻击,其中旋转攻击既改变图像的像素值又改变像素的位置,是大部分水印算法的短板。另再采用组合攻击,马赛克攻击,篡改攻击测试其性能,其中具体组合攻击参数如下:(a)均值为0,方差为0.01的椒盐噪声+旋转10°;(b)压缩因子为50的JPEG压缩+右上剪切1/16; (c) 均值为0,方差为0.005的高斯噪声+左上1/4剪切;(d)左上剪切1/16+旋转10°。对图像分别做左上篡改1/16和中心篡改1/4攻击、8×8和16×16马赛克攻击。测试结果见表2,选取部分攻击和提取效果图见图8、图9。
图8 受到攻击的图像
Fig.8 Image under attack
图9中(a)～(l)的水印分别对应图8中(a)～(l)受到攻击的载体图像所提取的水印信息。对于旋转攻击,由于本文算法应用Radon变换进行旋转校正,所提取的水印NC值均大于0.9258,如图8(b)未进行旋转校正所提取的水印如图9(b)所示,已经完全失真。如图8(c)进行旋转校正所提取的水印如图9(c)所示,水印信息可以较好的恢复,所以本文算法可以有效的抵抗旋转攻击。对于剪切攻击,在剪切1/16,和1/4的情况下,提取效果稳定,在剪切1/2时如图8(h)由于图像信息损失过多,效果不佳,这也符合客观情况。对于组合攻击,对图像改变很大,但本算法所提取的NC依旧在0.9左右,表现出良好的鲁棒性。从表2和图8(k)看出,即使篡改1/4也能很好的恢复水印。马赛克攻击是用块像素的均值代替原始像素值,在8×8马赛克攻击时,提取效果良好,NC大于0.95,而在16×16马赛克攻击时,由于像素值改变太多导致NC值下降至0.8左右。本文算法能有效抵抗几何攻击,是因为采用Baker映射+CML的方式将水印均匀的置乱,使得错误分散开来,补偿剪切攻击带来的大面积0像素值;采用Radon变换获取图像的角度信息以此校正旋转攻击导致图像大幅度的改变;采用CT-QR双变换域能够有效的提取图像特征。综上所述,本文算法对大部分攻击在一定范围内具有较强的鲁棒性。
表2 不同攻击下水印提取NC值
Tab.2 Extracting NC value of watermark under different attacks
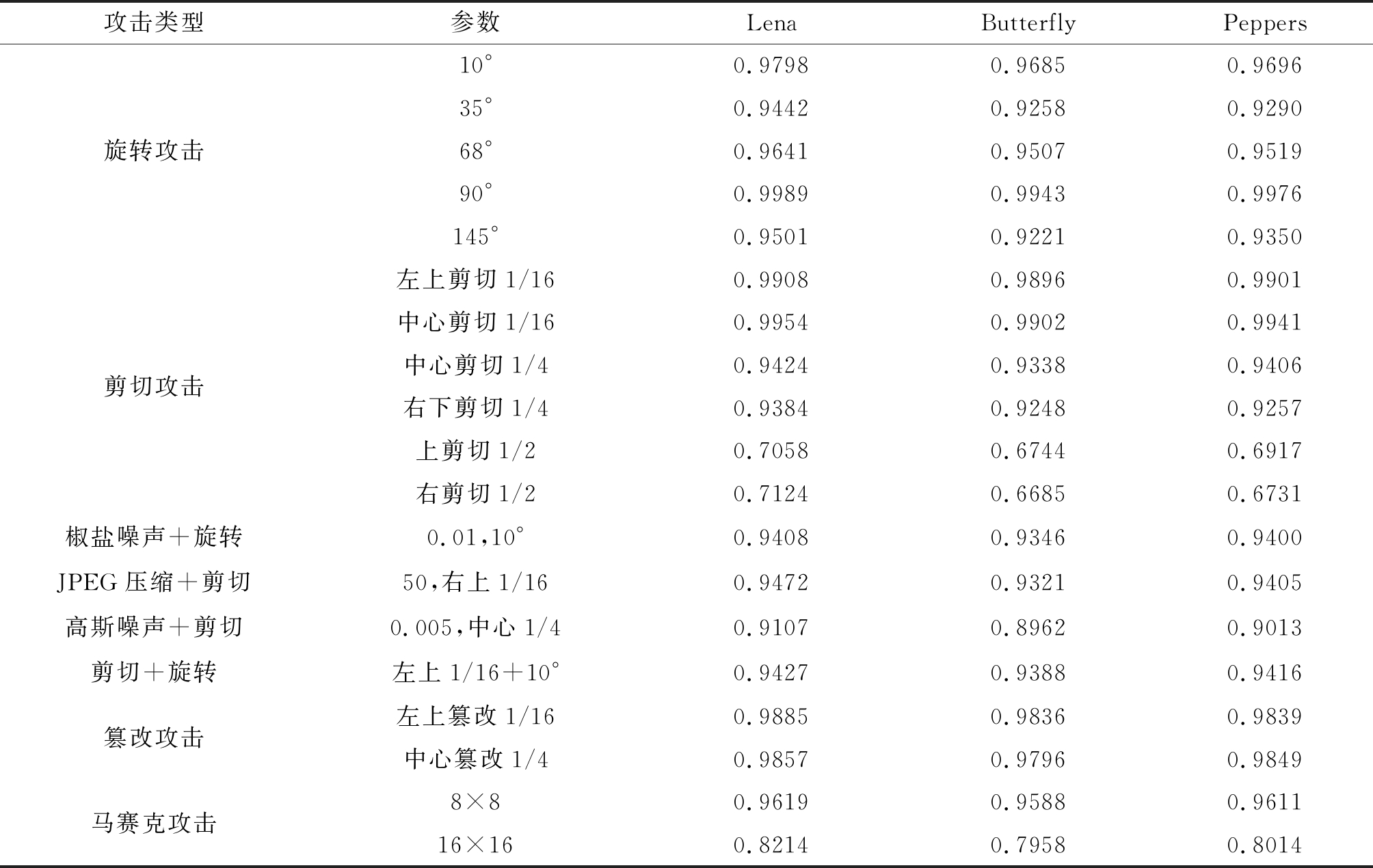
攻击类型参数LenaButterflyPeppers旋转攻击10°0.97980.96850.969635°0.94420.92580.929068°0.96410.95070.951990°0.99890.99430.9976145°0.95010.92210.9350剪切攻击左上剪切1/160.99080.98960.9901中心剪切1/160.99540.99020.9941中心剪切1/40.94240.93380.9406右下剪切1/40.93840.92480.9257上剪切1/20.70580.67440.6917右剪切1/20.71240.66850.6731椒盐噪声+旋转0.01,10°0.94080.93460.9400JPEG压缩+剪切50,右上1/160.94720.93210.9405高斯噪声+剪切0.005,中心1/4 0.91070.89620.9013剪切+旋转左上1/16+10°0.94270.93880.9416篡改攻击左上篡改1/160.98850.98360.9839中心篡改1/40.98570.97960.9849马赛克攻击8×80.96190.95880.961116×160.82140.79580.8014
图9 不同攻击下水印的提取效果
Fig.9 Effect of watermark extraction under different attacks
6.3 对比实验
为验证本文算法的优越性,将本文算法和近来较先进的水印算法文献[13]、[14]中没有设密钥的算法相比较,选取Lena图像,进行其几何攻击与非几何攻击测试,实验结果如表3。
从表3中可以看出,仅在高斯噪声攻击下,NC值略低于文献[13]、文献[14],在其他攻击下均有强鲁棒性,尤其在旋转、剪切攻击上具有明显的优势,水印提取NC值达0.94以上。相比文献[13]、[14]算法,本文算法在几何攻击与非几何攻击,更加具有强鲁棒性。
表3 鲁棒性对比实验(NC)
Tab.3 Robustness comparison experiment (NC)
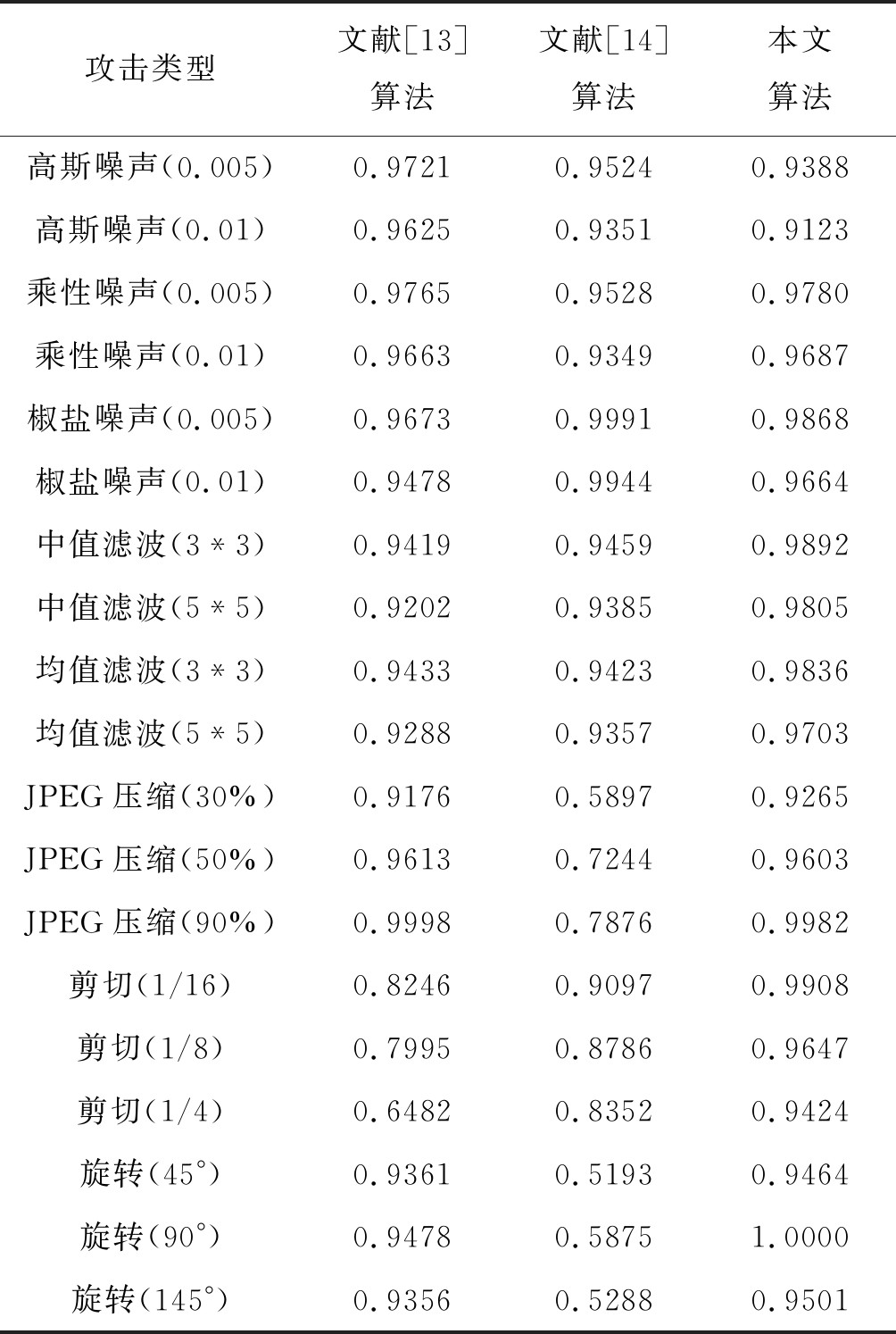
攻击类型文献[13]算法文献[14]算法本文算法高斯噪声(0.005)0.97210.95240.9388高斯噪声(0.01)0.96250.93510.9123乘性噪声(0.005)0.97650.95280.9780乘性噪声(0.01)0.96630.93490.9687椒盐噪声(0.005)0.96730.99910.9868椒盐噪声(0.01)0.94780.99440.9664中值滤波(3*3)0.94190.94590.9892中值滤波(5*5)0.92020.93850.9805均值滤波(3*3)0.94330.94230.9836均值滤波(5*5)0.92880.93570.9703JPEG压缩(30%)0.91760.58970.9265JPEG压缩(50%)0.96130.72440.9603JPEG压缩(90%)0.99980.78760.9982剪切(1/16)0.82460.90970.9908剪切(1/8)0.79950.87860.9647剪切(1/4)0.64820.83520.9424旋转(45°)0.93610.51930.9464旋转(90°)0.94780.58751.0000旋转(145°)0.93560.52880.9501
7 结论
本文将Baker映射和时空混沌系统对图像加密的方式运用于双彩色水印系统,结合Contourlet-QR分解的优势,利用Radon变换对图像进行旋转攻击的校正,建立了一种具有强鲁棒性的可实现盲提取的水印方案,该方案具良好的实用价值。大量实验表明,在常规攻击下,NC值最低0.8852,最高可达0.9989,单一的几何攻击NC也在0.92以上,在旋转+剪切双重几何攻击下,水印提取NC值最低可达0.9388。故本文算法在具有良好的不可见性的同时,能抵抗加噪、JPEG压缩、滤波、旋转、剪切、篡改、马赛克攻击、组合攻击等图像攻击方式,具有强鲁棒性。
[1] 丁兴号, 章登峰, 钱坤, 等. 基于无下采样Contourlet变换和人眼视觉系统的稳健盲水印算法[J]. 光学学报, 2009, 29(12): 3344-3350.
DING Xinghao, ZHANG Dengfeng, QIAN Kun, et al. A robust blind watermarking algorithm based on non-subsampled contourlet transform and human visual system[J]. Acta Optica Sinica, 2009, 29(12): 3344-3350.(in Chinese)
[2] TOMAR R, SHARMA H K, DUMKA A, et al. Blind watermarking technique for greyscale image using DCT and 1-D Walsh coding[C]∥2015 1st International Conference on Next Generation Computing Technologies (NGCT). Dehradun, India. IEEE, 2015: 365-369.
[3] ZHANG Guoyin, KOU Liang, ZHANG Liguo, et al. A new digital watermarking method for data integrity protection in the perception layer of IoT[J]. Security and Communication Networks, 2017, 2017: 1-12.
[4] 马玲, 张晓辉. 基于内积空间非空子空间变换关系的含水印彩色图像特征分析[J]. 计算机学报, 2017, 40(5): 1203-1217.
MA Ling, ZHANG Xiaohui. Characteristics of color images with watermark based on the relationship between non-void subspaces of inner space[J]. Chinese Journal of Computers, 2017, 40(5): 1203-1217.(in Chinese)
[5] 尚福华, 李盼池. 彩色图像的量子水印算法[J]. 信号处理, 2017, 33(11): 1424-1435.
SHANG Fuhua, LI Panchi. Quantum watermarking algorithm for color images[J]. Journal of Signal Processing, 2017, 33(11): 1424-1435.(in Chinese)
[6] 白韬韬, 刘真, 卢鹏. 基于QR码的Contourlet域数字水印算法[J]. 光电子.激光, 2014, 25(4): 769-776.
BAI Taotao, LIU Zhen, LU Peng. Digital watermarking scheme in Contourlet domain based on QR code[J]. Journal of Optoelectronics Laser, 2014, 25(4): 769-776.(in Chinese)
[7] LIU Shuai, PAN Zheng, SONG Houbing. Digital image watermarking method based on DCT and fractal encoding[J]. IET Image Processing, 2017, 11(10): 815- 821.
[8] ROY S, PAL A K. A robust blind hybrid image watermarking scheme in RDWT-DCT domain using Arnold scrambling[J]. Multimedia Tools and Applications, 2017, 76(3): 3577-3616.
[9] LI Jingyou, ZHANG Chaozhu. Blind and robust watermarking scheme combining bimodal distribution structure with iterative selection method[J]. Multimedia Tools and Applications, 2020, 79(1): 1373-1407.
[10]周琳, 张天骐, 冯嘉欣, 等. Blob-Harris特征区域结合CT-SVD的鲁棒图像水印算法[J]. 信号处理, 2020, 36(4): 520-530.
ZHOU Lin, ZHANG Tianqi, FENG Jiaxin, et al. Image watermarking algorithm based on blob-Harris feature region and CT-SVD[J]. Journal of Signal Processing, 2020, 36(4): 520-530.(in Chinese)
[11]陈青, 卜莹, 李伟. 基于BSVD分解和Radon变换的NSCT域鲁棒水印算法[J]. 包装工程, 2019, 40(13): 233-238.
CHEN Qing, BU Ying, LI Wei. Robust watermarking algorithm in NSCT domain based on BSVD decomposition and Radon transform[J]. Packaging Engineering, 2019, 40(13): 233-238.(in Chinese)
[12]SU Qingtang, YUAN Zihan, LIU Decheng. An approximate schur decomposition-based spatial domain color image watermarking method[J]. IEEE Access, 2019, 7: 4358- 4370.
[13]SU Qingtang, WANG Gang, ZHANG Xiaofeng, et al. A new algorithm of blind color image watermarking based on LU decomposition[J]. Multidimensional Systems and Signal Processing, 2018, 29(3): 1055-1074.
[14]KHANAM T, DHAR P K, KOWSAR S, et al. SVD-based image watermarking using the fast Walsh-hadamard transform, key mapping, and coefficient ordering for ownership protection[J]. Symmetry, 2019, 12(1): 52.
[15]PICHLER F, SCHARINGER J. Finite dimensional generalized baker dynamical systems for cryptographic applications[M]. Computer Aided Systems Theory — EUROCAST′95. Berlin, Heidelberg: Springer Berlin Heidelberg, 1996: 465- 476.
[16]张雪. 基于DNA序列和DWT的双彩色图像盲水印研究[D]. 开封: 河南大学, 2017.
ZHANG Xue. Research on blind watermarking of double color images based on DNA sequences and DWT[D]. Kaifeng: Henan University, 2017. (in Chinese)
[17]刘卓, 王永. 基于二维耦合映像格子模型的图像压缩加密方案[J]. 重庆邮电大学学报(自然科学版), 2020, 32(6): 1048-1057.
LIU Zhuo, WANG Yong. Image compression and encryption scheme based on the two-dimensional coupled map lattice model[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2020, 32(6): 1048-1057.(in Chinese)
[18]DO M N, VETTERLI M. The contourlet transform: An efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing, 2005, 14(12): 2091-2106.
[19]SU Qingtang, NIU Yugang, LIU Xianxi, et al. Embedding color watermarks in color images based on Schur decomposition[J]. Optics Communications, 2012, 285(7): 1792-1802.
[20]GUO Yong, LI Bingzhao. Blind image watermarking method based on linear canonical wavelet transform and QR decomposition[J]. IET Image Processing, 2016, 10(10): 773-786.
[21]ESSAIDANI D, SEDDIK H, BEN BRAIEK E. Exploiting asynchronous invariance for resistant encrypted watermark embedded in Radon field[C]∥2013 World Congress on Computer and Information Technology (WCCIT). Sousse, Tunisia. IEEE, 2013: 1- 8.
