1 引言
高光谱图像包含有丰富的光谱信息,目前已经广泛地应用到地物信息提取等方面。由于空间分辨率低、地形复杂等原因,一个像元总是包含着不同的地物,这种现象被称为“混合像元”。因此,一般采用高光谱解混对高光谱数据进行预处理操作。高光谱解混就是将混合的像元分解成端元和对应丰度的过程,丰度表示每种端元在混合像元中所占的比例[1]。
目前,混合像元分解使用的模型主要是线性混合模型[2](Linear Mixing Model,LMM)和非线性混合模型[3](Nonlinear Mixting Model,NMM)。相比于非线性混合模型,线性混合模型因其简单且物理意义明确而被广泛的使用。在线性混合模型的基础上,常用三类方法进行像元的分解:第一类是基于单纯形几何理论的方法[4],第二类是基于字典稀疏回归的方法[5],第三类是基于统计的方法[6]。第一类方法认为高光谱数据构成了单纯形,端元是单纯形的顶点。因此,几何方法常用来做端元的提取。N-FINDR[7]和顶点分量分析[8](Vertex Component Analysis,VCA)是比较流行的几何方法。虽然这些方法简单快捷,但是有一个很大的缺点,需要满足光谱的数据中有纯端元的假设。而且这些方法主要集中于端元的提取,丰度的估计一般采用完全约束的最小二乘算法[9](Fully Constrained Least Squares,FCLS)。第二类方法是在已知端元谱库的基础上估计光谱图像中出现的端元所对应的丰度。随着美国地质调查局光谱库的出现,基于字典稀疏回归的方法越来越受到重视。
第三类方法是在有一定约束条件下求解线性混合模型,能够同时得到端元和对应的丰度。独立成分分析[10](Independent Component Analysis,ICA)和非负矩阵分解[11](Nonnegative Matrix Factorization,NMF)是两种典型的统计方法。ICA可以从混合的高光谱数据中提取出独立的源,并且它假设丰度是独立的。但是,实际情况中丰度要满足和为1的约束,与丰度独立的假设矛盾,所以假设不成立。NMF将一个高维的数据分解成两个非负的矩阵:一个由基向量组成,另外一个由系数向量组成。NMF用于高光谱解混不需要假设有纯像元的存在,而且也可以同时确定端元和对应的丰度。因为这些优点,NMF在高光谱图像领域得到了广泛的应用。然而,NMF的目标函数具有非凸性,所以往往容易陷入到局部最小值中。仅有非负约束是远远不够的,为了得到更加精确的分解效果,需要考虑到更多的约束条件。通过对光谱特性等方面的研究,很多不同的约束已经应用在了高光谱解混当中。其中一种方法是最小体积和丰度稀疏约束的NMF[12],该方法在NMF模型的基础上引入了端元的几何特征和丰度的稀疏性作为约束条件。另外一种方法是端元的差异性约束的NMF[13],所提出的约束可以测量端元之间的差异性并且约束端元的平滑性。Qian等[14]使用L1/2范数对丰度的稀疏性进行约束,不仅有很好的稀疏性,而且满足丰度和为一的约束。祝等[15]提出了全变差和加权稀疏约束的NMF,同时利用了丰度行的分段平滑性和列的稀疏性。Huang等[16]提出了一种结合L2,1范数和L1,2范数的NMF模型,可以同时实现对带噪声和像素噪声的鲁棒性。
上面提到的这些方法,虽然取得了不错的效果,但是都忽略了高光谱的空间信息。Lu等[17]和Yang等[18]考虑了高光谱内部的流行结构,并通过图模型理论将其嵌入到NMF模型,使相似性比较高的邻近像元可以联合在一起实现解混。Tong等[19]和甘等[20]考虑到了高光谱数据的欧氏距离内部结构和黎曼几何结构,提出了图约束的NMF。Wang等[21]、Lu等[22]对原有的高光谱数据集进行聚类,使用聚类标签强化相似性和相异性特征。Liu等[23]提出了一种四邻域加权约束的非负矩阵分解,尽管也取得了不错的效果,但是邻域结构固定,对空间信息的利用不够充分。虽然上述方法对空间信息的使用进行了一些尝试,但是如何有效地利用空间和光谱信息仍然是一个很大的挑战。
本文提出了一种新的基于自适应局部邻域加权约束的非负矩阵分解(Nonnegative Matrix Factorization Based on Adaptive Local Neighborhood Weighting Constraint,NMF-ALNWC),不仅根据丰度的数据特点设计了一种有效地确定局部邻域的方法,而且在邻域内计算的权重充分地利用了空间光谱信息。提出的方法大致可以分为三个步骤:首先,根据丰度的数据特点,确定给定像元的局部邻域范围。其次,在邻域范围内,利用空间距离和相关性计算给定像元和邻域像元的权重。最后,将给定像元的丰度与其邻域内像元的丰度之间的相似性作为约束项加到NMF模型中,并用权重对约束项进行加权操作。
本文的其余部分安排如下。第2部分介绍NMF解混的原理。第3部分详细介绍局部邻域的确定以及权重的计算。第4部分提出了基于自适应局部邻域加权约束的非负矩阵分解模型。在第5部分,利用Japser Ridge数据集和Urban数据集进行了实验和分析。最后,第6部分对本文进行了总结,并对未来的研究提出了一些建议。
2 NMF解混原理
2.1 线性混合模型
LMM假定像元是由端元及其相应的丰度以线性组合的方式产生的,基于LMM,高光谱的数据可以表示为:
Y=AS+n
(1)
其中,Y∈RL×N表示L个波段、N个像元的高光谱数据矩阵,A∈RL×P为端元矩阵,P是端元数,S∈RP×N为丰度矩阵,n∈RL×N表示高斯噪声。一般,LMM有两个约束条件:丰度的非负性约束以及和为1约束。具体的表述如下:
S≥0
(2)
(3)
其中![]() 和
和![]() 表示元素均为1的行向量。
表示元素均为1的行向量。
2.2 非负矩阵分解
线性混合模型将高光谱数据矩阵分解成端元矩阵和丰度矩阵,而非负矩阵分解是将高维的原始矩阵分解成两个低维非负矩阵,形如:
X≈WH
(4)
矩阵X∈Rm×n分解成两个矩阵W和H,W∈Rm×t,H∈Rt×n,并且满足t
由此可以看出,非负矩阵分解的表达形式和线性混合模型十分的契合,所以将非负矩阵分解的方法应用于高光谱解混中。为了衡量近似程度,常用的方式是计算X和WH的欧式距离来建立目标函数,如式(5)所示:
(5)
其中,||·![]() 是表示Frobenius范数。目标函数式(5)同时对W和H估计为非凸函数,但是单独对W和H估计可转化为两个凸函数。因此,在求解全局最优解时,Lee等文章常采用梯度下降法推导出的乘法迭代规则[24]。式(5)的乘法迭代规则表示为:
是表示Frobenius范数。目标函数式(5)同时对W和H估计为非凸函数,但是单独对W和H估计可转化为两个凸函数。因此,在求解全局最优解时,Lee等文章常采用梯度下降法推导出的乘法迭代规则[24]。式(5)的乘法迭代规则表示为:
W←W.*XHT./WHHT
(6)
H←H.*WTX./WTWH
(7)
每次迭代过程中H都要满足非负性以及和为1约束。
3 局部邻域权重
在这一部分将具体介绍如何利用丰度的数据特点自适应地确定给定像元的局部邻域以及如何计算给定像元和邻域像元的权重。
3.1 局部邻域思想的引入
事实上,同质区域像元之间都存在一定的相似性,但是考虑到算法的复杂度和计算量,不能计算同质区域内所有像元之间的相似性。因此,提出了局部邻域,在考虑像元yi相似性时,仅考虑yi的局部邻域N(i)内的像元,yi表示高光谱数据矩阵Y∈RL×N的第i列。
局部邻域N(i)的选取有多种形式,常见的有方形结构[25]和圆形结构,优点是操作简单,但是结构固定,在处理过渡区域、边界区域时不能很好地利用空间信息。通过对丰度数据特点的深入研究,本文提出了一种可以充分利用空间信息确定邻域的方法。

图1 局部区域划分图
Fig.1 Local area division diagram
该方法依据的原理为:整幅高光谱图像可以分成许多不同的相似区域,每一个相似区域都比较接近于一种地物,即一种端元。图1为高光谱图像一个局部区域的划分图。假设在区域1的地物比较接近于端元K,那么端元K对应的丰度图在区域1的丰度值就比较大,而其他端元对应的丰度图在该区域的丰度值比较小。因此,通过比较不同丰度图在同一位置的丰度值即可判断出与该位置像元相近的端元。然后,利用相似区域内对应端元的丰度值比较接近的特点确定局部邻域。下面将对该方法进行详细说明。
3.2 确定局部邻域
首先,确定每一个像元的空间坐标。假设高光谱图像排列在一个r×c的网格上,并有r×c=N,网格上的每一个位置都对应一个L维的像素向量,即一个像元。将高光谱数据矩阵Y∈RL×N的N个像元按照从左到右,从上到下的顺序排列到网格当中。这样,就可以得到像元yi和它空间位置(p,q)的关系
i=(p-1)*r+q
(8)
i=(q-1)*c+p
(9)
其次,为了得到临近像元之间的空间关系,必须暂时改变丰度数据的表示方式。将丰度矩阵S的每一行,按照其像元的空间位置整理成对应的矩阵。以其中任意一个端元的丰度SQ∈R1×N为例,设其被整理为![]() 其中r和c分别表示矩阵的行数和列数。P个端元对应的P行丰度分别被整理成
其中r和c分别表示矩阵的行数和列数。P个端元对应的P行丰度分别被整理成![]() 中的元素表示为
中的元素表示为![]() 元素值的大小等于丰度值。
元素值的大小等于丰度值。
然后,在确定空间坐标为(i, j)的给定像元的局部邻域之前,需要先判断该像元接近于哪种端元。通过比较空间坐标为(i, j)的各丰度矩阵对应的丰度值![]() 的大小,找到最大的
的大小,找到最大的![]() 即可判断该像元比较接近于端元K。
即可判断该像元比较接近于端元K。
最后,根据相似区域对应丰度值比较接近的特点,在端元K对应的丰度矩阵![]() 中,以
中,以![]() 为中心,3×3窗口内找到所有丰度值在
为中心,3×3窗口内找到所有丰度值在![]() 范围内的位置作为局部邻域N(i),τ是一个可控的参数。遍历每一个像元即可得到每一个像元的局部邻域。
范围内的位置作为局部邻域N(i),τ是一个可控的参数。遍历每一个像元即可得到每一个像元的局部邻域。
3.3 计算权重
为了确定局部邻域像元yj(j∈N(i))对给定像元yi的贡献,需要考虑两个因素:空间距离和局部邻域像元的相似性。由于局部邻域内的像元对应的丰度比较接近,将通过丰度的相似性来衡量像元的相似性。基于上述的分析,局部邻域像元yj对yi权重的贡献可以定义为:
(10)
其中,α表示像元之间的空间距离,β表示像元之间的相似性,![]() 和β的取值范围都在(0,1],属于同一个量级。假设第i个像元和第j个像元的空间坐标分别是(r,s)和(k,l),我们简单地定义α和β为:
和β的取值范围都在(0,1],属于同一个量级。假设第i个像元和第j个像元的空间坐标分别是(r,s)和(k,l),我们简单地定义α和β为:
α=|r-k|+|s-l|
(11)
β=〈si·sj〉
(12)
其中,|·|表示绝对值,〈·〉表示内积,α表示像元yi和yj之间的曼哈顿距离,β表示丰度si和sj的相似性,si表示的丰度矩阵S的第i列。当距离比较近,丰度相似度比较高时,第j个像元对第i个像元的影响就越大。显然,wij可以衡量第j个像元在空间距离和相似性方面对第i个像元的贡献。
对于给定像元yi,局部邻域内的全部像元对它的影响可以表示为χi,χi可以通过计算每个邻域像元yj(j∈N(i))对yi贡献的和来表示。例如:
(13)
4 基于自适应局部邻域加权约束的非负矩阵分解模型
由于NMF模型的目标函数的非凸性[24],将NMF算法直接应用于高光谱解混会导致局部极小值问题。为了更好的对端元A和丰度S估计,就需要在NMF的模型中加入一些辅助约束。在这里,根据给定像元的丰度与局部邻域内像元的丰度相似的特点,将局部邻域丰度的先验信息作为约束项,并对其进行加权操作,充分地利用了高光谱的空间信息和局部邻域像元的相似性,提高了解混的精度。基于自适应局部邻域加权约束的NMF模型为
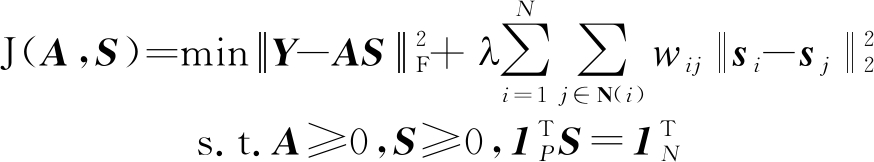
(14)
其中λ是一个可调参数用于平衡近似误差和约束项,wij在2.3节已经提出,给定像元的丰度和局部邻域像元丰度相似性越高,对应的权重也越大,反之,相似性越低,对应的权重就越小。接下来,目标函数式(14)的求解采用梯度下降法,将式(14)的优化分解为以下两个子问题:
(15)
(16)
提出来的方法包含两个步骤:1)端元估计;2)丰度估计;下面将详细说明迭代更新规则。
4.1 迭代更新规则
1)端元估计:估计端元的目标函数最小化公式如下:
J(A)=min||Y-AS![]() +Tr(ψA)
+Tr(ψA)
(17)
在式(17)中,对目标函数增加了非负约束,ψ∈RL×P是一个矩阵形式的拉格朗日乘子。为了找到式(17)的最小值,常用的方法是直接对式(17)求导,并设置它的偏导数为0。根据Karush-Kuhn-Tucker(K-K-T)条件,得到如下的线性方程:
▽AJ(A)=2ASST-2YST+ψ=0
(18)
A.*ψ=0
(19)
其中.*表示矩阵对应元素相乘,(·)T表示矩阵的转置。式(17)的左右两边同时.*矩阵A,可以得到如下方程式:
A.*(2ASST)-A.*(2YST)+A.*ψ=0
(20)
把式(19)代入到式(20),就得到了端元的更新规则
A←A.*(YST)./(ASST)
(21)
其中./表示矩阵对应元素相除。
2)丰度估计:估计丰度的目标函数最小化表示为:
J(S)=min||Yf-AfS![]() +
+![]()
(22)
其中,Yf和Af是增广矩阵,拉格朗日乘子Γ∈RP×N。
(23)
式中δ是一个正常数,用于调整丰度和为1的约束,δ越大,S的每一列的和越接近1,在实验中δ都设置为15。数学上,最小化式(22)的K-K-T条件表示为
(24)
S.*Γ=0
(25)
类似地,式(24)的左右两边同时.*矩阵S,可以得到更新规则
S←S.![]()
(26)
其中,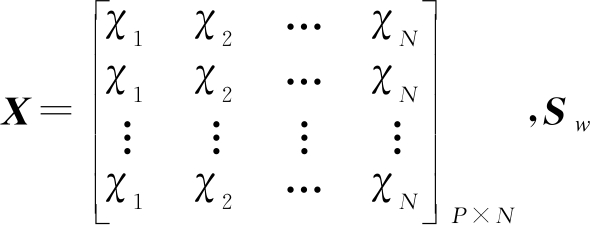 的第i列表示为
的第i列表示为![]()
4.2 收敛性的证明
NMF-ALNWC的目标函数如式(14)所示。这一小节的目的是证明目标函数在更新步骤中是单调非增的。也就是说,如果Ak,Sk是第k次迭代的值,Ak+1,Sk+1是第k+1次迭代的值,需要证明
J(Ak+1,Sk)≤J(Ak,Sk)
(27)
J(Ak+1,Sk+1)≤J(Ak+1,Sk)
(28)
其中更新规则分别是式(21)和式(26)。不等式(27)的证明Lee和Seung已经给出。现在对不等式(28)的证明如下。
因为目标函数在S的列中是可分离的,所以只关注S的每一列来证明不等式,然后目标函数变成了
(29)
为了证明不等式,首先定义一个辅助函数G(s,sk),这个辅助函数需要满足G(sk,sk)=J(sk),G(s,sk)≥J(s)和![]() 因此,在每一次更新中J(sk+1)≤G(sk+1,sk)≤G(sk,sk)=J(sk)保证了不等式的成立。
因此,在每一次更新中J(sk+1)≤G(sk+1,sk)≤G(sk,sk)=J(sk)保证了不等式的成立。
根据[26],我们定义辅助函数G为
G(s,sk)=J(sk)+(s-sk)(▽J(sk))T+![]()
(30)
其中,K(sk)=diag((ATAsk+λχisk)./sk)。
显然,辅助函数G满足G(sk,sk)=J(sk)。接下来,要证明函数G第二个条件G(s,sk)≥J(s)也是满足的。J(s)在sk点的泰勒展开式为
J(s)=J(sk)+(s-sk)(▽J(sk))T+![]()
(31)
根据式(30)和式(31),可以得到
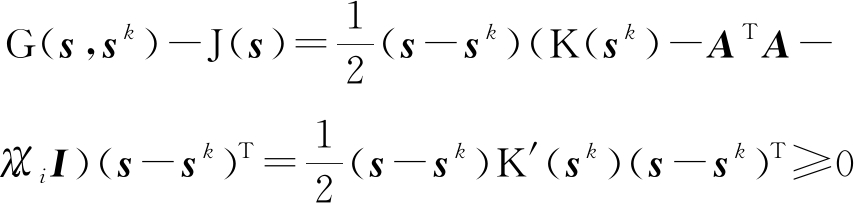
(32)
其中K′(sk)=diag(ATAsk./sk)-ATA,这已经在[24]被证明是半正定矩阵。因此,辅助矩阵(30)的最小值sk+1满足J(sk+1)≤J(sk)。收敛性的证明已完成。
由于函数G是一个半正定的二次矩阵,很容易计算它的最小值sk+1
sk+1=sk-▽J(sk)K-1(sk)=sk-![]()
![]()
(33)
这是所需的更新规则。
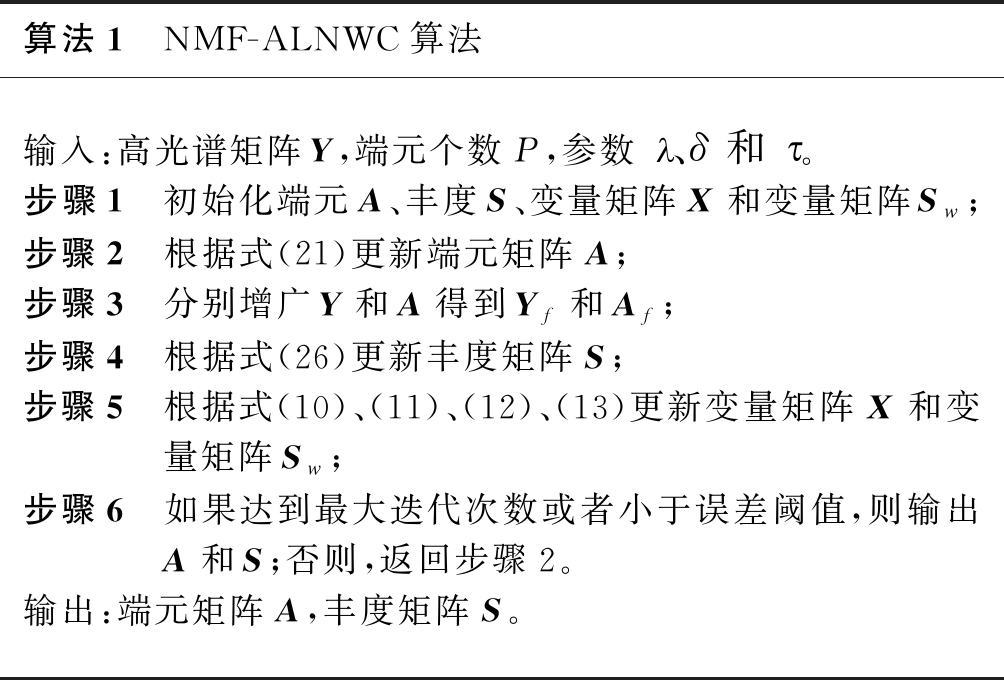
4.3 算法及参数设置
本节讨论NMF-ALNWC算法具体实现的一些问题,包括端元数目估计、端元初始化、丰度初始化、终止条件以及具体的算法步骤。
端元数目估计使用最小信号子空间识别算法(Hysime)[27]。端元的初始化采用VCA算法,丰度的初始化采用FCLS算法。NMF-ALNWC算法的终止条件采用两个常用的标准:设置最大迭代次数Tmax,当迭代的次数大于预先设置的Tmax时,迭代停止,Tmax设置为500。设置误差阈值ε,定义近似误差为:
d=||Y-AS![]()
(34)
在迭代过程中,当d的值小于预先设定的误差阈值ε时,迭代结束,ε设置为1×10-3。最后,本文所提出的NMF-ALNWC模型如算法1所示。
5 实验结果和讨论
在这一节,使用Japser Ridges数据集和Urban数据集来评估算法的性能,具体的评价指标有两个:光谱角距离(SAD)和均方根误差(RMSE)。对于第k个端元而言,SAD用于比较真实的端元Ak和估计的端元![]() 的相似性,可以定义为
的相似性,可以定义为
(35)
另一方面,均方根误差(RMSE)用于比较真实图像和重构图像的相似性。RMSE被定义为
(36)
其中,yij是真实图像的像素值,![]() 是重构图像的像素值。RMSE越小表示真实图像和重构图像的误差越小,即解混精度越高。
是重构图像的像素值。RMSE越小表示真实图像和重构图像的误差越小,即解混精度越高。
5.1 Japser Ridge数据集实验
将NMF-ALNWC算法应用于Japser Ridge高光谱数据集。该数据集原本包含224个波段,波长范围从0.38~2.5 μm,由于密集的水蒸气和大气效应,移除了1~3,108~112,154~166和220~224波段,剩余198个波段,使用100×100像素的数据区域。数据集主要包含了4种地物:树木、水体、土壤和道路。在这个场景中,提出的NMF-ALNWC算法要和EDCNMF[13],L1/2-NMF[14],SSRNMF[16],WNMF[23]和VCA-FCLS进行比较。不同算法的SAD值和RMSE是50次重复实验的平均值。NMF-ALNWC算法的参数λ设置为0.8,阈值τ设置为0.1。
下面,我们给出了不同算法应用于Japser Ridge数据集的实验结果。表1是不同算法在Japser Ridge数据集下的SAD值,前四行分别显示了水体,树木,土壤和道路在不同方法下的SAD值,最后一行显示了不同方法下所有地物SAD的均值。其中,最小的值用加粗的数字表示。通过观察表1,我们可以看出,NMF-ALNWC算法比其他算法获得更好的SAD值。图2显示了不同算法提取的端元和真实端元的对比,不同符号表示不同的算法。该图显示了NMF-ALNWC算法有较好的端元提取效果。图3是不同算法估计的丰度图和真实丰度图之间的对比,其中,纯黑部分的丰度值为0,纯白部分的丰
表1 Japser Ridge数据集下不同算法的SAD值
Tab.1 SAD values for different algorithms under the Japser Ridge data set
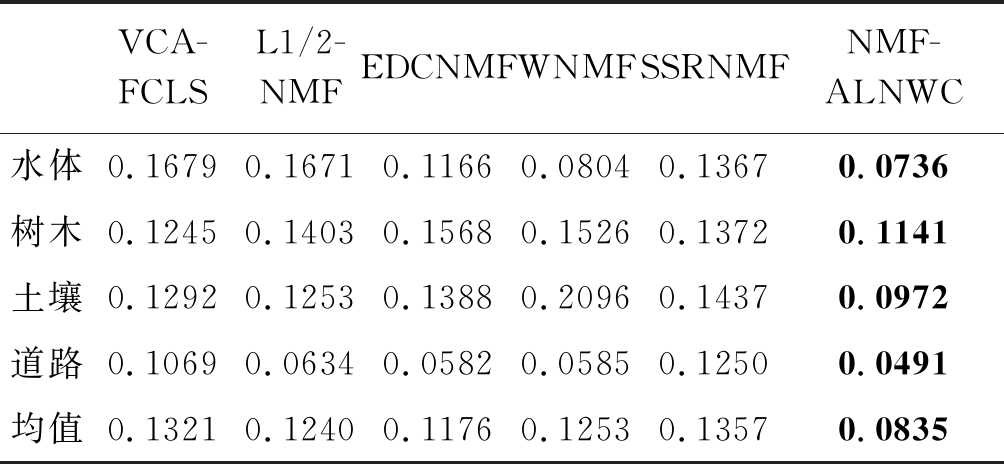
VCA-FCLSL1/2-NMFEDCNMFWNMFSSRNMFNMF-ALNWC水体0.16790.16710.11660.08040.13670.0736树木0.12450.14030.15680.15260.13720.1141土壤0.12920.12530.13880.20960.14370.0972道路0.10690.06340.05820.05850.12500.0491均值0.13210.12400.11760.12530.13570.0835
度值为1。通过对比,可以看出NMF-ALNWC算法比其他算法有更好的表现。表2显示了在不同方法下的RMSE值,NMF-ALNWC算法计算的均方根误差最小,即重构的图像更加接近于真实的图像。综上所述,在Japser Ridge数据集下NMF-ALNWC算法有较好的解混效果。
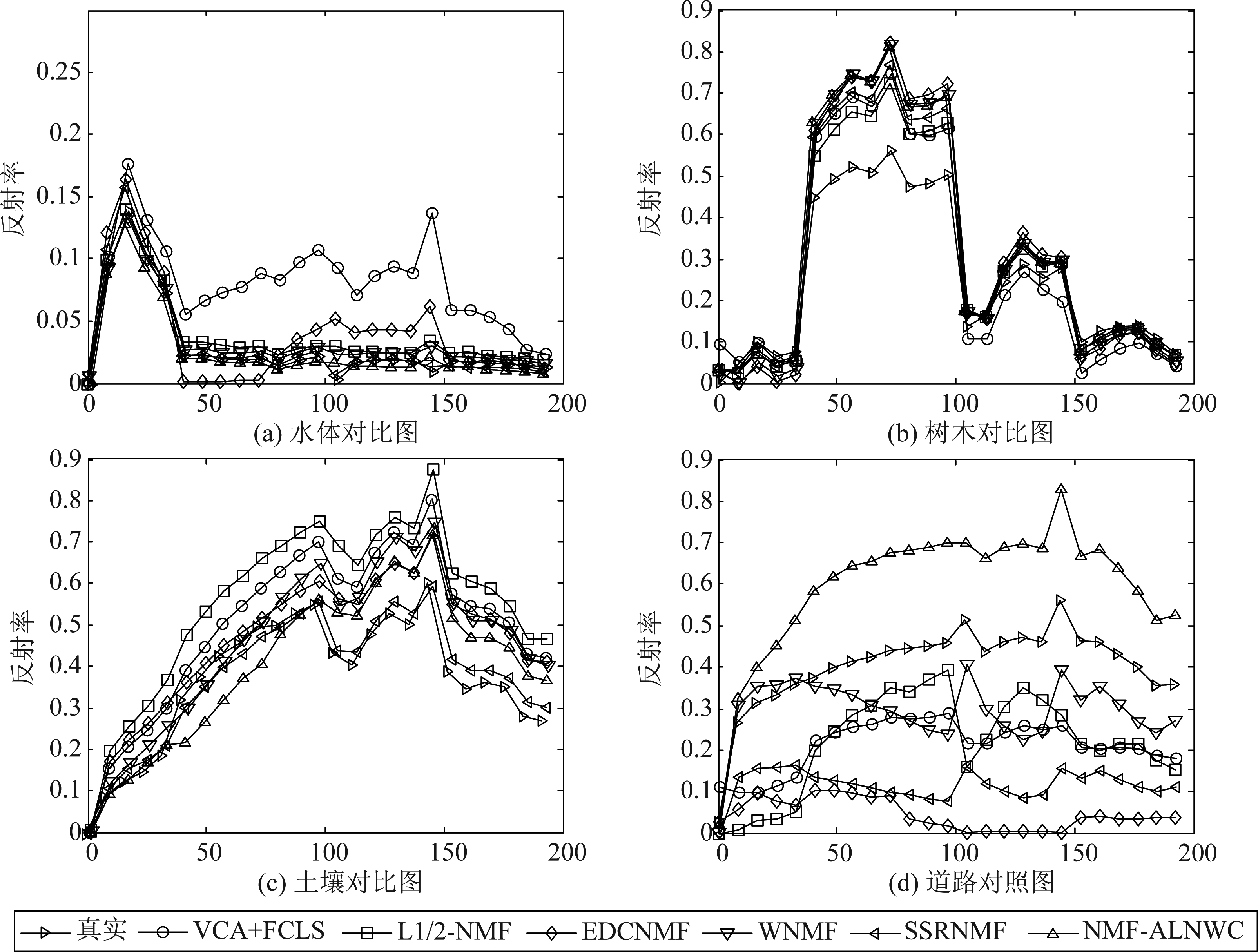
图2 Japser Ridge数据集下真实端元和不同算法提取端元的对比图
Fig.2 A comparison graph of real endmembers and endmembers extracted by different algorithms under the Japser Ridge data set

图3 Japser Ridge数据集下真实丰度和不同算法估计丰度的对比图
Fig.3 A comparison graph of real abundance and abundance estimated by different algorithms under the Japser Ridge data set
表2 Japser Ridge数据集下不同算法的RMSE值
Tab.2 RMSE values for different algorithms under the Japser Ridge data set
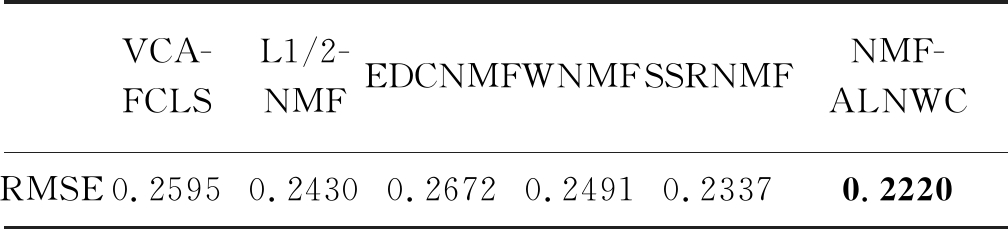
VCA-FCLSL1/2-NMFEDCNMFWNMFSSRNMFNMF-ALNWCRMSE0.25950.24300.26720.24910.23370.2220
5.2 Urban数据集实验
在这一节,我们将使用Urban高光谱数据集。Urban是高光谱解混研究中使用的最广泛的高光谱数据之一。数据集由210个波段组成,但是由于水蒸气和大气的影响,存在一些低信噪比的噪声带,包括1~4、76、87、101~111、136~153和198~210。除去这些噪声带,我们使用的Urban数据集包含了162个有效波段。该场景主要由道路、草地、树木、屋顶和土壤等地物组成,大小为307×307像素。
为了验证所提出的NMF-ALNWC算法的性能,使用EDCNMF,L1/2-NMF,WNMF和VCA-FCLS四种算法进行对比。同样地,不同算法得到的SAD值和RMSE值是50次重复实验的平均值。NMF-ALNWC算法的参数λ设置为0.6,阈值τ设置为0.1。表3显示了不同地物在不同方法下的SAD值,通过数值之间的比较可以看出NMF-ALNWC算法取得更小的SAD值,即NMF-ALNWC算法提取的端元更加接近于真实的端元。表4是Urban数据集在不同算法下的RMSE值,比较前四种算法,可以发现利用空间信息的WNMF比其他算法取得更好的解混结果,不过WNMF对于空间信息的利用不够充分,本文提出的NMF-ALNWC算法能够更加充分地利用空间信息,因此,也取得了更好的解混效果。图4是不同算法估计的丰度图和真实丰度图之间的对比,通过观察,可以看出我们提出的算法比其他对比算法获得更好的丰度估计效果。综上所述,在Urban数据集下,NMF-ALNWC算法有不错的解混性能。

图4 Urban数据集下真实丰度和不同算法估计丰度的对比图
Fig.4 A comparison graph of real abundance and abundance estimated by different algorithms under the Urban data set
表3 Urban数据集下不同算法的SAD值
Tab.3 SAD values for different algorithms under the Urban data set
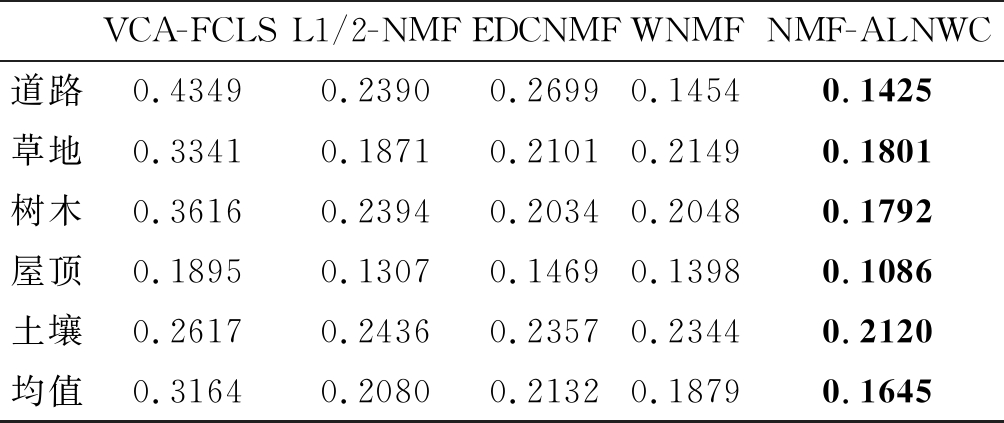
VCA-FCLSL1/2-NMFEDCNMFWNMFNMF-ALNWC道路0.43490.23900.26990.14540.1425草地0.33410.18710.21010.21490.1801树木0.36160.23940.20340.20480.1792屋顶0.18950.13070.14690.13980.1086土壤0.26170.24360.23570.23440.2120均值0.31640.20800.21320.18790.1645
表4 Urban数据集下不同算法的RMSE值
Tab.4 RMSE values for different algorithms under the Urban data set
VCA-FCLSL1/2-NMFEDCNMFWNMFNMF-ALNWCRMSE0.41560.37160.38920.34940.3064
6 结论
本文提出了一种新的高光谱解混算法NMF-ALNWC。NMF-ALNWC算法根据丰度的数据特点确定了给定像元的局部邻域,并在邻域范围内利用空间距离和像元的相似性计算给定像元和邻域像元的权重。有效地利用了高光谱的空谱信息,提高了解混的精度。通过实验,将提出的方法与其他解混方法进行对比,验证了NMF-ALNWC算法的优越性。然而,提出的算法还有提升的空间,例如,权重的空间距离可以考虑用一种非线性的方式来计算。另外,算法中具有丰富先验信息的端元未被使用。而且,NMF-ALNWC使用的是单层NMF,NMF隐藏层的信息也未被开发。因此在未来的工作中,可以尝试解决这些问题。
[1] 张兵. 高光谱图像处理与信息提取前沿[J]. 遥感学报, 2016, 20(5): 1062-1090.
ZHANG Bing. Advancement of hyperspectral image processing and information extraction[J]. Journal of Remote Sensing, 2016, 20(5): 1062-1090.(in Chinese)
[2] 袁静, 章毓晋, 高方平. 线性高光谱解混模型综述[J]. 红外与毫米波学报, 2018, 37(5): 553.
YUAN Jing, ZHANG Yujin, GAO Fangping. An overview on linear hyperspectral unmixing[J]. Journal of Infrared and Millimeter Waves, 2018, 37(5): 553.(in Chinese)
[3] 杨斌,王斌.高光谱遥感图像非线性解混研究综述[J].红外与毫米波学报, 2017, 36(2): 173-185.
YANG Bin, WANG Bin. Review of nonlinear unmixing for hyperspectral remote sensing imagery[J]. Journal of Infrared and Millimeter Waves, 2017, 36(2): 173-185.(in Chinese)
[4] LI Huali, LI Shutao, ZHANG Liangpei. Adaptive endmember extraction based sparse nonnegative matrix factorization with spatial local information[C]∥2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Milan, Italy. IEEE, 2015: 1753-1756.
[5] 张作宇, 廖守亿, 孙大为, 等. 稀疏差异先验信息支持的高光谱图像稀疏解混算法[J]. 测绘学报, 2020, 49(8): 1032-1041.
ZHANG Zuoyu, LIAO Shouyi, SUN Dawei, et al. Sparse hyperspectral unmixing algorithm supported by sparse difference prior information[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 1032-1041.(in Chinese)
[6] ZANOTTA D C, HAERTEL V, SHIMABUKURO Y E, et al. Linear spectral mixing model for identifying potential missing endmembers in spectral mixture analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 3005-3012.
[7] WINTER M E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data[C]∥SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation. Proc SPIE 3753, Imaging Spectrometry V, Denver, CO, USA. 1999, 3753: 266-275.
[8] NASCIMENTO J M P, DIAS J M B. Vertex component analysis: A fast algorithm to unmix hyperspectral data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 898-910.
[9] HEINZ D C, Chein-I-Chang. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 529-545.
[10]XIA Wei, LIU Xuesong, WANG Bin, et al. Independent component analysis for blind unmixing of hyperspectral imagery with additional constraints[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2165-2179.
[11]TONG Lei, ZHOU Jun, QIAN Yuntao, et al. Nonnegative-matrix-factorization-based hyperspectral unmixing with partially known endmembers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(11): 6531- 6544.
[12]王伞, 韩月, 王立国. 体积约束的稀疏NMF高光谱解混[J]. 哈尔滨工程大学学报, 2019, 40(12): 2077-2082.
WANG San, HAN Yue, WANG Liguo. Hyperspectral unmixing of sparse non-negative matrix factorization based on volume constraints[J]. Journal of Harbin Engineering University, 2019, 40(12): 2077-2082.(in Chinese)
[13]WANG Nan, DU Bo, ZHANG Liangpei. An endmember dissimilarity constrained non-negative matrix factorization method for hyperspectral unmixing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 554-569.
[14]QIAN Yuntao, JIA Sen, ZHOU Jun, et al. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4282- 4297.
[15]祝伟, 王雪, 黄岩, 等. 重加权稀疏和全变差约束下的深度非负矩阵分解高光谱解混[J]. 遥感学报, 2020, 24(4): 401- 416.
ZHU Wei, WANG Xue, HUANG Yan, et al. Reweighted sparsity regularized deep nonnegative matrix factorization with total variation toward hyperspectral unmixing[J]. Journal of Remote Sensing, 2020, 24(4): 401- 416.(in Chinese)
[16]HUANG Risheng, LI Xiaorun, ZHAO Liaoying. Spectral-spatial robust nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 8235- 8254.
[17]LU Xiaoqiang, WU Hao, YUAN Yuan, et al. Manifold regularized sparse NMF for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 2815-2826.
[18]YANG Shuyuan, ZHANG Xiantong, YAO Yigang, et al. Geometric nonnegative matrix factorization (GNMF) for hyperspectral unmixing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2696-2703.
[19]TONG Lei, ZHOU Jun, QIAN Bin, et al. Adaptive graph regularized multilayer nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 434- 447.
[20]甘玉泉, 刘伟华, 冯向朋, 等. 一种稀疏约束的图正则化非负矩阵光谱解混方法[J]. 光谱学与光谱分析, 2019, 39(4): 1118.
GAN Yuquan, LIU Weihua, FENG Xiangpeng, et al. A sparse constrained graph regularized nonnegative matrix factorization algorithm for hyperspectral unmixing[J]. Spectroscopy and Spectral Analysis, 2019, 39(4): 1118.(in Chinese)
[21]WANG Wenhong, QIAN Yuntao, LIU Hongfu. Multiple clustering guided nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 5162-5179.
[22]LU Xiaoqiang, DONG Le, YUAN Yuan. Subspace clustering constrained sparse NMF for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(5): 3007-3019.
[23]LIU Junmin, ZHANG Jiangshe, GAO Yuelin, et al. Enhancing spectral unmixing by local neighborhood weights[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(5): 1545-1552.
[24]LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-791.
[25]ZORTEA M, PLAZA A. Spatial preprocessing for endmember extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2679-2693.
[26]HOYER P O. Non-negative sparse coding[C]∥Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing. Martigny, Switzerland. IEEE, 2002: 557-565.
[27]BIOUCAS-DIAS J M, NASCIMENTO J M P. Hyperspectral subspace identification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(8): 2435-2445.
