1 引言
无线通信技术的快速发展使得同频段的不同信号间相互干扰的情况不可避免,宽频带的OFDM系统极易受到同频段其他窄带信号的影响发生频谱混叠现象,从而使系统性能下降,影响正常通信[1-3]。当前对窄带干扰的时域抑制方法主要包括窗函数法[4-5]和滤波法[6-7]两种:窗函数法从中间向两边衰减的特性可在一定程度上降低窄带干扰频谱泄露带来的影响,但加窗会使信号畸变带来额外信噪比损失且无法彻底消除干扰;滤波法可有效避免窄带干扰的频谱泄露现象,但受滤波器系数收敛时间影响会造成一定程度的延时。频域干扰抑制方法主要包括门限法[8-9]和置零法[10-11],门限法简单易实现,但在实际应用中,当设置的门限值过高时会造成干扰信号的漏检,设置的门限值过低时又会出现误检造成有用信号的丢失;置零法的干扰抑制效果会随着系统中受干扰频点个数的增加而逐渐变差,同时该方法还会造成部分有用信号的损失;预编码[12-13]干扰抑制方法高效且不会引起额外的性能损失,但该方法仅适用于干扰功率较低的场景,当干扰功率较高时,该方法的处理复杂度较高、抑制效果较差。另外,采用压缩感知方法[14-15]抑制干扰也成为了研究热点,但该方法仅可抑制OFDM信号中具有较高稀疏度的干扰分量。
在同一频段内,当OFDM信号与干扰信号在频域发生频谱混叠时,可通过信号的稀疏表示[16-18]理论实现OFDM信号带内干扰的抑制问题。稀疏表示理论的基础和前提是过完备字典的构造,包括分析字典和学习字典,学习字典较分析字典而言有更好的自适应性且表达形式繁多。若使用同一字典对混合信号进行稀疏表示,往往难以区分有用信号和干扰信号。因此,为确保各信号间的有效区分,可根据不同信号之间形态成分的差异性,将不同的信号用不同的字典进行稀疏表示。对于符号同步的OFDM系统,干扰信号会在一个OFDM符号内呈现多个周期,为得到干扰信号的最佳稀疏表示,可先利用符号同步信息对干扰样本信号按照符号周期进行分段,再使用OMP算法进行稀疏分解,继而实现干扰信号的精确重构。
本文对OFDM信号带内多路单载波通信干扰的抑制问题进行研究。根据OFDM信号和干扰信号形态成分的差异性,对不同的信号采用不同的学习字典进行稀疏表示,并结合符号同步信息设计了OFDM信号带内多路单载波通信干扰的抑制方法,仿真结果验证了本文算法的有效性。
2 多路单载波通信干扰场景下的OFDM接收信号模型
假设OFDM系统的子载波个数为N,则发射机的输出信号可以表示为:
(1)
式中,X(m)为第m个子载波上的调制信号。在OFDM系统的接收端,符号定时的变化会使系统产生相应的时延扩展,造成FFT运算窗的延时从而影响其他OFDM符号的传输,受时延扩展影响的OFDM信号可表示为x(n+τ)。当OFDM系统中存在加性高斯白噪声w(n)和带内干扰信号i1(n)与i2(n)时,系统的接收信号为:
![]()
w(n)+i1(n)+i2(n)
(2)
式中,H(m)为子载波m的信道响应,本文以MSK、2PSK、2FSK三类单载波通信信号作为带内干扰信号,随机选取两类信号进行组合,构造了两种多路干扰模型,分别为:
(1)2PSK和MSK干扰模型:
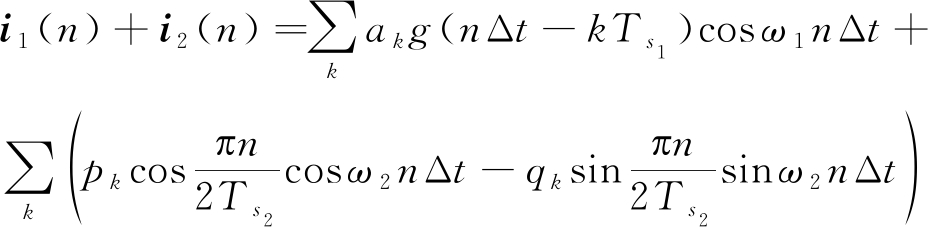
(3)
式中,Ts1和Ts2为2PSK、MSK信号的码元持续时间,Δt为采样间隔,g(nΔt-kTs1)为2PSK信号的基带脉冲波形,ak随发送的二进制符号变化;当MSK信号中的k为奇数时,pk发生改变、qk保持不变。
(2)2PSK和2FSK干扰模型:
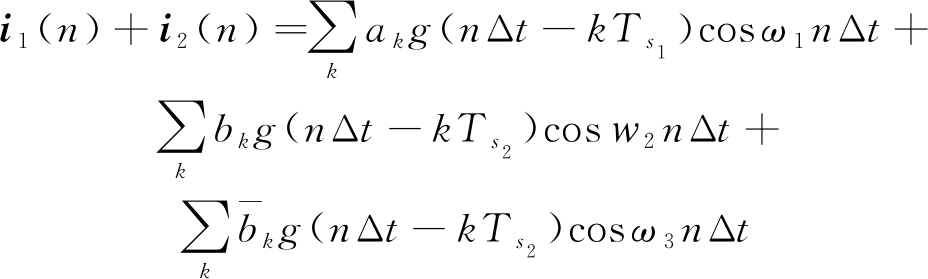
(4)
式中,![]() 和bk互为反码。仅考虑时延扩展对系统的影响,则经过FFT解调后,子载波m上的输出信号可表示为:
和bk互为反码。仅考虑时延扩展对系统的影响,则经过FFT解调后,子载波m上的输出信号可表示为:
![]()
X(m)H(m)+W(m)+I1(m)+I2(m)
(5)
式中,W(m)、I1(m)、I2(m)为子载波m上叠加的噪声分量和干扰分量。由式(5)可知,时延扩展的存在会使接收信号产生相应的相位偏移,使解调后的子载波相位发生变化,引起信号弥散。因此,在干扰抑制前有必要先进行系统的符号同步。假设同步后的多路干扰信号在一个OFDM符号内呈现λ1、λ2个周期,则有:
Ts=λ1Ts1=λ2Ts2
(6)
定义干信比为时域干扰信号功率与OFDM信号功率之比,随着干信比的增大,OFDM系统性能会逐渐下降,只有有效的抑制或分离接收信号中的干扰信号,才能最大程度得到所需要的有用信号。
3 带内多路单载波通信干扰抑制方法
本文根据不同信号间形态成分的差异性,使用K-SVD算法[19]训练OFDM信号和多路干扰信号的过完备字典,确保各信号间的有效区分:

(7)
式中,Θ、Φ、Ψ为过完备字典,l1、l2、l3为字典原子个数。
3.1 过完备字典的构造
K-SVD算法包括稀疏编码和字典更新两大步骤,稀疏编码阶段可表示为:
(8)
式中,y为样本信号,D为初始化字典,α为稀疏系数矩阵。在字典更新阶段,该算法的目标函数为:
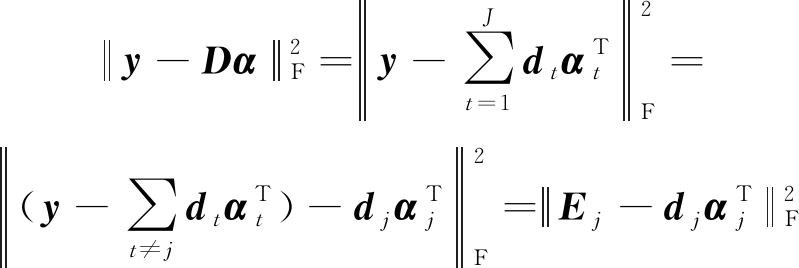
(9)
式中,dj为D上的第j列原子,![]() 为第j行稀疏系数矩阵,Εj表示误差。定义集合ωj={Γ|1≤Γ≤N,αj(Γ)≠0},为字典原子dj成分的样本索引集;选择Εj中ωj对应的列,记为
为第j行稀疏系数矩阵,Εj表示误差。定义集合ωj={Γ|1≤Γ≤N,αj(Γ)≠0},为字典原子dj成分的样本索引集;选择Εj中ωj对应的列,记为![]() 对
对![]() 进行SVD分解,更新字典原子和系数矩阵:
进行SVD分解,更新字典原子和系数矩阵:
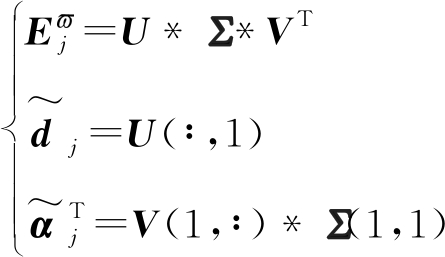
(10)
式中,U(∶,1)和V(1,∶)分别表示U和V的第一列和第一行元素;不断更新字典直至到达停止条件,终止迭代,完成过完备字典的构造。
3.2 信号的稀疏分解算法
直接使用过完备字典对全部样本信号进行稀疏分解,不易得到原始信号的最佳稀疏表示。因此,区别于传统的分解方法,本文在对OFDM信号的过完备字典进行稀疏分解时,先按照系统的符号个数对OFDM样本信号进行划分,再利用OMP算法进行稀疏分解,继而实现OFDM信号的精确重构。但因干扰信号会在一个OFDM符号内呈现多个周期,为提高干扰信号的分解精度,本文先利用符号同步信息将每个OFDM符号内的干扰样本进行符号周期分段,再使用OMP算法进行稀疏分解。OMP算法在提升迭代速度的同时可有效确保迭代后的残差与其他原子间的正交性。给定过完备字典D,原子参数集合γ,一个OFDM符号内的干扰样本信号{y(n),n∈1,…,P},假设y(n)中包含λ个整数倍周期的干扰分量,则可将其划分为:
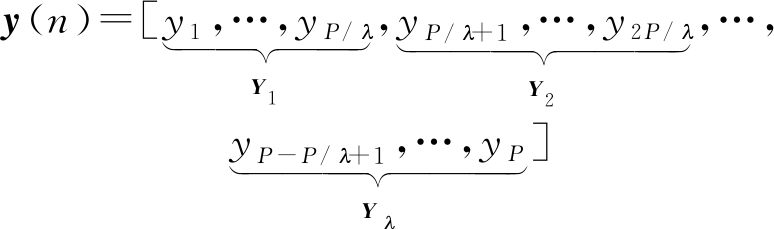
(11)
对于输入的任一样本{Yη,η∈1,…,λ},记初始残差r0Yη=Yη,对Yη求解最优原子dγ0:
r0Yη=〈r0Yη,rγ0〉dγ0+r1Yη
(12)
式中,〈r0Yη,dγ0〉dγ0是r0Yη在dγ0上的投影,r1Yη为经过一次分解后的残差,此时的dγ0与r1Yη正交,则:
||r0Yη||2=|〈r0Yη,dγ0〉|2+||r1Yη||2
(13)
记u0=dγ0,最大迭代次数为H,则最优原子dγh经过Gram-Schmidt正交化后的表达式为:
(14)
将残差rhYη投影到经过归一化处理uh上,可得:
rhYη=〈rhYη,uh〉uh+rh+1Yη
(15)
经过迭代后的稀疏系数可表示为:
(16)
依次对所有OFDM符号内的干扰样本进行分解,将分解得到的稀疏系数矩阵进行级联组合,可得:
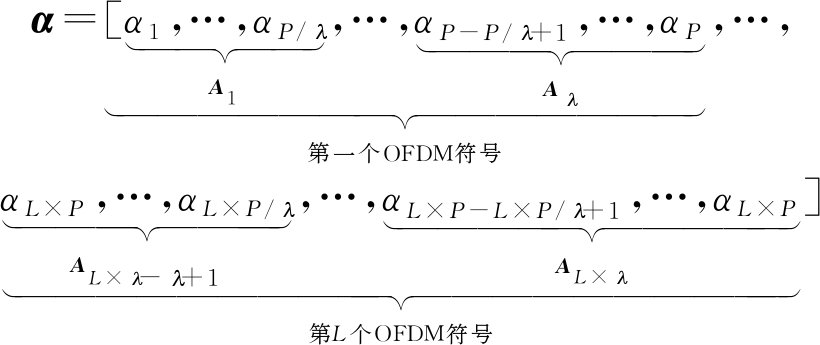
(17)
3.3 带内多路干扰信号的重构与抑制
通过字典原子与相应系数间的线性组合便可重构原始分段信号,将所有OFDM符号内分段重构后的干扰信号分量进行级联便可得到完整的重构干扰信号。假设一个OFDM符号内干扰信号i1(n)的样本长度为P1,则L个OFDM符号内i1(n)的重构信号为:
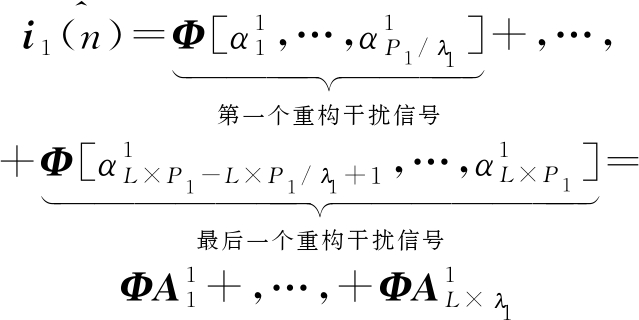
(18)
同理,假设在一个OFDM符号内干扰信号i2(n)的样本长度为P2,则i2(n)的重构信号可表示为:
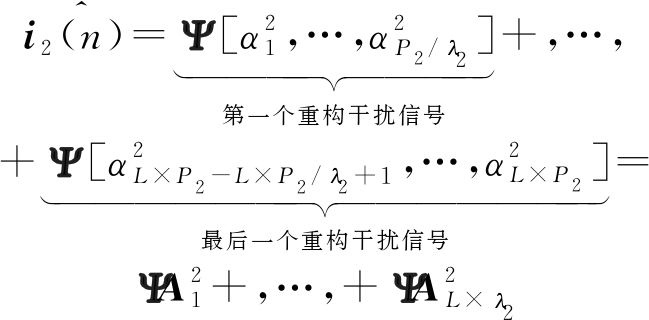
(19)
重构后的带内多路干扰信号,可在接收端通过对消法依次进行抑制,得到含有加性高斯白噪声的OFDM信号:
(20)
OFDM信号带内多路单载波通信干扰的抑制流程图如图1所示,首先,使用K-SVD算法依次对输入的干扰样本信号进行过完备字典的构造,对不同的干扰信号采用不同的学习字典进行稀疏表示。其次,为了提高干扰信号的分解精度,先利用符号同步信息对干扰样本信号进行符号周期分段,再使用OMP算法进行稀疏分解,继而实现干扰信号的精确重构。最后,在系统接收端使用对消法依次对重构后的干扰信号进行抑制。
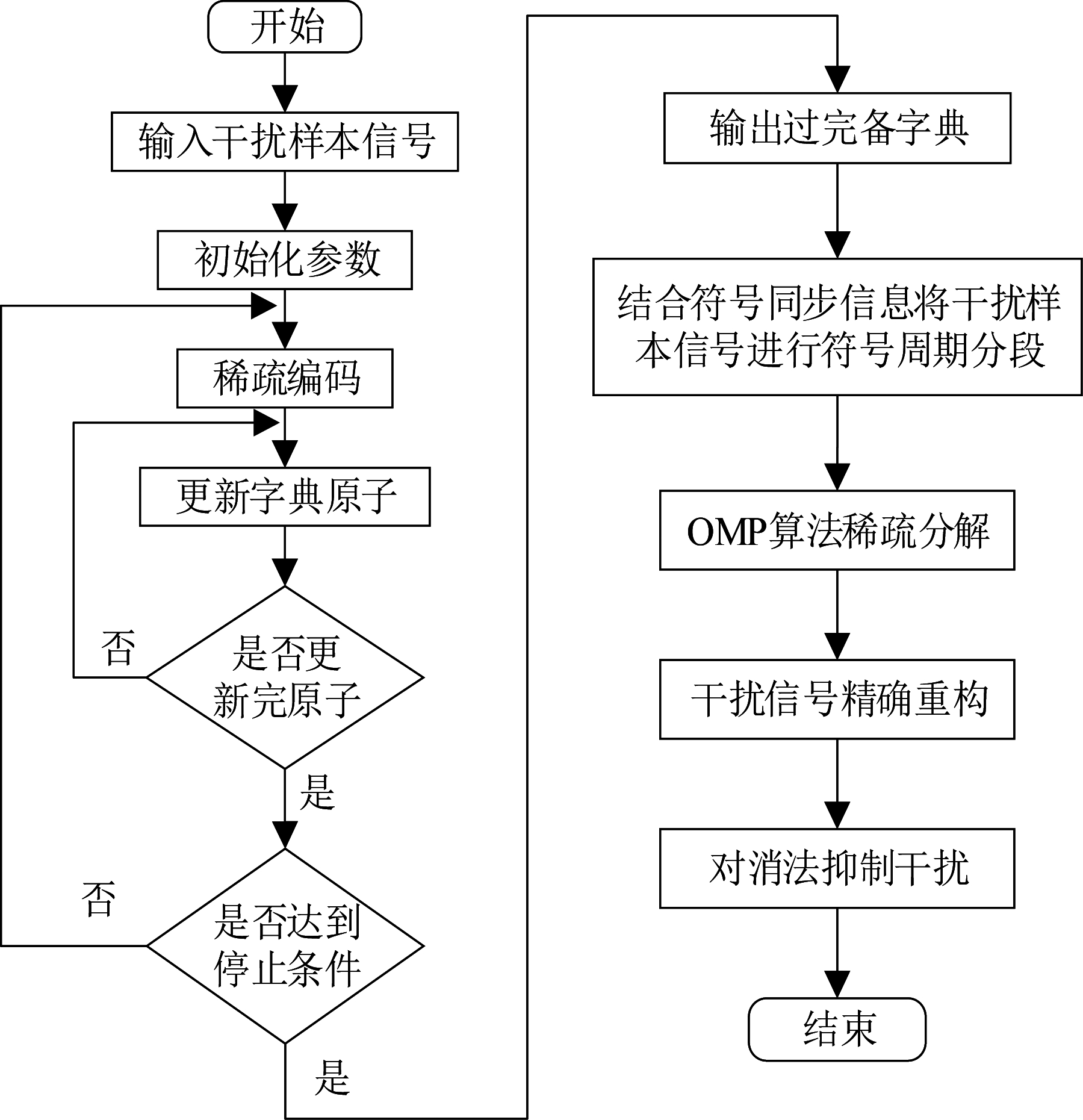
图1 干扰抑制流程图
Fig.1 Flow chart of interference suppression
4 仿真结果与分析
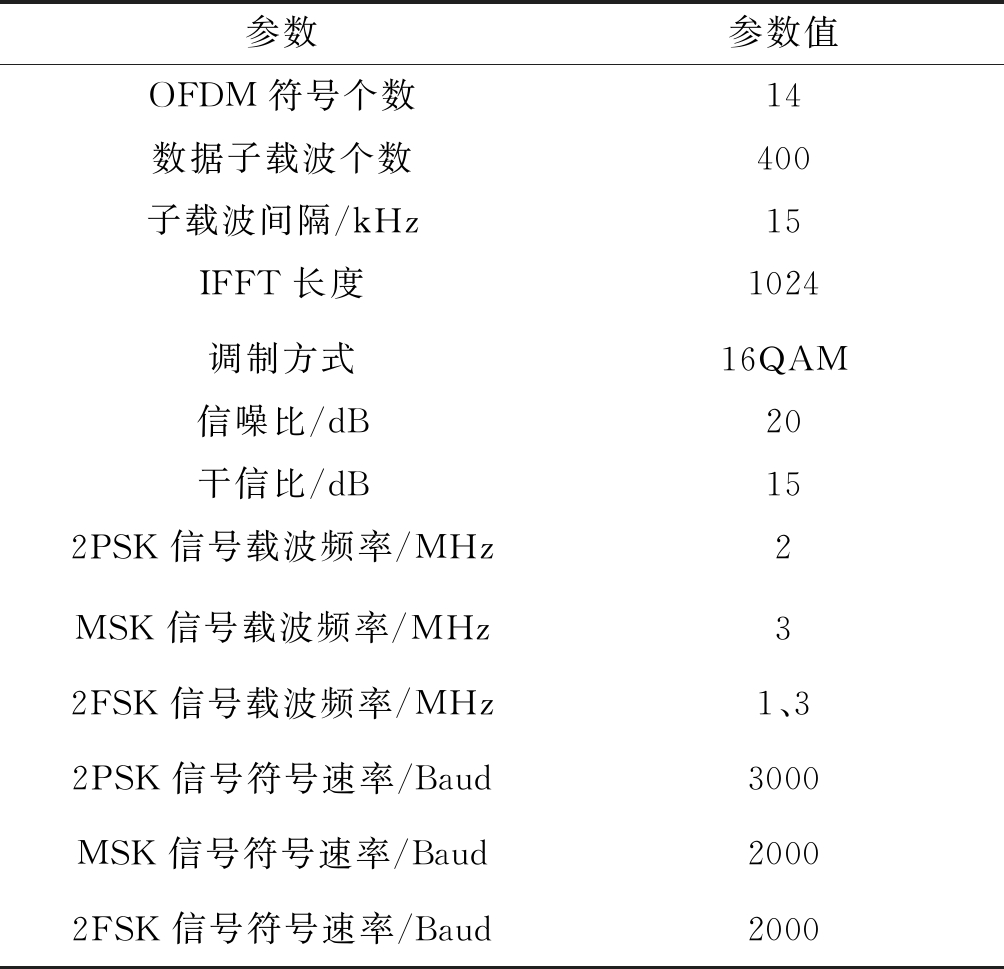
为验证所提方法对OFDM信号带内多路单载波通信干扰的抑制情况,以2PSK和MSK、2PSK和2FSK作为带内多路干扰模型进行仿真实验。主要仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
参数参数值OFDM符号个数14数据子载波个数400子载波间隔/kHz15IFFT长度1024调制方式信噪比/dB干信比/dB2PSK信号载波频率/MHz16QAM20152MSK信号载波频率/MHz32FSK信号载波频率/MHz1、32PSK信号符号速率/Baud3000MSK信号符号速率/Baud20002FSK信号符号速率/Baud2000
4.1 2PSK和MSK干扰模型
2PSK和MSK干扰模型的频谱范围为1.96 MHz~2.04 MHz和2.94 MHz~3.06 MHz,干扰抑制前后系统的归一化频谱图和星座图如图2、图3、图4、图5所示。
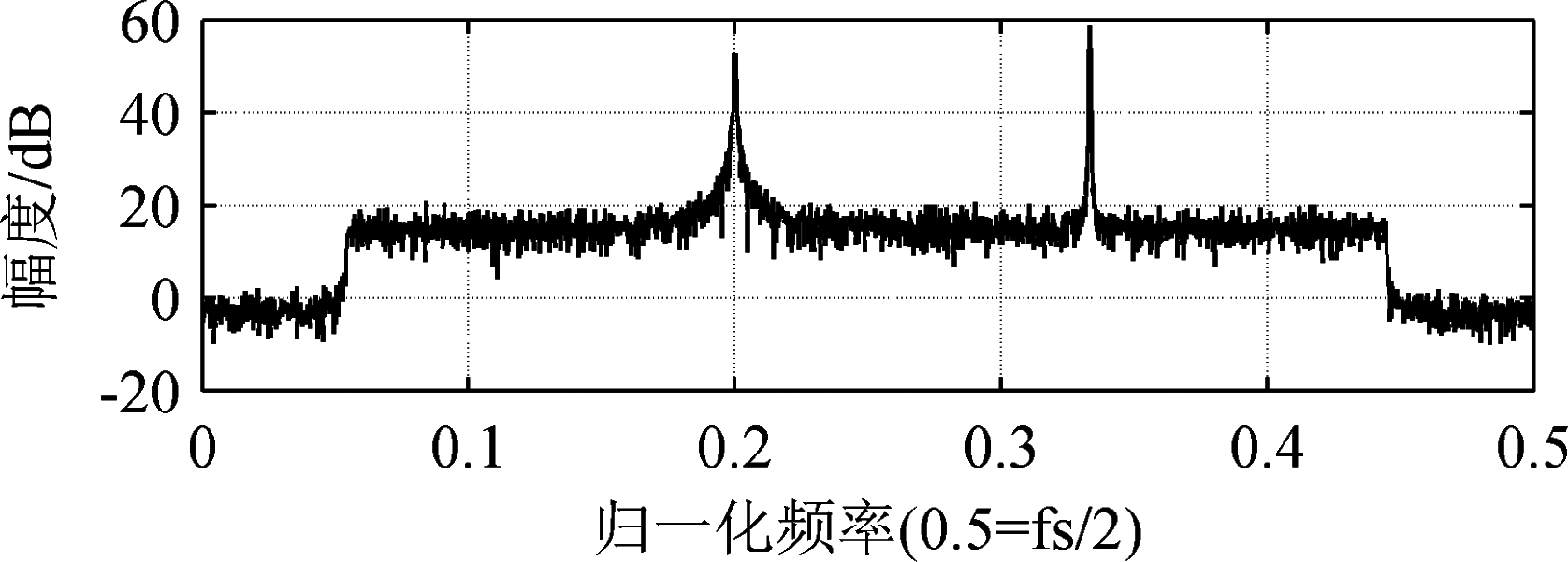
图2 2PSK和MSK干扰模型抑制前系统归一化频谱图
Fig.2 System normalized spectrum before 2PSK and MSK interference model suppression
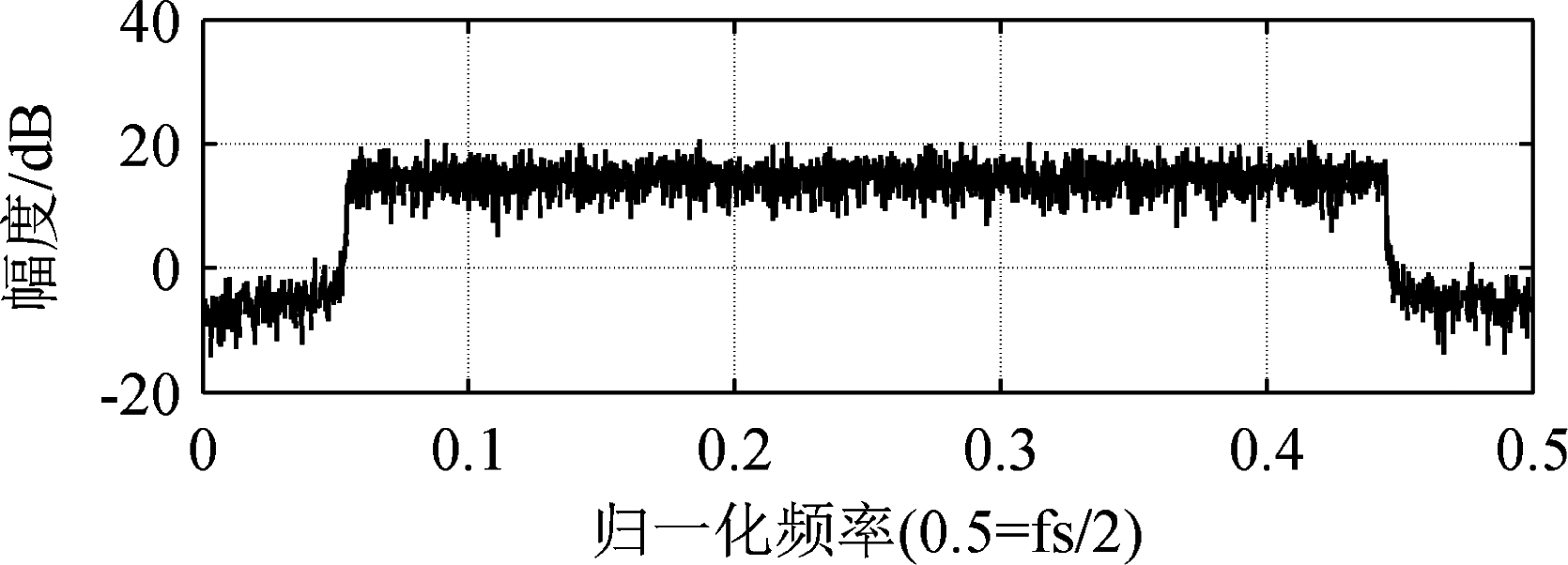
图3 2PSK和MSK干扰模型抑制后系统归一化频谱图
Fig.3 System normalized spectrum after 2PSK and MSK interference model suppression
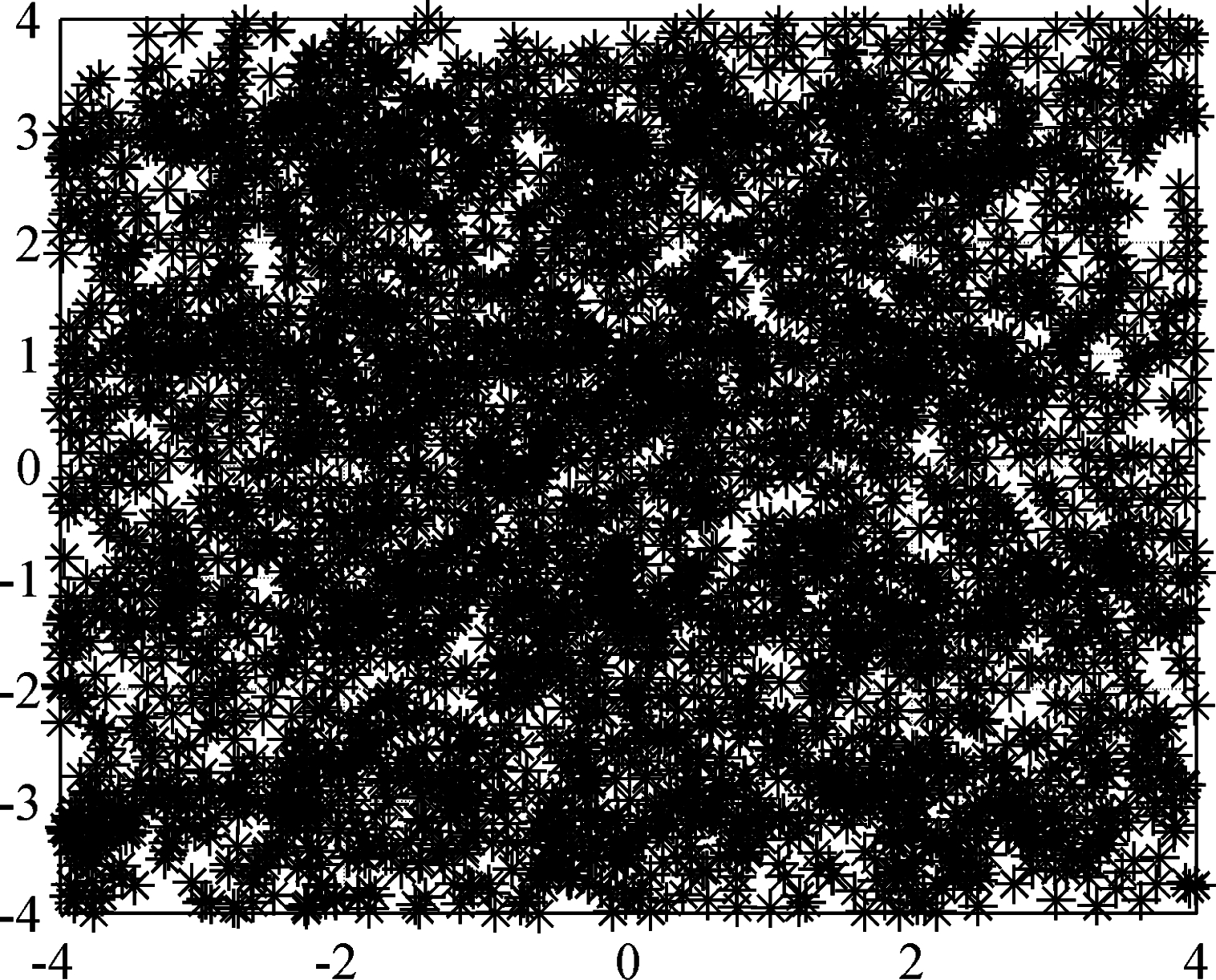
图4 2PSK和MSK干扰模型抑制前系统星座图
Fig.4 System constellation diagram before 2PSK and MSK interference model suppression
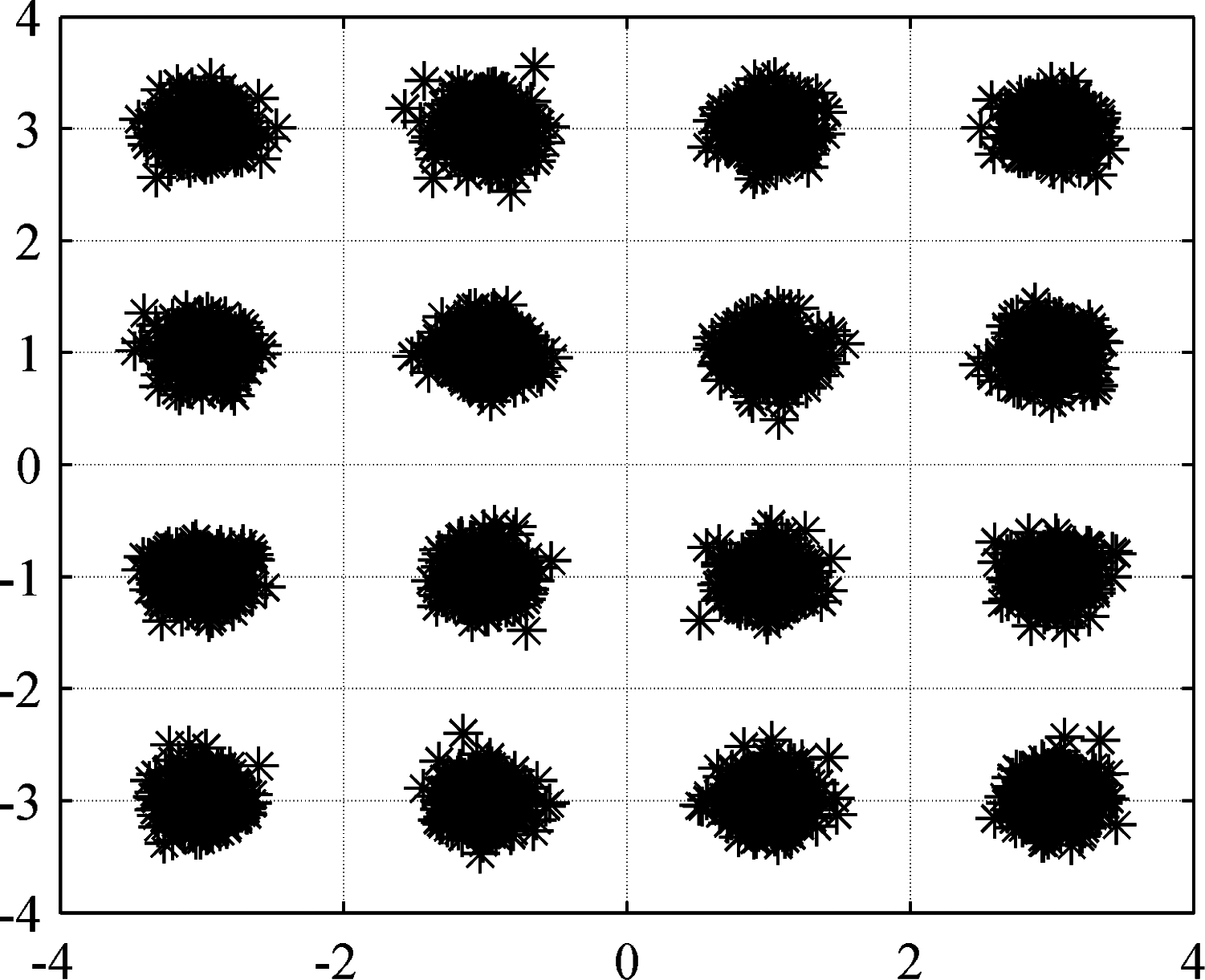
图5 2PSK和MSK干扰模型抑制后系统星座图
Fig.5 System constellation diagram after 2PSK and MSK interference model suppression
由图2可以看出,受2PSK和MSK干扰模型影响,系统归一化频谱图中会出现大小分别为52.57 dB和58.83 dB的两处峰值,经本文算法进行干扰抑制后,峰值下降至图3中的19.32 dB和18.21 dB;结合
图4、图5可以看出,经过干扰抑制后,系统的星座图由散乱无序变为了聚集排列的状态。仿真结果表明本文算法可有效减少2PSK和MSK干扰模型对OFDM信号所造成的影响,且抑制效果较为理想。
4.2 2PSK和2FSK干扰模型
2PSK和2FSK干扰模型的频谱范围为480 kHz~1.52 MHz,1.96 MHz~2.04 MHz,2.48 MHz~3.52 MHz,干扰抑制前后系统的归一化频谱图和星座图如图6、图7、图8、图9所示。
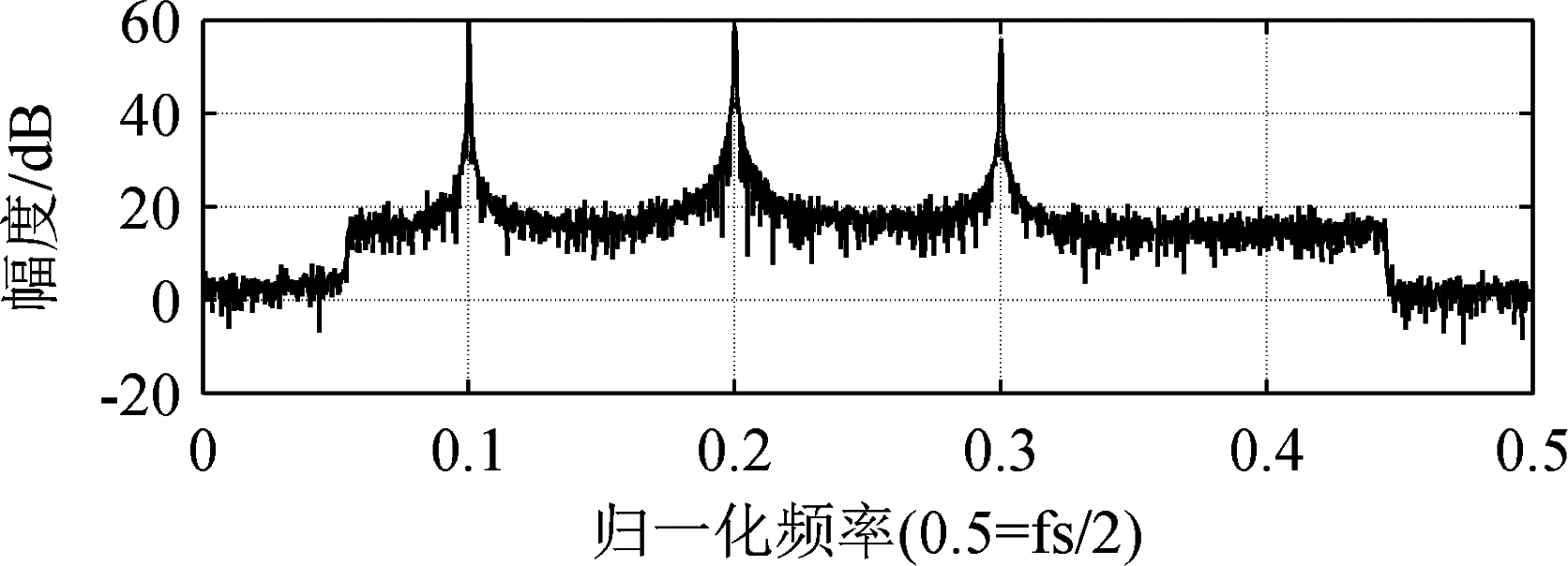
图6 2PSK和2FSK干扰模型抑制前系统归一化频谱图
Fig.6 System normalized spectrum before 2PSK and 2FSK interference model suppression
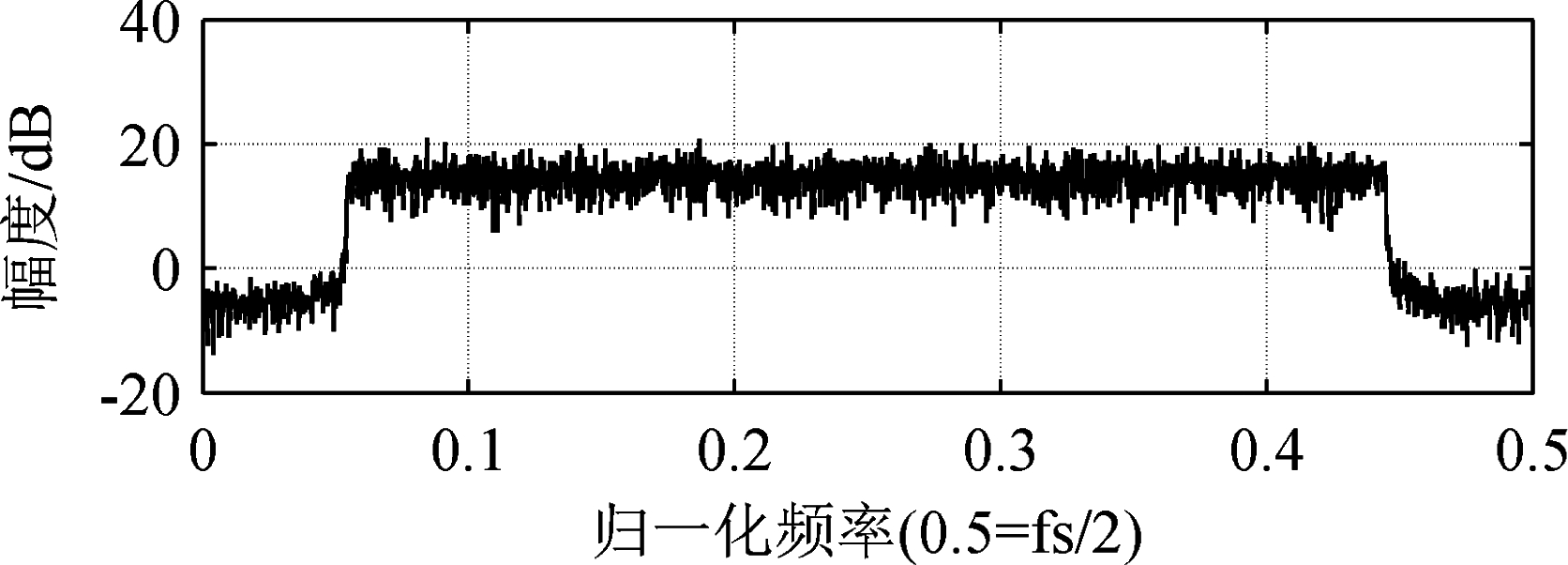
图7 2PSK和2FSK干扰模型抑制后系统归一化频谱图
Fig.7 System normalized spectrum after 2PSK and 2FSK interference model suppression
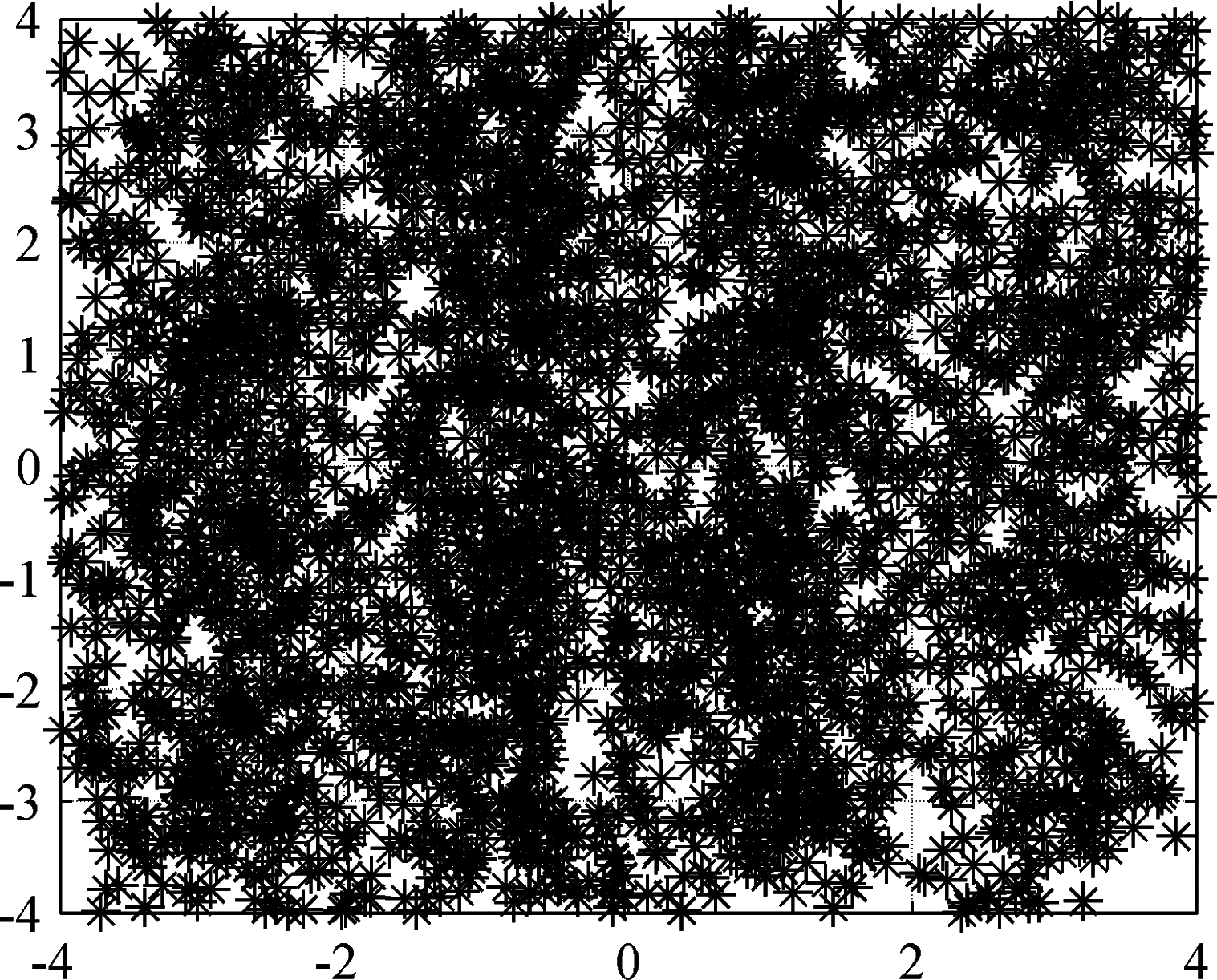
图8 2PSK和2FSK干扰模型抑制前系统星座图
Fig.8 System constellation diagram before 2PSK and 2FSK interference model suppression
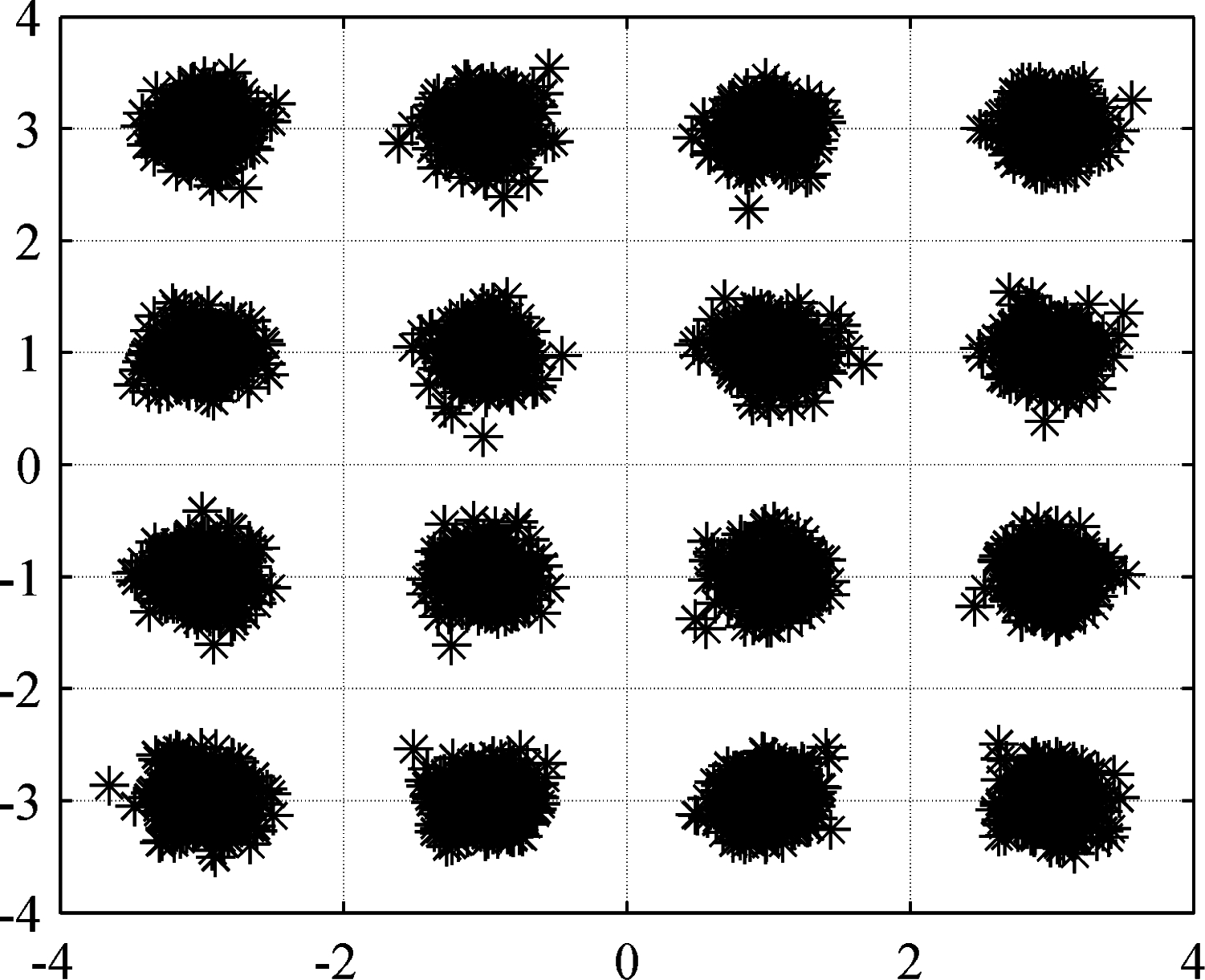
图9 2PSK和2FSK干扰模型抑制后系统星座图
Fig.9 System constellation diagram after 2PSK and 2FSK interference model suppression
对比图6、图7可以看出,经过本文算法进行干扰抑制后,OFDM系统归一化频谱图中的峰值分别从59.28 dB、58.59 dB和55.94 dB降低为18.19 dB、17.92 dB、16.73 dB。结合图8、图9可以看出,受干扰信号的影响系统星座点会发生弥散,在经过干扰抑制后星座点呈现聚集排列的状态。仿真结果表明,本文算法可有效减少2PSK和2FSK干扰模型对OFDM信号所造成的影响,且具有良好的抑制效果。
4.3 算法性能分析
对信号进行重构时,重构概率会受到信号稀疏度和OMP算法迭代次数的影响,现以训练得到的OFDM信号过完备字典为例,对不同稀疏度下OFDM信号的重构概率进行仿真分析,结果如图10所示。
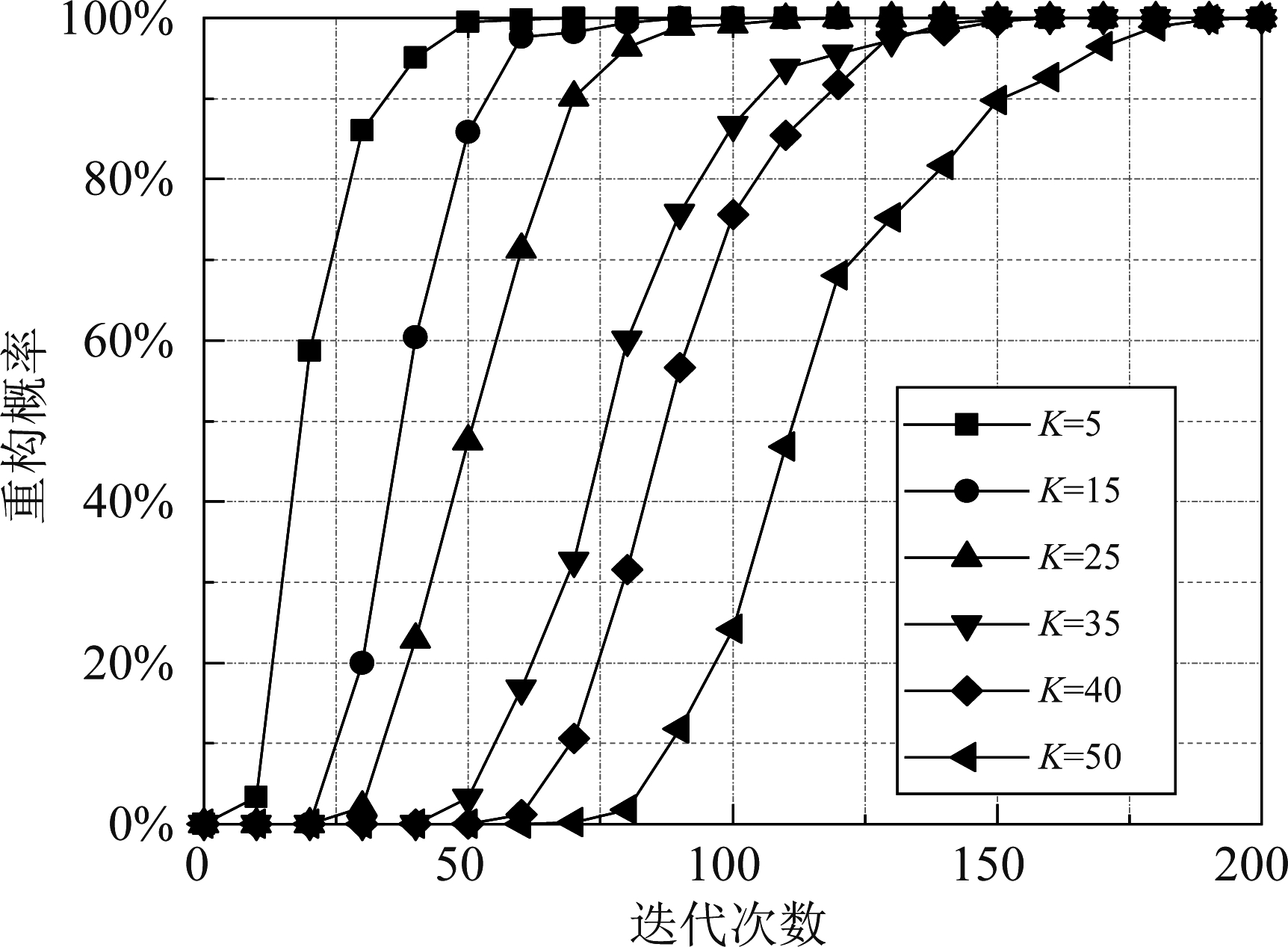
图10 重构概率分析图
Fig.10 Reconstruction probability analysis diagram
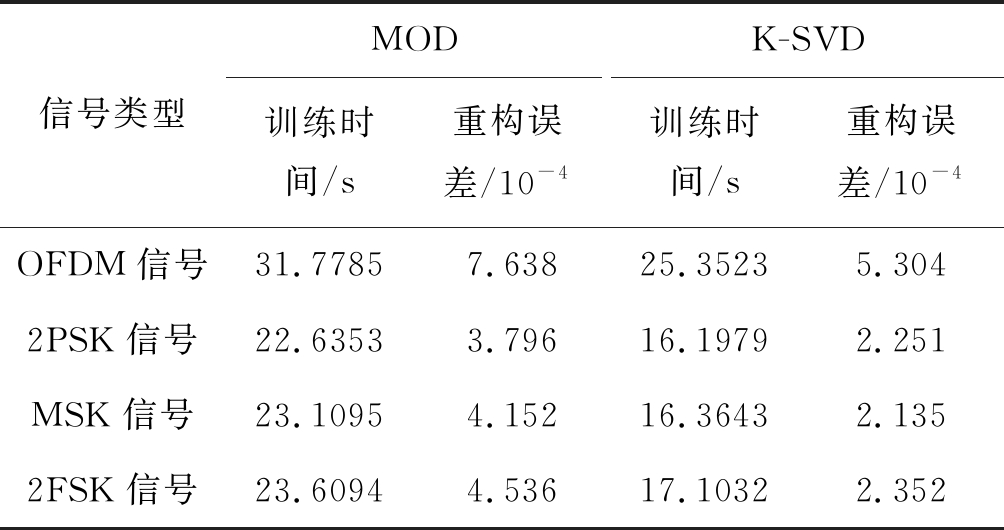
由图10可以看出,当迭代次数相同时,信号的稀疏度越小,信号的重构概率越高;当重构概率相同时,信号越稀疏,重构该信号所需的迭代次数就越少。为验证使用K-SVD算法训练过完备字典的有效性,分别使用最优方向法(Method of Optimal Directions,MOD)和K-SVD算法构造带内各信号的过完备字典,并将字典的训练时间及信号的重构误差进行对比,结果如表2所示。
表2 MOD和K-SVD字典学习算法对比
Tab.2 Comparison of MOD and K-SVD dictionary learning algorithms
信号类型MOD训练时间/s重构误差/10-4K-SVD训练时间/s重构误差/10-4OFDM信号31.77857.63825.35235.3042PSK信号22.63533.79616.19792.251MSK信号23.10954.15216.36432.1352FSK信号23.60944.53617.10322.352
由表2可知,K-SVD算法较MOD而言,有更短的训练时间和更小的重构误差,这是因为在训练字典时,K-SVD算法避免了MOD中大量的矩阵求逆运算,计算复杂度较低,可以更好地提高带内各信号的适应性。
4.4 干扰抑制效果分析
为验证本文算法在0 dB~20 dB信噪比范围内对两种干扰模型的抑制情况,设置干信比大小为20 dB,对系统无干扰、无干扰抑制措施、采用频域置零法抑制干扰及使用本文算法抑制干扰四种情况下的系统误比特率曲线进行绘制,仿真结果如图11、图12所示。
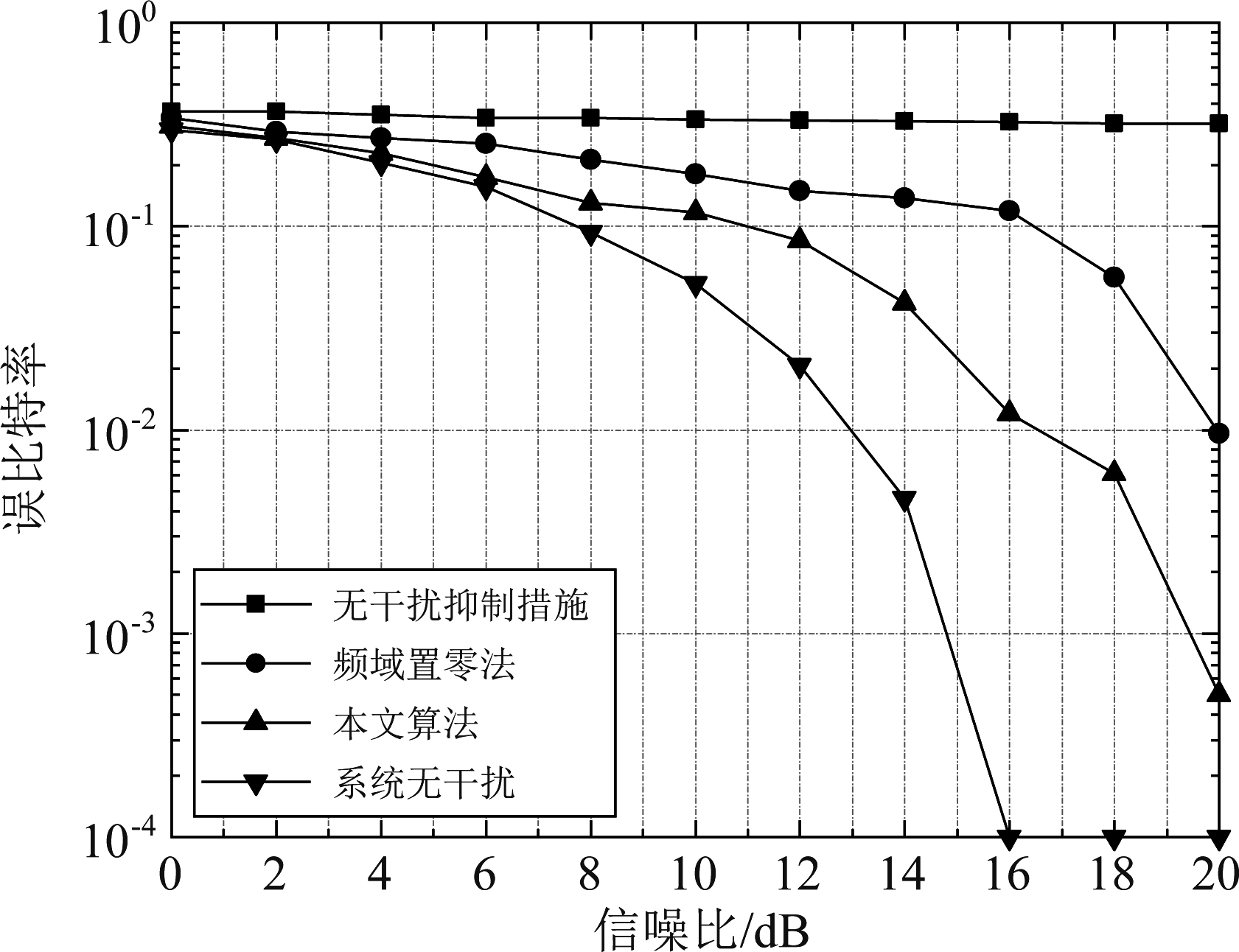
图11 2PSK和MSK干扰模型抑制效果分析图
Fig.11 2PSK and MSK interference model suppression effect analysis diagram
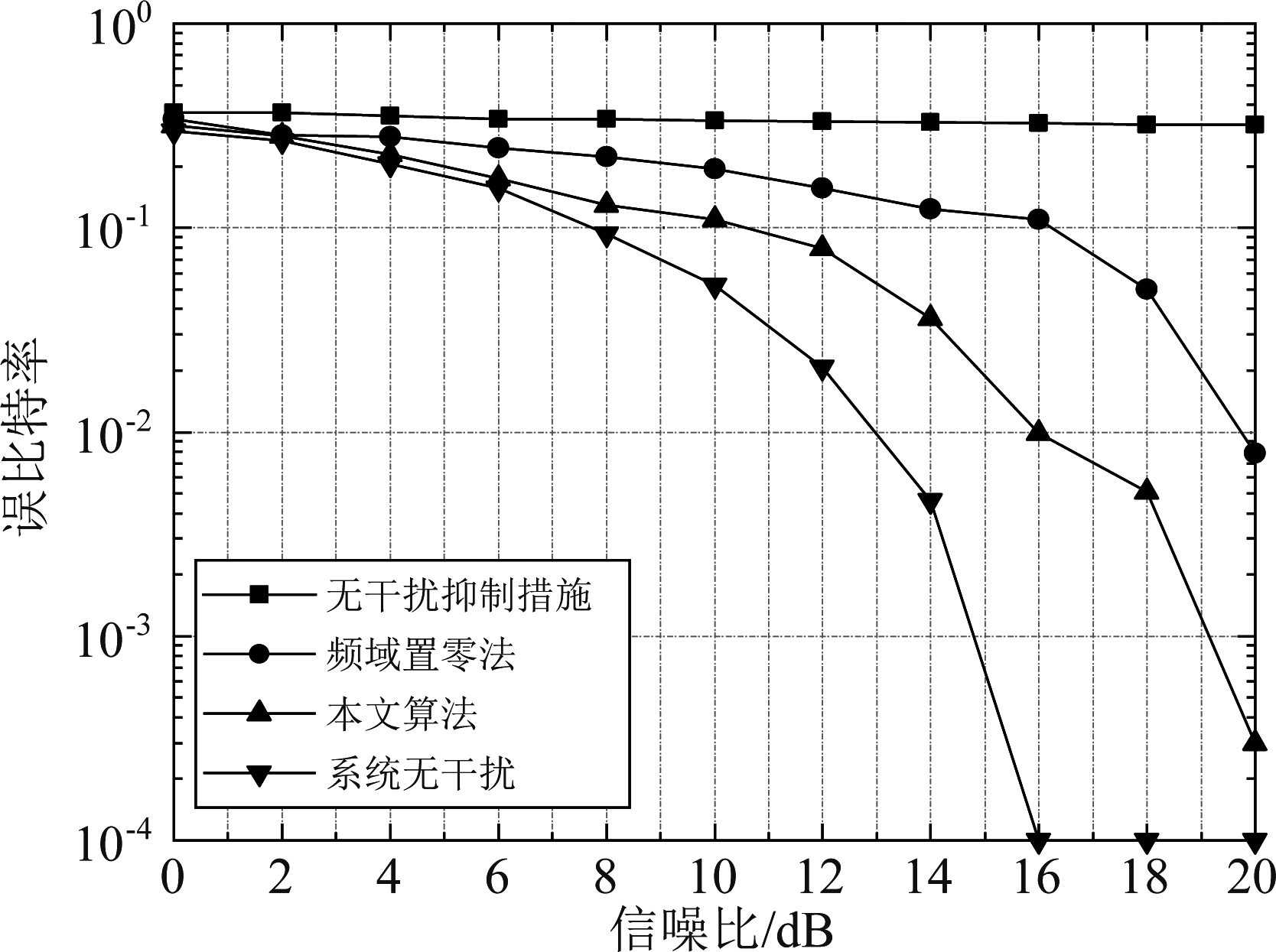
图12 2PSK和2FSK干扰模型抑制效果分析图
Fig.12 2PSK and 2FSK interference model suppression effect analysis diagram
对比图11、图12可知,在任意信噪比情况下,本文提出的干扰抑制方法较传统频域置零法可大幅降低系统的误比特率、有更好的抑制效果。这是由于频域置零法仅在OFDM信号中受干扰的子载波个数较少时有良好的抑制效果,而本文所使用的干扰模型具有一定的连续带宽,会使OFDM信号中受干扰子载波的数目大幅增加,此时使用频域置零法抑制效果不理想且极易引起有用信号的丢失。而本文算法充分利用了信号的稀疏特性,在提高干扰信号重构精度的同时可有效减少不必要的损失。
5 结论
本文提出了基于学习字典和符号同步信息的OFDM信号带内多路单载波通信干扰抑制方法,首先通过K-SVD算法进行OFDM信号和干扰信号过完备字典的构造,使各信号仅能使用相对应的学习字典进行稀疏表示,达到区分有用信号和干扰信号的目的。其次,将符号同步信息与OMP算法相结合,提高了带内各信号的分解精度,确保了各信号的高概率重构。最后,在接收端使用对消法完成多路干扰信号的抑制。与传统的干扰抑制方法不同,所提方法充分利用了信号的稀疏特性,适用于大多数场景下OFDM信号带内干扰的抑制问题。仿真结果表明,所提方法较传统置零法可有效提升系统性能,具有一定的实用性。
[1] JADAV N K. A survey on OFDM interference challenge to improve its BER[C]//2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA). Coimbatore, India. IEEE, 2018: 1052-1058.
[2] KIM K H. NBI spectral leakage mitigation based on compressed sensing in OFDM systems[J]. IEEE Transactions on Broadcasting, 2016, 62(2): 409- 416.
[3] KIM I H, PANDE T. SINR analysis of a narrowband interference cancellation scheme in OFDM communication systems[C]//2015 IEEE Global Communications Conference (GLOBECOM). San Diego, CA, USA. IEEE, 2015: 1- 6.
[4] ECHIZENYA D, OHNO K. A consideration on spectrum forming and interference mitigation by Gaussian windowed OFDM[C]//2018 21st International Symposium on Wireless Personal Multimedia Communications (WPMC). Chiang Rai, Thailand. IEEE, 2018: 583-587.
[5] 孟东, 缪玲娟, 张希. 反加窗算法及其在扩频系统窄带干扰抑制中的应用[J]. 电子与信息学报, 2015, 37(10): 2349-2355.
MENG Dong, MIAO Lingjuan, ZHANG Xi. Inverse windowing algorithm and its application to narrow-band interference suppression in direct sequence spectrum system[J]. Journal of Electronics & Information Technology, 2015, 37(10): 2349-2355.(in Chinese)
[6] COULSON A J. Bit error rate performance of OFDM in narrowband interference with excision filtering[J]. IEEE Transactions on Wireless Communications, 2006, 5(9): 2484-2492.
[7] ZHANG Chengwen, HU Xudong, LIU Yutao, et al. Multiple interacting narrowband interferences suppression algorithm for OFDM systems[J]. IEEE Access, 2020, 8: 62310- 62321.
[8] 黄李峰, 田亚飞. OFDM系统中基于最优门限选取的窄带干扰抑制方法[J]. 信号处理, 2015, 31(3): 259-266.
HUANG Lifeng, TIAN Yafei. Narrowband interference suppression based on optimal threshold selection in OFDM systems[J]. Journal of Signal Processing, 2015, 31(3): 259-266.(in Chinese)
[9] 汪勃, 谌明, 梁光明, 等. 自适应三门限窄带干扰抑制算法[J]. 电子学报, 2015, 43(1): 13-17.
WANG Bo, CHEN Ming, LIANG Guangming, et al. Adaptive tri-threshold narrowband interference suppression algorithm[J]. Acta Electronica Sinica, 2015, 43(1): 13-17.(in Chinese)
[10]YAO Rugui, CHEN Yun, LI Geng, et al. Iterative threshold algorithm for narrow-band interference suppression[C]//2013 22nd Wireless and Optical Communication Conference. Chongqing, China. IEEE, 2013: 252-256.
[11]胡旭东, 张成文, 刘玉涛, 等. 面向OFDM系统的高精度窄带干扰抑制算法[J]. 西安交通大学学报, 2019, 53(8): 114-120,128.
HU Xudong, ZHANG Chengwen, LIU Yutao, et al. A high precision suppression algorithm of narrowband interferences for OFDM systems[J]. Journal of Xi’an Jiaotong University, 2019, 53(8): 114-120,128.(in Chinese)
[12]POPESCU O, POPESCU D C. On the performance of sub-band precoded OFDM in the presence of narrowband co-channel interference[J]. IEEE Transactions on Broadcasting, 2016, 62(3): 736-743.
[13]刘凤威, 赵宏志, 唐友喜. 窄带干扰下MIMO系统的特征域传输方案[J]. 电子与信息学报, 2016, 38(6): 1385-1390.
LIU Fengwei, ZHAO Hongzhi, TANG Youxi. An eigen domain transmission scheme for MIMO systems under narrowband interference[J]. Journal of Electronics & Information Technology, 2016, 38(6): 1385-1390.(in Chinese)
[14]李冬霞, 王召, 刘海涛. 联合两级滤波与压缩感知的测距仪干扰抑制方法[J]. 信号处理, 2020, 36(7): 1118-1126.
LI Dongxia, WANG Zhao, LIU Haitao. DME impulse interference mitigation method based on joint two-stage filtering and compressed sensing[J]. Journal of Signal Processing, 2020, 36(7): 1118-1126.(in Chinese)
[15]张永顺, 朱卫纲, 贾鑫, 等. 大带宽通信压缩域干扰抑制方法综述[J]. 兵器装备工程学报, 2019, 40(11): 103-110.
ZHANG Yongshun, ZHU Weigang, JIA Xin, et al. Survey of interference suppression method for broadband communication in compressed domain[J]. Journal of Ordnance Equipment Engineering, 2019, 40(11): 103-110.(in Chinese)
[16]ZHANG Zheng, XU Yong, YANG Jian, et al. A survey of sparse representation: Algorithms and applications[J]. IEEE Access, 2015, 3: 490-530.
[17]练秋生, 石保顺, 陈书贞. 字典学习模型、算法及其应用研究进展[J]. 自动化学报, 2015, 41(2): 240-260.
LIAN Qiusheng, SHI Baoshun, CHEN Shuzhen. Research advances on dictionary learning models, algorithms and applications[J]. Acta Automatica Sinica, 2015, 41(2): 240-260.(in Chinese)
[18]LIU Gaohui, HU Yujie. In-band interference suppression method of OFDM signal based on double sparsity K-SVD algorithm joint dictionary learning[C]//2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC). Xi’an, China. IEEE, 2019: 1-3.
[19]AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311- 4322.

