1 引言
对物体、人脸以及场景的识别在工程上一直是一个复杂而重要的问题。而现有的深度神经网络(Deep Neural Networks, DNN)对输入的微小变化的鲁棒性较差。通过在特定位置放置贴纸,可使深度神经网络误读停车标志[1];深度神经网络对微小的位姿扰动十分敏感[2];而一些来源于真实环境中的对抗样本也有可能使分类器失灵[3]。这主要源于现有的深度神经网络往往关注于色彩、纹理等低级特征,然后再逐层从低级特征中提取、抽象出高级特征,而不能如同大脑,直接对高级特征进行学习[4]。另一方面,现有的深度学习方法需要大量的样本进行训练,计算成本高。而大脑能够执行现有计算机无法完成的复杂任务,例如同时识别多个目标、推理、控制与移动,且计算成本较低[5]。研究并模拟大脑的结构及功能,是现有识别算法的发展趋势之一。如Poggio 等人[6]于 1999年提出的HMAX模型这一个类脑识别模型,此后包括Serre等人[7]在内,对该模型进行了改进,此类算法训练样本小,速度快,识别率高。但这类模型还是如同传统的模式识别算法一样[8],采用通过Gabor滤波器或小波变换提取高维的低级特征,再逐层降维的思路,仍没有直接模仿人脑直接识别高级特征的行为。
海马结构是高等哺乳动物大脑中重要组成部分,负责大脑中记忆、识别、导航、学习等重要功能,是研究啮齿类乃至灵长类动物大脑认知功能的关键部位。海马结构由内嗅皮层、海马区、齿状回以及下托综合体构成。1971年,O’Keefe等人在自由活动的大鼠海马区首次发现了具有空间定位功能的位置细胞神经元[9],并发现了哺乳动物直接利用空间内部表征导航到目标位置的能力。2005年,Moser夫妇在内侧内嗅皮层(Medial Entorhinal Cortex, mEC)发现了网格细胞,该细胞具有在空间固定区域重复规律性放电的特性[10],其放电在空间中呈六边形对称。而最近的研究发现,网格细胞不仅在空间导航中发挥作用。在视觉空间中,经过高度受控的视觉跟踪任务,内嗅皮层的功能性磁共振成像(Functional Magnetic Resonance Imaging, fMRI)数据显示了类似网格细胞的六边形放电特征信号[11]。另一方面,通过对行为与知觉关系的长期研究,人们发现识别过程与认知主体的眼部运动具有关联性。罕见病理学数据则表明,眼睛无法运动的患者,会采用头部运动来代替眼部扫视[12]。据此可提出一种假设,即大脑对目标进行认知时,人眼对目标进行扫视,通过记忆预测对象身份,并通过反馈的视觉信息,对预测进行确认,最终成功识别对象。而扫视轨迹处于二维平面,与空间导航具有一致性。最近的研究表明,在视觉活动中,海马体的内嗅皮层有类似网格细胞的神经元反应。基于此,提出了由网格细胞神经元驱动的特征编码的目标识别机制,提供了一种可行的大脑视觉识别机制模型。
模型中,识别的关键在于相应特征的几何分布情况,只有能在对应的位置检测到本应存在的特征,才能识别该对象。模型对目标的特征群进行基于网格细胞的坐标编码,进而记录特征之间的相对位置,导出扫视向量。在识别过程中,依据扫视向量,并借助NCC特征匹配算法,依次对特征进行匹配。特征匹配成功次数累积超过一定阈值,则识别成功。
本文在特征匹配模块,采用了工程实践中已然成熟的归一化互相关匹配算法(Normalized Cross Correlation, NCC),提高了单个特征匹配精度,进而整体提升了模型的速度,并能抵消灰度变化带来的影响。
2 类脑视觉识别模型
人的识别过程依赖于眼球运动,而眼球运动的引导可能与网格细胞有关。基于此,可提出一种类脑的视觉识别模型。该模型由三部分构成:计算识别对象特征与记忆对象特征相似程度的特征匹配模块、进行坐标编码以及输出眼球运动信号的矢量导航模块、标记记忆对象特征与对象身份的标签模块。模型具体过程如下:
在识别之前,需要预先学习并记忆对象的相关特征,并对每个特征的中心位置以网格细胞编码其坐标,之后用特征标签细胞标记相关特征,身份细胞标记该对象,并与相对应对象特征的多个特征细胞关联,表示某一身份的对象具有相对应的视觉特征。
第一步,在识别对象过程中,首先眼球会注视对象的某一显著特征(图像梯度较高的区域),此时视觉信号通过眼球到达视网膜,由视网膜采集图像,然后感知细胞检测其特征。
第二步,接收的特征信息会激活相应的特征标签细胞;此时标签细胞处于竞争状态,最活跃的特征标签细胞驱动相应的身份细胞。而模型根据特征标签细胞的激活情况,对识别对象的身份有一个预先的假设,身份细胞象征此种假设。
第三步,最活跃的身份细胞随机驱动另一特征标签细胞,特征标签细胞与之前由特征信息激活的标签细胞,各自激活相对应的网格细胞,网格细胞输出坐标至距离细胞,由距离细胞处理后得到眼动神经信号,驱动眼球扫视,观察下一区域。
多次重复以上过程,每次过程都会刺激相应的身份细胞,其激活率会累积,为之前的假设提供支持;当身份细胞激活率超过判决阈值,则模型认为已识别对象。若连续数次观察对象不同区域,身份细胞都未达到阈值,则认为该识别对象是一个陌生对象。由主导目前的身份细胞来决定模型的扫视模式,多次扫视的结果决定特征匹配的区域;而特征匹配的结果会影响哪些特征标签细胞被激活,进而决定身份细胞的激活情况,这就是多次扫视与特征匹配过程及身份细胞之间的转换关系。
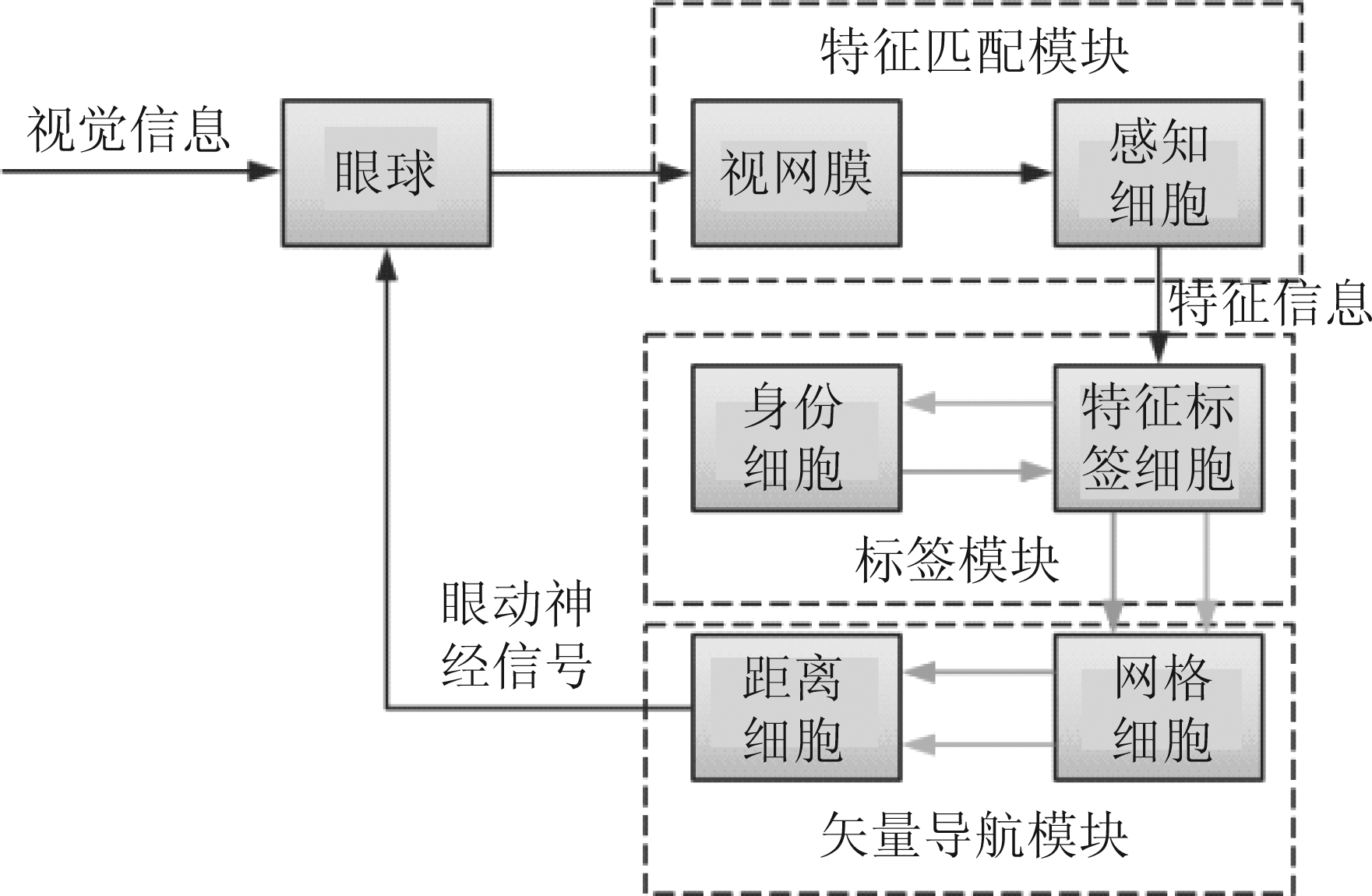
图1 类脑视觉识别模型
Fig.1 Brain-inspired visual recognition module
2.1 特征匹配模块
模型所定义的感知细胞,是用于检测识别过程中观察的特征区域是否与记忆中的某些特征相似。此处采用的计算图像之间的相似程度的方法,是较为经典的图像匹配的算法。
归一化互相关匹配算法(Normalized Cross Correlation, NCC)是一种较为常用且性能较强的图像匹配算法,最早由Roche等人提出[13]。该算法的计算结果固定在[-1,1]之间,经过简单的阈值处理即可作为激活率输出;且抗干扰能力强,对灰度值的线性变化有很好的鲁棒性;对垂直与水平平移的图像,以及轻微旋转(18度以内)与尺度变换(1.5倍以内)的图像,仍有较好的匹配结果[14]。该算法被广泛运用于如医学图像分析、视频处理、交通控制以及工业生产检测等领域[15-16]。
设记忆图像与待检测区域大小皆为a×a,则两图像的相似程度Rf为:
Rf=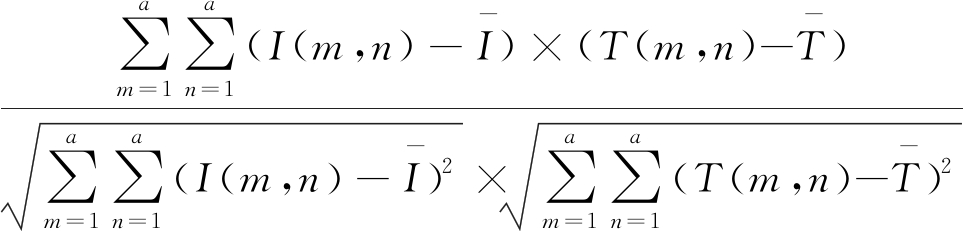
(1)
其中I(m,n)表示图像匹配区域的坐标(m,n)的像素值,T(m,n)表示模板的坐标(m,n)的像素值,![]() 为匹配区域所有像素值的均值,
为匹配区域所有像素值的均值,![]() 为模板所有像素的均值。从式(1)可以看出,当图像的灰度值整体增加或减小,通过减去均值这一步骤,抵消了灰度值变化对相似程度计算的影响。在正式环境中对图像进行采集时,往往因环境变化导致亮度变化,而该算法能很好地解决此问题,因此在实际过程中被广泛运用。
为模板所有像素的均值。从式(1)可以看出,当图像的灰度值整体增加或减小,通过减去均值这一步骤,抵消了灰度值变化对相似程度计算的影响。在正式环境中对图像进行采集时,往往因环境变化导致亮度变化,而该算法能很好地解决此问题,因此在实际过程中被广泛运用。
当Rf=1或者接近于1时,两幅图像相似程度较高;当Rf≤0或者接近于0时,则两者相似程度低,无法匹配。
2.2 矢量导航模块2.2.1 网格细胞
网格细胞的空间特征由三个变量表征:位相φ、网格方向θ、网格间距λ。其中,位相表示网格节点相对于空间绝对参考系原点的偏移量;网格方向表示网格样式相对参考系轴的倾斜度;网格间距为网格放电野中心之间的间距。图2表示的是大鼠海马体中电极采集的放电信号情况,黑色线条表示大鼠在1 m见方的范围内的运动轨迹,而红点表示该位置处网格细胞放电情况,且网格细胞在内侧内嗅皮层(middle entorhinal cortex, mEC)中,沿背腹轴呈现不同网格间距的网格细胞放电,即网格细胞随相同的运动速度呈现不同距离周期的放电。通过不同间距的网格细胞的周期性放电,可实现用较小尺度的网格细胞表示较大尺度的空间,目前所记录的最大尺度超过300 cm且可能仅为其所能表征空间大小的一半左右[17]。
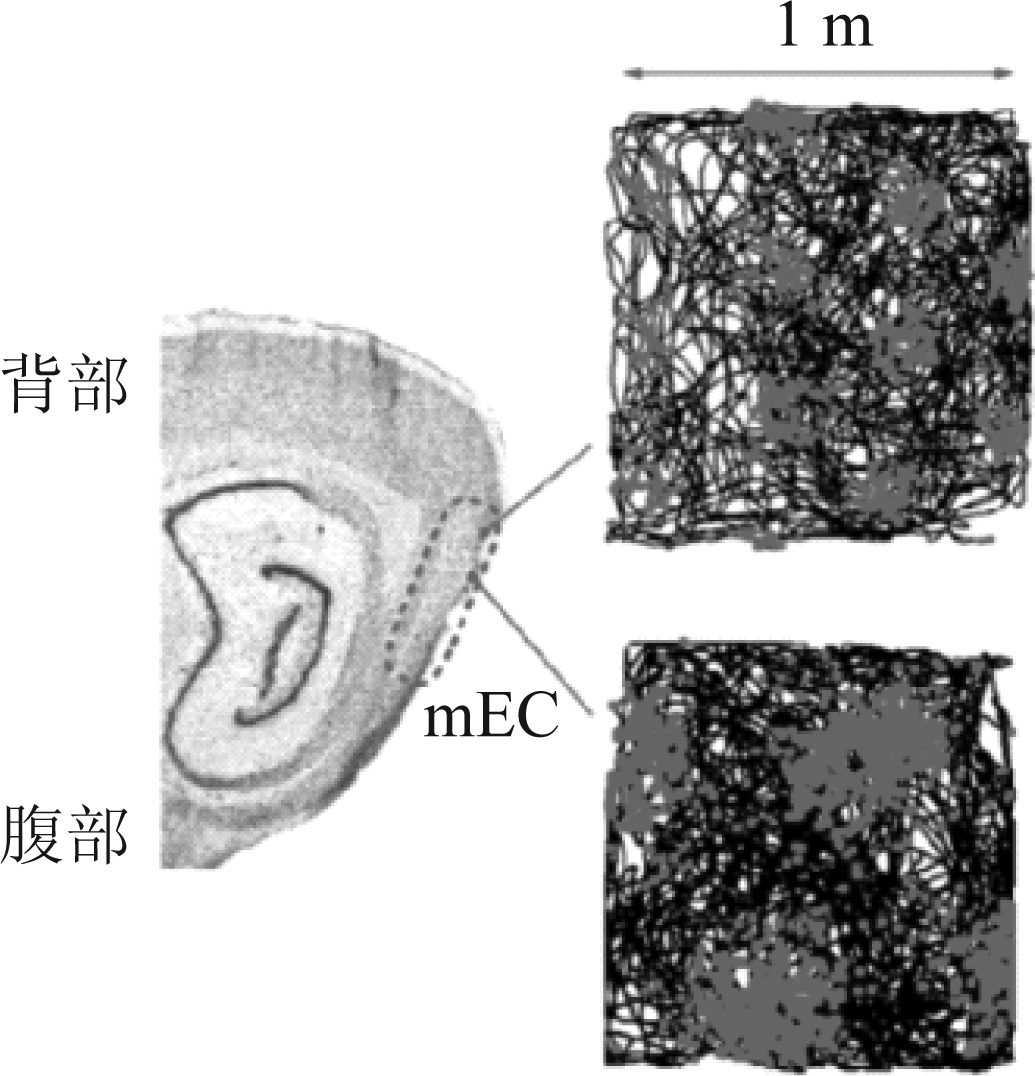
图2 大鼠活动轨迹与网格细胞放电关系[18]
Fig.2 The relationship between rat activity trajectory and grid cell firing[18]
大鼠内嗅皮层网格细胞随空间位置程六边形放电,现有的网格细胞模型,旨在模仿这种六边形放电行为,呈现二维空间上的六边形规则斑图,如图3,通过不同周期的网格细胞放电的组合排列来唯一编码空间位置。在模拟网格细胞放电时,通常采用振荡干涉模型或连续吸引子网络模型。此处采用Yoram Burak等人提出的连续吸引子网络模型[19]。

图3 网格细胞六边形放电仿真图
Fig.3 Grid cell hexagonal firing simulation
网格细胞模型中,二维平面排布的网格细胞如式(2)所示进行自组织:
(2)
式中,τ为时间常数,si、sj分别为第i个与第j个网格细胞的放电率,p是激活函数,此处采用线性整流函数(Rectified Linear Unit, ReLU)。Bi为前馈输入,通过调节前馈输入可以使得网格细胞的六边形放电图样实现整体的平移。而Wij为第i个与第j个网格细胞之间的连接权重,由式(3)决定:
Wij=W0(xi-xj-leθj)
W0(x)=ae-γ|x|2-e-β|x|2
(3)
式中,xi与xj为第i个与第j个网格细胞的平面坐标,l为偏置量的模,eθj为网格细胞j的优选方向的单位矢量。W0是墨西哥帽函数,a决定了网格细胞之间的兴奋性连接权重的大小,γ、β决定了兴奋性连接与抑制性连接的空间范围,可通过改变γ、β来形成不同空间周期的网格细胞群,以模仿沿背腹轴呈现不同网格间距的网格细胞放电。需要说明,识别模型中仅仅使用静态网格细胞对图像像素进行位置编码,而不宜移动,故前馈输入为固定值1,l为0。
2.2.2 距离细胞
由Daniel Bush等人提供的距离细胞模型[18],其中距离细胞可能与齿状回中的位置细胞相对应[20]。距离细胞接受来自网格细胞的信号,用以输出从当前位置到目标位置的移动矢量。一组距离细胞沿某一维轴编码轴上特定的位置,并从沿该轴的每个位置活动的网格细胞接收输入。当网格细胞编码某一位置时,它们激活一个单独的距离细胞来编码其在轴上的位置。之后再运用赢者通吃算法,动态消除了其他距离细胞中的活动。则沿一维轴的一组距离细胞的激活率v为:
vcx=f(g[WDCx·Gc(x1,y1)])
vtx=f(g[WDCx·Gv(x2,y2)])
vcy=f(g[WDCy·Gc(x1,y1)])
vty=f(g[WDCy·Gv(x2,y2)])
(4)
式中, f为赢者通吃算法的函数,激活率最大的距离细胞激活率为1,其余为0。g是归一化函数,WDCx与WDCy是网格细胞到距离细胞分别沿x与y轴的突触权值,Gc是当前位置网格细胞编码坐标,Gt是目标位置网格细胞编码坐标。(x,y)为该位置在空间绝对参考系下坐标。vcx、vtx、vcy、vty为当前位置与目标位置沿x与y轴的一组距离细胞激活率。
每一个距离细胞都为其对应的读出细胞提供输入,其突触权值强度随轴向移动方向而线性增加或减小。那么该读出细胞的触发率可以编码从原点到目标位置沿某一轴的位移。为保证误差较小,采取将两个反方向的距离细胞阵列求取平均值的方式,求解沿该轴的位移。一列为距离细胞解码的起始位置,另一列为解码的目标位置。每个距离细胞列投射到一个“向上移动”(左)和一个“向下移动”(右)的读出细胞,其突触权值W沿轴向反方向线性变化。设突触权值由1至q线性变化,各权值之间间隔为1,则读出细胞输出位移为:
![]()
![]()
Wcu=(q:1) Wtu=(1:q)
Wcd=(1:q) Wtd=(q:1)
(5)
Δx与Δy为位移沿x与y轴的值,(Wcu,Wtu)与(Wcd,Wtd)分别为当前位置与目标位置的距离细胞所连接的沿不同方向变化的突触权值。如果能得知两个不共线的轴上的位移,那么就可以求解起始到目标位置的二维平面位移。
2.3 标签模块
标签模块由两部分构成,身份细胞与特征标签细胞。其中,身份细胞用来标记记忆中相关对象的身份,而特征标签细胞用于标记相对应身份下的图像特征。
特征标签细胞与记忆中的特征一一对应。当通过NCC算法,依次与记忆中的图像计算得到相似程度后,经阈值处理h,g为归一化函数,输出为一组特征标签细胞的激活率F:
F=h(g[Rf1,Rf2,…,Rfn]T)![]()
(6)
其中T为大小接近1的阈值。
将身份细胞激活率记作I。设特征标签细胞到身份细胞的突触权重为WL2I,有:
In+1=In+t×(WL2I·F)
(7)
t为特征标签细胞与身份细胞的耦合程度。通过调节该值,可以调整理想状态下识别过程中的扫视次数。n为当前扫视次数。
3 仿真分析
3.1 仿真条件
(1)仿真采用YALE人脸数据集,该数据集包含15人,每人包含11张光照、姿势及表情皆不相同的图片,图像归一化为100×100。实验采取10人个人的图片作为训练集,每人一张;之后采用K张图片进行测试。实验重复十次,取平均值作为结果。
(2)仿真对每个对象选取九个特征区域进行匹配,匹配区域大小为13×13像素。
(3)仿真基于matlab R2017b仿真平台进行仿真。计算机为Ubuntu 16.04操作系统,内存8 GB,CPU为Intel 酷睿i7- 6700HQ。
(4)表1中所列为仿真实验中所使用的部分参数具体数值,t为特征标签细胞与身份细胞的耦合程度,T为2.3节中阈值处理的阈值,q为距离细胞与读出细胞连接权重的变化范围大小。
表1 仿真中部分参数
Tab.1 Parameters in the simulation

参数数值耦合程度t0.4阈值T0.85突触权值范围q100
3.2 模型算法流程
模型算法流程如图4所示。首先,在选定特征较明显(灰度梯度较大)的初始匹配区域后,采用运用NCC算法的特征检测器匹配该区域,驱动特征标签细胞,而与之相关联的身份细胞进而也被激活,身份细胞选择另一特征标签细胞,与这两个特征标签细胞相关联的网格细胞,输出编码至距离细胞,依据距离细胞生成的矢量移动到下一特征检测区域,再次进行以上流程。若连续移动两次特征检测区域后都匹配失败,或身份细胞激活率之和大于5时,则重新在图像中寻找显著特征作为初始匹配区域。而当连续超过9次选择初始匹配区域,则认为是陌生对象。
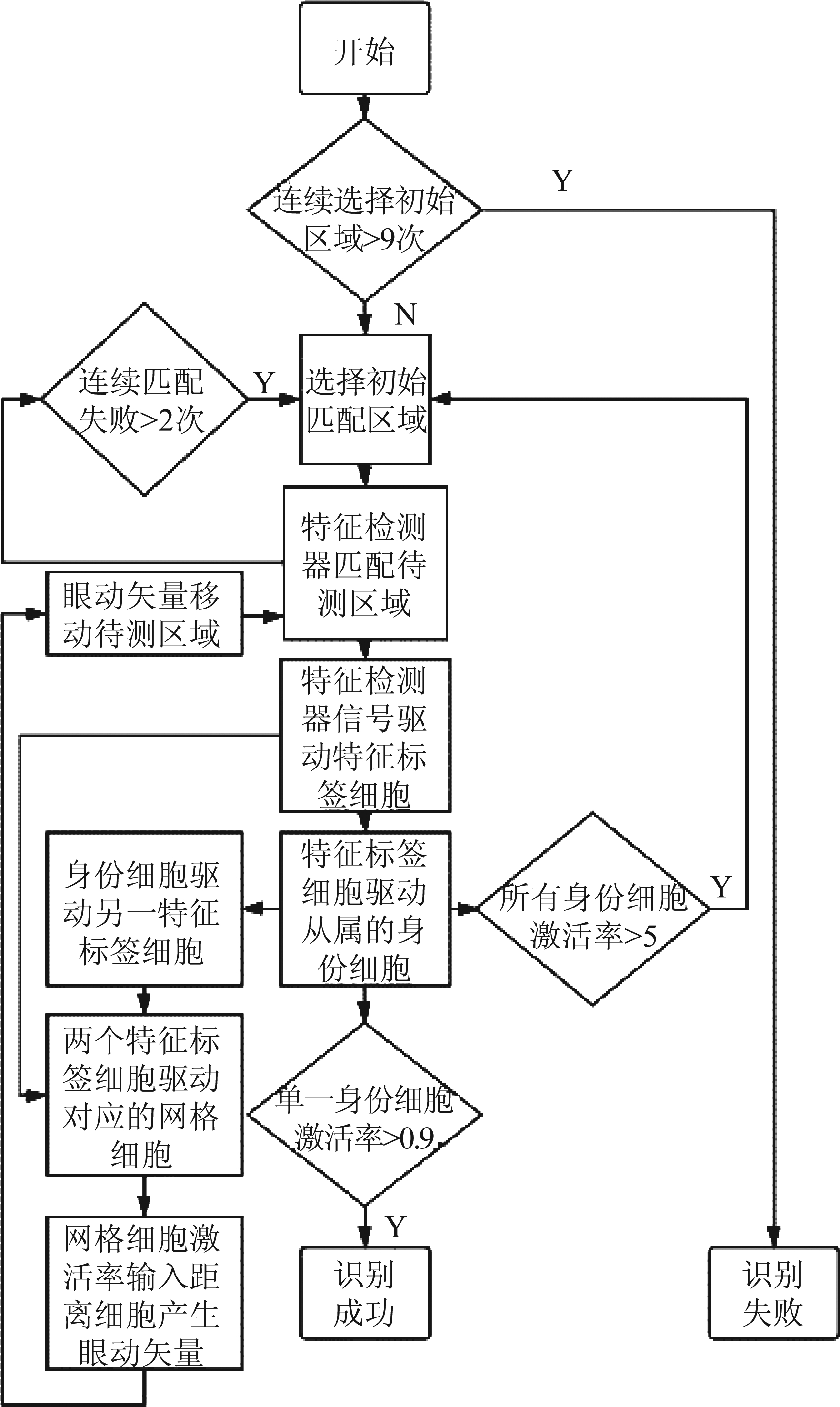
图4 模型算法流程图
Fig.4 Model algorithm flow chart
3.3 结果与分析
图5给出了模型的扫视识别过程。可以发现,NCC算法的精度较好,只有相似的特征区域才有较高的匹配值,因而正确的特征标签细胞能很快地在竞争中取得优势,而身份细胞也能在较短的扫视次数中积累足够的激活率。

图5 模型扫视识别过程
Fig.5 Model scanning recognition process
3.3.1 算法对比实验
实验同超香肠神经元模型、多自由度神经元模型以及支持向量基算法[21]进行比较,比较结果如下表:
表2 YALE数据集算法对比实验结果
Tab.2 Experimental results of algorithm comparison by YALE dataset
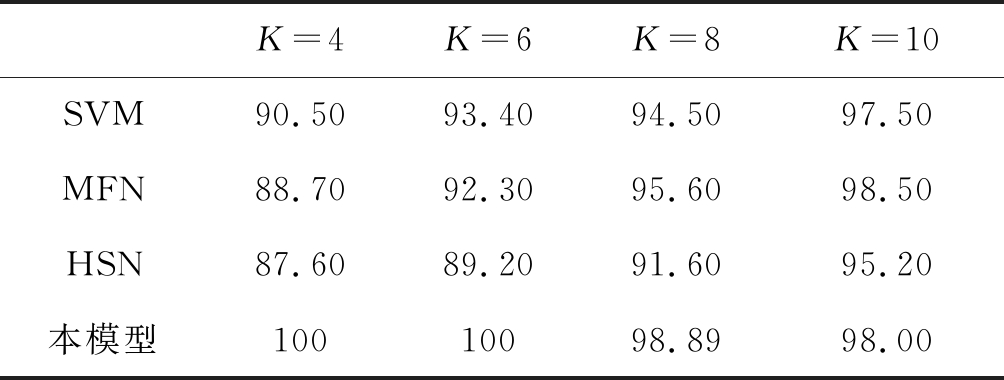
K=4K=6K=8K=10SVM90.5093.4094.5097.50MFN88.7092.3095.6098.50HSN87.6089.2091.6095.20本模型10010098.8998.00
可以看出,本实验模型在测试样本较小的情况下较其他算法,识别率较高且稳定。但存在测试对象越多,识别率逐渐下降的问题,可能原因是在识别对象增加的情况下,相互竞争的特征标签细胞增多,正确的特征标签细胞就更难以在竞争中获取优势。另一方面,模型的识别时间为2.79 s/幅,速度较其他识别模型而言慢。
3.3.2 灰度变化对比实验
本文针对灰度变化进行了对比实验。实验仍采用YALE人脸数据集,取K=10进行实验。实验结果如表3所示。实验结果表明,采用NCC特征匹配算法后,模型对灰度变化具有较好鲁棒性。实验中,在对图像整体改变灰度后(整体下降40),识别率有所降低但并不明显,平均扫视次数及用时都略有增加。
表3 灰度变化前后对比结果
Tab.3 Comparison results before and after gray level change
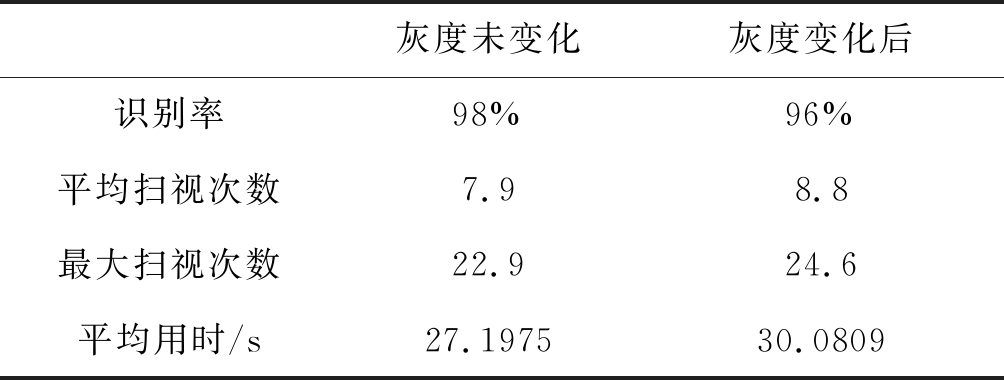
灰度未变化灰度变化后识别率98%96%平均扫视次数7.98.8最大扫视次数22.924.6平均用时/s27.197530.0809
图6对灰度变化前后的扫视识别过程进行了对比。可以看出,灰度值前后变化程度十分明显,但模型的识别过程并未受到较大的影响。这说明NCC算法对于图像灰度整体的线性变化鲁棒性较强。
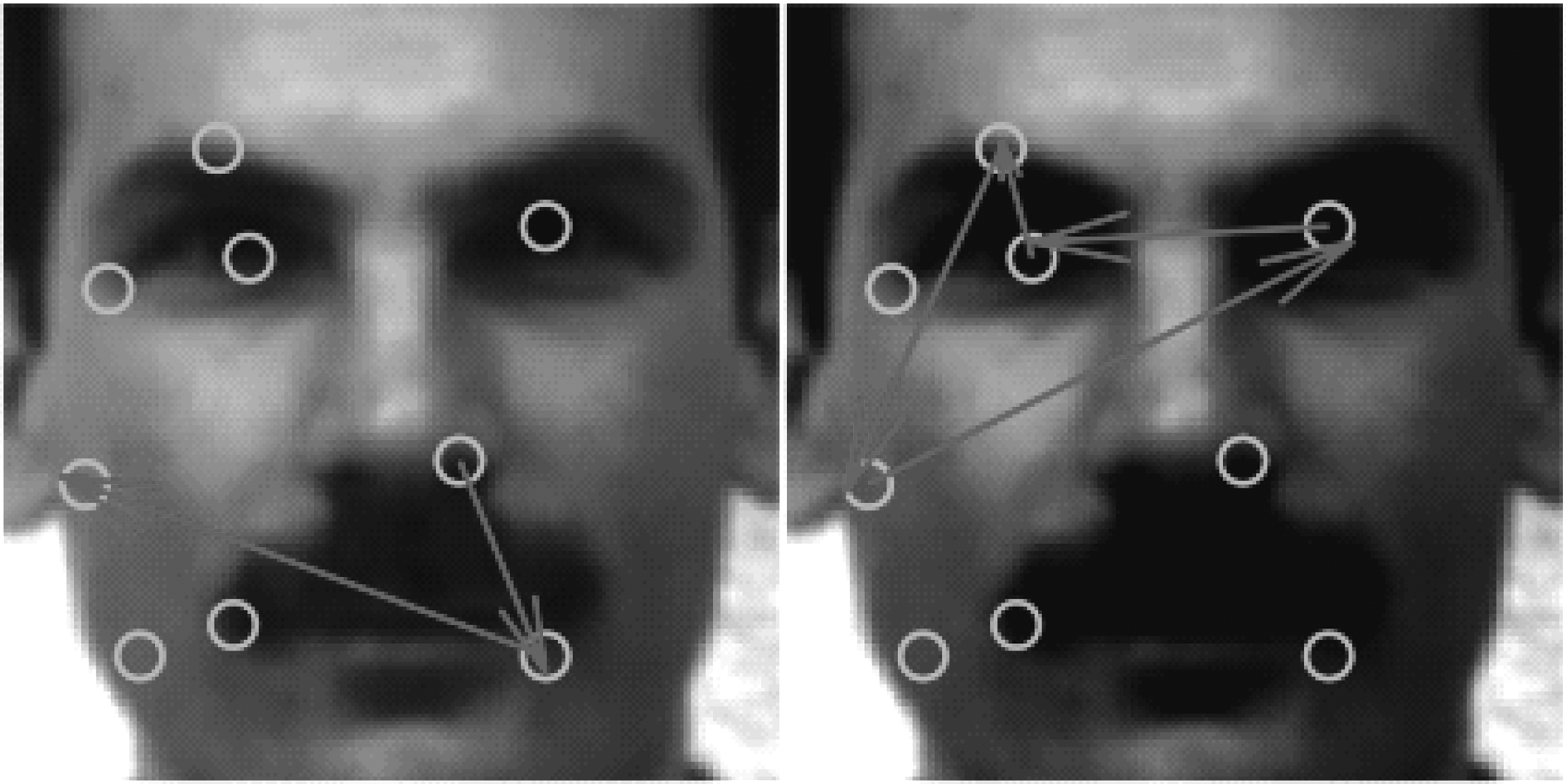
图6 灰度变化前后扫视识别过程对比
Fig.6 Comparison of scanning recognition process before and after gray level change
4 结论
本文提出一种基于NCC特征匹配的类脑视觉识别模型。在分析现有的生理学数据后,该模型提出通过连续吸引子网络的网格细胞模型实施坐标编码,以距离细胞输出位移矢量,驱动图像特征匹配区域变化,进行选择性特征匹配。另一方面,运用NCC特征匹配算法,在提高匹配速度与准确度的同时,还加强了匹配过程对于灰度变化的鲁棒性,提高了模型整体性能。该模型为识别算法提供一种可能的思路,为进一步研究奠定基础。
[1] EYKHOLT K, EVTIMOV I, FERNANDES E, et al. Robust physical-world attacks on deep learning visual classification[C]∥2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA. IEEE, 2018: 1625-1634.
[2] ALCORN M A,LI Qi,GONG Zhitao,et al.Strike (with) a pose: Neural networks are easily fooled by strange poses of familiar objects[C]∥2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, CA, USA. IEEE, 2019: 4840- 4849.
[3] HENDRYCKS D,ZHAO K,BASART S,et al.Natural adversarial examples[J].arXiv preprint arXiv,2019:1907.07174.
[4] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436- 444.
[5] ROY K, JAISWAL A, PANDA P. Towards spike-based machine intelligence with neuromorphic computing[J]. Nature, 2019, 575(7784): 607- 617.
[6] RIESENHUBER M, POGGIO T. Hierarchical models of object recognition in cortex[J]. Nature Neuroscience, 1999, 2(11): 1019-1025.
[7] SERRE T, WOLF L, BILESCHI S, et al. Robust object recognition with cortex-like mechanisms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(3): 411- 426.
[8] 杨欣, 费树岷, 陈丽娟. 小样本条件下基于全局和局部特征融合的人脸识别[J]. 信号处理, 2008, 24(1): 49-53.
YANG Xin, FEI Shumin, CHEN Lijuan. Global and local feature extraction based face recognition in small samples[J]. Signal Processing, 2008, 24(1): 49-53.(in Chinese)
[9] O’KEEFE J, DOSTROVSKY J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat[J]. Brain Research, 1971, 34(1): 171-175.
[10]HAFTING T, FYHN M, MOLDEN S, et al. Microstructure of a spatial map in the entorhinal cortex[J]. Nature, 2005, 436(7052): 801- 806.
[11]NAU M, NAVARRO SCHRÖDER T, BELLMUND J L S, et al. Hexadirectional coding of visual space in human entorhinal cortex[J]. Nature Neuroscience, 2018, 21(2): 188-190.
[12]GILCHRIST I D, BROWN V, FINDLAY J M. Saccades without eye movements[J]. Nature, 1997, 390(6656): 130-131.
[13]ROCHE A,MALANDAIN G,PENNEC X,et al.The correlation ratio as a new similarity measure for multimodal image registration[C]∥International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer,Berlin,Heidelberg,1998:1115-1124.
[14]李姣. 基于归一化互相关匹配的图像配准技术研究[D]. 兰州: 西北师范大学, 2018.
LI Jiao. Research on image registration based on normalized cross-correlation matching[D].Lanzhou: Northwest Normal University, 2018.(in Chinese)
[15]谢维达, 周宇恒, 寇若岚. 一种改进的快速归一化互相关算法[J]. 同济大学学报(自然科学版), 2011, 39(8): 1233-1237.
XIE Weida, ZHOU Yuheng, KOU Ruolan. An improved fast normalized cross correlation algorithm[J]. Journal of Tongji University (Natural Science), 2011, 39(8): 1233-1237.(in Chinese)
[16]王恩国, 吴树范. NCC边缘信息快速匹配算法[J]. 电子技术, 2017, 46(12): 19-21.
WANG Enguo, WU Shufan. Fast matching algorithm based on edge information[J]. Electronic Technology, 2017, 46(12): 19-21.(in Chinese)
[17]BLUM K I, ABBOTT L F. A model of spatial map formation in the hippocampus of the rat[J]. Neural Computation, 1996, 8(1): 85-93.
[18]BUSH D, BARRY C, MANSON D, et al. Using grid cells for navigation[J]. Neuron, 2015, 87(3): 507-520.
[19]BURAK Y, FIETE I R. Accurate path integration in continuous attractor network models of grid cells[J]. PLoS Computational Biology, 2009, 5(2): e1000291.
[20]HUHN Z, SOMOGYVARI Z, KISS T, et al. Extraction of distance information from the activity of entorhinal grid cells: A model study[C]∥2009 International Joint Conference on Neural Networks. Atlanta, GA, USA. IEEE, 2009: 1298-1303.
[21]肖潇. 高维仿生信息几何学研究及其在模式识别中的应用[D]. 杭州: 浙江工业大学, 2012.
XIAO Xiao. High-dimension biomimetic information science and its application in pattern recognition[D]. Hangzhou: Zhejiang University of Technology, 2012.(in Chinese)


