1 引言
随着科技水平的进步,全球导航卫星系统(Global Navigation Satellite System, GNSS)已经被广泛的应用在各个领域,其中北斗导航定位系统(Beidou system,BDS)是我国独立研发的[1-2],该系统也应用了性能更加优越的二进制偏移载波信号[14]。在实际的通信环境中,信号在传输过程中难免会因为遇到树木、建筑物等而发生散射、反射等现象[16],因此,多径成为了一种难以避免的情况,而且多径也是影响定位精度的一个主要因素,基于此种情况,对多径环境下的信号的处理成为了十分重要的一件事,然而对信号进行处理的首要步骤是对信号的捕获,因此,对多径环境下信号的捕获的研究是十分有必要的。
目前存在的文献大多数是对不存在多普勒变化率的多径信号的捕获或跟踪,对存在一阶多普勒变化率的多径信号的捕获算法并不多,文献[3]通过滑动相关的方法完成了对多径情况下接收信号的捕获,但是该方法需要的捕获时间长,实时性较差,并且对噪声和干扰较为敏感。文献[4]应用PMF的方法对接收信号在多径情况下的捕获性能进行了分析,该方法需要的捕获时间比文献[3]短,但是该方法却需要占用大量硬件资源来实现。文献[5]采用PMF与FFT相结合的方法实现了对存在多普勒频偏的单径信号的快速捕获,文献[6]对文献[5]进行了拓展,对PMF与FFT相结合的方法在多径情况下接收信号的捕获性能进行了分析,但是该方法只能对存在多普勒频偏的信号进行捕获,对存在一阶多普勒变化率的信号的捕获却无能为力。文献[7-10]采用PMF和FRFT相结合的方法完成了对存在一阶多普勒变化率的信号的捕获,但是上述文献[7-10]仅仅讨论了在单径情况下该方法对信号的捕获性能,完全没有涉及该算法在多径情况下的捕获性能的讨论。
对于多径情况下且存在一阶多普勒变化率的高动态BOC信号捕获困难的问题,本文提出了基于PMF和FRFT相结合的多径情况下高动态BOC信号的捕获算法,该方法首先利用PMF的方法对信号进行分段积分处理,通过减少积分时间来减小多普勒频偏影响的同时降低后续操作的运算量,然后对积分结果进行FRFT运算,确定直达信号所对应的最佳FRFT阶数,最后在直达信号能量最集中的FRFT域完成对存在一阶多普勒变化率的多径信号的捕获。
2 信号模型
2.1 单径BOC信号模型
BOC调制信号是一种具有频谱分裂特性以及更强抗干扰能力的信号。BOC基带信号的产生是通过扩频伪码和副载波以及基带数据相乘后得到的。BOC调制信号的产生是通过载波与BOC基带信号相乘之后得到的[10],其产生框图如图1。
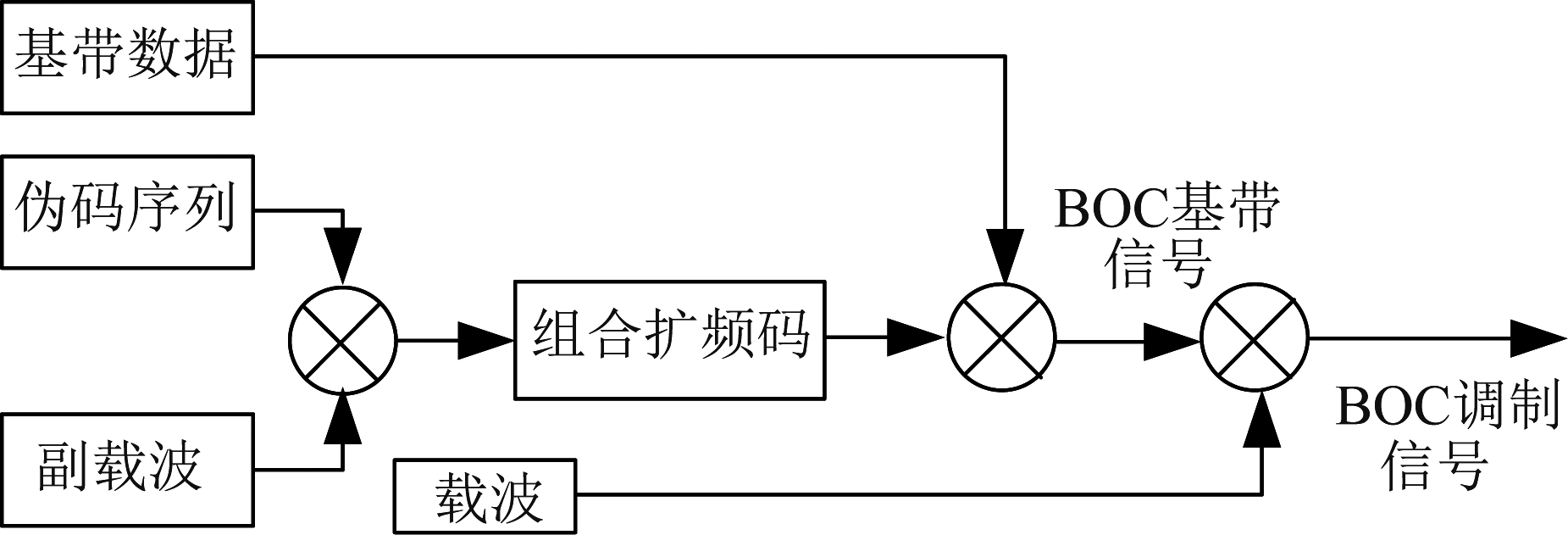
图1 BOC调制信号原理框图
Fig.1 BOC Modulation Signal Principle Block
单径情况下存在一阶多普勒变化率的BOC信号可以表示如下:
r(t)=Ad(t)c(t)sc(t)exp[j 2πφ(t)+φ0]+n(t)=
Ad(t)s(t)exp[j 2πφ(t)+φ0]+n(t)
(1)
其中A代表信号的幅度,d(t)代表基带数据,c(t)代表扩频伪码,sc(t)=sgn[sin(2πfsct)]代表副载波, fsc代表副载波频率,s(t)=c(t)sc(t)代表组合扩频码,φ0代表初始相位,φ(t)=(fi+fd)t+kdt2, fi代表中频频率, fd代表多普勒频移,kd代表一阶多普勒变化率。n(t)代表高斯白噪声。
2.2 多径BOC信号模型
多径情况下存在一阶多普勒变化率的BOC信号可以表示如下:
x(t)=r(t)⊗h(τ,t)+n(t)
(2)
(3)
其中式(2)中的r(t)代表上文所描述的存在一阶多普勒变化率的单径BOC信号,式(2)和式(3)中的h(τ,t)代表时变信道模型,ak(t)以及τk(t)代表第k条路径在时刻t所对应的信号的幅度衰落和传输时延,δ(t)代表单位冲激函数[5]。
一般而言,脉冲的变化速率和信道的变化速率比起来会快很多[13],因此我们可以将h(τ,t)等效为如下表达式:
(4)
综上所述,可将上述BOC信号在多径情况下的信号模型表示如下:
x(t)=Ad(t)s(t)exp[j 2π(fdt+kdt2)+φ0]⊗![]()
(5)
将式(5)以伪码速率进行采样后可表示如下:
x(i)=Ad(i)s(i)exp[j 2π(fdi+kdi2)+φ0]⊗![]()
(6)
3 捕获算法原理
3.1 部分匹配相关原理
因为扩频信号具有优良的相关特性,所以将采样后的信号和扩频信号进行相关运算是完成信号捕获的常用方法,但是当多普勒频移增大时,相关运算的幅值也会相应的减小,影响信号的捕获,因此,本文采取部分匹配相关的方法,减小相关运算的长度,一方面可以通过减小积分运算的时间减小多普勒频移的影响,另一方面又可以减小下一步FRFT的运算点数,从而减小计算的复杂度。
部分匹配相关运算的实质是将接收信号与扩频信号进行分段并行相关运算,假设每个匹配滤波器的长度是p,共有R个部分匹配滤波器,则运算的总长度L=pR。为了使下文的分析更加方便,假设信号幅度A等于1且在部分相关运算的过程中信号的信息位不发生改变,因此,多径信号与扩频信号的第r(0≤r≤R-1)个部分相关运算可以表示如下[5]:
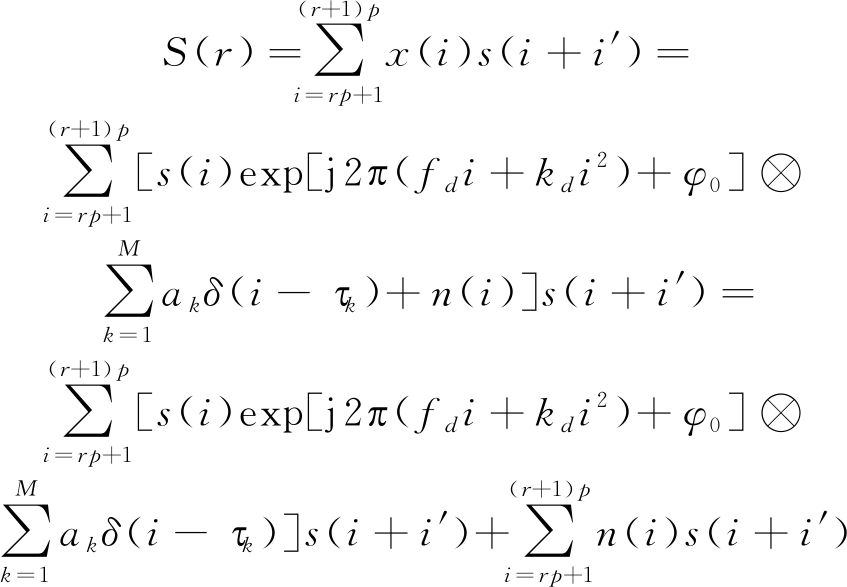
(7)
将式(7)经过化简后,可以得到下式:
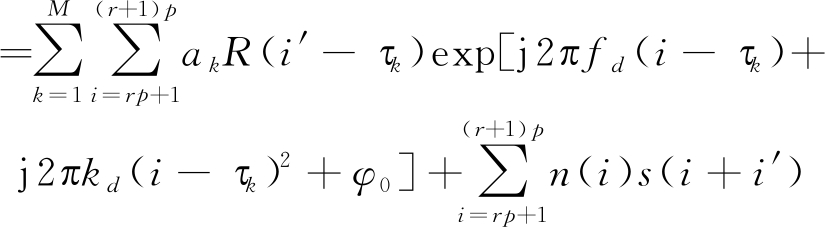
(8)
由式(8)可以看出,存在一阶多普勒变化率的多径信号的部分相关结果是不同时延的单径信号的部分相关结果之和。由参考文献[12]可得存在一阶多普勒变化率的单径信号的部分相关结果可以看为LFM信号,具体表达式如下所示:
s(r)=R(Δτ)sin c[fdp+kdp2]
exp[j 2πfd(i-τ)+j 2πkd(i-τ)2+φ0]
(9)
因此,存在一阶多普勒变化率的多径BOC信号的部分相关结果可以化简为不同LFM信号之和,具体表达式如下所示:
![]()
exp[j 2πfd(i-τk)+j 2πkd(i-τk)2+φ0]+![]()
(10)
3.2 FRFT原理
存在一阶多普勒变化率的LFM信号在频域存在频谱展宽的问题,不能同时估计多普勒频移和多普勒变化率。LFM信号的Wigner分布在时频平面是一条斜直线,而且一个LFM信号的Wigner分布在FRFT域的直线积分投影恰恰是该信号在FRFT域上的模的平方,因此,在和该条斜直线相垂直的FRFT域上求FRFT将会有明显的峰值出现,而噪声的能量则会均匀的分布在整个时频平面内,不会出现能量聚集[18],因此可以通过FRFT的能量聚集的特性实现对存在一阶多普勒变化率的信号的多普勒频偏以及一阶多普勒变化率的估计。
FRFT对于LFM信号的另外一个优点是当存在多分量LFM信号时,不同的LFM信号在FRFT域不会出现交叉项,不同的LFM信号会在不同的FRFT阶数下出现能量聚集。对于所接收到的卫星信号来说,通常情况下总是存在一条直达信号和多条反射信号的,而且由于反射路径上所造成的损耗,一般而言,直达信号的能量是大于反射信号的能量的,因此我们可以首先利用不同的LFM信号在不同的FRFT阶数下产生能量聚集的特性以及不同多径信号的能量强弱的关系得到直达信号能量聚集时所对应的FRFT阶数,然后利用直达信号在该阶数下产生能量聚集而噪声和除直达信号之外的反射信号等多径信号则不会在该阶数下产生明显的能量聚集的特性实现对多径信号的捕获。
通过文献[16]可得,信号x(t)所对应的FRFT的定义可表述如下:
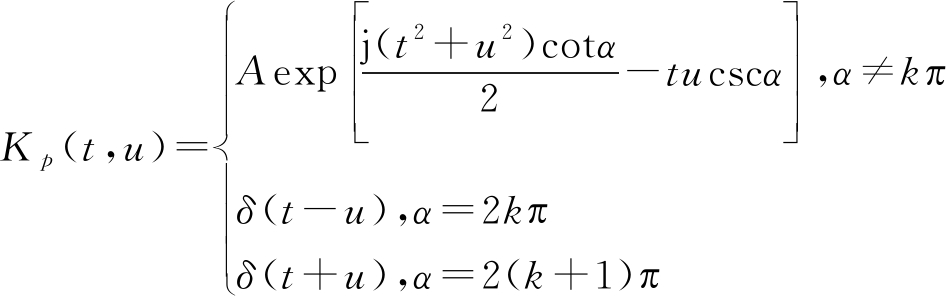
(11)
其中,![]() 表示整数,p表示FRFT变换的阶数,α=pπ/2表示旋转的角度,位于(t, f)平面的LFM信号经过α的旋转角度后会在(u,ν)平面产生能量聚集。
表示整数,p表示FRFT变换的阶数,α=pπ/2表示旋转的角度,位于(t, f)平面的LFM信号经过α的旋转角度后会在(u,ν)平面产生能量聚集。
离散化是将FRFT应用到实际的工程中所必不可少的步骤,离散信号S(n)的N点离散FRFT可以表示如下[12]:

(12)
将部分匹配相关结果进行FRFT后能量峰值所对应的位置可以表示如下:
(13)
其中![]() 表示旋转角度的估计值,
表示旋转角度的估计值,![]() 表示频率误差的FRFT输出阶数的估计值,多普勒频偏的估计值
表示频率误差的FRFT输出阶数的估计值,多普勒频偏的估计值![]() 和一阶多普勒变化率的估计值
和一阶多普勒变化率的估计值![]() 可以表示如下[12]:
可以表示如下[12]:
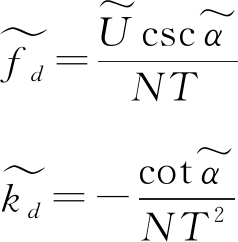
(14)
3.3 捕获算法框图
本文所提出的对存在一阶多普勒变化率的多径BOC信号的具体捕获算法框图如图2。
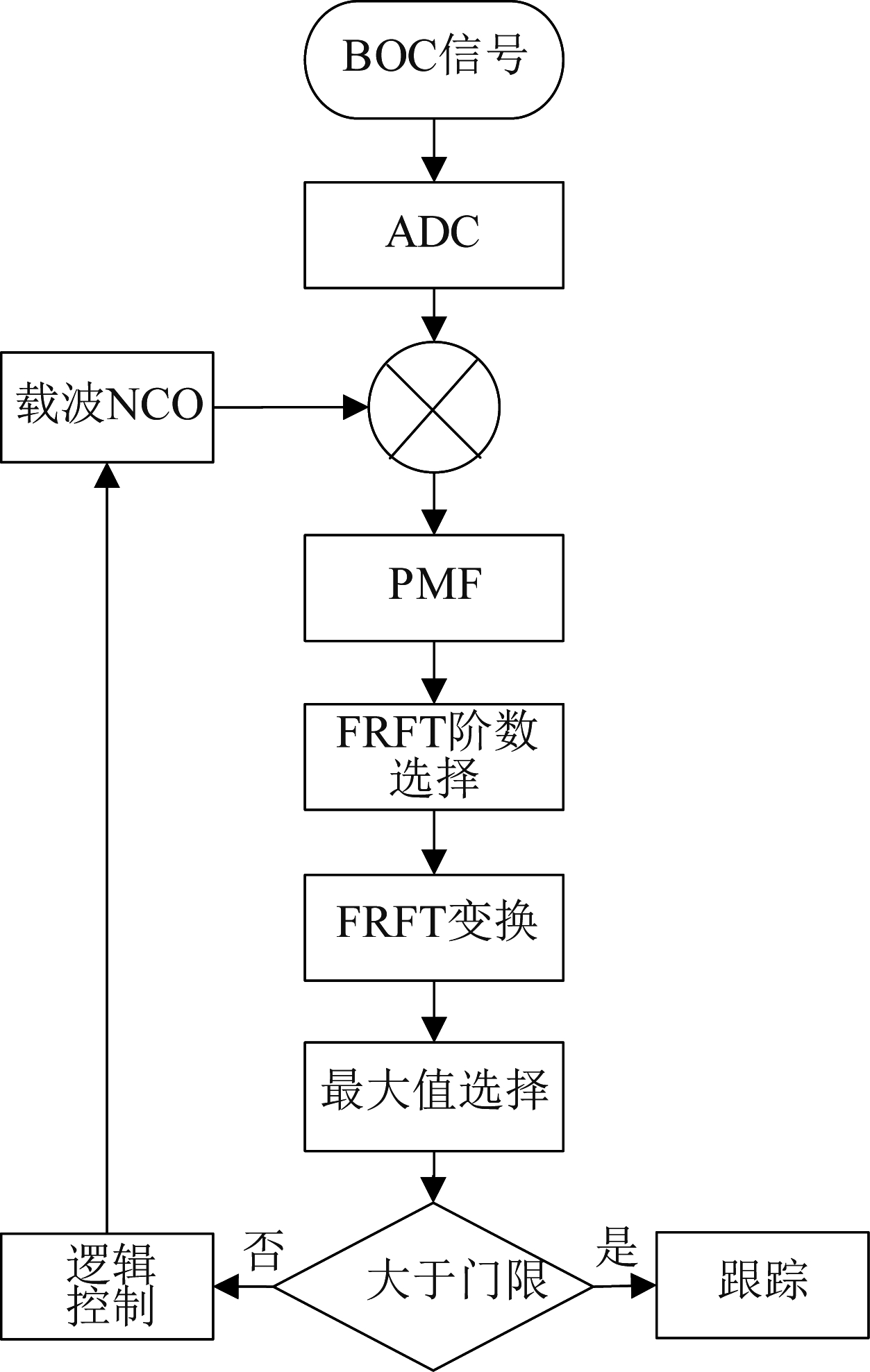
图2 整体捕获算法框图
Fig.2 Block diagram of overall acquisition algorithm
捕获算法步骤如下:
步骤1 将接收到的存在一阶多普勒变化率的多径BOC信号进行下变频、模数转换以及离散化采样,得到离散信号。
步骤2 将采样后得到的离散信号经过本地载波控制振荡器(NCO,numerically controlled oscillator)进行载波剥离。
步骤3 将每一段中经过载波剥离后的BOC信号与组合扩频码进行分段相关运算。
步骤4 将分段相关运算结果进行FRFT处理,得到直达信号所对应的最佳FRFT阶数。
步骤5 在最佳FRFT阶数下对分段相关运算的FRFT结果进行取模运算且进行峰值的搜索。
步骤6 将取模运算后的最大峰值和判决门限进行比较,若最大值超过了预先设定的门限,则说明本地扩频码和接收信号的扩频码已经对齐,完成了对信号的捕获,如果没有超过预先设定的门限值,根据式(14)所获得的参数对多普勒频偏进行补偿,同时滑动本地扩频码。
步骤7 重复步骤3到步骤6的操作,直到扩频码相位对齐。
4 仿真实验
为了检测所提出的算法对多径BOC信号的捕获性能,本文对BOC(1,1)信号进行了仿真实验,在本次仿真实验中,将信号的采样频率设置为16.368 MHz,码元速率设置为1.023 MHz,码片的长度设置为1024,PMF时间为16 ms,多普勒频偏设置为5 kHz,一阶多普勒变化率设置为2 kHz。
实验1 谱峰对比仿真
本实验对多径条件下的BOC信号进行了PMF-FFT变换以及直达信号所对应的最优FRFT阶次下的PMF-FRFT变换,结果如图3的(a)图和(b)图。
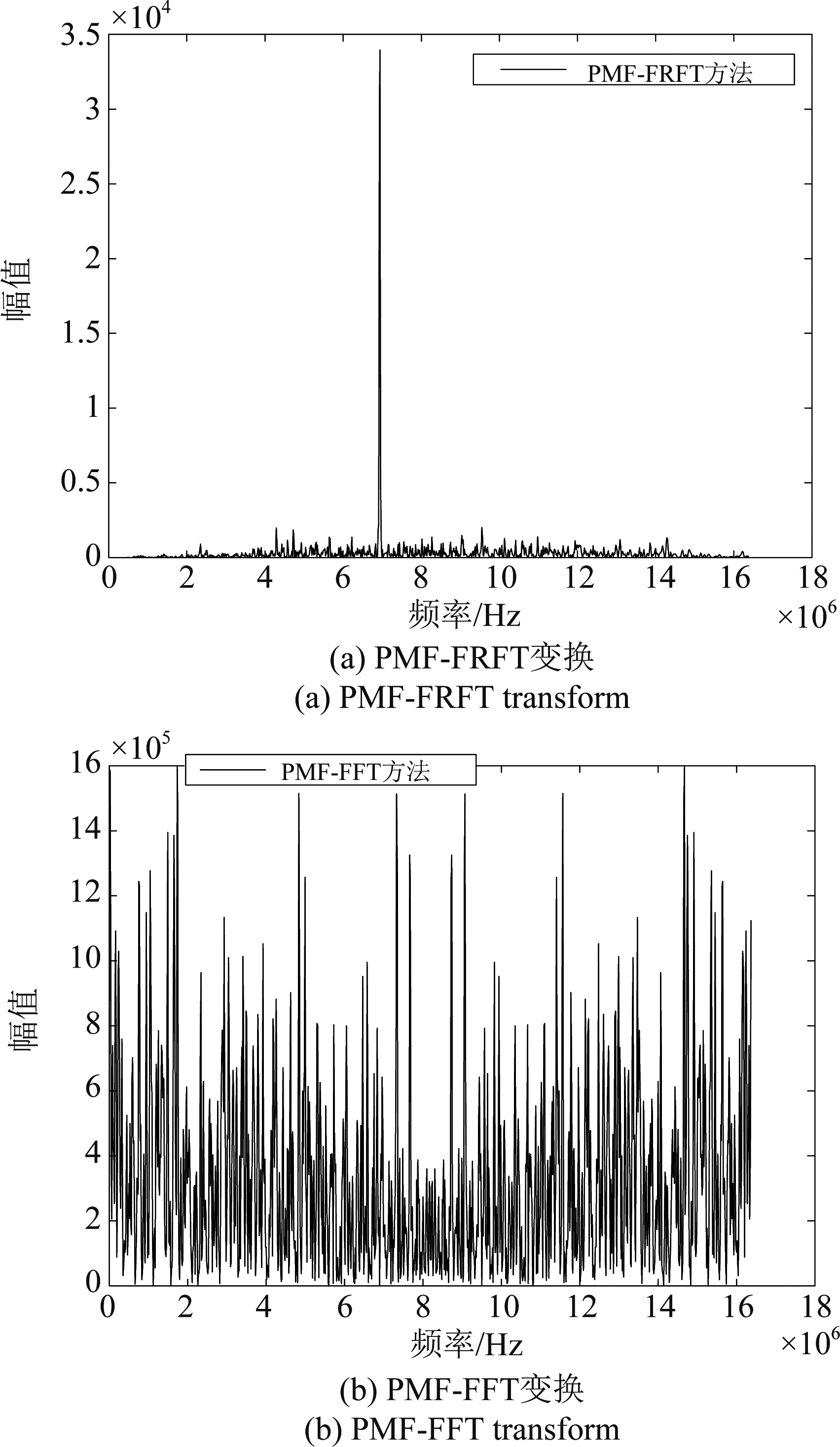
图3 峰值仿真对比图
Fig.3 Peak simulation comparison chart
从图3中的(a)图和(b)图可以看到PMF-FRFT的方法由于能量聚集的特性有明显的峰值出现,能够对存在一阶多普勒变化率的多径信号实现直接捕获,而PMF-FFT方法的主峰和副峰之间则相隔非常接近,难以实现对存在一阶多普勒变化率的多径信号的直接捕获。
实验2 分段数对比仿真
本实验对长度为L=1024的数据进行了不同分段数的分段相关运算,假设分段数用R表示,每一段的长度用p表示,则可以得到L=pR,实验中所取的分段数分别为R=4,R=8,R=16,仿真结果如图4。
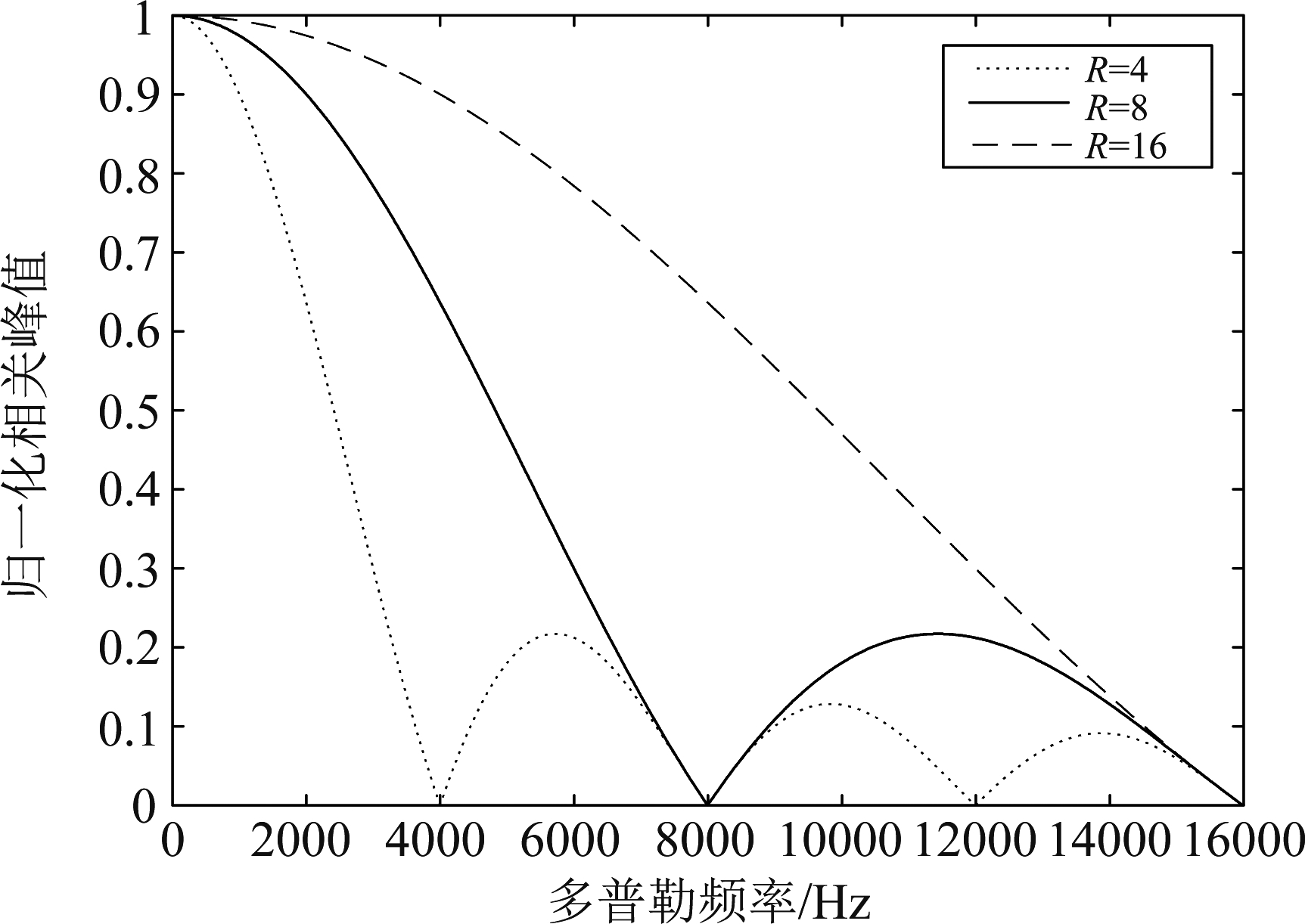
图4 分段数仿真对比图
Fig.4 Simulation comparison diagram of segmentation number
通过图4可以看到,当实验中所取的分段数增多的时候,相关峰的衰减将会变的缓慢,这是因为相关运算的结果会随着相关运算时间的延长而增加对多普勒频移的积累,因此缩短相关运算的点数可以增大相关运算结果对多普勒频移的容差性[15],从而可以达到减小相关峰的衰减的目的。
实验3 窗函数影响仿真
本实验分别对不加窗,加哈明窗,加汉宁窗,加凯撒窗时的BOC信号的检测概率进行了仿真实验,仿真结果如图5。
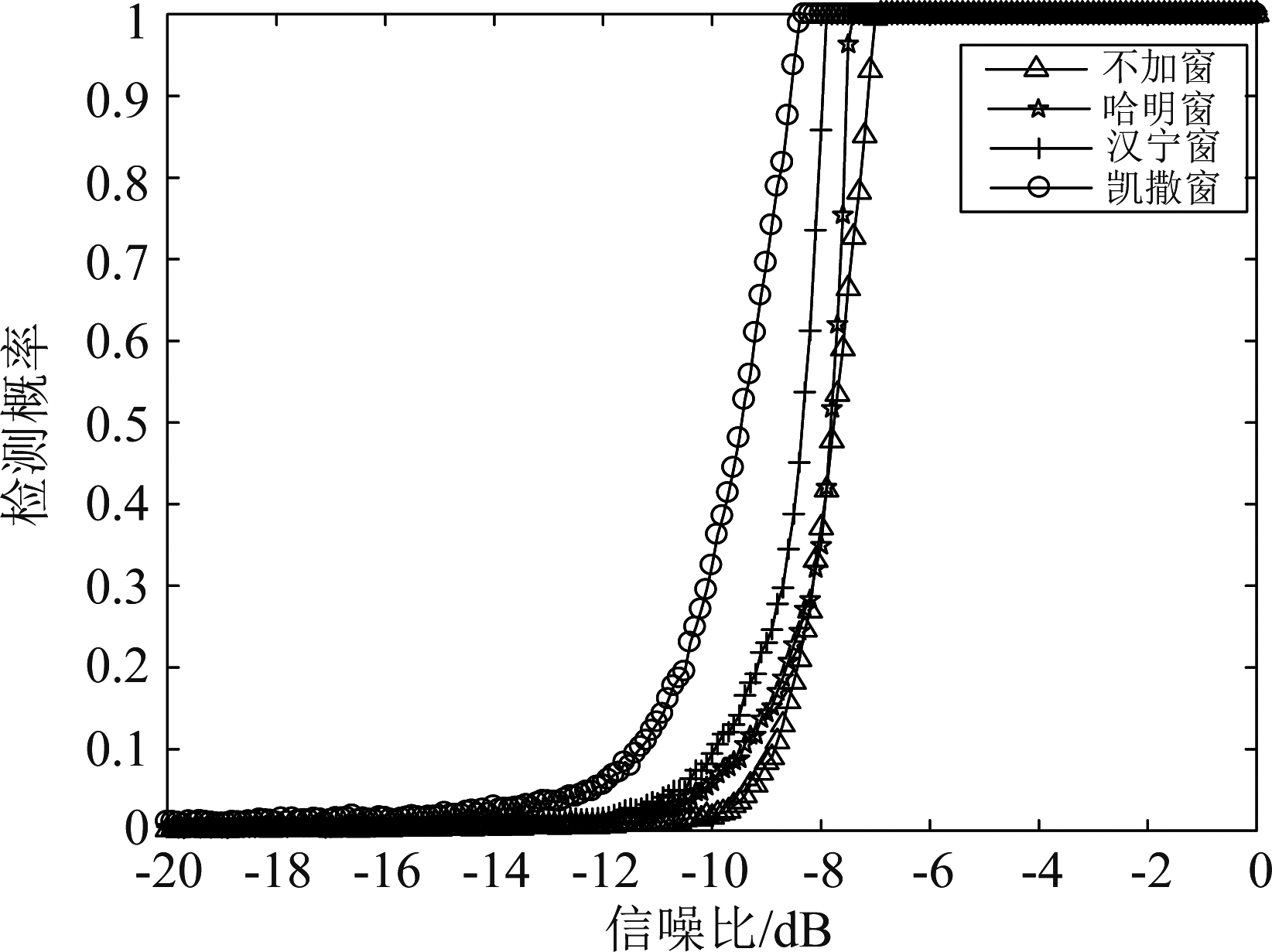
图5 不同加窗仿真对比图
Fig.5 Comparison diagram of different windowing simulation
从图5中可以看到,加窗后的检测概率高于不加窗时的检测概率,其中加哈明窗的检测概率比不加窗时的检测概率高0.4 dB,加汉宁窗的检测概率比不加窗时的检测概率高0.9 dB,加凯撒窗时的检测概率最高,比不加窗时的检测概率高1.3 dB,加窗后可以提高检测概率的原因是对FRFT的运算通常是采用基于FFT分解的快速计算方法来实现的,但是FFT运算存在频谱泄露的问题,因此将FRFT的快速算法应用到实际工程运算中的时候,也难免会出现频谱泄漏的问题,因此在运算的过程中进行加窗处理可以减小频谱泄漏,提高检测概率。
实验4 不同莱斯因子仿真
本实验分别对多径数为L=3,莱斯因子K=1,K=5,K=10时的BOC信号进行了仿真实验,仿真结果如图6。
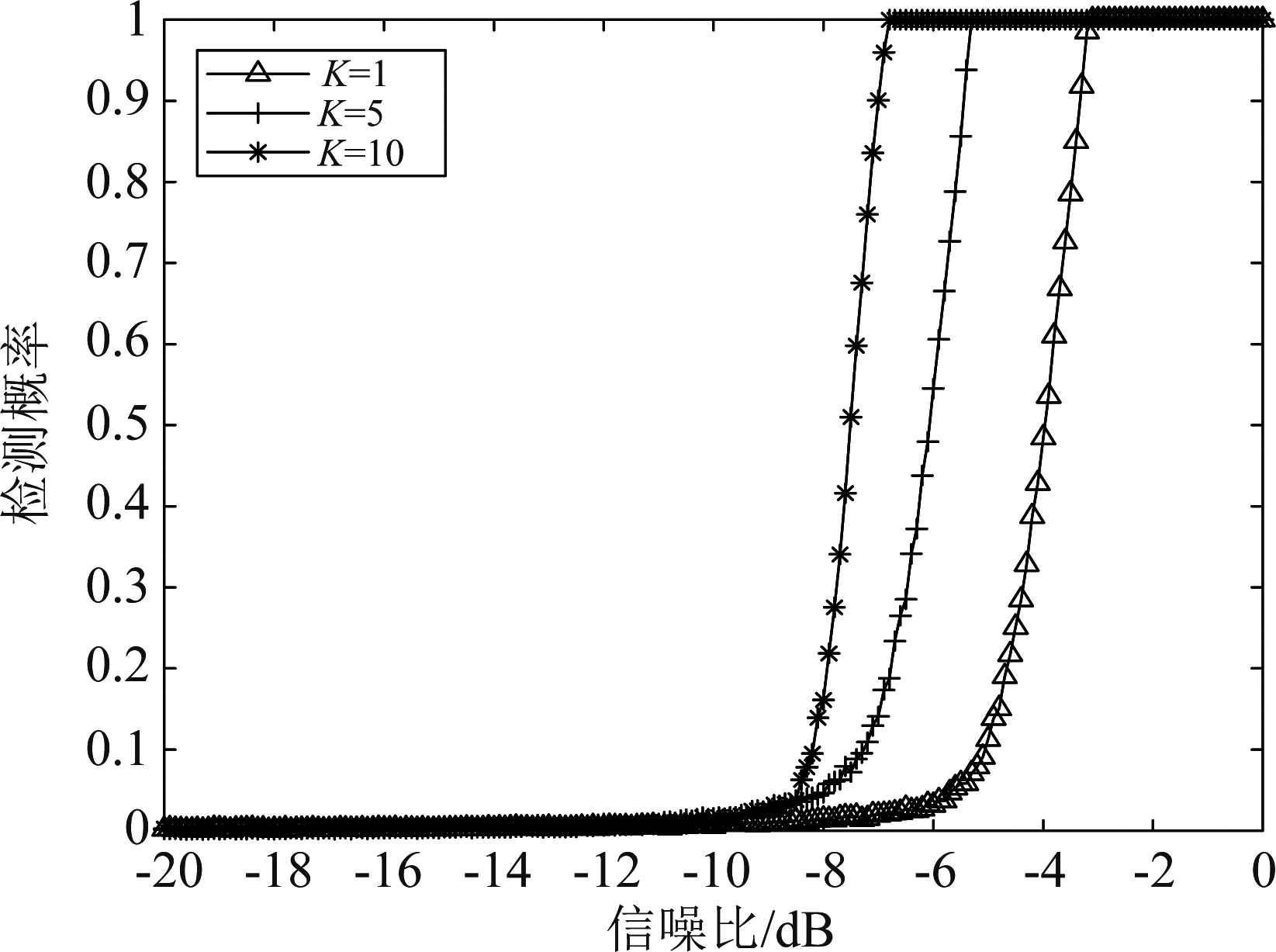
图6 莱斯因子仿真对比图
Fig.6 Rice factor simulation comparison chart
从图6可以看到,随着莱斯因子数的增大,检测概率逐渐增大,其中K=5时的检测概率比K=1时的检测概率高2.1 dB,K=10时的检测概率比K=5时的检测概率高1.5 dB。这是因为莱斯因子所描述的是直射分量的能量和散射波的能量和的比例,当莱斯因子数增大的时候,直射信号所占的能量相比于其他反射,散射等信号所占的能量的比例增大,随着直达信号所占能量的增大,多径信号对直达信号的影响也会相应的减小,检测概率也会随之而增大。
实验5 不同多径数仿真
本实验分别对莱斯因子数为K=5,多径数L=2,L=5,L=7时的BOC信号进行了仿真实验,仿真结果如图7。
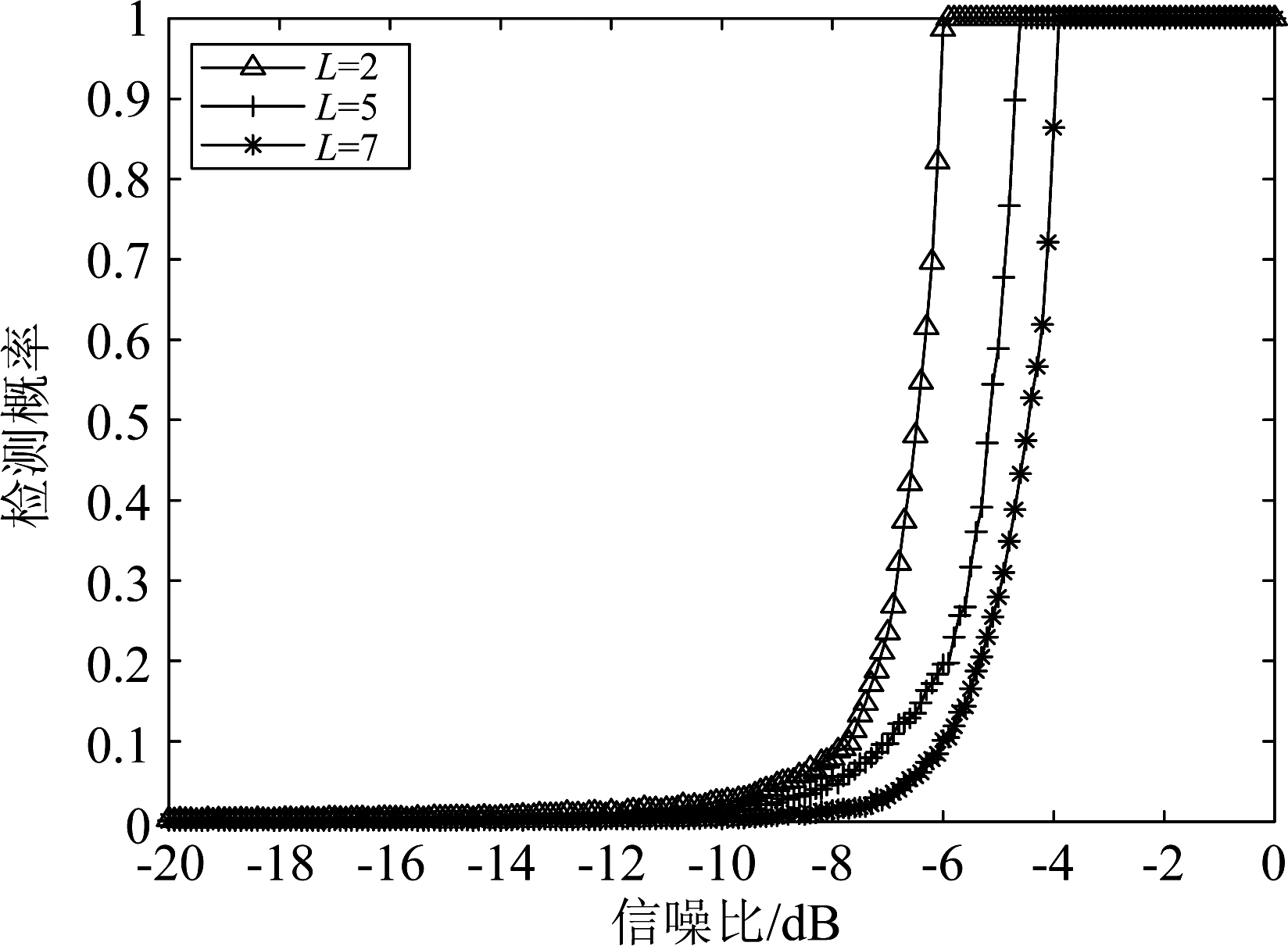
图7 多径数仿真对比图
Fig.7 Comparison diagram of multipath number simulation
从图7可以看到,随着多径数的增多,检测概率随之减小,其中L=2时的检测概率比L=5时的检测概率高1.3 dB,L=5时的检测概率比L=7时的检测概率高0.7 dB,这是因为随着多径数的增多,多径信号对直达信号的干扰就会随之增大,因此,随着多径数的增多,检测概率也会随之下降。
实验6 不同多普勒频偏仿真
本实验对一阶多普勒变化率分别为a2=1K,a2=2K,a2=3K时的多径信号的检测概率进行了仿真实验,仿真结果如图8。

图8 多普勒频偏仿真对比图
Fig.8 Comparison diagram of Doppler frequency offset simulation
从图8可以看到,随着一阶多普勒变化率的增高,检测概率随之减小,其中a2=1K时的检测概率比a2=2K时的检测概率高2.1 dB,a2=2K时的检测概率比a2=3K时的检测概率高1.5 dB,这是因为多普勒变化率会对部分相关结果产生影响,随着多普勒变化率的增大,相关峰会发生衰减,而FRFT运算的峰值和相关运算的幅值的平方成正比[17],所以随着一阶多普勒变化率的增大,检测概率也会随之减小。
实验7 不同算法对比仿真
本实验在莱斯因子数K=1,多径数L=5时分别应用本文算法和DPT-PMF-FFT算法以及并行码FFT算法对BOC信号进行了仿真实验,仿真结果如图9。
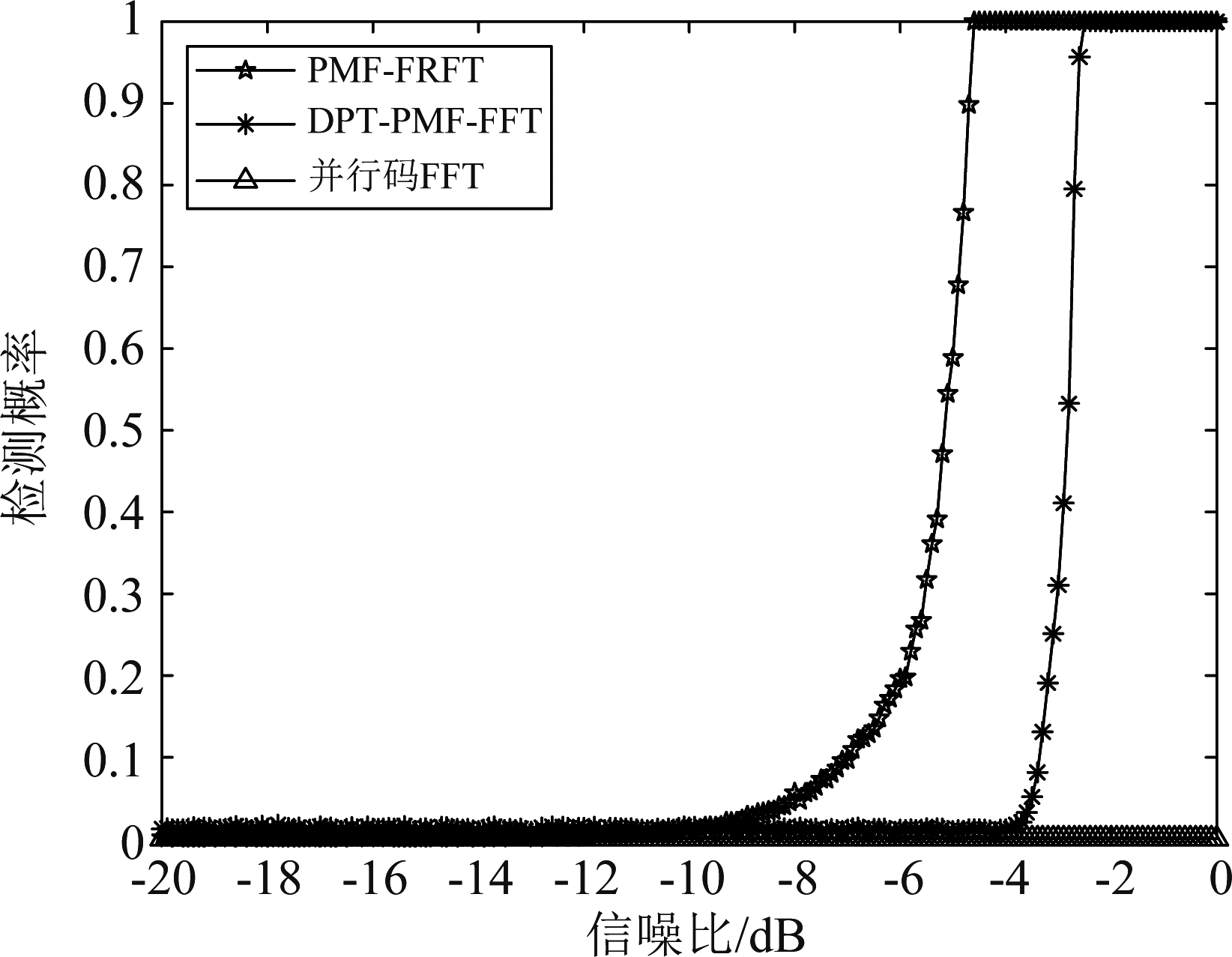
图9 不同算法对比仿真图
Fig.9 Comparison of different algorithms
从图9可以看出,本文所提算法所得到的检测概率最高,其次是DPT-PMF-FFT算法,本文算法的检测概率比DPT-PMF-FFT算法的检测概率高将近2 dB的原因是经过降阶处理后会引入一部分噪声,从而造成检测概率的降低,基于并行码的FFT算法因为不能对一阶多普勒变化率进行补偿,所以难以实现对存在一阶多普勒变化率的多径信号的捕获。
5 结论
本文拓展了PMF和FRFT相结合的单径信号捕获方法,利用多分量LFM信号在FRFT域不存在交叉项以及多径分量直达信号与除直达信号外的多径分量能量不同的优点,先确定直达信号所对应的最佳FRFT阶数,然后在此最佳FRFT阶数下实现了对多径信号抑制的同时完成对直达信号的捕获。仿真结果表明,在莱斯因子数为1,多径数为3,一阶多普勒变化率为2K的时候,本文算法可以在SNR=-7 dB的情况下完成对多径BOC信号的捕获,因此,通过仿真试验,可以认为本算法可以完成对存在一阶多普勒变化率的多径BOC信号的捕获,且通过仿真发现本文算法比DPT-PMF-FFT算法有将近2 dB的检测概率的提升。
[1] KIM S, CHONG D, YOON S. A new GNSS synchronization scheme[C]∥VTC Spring 2009-IEEE 69th Vehicular Technology Conference. Barcelona, Spain. IEEE, 2009: 1-5.
[2] YAO Yibin, LIU Lei, KONG Jian , et al. Global ionospheric modeling based on multi-GNSS, satellite altimetry, and Formosat-3/COSMIC data[J]. Gps Solutions, 2018, 22(4):104.
[3] 黄振, 陆建华, 杨士中. 基于DMF直扩系统捕获性能的研究[J]. 电路与系统学报, 2002, 7(1): 92-95.
HUANG Zhen, LU Jianhua, YANG Shizhong. Performance of acquisition in a matched-filter for DSSS[J]. Journal of Circuits and Systems, 2002, 7(1): 92-95.(in Chinese)
[4] 谭晓衡, 杨力生, 王韬. 基于DMF捕获系统频率选择性信道下捕获性能的分析[J]. 电路与系统学报, 2004, 9(6): 13-18.
TAN Xiaoheng, YANG Lisheng, WANG Tao. Acquisition performance analysis based on digital matched-filter over frequency-selective channel[J]. Journal of Circuits and Systems, 2004, 9(6): 13-18.(in Chinese)
[5] 刘燕丽, 张天骐, 苗圃, 等. 部分相关与功率谱相结合的伪码快捕算法[J]. 测控技术, 2009, 28(11): 14-18,31.
LIU Yanli, ZHANG Tianqi, MIAO Pu, et al. Rush capture of PN code based on method of partial correlation and power spectrum[J]. Measurement & Control Technology, 2009, 28(11): 14-18,31.(in Chinese)
[6] 杜晓华, 张天骐, 庞统, 等. 多径环境下直扩信号PN码捕获性能分析[J]. 计算机应用研究, 2010, 27(8): 2913-2917.
DU Xiaohua, ZHANG Tianqi, PANG Tong, et al. Analysis on PN code acquisition performance in DS-SS over multipath environment[J]. Application Research of Computers, 2010, 27(8): 2913-2917.(in Chinese)
[7] LUO Yiran, ZHANG Lei, EL-SHEIMY N. An improved DE-KFL for BOC signal tracking assisted by FRFT in a highly dynamic environment[C]∥2018 IEEE/ION Position, Location and Navigation Symposium (PLANS). Monterey, CA. IEEE, 2018: 1525-1534.
[8] LUO Yiran, ZHANG Lei, RUAN Hang. An acquisition algorithm based on FRFT for weak GNSS signals in A dynamic environment[J]. IEEE Communications Letters, 2018, 22(6): 1212-1215.
[9] XIA Xuan, ZHAO Jiankang, LONG Haihui, et al. Fractional Fourier transform-based unassisted tracking method for Global Navigation Satellite System signal carrier with high dynamics[J]. IET Radar, Sonar & Navigation, 2016, 10(3): 506-515.
[10]QI Jianzhong, LUO Feixiang, SONG Qingping. Fast acquisition method of navigation receiver based on folded PMF-FFT[C]∥2014 IEEE Computers, Communications and IT Applications Conference. Beijing, China. IEEE, 2014: 62- 66.
[11]张天骐, 袁帅, 刘董华, 等. 基于批处理和Teager-Kaiser算子的BOC信号联合捕获算法[J]. 系统工程与电子技术, 2019, 41(2): 259-265.
ZHANG Tianqi, YUAN Shuai, LIU Donghua, et al. BOC signal combined acquisition algorithm based on batch processing and Teager-Kaiser operator[J]. Systems Engineering and Electronics, 2019, 41(2): 259-265.(in Chinese)
[12]潘毅, 张天骐, 张刚, 等. 高动态BOC信号捕获算法[J]. 通信学报, 2019, 40(6): 82- 89.
PAN Yi, ZHANG Tianqi, ZHANG Gang, et al. Acquisition algorithm for BOC signals in high dynamic environment[J]. Journal on Communications, 2019, 40(6): 82- 89.(in Chinese)
[13]潘毅, 张天骐, 李军伟, 等. 多径衰落信道下BOC信号捕获性能分析[J]. 光通信研究, 2013(5): 67-70.
PAN Yi, ZHANG Tianqi, LI Junwei, et al. Analysis of BOC signal acquisition performance in multipath fading channels[J]. Study on Optical Communications, 2013(5): 67-70.(in Chinese)
[14]XIONG Hailiang, WANG Songhua, GONG Shu, et al. Improved synchronisation algorithm based on reconstructed correlation function for BOC modulation in satellite navigation and positioning system[J]. IET Communications, 2018, 12(6): 743-750.
[15]宁海涛. 弱GPS信号捕获远近场效应研究[J]. 计算机应用与软件, 2014, 31(2): 144-148,229.
NING Haitao. On near-far field effect of GPS signal capture[J]. Computer Applications and Software, 2014, 31(2): 144-148,229.(in Chinese)
[16]冯亚丽, 刘成, 张祥斌. Chirp信号多径时延估计算法研究[J]. 计算机应用研究, 2020, 37(6): 1638-1641.
FENG Yali, LIU Cheng, ZHANG Xiangbin. Research on multipath delay estimation algorithm for Chirp signal[J]. Application Research of Computers, 2020, 37(6): 1638-1641.(in Chinese)
[17]刘建成, 刘忠, 王雪松, 等. 高斯白噪声背景下的LFM信号的分数阶Fourier域信噪比分析[J]. 电子与信息学报, 2007, 29(10): 2337-2340.
LIU Jiancheng, LIU Zhong, WANG Xuesong, et al. SNR analysis of LFM signal with Gaussian white noise in fractional Fourier transform domain[J]. Journal of Electronics & Information Technology, 2007, 29(10): 2337-2340.(in Chinese)
[18]金翔. 分数阶Fourier变换的高动态信号参数估计[D]. 重庆: 重庆邮电大学, 2011.
JIN Xiang. High dynamic signal parameter estimation based on the fractional Fourier transform[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2011.(in Chinese)



