1 引言
作为常用扩谱通信方式之一,跳频通信凭借其强抗干扰能力、低截获率、多址组网能力、抗衰落等特点,成为军事通信中的关键技术。同时,它的兴起也对通信侦察带来巨大考验,因此对跳频信号进行准确检测具有重要的军事意义。
近年来国内外已有许多跳频信号检测方法,主要可分为非盲检测和盲检测两大类。文献[1]提出一种基于能量的检测方法,使用辐射计在各个通道进行测量,根据各信道检测结果判断是否存在跳频信号,但抗噪性能差。文献[2]针对信道化接收中由于无法保证收发双方的时间同步而导致的检测性能恶化问题,提出一种利用重叠滑动窗法生成门限值的方法,显著地降低了虚警概率。文献[3]提出的基于压缩接收机检测法,与信道化接收机相比,该方法易于实现,但处理的跳频信号带宽有一定的限制。文献[4-5]提出的基于自相关检测是一种基于功率采样判决的检测算法,采用了粗略信道化处理,与信道辐射计相比具有更好的检测性能。文献[5]在文献[4]的基础上引入一个只与噪声分布相关的特征量ρ作为考察参数,缓解了噪声的影响,在较低信噪比下具有良好检测效果。文献[6]利用跳频信号和定频信号在时频矩阵上的聚集差异性,通过设置合适局部自适应阈值剔除定频信号,具有较低的计算复杂度,但无法在低信噪比情况下实现跳频信号的检测。文献[7]将接收数据映射到能量域,通过白化、主成分分析、信道化处理以及短时能量对消依次将有色噪声、突发信号、定频干扰进行剔除实现跳频信号检测,具有较低的虚警概率。
上述检测方案都是在已知信号的跳速、跳时或候选频率集等参数的基础上实现的,而通常获取这类先验信息是一项极具挑战性的任务,因此无须先验知识的盲检测更适用于实际战场中。文献[8]利用跳频信号与定频信号功率谱对消比大小的差异,可以实现跳频信号与定频信号发生频率碰撞的跳频信号检测。文献[9]改进文献[8]传统功率谱对消法,将信号直接分成两段计算功率对消比,在实现跳频信号和定频信号检测的同时减少了计算量,但在存在突发干扰和低信噪比条件下识别性能急剧下降。文献[10-11]利用跳频信号和噪声具有不同的自相关特性,文献[10]根据接收信号的自相关峰值进行跳频信号盲检测,文献[11]根据接收信号与含噪模板在频域的自相关统计量进行检测,但这类方法只能在背景噪声中检测跳频信号,无法在含有其他干扰信号时实现跳频信号的检测。文献[12-13]将信号经短时傅里叶变换后得到的时频图作为二维图像进行分析,分别利用图像边缘检测原理和形态学预处理方法有效剔除背景噪声和定频干扰,提高跳频信号检测性能,但在多个跳频信号同时存在或低信噪比等情况下性能恶化。文献[14]在信号的时频瀑布图上提取方向梯度直方图特征,利用Adaboost算法实现跳频信号自动化检测,但在低信噪比的环境下,跳频信号容易被误检为定频信号。
从以上论述可看出,大多盲检测算法都是在相对简单的电磁环境中检测跳频信号,且在低信噪比条件下检测性能急剧下降甚至方法失效。考虑到跳频信号的非平稳性,本文从时频分析角度出发,充分利用各信号的时频分布特点,根据各信号在时频对消比上的差异,在高斯白噪声背景下实现对多个跳、定频信号的检测,且在复杂电磁背景和低信噪比条件下具有优越的跳频信号检测性能。
2 短时傅里叶变换与信号模型
时频分析技术能够描述信号在不同时间里频率变化的情况,同时它又能从时域、频域两个维度反映观测信号能量强度,故十分适用于对跳频信号分析处理[15-16]。本文选用简单直观、无交叉项干扰的短时傅里叶变换(STFT)对跳频信号进行实时处理分析。
对于给定的连续信号x(t),其短时傅里叶变换定义如下:
STFTx(f,t)=
x(τ)h*(τ-t)e-j2πfτdτ
(1)
其中h(t)是窗函数,h*(t)是它的共轭形式。
从上式可看出,STFT实际上是将x(t)与一个以t为中心的窗函数相乘再做傅里叶变换的过程,最后得到的是x(t)在“t”附近的“局部频谱”。窗函数的形状和长度影响时频域分辨率,应结合实际应用情况,在时间和频率分辨率上进行权衡,选择合适的窗函数。
假设接收机在观测时间T内接收到的信号为x(t),对其进行离散化处理,用以下数学模型表示:
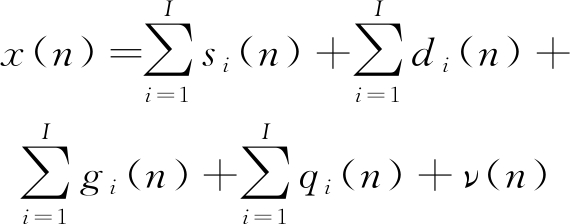
(2)
其中,si(n)表示第i个跳频信号,i=1,2,3,...,I;di(n)表示第i个定频信号,i=1,2,3,...,I;gi(n)表示第i个扫频信号,i=1,2,3,...,I;qi(n)表示第i个突发信号,i=1,2,3,...,I;ν(n)是均值为0、方差为
的高斯白噪声;信号长度为L。选取长度为W的窗函数对x(n)进行STFT处理,得到STFTx(m,n),令其时频谱为:
(3)
其中m=1,2,...,M为离散频率点;n=1,2,...,N为时刻点。
3 时频对消原理与方法
由于跳频信号和定频信号的时频图具有不同特性,因此做如下处理得到时频对消比。先将接收信号时频谱的不同频率分量在所有时间点的功率进行累加,得到只与频率相关的平均功率谱
(4)
然后在原时频谱上减去对应频率的平均功率谱,得到时频对消谱:
(5)
最后利用原时频谱和时频对消谱功率总和,构造信号的时频对消比统计量η如下:
(6)
3.1 时频对消法原理
(1)跳频信号的时频对消比
跳频信号的频率是随时间不断跳变的,且其跳变周期远小于接收信号长度,即它在某一频率上停留的时间远短于观测时间,故按照式(4)计算可知它的平均功率谱是非常小的,因此时频对消谱保留了信号的原时频特性。以H=1为例,可得跳频信号时频对消比如下:
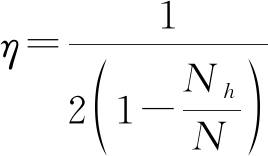
(7)
其中Nh为跳频信号一跳周期内所占时间点数,每个时间点上的功率大小为a,N为时频谱的时间点数。由于Nh≪N,由式(7)可知跳频信号的时频对消比η为
(2)定频信号的时频对消比
由于定频信号是以某一恒定不变的频率存在于整个观测时间内,它的时频谱是相对均匀地分布在各频率的每个时间点上,则
恒成立,通过式(5)时频对消后得到Psub(m,n)=0,可将定频信号剔除。那么对于定频信号而言,其时频对消比的分母趋近于0,分子是原时频谱的功率总和,故理论上所得对消比的值η=∞。
(3)高斯白噪声的时频对消比统计量
利用不等式关系可得
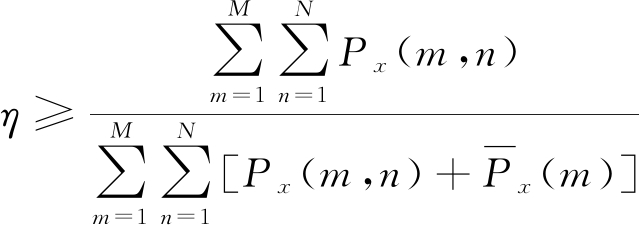
(8)
令
对于服从
分布的高斯白噪声ν(n),其功率谱Px(m,n)和平均功率谱
分别服从自由度为2和2N的中心卡方分布[17]。可知q1和q2服从自由度分别为2MN和2(N+1)MN的中心卡方分布,则r1服从F分布[17],其统计均值为
(9)
由式(4)和(5)可知,
又由于
所以
因此当M和N较大时,由式(6)和式(9)可得η的统计均值E{η}是大于1的有限值。
(4)其他干扰信号的时频对消比
突发信号会以任意频率随机出现在观测时间内,具有类似于跳频信号的频域特征,但其存在时间一般比跳频周期短[18],即有Nq<Nh≪N,其中Nq为突发信号持续时间点数,故
的取值近似为0,根据式(7)可得突发信号的时频对消比近似为0.5。
同理,对于扫频信号,可将它视为线性分布在不同频率的突发信号,其在某一频点停留的时间为Ng,同样有Ng<Nh≪N,故扫频信号的对消比也近似为0.5。
由上述分析可知,跳频信号、定频信号和高斯白噪声的时频对消比具有明显差异,因此可以在高斯噪声背景下利用η检测跳频信号和定频信号。由于突发和扫频干扰信号的时频对消比与跳频信号比较接近,将影响跳频信号检测性能,本文后续将分析其影响情况。
3.2 算法流程
当扫频和突发干扰信号不存在时,本文简称为高斯白噪声背景。根据纽曼皮尔逊准则,给定虚警概率,通过蒙特卡洛仿真得到高斯白噪声背景下检测门限u1和u2,则本文所提出的基于时频对消比的定频信号和跳频信号检测算法(简记为TFC)流程图如图1。
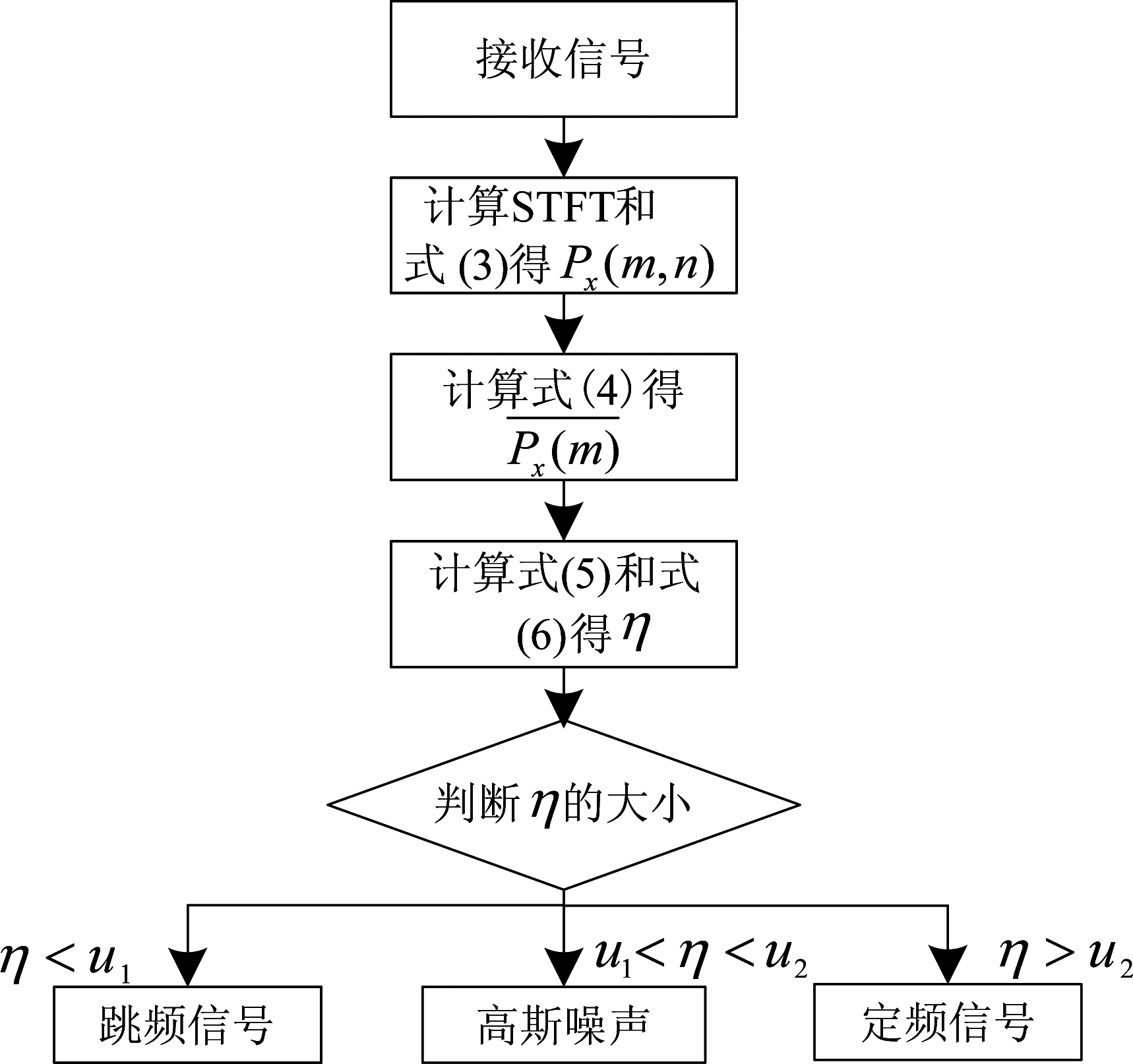
图1 时频对消算法流程图
Fig.1 Flow chart of time-frequency cancellation algorithm
4 算法仿真及性能分析
假设信号的采样率为10 MHz,接收信号长度为100000点。高斯白噪声背景下的接收信号包含(1)三个定频信号频率,其分别为800 kHz、2500 kHz和3000 kHz;(2)两个跳频信号,跳频周期分别为0.5 ms、1 ms,跳频频率集分别为[2800 1400 600 300 1200 450 1850 2500 1550 750 2100 1750 1950 1000 1250 2300 500 2200 800 1600]kHz和[2000 900 1700 1300 1800 400 1900 1500 700 2650]kHz。复杂电磁环境下的接收信号另外增加了扫频范围为100～500 kHz,扫频周期为4 ms的扫频信号、三个持续时长为0.1 ms频率分别为980、1600和2700 kHz的突发干扰。
4.1 时频对消比分析
选定窗长为1024的Hamming窗,滑动步长为窗长的25%。
当接收信号为两个跳频信号和三个定频信号时,时频对消前后的时频谱图如图2所示。从图2可以看出,即使在定频信号与跳频信号发生频率碰撞的情况下,经时频对消,也能基本抵消定频信号,同时保留跳频信号,仿真结果与理论分析一致。图2(b)中若隐若现的长线条是跳频信号的时间平均功率对消后的残留,其值大小随着观测时间的增长而减小。
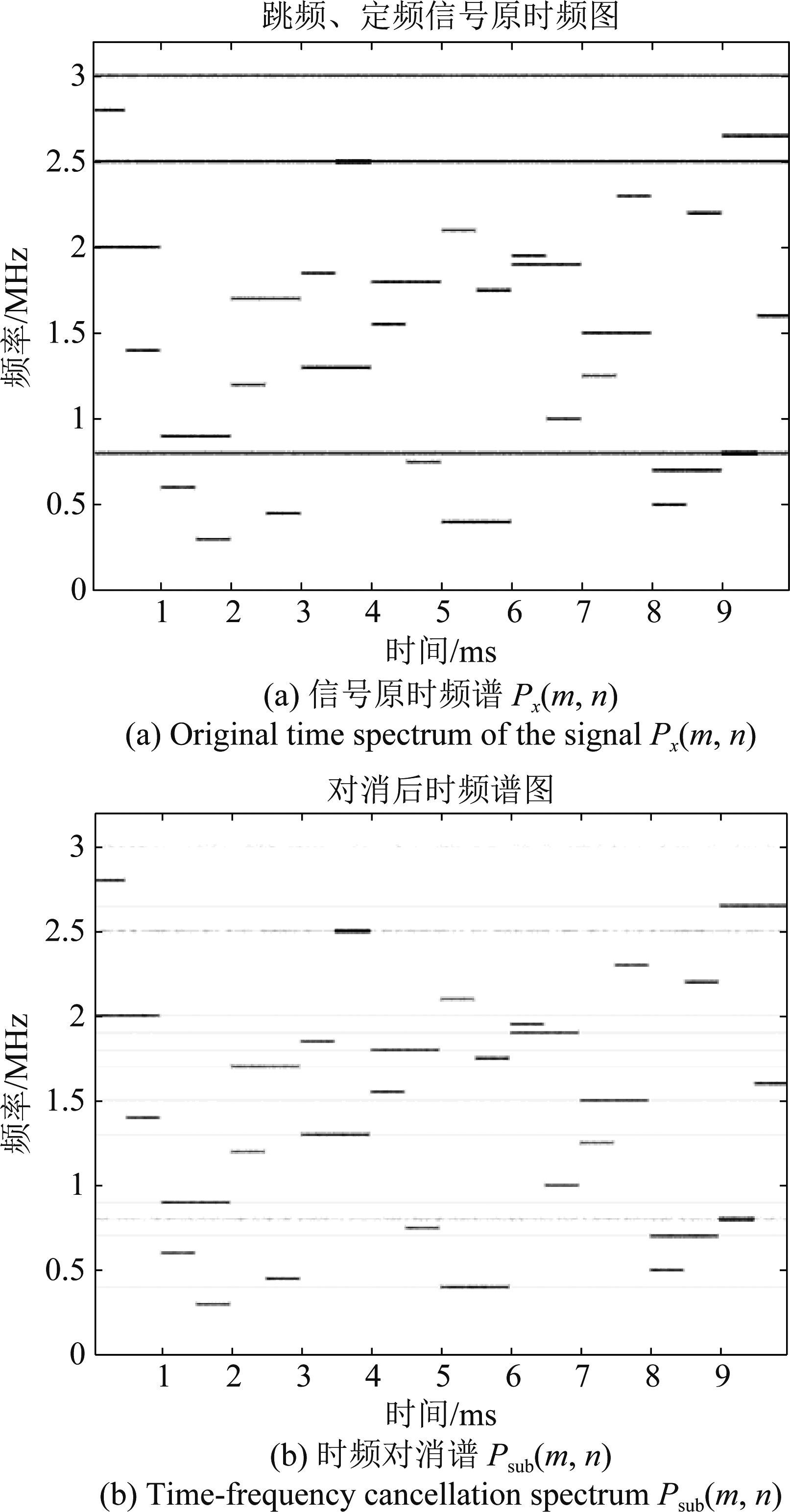
图2 接收信号时频对消前后的时频图
Fig.2 The time-frequency diagram of the received signal before and after the cancellation
根据3.1节可知,纯定频信号的时频对消比理论上为无穷大。104次蒙特卡洛实验得到不同功率下周期为1 ms的纯跳频信号、纯扫频和突发信号以及纯高斯白噪声的时频对消比,结果表明,纯跳频信号的时频对消比为0.558,纯扫频和突发信号的时频对消比为0.515,纯高斯白噪声的时频对消比在1.362上下浮动。
由3.1节可知时频对消可基本剔除定频信号,故定义跳频信号功率与扫频、突发信号功率之和的比值为信干比(SIR),扫频、突发信号的功率之和与高斯白噪声功率的比值为干噪比(JNR)。
复杂电磁环境下的接收信号包括跳频信号、定频信号、扫频和突发信号以及高斯白噪声,不同SIR下接收信号的时频对消比如图3所示。由图3可看出,随着干噪比或信噪比的增加,复杂电磁环境下的接收信号时频对消比减小;低干噪比时,高斯白噪声影响大,接收信号时频对消比会随着干噪比或信噪比的降低而增大,并向高斯白噪声的时频对消比逼近;在干噪比或信噪比较大时,扫频、突发干扰信号或跳频信号的时频对消比是主要成分,接收信号的时频对消比随着干噪比的增加而减小,并最终趋向于稳定值。
图3 信号时频对消比
Fig.3 Time-frequency cancellation of signals
4.2 高斯白噪声背景下定频信号和跳频信号的检测
(1)判决门限的确定
为了确定检测门限值和分析噪声方差对门限的影响,分别对噪声方差
为1～10的高斯白噪声的时频对消比各进行104次蒙特卡洛实验,虚警概率为10-4时得到检测门限u1和u2与方差的关系如图4所示。
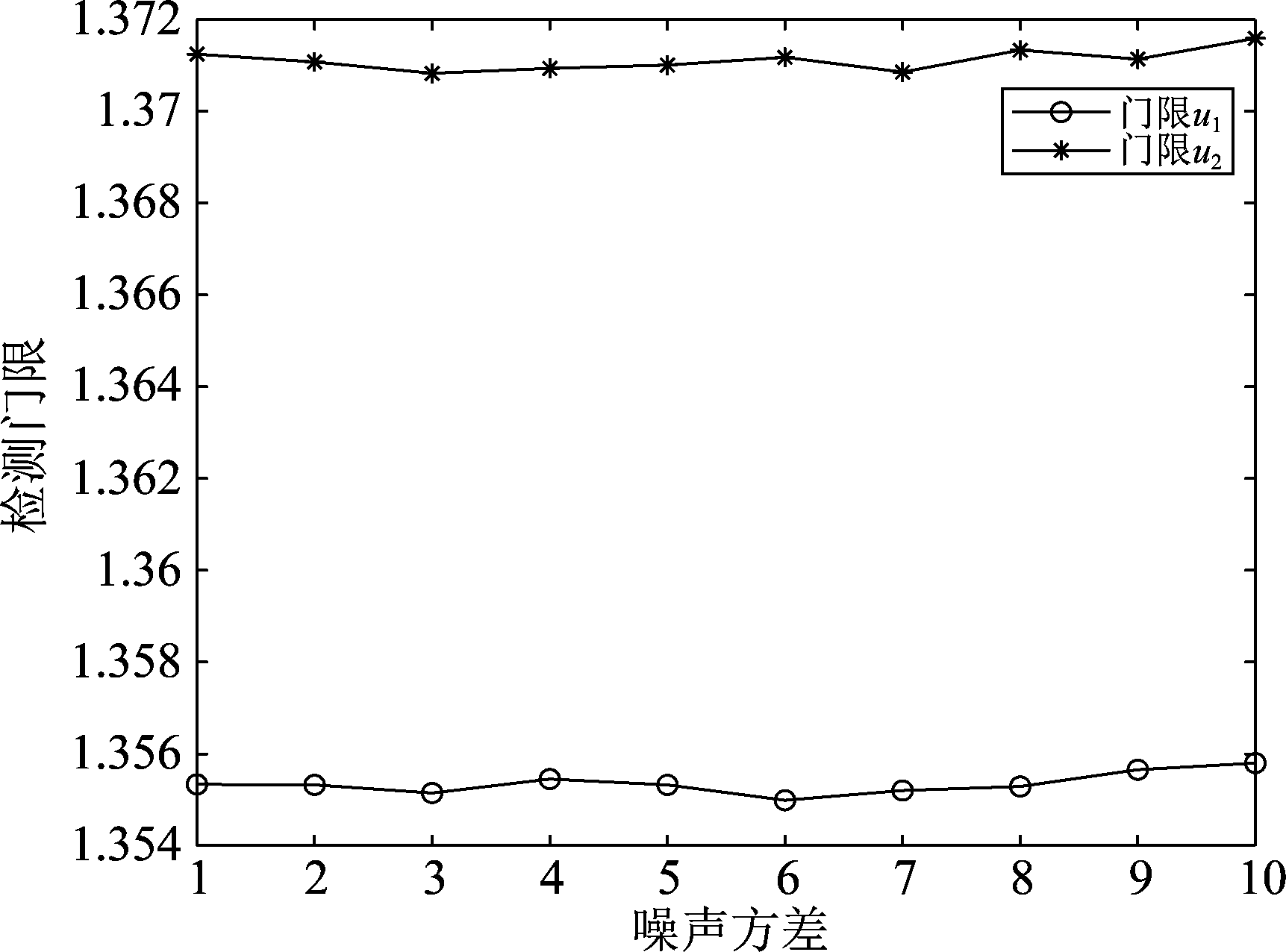
图4 不同方差下的门限值
Fig.4 Threshold under different variances
由上图可知,门限u1在1.354～1.356之间,u2在1.370～1.372上下轻微波动,由此可知,本文提出的TFC法的检测门限不受噪声方差的影响,也就表明本文算法具有抗噪声功率不确定性能。在以下实验中,均选取方差
的高斯白噪声所对应的门限值u1=1.355,u2=1.371。
(2)窗长对检测性能的影响
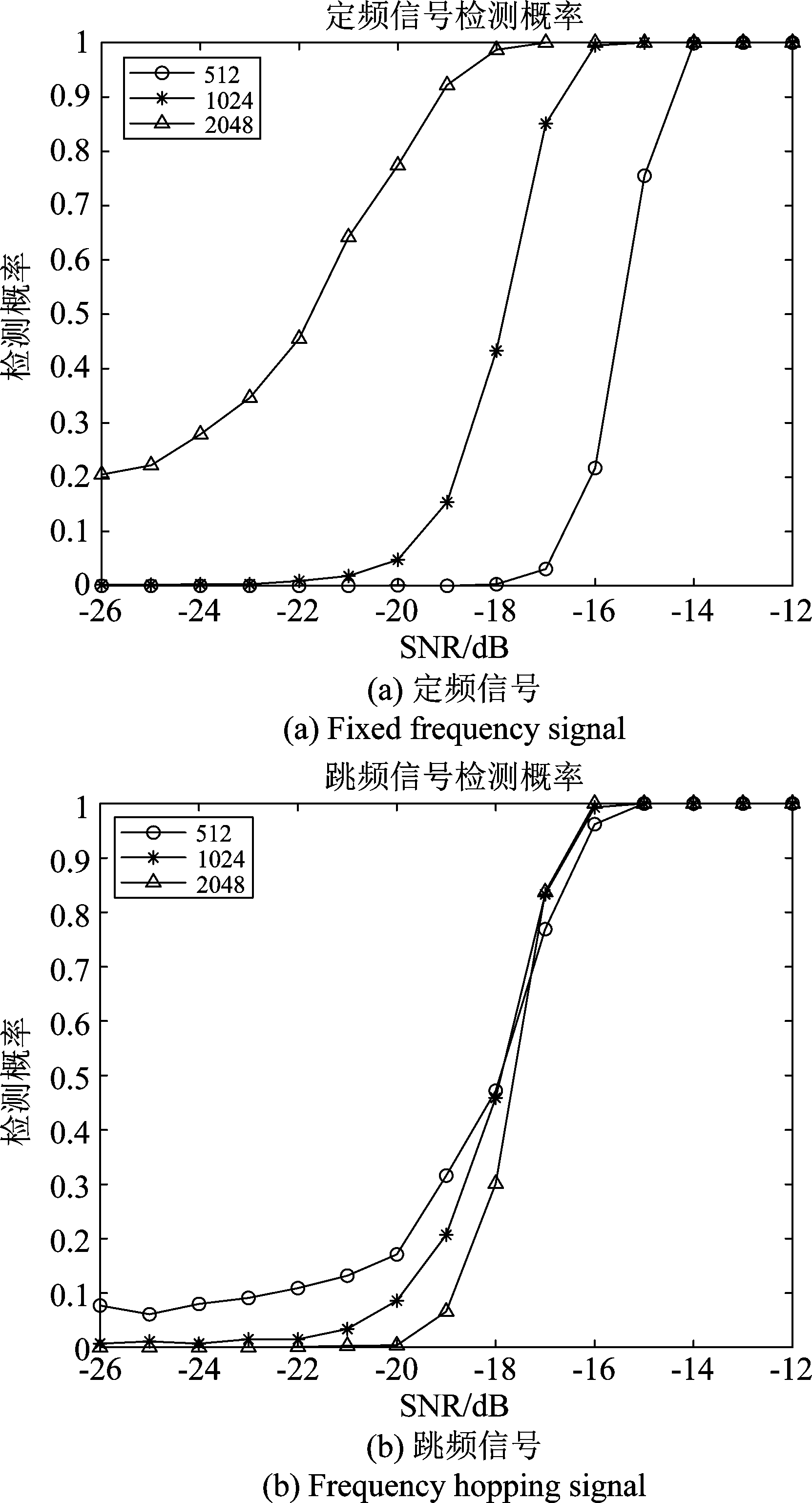
图5 不同窗长下的检测概率
Fig.5 Detection probability under different window lengths
选定Hamming窗,窗长分别为512、1024、2048,滑动步长为窗长的25%,其他参数不变。在高斯噪声背景下,分别针对三个定频信号和两个跳频信号进行检测,得到的检测概率曲线如图5所示。可以看出定频信号的检测性能会随着窗长的增加而提高,窗长越长,频率分辨率越高,但计算量增大,从而影响算法的实时性,并且时间分辨率也会随之降低。当信噪比大于-17 dB时,窗长对跳频信号的检测性能影响较小。综合考虑,下文取窗长为1024。
(3)滑动步长对检测性能影响
选定窗长为1024的Hamming窗,滑动步长分别取窗长的25%、50%、75%,信号参数及条件同(2),分别得到针对三个定频信号和两个跳频信号的检测概率如图6所示。由图6可知,当信噪比低于-16 dB时,定频信号的检测概率会随着滑动步长的缩短而降低;当信噪比在-19 dB～-15 dB之间时,跳频信号的检测概率会随着滑动步长的缩短而增加。滑动步长缩短,计算量增大。综合考虑,下文选取滑动步长为窗长的25%。
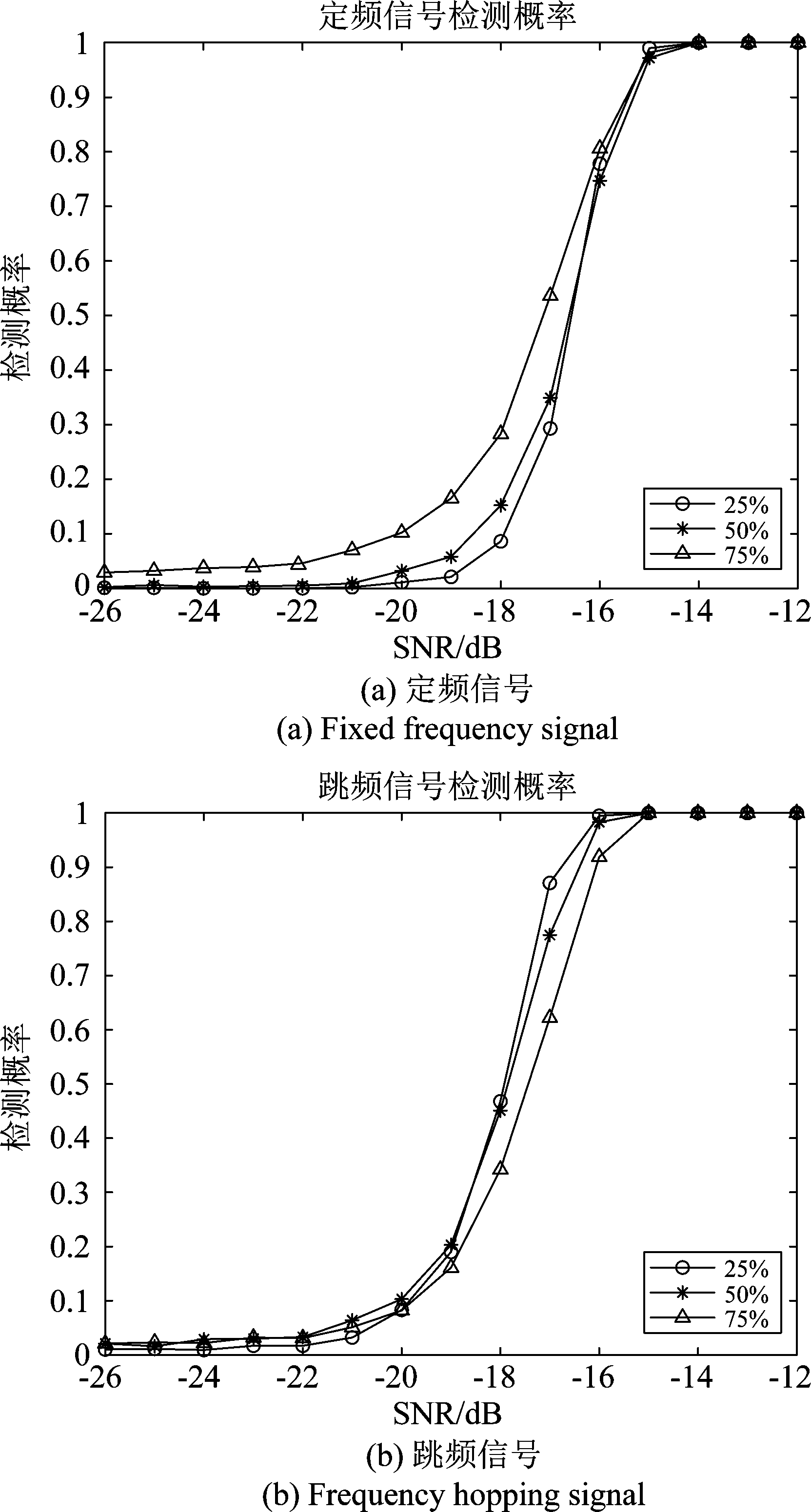
图6 不同滑动步长下的检测概率
Fig.6 Detection probability under different sliding steps
(4)算法性能对比
选取Hamming窗函数,窗长为1024,滑动步长为25%,其他参数同(2)。在高斯背景下,分别对三个定频信号和两个跳频信号进行检测,本文算法和文献[9]改进型功率谱对消算法(简记为IPC)对定频和跳频信号的检测概率如图7所示。从图中可看出,本文算法对定频信号和跳频信号具有几乎相同的检测性能,且优于对比算法。对于定频信号检测,本文算法提高了信噪比1 dB,对于跳频信号检测,本文算法提高信噪比2～3 dB。
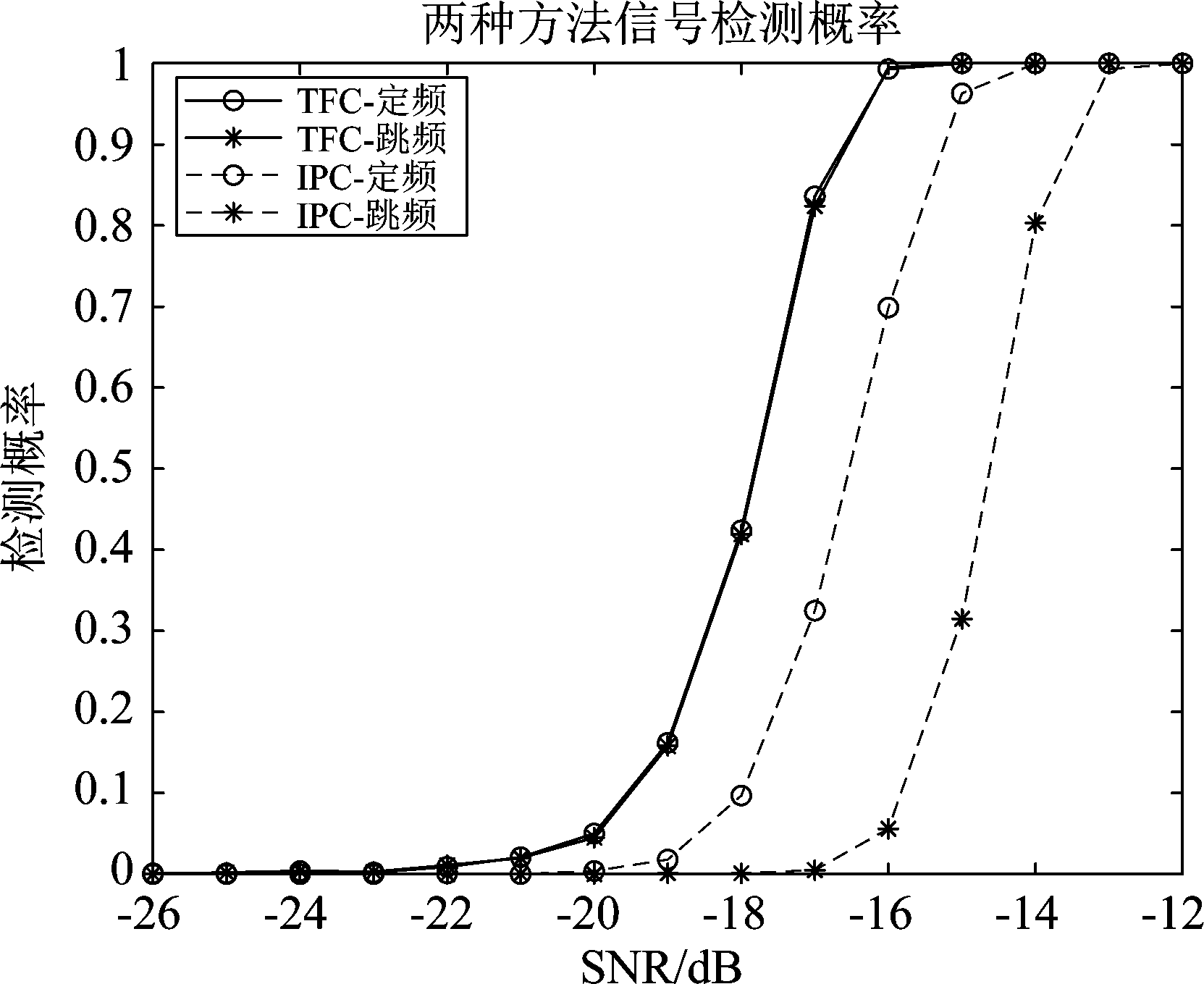
图7 两种算法检测概率对比
Fig.7 Comparison of detection probabilities between two algorithms
4.3 复杂电磁背景下跳频信号的检测
实际电磁环境是比较复杂的,并不仅仅只有噪声,可能还存在着大量的定频信号、频率线性变化的扫频信号和随机出现的突发干扰,并且会与跳频信号产生频率碰撞。由于信号时频对消后可将定频信号基本剔除,故主要分析以扫频、突发信号和高斯白噪声为背景的干扰对跳频信号检测性能的影响。
(1)检测规则及判决门限
由第3节、4.1节及4.2节实验(1)结果可知,复杂电磁背景下跳频信号的检测规则应为:当u0<η<u1 时,判决为存在跳频信号;否则判决为不存在跳频信号。其中u1=1.355,u0确定如下。
由图3可知,当接收信号为扫频、突发信号和高斯白噪声时,其对消比不再像纯高斯白噪声时一样具有抗功率不确定性,而是会随着干噪比的改变而变化。又由于实际电磁环境中无法确定扫频、突发信号的功率大小,故取干噪比为0 dB时的接收信号对消比作为检测跳频信号的门限下限u0。由4.1节仿真结果得到u1=0.785。
(2)算法性能对比及分析
当接收信号为跳频、定频、扫频、突发信号以及高斯白噪声的混合信号,SIR分别取8 dB、5 dB、2 dB和0 dB时,本文的TFC法和文献[9]IPC法对两个跳频信号的检测概率如图8所示。可以看出,随着信噪比和信干比增大,两种算法检测性能都有所提高,且本文算法的检测性能优于IPC法。与图7相比可知,由于定频信号、扫频信号和突发信号的影响,对比算法(IPC)的检测率急剧下降,在信干比低于2 dB时,该算法完全失效,而本文算法在信干比为0 dB且信噪比为-9 dB时达到100%的检测成功率。
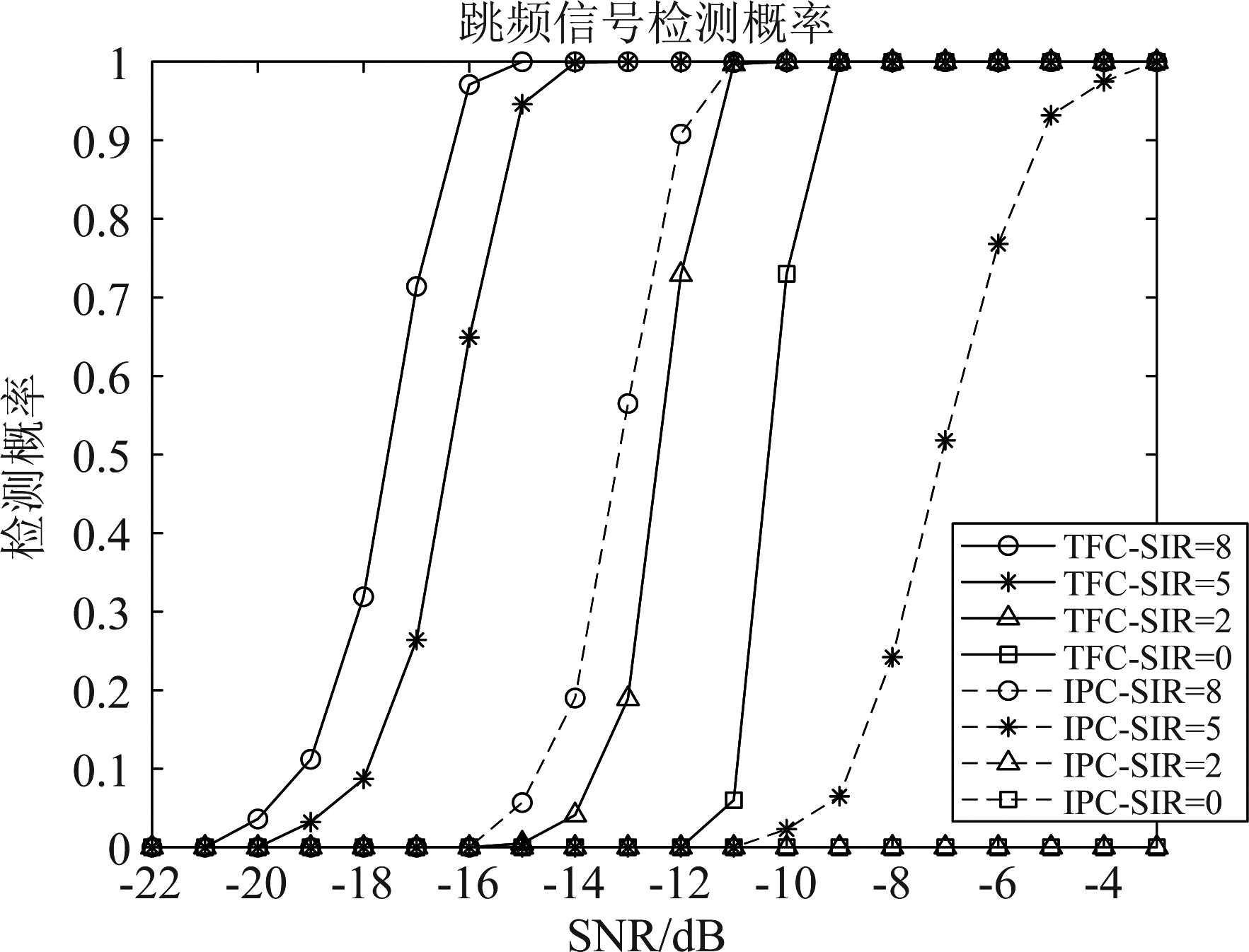
图8 复杂环境下两种算法的跳频检测概率
Fig.8 Probability of frequency hopping detection by two algorithms in complex environment
最后,对仅存在突发、扫频干扰和噪声时,本文算法进行了大量仿真。仿真结果表明,本文算法将突发和扫频干扰信号误检为跳频信号的虚警概率随着干噪比的提高而降低,且在干噪比为0 dB附近时,虚警概率发生骤变:在干噪比为0 dB时的虚警概率为50.7%,在干噪比为0.05 dB时的虚警概率几乎为0。
5 结论
本文利用短时傅里叶变换构造的时频对消比作为检测统计量,通过蒙特卡洛仿真得到检测门限,实现了高斯背景下跳频、定频信号的盲检测检测,该算法具有抗噪声功率不确定性,在低信噪比条件下,对两种信号的检测性能都优于改进型功率谱对消法。该算法能够实现复杂电磁环境中多跳频信号检测,其检测性能远优于改进型功率谱对消法。
[1] LEHTOMAKI J J. Maximum based detection of slow frequency hopping signals[J]. IEEE Communications Letters, 2003, 7(5): 201-203.
[2] 张东伟, 郭英, 霍文俊, 等. 一种改进的跳频信号信道化检测方法[J]. 火力与指挥控制, 2012, 37(8): 58- 61,65.
ZHANG Dongwei, GUO Ying, HUO Wenjun, et al. An improved channelized detection mothod of frequency-hopping signals[J]. Fire Control & Command Control, 2012, 37(8): 58- 61,65.(in Chinese)
[3] LI K H, MILSTEIN L B. On the use of a compressive receiver for signal detection[J]. IEEE Transactions on Communications, 1991, 39(4): 557-566.
[4] CHUNG C D, POLYDOROS A. Parameter estimation of random FH signals using autocorrelation techniques[J]. IEEE Transactions on Communications, 1995, 43(2/3/4): 1097-1106.
[5] 董占奇, 胡捍英. 基于ρ判决的跳频信号多跳自相关检测[J]. 现代电子技术, 2007, 30(7): 25-27.
DONG Zhanqi, HU Hanying. Multi-hop autocorrelation detection of Frequency-Hopping signals based on ρ decision[J]. Modern Electronics Technique, 2007, 30(7): 25-27.(in Chinese)
[6] 张盛魁, 姚志成, 范志良, 等. 基于局部自适应阈值的跳频信号提取和检测[J]. 电光与控制, 2020, 27(1): 68-72.
ZHANG Shengkui, YAO Zhicheng, FAN Zhiliang, et al. Frequency hopping signal extraction and detection based on local adaptive threshold[J]. Electronics Optics & Control, 2020, 27(1): 68-72.(in Chinese)
[7] 李硕, 李天昀. 短波信道下的跳频信号检测[J]. 电子学报, 2019, 47(3): 623- 629.
LI Shuo, LI Tianyun. Frequency hopping signal detection over the short-wave channel[J]. Acta Electronica Sinica, 2019, 47(3): 623- 629.(in Chinese)
[8] 高宪军, 李德鑫, 李娜, 等. 基于功率谱对消的跳频信号检测算法[J]. 吉林大学学报(信息科学版), 2008, 26(3): 238-243.
GAO Xianjun, LI Dexin, LI Na, et al. Algorithm for frequency-hopping signals detection based on suppressing power spectrum[J]. Journal of Jilin University (Information Science Edition), 2008, 26(3): 238-243.(in Chinese)
[9] 刘旭波. 基于功率谱分段对消算法的跳频信号检测[J]. 自动化技术与应用, 2017, 36(11): 69-73.
LIU Xubo. Frequency hopping signal detection based on power spectrum cancellation algorithm[J]. Techniques of Automation and Applications, 2017, 36(11): 69-73.(in Chinese)
[10]CHUNG C D, POLYDOROS A. Detection and hop-rate estimation of random FH signals via autocorrelation technique[C]∥MILCOM 91-Conference record. McLean, VA, USA. IEEE, 1991: 345-349.
[11]LEE K G, OH S J. Detection of fast frequency-hopping signals using dirty template in the frequency domain[J]. IEEE Wireless Communications Letters, 2019, 8(1): 281-284.
[12]陈硕, 李天昀, 葛临东. 一种基于边缘检测的跳频检测算法研究[J]. 信息工程大学学报, 2006, 7(3): 264-266,270.
CHEN Shuo, LI Tianyun, GE Lindong. Study on frequency-hopping detection algorithm based on edge detection[J]. Journal of Information Engineering University, 2006, 7(3): 264-266,270.(in Chinese)
[13]陈含欣, 江桦, 崔伟亮. 一种基于形态学预处理的时频检测算法[J]. 信息工程大学学报, 2010, 11(4): 438- 442.
CHEN Hanxin, JIANG Hua, CUI Weiliang. Novel TF detection algorithm based on morphology pre-processing[J]. Journal of Information Engineering University, 2010, 11(4): 438- 442.(in Chinese)
[14]孙德刚, 王友军, 王文, 等. 基于HOG的跳频信号自动化检测模型[J]. 通信技术, 2018, 51(4): 758-762.
SUN Degang, WANG Youjun, WANG Wen, et al. Automatic detection model for HOG-based frequency hopping signal[J]. Communications Technology, 2018, 51(4): 758-762.(in Chinese)
[15]李雷, 郭英, 张坤峰, 等. 块稀疏贝叶斯模型下的跳频信号时频分析[J]. 信号处理, 2018, 34(1): 107-113.
LI Lei, GUO Ying, ZHANG Kunfeng, et al. Time-frequency analysis of frequency-hopping signals based on block sparse Bayesian model[J]. Journal of Signal Processing, 2018, 34(1): 107-113.(in Chinese)
[16]辛吉荣, 陆路希, 包昕, 等. 基于时频稀疏性的跳频信号背景噪声估计算法[J]. 电子学报, 2014, 42(10): 1932-1937.
XIN Jirong, LU Luxi, BAO Xin, et al. Noise energy estimator based on sparseness of time-frequency domain for broadband frequency-hopping signal[J]. Acta Electronica Sinica, 2014, 42(10): 1932-1937.(in Chinese)
[17]宗序平, 等.数理统计学及其应用[M].北京：机械工业出版社, 2016.
ZONG Xuping, et al. Mathematical statistics with applications[M]. Beijing: China Machine Press, 2016. (in Chinese)
[18]李红光, 郭英, 齐子森, 等. 复杂电磁环境下多跳频信号盲检测[J]. 华中科技大学学报(自然科学版), 2020, 48(7): 13-19.
LI Hongguang, GUO Ying, QI Zisen, et al. Blind detection of multi-frequency hopping signals under complex electromagnetic environment[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(7): 13-19.(in Chinese)
