1 引言
新兴多媒体应用的引入以及无线数据需求的急剧增长给现有的无线网络带来了沉重的负担[1]。非正交多址(NOMA)具有实现增强用户公平性、提高频谱利用率、降低接入延迟以及促进多样化服务质量(QoS, quality of service)的潜力,受到了极大的关注,非常有望在下一代无线通信网络中使用[2-3]。在实际通信过程中,如果发送源与目的端之间距离过远,会造成通信性能下降等问题。协作NOMA由于其提高覆盖范围、吞吐量和系统可靠性的能力而成为热点研究领域之一。文献[4]提出了一种两阶段叠加编码的协作NOMA中继方案,提高了NOMA中继系统的性能;文献[5]研究了一种认知无线电(CR, Cognitive Radio)下的协作NOMA网络,证明了CR-NOMA相比于协作正交多址的优越性。文献[6]研究了中继选择方案对协作下认知非正交多址(CR-NOMA)网络中断性能的影响,提出了一种两级中继选择方案,证明了两级中继选择策略可以达到更好的中断性能和更大的分集增益。
然而,上述所提到的协作NOMA方案都是基于单向中继,其中消息仅在一个方向上传递。文献[7]研究了一种双向中继(TWR, Two-Way Relay)非正交多址接入系统,其中两组NOMA用户借助半双工解码转发中继交换消息。文献[8]提出了一种新颖的全双工协作NOMA接入系统,证明了低信噪比时突出的性能。文献[9]提出协作NOMA与物理层网络编码结合,实现一对NOMA用户之间的信息交换。文献[10]研究了双向中继NOMA系统的安全性能,当窃听者靠近用户之一时,遍历保密和速率性能下降。文献[11]结合NOMA与双向中继设计了一个混合双向中继系统(TWRS),通过利用网络编码带来的无损压缩增益显著提高了系统吞吐量。文献[12]优化功率和时间分配,结合网络编码,提高了中断概率和遍历速率性能。文献[13]研究了一种多天线双向中继NOMA系统,用户通过多天线中继支持双向叠加传输。文献[14]提出了一种基于放大转发(AF, Amplify-and-forward)的协作NOMA双向中继传输系统,同时考虑信号的上行和下行,在两个时隙内完成基站和用户之间的双向信息交换。文献[15]提出一种双向中继NOMA传输方案,两个用户之间存在直通链路,共使用三个时隙完成双向信息交换。文献[16]将双向中继NOMA与认知无线电结合,实验结果表明,缩短次用户和中继之间的距离或升高干扰约束阈值均可以提高系统性能。
与文献[7]不同的是,文献[7]按照信道条件的不同将NOMA用户分为两组,两组用户在一个中继节点的帮助下交换信息,所提系统中不存在基站。与文献[11]中基站和用户之间不存在协作链路不同的是,本文考虑基站和信道条件较差的用户之间存在中继,更符合实际,但同时也增加了系统的复杂度。与文献[13]不同的是,文献[13]中用户与中继均配备多根天线,两个用户通过中继节点交换消息,且不存在基站,本文基站与用户均配备单根天线。与文献[14]不同的是,文献[14]仅仅在完美CSI下研究了下行信号的遍历和速率而未考虑系统的中断性能,且该系统涉及上下行信号的同时传输,对上行信号的研究同样至关重要。本方案采用解码转发(DF)协议,为近端用户分配较大的功率,进一步考虑了在不完美CSI下,中继利用串行干扰消除(SIC, Successive Interference Cancellation)技术将信号逐级解码,结合网络编码原理,将信号重新编码后发送到用户和基站。本文对系统上下行信号均进行了研究,推导了上下行信号遍历和速率及中断概率闭合表达式。仿真结果表明,相比于传统单向中继NOMA和时分多址OMA网络,该方案有显著的性能提升。
文章的后续结构如下:第2节给出了系统模型;第3节推导了遍历和速率及中断概率闭合表达式;第4节给出了计算机仿真结果;第5节总结全文。
2 系统模型
2.1 本文系统模型
系统模型如图1所示,包含一个基站,一个双向中继R和两个用户U1、U2,中继采用解码转发协议(DF),均配备单根天线。假设其中U1为远端用户,信道条件较差,为了实现更好的通信,在此通过采用中继与基站进行通信;U2为近端用户,信道条件较好,与基站直接通信,且U1和U2之间,中继和U2之间不存在干扰。设hi, j表示瑞利衰落信道,其中i≠j,i, j={S,R,1,2}。不失一般性,本文假设下行信道条件为|hR,1|2<|hS,2|2<|hS,R|2,上行信道条件为|h1,R|2<|h2,S|2<|hR,S|2。本方案上下行信号占用相同的频率资源在不同的时隙内传输,假设上下行信号在相对较短的时间内完成传输,可近似认为上行链路和下行链路的传输信号所经历的信道衰落相同,即信道具有互易性[17]。
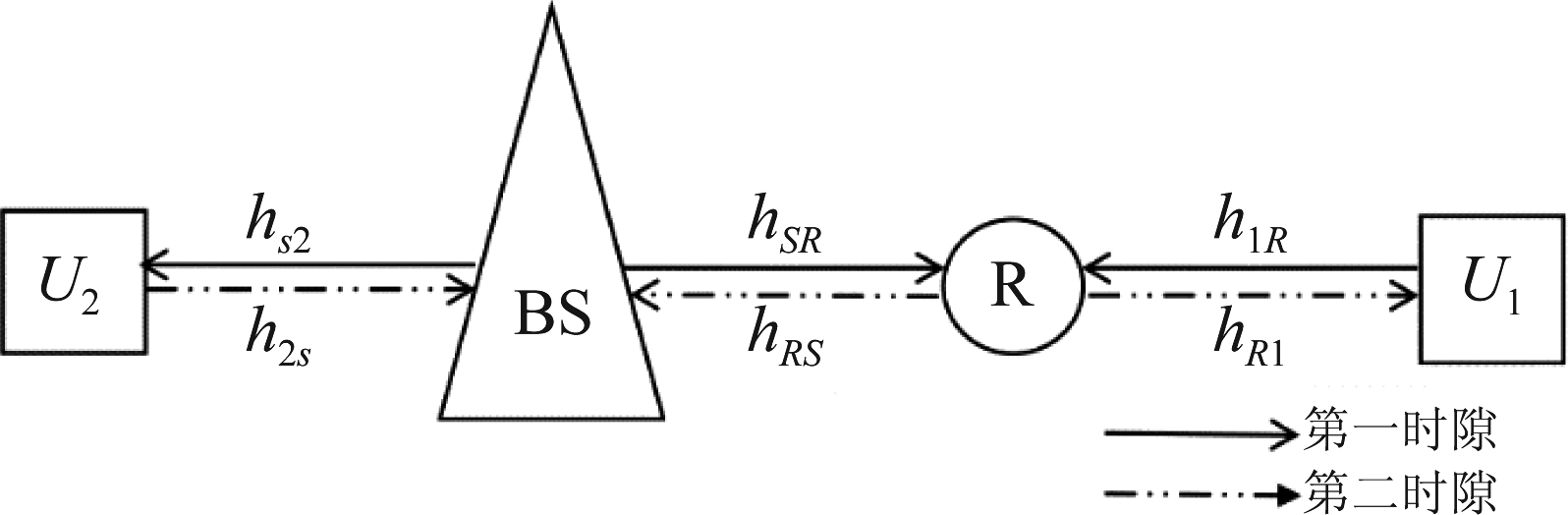
图1 本文系统模型
Fig.1 The system model of this paper
在实际系统中,由于主要由反馈延迟引起的信道估计误差,很难获得完美CSI。假设信道hi, j的估计为
于是信道参数可以表示为
其中,
表示信道误差,可近似为高斯随机变量[4],k表示信道误差系数。假设独立同分布的加性高斯白噪声(AWGN)表示为nk～(0,σ2),k={S,R,1,2}。PS、PR、P1、P2分别表示基站、中继以及两个用户的发送功率,发送信噪比定义为ρl=Pl/σ2,l={S,R,1,2}。
本方案设计的系统考虑了实际应用场景,许多也是具有上下行双向传输任务的通信系统。即BS分别向U1和U2发送下行信号x1和x2,U1和U2分别需要向BS发送上行信号y1和y2。本文系统模型完成整个通信过程一共只需要两个时隙,实线代表第一时隙,虚线代表第二时隙。第一时隙中,BS向R和U2发送x1和x2的功率复用NOMA信号x,U1向R发送上行信号y1。x是信号x1和x2的叠加编码信号,表示为:
(1)
a1和a2分别代表x1和x2功率分配因子,有a1+a2=1,E(|x1|2)=E(|x2|2)=1。由于第一时隙x1并未到达终端U1,且hS,R信道条件较好,为首先保证U2接收信号的质量,有a1<a2。R接收信号为:
(2)
同时U2接收信号为:
ybs,2=hS,Rx+n1
(3)
第一时隙中,R接收来自基站和U1的信号,此时相当于上行NOMA。同文献[18],假设x2、x1、y1进行多用户叠加编码,根据NOMA解调原理,接收机使用串行干扰消除(SIC)技术,把小功率信号视为噪声,对大功率信号进行解码,然后将成功解码的大功率信号剔除,再对小功率信号进行解码,从而实现多用户信号检测。由于R采用DF转发协议解码信号,因此R存在处理时延τ。同文献[13],假设R处理时延相较于总的传输时间可以忽略不计。考虑到实际情况,本文假设基站发送功率远大于用户,保证在R端接收到信号功率大小依次为x2、x1、y1,解码过程如下:
R解码x2:由于a2>a1,在R处信号x1和y1被当作噪声,直接对x2进行解码。此时R端解码x2的SINR为:
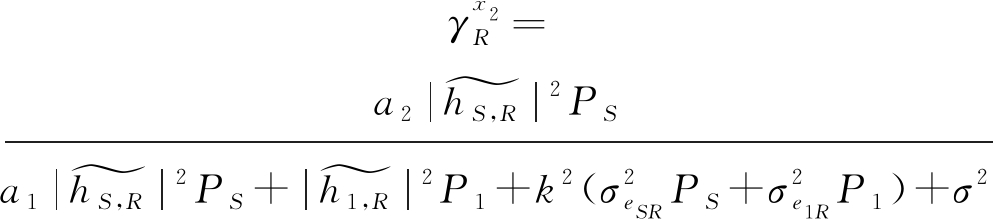
(4)
R解码x1:成功解码x2并将其去除后,对x1进行解码,y1被视为噪声。此时R端解码x1的SINR为:
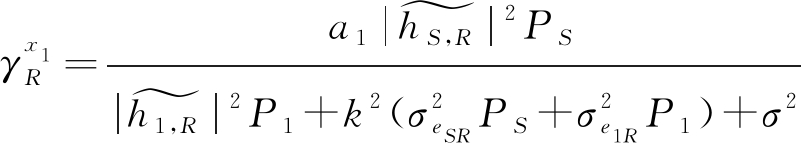
(5)
R解码y1:成功解码x1并将其去除后,对y1进行解码。此时R端解码y1的SINR为:
(6)
U2解码x2:此时x1被当作噪声,直接对x2进行解码。U2解码x2的SINR为:
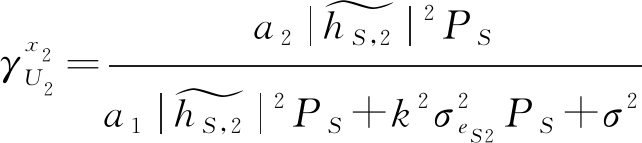
(7)
由于中继采用解码转发(DF)协议,信号x1、x2和y1被R成功解码后,结合网络编码原理,R将x1和y1进行异或相加得到新的信号y=x1⊕y1。第二时隙,R将y分别发送给基站和U1;同时,U2将y2发送到基站。第二时隙中,U1接收信号表示为:
(8)
基站同时接收来自R和U2的混叠信号,接收信号可以表示为:
(9)
U1解码y的SINR为:
(10)
U1通过异或运算对检测到的位序列进行编码,最终得到来自基站的信息,表示为x1=y1⊕y。
在基站侧,由于中继发射功率大于用户,基站首先视y2为噪声,对y进行解码。BS解码y的SINR为:
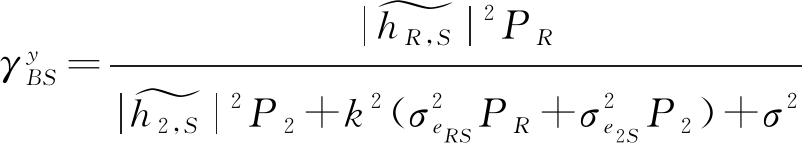
(11)
经过异或运算,基站得到来自U1的信号y1=x1⊕y。成功解码y后将其去除,BS解码y2的SINR为:
(12)
对于两跳的协作中继系统,信号可达速率受较弱的一跳决定,x1、x2、y1、y2可达速率可表示为:
(13)
(14)
(15)
(16)
其中,乘子1/2是因为该系统完整的通信过程只需要两个时隙。
2.2 对比策略系统模型
图2展示了基于单向中继的传统协作NOMA场景。它使用4个时隙来完成信息交换。在第一时隙中,基站分别发送叠加编码的消息到中继和U2;由于中继采用解码转发(DF)协议,第二时隙中继将x1解码后重新编码发送到U1;第三时隙,U1发送y1并被中继接收。在第四个时隙中,中继站将先前接收的y1解码重传到基站,同时U2传输上行信号y2。
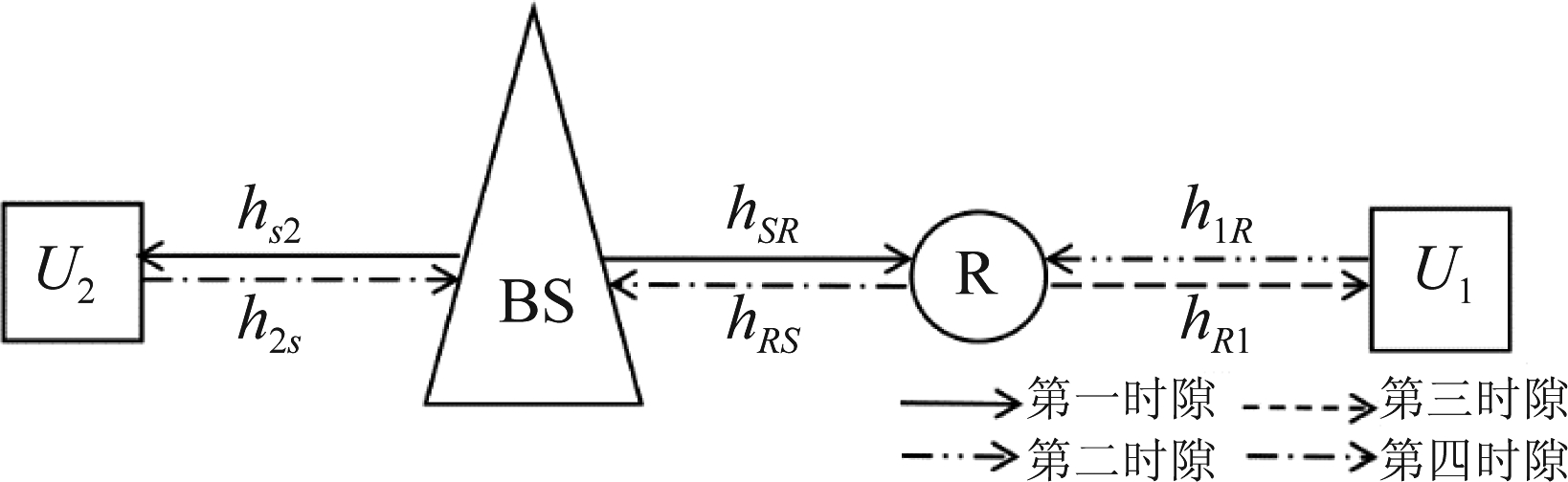
图2 传统单向中继系统模型
Fig.2 Traditional one-way relay system model
图3展示了传统OMA场景,利用6个时隙来完成从下行链路到上行链路的信息交换,其中每个消息都使用一个专用时隙来发送。
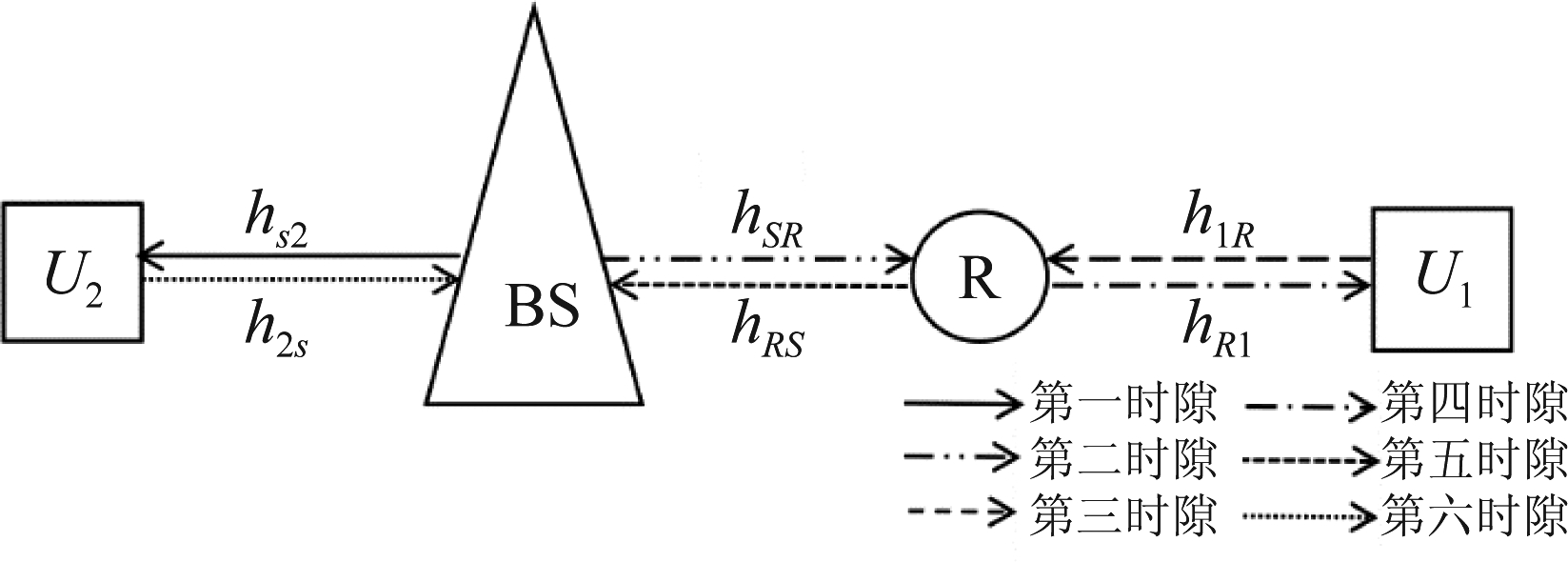
图3 时分复用OMA系统模型
Fig.3 Time division multiplexing OMA system model
3 性能分析
本节对系统上下行信号的遍历和速率和中断概率进行公式推导,为仿真实验做理论准备。
3.1 下行遍历和速率
记γi的概率密度函数(Probability Density Function, PDF)为fγi(x),其对应的累计分布函数(Cumulative Distribution Function, CDF)为Fγi(x),其中i={1,2,3,4}。根据公式
式(13)～(16)可以表示为
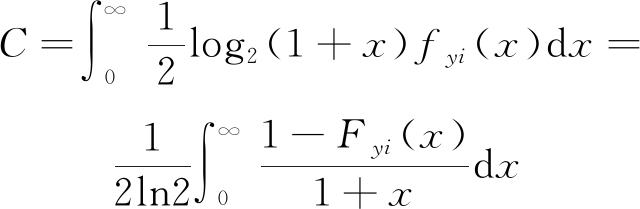
(17)
定理1 下行信号遍历和速率为:
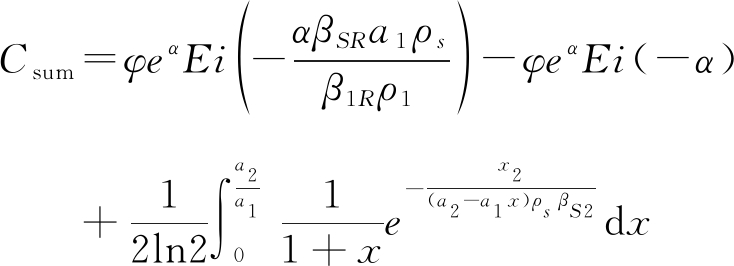
(18)
其中,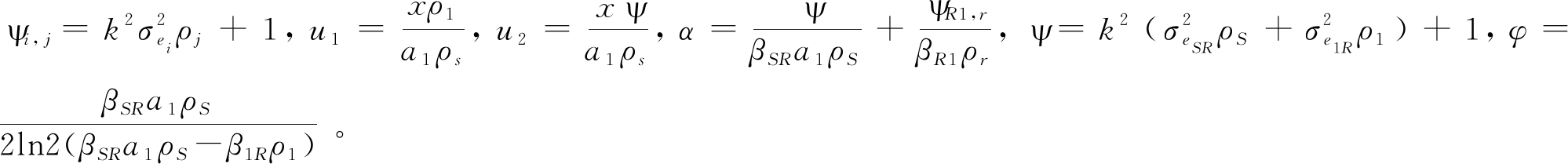
证明 定理1的证明过程详见附录A。
3.2 下行中断概率与吞吐量分析
定义R1和R2分别为信号x1和x2的目标传输速率,中断互补事件表述如下:1) U2成功解码x2。2) 成功解码x1的条件:R成功解码x2和x1;U1成功解码x1。下面分别给出x1和x2的中断概率表达式。
定理2 下行信号中断概率为:
Pout=
(19)
其中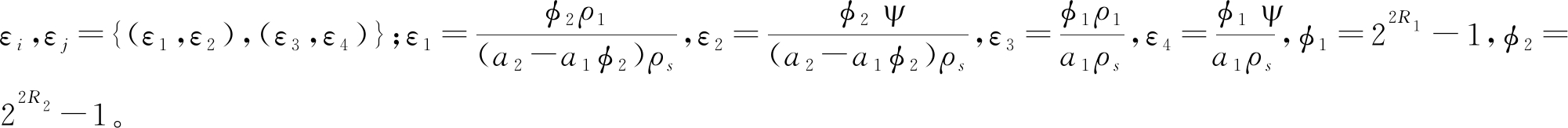
证明 定理2的证明过程详见附录B。
根据文献[19],吞吐量是传输速率和信息传输成功的概率之积。本章所提出的TWR-NOMA方案所能达的下行信号的系统吞吐量为:
Rout=(R1+R2)(1-Pout)=(R1+R2)
(20)
3.3 上行遍历和速率
定理3 上行信号遍历和速率为:
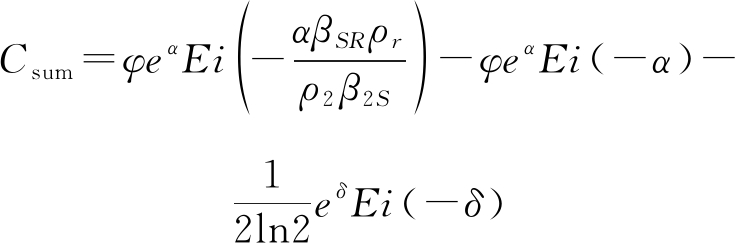
(21)
其中,
证明 定理3的证明过程详见附录C。
3.4 上行中断概率
定义R3和R4分别为信号y1和y2的目标传输速率,中断事件互补事件表述如下:1) BS成功解码y2。2)成功解码y1的条件:R成功解码x2、x1和y1;BS成功解码y1。下面给出y1和y2中断概率表达式。
定理4 下行信号中断概率为:
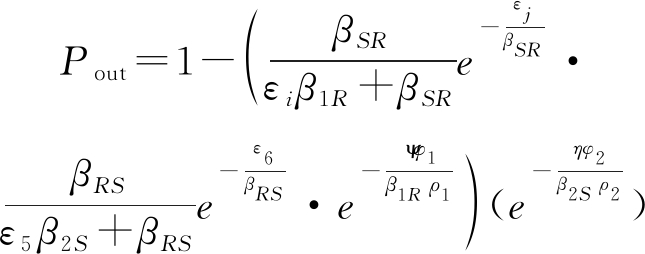
(22)
其中,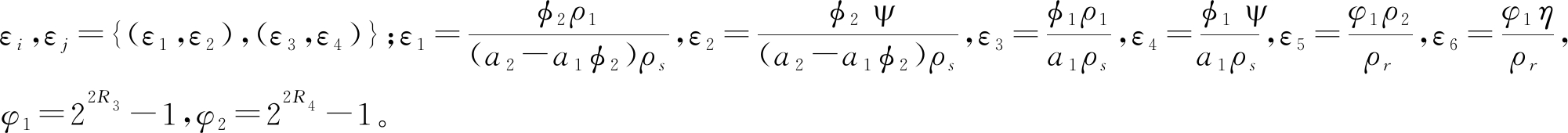
证明 定理4的证明过程详见附录D。
4 仿真结果及分析
本节使用Matlab对本方案的各项性能进行Monte Carlo 仿真,对前文所推导的表达式进行了验证。仿真信道采用瑞利衰落信道,信道参数设置βSR=15, βR1=5,βS2=10;功率分配因子a1=0.2,a2=0.8;方差
其中i≠j,i, j={S,R,1,2};下行信号目标速率R1=R2=0.5 bps/Hz,上行信号目标速率R3=R4=0.1 bps/Hz;非特殊说明,中继发送信噪比ρr=10 dB,用户发送信噪比ρ1=ρ2=3 dB。
本文对比策略为文献[14]中所提方案、传统单向中继NOMA(OWR-NOMA)和时分复用OMA,分别在完美CSI(k=0)和不完美CSI(k=0.1)条件下与这两种方案对各项性能进行了对比,实验中设置四种方案信道条件与各项参数均相等。欲完成同等传输任务,OWR-NOMA和OMA分别需使用4个和6个时隙,同文献[20],若在相同时间内完成整个通信过程且时隙均匀分配,则OWR-NOMA和OMA可达速率需乘时隙分配因子1/4与1/6,若可达速率低于目标速率,则系统发生中断事件。
4.1 下行信号仿真结果及分析
图4展示了各项方案下行遍历和速率随发送信噪比(即ρs)变化曲线,实线表示完美CSI(k=0),虚线表示不完美CSI(k=0.1)。从图中可以得出如下结论:1)本方案遍历和速率随发送端信噪比的升高而升高,逐渐趋于某一定值;相较于文献[14],本文方案在低信噪比时能够取得较好的性能;而相比于 OWR-NOMA与OMA,本方案有着显著的性能优势,其原因是 OWR-NOMA和OMA分别需要六个和四个时隙完成整个通信过程,而TWR-NOMA方案只需两个时隙,极大地提高了资源利用率。2)当信道CSI变得不完美时,TWR-NOMA受影响较小,即本方案鲁棒性能较好。
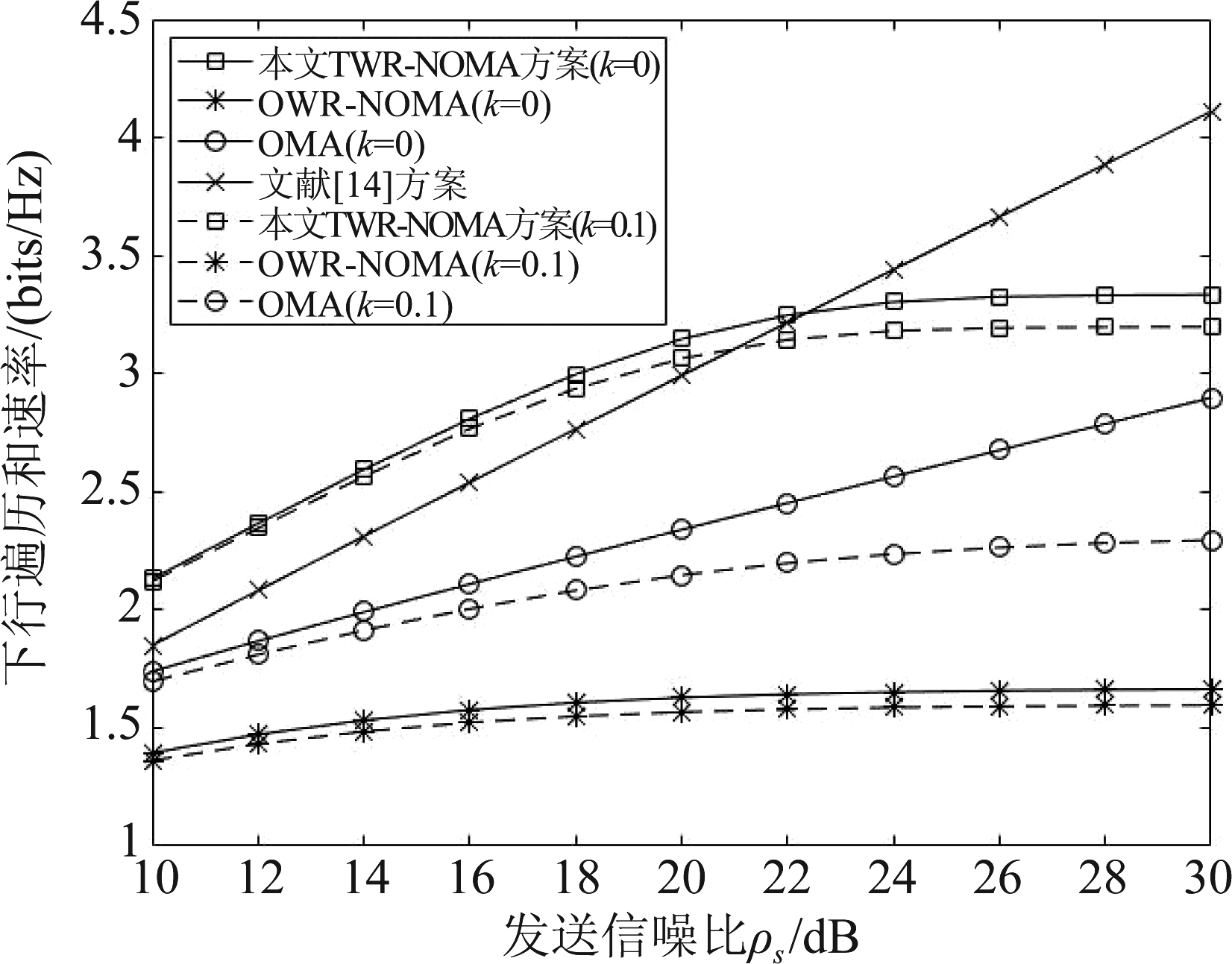
图4 不同发送信噪比时的下行和速率
Fig.4 Downlink ergodic sum rate of different transmission SNR
图5(a)展示了不同CSI下本方案下行中断概率随发送信噪比(即ρs)的变化曲线,实线表示经过公式推导得出的理论曲线,虚线表示Monte Carlo 仿真曲线。从图中可以看出,公式推导结果与仿真结果一致,验证了理论推导的正确性。随着ρs的提高,中断概率不断减小。图5(b)展示了四种方案下行中断概率随ρs变化曲线,从图中可以得出如下结论:1)四种方案中断概率均随发送端信噪比的增加而降低;在完美 CSI下,TWR-NOMA方案略次于文献方案;当发送信噪比较高时,TWR-NOMA方案明显优于OWR-NOMA和OMA系统,获得了较低的中断概率。这主要是由于OWR-NOMA和TDMA模式下的OMA必须提高其传输速率,才能与TWR-NOMA系统保持相同的遍历和速率,从而导致中断概率升高。而发送信噪比较低时,TWR-NOMA中断概率略高于OMA,这是由于TWR-NOMA方案是否发生中断很大程度取决于能否对信号实现正确解码,较低的发送信噪比增加了正确解码的困难程度。2)当CSI变得不完美时,本文TWR-NOMA方案受影响较小,鲁棒性较好。
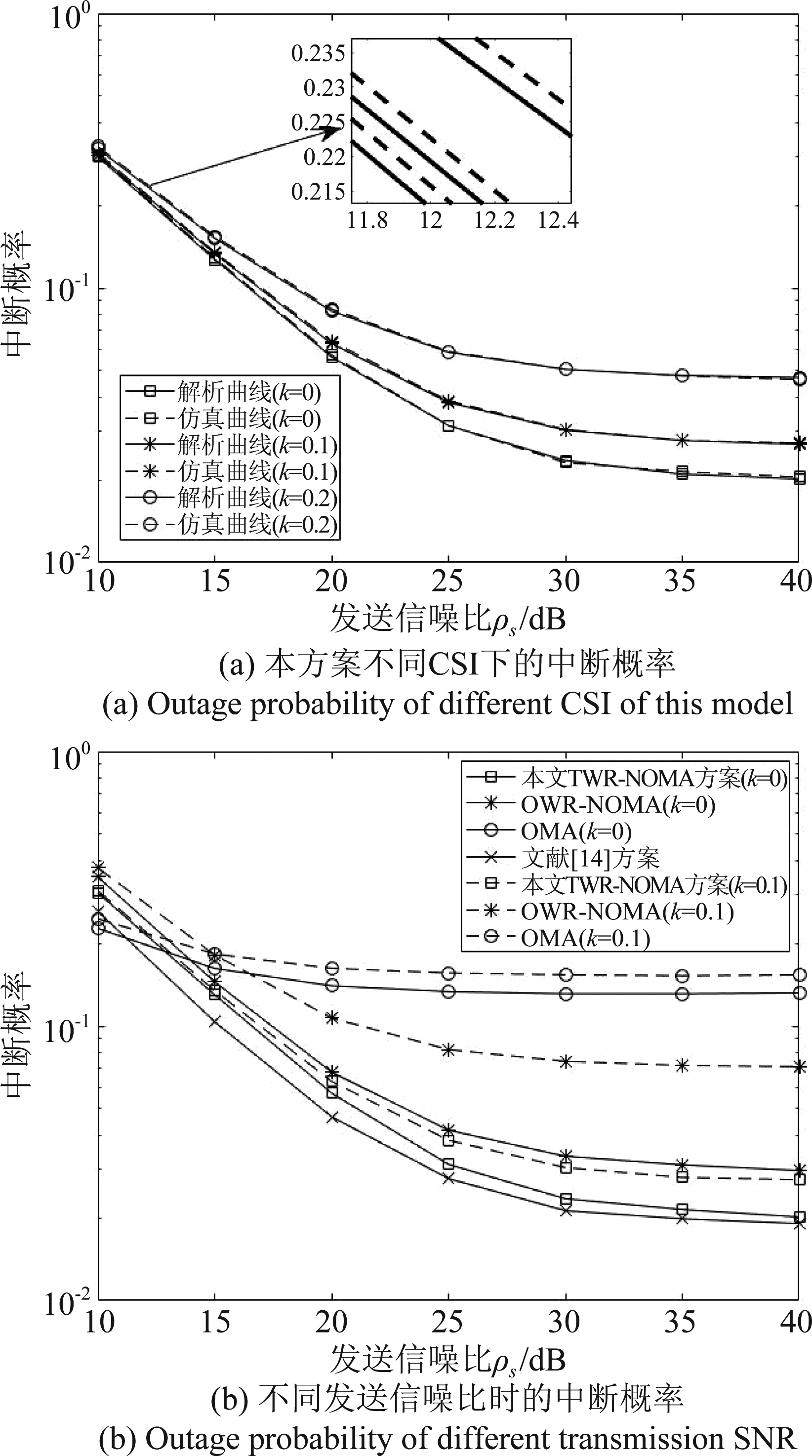
图5 下行中断概率变化曲线
Fig.5 Downlink outage probability curve
图6展示了下行链路吞吐量随ρs之间变化曲线,实线表示完美CSI(k=0),虚线表示不完美CSI(k=0.1)。当目标速率相同时,由于低信噪比下TWR-NOMA中断概率略高于OMA, TWR-NOMA吞吐量略低于OMA。而随着ρs的增加,三种方案的吞吐量均逐渐趋于一个上限值,且TWR-NOMA方案的上限值要高于其他两种方案。这是由于随着ρs的增加,信息传输成功的概率(1-Pout)趋近于1,因此ρs较高时系统吞吐量的大小主要取决于目标传输速率R的大小。
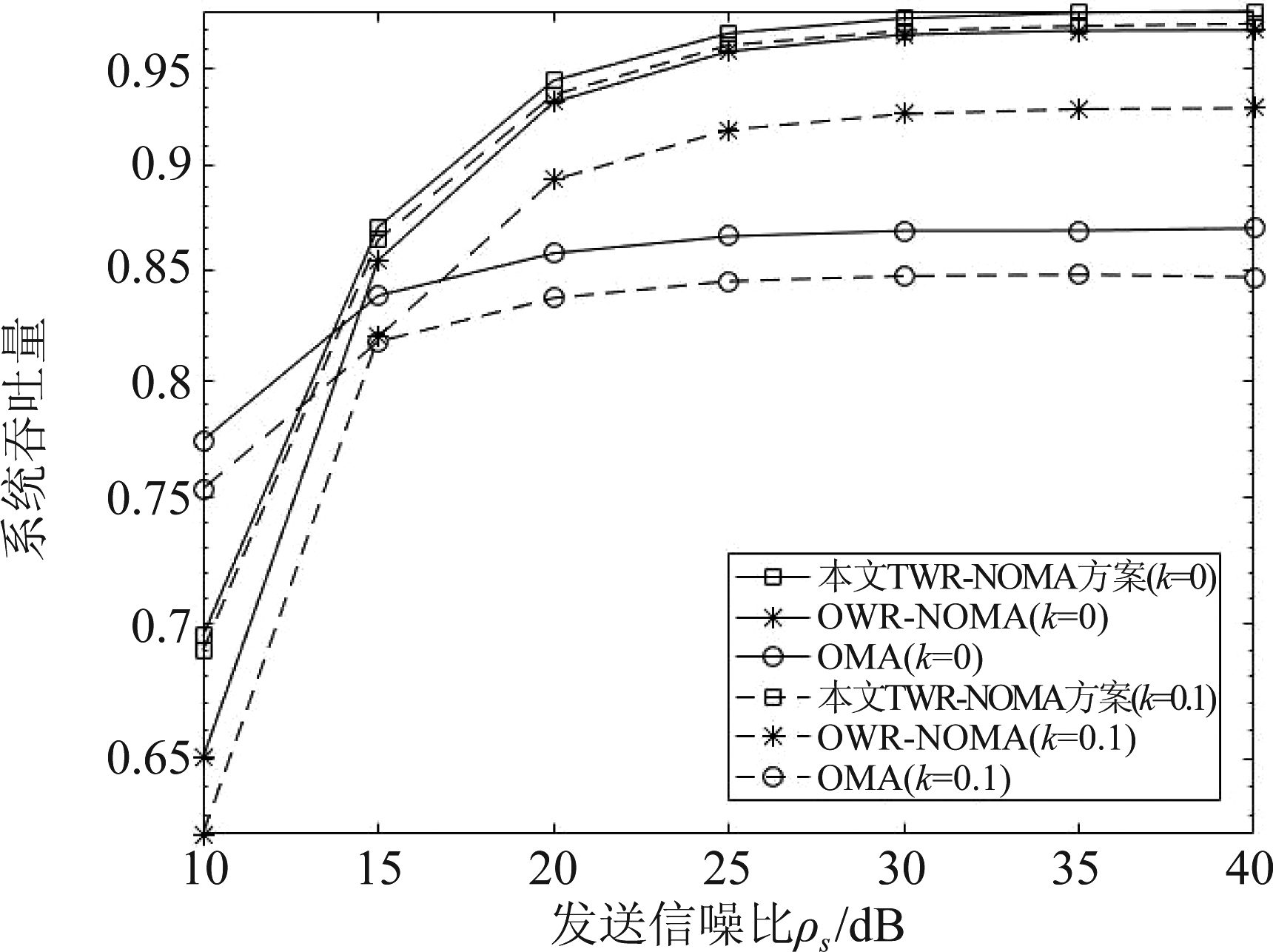
图6 不同发送信噪比时的吞吐量
Fig.6 System throughput of different transmission SNR
图7展示了完美CSI下中断概率随目标速率的变化曲线,其中ρs=20 dB,ρr=10 dB。随着信号目标速率的升高,系统中断概率随之升高。而且TWR-NOMA的性能优势越来越显著。这说明对目标速率进行适当设置可以有效改善系统中断性能。
图7 不同目标速率时的中断概率
Fig.7 Outage probability of different target rate
图8展示了不同目标速率下,当发送端功率分配因子发生改变时中断概率的变化曲线。从图中同样可以看出,随着信号目标速率的升高,系统中断概率随之升高;在一定范围内提高a1,系统中断概率会降低;而在超过某一阈值后,中断概率开始增大。这说明调整功率分配参数可使系统获得最优的中断性能。
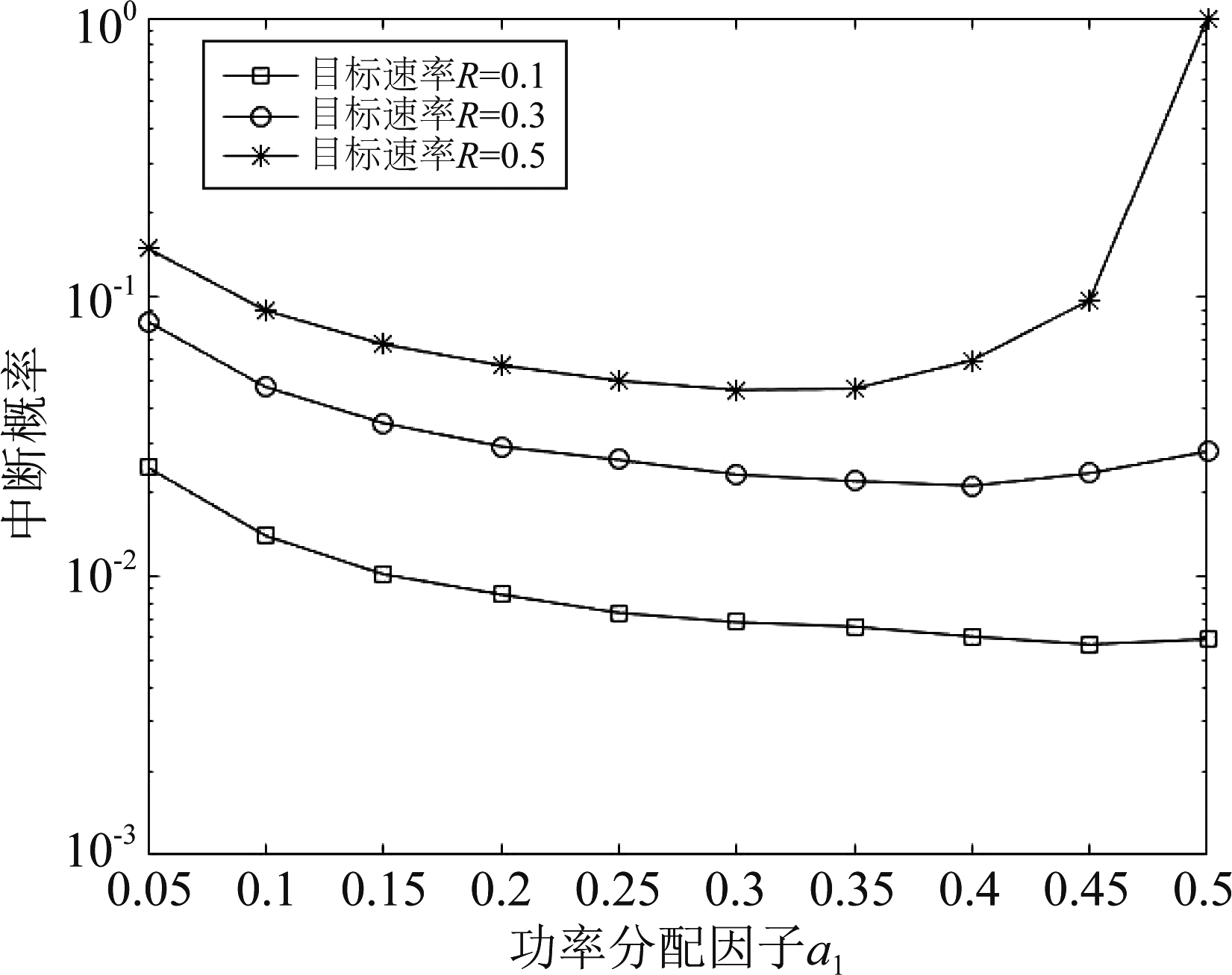
图8 功率分配因子对中断概率的影响
Fig.8 Outage probability of different power allocation factors
4.2 上行信号仿真结果及分析
由于本文TWR-NOMA方案同时涉及上行与下行信号的传输,因此需要对上行信号进行分析。ρs=20 dB,ρr=10 dB。
图9 (a)展示了不同CSI下本方案上行中断概率随用户发送信噪比(即ρ1)变化曲线,实线表示经过公式推导得出的理论曲线,虚线表示Monte Carlo 仿真曲线。从图中可以看出,公式推导结果与仿真结果一致,验证了理论推导的正确性。随着ρ1的提高,中断概率不断减小。图9(b)分别展示了四种方案上行中断概率随ρ1变化曲线,实线表示完美CSI(k=0),虚线表示不完美CSI(k=0.1),从图中可以得出如下结论:四种方案中断概率均随用户端信噪比的增加而降低; TWR-NOMA方案明显优于其余三种方案,获得了最好的中断性能。
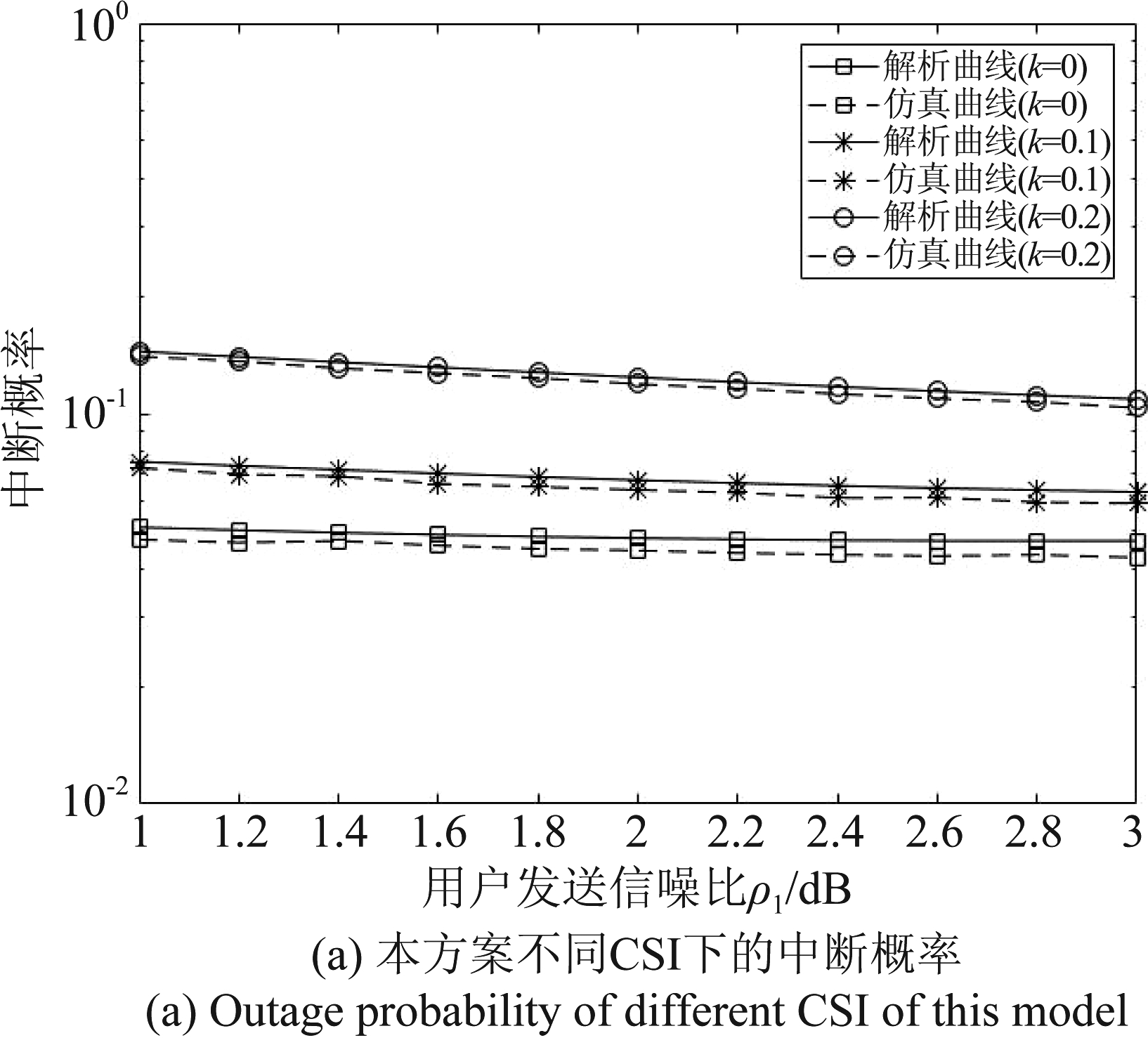
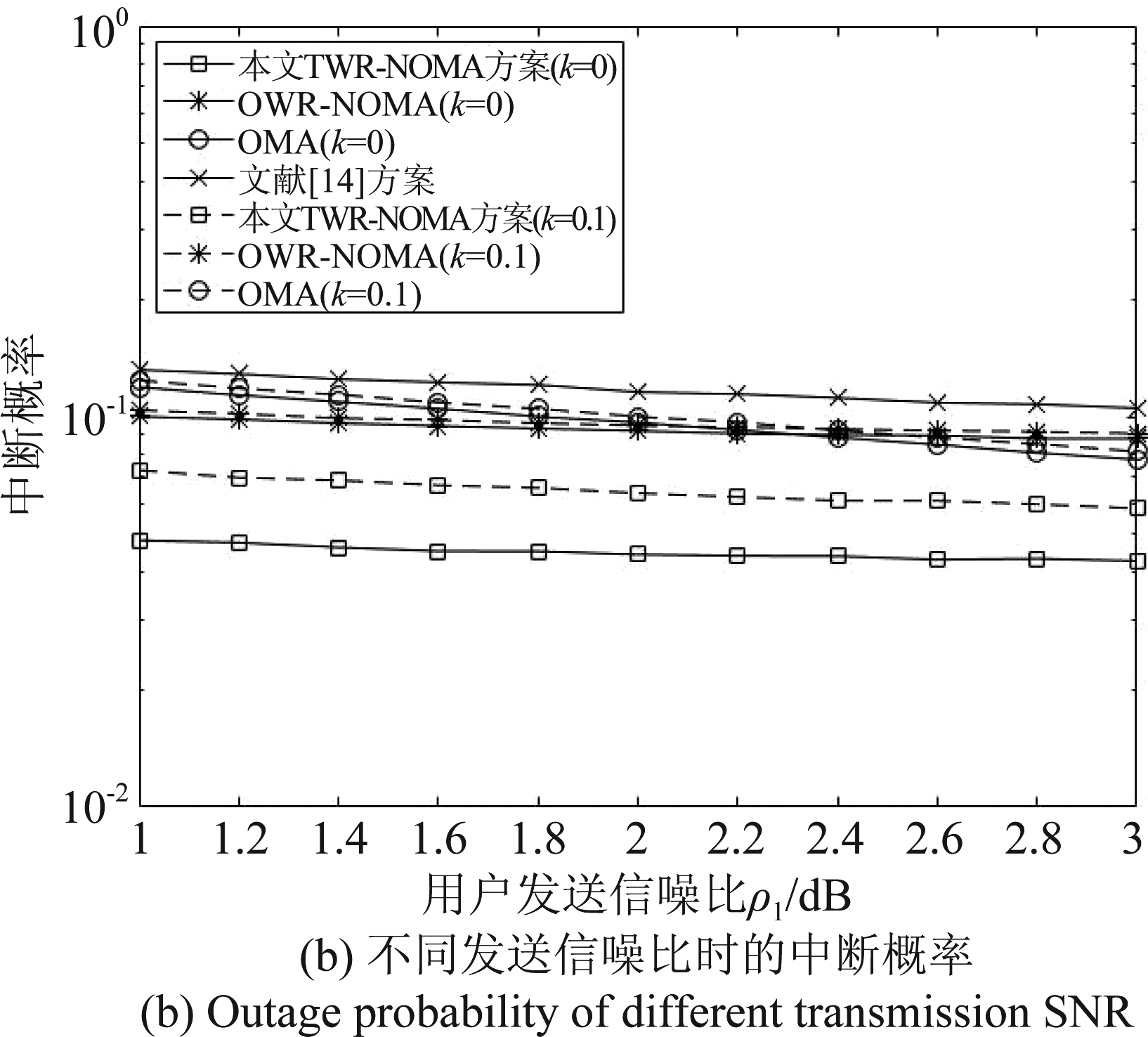
图9 上行中断概率变化曲线
Fig.9 Uplink outage probability curve
图10分析了上行信号遍历和速率与用户端发送信噪比(即ρ1)之间的关系,从图中可以看出:系统的上行遍历和速率随用户发送信噪比的升高而升高;TWR-NOMA方案明显优于其余三种方案,可以达到最高的遍历和速率。
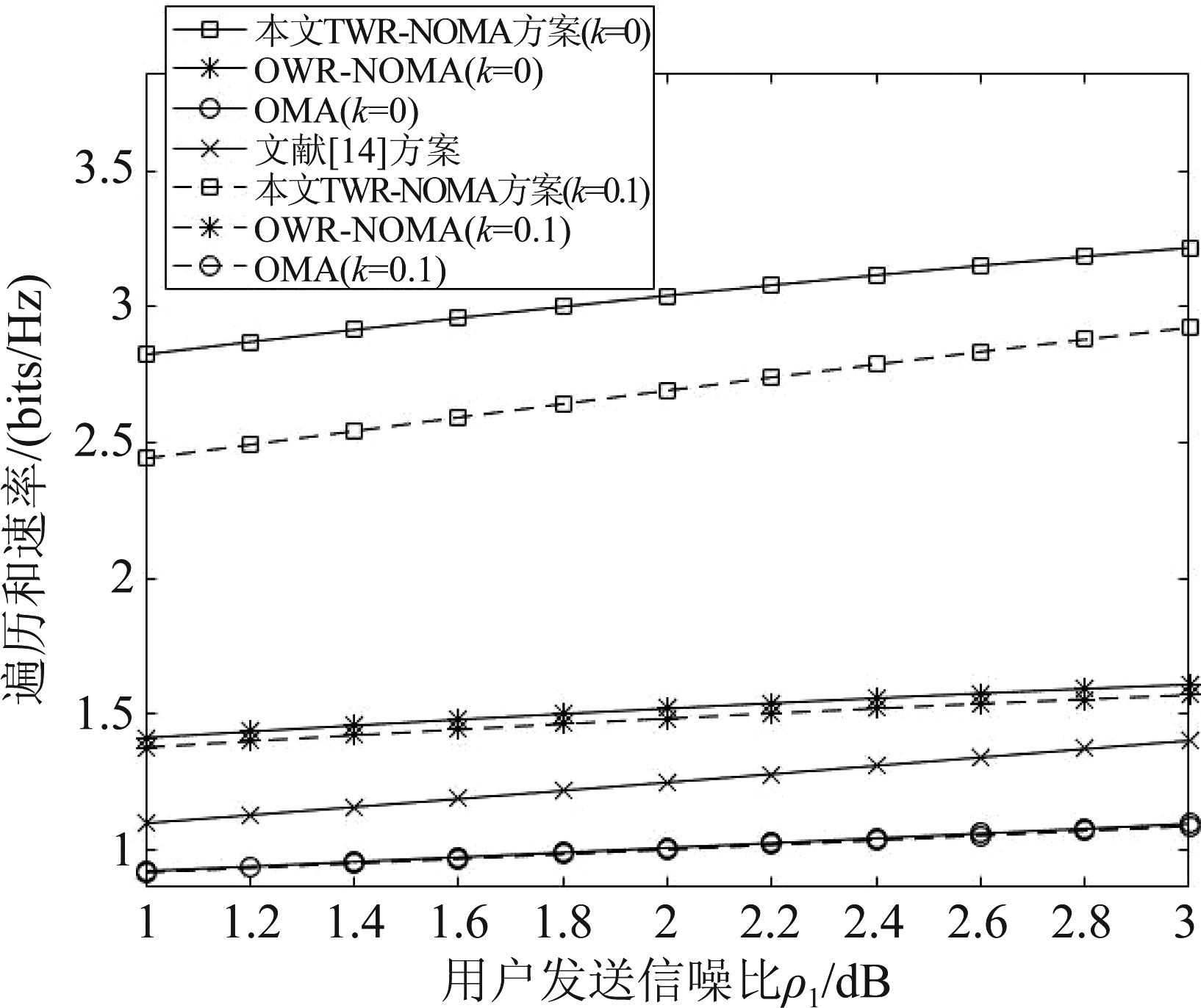
图10 不同发送信噪比时的上行和速率
Fig.10 Uplink ergodic sum rate of different transmission SNR
5 结论
本文提出一种基于双向中继、NOMA和网络编码结合的传输方案,实现最短时隙双向信息传输。并研究了不完美信道状态信息下解码转发(DF)的双向中继NOMA系统性能。与传统方案相比,本文方案只需要两个时隙来完成双向信息交换,极大地提高了资源利用率。仿真结果表明,相比于传统方案,无论对于上行还是下行信号,该方案的遍历和速率和中断性能均得到显著提升。
附录 定理证明:
A 定理1的证明
γ的CDF函数可以表示为:
Fγ(x)=Pr{γ<x}=1-Pr{γ>x}
(A.1)
表示γi的互补累积分布函数(Complementary Cumulative Distribution Function, CCDF)
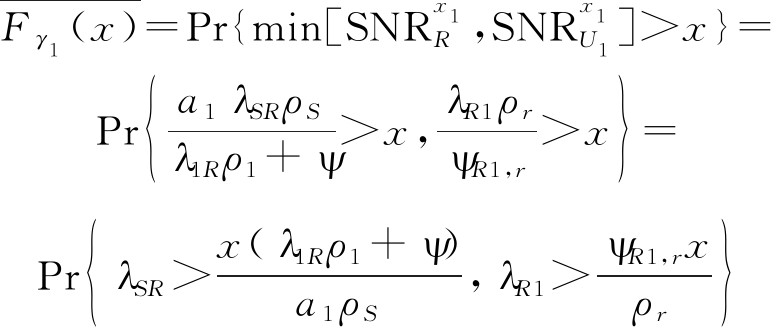
(A.2)
将各路信道的信道增益定义为
其CDF表达式为
其中i≠j,i, j={S,R,1,2},简写为λij。则γ1的CCDF为:
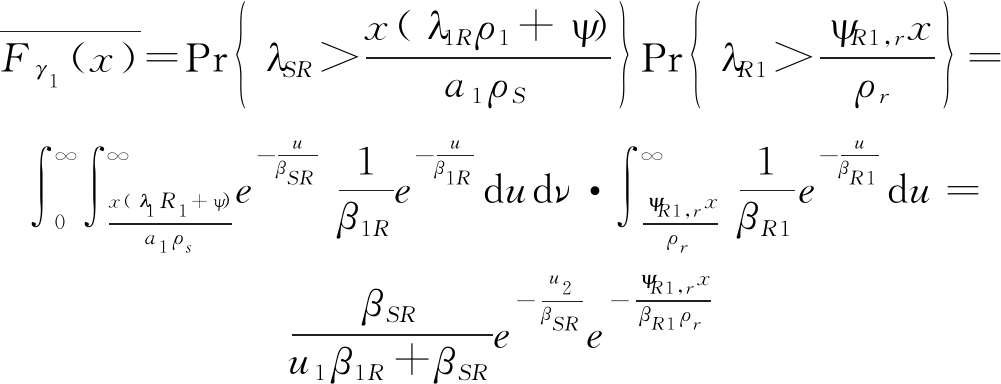
(A.3)
将(A.3)带入式(17),可以得到:
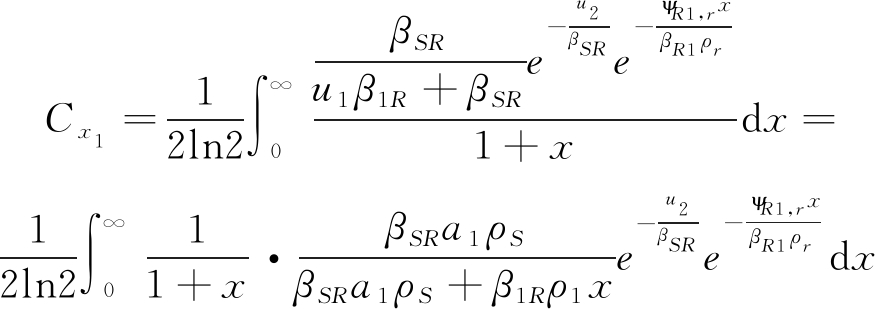
(A.4)
将上式进行因式分解:
(A.5)
上式利用等式
来获取表达式。
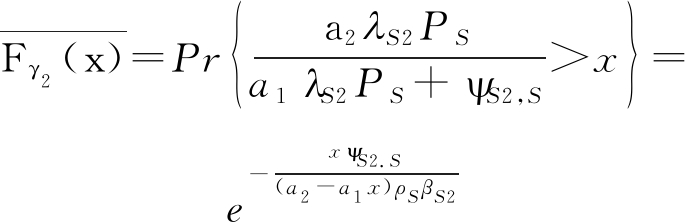
(A.6)
其中,式(26)必须满足a2-a1x>0,否则
故
(A.7)
下行信号遍历和速率Csum=Cx1+Cx2,证毕。
B 定理2的证明
将中断概率Px1的互补概率定义为
可以求得
为:
(B.1)
从公式(B.1)可以看出,当a2-a1φ2≤0或a1=0时,有
同时a1+a2=1,即当
或a1=0时,Px1=1。
分情况讨论,当
时,式(B.1)为:
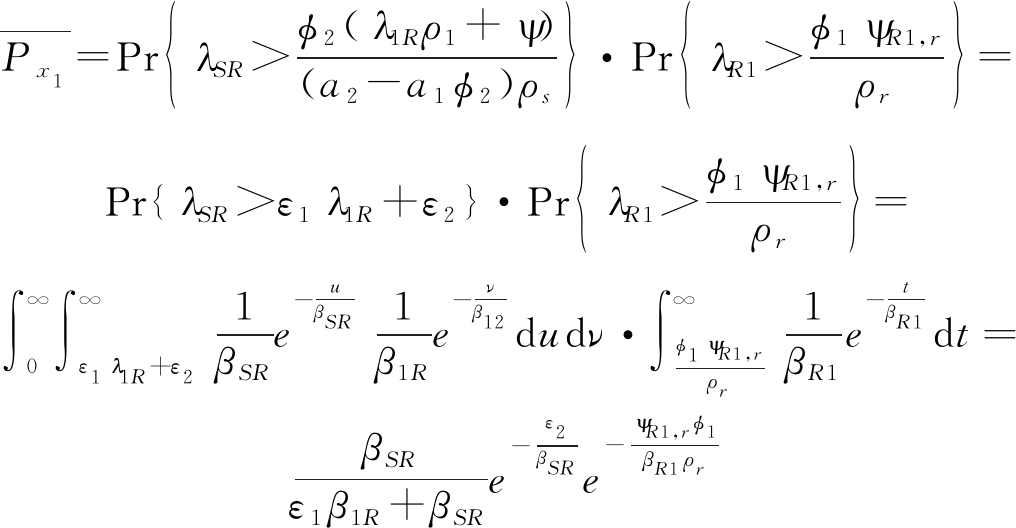
(B.2)
反之,当
时,式(B.1)为:
(B.3)
综上,
(B.4)
故TWR-NOMA方案下行中断概率:Pout=Px1+Px2-Px1·Px2。证毕。
C 定理3的证明
γ3的CCDF为:
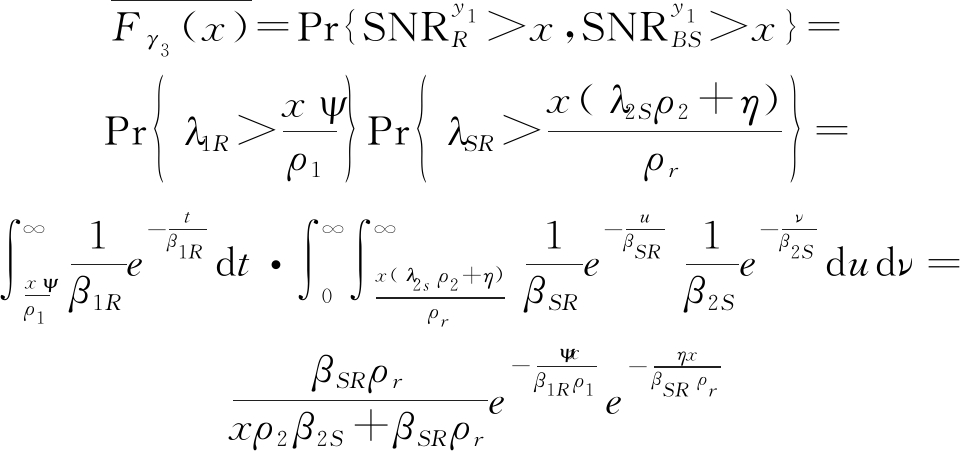
(C.1)
将式(C.1)带入式(17),可以得到:
(C.2)
类比式(A.5),将上式进行因式分解:
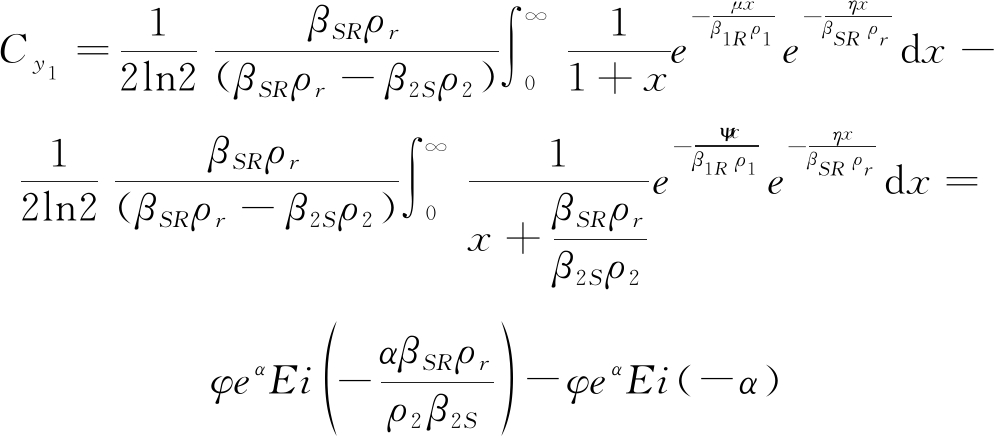
(C.3)
对于y2:
(C.4)
故γ4的各态历经和速率表达式为:
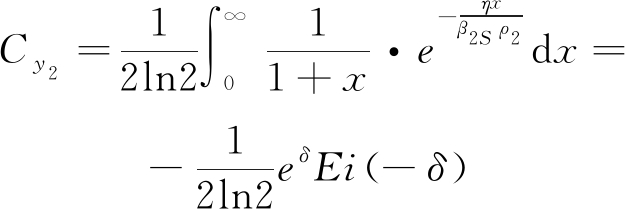
(C.5)
上行信号遍历和速率为Csum=Cy1+Cy2,证毕。
D 定理4的证明
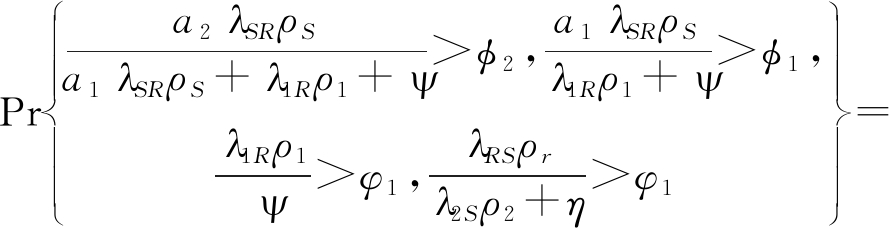
(D.1)
同样地,当或a1=0时,Py1=1。其中,
的计算同式(B.2)(B.3)。而
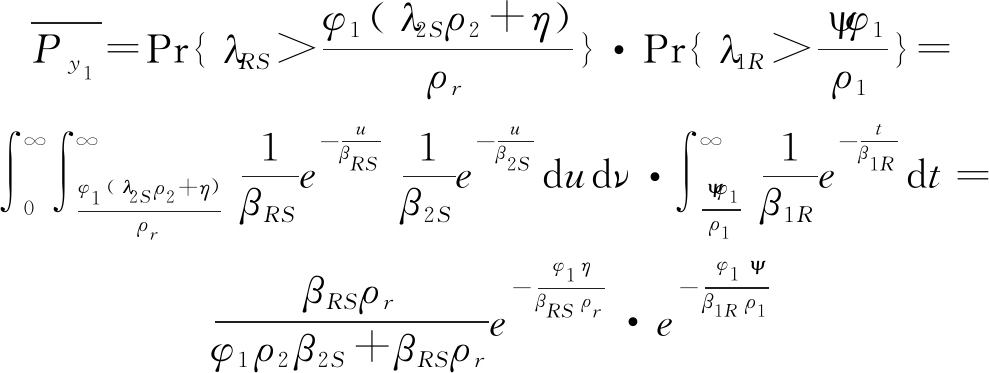
(D.2)
故
其中εi,εj={(ε1,ε2),(ε3,ε4)}。
(D.3)
综上,TWR-NOMA方案上行中断概率:Pout=Px1+Px2-Px1·Px2。证毕。
[1] DING Zhiguo, LIU Yuanwei, CHOI J, et al. Application of non-orthogonal multiple access in LTE and 5G networks[J]. IEEE Communications Magazine, 2017, 55(2): 185-191.
[2] DING Zhiguo, YANG Zheng, FAN Pingzhi, et al. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users[J]. IEEE Signal Processing Letters, 2014, 21(12): 1501-1505.
[3] DING Zhiguo, PENG Mugen, POOR H V. Cooperative non-orthogonal multiple access in 5G systems[J]. IEEE Communications Letters, 2015, 19(8): 1462-1465.
[4] ZHANG Yingying, YANG Zhen, FENG Youhong, et al. Performance analysis of cooperative relaying systems with power-domain non-orthogonal multiple access[J]. IEEE Access, 2018, 6: 39839-39848.
[5] ARZYKULOV S, TSIFTSIS T A, NAURYZBAYEV G, et al. Outage performance of cooperative underlay CR-NOMA with imperfect CSI[J]. IEEE Communications Letters, 2019, 23(1): 176-179.
[6] 乔宇航, 贺玉成, 杨键泉, 等. 两级中继选择的协作CR-NOMA网络性能分析[J]. 信号处理, 2020, 36(2): 196-202.
QIAO Yuhang, HE Yucheng, YANG Jianquan, et al. Performance analysis for cooperative CR-NOMA with two-stage relay selection[J]. Journal of Signal Processing, 2020, 36(2): 196-202.(in Chinese)
[7] YUE Xinwei, LIU Yuanwei, KANG Shaoli, et al. Modeling and analysis of two-way relay non-orthogonal multiple access systems[J]. IEEE Transactions on Communications, 2018, 66(9): 3784-3796.
[8] SUN Yan, NG D W K, SCHOBER R. Resource allocation for MC-NOMA systems with cognitive relaying[C]∥2017 IEEE Globecom Workshops (GC Wkshps). Singapore. IEEE, 2017: 1-7.
[9] FANG Zhaoxi, LI Jun, LU Yingzhi. Cooperative non-orthogonal multiple access for two-way relay networks[J]. AEU-International Journal of Electronics and Communications, 2020, 115(1):1434-1439.
[10]SHUKLA M K, NGUYEN H H. Ergodic secrecy sum rate analysis of a two-way relay NOMA system[J]. IEEE Systems Journal, 2020, 4(3): 1- 4.
[11]WEI Fanbo, ZHOU Ting, XU Tianheng, et al. Modeling and analysis of two-way relay networks: A joint mechanism using NOMA and network coding[J]. IEEE Access, 2019, 7: 152679-152689.
[12]BAE Jimin, HAN Y. Joint power and time allocation for two-way cooperative NOMA[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 12443-12447.
[13]LV Lu, YE Qiang, DING Zhiguo, et al. Multi-antenna two-way relay based cooperative NOMA[J]. IEEE Transactions on Wireless Communications, 2020, 19(10): 6486- 6503.
[14]HO C Y, LEOW C Y. Cooperative non-orthogonal multiple access using two-way relay[C]∥2017 IEEE International Conference on Signal and Image Processing Applications (ICSIPA). Kuching, Malaysia. IEEE, 2017: 459- 463.
[15]HESAM A, BASTAMI A H. NOMA-based transmission in half-duplex two-way relay network[C]∥2020 28th Iranian Conference on Electrical Engineering (ICEE). Tabriz, Iran. IEEE, 2020: 1- 6.
[16]ANH N D, SON P N. Performance analysis and evaluation of underlay two-way cooperative networks with NOMA[C]∥2020 5th International Conference on Green Technology and Sustainable Development (GTSD). Ho Chi Minh City, Vietnam. IEEE, 2020: 103-108.
[17]PENG Linning, LI Guyue, ZHANG Junqing, et al. An investigation of using loop-back mechanism for channel reciprocity enhancement in secret key generation[J]. IEEE Transactions on Mobile Computing, 2019, 18(3): 507-519.
[18]JIANG Ling, DONG Bing, SI Zhongwei, et al. Optimization of power allocation for multi-user superposition transmission systems[C]∥2018 IEEE International Conference on Communications Workshops (ICC Workshops). Kansas City, MO, USA. IEEE, 2018: 1- 6.
[19]NASIR A A, ZHOU Xiangyun, DURRANI S, et al. Relaying protocols for wireless energy harvesting and information processing[J]. IEEE Transactions on Wireless Communications, 2012, 12(7): 3622-3636.
[20]FENG Youhong, YAN Shihao, LIU Chenxi, et al. Two-stage relay selection for enhancing physical layer security in non-orthogonal multiple access[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(6): 1670-1683.
